1 Introduction

During the last decades, the increasing demand for surgical services along with the ever-rising nursing costs leads to an acute shortage of surgical nurses for operating room (OR) suites (Oulton 2006; Beliën and Demeulemeester 2008). In China, the aging population results in significant increases in surgical demand and hence exacerbates the surgical nurse shortage, said to be 218,000 in 2011, i.e., 11 % of the total number of registered nurses, and expected to grow to 450,000 by 2020, i.e., 15 % of the estimated total number of registered nurses (National Health Services Statistics in China 2011). Therefore, it is of vital importance for OR suites to use surgical nurses as efficiently as possible in delivering surgical services.

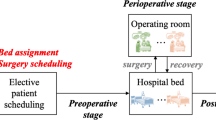
Optimal use of surgical nurses is a complicated task for OR suites due to the strong dependencies between the daily surgery and nurse scheduling. Surgery scheduling allocates a set of elective surgeries to ORs and sequences elective surgeries in each OR (Denton et al. 2010; Min and Yih 2010). Then, nurse scheduling assigns a set of surgical nurses to each elective surgery based on their specific demands, functioning in scrub or circulating roles during surgery. Surgery scheduling consequently determines surgical nurse demands among ORs and obviously has an important impact on nurse scheduling. Besides, a high volume of elective surgeries with time windows (i.e., release time and deadline), and a multiple OR setting with fixed regular working hours give rise to a difficult integrated scheduling problem in highly constrained environments.

In this paper, we focus on the integrated scheduling of elective surgeries and surgical nurses, which is a fundamental, but understudied aspect of OR scheduling. The purpose of this paper is to evaluate the benefit of integrating elective surgery and surgical nurse scheduling in terms of nurse utilization, comparing with a two-stage approach that is frequently used (Jebali et al. 2006; Testi et al. 2007; Roland and Riane 2011). The two-stage approach optimizes the surgery scheduling problem and the nurse scheduling problem sequentially while ignoring their strong dependencies, which could lead to poor utilization of surgical nurses. It is our belief that integrating elective surgery and surgical nurse scheduling is an effective way to improve surgical nurse use for OR suites.

To the best of our knowledge, most previous studies on surgery scheduling only consider the aggregated capacity (i.e., total working hours per workday) of nurses, and neglect the important impact of surgery scheduling on nurse scheduling. Guinet and Chaabane (2003) propose an assignment model with surgical nurse capacity constraint for assigning elective surgeries to ORs over a planning horizon. Jebali et al. (2006) develop a two-step approach for allocation and sequencing of elective surgeries with the objective of improving OR utilization. They take into consideration the availabilities of surgical nurses. Roland et al. (2010) apply the resource constrained project scheduling model to formulate the allocation and sequencing of elective surgeries. Several constraints regarding human resources’ availabilities and preferences are included in their model. Fei et al. (2010) formulate the surgery scheduling problem as a set partitioning problem, taking into account the maximal working hours of surgical nurses. Pham and Klinkert (2008) treat the surgery scheduling problem as a multi-mode job shop problem. A mode is defined as a possible choice of resource set that includes both personnel and facilities. Mode availability is also considered. Lamiri et al. (2009) study the surgery scheduling problem for ORs shared between elective and emergency patients. Staffed OR capacity is considered in the constraints. Marques et al. (2011) develop an integer linear programming model for scheduling elective surgeries with time-window constraints. Surgical nurses’ regular working hours are considered in the model.

The extreme importance of optimal use of surgical nurses has been emphasized by several researchers. Beliën and Demeulemeester (2008) formulate the nurse rostering problem using a branch and price approach, combined with different surgery workload patterns. He et al. (2012) propose a newsvendor framework to determine the optimal nurse staffing levels for an OR suite. Different surgery information sets are considered at the time of decision: no information, information on number of surgeries, and information on number and types of surgeries. Altamirano et al. (2012) propose a particle swarm optimization algorithm to determine the shift (i.e., elective-day, emergency-day and emergency-night) assignment of surgical nurses at a French public hospital. However, these studies fall into the category of tactical nurse rostering problem (NRP), which involves producing a periodic (i.e., weekly, fortnightly, or monthly) duty roster for nursing staff, subject to legal regulations, personnel policies, nurses’ preferences and many other hospital-specific requirements (Cheang et al. 2003; Burke et al. 2004; Ernst et al. 2004). In contrast, the nurse scheduling problem concerned in this paper lies on a daily basis and is based on the rostering of surgical nurses. Specifically, nurse scheduling in OR suites assigns surgical nurses of elective-day (emergency-day and emergency-night) shift to elective (emergency) surgeries on each workday.

Our work differs from the aforementioned studies in the following ways. First, we propose an integer programming (IP) model for integrating the elective surgery and the surgical nurse scheduling processes with the objective of improving nurse utilization. So far as we know, no models have been proposed to integrate both areas of decision making. Second, we develop a genetic algorithm (GA) based on the IP formulation to solve the problem more efficiently. The use of a GA is notably justified by its advantage of proposing a population of good solutions in a reasonable time. Finally, in order to evaluate the practical benefit of integrated scheduling of elective surgeries and surgical nurses, we test the IP model and the GA against the two-stage approach in various problem settings.

The remainder of the paper is organized as follows. In Sect. 2, we describe both the IP model and the two-stage approach. Section 3 presents a GA to solve the IP model. In Sect. 4, we describe a case study for testing the IP model and the GA against the two-stage approach. The results of the case study are discussed in Sect. 5. Finally, in Sect. 6 we give concluding remarks and directions for future work.

2 Problem statement and formulation

The problem addressed in this paper involves daily scheduling of elective surgeries and surgical nurses for OR suites. Specifically, at a specified cutoff time (e.g., 10 A.M. the workday before surgery), a set of elective surgeries submitted by surgeons are allocated into ORs and given predicted start times. Then each elective surgery is assigned with a set of surgical nurses. Here we use block to define groups of one or more elective surgeries done consecutively in an OR by the same surgeon (Denton et al. 2010; Batun et al. 2010). We schedule elective surgeries in blocks because in practice, a given surgeon’s elective surgeries on a workday are scheduled consecutively and assigned with the same set of surgical nurses.

Scheduling of elective surgeries and surgical nurses has to satisfy various constraints such as regular working hours, time windows of surgeries, surgical nurse demands of surgeries. And the objective is to use as few surgical nurses and ORs as possible for a given set of elective surgeries, which is equivalent to improving OR and nurse utilization. This is for two reasons. First, free surgical nurses and ORs may allow the OR suite to increase its surgery volume, which can be easily translated to significant increase in revenue (Guerriero and Guido 2011). Second, free surgical nurses and ORs can also absorb unforeseen events like large lateness or arrivals of emergency (Lamiri et al. 2009; Persson and Persson 2010). This should prevent the surgery schedule from being too much disrupted, and therefore improve service quality.

The integrated scheduling of elective surgeries and surgical nurses addressed in this paper is formulated as a discrete time integer programming model, which is presented below.

2.1 Notations

The notations used for formulating the problem are as follows:

B

number of blocks to be scheduled, b = 1, …, B;

N

number of available surgical nurses, n = 1, …, N;

J

number of available ORs, j = 1, …, J;

T

number of time periods of a regularly scheduled workday, t = 1, …, T;

p b

duration of block b;

r b

release time of block b;

d b

deadline of blockb;

h b

surgical nurse demand of block b;

Decision variables:

x bjt

1 if block b is allocated to OR j, starting at time period t; 0 otherwise;

y nb

1 if surgical nurse n is assigned to block b; 0 otherwise;

X j

1 if OR j is open; 0 otherwise;

Y n

1 if surgical nurse n is used; 0 otherwise.

2.2 Integer programming model

We first introduce the IP model that integrates the nurse and the surgery scheduling process.

$${\text{Minimize}}\quad \sum\limits_{j = 1}^{J} {X_{j} + w} \sum\limits_{n = 1}^{N} {Y_{n} }$$
(1)

Subject to:

$$\sum\limits_{j = 1}^{J} {\sum\limits_{{t = r_{b} }}^{{d_{b} - p_{b} + 1}} {x_{bjt} } } = 1,\quad \forall b = 1, \ldots , B$$
(2)
$$x_{bjt} \le X_{j} ,\quad \forall b = 1, \ldots , B,\forall j = 1, \ldots , J,\forall t = 1, \ldots , T$$
(3)
$$\sum\limits_{b = 1}^{B} {\sum\limits_{{\tau = t - p_{b} + 1}}^{t} {x_{bj\tau } } } \le 1,\quad \forall j = 1, \ldots , J,\forall t = 1, \ldots , T$$
(4)
$$\sum\limits_{n = 1}^{N} {y_{nb} = h_{b} } ,\quad \forall b = 1, \ldots , B$$
(5)
$$y_{nb} \le Y_{n} ,\quad \forall n = 1, \ldots , N,\forall b = 1, \ldots , B$$
(6)
$$\sum\limits_{j = 1}^{J} {\sum\limits_{{\tau = t - p_{b} + 1}}^{t} {x_{bj\tau } } } + \sum\limits_{j = 1}^{J} {\sum\limits_{{\tau = t - p_{{b^{{\prime }} }} + 1}}^{t} {x_{{b^{{\prime }} j\tau }} } } \le 3 - y_{nb} - y_{{nb^{{\prime }} }} ,\quad \forall b, b^{{\prime }} = 1, \ldots , B,\forall n = 1, \ldots , N,\forall t = 1, \ldots , T$$
(7)
$$x_{bjt} \in \{ 0,1\} ,\quad \forall b = 1, \ldots , B,\forall j = 1, \ldots , J,\forall t = 1, \ldots , T$$
(8)
$$X_{j} \in \{ 0,1\} ,\quad \forall j = 1, \ldots , J$$
(9)
$$y_{nb} \in \{ 0,1\} ,\quad \forall b = 1, \ldots , B,\forall n = 1, \ldots , N$$
(10)
$$Y_{n} \in \{ 0,1\} ,\quad \forall n = 1, \ldots , N$$
(11)

The above IP model schedules elective surgeries and surgical nurses simultaneously with the objective function (1) of minimizing the number of ORs and surgical nurses used. We set w in Eq. (1) at 0.5 because in practice, the planning ratio of surgical nurse to OR is usually 2, i.e., one OR is staffed with two surgical nurses on average.

For surgery scheduling, Constraints (2) ensure that each block is allocated to one OR and starts within the time window defined by release time and deadline. Constraints (3) state that blocks can only be allocated to open ORs. Constraints (4) prevent the allocation of overlapping blocks in one OR. For nurse scheduling, Constraints (5) guarantee that the surgical nurse demand of each block is satisfied. Constraints (6) indicate used surgical nurses. Constraints (7) link the two scheduling processes by preventing the assignment of surgical nurses to blocks that overlap in time. Constraints (8–11) are the integrality constraints.

2.3 Two-stage approach

We also present the two-stage approach for evaluating the benefit of integrating elective surgery and surgical nurse scheduling. The two-stage approach proceeds as follows:

Stage 1: Surgery scheduling

By using the notations defined in Sect. 2.1, the surgery scheduling problem can be formulated as follows:

$${\text{Minimize}}\quad \sum\limits_{j = 1}^{J} {X_{j} }$$
(12)
$${\text{Subject}}\,{\text{to: (2)}}\sim (4),(8)\sim (9)$$

The objective function (12) seeks to minimize the number of ORs used. The resulting schedule determines the OR and start time of block b, which are denoted as o b and s b , respectively.

Stage 2: Nurse scheduling

Given the schedule generated in stage 1, the nurse scheduling problem can be formulated as follows:

$${\text{Minimize}}\quad \sum\limits_{n = 1}^{N} {Y_{n} }$$
(13)
$${\text{Subject}}\,{\text{to: (5)}}\sim (6),(10)\sim (11)$$
$$y_{nb} + y_{{nb^{{\prime }} }} \le 1,$$
$$\forall n = 1, \ldots , N,\forall b, b^{{\prime }} = 1, \ldots , B\quad {\text{with}}\quad o_{b} \ne o_{{b^{{\prime }} }} \quad {\text{and}}\;\hbox{max} \left( {s_{b} , s_{{b^{{\prime }} }} } \right) < \hbox{min} \left( {s_{b} + p_{b} , s_{{b^{{\prime }} }} + p_{{b^{{\prime }} }} } \right)$$
(14)

The objective function (13) minimizes the number of surgical nurses used. Constraints (14) prevent the assignment of surgical nurses to overlapping blocks in different ORs.

3 Genetic algorithm

Due to the complexity of the integrated scheduling problem, finding the optimal solution of the IP model is computationally intractable given practical-sized problem. Therefore, a genetic algorithm based on the IP formulation is developed to generate good surgery schedules (i.e., that satisfy all the constraints and produce a satisfactory objective) in a reasonable time.

3.1 The basic architecture of the GA

The procedure of our GA is described below, where G(t) is the current population, popsize is the population size. This procedure is repeated until a number maxgen of generations is reached.

Procedure of the GA

  1. 1.

    t: = 0;

  2. 2.

    Initialize popsize individuals in G(t);

  3. 3.

    Repeat

  4. 4.

    Evaluate G(t);

  5. 5.

    t: = t + 1;

  6. 6.

    Repeat

  7. 7.

    Select parents from G(t -1) into the mating pool;

  8. 8.

    Apply crossover and mutation to the individuals in the mating pool;

  9. 9.

    Until popsize offsprings are created

  10. 10.

    Copy popsize best individuals from G(t -1) and the mating pool to G(t);

  11. 11.

    Until t > maxgen

3.2 Chromosomal representation of individuals

Each individual is modeled by three uncorrelated chromosomes,I = (α, β, γ), which correspond to the three decisions to be made in surgery and nurse scheduling (i.e., block allocation and sequence; surgical nurse assignment). Each chromosome has B genes representing B blocks.

$$I = \left( {\begin{array}{*{20}c} \alpha \\ \beta \\ \gamma \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {j_{1} , \ldots ,j_{B} } \\ {t_{1} , \ldots ,t_{B} } \\ {n_{1} , \ldots ,n_{B} } \\ \end{array} } \right)$$

A combination (j b , t b , n b ) means that block b is allocated to OR j b , starting at time period t b , and assigned with surgical nurses in set n b . The size of n b equals h b , which is the surgical nurse demand of block b.

3.3 Initial population

The initial population composed of popsize individuals is generated in the following way. The OR j b of block b is randomly selected from the set of available ORs. The start time t b is randomly chosen within the time window of block b, i.e., [r b , d b  − p b  + 1]. The set of surgical nurses n b assigned to block b is selected randomly without replacement from the set of available surgical nurses.

3.4 Fitness evaluation

Based on the IP formulation (see Sect. 2.2), the fitness value of an individual I is computed according to the satisfaction of the non-overlap constraints with respect to blocks and surgical nurses, i.e., constraints (4) and (7). We define two variables R B and R N to represent the number of violations of the two sets of constraints. The fitness function of an individual I is defined as:

$$f(I) = \left\{ {\begin{array}{*{20}l} {C(I){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} I{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{is}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{feasible}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {M + R^{B} + R^{N} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{otherwise}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ \end{array} } \right.$$

where C(I) is the objective function value (i.e., Eq. (1)) associated with feasible individual I, and M is the upper bound of the objective function value. Here M is computed considering the situation that all ORs and surgical nurses are used. Given this fitness function, the goal of the GA is to minimize the fitness value.

3.5 Selection

We choose among the three selection methods well known in the GA literature to select the individuals to be included in the mating pool: binary tournament, n-size tournament and linear ranking. Computational experience proves that binary tournament gives the best results among the three selection methods. The chosen selection method has to be repeated until the number of individuals in the mating pool equals the population size. Then pairs of individuals (i.e., the parents) are randomly selected from the mating pool for offspring generation with probability p c  = 0.8.

3.6 Offspring generation

Once the parents have been selected, the crossover and mutation operators are applied to create and modify new individuals.

3.6.1 Crossover

This operator generates two offsprings I D and I S from two parents I F and I M by applying the single-point crossover to each of the three chromosomes in I F and I M.

We first draw three random integers q 1 , q 2 and q 3 such that 1 ≤ q 1, q 2, q 3 ≤ B. Taking the daughter I D = (α D, β D, γ D)for example, the first q 1 genes of α D are taken from the mother I M:

$$j_{b}^{D} : = j_{b}^{M}, \quad \forall b = 1, \ldots ,q_{1}$$

The remaining genes q 1  + 1,…, B are then derived from the father I F:

$$j_{b}^{D} : = j_{b}^{F}, \quad \forall b = q_{1} + 1, \ldots ,B$$

The same applies to the other two chromosomes β D and γ D of the daughter I D using q 2 and q 3 , respectively. The son I S is created following the same way by inverting father and mother.

3.6.2 Mutation

The mutation operator is then applied to each offspringI = (α, β, γ)with probability p m  = 0.1, following the same way we generate the initial population (see Sect. 3.3).

The offspring generation phase terminates when the population size of the mating pool is reached. Then we retrieve the best popsize individuals (based on their fitness values) from the current population and the mating pool to form the next generation.

4 Case study

A case study from the OR suite in a Chinese hospital is used to evaluate the benefit (in terms of savings in nursing costs) of integrating surgery and nurse scheduling using the IP model and the GA. The two-stage approach is used as the standard against which the IP model and the GA are compared.

The OR suite has 13 multifunctional ORs, i.e., a block can be assigned to any available OR, and 25 surgical nurses are employed on a long-term basis (i.e., annually). A dataset composed of 200 blocks is obtained from the OR suite given the historical surgery application sheets that contain detailed information of surgeries, such as surgeon, duration, release time and deadline, surgical nurse demand and so on. Each regularly scheduled workday (8 h) is composed of 32 time periods (of 15 min), because in practice the head nurse of the OR suite schedules blocks in increments of 15 min. The durations of the blocks range from 3 to 27 time periods, with a mean of 12.3 time periods and a standard deviation of 5.7 (see Fig. 1). The surgical nurse demands of the blocks range from 1 to 3, with a mean of 2.1 and a standard deviation of 0.9 (see Fig. 2).

Fig. 1
figure 1

Histogram of the block durations

Full size image
Fig. 2
figure 2

Histogram of the surgical nurse demands

Full size image

The performance of the IP model and the GA is tested on both large and small problems (see Table 1). For large problem, we generate 10 instances, each composed of 25 blocks that are randomly selected from the dataset. For small problem, we also generate 10 instances, each composed of 10 blocks that are randomly selected from the dataset.

Table 1 Number of blocks by workday of week (all workdays between August 1 and 31, 2011)
Full size table

All computational tests are carried out on a Windows desktop machine with 2.00 GB of memory running at 2.4 GHz on an Intel Core 2 CPU processor. The mathematical models are coded in C++ and solved using the Cplex 12.1, and the GA is coded in C++.

5 Discussion of results

5.1 Efficiency of the IP model and the GA

The computational efficiency of the IP model and the GA is validated on both large and small instances. Due to the complexity of the problem, we expect long computation time for solving the IP model on large instances. Hence, we limit the computation time of solving the IP model to 10 h per large instance after trials. We report the classical outputs of the Cplex solver, i.e., the objective value (Obj.), the relative gap between the current best integer solution and the lower bound (Gap), and the computation time in minutes.

The GA is applied ten times to each instance with parameters popsize (of individuals) and maxgen (of generations) chosen based on computational experience. Specifically (popsize, maxgen) is set at (100, 400) and (100, 200) for large and small instances, respectively. The average (Avg.), best and worst objective values over ten runs are reported. The number of times that the GA finds the optimum (#OPT) over ten runs, and the average time to get the final population are mentioned. In order to assess the efficiency of the GA, we report the average improvement (Impv.) achieved by the GA over initial solutions. We also give the average difference between the GA and the IP model, i.e.,Δ GA–IP . \(\varDelta_{GA - IP} = ({\text{Obj}}_{GA} - {\text{Obj}}_{IP} )/{\text{Obj}}_{IP} \times 100\,\%\). Table 2 presents the computational results.

Table 2 Comparisons between the IP model and the GA
Full size table

Table 2 shows that the IP model provides better objective values (as indicated byΔ GA–IP ) for both large and small instances. However, it is proved to be quite time-consuming, especially for large instances. Therefore, it is necessary to find a compromise between computational efficiency and solution quality, and this goal is achieved by the GA. The GA can find good solutions (within 10.77 % of global optimality on average) in a much shorter computation time as compared with the IP model. Moreover, for small instances, the GA finds the optimal solutions at high percentages. Whereas the optimal solutions for large instances (if found by the IP model) are harder for the GA to find. The GA also obtains significant improvements in solution quality, especially for large instances.

The GA also shows its distinctive ability to generate a set of feasible surgery schedules in a reasonable time. At the last generations, 29.4 and 17.1 feasible surgery schedules can be produced on average per small and large instance, respectively. In practice, these feasible surgery schedules can provide the head nurse of the OR suite with the option of selecting the most appropriate schedule based on various considerations, i.e., surgeons’ and nurses’ preferences and unforeseen events like large lateness or arrivals of emergency surgeries.

5.2 Benefit of integrating surgery and nurse scheduling

The benefit of integrating surgery and nurse scheduling by the IP model and the GA is validated through comparison with the two-stage approach on both large and small instances. The parameter settings of the IP model and the GA are the same as those in Sect. 5.1. Table 3 gives the average improvements of the IP model and the GA over the two-stage approach, i.e., Δ2SA–IP and Δ2SA–GA , where \(\Delta_{2SA-IP} = ({\text{Obj}}_{2SA}\hbox{--}{\text{Obj}}_{IP} )/{\text{Obj}}_{IP} \times 100\,\% \quad {\text{and}}\quad \Delta_{2SA-GA} = ({\text{Obj}}_{2SA}-{\text{Obj}}_{GA} )/{\text{Obj}}_{GA} \times 100\,\%\)

Table 3 Comparisons between the two-stage approach and the integrated approaches
Full size table

As we can see from Table 3, for both large and small instances, applying the IP model and the GA leads to better objective values as compared with the two-stage approach. Specifically, the IP model gives the best solutions, however, at the cost of long computation time (see Table 2). And the savings achieved by the IP model and the GA are more significant for large instances, which suggests a greater potential of improvements in large size problems.

We also present the detailed use of ORs and surgical nurses by the IP model, the GA and the two-stage approach. Table 4 gives the average OR utilization (UOR) and surgical nurse utilization (USN) by the two-stage approach, which are frequently used as OR suite performance measures in practice (Jeang and Chiang 2012). Utilization is calculated as the time that an OR (or a surgical nurse) is used, divided by the regularly scheduled hours per workday (8 h). The average improvements of the IP model and the GA over the two-stage approach in OR and surgical nurse utilization are reported.

Table 4 Utilization of ORs and surgical nurses
Full size table

Table 4 clearly shows that with respect to the use of ORs, no significant difference is measured between the integrated approaches (the IP model and the GA) and the two-stage approach, and the two-stage approach performs slightly better than the IP model and the GA. This can be easily understood by the fact that the two-stage approach optimizes surgery scheduling alone without considering nurse scheduling and their strong dependencies. To the contrary, both the IP model and the GA achieve significant higher utilization in the use of surgical nurses as compared with the two-stage approach. Specifically, the utilization improvements are even greater for the IP model and for large instances.

This comparative study clearly reveals that integrating surgery and nurse scheduling may yield important savings in nursing costs for OR suites. Actually, by scheduling elective surgeries and surgical nurses simultaneously, the important impact of surgery scheduling on nurse scheduling, i.e., the distribution of surgical nurse demands among ORs, can be considered explicitly in surgery scheduling. This imposes modifications on surgery scheduling and hence leads to improvements on nurse scheduling.

6 Conclusions

This paper tackles the integrated scheduling of elective surgeries and surgical nurses for OR suites, which is a fundamental, but understudied aspect of OR scheduling. The objective is to optimize the use of surgical nurses given the close interactions between the surgery and the nurse scheduling process. To this aim, an integer programming model is proposed for scheduling elective surgeries and surgical nurses simultaneously. Moreover, a genetic algorithm is developed based on the IP formulation to solve the problem more efficiently. In order to demonstrate the benefit of integrating nurse and surgery scheduling in terms of surgical nurse utilization, both the IP model and the GA are tested against a two-stage approach which is typically used to schedule surgeries and nurses sequentially while ignoring their dependencies.

The computational results from a real-life case study show that considerable improvements in surgical nurse utilization can be achieved by the IP model and the GA as compared with the two-stage approach, meanwhile no significant differences in the use of ORs are observed. Moreover, compared with the IP model that gives the optimal solution in a long computation time, the GA can achieve promising compromise between solution quality and computational efficiency.

In this paper, we assume deterministic surgery duration. Other studies showed that lognormal or normal distribution is a better approximation of surgery duration in practice (Hans et al. 2008). Indeed, uncertainty involved in surgery durations can lead to sub-optimality even infeasibility of the surgery schedules proposed by the IP model and the GA. This scenario arises commonly when a surgical nurse is assigned to several blocks in different ORs. If former blocks finish later than scheduled, all latter blocks of the surgical nurse could be delayed. In order to avoid such delays, which are most undesirable for surgeons and patients in practice, uncertainty in surgery durations needs to be considered explicitly in further works.