1 Introduction

Over the recent years the world economic situation has been rather unstable and uncertain. Seaborne trade is highly dependent on macroeconomic factors and most operators in international maritime transportation have experienced decreased demand for their services, high competition from other shipping companies and high fuel prices. For example, from June 2008 to December 2008 the dry bulk freight indices were down by approximately 80 percent (UNCTAD 2011). Under such conditions, proper routing and scheduling of the fleet is crucial for obtaining a profit.

In this paper we study a real ship routing and scheduling problem for the Norwegian shipping company Saga Forest Carriers, which are specializing in the world wide transportation of forest products and break bulk cargoes. In the literature of maritime transportation it is common to categorize the operation of commercial ships into three basic modes: liner, tramp and industrial (Lawrence 1972). The tactical planning problem of the company is difficult to categorize this way as it contains aspects from both liner and tramp shipping. Like a liner shipping company, Saga Forest Carriers operate on several trade routes on which the ships sail regularly. In addition to operating their regular routes, they also act like a tramp shipping operator in the spot market. Their fleet deployment problem includes assigning the fleet both to regular routes and to available spot voyages to which their ships can be chartered out to perform.

The purpose of this paper is to introduce a new extension to the fleet deployment problem, namely the voyage separation requirement, to present new mathematical models for this problem, and to evaluate these models by the means of a computational study.

The remainder of this paper is outlined as follows. In Sect. 2 a presentation of the fleet deployment problem with voyage separation requirements is given. Section 3 contains a description of relevant, existing literature. Mathematical formulations for the fleet deployment problem with voyage separation requirements are presented in Sect. 4. In Sect. 5 we present a computational study, while concluding remarks are given in Sect. 6.

2 Problem description

We will now give a description of the fleet deployment problem with voyage separation requirements as faced by Saga Forest Carriers. A general fleet deployment problem is described by Christiansen et al. (2007). However, in this article we will extend the model to reflect the world of this particular shipping company.

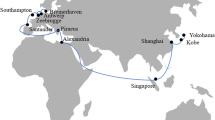
The company operates several intercontinental trades or trade routes, where cargo is loaded in one geographical region and discharged in another region. Figure 1 depicts two examples of trade routes that Saga Forest Carriers operate. In the SAM-FE trade cargo is picked up in South America and delivered at several ports in the Far East. Similarly, the EUR-EC trade goes from ports in Europe to the US East Coast.

Fig. 1
figure 1

Example of two trade routes

Full size image

For each trade route there is a set of voyages that are to be sailed throughout the planning period. Geographically, a voyage is similar to a trade route, and consists of one or more port calls in the loading region where cargo is to be picked up and one or more port calls in the discharge region where the cargo is to be delivered. The voyages for a specific trade route have an estimated duration, which includes sailing between all ports along the voyage as well as the time spent in the ports. Because the ships may have different service speeds, the duration of a voyage can be ship dependent.

The voyages for a given trade route are defined based on expected cargo availability and on long term contracts made with cargo owners (charterers). These contracts of affreightment (COAs) typically specify, besides the economic agreements, the total amount of goods that should be transported, the number of voyages that should be performed per year, or both. It is up to the ship operator to schedule when each voyage will start, but his degrees of freedom are not unlimited. The ship operator does not control the inventories at the loading ports, hence inventory costs are not relevant for the planning of his fleet deployment. For the charterers, however, it is important to balance the inventory level as evenly as possible to reduce the inventory costs. Therefore, a COA usually includes a clause specifying that the starting days of voyages for the same trade should be, using shipping terminology, fairly evenly spread in time. That is, the cargo owners expect that the goods will be shipped out at regular intervals. Even though the COAs usually do not specify exactly what fairly evenly spread means, the scheduler must take this into account when deploying the fleet.

One way of forcing spread of the voyages on the same trade is to give each voyage a time window. This time window defines the earliest and the latest start of loading in the first port call of the voyage. For example, consider a trade route where the ship operator has agreed to sail three voyages every month. One possible set of time windows could be to say that the first voyage should start between day 1 and 10 in the month, the second should start between day 11 and 20, and the third should start between day 21 and 30. However, in such a case the fleet operator is allowed to start one voyage on day 10, one on day 11 and the last on day 30. This can hardly be considered evenly spread, and will not be accepted by the charterer. To ensure a better spread on voyages on this trade one could tighten the time windows. However, this would restrict the ship operator’s flexibility and most often result in poor fleet utilization.

In order to cope with the the requirement of fairly evenly spread voyages, trade specific time separation limits are defined. These limits define the minimum acceptable time between two consecutive voyages on a given trade. Scheduling two voyages on a trade very tightly will not cause any direct costs, but the shipping company can lose goodwill and too little time between voyages can also make it more difficult to find spot cargo to utilize spare ship capacity. Furthermore, the cargo owner may face increased inventory costs when the voyages are not evenly spread in time. It is therefore important to ensure that voyages on the same trade are evenly spread in time when the fleet deployment plans are made.

Saga Forest Carriers have a heterogeneous fleet of ships, with individual load capacities, cargo handling equipment, sailing speeds, draft restrictions, operating costs and positions at the start of the planning period. This might put restrictions on which ships that are allowed to carry out a given voyage. Some ships also have maintenance requirements that have to be considered in the scheduling process. In order to renew its certificates, a ship has to go through an extensive survey at regular intervals. Each ship has a 4–6 months wide time window specifying when it has to visit a ship yard in Korea or China to go in a dry dock. Typically, the duration of such a survey is 25 days and must be carried out every second year.

The sailing speed of each ship can be considered fixed as it is determined at a higher level prior to the fleet deployment. This fixed planning speed is determined based on several factors, such as ship design, expected future fuel prices and freight rate forecasts. Naturally, in a poor freight market this speed will be lower than in a booming market. For a given ship this planning speed will typically be 13–14 knots, and even though it is physically possible for the ship to sail at a higher speed, it would be rather costly and the planners dealing with the fleet deployment are not allowed to exceed this speed when scheduling the fleet. Psaraftis and Kontovas (2013) give several examples of research done in the field of optimizing speed in maritime transportation. In the case of Saga Forest Carriers, however, determining the speed for each sailing leg of a ship’s route is done together with the detailed port rotation planning after the fleet deployment problem has been solved, hence speed optimization is not a part of the fleet deployment problem studied in this article.

In the shipping company’s portfolio of COAs there is an imbalance in the supply and demand among the regions. For instance, in the fleet deployment problem of Saga Forest Carriers there are more voyages starting in South America than ending up there. Hence, it is not possible to find a fleet schedule that completely avoid any ballast sailing (sailing with no cargo on board) by only sailing the contracted voyages. Therefore, the company is constantly looking to the spot market to charter out their ships to voyages that can give additional freight income while repositioning the ships. The fleet deployment problem therefore has two sets of voyages, one that consists of the contracted voyages that the shipping company is obliged to carry out, and one that consists of optional spot voyages which can be taken if there is sufficient fleet capacity and it is profitable.

The fleet deployment problem is to assign and schedule ships in a fleet to a set of voyages on predefined trade routes for the next planning period in order to maximize the profit. If the shipping company’s fleet does not have sufficient capacity, it is possible to charter in spot vessels on a short term contract to perform some of the contracted voyages.

3 Literature

The planning problem faced by Saga Forest Carriers can be classified as a fleet deployment problem, which has received some attention in the research literature, although mostly for container shipping. Gelareh and Meng (2010) present a mathematical model for a container shipping fleet deployment problem that incorporates speed decisions on sailing legs along each route. They also extend their model to let the service frequency on each liner route be a decision variable, and to handle the possibility of maximal travel time requirement between port pairs (e.g. in case of perishable products). Wang et al (2011) later modified the model by Gelareh and Meng (2010), while Meng and Wang (2011) extended it to consider uncertainty in container shipment demand by imposing chance constraints for each liner service route to guarantee that the ships assigned to that route can satisfy the demand with a given probability. Liu et al (2011) present a joint model for container flow management and fleet deployment, while Wang and Meng (2012) propose a model that accommodates container transshipment operations in ports.

None of the studies referred to above include requirements for evenly spread voyages. They also rely on a number of other assumptions typical for container shipping that may be too restrictive in our problem. The most important limitations of the models from these studies are (1) that each ship is assigned to only one single trade route during the whole planning horizon, and (2) that ships are considered as groups of ship types. The latter assumption can be a problem in short-term planning problems as it may result in solutions that are practically infeasible as initial positions or ongoing voyages may restrict some ships from performing the number of voyages on the route calculated by the models. Fagerholt et al (2009) study the fleet deployment problem for a Roll-on Roll-off shipping company. In their model, each ship is modeled individually with a given initial open position and time for when it is available for new assignments. Like in our problem, each voyage on a trade route is modeled explicitly with a time window in which the voyage must start. However, they do not consider evenly spread of voyages on the same route.

A few examples of time separation constraints can be found in the literature. Bélanger et al (2006) study a periodic airline fleet deployment problem where the goal is to assign aircraft types to each flight in order to generate a schedule that can be repeated on a daily basis. A penalty cost is added to the objective function when the departure of two flights with the same origin and destination airports are scheduled too closely. An example from maritime transportation is Sigurd et al (2005). They consider a general pickup and delivery problem with time separation requirements on recurring visits to the same port, but in a different context than ours.

4 Mathematical models

In this section two different mathematical formulations for the fleet deployment problem will be given, one based on arc flows, and one based on path flows. The problem’s objective is to maximize profit, while ensuring that all the contractual voyages are sailed. Two alternative formulations of the voyage separation requirement, that apply for both models, will be presented.

4.1 An arc flow formulation

Let \({{\mathcal{V}}}\) be the set of ships. Even though some of the ships have almost identical physical properties, they must be treated individually. This is because they have individual starting positions and individual maintenance schedules, which could lead to infeasible solutions if they were treated as groups of ships. Let \({{\mathcal{R}}}\) be the set of trade routes. The problem is defined on a graph \({{\mathcal{G}}({\mathcal{N}},{\mathcal{A}})}\). The set \({{\mathcal{N}}}\) contains four types of nodes: Origin nodes, destination nodes, voyage nodes and maintenance nodes. For each ship \({v \in {\mathcal{V}}, o(v)\in{\mathcal{N}}}\) represents the starting position and d(v) represents an artificial ending position, which geographically will correspond to the ship’s ending position. The distance from any node to d(v) is zero. Each voyage i on trade route r is represented by a node \({(r,i) \in {\mathcal{N}}}\). The set \({{\mathcal{I}}_r=\left\{1, 2, {\ldots},n_r\right\}}\) is the set of voyages on trade route \({r\in{\mathcal{R}}}\), where n r is the number of voyages on trade route r that must be performed during the planning period. The two disjoint subsets of \({{\mathcal{N}}, {\mathcal{N}}^C}\) and \({{\mathcal{N}}^O}\) represent the contracted (compulsory) voyages and the spot (optional) voyages, respectively. Let \({{\mathcal{N}}_v^M}\) be the set of nodes that correspond to required ship yard maintenance visits for ship v. Like the voyage nodes, the maintenance nodes have two indices (r, i). An arc \({((r,i),(q,j)) \in {\mathcal{A}}}\) corresponds to sailing voyage (or visiting maintenance node) (r, i) and then sailing empty from the end of voyage (or maintenance node) (r, i) to the start of voyage (or maintenance node) (q, j). Included in \({{\mathcal{A}}}\) are also the arcs (o(v), (r, i)) and ((r, i), d(v)). The arcs (o(v), (r, i)) represent traveling directly from the starting position of ship v to the start of voyage i on trade r or to the maintenance node (r, i), while ((r, i), d(v)) represent sailing directly from the end of voyage i on trade r (or maintenance node) (r, i) to the artificial ending point of ship v. Finally, the arc (o(v), d(v)) represents sailing directly from the starting position of ship v to the artificial ending point, which means that the ship will not be used at all. The graph \({{\mathcal{G}}_v({\mathcal{N}}_v,{\mathcal{A}}_v)}\) is the subgraph of \({{\mathcal{G}}}\) for ship v. The set \({{\mathcal{N}}_v}\) consists of all the nodes in \({{\mathcal{N}}}\) which correspond to voyages that ship v can service.

Figure 2 shows an example of a graph \({{\mathcal{G}}_v}\) representing a planning problem with two trade routes \({{\mathcal{R}}=\{1,2\}}\), each with two voyages, \({{\mathcal{I}}_1=\{1,2\}}\) and \({{\mathcal{I}}_2=\{1,2\}}\). This example does not include any maintenance nodes. Note that not all nodes are connected with arcs, due to time window constraints in the nodes.

Fig. 2
figure 2

A graph for a given ship with two trades, and two voyages on each trade

Full size image

The time it takes ship v to sail along arc ((r, i), (q, j)) is T B vriqj . This represents sailing empty from the last discharge port of voyage (r, i) to the first loading port of voyage (q, j). Let C vriqj be the corresponding cost. Let T B o(v)ri and C o(v)ri be the time and cost, respectively, of ship v sailing empty from its origin to the start of voyage (r, i). The duration of sailing voyage (r, i) with ship v is T V vri , which corresponds to sailing between all ports on a trade route and the service time of all the port calls. Let P vri be the corresponding profit, that is, the estimated freight income minus the voyage costs, which mainly consists of fuel, port and canal costs. Let C S ri be the cost of chartering a spot vessel to service voyage i on trade r.

Each voyage must start at its first port within a time window. Let E ri and L ri be the earliest and the latest time for starting voyage i on trade r, respectively. Let E o(v) be the earliest time ship v can start from its initial position. Let B r be the minimum accepted time between two consecutive voyages on trade r.

The binary flow variable x vriqj is 1 if ship v travels directly from node (r, i) to node (q, j), and 0 otherwise. The binary variable x o(v)ri is 1 if ship v goes from its origin to node (r, i), and 0 otherwise. Let x rid(v) equal 1 if node (r, i) is the last node ship v visits before it goes to d(v). Similarly, let x o(v)d(v) be 1 if ship v does not service any voyages at all, and 0 otherwise. Let s ri equal 1 if voyage i on trade r is serviced by a chartered spot vessel, and 0 otherwise. The variable t ri is the time for start of voyage i of trade r and t o(v) is the time when ship v leaves its initial position.

This model, with one node for each voyage, resembles a multi-vehicle traveling salesman problem with time windows (m-TSPTW), with some optional nodes and asymmetric distances. The maritime fleet deployment problem with voyage separation requirements can now be formulated as follows:

$$ \max \quad \quad \sum_{v\in{{\mathcal{V}}}}\sum_{r\in{{\mathcal{R}}}_v}\sum_{i\in{{\mathcal{I}}}_r} (P_{vri} - C_{o(v)ri}) x_{o(v)ri} +\sum_{v\in{{\mathcal{V}}}}\sum_{r\in{{\mathcal{R}}}_v}\sum_{i\in{{\mathcal{I}}}_r}\sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_q} (P_{vri} - C_{vriqj})x_{vriqj} - \sum_{r\in{{\mathcal{R}}}}\sum_{i \in{{\mathcal{I}}}_r} C^S_{ri}s_{ri}, $$
(1)

subject to

$$ \sum_{v\in{{\mathcal{V}}}_r}\left[\sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_r}x_{vriqj} +x_{rid(v)} \right]+s_{ri} = 1,\quad(r,i)\in{{\mathcal{N}}}^C, $$
(2)
$$ \sum_{v\in{{\mathcal{V}}}_r}\left[\sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_r}x_{vriqj} +x_{rid(v)} \right]\leq 1,\quad(r,i)\in{{\mathcal{N}}}^O, $$
(3)
$$ \sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_r}x_{vriqj} +x_{rid(v)} = 1, v \in {{\mathcal{V}}},\quad (r,i)\in{{\mathcal{N}}}_v^M, $$
(4)
$$ x_{o(v)d(v)}+\sum_{r\in{{\mathcal{R}}}_v}\sum_{i\in{{\mathcal{I}}}_r}x_{o(v)ri} = 1,\quad v\in{{\mathcal{V}}}, $$
(5)
$$x_{rid(v)} + \sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_q}x_{vriqj} - \sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_q}x_{vqjri} - x_{o(v)ri}=0,\quad v\in{{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v,\quad i\in{{\mathcal{I}}}_r, $$
(6)
$$ x_{o(v)d(v)}+\sum_{r\in{{\mathcal{R}}}_v}\sum_{i\in{{\mathcal{I}}}_{r}}x_{rid(v)} = 1,\quad v\in{{\mathcal{V}}} $$
(7)
$$ t_{o(v)} + T^B_{o(v)ri} - t_{ri}-M_{o(v)r}(1-x_{o(v)ri})\leq 0,\quad v \in {{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v, \quad\in{{\mathcal{I}}}_r , $$
(8)
$$ t_{ri} + T^V_{vri} + T^B_{vriqj} - t_{qj} -M_{rq}(1-x_{vriqj}) \leq 0,\quad v \in {{\mathcal{V}}},\quad((r,i),(q,j)) \in {{\mathcal{A}}}_v , $$
(9)
$$ t_{o(v)} \geq E_{o(v)},\quad v\in{{\mathcal{V}}}, $$
(10)
$$ E_{ri} \leq t_{ri} \leq L_{ri},\quad r \in {{\mathcal{R}}},\quad i \in {{\mathcal{I}}}_{r}, $$
(11)
$$ t_{r,i+1} - t_{ri} \geq B_{r},\quad r \in {{\mathcal{R}}},\quad i \in {{\mathcal{I}}}_{r}\setminus \left\{n_r\right\}, $$
(12)
$$ x_{o(v)d(v)} \in\{0,1\},\quad v \in {{\mathcal{V}}} , $$
(13)
$$ x_{o(v)ri} \in\{0,1\},\quad v \in {{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v,\quad i\in{{\mathcal{I}}}_r , $$
(14)
$$ x_{rid(v)} \in\{0,1\},\quad v \in {{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v,\quad i\in{{\mathcal{I}}}_r , $$
(15)
$$ x_{vriqj} \in\{0,1\},\quad v \in {{\mathcal{V}}},\quad ((r,i),(q,j))\in{{\mathcal{A}}}_v , $$
(16)
$$ s_{ri} \in\{0,1\},\quad r \in {{\mathcal{R}}}_v,\quad i \in {{\mathcal{I}}}_r. $$
(17)

The objective function (1) sums up the profit from servicing the voyages minus the costs of sailing from the ships’ starting positions to their first voyage and the costs of chartering spot ships if needed.

Constraints (2) state that each contractual voyage must be serviced, either by a ship in the fleet or by a spot ship, while constraints (3) say that each optional voyage can be taken at most once by the fleet’s ships. Constraints (4) ensure that all required ship maintenance operations are carried out. The network flow for each ship is ensured by constraints (5), (6) and (7).

Constraints (8) ensure the time spent sailing from a ship v’s initial position o(v) to a first voyage (r, i) does not exceed the latest start time for the voyage. These constraints have been linearized by using the well known big-M method by introducing a big number M o(v)r . Constraints (9) state that the time spent servicing voyage (r, i) plus the time spent ballast sailing from the end of voyage (r, i) to the start of voyage (q, r) cannot exceed the start time for voyage (q, j). These constraints also function as sub-tour elimination constraints that will make sure that no closed cycles between a subset of voyages will appear in the solution. These constraints have also been linearized by applying the big-M method. The big-M parameters in constraints (8) and (9) have been calculated as follows:

$$ M_{o(v)r} = E_{o(v)} + T^B_{o(v)ri},\quad v \in {{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v,\quad i\in{{\mathcal{I}}}_r, $$
(18)
$$ M_{rq} = L_{ri} + T^V_{vri} +T^B_{vriqj} - E_{qj},\quad v \in {{\mathcal{V}}},\quad((r,i),(q,j)) \in {{\mathcal{A}}}_v. $$
(19)

Constraints (10) state that a ship v cannot start leaving its initial position before it is available, while constraints (11) will ensure that the time window for each voyage is not violated. The minimum accepted time between two consecutive voyages on a trade will be taken care of by constraints (12). Constraints (13), (14), (15) and (16) impose binary requirements on all the flow variables.

4.2 A path flow formulation

The arc flow formulation in Sect. 4.1 can be reformulated as a path flow model where the flow variables are replaced by variables that describes paths through the graph. The problem will be decomposed into a master problem where the allocation of paths to the ships is done and one subproblem for each ship, where feasible paths are generated. The ship specific subproblem contains the flow constraints and the time constraints. Only paths that visit the required maintenance nodes for each ship are generated. Due to the voyage spread requirement the schedules for the ships are not independent of each other, and the time constraints in this formulation cannot be handled solely in the subproblems.

In addition to the notation already presented for the arc flow model, a few more symbols must be declared in order to formulate the path flow model. Let \(\mathcal{P}_v\) be the set of feasible paths for ship v. Let \(\mathcal{P}_{vriqj}\) be a subset of \(\mathcal{P}_v\) which contains all the paths where ship v do voyage j of trade q directly after voyage i of trade r. Let z vp be a binary decision variable that equals 1 if ship v is following path p, and 0 otherwise. Let A vpri be a binary parameter that equals 1 if path p for ship v includes sailing voyage i on trade r. Let E vpri be the earliest service start for voyage i on trade r if performed by ship v on path p. Let P vp be the profit from letting ship v sail path p, i.e. the freight income minus sailing costs. Let C S ri be the cost of chartering in a spot vessel to service voyage (r, i). Further, let t vri be a decision variable that denotes the start of voyage i on trade r for ship v. Let t S ri denote the start of voyage i on trade r if it is assigned to a spot vessel, and 0 otherwise.

A path flow model describing the fleet deployment problem with voyage separation constraints can now be stated as follows.

$$ \hbox{maximize} \sum_{v\in{{\mathcal{V}}}}\sum_{p\in{\mathcal{P}}_v}P_{vp} z_{vp} - \sum_{r\in{{\mathcal{R}}}}\sum_{i\in{{\mathcal{I}}}_r)}C^S_{ri} s_{ri} , $$
(20)

subject to

$$ \sum_{v\in{{\mathcal{V}}}_r}\sum_{p\in{\mathcal{P}}} A_{vpri} z_{vp} + s_{ri} = 1,\quad (r,i)\in{{\mathcal{N}}}^C, $$
(21)
$$ \sum_{v\in{{\mathcal{V}}}_r}\sum_{p\in{\mathcal{P}}} A_{vpri} z_{vp} \leq 1,\quad (r,i)\in{{\mathcal{N}}}^O, $$
(22)
$$ \sum_{p\in{\mathcal{P}}_v} z_{vp} = 1,\quad v\in{{\mathcal{V}}} $$
(23)
$$ \sum_{p\in{\mathcal{P}}_v}E_{vpri} z_{vp} \leq t_{vri} \leq \sum_{p\in{\mathcal{P}}_v}A_{vpri}L_{ri}z_{vp} ,\quad v \in {{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v,\quad i \in{{\mathcal{I}}}_r $$
(24)
$$ E_{ri} s_{ri} \leq t^S_{ri} \leq L_{ri} s_{ri},\quad r \in{{\mathcal{R}}} ,\quad i \in{{\mathcal{I}}}_r, $$
(25)
$$ t^B_{o(v)}+\sum_{p\in{\mathcal{P}}_v}(T_{o(v)ri} +L_{ri})z_{vp}-L_{ri}\leq t_{vri},\quad v\in{{\mathcal{V}}},\quad r \in{{\mathcal{R}}}_v,\quad i \in{{\mathcal{I}}}_r, $$
(26)
$$ t_{vri} + z_{vp} \sum_{p \in {\mathcal{P}}_{vriqj}}(T^V_{vri}+T^B_{vriqj}+L_{ri}) - L_{ri}-t_{vqj} \leq 0,\quad v\in{{\mathcal{V}}},\quad r\in{{\mathcal{R}}}_v, \quad i\in{{\mathcal{I}}}_r, \quad q\in{{\mathcal{R}}}_v,\quad j\in{{\mathcal{I}}}_q, $$
(27)
$$ B_r + \sum_{v\in{{\mathcal{V}}}_r}t_{vri} + t^S_{ri}-\sum_{v\in{{\mathcal{V}}}_r}t_{vr,i+1}-t^S_{r,i+1}\leq 0,\quad r \in{{\mathcal{R}}} ,\quad i \in{{\mathcal{I}}}_r\setminus\left\{n_r\right\}, $$
(28)
$$ t_{o(v)} \geq E_{o(v)},\quad v \in {{\mathcal{V}}}, $$
(29)
$$ z_{vp} \in\{0,1\},\quad v \in {{\mathcal{V}}}, \quad p\in{\mathcal{P}}_v , $$
(30)
$$ s_{ri} \in\{0,1\},\quad r \in {{\mathcal{R}}}_v,\quad i \in {{\mathcal{I}}}_r. $$
(31)

The objective function (20) maximizes the total profit by choosing the most profitable combination of paths for the fleet and the most favorable spot ship options. Constraints (21) state that each contractual voyage must be serviced, either by a ship in the fleet or by a spot ship, while constraints (22) say that each optional voyage can be taken at most once by the fleet’s ships. Constraints (23) state that each ship must follow one and only one path. Constraints (24) ensure that the voyages start within their time windows. To tighten the problem, the earliest start of a voyage, E ri , has been replaced by the ship and path dependent parameter E vpri , since a ship on a given path may not be able to reach (r, i) within E ri . Constraints (25) state that a voyage must start within its time window if it is taken by a spot ship. Constraints (26) ensure that a ship does not start serving its first voyage before it has sailed empty from its starting position, while constraints (27) state that a ship cannot start service of a voyage before it has finished the preceding one and then sailed empty to the start port of the voyage. Minimum spread between two consecutive voyages on a trade is ensured by constraints (28). Constraint (29) state that a ship cannot start on its path before it is available in its starting position. Finally, constraints (30) and (31) state that z vp and s ri are binary variables.

4.3 An alternative formulation of the voyage separation requirement

One disadvantage with the model formulations presented, is that it is very difficult for the fleet planners to decide what value the minimum spread parameter B r should have for each trade. The minimum separation time is normally not defined in the contract. Giving these parameters too high value will certainly ensure that the schedule will be accepted by the charterers, but also reduce the flexibility and probably lead to a more costly solution for the shipping company than necessary. On the other hand, if the value of B r is set too low, it might cause dissatisfied charterers and not optimal cargo availability. Since it is difficult to specify an absolute limit for the time between voyages of a trade, a soft constraint might provide a better model of the real world. We will now extend the path flow formulation to include a soft constraint for the voyage separation. There will still be a hard bound for the separation variable, but in addition there is a tighter preferred soft bound that can be violated. The penalty cost for violating the soft constraint will be linearly dependent on the magnitude of the violation, as illustrated in Fig. 3.

Fig. 3
figure 3

Penalty cost function for time between consecutive voyages on a trade

Full size image

Let D r be the preferred minimum time between two consecutive voyages on trade r and C P r be the artificial penalty cost for violating D r by one time unit. Let y ri be a variable that represents the number of time units the preferred separation limit D r is violated by voyage i on trade r.

The arc flow formulation in Sect. 4.1 can be extended to include soft time spread restrictions by adding constraints (33) and (34). The objective function (1) should be replaced by the revised one (32).

$$ \begin{aligned} &\max \sum_{v\in{{\mathcal{V}}}}\sum_{r\in{{\mathcal{R}}}_v}\sum_{i\in{{\mathcal{I}}}_r} (P_{vri} - C_{o(v)ri}) x_{o(v)ri} \\ &+\sum_{v\in{{\mathcal{V}}}}\sum_{r\in{{\mathcal{R}}}_v}\sum_{i\in{{\mathcal{I}}}_r}\sum_{q\in{{\mathcal{R}}}_v}\sum_{j\in{{\mathcal{I}}}_q} (P_{vri} - C_{vriqj})x_{vriqj}\\ &- \sum_{r\in{{\mathcal{R}}}}\sum_{i \in{{\mathcal{I}}}_r} C^S_{ri}s_{ri} - \sum_{r\in{{\mathcal{R}}}}\sum_{i\in{{\mathcal{I}}}_r}C^P_{r} y_{ri}, \end{aligned} $$
(32)
$$ D_r + t_{ri} - t_{r,i+1} - y_{ri}\leq 0,\quad r \in{{\mathcal{R}}} ,\quad i \in{{\mathcal{I}}}_r\setminus \left\{n_r\right\}, $$
(33)
$$ y_{ri} \geq 0,\quad r \in{{\mathcal{R}}} ,\quad i \in{{\mathcal{I}}}_r. $$
(34)

For the path flow formulation in Sect. 4.2 we can add the constraints (36) and (37), while the revised objective function (35) replaces the original one (20).

$$ \max \sum_{v\in{{\mathcal{V}}}}\sum_{p\in{\mathcal{P}}_v}P_{vp} z_{vp} - \sum_{r\in{{\mathcal{R}}}}\sum_{i\in{{\mathcal{I}}}_r}C^S_{ri} s_{ri}- \sum_{r\in{{\mathcal{R}}}}\sum_{i\in{{\mathcal{I}}}_r}C^P_{r} y_{ri}, $$
(35)
$$ D_r + \sum_{v\in{{\mathcal{V}}}}t_{vri} + t^S_{ri} -\sum_{v\in{{\mathcal{V}}}}t_{vr,i+1} - t^S_{r,i+1}\leq y_{ri},\quad r \in{{\mathcal{R}}} ,\quad i \in{{\mathcal{I}}}_r \setminus \left\{n_r\right\}, $$
(36)
$$ y_{ri} \geq 0,\quad r \in{{\mathcal{R}}} ,\quad i \in{{\mathcal{I}}}_r. $$
(37)

5 Computational study

We have performed several computational experiments in order to evaluate the proposed models. First, in Sect. 5.1 a description of how the models are implemented is given. In Sect. 5.2 the test instances are presented. Then we compare the performance of the arc flow and the path flow models in Sect. 5.3 In Sect. 5.4 the effect of adding voyage separation constraints is studied, while in 5.5 we analyze the effect of adding the soft formulation of the time separation constraints. Finally, in Sect. 5.6 we discuss the impact of using optimization based solution methods by comparing the solution of a real life problem instance with a schedule made manually by the schedulers at Saga Forest Carriers.

5.1 Implementation

The optimization models presented in Sect. 4 have been implemented in Xpress MP 7.0 64 bit. In order to generate the parameters for the path flow model a path generator program has been implemented. All feasible paths for each ship are generated a priori to the optimization. Since the required maintenance operations and also some the voyages can have quite wide time windows, there may be several feasible sequences or paths a ship can follow while performing the same set of voyages. A simple dominance test is therefore performed to make sure that only the most profitable one is passed on to the optimization model.

The path generation has been implemented in C#. Both the path generation and the optimization is performed on a DELL Latitude Laptop with Intel Core i5 CPU (4 × 2.40 GHz), 4 GB DDR2 RM running on Windows 7.

5.2 Test problem instances

The real planning problem faced by Saga Forest Carriers includes 25 ships, 10 trades and approximately 50 voyages over a planning horizon of three to four months. To provide a sufficiently large set of problem instances for testing the models, a test instance generator has been developed. Based on parameters describing the number of ships, the number of trades and the length of the planning horizon, the generator randomly selects a subset of the fleet’s ships and trades, and generates a set of voyages with corresponding time windows. The width of the time windows are dependent on the frequencies of the voyages. For instance, a trade with three voyages every month will have 10 days non-overlapping time windows, while a trade with only one monthly voyage will have a 30 days window. Furthermore, the instance generator calculates sailing times and costs based on distances, fuel costs, freight rates and ship data from the shipping company’s fleet management system. The output from the generator is flat text files that can be read by the path generator program and by the Xpress MP optimization software. Table 1 provides a summary of the generated test instances. The columns Ships and Trades display the number of ships in the fleet and the number of different trade routes, respectively. The column Voyages shows the total number of voyages, with the number of optional voyages in parenthesis. The length of the planning horizon in days is given in the column Horizon. Note that this horizon defines the period that covers the start of the time windows for the generated voyages. This means that the actual planning period for the scheduling problem is longer, as a voyage can have a latest starting time outside the horizon. In addition, the voyages also have to be finished. The columns Var. and Constr. shows the number of variables and constraints, respectively, for both the arc flow and the path flow formulations.

Table 1 Summary of test instances
Full size table

5.3 Comparing arc flow and path flow formulations

The 18 test problem instances in Table 1 have been solved by both the arc flow and the path flow based solution approaches. In this test both models contain only the hard voyage separation constraints. The results of these comparisons are displayed in Table 2. The columns Obj show the best solutions found by the two models. The columns Gap show the gap in percent between the best integer solution and the best bound found after the maximum solution time of 1 h (3,600 s). The columns Seconds report the computational time in seconds, if optimum is reached before the time limit. For the path flow formulation, the first number is the total solution time, while the number in parentheses is the time spent generating the paths.

Table 2 Comparison of the arc flow and the path flow model
Full size table

From the results in Table 2 we see that for the smallest problem instances (1 to 12) there are no significant difference between the models. They both find the optimal solution to the problems and they both solve the problems quickly. For the larger problem instances, however, there is a tendency that the path flow model is faster than the arc flow model. For several of the instances, the arc flow model does not prove optimality within the 1 h time limit. However, the gap is less than 1 , and when we compare the solutions of the arc flow model to the optimal ones provided by the path flow model, we see that for all but one of the instances the arc flow model finds the optimal solutions, but is just not able to close the gap to the best bound. The conclusion from this comparison is still that for larger instances, the path flow model is faster.

5.4 Effect of voyage separation requirements

To provide an example of the effect of including voyage separation requirements in the model, we have solved instance 17 from Table 1 without the voyage separation constraints and compared the solution with the one obtained by using the path flow model in Table 2. In this problem instance the SAM-EUR trade has 18 voyages, all with 7 days wide time windows. For this trade, the minimum accepted time between two voyages is 5 days. Figure 4 depicts how the voyages are spread out along the time line. We see that without the voyage separation constraints some of the consecutive voyages start very close in time to each other, which would probably not be accepted by the charterer. In Table 3, which compares the two solutions, we see that adding the separation constraint hardly reduces the objective value at all, approximately only by 0.01 percent. The ideal separation, that is, perfectly evenly spread, for this trade is 7 days, which is the time between the start of each time window. The table also shows the standard deviation of the separation times. We see that with separation constraints, the separation times deviates significantly less from the ideal time. Even though we have only shown one trade in one instance, the conclusion from our experiments is that it seems that adding voyage separation requirements significantly improves the spread of voyages without only marginal reductions in profit. It therefore provides solutions that are much better in practice.

Fig. 4
figure 4

Starting days for voyages on the SAM-EUR trade

Full size image
Table 3 The effect of adding separation constraints
Full size table

5.5 Analysis of soft voyage separation requirements

Just adding the soft restrictions without relaxing the hard constraints will obviously always provide solutions with objective values that are worse or equal compared to the formulation with the hard constraint only. Furthermore, it adds complexity to the model and will probably increase the computational time. When comparing the hard and the soft formulations one must therefore choose different values for the minimum time spread, B r .

In order to analyze the effect of adding the soft constraints we study a problem instance with ten ships, three trades and a total of 35 voyages over a 120 day planning horizon. The problem is first solved six times by the hard formulation, then twelve times by the soft formulation, each time with different parameter settings, providing different penalty cost functions. We recall from Sect. 4.3 that D r is the preferred minimum separation time between voyages of trade r. For this experiment we fix D r to the values that is specified by the shipping company. Table 4 shows the parameter settings and the results of the optimization. The values of B r are obtained by multiplying the values of D r with the coefficient shown in column B.

Table 4 Comparison of hard and soft voyage spread constraints
Full size table

For example, assume that D r for a given trade in the test instance has the value of 10 days. For test 1 B r will have the same value, while in test 2 it will be set to 8 days and so on. We also test for two different penalty costs. The penalty for violating the preferred separation limit D r by 1 day is given in column C P. The column Real obj. reports the objective value without any penalty costs. The column Penalty contains the artificial penalty costs associated with the solution. The number of chartered in spot ships in the solution is given in column Spot ships. Finally, the computational time is displayed in Seconds. The path flow based model has been used for all the tests.

Figure 5 shows a graphical representation of the results in Table 4. There are three functions, one for the hard model (test 1 to 6) one for the soft model with penalty coefficient C P r  = 10,000 (test 7–12), and one for the soft model with C P r  = 40,000 (test 13–18). The figure shows the real objective value, i.e. without the artificial penalty costs. Due to the integral properties of the fleet deployment problem, these functions take the shape of a step function. Both the results in the table and the figure show that as the value of B r increases, the optimal objective value decreases. We also see that the higher the penalty rate, the lower the objective value.

Fig. 5
figure 5

Objective values (without penalty) as function of minimum allowed spread

Full size image

For the quite small problem instance studied in this experiment, we cannot draw any final conclusion about the relationship between the parameter settings and the computational time. It seems, however, to be a trend that the smaller the value of the parameters B r , the faster the optimal solution is found. It also seems like the model with the soft constraints is slightly more time consuming to solve than the model with only the hard constraints.

Even though only one problem instance has been analyzed in this computational study, the conclusion is that the soft formulation is more flexible in finding good solutions and does not increase the computational time very much. The user should however be very careful in choosing the parameters, as slightly different penalty costs or minimum voyage separation times might lead to significantly different solutions.

5.6 Analysis of a real life fleet deployment problem

In order to evaluate the effects of introducing optimization based tools for solving the fleet deployment problem of Saga Forest Carriers, we have compared a real life schedule made by their own schedulers with the results from our proposed path flow model. In their planning process, the schedulers use advanced spreadsheet models. These spreadsheets can download updated positions for all the ships, but do not include any optimization features. The schedulers manually assign available ships to the voyages and the spreadsheets automatically update open dates and positions for the ships, helping the schedulers to visualize the plan.

In this experiment a three month schedule has been studied. The problem consists of 24 ships and seven trades with 42 voyages in total. In addition, the chartering department has identified 14 possible spot voyages in the market. Since Saga’s schedulers do not use a model that contains soft constraints for the voyage separation requirements, the path flow formulation with hard separation constraints has been used in the comparison.

The results from the experiment can be found in Table 5. The column Manual schedule refers to the schedule produced by Saga’s own schedulers, while Optimized schedule refers to the schedule obtained from solving the path flow based formulation of the problem. As expected, the optimization based method finds the best schedule. The difference is 2.9 percent or approximately 1.2 million USD. We see that the optimized schedule does not take all the spot cargoes, resulting in a lower gross freight income. Instead the optimized solution has ship routes with less ballast sailing and hence much lower fuel costs.

Table 5 Comparison of manual scheduling and optimization based scheduling
Full size table

A perhaps more important advantage of the optimization based method is that it solves the problem quite quickly. The optimal schedule was found after 16 s and optimality was proven after 68 s. Generating the schedule manually takes roughly a full working day. It is obvious that using optimization based decision support tools can save a lot of time. This allows the schedulers to spend more time on other tasks, for instance rescheduling when ships are delayed or searching the spot market for profitable charter-out opportunities.

6 Concluding remarks

We have studies a real planning problem faced by the shipping company Saga Forest Carriers. This problem can be considered as a fleet deployment problem similar to what can be found in the liner shipping literature, except that here we have time separation requirements for voyages of the same trade. Two mathematical formulations of the problem have been presented, one arc flow and one path flow model.

The fleet deployment problem is an important tactical planning problem and its purpose is to determine the fleet schedule for the next few months. Even though the planning period is relatively long, rescheduling is needed quite often due to updated information about the future. Hence the response time for the decision support system is crucial. Computational studies of 18 test problem instances show that both models work well on small problem instances. However, the path flow based model, with all possible paths generated a priori, is in addition capable of solving real life sized problem instances to optimality within an acceptable time.

The computational results show that introducing voyage separation requirements provides solution that have much better spread of voyages, and this comes at only a marginal reduction in profit. Good spread of voyages is important in this planning problem, hence these solutions are much better in practice.

Since the contractual clause stating that voyages should be fairly evenly spread does not specify exactly what is acceptable time between two voyages, we have also presented an alternative formulation of the voyage separation requirement. This is a soft constraint which adds an artificial penalty to the objective function. A computational study shows that using the soft constraint formulation will improve the solutions without increasing the computational time very much.

Compared with the spreadsheet based scheduling tool currently used by Saga Forest Carriers, the optimization based methods proposed in this paper provides solutions with better profit and better voyage separation. In addition, using these methods is much faster than manual scheduling and could therefore free up time for the schedulers.