1 Introduction

A train timetable includes the arrival and departure times of a set of trains at stations and the assignment of tracks and platforms. The timetable optimization is generally divided into a scheduling process and a rescheduling process. For scheduling process, the railway company would like to minimize the operational cost by meeting the safety constraint and the requirements of passengers. For example, Kraay et al. (1991) formulated a mixed integer programming (MIP) model to minimize the energy cost and delay, Higgins et al. (1995) proposed a MIP model to minimize the delay cost. Ghoseiri et al. (2004) proposed a two-objective optimization model for railway network which minimizes the fuel consumption cost and the total passenger-time. Yang et al. (2009) proposed a fuzzy expected value programming model by minimizing the delay time and the total passenger-time on the assumption that the numbers of passengers at stations are fuzzy variables. The authors designed a branch and bound algorithm to solve the fuzzy optimization model. Chien et al. (2011) developed a modular fuzzy ranking framework that can systematically decompose the fuzzy ranking methods into specific modules. Furthermore, Li et al. (2011) studied another fuzzy expected value programming model which minimizes the average energy consumption under the maximal allowable velocity constraint and traversing time constraint. The authors designed an iterative algorithm based on the Karush–Kuhn–Tucker optimality conditions. The numerical examples illustrated that the fuzzy optimization technique can further save energy 3.75 % in average.

As the uncertain disturbances arising from bad weather conditions, equipment faults and unexpected passengers, the original timetable obtained at the scheduling process may be suboptimal or infeasible during the operation process. Therefore, a rescheduling procedure is needed to suggest new arrival/departure times and a new assignment of railway resources within a reasonable computation time. In this case, the main objective is to assure that the reassignment is as similar as possible to the original timetable, e.g., minimizing the negative effect of the disturbances. For example, Tonquist and Persson (2007) formulated a complex MIP model to minimize a discontinuous delay cost on the last station for each train, which allows for the modeling of a highly complex multi-bidirectional-tracks network in which each track consists of several blocks. The authors analyzed the connections constraints and tolerance of delays. In contrast to previous approaches, the authors analyzed how the approach performs for large and real problem instances. Acuna-Agost et al. (2011) proposed a MIP model to minimize the differences between the original plan and the new provisional plan. The objective function is defined as a weighted sum of the costs of delays, changes of tracks/platforms, and unplanned stops. It supports bidirectional lines, multi-track lines and extra time for accelerating and braking. Since the large number of variables and constraints, an approach called Statistical Analysis of Propagation of Incidents is developed to tackle the problem.

The train fueling cost minimization is a special type of timetable optimization problem, which studies how to find a scheduling and fueling strategy for trains on a corridor such that the fueling cost is minimized and no train runs out of fuel. As the continuously increasing of fuel price in the world, railway companies pay more and more money for purchasing fuel to keep their trains running. Generally speaking, fuel price is affected by many factors, for example, crude oil price, refining cost, distribution and marketing, and fuel tax, where crude oil price dictates the fuel price varies over time, and the other three factors dictate the fuel price varies across locations. In addition, the official adjustment policy also has an important influence on the fuel price. For example, the Chinese average diesel fuel price had been increasing from month to month in 2009, one liter of diesel fuel costs 4.11 RMB on January, 4.26 RMB on March, 4.60 RMB on June, 4.93 RMB on July, 5.18 RMB on September, and 5.43 RMB on November. On the other hand, the fuel prices in different provinces are also different, take the date July 8, 2010 for example, one liter of diesel fuel costs 6.69 RMB in Beijing, 5.58 RMB in Shanghai, 6.23 RMB in Tianjin, 6.31 RMB in Chongqin, and 6.76 RMB in Tibet. These two characteristics of fuel price impact the train fueling cost minimization problem as follows: the variation over time makes it necessary to treat the fuel price as an uncertain variable, then the fueling cost minimization model should be an uncertain optimization model; the variation across locations dictates the optimal fueling strategy avoids fuel purchases at high price stations, and dictates the optimal scheduling strategy reduces the amount of energy consumption when trains pass high price stations as much as possible.

Traditionally, fueling stations are generally assumed to have a common fuel price. Then the fueling cost minimization problem is equivalent to the fuel consumption minimization problem. For example, Chang and Sim (1997) investigated a coasting control optimization model for saving fuel consumption, Howlett (2000) investigated a fuel consumption minimization model with a traversing time constraint, and designed a numerical algorithm based on the Karush–Kuhn–Tucker conditions for the optimal solution, Effati and Roohparvar (2006) presented a linear programming approach and a dynamic programming approach to solve the fuel consumption minimization problem. A survey on fuel consumption minimization model and algorithm was given by Miyatake and Ko (2010), and the latest developments may consult literatures (Bai et al. 2009; Howlett et al. 2009; Khmelnitsky 2000; Liu and Golovitcher 2003).

Recently, Nourbakhsh and Ouyang (2010) proposed an optimal fueling strategy model for locomotive fleets in railway networks, which first considers the variation of fuel price across locations, but does not consider the variation over time. In their work, the authors studied the fueling strategy problem with a given train scheduling strategy. Since the fueling cost depends on the the amount of fuel consumption, while the amount of fuel consumption is determined by the speeds of trains, it is reasonable to study the fueling strategy problem and the train scheduling problem in an integrated formulation. To the best of our knowledge, the integrated problem has not been studied before. The purpose of this paper is to formulate a mathematical model to determine an optimal scheduling and fueling strategy such that the fueling cost is minimized. Since the fueling strategy will be used by many trains over a long period of time, during which the fuel prices at the refueling points will vary, we employ fuzzy variables to model the fuel prices and thus proposed this approach, which has not been seen in the literature to our best knowledge.

The rest of this paper is organized as follows. Section 2 proposes a fuzzy fueling cost minimization model which minimizes the expected value of the fuzzy fueling cost under the traversing time constraint, the maximal allowable speed constraint, the tank capacity constraint and so on. Section 3 describes the proposed approach as a nonlinear scheduling strategy model and a linear fueling strategy model. Based on the Karush–Kuhn–Tucker conditions, we design an iterative algorithm to solve the scheduling model, and then design a numerical algorithm to solve the fueling cost minimization model. Section 4 presents two numerical examples to show the efficiency of the proposed model and algorithm. Section 5 concludes with discussions of contributions and future research directions.

2 Mathematical model

This paper studies the fuzzy train fueling cost minimization problem within the framework of credibility theory (Liu 2007; Li and Liu 2006), which is a powerful tool for dealing with fuzzy phenomena.

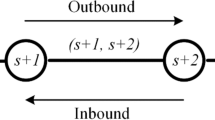
Suppose that there is a railway line consisting of n + 1 stations (see Fig. 1). Without loss of generality, we assume that trains may purchase fuel at the first n stations with different prices. In this section, we shall formulate an optimization model for determining a scheduling and fueling strategy, which minimizes the fueling cost and ensures that no train runs out of fuel. In addition, the traversing time constraint, the maximal allowable speed constraint, and the tank capacity constraint will be also considered. First, we introduce some parameters and the decision variables.

Fig. 1
figure 1

A rail line which consists of n + 1 stations

Full size image

2.1 Parameters and decision variables

n::

number of fueling stations along the rail line

l i ::

link between the ith station and the (i+1)th station

d i ::

length of link l i

m::

weight of the train

r i0::

resistance coefficient due to grade and rolling resistance on link i

r i1::

resistance coefficient due to rail friction on link i

r i2::

resistance coefficient due to air friction on link i

s::

amount of fuel consumption per joule of power

T::

the predetermined traversing time for the train

b::

the tank capacity for the train

ξ i ::

fuel price at fueling station i, which is treated as a fuzzy variable

u max i ::

the maximal allowable speed on the ith link

u i ::

train average speed on the ith link, which is the decision variable

w i ::

amount of fuel purchased at fueling station i, which is the decision variable.

2.2 Assumptions

  1. (a)

    Since we consider trains with high power/weight ratio travelling long distances, they are assumed to run with constant speeds on all links.

  2. (b)

    The fueling stations are assumed to be located such that a full tank of fuel can avoid the train running out of fuel between any two adjacent stations.

  3. (c)

    The dwell time for each train at each station is fixed and predetermined for satisfying the loading/unloading requirements, which is larger than the fueling operation time.

2.3 Fuzzy fueling cost minimization model

If the link between the ith station and the (i + 1)th station is labeled with its starting station, then there are n links along the rail line. We use u i to denote the average speed of the train when it runs on the ith link. If the gradient is constant and the train travels at a constant speed then the resistance force on the train can be modeled by the Davis formula (Ghoseiri et al. 2004), a quadratic m(r i0 + r i1 u i  + r i2 u 2 i ), where m is the mass of the train, r i0 is the resistance coefficient due to grade and rolling resistance, r i1 is the resistance coefficient due to rail and bearing friction, and r i2 is the resistance coefficient due to air friction. If the length of the ith link is d i , then the fuel consumption will be

$$ e_i=m\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right) d_i s, $$
(1)

where s is the fuel consumption per joule of energy. More generally, the fuel use on a link with varying gradients and varying train speed will increase with average speed. The relationship between fuel use and average speed can be found by simulation, then approximated by a quadratic similar to Eq. (1).

We use w i to denote the amount of fuel purchased at the ith fueling station. In order to avoid the train running out of fuel, for each 1 ≤ k ≤ n, the total amount of fuel purchased at the first k stations should be larger than the amount of fuel consumption, that is,

$$ \sum\limits_{i=1}^{k}\left(w_i-m\left(r_{i0}+r_{i1} u_i+r_{i2}u_i^2\right)d_is\right)\geq0. $$
(2)

In addition, since the tank capacity is finite, the amount of fuel purchased at the kth station should not exceed the maximal allowable value. That is, for each 1 ≤ k ≤ n, we have

$$ \sum\limits_{i=1}^{k-1}\left(w_i-m\left(r_{i0}+r_{i1} u_i+r_{i2}u_i^2\right)d_is\right)+w_k\leq b, $$
(3)

where the sum item denotes the amount of fuel left in the tank when the train arrives at the kth fueling station, and b denotes the tank capacity.

Since the fuel prices at fueling stations generally vary from month to month affected by the crude oil price and the adjustment policy based on regional concerns, it is unreasonable to estimate the future fuel prices by crisp numbers when making the fueling strategy. In this paper, we use fuzzy variables \(\xi_1,\xi_2,\ldots,\xi_n\) to model them. Then the fueling cost \(\xi_1w_1+\xi_2w_2+\cdots+\xi_nw_n\) is also a fuzzy variable. If the decision-maker would like to minimize its expected value, that is, the average fueling cost, then we get the following fuzzy fueling cost minimization model (FCM)

$$ \left\{\begin{array}{ll} \min E\left[\xi_1w_1+\xi_2w_2+\cdots+\xi_nw_n\right]\\ s.t. \displaystyle\sum\limits_{i=1}^{k-1}(w_i-m\left(r_{i0} +r_{i1}u_i+r_{i2}u_i^2\right)d_is)+w_k\leq b,\quad \forall k=1,2,\ldots,n\\ \quad \displaystyle\sum\limits_{i=1}^{k}(w_i-m\left(r_{i0} +r_{i1}u_i+r_{i2}u_i^2\right)d_is)\geq 0, \quad\forall k=1,2,\ldots,n\\ \quad \displaystyle\sum\limits_{i=1}^nd_i/u_i=T\\ \quad u_i^{\max}\geq u_i>0,\quad \forall i=1,2,\ldots,n\\ \quad w_i\geq0, \quad \forall i=1,2,\ldots,n, \end{array}\right. $$
(4)

where the first constraint is the tank capacity constraint, the second constraint ensures that no train runs out of fuel, the third constraint ensures that the traversing time is equal to a predetermined value, and the fourth constraint ensures that the running speeds for the train are less than the maximal allowable values.

3 Algorithms

If fuzzy variables \(\xi_1,\xi_2,\ldots,\xi_n\) are not independent, the fuzzy simulation technique (Liu and Liu 2002) can be well used to approximate the expected fueling cost, and the FCM model can be solved with a hybrid intelligent algorithm (Li et al. 2009). In what follows, we assume that fuzzy variables \(\xi_1,\xi_2,\ldots,\xi_n\) are independent. Then it follows from the linearity of expected value that

$$ E\left[\xi_1w_1+\xi_2w_2+\cdots+\xi_nw_n\right] =E[\xi_1]w_1+E[\xi_2]w_2+\cdots+E[\xi_n]w_n. $$

The FCM model contains two decision vectors, that is, fueling strategy and scheduling strategy. For each given feasible scheduling strategy \((u_1,u_2,\ldots,u_n),\) the FCM model is a linear programming model on fueling strategy. Now, let us analyze its optimal solution. For simplicity, we denote k 1 = 1, use L i to denote the amount of fuel left in the tank when the train arrives at the ith station, and use F(i, j) to denote the amount of fuel required to travel from station i to station j. For all 1 ≤ i < j ≤ n + 1, it is easy to prove that

$$ L_{i}=\sum_{k=1}^{i-1}\left(w_k-m \left(r_{k0}+r_{k1}u_k+r_{k2}u_k^2\right)d_ks\right), $$
(5)
$$ F(i,j)=\sum_{k=i}^{j-1}m\left(r_{k0}+r_{k1}u_k+r_{k2}u_k^2\right)d_ks. $$
(6)

When the train prepares to start its travel at station k 1, let i 1 be the smallest index satisfying E[\(\xi _{{i_{1} }}\)] < E[\(\xi _{{k_{1} }}\)]. In the case of there is no station with smaller average fuel price than station k 1, we set i 1 = n + 1. If the amount of fuel consumption for the subjourney from station k 1 to station i 1 is less than the tank capacity, that is, F(k 1, i 1) ≤ b, then we should purchase all the required fuel at station k 1 since it has a lower price. In this case, the train will perform the next fueling operation at station k 2 = i 1 with \(L _{{k_{2} }}\) = 0. Otherwise, we have F(k 1,i 1) > b. It is clear that we should fill the tank fully at station k 1, and consider the next fueling operation at station k 2 = k 1 + 1. When the train arrives at station k 2, the amount of fuel left in the tank is \(L _{{k_{2} }}\) = b − F(k 1,k 2). In general, we have

$$ w_{k_{1}}=\left\{\begin{array}{ll} F(k_1,i_1),& \, \hbox{if}\, F(k_1,i_1)\leq b\\ b, & \,\hbox{if}\, F(k_1,i_1)>b,\\ \end{array}\right. $$
(7)
$$ k_2=\left\{\begin{array}{ll} i_1, &\,\hbox{if}\, F(k_1,i_1)\leq b\\ k_1+1, &\, \hbox{if}\, F(k_1,i_1)>b, \end{array}\right. $$
(8)
$$ L_{k_{2}}=\left\{\begin{array}{ll} 0, &\, \hbox{if}\, F(k_1,i_1)\leq b\\ b-F(k_1,k_2), &\, \hbox{if}\, F(k_1,i_1)>b.\\ \end{array}\right. $$
(9)

In addition, for each k 1 < i < k 2, the optimal amount of fuel purchased at station i should be w i  = 0. Now, suppose that the train has fueled at station k l−1, and we consider the fueling operation at the k l th station. Let i l be the smallest index satisfying i l  > k l and E[\(\xi _{{i_{l} }}\)] < E[\(\xi _{{k_{l} }}\)]. In the case of E[ξ i ] ≥ E[\(\xi _{{k_{l} }}\)] for all i > k l , we set i l  = n + 1. If F(k l , i l ) ≤ \(L _{{k_{l} }}\), that is, the left fuel in the tank is enough for providing the train runs from station k l to station i l , then we should not purchase fuel at station k l since it has a higher fuel price than station i l . If \(L _{{k_{l} }}\)< F(k l , i l ) ≤ b, then the optimal amount of fuel purchased at the k l th station should be F(k l , i l ) − \(L _{{k_{l} }}.\)For these two cases, we perform the next fueling operation at station i l . If F(k l , i l ) > b, we should fill the tank fully at station k l , and consider the next possible fueling operation at station k l  + 1. In general, we have

$$ w_{k_{l}}=\left\{\begin{array}{ll} 0, & \, \hbox{if} F(k_l,i_{l})\leq L_{k_{l}}\\ F(k_l,i_{l})-L_{k_{l}}, & \, \hbox{if}\, L_{k_{l}}<F(k_l,i_{l})\leq b\\ b-L_{k_{l}}, & \, \hbox{if}\, F(k_l,i_{l})>b, \end{array}\right. $$
(10)
$$ k_{l+1}=\left\{\begin{array}{cl} i_l, &\, \hbox{if}\, F(k_l,i_{l})\leq L_{k_{l}}\\ i_l, &\, \hbox{if}\, L_{k_{l}}<F(k_l,i_{l})\leq b\\ k_l+1, &\, \hbox{if}\, F(k_l,i_{l})>b, \end{array}\right. $$
(11)

and the amount of fuel left in the tank when the train arrives at the k l+1th station is

$$ L_{k_{l+1}}=\left\{\begin{array}{ll} L_{k_{l}}-F(k_l,i_{l}), &\, \hbox{if}\,F(k_l,i_{l})\leq L_{k_{l}}\\ 0,&\, \hbox{if}\, L_{k_{l}}<F(k_l,i_{l})\leq b\\ b-F(k_l,k_{l+1}), &\, \hbox{if}\, F(k_l,i_{l})>b,\end{array}\right. $$
(12)

For each k l  < i < k l+1, the optimal amount of fuel purchased at station i should be w i  = 0. Since the number of fueling stations is finite, the optimal fueling strategy and the minimum fueling cost with given scheduling strategy \((u_1,u_2,\ldots,u_n)\) may be solved by at most n loops.

Theorem 1

For each given scheduling strategy \((u_1,u_2,\ldots,u_n), \) let \((w_1,w_2, \ldots,w_n)\) be the optimal fueling strategy of the FCM model. Then there is a constant c such that the minimum fueling cost is

$$ \sum_{i=1}^nE[\xi_i]w_i=\sum_{i=1}^n\alpha_im\left(r_{i0} +r_{i1}u_i+r_{i2}u_i^2\right)d_is+c $$
(13)

where \(\alpha_i\in\left\{{ E[\xi_1],E[\xi_2],\ldots,E[\xi_n]}\right\}\) for all 1 ≤ i ≤ n.

Proof

Assume that the train performs the fueling operations at stations \(k_1,k_2,\ldots,k_L\) along its trip, that is, we have F(k l , i l ) > \(L _{{k_{l} }}\) for all 1 ≤ l ≤ L. For each 2 ≤ l ≤ L, we will prove that there is a constant c l such that

$$ \begin{aligned} \sum_{j=1}^lE[\xi_{k_{j}}]w_{k_{j}}&=\sum_{i=1}^{k_{l}-1}\alpha_im\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is\\ & \quad +E[\xi_{k_{l}}]\min\left\{F(k_l,i_{l}), b\right\}+c_l, \end{aligned} $$
(14)

where \(\alpha_i\in\left\{{ E[\xi_1],E[\xi_2],\ldots,E[\xi_n]}\right\}\) for all 1 ≤ i ≤ n. For l = 2, the argument breaks down into two cases.

Case 1. F(k 1,i 1) ≤ b. In this case, we have k 2 = i 1, the amount of fuel purchased at the k 1th station is F(k 1,i 1). When the train arrives at station k 2, the amount of fuel left in the tank is \(L _{{k_{2} }}\) = 0. Then it is easy to prove that

$$ \begin{aligned} \sum_{j=1}^lE[\xi_{k_{j}}]w_{k_{j}}& =E[\xi_{k_{1}}]F(k_1,i_1)+ E[\xi_{k_{2}}]\min\left\{F(k_2,i_2),b\right\}\\ & =\sum_{i=1}^{k_2-1}\alpha_i m\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is +E[\xi_{k_{2}}]\min\left\{F(k_2,i_2),b\right\}+c_2, \end{aligned} $$
(15)

where c 2 = 0 and α i  = E[\(\xi _{{k_{1} }}\)] for all 1 ≤ i ≤ k 2 − 1.

Case 2. F(k 1,i 1) > b. It is easy to prove that the amount of fuel purchased at the k 1th station is b, and the amount of fuel left in the tank is \(L _{{k_{2} }}\) = b − F(k 1,k 2) when the train arrives at station k 2, which implies that

$$ \begin{aligned} \sum_{j=1}^lE[\xi_{k_{j}}]w_{k_{j}} & =E[\xi_{k_{1}}] b+E[\xi_{k_{2}}]\left(\min\left\{F(k_2,i_2),b\right\}-L_{k_{2}}\right)\\ & =\sum_{i=1}^{k_{2}-1}\alpha_i m\left(r_{i0}+r_{i1}u_i+r_{i2}u_{i}^{2}\right)d_is +E[\xi_{k_{2}}]\min\left\{F(k_2,i_2),b\right\}+c_2,\\ \end{aligned} $$
(16)

where \(c_2=\left(E[\xi_{k_{1}}]-E[\xi_{k_{2}}]\right)\times b\) and α i  = E[\(\xi _{{k_{2} }}\)] for all 1 ≤ i ≤ k 2 − 1.

Now, assume that formulation (14) holds for l = h, then there are parameters \(c_h,\alpha_1,\alpha_2,\ldots,\alpha_{k_{h}-1}\) such that

$$ \begin{aligned} \sum_{j=1}^{h}E[\xi_{k_{j}}]w_{k_{j}}&=\sum_{i=1}^{k_{h}-1} \alpha_im\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is\\ & \quad +E[\xi_{k_{h}}]\min\left\{F(k_h,i_{h}),b\right\}+c_h.\\ \end{aligned} $$
(17)

We will prove that (14) still holds for l = h + 1. The argument breaks down into two cases.

Case 1. F(k h , i h ) ≤ b. In this case, it is easy to prove that k h+1 = i h+1, the amount of fuel purchased at the k h th station is F(k h , i h ), and the amount of fuel left in the tank is \(L _{{k_{h+1} }}\) = 0 when the train arrives at station k h+1, then

$$ \begin{aligned} & \sum_{j=1}^{h}E[\xi_{k_{j}}]w_{k_{j}}+E[\xi_{k_{h+1}}]w_{k_{h+1}}\\ & =\sum_{i=1}^{k_{h}-1}\alpha_im\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right) d_is+E[\xi_{k_{h}}]F(k_h,i_{h+1})+c_h\\ & +E[\xi_{k_{h+1}}]\min\left\{F(k_{h+1},i_{h+1}),b\right\}\\ & =\sum_{i=1}^{k_{h+1}-1}\alpha_im\left(r_{i0} +r_{i1}u_i+r_{i2}u_i^2\right)d_is+c_{h+1}\\ & +E[\xi_{k_{h+1}}]\min\left\{F(k_{h+1},i_{h+2}),b\right\}, \end{aligned} $$
(18)

where c h+1 = c h and α i  = E[\(\xi _{{k_{h} }}\)] for all k h  ≤ i ≤ k h+1 − 1.

Case 2. F(k h , i h ) > b. It is easy to prove that the amount of fuel purchased at the k h th station is b, and the amount of fuel left in the tank is \(L _{{k_{h+1} }}\) = b − F(k h ,k h+1) when the train arrives at station k h+1, then we have

$$ \begin{aligned} &\sum_{j=1}^{h}E[\xi_{k_{j}}]w_{k_{j}}+E[\xi_{k_{h+1}}]w_{k_{h+1}}\\ &\!\!\!\!\!\!=\sum_{i=1}^{k_{h}-1}\alpha_im\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is\\ & +E[\xi_{k_{h}}]b+c_h+E[\xi_{k_{h+1}}]\left(\min\left\{F(k_{h+1},i_{h+1}),b\right\}-L_{k_{h+1}}\right)\\ &\!\!\!\!\!\!=\sum_{i=1}^{k_{h+1}-1}\alpha_im\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is+c_{h+1}\\ &+E[\xi_{k_{h+1}}]\min\left\{F(k_{h+1},i_{h+1}),b\right\}, \end{aligned} $$
(19)

where c h+1 = c h  + (E[\(\xi _{{k_{h} }}\)] − E[\(\xi _{{k_{h+1} }}\)]) × b and α i  = E[\(\xi _{{k_{h+1} }}\)] for all k h  ≤ i ≤ k h+1 − 1.

Hence, formulation (14) holds for all 2 ≤ l ≤ L. In particular, take l = L, since i L  = n + 1 and F(k L , i L ) ≤ b, it is easy to prove that (13) holds. The proof is complete.

For each given scheduling strategy \((u_1,u_2,\ldots,u_n), \) if the average fuel prices at fueling stations are decreasing, i.e., \(E[\xi_1]>E[\xi_2]>\cdots>E[\xi_n], \) then it is easy to prove that the optimal amount of fuel purchased at the ith station is w i  = m(r i0 + r i1 u i  + r i2 u 2 i )d i s, and the minimum fueling cost is

$$ \sum_{i=1}^nE[\xi_i]w_i=\sum_{i=1}^nE[\xi_i]m \left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is. $$
(20)

According to Theorem 3.1, we may decompose the FCM model into a scheduling strategy model (FCM-I)

$$ \left\{\begin{array}{l} \min \displaystyle\sum\limits_{i=1}^{n}\alpha_im\left(r_{i0}+ r_{i1}u_i+r_{i2}u_i^2\right)d_is\\ s.t. \displaystyle\sum\limits_{i=1}^nd_i/u_i=T\\ u_i^{\max}\geq u_i>0,\quad \forall i=1,2,\ldots,n\\ \end{array}\right. $$
(21)

where \(\alpha_1,\alpha_2,\ldots,\alpha_n\) are determined by \((u_1,u_2,\ldots,u_n), \) and a linear fueling strategy model (FCM-II)

$$ \left\{\begin{array}{l} \min \displaystyle\sum\limits_{i=1}^{n}E[\xi_i]w_i\\ s.t. \displaystyle\sum\limits_{i=1}^{k-1}\left(w_i-m\left(r_{i0}+r_{i1}u_i +r_{i2}u_i^2\right)d_is\right)+w_k\leq b, \forall k=1,2,\ldots,n\\ \displaystyle\sum\limits_{i=1}^{k}\left(w_i-m \left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is\right)\geq 0, \forall k=1,2,\ldots,n\\ w_i\geq0, \forall i=1,2,\ldots,n. \end{array}\right. $$
(22)

For each given scheduling strategy \((u_1,u_2,\ldots,u_n), \) according to the analysis in above section, the optimal fueling strategy \((w_1,w_2,\ldots,w_n)\) and parameter \((\alpha_1,\alpha_2,\ldots,\alpha_n)\) may be solved by the following two algorithms.

Algorithm 31

A numerical algorithm for solving \((w_1,w_2,\ldots,w_n)\) with a given scheduling strategy \((u_1,u_2,\ldots,u_n)\) is summarized as follows:

  • Step 1. Set i 0 = 1, L = 0, and w i  = 0 for all \(i=1,2,\ldots,n\).

  • Step 2. Define \(i_1=\min\{i_0<i\leq n+1\mid E[\xi_{i}]<E[\xi_{i_0}]\}\) where E[ξ n+1] = 0.

  • Step 3. If F(i 0, i 1) ≤ L, set L = L − F(i 0,i 1) and i 0 = i 1.

  • Step 4. If L < F(i 0, i 1) ≤ b, set w i_0 = F(i 0, i 1) − L, L = 0 and i 0 = i 1.

  • Step 5. If F(i 0, i 1) > b, set w i_0 = b − L, L = b − F(i 0, i 0 + 1) and i 0 = i 0 + 1.

  • Step 6. If i 0 = n + 1, return \((w_1,w_2,\ldots,w_n)\). Otherwise, goto step 2.

Algorithm 32

A numerical algorithm for solving \((\alpha_1,\alpha_2,\ldots,\alpha_n)\) with given scheduling strategy \((u_1,u_2,\ldots,u_n)\) and fueling strategy \((w_1,w_2,\ldots,w_n)\) is described as follows:

  • Step 1. Set i 0 = 1 and α i  = 0 for all \(i=1,2,\ldots,n\).

  • Step 2. Define \(i_1=\min\{i_0<i\leq n+1\mid E[\xi_{i}]<E[\xi_{i_0}]\}\) where E[ξ n+1] = 0.

  • Step 3. If F(i 0, i 1) ≤ b, set α i  = E[ξ i_0] for all i 0 ≤ i ≤ i 1 − 1 and i 0 = i 1.

  • Step 4. If F(i 0, i 1) > b, define \(k=\min\{i_0<k\leq n+1\mid w_k>0\}\). Set α i  = E[ξ k ] for all i 0 ≤ i ≤ k − 1 and i 0 = k.

  • Step 5. If i 0 = n + 1, return \((\alpha_1,\alpha_2,\ldots,\alpha_n)\). Otherwise, goto step 2.

In the following, we shall design an iterative algorithm for solving the FCM-I model based on the Karush–Kuhn–Tucker conditions. Let \((\alpha_1,\alpha_2,\ldots,\alpha_n)\) be a given parameter vector. For each positive real number S and index subset \(I\subseteq\{1,2,\ldots,n\}, \) we denote FCM-I(S, I) as the following nonlinear programming model

$$ \left\{\begin{array}{ll} \min \displaystyle\sum\limits_{i\in I}\alpha_im\left(r_{i0}+r_{i1}u_i+r_{i2}u_i^2\right)d_is\\ s.t. \displaystyle\sum\limits_{i\in I}d_i/u_i=S\\ \quad u_i>0, \forall i\in I. \end{array}\right. $$
(23)

First, let us consider how to solve the FCM-I(S,I) model. Since it is a convex programming, according to the Karush–Kuhn–Tucker conditions, \((u_1,u_2,\ldots,u_n)\) is an optimal solution if and only if there is a real number λ such that

$$ \left\{\begin{array}{l} \alpha_im\left(r_{i1}+2r_{i2}d_iu_i\right)s-\lambda d_i/u_i^2=0,\quad \forall i\in I\\ \displaystyle\sum_{i\in I}d_i/u_i-S=0. \end{array}\right. $$
(24)

For each 1 ≤ i ≤ n, applying Kaerdannuo formula to the first equation of (24), the optimal velocity u i is determined by parameter λ as

$$ \begin{aligned} u_i =\sqrt[3]{\lambda/4r_{i2}\alpha_ims\!-\!\left(r_{i1}/6r_{i2}\right)^3\! +\!\sqrt{\left(\lambda/4r_{i2}\alpha_ims\!-\!2\left(r_{i1}/6r_{i2}\right)^3\right) \lambda/4r_{i2}\alpha_ims}}\\ &\!+\sqrt[3]{\lambda/4r_{i2}\alpha_ims\!-\!\left(r_{i1}/6r_{i2}\right)^3\! -\!\sqrt{\left(\lambda/4r_{i2}\alpha_ims\!-\!2\left(r_{i1}/6r_{i2}\right)^3\right) \lambda/4r_{i2}\alpha_ims}}\\ &-r_{i1}/6r_{i2}.\\ \end{aligned} $$
(25)

On the other hand, according to the second equation of (24), it is easy to prove that parameter λ is determined by \((u_1,u_2,\ldots,u_n)\) via the following formulation

$$ \lambda=\sum_{i\in I}\alpha_im\left(r_{i1}u_i+2r_{i2}u_i^2\right)d_is/S. $$
(26)

Then we may solve the model by finding a number λ and vector \((u_1,u_2,\ldots,u_n)\) satisfying conditions (25) and (26).

Now, we consider the problem on how to solve the FCM-I model. First, let S 1 be the predetermined traversing time T, and let I 1 be the universal set \(\{1,2,\ldots,n\}\). We solve the optimal solution \((u_1,u_2,\ldots,u_n)\) of the FCM-I(S1,I1) model. If it satisfies the maximal allowable speed constraint, then it is the optimal solution of the FCM-I model. Otherwise, we denote \(I'=\left\{i\in I_1\mid u_i>u_i^{\max}\right\}\). Since Li et al. (2011) proved that the optimal solution of the FCM-I model should satisfy u i  = u max i for all \(i\in I',\) we modify u i  = u max i for all \(i\in I'\). Now, let us consider the second modification. Set

$$ I_2=I_1\setminus I^{\prime},S_2=S_1-\sum_{i\in I^{\prime}}d_i/u_i^{\max}, $$
(27)

then we get a new optimization model FCM-I(I2, S2). If its optimal solution \(\{u_i,i\in I_2\}\) satisfies the maximal allowable speed constraint, then \((u_1,u_2,\ldots, u_n)\) is the optimal solution of the FCM-I model. Otherwise, we modify the optimal solution, and goto the next loop. Since the optimal solution consists of n components, the FCM-I model may be solved by at most n loops.

Algorithm 33

An iterative algorithm for solving the FCM-I model is described as follows:

  • Step 1. Set \(\varepsilon=0.001, I=\{1,2,\ldots,n\}\) and S = T.

  • Step 2. Initialize a feasible solution \(v=\{v_i,i\in I\}\) of the FCM-I(I,S) model, and calculate the parameter λ0 by (26);

  • Step 3. Calculate a new feasible solution \(\{u_i,i\in I\}\) with λ0 by (25);

  • Step 4. Corresponding to feasible solution u, update parameter λ by (26);

  • Step 5. If \(|\lambda_0-\lambda|>\varepsilon,\) set λ0 = λ, and goto step 3.

  • Step 6. Define \(I'=\left\{i\in I\mid u_i>u_i^{\max}\right\}\). If I′ ≠ ∅, set u i  = u max i for all \(i\in I'\). Reset \(I=I\setminus I^{\prime}, S=S-\sum_{i\in I^{\prime}}d_i/u_i^{\max},\) and goto step 2.

  • Step 7. Return \((u_1,u_2,\ldots,u_n)\) as the optimal solution of the FCM-I model.

By integrating Algorithms 4.1, 4.2, and 4.3, a numerical algorithm for solving the FCM model is designed in the following. A flow chart for the algorithm is illustrated in Fig. 2.

Fig. 2
figure 2

Flow chart for the numerical algorithm, where \(c=\left(E[\xi_1],E[\xi_2],\ldots,E[\xi_n]\right)\)

Full size image

Algorithm 34

An algorithm for the FCM model is described as follows:

  • Step 1. Initialize some parameters, including resistance coefficients r i0, r i1, r i2, tank capacity b, train’s weight m, length of link \((d_1,d_2,\ldots,d_n), \) fuel price \((\xi_1,\xi_2,\ldots,\xi_n), \) and maximal allowable speed \((u_1^{\max},u_2^{\max},\ldots,u_n^{\max})\).

  • Step 2. Set \((E[\xi_1],E[\xi_2],\ldots,E[\xi_n])\) as the initialized parameter vector α0.

  • Step 3. Calculate the optimal solution u of the FCM-I model with parameter α0 by using Algorithm 4.3.

  • Step 4. Calculate a new parameter vector α by using Algorithm 4.2.

  • Step 5. If α ≠ α0, then set α0 = α and goto step 3.

  • Step 6. If α = α0, calculate the optimal solution w of the FCM-II model by Algorithm 4.1, and return (w, u) as the optimal solution of the FCM model.

4 Numerical example

In order to show the efficiency of the FCM model on saving fueling cost, we illustrate two numerical examples in this section, which consider the optimal scheduling and fueling strategy for a passenger train and a freight train, respectively. In these examples, some basic parameters are listed as follows: resistance coefficient due to grade and rolling resistances r i0 = 16.6 for all i, resistance coefficient due to rail friction r i1 = 0.366 for all i, resistance coefficient due to air friction r i2 = 0.0261 for all i, and quantity of fuel consumption for providing per joule of power s = 2.89 × 10−5 L.

Example 1

In this example, we consider the optimal fueling and scheduling strategy for a passenger train. Along the trip, the train will stop for fueling operations at seven stations. Table 1 shows the basic information for the train, where the lengths of links and the initialized speeds consults train T27 in Chinese railway system, and the fuel prices on different stations consults the website http://oil.usd-cny.com/, which lists the daily fuel prices for the main cities in China. If the train runs with the initialized speed, it is easy to calculate that the traversing time for the train is 43.93h, which is selected as the traversing time parameter in the FCM model. In addition, the weight of train is assumed to be m = 2 × 106 kg, and the tank capacity is assumed to be b = 2 × 107 L.

Table 1 Database for numerical example 5.1
Full size table

Now, let us calculate the optimal fueling strategy and scheduling strategy for the train. By performing Algorithm 4.4 on the database, it is easy to calculate that the optimal scheduling strategy is

$$ u_1=94.41, u_2=96.84, u_3=96.95, $$
$$ u_4=97.22, u_5=93.94, u_6=85.00, u_7=85.00, $$

the optimal fueling strategy is

$$ w_1=0.45\times10^7, w_2=1.58\times10^7, w_3=1.16\times10^7, w_4=2.00\times10^7, $$

and the corresponding minimum fueling cost is 4.08 × 107 RMB. If we use the initialized speed shown in Table 1, a run of Algorithm 4.1 shows that the minimum fueling cost is 4.27 × 107 RMB. It can be readily proved that the FCM model reduces the fueling cost by (4.27–4.08)/4.27 × 100 % = 4.45 %.

Example 2

In this example, we consider the optimal fueling and scheduling strategy for a freight train in Chinese railway system, which runs from Datong station to Qinhuangdao station. Along its trip, there are thirty-two stations where the train may stop for fueling. Table 2 shows the distance between each station and Qinhuangdao station. According to the data on website http://oil.usd-cny.com/, the fuzzy fuel prices on different fueling stations are also given in this table. It follows from Table 2 that the total length for the trip is 653 km. If the average speed for the train is 80km/h, then the traversing time is 8.16 h, which is selected as the traversing time parameter in the FCM model. In addition, different links are assumed to have a common maximal allowable speed u max = 100 km/h, the weight of train is assumed to be m = 2 × 107 kg, and the tank capacity is assumed to be b = 8 × 106 L.

Table 2 Database for numerical example 5.2
Full size table

In order to solve the optimal scheduling strategy and fueling strategy for the train, we perform Algorithm 4.4 on the database. The computational results are summarized in Table 3. For each station, the scheduling strategy denotes the speed of the train runs from this station to the next station, and the fueling strategy denotes the amount of fuel purchased at this station. It is easy to prove that the minimum fueling cost is 5.00 × 108 RMB. If the train runs uniformly with speed 80 km/h, the minimum fueling cost is 5.32 × 108 RMB, which implies that the FCM model reduces the fueling cost by (5.32–5.00)/5.32 × 100 % = 6.02 %.

Table 3 Optimal solution for numerical example 5.2
Full size table

5 Conclusions

In this paper, we study the train fueling cost minimization problem, in which the fuzziness of fuel prices is first considered. First, we propose a fuzzy fueling cost minimization model by minimizing the expected value of the fuzzy fueling cost. In order to solve the model, we decompose it into a scheduling strategy model and a fueling strategy model. Then we design an iterative algorithm to solve the scheduling strategy model based on the Karush–Kuhn–Tucker conditions, and design a numerical algorithm to solve the fuzzy fueling cost minimization model. Finally, we prove that our model may reduce the fueling cost significantly in terms of numerical examples.