1 Introduction

This paper presents comparisons of simulations using the one-dimensional turbulence (ODT) model to experimental data measured in an ethylene wall fire. Wall fires are important in their own right, but the principal motivation of this study arose from flame propagation in wildland fires, especially in fine fuels, such as occur in grass fires [1].

Understanding the mechanism of flame propagation in wildland fires is important for developing accurate fire models to predict fire behavior. In general, radiation has been noted as the principal heat transfer mechanism for flame front propagation through an unburnt fuel bed [2]. However, several studies have suggested that radiative heat transfer is not sufficient to heat wildland fuels to ignition, but that additional heat transfer methods are required [3–5]. Recent experiments and observations indicate the importance of convective heating by direct flame contact [6]. For instance, Cohen and Finney [7] demonstrated preferential ignition of large diameter fuels over fine fuels exposed to the same radiative source. Indeed, fine fuels failed to ignite or significantly char. It was argued that convection induced by buoyant acceleration at the heat source resulted in higher convective heat losses relative to radiative input for the finer fuels than the larger diameter fuels. The implication is that fine fuels in some flame propagation environments may require direct flame contact through convective heating to ignite.

Flame propagation by convective heating of unburnt fuel through direct flame contact is a complex process influenced by many factors. The Reynolds numbers in fires are large enough that the flows are nearly always turbulent, with the flow driven by buoyant acceleration in the flame zone and wind effects [3]. Turbulent flames involve (by definition) a wide range of time and length scales, ranging from sub-millimeter flames to scales as large as the fire itself—tens of meters in forest crown fires. Individual flames that occur at turbulent dissipation scales involve many differentially-diffusing species whose identity and chemical reaction mechanisms may be unknown. Soot formation and radiative transport further complicate the process. The propagation of the flame front is unsteady, with intermittent turbulent flames in fuel beds with complex spatial distributions, often involving heterogeneous fuels with unknown physical properties. Heat release during combustion results in gas expansion primarily through reduced density as temperature increases. In a nominally vertical fire in a fuel bed with fuel released throughout the height of the fuel bed, the flame/air interface is inclined towards the ambient air due to flame expansion via heat release, increasing fuel with increasing height, and turbulent mixing. Excursions of flame into unburnt fuel, enhanced by this inclined flame front, have been shown to result directly in fuel ignition and subsequent flame propagation [8].

This complexity of fire phenomena and the need for predictive models that can perform under broad conditions has motivated a trend towards physics-based models that capture the detailed interaction between turbulent flow, heat transfer, and chemistry. In “The Further History of Fire Science,” Emmons [9] outlined the complexity of fire systems and the technological improvements needed, and predicted a transition to physics-based models using high performance computing. Morvan [10] has reviewed physical mechanisms and length scales in wildland fires, discussing regimes and relevant length scales of surface fire propagation. He noted the need to “introduce more physics in a new generation of fire models,” and discussed capabilities of several fully physical fire models such WFDS [11]. In discussing fire eruption in wildland fires, Viegas [12] concluded that “more modelling [has] to be conducted in order to better understand the set of parameters driving eruptive fire behaviour” and that we should “include more fire science in the study of extreme wildfires.”

This paper is part of a larger study of the fundamentals of fire propagation in fuel beds. To capture flame propagation by direct flame contact, the turbulent flame itself must be resolved. The only simulation approach that can resolve flames in turbulent flows is direct numerical simulation (DNS), which is prohibitively expensive to run at fire scales. RANS and LES approaches can capture the fire scales, but cannot resolve individual flames. The ODT model is applied in this study because it is able to resolve all of the length and time scales (from the fire scale to individual flamelets), but in a single dimension so that the model is computationally efficient. The ODT model solves reaction-diffusion equations for mass, momentum, species, and energy, on a notional line-of-sight through a flow. Turbulent advection is modeled in ODT using a stochastic domain remapping process that simulates the effect of eddies. The model is described further below, but the key point is that it is able to resolve individual flames with realistic turbulence statistics. The ODT model has been widely applied to many reacting and non-reacting flows including homogeneous turbulence [13], mixing layers [14], channel flow [15], Reyleigh-Benard convection [16], and double diffusive interfaces [17] to name a few. Dreeben and Kerstein [18] modeled buoyant heat transfer in a vertical slot. Several researchers have studied turbulent jet flames with ODT including effects of flame extinction and reignition using several fuels [19–23]. Of direct relevance to the present study, Ricks et al. [24] modeled soot and enthalpy evolution in buoyant pool fires. Shihn and DesJardin [25] used ODT to simulate a buoyant, isothermally heated wall. These authors also studied near-wall behavior of vertical wall fires with acetylene and propane fuels to demonstrate ODT as a possible sub-grid closure model for LES [26]. Other studies using ODT as an LES sub-grid model include [27–30]. Because ODT is one-dimensional, it is best suited to temporally-evolving one-dimensional flows, or to two-dimensional statistically steady flows. That is, flows that can be approximated by boundary layer assumptions. The wall fire may be approximated as a boundary-layer flow and is amenable to study using ODT. Ignoring the transverse boundaries, the wall fire is statistically two-dimensional with property variations in the vertical and wall-normal directions. The vertical velocity component is dominant and gradients in properties such as velocity and temperature are highest in the wall-normal direction. The ODT line is oriented in this direction, and advanced vertically, consistent with a boundary-layer assumption, as discussed further below.

The complexity of fires necessitates simplified fuels and configurations amenable to experimental investigation and model validation. In this paper a wall fire is studied because it adds fuel to the system with height, which approximates the behavior of a buoyantly-driven flame front inclined by gas expansion. This stationary configuration eases setup and data collection. While many studies have been done on wall fires, most of them focus on the burning rates along the wall rather than the turbulent, intermittent statistics away from the wall. Ahmad and Faeth [31] studied burning rates in wall fires, where the burning surface was simulated by a fuel soaked wick. Markstein and De Ris [32] measured radiative emission from porous metal wall burners using several fuels. Quintiere [33] developed a framework for modelling flame spread rates along a vertical wall using a zone method. Delichatsios [34] studied pyrolysis/burning rates and flame heights of wall fires using a two-layer integral model. Joulain [35] studied flame propagation, burning rates, and mean temperatures and velocities present in vertical wall fires. One study by Wang et al. [36] focused on the turbulent, intermittent statistics away from the wall. This study used LES to investigate the transport characteristics and flame structures of vertical wall fires. As LES is a filtered model, the small scales were not resolved and a sub-grid model was used in this approach.

Recent experiments were performed by Finney et al. [6] of a vertical wall flame with ethylene fed uniformly through a porous ceramic burner to study properties at the intermittent flame/air interface. Instantaneous temperature measurements were made at four vertical stations and six wall-normal positions for several fuel flow rates.

This work simulates the experimental configuration using the ODT model. We present results of the model including velocity, temperature, and soot profiles. Mean and fluctuating distributions are also given, along with sensitivity to model variations. Model results are compared to experimental data for mean and fluctuating temperature profiles.

This work represents an extension of the ODT model in terms of the complexity of the configuration considered and is the first application of the formal spatial implementation of ODT [37] to reacting wall-bounded flows. (Application to a nonreacting isothermal wall was performed in [38].) Beyond this study, the successful application of ODT to buoyantly-driven, wall-bounded flows is important and would allow, e.g., detailed wall heat transfer studies.

2 Experimental Configuration

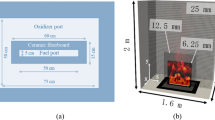
The ethylene wall fire experiments are described in [6]. A summary is provided here. The experimental wall burner consists of a a Cordierite\(^\mathrm{\mathrm{TM}}\) (Sud Chemie Hi-Tech Ceramics Corp., Alfred, New York) porous ceramic foam 2.5 cm thick with a porosity of 17.7 pores/cm [6]. The burner dimensions are 1.83 m tall, and 0.61 m wide. A fiberglass cloth borders the burner assembly in the plane of the burner. Ethylene flow rates range from 115 to 470 standard L/min. Flow rates of 235, 390 and 470 L/min are studied here, with corresponding heat release rates of 217, 361, and 435 kW, respectively. Ethylene was chosen because its molecular weight is close to that of air, so that uneven flow distribution due to hydrostatic pressure was avoided. Ethylene combustion also conserves moles so that density differences are due to temperature effects.

Figure 1
figure 1

Schematic of the ethylene wall fire configuration

Full size image

Figure 1 shows a schematic of the configuration. In the simulations, the ODT domain is oriented horizontally and is perpendicular to the wall. The solution is evolved by marching the ODT domain upwards, described further below. As the line is marched upwards, fuel is added to the domain, combustion gases expansion, and turbulent eddies (modeled through stochastic triplet maps) cause wall-normal mixing. Buoyant acceleration drives the vertical velocity, which in turn drives the turbulence.

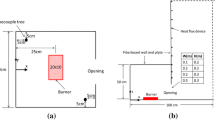
Temperature measurements were made at four heights up the wall. At each height, a set of six 0.00508 cm diameter type-K thermocouples were spaced horizontally at varying distances from the vertical wall. The temperature measurements were made at heights of 0.35, 0.78, 1.23, and 1.69 m. At the first height, the six thermocouples were placed at distances of 3, 5, 7, 9, 11, and 13 cm from the wall. At the other three heights the six thermocouples at each height were placed at 4, 6, 8, 10, 12, and 14 cm from the wall. The measured response time of the thermocouples in 5 m/s moving air was approximately 50 ms. The thermocouples were connected to a National Instruments Inc. SCXI 1102B module in the data acquisition system with a sensor bandwidth of approximately 3 Hz.

3 Model Formulation

A brief overview of ODT is presented here. A detailed description of the ODT formulation and implementation used here is available in [38] with additional details in [14, 37].

3.1 ODT Model

ODT solves two concurrent processes: (1) advancement of one-dimensional reaction-diffusion equations for mass, momentum, energy, and chemical species; and (2) turbulent advection modeled through stochastic eddy events consisting of a domain remapping process. There are two formulations of ODT: temporal and spatial. In temporal ODT, the one-dimensional domain is evolved in time. In spatial ODT, the domain is advanced in a spatial coordinate perpendicular to the line, and a steady state solution is assumed. In both cases the system is parabolic. Here, the spatial formulation of ODT is used, but the presentation below is given for the temporal formulation, then adapted to the spatial formulation.

Turbulent advection is modeled stochastically with domain remapping processes, called eddy events, that are implemented through triplet maps. A turbulent eddy is modeled as having a size \(l\), location \(x_0\), and timescale \(\tau \). A given eddy event is implemented using a triplet map by replacing original property profiles in the eddy region with three copies of the profiles, each spatially compressed by a factor of three, with the center copy spatially mirrored. This retains key turbulent processes of increasing gradients and surface area, while all properties are conserved and profiles are continuous. Eddy events are selected using a thinning process [39] based on the rejection method [40]. Candidate eddies are drawn from a presumed eddy size \(l\) and location \(x_0\) distribution \(P(x_0,l)\) and accepted with probability

$$\begin{aligned} P_a = \frac{\Delta t_s}{\tau P(x_0,l)l^2}. \end{aligned}$$
(1)

The specification of \(P(x_0,l)\) affects the efficiency of the model, but not the accuracy. Candidate eddies are sampled in time as a Poisson processes with rate \(1/\Delta t_s\). In Eq. (1), \(\tau \) is the eddy timescale, computed as

$$\begin{aligned} \frac{1}{\tau } = C\left[ \frac{2}{\rho _0 l^3}(E_{{kin}}-ZE_{{vp}}+E_{DL})\right] ^{1/2}, \end{aligned}$$
(2)

which is based on the one-dimensional scaling \(E\sim \frac{1}{2}\rho _0 l^3/\tau ^2\), where \(\rho _0=\frac{1}{l^3}\int \rho K(x)^2dx\) and \(K(x)\) is a kernel function that is the difference in final and initial locations defined by the triplet map [14, 37]. The \(E_{{kin}}\) term is a measure of the kinetic energy within the eddy interval and is specified as in [37]. The \(E_{\text{ vp }}\) term is a viscous penalty introduced to suppress small eddies subject to strong viscous damping, modeled as \(E_{vp}=\frac{1}{2}\bar{\mu }^2/\bar{\rho }l\), where \(\bar{\mu }\) and \(\bar{\rho }\) are the average viscosity and density in the eddy region, respectively. \(C\) and \(Z\) in Eq. (2) are the adjustable eddy rate and viscous penalty parameters, respectively. \(E_{DL}\) is a new term that models the Darrieus–Landau (DL) combustion instability, described below.

In the spatial formulation used in this paper, the sample time \(\Delta t_s\) is replaced by a spatial increment \(\Delta y_s\), and \(\tau \) is converted to an eddy length scale by multiplying by the Favre-mean velocity \(\tilde{V}\) in the eddy region. In addition, kernel operations, as in the calculation of \(\rho _0\) above, and \(E_{kin}\) include the local velocity in the integral (\(\rho v(x)\) instead of \(\rho \)) since mass flux, not mass is the key quantity in the spatial formulation [37], discussed further below. A large eddy suppression mechanism is used to prevent unphysically large eddies from occurring. Several models are possible; here, we use the criteria \(y>\beta l\), where \(\beta \) an adjustable parameter.

As noted above, \(Z\), \(C\), and \(\beta \) are adjustable ODT parameters that introduce a small degree of empiricism connecting the model representation of turbulent advection to the reality of the flow. \(Z\) is the viscous penalty parameter that scales the suppression of small eddies that are subject to strong viscous damping. Eddies are suppressed if \(ZE_{vp}>E_{kin}+E_{DL}\). \(C\) scales the eddy rate \(1/\tau \) and hence the acceptance probability of sampled eddies. This can be thought of as scaling the “time” of a flow insofar as the flow evolution is determined by the rate of turbulent mixing. As noted in [38], \(C\) “is roughly analogous to the coefficient of an eddy viscosity formula.” The large eddy suppression parameter \(\beta \) limits the size of large eddies. There are other large eddy suppression mechanisms that have been applied such as the scale reduction and median methods [37]. The method used here, termed the elapsed time method (here extended to space), has been successful in simulating flows such as jets [19, 21, 23]. Larger values of \(\beta \) tend to result in less mixing due to a reduced large eddy size, but this can be partially offset by larger values of \(C\) (see [21]). The parameters are normally tuned for a given configuration using previously applied values as a starting point. Here, parameters were adjusted to match the mean and fluctuating temperature data. Baseline values are given below in Table 1, with further discussion in Sect. 4.2. These parameters are discussed at length in the cited literature.

Spatial ODT advances the horizontal (wall-normal) line up the wall instead of advancing in time. The flow is assumed steady, except for the stochastic eddy events, and is evolved in the downstream direction parabolically using the boundary layer assumption neglecting streamwise (vertical) diffusion of heat, mass, and momentum in comparison to wall-normal diffusion of these quantities. The ODT code used is described in [38]. The code is written in C++ and uses an adaptive mesh. The diffusive advancement uses a Lagrangian finite volume formulation in which cells expand or contract such that the total vertical mass flux in a given cell is constant: \(\rho v \Delta x=c\), which is the result of the continuity equation applied to the cells. Other transport equations for species mass fractions, vertical momentum, and enthalpy in a given grid cell, are given, respectively, by

$$\begin{aligned} \frac{d Y_k}{d y}&= -\frac{j_{k,\,e} - j_{k,\,w}}{\rho v \Delta x} + \frac{\omega _k}{\rho v}, \end{aligned}$$
(3)
$$\begin{aligned} \frac{d v}{d y}&= -\frac{\tau _{e} - \tau _{w}}{\rho v \Delta x} + \frac{(\rho _{\infty }-\rho )g}{\rho v},\end{aligned}$$
(4)
$$\begin{aligned} \frac{d h}{d y}&= -\frac{q_{e} - q_{w}}{\rho v \Delta x} + \frac{S_{rad}}{\rho v}. \end{aligned}$$
(5)

Here, \(y\) is the vertical direction and \(x\) is wall-normal (horizontal). Subscripts \(e\) and \(w\) denote cell face values. The momentum flux is modeled as \(\tau =-\mu (dv/dx)\), and the species mass flux is modeled as \(j_k=-(\rho Y_kD_k/X_k)dX_k/dx\), where \(X_k\) is a species mole fraction and \(D_k\) is the binary diffusion coefficient. Heat flux is given by \(q=-\lambda dT/dy + \sum _kh_kj_k\), where \(\lambda \) is the thermal conductivity, and \(h_k\) is the enthalpy of species \(k\). The division by \(\rho v\Delta x\) in the above equations follows from \(\rho v\Delta x=c\). This relation is used to specify how changes in \(v\) and \(\rho \) affect the grid size \(\Delta x\). In the spatial advancement of the ODT line, grid cells with smaller velocities have an implied larger residence time (\(\Delta t = \Delta y/v\)). Ideal gases are assumed, and temperature is related to enthalpy through the auxiliary relation \(h=h(T,Y_i)\) using composition and temperature dependent heat capacities. Cantera is used to determine all thermochemical and transport properties [41]. The source term \(\omega _k\) in the mass conservation equation is the species reaction rate, and \(S_{rad}\) is the radiative source term in the energy equation.

The ODT code is solved using a first order explicit spatial advancement (a forward difference, appropriate for the parabolic advancement), with central difference approximations used for spatial derivatives appearing in flux terms (appropriate for diffusive fluxes). The advancement step \(\Delta y\) is small enough that no changes are apparent when using a second order trapezoidal spatial advancement. Mean chemical source terms (used in the explicit advancement) are computed with a high order implicit method using CVODE [42] with constant cell fluxes. This eliminates chemical stiffness and allows advancement at the diffusive CFL.

The adaptive mesh approach is applied by merging and splitting grid cells in a manner that conserves vertical fluxes of transported quantities: mass, momentum, thermal energy, and soot. Mesh adaption normally occurs after eddy events and diffusive advancement, but may occur during the diffusive advancement if the cells contract below the specified minimum size noted below. The grid is adapted based on a nominally uniform distribution of grid points along the arc length of the temperature, velocity, and soot profiles. The profiles are centered and scaled so that the domain and range vary on \([0,\, 1]\). A grid density factor (here chosen to be 60) is applied that gives nominally 60 points per unit normalized arc length. The profile that the arc length is based on (velocity, temperature, or soot) is chosen locally depending on which profile will yield the highest local grid refinement. The resulting grid is then constrained by a minimum cell size and refined so that the ratio of cell sizes between subsequent cells is greater than 0.4 and less than 2.5. Details can be found in [38]. A minimum grid cell size of 100 \(\upmu {\mathrm{{m}}}\) is used, which is sufficiently small that no significant differences in modeled versus experimental results are observed when doubling the number of grid cells. With the grid density factor of 60, the largest possible cell size is 16.67 mm (corresponding to a uniform profile) though most cells are much smaller due to property variations. (See Figure 3 below for an example of the profile resolution.)

3.2 Darrieus–Landau instability

Buoyant forces arise in a fluid for which there are density gradients and a body force. In the case of the Rayleigh–Taylor instability, density gradients are due to temperature gradients, such that heavy fluid is above light fluid, and the body force acting is gravity. Similarly, in a reactive flow, planar flames are intrinsically unstable due to acceleration of the variable-density fluid caused by thermal expansion across the burning front. This instability is termed the DL instability. Using the analogy to Rayleigh–Taylor instability allows an existing ODT representation of the Rayleigh–Taylor instability [43] to be modified in order to incorporate the DL instability mechanism into ODT. Namely, a formal analog of gravitational potential energy is introduced. In the present case, the constant acceleration of the gravity is replaced by the varying dilatation-induced acceleration on the line. The DL potential energy is then defined as

$$\begin{aligned} E_{DL} = \frac{8}{27}\int _{x_0}^{x_0+l}a(x)K(x)(\rho (x)-\bar{\rho })dx, \end{aligned}$$
(6)

where the factor 8/27 arises due to the variable density formulation and \(\bar{\rho }\) is a reference density defined as the average density over the interval \([x_0,\, x_0+l]\). This potential energy is nonzero only where the density varies, as it is the interaction of the dilatation-induced pressure gradient and the density gradient that is the cause of this instability mechanism. \(E_{DL}\) is not a potential energy in the same sense as in a buoyant flow, because it is not based on an external energy source. For this reason, it is only used to effect the probability of acceptance of an eddy. It is however, a formal analog to the treatment of energy in the buoyant flow, and therefore a tunable coefficient is not required.

It is interesting to note ODT allows explicit specification of physical effects such as the DL instability based on flow energetics, so that such effects may be studied directly. This is not as easily studied in Navier–Stokes-based solution approaches.

3.3 Chemical Mechanism

Arbitrarily complex combustion mechanisms can be incorporated within the ODT model formulation. The results presented are based on a global one-step mechanism that captures overall flame heat release [44]. Combustion timescales are fast compared to mixing timescales in the flames studied and finite rate kinetic effects are minor. The chemical mechanism reacts ethylene with oxygen to produce water and carbon dioxide and \(\text {C}_2\text {H}_4\), \(\text {O}_2\), \(\text {N}_2\), \(\text {CO}_2\), and \(\text {H}_2\text {O}\) are transported. Results are also presented comparing the one-step mechanism to a reduced mechanism consisting of 19 transported species, 10 quasi-steady species, and 167 reactions [45].

3.4 Soot Model

The soot model applied is that of Leung et al. [46], which is a semi-empirical four-step model that has been applied in many studies of turbulent, nonpremixed flames. The model assumes a monodispersed size distribution of soot particles and transports the first two moments of the soot size distribution: number density \(n\) and mass fraction \(Y_s\). Here, moments per mass are transported:

$$\begin{aligned} \frac{d M_k/\rho }{d y}&= -\frac{j_{k,\,e} - j_{k,\,w}}{\rho v \Delta x} + \frac{S_k}{\rho v}, \end{aligned}$$
(7)

where \(M_k\) is one of \(M_0=n\) or \(M_1=\rho Y_s\) The soot fluxes consist of thermophoretic transport and are given by \(j_k=-(0.554M_k \mu /\rho T)dT/dx\). Soot source terms are taken from [46]. The nucleation and growth species in the Leung model is acetylene. Because there is no acetylene in the one-step mechanism, acetylene was computed using a lookup table parameterized by mixture fraction and heat loss (defined as the local enthalpy defect from adiabatic normalized by the local adiabatic sensible enthalpy) with streams at 1 atm and 298.15 K. The table was generated with a steady laminar flamelet model [47] using the reduced mechanism noted above.

3.5 Radiation Model

The radiative source term in the enthalpy equation is computed using the Schuster–Schwarzchild approximation [48] (two-flux model) which is well suited to ODT in a boundary-layer-like flow. The outgoing (from the wall) heat flux \(q^+\) and incoming heat flux \(q^-\) are given by

$$\begin{aligned} \frac{dq^+}{dx}&= 2k\sigma T^4 - 2kq^+, \end{aligned}$$
(8)
$$\begin{aligned} \frac{dq^-}{dx}&= -2k\sigma T^4 + 2kq^-. \end{aligned}$$
(9)

The surrounding emissivity is unknown, but is set to 1.0. The wall emissivity is set to unity since the wall is covered with a black soot. The absorption coefficient is the sum of gas and soot components: \(k=k_g+k_s\). Temperature-dependent Planck mean absorption coefficients are taken for gas species \(\text {CO}_2\), CO, \(\text {CH}_4\), and \(\text {H}_2\text {O}\) [49], with \(k_g=\sum _ik_iP_i\). The soot absorption coefficient is taken as \(k_s=1863f_vT\).

3.6 Boundary and Initial Conditions

The initial velocity field is simply a uniform profile of magnitude 0.05 m/s, which is less than 1% of the peak mean velocity evolved. The flame is initialized by specifying an initial mixture fraction profile \(\xi (x)\), which is set using a hyperbolic tangent varying from nominally one at the wall to zero in the air. \(\xi =1\) is pure ethylene, and \(\xi =0\) is air. The transition width is 5 mm and its center is 5 mm from the wall. The initial composition profiles are taken as products of complete combustion, with temperature following from the known \(h(\xi )\) relation and the composition. Results were not found to be sensitive to the initial velocity and mixture fraction profiles. The ambient temperature and pressure are set to 298.15 K and 90,143 Pa, respectively. Ethylene enters through the wall at 298.15 K. Ethylene flow rates of 235, 390, and 470 standard L/min are studied, which correspond to wall flow velocities of 3.944, 6.545, and 7.888 mm/s, respectively. The wall is assumed adiabatic and diffusive species mass fluxes are assumed zero at the wall. The divergence of the soot flux is set to zero at the wall. All diffusive fluxes are assumed zero at the outlet boundary in the free stream.

4 Results

A number of simulations were performed to test the model and compare to available experimental data. The simulation cases are summarized in Table 1. Baseline parameters are specified and individual cases represent variations from the baseline.

Table 1 Summary of Simulation Cases and Parameters
Full size table

Simulations were performed at the Fulton Supercomputing Laboratory at Brigham Young University on 2.8 GHz Intel Nehalem processors. The average simulation time per realization for Case 2 was 0.93 h. Other cases are similar except Case 12, which is the reduced mechanism case and had a mean simulation time of 8.0 h.

Figure 2(a) shows contours of temperature for a single typical realization, and Figure 2(b) shows eddy sizes and locations for the same realization. The effect of triplet maps on the temperature contours, Figure 2(a), is shown, which cause intermittency in the flame. Buoyancy causes an upward acceleration of the flow, which draws in surrounding air. This is observed by the contraction of the flame, which is imposed by the conservation of upward mass flux. Buoyant acceleration tends to cause horizontal (wall-normal) contraction of the flow, and is opposed by flame dilatation from heat release which expands the flow. The occurrence of eddy events spreads the flame outward from the wall. While the mean temperature profiles will be concentrated relatively close to the wall, it is clear that intermittent flame zones are present farther from the wall.

Figure 2(b) shows the size and location of eddies. Each eddy is represented by a horizontal (wall-normal) line segment with two small vertical bars at the ends of the segment. These line segments give the wall-normal extent of the eddy. The wall-normal location of an eddy on the ODT line is the \(x\) location of the center of the line segment. The vertical position \(y\) of the line segment is the downstream location of the eddy occurrence (as the ODT line is marched vertically upwards during the evolution of the solution). A wide range of eddies occur as indicated in the figure. The eddies are concentrated towards the outer edges of the fire plume near the fire-ambient air interface. This is a region of high shear (which favors turbulence production, see Figure 5, below) and lower temperatures (which gives lower kinematic viscosity and higher Reynolds numbers, also favoring turbulence, see Figure 4, below). In this region, the velocity profile is lower than the peak value that occurs in the vicinity of the peak temperature (discussed below, see Figures 4 and 5). A lower velocity implies a higher residence time for fluid in this region and a higher probability of eddy occurrences. At any given height, the wall-normal region of the plume in which eddies occur is similar to the spread of the plume from the wall when considering the mean and RMS temperature, velocity, and soot fields (see Figure 4, discussed below). For instance, at \(y=1.69\,\text {m}\) , most of the eddy locations occur at or below \(x=0.25\,\text {m}\) , which is similar to the extent of the spread in the mean temperature and velocity fields, shown below. The DL model also affects the eddy locations, and is discussed in Sect. 4.4.

Figure 2
figure 2

Temperature contours (a) and eddy sizes and locations (b) for a single ODT realization for Case 2. Temperature contours have units of kelvin. In (a), leftward and rightward sweeps of temperature iso-contours reflect buoyancy-induced contraction and dilatation-induced expansion, respectively

Full size image
Figure 3
figure 3

Profiles temperature, velocity, and soot mass fraction for a single realization for Case 2 at \(y=1.8\,\text {m}\)

Full size image

Wall-normal scalar profiles for a given realization at a height of 1.8 m (at the top of the wall) are show in Figure 3. The symbols in the plots are positioned at the center of control volumes that comprise the computational grid. The \(x\) location of these symbols gives an indication of the grid spacing. The adaptive grid places many more points in regions of high fluctuations. For example, in the region \(0.05\le x\le 0.1\) there is a high degree of fluctuation in the soot profile resulting in many closely spaced points (199 grid points). The temperature and velocity fields have fewer fluctuations in the same region, but are captured on the same grid as the soot, and the grid points are (in some regions) too closely spaced to be individually distinguished. In contrast, in the region \(0.15\le x\le 0.2\), the profiles of temperature, velocity, and soot are fairly flat and there are only 44 grid points (with a relatively large span in the same region containing only 5 points). The temperature and velocity profiles are qualitatively similar with velocities higher in regions of higher temperature due to buoyant acceleration. The magnitude and wavelength of fluctuations is also similar for the velocity and temperature due to the similarity in the thermal and momentum diffusivities. In contrast, the soot mass fraction is highly intermittent with very fine fluctuations owing to the relatively low diffusivity of the soot particles. Resolving such fluctuations is a challenge in turbulent combustion modeling, as is accounting for the interactions between the soot, temperature, and radiative fields. The ability of ODT to capture fine scale fluctuations provides great opportunity to study and model such interactions.

Mean and root mean square (RMS) fluctuations of temperature, soot, and velocity are shown in Figure 4 as contour plots for Case 2. Means are computed using ensemble averages over all ODT realizations. Because each ODT realization is on a separate grid with variable number of grid cells, the results for each realization are mapped to a uniform grid of 500 points prior to averaging using cubic spline interpolation. Results were virtually the same when interpolating to a uniform grid of 10,000 points (corresponding to the finest possible grid in the ODT simulations). RMS profiles for e.g., temperature, are computed as as \(T_{RMS} = (\langle T^2\rangle -\langle T\rangle ^2)^{1/2}\), where \(\langle \cdot \rangle \) denotes an ensemble average; velocity and soot are computed similarly. In statistically-stationary flows, such as the present case, temporal and ensemble mean and RMS quantities are the same [50]. Wall-normal mean and RMS profiles are computed at 23 vertical locations, and the contours in Figure 4 were generated using these 23 profiles.

In Figure 4, consider the temperature along the wall-normal direction at a given height. The temperature profile is low at the wall, increases to a maximum, then decreases again towards the ambient air. The peak mean temperature along these profiles decreases with increasing height, and the wall-normal location of the peak along these profiles moves further from the wall with increasing height. At vertical locations above \(y=0.35\,\text {m}\), (below which the flow is developing from the initial condition, see below), the peak mean temperature varies from 1,643 K at \(y=0.35\,\text {m}\), \(x=0.012\,\text {m}\) to 1,565 K at \(y=1.8\,\text {m}\), \(x=0.02\,\text {m}\). Considering all 512 realizations for Case 2, the peak temperature along the 23 wall-normal profiles fluctuates but generally decreases with increasing height with a range of 2,017 K to 2,201 K. There is no correlation of the wall-normal location of the peak temperature along the 23 wall-normal profiles with increasing height, but the peak location is in the range of \(0.0064\le x\le 0.0893\) m. These peak temperatures are significantly less than the mean peak temperatures, and the range of distances from the wall that these peak temperatures occur overlaps, but it much wider than the range of wall-normal locations where the peaks in the mean temperature profiles occur.

Figure 4
figure 4

Temperature (a), (d), vertical velocity (b), (e), and soot mass fraction (c), (f) profiles. Top row means, (a), (b), and (c); bottom row RMS (d), (e), (f), for Case 2, (a) mean T, K , (b) mean \(\text {Y}_s\), (c) mean v, m/s (d) RMS T, K ,(e) RMS \(\text {Y}_s\) , (f) RMS v, m/s

Full size image

While the peak temperature remains relatively close to the wall, the temperature profile is observed to spread significantly. This is mirrored by the RMS profile, with higher values penetrating farther into the free stream. The peak RMS temperature \((\approx 400\text {K})\) occurs near the base of the wall as the turbulent eddies first wrinkle the initial flame.

The soot field does not appear to spread as much as the temperature and velocity fields. The mean soot field is concentrated near the wall on the fuel-rich side of the flame where the soot is formed. This is on the wall side of the peak mean temperature within 2 cm of the wall. At \(y=1.8\,\text {m}\) the peak mean soot mass fraction is 0.009, which corresponds to a soot volume fraction of 1.8 ppmv (assuming \(\rho _s=1850\,\text {kg/m}^3\)). While the soot is concentrated near the wall, lower levels of soot are observed further from the wall, out to 25 cm, where the average composition is fuel-lean. Soot is generally oxidized in fuel-lean environments, but soot may be present there if it is able to break through the flame without being oxidized. In the simulations, very little soot is observed at lean mixture fractions suggesting that the soot is largely oxidized as it is transported from fuel-rich regions to lean regions. Conversely, the presence of soot in environments that are fuel-lean on average does not imply that soot is present locally in fuel-lean environments since there are rich and lean fluctuations in composition about an overall lean value. In lean regions of the flame (on the ambient air side of the peak mean temperature) The soot RMS fluctuations are higher than the corresponding mean values and indicate the extent of spreading of the soot field. At \(y=1.8\,\text {m}\) the RMS soot mass fraction has a value of 0.0037 with a corresponding volume fraction of 0.4 ppmv.

Soot concentrations in flames and fires are difficult to measure and notoriously difficult to model accurately. For instance Mehta et al. [51] compared soot models in eight laminar premixed and nonpremixed flames in four separate burners with 36 combinations of detailed gas and soot models. They noted that “While no model gave soot volume fractions within a factor of five from experimental values for all eight flames, several models are within a factor of 10 for all eight flames.” The soot concentrations in our simulations of around 2 ppmv are reasonable and consistent with measurements in turbulent ethylene flames [52]. For reference, the laminar smoke point of ethylene is 5.9 ppmv [53].

The mean vertical velocity profile for Case 2 in Figure 4, shows a steady increase, both in magnitude and in width. The velocity increases due to buoyant acceleration. As the mean velocity increases, the RMS fluctuations also increase, with fluctuations around 10% of the mean values.

The fluctuations in the temperature, soot, and velocity fields all peak farther from the wall than the corresponding mean values. All things being equal, fluctuations in a quantity tend to be higher when the mean value of the quantity is higher. On the air side of the flame, the mean values of temperature, velocity, and soot decease with distance from the wall, suggesting a decrease in the RMS fluctuation. But fluctuations are driven by the turbulent mixing, which occurs further from the wall than the location of the peak values of temperature, soot, and velocity. This would tend to result in increased RMS fluctuations in the given quantities with distance from the wall (on the air side of the flame). At the top of the wall eddies are most strongly concentrated around \(x=0.25\,\text {m}\) , as indicated in Figure 2(b). As a result of these competing effects, the peak fluctuations in temperature, soot, and velocity each occur between the location of the peak mean value of the respective quantity and \(x=0.25\,\text {m}\) where mixing is high.

Figure 5
figure 5

Case 2 mean vertical velocity profiles for Case 2 at four heights (a), and the same velocity profiles scaled by the max mean values and the profile widths (evaluated as the full width at half maximum, fwhm) at each height (b)

Full size image

Figure 5(a) shows wall-normal profiles of the vertical velocity at four heights in the flame for Case 2. At any given height the mean velocity profile rises from zero at the wall, peaks a short distance away from the wall, and then decays again to the outer edge of the fire. At a given distance from the wall the mean velocity increases with height. At a height of 1.69 m (near the top of the wall), the mean velocity peaks at 6.26 m/s. Figure 5(b) shows the velocity profiles scaled by the peak mean values at each height, with the line position scaled by the profile width taken as the full width at half the maximum (fwhm). Above a height of 35 cm, these scaled profiles collapse to a single curve, indicating the self-similar behavior expected downstream in a boundary-layer flow. This similarity is consistent with previous wall fire reports [31, 34] and an isothermal wall previously studied with ODT and compared to experiments [25, 38]. The scaled profile predicted for 35 cm above the fire base does not quite follow the same behavior, indicating that the flow is likely still developing at this point in the fire.

The mean and RMS temperature profiles are compared to the available experimental data for Cases 1 to 3, with flow rates of 234, 390, and 470 L/min. The results for the mean temperatures are presented in Figure 6. The figure shows profiles at the four measurement heights of 35, 78, 123, and 169 cm, similar to the vertical velocity profiles shown above in Figure 5. The peak temperatures are similar for the three flow rates and at the three heights, though there is a small decrease in the peak temperature with increasing flow rate (due to enhanced mixing), and with height due to mixing and radiative losses. The location of the peak temperature moves away from the wall with increasing flow rate. Similarly, the temperature at any distance from the wall on the air side of the peak, in the measurement region, increases with increasing flow rate as the width of the flame brush increases. Comparison of the ODT simulation results with the experimental data shows good agreement in both magnitude and trends. At a given height and distance from the wall, the measured spread of the wall fire for different fuel flow rates is closely matched by the spread predicted by the ODT simulation. At 35 mm, where the flow is developing, the ODT simulations underpredict the spread as compared to the experimental results, while at the highest positions the fire plume spread is overpredicted by the ODT model in comparison with experimental results. Generally, the structure of the flame in terms of the velocity and temperature fields are similar to previous reports of wall fires [34, 35].

Figure 6
figure 6

Mean temperature profiles for three flow rates comparing the ODT simulations (lines) to the experiments (symbols). Four plots shown at increasing height

Full size image

These results are somewhat dependent on the ODT parameters, and slightly better experimental agreement is obtained using C = 5, as shown in Figure 9 below. Furthermore, while the agreement presented is fairly good, we emphasize the complexity of the physical phenomena and modeling uncertainties. These include the treatment of soot formation, radiative transport, chemistry modeling, boundary conditions, and modeling the turbulent advection. An ongoing research effort will investigate these processes, including model sensitivities and interactions. The resolution available in ODT can help address such issues, especially when coupled with experiments, and DNS and LES simulations as well.

Figure 7
figure 7

RMS temperature profiles for three flow rates comparing the ODT simulations (lines) to the experiments (symbols). Four plots shown at increasing height

Full size image

Figure 7 shows the RMS temperature fluctuations and is similar to Figure 6. The wall-normal location of the peak in the RMS increases with height and flow rate. Generally, the peak RMS temperature is higher for the higher flow rates. The trend in the ODT results matches the experiments, including the crossover of the low flow rate as the wall is approached. The wall-normal location of the peak is lower for the ODT than for the experiments, but they are similar at \(y=1.69\,\text {m}\) . As for the mean profiles, the spread is smaller at \(y=0.35\,\text {m}\) . At the upper locations, the shape of the profiles is very similar. The magnitude of the RMS temperatures predicted using the ODT simulation results is higher than the experiments. It is noted that experimental results were obtained using type-K thermocouples whose upper range of around 1,600 K is not high enough to accurately capture peak flame temperatures, (though type-K thermocouples may read higher values for short time periods). The time-dependent experimental data did not have any temperatures higher than 1,663 K, while the model predicted intermittent temperatures as high as 2,000 K. If the local time-varying experimental temperature measurements were subject to truncation of high instantaneous flame temperatures (down to around 1,600 K, say), the measured local RMS temperatures would be too low. The thermocouple response time and bandwidth may also affect the comparison, with longer response times and smaller bandwidth tending to reduce reported RMS fluctuations. This is discussed further in Sect. 4.5.

4.1 Heat Flux

While the motivation for the experiments in this study was an examination of the fluctuating turbulent flame brush at the flame-ambient air interface, wall heat flux is an important quantity in many fire applications. The resolution of ODT lends itself to modeling heat flux at the wall. Indeed, ODT has been applied as a near-wall LES closure model (for momentum transport) [15]. Figure 8 shows heat flux data from the results of Case 10 (but run for 512 realizations). Plot (a) shows mean and RMS conductive and net radiative heat flux to the wall as a function of height. The mean radiative wall heat flux increases with height as the flame brush becomes wider (in the wall normal direction) and the optical thickness increases. The mean heat flux to the wall increases from \(4.3\,\text {kW/m}^2\) at \(y=0.1\,\text {m}\) to \(14.4\,\text {kW/m}^2\) at \(y=1.8\,\text {m}\) . The conductive heat flux is similar in magnitude to the radiative flux, but increases less dramatically with distance up the wall; the conductive heat flux increases from \(9.9\,\text {kW/m}^2\) at \(y=0.1\,\text {m}\) to \(13.2\,\text {kW/m}^2\) at \(y=1.8\,\text {m}\) . The conductive heat flux increases with height as the velocity increase with height, resulting in higher shear and higher temperature gradients (which drive conduction) at the wall. The RMS profiles are also similar for the conductive and radiative fluxes, and both rise from zero at \(y=0.1\,\text {m}\) where there is little fluctuation as the flame is developing, to approximately \(7.7\,\text {kW/m}^2\) at \(y=1.8\,\text {m}\) .

Figure 8
figure 8

Wall heat flux for Case 10, plot (a), showing mean and RMS heat flux as a function of height for conduction and radiation. Plot (b) shows the mean wall-normal radiative heat flux profiles at four heights

Full size image

Figure 8(b) shows the mean wall-normal radiative heat flux profile at four vertical locations. Positive values are directed away from the wall. Near the wall, the heat flux towards the wall increases with height, consistent with plot (b); similarly, away from the wall, the heat flux also increases with height. Again, this is due to the increased volume of flame at higher locations where the flame brush is wider, and the increased optical thickness of the flame. The radiative heat flux away from the wall at \(x=0.25\,\text {m}\) and \(y=78\,\text {cm}\) is \(12\,\text {kW/m}^2\), consistent with values reported in [32]. The heat flux changes direction, passing through zero at an increasing wall-normal location with increasing height. This transition occurs in the vicinity of the peak mean temperature, but at slightly higher \(x\) locations. At heights of 35, 78, 128, and 169 cm, the net mean radiative heat flux passes through zero at wall-normal locations of 0.015, 0.023, 0.031, 0.035 m, respectively; and the wall-normal location of the peak mean temperature occurs at 0.01, 0.014, 0.016, and 0.018 m, respectively. The RMS mean radiative heat flux profiles (not shown) are relatively constant at around \(6\,\text {kW/m}^2\).

Figure 9
figure 9

Sensitivity to ODT parameters at \(y=1.69\,\text {m}\)

Full size image

4.2 Parameter Sensitivity

A sensitivity study was performed in which the three ODT parameters C, Z, and \(\beta \) were varied. These are Cases 2, 4 to 9 in Table 1. With Case 2 as a baseline, each parameter was increased and decreased by a factor of two. Figure 9 shows results comparing the mean temperature at \(y=1.69\,\text {m}\) . Increasing the eddy rate parameter C results in more eddies and a higher mixing rate. This causes higher temperatures and a wider flame brush with increasing C. Using C = 5 gives slightly better results than C = 10. There is very little sensitivity of the results to variation of the Z parameter. Variation of the \(\beta \) parameter shows a higher sensitivity than the other two parameters, with increasing \(\beta \) restricting eddy size and resulting in lower temperatures near the wall, higher temperatures for \(x\) between the peak and approximately 0.1 m, and lower temperatures for \(x\) greater than 0.1 m. These results suggest that the fire evolution is largely controlled by the large eddies.

As noted above, the parameter values chosen were adjusted to provide reasonable agreement between the simulated and experimental temperatures. Initial values were chosen based on previous simulations. Results are generally not sensitive to \(Z\), and a value of 400 is typical, though other values have been used. \(C\) is usually in the range of 3 to 10. Values of beta are usually in the range of 0.3 to 2.4. These flows include reacting temporal jets, homogeneous decaying turbulence, planar channel flow, nonreacting round jets, and an isothermally heated wall. The configuration affects the parameters chosen. In comparing to the literature, one should be careful to consider differences in the ODT model formulation.

While the results presented in Figure 9 show some quantitative sensitivity to the model parameters, the qualitative results are quite similar. The strength of ODT lies in its ability to resolved a full range of scales (in one dimension), which can provide useful information that is difficult or impossible to obtain using other modeling approaches. Ultimately, the most effective approach to investigating certain fire behavior may be the application of a combination of complementary tools, for instance, experiments, LES (which can capture three-dimensional flow structures, but requires subgrid modeling), and ODT, which models models turbulent mixing, but resolves the fine scales without requiring a subgrid model.

Figure 10
figure 10

Mean temperatures at \(y=1.69\,\text {m}\) for two chemical mechanisms, and for two boundary conditions

Full size image

4.3 Chemistry and Boundary Condition Sensitivity

The effect of the gas chemistry model is evaluated by comparing the mean temperature and soot profiles using the 1-step and reduced mechanisms. Figure 10 shows the mean temperature profiles at \(y=1.69\,\text {m}\) on the right hand side (RHS) axis, and mean soot mass fraction profiles at the same height on the left hand side (LHS) axis. The results are nearly identical for the two mechanisms, with small variation occurring near the wall on the rich side of the flame. The soot concentrations are nearly identical for the two mechanisms in this region of the flame. On the air side of the flame, the soot concentrations are higher with the reduced mechanism, and given the close agreement of the temperature, the differences in the soot concentration are attributed to differences in the acetylene and oxygen concentrations between the reduced model and the one step model with table lookup for acetylene.

The effect of using an isothermal (298 K) wall boundary condition was also tested and results are shown in Figure 10. Referring to the RHS axis in the figure, the simulated mean temperatures for the isothermal boundary condition are lower than those using the adiabatic boundary condition by an average of 83 K for \(0<x<0.25\,\text {m}\) . For the isothermal boundary condition, the soot concentration, shown on the LHS axis in the figure, is less than half of that for the adiabatic boundary condition. The temperature profiles are lower for the isothermal boundary condition due to heat losses to the cold wall. The lower temperature results in lower soot formation rates in the fuel-rich region near the wall, and hence a lower soot concentration.

Figure 11
figure 11

Mean temperatures at \(y=1.69\,\text {m}\) with and without the Darrieus–Landau model (a), and eddy map (b)

Full size image

4.4 Darrieus–Landau Model Sensitivity

The sensitivity of the results to the DL model is shown in Figure 11, which compares Cases 2 and 11 in Table 1 at \(y=1.69\,\text {m}\) . The figure shows the mean temperature at \(y=1.69\) with and without the DL model, (a), and the eddy maps, (b), (as in Figure 2). Without the DL model, the temperature profile is reduced near the wall and at the furthest measurement positions. The DL model acts on density differences in an accelerating flow. As the wall is stationary, the effects of dilatation are cumulative in accelerating the flow away from the wall. Conversely, as the flow is accelerated upwards due to buoyancy, fluid is drawn in from the surroundings which tends to counteract the positive dilatation of heat release. Figure 11(b) shows the eddy maps for the DL and no DL cases. Without the DL model there are fewer eddies, and the eddies occur at locations nearer the wall.

Because the ODT model slightly overpredicts the mean temperature, the reduction in the temperature without the DL model improves the agreement for some of the data points. This is largely dependent on the choice of ODT parameters. As noted in Sect. 4.2, using C = 5 gives somewhat better agreement, and in that case the reduction in temperature without the DL model would reduce the agreement, especially at higher \(x\) locations.

The DL model is not strictly necessary in ODT of combustion problems and many ODT have been performed without it. However, we believe that including the model is an improvement, and the results generally support this.

The reason for the differences in temperature between the results with and without the DL model is primarily due to the differences in mixing. More eddies occur with the DL model, and more eddies imply higher mixing rates. With the DL model, the temperature is higher on both the fuel side of the flame near the wall and on the air side of the flame away from the wall (\(x>0.1\,\text {m}\) ) since the hot combustion products are more vigorously mixed into the cold fuel and ambient air. In both regions, the mean mixture fraction is closer to stoichiometric with the DL model, whereas the mean temperature conditioned on mixture fraction is nearly the same, supporting the idea that the differences are due to mixing.

4.5 Thermocouple Analysis

In the previous results, the modeled gas temperature is compared to the experimental thermocouple reading. A model thermocouple temperature for Case 2 is implemented and tested here. This is done assuming equilibrium between a model thermocouple and the surrounding gas temperature, that is, the net heat transfer to the thermocouple is zero,

$$\begin{aligned} \epsilon \left( \frac{1}{2}q^+ + \frac{1}{2}q^- -\sigma T_t^4\right) + h_{c}(T_g-T_t) = 0, \end{aligned}$$
(10)

where \(\epsilon \) is the thermocouple emissivity, \(h_c\) is the heat transfer coefficient, \(\sigma \) is the Stefan–Boltzmann constant, and \(T_g\), and \(T_t\) are the gas and thermocouple temperatures, respectively. Here, a model thermocouple temperature corresponding to the model gas temperature is evaluated at every point in the domain for each realization, and the results are averaged. The heat transfer coefficient \(h_c\) is computed from \(Nu=hD/\lambda \) and \(Nu=2+0.6Re^{1/2}Pr^{1/3}\), where local composition, temperature, and pressure dependent properties are used. The thermocouple bead diameter is taken as 2.5 times the wire diameter, and the emissivity is taken as 0.6, as oxidized alumel and chromel. The difference between the mean gas and thermocouple temperatures are shown in Figure 12. The difference is fairly small in the measurement region. The maximum difference of the mean temperatures in Figure 12 in the measurement region is 40 K and 29 K at \(y=0.35\) and \(y=1.69\,\text {m}\) , respectively. The average difference in the measurement region is 30 K and 11 K at \(y=0.35\) and \(y=1.69\,\text {m}\) , respectively. Lower emissivities result in smaller differences. Using \(\epsilon =0.2\) as suggested in [54] for type-K thermocouples, the maximum difference of the mean temperatures in the measurement region is 14 K and 11 K at \(y=0.35\) and \(y=1.69\,\text {m}\) , respectively. The differences were also smaller for the isothermal boundary condition Case 10.

Figure 12
figure 12

Temperature difference profile between the gas and thermocouple model for Case 2 at four heights. Symbols correspond to the location of the experimental measurements

Full size image

The upper range of a type-K thermocouple is around 1,600 K, and the maximum temperature measured was was 1,663 K. The effect of limiting the upper temperature was tested by processing the ODT with all temperatures above above 1,600 K truncated to 1,600 K. Figure 13 compares mean and RMS temperature profiles with and without temperature truncation. There is little variation in the mean temperature, though the RMS profile decreases by up to 70 K when the temperature is truncated. The differences are less at lower heights, and at lower flow rates.

Figure 13
figure 13

Comparison of mean (a) and RMS (b) temperature profiles at \(y=1.69\,\text {m}\) when temperature data is truncated downwards to 1,600 K

Full size image

The thermocouples have a reported response time of 50 ms in air at 5 m/s (which is close to the simulated peak mean velocity). The following expression may be used to relate the RMS thermocouple temperature to the RMS gas temperature [55]:

$$\begin{aligned} \frac{T_{rms,g}}{T_{rms,t}} = \sqrt{1+\omega ^2\tau ^2}, \end{aligned}$$
(11)

where \(\omega \) is the fluctuating gas frequency and \(\tau \) is the thermocouple response time. Here, \(dT_t/dt = (T_g-T_t)/\tau \) is used. Finney et al. [6] reported power spectra with frequencies up to 20 Hz. At 5, 10, and 20 Hz, the RMS gas temperature would be 3, 12, and 41% higher than the reported RMS thermocouple temperature, respectively. Any limitations in data sampling frequency would further reduce measured RMS temperatures.

5 Conclusions

ODT simulations using a consistent spatial formulation have been performed of an ethylene wall flame. The predicted results were compared with experimental data in which ethylene is fed at varying flow rates through a porous wall burner. The configuration was chosen to mimic the behavior of a turbulent flame brush similar to that which might occur at the flame/fresh fuel interface of a nominally vertical flame front in a wildland fire propagating through a dense fuel bed. In such fires, the advancing flame front is inclined towards the unburned fuel due to lateral turbulent mixing, an increase in the total gaseous fuel released with increasing height, and expansion of combustion gases as they burn. Similar inclination of the flame/air interface occurs in the wall fire studied. Results presented are also relevant to simulating the behavior of wall fires in other applications.

The ODT model resolves diffusion–reaction flame structures in one dimension, with physically realistic turbulent statistics arising through the advective processes in the model. This allows details of temperature fluctuations to be modeled. ODT simulation results were presented of mean and fluctuating temperature, soot, and velocity profiles. Agreement with experimental results is generally good.

A new DL instability model was implemented within ODT that accounts for instabilities arising from dilatation-induced acceleration in a variable density flow. The model had a significant effect on the results. This model can be applied to any ODT of combustion processes.

A number of simulations were performed in which flow rate, ODT parameters, boundary conditions, chemistry model, and the DL instability were varied or tested. ODT showed correct trends with increasing flow rate, and results were found to be most sensitive to the \(\beta \) parameter, followed by the C parameter, with little sensitivity to Z. Small-to-modest variations in mean temperatures were found when varying the boundary condition, and chemistry model. Thermocouple temperatures were estimated to differ from gas temperatures by less than 40 K in the measurement region.

The detailed flame structure information, and multiscale resolution capabilities of ODT, combined with the relative cost-effectiveness are advantages of the model. Further applications towards model validation and development, such as quantifying subgrid uncertainties in chemistry, soot, and radiation models are areas of future interest.