1 Introduction

The use of Computational Fluid Dynamics (CFD) in fire simulations is becoming more and more popular. Despite the wide range of applicability, one important challenge is to be able to predict concentrations of major and minor species in the case of under-ventilated compartment fires. It is known that under-ventilated fires would result in the development of minor species and can lead to complex scenarios involving flame extinction (Maragkos and Merci 2019). Therefore, it is important to establish a strong basis in the choice of CFD models when simulating such scenarios.

To date, the most common approach to model turbulent combustion in fire simulations is the Eddy Dissipation Model (EDM) (Magnussen and Hjertager 1977), and the Eddy Dissipation Concept (EDC) (Magnussen 2005). With the former, the assumption is that the chemical reactions are infinitely fast, leaving the fuel reaction rate being governed only by a mixing time scale. While this approach is appealing because of its simplicity and the fact that it is relatively computationally inexpensive, minor species, which are important in incomplete combustion, cannot always be obtained with satisfactory accuracy. Within this framework, a simplified two-step reaction scheme for the prediction of CO in under-ventilated fires has been recently proposed in the literature (McGrattan et al. 2022) in the context of infinitely fast chemistry. Nevertheless, the use of finite rate chemistry towards predicting flame extinction has not been sufficiently explored in the literature. Therefore, the present study explores the potential of the EDC approach with finite rate chemistry, combined with LES turbulence modelling, to a flame that resembles a fire flame, namely the UMD line burner (White et al. 2015). For this test case, detailed reaction mechanisms with multiple species and reactions could be explored, but keeping the practical application of CFD simulations of (potentially under-ventilated) compartment fires in mind, this is not explored in the present study.

As a first step toward this goal, a preliminary study on the use of the EDC/LES approach with 2-step finite rate mechanisms was presented in Thabari et al. (2022), for the same flame as in the present study. This previous study illustrated that kinetics parameters can have a noticeable effect on the flame temperature and the resulting flow field. As a continuation of that study, the impact of the LES sub-grid scale turbulence model is assessed here, combined with the 2-step finite rate chemistry mechanism of Westbrook and Dryer (1981). The CFD predictions (i.e., flame temperatures, flow fields and reaction rates) will also be compared to results obtained with EDM in order to examine the effect of turbulence modelling when combined with infinitely fast and finite-rate chemistry. An initial attempt to simulate flame extinction with EDC, with varying levels of oxygen mole fraction in the co-flow, is also presented. The analysis is done on the basis of the predicted combustion efficiency for three different conditions: 1. far from extinction (21–18% vol. O2); 2. onset of extinction (14.5% vol. O2); 3. Extinction (13–12% vol. O2). A relatively simple approach for modelling radiation is used by prescribing the radiative fraction based on the reported experimental data.

2 Governing Equations

The CFD simulations are performed with OpenFOAM version 1912 using the FireFOAM solver. The code solves the Navier–Stokes equations along with transport equations for species mass fractions and sensible enthalpy (Thabari et al. 2022; Maragkos and Merci 2020):

$$ \frac{{\partial \overline{\rho }}}{\partial t} + \nabla \cdot \left( {\overline{\rho }\tilde{u}} \right) = 0 $$
(1)
$$ \frac{{\partial \left( {\overline{\rho }\tilde{u}} \right)}}{\partial t} + \nabla \cdot \left( {\overline{\rho }\tilde{u}\tilde{u}} \right) = - \nabla \overline{\rho } + \nabla \cdot \left[ {\mu_{eff} \left( {\nabla \tilde{u} + \left( {\nabla \tilde{u}} \right)^{T} - \frac{2}{3}\left( {\nabla \cdot \tilde{u}} \right)I} \right)} \right] + \overline{\rho }g $$
(2)
$$ \frac{{\partial \left( {\overline{\rho }\tilde{Y}_{k} } \right)}}{\partial t} + \nabla \cdot \left( {\overline{\rho }\tilde{u}\tilde{Y}_{k} } \right) = \nabla \cdot \left[ {\overline{\rho }\left( {D_{k} + \frac{{\nu_{sgs} }}{{Sc_{t} }}} \right)\nabla \tilde{Y}_{k} } \right] + \overline{{\dot{\omega }^{\prime\prime\prime}_{k} }} , \left( {k = 1, \ldots ,N_{s} - 1} \right) $$
(3)
$$ \frac{{\partial \left( {\overline{\rho }\tilde{h}_{s} } \right)}}{\partial t} + \nabla \cdot \left( {\overline{\rho }\tilde{u}\tilde{h}_{s} } \right) = \frac{{\overline{Dp} }}{Dt} + \nabla \cdot \left[ {\overline{\rho }\left( {D_{th} + \frac{{\nu_{sgs} }}{{Pr_{t} }}} \right)\nabla \tilde{h}_{s} } \right] - \nabla \cdot \overline{{\dot{q}^{\prime\prime}_{r} }} + \overline{{\dot{q}^{\prime\prime\prime}_{c} }} $$
(4)

Within the FireFOAM code, differential diffusion effects are neglected (i.e., \({D}_{k}=D\)), a unity Lewis number is employed (i.e., \(D={D}_{th}\)) while \({Sc}_{t}=P{r}_{t}=0.5\).

3 Turbulence Modelling

Three different turbulent models are compared: Smagorinsky (Smagorinsky 1963a); one equation (Yoshizawa 1986); and the dynamic one equation model (Menon et al. 1996). These models are well-known in the literature and have been used to simulate fire scenarios in the past (Kruljevic et al. 2020a; Vilfayeau 2015).

3.1 Smagorinsky Model

The implemented version of the Smagorinsky model (Smagorinsky 1963b) in OpenFOAM calculates the sub-grid scale viscosity as:

$$ \nu_{sgs} = c_{k} \Delta \sqrt {k_{sgs} } $$
(5)

where \({c}_{k}=0.05\) (Menon et al. 1996) is a model constant and \(\Delta ={\left(\Delta x\Delta y\Delta z\right)}^\frac{1}{3}\) is the filter width.

The sub-grid kinetic energy, \({k}_{sgs}\), is calculated, considering a local equilibrium, from the solution of a quadratic equation:

$$ ak_{sgs}^{2} + bk_{sgs} + c = 0 $$
(6)

where \(a = \frac{{c_{\varepsilon } }}{{\Delta }}\), \(b = \frac{2}{3}tr\left( {\tilde{S}} \right)\), \(c = 2c_{k} {\Delta }\left( {dev\left( {\tilde{S}} \right):\tilde{S}} \right)\) and \(\tilde{S} = \frac{1}{2}\left( {\nabla \tilde{u} + \nabla \left( {\tilde{u}} \right)^{T} } \right)\).

The sub-grid scale dissipation rate, \(\varepsilon_{sgs}\), is modelled as:

$$ \varepsilon_{sgs} = c_{\varepsilon } \frac{{k_{sgs}^{3/2} }}{\Delta } $$
(7)

where \({c}_{\varepsilon }=1.048\) is a model constant (Maragkos et al. 2017).

3.2 One Equation Model

The one equation model (Smagorinsky 1963b) calculates the sub-grid scale viscosity as:

$$ \nu_{sgs} = c_{k} \Delta \sqrt {k_{sgs} } $$
(8)

where \({c}_{k}=0.05\) (Menon et al. 1996) is a model constant and \(\Delta ={\left(\Delta x\Delta y\Delta z\right)}^\frac{1}{3}\) is the filter width.

The sub-grid kinetic energy, \({k}_{sgs}\), is calculated from a transport equation which reads:

$$ \frac{{\partial \left( {\overline{\rho }k_{sgs} } \right)}}{\partial t} + \nabla \cdot \left( {\overline{\rho }\tilde{u}k_{sgs} } \right) - \nabla \cdot \left[ {\overline{\rho }\left( {\nu + \nu_{sgs} } \right)\nabla k_{sgs} } \right] = P - \varepsilon_{sgs} $$
(9)

where \(P\) is the production term, \({\varepsilon }_{sgs}={c}_{\varepsilon }\frac{\overline{\rho }{k}_{sgs}^{3/2}}{\Delta }\) is the dissipation term and \({c}_{\varepsilon }=1.048\) is a model constant (Maragkos et al. 2017).

3.3 Dynamic One Equation Model

This model is the same as the one equation model described above only in this case the model parameters, \({c}_{k}\) and \({c}_{\varepsilon }\), are not constant but vary dynamically in space and time.

The model parameter, \({c}_{k}\), is calculated as:

$$ {\text{c}}_{{\text{k}}} = \frac{{\frac{1}{2}{\text{L}}_{{{\text{ij}}}} {\text{ M}}_{{{\text{ij}}}} }}{{{\text{M}}_{{{\text{ij}}}} {\text{M}}_{{{\text{ij}}}} }} $$
(10)

where \({L}_{ij}=dev\left(\widehat{{\widetilde{u}}_{i}{\widetilde{u}}_{j}}-\widehat{{\widetilde{u}}_{i}}\widehat{{\widetilde{u}}_{j}}\right)\), \({M}_{ij}=-2\Delta \sqrt{{K}_{ij}}\widehat{\widetilde{S}}\) and \({K}_{ij}=0.5\left(\widehat{{\widetilde{u}}_{i}{\widetilde{u}}_{j}}-\widehat{{\widetilde{u}}_{i}}\widehat{{\widetilde{u}}_{j}}\right)\).

The model parameter, \({c}_{\varepsilon }\), is calculated as:

$$ {\text{c}}_{{\upvarepsilon }} = \frac{{\left( {{\upnu } + {\upnu }_{{{\text{sgs}}}} } \right)2{\Delta }\left[ {\widehat{{\frac{{\partial {\tilde{\text{u}}}_{{\text{i}}} }}{{\partial {\text{x}}_{{\text{j}}} }}\frac{{\partial {\tilde{\text{u}}}_{{\text{i}}} }}{{\partial {\text{x}}_{{\text{j}}} }}}} - \left( {\frac{{\partial \widehat{{\widetilde{{{\text{u}}_{{\text{i}}} }}}}}}{{\partial {\text{x}}_{{\text{j}}} }}\frac{{\partial \widehat{{\widetilde{{{\text{u}}_{{\text{i}}} }}}}}}{{\partial {\text{x}}_{{\text{j}}} }}} \right)} \right]}}{{{\text{k}}_{{{\text{test}}}}^{3/2} }} $$
(11)

where the resolved kinetic energy at the test filter level is defined as \({k}_{test}=\frac{1}{2}\left(\widehat{{\widetilde{u}}_{k}{\widetilde{u}}_{k}}-{\widehat{\widetilde{u}}}_{k}{\widehat{\widetilde{u}}}_{k}\right)\).

4 Combustion Models

Two models are employed for modelling turbulent combustion: the Eddy Dissipation Model (EDM) (Magnussen and Hjertager 1977); and the Eddy Dissipation Concept (EDC) (Magnussen 2005).

The EDM is combined with infinitely fast chemistry, through a 1-step irreversible chemical reaction, with the reaction rate for the fuel expressed as:

$$ \overline{{\dot{\omega }^{\prime\prime\prime}_{F} }} = - \overline{\rho }\frac{{{\text{min}}\left( {\tilde{Y}_{F} ,\frac{{\tilde{Y}_{{O_{2} }} }}{s}} \right)}}{{\tau_{EDM} }} $$
(12)

where \(s\) is the stoichiometric oxygen-to-fuel ratio. The reaction rates for the others species are obtained through simple stoichiometric relations.

The mixing time scale is calculated as:

$$ \tau_{EDM} = {\text{min}}\left( {\frac{{k_{sgs} }}{{C_{EDM} \varepsilon_{sgs} }},\frac{{\Delta^{2} }}{{C_{diff} \alpha }}} \right) $$
(13)

with the model parameters \({C}_{EDM}\) and \({C}_{diff}\) both set to 4 (Maragkos et al. 2017).

On the other hand, a finite-rate chemistry scheme is introduced with EDC, considering a 2-step chemical reaction mechanism.

The reaction rate term for the chemical species reads:

$$ \overline{{\dot{\omega }^{\prime\prime\prime}_{k} }} = - \overline{\rho }\frac{{\gamma^{2} \chi }}{{\tau_{EDC} \left( {1 - \gamma^{2} \chi } \right)}}\left( {\tilde{Y}_{k} - Y_{k}^{*} } \right) $$
(14)

where \(\gamma \) is the size of fine structures, \({\tau }_{EDC}\) is the EDC mixing time scale, \(\chi \) is the reacting fraction of the fine structures, while \({\widetilde{Y}}_{k}\) and \({Y}_{k}^{*}\) are the filtered mass fractions of the species and the mass fractions of the species in the fine structures, respectively.

The size of the fine structures is determined as:

$$ \gamma = C_{\gamma } \left( {\frac{{\nu \varepsilon_{sgs} }}{{k_{sgs}^{2} }}} \right)^{\frac{1}{4}} $$
(15)

with \({C}_{\gamma }=2.1377\) a model constant and the size of fine structures limited to \(\gamma \le 1\) (Maragkos and Merci 2019).

The EDC mixing time scale, \({\tau }_{EDC}\), is based on the original energy cascade model, and it is assumed to be in the order of the Kolmogorov time scale:

$$ \tau_{EDC} = C_{\tau } \left( {\frac{\nu }{{\varepsilon_{sgs} }}} \right)^{\frac{1}{2}} $$
(16)

where \({C}_{\tau }=0.4803\) is a model constant (Parente et al. 2016).

As in Thabari, et al. (2022), \({Y}_{k}^{*}\) is calculated considering a Plug Flow Reactor (PFR) (Bösenhofer et al. 2018), through equations for enthalpy, pressure and chemical species:

$$ \frac{dh}{{dt}} = 0 $$
(17)
$$ \frac{dp}{{dt}} = 0 $$
(18)
$$ \frac{{dY_{k}^{*} }}{dt} = \frac{{\dot{\omega }_{k}^{{*^{\prime\prime\prime}}} }}{{\rho^{*} }} $$
(19)

where \({\dot{\omega }}_{k}^{{\prime}{\prime}{\prime}*}\) is evaluated from a chemical reaction mechanism (Eqs. (20)–(22)). With finite-rate chemistry, the reacting fraction of the fine structures is often set to \(\chi =\) 1 (i.e., the reacting fraction of the fine structures is controlled by chemistry (Shiehnejadhesar et al. 2014)).

The 2-step chemical reaction mechanism used with EDC reads as follows:

4.1 Reaction 1: \({\text{CH}}_{4} + 1.5{\text{O}}_{2} \to {\text{CO}} + 2{\text{H}}_{2} {\text{O}}\)

$$ \dot{\omega }_{k\;1}^{{*^{\prime\prime\prime}}} = 6.7 \times 10^{12} \exp \left( {\frac{{ - 4.84 \times 10^{4} }}{RT}} \right)\left[ {{\text{CH}}_{4} } \right]^{0.2} \left[ {{\text{O}}_{2} } \right]^{1.3} $$
(20)

4.2 Reaction 2: \({\text{CO}} + 0.5{\text{O}}_{2} \leftrightarrow {\text{CO}}_{2}\)

$$ \dot{\omega }_{k\;2 - forward}^{\prime \prime \prime *} = 3.98 \times 10^{14} \exp \left( {\frac{{ - 4.0 \times 10^{4} }}{RT}} \right)\left[ {{\text{CO}}} \right]^{1} \left[ {{\text{H}}_{2} {\text{O}}} \right]^{0.5} \left[ {{\text{O}}_{2} } \right]^{0.25} $$
(21)
$$ \dot{\omega }_{k\;2 - backward}^{\prime \prime \prime *} = 5.0 \times 10^{8} \exp \left( {\frac{{ - 4.0 \times 10^{4} }}{RT}} \right)\left[ {{\text{CO}}_{2} } \right]^{1} $$
(22)

where the reaction rates for the chemical species have been calculated considering an Arrhenius type of reaction in the form of \({{\dot{\omega }}_{k}}^{{\prime}{\prime}{\prime}*}=A\mathrm{exp}\left(-\frac{{E}_{a}}{RT}\right){\left[Fuel\right]}^{a}{\left[Oxidizer\right]}^{b}\) and the units are (cm3/mole)r−1 s−1 for \(A\) and (cal/mole) for \({E}_{a}\).

5 Radiation Modelling

Radiation is considered by solving the radiative transfer equation (RTE) with the finite volume discrete ordinates method (fvDOM), assuming a non-absorbing optically thin medium. In this case, the radiative heat fluxes in the sensible enthalpy equation (Eq. (4)) are calculated as:

$$ \nabla \cdot \overline{{\dot{q}^{\prime\prime}_{r} }} = \chi_{r} \overline{{\dot{q}^{\prime\prime\prime}_{c} }} $$
(23)

where \({\chi }_{r}\) is the radiative fraction of the fuel and is obtained from the experimental data (White et al. 2015).

6 Test Case Description

The UMD line burner (White et al. 2015), a well-documented experiment which is part of the MaCFP workshop, is chosen as a validation test case for the numerical simulations. Only cases with CH4 as fuel are considered in the present study in order to avoid the need for soot modelling. The injected mass flow rate from the fuel port (i.e., 1 g/s) results in a heat release rate of 50 kW (for an unsuppressed flame) while the co-flowing oxidizer is introduced with a mass flow rate of 85 g/s (see Fig. 1a). A ceramic fibreboard wall acts as a separation between the fuel port and the oxidizer stream. For comparison purposes, 10% and 20% uncertainties have been considered for the mean and rms temperature measurements, respectively. For the suppressed flame scenario, N2 was employed as the extinguishing agent. To reach extinction, nitrogen was added to the co-flow resulting in a decreasing oxygen mole fraction from 21 to 11% while keeping the mass flow rate of air constant. More details regarding the scenario, as well as the available experimental data, can be found in MaCFP.

Fig. 1
figure 1

a Top view of the UMD line burner (adapted from (Maragkos and Merci 2019)) and b computational domain, illustrating the different levels of grid refinement together with an instantaneous temperature plot in the mid-plane

Full size image

7 Numerical Set Up

The computational domain (see Fig. 1b) is a rectangular box of 1.6 m × 1 m × 2 m (length x width x height), using 25 mm cubic cells as base. A local grid refinement strategy is employed refining the mesh to 12.5 mm cubic cells up to a height of 0.6 m in a 0.8 m × 0.8 m × 0.6 m region, and to 6.25 mm cubic cells in a 0.6 m × 0.6 m × 0.4 m region. The total number of cells is approximately 739,500. The finest grid size used in the flame region has been previously reported to be sufficiently small in another study on the same test case with the use of infinitely fast chemistry (Thabari et al. 2022; White et al. 2017). It is also worth noting that the resolved turbulence resolution in the numerical simulations (not shown here) remained close or above 80% in the main regions of interest (i.e., in the flame region). The fuel and co-flowing oxidizer mass flow rates were set to the corresponding experimental values. The ambient temperature and pressure were 293 K and 101,325 Pa, respectively. The ceramic fibreboard plate (separating the fuel port and co-flow air at y = 0) was treated as an isothermal wall with a no-slip boundary condition for the velocity. For the solution of the RTE, 72 solid angles were used for angular discretization. All simulations were set to run for 35 s (averaged over the last 30 s to produce mean results), with a varying time step, based on a maximum CFL number of 0.9. The equations were advanced in time using a second order backward scheme. A second order filtered linear (i.e., filteredLinear2V) was used for the convective term in the momentum equations while a second order limited linear (i.e., limitedLinear) scheme was employed for the convective term in the transport equations for the scalars. The choice of these discretization schemes was based on (Maragkos et al. 2022). The bottom plane (y = 0), outside the co-flowing air, along with the sides of the computational domain were set to be open allowing for air to be freely entrained. A flame anchoring strategy was employed, so that the minimum value of the temperature in the first row of cells above the burner was 900 K. For simulations with infinitely fast chemistry (EDM), this approach was not necessary.

8 Results

8.1 No Extinction

Numerical results for the scenarios not involving any flame extinction are first presented here. Figure 2 provides contour plots of the predicted mean temperatures in the mid plane for EDC with the 2-step finite rate reaction mechanism (top) and the EDM (bottom) for the three different sub-grid scale turbulence models (i.e., Smagorinsky, one equation and dynamic one equation).

Fig. 2
figure 2

Contour plots of mean temperature in the mid plane with EDC (Top) and EDM (Bottom). From left to right: Smagorinsky, one equation, dynamic one equation

Full size image

Overall, there is a significant impact of the applied turbulence model, altering the flame temperature near the burner, for both EDC and EDM, particularly when the dynamic one equation model is applied. The dynamic calculation of the turbulence model parameter, \({c}_{\varepsilon }\), has an impact on the calculated mixing time scales, hence, the reaction rates and the resulting flame temperatures. Furthermore, there is also a significant difference between EDM and EDC, regardless of the sub-grid scale turbulence model employed. In this case, the maximum temperature is higher with the EDC approach than with EDM; the high-temperature region is larger and also extends very close to the burner with EDC, in contrast to EDM which occurs a few centimeters downstream. This temperature difference is also attributed to the flame anchoring strategy imposed with EDC (finite-rate chemistry approach). In this respect, the EDM predictions are more in line with what is reported in the experiments (i.e., a quantitative comparison is provided in the next section). Overall, these observations and the qualitative/quantitative differences between the models are further explained below on the basis of the resulting turbulence model parameters (i.e., \({c}_{k}\), \({c}_{\varepsilon }\)) as well as the predicted heat release rate per unit volume (HRRPUV).

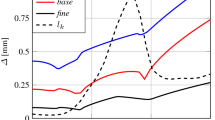
Figure 3 presents the predicted mean / rms temperatures and axial velocities on the centerline, as well as the radial profiles at a selected height of 0.25 m above the line burner, with different turbulence models. The available experimental data (i.e., limited only to thermocouple temperature measurements) are depicted with symbols in the graphs in order to have a more quantitative comparison between the numerical predictions and the experiments.

Fig. 3
figure 3

Mean results with different turbulence models: a centerline temperature; b radial temperature at 0.25 m height; c centerline velocity; d radial velocity at 0.25 m height

Full size image

As previously mentioned in the discussion of Fig. 2, both EDM and EDC model predictions are sensitive to the sub-grid scale turbulence model, although the former has the advantage that is less sensitive with respect to grid size variation (Thabari et al. 2022). Interestingly, Fig. 3 reveals that with the use of static turbulence models (i.e., Smagorinsky, one equation model), the EDM results do not deviate significantly from each other. The flame temperatures are fairly well predicted and remain close to the experimental data throughout the centerline (i.e., from the region close to burner up until further downstream). On the other hand, the dynamic one equation significantly under-predicts the maximum flame temperatures close to the burner and only shows good agreement further downstream (Fig. 3a). This behaviour is linked to the dynamic calculation of the turbulence model parameter \({c}_{\varepsilon }\) which directly affect the calculated reaction rates. Furthermore, the EDC predictions are consistently higher compared to EDM for all turbulence models. This observation is in line with what has been previously reported in the literature when comparing the EDM/EDC models on the same test case (Maragkos and Merci 2019). It is obvious, that the differences between the EDM/EDC models (i.e., reaction rate expressions, dependence on sub-grid scale quantities), in combination with the dynamically determined turbulence model parameters \({c}_{k}\) and \({c}_{\varepsilon }\), lead to differences in the resulting flame temperatures. The dynamic one equation model predicts lower \({c}_{k}\) values compared to the static model (i.e., Fig. 4a) making the fire plume more turbulent. In addition, it also predicts lower \({c}_{\varepsilon }\) values (i.e., Fig. 4b) which lead to lower values for the sub-grid scale dissipation rate. Both these aspects directly affect the predicted reaction rates and result in lower maximum flame temperatures. This aspect is further supported by examining the predicted heat release per unit volume (HRRPUV) values presented in Fig. 5 for the different cases. It is clear, that the performance of the dynamic one equation with both EDC and EDM models results in significantly less heat being released due to combustion, hence, resulting in lower temperatures as well. Unlike EDM, the HRRPUV with finite-rate EDC does not solely rely on turbulent mixing (see Eq. (16)) but also on the Arrhenius-type of chemical reaction rate (see Eqs. (20–22)). The predicted rms values are in line with the previous observations, i.e., the EDC, having higher mean flame temperatures, also has higher rms values compared to EDM. Overall, the rms predictions with EDC tend to be closer to the experimental data at axial locations close to the burner (y < 0.1 m) but are over-predicted further downstream (0.1 m < y < 0.5 m). On the other hand, the EDM predictions are under-predicted close to the burner but compare better further downstream. A similar trend is also seen in the predicted mean / rms axial velocities with the EDC predictions being higher than EDM, a direct consequence of the higher flame temperatures as well. Nevertheless, given that there are no velocity measurements to compare against, no further comments can be made regarding the accuracy of these numerical predictions.

Fig. 4
figure 4

Predicted a \({c}_{\varepsilon }\) and b \({c}_{k}\) turbulence model parameters with the dynamic one equation turbulence model along the centerline (with the EDM combustion model)

Full size image
Fig. 5
figure 5

Predicted Heat Release Rate per Unit Volume (HRRPUV) along the centerline with a EDM and b EDC

Full size image

8.2 Extinction

Numerical results for scenarios involving flame extinction are presented here focusing only on EDC since the use of EDM would require additional extinction /re-ignition modelling. Figure 6 presents a comparison, between the experiments and the simulations, of the radial profiles of the O2 mole fractions for a case with 18% vol. injected from the co-flow. The numerical predictions with static models follow closely the experimental profiles at both downstream distances. The only difference between the static cases is observed around the centerline at height y = 0.125 m where the concentration with the Smagorinsky model is lower compared to the other models. However, the dynamic model fails to capture well the mole fractions because the fuel is not burnt completely.

Fig. 6
figure 6

Radial profile of O2 mole fractions with 18% vol. O2 in the co-flow at height a y = 0.125 m and b y = 0.25 m

Full size image

Figure 7 shows a comparison between the numerical simulations and the experimental values for the combustion efficiency \(\eta \), defined as the ratio of integrated heat release rate (HRR) inside the domain over the theoretical HRR without extinction, as a function of the O2 oxygen mole-fraction in the co-flow. The experimental data show that the combustion efficiency is not significantly affected in the range \(0.145<{X}_{{O}_{2}}<0.21\) and that flame extinction occurs at approximately \({X}_{{O}_{2}}\approx 0.122\) (White et al. 2015). The predictions with all turbulent models are fairly close and show a relatively good agreement with the experiment data during two conditions: far from extinction (\({X}_{{O}_{2}}=0.18\)) and extinction (\({X}_{{O}_{2}}=0.12\)). Nevertheless, the simulations are less accurate in predicting the onset to flame extinction occurring at around \({X}_{{O}_{2}}\approx 0.13-0.15\). A possible reason for this discrepancy could be the simplified way of radiation modelling (i.e., constant radiative fraction) employed in this case. Even though the employed approach guarantees that the correct amount of heat is released due to radiation (i.e., as opposed to trying to predict the radiative fractions), it also has its limitations as it assumes an optically thin flame and neglects absorption. This aspect has been previously reported in the literature for the same test case (Kruljevic et al. 2020b). One of the main reasons mentioned is that when the residence time of the chemical species is not short (low scalar dissipation rates), radiation will lower the temperature and slow down the chemical reactions, hence, resulting in lower heat release rates as well. For the case with reduced O2 oxygen mole-fraction in the co-flow, it is possible that radiation is less significant as the radiation source term becomes negligible (White et al. 2015) (i.e., due to reduced flame temperatures). Another possible reason for the discrepancies is that a more detailed reaction mechanism is needed in order to capture flame extinction correctly around the onset of flame extinction. It is worth noting that the same study (Kruljevic et al. 2020b) highlighted the failure of simplified global mechanisms to accurately simulate flame extinction in the case of fire scenarios. Therefore, considerations of more advanced radiation models (i.e., WSGG type of models, including absorption) and more detailed chemical mechanisms might be important to take into account in the future.

Fig. 7
figure 7

Combustion efficiency at selected O2 mole fractions in the co-flow with EDC and different turbulent models

Full size image

9 Conclusion

The effect of turbulence modelling (i.e., Smagorinsky, one equation, dynamic one equation), combined with the use of infinitely fast (EDM) and finite-rate (EDC) chemistry, has been studied in LES of a turbulent line burner case and focusing on various levels of flame extinction.

The numerical predictions showed that the performance of the dynamic one-equation sub-grid scale turbulence model is not satisfactory, with either of the combustion models, with and without extinction. It was revealed for cases without extinction that the dynamic calculation of the turbulence model parameters has a significant effect on the reaction rates and, hence, on the resulting flame temperatures.

The predicted turbulence model parameters in this case were significantly lower compared to the values often used in the literature for highly turbulent flows.

For extinction cases, both static sub-grid scale turbulence models, combined with EDC and finite-rate chemistry, showed very similar predictions, although their impact is not negligible.

With the simulation set-up, reasonable accuracy has been obtained for the cases far away from extinction. The transition to extinction is not captured very accurately by the models, so there is room for improvement for that aspect.

The results presented in the paper show that the use of finite-rate chemistry has great potential in capturing flame extinction without the need for additional modelling, in contrast to the use of infinitely fast chemistry (i.e., which requires additional modelling for flame extinction and re-ignition). The use of a more advanced radiation model, which considers absorption, as well as the inclusion of a more detailed reaction mechanism are expected to further improve the current numerical predictions.