Introduction

Traditional quantitative genetics studies organisms on the basis of phenotypic observations and tries to reach conclusions about their genotype, in particular about the way in which quantitative traits are inherited. This is usually accomplished by describing the gene action by genetic parameters, functions of phenotypic means and variances (Falconer and Mackay 1996). One of these parameters is the effect of additive gene action, usually denoted by a, and defined as half of the difference between the genotypic values of two homozygotes. Additive effects are fixed in the population as it increases its homozygosity in succesive generations. Therefore, a significant additive gene action effect in certain population means that selection begining in the early generations gives hope for obtaining transgressive homozygous lines (Mather 1949; Surma 1996).

The progress of experimental methods allows now for exploration of the genome. It is possible to analyze individuals with respect to the molecular markers reflecting their genomic constitution. It is also possible to combine methods of quantitative genetics and of molecular genetics for localization of quantitative trait loci (QTL) relative to markers and for estimation of their effects. In most studies, homozygous lines are used for QTL analysis. In consequence, attention is mainly paid to estimation and interpretation of additive gene effects.

The two methods of estimation of the additive genetic effect: first, using just phenotypic data, and the second, which additionally takes into account the genotypic marker data, are both based on the polygenic model of inheritance. The “phenotypic” method estimates the total additive effect of all loci affecting the trait under study, while the “genotypic” method allows for estimation of the contributions of individual genes. Comparison of these two methods with respect to obtained estimates and breeding recommendations has not been adequately considered in the literature. To our knowledge, only Snape (1997, p. 44, Table 6) discussed briefly this issue on the basis of one experiment with barley doubled haploid lines and one trait—flowering time. He found the “phenotypic” estimate of a to be smaller than the “genotypic” one, and proposed as the explanation an inadequate representation of the population extremes in the examined sample of lines.

The aim of the study reported in this paper was comparison of two methods of estimation of the parameter connected with the additive gene action: the phenotypic method, used traditionally in quantitative genetics, and the genotypic method, which is based on marker observations and now is used routinely in many species. The comparison was performed by analytical methods, by analyses of real data sets and by a simulation study. Also, a modification of estimation of the additive gene action effect by using weighted multiple linear regression was considered with the aim to set a bridge between the two compared methodologies.

In our considerations we use the form of the additive gene action effect estimator based on phenotypic observations of biparental homozygous progeny and mean values for groups of extreme lines described by Surma et al. (1984). Genetic and mathematical interpretation of additive and other genetic parameters was presented e.g. by Falconer and Mackay (1996, chapter 7).

As to the QTL mapping method, we use the multiple linear regression model (Jansen 1993; Haley et al. 1994) of trait values on marker observations acting as explanatory variables (Jansen 1996). It permits for elimination of markers which reveal linkage to a QTL when tested one by one, but in multiple analyses are not characterized by any influence on the phenotypic trait. It assumes that the QTL are located at marker positions.

Material and methods

Estimation methods

If in the experiment we observe n biparental homozygous (recombinant inbred or doubled haploid) plant lines, we get an n-vector of phenotypic means y = [y 1, y 2, …, y n ]′ and q n-vectors of marker genotype observations m l , l = 1, 2,…, q. The i-th element (i = 1, 2, …, n) of vector m l is equal to −1 or 1, depending on the parent’s genotype exhibited by the i-th line.

Estimation of the additive gene effect on the basis of phenotypic observations y requires identification of the groups of extreme lines, i.e., lines with minimal and maximal expression of the observed trait. In this paper we identify the groups of extreme lines using the quantile method (Bocianowski et al. 1999), in which as minimal (maximal) lines are taken the ones with the mean values smaller (bigger) than 0.03 (0.97) quantile of the empirical distribution of means. On the assumption that the minimal and maximal lines contain, respectively, only alleles decreasing and only alleles increasing the value of the trait (Choo and Reinbergs 1982), the total additive efect a of all genes controlling the trait (Mather 1949) can be estimated by the formula (Surma et al. 1984)

$$ \hat a_{F} = \frac{1}{2}\left( {\bar L_{{\max }} - \bar L_{{\min }} } \right), $$
(1)

where \( \bar L_{{\min }} \) and \( \bar L_{{\max }} \) denote the means for the groups of minimal and maximal lines, respectively.

In the presence of observations of molecular markers, estimation of a is made on the assumption that the genes responsible for the trait are completely linked to observed markers. After deciding which p markers out of all observed sufficiently well explain the variability of the trait, we can model phenotypic observations for the lines as

$$ {\mathbf{y}} = {\mathbf{X}}\beta + {\mathbf{e}}, $$
(2)

where X denotes the n × (p + 1)-dimensional matrix of the form \( {\mathbf{X}} = [{\mathbf{1}},{\mathbf{m}}_{{l_{1} }} ,{\mathbf{m}}_{{l_{2} }} , \ldots ,{\mathbf{m}}_{{l_{p} }} ], \) l 1 , l 2 , …, l p ∈ {1, 2, …, q}, β denotes the (p + 1)-dimensional vector of unknown parameters of the form \( {\varvec{\beta}} = \left[ {\mu ,a_{{l_{1} }} ,a_{{l_{2} }} , \ldots ,a_{{l_{p} }} } \right]^{\prime } , \) and e denotes the n-dimensional vector of random variables of the form \( {\mathbf{e}} = \left[ {e_{1} ,e_{2} , \ldots ,e_{n} } \right]^{\prime } \) such that E(ei) = 0, Var(ei) = σ2, Cov(ei,ej) = 0 for i ≠ j, i,j = 1, 2, …, n. The parameters \( a_{{l_{1} }} ,a_{{l_{2} }} , \ldots ,a_{{l_{p} }} \) are the additive effects of the genes controlling the trait. If X is of full rank, the estimate of β is given by (Searle 1982)

$$ \hat {\varvec{\beta}} = \left( {{\mathbf{X}}^{\prime } {\mathbf{X}}} \right)^{{ - 1}} {\mathbf{X}}^{\prime } {\mathbf{y}} $$
(3)

The total additive effect of genes influencing the trait, defined as the sum of absolute values of individual effects, can by found as

$$ \hat a_{G} = \sum\limits_{{k = 1}}^{p} {\left| {\hat a_{{l_{k} }} } \right|} . $$
(4)

Selection of markers chosen for model (2) can be made, e.g., by a stepwise regression procedure (Charcosset et al. 2001). Here we used a three-stage algorithm, in which: first, selection was made by a backward stepwise search independently inside all linkage groups; then, markers chosen in this way were put in one group and subjected to the second backward selection (see Jansen and Stam 1994). Finally, at the third stage, we considered situations, in which chosen markers were located on the chromosome very close to each other (closer than 5 cM). Because these markers are linked probably to one QTL, only the marker with the largest value of the test statistic was retained in the set. At the first and second stages we used the critical significance level equal to 0.001, resulting from a Bonferroni correction.

The modified version of trait regression on marker data in this paper, used only in simulations, is considered by taking a weighted multiple linear regression, that is, regression with a diagonal matrix W of unknown variances of observations, which, however, may be empirically found by estimation. In this model the estimate of β is

$$ \hat {\varvec{\beta}} = \left( {{\mathbf{X}}^{\prime}{\mathbf{W}}^{{ - 1}} {\mathbf{X}}} \right)^{{ - 1}} {\mathbf{X}}^{\prime}{\mathbf{W}}^{{ - 1}} {\mathbf{y}}, $$

where W = (w ii ), with w ii being the estimated variance for i line, i = 1, 2, …, n. Selection of markers for the weighted regression is made by the same method as described for the unweighted case.

Data sets

To compare the estimates of a obtained by different methods the following data sets were used.

Data set 1

Doubled haploid lines of barley (cross Steptoe × Morex). The data concern 150 DH lines of barley obtained from the Steptoe × Morex cross, used in the NABGM project and tested at 16 environments (Kleinhofs et al. 1993; Romagosa et al. 1996; http://wheat.pw.usda.gov/ggpages/SxM). The linkage map used consisted of 223 molecular markers, mostly RFLP, with mean distance between markers equal to 5.66 cM. The lines were analysed for eight phenotypic traits (alpha amylase, AA; diastatic power, DP; grain protein, GP; grain yield, GY; height, HE; heading date, HD; lodging, LO; malt extract, ME; Hayes et al. 1993). Grain protein, lodging and malt extract were transformed by \( \arcsin \sqrt {{x \mathord{\left/ {\vphantom {x {100}}} \right. \kern-\nulldelimiterspace} {100}}} . \) Missing marker data were estimated by the method of Martinez and Curnow (1994), that is, using non-missing data of flanking markers.

Data set 2

Doubled haploid lines of barley (cross Harrington × TR306). The data come also from the NABGM project (Tinker et al. 1996, http://wheat.pw.usda.gov/ggpages/maps/Hordeum) and concern 145 DH lines of barley obtained from the cross Harrington × TR306. The lines were analysed for seven phenotypic traits (weight of grain harvested per unit area, GY; number of days from planting until emergence of 50% of heads on main tillers, HD; number of days from planting until physiological maturity, NM; plant height, HE; lodging transformed by \( \arcsin \sqrt {{x \mathord{\left/ {\vphantom {x {100}}} \right. \kern-\nulldelimiterspace} {100}}} , \) LO; 1000 kernel weight, KW; test weight, TW). We used the map composed of 127 molecular markers (mostly RFLP) with the mean distance between markers equal to 10.62 cM. Results shown below concern observations from five environments (in four environments observations were made over 2 years).

Data set 3

Recombinant inbred lines of maize (cross B73 × H99). The data used for this example concern 138 RI lines of maize, derived from the cross B73 × H99 at Department of Genetics and Microbiology, University of Milan (for details see Frova et al. 1999; Sari-Gorla et al. 1999). The lines were investigated with respect to nine phenotypic traits (ear length, EL; ear weight, EW; kernel weight per ear, KWE; kernel number per ear, KN; 50-kernel weight, 50 KW; male flowering time, MFT; female flowering time, FFT; anthesis-silking interval, ASI; plant height, PH), in drought conditions and under irrigation. Trait observations were transformed to tolerance indices, i.e., the ratios of observations obtained in two different conditions. We use observations of 144 molecular markers (RFLP, SSR and AFLP). The mean distance between markers in the map was equal to 15.13 cM.

Simulation studies

In the simulation studies comparing the “phenotypic” and “genotypic” estimates of the additive gene action effect the following variants of assumed parameters were adopted. The true value of the parameter was set to 10 (a = 10) and the total mean value of the trait to 100. 150 homozygous lines were analyzed and 150 markers. Markers were located in 5, 7 or 10 linkage groups (LG). LG contained 30 (for 5 groups) or 15 (for 10 groups) markers; for seven LG the numbers of markers in individual groups were 21, 21, 21, 21, 22, 22 and 22. Distances between markers were all equal (12 cM) or unequal (for 5 groups: 10, 11, 12.5, 14 and 15 cM; for 7 groups: 10, 11, 11.5, 12.5, 13.5, 14 and 15 cM; for 10 groups: 10, 10.5, 11, 11.5, 12, 13, 13.5, 14, 14.5 and 15 cM). The number of QTL affecting the trait was assumed to be 1, 4 or 10. The QTL were (i) distributed on the whole genome, (ii) located in one LG or, in the case of 10 genes and seven- or 10-chromosome genome, (iii) in the two LG. Effects of individual genes were assumed to be: (i) equal for all genes or (ii) one QTL effect was much larger than others. The error variance was equal to 5 or 10. For each combination of the parameters, 1000 data sets containing the vector of phenotypic observations and vectors of marker genotype observations were generated. For each data set the additive gene action effect estimates \( \hat a_{{jF}} \) and \( \hat a_{{jG}} , \) j = 1, 2, …, 1000, were calculated by the methods presented above. Then, mean values of parameter estimates \( \overline {\hat a} _{F} , \) \( \overline {\hat a} _{G} \) for each series were calculated, together with the mean squared errors.

In the simulations concerning the weighted regression, the situation in which each homozygous line is represented by five plants was analyzed. The same values of the additive gene effect and of the total mean were assumed as for the unweighted case. The simulations were limited to the case of seven linkage groups with distances between markers equal to 12 cM. The trait was assumed to be determined by four or 10 QTL with equal values of the additive effect. These QTL were located in one (for four QTL), two (for 10 QTL) or in many LG. The variance for lines was assumed according to four variants: (i) equal for all lines, (ii) greater for extreme lines than for other lines, (iii) smaller for extreme lines than for other lines, (iv) different for minimal lines, maximal lines and other lines. The error variance was equal to 5 for all generated observations. For each combination of parameters, 2000 random generations of the data set containing the vector of phenotypic observations and vectors of marker genotype observations were made. For each data set, the line variances were estimated, and the total additive gene effect was estimated by the phenotypic method and by unweighted and weighted version of the genotypic method. The results were summarised by mean values for series of simulations and mean squared errors.

Results

Analytical comparison

Analytical comparison of formulae (1) and (4) is possible with the two genetic assumptions:

  1. (i)

    that the markers are unlinked, that is, for any two markers probability of encountering a line with observations (1,1) or (−1, −1) is the same as observing a line with (1, −1) or (−1,1);

  2. (ii)

    that the segregation of each marker is concordant with the genetic model appropriate for the analysed population, which in our case means that the probability of observing “−1” is the same as observing “1” (1:1 segregation).

If the marker data satisfied exactly assumptions (i) and (ii), we would have X′X = n I, where I is the identity matrix, and the estimator (4) could be written as

$$ \hat a_{G} = \sum\limits_{{k = 1}}^{p} {\left| {\frac{1}{2}\left( {\bar y_{{l_{k} }} ^{{\left( + \right)}} - \bar y_{{l_{k} }} ^{{\left( - \right)}} } \right)} \right|} , $$
(5)

where \( \bar y_{{l_{k} }} ^{{\left( + \right)}} \) and \( \bar y_{{l_{k} }} ^{{\left( - \right)}} \) denote the mean values for lines with observations of the l k-th marker equal to 1 and −1, respectively, with k = 1, 2, …, p.

Practically, the marker data do not fulfill exactly the assumptions taken above as leading to (5). The assumption (i) is, however, approximately true if the markers chosen to model (2) are weakly linked, that is, if they are far from each other in the linkage map (e.g., in different linkage groups). The assumption (ii) is usually tested by a χ2 test before any linkage analysis is done. Therefore, in practice the estimates of the parameters \( a_{{l_{k} }} , \) additive effects of the individual loci, are close to the values which would be used in the simplified formula (5).

Note that (5) is similar in form to (1), the difference being that in (1) means for phenotypically extreme lines are used, while in (5) the means for genotypic classes are taken. Note also that each component of (5) is smaller than the estimator \( \hat a_{F} \) obtained by (1). Thus, analytical comparison of the methods of estimation shows that comformity of the estimates obtained by (1) and (4) can be achieved by summing a right number of individual gene effects.

Numerical comparison

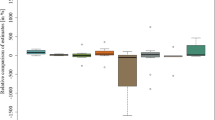
Figure 1a shows the summary of the comparisons between genotypic and phenotypic estimates of the total additive effect in the form of a box-and-whisker diagram of the observed values \( \left( {{{\hat a_{G} } \mathord{\left/ {\vphantom {{\hat a_{G} } {\hat a_{F} }}} \right. \kern-\nulldelimiterspace} {\hat a_{F} }}} \right) \times 100 \) for data set 1 (variability over 16 environments). In most of the considered situations the total additive effect calculated on the basis of the marker observations was smaller than the total additive effect obtained from phenotypic observations only. However, the range of the calculated coefficients is quite large, from 34.14% for GY in one of the environments, to 153.3% for GP. The smallest range of values was observed for the trait HD.

Fig. 1
figure 1

Relative comparison of phenotypic and genotypic estimates of the total additive effect: box-and-whisker diagram of the values \( \left( {{{\hat a_{G} } \mathord{\left/ {\vphantom {{\hat a_{G} } {\hat a_{F} }}} \right. \kern-\nulldelimiterspace} {\hat a_{F} }}} \right) \times 100, \) classified by the observed phenotypic traits; (a) data set 1, (b) data set 2

Full size image

In Fig. 1b a similar summary for data set 2 is shown. Again, most of the genotypic estimates were smaller than the phenotypic ones. The range of the comparative coefficients was from 0% for TW in one of the environments (i.e., no significant markers were found for the trait), to 148.3% for GY. The smallest range of the values was observed again for the trait HD.

Figure 2 summarizes comparison of estimates of a, scaled by the trait mean value, obtained for data set 3. Here, the estimates based on the genotype were much smaller than the ones based just on the phenotype. For four of the traits, the phenotypic estimate exceeded 50% of the mean value; the total genotypic effect was never larger than 18% of the mean.

Fig. 2
figure 2

Scatterplot of genotypic estimates of the total additive effect vs. corresponding phenotypic estimates (both values expressed as % of the mean value of the trait)

Full size image

Simulation study

Table 1 summarizes results of simulations performed to compare the estimates obtained by the phenotypic and genotypic methods.

Table 1 Phenotypic and genotypic estimates of the total additive effect obtained in the simulation study
Full size table

The mean phenotypic estimate was always bigger than 10, the true value (only for 10 QTL in many linkage groups the effect was 9.42). The largest values were obtained for 1 QTL, which may be explained by the fact that in this situation there is 50% of minimal and 50% of maximal lines, not 3% as the method assumes, and the difference between extreme lines is overestimated. Also, a large value was obtained for QTL located in one linkage group, as in this situation all QTL are linked, and their effects are accumulated in an additive way, which increases the difference between extreme lines. We observe also that increasing the error variance results in an increase of the phenotypic estimate, which is a result of a bigger range of mean values for lines.

As to the mean genotypic estimates in Table 1, they were smaller than 10, unless there was 1 QTL or one linkage group. The values decreased with increasing number of QTL or linkage groups, that is, when it was more difficult to find all assumed significant QTL with the stepwise regression. The mean genotypic estimates were also smaller when QTL effects were not equal, which is caused by a difficulty with finding smaller effects.

The mean difference between the phenotypic estimate and the genotypic estimate was always positive and was the smallest when many QTL were assumed.

The last two columns of Table 1 show that, in general, a decrease of the estimates was accompanied by an increase of their mean squared error.

Tables 2 and 3 contain results of simulations performed to analyse properties of the genotypic estimates based on weighted regression. They were always bigger than the “unweighted” ones. In Table 2 it is seen that a difference exist is also in the situation when the assumed variances for lines were all equal; it was observed that this was caused by a bigger number of markers selected as significant by the weighted regression. This property probably caused the weighted effect to be bigger in the situation when the variance of extreme lines was larger. Theoretically, the larger variance of extreme lines, and, consequently, their smaller weights in regression, decrease the regression coefficients. This is because the means of marker classes are shifted towards non-extreme values. An opposite effect of increasing the estimate by assuming smaller variance for extreme lines was correctly observed. If all assumed variances were different, just a shift of weighted means for extreme lines was observed, without a big change of the estimate of the additive effect. The mean squared errors of the weighted estimates were bigger. The weighted estimates were always closer to the phenotypic estimates than the unweighted ones.

Table 2 Phenotypic and genotypic estimates of the total additive effect obtained in the simulations performed to study the performance of weighted regression
Full size table
Table 3 Phenotypic and genotypic estimates of the total additive effect obtained in the simulations performed to study the performance of weighted regression
Full size table

In Table 3 it can be seen that the difference between unweighted and weighted estimates decreased when the number of QTL and the number of linkage groups with QTL increased. The weighted estimates were closer to the phenotypic ones than unweighted estimates in all situations except for the last case, when the number of QTL and linkage groups was large; here, the weighted estimate was closer to the true value of 10.

Discussion

The aim of the breeding process is obtaining new genotypes with characteristics improved over the parental forms. The parameter connected with the additive gene action can influence decisions about usefulness of the breeding material for that purpose. In this paper the methods of estimation of the total additive gene action effect were compared analytically, numerically and by simulations.

The analytic comparison shows that, under the assumption of correct segregation and no linkage between markers, the formulae for the phenotypic and genotypic estimators are comparable, and that the additive effect of each individual QTL is smaller than the phenotypic effect. Therefore, the number of declared QTL is mostly responsible for the relation between phenotypic and genotypic estimators.

The numerical comparison of estimates of the additive gene action effect was based on three examples: two concerning doubled haploid lines of barley and one concerning recombinant inbred lines of maize. In total 162 sets of observations were analyzed. The comparison shows that usually the genotypic estimate of a is smaller than the phenotypic one. So, the situation is different than in the case study reported by Snape (1997). But our results agree with the intuition, because the phenotypic estimate is an estimate of the total additive effect of all genes influencing the trait, whereas the estimate obtained on the basis of genotypic observations is an estimate of the additive action of only selected genes. The range of differences between the two estimates observed in our study is most probably a consequence of considering a large variety of experimental situations, traits and environments.

The simulation study performed to compare the estimation methods could not, obviously, take into account all possible experiemental situations. In our opinion, however, the applied combinations of parameters correspond to the cases often met in real QTL studies. The results obtained from the simulation study show some stability of the properties of both methods of estimation over different types of genetic material. The lack of influence of the number of chromosomes on estimation of additive gene action effect by both methods and on conclusions concerning the comparison of proposed methods of estimation, shows good prospect for application of our conclusions for different plant species. Moreover, the lack of influence of the distance between markers shows a possibility of using those methods for different genetic maps.

In contrary, the number of assumed QTL and their assumed positions, in one or many linkage groups, were found to have a large effect on the estimates and their comparison. The phenotypic estimate decreased towards the true value of a when the number of assumed QTL was increasing, that is, when the applied criterion of selection of extreme lines (3%) became realistic. For the largest number of QTL, 10, it could be smaller than the true value, as the genotypic combinations generating extreme lines were not adequately represented in the simulated sample. Also, the phenotypic estimate tended to the true value when the number of linkage groups with QTL increased, that is, when no excessive accumulation of linked individual effects took place. The genotypic estimate decreased its value in approximately the same way as the phenotypic one. However, it could become smaller than the true value already for a moderate number of QTL, 4, and for a moderate number of linkage groups, 2, that is, when, in addition to underrepresentation of the tails of the distribution, also the problems with identifying all significant QTL were accumulating. The difference between the phenotypic and the genotypic estimate was the smallest when there was many QTL, that is, when a model closest to a truly polygenic one applied.

The discrepancy between phenotypic and genotypic estimates of the total additive effect, observed in both our numerical and simulated comparisons, comes partially from the fact that, obviously, the genotypic methods does not find all genes affecting the trait. Our study of weighted regression shows, however, that the difference between the phenotypic and genotypic estimate can be decreased when we agree that a natural possibility of a smaller variance of the minimal and maximal lines, located at the extremes of the phenotypic distribution, exists. When appropriate bigger weights are used in regression of the trait on marker data, the individual QTL effects are increased, and the number of QTL found is bigger than in ordinary regression. As a result, the total genetic effect is expected to be closer to the true value.

With respect to the weighted regression, it is also interesting to note that the phenotypic estimate of the additive effect a given by (1) is equivalent to the coefficient of regression of phenotypic values of extreme lines on a dummy variable with elements 1 and −1 for, respectively, maximal and minimal lines. In other words, its calculation is equivalent, theoretically, to performing weighted regression of phenotypic observations on one hypothetical marker, with weights equal to 1 for extreme lines and 0 for other lines. Now, QTL localization methods by ordinary regression use many markers and weights equal for all lines. So, the weighted regression can be seen as an intermediate approach, which can give more weight to the extreme lines, thus closing the gap between the phenotypic and genotypic estimates of the additive effect. We see this fact as interesting from theoretical rather than practical point of view. The weighted regression can rarely be applied in practice, as usually only the plot data are available, or the number of measured plants is small, which may affect the quality of the variance estimates.

We admit that, to some extent, the results obtained by the estimation method utilizing the genotypic information depend on the QTL localization method used. The method used here was a simple one, of stepwise regression. However, a comparison with the sources reporting analysis of the same data by using other methods, also interval mapping (Frova et al. 1999; Hayes et al. 1993; Hayes and Iyarnabo 1994; Sari-Gorla et al. 1999; Tinker et al. 1996) shows that comparable results were obtained, with respect to the number of QTL and amount of variability explained by the model. This suggests that in our computations no downward bias, resulting from an incomplete linkage between markers and QTL, was observed. Also, the model used for estimation of additive effects does not take into account epistasis. Preliminary computations using a model with QTL × QTL interactions suggest that in such a model the estimated additive effect is usually decreased. So, the conclusions reached here should not be changed when epistasis is considered. However, this has not been proved yet by simulations.

Note that our results obtained from the data analysis, showing that usually the genotypic estimate was smaller than the phenotypic one, and results of simulations, showing that it was smaller than the true value, suggest that no upward bias, in the sense of Melchinger et al. (1998), was observed. Therefore, no cross-validation described by these authors was used.

The general conclusion from our results is that, in practical studies, estimates of the total additive effect for quantitative trait loci smaller than the total phenotypic estimate should be expected. If an opposite situation is found, it should be analysed, for example, if the genetic assumptions of correct segregation and no close linkage among markers are fulfilled.