1 Introduction

Starting an investment plan is the beginning of entering the business world. To survive and succeed in the complex environment of the global business, steps must be firmly taken from the beginning, along with optimal decisions (Hornstein 2015). A project involves an organization of individuals that collects resources to achieve a specific goal (Svejvig and Andersen 2015). The project management can also be defined as programming, directing, and controlling resources to achieve specific goals (Mir and Pinnington 2014). Time, cost, risk, quality, environmental impacts, social influences, etc., are the main criteria of a project that all project managers always seek to complete projects in the shortest possible time, with the lowest possible cost, with the lowest risk, and at the highest level of quality; but the question is how can these goals be achieved? (Nicholas and Steyn 2017). The main challenge for project managers is to select an appropriate approach to find the optimal combination of time, cost, risk, and quality of project activities in order to achieve the above goals (Marcelino-Sádaba et al. 2015). The emergence of new contracts that increase the quality of project execution operations while reducing their time, cost, and risk requires developed models that consider not only time, cost, and risk but also the quality factor in the evaluation and the optimization of project execution procedures (Kaiser et al. 2015). Reducing the risk, cost, and time of execution and improving its quality are different objectives of management that are not consistent with each other. This is the task of management accountants, who help construction engineers to solve the time, cost, risk, and quality trade-off in investment plans and construction projects (Hazır 2015). Project management is a collection of knowledge, skills, tools, and techniques dealing with a project’s activities by integrating some related processes including initial processes, scheduling, implementation, control, and finalization of project objectives (Kerzner 2017). In an exclusive project management approach, traditional project management practices are used to lead and direct the project team. In this approach, it is assumed that the project manager is the best person for scheduling, controlling, and managing the team. In this way, the project manager schedules the activities and assigns them to the team members. The relationship between the team members and the project manager is often unilateral, and the project manager is responsible for solving all project problems (Turner 2014). Tavana et al. (2014) presented a multi-objective multi-mode model for solving preemptive time–cost–quality trade-off project programming problems using generalized assumptions and predecessor relationships. The proposed model had three unique attributes: (1) the default activity (taking into account some limitations such as the minimum time before the first interruption, the maximum number of interruptions for each activity, and the maximum time interval and restart); (2) simultaneous optimization of conflicting objectives (such as time, cost, and quality); and (3) general preconditions of relationships between activities. Zhu (2016) developed mathematical models of cost–time–quality trade-off project. The parameters of project activities were clearly estimated on the basis of gray numbers. The most important aspect of the proposed model was to consider the uncertainty in project programming data in the form of gray numbers. Hornstein (2015) applied a novel theory for the first time in the project scheduling area to identify the best Pareto-based solutions for preemptive time–cost–quality trade-off projects. A framework for integrating multi-criteria decision-making (MCDM) approaches with multi-objective optimization techniques was also proposed in this study. Kaiser et al. (2015) investigated the multi-objective bees algorithm with differential evolutions for the project quality–time–cost trade-off using the resource-constrained project programming. Koo et al. (2015) developed an integrated multi-objective optimization model to provide the Pareto front in six steps: (1) statement of the problem, (2) definition of optimization goals, (3) creating a data structure, (4) standardization of optimization goals, (5) definition of fitness function, and 6) introduction of genetic algorithm. Mohammadipour and Sadjadi (2016) reviewed the project cost–quality–risk trade-off analysis in a time-constrained problem. They proposed a multi-objective mixed-integer linear programming for minimizing “project total extra cost,” “project risk enhancement,” and “project total quality reduction” because of time constraint. Muriana and Vizzini (2017) presented a multi-objective gray linear model to find the critical path of the project using risk, time, cost, and quality parameters of the project. Tran and Long (2018) reviewed the project time–cost trade-off and its application in a major construction project and introduced risk–source trade-off as the innovation of their own study. Tabrizi (2018) evaluated the project risk–quality–time–cost trade-off with the help of dolphin technique. In this paper, Dolphin’s group hunting algorithm was presented as a new evolutionary optimization method. The proposed algorithm was inspired by clever and collective hunting of dolphins. Zou et al. (2018) evaluated the balance between time and cost of the project using Bayes’ theorem to update project time and cost estimation, taking into account the cost, time, and resource constraints under conditions of uncertainty. They also used a meta-heuristic to solve the problem which saved time considerably. Farazmand and Beheshtinia (2018) analyzed the time–cost–environment balance with an integrated genetic algorithm. The purpose of the research was to minimize the environmental impact costs and also to minimize the entire project time in order to minimize late payment fees. Since exact solution methods had no high efficiency, they used genetic algorithm to obtain optimal solutions for large size problems.

Mahmoudi and Feylizadeh (2018) evaluated project programming with benefit–time trade-off. They considered several discrete times with four payment methods. The final benefit depends on end time because the cost would be reduced by decreasing project time. Since it was an NP-hard problem, the variable neighborhood search method was used to solve the problem.

Rui et al. (2018) examined the programming project of oil and gas development using cost–time–quality trade-off approach with the goal of minimization of project total time and maximization of project quality under conditions of uncertainty. They addressed the problem with a multi-objective approach and Pareto front solutions and used fuzzy theory to counteract the uncertainty of the parameters.

One of the important goals in scheduling a project is to analyze the impacts among the various components of the project. After creating a CPM (critical path method), the influence of time and budget shortages has been firstly introduced (as compared to other issues) as one of the frequent issues discussed in the literature. Badiru and Osisanya (2016) developed an analytical model for the cost–time problem using the optimal control theory in the Markov logic network. Ke et al. (2015) removed the hypothesis of the fixed costs of activity over the project time and spent the estimated cash flow for the cost–time optimization. Tran and Long (2018) proposed a different method for consolidated cost–time analysis in a project network in fuzzy environments. Zhang and Fan (2014) developed a linear programming model to reduce the initial period of the project according to the cost optimization approach. Liu et al. (2016) developed an effective time–cost optimization method for resource-constrained project scheduling where activities have been completed with limited resources.

According to the literature review, there is no research in the area of scheduling projects considering sustainable development concepts. Moreover, some limited researchers studied the scheduling problems under uncertain conditions. As a consequence, this paper intends to optimize the duration of projects’ activities with respect to socio-environmental factors under uncertain conditions. One of the new approaches in modeling the project management in the field of cost–time balance, scheduling, and resource allocation is robust programming. This approach tries to bring matters closer to real-world conditions by taking into account the value of parameters in non-realistic quantities. Robust programming is mainly applied in the field of project scheduling, for example the works of Demeulemeester and Herroelen (2011), Van de Vonder et al. (2008), Lambrechts et al. (2011), and Herroelen and Leus (2005).

In the resource allocation discussion, several studies including Alcaraz and Maroto (2001), Deblaere et al. (2007), Ali et al. (2004), and Boshkovska et al. (2017) applied robust programming. The application of robust programming methods has been less considered in the optimization of project management, emphasizing time–cost–risk trade-off, and considering sustainable development criteria, and no research has been found according to the literature review. However, the parameters under the conditions of uncertainty can be much closer to the real-world conditions (Ben-Tal et al. 2009).

In this research, a multi-objective mathematical model under uncertainty is presented taking into account cost, risk, and sustainable development criteria including environmental and social factors. According to the literature research, this study examines project scheduling considering socio-environmental factors for the first time. Given the variety of methods used to deal with the uncertainty of the parameters, one of the most common and most practical methods based on the robust programming provided by Bertsimas and Sim (2003) is employed in this study. According to Mulvey et al. (1995), Ben-Tal et al. (2009), and Beyer and Sendhoff (2007), in the robust programming method, the uncertainty parameters are placed in distinct intervals whose distribution function is not considered previously. The newly developed version of the epsilon-constraint method proposed by Mavrotas and Florios (2013) is used to solve the problem.

The structure of the paper is organized as follows. Section 2 describes the statement of problem, and Sect. 3 states the presented model under the conditions of uncertainty using the proposed robust programming. Section 4 details the problem-solving method, and Sect. 5 is related to the computational results and required analyses. The final section summarizes the findings.

2 The statement of problem

These days, the organizations are faced with different projects, and it is important to accomplish the project in a timely manner, taking into account the predecessors for activities and resources to maximize organizational profit. One of the most difficult parts of the project is customer satisfaction while scheduling based on the time horizon of the project. There are numerous challenges when the customers ask contractors to shorten the duration of the project and it will have different implications for the quality and profitability of the project. Therefore, the project executives need to make changes at the start and end of the project’s activities to meet the needs of the project owners. These objectives generally include time delays cost, risk factors, and effective factors in sustainable development, such as socio-environmental ones. In the following, the paper outlines each of the factors that are actually the objective functions of the proposed mathematical model.

2.1 Minimize the cost of time delays in project

In any construction or industrial project, some customers want to reduce the duration of the project execution. Failure to fulfill customers’ demands confronts the organization with delays in the implementation of the project. Therefore, the first objective function is to minimize the maximum delay time in the project. These delays usually lead to some penalties and consequently cost estimate problems (Orm and Jeunet 2018).

2.2 Minimize the risk

The second goal is to minimize the entire project risk. According to the definition of Project Management Body of Knowledge (PMBOK), risk is said to be an event in the future that is likely to occur, and if it occurs, it will have a positive or negative effect on the project. The risks that have a positive impact are called desired risks or opportunities, and the risks that have negative effects are called undesirable risks or threats. In this research, the risk was considered as a threat (Mohammadipour and Sadjadi 2016).

2.3 The sustainable development in the proposed problem

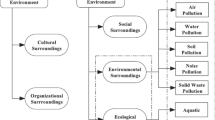
One of the most important aspects of innovation in this research is considering the objectives of sustainable development as objective functions. These objectives will include environmental impacts (Kivilä et al. 2017) and social impacts (Silvius et al. 2017). The proposed model tries to optimize resource allocation, activity scheduling, and other constraints related to the defined objectives. In the following, we describe each of the dimensions of sustainable development.

2.3.1 Minimization of environmental destructive effects

Some of the important functions of environmental impact assessment (EIA) are the implementation of construction activities in projects and the prevention of excessive construction waste and carbon dioxide produced by construction machinery (Kivilä et al. 2017). Evaluation of environmental impacts is an operationally integrated vision for sustainable development, a view that considers the interconnected system to be sustainable in and with the environment (Kerzner 2017). In this system, each type of activity is interconnected in the economic, social and environmental dimensions, and the others. This concept has been expressed in the most expressive and explicit form in the article 50 of the constitution of Iran (Asasi 1980). Since the EIA is one of the most appropriate criteria for sustainable development and environmental management in the world, it should be in the form of legal requirements. There are currently laws, regulations, and approvals in the field of EIA in Iran. Some of them directly and explicitly monitor the obligations of construction and development projects for EIA. On the other hand, some others do not directly refer to the EIA, but they can be regarded as equivalent to the EIA regulations because of having the same concepts and preventive aspects. Some of the rules and regulations that directly concern EIA are: Article 105 of the Third Plan of Economic, Social and Cultural Development of the Islamic Republic of Iran, Article 71 of the Fourth Development Plan Act, Article 10 of the Noise Pollution Prevention Regulations, and Decrees No. 138, 156, 166, 196, 237, 249, and 250 of the Supreme Council for the Protection of the Environment. Other relevant laws and regulations are Articles 60, 85, and of the Third Development Plan Law, Articles 12 and 13 of the Law on the Prevention of Air Pollution, and Article 11 of the Water Pollution Prevention Regulations. With regard to the criteria for differences in the legal systems, Germany and France among the countries subject to the Romano-Germanic Legal System, and Canada and the United States among the countries governed by the Anglo-Saxon legal system are selected to investigate the EIA regulations. By examining the EIA regulations of developed countries and comparing them with the existing laws in Iran, it is generally concluded that the EIA consequences in Iran are of a general but not integrated level. Although the European Union (EU) countries, including Germany, France, and Canada, have different administrative and political systems, they have essentially comprehensive integrated environmental regulations.

2.3.2 Minimization of social destructive effects

Social assessment is the process of providing a framework for prioritizing, collecting, analyzing, and categorizing social information and participating in the design and provision of executive operations for the construction project.

In other word, social impacts of construction projects indicate how projects can satisfy the current and future needs of people (Wang et al. 2016). Unpredictable consequences of construction projects can severely reduce the benefits of these projects, highlighting the importance of assessing social impacts. With respect to the type of construction projects, different aspects of social impacts should be considered. For example, Tilt et al. (2009) investigated some factors such as land acquisition, resettlement of people near the projects, and resource depletion on the dam projects. Capital performance, health and safety issues, accessibility to the site, usability psychology are some criteria developed by Almahmoud and Doloi (2015) according to the stakeholders’ perspective. Xiahou et al. (2018) proposed a framework based on fuzzy AHP to assess the social impact of construction projects. They defined five categories including socio-economy development, socio-environment development, social flexibility, public service development, and environment and resource conservation for social assessment of construction projects. Considering the importance of social impacts, this paper intends to investigate this topic. Moreover, all implications of the plan are rated based on their impact on the social environment. Finally, the optimization approach is developed based on these ratings (Chawla et al. 2018).

3 The proposed mathematical model

All the economic, environmental, social, and risk objective functions are considered in this model. A comprehensive mathematical model with four objective functions is proposed to optimize the resource allocation and scheduling the execution of the activities in the construction projects. The purpose of proposing such a model is considering all the effects imposed by the economic, environmental, social, and risk criteria on the final decision-making of managers.

Indices, parameters, and variables are presented as follows. It should be noted that the model structure is firstly proposed by consideration of deterministic parameters and then is described under uncertainty.

3.1 Indices

\(i\): Predecessor activity index.

\(j\): Activity index.

\(k\): Successful activity \({\text{k}}\) index.

\(r\): Risk-affected activity index.

\(t\): Number of delayed time units of activities index.

\(l\): Last activity index.

3.2 Parameters

\({\text{Cost}}_{{\text{j}}}\): Cost of increase or decrease in the delay of one time unit in activity j.

\({\text{T}}_{{\text{j}}}\): Execution time of activity j.

\({\text{MD}}_{{\text{j}}}^{{{\text{max}}}}\): The maximum allowable delay time unit for activity j.

\({\text{FT}}_{0}\): Project completion time which is defined by customer.

\({\text{ADfS}}_{{{\text{ij}}}}^{{{\text{min}}}}\): The minimum time between finish time of activity i and start time of activity j.

\({\text{ADSS}}_{{{\text{ij}}}}^{{{\text{min}}}}\): The minimum time between start time of activity i and start time of activity j.

\({\text{ADff}}_{{{\text{ij}}}}^{{{\text{min}}}}\): The minimum time between finish time of activity i and finish time of activity j.

\({\text{ADSf}}_{{{\text{ij}}}}^{{{\text{min}}}}\): The minimum time between start time of activity i and finish time of activity j.

\({\text{RP}}_{{{\text{jt}}}}\): The project risk probability by reducing the time t in activity j.

\({\text{RE}}_{{{\text{jrt}}}}\): The risk effect on activity j affected by r with t unit of delay.

3.3 Decision variables

\({\text{X}}_{{{\text{jt}}}}\): If activity j delays t unit, it will be one otherwise will be zero.

\({\text{ET}}_{{\text{j}}}\): The earliest start of activity j.

\({\text{LT}}_{{\text{j}}}\): The latest finish of activity j.

3.4 The structure of model

Model 1

$$\min Z_{1} = \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{{MD_{jn}^{\max } }} \left( {t {\text{Cos}} t_{j} X_{jt} } \right)$$
(1)
$$\min {\text{Z}}_{1} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{MD_{jn}^{max} }} \left( {{\text{t Cost}}_{{\text{j}}} {\text{X}}_{{{\text{jt}}}} } \right)$$
(2)
$$\min {\text{Z}}_{3} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{MD_{jn}^{max} }} \left( {{\text{t }}SOC_{j} {\text{X}}_{{{\text{jt}}}} } \right)$$
(3)
$$\min {\text{Z}}_{4} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{TR}}_{{\text{j}}}^{{{\text{max}}}} }} \mathop \sum \limits_{{{\text{r}} = 1}}^{{\text{R}}} {\text{RP}}_{{{\text{jt}}}} {\text{ I}}_{{{\text{rjt}}}} {\text{ X}}_{{{\text{jt}}}}$$
(4)
$${\text{LT}}_{{\text{l}}} = {\text{FT}}_{0}$$
(5)
$$\mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{TR}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{X}}_{{{\text{jt}}}} \le 1\forall {\text{j}}$$
(6)
$${\text{LT}}_{{\text{j}}} - {\text{ET}}_{{\text{j}}} \ge \left( {{\text{T}}_{{\text{j}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right)\forall {\text{j}},{\text{n}}$$
(7)
$${\text{ES}}_{{\text{j}}} - {\text{ET}}_{{\text{j}}} \ge \left( {{\text{T}}_{{\text{j}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) + {\text{ADfS}}_{{{\text{ij}}}}^{{{\text{min}}}} \forall {\text{i}},{\text{j}},{\text{n}}$$
(8)
$${\text{LT}}_{{\text{k}}} - {\text{LT}}_{{\text{j}}} \ge \left( {{\text{T}}_{{\text{k}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) + {\text{ADfS}}_{{{\text{ij}}}}^{{{\text{min}}}} \forall {\text{i}},{\text{j}},{\text{n}}$$
(9)
$${\text{ET}}_{{\text{j}}} - {\text{ET}}_{{\text{i}}} \ge {\text{SS}}_{{{\text{ij}}}}^{{{\text{min}}}} \forall {\text{i}},{\text{j}}$$
(10)
$${\text{LT}}_{{\text{k}}} - {\text{LT}}_{{\text{j}}} \ge \left( {{\text{T}}_{{\text{k}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) - \left( {{\text{T}}_{{\text{k}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) + {\text{SS}}_{{{\text{jk}}}}^{{{\text{min}}}} \forall {\text{j}},{\text{k}}$$
(11)
$${\text{ET}}_{{\text{j}}} - {\text{ET}}_{{\text{i}}} \ge \left( {{\text{T}}_{{\text{i}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) - \left( {{\text{T}}_{{\text{j}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) + {\text{FF}}_{{{\text{jk}}}}^{{{\text{min}}}} \forall {\text{j}},{\text{k}}$$
(12)
$${\text{LT}}_{{\text{k}}} - {\text{LT}}_{{\text{j}}} \ge {\text{ADff}}_{{{\text{ij}}}}^{{{\text{min}}}} \forall {\text{j}},{\text{k}}$$
(13)
$${\text{ET}}_{{\text{j}}} - {\text{ET}}_{{\text{i}}} \ge {\text{ADSS}}_{{{\text{ij}}}}^{{{\text{min}}}} - \left( {{\text{T}}_{{\text{j}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right) \forall {\text{i}},{\text{j}}$$
(14)
$${\text{LT}}_{{\text{k}}} - {\text{LT}}_{{\text{j}}} \ge {\text{ADSf}}_{{{\text{ij}}}}^{{{\text{min}}}} - \left( {{\text{T}}_{{\text{j}}} - \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{MD}}_{{\text{j}}}^{{{\text{max}}}} }} {\text{t X}}_{{{\text{jt}}}} } \right)\forall {\text{j}},{\text{k}}$$
(15)
$$LT_{j} ,{ }ET_{j} \ge 0,{ }X_{jt} \in \left\{ {0,1} \right\} \forall {\text{j}},{\text{t}}$$
(16)

As it can be seen, the problem studied in this research consists of four objective functions. The objective function (1) minimizes the total time delays in the project activities execution. The objective function (2) minimizes the delay risk in the project activities execution. The objective function (3) minimizes the destructive environmental effects and the objective function (4) minimizes the destructive social effects caused by the delay in each one of the intended project activities. Indeed, these objective functions try to prevent the model from delays, which cause environmental pollution or huge social unsatisfactory. Constraint (5) defines the time limitation specified by the customer for the project. This constraint, in fact, guarantees that the whole project is finished before the maximum time specified by the customer. Constraint (6) guarantees that if one activity is going to delay, this delay occurs only in one of the time intervals defined for the project. Constraints (7) to (15) calculate the critical time of the project and assign the suitable start and finish time of each activity in each project.

3.4.1 Describing the problem structure under uncertainty

Since the cost parameters of delay time, the project risk probabilities, and the amount of risk effect on the activities are uncertain, the robust programming proposed by Bertsimas and Sim (2003) is used in this paper. In this approach, the parameters have interval values instead of a certain value. All the uncertain parameters are as follow:

$$\widetilde{Cost}_{j} = \left[ {Cost_{j} - \widehat{Cost}_{j} ,Cost_{j} + \widehat{Cost}_{j} } \right]$$
$$\widetilde{RP}_{jt} = \left[ {RP_{jt} - R\hat{P}_{jt} .RP_{jt} + \widehat{RP}_{jt} } \right]$$
$$\widetilde{{{\text{ENV}}}}_{j} = \left[ {{\text{ENV}}_{j} - \widehat{{{\text{ENV}}}}_{j} .{\text{ENV}}_{j} + \widehat{{{\text{ENV}}}}_{j} } \right]$$
$$\widetilde{{{\text{SOC}}}}_{j} = \left[ {{\text{SOC}}_{j} - \widehat{{{\text{SOC}}}}_{j} .{\text{SOC}}_{j} + \widehat{{{\text{SOC}}}}_{j} } \right]$$

where for each parameter, the value having \(\left( \sim \right)\) sign is the final value of uncertainty, the value having \(\left( \sim \right)\) sign represents the variation in the interval, and the value without any sign represents the average value of the parameter.

3.4.2 Robust programming approach

Transforming a deterministic model into a robust one using the Bertsimas and Sim (2003) method is not dependent on the number of objective functions, and only the proved constraints of each objective function are added to the problem for other objective functions (Raith et al. 2018). Therefore, the robust optimization structure is first described and proved for the first objective function and then developed for other objective functions.

Generally, suppose \(\widetilde{Cost}_{j} = \left[ {Cost_{j} - \widehat{Cost}_{j} ,Cost_{j} + \widehat{Cost}_{j} } \right]\) presents the uncertainty for the first objective function. Moreover, index \(\left( {{\text{Jr}}} \right)\) denotes \(\widetilde{Cost}_{j}\) in which \(\widehat{Cost}_{j} \ne 0\). Thus, one can say \({\text{Jr}} = \left\{ {\left( {{\text{i}},{\text{j}}} \right):\widehat{Cost}_{j} > 0,{\text{j}} = 1, \ldots ,{\text{J}}} \right\}\). In order to control the uncertainty in obtaining the final solution, the parameter \({\Gamma }\) is used as the robust parameter. This parameter is in the \(\left[ {0,\left| {{\text{Jr}}} \right|} \right]\) interval and does not necessarily have an integer value. The main role of this parameter is to determine the number of coefficients that are at their maximum values (the worst possible condition). Indeed, \({\Gamma }\) number of coefficients \(\widehat{{{\text{Cost}}}}_{{\text{j}}} > 0\) will be at their maximum values and other parameters in the \({\text{Jr}}\) have a coefficient \(\Gamma - \Gamma\) and their varying values in the \(\widetilde{Cost}_{j} = \left[ {Cost_{j} - \widehat{Cost}_{j} ,Cost_{j} + \widehat{Cost}_{j} } \right]\) interval. Therefore, the structure of objective function is changed into the following.

Model 2

$${\text{M}}inZ = \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{{MD_{jn}^{max} }} \left( {t Cost_{jn} X_{jtn} } \right) + \mathop {\max }\limits_{{\left\{ {\begin{array}{*{20}c} {S:S \subseteq J, \left| S \right| \le \Gamma } \\ {\left( {j_{t} ,t_{t} } \right) \in \frac{J}{S}} \\ \end{array} } \right\}}} \left( {\mathop \sum \limits_{j = 1} \mathop \sum \limits_{t = 1} t \widehat{Cost}_{j} X_{jt} - \left( {\Gamma - \Gamma } \right) \widehat{Cost}_{{i_{t} j_{t} }} X_{{j_{t} t_{t} }} } \right)$$
(17)

Based on the structure of the changed objective functions and the above explanations, it is clear that if \(\Gamma =\left|Jr\right|\), then the proposed robust programming is equivalent to the Soyster (1973) robust programming (considering the worst case). Moreover, if \(\Gamma =0\), then no uncertainty is allowed in the model and the proposed robust programming is equivalent to the main deterministic model. Applicability of this method is in obtaining the results for intermediate values. But by slightly changing the structure of model 2 and using the basic concepts of operation research (OR), one can prove that model 2 is equivalent to a linear programming problem.

Theorem:

The proposed model 2 is equivalent to the following linear programming model.

Model 3

$${\text{M}}inZ\mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{t = 1}^{{TR_{j}^{max} }} \left( {t Cosr_{jn} X_{jtn} } \right) + \Gamma_{1} U_{1} + \mathop \sum \limits_{j,t} U1_{jt}$$
(18)
$$t \widehat{Cost}_{j} X_{jt} + U_{1} + U1_{jt} \ge 0,$$
(19)
$$U1_{jt} \ge 0,$$
(20)
$$U_{1} \ge 0,$$
(21)

Proof:

In order to prove this theorem, one can change the nonlinear terms of objective functions of model 2 into linear terms by introducing variable \(Z1_{jt}\) where \(\mathop \sum \limits_{{{\text{jtn}}}} Z1_{jt} \le \Gamma\). It should be noted that \(0 \le Z1_{jt} { } \le 1\).

Model 4

$$Min \mathop \sum \limits_{j = 1} \mathop \sum \limits_{t = 1} t \hat{C}ost_{j} X_{jt} Z1_{jt}$$
(22)
$$\mathop \sum \limits_{{{\text{jtn}}}} Z1_{jt} \le \Gamma ,$$
(23)

It is clear that the problem should have \(\Gamma\) number of variable \(Z1_{jt} = 1\) and one parameter \(Z1_{jt} = \Gamma - \Gamma\) in the optimal situation, which is equivalent to the nonlinear parts of objective function of the model 4. Using the strong duality theorem for variable \(\left( {X_{jt} } \right)_{{j = 1, \ldots ,J{ },{ }t = 1, \ldots ,T}}\) will have:

Model 5

$$Min \left( {\Gamma U_{1} } \right) + \left( {\mathop \sum \limits_{j.t} U1_{jt} } \right)s.t$$
(24)
$$t \widehat{Cost}_{j} X_{jt} + U_{1} + U1_{jt} \ge 0,$$
(25)
$$U1_{jt} \ge 0,$$
(26)
$$U_{1} \ge 0,$$
(27)

By combining Model 5 and the initial model, one can prove the theorem.

Similar to theorem 1, the robust optimization structure can be proved for other objective functions. Thus, model 6 is the final structure of the robust programming of the proposed model.

4 Model 6

$$M{\text{inZ}}_{1} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{TR}}_{{\text{j}}}^{{{\text{max}}}} }} \left( {{\text{t Cost}}_{{{\text{jn}}}} {\text{X}}_{{{\text{jtn}}}} } \right) + {\Gamma }_{1} {\text{ U}}_{1} + \mathop \sum \limits_{{{\text{j}},{\text{t}}}} {\text{U}}1_{{{\text{jt}}}}$$
(28)
$$\min {\text{Z}}_{2} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{MD_{jn}^{max} }} \left( {{\text{t }}ENV_{j} {\text{X}}_{{{\text{jt}}}} } \right) + {\Gamma }_{2} {\text{ U}}_{2} + \mathop \sum \limits_{{{\text{j}},{\text{t}}}} {\text{U}}2_{{{\text{jt}}}}$$
(29)
$$\min {\text{Z}}_{3} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{MD_{jn}^{max} }} \left( {{\text{t }}SOC_{j} {\text{X}}_{{{\text{jt}}}} } \right) + {\Gamma }_{3} {\text{ U}}_{3} + \mathop \sum \limits_{{{\text{j}},{\text{t}}}} {\text{U}}3_{{{\text{jt}}}}$$
(30)
$$\min {\text{Z}}_{4} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{J}}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{TR}}_{{\text{j}}}^{{{\text{max}}}} }} \mathop \sum \limits_{{{\text{r}} = 1}}^{{\text{R}}} {\text{RP}}_{{{\text{jt}}}} {\text{ I}}_{{{\text{rjt}}}} {\text{ X}}_{{{\text{jt}}}} + {\Gamma }_{4} {\text{ U}}_{4} + \mathop \sum \limits_{{{\text{j}},{\text{t}}}} {\text{U}}4_{{{\text{jt}}}}$$
(31)
$${\text{Equations }}\left( {5 - 15} \right)$$
(32)
$${\text{t }}\widehat{{{\text{Cost}}}}_{{\text{j}}} {\text{X}}_{{{\text{jt}}}} + {\text{U}}_{1} + {\text{U}}1_{{{\text{jt}}}} \ge 0,$$
(33)
$${\text{U}}1_{{{\text{jt}}}} \ge 0,$$
(34)
$${\text{U}}_{1} \ge 0,$$
(35)
$${\text{t }}\widehat{ENV}_{{\text{j}}} {\text{X}}_{{{\text{jt}}}} + {\text{U}}_{2} + {\text{U}}2_{{{\text{jt}}}} \ge 0,$$
(36)
$${\text{U}}2_{{{\text{jt}}}} \ge 0,$$
(37)
$${\text{U}}_{2} \ge 0,$$
(38)
$${\text{t }}\widehat{SOC}_{{\text{j}}} {\text{X}}_{{{\text{jt}}}} + {\text{U}}_{3} + {\text{U}}3_{{{\text{jt}}}} \ge 0,$$
(39)
$${\text{U}}3_{{{\text{jt}}}} \ge 0,$$
(40)
$${\text{U}}_{3} \ge 0,$$
(41)
$$t \widehat{RP}_{jt} \hat{I}_{rjt} X_{jt} + U_{4} + U4_{jt} \ge 0,$$
(42)
$${\text{U}}4_{{{\text{jt}}}} \ge 0,$$
(43)
$${\text{U}}_{4} \ge 0,$$
(44)

5 Solution method

The epsilon-constraint method is one of the known approaches to deal with multi-objective problems, and it solves this type of problems by transferring all the objective functions in each step to the constraint except one objective function.

In this method, one of the objectives is optimized while the other objectives are added to the problem as constraints. One of the difficulties with this method is its high dependence on the constraints’ values or the epsilons. Mavrotas and Florios (2013) transformed the constraints of objective functions into equalities using covariates in order to prevent production of weak values in the effective solutions, and the sum of these covariates is simultaneously inserted into the objective function as the second term with lower weight. Assume the following problem:

$$\begin{gathered} \max \left( {f_{1} \left( x \right),f_{2} \left( x \right), \ldots ,f_{p} \left( x \right)} \right)\; \hfill \\ s.t\; \hfill \\ x\smallint S \hfill \\ \end{gathered}$$
(45)

where x is the decision variable vector, \({\text{f}}_{1} \left( {\text{x}} \right),{\text{f}}_{2} \left( {\text{x}} \right), \ldots ,{\text{f}}_{{\text{p}}} \left( {\text{x}} \right)\) are the objective functions, and S is the feasible region. One of the objective functions is selected for optimization in the epsilon-constraint method, and the other objective functions turn to constraints with an upper constraint of \({\upvarepsilon }\).

$$\begin{gathered} \max f_{1} \left( x \right) \hfill \\ s.t \hfill \\ f_{2} \left( x \right) \ge e_{2} \hfill \\ f_{3} \left( x \right) \ge e_{3} \hfill \\ f_{p} \left( x \right) \ge e_{p} \hfill \\ x\smallint S \hfill \\ \end{gathered}$$
(46)

The augmented problem in the epsilon-constraint method is obtained as follows:

$$\begin{gathered} \max \left( { f_{1} \left( x \right) + eps \times \left( {\frac{{s_{2} }}{{r_{2} }} + \frac{{s_{3} }}{{r_{3} }} + \ldots + \frac{{s_{p} }}{{r_{p } }}} \right)} \right) \hfill \\ s.t \hfill \\ f_{2} \left( x \right) - s_{2} = e_{2} \hfill \\ f_{3} \left( x \right) - s_{3} = e_{3} \hfill \\ f_{p} \left( x \right) - s_{p} = e_{p} \hfill \\ x\smallint S \hfill \\ s_{i} \smallint R \hfill \\ \end{gathered}$$
(47)

where \({e}_{2}\) are the parameters of the values on the right-hand side and \(r_{2} ,r_{3} , \ldots ,r_{p}\) are the objective function ranges. \(s_{2} ,s_{3} , \ldots ,s_{p}\) are the covariates of the constraints and epsilon can set between 10–6 and 10–3.

But the objective function changes as follows by developing the augmented epsilon-constraint method:

$$\max \left( {{ }f_{1} \left( x \right) + eps \times \left( {\frac{{s_{2} }}{{r_{2} }} + 10^{ - 1} \times \frac{{s_{3} }}{{r_{3} }} + \ldots + 10^{{ - \left( {p - 2} \right)}} \times \frac{{s_{p} }}{{r_{{p{ }}} }}} \right)} \right)$$
(48)

A sort of lexicographic optimization is performed on other objective functions where there may be other optimums. For instance, with this formula, the solver will find the optimum solution for \(f_{1}\) and then try to optimize \(f_{2}\) and then \(f_{3}\) and others. But the sequence of optimizing \(f_{2} \ldots f_{3}\) is different from the previous formulation method. While in this method, we force the constrained objective functions to sequentially optimize. First, the variation ranges of \(p - 1\) objective functions which will be used in the constraint are obtained using the balance table. Then, the \(kth\) objective function range is divided into \(q_{k}\) equal intervals and thus all the grid points are \(q_{k} + 1\) where the \(kth\) objective function is used to change the parameter of the right-hand side values \(e_{p}\). The total number of elements is \(\left( {q_{1} + 1} \right) \times \left( {q_{2} + 1} \right) \times \ldots \left( {q_{p} + 1} \right)\) and \(r_{k}\) is the range of the objective function. We calculate \(2, \ldots ,{\text{p}}\) objective function range for each objective function. Then, we divide the range of the \(kth\) objective function by the equal distances of \(q_{k}\). \(r_{k}\) would be the range of the \(kth\) \(\left( {k = 2, \ldots ,p} \right)\) objective function. The decomposition step for this objective function is defined as follows:

$$step_{k} = r_{k} /q_{k}$$
(49)
$$e_{kt} = fmin_{k} + t \times step_{k}$$
(50)

The right-hand side values for the corresponding constraint in the \(tth\) iteration in the objective function are as follows:

\(fmin_{k}\) is the minimum of the objective function and \(t\) is the number of the specific objective function. After the optimization, the surplus variable and the bypass coefficient are calculated as \(b = int\left( {s_{2} /step2} \right)\) where \(int()\) is the floor function. When the surplus variable \(s_{2}\) is higher than \(step2\), the next iteration yields the same result except for the surplus variable, which now possesses value of s2-step2, causing the iteration to be redundant; consequently, the bypass coefficient shows how to ignore many of the successive iterations. The aim of this method is to propose and optimally evaluate the main epsilon-constraint method, which is suitable to deal with multi-objective integer programming problems. This method has proved that it is more effective in providing an exact Pareto set of solutions in the integer programming problem compared to its previous version and some other common methods (Mavrotas and Florios 2013).

6 Computational results

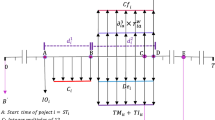
In this section, a numerical example is solved using the proposed model based on the information from an industrial project and the results are discussed. It should be noted that since the project has 21 activities, it can be solved using the CPLEX solver (which is an optimization software package) and the improved epsilon-constraint method. The initial information of this project is presented in Table 1.

Table 1 Information about the project
Full size table

The activity number is in the first column and the title of each activity is described in the second column of Table 1. The delay cost in each time unit of each activity execution is presented in the third column, and the execution time and the allowed time for each activity delay are presented in the fourth and fifth columns, respectively. According to Fig. 1 which is the Gantt chart of the project activities, it can be seen that the total project execution time is 27 days. This time should be reduced by four time units so the project could be delivered based on the customer desire. Other information associated with the project is presented in Tables 2, 3, 4, 5, and 6.

Fig. 1
figure 1

Gantt chart of implementing the project activities

Full size image
Table 2 Probability of project risk by reducing each unit time per activity
Full size table
Table 3 The minimum time between finishing one activity and starting another activity
Full size table
Table 4 The minimum time between the start of an activity and the start of another activity
Full size table
Table 5 The minimum time between the end of an activity and the end of another activity
Full size table
Table 6 The minimum time between the start of an activity and the end of another activity
Full size table
Table 7 The mean and uncertainty level of the parameters in the objective functions of the problem
Full size table

Based on the information in Table 2, the probability of the risk occurrence in the time unit reduction is a value between 0 and 1 which denotes the risk percentage. For instance, if activity 5 experiences 2 days of time reduction, the project execution risk is increased by 20 percent. Other information is analyzed with the same procedure. To reach this information, expert judgment can be a good solution in each project.

The minimum time between finishing one activity and starting another activity is described in Table 3. For instance, the minimum time between finishing activity 3 and starting activity 7 would be equal to 8 time units. However, the time difference between starting activity 3 and starting activity 7 is equal to 9 time units which is presented in Table 4. There are similar analyses for other activities.

The minimum time between finishing one activity and finishing another and the minimum time between starting one activity and finishing another activity are presented in Tables 5 and 6, respectively. For instance, based on Table 5, \(FF\left( {4 - 7} \right) = 12\) and based on Tables 6 and 7, \(SF\left( {4 - 7} \right) = 13\) are the time units. Thus, the execution time of activity 4 should be equal to one time unit which is calculated correctly based on Table 1.

It should be noted that values related to the parameters of the objective function are randomly in the following unknown interval.

The upper bound of robust parameters \(\Gamma_{1} , \Gamma_{2} , \Gamma_{3} ,\) and \(\Gamma_{4}\) should be first specified. Since the upper limit of each robust parameter is equal to the maximum number of parameters having uncertainty in the related objective function, one can say that \(\Gamma_{1} \in \left[ {0,21} \right], \Gamma_{2} \in \left[ {0,420} \right], \Gamma_{3} \in \left[ {0,21} \right]\), and \(\Gamma_{4} \in \left[ {0,21} \right]\). These numbers are obtained by calculating the number of parameters in each objective function, which is the multiplication of the indices of the related parameters. For instance, the upper limit of parameter numbers of \(\Gamma_{2}\) is equal to the multiplication of \(j = 21\) by \(t = 20\) which is \(420\). Similar calculations are performed for other robust parameters.

The exact determination of the robust parameters is very difficult and it is always dependent on the opinion of the decision-maker and thorough knowledge about the research problems (Raith et al. 2018). Thus, one cannot consider a unique value for these parameters. Therefore, solving the research problem is done in different scenarios and with different values of robust parameters.

6.1 The first scenario: the average value of all robust parameters \(\left( {{\varvec{\varGamma}}_{1} = 10.5} \right),\user2{ }\left( {{\varvec{\varGamma}}_{2} = 210} \right),\user2{ }\left( {{\varvec{\varGamma}}_{3} = 10.5} \right),\user2{ }\left( {{\varvec{\varGamma}}_{4} = 10.5} \right)\)

Nearly half of the parameters in the objective functions would have uncertainty in solving the proposed example using the average value of the robust parameters. Thus, one can say that the first scenario represents a semi-definite condition for the problem. After solving the problem using the epsilon-constraint method and the CPLEX solver which is currently the most powerful solver for MIP (mixed-integer programming) problems (CPLEX 2003), the results are illustrated as the Pareto front in Fig. 2. It should be noted that the Pareto front is a 4D figure and cannot be directly shown, thus the obtained Pareto front is demonstrated in the form of unrepeated 3D combinations. The value of each objective function is also reported between zero and one based on the standard.

Fig. 2
figure 2

Triple compounds from Pareto front scenario 1

Full size image

The Pareto front of the first, the second, and the third objective functions is illustrated in Fig. 2-a. As can be seen, all the objective functions have a value between \(0.5\) and \(0.9\). These values are standardized, and their real values can be produced by the following transformation function.

$$X = \frac{{x - \left( {x_{max} + x_{min} } \right)/2}}{{\left( {x_{max} - x_{min} } \right)/2}}$$
(51)

where \(X\) denotes the standardized value, \(x\) is the main value of the parameter, and \({x}_{max}\) and \({x}_{min}\) are the maximum and minimum values of the parameters, respectively. The main and standardized values of the parameters can be found in Table 8.

Table 8 Home values and standardized parameters
Full size table

A number of 50 Pareto members are produced in this scenario, and each of them can be implemented in the system as a final solution. However, the final selection of the Pareto member is done based on the opinion of project managers, and the main decision-makers thus all the Pareto members should be proposed to them in order to select the final member.

Based on Table 9, the values of the first to the fourth objective functions are shown in columns two to five. The values of the decision variables are presented in the sixth column among which activities 1, 18, 2, and 14 have been mostly selected with comparison to other activities. In fact, these activities have suitable properties to reduce the total project time and can create desired levels in terms of different objective functions. When assessing the results of each member, one can see that all the solutions can reduce the total project execution time for at least 4 time units and this reduction is exactly in agreement with the time requested by the project owner. Thus, one can say that the produced solutions are feasible and they are members of the Pareto optimal set based on the structure of the epsilon-constraint method.

Table 9 Members of the Pareto front for scenario
Full size table
Table 10 The real and standardized values of robust parameters
Full size table

6.2 The second scenario: parameters of the first and the third objective functions at their maximum value and the second and fourth function at their average value

Based on this scenario, the robust parameters for the first and the third objective functions are equal to \(\left( {\Gamma_{1} = 21} \right) {\text{and}} \left( {\Gamma_{3} = 21} \right)\) and they are equal to \(\left( {\Gamma_{2} = 420} \right) {\text{and}} \left( {\Gamma_{4} = 21} \right)\) for the second and the fourth objective functions. All the parameters of the first and the third objective functions have uncertainty and this condition is “the worst case” presented in Soyster (1973). The first and the third objective functions are in the worst condition. The Pareto front obtained from solving this scenario is illustrated in Fig. 3.

Fig. 3:
figure 3

3D components of the Pareto front of scenario 2

Full size image

Figure 3 shows that 46 Pareto members are produced in solving this example which is a lower number compared to the first scenario. The reason for this can be attributed to considering the first and the third objective functions in the worst condition. The decision-making for the first and the third objective functions in this scenario is, in fact, very limited and the model is not able to produce different decisions. Thus, a lower number of solutions are produced as the Pareto members. It can be seen that the first and the third objective functions have more concentration on the solution boundary points. In other words, they have produced solutions with higher values of objective functions. This fact could be predicted beforehand because considering “the worst case” for these functions cannot provide decision-makers with a suitable choice compared to the first scenario.

6.3 The third scenario: the first and the second objective functions at the maximum value and the third and the fourth objective functions at the average value

This scenario can be considered as a sustainable scenario; because it particularly pays attention to the third and the fourth objective functions, which are the ones related to sustainable development. In this scenario, the cost and risk levels are in the worst decision-making condition and managers cannot have diverse choices to make. However, there is a different analysis for the sustainable development functions. Since only half of the parameters in these objective functions are uncertain, pretty diverse decisions will be made for these objectives in the Pareto front. It can also be stated that the number of these solutions is more than that of the first scenario; because all the functions in the first scenario are at their middle levels and the decisions are affected by all the objectives. But in this scenario, only the sustainable development functions can cause diversity in the Pareto member’s value and consequently produce more solutions. Figure 4 shows the Pareto front structure of this scenario.

Fig. 4:
figure 4

3D components of the Pareto front of scenario 3

Full size image

Figure 4 shows that solution diversity in the second and the fourth objective functions is high, and the first and the third objective functions have values between 0.5 and 0.65 except for a few cases. Therefore, one can say that most of the decisions are made by the sustainable development functions when considering the first and the second functions to be in “the worst condition” and managers have the opportunity to exclusively decide about these objective functions.

6.4 Analyzing the sensitivity of the robust parameters in producing Pareto solutions

In order to assess the behavior of the robust parameters in producing Pareto solutions, which are the different cases of the manager optimum decisions, the results of the first to the third scenarios and the other two scenarios are compared to each other in this section. Thus, the fourth and the fifth scenarios can be briefly described. The fourth scenario: The first and the second objective functions are at the average values, and the third and the fourth functions are at the highest values. The fifth scenario: All the objective functions are at the highest value.

Since the analysis of the results obtained from these two scenarios is similar to that of the first to the third scenarios, these scenarios are only used to assess the behavior of the robust parameters compared to different cases. One method to compare the behavior of the robust parameters in producing the solution is to directly compare the Pareto front produced in different scenarios. The performance of the objective functions in producing different solutions can be observed in this comparison. For this purpose, Fig. 5 presents these results.

Fig. 5
figure 5

Comparison the Pareto front generated by various scenarios

Full size image

Figure 5 shows that the distribution level of solutions is different for different scenarios. The concentration of the solution production is different in each objective function in each scenario proportional to the defined range of robust parameter. For instance, it can be observed that scenario 1 nearly dominates all the other scenarios in producing the solutions. In other words, the solutions produced in scenario 1 have the greatest diversity. However, this diversity reaches its minimum value in scenario 5 and approximately all the objective functions are concentrated in a small interval. In conclusion, one can say that the robust parameters can directly affect the production of solutions having various qualities. Some numerical examples with different combinations of robust parameters have been produced to suitably compare the effectiveness of each robust parameter in producing the final solutions and then the quality of solutions is measured using the criterion designed in the following. This criterion can help decision-makers to finally select the level of uncertainty for each parameter. In order to produce suitable combinations and perform the calculations needed for obtaining the optimal values of the robust parameters, the method of Design of Experiment is used along with the response surface method (RSM).

6.5 Design of experiments to calculate the robust parameter’s values

In this section, some experiments are designed to determine the optimal level of each robust parameter and then the obtained results are compared using the criterion of measuring the solution quality (Fig. 6).

Fig. 6
figure 6

Optimal level for robustness parameters

Full size image

6.5.1 Designing the criterion for measuring the solution quality

A criterion is designed based on measuring the diversity of the produced solutions to assess the quality of them. In this criterion, the absolute value of the distance between each Pareto member and the average distance is calculated and is divided by the total average. This criterion is proposed as follows:

$$Quality Measure = \frac{{\mathop \sum \nolimits_{i = 1}^{N - 1} \left| {d_{mean} - d_{i} } \right|}}{{\left( {N - 1} \right) \times d_{mean} }}$$
(52)

where \(d_{i}\) is the Euclidean distance from \(ith\) member of the Pareto front to the optimal boundary. Moreover, \(d_{mean}\) denotes the average value of these distances. The solution diversity can be measured using this criterion. It is clear that the more distribution of the solutions around the distance averages, the lower the criterion value would be.

6.5.2 Analysis of the results of the design of experiments

The design of experiment method of RSM which is based on the Box–Behnken design is used in this research which is one of the most effective tools in this field. The first step in RSM is to specify parameters and their levels. Since parameters have different units, they should be first standardized as values between 0 and 1 using Eq. 51. The main and standard values of parameters are shown in Tables 9 and 10.

Then, a three-level four-variable is presented by the Box–Behnken method, and 29 experiments are conducted in accordance with Table 2. The number of tests required can be calculated according to the equation given as follows.

$${\text{N}} = 2{\text{k}}\left( {{\text{k}} - 1} \right) + {\text{C}}_{0}$$
(53)

where \(N\) is the number of experiments, \(k\) shows the variables, and \({C}_{0}\) shows the central points. Design-Expert software (trial version of v.10, Stat-Ease Inc., Minneapolis, MN, USA) is used to evaluate the design and analysis of data regression and to plot the charts.

6.6 Statistical results from RSM

In this study, a multivariable regression is applied to evaluate the experimental results. The best model that fits all the design points is quadratic. The analysis of variance (ANOVA) test is used to estimate the impacts and interactions of the variables. The obtained results are presented in Table 11. The expressions of “significant” shown in the model after the analysis of variance include \(A, B, C, D, AD, A^{2} ,B^{2} ,C^{2} , {\text{and}} D^{2}\) with \(P value < 0.05\). Other terms do not significantly affect the quality index value and are removed from the model. Therefore, the polynomial function was determined in order to estimate the quality index according to the equation given as follows.

$$Y = 11.807 + 0.440 A - 0.407 B - 0.967 C + 0.451 D + 0.692 AB + 1.242 BC - 1.076 BD + 1.116 CD + 0.328 B^{2} - 0.037 C^{2}$$
(54)
Table 11 Experiments designed by Box–Behnken and response surface values
Full size table

where \(Y\) is the quality index, \(A, B, C, and D\) represent \(\Gamma_{1} , \Gamma_{2} , \Gamma_{3} , {\text{and}} \Gamma_{5}\), respectively. As shown in the ANOVA table (Table 11), \(p value < 0.0001\) and the insignificant lack of fitness (0.042) indicate that the experimental data have an appropriate fitness with the proposed model. In addition, high adjusted R-squared and predicted R-squared, which have values of 0.974 and 0.926, respectively, confirm the efficiency of the model.

6.7 Investigating the effect of variables on spinning consistency and optimizing the surface of each of the parameters

Based on the ANOVA results, the response surface of the model shows that the parameter \(\Gamma_{3}\) has the greatest impact on the quality index. In fact, any change in the linear density of spinning (while other parameters are in their mean) causes a significant change in the quality index, whereas the changes in \(\Gamma_{2}\) and \(\Gamma_{3}\) parameters have a relative effect on the quality index. The parameter \(\Gamma_{1}\) also has the least effect.

Finally, it can be stated the optimum numerical values for the robust objective functions of the first, the second, the third, and the fourth parameters are 0.035, 0.260, 0.923, and 0.400, respectively, which represent \(\left( {\Gamma_{1} = 12.8} \right), \left( {\Gamma_{2} = 155} \right), \left( {\Gamma_{3} = 2.8} \right), {\text{and}} \left( {\Gamma_{4} = 5.3} \right)\). At this level of parameters, the amount of response dispersion will be generated by the response quality index (Table 12).

Table 12 Analysis of variance (ANOVA) for response surface of quadratic model of spinning consistency
Full size table

7 Discussion

Two aspects of the results, including methodology and practical implications, can be discussed as follows:

Regarding the proposed methodology, two concepts should be considered. The first one is modeling the socio-environmental concept of projects for the first time in the scheduling problems. By minimizing the destructive environmental and social effects caused by the delay in each of the intended project activities, the sustainability project performance will be promoted. Although the socio-environmental concept has different aspects, working on delay is a realistic approach when the problem is scheduling. By minimizing projects’ duration, some adverse environmental effects of projects, such as waste, noise, dust, solid wastes, toxic generation, air pollution, water pollution, will be decreased. Accordingly, minimizing the delay can influence the social aspect of projects. For example, completing projects sooner causes to increase project’s access speed for people, or the possibility of health and safety issues will be decreased. As a consequence, minimizing delay is an excellent strategy to promote project sustainability indicators. The second point should be discussed about the methodology is uncertainty. In order to model the natural uncertainty existed in the scheduling problem, this paper applied the robust programming method proposed by Bertsimas and Sim (2003) as a tool for transforming a deterministic model into a probabilistic one. The main advantage of this model is its ability to analyze the different levels of robust parameters. According to the users’ request, several scenarios can be developed to investigate the effect of parameters’ uncertainty on the projects’ schedule. For instance, this paper developed three scenarios for its own numerical example to reach the users’ request, which is decreasing the total time of the project by four units. According to the results of the first scenario, it can be observed that all solutions reduce the total time of the project implementation by at least four units, which is exactly the duration of the project owner’s request. Therefore, it can be claimed that the generated solutions are feasible and they are members of the Pareto front according to the structure of the epsilon-constraint method. In the second scenario, 46 Pareto members are produced. In fact, in this scenario, the level of decision-making about the first and the third objective functions is very limited and the model cannot produce different decisions. Considering the objective function values, it is found that the first and the third objective functions are more focused on the boundary points of the solutions. In other words, they generate solutions with more objective function values. In the third scenario, the diversity of solutions in the second and the fourth objective functions is high, and the first and the third functions are often set in the range of 5.0–6.05, except for some cases. Therefore, it can be said that by considering the first and the second objective functions in the “worst condition,” most decisions are made by sustainable development functions, and managers have the opportunity to decide specifically about these objective functions. Sensitivity analysis is carried out in the form of the fourth and the fifth scenarios in order to accurately study the model behavior in different conditions. In these scenarios, the dispersion surface of solutions varies for different scenarios. In fact, in each scenario, the focus of producing solutions in each objective function is a significant difference proportional to the robust parameter defined range, indicating the great impact of robust parameters on the results. Finally, the response surface methodology is used to determine the optimal surface of the robust parameters, and the final values\(\left( {\Gamma_{1} = 12.8} \right), \left( {\Gamma_{2} = 155} \right), \left( {\Gamma_{3} = 2.8} \right),and \left( {\Gamma_{4} = 5.3} \right)\) are reported for the final use of managers. Given that the sustainable development criteria can influence greatly the outcomes; it is suggested that other aspects of sustainable development as constraints or objective functions should be investigated. In addition, other robust programming methods can be applied to deal with the conditions of uncertainty in order to analyze and compare the results.

Regarding the practical implications of the proposed methodology, users can be assured that this model’s outcomes satisfy their needs in three main aspects, including time, cost, and socio-environmental area. Moreover, the ability of robust programming in working with different levels of uncertainty can bring a useful tool for users to investigate real situations of projects and apply the right strategy for scheduling their own projects. Since the outcomes of the model optimized the duration of each activity in the project with respect to three objectives, the results are applicable for the planning and scheduling unit of each project.

8 Conclusion and suggestions

This paper examined a multi-objective mathematical model to schedule the projects’ activities with respect to minimizing cost, risk, and socio-environmental effects under uncertainty conditions. In this study, the project scheduling problem considering socio-environmental criteria is proposed as an optimization problem for the first time to the best of our knowledge. The socio-environmental criteria have been considered by the concept of minimizing the delay of projects. One of the advantages of the proposed methodology is considering some main parameters of the problem under uncertainty to be close to the real-world projects. In order to deal with uncertainty, robust programming is used as a useful tool to create robust solutions. Some objective functions for minimizing the cost of delay, destructive environmental and social effects, and finally, risk of increasing the delay of projects are presented as a multi-objective model. The epsilon-constraint method was applied to solve the multi-objective model of this paper. In this method, one of the objectives is optimized while the other objectives are added to the problem as constraints. In order to understand how the proposed methodology works, a numerical example was presented. According to the different level of robust parameters, three scenarios were developed and solved. The results based on the Pareto front diagram showed that the first scenario which is nearly half of the parameters had uncertainty in the example and using the average value of the robust parameters almost dominates all the other scenarios in producing the solutions. In other words, the solutions produced in scenario 1 have the greatest diversity. Since the robust parameters can directly affect the quality of solutions, creating suitable combinations of the robust parameters’ optimal values is necessary. This paper proposed to apply the method of design of experiment along with the RSM. The outcomes of the optimal surface of the robust parameters are crucial criteria for managers to set their projects’ schedule.

Given that the sustainable development criteria can influence the outcomes greatly, it is suggested that other aspects of sustainable development as constraints or objective functions should be investigated. In addition, other robust programming methods can be applied to deal with uncertainty conditions to analyze and compare the results.