1 Introduction

Oil is comprised of many different toxic compounds which endanger the marine environment involved in a spill, however there are many natural, native microorganisms which are not only capable, but thrive on the decomposition of these toxic compounds. This process of using microorganisms for such cleanup efforts in shorelines is known as bioremediation, and it has proven to be a successful method for the cleanup of marine areas affected by oil spills [5].

There are two different types of bioremediation used for oil spill cleanup: bioaugmentation and biostimulation. Bioaugmentation is the addition of microorganisms capable of degrading the toxic hydrocarbons, in order to achieve a reduction of the pollutants. Biostimulation is the addition of nutrients needed by indigenous hydrocarbon-degrading microorganisms in order to achieve maximum degradation of toxic compounds present in the oil. The degradation of hydrocarbons (biodegradation) begins by the conversion of the alkane chain or polycyclic aromatic hydrocarbon (PAH) into alcohol. Oxidation then converts the compound to an aldehyde and then into an acid and eventually into water, carbon dioxide, and biomass. In the case of the PAH, fission occurs which ultimately leads to mineralization [39]. More than 170 genera of microorganisms have been identified in the environment which are able to degrade hydrocarbons, due to such diversity and different conditions at the spill site, hydrocarbons are not all biodegraded at similar rates, and not all hydrocarbons are degradable, but estimates for the biodegradability of different crude oils range from 70 to 97 %. What remain are principally the asphaltenes and resin compounds, which are essentially biologically inert [31].

Although biodegradation is a particularly important mechanism for removing the non-volatile components of oil from the environment, this is a relatively slow natural process and may require months to years for microorganisms to degrade a significant fraction of oil stranded in shorelines, within the sediments of marine and/or freshwater environments [44]. The simplest way of stimulating biodegradation, and the only one that has achieved experimental verification in the field, is to carefully add nitrogen and phosphorus nutrients. This was first used on a large scale in Alaska, following the 1989 spill from the Exxon Valdez [4, 29, 30]. Two fertilizers were used in the large-scale applications: an oleophilic liquid product designed to adhere to oil, named Inipol EAP22 [17]; and a slow-release granular agricultural product called Customblen [31].

The bioremediation was very successful, as shown in a joint monitoring program conducted by Exxon, the USEPA and the Alaska Department of Environmental Conservation [30]. The fertilizer applications were successful at delivering nutrients throughout the oiled part of the shorelines, microbial activity was enhanced, and oil biodegradation was stimulated two- to fivefold [4, 29, 30]. Furthermore, this was achieved with no detectable adverse environmental impact [4, 29, 30]. Since then, bioremediation has been used on a limited site as part up of the cleanup of the Sea Empress spill [38], and has been demonstrated on experimental spills in marine or brackish environments on the Delaware Bay [40], a Texas wetland [24], a fine-sand beach in England [37], mangroves in Australia [33], and an Arctic shoreline in Spitsbergen [28].

Due to these successes, it is desirable to include bioremediation in responses to future spills where oil strands on rocky or inaccessible shorelines. In this situation currents can be used to carry the nutrients to the polluted zones instead of release it directly on the site. For such case, an important factor in achieving successful biostimulation is obtaining an ideal (critical) concentration of nutrients needed for maximum growth of the organisms, and keeping this concentration present for the organisms as long as possible. This can become a difficult task taking into account that appropriate point for releasing the nutrients is unknown, and also because of physical influences, such as differences in densities, wave movements, and tidal influences. Tracer studies are often used to examine how the motion of the water and nutrients are influenced under different situations [2, 3].

In this work, a strategy is proposed for the remediation of oil-polluted marine environments which uses the fluid dynamic in a limited water region D to distribute a nutrient (nitrogen or phosphorus) and stimulate biodegradation in some important internal ecological zones Ω i  ⊂ D such as recreation or aquaculture areas. By the strategy, the nutrient released at point r 0 of domain D with a discharge rate Q(t) spreads by currents and turbulent diffusion and reaches all the contaminated zones. Moreover, a critical mean concentration of nutrient c i (higher than the natural concentration) should be achieved and maintained in each zone Ω i (1 ≤ i ≤ N) within a certain time to properly stimulate the growth of the oil degrading microorganisms [2]. This time interval is denoted below as [T–τ,T]. It should be noted that an adequate release rate Q(t) does not always exist, that is, at times, this strategy fails. In particular, this can happen when the release point r 0 is improperly chosen with respect to the flow and the location of zones, or when the time T is not large enough to let the nutrient to reach all the zones. A strategy is called optimal if it solves the problem and, at the same time, minimizes the discharge rate Q(t) to mitigate the impact of nutrients on the marine environment and to decrease the remediation cost. Thus, by introducing the least amount of nutrients, the optimal control not only cleans the zones, but also protects the whole ecosystem.

All these things considered, the variational formulation of optimal remediation strategy is as follows:

$$ {\text{minimize}}\quad m(Q) = \int\limits_0^T {Q(t)dt} $$
(1)
$$ {\text{subject}}\;{\text{to}}:\quad {c_i} \leqslant {J_i}\left( \phi \right) = \frac{1}{{\tau \left| {{\Omega_i}} \right|}}\int\limits_{{T - \tau }}^T {\mathop{\smallint }\limits_{{{\Omega_i}}} \;\phi \left( {r,t} \right)drdt} \leqslant {c_i} + {\varepsilon_i},\quad 1 \leqslant i \leqslant N $$
(2)
$$ {J_0} = \frac{1}{{T\left| D \right|}}\int\limits_0^T {\mathop{\smallint }\limits_D \;\phi \left( {r,t} \right)drdt} \leqslant {c_0};\quad 0 \leqslant Q(t) \leqslant {Q_0}(t),\quad 0 \leqslant t \leqslant T $$
(3)

where m(Q) is the functional that represents the total mass of nutrient released into the system within time interval [0,T], \( \phi = \phi \left( {r,t} \right) \) is the concentration of nutrient in D (it will be determined with a dispersion model described in Section 2) and \( {J_i}\left( \phi \right) \) is the mean concentration of nutrient in ith zone Ω i , 1 ≤ i ≤ N, within time interval [T–τ,T]. By convenience, all the zones Ω i considered in this work are nonintersecting. The constraints in (2) are imposed to maintain J i equal to or slightly above the critical concentration c i  > 0 required for biodegradation (1 ≤ i ≤ N). Also, note that the introduction of small parameters ε i  > 0 increases the number of feasible solutions for problem (1)–(3), and therefore, this model is less restrictive than that described by Parra-Guevara and Skiba in [25, 26]. The integral condition in (3) represents an ecological constraint that limits the mean concentration of the nutrient in the whole region, while the mass released at the point of discharge is bounded by function Q 0 according to the inequality in (3). Finally, we note that the formulation (1)–(3) can also be used to determine the optimal release parameters in a fairly common case, when the repeated application of nutrients is required in the contaminated areas due to the slow degradation of oil in the marine environment. Sufficient conditions for such a methodology are given in Section 3.

2 Dispersion Model

The concentration of nutrient \( \phi \left( {r,t} \right) \) in a domain D ⊂ ℝ3 and time interval [0,T] is estimated by the following dispersion model

$$ \frac{{\partial \phi }}{{\partial t}} + \overrightarrow U \cdot \nabla \phi - \nabla \cdot \mu \nabla \phi + \sigma \phi + \nabla \cdot {\overrightarrow \phi_s} = Q(t)\delta \left( {r - {r_0}} \right) $$
(4)
$$ {\overrightarrow \phi_s} = - {v_s}\phi \overrightarrow k \;in\;D $$
(5)
$$ \mu \frac{{\partial \phi }}{{\partial n}} = {\overrightarrow \phi_s} \cdot \overrightarrow n - \zeta \phi \overrightarrow k \cdot \overrightarrow n \quad {\text{on}}\quad {S_T} $$
(6)
$$ \mu \frac{{\partial \phi }}{{\partial n}} = 0\quad {\text{on}}\quad {S^{ + }} $$
(7)
$$ \mu \frac{{\partial \phi }}{{\partial n}} - {U_n}\phi = 0\quad {\text{on}}\quad {S^{ - }} $$
(8)
$$ \mu \frac{{\partial \phi }}{{\partial n}} = 0\quad {\text{on}}\quad {S_B} $$
(9)
$$ \phi \left( {r,\;0} \right) = {\phi^0}(r)\quad {\text{in}}\quad D $$
(10)
$$ \nabla \cdot \overrightarrow U = 0\quad {\text{in}}\quad D $$
(11)

Here (4) is the advection–diffusion equation, \( \overrightarrow U \left( {r,\;t} \right) \) is the current velocity that satisfies the incompressibility condition (11), μ(r,t) is the turbulent diffusion coefficient, σ(r,t) is the chemical transformation coefficient characterizing the decay rate of nutrient in water. Note that the first-order (linear) kinetics \( \sigma \phi \) describing the process of chemical transformation is a reasonable approximation for such nutrients in water as the nitrogen and phosphorus. The term \( \nabla \cdot {\overrightarrow \phi_s} \) in (4), describes the change of concentration of nutrient per unit time because of sedimentation with constant velocity v s  > 0, and δ(r–r 0) is the Dirac delta centered at the discharge point r 0. Equation (6) is the boundary condition on the free surface S T of domain D, where ζ(r,t) is the coefficient characterizing the process of evaporation of nutrient, and (9) represents the boundary condition on the bottom S B of domain D. Equations (7) and (8) are the corresponding conditions on the lateral boundary of D, besides S + is the rigid or outflow part of boundary where \( {U_n} = \overrightarrow U \cdot \overrightarrow n \geqslant 0 \), and S – is its inflow part where U n  < 0. Finally, the Eq. (10) represents the initial distribution of the nutrient at t = 0. In all equations, \( \overrightarrow n \) is the unit outward normal vector to the boundary \( \partial D = {S_T} \cup {S^{ + }} \cup {S^{ - }} \cup {S_B} \) of domain D, ∂/∂n is the derivative in the normal direction, and \( \overrightarrow k = {\left( {0,\;0,\;1} \right)^t} \) is the unit vector directed upward in the Cartesian coordinate system. We observe that

$$ \overrightarrow k \cdot \overrightarrow n = 0\;{\text{on}}\;{S^{ + }} \cup {S^{ - }}\;{\text{and}}\;\overrightarrow U \cdot \overrightarrow n = 0\;{\text{on}}\;{S_T} \cup {S_B} $$
(12)

Also, note that the boundary conditions (6)–(9) are general (i.e., not only for horizontal free and bottom surfaces S T and S B ), and hence, the dispersion model can take into account free surface wave motion and marine topography.

First, we show that the solution of dispersion model (4)–(11) satisfies the mass balance equation. Indeed, integrating Eq. (4) over domain D we get:

$$ \frac{\partial }{{\partial t}}\mathop{\smallint }\limits_D \phi dr + \mathop{\smallint }\limits_D \overrightarrow U \cdot \nabla \phi dr - \mathop{\smallint }\limits_D \nabla \cdot \mu \nabla \phi dr + \mathop{\smallint }\limits_D \sigma \phi dr + \mathop{\smallint }\limits_D \nabla \cdot {\overrightarrow \phi_s}dr = \mathop{\smallint }\limits_D Q(t)\delta \left( {r - {r_0}} \right)dr $$

Applying the divergence theorem [16], it is possible to rewrite some integrals as follows:

$$ \mathop{\smallint }\limits_D \overrightarrow U \cdot \nabla \phi dr = \mathop{\smallint }\limits_D \nabla \cdot \left( {\overrightarrow U \phi } \right)\;dr = \mathop{\smallint }\limits_{{\partial D}} \overrightarrow U \cdot \overrightarrow n \phi dS $$
$$ \mathop{\smallint }\limits_D \nabla \cdot \mu \nabla \phi dr = \mathop{\smallint }\limits_{{\partial D}} \mu \nabla \phi \cdot \overrightarrow n dS = \mathop{\smallint }\limits_{{\partial D}} \mu \frac{{\partial \phi }}{{\partial n}}dS $$
$$ \mathop{\smallint }\limits_D \nabla \cdot {\overrightarrow \phi_s}dr = \mathop{\smallint }\limits_{{\partial D}} {\overrightarrow \phi_s} \cdot \overrightarrow n dS $$

Finally, dividing each integral over boundary ∂D into the four integrals over S T , S +, S –, and S B , and applying Eqs. (6) to (9) and observation (12), we obtain the mass balance equation:

$$ \frac{\partial }{{\partial t}}\mathop{\smallint }\limits_D \phi dr = Q(t) - \mathop{\smallint }\limits_D \sigma \phi dr - \mathop{\smallint }\limits_{{{S^{ + }}}} {U_n}\phi dS - \mathop{\smallint }\limits_{{{S_T}}} \zeta \phi \overrightarrow k \cdot \overrightarrow n dS + \mathop{\smallint }\limits_{{{S_B}}} {\nu_s}\phi \overrightarrow k \cdot \overrightarrow n dS $$
(13)

Since \( \overrightarrow k \cdot \overrightarrow n > 0 \) at S T and \( \overrightarrow k \cdot \overrightarrow n < 0 \) at S B , the total mass of the nutrient increases due to the discharge rate Q(t), and decreases because of chemical transformation, advective outflow through S +, superficial evaporation, and sedimentation.

We now show that the dispersion problem (4)–(11) is well posed. Indeed, the model operator is:

$$ A\phi = \overrightarrow U \cdot \nabla \phi - \nabla \cdot \mu \nabla \phi + \sigma \phi + \nabla \cdot {\overrightarrow \phi_s} $$
(14)

Defining the inner product in L 2(D) as \( \left( {A\phi, \;\phi } \right) = \mathop{\smallint }\limits_D \phi A\phi dr \), we obtain the expression

$$ \left( {A\phi, \;\phi } \right) = \mathop{\smallint }\limits_D \phi \overrightarrow U \cdot \nabla \phi dr + \mathop{\smallint }\limits_D \sigma {\phi^2}dr - \mathop{\smallint }\limits_D \phi \nabla \cdot \mu \nabla \phi dr + \mathop{\smallint }\limits_D \phi \nabla \cdot {\overrightarrow \phi_s}dr $$

The divergence theorem allows modifying some integrals in the last equation:

$$ \mathop{\smallint }\limits_D \phi \overrightarrow U \cdot \nabla \phi dr = \frac{1}{2}\mathop{\smallint }\limits_{{\partial D}} {\phi^2}\overrightarrow U \cdot \overrightarrow n dS $$
$$ \mathop{\smallint }\limits_D \phi \nabla \cdot \left( {\mu \nabla \phi } \right)\;dr = \mathop{\smallint }\limits_{{\partial D}} \phi \mu \frac{{\partial \phi }}{{\partial n}}dS - \mathop{\smallint }\limits_D \mu {\left| {\nabla \phi } \right|^2}dr $$
$$ \mathop{\smallint }\limits_D \phi \nabla \cdot {\overrightarrow \phi_s}dr = \frac{1}{2}\mathop{\smallint }\limits_{{\partial D}} \phi {\overrightarrow \phi_s} \cdot \overrightarrow n dS $$

Finally, dividing each integral over ∂D into the four integrals over S T , S +, S –, and S B , and applying the conditions (6)–(9) and (12), we get

$$ \matrix{{*{20}{c}} {\left( {A\phi, \;\phi } \right) = \mathop{\smallint }\limits_D \sigma {\phi^2}dr + \mathop{\smallint }\limits_D \mu {{\left| {\nabla \phi } \right|}^2}dr + \mathop{\smallint }\limits_{{{S_T}}} \zeta {\phi^2}\overrightarrow k \cdot \overrightarrow n dS} \\ { + \frac{1}{2}\left\{ {\mathop{\smallint }\limits_{{{S^{ + }}}} {U_n}{\phi^2}dS - \mathop{\smallint }\limits_{{{S^{ - }}}} {U_n}{\phi^2}dS + \mathop{\smallint }\limits_{{{S_T}}} {v_s}{\phi^2}\overrightarrow k \cdot \overrightarrow n dS - \mathop{\smallint }\limits_{{{S_B}}} {v_s}{\phi^2}\overrightarrow k \cdot \overrightarrow n dS} \right\}} \\ } $$
(15)

Since U n  < 0 in S –, \( \overrightarrow k \cdot \overrightarrow n > 0 \) at S T and \( \overrightarrow k \cdot \overrightarrow n < 0 \) at S B , Eq. (15) can be rewritten as

$$ \left( {A\phi, \;\phi } \right) = \mathop{\smallint }\limits_D \sigma {\phi^2}dr + \mathop{\smallint }\limits_D \mu {\left| {\nabla \phi } \right|^2}dr + \mathop{\smallint }\limits_{{{S_T}}} \zeta {\phi^2}\overrightarrow k \cdot \overrightarrow n dS + \frac{1}{2}\left\{ {\mathop{\smallint }\limits_{{{S^{ + }} \cup {S^{ - }}}} \left| {{U_n}} \right|{\phi^2}dS + \mathop{\smallint }\limits_{{{S_T} \cup {S_B}}} {v_s}{\phi^2}\left| {\overrightarrow k \cdot \overrightarrow n } \right|dS} \right\} $$

Thus, operator A is positive semidefinite: \( \left( {A\phi, \phi } \right) \geqslant 0 \).

Taking the inner product of every term of Eq. (4) with \( \phi \), we obtain

$$ \left( {\frac{{\partial \phi }}{{\partial t}},\;\phi } \right) = \left( {f,\;\phi } \right) - \left( {A\phi, \;\phi } \right),\;f\left( {r,\;t} \right) = Q(t)\delta \left( {r - {r_0}} \right) $$

Using the condition \( \left( {A\phi, \phi } \right) \geqslant 0 \) and Schwarz inequality [15], the last equation implies the inequality.

$$ \left( {\phi, \;\frac{{\partial \phi }}{{\partial t}}} \right) \leqslant \left\| \phi \right\|\left\| f \right\|,\quad \left\| \phi \right\| = \sqrt {{\left( {\phi, \;\phi } \right)}} $$

Further,

$$ \left( {\phi, \frac{{\partial \phi }}{{\partial t}}} \right) = \frac{1}{2}\frac{\partial }{{\partial t}}{\left\| \phi \right\|^2} = \left\| \phi \right\|\;\frac{\partial }{{\partial t}}\left\| \phi \right\| $$

and hence, \( \frac{\partial }{{\partial t}}\left\| \phi \right\| \leqslant \left\| f \right\| \). Finally, the integration over time interval (0,T) leads to

$$ \left\| \phi \right\| \leqslant T\mathop{{\max }}\limits_{{0 \leqslant t \leqslant T}} \left\| {Q(t)\delta \left( {r - {r_0}} \right)} \right\| + \left\| {{\phi^0}(r)} \right\| $$
(16)

Since the dispersion model (4)–(11) is linear with respect to \( \phi \), estimation (16) guarantees that the solution of problem (4)–(11) is unique and continuously depends on the initial conditions and forcing. Also, using the method described by Skiba and Parra-Guevara in [36], it is possible to prove the existence of generalized solution of problem (4)–(11), that is, the model (4)–(11) is well posed in the sense of Hadamard [11]. Also note that the positive semidefiniteness of operator A allows us to split the operator A in coordinate directions, and with the help of numerical schemes by Marchuk [20] and Crank-Nicolson [6] construct unconditionally stable and efficient numerical algorithm of second approximation order in space and time for the solution of problem (4)–(11) [34].

3 Adjoint Functions and the Duality Principle

It is rather difficult to analyze and solve variational problem (1)–(3) because the constraints in (2)–(3) are related with the solution Q of control problem implicitly through the solution \( \phi \) of dispersion model (4)–(11). In order to establish an explicit dependence of the constraints on Q, we now introduce one more model which is adjoint to the dispersion model (4)–(11). Its operator A * is adjoint to the operator A of model (4)–(11) in the sense of Lagrange identity

$$ \left( {A\phi, \;g} \right) = \left( {\phi, \;{A^{ * }}g} \right) $$

where (∙,∙) is the inner product in L 2(D) [20]. Solutions of this adjoint model will be used to establish a duality principle for the mean concentration of the released nutrient in the marine environment. Let us construct the operator A *. The inner product (Aϕ, g) is

$$ \left( {A\phi, \;g} \right) = \mathop{\smallint }\limits_D g\overrightarrow U \cdot \nabla \phi dr + \mathop{\smallint }\limits_D \sigma g\phi dr - \mathop{\smallint }\limits_D g\nabla \cdot \mu \nabla \phi dr + \mathop{\smallint }\limits_D g\nabla \cdot {\overrightarrow \phi_s}dr $$

The integrals in the last expression can be rewritten with the divergence theorem as

$$ \mathop{\smallint }\limits_D g\overrightarrow U \cdot \nabla \phi dr = \mathop{\smallint }\limits_{{\partial D}} g\phi \overrightarrow U \cdot \overrightarrow n dS - \mathop{\smallint }\limits_D \phi \overrightarrow U \cdot \nabla gdr $$
$$ \mathop{\smallint }\limits_D g\nabla \cdot \mu \nabla \phi dr = \mathop{\smallint }\limits_{{\partial D}} g\mu \frac{{\partial \phi }}{{\partial n}}dS - \mathop{\smallint }\limits_{{\partial D}} \phi \mu \frac{{\partial g}}{{\partial n}}dS + \mathop{\smallint }\limits_D \phi \nabla \cdot \mu \nabla gdr $$
$$ \mathop{\smallint }\limits_D g\nabla \cdot {\overrightarrow \phi_s}dr = \mathop{\smallint }\limits_{{\partial D}} g{\overrightarrow \phi_s} \cdot \overrightarrow n dS - \mathop{\smallint }\limits_D \phi \nabla \cdot {\overrightarrow g_s}dr $$

where \( {\overrightarrow g_s} = - {v_s}g\overrightarrow k \). Then

$$ \left( {A\phi, \;g} \right) = \mathop{\smallint }\limits_D \phi \left( { - \overrightarrow U \cdot \nabla g - \nabla \cdot \mu \nabla g + \sigma g - \nabla \cdot {{\overrightarrow g }_s}} \right)\;dr + \mathop{\smallint }\limits_{{\partial D}} g\phi \overrightarrow U \cdot \overrightarrow n dS + \mathop{\smallint }\limits_{{\partial D}} \phi \mu \frac{{\partial g}}{{\partial n}}dS - \mathop{\smallint }\limits_{{\partial D}} g\mu \frac{{\partial \phi }}{{\partial n}}dS + \mathop{\smallint }\limits_{{\partial D}} g{\overrightarrow \phi_s} \cdot \overrightarrow n dS $$

Dividing the integrals over boundary ∂D into four integrals over S T , S +, S –, and S B , and using conditions (6)–(9) and (12), we obtain that

$$ \left( {A\phi, \;g} \right) = \mathop{\smallint }\limits_D \phi \left( { - \overrightarrow U \cdot \nabla g - \nabla \cdot \mu \nabla g + \sigma g - \nabla \cdot {{\overrightarrow g }_s}} \right)\;dr $$

provided that function g satisfies the boundary conditions (20)–(23). Thus, the Lagrange identity is fulfilled if

$$ {A^{ * }}g = - \overrightarrow U \cdot \nabla g - \nabla \cdot \mu \nabla g + \sigma g - \nabla \cdot {\overrightarrow g_s} $$

On the other hand, multiplying (4) by g and taking the integral over space–time domain D × (0,T), we get

$$ \mathop{\smallint }\limits_0^T \mathop{\smallint }\limits_D g\frac{{\partial \phi }}{{\partial t}}drdt + \mathop{\smallint }\limits_0^T \mathop{\smallint }\limits_D gA\phi drdt = \mathop{\smallint }\limits_0^T \mathop{\smallint }\limits_D gQ(t)\delta \left( {r - {r_0}} \right)drdt $$

Integrating by parts the first integral and using conditions (10) and g(r, T) = 0 leads to

$$ \mathop{\smallint }\limits_0^T \mathop{\smallint }\limits_D g\frac{{\partial \phi }}{{\partial t}}drdt = - \mathop{\smallint }\limits_D g\left( {r,\;0} \right){\phi^0}(r)dr - \mathop{\smallint }\limits_0^T \mathop{\smallint }\limits_D \phi \frac{{\partial g}}{{\partial t}}drdt $$

Applying now Eq. (4), Lagrange identity and well-known property of Dirac delta one can get

$$ \mathop{\smallint }\limits_0^T \mathop{\smallint }\limits_D \phi \left\{ { - \frac{{\partial g}}{{\partial t}} + {A^{ * }}g} \right\}drdt = \mathop{\smallint }\limits_0^T Q(t)g\left( {{r_0},\;t} \right)dt + \mathop{\smallint }\limits_D g\left( {r,\;0} \right){\phi^0}(r)dr $$
(17)

In order to take advantage of Eq. (17), which explicitly relates the discharge rate of nutrient Q(t) with the concentration of nutrient \( \phi \left( {r,t} \right) \) through the function g, we consider the following adjoint dispersion model:

$$ - \frac{{\partial g}}{{\partial t}} - \overrightarrow U \cdot \nabla g - \nabla \cdot \mu \nabla g + \sigma g - \nabla \cdot {\overrightarrow g_s} = p\left( {r,\;t} \right) $$
(18)
$$ {\overrightarrow g_s} = - {v_s}g\overrightarrow k \;{\text{in}}\;D $$
(19)
$$ \mu \frac{{\partial g}}{{\partial n}} + \zeta g\overrightarrow k \cdot \overrightarrow n = 0\;{\text{on}}\;{S_T} $$
(20)
$$ \mu \frac{{\partial g}}{{\partial n}} + {U_n}g = 0\;{\text{on}}\;{S^{ + }} $$
(21)
$$ \mu \frac{{\partial g}}{{\partial n}} = 0\;{\text{on}}\;{S^{ - }} $$
(22)
$$ \mu \frac{{\partial g}}{{\partial n}} = - {\overrightarrow g_s} \cdot \overrightarrow n \;{\text{on}}\;{S_B} $$
(23)
$$ g\left( {r,\;T} \right) = 0\;{\text{in}}\;D $$
(24)

Note that the boundary conditions (19)–(23) and final condition (24) imposed on the solution are those that guarantee the fulfilment of the Lagrange identity. Besides, this model is similar to model (4)–(11), but with advection and sedimentation velocities in opposite direction. Thus, the adjoint model (18)–(24) being solved backward in time (from t = T to t = 0) also has a unique solution, which continuously depends on the forcing p(r,t). This result can be immediately shown by the transformation of variable t′ = T–t [36].

Moreover, the forcing p(r,t) of Eq. (18) will be defined so that the mean concentration of nutrient

$$ {J_i}(\phi ) = \frac{1}{{\tau \left| {{\Omega_i}} \right|}}\int\limits_{{T - \tau }}^T {\int\limits_{{{\Omega_i}}} {\phi (r)dr} } dt $$

in a contaminated zone Ω i  ⊂ D will be explicitly related with the discharge rate Q(t) and initial concentration of nutrient \( {\phi^0}(r) \) through the adjoint solution g. Indeed, let us take

$$ p\left( {r,\;t} \right) = \left\{ {\matrix{{*{20}{c}} {\frac{1}{{\tau \left| {{\Omega_i}} \right|}}{ },\;r \in {\Omega_i}\;{\text{and}}\;t \in \left( {T - \tau, \;T} \right)} \hfill \\ {{ }0,\;{\text{otherwise }}} \hfill \\ } } \right. $$

where \( \left| {{\Omega_i}} \right| \) is the volume of oil-polluted zone Ω i , and τ is the time required for the nutrient to reach its critical concentration in the zone. Then the use of this formula in (17) leads to

$$ {J_i}\left( \phi \right) = \mathop{\smallint }\limits_0^T {g_i}\left( {{r_0},\;t} \right)Q(t)dt + \mathop{\smallint }\limits_D {g_i}\left( {r,\;0} \right){\phi^0}(r)dr $$
(25)

also known as the duality principle. Provided that ϕ 0(r) = 0 for the first discharge of nutrient, the last formula is reduced to

$$ {J_i}\left( \phi \right) = \mathop{\smallint }\limits_0^T {g_i}\left( {{r_0},\;t} \right)Q(t)dt $$
(26)

The use of (26) in (2) for each zone Ω i (i = 1,…,N) , and in (3) for the region D, transforms the variational problem (1)–(3) to a more convenient form for the analysis:

$$ {\text{minimize}}\;m(Q) = \int\limits_0^T {Q(t)dt} $$
(27)
$$ {\text{subject}}\;{\text{to}}:{c_i} \leqslant \mathop{\smallint }\limits_0^T {g_i}\left( {{r_0},t} \right)Q(t)dt \leqslant {c_i} + {\varepsilon_i},\;1 \leqslant i \leqslant N $$
(28)
$$ \mathop{\smallint }\limits_0^T {g_0}\left( {{r_0},t} \right)Q(t)dt \leqslant {c_0};\;0 \leqslant Q(t) \leqslant {Q_0}(t),\;0 \leqslant t \leqslant T $$
(29)

Note that this model can be simplified if the following relationship between the limit Q 0 of the discharge rate and the global limit c 0 of the mean concentration is satisfied

$$ \mathop{\smallint }\limits_0^T {g_0}\left( {{r_0},t} \right){Q_0}(t)dt \leqslant {c_0} $$

in such a case the integral constraint in (29) can be omitted. However, since these parameters can vary according to the conditions of the marine environment, this simplification is not always possible.

However, if a repeated discharge of nutrient is needed for degrading oil residuals, then the nonzero initial concentration of the nutrient must be taken into account (see (25)). It should be noted that, due to microbial intake of nutrient in the oil-polluted zones and the water outflow from region D, the concentration of nutrient decreases in region D towards its natural value. Therefore, the following conditions for the mean concentration of nutrient must be fulfilled since the moment t 0 > T:

$$ \frac{1}{{\left| D \right|}}\int\limits_D {\phi \left( {r,t} \right)dr < {c_0}}, \;\frac{1}{{\left| {{\Omega_i}} \right|}}\int\limits_{{{\Omega_i}}} {\phi \left( {r,t} \right)dr < {c_i} + {\varepsilon_i}}, \;i = 1,...,N,\;t \geqslant {t_0} $$
(30)

The moment t 0 can be determined through monitoring the mean concentration of nutrient in region D or by using the solution ϕ forecasted by the model (4)–(11) with the forcing Q(t) equal to zero for t > T. Once conditions (30) are fulfilled, the initial concentration for modeling the next application of nutrient is chosen as

$$ {\varphi^0}(r) = \phi \left( {r,{t_0}} \right) $$
(31)

and the next time interval for such modeling is [t 0, t 0 + T]. Due to conditions (30), the contribution of φ 0(r) to the mean concentrations of nutrient during time interval [t 0 + T − τ,t 0 + T] is less than the upper bounds c 0 (in D) and c i  + ε i (in Ω i , i = 1,…,N). Note that without these last conditions, the feasibility space for problem (1)–(3) is empty and there is no solution to the control problem.

Thus, once conditions (30) are fulfilled and assuming that t 0 = 0, again the problem (27)–(29) can be considered with the following positive parameters to modeling the second discharge of nutrient

$$ c_0^{\prime } = {c_0} - \mathop{\smallint }\limits_D {g_i}\left( {r,\;0} \right){\varphi^0}(r)dr\;{\text{and}}\;c_i^{\prime } = {c_i} - \mathop{\smallint }\limits_D {g_i}\left( {r,\;0} \right){\varphi^0}(r)dr,{ }i = 1, \ldots, N $$
(32)

Where the adjoint functions in (32) must be calculated in time interval [t 0, t 0 + T]. Without loss of generality, we have assumed that negative values on the left side of constraints (28) have been switched to zero, when they appear. Taking into account these remarks, the variational problem (27)–(29) is a general representation of the remediation strategy when it is to be applied once or many times.

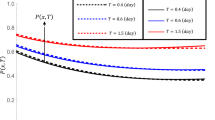
It is important to note that all the adjoint solutions g i (r 0,t) which figure in constraints (28) and (29) are independent of the discharge rate Q(t). This non-negative solutions are determined by the flow dynamics in region D and serve in constraints (28) and (29) as certain weight functions characterizing the impact of the discharge of nutrient at point r 0 on each zone Ω i (see Fig. 1). In other words, the adjoint solutions are the influence functions (or information functions) in the control theory. That is why the adjoint problem solutions are widely used in the sensitivity study of various models, and in particular, in the atmosphere and ocean model, weather forecast and climate theory [19, 22], data assimilation problems [21], problems of identification of unknown pollution sources, like nuclear accidents [32, 42], simulation of oil pollution [7, 35], and optimal control in pollution problems [1, 13, 14, 18, 20, 27, 41].

Fig. 1
figure 1

Adjoint functions for region D (g 0) and Ω i zones (g i , i = 1, 2, 3)

Full size image

4 Analytical and Numerical Results

In order to determine the features of a variational problem (27)–(29), we first analyze this problem for a fixed point r 0∈D, and then consider the problem of choosing the optimal discharge point.

The feasibility space Θ for problem (27)–(29) is given as

$$ \Theta = \left\{ {Q \in {L_2}\left( {0,T} \right){\text{such}}\;{\text{that}}\;{\text{conditions}}\;\left( {{28}} \right)\;{\text{and}}\;\left( {{29}} \right){\text{are}}\;{\text{fulfilled}}} \right\} $$

where functions Q 0 and g i (r 0,t), i = 1,…, N, belong to the Hilbert space H = L 2(0,T). Since each function g i (r 0,t) is non-negative in [0,T] and c i  > 0 (i = 1,…, N), it is concluded from (28) that the feasibility space Θ is non-empty only if

$$ {g_i}\left( {{r_0},t} \right) > 0\;{\text{in}}\;{\text{an}}\;{\text{open}}\;{\text{interval}}\quad {I_i} \subset \left( {0,T} \right),{ }1 \leqslant i \leqslant N $$
(33)

This is a necessary condition for the existence of solution to the control problem, such a condition suggests that the optimal discharge point should be chosen only among such points r ∈ D that satisfy (33). However, condition (33) is not sufficient for the existence of a solution to problems (27)–(29). Indeed, (33) is satisfied if 0 < g j (r 0, t) < g k (r 0, t), 0 ≤ t ≤ T. However, the feasibility space Θ is empty if c j  > c k  + ε k .

On the other hand, the feasibility space Θ is a convex, bounded and closed set in H. To show this, we observe that for any Q 1 and Q 2 in H, and λ ∈ (0,1),

$$ \matrix{{*{20}{c}} {\mathop{\smallint }\limits_0^T \left( {\lambda {Q_1} + \left( {1 - \lambda } \right){Q_2}} \right){g_i}\left( {{r_0},t} \right)dt = \lambda \int\limits_0^T {{Q_1}{g_i}\left( {{r_0},t} \right)} dt + \left( {1 - \lambda } \right)\int\limits_0^T {{Q_2}{g_i}\left( {{r_0},t} \right)} dt} \hfill \\ { \leqslant \lambda \left( {{c_i} + {\varepsilon_i}} \right) + \left( {1 - \lambda } \right)\left( {{c_i} + {\varepsilon_i}} \right) = {c_i} + {\varepsilon_i}} \hfill \\ } $$

and

$$ 0 \leqslant \lambda {Q_1} + \left( {1 - \lambda } \right){Q_2} \leqslant \lambda {Q_0} + \left( {1 - \lambda } \right){Q_0} = {Q_0},\quad 0 \leqslant t \leqslant T $$

The term λ Q 1 + (1 − λ)Q 2 satisfies the constraints (28)–(29) as well, and hence Θ is a convex set.

Also, due to the last constraint in (29), \( \left\| Q \right\| \leqslant \left\| {{Q_0}} \right\| = const \) for all Q of Θ, and therefore, the feasibility space Θ is bounded.

Finally, in order to show that Θ is a closed set in H, we now prove that \( \overline \Theta \subset \Theta \) [9]. Let Q be any element of \( \overline \Theta \). Then there is a sequence \( \left\{ {{Q_k}} \right\}_{{k = 1}}^{\infty } \) in Θ such that

$$ \left\| {{Q_k} - Q} \right\| \to 0\;{\text{as}}\;k \to \infty $$
(34)

Assume that Q(t) < 0 in some interval I ⊂ (0,T) of positive measure |I| > 0. Then

$$ {\left\| {{Q_k} - Q} \right\|^2} = \int\limits_0^T {{{\left( {{Q_k} - Q} \right)}^2}} dt \geqslant \int\limits_I {{{\left( {{Q_k} - Q} \right)}^2}dt \geqslant \int\limits_I {{Q^2}} } dt = l > 0 $$

The last inequality contradicts the convergence of \( \left\{ {{Q_k}} \right\}_{{k = 1}}^{\infty } \) in H, and hence, Q is a non-negative function in (0, T).

Now, we assume that Q(t) > Q 0(t) in some interval I ⊂ (0, T) of positive measure |I| > 0. Then

$$ {\left\| {{Q_k} - Q} \right\|^2} = \int\limits_0^T {{{\left( {{Q_k} - Q} \right)}^2}} dt \geqslant {\int\limits_I {{{\left( {{Q_k} - Q} \right)}^2}dt \geqslant \int\limits_I {\left( {Q - {Q_0}} \right)} }^2}dt = {l^{\prime }} > 0 $$

The last inequality contradicts the convergence of \( \left\{ {{Q_k}} \right\}_{{k = 1}}^{\infty } \) in H, and hence, Q(t) ≤ Q 0(t) in (0,T).

On the other hand, the Schwarz inequality [15] leads to

$$ \left| {\int\limits_0^T {{Q_k}(t){g_i}\left( {{r_0},t} \right)} dt - \int\limits_0^T {Q(t){g_i}\left( {{r_0},t} \right)} dt} \right| \leqslant \int\limits_0^T {\left| {{Q_k}(t) - Q(t)} \right|} {g_i}\left( {{r_0},t} \right)dt \leqslant \left\| {{Q_k} - Q} \right\|\left\| {{g_i}\left( {{r_0},t} \right)} \right\| $$

and, due to (34), we get that \( \mathop{{\lim }}\limits_{{k \to \infty }} \int\limits_0^T {{Q_k}{g_i}\left( {{r_0},t} \right)} dt = \int\limits_0^T {Q{g_i}\left( {{r_0},t} \right)} dt \). By (28), the sequence \( \left\{ {\int\limits_0^T {{Q_k}{g_i}\left( {{r_0},t} \right)} dt} \right\}_{{k = 1}}^{\infty } \) belongs to the closed interval [c i , c i  + ε i ], and hence this interval contains its limit point [9]. Thus

$$ {c_i} \leqslant \int\limits_0^T {Q(t){g_i}\left( {{r_0},t} \right)} dt \leqslant {c_i} + {\varepsilon_i}{,}\quad 1 \leqslant i \leqslant N $$

The constraint \( 0 \leqslant \int\limits_0^T {Q(t){g_0}\left( {{r_0},t} \right)} dt \leqslant {c_0} \) is proved in a similar way, and therefore, Q ∊ Θ.

To prove the existence of solution to problem (27)–(29), we consider a finite-dimensional subspace Г of H. Since H is a normed space, Г is a closed set in H [15]. So, the intersection \( \Pi = \Gamma \cap \Theta \) of closed sets is a closed set in H [9]. In fact, П is a closed set in Г, as well [9]. Also, note that П is a bounded subset of Г, because Π ⊂ Θ, and Θ is bounded in the norm of H. Since Г is a finite-dimensional normed space, and П is a bounded and closed subset of Г, П is a compact subset in Г[15].

On the other hand, Schwarz inequality leads to

$$ \left| {m(q) - m(Q)} \right| \leqslant \int\limits_0^T {\left| {q(t) - Q(t)} \right|dt} \leqslant \sqrt {T} \left\| {q - Q} \right\| $$

where m(Q) is the mass functional (27). Using the last inequality, and choosing \( \delta = {{\varepsilon } \left/ {{\sqrt {T} }} \right.} \) for the continuity definition, one concludes that m(Q) is a continuous functional on H, and hence, it is also continuous on П. Since П is a compact subset of the metric space Г, and m is a continuous functional on \( \Pi \ne \phi \), there exists a point Q * ∊ Π that minimizes functional m [15]. This point Q * = Q *(t; r 0) is the optimal discharge rate of the nutrient at the point r 0.

Note that the functional m(Q) is linear and convex, but not strictly convex, and hence, there may exist more than one optimal solution, that is, Q * is not necessarily unique. However, the space of optimal solutions is a convex set in П. To show this, note that П is a convex set as the intersection of convex sets [12]. Thus, if Q 1 and Q 2 are optimal solutions of П, and λ ∊ (0, 1), then λ Q 1 + (1 − λ)Q 2 also belongs to П, and

$$ m\left( {\lambda {Q_1} + \left( {1 - \lambda } \right){Q_2}} \right) = \lambda m\left( {{Q_1}} \right) + \left( {1 - \lambda } \right)m\left( {{Q_2}} \right) = \lambda m\left( {{Q^{ * }}} \right) + \left( {1 - \lambda } \right)m\left( {{Q^{ * }}} \right) = m\left( {{Q^{ * }}} \right), $$

that is, solution λQ 1 + (1 − λ)Q 2 is also optimal.

This property is useful, since it permits choosing, at the same cost m(Q *), an optimal solution among the functions λ Q 1 + (1 − λ)Q 2, 0 < λ < 1, where Q 1 and Q 2 are two given optimal solutions. The criterion for such a choice could be the easiness to implement the discharge rate in a real situation of bioremediation.

In this work, the finite-dimensional subspace Г is generated by the ‘tent’ functions, which are given as

$$ {\gamma_k}(t) = \left\{ \begin{gathered} {{{1 + \left( {t - {t_k}} \right)}} \left/ {{\Delta t,\;{t_{{k - 1}}} \leqslant t \leqslant {t_k}}} \right.} \hfill \\ {{{1 - \left( {t - {t_k}} \right)}} \left/ {{\Delta t,\;{t_k} \leqslant t \leqslant {t_{{k + 1}}}}} \right.} \hfill \\ 0,\;{\text{otherwise}} \hfill \\ \end{gathered} \right. $$
(35)

where the nodes t k  = k ⋅ Δt, k = 0, 1, …, L, Δt ⋅ L = T, form a regular mesh in interval [0,T], and the functions γ 0 and γ L are equal to zero outside [0,T]. The basic functions γ k , k = 0, 1, …, L, have the following useful properties:

$$ {\gamma_i}\left( {{t_j}} \right) = \left\{ \begin{gathered} 1,\quad i = j \hfill \\ 0,\quad i \ne j \hfill \\ \end{gathered} \right.,\;i,j = 0,1,...,L $$

and

$$ \int\limits_0^T {{\gamma_0}(t)dt = \int\limits_0^T {{\gamma_L}(t)dt = \frac{{\Delta t}}{2}}, \quad } \int\limits_0^T {{\gamma_k}(t)dt = \Delta t,\;k = 1,...,L - 1} $$

Taking into account these remarks, one can conclude that the discharge rate of nutrient Q∊П is given by a linear combination of basic functions

$$ Q(t) = \sum\limits_{{k = 0}}^L {{x_k}{\gamma_k}(t)} $$
(36)

and the optimal solution Q * of control problem is the solution of the following linear programming problem

$$ {\text{minimize}}\quad m\left( {{x_0},...,{x_L}} \right) = \left( {{{{\Delta t}} \left/ {2} \right.}} \right)\left[ {{x_0} + 2\sum\limits_{{k = 1}}^{{L - 1}} {{x_k}} + {x_L}} \right] $$
(37)
$$ {\text{subject to}}:\quad {c_i} \leqslant \sum\limits_{{k = 0}}^L {{a_{{ik}}}{x_k} \leqslant {c_i} + {\varepsilon_i}}, \quad 1 \leqslant i \leqslant N $$
(38)
$$ { }\sum\limits_{{k = 0}}^L {{a_{{0k}}}{x_k} \leqslant {c_0}}, \quad 0 \leqslant {x_k} \leqslant {Q_0}\left( {{t_k}} \right),\quad 0 \leqslant k \leqslant L $$
(39)

where the coefficients a ik are given as

$$ {a_{{ik}}} = \int_{{{t_{{k - 1}}}}}^{{{t_{{k + 1}}}}} {{g_i}\left( {{r_0},t} \right){\gamma_k}(t)dt,\quad 0 \leqslant i \leqslant N,\quad 0 \leqslant k \leqslant L} $$
(40)

and the feasibility space П is determined by (36) and (38)–(40).

Thus, the variational problem (27)–(29) has been reduced to the linear programming problem (37)–(40) with L + 1 real variables \( \left\{ {{x_k}} \right\}_{{k = 0}}^L \), and 2(L + N) + 3 constraints. The solution of this problem can be obtained with a large-scale optimization method based on LIPSOL, Linear Interior Point Solver [43], which is a variant of Mehrotra’s predictor–corrector algorithm [23], a primal–dual interior-point method. Also, for medium-scale optimization can be applied a projection method which is a variation of the well-known simplex method for linear programming [8, 12]. The interior-point method reduces the computing time in the large size problems [43] and represents a good alternative when the number of grid points in the control problem is too large. In this work, both methods above mentioned have been implemented with the linprog subroutine of MATLAB.

Note that, in order to simplify the linear programming problem (37)–(40), we can approach the coefficients a ik through second order formulas, like trapezoidal rule, as follows

$$ {a_{{i0}}} = \left( {{{{\Delta t}} \left/ {2} \right.}} \right){g_i}\left( {{r_0},{t_0}} \right){,}\quad {a_{{iL}}} = \left( {{{{\Delta t}} \left/ {2} \right.}} \right){g_i}\left( {{r_0},{t_L}} \right),\quad {a_{{ik}}} = \Delta t \cdot {g_i}\left( {{r_0},{t_k}} \right)\quad 1 \leqslant i \leqslant N,\quad 1 \leqslant k \leqslant L. $$

Once the optimal discharge rate Q *(t;r 0) can be built for any r 0∊D, the choice of a suitable release site is considered. We point out that the criterion to select the optimal discharge point \( r_0^{ * } \) is to minimize the mass of the nutrient entering the marine environment. Note that in this case, the objective function is a non-linear function \( m\left( {{Q^{ * }}} \right) = \int_0^T {{Q^{ * }}\left( {t;{r_0}} \right)dt} \) of three real variables being the coordinates of r 0 = (x 0, y 0, z 0), and it can be evaluated when all the adjoint functions g i are already determined and the linear programming model (37)–(40) has been solved. Besides, while minimizing this function, it is a computationally advantageous to narrow the search area only to those points r 0∊D in which the indicative function

$$ {\text{P}}\left( {{r_0}} \right) = \mathop{\Pi }\limits_{{i = 1}}^N \int_0^T {{g_i}\left( {{r_0},t} \right)} dt $$
(41)

is positive, that is , the minimum \( r_0^{ * } \) must be searched only within the support of function P [10], where the necessary condition (33) is fulfilled. The case P(r 0) = 0 means that, due to the flow dynamics in D, the nutrient discharge at the point r 0 cannot reach all the oil-polluted zones during the time interval [T − τ,T].

4.1 Examples of Remediation in a Channel

In order to illustrate the method developed, we now consider a simple example of bioremediation in a channel of 120 m long [0,120], 10 m wide [0,10], and 4 m deep [0,4], H = 4. The channel contains three oil-polluted zones: \( {\Omega_{{1}}} = \left[ {20,30} \right] \times \left[ {9,10} \right] \times \left[ {0,4} \right] \), \( {\Omega_{{2}}} = \left[ {70,80} \right] \times \left[ {9,10} \right] \times \left[ {0,4} \right] \) and \( {\Omega_{{3}}} = \left[ {95,100} \right] \times \left[ {0,2} \right] \times \left[ {0,4} \right] \).

The critical nutrient concentrations c i (grm −3) in the zones vary from one experiment to another (Table 1) and generate different optimal discharge rates \( Q_j^{ * } \) (Fig. 2). The parameters of adjoint model (18)–(24) have been taken as follows: The velocity vector \( \overrightarrow U \) is directed along the channel and is equal to \( \overrightarrow U = 0.0083\overrightarrow i { }m{s^{{ - 1}}} \), \( \overrightarrow i = {\left( {1,0,0} \right)^t} \), μ = 0.0017 m2s−1, σ = 0.00027 s−1 and ζ = v s  = 0.

Table 1 Numerical details of linear programming problem solution (37)–(40)
Full size table
Fig. 2
figure 2

Optimal discharge rates Q j for data j = 1, 2, 3, and 4

Full size image

The nutrient is released at the point r 0 = (3,2.2,2) during 4 h (T = 14,400 s), the total time interval is 4 h: (0,T) = (0,14400), and the mean concentration is controlled within the last 1-h interval [T − τ, T] = [10,800, 14,400], i.e., τ = 3,600 s. The adjoint functions g i (r 0, t) for the three zones (i = 1, 2, 3), and adjoint function g 0(r 0, t) for region D, are given in Fig. 1.

In all the examples (j = 1, 2, 3, and 4), the linear programming problem (37)–(40) is solved with the following parameters ε i  = 0.05(grm −3), c 0 = 3.5(grm −3),

$$ {Q_0}(t) = \left\{ \begin{gathered} {\alpha_j},\;0 \leqslant t < 7,200 \hfill \\ {\beta_j},\;{7,200} \leqslant t \leqslant 14,400 \hfill \\ \end{gathered} \right., $$

where α 1 = 7.77 and β 1 = 9.44; α 2 = 7.22 and β 2 = 9.77; α 3 = 12.22 and β 3 = 5.33; and α 4 = 10.00 and β 4 = 12.44. Finally, the spatial mesh size for numerical solution of adjoint problem (18)–(24) is Δx = Δy = 0.4 m with a time step Δt = 36 s, and hence, L = 400 for the linear programming problem.

The computing time to get each adjoint problem solution using the workstation HP-XW8200 was about 370 s. Table 1 shows the time required to solve the linear programming problem (37)–(40) through linprog subroutine of MATLAB. It is important to note that the interior point method is, approximately, 100 times faster than the simplex method, and both methods determine the same solution (see relative errors in Table 1). We conclude that, for each example, the computing time required to find the optimal discharge rate was about 1,500 s. Figure 2 shows the optimal discharge rates \( Q_j^{ * } \) for the four examples (j = 1, 2, 3, and 4). Each release rate is simply a combination of step functions. The nonzero values of step functions are defined in the intervals where the adjoint functions are positive, besides the height of the steps is determined by the limit function Q 0.

5 Conclusions and Final Remarks

The main objectives of the mathematical modeling in the environment protection are the prediction of concentrations of different substances (pollutants, cleanears, nutrients, etc.), the development of the methods which help to prevent dangerous pollution levels (control of emissions) and the development of the strategies for the remediation of polluted zones. In this work, we have presented a method of cleaning the oil-polluted marine environment through bioremediation. It is assumed that oil is stranded in some zones at the shoreline and the goal is to release a nutrient into aquatic system in order to increase the amount of indigenous microorganisms which degrade the pollutants in such zones. Thus, the specific objectives are to determine the appropriate parameters of releasing a nutrient, namely, r 0 (discharge site) and Q (discharge rate), in order to reach necessary concentration of the nutrient in the polluted zones. Both unknown parameters are chosen so that to minimize the total mass of the nutrient, with the aim to minimize the impact on the environment and the cost of remediation. To this end, for each point r 0, the optimal discharge rate Q * = Q *(t; r 0) is obtained through the solution of a linear programming problem. We have shown the existence of such a solution. Then the optimal discharge site r 0 is selected as such a point which minimizes the function m(Q *(t; r 0)). To reduce the computational efforts, the search is limited to the points r 0 ∊ D at which the indicative function P is positive.

To determine the discharge rate of the nutrient Q *(t; r 0), it is necessary first to solve N + 1 adjoint problems (where N is the number of contaminated zones), and then a linear programming problem with L + 1 positive variables and 2(L + N) + 3 constraints (where L + 1 is the number of nodes of regular mesh in interval [0, T]). This procedure is shown to be computationally efficient. Also, the numerical examples show that in the case when the limit Q 0 is constant, Q *(t; r 0) has a simple form (combination of step functions). This is important advantage of the method in its practical application in bioremediation.

This new remediation method is strongly based on the adjoint estimates, but it also uses the direct concentration estimates of the nutrient in polluted zones when multiple discharges of the nutrient are needed. These equivalent estimates complement each other well at the assessment of the nutrient and pollution control. The direct estimates, utilizing the solution of the transport problem, enable making the comprehensive analysis of ecological situation in the whole area. On the other hand, the adjoint estimates use the adjoint problem solutions and explicitly depend on the discharge rate of the nutrient and its initial distribution in the region. Besides, the solutions of adjoint problem serve as influence functions, which show the impact of the discharge point location on the concentration of nutrient in each oil-polluted zone. Therefore, the adjoint estimates are effective and economical in the study of the sensitivity of the concentrations of the nutrient to variations in the model parameters.

Owing to special boundary conditions, both the main and adjoint problems are well-posed according to Hadamard, that is, any solution of either problem is unique and stable to initial perturbations. These conditions are reduced to the well-known and natural boundary conditions in the non-diffusion limit (pure advection problem) and in the case of a closed sea basin whose boundary is the coast line.

We now make a final remark. In this work, we suppose that the nutrient released into the marine environment is a liquid, for example, the product named Inipol EAP22 [17]. Therefore the sedimentation velocity v s is very small or zero, and the sediment of nutrient mass on the bottom S B of the marine region D is not significant, namely, the nutrient is totally dissolved in the water. That is why we control the mean concentration of nutrient in the tridimensional marine oil-polluted zones Ω i , which are located at the shoreline but not at the bottom of the marine region D. On the other hand, when the oil is concentrated on the marine floor, the bioremediation is required in some two-dimensional zones \( \Omega_B^i \), located on the sea bottom S B of region D, the nutrient should be released in granular form, as the Customblen product [31]. In this case, the sedimentation velocity v s is not zero, and the mass of the nutrient, deposited on S B , increases, which favors the remediation process in the polluted zones \( \Omega_B^i \). Therefore, the control of the nutrient mass deposited on S B is more adequate than control of the nutrient concentration per volume.

To study this problem, we also consider the variational problem (1)–(3) and dispersion model (4)–(11), but the functional J i , given by constraints in (2), is redefined as

$$ {J_i} = - \frac{1}{{\left| {\Omega_B^i} \right|}}\int\limits_0^T {\int\limits_{{\Omega_B^i}} {{v_s}} } \phi \overrightarrow k \cdot \overrightarrow n dSdt $$

According to the mass balance Eq. (13), this functional estimates the mass of the deposited nutrient, per superficial unit, on the polluted zone \( \Omega_B^i \subset {S_B} \), during the interval of discharge [0, T]. Note that J i is a non-negative function because \( \overrightarrow k \cdot \overrightarrow n < 0{\text{ on }}{S_B} \).

In order to extend to this case the methodology described in this work, we must change the adjoint model (18)–(24) as follows. The forcing in the transport Eq. (18) is redefined as

$$ p\left( {r,t} \right) = 0,\quad r \in D,\quad 0 < t < T $$

and the boundary condition given by (23) is redefined as

$$ \mu \frac{{\partial g}}{{\partial n}} + \overrightarrow g \cdot \overrightarrow n = \left\{ \begin{gathered} { } - \frac{{{v_s}}}{{\left| {\Omega_B^i} \right|}}\overrightarrow k \cdot \overrightarrow n {, }\quad {\text{if}}\quad r \in \Omega_B^i{ } \hfill \\ { 0, }\quad {\text{if}}\quad r \in {S_B} - \Omega_B^i \hfill \\ \end{gathered} \right.\;{\text{on}}\;{S_B} $$

Taking into account these considerations, it is shown that the duality principle (25) also holds for the new functional J i , and hence, the variational problem (27)–(29) and the linear programming problem (37)–(40) can be applied to determine the optimal discharge parameters of the bioremediation problem. We observe that this adjoint model also has unique solution that continuously depends of the parameters determining the flow through the boundary S B .