1 Introduction

Surface water pollution by chemical, physical, and biological contaminants all over the world can be considered as a worldwide problem [1, 2]. Anthropogenic inputs such as municipal, industrial, and agricultural wastewater discharge and natural processes, i.e., weathering and soil erosion, are major factors determining the quality of the water resources. Many studies have been done on anthropogenic contamination of ecosystems [3, 4]. However, due to spatial and temporal variations in water quality, which are often difficult to interpret, a monitoring program providing a representative and reliable estimation of the quality of surface waters is necessary [5]. Literature demonstrated that chemometric data analysis methods such as canonical correlation analysis (CCA), principal component analysis (PCA), and principal factor analysis (PFA) are suitable techniques to achieve the goals. Through the CCA approach, Larson et al. [6] analyzed an 11-year-long measurement time series of waves and profiles from Duck North Carolina in order to determine covariability between waves and profile response. Gangopadhyay et al. [7] applied the PCA and PFA techniques to identify importance of monitoring wells predicting dynamic variations related to potentiometric head at a location in Bangkok, Thailand. Simeonov et al. [8] using PCA, clustering analysis (CA), and principal component regression interpreted a large and complex data matrix of surface water parameters in northern Greece. However, water quality data set from alluvial region in northern India have been analyzed by means of PCA, discriminate analysis, and partial least squares in order to investigate the three parts: first compositional differences between surface and groundwater samples; second spatial variations in groundwater composition; and finally influence of natural and anthropogenic factors [9]. Sarbu and Pop [10] illustrated a data set concerning the water quality in the Danube River through a robust fuzzy PCA algorithm. Ouyang [11] adopted PCA and PFA to identify important water quality parameters in 22 stations located at the main stem of the lower St. Johns River in Florida, USA. Results revealed that total organic carbon, dissolved organic carbon, total nitrogen, dissolved nitrate and nitrite, orthophosphate, alkalinity, salinity, magnesium, and calcium were the most important parameters in assessing variations of water quality in the river. Through the PCA and geographical information system approaches, Terrado et al. [12] analyzed the main contamination sources of heavy metals, organic compounds, and other physicochemical parameters in Ebro River surface waters. Furthermore, they evaluated their temporal and spatial distributions. Noori et al. [13] applied PCA and PFA techniques for selecting the monitoring stations in assessing annual variations of river water quality. They selected eight monitoring stations, located at the Karoon River in Iran. Finally, authors suggested that PCA and PFA techniques were useful tools for identifying the importance of surface water quality monitoring stations. Sherestha and Kazama [14] applied CA, PCA, PFA, and discriminant analysis techniques to evaluate temporal and spatial variations and interpret a large complex water quality data set of the Fuji River basin. Liu et al. [15] applied CCA to investigate relationship between personal exposure to ten volatile organic compounds and biochemical liver tests. Noori et al. [16] proposed a multivariate statistical method, i.e., canonical correlation analysis for investigating the relationship between physical and chemical parameters of the Karoon River.

However, it is pointed out that previous studies try to identify annual variations of the water quality parameters in the water quality monitoring networks. It is clear that water quality parameters are affected by arid, semi-arid, and wet conditions; thus they can be different in each season of the year. So it is an important task to investigate the seasonal variations of the water quality in the monitoring networks. Hence, the research aims are to analyze seasonal variations of 11 physio-chemical parameters recorded in seven surface water quality monitoring stations for 7 years in the Gorganrud River, Iran, by means of PCA and PFA techniques. In addition, investigation of the relationship between physical and chemical parameters in the Gorganrud River is carried out using CCA method.

2 Materials and Methods

2.1 Case Study and Data

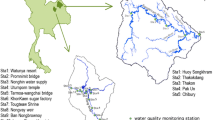
The Gorganrud River basin (between 54°00′ to 56°07′ E and 36°36′ to 37°47′ N) is located in Golestan province, northern part of Iran (Fig. 1). Gorganrud River originates from the Alborz Mountains and after passing from the residential, agricultural, and industrial areas flows down to the Caspian Sea. It has a catchment area of 10,200 km2 and average annual rainfall of 500 mm. The main stream length of the Gorganrud River catchment is 350 km. The Increasing water withdrawal that leads to enhance wastewater discharge to the river endangered the aquatic life of this ecosystem. As a result, there is an increasing trend gap between current water quality and standard water quality. Agricultural and agro-industrial return flows, domestic wastewater of the cities–rural area, and industrial wastewaters are known as the main pollution sources of the surface and groundwater resources in the Gorganrud River basins.

Fig. 1
figure 1

Territorial layout of the Gorganrud River basin and the location of the river sampling sites

Full size image

In this study, 11 physio-chemical parameters related to seven monitoring stations are used for chemometric analysis (Table 1).

Table 1 Water quality parameters for surface water of the Gorganrud River basin
Full size table

2.2 CCA Method

In some sets of multivariate data, the variables are divided naturally into two groups (i.e., response data and predictor variable). A canonical correlation analysis can then be used to investigate relationships between the two groups. As an exploratory tool, it is used as a data reduction method. The goal of CCA is to construct two new sets of canonical variates U = αX and V = βY that are linear combinations of the original variables such that the simple correlation between U and V is maximal, subject to the restriction that each canonical variate U and V has unit variance (to ensure uniqueness, except for sign) and is uncorrelated with other constructed variates within the set [17]. Assume that the \( \left( {p + q} \right) \times \left( {p + q} \right) \) correlation matrix between the variables X 1 , X 2 , …, X p and Y 1 , Y 2 , …, Y q takes the following form when it is calculated from the sample for which the variables are recorded:

figure a

From this matrix, a q × q matrix B −1 C′A −1 C can be calculated, and the eigenvalue problem can be considered as [18]:

$$ \left( {{{\mathbf{B}}^{{ - {\mathbf{1}}}}}{\mathbf{C}}\prime {{\mathbf{A}}^{{ - {\mathbf{1}}}}}{\mathbf{C}} - \lambda {\mathbf{I}}} \right){\mathbf{b}} = 0 $$
(2)

It turns out that the eigenvalues λ 1 > λ 2 > … > λ r are then the squares of the correlations between the canonical variates. The r subscript is smaller than p and q. The corresponding eigenvectors b 1, b 2, …, b r give the coefficients of the Y variables for canonical variates. The coefficients of linear combination of X variables (U i ) and the ith canonical variate for the X variables are given by the elements of the a i vector [19].

$$ {{\mathbf{a}}_{\text{i}}} = {{\mathbf{A}}^{{ - {\mathbf{1}}}}}{\mathbf{C}}{{\mathbf{b}}_{\text{i}}} $$
(3)

In these calculations, it is assumed that the original X and Y variables are in a standardized form with a mean of zero and standard deviation of unity. The coefficients of the canonical variates are for these standardized X and Y variables.

2.3 PCA and PFA

PCA and PFA are multivariate statistical methods which can be used for reducing complexity of input variables when there are large volumes of information and it is intended to have a better interpretation of variables [20, 21]. In mathematical terms, PCA and PFA involve the following five major steps: (1) start by coding the variables X 1 , X 2 ,…, X p to have zero means and unit variance; (2) calculate the correlation matrix R; (3) find the eigenvalues λ 1 , λ 2 ,…, λ p and the corresponding eigenvectors a 1 , a 2 ,…, a p by solving Eq. 4:

$$ \left| {R - I\lambda } \right| = 0. $$
(4)

(4) Discard any components that only account for a small proportion of the variation in datasets and (5) develop the factor loading matrix and perform a Varimax rotation on the factor loading matrix to infer the principal parameters [22]. Details for mastering the art of PCA and PFA are published elsewhere [23–25].

3 Results and Discussion

3.1 Relationship Between Physical and Chemical Parameters

According to Table 1 there are five variables in the response data set, i.e., physical parameters including T, DO, TDS, Turb, TSS, and six variables in the predictor set, i.e., chemical parameters including BOD5, COD, \( {\text{NO}}_{{3}}^{ - } \), TP, EC, and pH. CCA results indicated that correlation coefficient for canonical variates 1, 2, and 3 were 0.94, 0.86, and 0.72, respectively. Correlation coefficients for fourth and fifth canonical variates were 0.38 and 0.45, and then they were neglected in conclusion. Among the first three canonical variates, only the first and second canonical correlation was statistically significant (p value < 0.05). Therefore, there is no real evidence of any relationships between the physical and chemical variables based on canonical variate 3. It is pointed out that the first and second canonical variates represent the most variations in the response and predictor data set. Thus based on correlation coefficients of the first and second canonical variates, it can be concluded that a strong relationship between physical and chemical parameters exists in the Gorganrud River.

3.2 Identification of Important Monitoring Stations

Early correlation symmetrical matrix R is formed with dimensions 7 × 7 (equivalent to the number of input variables or stations) for PCA application. From solving Eq. 4, seven eigenvalues are obtained. Then for each of the eigenvalue, seven eigenvectors are calculated. Finally, using obtained eigenvectors, seven principal components (PCs) are computed. The characteristics of the PCs are presented in Table 2.

Table 2 Descriptive statistics of created PCs
Full size table

In this table, eigenvalues, variance proportion, and cumulative variance proportion are shown. Clearly, the first three components accounted approximately 48.59%, 31.35%, and 19.49% of the total variance in the data sets, respectively. These three components together accounted for about 99.43% of the total variance and the rest only accounted for about 0.57%. Therefore, our discussions will focus only on the three components calculated as:

$$ \begin{array}{*{20}{c}} {{\text{PC}}1 = 0.242{\text{S}}{{\text{T}}_1} + 0.262{\text{S}}{{\text{T}}_2} + 0.644{\text{S}}{{\text{T}}_3} + 0.780{\text{S}}{{\text{T}}_4} + 0.822{\text{S}}{{\text{T}}_5} + 0.905{\text{S}}{{\text{T}}_6} + 0.869{\text{S}}{{\text{T}}_7}} \\ {{\text{PC}}2 = 0.065{\text{S}}{{\text{T}}_1} + 0.950{\text{S}}{{\text{T}}_2} + 0.763{\text{S}}{{\text{T}}_3} + 0.620{\text{S}}{{\text{T}}_4} + 0.358{\text{S}}{{\text{T}}_5} + 0.292{\text{S}}{{\text{T}}_6} + 0.326{\text{S}}{{\text{T}}_7}} \\ {{\text{PC}}3 = 0.968{\text{S}}{{\text{T}}_1} + 0.169{\text{S}}{{\text{T}}_2} + 0.103{\text{S}}{{\text{T}}_3} - 0.040{\text{S}}{{\text{T}}_4} + 0.433{\text{S}}{{\text{T}}_5} + 0.307{\text{S}}{{\text{T}}_6} + 0.338{\text{S}}{{\text{T}}_7}} \\ \end{array} $$
(5)

where ST i is the monitoring station, the subscripts denote the station numbers, and the coefficients are the eigenvectors. PC1 (Eq. 5) indicated that there are difference between ST1 and ST2 coefficients and other coefficients. So the two coefficients have little effects on PC1 leading to realize that these stations are less important in monitoring water quality variations. In addition, based on the results of PC2, ST has lowest absolute loading (eigenvector) values and a similar trend could be obtained for PC3. However, any conclusion based upon the PC1, PC2, and PC3 would be inappropriate since they only accounted for 48.59%, 31.35%, and 19.49% of the total variance, respectively. For determining the important water quality stations, a PFA technique should be established. In the PFA technique, similar to PCA, the number of factors is equal to the number of variables. Table 3 shows the eigenvectors, which assess the coefficients for formation of factors. In the research, the correlation coefficient considered significant is the one that is greater than 0.75 (or >75%). The main reason of selecting the conservative criterion is that the study area (Gorganrud River basin) is large and the river system is highly nonlinear and dynamic. In addition, some researchers [11, 16] proposed approximately similar value which is used in this research. The stations with less rotated factor correlation coefficients than mentioned value are not considered principal stations. Table 3 indicated that all monitoring stations have coefficient values which are greater than 0.75. Therefore, to explain the annual variation of the data set, all water quality monitoring stations are considered important and thereby their location in the river system could be suitable.

Table 3 Eigenvectors obtained through PFA application
Full size table

3.3 Data Analysis Based on Seasonal Water Quality Parameters

Eleven variables related to water quality parameters have been used for each season. So there are four seasonal correlation symmetrical matrixes for spring, summer, autumn, and winter seasons. Similar to previous section, after solving Eq. 4 for correlation matrixes, the characteristics of 11 PCs for each season is calculated (Tables 4 and 5). In this section, according to PCA results, PCs with eigenvalues higher than 1 are selected, as a result, only four PCs for spring and summer and three for autumn and winter are allocated. The PCs indicated 92.29%, 98.10%, 93.29%, and 89.80% of total variance proportion of input variables in spring, summer, autumn, and winter seasons, respectively. In addition, eigenvectors are obtained through PCA application (Tables 6 and 7) for each season. It should be pointed out that for retaining the PCs, a criterion equal to 10−6 is used. It resulted to six PCs for each season (Tables 6 and 7). In these tables, most effective variables to form the PCs are shown by bold font. Table 6 shows that T and TSS as two water quality parameters that have the highest absolute loading (eigenvector) values for the first component (PC1) in spring season. However, important parameters based on PC1 for summer are pH, EC, BOD5, and COD. Furthermore, the important parameters for autumn and winter seasons are presented by bold font in Table 7. Similar to the previous section, any conclusion based on PC1 in all seasons would be inappropriate since they only accounted for 41.18%, 50.04%, 55.66%, and 41.55% of the total variance in spring, summer, autumn, and winter seasons, respectively. For example, in order to select the important parameter in spring season, although T is the most important parameter in formation of PC1, it has the lowest effect on formation of PC2 (0.077). Also, in the winter, although EC is the most important parameter based on PC1, it is one of the few parameters which affected PC2. Many details are available in Tables 6 and 7.

Table 4 Descriptive statistics of created PCs for spring and summer seasons
Full size table
Table 5 Descriptive statistics of created PCs for autumn and winter seasons
Full size table
Table 6 PCs correlation coefficients for spring and summer seasons
Full size table
Table 7 PCs correlation coefficients for autumn and winter seasons
Full size table

3.4 Extraction of Important Seasonal Water Quality Parameters

As demonstrated in the previous section, the PCA is not proper technique for extracting the important seasonal water quality parameters and it should be carried out by means of the PFA technique. Thus, using PFA method, results of the eigenvalues for each season are plotted in Figs. 2, 3, 4, and 5. Also, Tables 8 and 9 contain the eigenvectors or rotated factor correlation coefficients for each season. Similar to previous section, a criterion as 10−6 is used to retain the principal factors. Furthermore, an absolute rotated factor correlation coefficient value equal to 0.95 (or >95%) is considered for selecting the important parameter contributing to seasonal variations of the water quality of Gorganrud River. It is pointed out, if the value of this criterion is selected close to 1, the numbers of less importance stations or parameters increase. Therefore, due to negative impact of ignored stations is more than ignored parameters, the value of 0.95 was considered for choosing the principal seasonal water quality parameters. Besides, another scenario is run by the value of 0.90 for selecting the principal seasonal water quality parameters.

Fig. 2
figure 2

Eigenvalues of principal factors in spring season

Full size image
Fig. 3
figure 3

Eigenvalues of principal factors in summer season

Full size image
Fig. 4
figure 4

Eigenvalues of principal factors in autumn season

Full size image
Fig. 5
figure 5

Eigenvalues of principal factors in winter season

Full size image
Table 8 Rotated factor (F.) correlation coefficients for spring and summer seasons
Full size table
Table 9 Rotated factor (F.) correlation coefficients for autumn and winter seasons
Full size table

According to Tables 8 and 9, for rotated factor correlation coefficient value equal to 0.95 (first scenario), the important parameters in contributing to water quality variations for one season may not be important for another season. The numbers of important variables in spring, summer, autumn, and winter seasons are 2, 5, 3, and 2 parameters, respectively. In contrast with other seasons, summer, and autumn seasons have the more important parameters because in these seasons, the Gorganrud River has the least amount of flow leading to deteriorate water quality of the river. However, water temperature parameter is one of the most important parameters in summer and winter seasons because in these seasons it affects water quality more than the other seasons. Furthermore, Table 8 denotes that in summer, TP and \( {\text{NO}}_{{3}}^{ - } \) are included in the important parameters. In the Gorganrud River basin, the most volumes of phosphate and nitrate fertilizers are commonly used in summer. In addition, in summer, activity of aquatic plants is very high. So the mentioned reasons cause TP and \( {\text{NO}}_{{3}}^{ - } \) to have more variations. Generally, the important parameters in the spring season are electrical conductivity and turbidity, while important parameters for summer season are water temperature, turbidity, total phosphorous, nitrate, and total suspended solids. However, the main parameters attributed to autumn are pH, total dissolved solids, and dissolved oxygen; and that attributed to winter are water temperature and dissolved oxygen.

In the second scenario, the rotated factor correlation coefficient value is selected to be 0.90. In this scenario, the numbers of important variables in spring, summer, autumn, and winter seasons achieved as five, seven, six, and six parameters, respectively. It concluded that the summer has the more important parameters. Generally, the important parameters in the spring season are electrical conductivity, turbidity, dissolved oxygen, total phosphorous, and nitrate while important parameters for summer season are water temperature, turbidity, total phosphorous, nitrate, total suspended solids, dissolved oxygen, and chemical oxygen demand. However, the main parameters attributed to autumn are pH, turbidity, total dissolved solids, total suspended solids, dissolved oxygen, and total phosphorous; and those attributed to winter are water temperature, total dissolved solids, total suspended solids, dissolved oxygen, total phosphorous, and nitrate.

4 Conclusions

In this research, water quality of the Gorganrud River basin from 1996 to 2002 is evaluated. To achieve this goal, canonical correlation analysis, principal component analysis, and principal factor analyses are used. The following conclusions are drawn in the study through:

  1. a.

    Generally, multivariate statistical techniques such as CCA, PCA, and PFA were effective tool for environmental quality assessment of the Gorganrud River.

  2. b.

    CCA results indicated strong relationship between physical and chemical parameters in the Gorganrud River.

  3. c.

    Results from the PFA technique showed that all water quality monitoring stations are considered important in explaining the annual variance of the data set, and thereby the location of them in the river system could be suitable.

  4. d.

    In the first scenario (rotated factor correlation coefficient value equal to 0.95) the important parameters in the spring season were EC and Turb, while important parameters for summer season were T, Turb, TP, \( {\text{NO}}_{{3}}^{ - } \), and TSS. However, the main parameters attributed to autumn were pH, TDS, and DO; and that attributed to winter were T and DO.

  5. e.

    In the second scenario (rotated factor correlation coefficient value equal to 0.90) the important parameters in the spring season were EC, Turb, DO, TP, and \( {\text{NO}}_{{3}}^{ - } \) while important parameters for summer season were T, Turb, TP, \( {\text{NO}}_{{3}}^{ - } \), TSS, DO, and COD. However, the main parameters attributed to autumn are pH, Turb, TDS, TSS, DO, and TP; and that attributed to winter were T, TDS, TSS, DO, TP, and \( {\text{NO}}_{{3}}^{ - } \).

  6. f.

    Generally, important parameters in contributing to water quality variations in the first and second scenario for one season may not be important for another season.

  7. g.

    The presented methodology in this study can be a good tool for authorities in order to program the monitoring stations and water quality parameters.