Effect of inclined magnetic field on natural convection and entropy generation of non-Newtonian ferrofluid in a square cavity having a heated wavy cylinder

Abstract

Magnetohydrodynamic (MHD) natural convection of non-Newtonian ferrofluid and entropy generation in a square enclosure containing a wavy cylinder was investigated. The inner wavy cylinder was assumed to be heated and the outer square enclosure to be cold. The ferrofluid's rheology was presented by the power-law model, while density fluctuations owing to thermal expansion were described using the Boussinesq approximation. Numerical calculations had been performed using dimensionless parameters such as Hartmann number, power-law index, Rayleigh number, wave number, and volume fraction. Results are discussed in terms of isotherms, velocity field, average Nusselt number, and entropy generation, taking into account the variations in physically significant parameters. Results indicate that thermal convection dominates the isotherms of shear-thinning fluids, while conduction is more prominent in shear-thickening fluids. The power-law index (n) greatly influences the streamlines and isotherms. The non-Newtonian ferrofluid's average Nusselt number ($\overline{\mathrm{Nu}}$) rises as the Hartmann number is reduced and the Rayleigh number (Ra) is increased. In this simulation, the maximum value of $\overline{\mathrm{Nu}}$ is found to be 8.38 because of the addition of ferroparticles. Additionally, the irreversibility caused by fluid friction, heat transfer, and magnetic field for the shear-thinning (n < 1), Newtonian (n = 1), and shear-thickening (n > 1) cases can be minimized by using the ideal parametric combination.

1 Introduction

Ferrofluids are nanofluids that contain a suspension of nanometer-sized solid ferromagnetic particles in a common heat transfer fluid. They are composed of 5% magnetic particles, 10% surfactants, and 85% carrier fluid [1] and usually contain iron oxides or iron salts such as magnetite (Fe₃O₄) and hematite (Fe₂O₃) [2]. Ferromagnetic particles have a diameter of 10 nm or less. They are classified as superparamagnetic because they can only be magnetized in the presence of magnetic dipoles. The temperature-dependent magnetic coupling of ferromagnetic nanofluids is one of its most prominent advantages [3]. Thermal efficiency of these fluids is controlled by manipulating the amplitude and direction of the magnetic field [4, 5]. Due to their exceptional thermo-physical properties, ferrofluids have numerous applications in engineering such as heat dissipation, dynamic sealing, doping, inertial and viscous damping, and heat transfer. In addition, there are many engineering and industrial applications for example condensers, building heating and cooling systems, refrigeration heat exchangers, and the gas and oil industry. Ferrofluids can be used to target drugs with magnets and for hypothermia and MRI contrast enhancement as well as magnetic cell separation in biomedicine [6].

A decade of research into ferrofluids' heat transfer [7] across irregular geometries has led to considerable gains in mass and heat transfer efficiency due to the uneven surface [8]. Heat transfer by natural convection and fluid flow between a square-shaped enclosure and a cylinder with wavy walls has always been a potential area of research. In addition, a wavy-walled cylinder placed in a square-shaped cavity has many applications in the field of biotechnology [9] such as plant cell wall engineering, microbial fuel cell architecture to improve fuel production biomaterials [10]; including various applications in geophysical systems and engineering, for example, power generation, heat conduction, insulation, natural circulation atmospheric, machinery cooling, solar panels, underground cabling, electrical equipment, etc. As a result of this, a number of researchers [11,12,13] investigated the natural convection of nanofluids in a square-shaped cavity containing a wavy cylinder. Dogonchi et al. [14] employed CVFEM to study the natural convection of nanofluids inside of a square-shaped cavity that contained a corrugated circular heater. Because of the waviness of the inner wall of the annulus, it was found that adding nanoparticles increased the rate of heat transmission. Abdulkadhim et al. [15] explored the heat transfer during fluid flows between sinusoidal cylinders inside a vertically walled enclosure filling with multilayers of nanofluid and a porous medium soaked with a similar nanofluid numerically. When the Darcy and Rayleigh numbers grow, the heat transfer rate of convection becomes dominating and the intensity of the fluid flow and the thickness of the shear layer increase.

Currently, magnetohydrodynamic natural convective heat transfer has become widespread. It has a wide variety of applications, including continuous casting and processes growing crystal, MHD pumps and flow meters, nuclear reactors, and electronic components. In order to improve the flow field's level of stability, it is customarily necessary to employ an external magnetic field. Few researchers [16,17,18] have shown that external magnetic fields can affect heat transmission in cavities. According to all of them, as the intensity of the magnetic field (Ha) increased, the coefficient of heat transfer due to convection decreased. Son and Park [19] studied the MHD natural convective heat transfer filling with ferrofluid having an insulating block inside a rectangular cavity and found that inserting a block improves heat transfer to a large extent some degree within the block size and Ha. Javed [20] numerically examined the effect of magnetic field on heat transport through ferrofluid within a square-shaped cavity having a heat source. When the intensity of the magnetic field is increased, resulting in the conduction regime taking control within the container for all values of Ha, provided that Ra is reduced.

Although most studies have focused on free convective heat transfer for a Newtonian fluid inside cavities, the impact of the non-Newtonian behavior of nanofluids on thermal distribution by free convection has not yet been examined. There are numerous applications for heat transmission via non-Newtonian fluid natural convection, including the design of chemical reactors, polymer engineering in paper manufacturing, and oil drilling. As a result, it is very important to know the basic physics behind how heat moves through non-Newtonian fluids. Many experts have tested free convection from an envelope with non-Newtonian fluids [21,22,23,24]. They studied the consequence of non-Newtonian effect on heat transfer by free convection. According to them, it is also possible to compare heat transfer via natural convection between non-Newtonian and Newtonian fluids. Kefayati [25] investigated the magnetic effect introduced externally to a non-Newtonian nanofluid with a non-Newtonian index of 0.6–1 using Pr = 100 which is based on the non-Newtonian behavior of the fluid, and experimented with varying non-Newtonian index, Rayleigh and Hartmann numbers to see how these affected heat transfer characteristics. Turan et al. [26] also examined laminar natural convective heat transfer of power-law fluids inside a square-shaped enclosure with variably heated sides exposed to a constant temperature. According to the findings of the simulations, an increase in Pr leads to a decrease in $\overline{\mathrm{Nu}}$ for a certain set of Ra (Rayleigh number), and n in the range 0.6–1.8.

A system's energy losses can be better understood by doing accurate entropy generation calculations, which can be used in many different industries to improve heat transfer design. Therefore, entropy generation is widely studied in the free convection of pure fluids [27, 28] and nanofluids [29,30,31,32]. Recently, entropy generation has also been explored on magnetohydrodynamic nanofluids. Mahmoudi et al. [33] found that copper Cu-water nanofluids can improve the rate of heat transfer and entropy generation in free convection inside a 2D trapezoidal enclosure when a constant magnetic field is applied. The results demonstrate that at Ra = 10⁴ and 10⁵, $\overline{\mathrm{Nu}}$ increases with Hartman number in the presence of nanoparticles, but a decrease is observed with a higher Rayleigh number. Furthermore, it was found that with the presence of nanoparticles entropy generation is reduced, but magnetic fields generally enhances the magnitude of entropy generation. Because nanoparticles have the potential to increase system stability, resulting in decreased disorder and reduced entropy generation. They also enable improved heat transfer, reducing irreversibilities and lowering entropy generation. In contrast, magnetic fields promote the movement of charged particles, which leads to increased energy dissipation and consequently higher entropy generation. Magnetic fields can additionally induce turbulence and mixing in fluid flows, further contributing to increased entropy generation. Mejri et al. [34] conducted research on laminar free convection in a square-shaped enclosure filling with water-Al₂O₃ nanofluids and analyzed the entropy generation with a magnetic field. According to the findings, the rate of heat transfer and entropy formation changes in proportion to the increase of volume fraction for Ra = 5 $\times$ 10⁴ and Ha = 20. It was claimed that the right selection of Ra and Ha might be capable of maximizing heat transfer rate while reducing entropy generation.

The above literature survey exhibits that the heat transfer behaviors of MHD natural convection of non-Newtonian ferrofluids in the square enclosure with a wavy wall cylinder have not been previously discussed. Even, irregular surfaces increase the heat transmission rate, they also complicate the interactions between enclosure walls and fluids within the domain. Wavy walls add an additional layer of complexity to these challenges, and the flow of ferrofluid between the square enclosure and the cylinder with wavy walls has not been subjected to a significant amount of research. As a result, the current work focuses on the non-Newtonian behavior of magnetohydrodynamic natural convection of ferrofluid between the square enclosure and the wavy wall cylinder, with Fe₃O₄ as the ferroparticle and H₂O as the base fluid. The intent of our study is to give a comprehensive analysis of flow fields, heat transfer, and entropy creation in order to measure the thermal performance of systems that are affected by magnetic force. The results obtained through current numerical studies can be used to obtain the optimum flow and geometric parameters in order to accomplish the development of effective heat transfer in the above system.

2 Mathematical formulation

2.1 The physical configuration

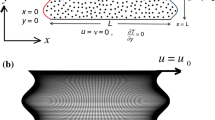
A 2D laminar unsteady natural convection of a non-Newtonian fluid is hypothesized to take place within a square cavity that contains a wavy heated cylinder while being subjected to an inclined magnetic field. The non-Newtonian ferrofluid (Fe₃O₄–H₂O) flows across the space between the square enclosure and the wavy cylinder.

Figure 1 illustrates the geometry of the current problem. The length and the height of the outer square enclosure are denoted by L. The functions of the wavy cylinder surface are:

$$ r_{1} \left( \eta \right) = \left( {r + A\cos \left( {2\pi N\eta } \right)} \right) \times \sin \left( {2\pi \eta } \right), $$

(1)

$$ r_{2} \left( \eta \right) = \left( {r + A\cos \left( {2\pi N\eta } \right)} \right) \times \cos \left( {2\pi \eta } \right). $$

(2)

Here, r denotes the radius of the smooth (base) circle, η denotes the angular coordinate, A and N are the amplitude of the wavy cylinder’s wave and number of waves. In this analysis, N and A are chosen as 5 and 0.07. It is presumed that the inner wavy cylinder is at a temperature of T_h, whereas the outer enclosure’s temperature is thought to be T_c.

Fig. 1

The physical model’s schematic diagram

2.2 Thermo-physical characteristics of non-Newtonian power-law ferrofluid

Here ferroparticles (Fe₃O₄) have been included in the water-based transport fluid. In Table 1, the thermo-physical characteristics of ferroparticles and water are listed.

Table 1 Thermo-physical properties of water and ferroparticles [40, 46,47,48,49]

Using the thermo-physical characteristics of the ferroparticles and water of Table 1, effective thermo-physical characteristics of ferrofluid are computed as defined below.

According to the mixing rule presented by Xuan et al. [35] and Ghanbarpour et al. [36], the effective density of ferrofluid is given by

$$ \rho_{{{\text{ff}}}} = \left( {1 - \phi } \right)\rho_{{\text{f}}} + \phi \,\rho_{{\text{s}}} . $$

(3)

Here, $\rho_{{\text{f}}}$ and $\rho_{{\text{s}}}$ denote the densities of the base fluid and the solid particle, respectively, and ϕ denotes the volume fraction of the ferroparticles.

The heat capacity $\left( {\rho C_{{\text{p}}} } \right)_{{{\text{ff}}}}$ and the thermal expansion coefficient $\left( {\rho \beta } \right)_{{{\text{ff}}}}$ of the ferrofluid are approximated from the mass average technique [36] as

$$ \left( {\rho C_{{\text{p}}} } \right)_{{{\text{ff}}}} = \left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} \left( {1 - \phi } \right) + \left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} \phi , $$

(4)

$$\left( {\rho \beta } \right)_{{{\text{ff}}}} = \left( {\rho \beta } \right)_{{\text{f}}} \left( {1 - \phi } \right) + \left( {\rho \beta } \right)_{{\text{s}}} \phi .$$

(5)

According to the Maxwell–Garnetts (MG) model, the electrical conductivity (σ_ff) and the effective thermal conductivity (k_ff) of the ferrofluid are

$$ \sigma_{{{\text{ff}}}} = \sigma_{{\text{f}}} \left[ {1 + \frac{{3\left( {\frac{{\sigma_{{\text{s}}} }}{{\sigma_{{\text{f}}} }} - 1} \right)\phi }}{{\left( {\frac{{\sigma_{{\text{s}}} }}{{\sigma_{{\text{f}}} }} + 2} \right) - \left( {\frac{{\sigma_{{\text{s}}} }}{{\sigma_{{\text{f}}} }} - 1} \right)\phi }}} \right], $$

(6)

$$ k_{{{\text{ff}}}} = k_{{\text{f}}} \frac{{k_{{\text{s}}} + 2k_{{\text{f}}} - 2\phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}}{{k_{{\text{s}}} + 2k_{{\text{f}}} + \phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}}. $$

(7)

The effective dynamic viscosity $\tilde{\mu }_{{\text{ff}}}$ of the ferrofluid can be computed using Brinkman model [37] along with the expansion for non-Newtonian power-law fluids, which reads as follows:

$$ \tilde{\mu }_{{{\text{ff}}}} = \frac{{\mu_{{\text{f}}} }}{{(1 - \phi )^{2.5} }}\left| {\tilde{\dot{\gamma }}} \right|^{\,n - 1} . $$

(8)

Here, n denotes the power-law index or flow behavior index and $\left| {\tilde{\dot{\gamma }}} \right|$ denotes the magnitude of the shear rate which can be expressed as follows:

$$ \left| {\tilde{\dot{\gamma }}} \right| = \left[ {2\left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}}} \right)^{2} + 2\left( {\frac{{\partial \tilde{v}}}{{\partial \tilde{y}}}} \right)^{2} + \left( {\frac{{\partial \tilde{v}}}{{\partial \tilde{x}}} + \frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right)^{2} } \right]^{\frac{1}{2}} . $$

(9)

The thermal diffusivity $\alpha_{{{\text{ff}}}}$ is calculated as

$$ \alpha_{{{\text{ff}}}} = \frac{{k_{{{\text{ff}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{ff}}}} }}. $$

(10)

2.3 Dimensional governing equations

According to the above-mentioned assertion as well as the Boussinesq approximation, the governing equations (11)–(14) are,

$$ \frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} + \frac{{\partial \tilde{v}}}{{\partial \tilde{y}}} = 0, $$

(11)

$$ \begin{aligned} \rho_{{{\text{ff}}}} \left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{t}}} + \tilde{u}\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right) = & - \frac{{\partial \tilde{p}}}{{\partial \tilde{x}}} + \frac{\partial }{{\partial \tilde{x}}}\left( {2\tilde{\mu }_{{{\text{ff}}}} \frac{{\partial \tilde{u}}}{{\partial \tilde{x}}}} \right) + \frac{\partial }{{\partial \overline{y}}}\left( {\tilde{\mu }_{{{\text{ff}}}} \frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right) + \frac{\partial }{{\partial \tilde{y}}}\left( {\tilde{\mu }_{{{\text{ff}}}} \frac{{\partial \tilde{v}}}{{\partial \tilde{x}}}} \right) \\ \; & + B^{2} \sigma_{{{\text{ff}}}} \left( { - \tilde{u}\sin^{2} \gamma + \tilde{v}\cos \gamma \sin \gamma } \right), \\ \end{aligned} $$

(12)

$$ \begin{aligned} \rho_{{{\text{ff}}}} \left( {\frac{{\partial \tilde{v}}}{{\partial \tilde{t}}} + \tilde{u}\frac{{\partial \tilde{v}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{v}}}{{\partial \tilde{y}}}} \right) = & - \frac{{\partial \tilde{p}}}{{\partial \tilde{y}}} + \frac{\partial }{{\partial \tilde{x}}}\left( {\tilde{\mu }_{{{\text{ff}}}} \frac{{\partial \tilde{v}}}{{\partial \tilde{x}}}} \right) + \frac{\partial }{{\partial \tilde{y}}}\left( {2\tilde{\mu }_{{{\text{ff}}}} \frac{{\partial \tilde{v}}}{{\partial \tilde{y}}}} \right) + \frac{\partial }{{\partial \tilde{x}}}\left( {\tilde{\mu }_{{{\text{ff}}}} \frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right) \\ \; &+ g\left( {\rho \beta } \right)_{{{\text{ff}}}} \left( {\tilde{T} - T_{{\text{c}}} } \right) + B^{2} \sigma_{{{\text{ff}}}} \left( { - \tilde{v}\cos^{2} \gamma + \tilde{u}\sin \gamma \cos \gamma } \right), \\ \end{aligned} $$

(13)

$$ \frac{{\partial \tilde{T}}}{{\partial \tilde{t}}} + \tilde{u}\frac{{\partial \tilde{T}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{T}}}{{\partial \tilde{y}}} = \alpha_{{{\text{ff}}}} \left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{x}^{2} }} + \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }}} \right). $$

(14)

Here, t̃ specifies the time, ũ and ṽ denote the velocities along the x̃-axis and ỹ-axis. Also, T̃, T_c, g and p̃ are the ferrofluid temperature, surrounding temperature, gravitational acceleration and pressure, respectively. Furthermore, B and γ is the strength and the angle of the magnetic field.

For the above-mentioned model

Initial conditions are:

$$ \tilde{u} = \tilde{v} = 0,\quad \tilde{T} = 0\quad {\text{at }}\tilde{t} = 0, $$

(15)

Boundary conditions are

$$ {\text{Inner}}\;{\text{cylinder:}}\quad\tilde{u} = \tilde{v} = 0,\;\tilde{T} = T_{{\text{h}}} \quad {\text{at }}\tilde{t} > 0, $$

(16)

$$ {\text{Outer}}\quad {\text{cylinder:}} \;\tilde{u} = \tilde{v} = 0,\,\tilde{T} = T_{{\text{c}}} \quad{\text{at }}\tilde{t} > 0. $$

(17)

2.4 Dimensionless governing equations

The following non-dimensional variables are introduced to transform the dimensional equations into dimensionless form:

$$ x = \frac{{\tilde{x}}}{L},\quad y = \frac{{\tilde{y}}}{L}, $$

(18)

$$ u = \frac{{\tilde{u}L}}{{\alpha_{{\text{f}}} }},\quad v = \frac{{\tilde{v}L}}{{\alpha_{{\text{f}}} }}, $$

(19)

$$ t = \tilde{t}\frac{{\sigma_{{\text{f}}} }}{{L^{2} }},\quad p = \tilde{p}\frac{{L^{2} }}{{\rho_{{{\text{ff}}}} \alpha_{{\text{f}}}^{2} }},\quad \theta = \frac{{\tilde{T} - T_{{\text{c}}} }}{{T_{{\text{h}}} - T_{{\text{c}}} }}, $$

(20)

$$ {\text{Ha}} = \sqrt {\frac{{\sigma_{{\text{f}}} \alpha_{{\text{f}}}^{1 - n} }}{{\mu_{{\text{f}}} }}} BL^{n} \quad \alpha_{{\text{f}}} = \frac{{k_{{\text{f}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\quad \nu_{{\text{f}}} = \frac{{\mu_{{\text{f}}} }}{{\rho_{{\text{f}}} }} ,$$

(21)

$$ \Pr = \frac{{\nu_{{\text{f}}} L^{2 - 2n} }}{{\alpha_{{\text{f}}}^{2 - n} }}, \quad {\text{Ra}} = \frac{{g\beta_{{\text{f}}} \Delta TL^{2n + 1} }}{{\nu_{{\text{f}}} \alpha_{{\text{f}}}^{n} }}, \quad \Delta T = T_{{\text{h}}} - T_{{\text{c}}} . $$

(22)

Using the relations (18)–(22), the dimensional governing equations can be transformed into the dimensionless form:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$

(23)

$$ \begin{aligned} \frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{{{\text{d}}u}}{{{\text{d}}y}} = & - \frac{\partial p}{{\partial x}} + \frac{\Pr }{{(1 - \phi )^{2.5} \lambda_{2} }}\left[ {2\frac{\partial }{\partial x}\left( {D\frac{\partial u}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {D\frac{\partial u}{{\partial y}}} \right) + \frac{\partial }{\partial y}\left( {D\frac{\partial v}{{\partial x}}} \right)} \right] \\ \; &+ {\text{Ha}}^{2} \frac{\Pr }{{\lambda_{2} }}\frac{{\sigma_{{{\text{ff}}}} }}{{\sigma_{{\text{f}}} }}\left( { - u\sin^{2} \gamma + v\cos \gamma \sin \gamma } \right), \\ \end{aligned} $$

(24)

$$ \begin{aligned} \frac{\partial v}{{\partial t}} + u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} = & - \frac{\partial p}{{\partial y}} + \frac{\Pr }{{(1 - \phi )^{2.5} \lambda_{2} }}\left[ {2\frac{\partial }{\partial y}\left( {D\frac{\partial v}{{\partial y}}} \right) + \frac{\partial }{\partial x}\left( {D\frac{\partial u}{{\partial y}}} \right) + \frac{\partial }{\partial x}\left( {D\frac{\partial v}{{\partial x}}} \right)} \right] \\ \; &+\frac{{\lambda_{1} }}{{\lambda_{2} }}\Pr {\text{Ra}}\theta + {\text{Ha}}^{2} \frac{\Pr }{{\lambda_{2} }}\frac{{\sigma_{{{\text{ff}}}} }}{{\sigma_{{\text{f}}} }}\left( { - v\cos^{2} \gamma + u\sin \gamma \cos \gamma } \right), \\ \end{aligned} $$

(25)

$$ \frac{\partial \theta }{{\partial t}} + u\frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}} = \frac{{\alpha_{{{\text{ff}}}} }}{{\alpha_{{\text{f}}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right), $$

(26)

where

$$ \begin{aligned} \lambda_{1} &= \left( {1 - \phi } \right) + \phi \frac{{\left( {\rho \beta } \right)_{{\text{s}}} }}{{\left( {\rho \beta } \right)_{{\text{f}}} }} \\ \lambda_{2}& = \left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}, \\ \end{aligned}$$

(27)

$$ D = \left| {\dot{\gamma }} \right|^{\,n\, - 1} = \left[ {2\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + 2\left( {\frac{\partial v}{{\partial y}}} \right)^{2} + \left( {\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)^{2} } \right]^{{\frac{n\, - 1}{2}}} . $$

(28)

The dimensionless initial and boundary conditions are:

$$ \begin{gathered} {\text{At}}\;t = \quad 0 \hfill \\ u = v = 0,\quad T = 0 \hfill \\ {\text{At}}\;t > \, 0, \hfill \\ \end{gathered} $$

(29)

$$ {\text{Inner}}\;{\text{cylinder:}} \ u = v = 0,\quad T = {1,} $$

(30)

$$ {\text{Outer}}\;{\text{enclosure:}} \ u = v = 0,\quad T = 0, $$

(31)

2.5 The rate of heat transfer

The heat transfer rate at the heated inner wavy wall in dimensionless form is calculated as $\overline{\mathrm{Nu}}$ (average Nusselt number) by using the following formula:

$$ \overline{{{\text{Nu}}}} = \frac{1}{s}\int\limits_{0}^{{\text{s}}} {{\text{Nu}}\left( \eta \right){\text{d}}\eta \quad {\text{where Nu}}\left( \eta \right) = - \frac{{k_{{{\text{ff}}}} }}{{k_{{\text{f}}} }}\frac{\partial \theta }{{\partial \eta }}} . $$

(32)

Here, η is the angular coordinate and s denotes the surface area of the inner cylinder.

2.6 Entropy generation

On the basis of the second law of thermodynamics, the estimation of entropy generation can be useful for designing a better energy system. In a convection process of fluid flow and heat transfer, the irreversibility is induced for fluid friction, heat transfer, and magnetic field. The total entropy profile of a laminar incompressible fluid flow can be calculated as the summation of the irreversibilities caused by thermal gradients, magnetic fields, and viscous dissipation using the following formula [38, 39]:

$$ \tilde{S}_{{\text{S}}} = \tilde{S}_{{\text{F}}} + \tilde{S}_{{\text{T}}} + \tilde{S}_{{\text{M}}} , $$

(33)

where S̅_F, S̅_T, and S̅_M, are the entropy generations by fluid friction, heat transfer, and magnetic field, respectively, and can be written as follows [40, 41]:

$$ \tilde{S}_{{\text{F}}} = \frac{{\mu_{{{\text{ff}}}} }}{{T_{0} }}\left[ {2\left( {\frac{{{\text{d}}\tilde{u}}}{{{\text{d}}\tilde{x}}}} \right)^{2} + 2\left( {\frac{{{\text{d}}\tilde{v}}}{{{\text{d}}\tilde{y}}}} \right)^{2} + \left( {\frac{{{\text{d}}\tilde{v}}}{{{\text{d}}\tilde{x}}} + \frac{{{\text{d}}\tilde{u}}}{{{\text{d}}\tilde{y}}}} \right)^{2} } \right], $$

(34)

$$ \tilde{S}_{{\text{T}}} = \frac{{k_{{{\text{ff}}}} }}{{T_{0}^{2} }}\left[ {\left( {\frac{{{\text{d}}\tilde{T}}}{{{\text{d}}\tilde{x}}}} \right)^{2} + \left( {\frac{{{\text{d}}\tilde{T}}}{{{\text{d}}\tilde{y}}}} \right)^{2} } \right], $$

(35)

$$ \tilde{S}_{{\text{M}}} = \frac{{\sigma_{{{\text{ff}}}} B^{2} }}{{T_{0} }}\left( {\tilde{u}\sin \gamma - \tilde{v}\cos \gamma } \right)^{2} . $$

(36)

After non-dimensionalizing these equations, the resulting equations are written as:

• Local entropy

  $$ S_{{\text{S}}} = S_{{\text{F}}} + S_{{\text{T}}} + S_{{\text{M}}} , $$

  (37)

• Entropy generation caused by fluid friction

  $$ \begin{aligned} S_{{\text{F}}} = & \tilde{S}_{{\text{F}}} \times \frac{{T_{0}^{2} L^{2} }}{{k_{{\text{f}}} \Delta T^{2} }} \\ S_{{\text{F}}} = & \varphi_{1} \left[ {2\left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)^{2} + 2\left( {\frac{{{\text{d}}v}}{{{\text{d}}y}}} \right)^{2} + \left( {\frac{{{\text{d}}v}}{{{\text{d}}x}} + \frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right]. \\ \end{aligned} $$

  (38)

• Entropy generation caused by heat transfer

  $$ \begin{aligned} S_{{\text{T}}} = & \tilde{S}_{{\text{T}}} \times \frac{{T_{0}^{2} L^{2} }}{{k_{f} \Delta T^{2} }} \\ S_{{\text{T}}} = & \frac{{k_{{{\text{ff}}}} }}{{k_{{\text{f}}} }}\left[ {\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}x}}} \right)^{2} + \left( {\frac{{{\text{d}}\theta }}{{{\text{d}}y}}} \right)^{2} } \right]. \\ \end{aligned} $$

  (39)

• Entropy generation caused by the magnetic field

  $$ \begin{aligned} S_{{\text{M}}} = & \tilde{S}_{{\text{M}}} \times \frac{{T_{0}^{2} L^{2} }}{{k_{{\text{f}}} \Delta T^{2} }},\\ S_{{\text{M}}} = & \frac{{\sigma_{{{\text{ff}}}} }}{{\sigma_{{\text{f}}} }}\lambda_{1} {\text{Ha}}^{2} \left( {u\sin \gamma - v\cos \gamma } \right)^{2} , \\ \end{aligned} $$

  (40)

  where

  $$ \lambda_{1} = \frac{{\mu_{{\text{f}}} \alpha_{{\text{f}}}^{n + 1} }}{{L^{2n} k_{{\text{f}}} \Delta T^{2} }},\quad \lambda_{2} = \frac{{T_{0} \alpha_{{\text{f}}}^{n + 1} \mu_{{\text{f}}} }}{{k_{{\text{f}}} L^{2n} \Delta T^{2} }},\quad \varphi_{1} = \frac{D}{{(1 - \phi )^{2.5} }}\lambda_{2} . $$

  (41)

Here, the parameters λ₁ and λ₂ are referred to as the distribution ratio of irreversibility, T₀ and D denote the bulk temperature and fluid viscosity. There is no fixed value for λ₁ and λ₂. Here, the constants λ₁ and λ₂ take the value 10^–4 like [27].

The local dimensionless Bejan number (Be) is calculated dividing the number of entropy generations for heat transfer by the total number of entropy generations. This calculation yields the following formula [42]:

$$ {\text{Be}} = \frac{{S_{{\text{T}}} }}{{S_{{\text{S}}} }}. $$

(42)

The overall non-dimensional entropy generation is given by numerically integrating the local dimensionless entropy generation over the entire domain [43]:

$$ \left( {S_{{\text{F}}} } \right)_{t} = \iint\limits_{A} {S_{{\text{F}}}\quad {\text{d}}A,}\left( {S_{{\text{T}}} } \right)_{t} = \iint\limits_{A} {S_{{\text{T}}}\quad {\text{d}}A,}\left( {S_{{\text{M}}} } \right)_{t} = \iint\limits_{A} {S_{{\text{M}}}\quad {\text{d}}A}, $$

(43)

$$ \left( {S_{{\text{S}}} } \right)_{{\text{t}}} = \iint\limits_{A} {S_{{\text{S}}}\quad {\text{d}}A,}{\text{Be}}_{{{\text{avg}}}} = \frac{{\iint\limits_{{\text{A}}} {{\text{Be}}\quad{\text{d}}A}}}{{\iint\limits_{A} {{\text{d}}A}}}. $$

(44)

3 Numerical solution

3.1 Solution procedure

This study uses the COMSOL Multiphysics software including the finite element approach to numerically solve the dimensionless governinge equations (23)–(26) subject to the boundary conditions (29)–(31). FEM-based software, COMSOL Multiphysics, is used for a wide range of physics and engineering simulations. For the continuity and the momentum equations (23)–(25) and the energy equation (26), COMSOL Multiphysics takes into account the laminar flow (spf) application mode as well as the heat transfer (ht) in fluid application mode. A triangular mesh is applied to the domain between the square enclosure and the inner wavy cylinder to generate meshes. In this case, the numerical calculations are performed using an extremely finer mesh, which is capable of adapting to fluid dynamic circumstances.

3.2 Grid independence test

For grid independency, several tests have been carried out to make sure that the results are free from the grid calibration. In this study, $\overline{\mathrm{Nu}}$ (average Nusselt number) around the heated wavy cylinder has been determined using COMSOL’s default mesh sizes for shear-thinning (n < 1), Newtonian (n = 1) and shear-thickening (n > 1) cases at ϕ = 0.06, Ha = 10, γ = π/4, Ra = 10⁵, t = 1, and Pr = 6.8377. The estimated results are tabulated in Table 2. Based on Table 2, an extremely fine mesh that contains 66,096 mesh elements is chosen for the entire simulation.

Table 2 Results of the grid independency test for ϕ = 0.06, Ha = 10, N = 5, γ = π/4, Ra = 10⁵, t = 1, and Pr = 6.8377

3.3 Validation of the numerical solution

To check the validity, the natural convection in a lower-temperature outer square cavity with the higher temperature circular cylinder at the cavity’s core was tested. The estimated surfaced averaged Nusselt numbers ($\overline{\mathrm{Nu}}$) are cross-checked with the benchmark values provided by Kim et al. [44], and Lee et al. [45] as displayed in Table 3. The current results are a good level of precision with the values estimated by Kim et al. [44] and Lee et al. [45].

Table 3 Comparison of $\overline{\mathrm{Nu}}$ at the hot inner cylinder for n = 1, Pr = 0.7, ϕ = 0.0, and Ha = 0 with those of the previous numerical results

Figure 2 is another comparison for natural convective flow of the non-Newtonian power-law fluids in one sided heated square-shaped enclosure for various Ra (10⁴ and 10⁵), power-law index (n = 0.6–1.8) while Pr = 100. From Fig. 2, it is found that the current findings are in perfect agreement with the equivalent results studied by Turan et al. [26] using ANSYS-Fluent software.

Fig. 2

Comparison of the current results with the findings obtained by Turan et al. [26] as $\overline{\mathrm{Nu}}$ (average Nusselt number) for various n, while Ra = 10⁴, 10⁵, Pr = 100, Ha = 0, and ϕ = 0.0

4 Results and discussion

This section presents computational results for isotherms, streamlines, local and average Nusselt numbers and entropy generation for various parameters, taking thermal Rayleigh numbers Ra = 10³,10⁴, and 10⁵, power-law index n = 0.6–1.4, Hartman number Ha = 0, 10, 20, volume fraction ϕ = 0, 0.03, 0.06, 0.09, Prandtl number Pr = 6.8377 and γ = π/4. These parameter choices allow us to comprehensively understand the phenomenon under study and provide a solid foundation for further analysis and interpretation. Detailed physical and theoretical descriptions of the gathered data and their graphical depiction, are provided in the following sections.

4.1 Influence of different inner cylinder shapes on streamlines and isotherms

The distribution of the flow field and isotherms for various values of the wave number (N) of the inner wavy cylinder are illustrated correspondingly in Figs. 3(a)–(h) and 4(a)–(h). Numerical studies are performed for Ha = 20, Ra = 10⁴ and 10⁵, γ = π/4, n = 0.6, ϕ = 0.06, t = 1, and Pr = 6.8377 to expose the mechanism for various values of N. In the case of Ra = 10⁴ and 10⁵, the maximum velocity magnitudes for N = 2, 3, 4, and 5 are (21.02, 220.23), (22.09, 215.52), (22.78, 255.15), and (21.99, 215.36) correspondingly. For n = 4, the maximum velocity magnitude is observed. This clearly demonstrates that increasing the size between the outer cavity and the inner wavy cylinder considerably impacts the velocities' strength. It can be seen in Fig. 4(a)–(h) that for increasing Ra, isotherms get denser around the inner cylinder along with the number of waves. So, the construction of the inner cylinder has a notable effect on the thermal transfer inside the enclosure.

Fig. 3

Streamlines for various shapes of inner cylinder: a N = 2, b N = 3, c N = 4, d N = 5 at Ra = 10⁴ and e N = 2, f N = 3, g N = 4, h N = 5 at Ra = 10.⁵, while n = 0.6, ϕ = 0.06, Ha = 20, γ = π/4, Pr = 6.8377

Fig. 4

Isotherms for various shapes of inner cylinder: a N = 2, b N = 3, c N = 4, d N = 5 at Ra = 10⁴ and e N = 2, f N = 3, g N = 4, h N = 5 at Ra = 10⁵, while n = 0.6, ϕ = 0.06, Ha = 20, γ = π/4, Pr = 6.8377

4.2 Influence of n and Ra on streamlines

As seen in Fig. 5(a)–(o), both the power-law index and Rayleigh number impact the velocity field. To illustrate the mechanism for a range of n and Ra, the other physical parameters N = 5, Ha = 10, ϕ = 0.06, t = 1, and Pr = 6.8377 are used. The maximum velocity magnitude corresponding to n = 0.6, 0.8, 1.0, 1.2 and 1.4 along with Ra = 10³, 10⁴, and 10⁵ are (1.60, 0.88, 0.58, 0.43, 0.35), (44.62, 14.07, 5.59, 2.94, 1.80) and (367.11, 153.31, 53.88, 20.19, 9.14). The fluid's effective viscosity rises together with the values of n, but the magnitude of velocity drops. As a result, the vortexes shrink in size and alter their shape. The streamlines also show that since the convective transport diminishes compared to viscous flow resistance, the magnification of n reduces the magnitude of fluid flow. Furthermore, when n increases, the momentum boundary layers get thinner. This means that when the fluid viscosity inside the domain goes up, the maximum value is reached for the shear-thickening case. And the strength of the speed rises with the addition of Ra. The fluid close to the heated body becomes hot since the inner cylinder inside the enclosure heats up. The density of the hot fluid is less than the density of the cold fluid. The thinner fluid then rises to the surface due to buoyant force. This causes the hot fluid to become denser at the top, making it cooler. The fluid then descends into the enclosure's lowest portion. For this reason, two strong opposing vortices are therefore created. The impact of buoyant force increases as Ra increases. So, the value of velocity magnitude is increased.

Fig. 5

Streamlines for different power-law index (n = 0.6, 0.8, 1.0, 1.2, 1.4), and Rayleigh numbers (Ra = 10³, 10⁴, 10.⁵) at Ha = 10, ϕ = 0.06

4.3 Influence of n and Ra on isotherms

Figure 6(a)–(o) shows that isotherms are influenced by n and Ra. When n = 0.6, isotherms become more curved, indicating that the convective heat transfer strength is becoming more significant. Whenever n = 1, isotherms become less curved, and the boundary layers shrink. Furthermore, it is seen that when n = 1.4, isotherms become thinner and more closely fit the inner cylinder. Accordingly, it can be said that thermal convection dominates the isotherms of shear-thinning fluid, and conduction dominates the isotherms of shear-thickening fluid. At Ra = 10³, it is noticeable that the isotherm's pattern appears to parallel near the wavy cylinder. As Ra rises, the scenario changes. Isotherms near the inner heated cylinders and the outer enclosure get denser as Ra rises because the higher Rayleigh number dominates the convective heat transfer procedure.

Fig. 6

Isotherms for various power-law index (n = 0.6, 0.8, 1.0, 1.2, and 1.4), and Rayleigh numbers (Ra = 10³, 10⁴, and 10.⁵) at Ha = 10, ϕ = 0.06

4.4 Influence of Ha and ϕ on streamlines

Figure 7(a)–(l) represents the effect of various values of Ha and ϕ on the distribution of the velocity field. The related parameters are taken as n = 0.8, Ra = 10⁵, t = 1, Pr = 6.8377, and γ = π/4 to describe the flow distribution for different values of Ha. Figure 7(a)–(l) shows that without a magnetic field (Ha = 0), velocity is distributed practically symmetrically, but with the presence of a magnetic field, the pattern of flow becomes asymmetric. The strength of the magnetic field gets more potent as Ha goes up. This causes the vortex to change shape and become longer in the direction of angle γ = π/4. The magnitude of the velocity corresponding to Ha = 0, Ha = 10, and Ha = 20 for ϕ = 0.06, Ra = 10⁵ are 184.74, 152.69, and 114.37, respectively. It can be perceived that the velocity magnitude decreases because of an increase in Ha, which indicates that the convection strength is weakened. When Ha is increased, the boundary layers thickness also increases. And when the concentration of ferroparticles goes from 0.0 to 0.09, the strength of the velocity field decreases as well as the convective force because the effective viscosity of the mixture increases.

Fig. 7

Streamlines for different Hartman numbers (Ha = 0, 10, 20), and volume fraction (ϕ = 0.00, 0.03, 0.06, 0.09) at Ra = 10⁵ and n = 0.8

4.5 Influence of Ha and ϕ on isotherms

The patterns of the isotherms contours have been demonstrated in Fig. 8(a)–(l) for different Hartman numbers Ha = 0, 10, 20, and volume fraction ϕ = 0.0, 0.03, 0.06, 0.09. Isotherms for Ha = 0 appear to be more curved than isotherms for Ha = 10 and 20, indicating that convective heat transfer is more robust without a magnetic field, as depicted in Fig. 8. The flow gets more controlled as Hartmann number rises. The physical reason is that a more extensive Ra controls the convective heat transfer mechanism. Higher values of Ha generate a stronger magnetic field known as the Lorentz force field, which acts against fluid flow, convection, and heat transfer. As a result, a magnetic field should be attached to the system to improve cooling. When the concentration of the ferroparticles increases from 0.0 to 0.09, the buoyancy layer’s thickness reduces, and the isotherms become less curved and fitted with the inner cylinder.

Fig. 8

Isotherms for different Hartman numbers (Ha = 0, 10, 20), and volume fraction (ϕ = 0.00, 0.03, 0.06, 0.09) at Ra = 10⁵ and n = 0.8

4.6 Influence of Ha and Ra on average Nusselt number

Figure 9 illustrates the influence of Ra = 10³, 10⁴, 5 × 10⁴, 10⁵, along with various Ha (0, 10, 20), and ϕ (0, 0.06) on $\overline{\mathrm{Nu}}$ while n = 0.8. Clearly, the values of $\overline{\mathrm{Nu}}$ grow massively when Ra increases from 10³ to 10⁵. On the other hand, the increased Ha leads to a decrease in $\overline{\mathrm{Nu}}$. With the rise in Ha from 0 to 20, $\overline{\mathrm{Nu}}$ decreases (i) 0.02% for pure fluid and 0.01% for ferrofluid, while Ra = 10³, (ii) 7.43% for pure fluid and 3.89% for ferrofluid, when Ra = 10⁴, and (iii) 23.69% for pure fluid and 25.63% for ferrofluid, while Ra = 10⁵. It is worth mentioning that $\overline{\mathrm{Nu}}$ = 8.38 and $\overline{\mathrm{Nu}}$ = 8.76 at Ha = 0 are the highest values found in the entire simulations for pure fluid and ferrofluid, respectively.

Fig. 9

$\overline{\mathrm{Nu}}$ against Rayleigh number (Ra) across various Ha taking ϕ = 0 (solid lines) and ϕ = 0.06 (dashed lines) while n = 0.8

4.7 Influence of Ha and ϕ on average Nusselt number

The influence of different ϕ on $\overline{\mathrm{Nu}}$ in the inner cylinder across Ha = 0, 10, 20 are illustrated in Fig. 10a for Ra = 10⁴ and in Fig. 10b for Ra = 10⁵ while n = 0.8. $\overline{\mathrm{Nu}}$ increases nonlinearly against ϕ. The increment in $\overline{\mathrm{Nu}}$ is caused by the increment in the fluid’s thermal conductivity and the gradual rise of buoyancy force. Meanwhile, the magnetic field's presence causes a decrease in the domain's convection intensity. The strength of the magnetic field has a notable influence on the thermal area. Greater Ha values result in a more powerful Lorentz force field, which works against convection, heat transfer and fluid movement.

Fig. 10

$\overline{\mathrm{Nu}}$ against various ϕ for different Ha = 0, 10, 20 at a Ra = 10⁴, b Ra = 10⁵ while n = 0.8

4.8 Influence of n, Ha, and ϕ on average Nusselt number

In Fig. 11(a)–(b), $\overline{\mathrm{Nu}}$ is plotted against various values of n (0.6–1.4) along with the variation of Ha (0, 10, 20) and ϕ = 0 and 0.06. For both Fig. 11(a) and (b), it is illustrated that, with an increase in n, the value of $\overline{\mathrm{Nu}}$ decreases exponentially. The fluid's viscosity increases from the shear-thinning phase to the shear-thickening phase. As a result, the rate of heat transfer decreases; in addition, the values of $\overline{\mathrm{Nu}}$ decrease with an increase in Ha.

Fig. 11

$\overline{\mathrm{Nu}}$ against various values of n for different Ha = 0, 10, 20 at a Ra = 10⁴, b Ra = 10.⁵ while ϕ = 0 (solid lines) and ϕ = 0.06 (dashed lines)

With the inclusion of ferroparticles, Fig. 11a shows the following statistics: For Ha = 0, $\overline{\mathrm{Nu}}$, increases up to (i) 3.47% at n = 0.6, (ii) 13.43% for n = 1 (Newtonian case), (iii) 14.01% at n = 1.4. Similarly, for Ha = 10, $\overline{\mathrm{Nu}}$, increases up to (i) 21.28% at n = 0.6, (ii) 13.79% for n = 1 (Newtonian case), (iii) 14.01% at n = 1.4. Lastly, for Ha = 20, $\overline{\mathrm{Nu}}$, increases up to (i) 11.61% at n = 0.6, (ii) 13.79% for n = 1 (Newtonian case), (iii) 14.01% at n = 1.4.

In Fig. 11(b), with the inclusion of ferroparticles, the percentages of variation in $\overline{\mathrm{Nu}}$ has also been computed. It is found that for Ha = 0, $\overline{\mathrm{Nu}}$, increases up to (i) 0.03% at n = 0.6, (ii) 0.05% for n = 1 (Newtonian case), (iii) 12.93% at n = 1.4. For Ha = 10, $\overline{\mathrm{Nu}}$, decreases up to (i) 0.65% at n = 0.6, increases up to (ii) 4.68% for n = 1 (Newtonian case), increases up to (iii) 12.96% at n = 1.4. For Ha = 20, $\overline{\mathrm{Nu}}$, increases up to (i) 0.98% at n = 0.6, (ii) 5.26% for n = 1 (Newtonian case), (iii) 13.06% at n = 1.4.

4.9 Influence of different shape of inner cylinder on average Nusselt number

Figure 12 demonstrates the influence of different inner cylinder shapes (wavy, circular, and square) on the average Nusselt number as the Rayleigh number is varied, considering parameters such as n = 0.8 Ha = 20, and ϕ = 0.06. The results show that the average Nusselt number increases exponentially with higher Rayleigh numbers. This suggests that as the convective motion of the fluid becomes more intense, heat transfer to the cylinder walls is enhanced. However, significant variations in heat transfer performance are observed when comparing the inner cylinder shapes. The circular shape exhibits the highest average Nusselt number, suggesting efficient heat transfer. In contrast, transitioning to square or wavy shapes results in a noticeable reduction in the average Nusselt number.

Fig. 12

$\overline{\mathrm{Nu}}$ against Rayleigh number (Ra) for different shapes of inner cylinder taking ϕ = 0 (solid lines) and ϕ = 0.06 (dashed lines) while n = 0.8 and Ha = 20

4.10 Influence of ϕ, Ra, and n on average Nusselt number

Based on different n and Ra, Table 4 shows the influence of variation in ϕ on $\overline{\mathrm{Nu}}$ for Ha = 10. It is shown that, for each volume fraction, $\overline{\mathrm{Nu}}$ is increased by the increment of Ra for each combination of power-law indexes. Further investigation reveals that for the shear-thinning scenario (n = 0.6), $\overline{\mathrm{Nu}}$ increases when Ra = 10³ and 10⁴, and that when Ra = 10⁵, $\overline{\mathrm{Nu}}$ falls. When compared to the shear-thickening situation, $\overline{\mathrm{Nu}}$ rises when Ra = 10⁵. However, for ferrofluid (ϕ = 3%, 6%, and 9%), the value of $\overline{\mathrm{Nu}}$ is directly proportional to all of the values of n. In all cases of Ra, the values of $\overline{\mathrm{Nu}}$ drop for pure and ferrofluid with the increase in n.

Table 4 Average Nusselt numbers ($\overline{\mathrm{Nu}}$) for Ha = 10 while Pr = 6.8377 across different Ra, n, and ϕ

4.11 Influence of Ha, Ra, and n on average Nusselt number

Table 5 represents the influence of $\overline{\mathrm{Nu}}$ for various Ra, Ha, and n for 10% volume fraction. It can be noticed that, for each case of Ra, $\overline{\mathrm{Nu}}$ decreases with the rise of Ha (0, 10, and 20) for shear-thinning case (n = 0.6, 0.8), Newtonian case (n = 1), and shear-thickening case (n = 1.2, 1.4). Moreover, with the increment of Ra, $\overline{\mathrm{Nu}}$ increases massively for all cases of n and Ha.

Table 5 Average Nusselt numbers ($\overline{Nu}$) for ϕ = 0.06 while Pr = 6.8377 across different Ra, Ha, and n

4.12 Influence of Rayleigh number and power-law index on entropy generation profiles

Entropy generation induced by fluid friction, heat transfer, and magnetic field has been represented by a graph in the subsequent sections to illustrate the variation of n with Newtonian case (n = 1.0), shear-thinning case (n = 0.6), and the shear-thickening case (n = 1.4) for various Rayleigh numbers (Ra = 10³, 10⁴, and 10⁵) and volume fraction ϕ = 0.06 while Ha = 10.

4.12.1 Entropy generation for fluid friction (SF)

Figure 13(a)–(i) demonstrates the entropy generation for fluid friction for non-Newtonian ferrofluid with varying Ra and n when the magnetic field is present (Ha = 10). As the applied shear rate is greater close to the wall, the contours of irreversibility caused by fluid friction reveal that the irreversibility is detected close to the wavy walls. Near the active walls, the local entropy regarding fluid friction is maximum. When the viscous effect is increased, the variation in the irreversibility caused by the fluid friction becomes obvious at the middle of the domain. This takes place concurrently with an increase in n. The amount of entropy generated by fluid friction increases as n increases. The fluid becomes more viscous as n grows, increasing the irreversibility of fluid friction (S_F). The contour graphs show that as Ra increases, more contour lines appear inside the domain, as well as the magnitudes of the contours increase because of Ra's magnification. Whenever, the fluid converts from Newtonian case to shear-thickening case, the local entropy that is caused by fluid friction decreases and spreads over the core region. This occurs because the cavity flow becomes weaker with the increment of power-law index n > 1, which means that the fluid is no longer Newtonian. Figure 13's contours demonstrate that the minimum values eventually become dissipated and move toward the core region of the enclosure as n increases in response to the increase in effective viscosity of the overall fluid.

Fig. 13

Contours of entropy generation caused by fluid friction (S_F) for various n = 0.6, 1, 1.4 across different Ra = 10³, 10⁴, 10.⁵ with ϕ = 0.06 while Ha = 10

4.12.2 Entropy generation for heat transfer (ST)

Figure 14(a)–(i) contains a mapping of entropy profiles that were caused by heat transfer. These entropy profiles were mapped using a variety of Ra and n. From the distribution of heat transfer, it can be noticed that for Ra = 10³, the contours are mainly confined to the inner cylinder because the convective rate of heat transfer is maximum in this location because of buoyancy-driven flow. Furthermore, since the convective rate of heat transfer is lower near the outer enclosure, some contours appear with reduced magnitude. Convective heat transfer was reduced as the power-law index increased due to an increase in effective viscosity and a reduction in fluid flow strength. At Ra = 10⁴ and 10⁵, the buoyancy force increases, resulting in a strengthening of the flow. This makes the contours look longer. Therefore, maximum heat transfer entropy is generated with a lower power-law index and higher Rayleigh number.

Fig. 14

Contours of entropy generation caused by heat transfer (S_T) for variious n = 0.6, 1, 1.4 across different Ra = 10³, 10⁴, 10.⁵ with volume fraction ϕ = 0.06 while Ha = 10

4.12.3 Entropy generation for magnetic field (SM)

Figure 15(a)–(i) represents the impact of magnetic field on the contours of entropy generation. The results reveal that the distribution of entropy production for the magnetic field is dominant close to the inner cylinder along with the direction of the magnetic field. For magnetic field, entropy generation decreases drastically with the increment of power-law index. Because the fluid's effective viscosity rises with increasing the power-law index, the strength of the entropy generation drops, and the flow weakens. Maximum magnetic field irreversibility persists at the surface of the inner wavy cylinder, whereas minimal magnetic field irreversibility is observed at the surface of the outer enclosure. Moreover, as Ra increases, the magnetic field's entropy generation also increases.

Fig. 15

Contours of entropy generation caused by magnetic field (S_M) for various n = 0.6, 1, 1.4 across different Ra = 10³, 10⁴, 10.⁵ with ϕ = 0.06 while Ha = 10

4.12.4 Local Bejan number (Be)

The local Bejan number (Be), which is the irreversibility for heat transfer divided by the total irreversibilities, has been shown in Fig. 16(a)–(i). On that account, the irreversibility for heat transfer becomes dominant when Be is larger than 0.5, whereas other irreversibilities become prominent when Be is significantly less than 0.5. With an increase in effective viscosity, this formation of contours becomes symmetrical about the inner cylinder. However, when Ra increases, the flow becomes stronger. The distribution of the Bejan number (Be) varies significantly when the power-law index rises. Additionally, as Ra increases, the Bejan number drops.

Fig. 16

Contours for Bejan number (Be) for various n = 0.6, 1, 1.4 across different Ra = 10³, 10⁴, 10.⁵ with ϕ = 0.06 while Ha = 10

4.12.5 Entropy values across various Ha, Ra, and ϕ

Table 6 displays the total entropy values of shear-thinning ferrofluid for various Ha (0, 10, 20) and Ra (10³, 10⁴, 10⁵) and ϕ (0.0, 0.03, 0.06, 0.09) with fixed value of n = 0.8 while Pr = 6.8377. For Ha = 0, it is depicted that, the values of (S_T)_t increase and the values of (S_F)_t decrease for adding the solid particles for each case of Ra. Also, because there is no presence of magnetic field, the value of the entropy generation for magnetic field, (S_M)_t is equal to zero. Ha = 10 demonstrates a slightly distinct phenomenon. Both the values of (S_F)_t and (S_M)_t reduce with the addition of ϕ for Ra = 10³, 10⁴, 10⁵ while the values of (S_T)_t increase. In addition, the increase of Ha for each case of Ra and ϕ results in a decrease of the (S_T)_t, (S_F)_t values. In contrast, the increment in Ra for each case of Ha and ϕ indicates a significant growth in entropy values.

Table 6 Total entropy at n = 0.8 across different Ha, Ra and ϕ while Pr = 6.8377

4.12.6 Entropy values across various n, Ha, and Ra

Table 7 displays the entropy profiles for different n, Ra, and Ha for ϕ = 0.06. For Ha = 0, it can be observed that the entropy generation caused by fluid friction and heat transfer reduces as the power-law index increases. Similarly, for Ha = 10 and 20, the entropy generation caused by heat transfer, fluid fraction, and magnetic field decrease with the increment of n. In addition, as Ra rises, the Bejan number drops, while the values (S_T)_t, (S_F)_t, (S_M)_t, and (S_S)_t grow substantially. In addition, a rise in Ha values decreases all entropy values for each values of Ra.

Table 7 Entropy profile for various n, across different Ha = 0, 10, 20, and Ra = 10⁴, 10⁵ while Pr = 6.8377 and ϕ = 0.06

5 Conclusion

Non-Newtonian ferrofluid in a square-shaped cavity having a wavy cylinder was numerically investigated for natural convection. The study was conducted using different values for Ra, Ha, ϕ, and n while holding the Prandtl number constant (Pr = 6.8377). Graphic and tabular representations of numerical results were used to convey physical and quantitative information about the answers. Benchmark solutions in the literature might be used to verify experimental results. The followings are some of the most significant outcomes of this investigation:

• Increasing the power-law index (n) and Hartmann number (Ha) reduced the convective heat transfer and average Nusselt number.

• With the increase of Rayleigh number (Ra), the heat transfer rate increased.

• Rayleigh number is directly related to the entropy values, whereas Hartmann number is inversely proportional to the entropy values.

• The addition of ferroparticles decreased heat transfer at n = 0.6 and augmented it at n = 1.4 for all values of Ha studied. Also, it enhanced the average heat transfer rate in both shear-thinning and shear-thickening instances.

• The total entropy decreased because of the Hartmann number and power-law index increment but increased with the Rayleigh number and volume fraction.

• (Be)_avg was reduced by 7% for the shear-thinning case, whereas it was increased up to 14% for the shear-thickening case.