Introduction

Ferrofluids are defined as magnetic nanofluids which can be used as passive control parameter in different energy systems such as solar energy, design of heat exchanger and cooling processes, see [29]. Fundamentals of preparation of the ferrofluids can be found in Berger et al. [11] and Shahsavar et al. [35].

Some of ducts have cavity for different applications in sanitaries, building applications, air conditioning systems and cooling of electronic equipments. Heat transfer of ferrofluids can be found in solar energy applications as Khosravi et al. [19]. In this context, Rahman et al. [28] worked on a numerical solution to find the magnetic field which affects in a duct with a cavity for different heater locations for laminar flow. They found that each heater location exhibits different flow field and temperature in the duct for air. After that, they solved the similar problem for partially heated duct with open cavity as given in Rahman et al. [28]. Selimefendigil et al. [33] performed a computational study on buoyancy-induced flow of ferrofluid in a partially heated square closed space by using finite element method and found that geometrical parameters for heater make an important effects on heat and fluid flow. Selimefendigil and Oztop [32] worked on the heat transfer of a rotating cylinder under the influence of magnetic field in the backward-facing ferrofluid. They found that the increase in Re number increases the local Nusselt number and decreases the magnetic field. The impact of the cylinder rotational on the local Nusselt number is more visible for lower values of Reynolds number. Job and Gunakala [17] examined the mixed convection of magnetite (\(\mathrm{Fe}_3\mathrm{O}_4\)) ferrofluid in a sinusoidally curvilinear duct with two porous blocks. They observed that the isoconcentrations go far from the heat sources by increasing \(h_1\) with small values.

Asadi et al. [9] solved a problem on 2D forced convection of water and \(\mathrm{Fe}_3\mathrm{O}_4\) in non-uniform magnetic field in a sinusoidal walled duct by using finite volume method (FVM). They found that the Nu number increases with wave amplitude, volume fraction of nanoparticles, and Re number. Job and Gunakala [17] performed a solution on mixed convection of ferrofluid through a corrugated channel with a porous partition. They applied various magnetic field to the system by applying the finite element technique. The flow field demonstrated that the recirculation zones expand near the heat sources as Darcy number (Da) increases, but decrease as thickness of porous block is increased. Shahsavar et al. [35] numerically explored the entropy production and heat transfer of hybrid nanofluid flow in a concentric horizontal annulus. Jhumur and Bhattacharjee [16] studied the time-dependent coupled convection in L-shaped cavity filled with ferrofluid under magnetic field. It was observed that the effect of Grashof number (Gr) becomes insignificant for the horizontal heated wall due to dominant heat conduction. Rabbi et al. [27] performed a computational study on mixed convection in a ferrofluid-filled lid-driven cavity in case of different heater geometries. They tried triangular and semicircular heated configuration on the bottom wall and found that the cavity produced a higher value of Nu for the semicircular notched cavity as compared to triangular notched cavity.

Bahiraei et al. [10] solved the problem of heat and fluid flow in a square cross-sectional duct under magnetic field in the presence of ferrofluid flow. At the end of their work, it was concluded that the average heat transfer coefficient with four magnets is approximately 40.79% and 58.19% higher than those of utilizing no magnet with ferrofluid and pure water, respectively. Salehpour et al. [31] experimentally investigated the mixed convection of ferrofluid under magnetic field in a porous-media-filled channel. Nessab et al. [26] used the ferrofluids as jet stream under magnetic field. They found that the heat transfer is increasing with the increase in the magnetic number and the reduction in the aspect ratio. Some recent articles on ferrofluids can be found in [7, 20, 25, 34]. Also, the MHD problems which are solved by finite element method can be found in literature as [12, 30].

The main aim of the present investigation is to explore the effects of governing parameters in a ferrofluid flow through channel with non-symmetric cavities. Based on author’s knowledge and the above literature survey, there is no work on non-symmetric cavities for both mixed and forced convection cases. [3,4,5,6]

The physical model

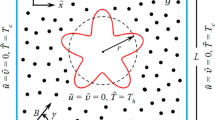
Consider the two-dimensional channel filled with ferrofluid under the effect of applied magnetic field in the horizontal direction. Two square cavities of length h are fixed on both the upper and lower walls of the channel (see Fig. 1). The bottom wall of cavity on lower side is controlled at hot temperature (\(T_\mathrm{h}\)), and the top wall of the cavity on the upper side is maintained at cold temperature (\(T_\mathrm{c}\)). The temperature of the ferrofluid entering from the inlet of the channel is \(T_\mathrm{c}\). An inflow velocity is provided at the inlet in the form of a parabolic profile which is fully developed hydrodynamically. On the other hand, the homogeneous Neumann boundary conditions for the velocity and temperature variables are prescribed at the outlet. For all other walls of the channel and cavities, the no-slip for velocity and adiabatic for temperature are imposed. As compared to the external magnetic field, the effect of the induced magnetic field is not taken into account. Moreover, the assumption of laminar, steady, incompressible and Newtonian fluid is also considered. The Joule heating and viscous dissipation phenomena are ignored in the energy equation. Thermophysical properties of water, iron oxide and the nanofluid are supposed to be constant (see Table 1) except for density. The variations in density are incorporated using Boussinesq approximation.

Fig. 1
figure 1

A schematic diagram of physical model under consideration

Full size image
Table 1 Physical properties of the base fluid and nanoparticles [27]
Full size table

The governing partial differential equations

The governing laws of mass, momentum and energy under the above-mentioned assumption lead to the following partial differential equations

$$\begin{aligned} \text {div}\; \mathbf {u}&= 0 , \end{aligned}$$
(1)
$$\begin{aligned} \rho _\mathrm{ff}(\mathbf {u}\cdot \nabla )\mathbf {u}&= \nabla p- \mu _\mathrm{ff}\triangle \mathbf {u}-\sigma _\mathrm{ff}B_{0}^2v\mathbf {e}\nonumber \\&\quad +(\rho \beta )_\mathrm{ff} g(T-T_\mathrm{c})\mathbf {e}, \end{aligned}$$
(2)
$$\begin{aligned} (\mathbf {u}\cdot \nabla )T&= \alpha _\mathrm{ff}\triangle T, \end{aligned}$$
(3)

where \(\mathbf {u}=(u, v)\) is the velocity vector and \(\mathbf {e}=(0, 1)\) represents the unit vector.

The investigated problem is subject to the following boundary conditions:

  • At the inlet:   \(u=u(y),\quad v=0, \quad T=T_\mathrm{c}.\)

  • At the bottom wall of lower cavity:   \(u= v=0, \quad T=T_\mathrm{h}.\)

  • At the top wall of upper cavity:   \(u= v=0, \quad T=T_\mathrm{c}.\)

  • At the outlet:    \(\frac{\partial u}{\partial x}=\frac{\partial v}{\partial x}=\frac{\partial T}{\partial x}=0\).

  • On all the other channel and cavity walls:  \(u=v=\partial T/\partial \mathbf {n}=0,\) where \(\mathbf {n}\) is used to denote the normal direction to the corresponding boundary.

The dimensionless partial differential equations

The following transformations are invoked to achieve the dimensionless form of governing model

$$\begin{aligned}&(X, Y)=\left( \frac{x}{H}, \frac{y}{H}\right) , \quad P=\frac{p}{\rho _\mathrm{ff}\overline{u}^2},\\&\quad \mathrm{Re}=\frac{\overline{u} H}{\nu _\mathrm{f}},\quad \mathrm{Ri}=\frac{\mathrm{Gr}}{Re^2} \\&\quad (U, V)=\left( \frac{u}{\overline{u}}, \frac{v}{\overline{u}}\right) ,\quad \theta =\frac{T-T_\mathrm{c}}{T_\mathrm{h}-T_\mathrm{c}}, \\&\quad \mathrm{Pr}=\frac{\nu _{\mathrm{f}}}{\alpha _\mathrm{f}}, \quad \mathrm{Ha}=B_{0}H\sqrt{\frac{\sigma _\mathrm{ff}}{\mu _\mathrm{ff}}}. \end{aligned}$$

With the above-introduced variables, the governing equations are reduced as follows

$$\begin{aligned} \text {div}\; {\mathbf {U}}&= 0 , \end{aligned}$$
(4)
$$\begin{aligned} ({\mathbf {U}}\cdot \nabla ){\mathbf {U}}&= \nabla P- \frac{1}{\mathrm{Re}} \frac{\mu _{\mathrm{ff}}}{\rho _{\mathrm{ff}}\nu _{\mathrm{f}}}\triangle {\mathbf {U}}-\frac{\rho _{\mathrm{f}}}{\rho _{\mathrm{ff}}}\frac{\sigma _{\mathrm{ff}}}{\sigma _{\mathrm{f}}}\frac{\mathrm{Ha}^{2}}{\mathrm{Re}}V\,{\mathbf {e}} \nonumber \\&\quad +{\mathrm{Ri}}\frac{\rho _{\mathrm{f}}}{\rho _{\mathrm{ff}}}\left( 1-\phi +\frac{\rho _{\mathrm{s}}\beta _{\mathrm{s}}}{\rho _{\mathrm{f}}\beta _{\mathrm{f}}}\phi \right) \theta \,{\mathbf {e}}, \end{aligned}$$
(5)
$$\begin{aligned} ({\mathbf {U}}\cdot \nabla )\theta&= \frac{1}{\mathrm{RePr}}\frac{\alpha _{\mathrm{ff}}}{\alpha _{\mathrm{f}}}\triangle \theta , \end{aligned}$$
(6)

where \(\mathbf {U}\) denotes the dimensionless velocity vector.

The corresponding boundary conditions read the following:

  • At the inlet:  \(U=U(Y),\quad V= \theta =0\).

  • At the bottom wall of lower cavity: \(U= V=0, \quad \theta =1\).

  • At the top wall of upper cavity:   \(U= V= \theta =0\).

  • At the outlet:    \(\frac{\partial U}{\partial X}=\frac{\partial V}{\partial X}=\frac{\partial \theta }{\partial X}=0\).

  • On all the other channel and cavity walls:    \(U=V=\partial \theta /\partial \mathbf {n}=0.\)

Thermophysical properties of nanofluid

The effective formulae for the thermophysical properties of the nanofluid employed in the present investigation are written as follows [1, 2, 18, 22, 36]

  • Density:    \(\rho _\mathrm{ff} = (1-\phi )\rho _\mathrm{f} + \phi \rho _\mathrm{s}\),

  • Thermal diffusivity:    \(\alpha _\mathrm{ff}=\frac{k_\mathrm{ff}}{(\rho C_\mathrm{p})_\mathrm{ff}}\),

  • Electrical conductivity:    \(\sigma _\mathrm{ff}=\sigma _\mathrm{f}\left[ 1+\frac{3(\sigma -1)\phi }{(\sigma +2)-(\sigma -1)\phi }\right] ,\,\sigma = \frac{\sigma _\mathrm{s}}{\sigma _\mathrm{f}}\)

  • Specific heat:    \((\rho C_\mathrm{p})_\mathrm{ff} = \left( 1-\phi \right) (\rho C_\mathrm{p}) _\mathrm{f}+ \phi (\rho C_\mathrm{p})_\mathrm{s}\),

  • Thermal conductivity:    \(\frac{k_\mathrm{ff}}{k_\mathrm{f}}=\frac{k_\mathrm{s}+2k_\mathrm{f}-2\phi (k_\mathrm{f}-k_\mathrm{p})}{ k_\mathrm{s}+2k_\mathrm{f}+\phi (k_\mathrm{f}-k_\mathrm{p})},\)

  • Thermal expansion coefficient:    \((\rho \beta )_\mathrm{ff} = (1-\phi )(\rho \beta )_\mathrm{f} + \phi (\rho \beta )_\mathrm{s}\),

  • Dynamic viscosity:    \(\mu _\mathrm{ff}=\frac{\mu _\mathrm{f}}{(1-\phi )^{2.5}}.\)

The Nusselt number

The local and average Nusselt numbers which are characterized by the ratio of the heat transfer due to the convection to conduction on the heated wall are defined as follows

$$\begin{aligned} \mathrm{Nu}=\frac{h_\mathrm{ff} H}{k_\mathrm{f}}, \end{aligned}$$
(7)

where \(h_\mathrm{ff}\) is given by

$$\begin{aligned} h_\mathrm{ff} = \frac{q}{T_\mathrm{h} - T_\mathrm{c}}. \end{aligned}$$
(8)

The wall heat flux q is expressed as

$$\begin{aligned}&q=-k_\mathrm{ff}\frac{(T_\mathrm{h}-T_\mathrm{c})}{H}\frac{\partial \theta }{\partial Y}\bigg |_{Y=0}, \end{aligned}$$
(9)
$$\begin{aligned}&\mathrm{Nu}=-\frac{k_\mathrm{ff}}{k_\mathrm{f}}\left( \frac{\partial \theta }{\partial Y}\right) , \end{aligned}$$
(10)

The average Nu can be computed by integrating the above equation over the length (\({\mathcal {L}}\)) of heated wall

$$\begin{aligned} {Nu}_{\text {avg}}=\int _{0}^{{\mathcal {L}}}\mathrm{Nu}\,\mathrm{d}X. \end{aligned}$$
(11)

Numerical approximation

The Galerkin-based higher-order and stable finite element method is implemented for the numerical approximation of the governing system of partial differential Eqs. (4)–(6). To this end, first of all an unstructured grid is designed with the help of DeViSoR Grid (http://www.featflow.de) to cover the computational domain. The coarsest grid at level \((\ell =1)\) is depicted in Fig. 2 having 24 quadrilateral elements, by which a sequence of grids is constructed with successive refinements. Any grid at higher level \(\ell =\ell +1\) is obtained from level \(\ell\) where each quadrilateral element is further decomposed into four quadrilateral elements. The discretization of equations is achieved in the similar way as in [14] utilizing higher-order LBB-stable \(Q_2/P_1^\mathrm{disc}\)-element pair (see [13, 15] for further details). That means the \(Q_2\)-element is implemented for the velocity and temperature components, and pressure is discretized with the help of discontinuous \(P_1^\mathrm{disc}\)-element. The discretization of Eqs. (4)–(6) leads to the nonlinear equations which are coped with the Newton’s method and the linearized equations in each step are computed using the Gaussian elimination approach (see [14, 15] for further details).

Fig. 2
figure 2

Sequence of grid structures and the refinement strategy

Full size image

The code validation

We inaugurate this section by performing the validity check for our code which is based on a finite element discretization discussed in the previous section. To this end, code has been tested against a similar configuration with some published data available in the literature. The computations are carried out for three different situations, namely assisting, opposing and horizontal flows [8, 21, 23, 24]. The results obtained for the Nusselt number agree well with the published data which ensures the reliability of the code (see Table 2). Moreover, a grid convergence study has also been carried out by considering a sequence of grids by a uniform refinement procedure producing four elements from one while moving from a coarser level (\(\ell\)) to a finer level (\(\ell +1\)), see Fig. 2. The benchmark quantities, the drag and lift coefficients are chosen as they depend on both velocity and pressure approximation. The results are presented in Table 3 for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \phi = 0.05\), which indicate that after a threshold of some refinement level (\(\ell =7\)), no significant change is there for the next finer level (\(\ell =8\)) showing the grid independency. Hence, we restrict our further simulations at mesh refinement level \(\ell =7\) to save the computational time and memory.

Table 2 Forced flow Code validation for the present study against Refs. [8, 21, 23, 24] for various values of Ri
Full size table
Table 3 The convergence analysis for the proposed problem
Full size table

Results and discussion

A computational analysis has been done on heat transfer, fluid flow and temperature distribution in a channel with non-symmetric cavities by using the Galerkin-based finite element method. The bottom wall of the bottom cavity is heated isothermally. The proposed problem is explored for different controlling parameters as nanoparticle volume fraction; \((0\le \phi \le 0.15\)), aspect ratio of the cavities; (\(0.2\le h/H \le 1.0\)), Richardson numbers; (0.01\(\le \mathrm{Ri} \le 10\)), Hartmann number; (0 \(\le \mathrm{Ha} \le\)100); and Reynolds number; (\(1\le \mathrm{Re} \le 200\)).

Figure 3 illustrates the effects of Hartmann number on streamlines (on the left) and isotherms (on the right) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0\) and \(\phi = 0.05\). If we can take base case as \(\mathrm{Ha} = 0\), it is seen that the bottom cavity behaves completely as lid-driven cavity flow and a small circulation cell is formed at the bottom right corner. On the contrary, single cell is formed at the top cavity and its flow strength is very high. It is noticed that the cavity is heated from the bottom of the bottom cavity, this heat does not penetrate to the channel. In other words, convection mode of heat transfer is dominant inside the bottom cavity. If value of Hartmann number is increased, namely \(\mathrm{Ha} = 20\), two symmetric cells are formed on the top cavity and strength of the flow becomes very weak for the bottom one. In other words, increasing of magnetic field inserts a negative impact on flow strength and the main cell moves to the top. For further values of Hartmann number, namely \(\mathrm{Ha} = 50\), isotherms become too flat and for \(\mathrm{Ha} = 100\), they are completely parallel to the duct. As seen from Fig. 1 that the magnetic field is applied to the bottom cavity laterally. It means that conduction mode of heat transfer becomes dominant to convection mode and the flow inside the top cavity becomes stronger and multiple cells are formed.

Figure 4 shows the results according to Richardson number for fixed value of Hartmann number as \(\mathrm{Ha} = 25\). It is highly interesting result that the flow inside the top cavity is not affected from the changing of Richardson number as heating part of the cavity is located at the bottom of the cavity. There is no enough space for moving the fluid inside the cavity. As seen clearly from the result that domination of natural convection onto forced convection becomes stronger with increasing Richardson number. It is very clear from the isotherms that the number and location of the circulating cells inside the bottom cavity strongly depend on variation of the Richardson number. When the cavity is heated from the bottom wall, domination of natural convection becomes stronger and the temperature variations can be seen clearly inside the cavity.

Effects of Reynolds number on streamlines and isotherms for fixed parameters are presented in Fig. 5 and it is shown from the figure, effects of Reynolds number become insignificant inside the top cavity for all cases because forced convection becomes dominant even at the highest value of Reynolds number. In other words, flow movements due to buoyancy are suppressed due to domination of forced convection. On the contrary, both location of the main cell and the number of cells are changed depending on the Reynolds number and multiple cells are formed in the bottom cavity for \(\mathrm{Re} = 200\). Further values of Re number are tested, but there is no change on flow field inside the cavity.

Effects of the cavity aspect ratio are presented in Fig. 6 for \(\mathrm{Pr} = 6.2, \mathrm{Ri} = 1.0, \mathrm{Re} = 100\) and \(\phi = 0.5\). It is noticed that dimensions for both of the cavities are chosen as constant for whole work. As shown in the figure, when the gaps are very small, namely \(h/H = 0.2\) and \(h/H = 0.4\), the flow passes over cavities directly. On the contrary, there is a circulation inside the cavities and dimension of the circulating cells are directly related to dimensions of the cavities. Thus, penetration of the heat from the bottom side of the bottom cavity is increased with increasing of the aspect ratio of the cavities. Especially for the narrow channel, the flow from the top side behaves as lid-driven flow or belt flow. Thus, effect of higher values of Re becomes insignificant.

Nanoparticle volume fraction effects on the fluid flow and temperature are presented in Fig. 7. It is observed that the variation of nanoparticle volume fraction inserts small effect on temperature distribution and its effects on flow field become insignificant up to \(\phi = 0.05\). After this ratio, a mini-circulation cell is formed at the right bottom corner of the bottom cavity. It means that the flow strength is increased with addition of the particle. Further values of nanoparticle volume fraction did not tested to be safe the single phase flow behaviour.

Figure 8 shows the effects of Hartmann number on average Nusselt number for different values of Richardson number. The trend of variation of Nusselt number becomes almost same up to \(\mathrm{Ri} = 1.0\). Then, as an interesting result, it is increased and a big jumping is occurred for \(\mathrm{Ri} = 5.0\) at \(\mathrm{Ha} = 50\). As a general view, the heat transfer is decreased with increasing Hartmann number. Also, for higher values of Hartmann number and lower values of Richardson number, values of Nusselt number go to 1, namely convection mode of heat transfer is decreased. In other words, application of the magnetic field decreases the strength of the kinetic energy of the flow.

Figure 9 illustrates the effects of nanoparticle volume fraction on average Nusselt number for \(\mathrm{Ri} = 1.0, \mathrm{Pr} = 6.2, \mathrm{Re} = 100\) and \(\phi = 0.5\) for the case of \(h=H = 1.0\). The figure showed the higher value of heat transfer for \(\mathrm{Ri} \ge 1.0\). It is increased linearly for lower values of Ri, and it becomes almost constant up to \(\phi = 0.1\). For the highest value of nanoparticle volume fraction, higher heat transfer is formed for \(\mathrm{Ri} = 5.0\). Finally, based on chosen viscosity model, heat transfer is increased with increasing nanoparticle volume ratio. In similar way, Fig. 10 presents the variation of mean Nusselt number with Reynolds number for the parameters of \(\mathrm{Pr} = 6.2, \mathrm{Ri} = 1.0, \mathrm{Ha} = 25, \phi = 0.05\) for the case of \(h=H = 1.0\). Normally, heat transfer increases with increasing Reynolds number, but this increment is affected from the higher values of Richardson number. Flow and temperature distribution are presented in Fig. 5. For \(\mathrm{Re} = 50\), the Nusselt number increases rapidly with the same values of Grashof number, but it gives the same value for \(\mathrm{Re} = 100\) because increasing of flow velocity makes an opposite effect on heat transfer. The flow moves fast from the cavity, and penetration of heat transfer is decreased from the bottom wall.

Effects of h / H ratio on heat transfer is given for different parameters as \(\mathrm{Ri} = 1.0, \mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ha} = 25, \phi = 0.05\) in Fig. 11. As seen from the figure, penetration of temperature increases with increasing h/H ratio and higher Reynolds number. In case of small values of h / H, the flow goes directly from the cavity. Thus, flow inside the cavity becomes almost motionless and flow penetration becomes very low. In other words, conduction mode of heat transfer start to play its role and lower heat transfer is obtained due to motionless flow. Also, changing of h / H value affects the circulation cell as seen in Fig. 6.

Fig. 3
figure 3

Impact of Ha on the isotherms (right) and streamlines (left) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \phi = 0.05\)

Full size image
Fig. 4
figure 4

Impact of Ri on the isotherms (right) and streamlines (left) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ha} = 25, \phi = 0.05\)

Full size image
Fig. 5
figure 5

Impact of Re on the isotherms (right) and streamlines (left) for \(\mathrm{Pr} = 6.2, \mathrm{Ri} = 1.0, \mathrm{Ha} = 25, \phi = 0.05\)

Full size image
Fig. 6
figure 6

Impact of the aspect ratio h / H on the isotherms (right) and streamlines (left) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \mathrm{Ha} = 25,\phi = 0.05\)

Full size image
Fig. 7
figure 7

Impact of \(\phi\) on the isotherms (right) and streamlines (left) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \mathrm{Ha} = 25\) for the case of \(h/H=1.0\)

Full size image
Fig. 8
figure 8

Impact of Ha on \(\mathrm{Nu}_{\text {avg}}\) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \phi = 0.05\) for the case of \(h/H=1.0\)

Full size image
Fig. 9
figure 9

Impact of \(\phi\) on \(\mathrm{Nu}_{\text {avg}}\) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \mathrm{Ha} = 25\) for the case of \(h/H=1.0\)

Full size image
Fig. 10
figure 10

Impact of Re on \(\mathrm{Nu}_{\text {avg}}\) for \(\mathrm{Pr} = 6.2, \mathrm{Ha} = 25, \mathrm{Ri} = 1.0, \phi = 0.05\) for the case of \(h/H=1.0\)

Full size image
Fig. 11
figure 11

Impact of the ratio h / H on \(\mathrm{Nu}_{\text {avg}}\) for \(\mathrm{Pr} = 6.2, \mathrm{Re} = 100, \mathrm{Ri} = 1.0, \mathrm{Ha}=25, \phi = 0.05\)

Full size image

Conclusions

The numerical simulations have been performed for the heat and fluid flow in a channel having non-symmetric cavities. Approximation of the governing equations is obtained using the higher-order LBB-stable finite element method for many governing parameters. The key observations can be listed as follows:

  • Variation of nanoparticle volume fraction makes minor effect on heat transfer and fluid flow, especially for the smaller values of Ri.

  • Heat transfer is increased with increasing Re, but it decreases with geometrical parameters.

  • Both the flow field and temperature variation behave as lid-driven cavities, and the flow circulating inside the cavity depends on bottom lid or top lid. Number of circulations is not affected from nanoparticle volume fraction.

  • Heat transfer is also decreased by increasing Ha, and penetration of temperature increases with increasing h / H ratio and higher Reynolds number.