1 Introduction

The Brazilian Test is broadly used to determine the tensile strength of brittle materials. Unlike the direct tensile test, there is no need to attach the sample to the jaw, avoiding premature sample failure during the test set-up. The indirect tensile test or Brazilian Test consists of diametrically loading a cylindrical sample using a mobile jaw that is gradually displaced at a controlled velocity, inducing stresses within the sample.

The first experimental application was carried out by professor Carneiro [1], who presented it in the 5th Congress of the “Associaçao Brasileira de Normas Técnicas (ABNT)”. A similar test was proposed in Japan by Akazawa [2] that same year. Eventually, it was admitted by the American Society for Testing Materials (ASTM) [3] and by the International Society for Rock Mechanics (ISRM) [4].

Even though the test appears in the middle of the twentieth century, the mathematical and theoretical bases needed for its development were established at the end of the nineteenth one. In particular, it was Boussinesq [5] who managed to calculate the expression of the stresses produced inside a semi-infinite solid with a flat surface subjected to a uniformly distributed load applied along a certain length. This progress allows Flamant [6] to demonstrate that for a given point the relation between stresses equals the relation between the distances to the origin, measured at each axis, thus distribution has to be radial.

Advancing in his analysis, Boussinesq [7] introduces a shear component in the load in order to calculate the stress field, considering any load orientation in uniform distributions.

Based on Flamant [6] and Boussinesq [5, 7], another key step was taken by Timoshenko and Goodier [8], who developed the case of a disk subjected to concentrated load in plane elasticity.

The next step forward is produced when Hondros [9] analytically determines the stress field in any point inside a disk subjected to a uniformly distributed load. His analysis consists of expanding the load distribution as Fourier series, whereupon he evaluates the Young modulus and Poisson coefficient of cement mortars and concrete. Hondros’s [9] work sets a precedent in the historical evolution of this test because it establishes the bases for further mathematical developments.

Then, analytic closed solutions for the stress, strain and displacement fields inside a sample subjected to partially distributed compressions are obtained by Hung and Ma [10, 11]. Later, Markides et al. [11] developed an alternative solution for the case of distributed radial load using the complex potential method [13,14,15], obtaining similar results to Ma and Hung [11]. However, their research stands out for highlighting a gradient or discontinuity in the limit between the loaded and unloaded areas of the disk, which was more evident in the displacement calculus. Thus, non-uniform load distributions were proposed to overcome this issue [16,17,18]. Furthermore, Markides et al. [19] have addressed the Brazilian Test as a contact problem, considering Hertz contact between the sample and the jaw, which shape determines the stress state inside the disk [20, 21]. This issue involves a circular distribution of the load that cannot be solved by the complex potential method.

In turn an equivalent parabolic distribution was introduced. In that sense, it could be considered that the contact problem has been solved by Markides et al. [19], which lead to similar conclusions to those of Timoshenko [8]. However, Markides et al. [19] consider some restrictions in their formulation, based on the hypothesis that the actual contact length is small enough to assume that the contact is developed along a flat surface. The influence in the theoretic models of the different loading techniques used in the Brazilian test (cushions, bearings, etc.) is still on topic. This paper proposes two new alternative distributions, which guarantee the absence of discontinuities and the compatibility equations not only inside the disk but also along its boundary. Even though formulations that do not match these conditions have proved to lead to useful results, these new restrictions encourage the load function to match higher levels of mathematical adequacy in relation to the elastic theory.

Current investigation lines show how the location of the point where the failure is initiated is influenced by the contact angle considered [22, 23]. These new insights plus the novel applications of this test in biomedical materials [24,25,26,27], ceramics [28] or even ductile alloys [29, 30] and the extension of the method to determine elastic properties of the material [31,32,33,34,35] or shear strength of layering [36] highlight the importance of the stress, strain and displacement fields within the body.

This paper establishes a new method in order to determine the stress field in a disk subjected to diametrical compression under any radial loading distribution. This method differs from the previous ones [9,10,11,12,13,14,15,16,17,18,19,20,21], in the handy implementation of the solving system. Load distributions are considered as an infinite number of differential concentrated loads. In this sense, the solution to any load distribution can be obtained by integrating the expressions for a given concentrated load [11] along the contact angle. Thus, the stress state of any point could be determined by adding the contributions of each load that is part of the distribution. The core innovation of this method determines the stress field of any radial distribution type, even if it has no symmetry with respect to the vertical axis. When closed-form analytic solutions cannot be achieved, the result could be estimated by numerical approximations. Since a unique integral is needed to determine the stress state, the error committed is that of the numerical method employed, so it can be bounded to high accuracy applications, therefore potentially broadening the possibilities of this technique in simulation software and engineering problems.

2 Approach to the method

Several analytic solutions for the calculus of the stress field in the Brazilian test can be found in literature [9,10,11,12,13,14,15,16,17,18,19,20,21]. However, each one is developed for a specific case, and no relation among them can be established. Special attention should be given to the concentrated load. Even though this is impossible to achieve in real conditions, as two elastic bodies in contact always suffer deformations that oblige the load to be distributed along the contact angle, from a theoretical point of view it can be exploited to generate the stress field of distributions with central symmetry. Considering that any load distribution is made of the sum of an infinite number of differential loads, Hung and Ma’s formulation for the concentrated load [11] can be integrated taking into account how the load changes along the boundary, giving as a result the analytic or numerical solutions for the stress field developed by the authors in this paper.

2.1 Preliminary aspects

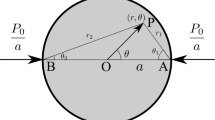
Stress in any point of the disk, when under a concentrated load, can be calculated by Hung and Ma’s formulation [11]. The expressions for the radial (\(\sigma _{\rho })\), hoop (\(\sigma _{\theta })\) and shear stresses (\(\tau _{\rho \theta })\) in polar coordinates are shown in Eqs. (1)–(3):

$$\begin{aligned} \sigma _{\rho }= & {} \frac{P\left( 1-\rho ^{2} \right) ^{2}{(\rho }^{4}+2\rho ^{2}-1+2\cos {2\theta })}{\pi Rt\left( \rho ^{4}+1+2\rho ^{2}\mathrm {cos}2\theta \right) ^{2}}, \end{aligned}$$
(1)
$$\begin{aligned} \sigma _{\theta }= & {} \frac{P\left[ \rho ^{8}+4\rho ^{4}-4\rho ^{2}-1-2(-2\rho ^{6}+\rho ^{4}+1)\cos {2\theta } \right] }{\pi Rt\left( \rho ^{4}+1+2\rho ^{2}\mathrm {cos}2\theta \right) ^{2}}, \end{aligned}$$
(2)
$$\begin{aligned} \tau _{r\theta }= & {} \frac{2P\left( 1-\rho ^{4} \right) \left( 1-\rho ^{2} \right) \sin {2\theta }}{\pi Rt\left( \rho ^{4}+1+2\rho ^{2}\mathrm {cos}2\theta \right) ^{2}}, \end{aligned}$$
(3)

where \(\rho =r/R\), being r the radial distance to the point and R the disk radius, t the thickness of the sample, P is the total applied load (equivalent to that of a concentrated case) and \(\theta \) the angle between the point position vector and the positive horizontal semi-axis.

Considering the whole distribution as formed by infinitely concentrated loads, the rotation with respect to the original application point must be taken into consideration. For that reason, a new angle \(\alpha \) is considered, representing the rotation with respect to the vertical diameter of the actuation line of the load. New variable \(P_{0}=P/t\) is introduced to graphically represent the variables, as shown in Fig. 1.

Fig. 1
figure 1

a Disk subjected to concentrated load acting along its vertical diameter and b angle \({{\varvec{\alpha }} }\) considered as both anticlockwise and c clockwise rotations

Full size image

As shown in Fig. 1b and c, \(\theta _{f}=\theta _{i}+\alpha \) is the angle to be considered, measuring \(\alpha \) with respect to the vertical diameter, being positive when it goes clockwise and negative when it goes anticlockwise. In order to simplify the notation and to homogenise the nomenclature with the existing one, from now on, \(\theta _{i}\) will be renamed \(\theta \), taking into account that it differs from the \(\theta \) used in Eqs. (1)–(3).

Taking all the above into account, stress components at any point of the disk can be expressed integrating a combination of two functions along the contact angle (\({2\omega }_{0}\)). The first, describes the shape of the distribution; and the second, is linked to the position of the point inside the disk. Mathematically, it can be formulated as follows:

$$\begin{aligned} \sigma _{\rho }= & {} \int _{{-\omega }_{0}}^{\omega _{0}} {\frac{P_{0}(\alpha )}{\pi }\times f_{1}\left( \rho ,\theta ,\alpha \right) \mathrm{{d}}\alpha ,} \end{aligned}$$
(4)
$$\begin{aligned} \sigma _{\theta }= & {} \int _{-\omega _{0}}^{\omega _{0}} {\frac{P_{0}(\alpha )}{\pi }\times f_{2}\left( \rho ,\theta ,\alpha \right) \mathrm{{d}}\alpha ,} \end{aligned}$$
(5)
$$\begin{aligned} \tau _{r\theta }= & {} \int _{-\omega _{0}}^{\omega _{0}} {\frac{P_{0}(\alpha )}{\pi }\times f_{3}\left( \rho ,\theta ,\alpha \right) \mathrm{{d}}\alpha ,} \end{aligned}$$
(6)

being \(P_{0}(\alpha )\) the radial stress function along the boundary; corresponding \(f_{1}\), \(f_{2}\) and \(f_{3}\) to Eqs. (1)–(3), respectively, after introducing the new variable \(\alpha \). This approach implies that no shear stresses are being applied along the periphery of the disk. Thus, boundary conditions can be summarised as follows:

$$\begin{aligned} \sigma _{\rho }= & {} P_{0}\left( \alpha \right) , \end{aligned}$$
(7)
$$\begin{aligned} \sigma _{\theta }= & {} \tau _{\rho \theta }=0. \end{aligned}$$
(8)

Even if shear stresses along the boundary do not influence the stress state at any point located far from the loaded rim; they induce significant deviations in the proximities of the load application area [16], therefore they must be taken into consideration when relevant to practical purposes. However, as the proposed method is based on the stress field caused by a concentrated radial load, shear stresses along the boundary will be neglected.

2.2 Load distributions considered

A clear difference should be made between load distributions that allow closed-form solutions and those which only allow numerical solutions. Nowadays, most of the attention is given to analytic results, leaving numerical calculations for simulation software. Main distributions are: uniform, sinusoidal and parabolic [17], which are shown in Eqs. (9)–(11), respectively,

$$\begin{aligned} P_{u}\left( \alpha \right)= & {} \frac{P}{2Rt\omega _{0}}, \end{aligned}$$
(9)
$$\begin{aligned} P_{s}\left( \alpha \right)= & {} \frac{P\left[ \cos \left( \alpha \right) -\mathrm {cos}\,\omega _{0} \right] }{2Rt\left( \sin \omega _{0}-\omega _{0}\,\mathrm {cos}\,\omega _{0} \right) }, \end{aligned}$$
(10)
$$\begin{aligned} P_{p}\left( \alpha \right)= & {} \sqrt{\frac{3\pi P}{32K_{rig}Rt}} \left( 1-\frac{{\mathrm {sin}}^{2}\alpha }{{\mathrm {sin}}^{2}\omega _{0p}} \right) . \end{aligned}$$
(11)

It is important to highlight that uniform distribution is a constant as it does not depend on \(\alpha \). However, it has been expressed as \(P(\alpha )\) because it represents the stress value along the loaded part of the boundary. The term \(K_{rig}\) involved in Eq. (11) considers the deformations produced along the contact during the test. It is a function of Muskhelishvili’s constants (k) and of the jaw (subindex one) and sample (subindex two) shear moduli (\(\mu \)):

$$\begin{aligned} K_{rig}=\frac{k_{1}+1}{4\mu _{1}}+\frac{k_{2}+1}{4\mu _{2}}, \end{aligned}$$
(12)

being \(k_{i}=3-4v_{i}\) in case of plane strain or \(k_{i}=\left( 3-v_{i} \right) /\left( 1+v_{i} \right) \) in the case of plane stress, being \(v_{i}\) the Poisson ratio of the material.

As a consequence of considering the elastic contact between the bodies, P and \(\omega _{0}\) are no longer two different parameters. The continuous deformation of both the sample and the jaw during the test makes the contact angle in the parabolic condition (\(\omega _{0p})\) vary as the load transferred increases. The relation between these parameters has been established by Markides and Kourkoulis [18]:

$$\begin{aligned} \omega _{0p}=\mathrm {asin}\sqrt{\frac{6K_{rig}P}{\pi Rt}} . \end{aligned}$$
(13)

Although parabolic load distribution is of special interest, as it involves the elastic properties of the jaw and the sample; its results are similar to the sinusoidal case for the same contact angle [17]. In fact, the parabolic distribution transforms into a sinusoidal one if the analysis is carried out from \(\alpha \).

2.2.1 Smooth transition distributions: the spline and new cosine distribution cases

Contact between the jaw and the sample generates displacements that depend on the stiffness relation between bodies. These displacements spread deformation progressively through the entire sample without discontinuities between any two infinitely close points. Thus, stress distributions should fulfil both continuity and smooth transition requirements, as well as compatibility conditions. In other words, a smooth transition must exist from the unloaded to the loaded part of the boundary from both a stress and a strain point of view. Experimental evidence of this phenomenon can be observed in Markides et al. [19], where radial displacements obtained by the digital image correlation technique clearly suggest that both strain and stress fields should also be smooth transition functions. However, they do verify the equilibrium equations of an elastic body in which the forces per volume unit are negligible [7]:

$$\begin{aligned}& \frac{\partial \sigma _{\rho }}{\partial \rho }+\frac{1}{\rho }\frac{\partial \tau _{\rho \theta }}{\partial \theta }+\frac{\sigma _{\rho }-\sigma _{\theta }}{\rho }=0, \end{aligned}$$
(14)
$$\begin{aligned}& \frac{1}{\rho }\frac{\partial \sigma _{\theta }}{\partial \theta }+\frac{\partial \tau _{\rho \theta }}{\partial \rho }+2\frac{\tau _{\rho \theta }}{\rho }=0. \end{aligned}$$
(15)

Taking all this into consideration, it must be discussed whether stronger restrictions should be imposed on functions that define stress state inside the sample. Smooth transition added to the fact that the greatest displacements located right above the vertical diameter can be mathematically expressed as a function \(y\left( \alpha \right) \) subjected to the following restrictions:

$$\begin{aligned}& \frac{\mathrm{{d}}y}{\mathrm{{d}}\alpha }\left( 0 \right) =0, \end{aligned}$$
(16)
$$\begin{aligned}& y\left( 0 \right) =1, \end{aligned}$$
(17)
$$\begin{aligned}& y\left( \omega _{0} \right) =0, \end{aligned}$$
(18)
$$\begin{aligned}& \frac{\mathrm{{d}}y}{\mathrm{{d}}\alpha }\left( \omega _{0} \right) =0, \end{aligned}$$
(19)
$$\begin{aligned}& y\left( -\omega _{0} \right) =0, \end{aligned}$$
(20)
$$\begin{aligned}& \frac{\mathrm{{d}}y}{\mathrm{{d}}\alpha }\left( {-\omega }_{0} \right) =0. \end{aligned}$$
(21)

Notice that six conditions are needed to represent the physical restrictions mentioned in Eqs. (16)–(21). However, the problem can be simplified as the desired function is even, therefore Eq. (16) does not need to be explicitly imposed. Taking into account that its derivatives vanish at the points \(\alpha ={\pm \omega }_{0}\), two different functions: a spline, \(y_{sp}(\alpha )\), and a new cosine distribution, \(y_{nc}(\alpha )\), are proposed in Eqs. (22) and (23) to match conditions in Eqs. (16)–(21):

$$\begin{aligned} y_{sp}\left( \alpha \right)= & {} \frac{1}{\omega _{0}^{4}}\alpha ^{4}-\frac{2}{\omega _{0}^{2}}\alpha ^{2}+1, \end{aligned}$$
(22)
$$\begin{aligned} y_{nc}\left( \alpha \right)= & {} \cos \left( \frac{\pi }{\omega _{0}}\alpha \right) +1. \end{aligned}$$
(23)

Up to this point only the shape of the function has been defined. However, it must also represent the total applied load. In order to match these conditions, a new function \(P_{sp,nc}\left( \alpha \right) =\gamma _{sp,nc}*y_{sp,nc}(\alpha )\), where subindexes sp and nc refers to spline and new cosine distributions, respectively, is defined. In this sense, \(\gamma _{sp,nc}\) is a constant that ensures the fulfilment of specific test conditions, maintaining the desired shape. As the area bounded by the function and the horizontal semi-axis represent the total applied load, Eq. (24) can be used to obtain \(\gamma _{sp,nc}\):

$$\begin{aligned} \int _{-\omega _{0}}^{\omega _{0}} {P_{sp,nc}\left( \alpha \right) \cos \left( \alpha \right) \,R\;\mathrm{{d}}\alpha } =\frac{P}{t}. \end{aligned}$$
(24)

Parameter \(\gamma \) for each distribution may be obtained by solving Eq. (24) for each case:

$$\begin{aligned} \gamma _{sp}= & {} \frac{15P}{16Rt\omega _{0}}, \end{aligned}$$
(25)
$$\begin{aligned} \gamma _{nc}= & {} \frac{P(\pi ^{2}-\omega _{0}^{2})}{2\pi ^{2}Rt\sin \left( \omega _{0} \right) }. \end{aligned}$$
(26)

A variable summary is depicted in Fig. 2, where, \(P_{0}(\alpha )=P(\alpha )/t\).

Fig. 2
figure 2

a Variable summary and b zoom to observe \(\upalpha \)

Full size image

2.3 Closed-form solutions

Concentrated formulation [10, 11] can be combined with the desired stress distribution shape along the boundary in order to obtain the stress field inside the disk. Expressions for uniformly distributed compressions are obtained by replacing Eq. (9) into Eqs. (4)–(6) and integrating them along the contact angle (\({2\omega }_{0})\), which means the interval \([{-\omega }_{0},\omega _{0}]\). Only \(P(\alpha )\) should be modified in Eqs. (4)–(6) to obtain the stress field due to any other load distribution. Results are in great agreement with previous literature [10, 11]. Only small differences caused by variable \(\theta \) exist. This is due to the fact that the position angle vanishes at horizontal semi-axis and increases anticlockwise in the proposed expressions, Eqs. (27)–(30), whereas in Ma and Hung [10, 11] formulation, it vanishes in the vertical diameter and increases clockwise. To homogenise all the stress fields proposed in this text, stress field in a disk subjected to uniformly distributed compressions is shown in Eqs. (27)–(30):

$$\begin{aligned}& \sigma _{\rho _{u}}= \frac{P}{2\pi Rt\omega _{0}}\left\{ \left( \rho ^{2}-1 \right) \left( \frac{\sin {2\left( \theta -\omega _{0} \right) }}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta -\omega _{0} \right) +1}}-\frac{\sin {2\left( \theta +\omega _{0} \right) }}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta +\omega _{0} \right) +1}} \right) \right. \nonumber \\&\qquad \,\, \left. +\,\hbox {atan }\left( \frac{1-\rho ^{2}}{1+\rho ^{2}}\tan \left( \theta -\omega _{0} \right) \right) -\hbox {atan }{\left( \frac{1-\rho ^{2}}{1+\rho ^{2}}\tan \left( \theta +\omega _{0} \right) \right) -\mathrm {\Phi }} \right\} , \end{aligned}$$
(27)
$$\begin{aligned}& \sigma _{\theta _{u}}=\frac{P}{2\pi Rt\omega _{0}}\left\{ \left( \rho ^{2}-1 \right) \left( -\frac{\sin {2\left( \theta -\omega _{0} \right) }}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta -\omega _{0} \right) +1}}+\frac{\sin {2\left( \theta +\omega _{0} \right) }}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta +\omega _{0} \right) +1}} \right) \right. \nonumber \\&\qquad \,\, \left. +\,\hbox {atan }\left( \frac{1-\rho ^{2}}{1+\rho ^{2}}\tan \left( \theta -\omega _{0} \right) \right) -\hbox {atan }{\left( \frac{1-\rho ^{2}}{1+\rho ^{2}}\tan \left( \theta +\omega _{0} \right) \right) -\mathrm {\Phi }} \right\} ,\end{aligned}$$
(28)
$$\begin{aligned}& {\Phi }=\left\{ {\begin{array}{cc} \uppi &{}\frac{{\uppi }}{{2}}{-}{\omega }_{{0}}{<}\uptheta \le \frac{{\uppi }}{{2}} \\ 0&{}{\uptheta \le }\frac{{\uppi }}{{2}}{-}{\upomega }_{{0}} \\ \end{array}}, \right. \end{aligned}$$
(29)
$$\begin{aligned}& \tau _{\rho \theta _{u}}=\frac{P\left( \rho ^{2}-1 \right) ^{2}\left( \rho ^{2}+1 \right) \left[ \cos {2\left( \theta -\omega _{0} \right) -\cos {2\left( \theta +\omega _{0} \right) }} \right] }{2\pi Rt\omega _{0}\left[ \rho ^{4}+2\rho ^{2}\cos {\mathrm {2}\left( \theta -\omega _{0} \right) }+1 \right] \left[ \rho ^{4}+2\rho ^{2}\cos {2\left( \theta +\omega _{0} \right) +1} \right] }. \end{aligned}$$
(30)

This result can also be used for further verification in the method. Making \(\omega _{0}\rightarrow 0\) in Eqs. (27)–(28) and Eq. (30), equivalent expressions to Eqs. (1)–(3) are obtained, proving that concentrated formulation is enclosed in the uniform distribution. Despite the fact that concentrated load physical meaning is limited to the contact case between two solids with infinite stiffness, that is to say infinite Young’s modulus, the method highlights the importance of this formulation as it can be used to obtain the stress field to arbitrary load. Similarity with previous expressions ensures valid displacements and strains after further mathematical treatment [11].

Sinusoidal and parabolic stress fields can be obtained in closed-form combining Eqs. (4)–(6) with Eqs. (10) and (11), respectively. In order to ease the computational implementation of the method, the expressions have been packed up in different variables.

Sinusoidal

$$\begin{aligned} \sigma _{\rho s}=\frac{-\,\omega _{0}\cos \left( \omega _{0} \right) }{\left[ \sin {\omega _{0}-\omega _{0}\mathrm {cos}(\omega _{0})} \right] }\sigma _{\rho u}+\frac{P\left( \rho ^{2}-1 \right) ^{2}}{8\pi Rt\left[ \sin {\omega _{0}-\omega _{0}\mathrm {cos}(\omega _{0})} \right] \rho ^{4}}\left[ \cos \left( \theta \right) \left( S_{1}+S_{2} \right) +\sin \left( \theta \right) \left( S_{3}+S_{4} \right) \right] \mathrm {,} \end{aligned}$$
(31)

where

$$\begin{aligned}& S_{1}= \frac{\sqrt{2} (A+B+2)}{2\sqrt{\left( B+1 \right) ^{3} }}\left[ \hbox {atanh}\left( \frac{\sqrt{2} \sin \left( \theta +\omega _{0} \right) }{\sqrt{ {B+1} }} \right) -\hbox {atanh }\left( \frac{\sqrt{2} \sin \left( \theta -\omega _{0} \right) }{\sqrt{{B+1}}} \right) \right] ,\end{aligned}$$
(32)
$$\begin{aligned}& S_{2}=\frac{A-B}{B+1}\left[ \frac{\mathrm {sin}(\theta +\omega _{0})}{B-2\sin {\left( \theta +\omega _{0} \right) ^{2}+1}}-\frac{\mathrm {sin}(\theta -\omega _{0})}{B-2\sin {\left( \theta -\omega _{0} \right) ^{2}+1}} \right] , \end{aligned}$$
(33)
$$\begin{aligned}& S_{3}=\frac{A-B}{B-1}\left[ \frac{\mathrm {cos}(\theta -\omega _{0})}{B+\cos {2(\theta -\omega _{0})}}-\frac{\mathrm {cos}(\theta +\omega _{0})}{B+\cos {2(\theta +\omega _{0})}} \right] , \end{aligned}$$
(34)
$$\begin{aligned}& S4=\frac{\sqrt{2} (A+B-2)}{2\sqrt{\left( B-1 \right) ^{3} }}\left[ \hbox {atan }\left( \frac{\sqrt{2} \cos \left( \theta -\omega _{0} \right) }{\sqrt{{B-1}}} \right) -\hbox {atan }\left( \frac{\sqrt{2} \cos \left( \theta +\omega _{0} \right) }{\sqrt{{B-1}} } \right) \right] , \end{aligned}$$
(35)
$$\begin{aligned}& A=\frac{\rho ^{4}}{2}+\rho ^{2}-\frac{1}{2}, \end{aligned}$$
(36)
$$\begin{aligned}& B=\frac{\rho ^{4}+1}{2\rho ^{2}}. \end{aligned}$$
(37)

The expression for sinusoidal hoop stress is

$$\begin{aligned} \sigma _{\theta s}=\frac{-\omega _{0}\cos \left( \omega _{0} \right) }{\left[ \sin {\omega _{0}-\omega _{0}\mathrm {cos}(\omega _{0})} \right] }\sigma _{\theta u}+\frac{P(2\rho ^{6}-\rho ^{4}-1)}{8\pi Rt\left[ \sin {\omega _{0}-\omega _{0}\mathrm {cos}(\omega _{0})} \right] \rho ^{4}}\left[ \cos \left( \theta \right) \left( S_{1}+S_{2} \right) +\sin \left( \theta \right) \left( S_{3}+S_{4} \right) \right] \mathrm {,} \end{aligned}$$
(38)

in this case, it is necessary to substitute A by

$$\begin{aligned} C=\frac{\rho ^{6}+\rho ^{4}+5\rho ^{2}+1}{2(2\rho ^{4}+\rho ^{2}+1)}, \end{aligned}$$
(39)

in Eqs. (32)–(35).

$$\begin{aligned} \tau _{\rho \theta s}=\frac{-\omega _{0}\cos \left( \omega _{0} \right) }{\left[ \sin {\omega _{0}-\omega _{0}\mathrm {cos}(\omega _{0})} \right] }\tau _{\rho \theta u}+\frac{P\left( \rho ^{6}-\rho ^{4}-\rho ^{2}+1 \right) }{8\pi Rt\left[ \sin {\omega _{0}-\omega _{0}\mathrm {cos}(\omega _{0})} \right] \rho ^{3}}\left[ \cos \left( \theta \right) \left( S_{5}+S_{6} \right) +\sin \left( \theta \right) \left( S_{7}+S_{8} \right) \right] \mathrm {,}\nonumber \\ \end{aligned}$$
(40)

where

$$\begin{aligned} S_{5}= & {} 2\rho \left( \frac{\mathrm {cos}(\theta +\omega _{0})}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta +\omega _{0} \right) }+1}-\frac{\mathrm {cos}(\theta -\omega _{0})}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta -\omega _{0} \right) }+1} \right) , \end{aligned}$$
(41)
$$\begin{aligned} S_{6}= & {} \frac{-1}{\rho ^{2}-1}\left[ \hbox {atan }\left( \frac{2\rho \cos \left( \theta +\omega _{0} \right) }{\rho ^{2}-1} \right) -\hbox {atan }\left( \frac{2\rho \cos \left( \theta -\omega _{0} \right) }{\rho ^{2}-1} \right) \right] , \end{aligned}$$
(42)
$$\begin{aligned} S_{7}= & {} 2\rho \left( \frac{\mathrm {sin}(\theta +\omega _{0})}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta +\omega _{0} \right) }+1}-\frac{\mathrm {sin}(\theta -\omega _{0})}{\rho ^{4}+2\rho ^{2}\cos {2\left( \theta -\omega _{0} \right) }+1} \right) , \end{aligned}$$
(43)
$$\begin{aligned} S_{8}= & {} \frac{-1}{\rho ^{2}+1}\left[ \hbox {atanh}\left( \frac{2\rho \sin \left( \theta +\omega _{0} \right) }{\rho ^{2}+1} \right) -\hbox {atanh}\left( \frac{2\rho \sin \left( \theta -\omega _{0} \right) }{\rho ^{2}+1} \right) \right] . \end{aligned}$$
(44)

Parabolic

$$\begin{aligned}& \sigma _{\rho p}={\sqrt{\frac{3P}{128K_{rig}Rt}}} \left\{ \frac{2\pi Rt\omega _{0p}}{P}\sigma _{\rho u}+\frac{\left( \rho ^{2}-1 \right) ^{2}}{4\rho ^{4}\mathrm {sin}(\omega _{0p})}\left[ \cos ^{2}{(\theta )}\left( S_{9}+S_{10} \right) -\frac{\sin {2\theta }}{2}S_{11}+\sin ^{2}\left( \theta \right) \left( S_{12}+S_{13} \right) \right] \right\} , \end{aligned}$$
(45)
$$\begin{aligned}& S_{9}=-2\omega _{0p}-\frac{A-B}{2\left( B-1 \right) }\left[ \frac{\sin {2\left( \theta +\omega _{0p} \right) }}{B+\cos {\mathrm {2}\left( \theta +\omega _{0p} \right) }}-\frac{\sin {2\left( \theta -\omega _{0p} \right) }}{B+\cos {2\left( \theta -\omega _{0p} \right) }} \right] , \end{aligned}$$
(46)
$$\begin{aligned}& S_{10}=-\frac{B^{2}-B+A-1}{\sqrt{\left( B-1 \right) ^{3}\left( B+1 \right) } }\left[ \hbox {atan }\left( \frac{\sqrt{{B-1}}}{\sqrt{B+1} }\tan \left( \theta +\omega _{0p} \right) \right) -\hbox {atan }\left( \frac{\sqrt{{B-1} }}{\sqrt{{B+1}} }\tan \left( \theta -\omega _{0p} \right) \right) \right] , \end{aligned}$$
(47)
$$\begin{aligned}& S_{11}=\log {\left( \frac{B+\cos {2\left( \theta -\omega _{0p} \right) }}{B+\cos {2\left( \theta -\omega _{0p} \right) }} \right) ,} \end{aligned}$$
(48)
$$\begin{aligned}& S_{12}=2\omega _{0}+\frac{A-B}{2(B+1)}\left[ \frac{\sin {2(\theta +\omega _{0p})}}{B+\cos {2(\theta +\omega _{0p})}}-\frac{\sin {2(\theta -\omega _{0p})}}{B+\cos {2(\theta -\omega _{0p})}} \right] , \end{aligned}$$
(49)
$$\begin{aligned}& S_{13}=\frac{-B^{2}-B+A+1}{\sqrt{\left( B-1 \right) \left( B+1 \right) ^{3}} }\left[ \hbox {atan }\left( \frac{\sqrt{B-1} }{\sqrt{B+1} }\tan \left( \theta +\omega _{0p} \right) \right) -\hbox {atan }\left( \frac{\sqrt{{B-1}}}{\sqrt{B+1} }\tan \left( \theta -\omega _{0p} \right) \right) \right] . \end{aligned}$$
(50)

Proceeding in a similar manner as in the sinusoidal distribution, A in Eqs. (46)–(50) must be substituted by Eq. (39), in order to obtain the analytic expression for the parabolic hoop stress, as shown in Eq. (51):

$$\begin{aligned}& \sigma _{\theta p}=\sqrt{\frac{3P}{128K_{rig}Rt}} \left\{ \frac{2\pi Rt\omega _{0p}}{P}\sigma _{\theta u}-\frac{2\rho ^{6}-\rho ^{4}-1}{4\rho ^{4}\sin \left( \omega _{0p} \right) }\left[ \cos ^{2}\left( \theta \right) \left( S_{9}+S_{10} \right) -\frac{\sin {2\theta }}{2}S_{11}+\sin ^{2}\left( \theta \right) \left( S_{12}+S_{13} \right) \right] \right\} ,\nonumber \\ \end{aligned}$$
(51)
$$\begin{aligned}& \tau _{\rho \theta p}=\sqrt{\frac{3\pi P}{128{\pi K}_{rig}Rt}} \left\{ \frac{2\pi Rt\omega _{0p}}{P}\tau _{\rho \theta u}-\frac{\left( \rho ^{2}-1 \right) ^{2}(\rho ^{2}+1)}{2\rho ^{4}\mathrm {sin}(\omega _{0p})}\left[ \frac{\sin \left( \theta \right) }{2}\left( S_{14}+S_{15} \right) +\mathrm {sin}(2\theta )\left( S_{16}+S_{17} \right) \right. \right. \nonumber \\&\qquad \,\,\, \left. \left. +\frac{\cos ^{2}\theta }{2}\left( S_{18}+S_{19} \right) \right] \right\} , \end{aligned}$$
(52)
$$\begin{aligned}& S_{14}=\log \left( \frac{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta +\omega _{0p} \right) +1}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta -\omega _{0p} \right) +1} \right) , \end{aligned}$$
(53)
$$\begin{aligned}& S_{15}=-\frac{\left( \rho ^{2}+1 \right) ^{2}}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta -\omega _{0p} \right) +1}+\frac{\left( \rho ^{2}+1 \right) ^{2}}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta +\omega _{0p} \right) +1}, \end{aligned}$$
(54)
$$\begin{aligned}& S_{16}=\frac{\rho ^{2}\sin {2\left( \theta +\omega _{0p} \right) }}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta +\omega _{0p} \right) +1}-\frac{\rho ^{2}\sin {2\left( \theta -\omega _{0p} \right) }}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta -\omega _{0p} \right) +1}-2\omega _{0p}, \end{aligned}$$
(55)
$$\begin{aligned}& S_{17}=\frac{\rho ^{4}+1}{\rho ^{4}-1}\left[ \hbox {atan }\left( \frac{\left( 1-\rho ^{2} \right) \sin {2\left( \theta -\omega _{0p} \right) }}{2\left( \rho ^{2}+1 \right) \cos \left( \theta -\omega _{0p} \right) ^{2}} \right) -\hbox {atan }\left( \frac{\left( 1-\rho ^{2} \right) \sin {2\left( \theta +\omega _{0p} \right) }}{2\left( \rho ^{2}+1 \right) \cos \left( \theta +\omega _{0p} \right) ^{2}} \right) \right] , \end{aligned}$$
(56)
$$\begin{aligned}& S_{18}=\log \left( \frac{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta -\omega _{0p} \right) +1}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta +\omega _{0p} \right) +1} \right) , \end{aligned}$$
(57)
$$\begin{aligned}& S_{19}=\frac{\left( \rho ^{2}-1 \right) ^{2}}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta -\omega _{0p} \right) +1}-\frac{\left( \rho ^{2}-1 \right) ^{2}}{\rho ^{4}+2\rho ^{2}\mathrm {cos}2\left( \theta +\omega _{0p} \right) +1}. \end{aligned}$$
(58)

As a consequence of the grouping chosen to integrate, sinusoidal and parabolic distributions imply computational problems when \(\rho =0\). However, this issue may be overcome by solving the limit of stress expressions when \(\rho \rightarrow 0\) or taking \(\rho =0\) before integration. Due to its simplicity, this second method has been selected, leading to Eqs. (59)–(64):

Sinusoidal distribution at the centre of the disk

$$\begin{aligned}& \sigma _{\rho _{s0}}=\frac{P}{\pi Rt\left[ \sin \left( \omega _{0} \right) -\omega _{0}\cos \left( \omega _{0} \right) \right] } \left[ \omega _{0}\cos \left( \omega _{0} \right) -\sin \left( \omega _{0} \right) -2\cos \left( 2\theta \right) \cos \left( \omega _{0} \right) ^{2}\mathrm {sin}(\omega _{0})\right. \nonumber \\&\qquad \,\,\, \left. +\frac{2}{3}\sin \left( \omega _{0} \right) \cos \left( 2\theta \right) \left( 2\cos {\left( \omega _{0} \right) ^{2}+1} \right) \right] , \end{aligned}$$
(59)
$$\begin{aligned}& \sigma _{\theta _{s0}}= \frac{P}{\pi Rt\left[ \sin \left( \omega _{0} \right) -\omega _{0}\cos \left( \omega _{0} \right) \right] }\left[ {\upomega }_{\mathrm {0}}\cos \left( {\upomega }_{\mathrm {0}} \right) \mathrm {-}\sin \left( {\upomega }_{\mathrm {0}} \right) \mathrm {-}\frac{\mathrm {2}}{\mathrm {3}}\cos \left( \mathrm {2}\uptheta \right) \sin \left( {\upomega }_{\mathrm {0}} \right) \mathrm {(2}\cos \left( {\upomega }_{\mathrm {0}} \right) ^{\mathrm {2}}\mathrm {+1)}\right. \nonumber \\&\qquad \,\,\, \left. +2\cos \left( {\upomega }_{\mathrm {0}} \right) ^{\mathrm {2}}\sin \left( {\upomega }_{\mathrm {0}} \right) \mathrm {cos}(2\uptheta ) \right] , \end{aligned}$$
(60)
$$\begin{aligned}& \tau _{\rho \theta _{s0}}=\frac{-\,4P\sin \left( 2\theta \right) \sin \left( \omega _{0} \right) ^{3}}{3\pi Rt\left[ \sin \left( \omega _{0} \right) -\omega _{0}\cos \left( \omega _{0} \right) \right] }. \end{aligned}$$
(61)

Parabolic distribution at the centre of the disk

$$\begin{aligned}& \sigma _{\rho _{p0}}=\sqrt{\frac{3P}{32K_{rig}Rt}} \left\{ \frac{2\omega _{0p}-\mathrm {sin}(2\omega _{0p})+2\hbox {cos}\left( 2\theta \right) \left[ \omega _{0p}-\sin \left( 2\omega _{0p} \right) +\frac{1}{4}\sin \left( 4\omega _{0p} \right) \right] }{2\hbox {sin}\left( \omega _{0} \right) ^{2}} \right. \nonumber \\&\qquad \,\,\, \left. -2\omega _{0}+2\mathrm {cos}(2\theta )\mathrm {sin}(2\omega _{0p}) \right\} , \end{aligned}$$
(62)
$$\begin{aligned}& \sigma _{\theta _{p0}}=\sqrt{\frac{3P}{32K_{rig}Rt}} \left\{ \frac{\omega _{0p}-\mathrm {sin}(2\omega _{0p})-\mathrm {cos}(2\theta )\left[ \omega _{0p}-\sin \left( 2\omega _{0p} \right) +\frac{1}{4}\mathrm {sin}(4\omega _{0p}) \right] }{\sin \left( \omega _{0p} \right) ^{2}}\right. \nonumber \\&\left. \qquad \,\,\, -2\omega _{0}-2\mathrm {cos}(2\theta )\,\mathrm {sin}(2\omega _{0p}) \right\} , \end{aligned}$$
(63)
$$\begin{aligned}& \tau _{\rho \theta _{p0}}= \sqrt{\frac{3P}{32K_{rig}Rt}} \frac{\mathrm {sin}(2\theta )\left[ \sin \left( 4\omega _{0p} \right) -4\omega _{0p} \right] }{4\sin \left( \omega _{0p} \right) ^{2}}. \end{aligned}$$
(64)

Other points where formulation leads to computational problems are along the periphery of the disk, because \(\rho =1\), therefore \(B=1\) and the denominator of some of the summands vanishes. However, this problem is easily overcome as stresses along the rim actually are the boundary conditions imposed in Eqs. (7) and (8).

Displacement and strain fields can be calculated in closed-form from Eqs. (33)–(36) applying the general laws of elasticity [11]. In addition, they can be solved numerically to all distributions; however, it was not carried out in order to avoid overloading this text.

2.4 Numerical cases

Despite the fact that analytic solutions cannot always be obtained (as in spline and new cosine distributions), numerical techniques can be used to determine the stress state in the disk, with the advantage of the error committed in the stress value being that of the numerical method used. That allows the error to remain below \({10}^{-6}\), which can even be accepted as exact solutions for engineering purposes. This is especially useful for simulation software as there is no influence on the type or number of elements. Furthermore, it is worth highlighting that circular distribution obtained after solving the contact problem [19] can also be addressed by using this technique, whereas no solution can be reached through complex potentials theory.

3 Results

The objective of this text is not to establish the real shape of the stress distribution generated along the contact between the sample and the jaw during the Brazilian test; however, once it is known this method can be employed in order to obtain its stress field. The proposed approach can also be used to analyse differences among any distributions, whatever they may be. In order to determine the influences that stress boundary conditions impose in the stress field inside the disk, a comparison between stress components in the whole disk is carried out.

Depending on the stress function considered along the boundary, integrals may not lead to analytical expressions. Nevertheless, numerical techniques can always be used to solve the problem. In that sense, no more than one integral is needed to obtain the strain or stress field, so the error can be accurately bounded, proving the method generates precise results with a handy implementation.

A detailed comparison of radial stresses along the loaded rim on each load distribution (Fig. 3) shows that spline and new cosine distributions are expected to generate higher compressions in the vicinity of the load application area and the vertical diameter as a consequence of their shape, even though uniformly distributed load will generate higher hoop and shear stresses at the edges of the contact between the bodies.

Fig. 3
figure 3

Stresses along the contact for different load distributions

Full size image

In order to determine the consequences of these assumptions over the stress field in the whole of the disk, both qualitative and quantitative comparisons between different load distributions and their variations will be carried out. Stress fields within the sample are obtained for the same total applied load, contact angle and for the same sample in uniform, sinusoidal, spline and new cosine distributions are plotted and discussed. Furthermore, a detailed analysis is carried out at the vertical and horizontal radii for being two sets of points of relevant interest in the Brazilian test. As parabolic distribution leads to similar results as the sinusoidal [17], it will not be considered to avoid overloading the present text. Finally, special attention is given to the centre of the sample, for being the point where tensile strength for brittle materials is determined, in order to evaluate how the shape of the distribution and the contact angle influence the stress state at this point. All calculus needed have been obtained by using a group of algorithms implemented in MATLAB.

3.1 Stress field in the whole of the disk

In order to determine how different loading conditions can influence the stress state in the whole of the disk, stress fields for each component and distribution have been compared. First, all stress fields are depicted for each component and normalised to the maximum value (either tensile or compressive) that is always reached in the radial and hoop stress components of the new cosine distribution. Secondly, a detailed analysis is carried out along the vertical and horizontal radii because of their relevance in the Brazilian test. All figures represent normalised stress components for a contact angle of \(30^{{\mathrm{o}}}\) , that is to say \(\omega _{0}=15^{{\mathrm{o}}}\).

3.1.1 \(\mathbf {\sigma }_{\mathbf {\rho }}\) field

Figure 4 shows that the radial component vanishes more progressively in the case of non-smooth distributions (especially for uniformly distributed compressions) as higher normalised stress values are reached along the vertical axis and through wider angles. All distributions imply a tensile area in the vicinity of the centre of the sample, its influence is more relevant in the case of non-smooth transitions, as it is a higher ratio between its maximum tensile and compressive stresses. Further, uniformly distributed compressions generate a more homogeneous stress state inside the disk, as its normalised radial stress vanishes more progressively inside the sample, except in the vicinity of the contact along the angular directions, where smooth distributions ease the transition from the loaded to the unloaded area.

Smooth transition distributions tend to concentrate the stresses over the vertical diameter, leading to relative stress differences up to 25% against sinusoidal distribution (Fig. 4b–d).

Fig. 4
figure 4

Normalised radial stress components in uniform (a), sinusoidal (b), spline (c) and new cosine (d) distributions

Full size image

3.1.2 \(\mathbf {\sigma }_{\mathbf {\theta }}\) field

Hoop stress shows qualitative differences in the proximity of the loaded arc, especially between uniformly distributed compressions and spline or new cosine distributions, which in fact are almost identical (Fig. 5). In similar fashion to the radial component, maximum normalised stresses are generated along wider angles in uniform and sinusoidal distributions, which also show higher normalised tensile stresses. Areas related to tensile stresses are very similar in all distributions, however, compressions in the vicinity of the contact show different behaviours in the case of uniformly distributed load, where two bulbs are generated in the area of high compressions, disturbing the smoother progression seen in sinusoidal, spline and new cosine.

Only high differences, in orders of magnitude between 30% and 50%, can be appreciated in the vicinity of the contact area. This phenomenon is also noticed between non-smooth and smooth transitions (Fig. 12); therefore, smoothness in the load distribution does not seem to be significant in the hoop stress field. Finally, only variations up to 7% in stress values are developed between spline and new cosine distributions in the immediate vicinities of the contact area (Fig. 5c, d), making the differences neglectable for most practical purposes.

Fig. 5
figure 5

Normalised hoop stress components in uniform (a), sinusoidal (b), spline (c) and new cosine (d) distributions

Full size image

3.1.3 \(\mathbf {\tau }_{\mathbf {\rho \theta }}\) field

Shear stresses are positive in the first and third quadrant and negative in the second and forth, that is to say that they point in the same direction but with opposing senses. However, to ease its graphical representation, all of them will be considered positive from now on. In addition, the colourmap used in Fig. 6 has been rescaled to optimise the shear stress field visualisation. Therefore, straight comparison among colours in Figs. 4, 5 and 6 cannot be done, but the normalised stress values indicate that maximum shear stresses are around 20% of those of radial component for non-smooth distributions and 25% for smooth ones.

Figure 6 shows that high shear stresses are developed near the periphery of the disk and they propagate to the centre vanishing in angular directions. Vertical and horizontal diameters are principal directions in all distributions, as shear stresses vanish in these sets of points. However, a shearing area is generated in the proximities of the centre of the sample, phenomenon that is reduced by smooth transitions in a significant manner. Thus, shear field is clearly influenced by the restriction of smoothness in the load distribution. In fact, the higher the smoothness, the larger the difference.

Non-smooth transitions impose higher stress values at the limits of the contact angle; however, smooth distributions generate higher compressive shear bulbs in the vicinity of the vertical diameter. Values do not differ significantly from one distribution to the other, specially between smooth transition distributions (Fig. 6c, d). Recent investigations show the influence of the stress state in this area over the point where the failure is initiated [22, 23], so this phenomenon could influence the mechanical strength of the sample as it modifies the stress field in the vicinity of the loading area.

Fig. 6
figure 6

Normalised shear stress components in uniform (a), sinusoidal (b), spline (c) and new cosine (d) distributions

Full size image

3.2 Differences among distributions

The differences among distributions can be considered as the error committed in the stress field depending on the selected distribution. Comparison is established among radial and hoop components along vertical and horizontal radii for all considered distributions.

3.2.1 Vertical radius

Radial stress distribution is clearly influenced in the vertical diameter. As the same load is applied over the same contact angle, smooth transitions reach higher values along the vertical axis. Especially significant is the difference among uniformly distributed and smooth transitions (spline and new cosine), where up to 50% of error is committed (Fig. 7). These results are in great agreement with the stress distribution comparison along the boundary (Fig. 3).

Fig. 7
figure 7

Normalised radial stress components in uniform, sinusoidal, spline and new cosine distributions along the vertical radius

Full size image

Uniformly distributed compressions generate the higher hoop stress field along the vertical radius, whereas \(\rho <0.90\) (Fig. 8). From that point onwards, smooth distributions show a quick stress increment with respect to the uniform case, reaching values twice as high in the area near the contact. Even though differences in hoop stresses between smooth distributions are neglectable for practical purposes (Fig. 8).

Fig. 8
figure 8

Normalised hoop stress components in uniform, sinusoidal, spline and new cosine distributions along the vertical radius

Full size image

It is worth to highlight that for values of \(\rho <0.5\) no relevant difference in the stress state along the vertical diameter is shown. However, deviations among distributions arise when the contact angle reaches higher values, as it is explained in Sect. 3.3.

3.2.2 Horizontal radius

Analysing the results of radial (Fig. 9) and hoop (Fig. 10) stress components along the horizontal radius has proven that all distributions predict similar values. In that sense, any distribution can be used without far-reaching effects on the stress field at this set of points.

Fig. 9
figure 9

Normalised radial stress components in uniform, sinusoidal, spline and new cosine distributions along the horizontal radius

Full size image
Fig. 10
figure 10

Normalised hoop stress components in uniform, sinusoidal, spline and new cosine distributions along the horizontal radius

Full size image

3.3 Stresses at the centre

All distributions considered accept closed-form analytical solutions at the centre point of the disk, broadening the application of the method to obtain partial analytical solutions for a certain set of points that may be of interest, even when it is not possible for the whole of the disk. In this case, stresses at the vertical diameter are considered. Subindex in Eqs. (65)–(72) means the analytic expressions are referred to the centre of the disk.

Uniform

$$\begin{aligned} \sigma _{\rho _{u0}}= & {} \frac{-P}{\pi Rt\omega _{0}}\left[ \mathrm {sin}\,(2\omega _{0})+\omega _{0} \right] , \end{aligned}$$
(65)
$$\begin{aligned} \sigma _{\theta _{u0}}= & {} \frac{P}{\pi Rt\omega _{0}}\left[ \mathrm {sin}\,(2\omega _{0})-\omega _{0} \right] . \end{aligned}$$
(66)

From Eqs. (40) and (41) further verifications can be developed. If small loading angles are considered, then \(\sin {\omega _{0}\sim \omega _{0}}\) and \(\sigma _{\rho }=-{3\sigma }_{\theta }\). On the other hand, if \(\omega _{0}=\frac{\pi }{2}\), which means biaxial stress state, then \(\sigma _{\rho }=\sigma _{\theta }\). In addition, shear stresses vanish along the vertical and horizontal diameters, which are in fact principal directions. These results are in great agreement with previous literature [8,9,10,11].

Sinusoidal

$$\begin{aligned} \sigma _{\rho _{s0}}= & {} \frac{P\left[ 2\cos \left( \omega _{0} \right) ^{2}\sin \left( \omega _{0} \right) -5\sin \left( \omega _{0} \right) +3\omega _{0}\mathrm {cos}(\omega _{0}) \right] }{3\pi Rt\left[ \sin \left( \omega _{0} \right) -\omega _{0}\mathrm {cos}(\omega _{0}) \right] }, \end{aligned}$$
(67)
$$\begin{aligned} \sigma _{\theta _{s0}}= & {} -\frac{P\left[ \sin \left( \omega _{0} \right) +2\cos \left( \omega _{0} \right) ^{2}\sin \left( \omega _{0} \right) -3\omega _{0}\cos \left( \omega _{0} \right) \right] }{3\pi Rt\left[ \sin \left( \omega _{0} \right) -\omega _{0}\cos \left( \omega _{0} \right) \right] }. \end{aligned}$$
(68)

Spline

$$\begin{aligned} \sigma _{{\rho }_{sp0}}= & {} -\frac{P\left[ \mathrm {45}\sin \left( 2\omega _{0} \right) -90\omega _{0}\cos \left( 2\omega _{0} \right) -60\omega _{0}^{2}\sin \left( 2\omega _{0} \right) +16\omega _{0}^{5} \right] }{16\pi Rt\omega _{0}^{5}}, \end{aligned}$$
(69)
$$\begin{aligned} \sigma _{\theta _{sp0}}= & {} -\frac{P\left[ 90\omega _{0}\cos \left( 2\omega _{0} \right) -45\sin \left( 2\omega _{0} \right) +60\omega _{0}^{2}\sin {\left( 2\omega _{0} \right) +16\omega _{0}^{5}} \right] }{16\pi Rt\omega _{0}^{5}}. \end{aligned}$$
(70)

New cosine

$$\begin{aligned} \sigma _{\rho _{nc0}}= & {} \frac{P\left( \pi ^{2}-\omega _{0}^{2} \right) }{4\pi ^{3}Rt\mathrm {sin}\left( \omega _{0} \right) }\left[ \frac{4\pi ^{2}\cos \left( 2\theta \right) \sin \left( 2\omega _{0} \right) }{-4\omega _{0}^{2}+\pi ^{2}}-4\omega _{0} \right] , \end{aligned}$$
(71)
$$\begin{aligned} \sigma _{\theta _{nc0}}= & {} \frac{P\left( \pi ^{2}-\omega _{0}^{2} \right) }{4\pi ^{3}Rt\mathrm {sin}\left( \omega _{0} \right) }\left[ -\frac{4\pi ^{2}\mathrm {cos}(2\theta )\mathrm {sin}(2\omega _{0})}{-4\omega _{0}^{2}+\pi ^{2}}-4\omega _{0} \right] . \end{aligned}$$
(72)

In order to evaluate Eqs. (65)–(72), the comparison between values predicted by concentrated load on radial (Fig. 11) and hoop (Fig. 12) stress components for each distribution has been carried out. Contact semi-angles between \(0^{{\mathrm{o}}}\) and \(90^{{\mathrm{o}}}\) have been considered in order to check the differences as \(\omega _{0}\) increases. Nevertheless, this calculus has been carried out only with comparison purposes, since the Brazilian test is recommended for small contact angles [3, 4].

The results show that all distributions suffer a deviation from the values predicted by the concentrated load, which increases when the contact semi-angle also increases (Figs. 11, 12). Hoop stress deviates steeper than radial stress, so the threshold angle where the error is neglectable varies from \(15^{{\mathrm{o}}}\) to 25º  depending on the component of interest in the uniformly distributed compression case, which is the distribution with the higher deviation respect to the concentrated load. Even though it is neglectable in values up to 15º  for all components and distributions, it has to be taken into account that there is always some uncertainty in the measure as a result of the elastic contact between the solids. This threshold value has been selected to maintain the deviation in hoop component below 10%, whatever the distribution selected is. Furthermore, for large values of \(\omega _{0}\) no tensile stress is located at the centre for uniform, sinusoidal and spline distributions as \(\sigma _{\theta }\) goes from positive to negative for a threshold contact semi-angle depending on the distribution shape, but always distant from the technical recommendations of the test [3, 4]. Special attention should be given to new cosine distribution which always generates a tensile stress in the centre of the disk.

As a consequence of the change from tensile to compressive hoop stress when the contact angle increases, the relation between stresses at the centre, which is accepted to be three [9], is actually discontinued for large values of \(\omega _{0}\) in uniform, sinusoidal and spline distributions. Although the Brazilian Test is recommended for small contact angles [3, 4], it must be highlighted that the more ductile the sample the more tendency to deviate from the concentrated solution. As an example, for uniformly distributed compressions, which is the most extended formulation, along a contact angle of \(60^{{\mathrm{o}}}\) (\(\omega _{0}=30^{\mathrm{o}})\), the deviation committed is 12% and 35% in radial and hoop stresses, respectively, which implies that stress relation at the centre of the disk \(\sigma _{\rho _{u0}}/\sigma _{\theta _{u0}}\) equals minus four instead of minus three. This leads to the fact that the stress relation at the centre of the sample has increased from minus three to slightly under minus four. For the threshold value of \(15^{{\mathrm{o}}}\) , the relation deviation is 7% for uniformly distributed compressions. This deviation is lower in the case of any other distribution, as the deviation from the concentrated case is not so pronounced (Figs. 11, 12).

Fig. 11
figure 11

Radial stress deviation from the concentrated case

Full size image
Fig. 12
figure 12

Hoop stress deviation from the concentrated case

Full size image

This is in agreement with Markides and Kourkoulis conclusions of the influence of jaw curvature in the stress state of the sample for the parabolic distribution case [21]. So, the present paper clarifies the influence of other types of distributions considered. It also worth to notice that dividing related expressions in Eqs. (65)–(72) and making \(\omega _{0}\rightarrow 0\), same results as in the concentrated case are obtained. Thus, any load application in an elastic body will introduce disturbances in the stress values as a result of deformation.

4 Conclusions

A method based on exploiting the concentrated load solution to generate stress fields due to arbitrary radial distributions has been exposed. Then, this technique was used to solve the stress field related to two new load distributions (spline and new cosine). Contrast of closed-form solution for uniformly distributed compressions along the boundary with accepted formulation has proved the validity of the method. When the complete integral cannot be solved, it even may be possible to obtain closed-form solutions for certain sets of points as follows: the centre of the sample, a given circumference inside the disk or a specific radius. Not only analytical but also numerical solutions can be obtained. In addition, only one integral is needed to determine each stress field component, so the error committed is bounded and known for being that of the numerical method used, leading to high accurate results. Even though concentrated load is referred to the contact case between two solids with infinite stiffness, the method highlights the importance of its formulation as it can be used to generate the stress field due to any radial load distribution along the boundary.

The study of stress state in the centre of the disk revealed that the accepted relation \(\sigma _{\rho }=-3\sigma _{\theta }\) is only valid for concentrated load, being acceptable for contact angles under \(15^{\circ }\) as the error induced is below 7%. Higher contact angles would imply deviations above 10% in hoop stress in the case of uniformly distributed compressions. However, different stress distributions along the boundary deviate in a different manner from this behaviour. Uniformly distributed stresses along the boundary induce the higher deviation, so they are not suitable for soft materials, as deformation induces larger values of \(\omega _{0}\). Uncertainty in stress values at the centre of the disk is a function of the contact angle whatever the imposed distribution may be, with the exception of the concentrated case that it is not reachable through experiments.

The radial stress field is strongly influenced by the shape of the distribution, especially in the vicinity of the load application area. This phenomenon slightly shows in hoop stresses, where significant deviations from one distribution to the other are reached in the area near the contact and the vertical axis. In addition, shear field differences are both qualitatively and quantitatively remarkable.

It should also be highlighted that the present method is applicable to radial load distributions and neglects shear stresses along the boundary for being based on concentrated radial loads acting along a diameter. However, shear stresses along the boundary should be considered depending on the practical application under interest. In that sense, it is worth to mention that friction will be influenced by the relative stiffness of the materials involved and the geometry of both the sample and the jaw. These two variables will determine the length of the loaded arc and the shape of the shear distribution along the boundary [19, 20]. Its influence is especially relevant in the area near the contact [20, 37, 38]. For that reason, failures initiated far from the centre of the disk should be carefully analysed and no tensile strength can be determined straightforward from laboratory results. The stress field generated by any shear distribution along the boundary is part of further investigation lines being developed by the authors.

The circular stress distribution, which is considered as the real one [19, 20], but cannot be solved in closed-form; however, its stress field can be numerically determined with high accuracy by using the technique shown in this paper. This method will even allow to determine the true failure initiation point [22, 23]. Accurate results plus a quick implementation make the method especially interesting for engineering applications. Finally, strain and displacement fields can be obtained through this method, therefore all the elastic fields of interest can be determined.