The Stress Field in a Standardized Brazilian Disc: The Influence of the Loading Type Acting on the Actual Contact Length

Abstract

The aim of the present study was to determine the stress field developed in a Brazilian disc under conditions closely approaching those of the actual test executed according to the standardized procedure suggested by the International Society for Rock Mechanics. Advantage is taken of a recently introduced analytic solution for a mixed fundamental contact problem where the disc and the jaw are considered as a system of two interacting elastic bodies. Using the outcomes of that study, the complex potentials method is employed here for the solution of a first fundamental problem for a Brazilian disc under a parabolic load distribution. Analytic full-field formulae for the components of the stress field developed in the disc are given. The solution is then applied for the case of a disc made from Dionysos marble. The results are compared to existing ones obtained from solutions adopting statically equivalent loads either in the form of distributed (uniform or sinusoidally) radial pressure acting along the actual contact rim or in the form of diametrically acting point (line) loads. While the stress field in the major part of the disc seems to be rather insensitive to the exact load application mode, critical differences are detected in the vicinity of the loaded arc of the disc. The solution is assessed according to the results of a short series of Brazilian disc tests with PMMA specimens. The agreement between theoretical predictions and experimental data is satisfactory. Finally, it is indicated that, as opposed to previous solutions, the stress field (even at the disc’s center) is a non-linear function of the externally applied load depending, among others, indirectly on the properties of the disc’s and jaw’s materials, the combination of which dictates the extent of the contact angle.

1 Introduction

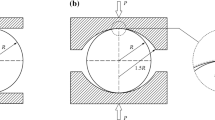
For the standardized execution of the Brazilian disc test, the International Society for Rock Mechanics (ISRM) proposed a “suggested” method based on the apparatus shown in Fig. 1 (ISRM 1988). It consists of two metallic jaws of curvature radius R ₂ equal to 1.5R ₁, where R ₁ is the disc’s radius. It is evident that if the own weight of the upper jaw is ignored, contact between specimen and jaw is realized along a mathematical line, i.e., the common generatrix of the cylindrical surfaces. Assuming now that the external load, applied by the loading frame on the upper jaw, increases gradually (and taking into account the inevitable deformability of both the jaw and the disc), the contact is realized along a curved surface, the projection on the disc’s cross section of which is a finite arc symmetric with respect to the vertical axis of symmetry of the arrangement.

Fig. 1

Vertical section of the ISRM suggested device for the standardized realization of the Brazilian disc test and the respective mathematical problem configuration

Existing analytic solutions for the stress field developed in the disc do not take into account this gradual change of the contact length considering either a point (line) load (Muskhelishvili 1963; Jianhong et al. 2009; Stefanizzi et al. 2009) or uniform radial pressure acting along an arc of arbitrarily predefined length (Hondros 1959; Markides et al. 2010). Although such approaches are rather rough approximations of reality, they are widely used for practical purposes. This is because it is generally accepted that the exact conditions in the immediate vicinity of the jaws–specimen interface do not seriously influence the stress field at the center of the disc. Unfortunately, this is not the case in the immediate vicinity of the load application area. Here, the local stress field is critically influenced not only by the magnitude of the contact length, but also by the exact distribution of the radial pressure and friction (Lavrov and Vervoort 2002; Markides et al. 2011), which vary according to the relative deformability of the jaws and the specimen.

In a recent study, shortly recapitulated is Sect. 2 (Kourkoulis et al. 2011), the mixed fundamental contact problem of two elastic bodies (corresponding to the disc and the jaw of the ISRM suggested device) was considered. Analytic formulae were obtained both for the actual length of the contact rim (in terms of R ₁ and R ₂, the elastic properties of the specimen’s and jaw’s materials and the load imposed), as well as for the exact variation of the radial pressure along this rim. Following the results of that study, an attempt is described here to obtain closed form expressions for the stress field developed in a circular disc under the influence of a radial pressure distribution closely resembling the form obtained by Kourkoulis et al. (2011) and acting along the actual contact length, as it is dictated by the geometry and the material properties. This configuration corresponds to a first fundamental problem of classic linear elasticity and is here solved using the complex potentials method introduced by Muskhelishvili (1963). The stress field obtained is considered in juxtaposition with existing ones, which ignore the actual loading and contact conditions at the jaw–disc interface. The cases comparatively considered include the diametral point load and the uniform and sinusoidal distributions of the radial pressure along the actual contact length (always assuming static equivalence between the overall loads). It is again concluded that at the disc’s center, the stress field is not very sensitive to the exact load application mode. However, according to the present solution, even at the center of the disc the stresses depend indirectly on the elastic properties of the disc’s and jaw’s materials (which define the contact angle) and vary non-linearly versus the load applied. As the loaded rim is approached, the situation changes dramatically and erroneous conclusions may be drawn in case the actual loading type is not taken into account.

2 The Standardized Brazilian Disc Test As a Contact Problem (Kourkoulis et al. 2011)

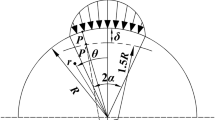
Following Muskhelishvili’s (1963) approach for the respective Hertz plane problem, consider the disc and jaw of the ISRM Brazilian test device as elastic bodies in frictionless contact. The respective mathematical regions S _j , j = 1, 2 lie in the complex plane z = x + iy (Fig. 1). Due to the load, P _o, parts (−ℓ, +ℓ) of their boundaries L _j , j = 1, 2 come in contact and the common arc after contact is realized is denoted as (−L, +L). A Cartesian system is introduced (Fig. 1) and τ denotes both point x and its abscissa. The contact length and the variation P(τ) of the contact stresses are to be determined. The following hold:

$$ \sigma_{{xy_{j} }}^{ \mp } = 0,\quad j = 1,2{\text{ on the entire }}x{\text{-axis}},{\text{i}}.{\text{e}}.{\text{ on }}L_{1} ,L_{2} , $$

(1)

$$ \sigma_{{yy_{j} }}^{ \mp } = 0,\quad j = 1,2{\text{ on }}x{\text{-axis except }}( - \ell , + \ell ) $$

(2)

$$ \sigma_{{yy_{j} }}^{ \mp } = - P(\tau ),\quad j = 1,2{\text{ along }}( - \ell , + \ell ).$$

(3)

Signs (−), (+) refer to boundary values for z tending to τ on x-axis from the lower and upper half-planes, respectively. With f(τ) = f ₂(τ) − f ₁(τ), f _j (τ), j = 1, 2 the equations of L _j before deformation and for small deformations, it can be seen that:

$$ v_{1}^{ - \prime } - v_{2}^{ + \prime } = f^{\prime } (\tau )\quad {\text{on }}( - \ell , + \ell ) $$

(4)

For the above boundary values and given the resultant force P _o (i.e., the overall external load P _dev normalized over the thickness w), a mixed fundamental plane problem is obtained. According to Muskhelishvili (1963), the solution consists in the determination of a single analytic function Φ _j (z), j = 1, 2, in terms of which stresses and displacements are expressed as:

$$ \sigma_{{yy_{j} }} - {\text{i}}\sigma_{{xy_{j} }} = \Upphi_{j} (z) - \Upphi_{j} \left( {\overline{z} } \right) + \left( {z - \overline{z} } \right)\overline{{\Upphi_{j}^{\prime } }} \left( {\overline{z} } \right),\quad j = 1,2 $$

(5)

$$ 2\mu_{j} \left( {u_{j}^{\prime } + {\text{i}}v_{j}^{\prime } } \right) = \kappa_{j} \Upphi_{j} (z) + \Upphi_{j} \left( {\overline{z} } \right) - \left( {z - \overline{z} } \right)\overline{{\Upphi_{j}^{\prime } }} \left( {\overline{z} } \right),\quad j = 1,2 $$

(6)

$$ 2\mu_{j} \left( {u_{j} + {\text{i}}v_{j} } \right) = \kappa_{j} \varphi_{j} (z) + \varphi_{j} \left( {\overline{z} } \right) - \left( {z - \overline{z} } \right)\overline{{\varphi_{j}^{\prime } }} \left( {\overline{z} } \right) + C,\quad j = 1,2 $$

(7)

C expresses rigid body displacements. Over-bar denotes complex conjugate values. κ _j , μ _j , j = 1, 2 are Muskhelishvili’s constants and shear moduli, respectively. Equations (1–7) for j = 1 yield:

$$ \Upphi_{1}^{ + } \left( \tau \right) + \Upphi_{1}^{ - } \left( \tau \right) = {\text{i}}f^{\prime } (\tau )/K{\text{ with }}K = (\kappa_{1} + 1)/4\mu_{1} + (\kappa_{2} + 1)/4\mu_{2} $$

(8)

Using function $\sqrt {\ell^{2} - z^{2} } = - {\text{i}}X(z)$ (where $X(z) = \sqrt {z^{2} - \ell^{2} }$ is a particular solution of $\Upphi_{1}^{ + } \left( \tau \right) + \Upphi_{1}^{ - } \left( \tau \right) = 0$), and assuming further that Φ₁(z) vanishes at infinity, Eq. (8) yields:

$$ \Upphi_{1} (z) = \frac{1}{{2\pi K\sqrt {\ell^{2} - z^{2} } }}\int\limits_{ - \ell }^{ + \ell } {\frac{{f^{\prime } (\tau )\sqrt {\ell^{2} - \tau^{2} } d\tau }}{\tau - z}} + \frac{{P_{\text{o}} }}{{2\pi \sqrt {\ell^{2} - z^{2} } }} $$

(9)

Using Plemelj formulae and Eqs. (5, 9) for j = 1, z → τ, yields for P(τ_ο) along (−ℓ, +ℓ):

$$ P\left( {\tau_{\text{o}} } \right) = \frac{1}{{\pi K\sqrt {\ell^{2} - \tau_{\text{o}}^{2} } }}\int\limits_{ - \ell }^{ + \ell } {\frac{{f^{\prime } (\tau )\sqrt {\ell^{2} - \tau^{2} } d\tau }}{{\tau - \tau_{o} }}} + \frac{{P_{\text{o}} }}{{\pi \sqrt {\ell^{2} - \tau_{\text{o}}^{2} } }} $$

(10)

For P(τ_ο) to remain bounded at points ±ℓ, Eqs. (9, 10) reduce to (Muskhelishvili 1963):

$$ \Upphi_{1} \left( z \right) = \frac{{\sqrt {\ell^{2} - z^{2} } }}{{2\pi {\rm K}}}\int\limits_{ - \ell }^{ + \ell } {\frac{{f^{\prime } (\tau )d\tau }}{{\left( {\tau - z} \right)\sqrt {\ell^{2} - \tau^{2} } }}} , \, P(\tau_{\text{o}} ) = \frac{{\sqrt {\ell^{2} - \tau_{\text{o}}^{2} } }}{\pi K}\int\limits_{ - \ell }^{ + \ell } {\frac{{f^{\prime } \left( \tau \right)d\tau }}{{\left( {\tau - \tau_{\text{o}} } \right)\sqrt {\ell^{2} - \tau^{2} } }}} $$

(11)

Clearly, P is actually zeroed at τ_ο = ±ℓ. Considering also Eq. (10), the following is obtained for ℓ:

$$ \int\limits_{ - \ell }^{ + \ell } {\frac{{f^{\prime } (\tau ){\text{d}}\tau }}{{\sqrt {\ell^{2} - \tau^{2} } }}} = 0,\int\limits_{ - \ell }^{ + \ell } {\frac{{f^{\prime } (\tau )\tau {\text{d}}\tau }}{{\sqrt {\ell^{2} - \tau^{2} } }}} = KP_{\text{o}} $$

(12)

Following Muskhelishvili (1963), the equal facing arcs (–ℓ, +ℓ) (before load is applied) that come into contact are considered (in their undeformed state) as parts of two parabolas, which at the vertex O have the same curvatures as the respective circular arcs and f _j (τ) = −(τ²/2R _j ). R _j , j = 1, 2 are the disc’s and jaw’s radii, respectively. Then Eqs. (12) reduce to a single condition for ℓ:

$$ \int\limits_{0}^{ + \ell } {\frac{{f^{\prime } (\tau )\tau {\text{d}}\tau }}{{\sqrt {\ell^{2} - \tau^{2} } }}} = \frac{{KP_{\text{o}} }}{2} $$

(13)

For R ₂ = 1.5R ₁, f′(τ) = τ/(3R ₁), the first of Eqs. (11) and (5) yield:

$$ \Upphi_{1} \left( z \right) = \frac{1}{{6R_{1} K}}\left( {\sqrt {\ell^{2} - z^{2} } + {\text{i}}z} \right), \, P(\tau ) = \frac{1}{{3R_{1} K}}\sqrt {\ell^{2} - \tau^{2} } $$

(14)

It is seen that P(τ) corresponds to a circular distribution of radial normal stresses (Fig. 2). Τhe contact length and the contact angle between the disc and the jaw are then obtained as:

$$ 2\ell = 2\sqrt {\frac{{6R_{1} KP_{\text{o}} }}{\pi }} ,\omega_{\text{o}} = \sqrt {\frac{{6KP_{\text{o}} }}{{\pi R_{1} }}}. $$

(15)

Fig. 2

The actual distribution of the radial pressure imposed by the jaw on the disc along the actual contact length (−ℓ, +ℓ)

3 The Stress Field Under Parabolic Radial Pressure Along the Actual Contact Length

3.1 The Problem

Knowing the actual variation of P, and ω_o, one could proceed to the solution of the first fundamental problem for the isolated Brazilian disc, using the method of complex potentials, to obtain the stress field developed in the disc. However for the circular distribution of P, a closed form solution is not possible (see "Appendix I"). Therefore, and within the accuracy considered, an alternative parabolic distribution is introduced (as described in "Appendix II") of the following form:

$$ P(\tau ) = \frac{\pi \ell }{8RK}\left[ {1 - \left( {\frac{\tau }{\ell }} \right)^{2} } \right] $$

(16)

where from now on R will stand for R ₁ (accordingly L will stand for L ₁). Taking now under consideration also the first of Eqs. (15), it follows that:

$$ \int\limits_{ - \ell }^{ + \ell } {\frac{\pi \ell }{8RK}\left[ {1 - \left( {\frac{\tau }{\ell }} \right)^{2} } \right]} {\text{d}}\tau = \int\limits_{ - \ell }^{ + \ell } {\frac{1}{3RK}\sqrt {\ell^{2} - \tau^{2} } } {\text{d}}\tau = P_{\text{o}} $$

(17)

insuring static equivalency between the circular and parabolic distributions (as in Fig. 3). It is emphasized at this point that the parabolic distribution given by Eq. (16) not only constitutes an efficient (from the point of view of reducing mathematical complexities) substitute of that given by the second of Eqs. (14), but perhaps it also approaches reality better: Indeed, the cyclic distribution of P has been obtained for an approximately straight contact segment (−ℓ, +ℓ) (Kourkoulis et al. 2011). It appears therefore that for an initially circular contact region (−ℓ, +ℓ), a parabolic distribution (of slightly increased intensity at the vertex and of slightly reduced intensity toward the end points of the loaded rim) is more reasonable compared to a perfectly circular one. The maximum value of the parabolic distribution is attained at the vertex point O (for τ = 0 in the Oxy Cartesian reference, Fig. 3), as:

$$ P_{\text{c}} = \frac{\pi \ell }{8RK} $$

(18)

Fig. 3

The actual (cyclic) distribution of the radial pressure in juxtaposition to the alternative one (parabolic) adopted in the present study

This value exceeds the respective one of the circular distribution P _c = ℓ/(3RK) by about 15%. Considering a Cartesian reference system with its origin at the center of the disc and taking into account that ω_o is very small (especially for brittle geomaterials tested using the ISRM device), the arcs τ, ℓ can be approximated by the respective straight segments τ′, ℓ′ (Fig. 4) as:

$$ \ell \approx \ell ^{\prime } = R\sin \omega _{o} ,\tau \approx \tau ^{\prime } = R\cos \vartheta $$

(19)

Fig. 4

The parabolic distribution along the loaded rim and further simplifying assumptions. The maximum value of the parabolic distribution in terms of P _o

Accordingly, ω_o of Eqs. (15) becomes:

$$ \omega_{\text{o}} = {\text{Arc}}\;{ \sin }\sqrt {\frac{{6KP_{\text{o}} }}{\pi R}} , $$

(20)

while P _c, from Eq. (18), is written as:

$$ P_{\text{c}} = \sqrt {\frac{{3\pi P_{\text{o}} }}{32KR}} $$

(21)

In the Cartesian reference introduced (Fig. 4), the end points ±ℓ of the loaded rim are denoted as t _j , j = 1, 2. Introducing Eqs. (18, 19, 21) in Eq. (16) P is written in terms of angle $\vartheta$ as:

$$ P(\vartheta ) = P_{\text{c}} \left( {1 - \frac{{{ \cos }^{2} \vartheta }}{{{ \sin }^{2} \omega_{o} }}} \right), $$

(22)

The boundary conditions for the stresses on the disc periphery L read as:

$$ \sigma_{rr}^{ + } (\vartheta ) = - P(\vartheta ) = - P_{\text{c}} \left( {1 - \frac{{{ \cos }^{2} \vartheta }}{{{ \sin }^{2} \omega_{\text{o}} }}} \right){\text{ on the loaded rims of }}L, $$

(23a)

$$ \sigma_{rr}^{ + } (\vartheta ) = 0{\text{ on the unloaded part of }}L $$

(23b)

Sign (+) indicates boundary values taken on L from the interior of the disc. Thus, one has arrived at a classical first fundamental problem for the intact Brazilian disc for the configuration shown in Fig. 5a.

Fig. 5

The mathematical configuration of the first fundamental problem for the disc and the conformal mapping

3.2 The Complex Potentials

Following Muskhelishvili’s (1963) complex potentials method, the disc is considered in the complex plane $z = r{\text{e}}^{{{\text{i}}\vartheta }}$. The origin of the Cartesian reference has been taken at the disc’s center and y-axis is the symmetry axis of the external load. The arbitrary point z on L is denoted by $t = {\text{Re}}^{{{\text{i}}\vartheta }}$ and t _j j = 1, 2, 3, 4 are the end points of the loaded rims. The problem is first solved for the unit disc in the complex plane $\zeta = \rho {\text{e}}^{{{\text{i}}\vartheta }}$, Fig. 5b. Points t _j of L correspond, through the conformal mapping z = Rζ, to points s _j on the unit circle γ, with $s = {\text{e}}^{{{\text{i}}\vartheta }}$ the arbitrary point ζ on it. In this context, Eqs. (23a, b) are rewritten for γ as:

$$ \sigma_{\rho \rho }^{ + } (\vartheta ) = - P(\vartheta ) = - P_{\text{c}} \left( {1 - \frac{{{ \cos }^{2} \vartheta }}{{{ \sin }^{2} \omega_{\text{o}} }}} \right){\text{ on the loaded rims of }}\gamma , $$

(24a)

$$ \sigma_{\rho \rho }^{ + } (\vartheta ) = 0{\text{ on the unloaded part of }}\gamma $$

(24b)

The complex potentials for the unit disc are written as (Markides et al. 2010, 2011):

$$ \Upphi (\zeta ) = \frac{1}{{2\pi {\text{i}}}}\int\limits_{\gamma } {\frac{{\sigma_{\rho \rho }^{ + } (s)}}{s - \zeta }} {\text{d}}s - \frac{1}{4\pi }\int\limits_{0}^{2\pi } {\sigma_{\rho \rho }^{ + } (\vartheta )} {\text{d}}\vartheta $$

(25)

$$ \Uppsi (\zeta ) = \frac{1}{{\zeta^{2} }}\Upphi (\zeta ) + \frac{1}{{\zeta^{2} }}\overline{\Upphi } \left( {\frac{1}{\zeta }} \right) - \frac{1}{\zeta }\Upphi^{\prime } (\zeta ) $$

(26)

Taking into account that ${ \cos }\vartheta = \left( {s + \overline{s} } \right)/2$, Eq. (24a) can be alternatively written as:

$$ \sigma_{\rho \rho }^{ + } (s) = - P_{\text{c}} \left[ {1 - \frac{1}{{4{ \sin }^{2} \omega_{\text{o}} }}\left( {2 + s^{2} + \frac{1}{{s^{2} }}} \right)} \right] $$

(27)

Combining Eqs. (24a, b, 27) with Eq. (25) provides Φ(ζ) as:

$$ \Upphi (\zeta ) = \frac{{P_{\text{c}} }}{{4\pi {\text{i}}\;{ \sin }^{2} \omega_{\text{o}} }}\left[ {\left( {\frac{{\zeta^{4} + 1}}{{2\zeta^{2} }} + { \cos }2\omega_{\text{o}} } \right)\ell n\frac{{s_{2}^{2} - \zeta^{2} }}{{s_{1}^{2} - \zeta^{2} }} - \left( {\frac{1}{{\zeta^{2} }} + { \cos }2\omega_{\text{o}} } \right)2{\text{i}}\omega_{\text{o}} } \right] $$

(28)

In turn, introducing Φ(ζ) from Eq. (28) in Eq. (26) gives for Ψ(z):

$$ \Uppsi (\zeta ) = \frac{{ - P_{\text{c}} }}{{4\pi {\text{i}}\;{ \sin }^{2} \omega_{\text{o}} }}\left[ {\frac{{\zeta^{4} - 1}}{{\zeta^{4} }}\ell n\frac{{s_{2}^{2} - \zeta^{2} }}{{s_{1}^{2} - \zeta^{2} }} + \left( {\frac{{\zeta^{4} + 1}}{{\zeta^{2} }} + 2{ \cos }2\omega_{\text{o}} } \right)\left( {\frac{1}{{s_{1}^{2} - \zeta^{2} }} - \frac{1}{{s_{2}^{2} - \zeta^{2} }}} \right) + \frac{{4{\text{i}}\omega_{\text{o}} }}{{\zeta^{4} }}} \right] $$

(29)

Reverting to the variable z through the conformal transformations ζ = z/R, s _j  = t _j /R, one obtains the complex potentials of the problem for the real disc of radius R as follows:

$$ \Upphi (z) = \frac{{P_{\text{c}} }}{{4\pi {\text{i}}\;{ \sin }^{2} \omega_{\text{o}} }}\left[ {\left( {\frac{{z^{4} + R^{4} }}{{2R^{2} z^{2} }} + { \cos }2\omega_{\text{o}} } \right) \cdot \ell n\frac{{t_{2}^{2} - z^{2} }}{{t_{1}^{2} - z^{2} }} - \left( {\frac{{R^{2} }}{{z^{2} }} + { \cos }2\omega_{\text{o}} } \right)2{\text{i}}\omega_{\text{o}} } \right] $$

(30)

$$ \begin{aligned} \Uppsi \left( z \right) & = \frac{{ - P_{\text{c}} }}{{4\pi {\text{i}}\;{ \sin }^{2} \omega_{\text{o}} }}\left[ {\frac{{z^{4} - R^{4} }}{{z^{4} }}\ell n\frac{{t_{2}^{2} - z^{2} }}{{t_{1}^{2} - z^{2} }}} \right. \\ & \quad + \left. {\left( {\frac{{z^{4} + R^{4} }}{{z^{2} }} + 2R^{2} { \cos }2\omega_{\text{o}} } \right)\left( {\frac{1}{{t_{1}^{2} - z^{2} }} - \frac{1}{{t_{2}^{2} - z^{2} }}} \right) + \frac{{4{\text{i}}R^{4} \omega_{\text{o}} }}{{z^{4} }}} \right] \\ \end{aligned}. $$

(31)

3.3 The Stress Field

Substitution of Eqs. (30, 31) in the familiar formula (Muskhelishvili 1963):

$$ \sigma_{rr} - {\text{i}}\sigma_{r\vartheta } = 2\Re \Upphi (z) - {\text{e}}^{{2{\text{i}}\vartheta }} \left[ {\overline{z} \Upphi^{\prime } (z) + \Uppsi (z)} \right] $$

(32)

($\Re$ denotes the real part of the function) gives the closed form expressions for the stress components in compact form as:

$$ \begin{aligned} \sigma_{{\begin{subarray} {rr} \\ {\vartheta \vartheta } \\ \end{subarray} }} & = \frac{{P_{\text{c}} }}{{4\pi { \sin }^{2} \omega_{\text{o}} }}\left\{ {\left. {\begin{array}{*{20}c} {\frac{{\left( {R^{2} - r^{2} } \right)^{2} }}{{2r^{4} }}} \\ {\frac{{2r^{6} - R^{6} - r^{4} R^{2} }}{{2r^{4} R^{2} }}} \\ \end{array} } \right\rangle \cdot { \sin }2\vartheta \cdot \ell n\frac{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} - \vartheta } \right)} \right)^{2} }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} + \vartheta } \right)} \right)^{2} }}} \right. \\ & \quad + \left\langle {\begin{array}{*{20}c} { + \frac{{4\omega_{\text{o}} R^{2} \left( {R^{2} - 2r^{2} } \right)}}{{r^{4} }}{ \cos }2\vartheta + \left( {\frac{{r^{4} - R^{4} + 2r^{2} R^{2} }}{{r^{4} }}{ \cos }2\vartheta + 2{ \cos }2\omega_{\text{o}} } \right)} \\ { - \frac{{4\omega_{\text{o}} R^{4} }}{{r^{4} }}{ \cos }2\vartheta + \left( {\frac{{2r^{6} + R^{6} - r^{4} R^{2} }}{{r^{4} R^{2} }}{ \cos }2\vartheta + 2{ \cos }2\omega_{\text{o}} } \right)} \\ \end{array} } \right\rangle \\ & \quad \cdot \left\langle {\begin{array}{*{20}c} {\left. \begin{gathered} 2\pi - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} - r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} + r{ \cos }\vartheta }} - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} + r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} - r{ \cos }\vartheta }} \hfill \\ - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} - r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} - r{ \cos }\vartheta }} - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} + r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} + r{ \cos }\vartheta }} \hfill \\ \end{gathered} \right\}{\text{region}}\;{\text{I}}} \\ {{\text{the same expression without }}2\pi {\text{ region II}}} \\ \end{array} } \right. \\ & \quad \pm \left( {R^{2} - r^{2} } \right)\left[ {\left( {\frac{{r^{2} }}{{R^{2} }}{ \sin }4\vartheta + 2{ \cos }2\omega_{\text{o}} { \sin }2\vartheta } \right)\left( {\frac{{ - R^{2} { \cos }2\omega_{\text{o}} - r^{2} { \cos }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} + \vartheta } \right)} \right)^{2} }}} \right.} \right. \\ & \quad \left. { + \frac{{R^{2} { \cos }2\omega_{\text{o}} + r^{2} { \cos }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} - \vartheta } \right)} \right)^{2} }}} \right) - \left( {\frac{{r^{2} }}{{R^{2} }}{ \cos }4\vartheta + 2{ \cos }2\omega_{\text{o}} { \cos }2\vartheta + \frac{{R^{2} }}{{r^{2} }}} \right) \\ & \quad \left. {\left. { \cdot \left( {\frac{{R^{2} { \sin }2\omega_{\text{o}} - r^{2} { \sin }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} + \vartheta } \right)} \right)^{2} }} + \frac{{R^{2} { \sin }2\omega_{\text{o}} + r^{2} { \sin }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} - \vartheta } \right)} \right)^{2} }}} \right)} \right] - 4\omega_{\text{o}} { \cos }2\omega_{\text{o}} } \right\} \\ \end{aligned} $$

(33)

$$ \begin{aligned} \sigma_{r\vartheta } & = \frac{{P_{\text{c}} \left( {R^{2} - r^{2} } \right)}}{{4\pi { \sin }^{2} \omega_{\text{o}} }}\left[ {\frac{{r^{4} - R^{4} }}{{2r^{4} R^{2} }}{ \cos }2\vartheta \ell n\frac{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} - \vartheta } \right)} \right)^{2} }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} + \vartheta } \right)} \right)^{2} }}} \right. \\ & \quad + \frac{{4\omega_{\text{o}} R^{2} }}{{r^{4} }}{ \sin }2\vartheta - \frac{{r^{4} + R^{4} }}{{r^{4} R^{2} }}{ \sin }2\vartheta \\ & \quad \cdot \left\langle {\begin{array}{*{20}c} {\left. \begin{gathered} 2\pi - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} - r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} + r{ \cos }\vartheta }} - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} + r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} - r{ \cos }\vartheta }} \hfill \\ - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} - r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} - r{ \cos }\vartheta }} - { \tan }^{ - 1} \frac{{R{ \cos }\omega_{\text{o}} + r{ \sin }\vartheta }}{{R{ \sin }\omega_{\text{o}} + r{ \cos }\vartheta }} \hfill \\ \end{gathered} \right\}{\text{region I}}} \\ {{\text{the same expression without }}2\pi {\text{ for region II}}} \\ \end{array} } \right. \\ & \quad + \left( {\frac{{r^{2} }}{{R^{2} }}{ \sin }4\vartheta + 2{ \cos }2\omega_{\text{o}} { \sin }2\vartheta } \right)\left( {\frac{{R^{2} { \sin }2\omega_{\text{o}} - r^{2} { \sin }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} + \vartheta } \right)} \right)^{2} }}} \right. \\ & \quad + \left. {\frac{{R^{2} { \sin }2\omega_{\text{o}} + r^{2} { \sin }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} - \vartheta } \right)} \right)^{2} }}} \right) + \left( {\frac{{r^{2} }}{{R^{2} }}{ \cos }4\vartheta + 2{ \cos }2\omega_{\text{o}} { \cos }2\vartheta + \frac{{R^{2} }}{{r^{2} }}} \right) \\ &\quad \left. { \cdot \left( {\frac{{ - R^{2} { \cos }2\omega_{\text{o}} - r^{2} { \cos }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} + \vartheta } \right)} \right)^{2} }} + \frac{{R^{2} { \cos }2\omega_{\text{o}} + r^{2} { \cos }2\vartheta }}{{\left( {R^{2} + r^{2} } \right)^{2} - \left( {2rR{ \sin }\left( {\omega_{\text{o}} - \vartheta } \right)} \right)^{2} }}} \right)} \right] \\ \end{aligned} $$

(34)

The limiting values of the stress components at the center of the disc (i.e., for r → 0) along a radius at any arbitrary angle ϑ are obtained through Eqs. (33, 34) as:

$$ \left. {\sigma_{rr} } \right|_{r = 0}^{\vartheta } = \frac{{P_{\text{c}} }}{{4\pi { \sin }^{2} \omega_{\text{o}} }}[4\omega_{\text{o}} { \cos }2\omega_{\text{o}} - 2{ \sin }2\omega_{\text{o}} + { \cos }2\vartheta (4\omega_{\text{o}} - { \sin }4\omega_{\text{o}} )] $$

(35)

$$ \left. {\sigma_{\vartheta \vartheta } } \right|_{r = 0}^{\vartheta } = \frac{{P_{\text{c}} }}{{4\pi { \sin }^{2} \omega_{\text{o}} }}[4\omega_{\text{o}} { \cos }2\omega_{\text{o}} - 2{ \sin }2\omega_{\text{o}} - { \cos }2\vartheta (4\omega_{\text{o}} - { \sin }4\omega_{\text{o}} )] $$

(36)

$$ \left. {\sigma_{r\vartheta } } \right|_{r = 0}^{\vartheta } = \frac{{ - P_{\text{c}} }}{{4\pi { \sin }^{2} \omega_{\text{o}} }}{ \sin }2\vartheta (4\omega_{\text{o}} - { \sin }4\omega_{\text{o}} ). $$

(37)

4 Results and Discussion

4.1 Loading Types

The above-developed solution is applied now for a disc of diameter 100 mm made from marble subjected to diametral compression using the ISRM standardized device. The mechanical properties assigned to the material are those of Dionysos marble (the material used extensively and almost exclusively in the restoration project of the Parthenon Temple in the Acropolis of Athens). Its modulus of elasticity was considered equal to E _D = 78 GPa and its Poisson’s ratio equal to ν_D = 0.26 (Kourkoulis et al. 1999). The jaws of the device are assumed to be made of steel with modulus of elasticity E _s = 210 GPa and Poisson’s ratio ν_s = 0.30. An overall compressive force P _dev equal to 11.45 kN is applied on the upper jaw of the ISRM device corresponding to the force causing a tensile stress equal to about 7.3 MPa at the center of the disc [according to the familiar formula σ_tension = (P _dev)/(πRw)]. The specific stress value is very close to the tensile fracture strength of Dionysos marble as it was obtained by a series of direct tension tests by Vardoulakis et al. (2002).

For the above combination of numerical values of the mechanical properties, geometrical characteristics and load, Eq. (20) yields a contact angle ω_o = 2.1°, justifying all assumptions about the smallness of the contact length (indeed, the contact length corresponding to the above combination is equal to about ℓ = 1.8 mm), while the maximum value P ^parabolic_c of the parabolic load distribution is given by Eq. (21).

At this point it was decided, for comparison reasons, to study in juxtaposition three additional loading cases, i.e., point load, uniformly distributed radial pressure and sinusoidally varying radial pressure.

(i) For the point load and for P _o = P _dev/w, the stress field components can be expressed by particularizing the Muskhelishvili’s (1963) general solution as:

$$ \begin{aligned} \sigma_{\begin{subarray}{l} rr \\ \vartheta \vartheta \end{subarray} } & = \frac{{P_{\text{o}} }}{\pi R}\left( {1 - 2\frac{{R^{4} + r^{2} R^{2} { \cos }2\vartheta }}{{R^{4} + r^{4} + 2r^{2} R^{2} { \cos }2\vartheta }}} \right) \\ & \quad \pm \frac{{2P_{\text{o}} R}}{\pi }\left( {R^{2} - r^{2} } \right)\frac{{{ \cos }2\vartheta \left( {R^{4} + r^{4} { \cos }4\vartheta + 2r^{2} R^{2} { \cos }2\vartheta } \right) + 2r^{2} { \sin }^{2} 2\vartheta \left( {R^{2} + r^{2} { \cos }2\vartheta } \right)}}{{\left( {R^{4} + r^{4} + 2r^{2} R^{2} { \cos }2\vartheta } \right)^{2} }} \\ \end{aligned} $$

(38)

$$ \sigma_{r\vartheta } = \frac{{2P_{\text{o}} R}}{\pi }\left( {R^{2} - r^{2} } \right){ \sin }2\vartheta \frac{{2r^{2} { \cos }2\vartheta \left( {R^{2} + r^{2} { \cos }2\vartheta } \right) - \left( {R^{4} + r^{4} { \cos }4\vartheta + 2r^{2} R^{2} { \cos }2\vartheta } \right)}}{{\left( {R^{4} + r^{4} + 2r^{2} R^{2} { \cos }2\vartheta } \right)^{2} }} $$

(39)

(ii) For the uniformly distributed radial pressure, the components of the stress field were given in closed form by Markides et al. (2010). In this case, it holds that (Fig. 6):

$$ {{P}}_{\text{c}}^{\text{uniform}} = \frac{{{{P}}_{\text{dev}} }}{{2{\text{R}}\omega_{o} {\text{w}}}} = \frac{{{{P}}_{\text{o}} }}{{2{\text{R}}\omega_{o} }}\,{\text{in}}\,\left[ {\frac{\text{kN}}{{{\text{m}}^{2} }}} \right] $$

(40)

where ω_o is considered as that obtained for the parabolic loading distribution by Eq. (20).

Fig. 6

Schematic representation of the loading types exerted on the disc

(iii) For a radial pressure sinusoidally varying according to the formula (Markides et al. 2011):

$$ P_{\text{sinusoidal}} (\vartheta ) = c\left( {{ \sin }\vartheta - { \cos }\omega_{\text{o}} } \right){\text{ in }}\left[ {\frac{\text{kN}}{{{\text{m}}^{2} }}} \right] $$

(41)

the static equivalence:

$$ \int\limits_{{{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} - \omega_{\text{o}} }}^{{{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} + \omega_{\text{o}} }} {P_{\text{sinusoidal}} (\vartheta )} Rw{\text{d}}\vartheta \equiv P_{\text{dev}} = P_{\text{o}} w $$

(42)

dictates that the maximum value reads as:

$$ P_{\text{c}}^{\text{sinusoidal}} = \frac{{P_{\text{o}} \left( {1 - { \cos }\omega_{\text{o}} } \right)}}{{2R\left( {{ \sin }\omega_{\text{o}} - \omega_{\text{o}} { \cos }\omega_{\text{o}} } \right)}}{\text{ in }}\left[ {\frac{\text{kN}}{{{\text{m}}^{2} }}} \right] $$

(43)

where again, ω_o corresponds to the one obtained from Eq. (20).

The four loading cases considered are recapitulated in Table 1 and schematically represented in Fig. 6.

Table 1 The loading cases considered

4.2 The Stress Field Along Some Characteristic Paths

The variation of the radial stress σ _rr along the ϑ = 90° radius (i.e., axis Oy in Fig. 6) is plotted in Fig. 7a for all four loading cases studied. As expected, the differences are absolutely negligible along the major part of the radius. Only for r values exceeding r = 0.95R, the distributions start deviating from each other as seen in the graph embedded in Fig. 7a. Clearly, the point load generates the (absolute) maximum radial stress equal to about −1,400 MPa for r = R. The stress values were (intentionally) not normalized to provide an estimation of their magnitudes (given that the material considered is widely used in praxis). On the contrary, the uniformly distributed load generates the minimum radial stress along the ϑ = 90° radius equal to about −300 MPa at r = R. The sinusoidal and the parabolic distributions yield identical results all along the ϑ = 90° radius and are equal to about −450 MPa at r = R.

Fig. 7

The variation of the radial (a) and the transverse (hoop) (b) stresses along the ϑ = 90° radius for all four loading types studied

Similar conclusions are drawn from Fig. 7b, in which the transverse (hoop) stress is plotted again along the ϑ = 90° radius. The stresses at r = R for the uniform load and the sinusoidal and parabolic distributions are exactly equal to the respective values of the radial stresses. The main difference concerns the stress distribution due to the point load, which is constant all over the ϑ = 90° radius. This constant value, equal to about 7 MPa, is identical for all four load types for r < 0.95R and provides an estimation of the tensile strength of the specific marble, which is very close to the one experimentally obtained from direct tension tests (Vardoulakis et al. 2002).

As a next step, the stress components’ variation is plotted along the radius ending at the end point of the contact arc (calculated according to the present method), i.e., along the radius with ϑ = 87.9° (Fig. 8). Again for r < 0.95R, all loading types yield identical results. For r → 0 (at the disc’s center), the value of the radial stress component is equal to about −21 MPa (Fig. 8a) and that of the transverse component is equal to about 7 MPa (Fig. 8b), while that of the shear component is equal to about −1 MPa (Fig. 8c). However as r → R, the situation changes dramatically. All stress components attain negative values and reach global extrema (around r ≈ 0.95R) equal to about −149.67 MPa for the radial stresses (for the uniform load), −124.57 MPa for the transverse stresses (for the point load) and about −98.21 MPa for the shear ones (again for the point load). The portion of the graphs around this global extremum is shown magnified in the embedded graphs. From this point on, the stress components increase abruptly and tend to zero (for all loading types) as r → R. It is to be noted that the differences for the four loading types are almost negligible for the transverse stress and very small (<5%) for the shear stress. On the contrary, the difference for the radial stress approaches 20% between the two extreme loading cases, i.e., the point load (−126.31 MPa) and the uniform distribution (−149.67 MPa).

Fig. 8

The variation of the radial (a), the transverse (hoop) (b) and the shear (c) stresses along the ϑ = 87.9° radius (i.e., along the radius ending at the end point of the contact arc) for all four loading types studied

To obtain a global view of the stress field, two additional radii are examined: one within the loaded arc (i.e., ϑ = 88.5°) and the other outside the loaded arc (i.e., ϑ = 60°). The results for the radius within the loaded arc are plotted in Fig. 9. All three stresses exhibit a qualitative behavior similar to that observed in Fig. 8. The main difference appears for the normal stresses in the immediate vicinity of the contact arc. The stress distribution for the uniform load and the parabolic and sinusoidal distributions do not exhibit an extreme value and the respective values keep decreasing up to the boundary of the disc (fulfilling the boundary conditions). Again, for clarity reasons, the areas of the graphs very close to the critical region (r → R) are shown in magnification in the embedded figures.

Fig. 9

The variation of the radial (a), the transverse (hoop) (b) and the shear (c) stresses along the ϑ = 88.5° radius (i.e., along an arbitrary radius ending at a point within the contact arc) for all four loading types studied

With respect to the stress distribution along the ϑ = 60° radius, plotted in Fig. 10a, the main conclusion is that any difference between the four loading types has been eliminated. It is thus indicated that outside the loaded arc, the influence of the exact load application mode is negligible and any one of the existing solutions for the stress field (ranging from the one introduced by Hondros (1959) to more sophisticated ones (Wijk 1978; Markides et al. 2010, 2011) can be safely used. In other words, it can be stated that no difference exists in this region of the disc between the actual problem and its mathematical simulations.

Fig. 10

The variation of the stress components along the ϑ = 60° (a) and the ϑ = 0° (b) radii for all four loading types studied (no differences can be detected)

As it is perhaps expected for the radius with ϑ = 0°, the situation is quite similar (Fig. 10b). No differences at all can be observed between the various loading modes, and therefore the simple solution for the point load (Eqs. 38, 39) appears adequate for practical purposes. Finally, the polar distribution of the normal stress components σ _rr and σ_ϑϑ along the arc with 85° < ϑ < 95° is plotted in Fig. 11 for the three load distributions (the point load is not included for clarity reasons, since it provides extremely higher absolute values). Recalling that on the disc’s periphery, i.e., for r = R it holds that σ _rr  = σ_ϑϑ, it can be concluded that the differences between the sinusoidal and parabolic distributions are negligible. On the other hand, the abrupt changes of the stress distribution in the case of the uniform load explains various erroneous results observed in the immediate vicinity of the terminal points of the loaded arc in all solutions adopting such a load type, accompanied by the linear elasticity assumption. Clearly, this inadequacy is cured by adopting either the sinusoidal or the parabolic load distribution (which are in fact much closer to reality).

Fig. 11

The distribution of the normal stresses σ _rr and σ_ϑϑ along the arc with 85° < ϑ < 95° (recall that on the disc’s periphery, i.e., for r = R, it holds that σ _rr  = σ_ϑϑ) for the three load distributions (the point load is not included since it shadows the figure’s clarity)

4.3 Experimental Validation and Use

The accuracy of the solution proposed here was assessed using the data from a short series of experiments carried out according to the ISRM suggestions. The disc-shaped specimens used were made from PMMA (E = 3.19 GPa and ν = 0.36). Their radius was R = 0.05 m and their width w = 0.01 m. PMMA was chosen since it was a more or less linear elastic material (at least for loads not approaching its fracture load) of isotropic and homogeneous nature, as opposed to most natural building stones. During the experiments, the strain field was determined using a 3D digital image correlation (DIC) system by LIMESS.

Characteristic experimental results concerning the transverse and radial strains along the ϑ = 90° radius are plotted in Fig. 12a for an external load P _dev = 20 kN. The experimental data are shown for 0 < r/R < 0.95, since as r/R → 1 the accuracy of the DIC technique is downgraded by optical effects due to the geometric discontinuity at r = R (the disc is thinner than the jaws).

Fig. 12

a The experimentally measured and the theoretically calculated radial and transverse strains along the ϑ = 90° radius. b The polar variation of the strain components for ϑ ∈ [70°, 90°] (and for ϑ ∈ [0°, 90°] in the embedded figure)

In the same figure, the theoretically calculated strain components are plotted as obtained using Eqs. (33) and Hooke’s generalized law. It is seen that the agreement between theory and experiment is almost excellent for ε_θθ for the whole r/R region, while for ε _rr some discrepancies appear as one approaches the specimen–jaw interface. However, even these discrepancies (maximized somewhere around r/R = 0.83) do not exceed 12% and could be attributed both to local deviations of the material from perfect linearity and also to the fact that the contact angle for PMMA for P _dev = 20 kN is around 12°; in other words, it is on the border line of validity of the small angle assumption (Eq. 19). Similar conclusions have been drawn from the comparison of the experimental data with the theoretical ones along any other radius. In fact, as one moves away from the critical region [ϑ − ω_ο, ϑ + ω_ο], the agreement becomes progressively better, while for the ϑ = 0° radius the two sets almost coincide with each other.

The polar variation of all three strain components for 0 < ϑ < 90° is plotted in the small figure embedded in Fig. 12b. It is seen that while for ϑ < 70° the strain components vary monotonically and smoothly, for ϑ > 75° strong fluctuations appear. In this direction, the 70° < ϑ < 90° part of the graph is plotted magnified in Fig. 12b together with the ϑ = 78.12° line corresponding to the specimen–jaw contact angle as determined from the second of Eq. (15). It is seen that in a relatively narrow band around this line, all three curves exhibit their local extrema (points A, B, C) and points of inflection (points D, E, F). It is reasonable to assume that at least some of these points are somehow related to the end of the disc–jaw contact region. Theoretically speaking, the end of the contact region can be defined as the point where the contact stresses are zeroed. Unfortunately from an experimental point of view, such a direct definition does not exist (stresses cannot be measured directly). Figure 12b offers a solution to this problem, since it is clear that any one of the points B, D or E (easily determined experimentally) can be used as the point corresponding to the end of the contact region, within a given degree of accuracy.

5 Conclusions

A closed form solution for the stress field developed in a disc subjected to diametral compression was obtained. The advantage of this solution (beyond the fact that it is a full-field closed form one) is that the loading type adopted (i.e., that of parabolic radial pressure distribution) approaches closely the actual loading form (as obtained from the solution of the mixed fundamental contact problem by Kourkoulis et al. 2011), i.e., the cyclic distribution of radial pressure. In addition, the load was applied along the actual contact length (instead of along an arbitrarily predefined arc) developed between the specimen and the metallic jaws, taking into account the inevitable deformability of both the specimen and the jaw. Finally it is emphasized at this point that according to a preliminary analysis, the displacement field due to the parabolic radial pressure distribution can be also obtained in closed form contrary to that of the sinusoidal distribution.

Perhaps, the most important outcome of the present study is that the dependence of the stress field components upon the externally applied load is not linear even at the center of the disc, contrary to what is predicted by previous approaches where the contact length was assumed constant (consider for example Eqs. (1–4) of Hondros’ (1959) pioneering paper). This can be easily concluded from Eqs. (35, 36), since the factor P _c (directly related to the external load P _dev) multiplying the expressions in square brackets is not constant but depends among others on the contact length ℓ (Eq. 18), which in turn depends on the load level (Eq. 20). This non-linear variation of the stress field on the load level is exhibited in Fig. 13a where the transverse (tensile) stress developed at the disc’s center is plotted versus the force, P _dev, externally exerted on the disc, both according to Hondros’ familiar formula σ_t = (P _dev/πRw) and also according to the present solution. For the needs of the present solution, the specimen was assumed to be made from PMMA, while the jaws from steel. It is seen from Fig. 13a that the tensile fracture stress of PMMA (estimated for the specific materials’ batch around 37 MPa from direct tension tests) corresponds according to the traditional formula to a load equal to 57.8 kN, while according to the present solution the respective load is equal to about 64 kN. The difference (exceeding 10%) is not negligible.

Fig. 13

The tensile (transverse or hoop) stress a at the discs’ center versus the external load, P _dev, according to the present solution and the σ_t = (P _dev/πRw) formula and b along the ϑ = 90° radius for P _dev = 10 kN and for specimens made from marble and PMMA

It can be argued of course at this point that PMMA is not a material representative of the materials tested using the Brazilian disc test. Clearly in case of geomaterials like marble, the deviation from linearity is not so striking and the traditional formula approaches experimental reality accurately enough. If for example Dionysos marble is considered (for which the maximum contact angle at the fracture load is about 2.1°), the predictions for the maximum load according to the present solution and according to the σ_t = (P _dev/πRw) formula almost coincide (the difference does not exceed 1%).

As one moves away from the disc’s center, the difference between the stresses developed in specimens made from different materials according to the present solution increase dramatically. This is indicated in Fig. 13b, where the transverse (hoop) stress is plotted along the ϑ = 90° for two materials, i.e., for marble and PMMA, for a common load level equal to 10 kN. It is seen that while for r/R < 0.75 the differences are negligible (embedded figure), for r/R → 1 they become enormous.

The results of the study indicate clearly that as long as one remains at points relatively far from the vicinity of the loaded portion of the disc’s periphery, all solutions for the stress field provide more or less acceptable results, in case of very brittle materials. This is true even for the gross approximation of reality corresponding to the point load simulation. However as one approaches the loading arc (i.e., for r → R and 90 − ω_ο < ϑ < 90 + ω_o), the stress field strongly deviates both from that predicted by the point load assumption and from that predicted for the uniform load. Similarly for materials of decreased ductility, the differences between existing approaches and that proposed here cannot be ignored even for the stresses at the disc’s center.

Of course, it is to be mentioned that even in case of loading distributions closely approaching reality (like the sinusoidal and the parabolic ones), the absolute values of the stresses developed in this region are very high, since linear elastic behavior of both the specimen’s and the jaw’s materials is assumed in the present solution. Although failure of the specimen is not studied at all in this paper, it is obvious and should be kept in mind that for specific combinations of the mechanical properties of the specimen and the jaw [especially those leading to very small contact angles, as determined from the second of Eqs. (15) or Eq. (20)], it is possible that premature failure starts in the vicinity of the loaded arc (especially close at its end points) undermining the validity of the test.

Beyond the linear elasticity assumption friction was ignored in the present study. This was done since existing studies (Lavrov and Vervoort 2002; Markides et al. 2011) indicate that the role of friction is again restricted very close to the loaded arc and cannot influence the stress field at the center of the disc. For a closed form solution of the friction problem, one should first answer the question concerning the type of friction developed at the jaw–specimen interface. Clearly a Coulomb-type friction (proportional to the normal radial pressure) is not adequate, because it yields maximized friction at the symmetry point of the load distribution where by intuition friction must be zeroed (Hooper 1971) since the relative motion tendency is eliminated due to symmetry. In any case, the fact that friction is ignored does not deteriorate the value of the present solution, which could be used (among others) for the validation of numerical models that could explore in a parametric manner various critical aspects of the Brazilian disc test.

Appendices

Appendix I

1.1 A Note on the Complex Potential in Case of Circular Load Distribution

Consider the circular distribution:

$$ P(\tau ) = \frac{1}{{3R_{1} K}}\sqrt {\ell^{2} - \tau^{2} } $$

Under the obvious simplifications: $\ell \approx \ell^{\prime } = R{ \sin }\omega_{\text{o}} ,\tau \approx \tau^{\prime } = R{ \cos }\vartheta$ (R = R ₁) becomes:

$$ P(\vartheta ) = \frac{1}{3K}\sqrt {{ \sin }^{2} \omega_{\text{o}} - { \cos }^{2} \vartheta } $$

Equivalently, since ${ \cos }\vartheta = \left( {s + \overline{s} } \right)/2$, it can be written as:

$$ P(s) = \frac{1}{3K}\sqrt {{ \sin }^{2} \omega_{\text{o}} - \frac{1}{2} - \frac{{s^{2} }}{4} - \frac{1}{{4s^{2} }}} ,\quad s = {\text{e}}^{{{\text{i}}\vartheta }} . $$

Therefore on the loaded rims (in the fictitious ζ-plane) it holds that:

$$ \sigma_{\rho \rho }^{ + } = - P(s) = - \frac{1}{3K}\sqrt {{ \sin }^{2} \omega_{\text{o}} - \frac{1}{2} - \frac{{s^{2} }}{4} - \frac{1}{{4s^{2} }}} . $$

Inserting the above value for $\sigma_{\rho \rho }^{ + }$ in the general formula:

$$ \Upphi (\zeta ) = \frac{1}{{2\pi {\text{i}}}}\int\limits_{\gamma } {\frac{{\sigma_{\rho \rho }^{ + } (s)}}{s - \zeta }} {\text{d}}s - \frac{1}{4\pi }\int\limits_{0}^{2\pi } {\sigma_{\rho \rho }^{ + } (\vartheta )} {\text{d}}\vartheta \quad \left( {{\text{Eq}}. \, 25} \right), $$

an integral appears of the form:

$$ \int {\frac{{\sqrt {C - s^{2} - \frac{1}{{s^{2} }}} }}{s - \zeta }} {\text{d}}s $$

A closed form solution for such an integral is not available.

Appendix II

2.1 An Alternative Load Distribution

Taking the squares of both sides of the second of Eqs. (14), for R ₁ = R, it follows that:

$$ P(\tau )^{2} + \left( {\frac{\tau }{3RK}} \right)^{2} = \left( {\frac{\ell }{3RK}} \right)^{2} , $$

which represents the equation of a circle of radius $\frac{\ell }{3RK}$.

A parabola (red color in the following figure) of the same area (demanded to insure static equivalence between the circular and the parabolic radial pressure distributions) that intersects the x-axis at the points $\mp \frac{\ell }{3RK}$ is described by the equation:

$$ P(\tau ) = \frac{\pi \ell }{8RK} - \frac{\pi }{8RK}\frac{\tau }{\ell }^{2} = \frac{\pi \ell }{8RK}\left[ {1 - \left( {\frac{\tau }{\ell }} \right)^{2} } \right]. $$

See Fig. 14.

Fig. 14

Cyclic versus parabolic pressure distribution