1 Introduction

The transport of a soluble substance in a flowing fluid has wide applications in the fields of chemical engineering, environmental engineering, biomedical engineering, and physiological fluid dynamics. The dispersion of a solute in a physiological fluid flow is of interest to understand the transport of nutrients, drugs, or toxins in blood. In his classic paper, Taylor [1] described the dispersion phenomenon of a diffusing solute in a fluid flowing through an impermeable circular pipe. Aris [2] considered Taylor’s classic model, removing restrictions made by Taylor to extend the longitudinal diffusion, and proposed the idea of using the method of moments to investigate the asymptotic behavior of the second-order moment about the mean. After a sufficiently long time of mixing across the tube, both authors noticed that the shape of the distribution of the diffusing material tends to a Gaussian distribution. Ananthakrishnan et al. [3] investigated the dispersion coefficient numerically and showed the long-time validity of the Taylor–Aris dispersion theory. Gill and Sankarasubramanian [4] reported a “generalized dispersion model” using a derivative expansion technique, which was valid for all times, to explore the dispersion in laminar flow. Furthermore, Barton [5] resolved certain technical difficulties in Aris’s method of moments and obtained the solutions of the second- and third-order moment equations for the distribution of the solute, being valid for all time.

The longitudinal dispersion of a solute in a time-dependent flow has been studied by a number of researchers. For unsteady flow, some have considered a periodic pressure gradient as the driving force of the flow (Aris [6], Watson [7], Mazumder and Das [8], Mukherjee and Mazumder [9], Roy et al. [10]). An exact solution of the diffusion equation was obtained by Chatwin [11] to examine the dispersion in an oscillatory flow. Using the method of moments, Bandyopadhyay and Mazumder [12] examined the effect of pulsatile flow on the dispersion process through a channel. Applying a homogenization technique, Barik and Dalal [13] obtained the transport coefficients in an oscillatory Couette flow with nonlinear chemical decay reactions. Sarkar and Jayaraman [14] and Mazumder and Mondal [15] investigated the impact of wall absorption on the dispersion in an oscillatory flow in an annular pipe and explained the application of their work to a catheterized artery. The dispersion of a solute in an unsteady flow through an annular curved tube was analyzed by Pedley and Kamm [16], and a similar kind of conduit was also considered by Jayaraman et al. [17] for the axial transport of a solute spreading due to a steady current and catalysis at the wall. The dispersion of contaminant molecules due to a turbulent shear flow over the surface of a rough bed was examined numerically by Mazumder and Bandyopadhyay [18], considering a solute released from an elevated line source. Recently, Al Mukahal et al. [19] investigated the transport process in terms of advection and dispersion of a passive solute in a steady unidirectional rivulet flow, and also obtained a general expression for the effective dispersion coefficient.

Based on previous studies, it is clear that dispersion phenomena have mostly been considered in Newtonian fluid flows under steady and periodic conditions in the presence or absence of chemical reactions in the past. A few attempts have also been made to study dispersion phenomena in non-Newtonian fluids, which has wide applications in polymer processing, biochemical processing, the cardiovascular system, etc. Agrawal and Jayaraman [20] provide a brief review on dispersion in power-law fluids in curved tubes using Taylor’s dispersion model. Considering wall absorption, Siddheshwar et al. [21, 22] studied dispersion in a power-law fluid in a channel or tube. A study of dispersion in non-Newtonian (Casson, Bingham plastic, and power-law) fluids was carried out by Sharp [23], considering conduits with the Taylor–Aris dispersion model. It was shown that, due to the non-Newtonian rheology of the fluid, the axial dispersion was reduced. For the case of larger arteries with high shear rate, the assumption of Newtonian behavior of blood is acceptable, according to Tu and Deville [24], whereas blood exhibits non-Newtonian behavior at low shear rate in small-diameter arteries (Long et al. [25]). Mathematical studies of blood flow are strongly supported by the Casson fluid model (e.g., Blair [26], Charm and Kurland [27], Dash et al. [28], Nagarani et al. [29], Sankar [30], Roy et al. [31]) for fixed hematocrits, anticoagulants, temperature, etc. Nagarani et al. [32] carried out exact analysis of unsteady convective diffusion in a Casson fluid flow in an annulus, with application to a catheterized artery. Rana and Murthy [33] investigated the dispersion process in a pulsatile flow of a Casson fluid flowing through a pipe in the presence of wall absorption. Recently, Debnath et al. [34] studied the transport of a chemically active solute through a multilayer (Casson–Newtonian) fluid model for steady flow; subsequently, Debnath et al. [35] extended their study by considering a pulsatile flow.

Because of the presence of conducting walls in lungs and blood vessels, it is vital to describe the dispersion procedure considering the wall characteristics to understand the indicator dilution technique and other mechanisms in the bronchial region. Many industrial (Alper [36]) and physiological (Kinne [37], El-Sayed et al. [38]) situations involve chemical reactions during mass transfer. Walker [39] described the steady diffusion of chemical species undergoing first-order heterogeneous and homogeneous reactions in a tubular flow. Further, Gupta and Gupta [40] studied the unsteady dispersion with a heterogeneous chemical reaction at the channel boundary and homogeneous reaction in the bulk of the flow. Purnama [41] analyzed the combined effects of retention and reactive boundary conditions on the dispersion phenomenon. Ng and Rudraiah [42] studied the solute dispersion process in the presence of wall retention and absorption using a generalized dispersion model. Using multiple scales of averaging, known as the homogenization method, Ng [43, 44] solved the transport equation considering both reversible and irreversible reactions, but the time variation of the dispersion coefficient was not considered. Furthermore, considering pulsatile flow through an annular pipe, Mazumder and Paul [45] investigated the dispersion phenomenon in the presence of reversible and irreversible reactions at the outer wall boundary. Recently, Debnath et al. [46] investigated the effect of the pipe’s annularity and flow pulsation for Poiseuille and Couette flows. They explored the mechanism of dispersion under the combined impact of kinetic reversible phase exchange and irreversible heterogeneous reactions between the species and inner wall. In the present paper, the following assumptions are made: (i) the pipe is annular with a periodic pressure gradient applied for flow pulsation, (ii) the non-Newtonian characteristic follows the Casson model, (iii) heterogeneous reversible phase exchange and irreversible absorption occur at the outer wall of the annulus, and (iv) a homogeneous first-order reaction occurs in the bulk flow.

It is clear that the present model has some practical significance for transport of species in blood flow through small-diameter arteries. More importantly, to the best of the authors’ knowledge, no efforts have been made to date to investigate dispersion under bulk homogeneous and heterogeneous reactions for a non-Newtonian fluid flowing through an annular tube. Due to the annular pipe flow, the present mathematical model can be used to understand the indicator dilution technique in a catheterized artery. The outer tube can be considered to represent the blood vessel, whereas the insertion of another smaller-diameter tube into the blood vessel results in the formation of an annular region between the catheter wall and the arterial wall. Such catheters are used to inject dye and withdraw blood samples for measurements (McDonald [47]); however, the introduction of a catheter into a blood vessel could be a potent cause of eddy formation and mixing of blood. Catheterization increases the frictional resistance to flow through the artery (Mazumder and Mondal [15]) and hence alters the flow field owing to changes in the hemodynamic conditions in the artery. Thus, the present study on dispersion affected by multiple kinds of reaction together with Casson fluid flow through an annular pipe is important for analysis of flow of blood or blood-like liquids in a catheterized artery, which may help to enhance understanding of the all-time behavior of such dispersion processes.

Fig. 1
figure 1

Schematic diagram of considered setup

Full size image

2 The considered problem

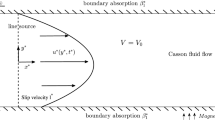
We consider unidirectional pulsatile flow of a Casson liquid through an annular pipe with radii \({\overline{a}}\) (outer) and \({\overline{b}}\) (inner) (\({\overline{a}} > {\overline{b}}\)), having radius ratio \(\eta ={{\overline{b}}}/{{\overline{a}}}\) (geometry of the annulus) and hydraulic radius \({\overline{d}}={\overline{a}}-{\overline{b}}\) (stream region). Figure 1 shows the flow geometry with a cylindrical coordinate system, where the axial and radial coordinates are by \({\overline{z}}\) and \({\overline{r}}\), respectively; the overbar denotes a dimensional quantity. The problem is defined under the following assumptions:

  1. (i)

    The flow is unsteady, laminar, axisymmetric, incompressible, and fully developed.

  2. (ii)

    The flow is driven by an imposed outward periodic pressure gradient. The pressure gradient at any \({\overline{z}}\) ( [33, 35, 48]) is represented by

    $$\begin{aligned} -\frac{\partial {{\overline{p}}}}{\partial {{\overline{z}}}}=A_0+A_1 \sin (\omega _\mathrm{p} {\overline{t}}), \end{aligned}$$
    (1)

    where \({\overline{p}}\) is the pressure, \(A_0\) and \(A_1\) are the steady and fluctuating components of the pressure gradient, \(\omega _\mathrm{p} \) is the frequency of the pressure pulsation, and \({\overline{t}}\) is time.

  3. (iii)

    Due to the infinite axial extent of the system, the aspect ratio \({L}/{{\overline{d}}}\) (ratio of the axial length L to the width \({\overline{d}}\)) at the annulus is infinite in this study, thus it is considered that the flow in the axial direction is fully developed. Therefore, \({\overline{u}}_{{\overline{r}}}={\overline{u}}_{{\overline{\theta }}}=0\) and \({\overline{u}}_{{\overline{z}}}={\overline{u}}\) (say). The continuity equation then reduces to \({\partial {\overline{u}}}/{\partial {\overline{z}}}=0.\) Also the axisymmetry of the flow ensures that \({\partial {\overline{u}}}/{\partial {\overline{\theta }}}=0\). Therefore, the velocity only has an axial component \({\overline{u}}={\overline{u}}({\overline{r}}, {\overline{t}})\), which satisfies the following momentum equation [33, 35, 48] in the axial direction:

$$\begin{aligned} \qquad \rho \frac{\partial {{\overline{u}}}}{\partial {{\overline{t}}}}=-\frac{\partial {\overline{p}}}{\partial {{\overline{z}}}} -\frac{1}{{\overline{r}}}\frac{\partial ({{\overline{r}}\; {\overline{\tau }})}}{\partial {{\overline{r}}}}, \end{aligned}$$
(2)

where \(\rho \), \({\overline{u}}({\overline{r}},{\overline{t}})\), and \({\overline{\tau }}\) are the density, axial component of velocity, and shear stress of the liquid, respectively.

As suggested by Fung [49] and Aroesty and Gross [50], the Casson constitutive equation is a nonlinear relation between the shear stress and shear rate and can be written as

$$\begin{aligned} \left. \begin{array}{ll} {{\overline{\tau }}}^\frac{1}{2}={{\overline{\tau }}_\mathrm{y}}^\frac{1}{2}+\left( -\mu \frac{\partial {{\overline{u}}}}{\partial {{\overline{r}}}}\right) ^ \frac{1}{2}\quad &{}\text{ if }\;{\overline{\tau }}>{\overline{\tau }}_\mathrm{y},\\ \frac{\partial {{\overline{u}}}}{\partial {{\overline{r}}}}=0\quad &{} \text{ if }\; -{\overline{\tau }}_\mathrm{y} \le {\overline{\tau }}\le {\overline{\tau }}_\mathrm{y},\\ {(-{\overline{\tau }})}^\frac{1}{2}={{\overline{\tau }}_\mathrm{y}}^\frac{1}{2}+\left( \mu \frac{\partial {{\overline{u}}}}{\partial {{\overline{r}}}}\right) ^ \frac{1}{2}\quad &{} \text{ if }\;{\overline{\tau }}<-{\overline{\tau }}_\mathrm{y}, \end{array}\right\} \end{aligned}$$
(3)

where \({\overline{\tau }}_\mathrm{y}\) is the yield stress and \(\mu \) is the viscosity of the Casson liquid (the viscosity at a higher rate of shear). In Eq. (3), the velocity gradient will be zero if \(-{\overline{\tau }}_\mathrm{y} \le {\overline{\tau }}\le {\overline{\tau }}_\mathrm{y}\), implying the existence of a plug-flow region.

The boundary conditions assumed for the problem under consideration are no-slip at both walls, that is,

$$\begin{aligned} {\overline{u}}({\overline{r}}, {\overline{t}})=0\quad \text{ at }\;{\overline{r}}={\overline{b}}\quad \text{ and }\; {\overline{r}}={\overline{a}}. \end{aligned}$$
(4)

Consider a chemical species suspended in a solvent which is completely miscible. The species takes part in multiple kinds of chemical reaction within the flow and at the boundary. Here, in the bulk of the flow, the species undergoes homogeneous first-order chemical kinetics with the fluid, with heterogeneous reversible phase exchange and irreversible absorption at the outer boundary of the annulus. We further consider that some portion of the species adheres to the tube wall, while the remaining portion moves with the fluid. The chemical substance that flows with the fluid and that is retained at the fluid–wall interface are in different forms, being referred to as the mobile and immobile phase, respectively. The homogeneous first-order reaction will then take place in the mobile phase, while the heterogeneous reversible and irreversible processes will occur in the immobile phase.

The concentration of mobile phase is denoted as \({\overline{C}}\) (mass of chemical per bulk volume of fluid), and the concentration of immobile phase as \({\overline{C}}_\mathrm{s}\) (mass of chemical per surface area of boundary wall). If they are in equilibrium state, they obey a constant ratio, i.e., \({\overline{\varOmega }}={{\overline{C}}_\mathrm{s}}/{{\overline{C}}}\), known as the partition coefficient, which can also be taken as a chemical-specific constant.

In the presence of the heterogeneous and homogeneous reactions specified above, when a chemically active solute is discharged into the mentioned flow through the annular gap of the tube, the transport equation for the concentration \({\overline{C}}({\overline{t}},{\overline{r}},{\overline{z}})\) is

$$\begin{aligned} \frac{\partial {\overline{C}}}{\partial {\overline{t}}}+{\overline{u}}({\overline{r}}, {\overline{t}})\frac{\partial {\overline{C}}}{\partial {\overline{z}}}=D\frac{\partial ^2 {\overline{C}}}{\partial {{\overline{z}}}^2}+\frac{D}{{\overline{r}}}\frac{\partial }{\partial {\overline{r}}}\left( {\overline{r}} \frac{\partial {\overline{C}}}{\partial {\overline{r}}}\right) -{\overline{\beta }}\;{\overline{C}}, \end{aligned}$$
(5)

where D is the molecular diffusivity (assumed constant) and \({\overline{\beta }}\) is the homogeneous reaction rate in the bulk flow.

The equation that governs \({\overline{C}}_\mathrm{s}({\overline{t}},{\overline{z}})\) is that of first-order kinetics describing the exchange of the mobile and immobile phases, given by

$$\begin{aligned} \frac{\partial {{\overline{C}}_\mathrm{s}}}{\partial {{\overline{t}}}}=K({\overline{\varOmega }} {\overline{C}}-{\overline{C}}_\mathrm{s}), \end{aligned}$$
(6)

where K is the reversible reaction rate constant. Equation (6) is an approximation of the diffusion model used to describe the mass transport in the wall layer. Schwarzenbach et al. [51] also showed the similarity of the solutions generated by the radial diffusion and first-order kinetic models. One of the important features of Eq. (6) is that the kinetics of the two reactions (kinetic reversible phase exchange and irreversible absorption) are not related in this setup and can thus be prescribed independently.

Following Rana and Murthy [33], the initial conditions for solving Eqs. (5) and (6) are

$$\begin{aligned} \left. \begin{array}{lll} {\overline{C}}(0,{\overline{r}},{\overline{z}})={\overline{C}}_0B({\overline{r}})\psi ({\overline{z}}), \quad ({\overline{b}}<{\overline{r}}< {\overline{a}}),\\ \psi ({\overline{z}})={\overline{d}}\;\delta ({\overline{z}}),\\ B({\overline{r}})=1,\\ {\overline{C}}_\mathrm{s}(0,{\overline{z}})=0,\\ \end{array} \right\} \end{aligned}$$
(7)

where \({\overline{C}}_0\) is the initial concentration of the slug input and \(\delta ({\overline{z}})\) is the Dirac delta function. The boundary conditions for the present problem can be expressed as

$$\begin{aligned}&{\overline{C}}=0\quad \text{ as }\;{\overline{z}}\rightarrow \pm \infty \; \text{ for } \text{ a } \text{ finite } \text{ extent } \text{ of } \text{ axial } \text{ distribution }, \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\partial {\overline{C}}}{\partial {\overline{r}}}=0 \quad \text{ at } \; {\overline{r}}={\overline{b}}, \end{aligned}$$
(9)
$$\begin{aligned}&-D\frac{\partial {\overline{C}}}{\partial {\overline{r}}}-{\overline{\varGamma }}{\overline{C}}=K({\overline{\varOmega }} {\overline{C}} -{\overline{C}}_\mathrm{s}) \quad \text{ at } \; {\overline{r}}={\overline{a}}, \end{aligned}$$
(10)

where \({\overline{\varGamma }}\) is the irreversible absorption parameter (representing the rate of loss at the outer wall).

We now introduce the following dimensionless quantities into Eqs. (1)–(10):

$$\begin{aligned}&t = \frac{D{\overline{t}}}{{\overline{d}}^2},\quad r = \frac{{\overline{r}}}{{\overline{d}}}, \quad z = \frac{D{\overline{z}}}{{\overline{d}}^2 U}, \quad U=\frac{{\overline{d}}^2 A_0 }{ 4{\mu }}, u=\frac{{\overline{u}}}{ U},\nonumber \\&\tau =\frac{{\overline{\tau }}}{{\mu }\left( \frac{U}{{{\overline{d}}}}\right) },\quad \tau _\mathrm{y}=\frac{{\overline{\tau }}_\mathrm{y}}{{\mu }\left( \frac{U}{{\overline{d}}}\right) }, \quad C=\frac{{\overline{C}}}{{\overline{C}}_0}, \quad C_\mathrm{s}=\frac{{\overline{C}}_\mathrm{s}}{{\overline{d}}\,{\overline{C}}_0}, \end{aligned}$$
(11)

where U is a reference velocity. Substituting the above dimensionless quantities into Eqs. (5)–(10) yields

$$\begin{aligned}&\frac{\partial C}{\partial t} + \ u(r, t)\frac{\partial C}{\partial z} = \frac{1}{r} \frac{\partial }{\partial r} \left( r \frac{\partial C}{\partial r} \right) +\frac{1}{\mathrm {Pe}^2} \frac{\partial ^2 C}{\partial z^2}-\beta C, \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial }{\partial t}C_\mathrm{s}(t,z)= \mathrm {Da}[\varOmega C(t,r_{\mathrm {o}},z)-C_\mathrm{s}(t,z)], \end{aligned}$$
(13)
$$\begin{aligned}&\left. \begin{array}{lll} {C}(0,r,z)=B(r)\psi (z), \quad (r_{\mathrm {i}}<r<r_{\mathrm {o}}),\\ \psi (z)=\frac{\delta (z)}{\mathrm {Pe}}, B(r)=1,\\ C_\mathrm{s}(0,z)=0,\\ \end{array} \right\} \end{aligned}$$
(14)
$$\begin{aligned}&C=0\quad \text{ as }\;z\rightarrow \pm \infty , \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\partial C}{\partial r}=0 \quad \text{ at } \; r=r_{\mathrm {i}}, \end{aligned}$$
(16)
$$\begin{aligned}&-\frac{\partial C}{\partial r}-\varGamma C=\mathrm {Da}(\varOmega C-C_\mathrm{s}) \quad \text{ at } \; r=r_{\mathrm {o}}, \end{aligned}$$
(17)

where \(r_{\mathrm {i}}\) (\(=\eta /(1-\eta )\)) and \(r_{\mathrm {o}}\) (\(=1/(1-\eta )\)) are the dimensionless inner and outer radius of the annular pipe, \(\mathrm {Pe}\) (\(={U {\overline{d}}}/{D}\)) is the Péclet number, \(\beta \) (\(={{\overline{\beta }} \ {\overline{d}}^2}/{D}\)) is the dimensionless homogeneous reaction rate, \(\mathrm {Da}\) (\(={K {\overline{d}}^2}/{D}\)) is the Damköhler number, \(\varGamma \) (\(={{\overline{\varGamma }} \ {{\overline{d}}}}/{D}\)) is the dimensionless irreversible reaction rate, and \(\varOmega \) (\(={{\overline{\varOmega }}}/{{\overline{d}}}\)) is the phase partition ratio (retention parameter), viz. the ratio of the chemical species distributed between the mobile and immobile phase.

The reactions considered in the present work are described by (a) the heterogeneous irreversible absorption (\(\varGamma \)) at the outer wall of the annulus, (b) the heterogeneous reversible phase exchange (\(\mathrm {Da}\)) there, and (c) the homogeneous first-order reaction (\(\beta \)) in the bulk flow. The prime aim of the present work is to carry out a comparative study of these reaction parameters, which are of great importance for the spreading of tracers in environmental and physiological processes. The irreversible absorption parameter \(\varGamma \) and bulk flow reaction parameter \(\beta \) are related to the mass depletion rate such that higher values of \(\varGamma \) and \(\beta \) indicate that a significant portion of the mass will be depleted in a very short duration. The Damköhler number \(\mathrm {Da}\) is the ratio of the phase exchange rate to the diffusion rate, with larger values of \(\mathrm {Da}\) indicating that the rate of reactions is higher than the diffusion rate. Each type of reaction may differ in its nature and completely in terms of its arena. Thus, they are compared to draw a definite conclusion regarding their relative effects on the dispersion process in a variety of flow conditions: steady, unsteady, and under the combined effect of steady and unsteady flows.

3 Velocity distribution

Using the dimensionless quantities given in Eq. (11), the momentum equation (2) reduces to

$$\begin{aligned} \epsilon \frac{\partial {u}}{\partial {t}}=4p(t)-\frac{1}{r}\frac{\partial ({r\tau })}{\partial {r}}, \end{aligned}$$
(18)

where \(\epsilon ={1}/{\mathrm {Sc}}\) is the inverse of the Schmidt number (\(\mathrm {Sc}={\nu }/{D}\)), \(p(t)=1+e \,\sin (\alpha ^2\;\mathrm {Sc}\;t)\), where \(e={A_1}/{A_0}\) (\(A_0\ne 0\)) is the amplitude of the fluctuating pressure component, and \(\alpha ={\overline{d}}\sqrt{{\omega _\mathrm{p}}/{({\mu }/{\rho })}}\) is the Womersley frequency parameter.

The nondimensional form of the Casson constitutive equation  (3) can be written as

$$\begin{aligned} \left. \begin{array}{ll} {{\tau }}^\frac{1}{2}={{\tau }_\mathrm{y}}^\frac{1}{2}+\left( -\frac{\partial {{u}}}{\partial {{r}}}\right) ^ \frac{1}{2}&{}\quad \text{ if }\;{\tau }>{\tau }_\mathrm{y},\\ \frac{\partial {{u}}}{\partial {{r}}}=0 &{}\quad \text{ if }\; -{\tau }_\mathrm{y} \le {\tau }\le {\tau }_\mathrm{y},\\ {(-{\tau })}^\frac{1}{2}={{\tau }_\mathrm{y}}^\frac{1}{2}+\left( \frac{\partial {{u}}}{\partial {{r}}}\right) ^ \frac{1}{2}&{}\quad \text{ if }\;{\tau }<-{\tau }_\mathrm{y}, \end{array}\right\} \end{aligned}$$
(19)

together with the boundary conditions (4)

$$\begin{aligned} u(r, t)=0\quad \text{ at }\; r=r_{\mathrm {i}}\quad \text{ and }\; r=r_{\mathrm {o}}. \end{aligned}$$
(20)

Following Sankar and Lee [52], the plug-flow region is represented by \(\lambda _1\le r\le \lambda _2\), where \(r_{\mathrm {i}}\le \lambda _1,\lambda _2\le r_{\mathrm {o}}\), and the two shear flow regions by \(r_\mathrm {i}\le r\le \lambda _1\) and \(\lambda _2\le r\le r_\mathrm {o}\); then, Eq. (19) will take the form

$$\begin{aligned} \left. \begin{array}{ll} \frac{\partial {u}}{\partial {r}}=\left( -\tau +\tau _\mathrm{y}-2\tau _\mathrm{y}^\frac{1}{2}\vert \tau \vert ^\frac{1}{2}\right) &{}\quad \text{ if } \; r_\mathrm {i}\le r\le \lambda _1\;\text{ and }\;{\tau }<-{\tau }_\mathrm{y},\\ \frac{\partial {u}}{\partial {r}}=0 &{}\quad \text{ if } \; \lambda _1\le r\le \lambda _2\; \text{ and }\; -{\tau }_\mathrm{y} \le {\tau }\le {\tau }_\mathrm{y}, \\ \frac{\partial {u}}{\partial {r}}=-\left( \tau +\tau _\mathrm{y}-2\tau _\mathrm{y}^\frac{1}{2}\tau ^\frac{1}{2}\right) &{}\quad \text{ if } \; \lambda _2\le r\le r_\mathrm {o}\; \text{ and }\;{\tau }>{\tau }_\mathrm{y}, \end{array}\right\} \end{aligned}$$
(21)

where \(\lambda _1\) and \(\lambda _2\) are the nondimensional yield plane locations in the flow field.

Because of the nonlinearity in the coupled equations (18) and (21), an exact solution is not possible, thus we proceed using a regular perturbation technique to solve these equations, considering \(\epsilon \) (\(={1}/{\mathrm {Sc}}\)) as the perturbation parameter. Consider a solution of the form

$$\begin{aligned} \left. \begin{array}{l} u(r, t)=u_{0}(r, t)+\epsilon \; u_{1}(r, t)+\cdots ,\\ u_\mathrm{p}(r, t)=u_{0\mathrm{p}}(r, t)+\epsilon \; u_{1\mathrm{p}}(r, t)+\cdots ,\\ \tau (r, t)=\tau _{0}(r, t)+\epsilon \; \tau _{1}(r, t)+\cdots .\\ \end{array} \right\} \end{aligned}$$
(22)

Utilizing Eq. (22) in Eqs. (18), (20), and (21) yields the following results:

Zeroth-order terms

$$\begin{aligned}&4p(t)-\frac{1}{r}\frac{\partial ({r \tau _0})}{\partial {r}}=0, \end{aligned}$$
(23)
$$\begin{aligned}&\frac{\partial {u_0}}{\partial {r}}=-\tau _0+\tau _\mathrm{y}-2\tau _\mathrm{y}^\frac{1}{2}\vert \tau _0\vert ^\frac{1}{2}\quad \text{ if }\; r_\mathrm {i}\le r\le \lambda _1, \end{aligned}$$
(24)
$$\begin{aligned}&\frac{\partial {u_0}}{\partial {r}}=0 \quad \text{ if }\; \lambda _1\le r\le \lambda _2, \end{aligned}$$
(25)
$$\begin{aligned}&\frac{\partial {u_0}}{\partial {r}}=-\left( \tau _0+\tau _\mathrm{y}-2\tau _\mathrm{y}^\frac{1}{2}\tau _0^\frac{1}{2}\right) \quad \text{ if }\; \lambda _2\le r\le r_\mathrm {o}. \end{aligned}$$
(26)

First-order terms

$$\begin{aligned}&\frac{\partial {u_0}}{\partial {t}}=-\frac{1}{r}\frac{\partial ({r\tau _1})}{\partial {r}}, \end{aligned}$$
(27)
$$\begin{aligned}&\frac{\partial {u_1}}{\partial {r}}=-\left( 1+\frac{\tau _\mathrm{y}^\frac{1}{2}}{\vert \tau _0\vert ^\frac{1}{2}}\right) \tau _1\quad \text{ if }\; r_\mathrm {i}\le r\le \lambda _1, \end{aligned}$$
(28)
$$\begin{aligned}&\frac{\partial {u_1}}{\partial {r}}=0 \quad \text{ if }\; \lambda _1\le r\le \lambda _2, \end{aligned}$$
(29)
$$\begin{aligned}&\frac{\partial {u_1}}{\partial {r}}=-\left( 1-\frac{\tau _\mathrm{y}^\frac{1}{2}}{\tau _0^\frac{1}{2}}\right) \tau _1 \quad \text{ if }\; \lambda _2\le r\le r_\mathrm {o}. \end{aligned}$$
(30)

Then, the boundary conditions for solving Eqs. (23)–(30) are

$$\begin{aligned} \left. \begin{array}{l} u_0(r=r_\mathrm {i})=0=u_0(r=r_\mathrm {o}),\\ -\tau _0(r=\lambda _1)=\tau _\mathrm{y}=\tau _0(r=\lambda _2),\\ u_0(r=\lambda _1)=u_{0\mathrm{p}}=u_0(r=\lambda _2),\\ u_1(r=r_\mathrm {i})=0=u_1(r=r_\mathrm {o}),\\ u_1(r=\lambda _1)=u_{1\mathrm{p}}=u_1(r=\lambda _2).\\ \end{array}\right\} \end{aligned}$$
(31)

Solving the boundary value problem of Eqs. (23)–(31) gives

$$\begin{aligned} \tau _0= 2p(t)\frac{r^2-\lambda ^2}{r}, \end{aligned}$$
(32)
$$\begin{aligned}&u_0^+(r, t)\!=\!2p(t)\left[ \lambda ^2 \log \left( \frac{r}{r_\mathrm {i}}\right) \!-\!\left( \frac{r^2-r_\mathrm {i}^2}{2}\right) \!+\!\frac{\varLambda }{2}(r-r_\mathrm {i})\right. \left. \!-\!(2\varLambda )^\frac{1}{2}\,\int _{r_\mathrm {i}}^{r}\left( \frac{\lambda ^2-r^2}{r}\right) ^\frac{1}{2}\mathrm {d}r\right] \text{ if } \; r_\mathrm {i}\le r\le \lambda _1, \end{aligned}$$
(33a)
$$\begin{aligned}&u_{0\mathrm{p}}^-(r, t)\!=\!2p(t)\left[ \lambda ^2 \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) \!-\!\left( \frac{\lambda _1^2-r_\mathrm {i}^2}{2}\right) \!+\!\frac{\varLambda }{2}(\lambda _1-r_\mathrm {i})\right. \left. \!-\!(2 \varLambda )^\frac{1}{2}\,\int _{r_\mathrm {i}}^{\lambda _1}\left( \frac{\lambda ^2-r^2}{r}\right) ^\frac{1}{2}\mathrm {d}r\right] \quad \text{ if } \; \lambda _1\le r\le \lambda _2, \nonumber \\ \end{aligned}$$
(33b)
$$\begin{aligned}&u_0^{++}(r, t)\!=\!2p(t)\left[ \left( \frac{r_\mathrm {o}^2-r^2}{2}\right) \!+\!\lambda ^2 \log \left( \frac{r}{r_\mathrm {o}}\right) \!+\!\frac{\varLambda }{2}(r_\mathrm {o}\!-\!r)\right. \left. -(2\varLambda )^\frac{1}{2}\, \int _{r}^{r_\mathrm {o}}\left( \frac{r^2\!-\!\lambda ^2}{r}\right) ^\frac{1}{2}\mathrm {d}r\right] \quad \text{ if } \; \lambda _2\le r\le r_\mathrm {o},\nonumber \\ \end{aligned}$$
(33c)

where \(\lambda ^2=\lambda _1\lambda _2\) and \(\lambda _2-\lambda _1={\tau _\mathrm{y}}/{p(t)}=\varLambda \). The superscripts “+” and “++” indicate the shear flow regions \(r_\mathrm {i}\le r \le \lambda _1\) and \(\lambda _2\le r \le r_\mathrm {o} \), respectively, while “-” represents the plug-flow region \(\lambda _1\le r\le \lambda _2\). Explicit equations for \(\lambda _1\) and \(\lambda _2\) cannot be obtained due to the nonlinearity in the Casson constitutive relation.

Now, using the continuity equation, \(u_0^{+}(r=\lambda _1)=u_{0\mathrm{p}}=u_0^{++}(r=\lambda _2)\) i.e. \(u_0^{++}(r=\lambda _2)-u_0^{+}(r=\lambda _1)=0\), thus

$$\begin{aligned}&2\varLambda ^2+4\varLambda \lambda _1-\left( r_\mathrm {o}+r_\mathrm {i}\right) \left( r_\mathrm {o}-r_\mathrm {i}+\varLambda \right) -2\lambda _1\left( \varLambda +\lambda _1\right) \log \left( \frac{(\varLambda +\lambda _1)r_\mathrm {i}}{r_\mathrm {o} \lambda _1}\right) \nonumber \\&\quad -2(2\varLambda )^\frac{1}{2}\left[ \int _{r_\mathrm {i}}^{\lambda _1}\left( \frac{\lambda _1(\varLambda +\lambda _1)-r^2}{r}\right) ^\frac{1}{2}\mathrm {d}r\right. \left. -\int _{\lambda _1+\varLambda }^{r_\mathrm {o}}\left( \frac{r^2-\lambda _1(\varLambda +\lambda _1)}{r}\right) ^\frac{1}{2}\mathrm {d}r\right] =0. \end{aligned}$$
(34)

This integral equation is solved numerically for \(\lambda _1\) using the Regula Falsi method. Once \(\lambda _1\) is known, \(\lambda _2\) and \(\lambda \) can be obtained immediately from \(\lambda _2-\lambda _1={\tau _\mathrm{y}}/{p(t)}=\varLambda \) and \(\lambda ^2=\lambda _1\lambda _2\). The complete flow field can then be evaluated from Eqs. (33a)–(33c).

We now obtain the corrections to the shear stress and velocity distributions due to small inertial effects. Let \(u_1\) and \(\tau _1\) be the first correction of the velocity and shear stress over \(u_0\) and \(\tau _0\). From Eq. (27), the first correction to the shear stress due to inertial effects is

$$\begin{aligned} \tau _1=\frac{1}{r}\,\int _{r}^{\lambda }\frac{\partial {u_0}}{\partial {t}}r\, \mathrm {d}r+\frac{D_1(t)}{r}, \end{aligned}$$
(35)

where \(D_1(t)\) is an unknown function to be determined. The detailed derivation of \(\tau _1\) is provided in the “Appendix.” Because of this corrected shear stress, the yield plane locations \(\lambda _1\) and \(\lambda _2\) are shifted. Let the corrected yield plane locations be \(\lambda _1+\epsilon \lambda ^\mathrm{c}_1 \) and \(\lambda _2+\epsilon \lambda ^\mathrm{c}_2\), where \(\lambda ^\mathrm{c}_1\) and \(\lambda ^\mathrm{c}_2\) are correction factors. Then, using the conditions for the yield stress gives

$$\begin{aligned} -(\tau _0+\epsilon \tau _1)(r=\lambda _1+\epsilon \lambda ^\mathrm{c}_1 )=\tau _\mathrm{y}=(\tau _0+\epsilon \tau _1)(r=\lambda _2+\epsilon \lambda ^\mathrm{c}_2 ). \end{aligned}$$
(36)

Using Taylor’s series expansion and noting that

$$\begin{aligned} -\tau _0(r=\lambda _1)=\tau _\mathrm{y}=\tau _0(r=\lambda _2), \end{aligned}$$

we obtain

$$\begin{aligned} \lambda ^\mathrm{c}_1(t)= & {} -\frac{\tau _1(\lambda _1,t)}{\frac{\partial \tau _0}{\partial r}(\lambda _1,t)}, \end{aligned}$$
(37a)
$$\begin{aligned} \lambda ^\mathrm{c}_2(t)= & {} -\frac{\tau _1(\lambda _2,t)}{\frac{\partial \tau _0}{\partial r}(\lambda _2,t)}. \end{aligned}$$
(37b)

For large values of \(\mathrm {Sc}\), the corrections to these approximations, obtained from Eqs. (37a) and (37b), are negligible.

The first correction to the velocity distribution obtained from Eqs. (28)–(30) is

$$\begin{aligned}&u_1^{+}(r,t)=-\int _{r_\mathrm {i}}^{r}\left[ 1+\frac{\tau _\mathrm{y}^\frac{1}{2}}{\vert \tau _0\vert ^\frac{1}{2}}\right] \tau _1\, \mathrm {d}r \quad \text{ if } \; r_\mathrm {i}\le r \le \lambda _1, \end{aligned}$$
(38a)
$$\begin{aligned}&u_{1\mathrm{p}}^{-}(r,t)=u_{1\mathrm{p}}\quad \text{ if } \; \lambda _1\le r \le \lambda _2, \end{aligned}$$
(38b)
$$\begin{aligned}&u_1^{++}(r,t)=\int _{r}^{r_\mathrm {o}}\left[ 1-\frac{\tau _y^\frac{1}{2}}{\tau _0^\frac{1}{2}}\right] \tau _1\,\mathrm {d}r \quad \text{ if } \; \lambda _2\le r \le r_\mathrm {o}. \end{aligned}$$
(38c)

The unknown function \(D_1(t)\) in Eq. (35) is obtained by using the boundary condition \(u_1^{+}(r=\lambda _1)=u_{1\mathrm{p}}^{-}=u_1^{++}(r=\lambda _2)\), which leads to the following implicit integral equation for \(D_1(t)\):

$$\begin{aligned} \int _{r_\mathrm {i}}^{\lambda _1}\left[ 1+\frac{\tau _\mathrm{y}^\frac{1}{2}}{\vert \tau _0\vert ^\frac{1}{2}}\right] \tau _1\, \mathrm {d}r+ \int _ {\lambda _2}^{r_\mathrm {o}}\left[ 1-\frac{\tau _\mathrm{y}^\frac{1}{2}}{\tau _0^\frac{1}{2}}\right] \tau _1\, \mathrm {d}r=0. \end{aligned}$$
(39)

Equation (39) is solved numerically by the Regula Falsi method to find \(D_1(t)\). Once \(D_1(t)\) is known, \(u_1^{+}\), \(u_{1\mathrm{p}}^{-}\), and \(u_1^{++}\) can be obtained completely from Eqs. (38a)–(38c) using the corrected values of \(\tau _1\) in their respective regions.

Using the first two terms of the perturbation series, we obtain the velocity distribution in the different regions as follows:

$$\begin{aligned} \left. \begin{array}{ll} u^{+}(r,t)=u_0^{+}+\epsilon u_1^{+} &{}\quad \text{ if } \; r_\mathrm {i}\le r \le \lambda _1, \\ u^{-}(r,t)=u_{0\mathrm{p}}^{-}+\epsilon u_{1\mathrm{p}}^{-} &{}\quad \text{ if } \; \lambda _1\le r \le \lambda _2,\\ u^{++}(r,t)=u_0^{++}+\epsilon u_1^{++} &{}\quad \text{ if } \; \lambda _2\le r \le r_\mathrm {o}. \end{array} \right\} \end{aligned}$$
(40)

The steady component of the velocity distribution is obtained from Eq. (40) by substituting \(e=0\) into \(p(t)=1+e \,\sin (\alpha ^2\;\mathrm {Sc}\;t)\) (i.e., \(p(t)=1\)); thus for purely unsteady flow, \(p(t)=e \,\sin (\alpha ^2\;\mathrm {Sc}\;t)\).

We now consider the Aris–Barton approach to study the dispersion of the reactive solute.

4 Aris–Barton approach

The pth moment of the distribution of the solute for the mobile phase in the axial flow at time t can be described, following Aris [2], as

$$\begin{aligned} C^{(p)}(t,r) = \int _{-\infty } ^{+\infty } z^p C(t,r, z)\,\mathrm {d}z, \end{aligned}$$
(41)

and likewise for the immobile phase we may assume that

$$\begin{aligned} {C_\mathrm{s}}^{(p)}(t) = \int _{-\infty } ^{+\infty } z^p C_\mathrm{s}(t,z)\,\mathrm {d}z. \end{aligned}$$
(42)

Using Eqs. (41) and (42), the diffusion equation (12) and the immobile mass distribution equation (13) can be written as

$$\begin{aligned}&\frac{\partial C^{(p)}}{\partial t} - \frac{1}{r} \frac{\partial }{\partial r} \left( r\frac{\partial C^{(p)}}{\partial r}\right) +\beta C^{(p)} = p \ u(r, t)\ C^{(p-1)} + \frac{1}{\mathrm {Pe}^2}p(p-1)C^{(p-2)}, \end{aligned}$$
(43)
$$\begin{aligned}&\frac{\mathrm {d} }{\mathrm {d} t}C_\mathrm{s}^{(p)}= \mathrm {Da}\left[ \varOmega C^{(p)}(t,r_\mathrm {o})-C_\mathrm{s}^{(p)}\right] , \end{aligned}$$
(44)

subject to the initial and boundary conditions

$$\begin{aligned}&\left. \begin{array}{lcl} C^{(p)}(0, r) = \left\{ \begin{array}{ll} \frac{1}{\mathrm {Pe}} &{} \text{ for }\, p=0,\\ 0 &{} \text{ for }\, p>0, \end{array} \right. \\ C_\mathrm{s}^{(p)}(0)=0,\\ \end{array} \right\} \end{aligned}$$
(45)
$$\begin{aligned}&\displaystyle \frac{\partial C^{(p)}}{\partial r} = 0 \quad \text{ at }\; r=r_\mathrm {i}, \end{aligned}$$
(46)
$$\begin{aligned}&\displaystyle -\frac{\partial C^{(p)}}{\partial r} -\varGamma C^{(p)} = \mathrm {Da}[\varOmega C^{(p)}-C_\mathrm{s}^{(p)}] \quad \text{ at }\; r=r_\mathrm {o}. \end{aligned}$$
(47)

The pth moment of the distribution of the solute in the mobile phase over the cross-section of the pipe is given by

$$\begin{aligned} \left\langle {C^{(p)}}(t)\right\rangle = \frac{2}{r_\mathrm {o}^2-r_\mathrm {i}^2}\int _{r_\mathrm {i}}^{r_\mathrm {o}} r C^{(p)}(t,r)\mathrm {d}r, \end{aligned}$$
(48)

where the angle bracket \(\langle \cdot \rangle \) denotes the cross-sectional mean. With this definition, Eq. (43) and Eq. (45) become

$$\begin{aligned} \frac{\mathrm {d} }{\mathrm {d}t} \left\langle {C^{(p)}}\right\rangle= & {} \frac{2 r_\mathrm {o}}{r_\mathrm {o}^2-r_\mathrm {i}^2}\left[ \mathrm {Da} C_\mathrm{s}^{(p)}(t)-\left( \varGamma +\mathrm {Da} \varOmega \right) C^{(p)}(t,r_\mathrm {o})\right] -\beta \left\langle {C^{(p)}}\right\rangle + \ p \left\langle {u(r,t) C^{(p-1)}}\right\rangle \nonumber \\&\quad + \frac{1}{\mathrm {Pe}^2}\ p(p-1) \left\langle {C^{(p-2)}}\right\rangle , \end{aligned}$$
(49)

and

$$\begin{aligned} \left. \begin{aligned} \left\langle {C^{(p)}}(0)\right\rangle= & {} \frac{1}{\mathrm {Pe}} \quad \text{ for } p=0,\\= & {} 0 \quad \text{ for } p>0. \end{aligned} \right\} \end{aligned}$$
(50)

The pth-order central moment about the mean of the concentration distribution can be defined as

$$\begin{aligned} {\mu }_p (t)= \frac{\int _{r_\mathrm {i}}^{r_\mathrm {o}} \int _{0}^{2\pi }\int _{-\infty }^{+\infty } r(z-z_\mathrm{g})^p C\, \text{ d }r\, \text{ d }{\theta }\,\text{ d }z}{\int _{r_\mathrm {i}}^{r_\mathrm {o}} \int _{0}^{2\pi } \int _{-\infty }^{+\infty } r C \,\text{ d }r\, \text{ d }{\theta }\,\text{ d }z}, \end{aligned}$$
(51)

where

$$\begin{aligned} z_\mathrm{g}=\frac{\int \int \int zC\,\text{ d }v }{\int \int \int C\, \text{ d }v}=\frac{\large {\langle {C^{(1)}}\rangle }}{\large {\langle {C^{(0)}}\rangle }} \end{aligned}$$

represents the centroid or first moment of the distribution of the solute and \(\langle {C^{(0)}}\rangle \) is the total mass of the chemical species in the flowing stream.

The higher-order central moments can be obtained from Eq. (51) as

$$\begin{aligned} \left. \begin{array}{lcl} \mu _2(t) &{} = &{} \frac{\large {\langle {C^{(2)}}\rangle }}{ \large {\langle {C^{(0)}}\rangle }} - z_\mathrm{g}^2, \\ \mu _3(t) &{} = &{} \frac{\large {\langle {C^{(3)}}\rangle }}{\large {\langle {C^{(0)}}\rangle }} - 3 z_\mathrm{g} \mu _2 - z_\mathrm{g}^3, \\ \mu _4(t) &{} = &{}\frac{\large {\langle {C^{(4)}}\rangle }}{\large {\langle {C^{(0)}}\rangle }}- 4 z_\mathrm{g} \mu _3 - 6 z_\mathrm{g}^2 \mu _2 -z_\mathrm{g}^4. \end{array} \right\} \end{aligned}$$
(52)

While explaining dispersion phenomena, Aris [2] revealed the physical significance of each of the integral moments of the concentration defined in Eq. (52). The integral moment equation (43) is a sequence of inhomogeneous equations for \(p=0,1,2,3,\ldots \) and can be solved for sufficiently high values of p to obtain the developed distribution to any degree of accuracy. Since the distribution finally tends to normal, the first two moments are ultimately sufficient to describe the distribution, where the third and fourth moments should be zero. A very useful picture of the progress of the dispersion can be obtained from the first three or four moments. Aris [2] showed that the rate of change of the variance is proportional to the sum of the molecular diffusion coefficient along the axial direction and the apparent dispersion coefficient (Taylor dispersion coefficient). Since the axial diffusion is negligible compared with the lateral diffusion, the apparent dispersion coefficient \(D_\mathrm{c}\) can be written as

$$\begin{aligned} D_\mathrm{c}=\frac{1}{2}\frac{\mathrm {d} \mu _2}{\mathrm {d}t}. \end{aligned}$$
(53)

To solve Eqs. (43)–(47), a standard finite-difference method based on a Crank–Nicolson implicit scheme is adopted due to the complexities in the moment equation. The whole width of the annulus is divided into \((M-1)\) equal parts of mesh size \(\varDelta r\), represented by the grid point j. Thus, the inner and outer walls of the annulus are addressed by \(j=1\) and \(j=M\), respectively, i.e., \({r_j = r_{\mathrm {i}} + (j-1) \times \varDelta r}\). Time is indexed by the grid point i, where each step size is assumed to be \(\varDelta t\). The general form of the time discretization is \({t_i = \varDelta t\times (i-1)}\), hence the initial time \(t=0\) corresponds to fixed \(i=1\). \(C^{(p)}(i,j)\) indicates the value of \(C^{(p)}\) at the ith grid point along the t-axis and jth grid point along the r-axis. The resulting finite-difference equations become simultaneous linear algebraic equations with a tridiagonal coefficient matrix:

$$\begin{aligned} P_j C^{(p)}(i+1, j+1) + Q_j C^{(p)}(i+1, j) + R_j C^{(p)}(i+1, j-1) = S_j, \end{aligned}$$
(54)

where \(P_j\), \(Q_j\), \(R_j\), and \(S_j\) are the matrix elements.

The concentration of immobile phase \(C_\mathrm{s}^{(p)}(i)\) can be computed from the relation

$$\begin{aligned} C_\mathrm{s}^{(p)}(i+1)=\frac{C_\mathrm{s}^{(p)}(i)+\mathrm {Da}\; \varDelta t \varOmega \;C^{(p)}(i+1,M)}{1+\displaystyle \mathrm {Da}\; \varDelta t}. \end{aligned}$$
(55)

The finite-difference form of the initial condition is

$$\begin{aligned} \left. \begin{array}{lcl} C^{(p)}(1, j) &{}=&{} \left\{ \begin{array}{ll} \frac{1}{\mathrm {Pe}} &{} \text{ for } p=0,\\ 0 &{} \text{ for } p>0, \end{array} \right. \\ C_\mathrm{s}^{(p)}(1)&{}=&{}0,\\ \end{array} \right\} \end{aligned}$$
(56)

while that of the boundary conditions is

$$\begin{aligned}&C^{(p)}(i+1,0) = C^{(p)}(i+1,2) \;\text{(at } \text{ the } \text{ surface } \text{ of } \text{ the } \text{ inner } \text{ cylinder) } \text{ and }\nonumber \\&C^{(p)}(i+1, M+1) = C^{(p)}(i+1, M-1) - 2\varDelta r(\varGamma +\mathrm {Da} \varOmega )C^{(p)}(i+1,M)+2\varDelta r \mathrm {Da} C_\mathrm{s}^{(p)}(i),\nonumber \\&\quad \text{(at } \text{ the } \text{ surface } \text{ of } \text{ the } \text{ outer } \text{ cylinder) }. \end{aligned}$$
(57)

Utilizing the Thomas algorithm (Anderson et al. [53]), a MATLAB code is developed to solve the tridiagonal coefficient matrices resulting from Eq. (54). First, the time-dependent axial velocity u is computed at all grid points using Eq. (40). Second, the concentration \(C^{(p)}\) is calculated from Eq. (43) as the value of u(r, t) at each of the grid points (\(i+1\), j) obtained in the previous step. Third, having the value of \(C^{(p)}\) from the second step, \(C_\mathrm{s}^{(p)}\) is calculated from Eq. (44). Finally, the value of \(\langle {C^{(p)}}(t)\rangle \) is calculated from Eq. (48) by Simpson’s one-third rule, using the known values from prior steps at their corresponding grid positions.

Numerical calculations are performed for steady, unsteady, and combined flow situations to study their effect on the dispersion process under variation of different parameters. The present scheme is linearly stable for any finite value of \(\varDelta t/(\varDelta r)^2\); sufficiently small mesh size of the spatial and temporal discretizations ensures precision of \(10^{-5}\) in the results. In all the cases, we take \(\alpha =0.5\), \(e=0.5\), and \(\mathrm {Pe}=\mathrm {Sc}= 1000\).

Fig. 2
figure 2

Variation of dispersion coefficient \(D_\mathrm{c}\) with time t when \(\eta \rightarrow 0\), \(e=0\), \(\tau _\mathrm{y}=0\), and \(\beta =0\)

Full size image

5 Results and discussion

To observe the effect of the heterogeneous and homogeneous reactions on the solute dispersion in a non-Newtonian liquid, a Casson liquid model is considered due to its application in analysis of the flow of blood-like liquids. The work described herein considers the Aris–Barton approach to dispersion analysis, examining the following cases to confirm the validity of the numerical scheme for the integral moment equation:

  1. Case (a):

    For the parameter values listed in Fig. 2, with radius ratio \(\eta \rightarrow 0 \) (i.e., \(r_\mathrm {i}\rightarrow 0\) and \(r_\mathrm {o}\rightarrow 1\)), yield stress \(\tau _\mathrm{y}=0\) (i.e., Newtonian fluid), amplitude of the fluctuating component \(e=0\) (i.e., steady flow), and bulk flow reaction rate \(\beta =0\) (i.e., no homogeneous reaction), the present result agrees well with Fig. 1 of Lau and Ng [54] both qualitatively and quantitatively.

  2. Case (b):

    To compare the results of the present dispersion model with that of Rana and Murthy [33], the following parameter values are considered: irreversible absorption rate \(\varGamma =0.01\) (i.e., presence of boundary absorption), bulk flow reaction rate \(\beta =0\) (i.e., no homogeneous reaction), and reversible phase exchange rate \(\mathrm {Da}=0\) (i.e., no reversible reaction at the boundary), where the flow field is obtained from Eq. (40) by applying \(\eta \rightarrow 0 \) (i.e., cylindrical pipe) and \(\alpha =e=0.5\) (i.e., unsteady flow), respectively. Figure 3a, b shows the temporal variation of the dispersion coefficient with the yield stress \(\tau _\mathrm{y}\); the model trend totally agrees qualitatively and quantitatively with the results of Rana and Murthy [33] (Fig. 3 coincides with Fig. 11 in Rana and Murthy [33]).

  3. Case (c):

    For \(\eta \rightarrow 0\), \(\tau _\mathrm{y}=0\), \(e=0\), and \(\mathrm {Da}=0\), the present work is equivalent to the model of Gupta and Gupta [40], where first-order irreversible chemical reactions are considered at the wall (heterogeneous reaction) and in the bulk flow (homogeneous reaction). Figure 4a applies for a homogeneous reaction in the bulk flow with no reaction at the walls, whereas Fig. 4b describes the coupled effect of both reaction parameters. The results in Fig. 4 clearly indicate that an increase in the reaction rate at the wall and bulk flow leads to a decrease in the dispersion coefficient. A similar kind of behavior was noted in the work of Gupta and Gupta [40] for laminar Newtonian flow between two parallel plates. The present model can thus be considered to represent a generalization of the work of Gupta and Gupta [40] to a non-Newtonian environment, representing a further validation of the model.

Fig. 3
figure 3

Variation of dispersion coefficient \(D_\mathrm{c}\) with time t for different values of yield stress \(\tau _\mathrm{y}\), when \(\eta \rightarrow 0\), \(\varGamma =0.01\), \(\beta =0\), \(\mathrm {Da}=0\), \(\alpha =0.5\), \(e=0.5\), and \(\mathrm {Sc}=1000\), for (a) short and (b) long times

Full size image
Fig. 4
figure 4

Variation of unsteady dispersion coefficient \(D_\mathrm{c}\) with (a) homogeneous reaction rate \(\beta \) for \(\varGamma =0\) and (b) heterogeneous reaction rate \(\varGamma \) for \(\beta =1\). At time \(t=0.5\), \(\eta \rightarrow 0\), \(\tau _\mathrm{y}=0\), \(e=0\), and \(\mathrm {Da}=0\)

Full size image

To show the coupled effects of the reaction parameters, viz. reversible phase exchange, irreversible absorption, and bulk flow reaction, for various velocity distributions, viz. steady, unsteady, and combined flows, figures are plotted for seven different combinations of \(\varOmega \), \(\mathrm {Da}\), \(\varGamma \), and \(\beta \) as listed in Table 1. Furthermore, the roles of the rheological parameter (yield stress) \(\tau _\mathrm{y}\) and radius ratio \(\eta \) in the dispersion process are also discussed.

Table 1 Values of controlling parameters considered in the present study
Full size table

5.1 Dispersion coefficient

Figure 5 shows the variation of the unsteady dispersion coefficient with respect to the steady component of the velocity distribution. The individual effect of the reaction parameters is considered without the presence of any other reactions, thus Fig. 5a demonstrates the effect of the phase exchange rate \(\mathrm {Da}\), whereas Fig. 5b, c shows the effects of the absorption parameter \(\varGamma \) and bulk flow reaction parameter \(\beta \) on the pipe boundary and in the bulk flow, respectively. It is clear from Fig. 5a that the reversible phase exchange rate increases the value of the dispersion coefficient \(D_\mathrm{c}\), where a fast phase exchange rate means that the steady state of \(D_\mathrm{c}\) appears in a short duration of time due to the strong retentive effect, which completely agrees with Lau and Ng [54]. As described in the work of Rana and Murthy [33], a high absorption rate here also diminishes the magnitude of the apparent dispersion coefficient \(D_\mathrm{c}\) (Fig. 5b). The temporal evolution of the dispersion coefficient due to the bulk flow reaction rate constant \(\beta \) is described in Fig. 5c. It is found that, with the homogeneous reaction in the bulk flow, the effective dispersion coefficient decreases with increase in the reaction rate constant \(\beta \), which agrees well with the findings of Gupta and Gupta [40]. From Fig. 5a–c, it can also be stated that the effect of the reaction in the bulk flow is less significant compared with the wall reactions.

Fig. 5
figure 5

Variation of dispersion coefficient \(D_\mathrm{c}\) with time t, when \(\eta =0.1\) and \(\tau _\mathrm{y}=0.04\) for a phase exchange rate \(\mathrm {Da}\), b irreversible absorption rate \(\varGamma \), and c bulk flow reaction rate \(\beta \)

Full size image

The coupled effect of the reactions on the dispersion as presented in Table 1 is investigated by discussing Fig. 6. The black colored line in Fig. 6 is for no reaction, whereas the solid color lines apply for lesser effect of the reactions and the dashed lines for their strong effect. A long time scale is considered to track the asymptotic behavior of the solute dispersion coefficient. Based on the results in Fig. 6, it is observed that the dispersion coefficient initially increases with time and reaches a stationary state after \(t = 0.783\), for case I without reactions. Cases II and III correspond to the analysis with slow and fast phase exchange rates, clearly revealing that the dispersion coefficient in case III reaches its steady-state point in a short duration of time compared with case II. The plots for cases IV and V suggest that the dispersion coefficient takes a long time to reach a steady value for weak absorption, whereas for the fast absorption rate, the dispersion coefficient rises to a local peak at \(t = 1.667\), before decreasing. According to cases VI and VII, the effect of the bulk flow reaction rate on the dispersion is similar to the effect induced by absorption at the outer boundary of the annulus. This kind of behavior of \(D_\mathrm{c}\), for the described reaction parameters, completely obeys the nature of physics, although some paradoxical behavior of the dispersion coefficient in the steady flow follows for cases II, V, and VII. Such an initial rise followed by a dramatic fall to a negative dispersion coefficient was also observed by Ng and Rudraiah [42] and Phillips et al. [55]. As the solute moves forward, the growing absorption and bulk flow reaction rate lead to an increase in the number of moles of reactive solute (i.e., an increase in the movement of the front cloud), while on the other hand, due to boundary retention, the concentration near the wall controls the trailing edge of the cloud, which hence can narrowly move far from the point of injection. Because of the high depletion rate, the mass loss at the front of the cloud is much quicker compared with at the trailing edge due to the slow wall retention, resulting in a large difference in concentration between the tailing and leading edges and thus a maximum value of the dispersion coefficient. Consequently, the approach of the dispersion coefficient towards negativity is perhaps due to the fast absorption rate rather than the slow wall retention (cases II, V, and VII in Table 1).

Fig. 6
figure 6

For steady flow, temporal evolution of the dispersion coefficient \(D_\mathrm{c}\) for the cases listed in Table 1, when \(\eta =0.1\) and \(\tau _\mathrm{y}=0.04\)

Full size image
Fig. 7
figure 7

For unsteady flow; descriptions as in Fig. 6

Full size image

The temporal evolution of the dispersion coefficient for the purely unsteady flow is documented in Figs. 7 and 8, at short and long times for the seven different combinations of the controlling parameters listed in Table 1. The colors used in Figs. 7 and 8 are similar to those in Fig. 6. It can be easily observed from Fig. 7 that, in a purely unsteady flow field, \(D_\mathrm{c}\) is reduced by all the reaction parameter, i.e., \(\mathrm {Da}\), \(\varGamma \), and \(\beta \), at short times. It can also be inferred that, during the initial time period, the rate of decrement of \(D_\mathrm{c}\) for the phase exchange rate and bulk flow reaction rate is not that significant, with the effect of the reactions in the bulk flow on the dispersion being less appreciable in particular. The fall and growth of the dispersion coefficient should not be taken as depending absolutely on the change of the reaction parameters, as the situation may also vary with the strength of the reactions, time span, yield stress, pulsation frequency, radius ratio, etc. At long times, similar qualitative effects of the absorption parameter on the dispersion coefficient can be seen in Fig. 8, although the fast phase exchange rate and strong bulk flow reaction rate cause an augmentation in the dispersion coefficient. It is noticeable that the responses of the dispersion coefficient seem to be more sensitive at long times.

Fig. 8
figure 8

Same as Fig. 7, for long times

Full size image
Fig. 9
figure 9

For combined flows; descriptions as in Fig. 6

Full size image

The coupled effect of the reaction parameters on the dispersion due to the combined (steady + unsteady) effect of the velocity distribution is shown in Figs. 9 and 10 at short and long times for the seven different combinations of the controlling parameters listed in Table 1. The results in Figs. 9 and 10 are similar to those in Figs. 7 and 8 for purely unsteady flows at both short and long times. The decrease in the dispersion coefficient with an increase in the value of the irreversible absorption parameter \(\varGamma \) is based on sound physical grounds. An increase in \(\varGamma \) leads to a growth in the number of moles of solute undergoing chemical reaction, resulting in a drop in the dispersion coefficient to all times. Compared with the other reaction parameters, the reversible reaction has the greatest impact on the dispersion at long times.

Fig. 10
figure 10

Same as Fig. 9, for long times

Full size image

In the present model, the role of the rheological parameter or yield stress \(\tau _\mathrm{y}\) is to capture the importance of non-Newtonian effects in the solute dispersion process. The rheological equation for a Casson liquid is defined in Eq. (3). If the shear stress is less than the yield stress, the fluid behaves like a solid body (i.e., plug-flow region), whereas if a shear stress greater than the yield stress is applied, it starts to move. The plug-flow region within the Casson liquid region is vital (Shaul and Kalman [56]), due to the significant advantages of transporting particulate material in plug form including low energy consumption, low particle attrition, and low pipe erosion. The yield stress of human blood is typically 0.04 \(\mathrm{dyn}/{\mathrm{cm}^2}\) at a hematocrit of 40\(\%\) (Merrill [57], McDonald [47], Merrill et al. [58]). For the combined flow situation, the effect of the yield stress \(\tau _\mathrm{y}\) on the dispersion coefficient \(D_\mathrm{c}\) is revealed by Fig. 11a, b. From Fig. 11a, b, it is completely understandable that an increase in yield stress decreases the value of the dispersion coefficient. This kind of behavior of \(D_\mathrm{c}\) appears due to the decrease in the flow velocity or the increase of the plug-flow region for larger yield stress values. A similar kind of behavior of \(D_\mathrm{c}\) with \(\tau _\mathrm{y}\) was found in the study of Nagarani and Sebastian [48]. At all times, the variation of the dispersion coefficient with the radius ratio is shown in Fig. 12, where larger values of \(\eta \) cause a significant decrement of \(D_\mathrm{c}\). At a given radial position, the velocity decreases with an increase in the radius ratio (figure not shown).

Fig. 11
figure 11

Variation of dispersion coefficient \(D_\mathrm{c}\) with time t for different values of yield stress \(\tau _\mathrm{y}\) when \(\eta =0.1\), \(\varOmega =0.05\), \( \mathrm {Da}=1\), \(\varGamma =1\), and \(\beta =1.5\) for a short and b long times

Full size image
Fig. 12
figure 12

Variation of dispersion coefficient \(D_\mathrm{c}\) with time t for different values of radius ratio \(\eta \) when \(\tau _\mathrm{y}=0.04\), \(\varOmega =0.05\), \( \mathrm {Da}=1\), \(\varGamma =1\), and \(\beta =1.5\) for a short and b long times

Full size image

Figure 13 presents a comparative study of the dispersion coefficient \(D_\mathrm{c}\) between the Newtonian and Casson fluid models. It is observed from Fig. 13a, b that, for the case of the Casson fluid (when \(\tau _\mathrm{y}=0.02\)), the magnitude of the dispersion coefficient is significantly lower than for the single-layer Newtonian fluid (when \(\tau _\mathrm{y}=0\)). Due to the presence of nonzero yield stress (\(\tau _\mathrm{y}\)) in the Casson fluid, resistance occurs, thus reducing the fluid velocity compared with the Newtonian fluid. Hence, a decrease in the dispersion coefficient is noticed at all times.

Fig. 13
figure 13

Variation of dispersion coefficient \(D_\mathrm{c}\) with time t when \(\eta =0.1\), \( \varOmega =0.05\), \( \mathrm {Da}=1\), \(\varGamma =1\), \(\beta =1.5\), and \(\tau _\mathrm{y}=0\) (Newtonian fluid) or \(\tau _\mathrm{y}=0.02\) (Casson fluid) for a short and b long times

Full size image

5.2 Mean concentration distribution

According to the very popular work of Taylor [1], for a shear-dependent flow, the distribution of the solute concentration is centered on a point that moves with the mean speed of the flow. The Taylor dispersion process refers to an asymptotic stage of the solute transport in a transversely confined flow region; during the process, the cross-sectional mean concentration forms a Gaussian distribution longitudinally. When convection is a major effect compared with dispersion, it is expected that the curve will be nearly Gaussian (Levenspiel and Smith [59]), so the concentration can be represented using a series of Hermite polynomials. Aris’s method of moments is useful for finding the central moments, and again using higher-order central moments, it is possible to approximate the mean axial concentration distribution \(C_\mathrm{m}(t, z)\) of a tracer within the flow region with the help of the Hermite polynomial representation for non-Gaussian curves (Mehta et al. [60], Mazumder and Das [8], Mazumder and Paul [45], Wang and Chen [61]). The cross-sectional mean concentration \(C_\mathrm{m}(t, z)\) is defined as

$$\begin{aligned} C_\mathrm{m}(t, z) = \left\langle {C}^{(0)}(t)\right\rangle \mathrm{e}^{-\xi ^2} \sum _{n=0}^\infty a_n(t) H_n(\xi ), \end{aligned}$$
(58)

where \( \xi = (z - z_\mathrm{g})/\sqrt{ 2 \mu _2}\), \(z_\mathrm{g} = {\langle {C}^{(1)}\rangle }/{\langle {C}^{(0)}\rangle }\), and the \(H_i\) are Hermite polynomials that satisfy the recurrence relation

$$\begin{aligned} H_{i+1}(\xi ) = 2\xi H_i(\xi ) - 2iH_{i-1}(\xi ), \quad i=0,1,2,\ldots \quad (H_0(\xi )=1). \end{aligned}$$

The coefficients \(a_i\) are given by

$$\begin{aligned} a_0 = 1/( 2 \pi \mu _2 )^{1/2}, \quad a_1=a_2=0,\quad a_3 = 2^{1/2} a_0 \nu _2 /24, \quad a_4 = a_0 \nu _3 /96. \end{aligned}$$
(59)

The mean concentration distribution \(C_\mathrm{m}(t, z)\) is plotted against the axial distance (\(z-z_\mathrm{g}\)) for the unsteady flow in Fig. 14a–d for the various combinations of the reaction parameters listed in Table 1 at dimensionless times of \(t=0.2\), 0.35, 0.5, and 0.65. From Fig. 14a–d, a strong absorption rate, fast phase exchange rate, and strong bulk flow reaction rate decrease the peak of the mean concentration distribution. Due to the consumption of the solute at the outer boundary of the annulus, a small amount of solute will get a chance to diffuse for high absorption, thus an increase in absorption will decrease \(C_\mathrm{m}\) in the axial direction. The wall retention reduces the amount of solute in the mobile phase, corresponding to a smaller area under the distribution curve. The increase of the homogeneous bulk-flow reaction parameter \(\beta \) ensures the depletion of the reactive material, thus the peak of the mean concentration distribution gradually decreases. Note that high absorption at the boundary of the annulus and strong reaction in the bulk flow may not have a constructive significance for long time, \(t=0.65\). From Fig. 15a, b, it is found that, as \(\tau _\mathrm{y}\) increases, so does the peak of the mean concentration distribution. Due to the increase in the yield stress in the fluid, the flow velocity reduces and hence the solute dispersion decreases. Therefore, the mean concentration of the solute increases in the axial direction.

Fig. 14
figure 14

Longitudinal distribution of mean concentration at different times against the axial distance for unsteady flow when \(\eta =0.1\), and \(\tau _\mathrm{y}=0.04\)

Full size image
Fig. 15
figure 15

Longitudinal distribution of mean concentration for different values of yield stress \(\tau _\mathrm{y}\) when \(\eta =0.1\), \(\varOmega =0.05\), \(\mathrm {Da}=1\), \( \varGamma =1\), and \(\beta =1.5\) at time a\(t=0.15\) and b\(t=0.5\)

Full size image

6 Conclusions

The convection–diffusion transport of a chemical species in a pulsatile flow through an annular pipe is investigated. In addition to heterogeneous (at the outer boundary of the annulus) and homogeneous (in the bulk flow) reactions, the analysis also considers a non-Newtonian Casson liquid as the carrier fluid, which is significant for analysis of flows of blood-like liquids. Aris’s method of moments is used for all-time dispersion analysis, utilizing a standard finite-difference implicit scheme to obtain the central moments. The numerical technique is first verified against some previous works. The following general conclusions can be drawn from the results of the present study:

  1. (i)

    The individual effects of a fast phase exchange rate \(\mathrm {Da}\), strong absorption rate \(\varGamma \), and strong bulk flow reaction rate \(\beta \) are found to decrease the dispersion coefficient \(D_\mathrm{c}\) at all times in the steady flow.

  2. (ii)

    For the case of steady flow with the coupled effect of the reaction parameters (i.e., \(\mathrm {Da}\), \(\varGamma \), and \(\beta \)), the dispersion coefficient reaches a steady value after a short duration for high reaction rates.

  3. (iii)

    Due to the fast absorption rate compared with the slow wall retention, the dispersion coefficient is found to be negative under the coupled effect of the reaction parameters.

  4. (iv)

    For the case of purely unsteady and combined flow, \(D_\mathrm{c}\) is found to decrease with \(\varGamma \) at short as well as long times, whereas \(D_\mathrm{c}\) varies with time due to the effects of the reversible reaction at the boundary and the first-order reaction in the bulk flow. At short times, \(D_\mathrm{c}\) is reduced by both \(\mathrm {Da}\) and \(\beta \), but at long times, the opposite effect occurs.

  5. (v)

    Among all the reactions, the minimal effect of the bulk flow reaction parameter on the dispersion is observed.

  6. (vi)

    The rheological parameter (yield stress) and the radius ratio of the annulus are found to reduce the value of the dispersion coefficient.

  7. (vii)

    Due to the stronger effect of all three reaction parameters, the peak of the mean concentration distribution diminishes. The peak of the mean concentration distribution increases with the yield stress.

  8. (viii)

    Due to the nature of the effects considered herein, this work is much closer to the physiological situation compared with several other works, as far as possible from a mathematical perspective, meriting its use in the clinical context.