Electric potential of a point charge in multilayered dielectrics evaluated from Hankel transform

Abstract

Electric potential of a point charge embedded in a three-layered dielectric system with infinite planar interfaces is determined. Using the technique of Hankel transform, the electric potentials in all domains are obtained in closed form. Nondimensionalization of the solution reduces the governing parameters into three scalars: a normalized charge location and two dielectric constant ratios. Numerical parametric study reveals interesting, coupled influences of these parameters on the distribution of electric potential. Due to the linear nature of the electrostatic problem, the solution here can be extended to similar multilayered dielectric systems with a distribution of charges.

1 Introduction

The applications of layered dielectric systems are common in energy storage and electrical insulation devices. Most of these devices consist of multiple layers of dielectric between grounded conducting plates or charged conductors [1, 2]. Microwave technologies such as antennas, transmission lines, computers, filters, power dividers, etc. are also made of several conductor–dielectric combinations. Studies on the performance of these electrical devices involve the calculation of electric potential and electric field as well as electrostatic force at the interfaces due to charge distribution in the system [3,4,5,6]. As one example, in order to determine the wave propagation properties of microstrip transmission lines, one must first obtain the electric field for a pair of charged conductors separated by a dielectric sheet [5]. Another very common physical phenomenon in layered dielectrics is adhesion (attractive force) between surfaces caused by contact charging [7, 8]. Calculation of the surface force first requires the knowledge of the electric potential in the space, which is occupied by dielectrics with different properties. Motivated by these applications, in this work we aim at establishing a theoretical framework of solving the electric potential in a multilayered dielectric system due to the presence of a point charge. Because of the linear nature of the problem, the solution can be easily extended to calculate electric potential induced by a distribution of charges.

Electrostatic problems involving a point charge in multilayered dielectrics have been studied in a number of previous works. Green’s function–moment method based on image theory is commonly used in literature to solve such problems. Pumplin [9] considered the problem of a parallel plate capacitor that consisted of two grounded plates and a point charge in between. The electric potential was solved using image charge method and presented in terms of Green’s function. Specifically, a distribution of point charges was introduced in the upper and lower spaces, with each charge having the same magnitude as the original point charge. The location of the image charges was solved to ensure that the electric potential on the two interfaces (grounded conducting plates) was zero. Pronic et al. [10] studied a multilayered dielectric system enclosed by a cylindrical conductor. An analogy was drawn to multistep electrical transmission line [4] which had a current source with its two ends short terminated. Based on the analogy, Green’s function satisfying the Poisson’s differential equation was obtained for a point charge in the structure and the solution for the electric potential was presented as a double infinite sum. Image charge method was also used in a number of other works to obtain the electric potential in a layered dielectric sphere [11], multiconductor transmission lines [3], etc.

Heubrandtner et al. [12] presented expressions for the electric field of a point charge in an infinite plane condenser. They mentioned its application in particle detection process through Parallel Plate Chambers (PPC) and Resistive Plate Chambers (RPC), which consisted of one and three homogeneous layers of dielectrics, respectively. The condenser was modeled as a single or multilayered dielectrics packed between two grounded conducting plates. Solution for the electric potential in the condenser was given, without detailed derivations, both in terms of infinite series and using an integral representation. The focus of Heubrandtner et al.’s study was to examine the convergence performance of the two forms of the solutions. Near the point of divergence, where the point charge is located, the integral representation of the solution gives overall better result than the series solution, due to the faster decay of the integrand and better performance in numerically evaluating the electric field when the electric potential needs to be differentiated.

Interests in problems involving a point charge in layered dielectric medium continued in recent years. A number of works considered the smooth transition between two dielectrics, i.e., these two dielectrics are separated by a middle layer (called diffuse interface) with a gradual change in dielectric permittivity from one side to the other. Xue and Deng [13] provided an excellent review of studies on diffuse interface and also revisited the problem containing a point charge in such three-layered dielectric system. They first obtained the Green’s function for a quasi-harmonic diffuse interface and then extended the results to general diffuse interfaces by dividing the transition layer into multiple quasi-harmonic sublayers. There were also studies that examined layered medium containing electrolyte solution, for instance to mimic biological membrane in electrolytic environment. Lin et al. [14] investigated such a system, with one dielectric layer (governed by Poisson’s equation) sandwiched between two electrolyte layers (governed by Poisson–Boltzmann equation). The electric potential due to a point charge in the middle layer was solved using the method of image charges.

The specific problem considered in this work is shown in Fig. 1. The space is separated into three dielectric domains, each being homogeneous and having dielectric constants of $\varepsilon _1$ (domain I, in the middle), $\varepsilon _2$ (domain II, in the lower domain), and $\varepsilon _3$ (domain III, in the upper domain), respectively. Because in the multilayered dielectric systems used in practice the horizontal dimension is typically much larger than the thickness of the middle layer (H), the three layers are approximated to be infinitely large in the horizontal direction. For the same reason, since the thicknesses of the top and bottom layers are usually much larger than H, the lower space (II) is assumed to extend downward to infinity, while the upper space (III) is assumed to extend upwards to infinity. These three domains are separated by hypothetical planar interface. A point charge of magnitude q is located at a distance d above the lower interface $(0<d<H)$. The objective is to solve for the electric potential in all three domains in terms of q, d, H, and the three dielectric constants $\varepsilon _1$, $\varepsilon _2$, and $\varepsilon _3$.

Fig. 1

Schematic of the electrostatic problem considered in this work

Although the problem shown in Fig. 1 appears to be a simple system, our extensive literature searches only found one previous work that considered the same situation [15]. The work was done by Barrera where the author started with the electric potential derived from the method of images, a series solution corresponding to an infinite array of image charges, and converted it into an integral form using two-dimensional Fourier transform. The original work contained mistakes, which was pointed out by an erratum published later [16], but without further examination.

It is clear that the method of image charges has been the most widely used approach to solve electrostatic problems in layered dielectrics. Even though some works attempted to improve convergence performance using solutions in integral form, the series solution obtained from image charges still served as a starting point. Given the apparent axisymmetry in many of those problems, it is surprising that there has been no attempt to tackle them using Hankel transform, a technique that is very useful for axisymmetric problems and has been used in mechanics (see ref. [17,18,19] for example).

In this paper, we demonstrate the application of Hankel transform in solving the problem shown in Fig. 1. A detailed and rigorous procedure is demonstrated in Sect. 2 including the formulation of the boundary value problem (BVP) for the electric potential, the mathematical treatment that reduces the dimension of the BVP, and the closed-form analytical solution for the electric potential. Section 3 contains nondimensionalization, validation of the solution, presentation of the results, and a parametric study. Conclusions are given in Sect. 4.

2 Formulation

It is clear from Fig. 1 that the problem possesses axisymmetry; therefore, it is most appropriate to use the cylindrical coordinates r, z, and $\theta$ as shown. Without loss of generality, the z-axis is placed so that the point charge is located directly on it. Due to axisymmetry, the electric potential $\phi$ is expected to be a function of r and z only.

In a homogeneous charge-free dielectric, the electric potential $\phi$ is governed by the Laplace equation:

$$\begin{aligned} \nabla ^2\phi (r,z)=0. \end{aligned}$$

(1)

Equation (1) applies to all the spatial points except for the location of the point charge q. The effect of point charge will be represented by a boundary condition (BC) given below. Accompanying Eq. (1) are several BCs:

$$\begin{aligned}&\lim \limits _{S_q\rightarrow 0}\oint _{S_q}(-\varepsilon _0 \varepsilon _1\nabla \phi )\cdot \mathbf {n}\mathrm{d}A=q, \end{aligned}$$

(2a)

$$\begin{aligned}&\lim \limits _{z\rightarrow 0^+}\phi =\lim \limits _{z\rightarrow 0^-}\phi ,\end{aligned}$$

(2b)

$$\begin{aligned}&\lim \limits _{z\rightarrow 0^+}\varepsilon _1\frac{\partial \phi }{\partial z}=\lim \limits _{z\rightarrow 0^-}\varepsilon _2\frac{\partial \phi }{\partial z}, \end{aligned}$$

(2c)

$$\begin{aligned}&\lim \limits _{z\rightarrow H^+}\phi =\lim \limits _{z\rightarrow H^-}\phi , \end{aligned}$$

(2d)

$$\begin{aligned}&\lim \limits _{z\rightarrow H^+}\varepsilon _3\frac{\partial \phi }{\partial z}=\lim \limits _{z\rightarrow H^-}\varepsilon _1\frac{\partial \phi }{\partial z}, \end{aligned}$$

(2e)

$$\begin{aligned}&\phi (r,z\rightarrow \infty )\rightarrow 0, \end{aligned}$$

(2f)

$$\begin{aligned}&\phi (r,z\rightarrow -\infty )\rightarrow 0. \end{aligned}$$

(2g)

Equation (2a) is the BC for the point charge, where $S_q$ is a closed surface enclosing q (see Fig. 1) and $\mathbf {n}$ is the outward normal of $S_q$. Equations (2b) and (2d) are the continuity conditions for the electric potential across the two interfaces, and Eqs. (2c) and (2e) describe the continuity for the normal electric displacement across the interfaces. Equations (2f) and (2g) are the far-field BCs, i.e., vanishing potential at infinity.

To solve the BVP, we start by denoting the electric potentials on the interfaces $z=0$ and $z=H$ by two unknown functions $\phi _{0}(r)$ and $\phi _{H}(r)$, respectively. This is warranted by the continuity conditions (2b) and (2d), and facilitates the construction of separate Dirichlet BVPs in all three domains. Next, we apply the zeroth-order Hankel transform to these BVPs on the radial coordinate r: $H_{_0}[\phi (r);\rho ]\equiv \int _0^\infty r\phi (r)J_{_0}(\rho r)\mathrm{d}r$, where $J_0(\rho r)$ is the zeroth-order Bessel function of the first kind. Making use of the property $H_0\left[ \frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial \phi }{\partial r});\rho \right] =-\rho ^2 H_0[\phi (r);\rho ]$, the BVPs in the upper and lower domains for the transformed electric potential $\varPhi (\rho ,z)$ now read

$$\begin{aligned}&\frac{\partial ^2\varPhi (\rho ,z>H)}{\partial z^2}-\rho ^2\varPhi (\rho ,z>H)=0, \end{aligned}$$

(3a)

$$\begin{aligned}&\varPhi (\rho ,z\rightarrow \infty )\rightarrow 0, \end{aligned}$$

(3b)

$$\begin{aligned}&\varPhi (\rho ,H)=\varPhi _H(\rho ) \end{aligned}$$

(3c)

and

$$\begin{aligned}&\frac{\partial ^2\varPhi (\rho ,z<0)}{\partial z^2}-\rho ^2\varPhi (\rho ,z<0)=0, \end{aligned}$$

(4a)

$$\begin{aligned}&\varPhi (\rho ,z\rightarrow -\infty )\rightarrow 0, \end{aligned}$$

(4b)

$$\begin{aligned}&\varPhi (\rho ,0)=\varPhi _0(\rho ), \end{aligned}$$

(4c)

where $\varPhi _0(\rho )$ and $\varPhi _H(\rho )$ are the Hankel transform of the functions $\phi _0(r)$ and $\phi _H(r)$, respectively. For the middle domain $(0<z<H)$, since it contains a singularity (point charge q), we first separate out the singular part of the electric potential $\phi _A(r,0<z<H)=q/4\pi \varepsilon _0\varepsilon _1\sqrt{r^2+(z-d)^2}$, which is the potential due to q in the absence of the interfaces, i.e., if the upper and lower domains had the same dielectric property as the middle domain. This gives the correct singularity at the location of the point charge and allows the BC (2a) to be satisfied. The second part of the electric potential, denoted as $\phi _B$, is nonsingular everywhere and is the difference between $\phi _A$ and the total electric potential in the middle domain. Applying Hankel transform to $\phi _B$ leads to the following BVP:

$$\begin{aligned}&\frac{\partial ^2\varPhi _B(\rho ,0<z<H)}{\partial z^2}-\rho ^2\varPhi _B(\rho ,0<z<H)=0, \end{aligned}$$

(5a)

$$\begin{aligned}&\varPhi _B(\rho ,0)=\varPhi _0(\rho )-\varPhi _{A0}(\rho ), \end{aligned}$$

(5b)

$$\begin{aligned}&\varPhi _B(\rho ,H)=\varPhi _H(\rho )-\varPhi _{AH}(\rho ). \end{aligned}$$

(5c)

Here $\varPhi _{A0}(\rho )$ is the Hankel transform of $\phi _{A0}(r)\equiv \phi _A(r,0)=q/4\pi \varepsilon _0\varepsilon _1\sqrt{r^2+d^2}$, which can be analytically evaluated to be $\varPhi _{A0}(\rho )=q\mathrm{e}^{-\rho d}/4\pi \varepsilon _0\varepsilon _1\rho$ [20]. Similarly, $\varPhi _{AH}(\rho )=q\mathrm{e}^{-\rho (H-d)}/4\pi \varepsilon _0\varepsilon _1\rho$ is the Hankel transform of $\phi _{AH}(r)\equiv \phi _A(r,H)=q/4\pi \varepsilon _0\varepsilon _1\sqrt{r^2+(H-d)^2}$.

So far, we have constructed separate Dirichlet BVP for each domain, and each BVP can be solved individually to obtain $\varPhi (\rho ,z)$ in terms of the unknown functions $\varPhi _{H}(\rho )$ and $\varPhi _{0}(\rho )$ . We have also made use of all BCs except (2c) and (2e), which will be used later to determine these two unknown functions.

It is straightforward to solve Eqs. (3a)–(3c) and (4a)–(4c) to obtain the transformed electric potential in the upper and lower domains:

$$\begin{aligned}&\varPhi (\rho ,z>H)=\varPhi _H(\rho )\mathrm{e}^{\rho (H-z)},\end{aligned}$$

(6)

$$\begin{aligned}&\varPhi (\rho ,z<0)=\varPhi _0(\rho )\mathrm{e}^{\rho z}. \end{aligned}$$

(7)

Taking the inverse Hankel transform in Eqs. (6) and (7), we obtain the expressions of electric potentials

$$\begin{aligned}&\phi (r,z>H)=\int _0^\infty \rho \varPhi _H(\rho )\mathrm{e}^{\rho (H-z)}J_0(\rho r)\mathrm{{d}}\rho , \end{aligned}$$

(8)

$$\begin{aligned}&\phi (r,z<0)=\int _0^\infty \rho \varPhi _0(\rho )\mathrm{e}^{\rho z}J_0(\rho r)\mathrm{{d}}\rho . \end{aligned}$$

(9)

Similarly, solving Eq. (5a) using the BCs (5b) and (5c) yields

$$\begin{aligned} \varPhi _B(\rho ,0<z<H)=\frac{[\varPhi _H(\rho )-\varPhi _{AH}(\rho )]\sinh (\rho z)+[\varPhi _0(\rho )-\varPhi _{A0}(\rho )]\sinh [\rho (H-z)]}{\sinh (\rho H)} \end{aligned}$$

(10)

which, after the inverse Hankel transform, leads to

$$\begin{aligned} \begin{aligned} \phi _B(r,0<z<H)&=\int _0^\infty \rho \frac{\varPhi _H(\rho )\sinh (\rho z)+\varPhi _0(\rho )\sinh [\rho (H-z)]}{\sinh (\rho H)}J_0(\rho r)\mathrm{{d}}\rho \\&\quad +\frac{q}{4\pi \varepsilon _0\varepsilon _1}\int _0^\infty \frac{\mathrm{e}^{-\rho (H-d)}\sinh (\rho z)-\mathrm{e}^{-\rho d}\sinh [\rho (H-z)]}{\sinh (\rho H)}J_0(\rho r)\mathrm{{d}}\rho . \end{aligned} \end{aligned}$$

(11)

Thus, the total electric potential in the middle domain is the sum of $\phi _A(r,0<z<H)$ and $\phi _B(r,0<z<H)$:

$$\begin{aligned} \phi (r,0<z<H)=\frac{q}{4\pi \varepsilon _0\varepsilon _1\sqrt{r^2+(z-d)^2}}+\phi _B(r,0<z<H). \end{aligned}$$

(12)

We can see from Eqs. (8), (9), and (12) that the solutions for all three domains are in terms of $\varPhi _H(\rho )$ and $\varPhi _0(\rho )$, which can be determined from the BCs (2c) and (2e). Specifically, substituting Eqs. (8), (9), and (12) into Eqs. (2c) and (2e), after some algebra $\varPhi _H(\rho )$ and $\varPhi _0(\rho )$ are found to be

$$\begin{aligned}&\varPhi _H(\rho )=\frac{q}{4\pi \varepsilon _0\rho }\frac{2\sinh [\rho (H-d)]+2\left[ \cosh (\rho H)+\frac{\varepsilon _2}{\varepsilon _1}\sinh (\rho H)\right] \sinh (\rho d)}{\sinh ^2(\rho H)\left[ (\varepsilon _2 + \varepsilon _3)\coth (\rho H)+\left( \frac{\varepsilon _2 \varepsilon _3}{\varepsilon _1}+\varepsilon _1\right) \right] }, \end{aligned}$$

(13)

$$\begin{aligned}&\varPhi _0(\rho )=\frac{q}{4\pi \varepsilon _0\rho }\frac{2\sinh (\rho d)+2\left[ \cosh (\rho H)+\frac{\varepsilon _3}{\varepsilon _1}\sinh (\rho H)\right] \sinh [\rho (H-d)]}{\sinh ^2(\rho H))\left[ (\varepsilon _2 + \varepsilon _3)\coth (\rho H)+\left( \frac{\varepsilon _2 \varepsilon _3}{\varepsilon _1}+\varepsilon _1\right) \right] }. \end{aligned}$$

(14)

With Eqs. (13) and (14), the solutions for the electric potential (Eqs. 8, 9, 12) are complete in all three domains, as they satisfy the governing equation and all BCs in the system.

3 Results and discussion

The electric potential formulated in the previous section will be numerically evaluated and presented below. To reduce the number of independent variables and allow broader application of the results, the following normalization is introduced:

$$\begin{aligned} \bar{\phi }=\frac{4\pi \varepsilon _0\varepsilon _1 H}{q}\phi ,\quad \bar{r}=\frac{r}{H},\quad \bar{z}=\frac{z}{H},\quad \bar{\rho }=\rho H,\quad \bar{d}=\frac{d}{H},\quad \varepsilon _{21}=\frac{\varepsilon _2}{\varepsilon _1},\quad \varepsilon _{31}=\frac{\varepsilon _3}{\varepsilon _1}. \end{aligned}$$

(15)

The normalized electric potential for the upper, lower, and middle domains are, respectively, given by

$$\begin{aligned}&\bar{\phi }(\bar{r},\bar{z}>1)=2\int _0^\infty { \frac{\sinh [\bar{\rho }(1-\bar{d})]+[\cosh (\bar{\rho })+\varepsilon _{21}\sinh (\bar{\rho })]\sinh (\bar{\rho }\bar{d})}{\sinh ^2(\bar{\rho })[(\varepsilon _{21}+\varepsilon _{31})\coth (\bar{\rho })+(\varepsilon _{21}\varepsilon _{31}+1)]}}\mathrm{e}^{\bar{\rho }(1-\bar{z})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }, \end{aligned}$$

(16a)

$$\begin{aligned}&\bar{\phi }(\bar{r},\bar{z}<0)=2\int _0^\infty {\frac{\sinh (\bar{\rho }\bar{d})+[\cosh (\bar{\rho })+\varepsilon _{31}\sinh (\bar{\rho })]\sinh [\bar{\rho }(1-\bar{d})]}{\sinh ^2(\bar{\rho })[(\varepsilon _{21}+\varepsilon _{31})\coth (\bar{\rho })+(\varepsilon _{21}\varepsilon _{31}+1)]}}\mathrm{e}^{\bar{\rho }\bar{z}}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }, \end{aligned}$$

(16b)

$$\begin{aligned}&\bar{\phi }(\bar{r},0<\bar{z}<1) = \frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}}\nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~+\,2\int _0^\infty {\frac{\sinh [\bar{\rho }(1-\bar{d})]+[\cosh (\bar{\rho })+\varepsilon _{21}\sinh (\bar{\rho })]\sinh (\bar{\rho }\bar{d})}{\sinh ^3(\bar{\rho })[(\varepsilon _{21}+\varepsilon _{31})\coth (\bar{\rho })+(\varepsilon _{21}\varepsilon _{31}+1)]}}\sinh {(\bar{\rho }\bar{z})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }\nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~+\,2\int _0^\infty {\frac{\sinh (\bar{\rho }\bar{d})+[\cosh (\bar{\rho })+\varepsilon _{31}\sinh (\bar{\rho })]\sinh [\bar{\rho }(1-\bar{d})]}{\sinh ^3(\bar{\rho })[(\varepsilon _{21}+\varepsilon _{31})\coth (\bar{\rho })+(\varepsilon _{21}\varepsilon _{31}+1)]}}\sinh [\bar{\rho }(1-\bar{z})]J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }\nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~-\int _0^\infty {\frac{\mathrm{e}^{-\bar{\rho }(1-\bar{d})}\sinh (\bar{\rho }\bar{z})+\mathrm{e}^{-\bar{\rho }\bar{d}}\sinh [\bar{\rho }(1-\bar{z})]}{\sinh (\bar{\rho })}}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }, \end{aligned}$$

(16c)

where $\varepsilon _{21}$ and $\varepsilon _{31}$, the ratios between dielectric constants that describe the relative permittivity of the three domains, and $\bar{d}$, the normalized location of the point charge, are the only three independent parameters.

Let us first consider a few special cases where the general solution given by Eqs. (16a)–(16c) can be reduced into analytical form. The first special case is where $\varepsilon _{21}=\varepsilon _{31}=1$, i.e., the three domains contain exactly the same dielectric material. It is expected that the electric potential in this case should simply be that of a point charge in a uniform dielectric, i.e.,

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z})=\frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}}. \end{aligned}$$

(17)

Now, substituting $\varepsilon _{21}=\varepsilon _{31}=1$ into Eq. (16a) and expanding the hyperbolic functions into exponentials gives

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z}>1)=\int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{z}-\bar{d})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }} \end{aligned}$$

(18)

with $\bar{z}-\bar{d}>0$. Similarly, for the lower domain, the electric potential from Eq. (16b) is simplified to

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z}<0)=\int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{d}-\bar{z})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }} \end{aligned}$$

(19)

with $\bar{d}-\bar{z}>0$. Both integrals in Eqs. (18) and (19) can be analytically evaluated to [20]

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z})=\int _0^\infty {\mathrm{e}^{-\bar{\rho }\left| \bar{z}-\bar{d}\right| }J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }}=\frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}}. \end{aligned}$$

(20)

For the middle domain, considering again the expansion of hyperbolic functions, all the terms in Eq. (16c) cancel except the first one which is $1/\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}$. Clearly, these results are the same as Eq. (17), the potential of a point charge in a uniform dielectric.

The second special case to be considered is where $\varepsilon _{21}\ne 1$ but $\varepsilon _{31}=1$. This corresponds to a system where the space is separated by one interface into two dielectric domains with the point charge located in the upper domain. Analytical solution for the electric potential in this case is also available [21], which in the normalized form is

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z}>0)=\frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}}-\left( \frac{\varepsilon _{21}-1}{\varepsilon _{21}+1}\right) \frac{1}{\sqrt{\bar{r}^2+(\bar{z}+\bar{d})^2}} \end{aligned}$$

(21)

applicable to domains I and III here, and

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z}<0)=\left( \frac{2}{\varepsilon _{21}+1}\right) \frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}} \end{aligned}$$

(22)

applicable to domain II. Considering $\varepsilon _{31}=1$ and simplifying Eqs. (16a) and (16c) result in the following two expressions for domains III and I, respectively:

$$\begin{aligned}&\bar{\phi }(\bar{r},\bar{z}>1)=\int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{z}-\bar{d})} J_0(\bar{\rho }\bar{r})\mathrm{d}\bar{\rho }}-\left( \frac{\varepsilon _{21}-1}{\varepsilon _{21}+1}\right) \int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{z}+\bar{d})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }}, \end{aligned}$$

(23)

$$\begin{aligned}&\bar{\phi }(\bar{r},0<\bar{z}<1)=\frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}}- \left( \frac{\varepsilon _{21}-1}{\varepsilon _{21}+1}\right) \int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{z}+\bar{d})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }}. \end{aligned}$$

(24)

Similar to Eq. (20), the integrals in Eqs. (23) and (24) can be analytically evaluated to [20] $\int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{z}-\bar{d})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }} =\left[ \bar{r}^2+(\bar{z}-\bar{d})^2\right] ^{-1/2}$ and $\int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{z}+\bar{d})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }}=\left[ \bar{r}^2+(\bar{z}+\bar{d})^2\right] ^{-1/2}$, which reduce both Eqs. (23) and (24) to

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z}>1)=\bar{\phi }(\bar{r},0<\bar{z}<1)=\frac{1}{\sqrt{\bar{r}^2+(\bar{z}-\bar{d})^2}}-\left( \frac{\varepsilon _{21}-1}{\varepsilon _{21}+1}\right) \frac{1}{\sqrt{\bar{r}^2+(\bar{z}+\bar{d})^2}}. \end{aligned}$$

(25)

Equation (25) is exactly the same as Eq. (21). Thus, our solutions for domains I and III agree with the known results under the condition of $\varepsilon _{21}\ne 1$ and $\varepsilon _{31}= 1$. Now, the simplified form of Eq. (16b) yields, for the normalized potential in domain II:

$$\begin{aligned} \bar{\phi }(\bar{r},\bar{z}<0)=\frac{2}{\varepsilon _{21}+1}\int _0^\infty {\mathrm{e}^{-\bar{\rho }(\bar{d}-\bar{z})}J_0(\bar{\rho }\bar{r})\mathrm{{d}}\bar{\rho }}. \end{aligned}$$

(26)

Evaluating the integral analytically as in Eqs. (20), (26) instantly reduces to Eq. (22). Thus, the solution in domain II is also verified by comparing it to the established solution.

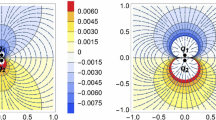
Now we consider more general situations and investigate the effect of the three dimensionless parameters $(\bar{d}$, $\varepsilon _{21}$ and $\varepsilon _{31})$ in detail. The integrals in the normalized electric potential (Eqs. 16a–16c) were evaluated numerically using recursive adaptive Lobatto quadrature, with the introduction of a finite upper bound $\bar{\rho }_{max}$ (i.e., cutoff) to replace infinity in the original expressions. A convergence test was conducted for this cutoff and it was found that increasing $\bar{\rho }_{max}$ beyond 50 did not introduce changes in the integrals greater than a small tolerance. Therefore, 50 was used as the cutoff for the numerical evaluation of the electric potential hereafter. Figure 2 shows the contour plots of electric potential due to a charge located at $\bar{d}=0.5$. For Fig. 2a, the dielectric constants of the materials in the upper and lower domains are considered equal and much higher than that of the middle layer ($\varepsilon _{21}=\varepsilon _{31}>>1$). It can be seen that the electric potential retains spherical symmetry near the point charge while it becomes distorted gradually at larger distance from the point charge where the effect of the different dielectrics becomes significant. For the configuration of the system considered in this figure, the electric potential is symmetric in both vertical and horizontal directions. The potential also decays at an equal rate in the upward and downward directions, but the decay is faster in the vertical direction than in the horizontal direction, which is due to the higher dielectric constant in the upper and lower domains. If $\varepsilon _{21}$ and $\varepsilon _{31}$ are further increased, we can expect that the system will approach the case where a uniform dielectric is sandwiched between two identical conductors. The electric field of charges in a dielectric between capacitors has been commonly studied in literatures. In the work of Pumplin [9], the equipotential surfaces were presented for a system with two grounded parallel plates and a point charge located midway between the plates. The results resemble the shape of the contours in Fig. 2a although they did not extend into the upper and lower domains due to the presence of conducting materials.

Fig. 2

Normalized electric potential of a single point charge in the middle layer of a three-layered dielectric system. The upper and lower interfaces are at the positions of $z/H=1$ and $z/H=0$, and marked by orange and blue lines, respectively. a $\varepsilon _{21}=10$ and $\varepsilon _{31}=10$, b $\varepsilon _{21}=0.1$ and $\varepsilon _{31}=10$. For all cases, $\bar{d}=0.5$

Fig. 3

Normalized electric potential, plotted against the dielectric constant ratio between the lower and middle domains, at three points $P_1(1, 0.5)$, $P_2(0, -0.5)$, and $P_3(0, 1.5)$, located in the middle, lower, and upper domains, respectively. For all cases, $\bar{d}=0.5$ and $\varepsilon _{31}=10$

Figure 2b represents a system with a very high dielectric constant in the upper domain $(\varepsilon _{31}\gg 1)$ and a much lower dielectric constant in the lower domain $(\varepsilon _{21}\ll 1)$ compared to that of the middle layer. Similar to Fig. 2a, spherical symmetry of the electric potential only retains very close to the point charge. Although the electric potential is symmetric about a vertical plane, unlike in Fig. 2a its rate of decay is different in the upward and downward directions, with much faster decay towards the upper interface due to the higher value of $\varepsilon _{31}$. It is interesting to observe that, although the value of $\varepsilon _{31}$ is the same in both figures, the values of $\bar{\phi }$ near the upper interface in Fig. 2b are drastically different from those in Fig. 2a. The smaller dielectric constant in the lower domain has caused a slower decay in both the upward and downward directions in Fig. 2b compared to Fig. 2a, which demonstrates the strong interactions among the dielectric materials in all three domains.

To more systematically study the effect of dielectric constant ratios, we plot the normalized potential as a function of $\varepsilon _{21}$ in Fig. 3 while fixing the other dielectric constant ratio $\varepsilon _{31}$, as well as the charge location $\bar{d}$. Due to symmetry, varying $\varepsilon _{31}$ with fixed $\varepsilon _{21}$ would correspond to the same result as if domains II and III were swapped. The electric potential is evaluated at three spatial points: $P_1(1, 0.5)$, $P_2(0, -0.5)$, and $P_3(0, 0.5)$ in the middle, lower, and upper domains, respectively. All three points are at equal distance from the point charge. It is clear that the electric potentials at all three points decrease with the increase of $\varepsilon _{21}$, indicating that the increase of dielectric constant in a single domain reduces the potential in all three domains, consistent with what was found in Fig. 2. On the other hand, the rate of decay with $\varepsilon _{21}$ is quite different at the three points. Since the dielectric is being varied in the domain where $P_2$ is located, the change of $\varepsilon _{21}$ has more direct impact on the potential at this point than at $P_1$ and $P_3$, leading to the highest rate of decay at $P_2$. The slowest decay is found at $P_3$ as this point is located at the furthest distance from the domain in which the dielectric constant is being changed. The curves for $P_2$ and $P_3$ intersect at $\varepsilon _{21}=10$, where the materials in the upper and lower domains become identical. Although the materials in the middle and lower domains become identical at $\varepsilon _{21}=1$, the potential at $P_1$ is still lower than that at $P_2$ when $\varepsilon _{21}=1$, because $P_1$ is closer to the upper domain with a higher dielectric constant and hence stronger screening. These two curves intersect at a $\varepsilon _{21}$ value greater than one.

The distance of the point charge from the interfaces also affects the distribution of electric potential in the system. In Fig. 4, $\bar{\phi }$ is plotted as a function of $\bar{d}$ where the location of point charge varies from 0.1 to 0.9 along the z-axis. At $\bar{d}=0.1$, the point charge is just above the lower interface and at $\bar{d}=0.9$ it is close to the upper interface. The same three locations $P_1$, $P_2$, and $P_3$ are chosen as before and the electric potential is presented for these points. Figure 4a represents the system in Fig. 2a which has two identical materials in the upper and lower domains with a higher dielectric constant $(\varepsilon _{21}=\varepsilon _{31}=10)$ than the middle one. The electric potential at $P_3$ monotonically increases as the point charge approaches from the lower to the upper interface, because the distance between the point charge and $P_3$ decreases. Similarly, at $P_2$, the electric potential decreases monotonically as the point charge moves away from it. Due to the identical dielectrics in the upper and lower domains, the rates of change of the electric potential at $P_2$ and $P_3$ have equal magnitude, and the two curves intersect at $\bar{d}=0.5$. The potential at $P_1$ first increases as its distance from the point charge decreases, reaches the maximum when the point charge is located midway between the two interfaces $(\bar{d}=0.5)$ and then starts decreasing due to the increase in distance from the point charge.

Fig. 4

Normalized electric potential, plotted against the normalized location $\bar{d}$, at three points $P_1(1, 0.5)$, $P_2(0, -0.5)$, and $P_3(0, 1.5)$ located in the upper, lower, and middle layers, respectively (see inset in Fig. 3). a $\varepsilon _{21}=10$ and $\varepsilon _{31}=10$, b $\varepsilon _{21}=0.1$ and $\varepsilon _{31}=10$

Fig. 5

Normalized electric potential at $P_1(1, 0.5)$, located in the middle layer, as a function of the normalized location $\bar{d}$ of the point charge. For all cases, $\varepsilon _{31}=10$

In Fig. 4b, we consider a different dielectric in each layer: the highest dielectric constant is in the upper domain and the lowest is in the lower domain. As the point charge approaches the upper interface, it comes closer to $P_3$ and hence the electric potential increases at this point. For the same reason, the electric potential at $P_2$ decreases as the point charge moves away from it. The most interesting phenomena is found at $P_1$. As the charge moves from the lower to the upper interface, the distance between the point charge and $P_1$ first decreases, and as it passes the midpoint $(\bar{d}=0.5)$, the distance increases. However, the electric potential at $P_1$ is found to monotonically decrease for the entire range of $\bar{d}$. To explain, as the charge moves towards the midway between the two interfaces, without considering the influence of the dielectrics in the upper and lower domains, the electric potential at $P_1$ should increase as the distance between the point charge and $P_1$ decreases. However, at the same time, the charge is approaching a domain with a higher dielectric constant, which tends to decrease its electric potential. These two competing effects can cause a complex relation between the charge location and the electric potential at $P_1$. For $\varepsilon _{21}=0.1$ and $\varepsilon _{31}=10$, the influence from the high dielectric constant in the upper domain appears to be dominant, which results in a net decrease in the electric potential at $P_1$. However, the rate of decay is quite small (see Fig. 4b), as a consequence of the two competing factors. After $\bar{d}=0.5$, the distance between the point charge and $P_1$ starts to increase and the point charge continues to approach the higher dielectric constant domain. Both tend to introduce a decay in the electric potential at $P_1$, and hence a faster decrease is observed from Fig. 4b.

To further investigate this interesting phenomenon, the normalized potential $\bar{\phi }$ at $P_1$ is plotted as a function of $\bar{d}$ in Fig. 5 for several different $\varepsilon _{21}$. The other dielectric constant ratio $\varepsilon _{31}$ remains at 10. The maximum for each curve, either as a local maximum in the interior of the domain or as a global maximum at the boundaries, is marked with *. As the charge approaches the upper interface, the change of $\bar{\phi }$ at $P_1$ is found to be quite different for different values of $\varepsilon _{21}$. For small $\varepsilon _{21}(<0.4)$, $\bar{\phi }$ monotonically decreases for the entire range of $\bar{d}$ although the distance between the point charge and $P_1$ decreases till $\bar{d}=0.5$. As discussed earlier, the effect of the high dielectric constant in the upper domain is dominant in this case, which reduces the net potential at $P_1$ as the point charge moves upwards. For $\varepsilon _{21}>0.4$, $\bar{\phi }$ shows a nonmonotonic change with the charge location and the maximum for each curve is found at a distance from the boundaries. In addition, as $\varepsilon _{21}$ increases, the local maximum shifts towards the upper interface due to the increased screening from the lower domain. Finally, for sufficiently large values of $\varepsilon _{21}(>10)$, the curves exhibit the trend of converging together as the lower domain approaches a conductor-like material.

The results above have demonstrated that the electric potential due to the point charge is strongly influenced by the dielectric materials used in the different layers, which can provide a means of modulating the electric potential in the multilayered system by adjusting material properties. Due to the linear nature of the electrostatic problem, the current work can be extended to study the electric potential due to a distribution of charges, for example, present in multilayered microstrips (used in microwave technologies) [22]. The expression for the electric potential can also be used directly to calculate other physical quantities such as polarization surface charge density (e.g., in Barrera. [15]) or surface force in contact adhesion.

4 Conclusion

The electric potential due to a point charge in a multilayered dielectric system is obtained in closed form using the technique of Hankel transform. Nondimensionalization of the solution reveals three dimensionless parameters that govern the normalized electric potential: $\bar{d}$, $\varepsilon _{21}$, and $\varepsilon _{31}$. A parametric study was performed to demonstrate the influence of these parameters. The results show that the electric potential and hence electric field in the system can be modulated, both quantitatively and qualitatively, by adjusting the governing parameters.