1 Introduction

Nanofluids are usually defined as fluids in which large numbers of small ferromagnetic particles having dimension of the order of \(10^{-9}\)m are dispersed. These particles are known as nanoparticles, and the fluid in which the particles are dispersed is called the base fluid. The term nanofluid in its present usage was apparently coined by Choi [1]. Water or any other organic solvent can be used as a base fluid [2]. The particles used in nanofluids are usually made up of metals, oxides, or carbon nanotubes. Recently, the interest in nanofluids has been revived for two reasons: first, they have become sufficiently cheap; second, large numbers of potential practical applications of nanofluids have been discovered [3]. Nanofluids possess a large number of interesting characteristic properties, and principal among them are an increase in the effective thermal conductivity and heat transfer enhancement. In [4] Eastman et al. reported a 40 % increase in the effective thermal conductivity in ethylene-glycol-based nanofluids. In alumina-water-based nanofluids, an enhancement of 10–30 % effective thermal conductivity was reported in [5].

Heat transfer enhancement by nanofluids, as expected, has attracted the attention of many researchers. Motivated to find an explanation for the anomalous heat transfer enhancement observed in nanofluids, Buongiorno [3] proposed a model taking into account the effects of Brownian diffusion (random diffusion of nanoparticles in the base fluid) and thermophoresis (motion of nanoparticles induced by a temperature gradient). He then observed that the anomalous heat transfer enhancement could not be attributed solely to nanoparticle dispersion and turbulent intensity. An alternative explanation for the increase of the heat transfer coefficient proposed by Buongiorno was that a significant decrease in the viscosity results within the boundary layer owing to the temperature gradient and thermophoresis, which leads to heat transfer enhancement. The same problem for the laminar free convection of Newtonian nanofluids was studied by Polidori et al. [6]. The Nusselt number (a dimensionless heat transfer coefficient) remains higher in the turbulent regime than in the laminar regime. Thus one is led to conclude that an increase in the Nusselt number in the turbulent regime could be one possible source of heat transfer enhancement. Another possible reason for anomalous heat transfer could be that Brownian motion and thermophoresis are considered to be two fundamental reasons for the free movement of nanoparticles in the base fluid. Natural convection, therefore, seems to be another possible source of enhancement of effective thermal conductivity because of the free movement of nanoparticles in base fluid [3, 7].

Most nanofluid properties are volume-fraction dependent (e.g., thermal conductivity). In [7] Tzou studied the critical Rayleigh number, which separates the laminar regime from the turbulent regime, for the onset of Rayleigh–Bénard instability in nanofluids, assuming the nanofluid properties are not dependent on the volume fraction of nanoparticles. In the absence of such a dependence, he reported a significant reduction in the critical Rayleigh number and thus the “dominance of turbulence.” The collective effect of Brownian motion and thermophoresis was shown to advance the onset of convection. Since the Nusselt number can be higher than that in laminar flows, the overall heat transfer rate can be higher in a turbulent regime than that in a regular laminar fluid. Using a Galerkin method, Dhananjay et al. [8] studied Rayleigh–Bénard convection in nanofluids when both boundaries are free. They also addressed the oscillatory case that had been missed earlier by Tzou [7, 9]. The onset of convection in a horizontal nanofluid layer of finite depth was studied by Nield and Kuznetsov [2]. They observed that the critical Rayleigh number decreased by a substantial amount if the basic nanoparticle distribution was top-heavy, and increased if the basic nanoparticle distribution was bottom-heavy, by the presence of nanoparticles. In the case where nanoparticles amass near the bottom of the nanofluid layer, oscillatory instability was observed to be possible. The instability of nanofluids in a shallow cavity heated from below was studied by Alloui et al. [10]. Both analytical and numerical studies were conducted. Among other things, they observed that heat transfer enhancement in nanofluids depended on the Rayleigh number and the volume fraction of the nanofluid.

Magnetic nanofluids (MNFs) are nanofluids placed in an ambient magnetic field. MNFs comprise a distinctive class of nanofluids that display both magnetic and fluid properties. This dual character of MNFs offers the prospect of controlling their flow and heat transfer properties via an externally applied magnetic field [11]. MNFs find applications in fields such as liquid seals in rotatory shafts for vacuum systems, hard-disk devices of personal computers, and the cooling and damping of loudspeakers, to name few.

The magnetic susceptibility of MNFs is a function of temperature; thus, the temperature gradient induces spatial gradients in magnetic susceptibility. Convection induced by these two gradients is known as thermomagnetic convection [11]. Finlayson [12] studied the instability in a ferrofluid layer heated from below. The linear stability problem was solved for shear–free and rigid–rigid boundaries. The results predicted that convection could also be driven by the magnetic forces alone, in the absence of gravity. Using a Galerkin method Gotoh and Yamada [13] investigated the linear instability in a horizontal magnetic fluid layer confined between two ferromagnetic boundaries and heated from below in an ambient vertical magnetic field. They obtained a relation between the critical Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) and magnetic number N, from which they deduced that \(\mathrm {Ra}_{\mathrm{c}}\) decreases as N increases. They further concluded that the effects of magnetic force and buoyancy compensate each other. For more on the convective instability problem and related heat transfer aspects, see [14–16] and references therein.

The problem of analyzing the instability of MNFs has been studied less extensively than the analogous problem of nanofluid convection. Using nonlinear stability analysis, Sunil and Mahajan [17] analyzed instability in a ferrofluid layer heated from below. Mahajan and Arora [18] investigated the effects of rotation at the onset of convection in a thin layer of a MNF using linear theory. The model used by them incorporated the effects of Brownian diffusion, thermophoresis, and magnetophoresis. They observed that magnetic forces dominate the buoyancy force in 1 mm thick fluid layers. For more studies related to thermomagnetic convection in MNF, the reader is referred to [19–22].

The heat transfer intensity of MNFs is characterized by the Rayleigh number \(\mathrm {Ra}\), which is the sum of thermomagnetic and thermogravitational parts, \(\mathrm {Ra}=\mathrm {Ra}_{\mathrm{m}}+ \mathrm {Ra}_{\mathrm{T}}\). Thus the intensity of thermomagnetic convection in general and the efficiency of devices made from MNFs in particular depend not only on magnetic and temperature field distributions but also on the thermophysical properties of MNFs and the extent of the dependence of magnetization on temperature [11]. Some previous works ignored the effects of a magnetic field on the thermophysical properties of MNFs. Recent studies have highlighted this dependence. The results of the study by Blum et al. [19] have confirmed the so-called additive action of thermogravitation and thermomagnetic forces on the heat transfer capacity of ferrofluids. Thus it is important to take into account the dependence of thermophysical properties of MNFs on externally applied magnetic fields while studying thermomagnetic convection in MNFs.

In this work, the effects of magnetic-field-dependent (MFD) viscosity on the onset of convection in MNFs are studied using linear stability theory. The Chebyshev pseudospectral method is used to solve the eigenvalue problem in gravity as well as in a microgravity environment for water- and ester-based MNFs.

2 Formulation

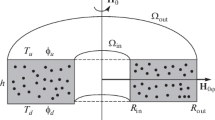
We consider an infinite horizontal layer of an incompressible MNF having a variable viscosity \(\mu _{1}=\mu (1+\varvec{\delta }\cdot {\varvec{B}})\) and heated from below. Here \(\mu _{1}\) is the MFD viscosity, \(\mu \) is the viscosity of the fluid in the absence of an applied magnetic field, \({\varvec{B}}\) is the magnetic induction, and \(\varvec{\delta }=\delta _1\mathbf {i}+\delta _2\mathbf {j}+\delta _3\mathbf {k}\) is the variation coefficient of viscosity, which we assume to be isotropic, i.e., \(\delta _1=\delta _2=\delta _3=\delta \). The fluid is assumed to occupy the layer \(z\in [0,d]\), with gravity, g, acting in the negative z-direction. The magnetic field \( {\varvec{H}}=H_{0}^\mathrm{{ext}} {\varvec{k}}\) acts outside the layer (Fig. 1).

Fig. 1
figure 1

Geometric configuration of problem

Full size image

The MNF is assumed to be incompressible, so the equation of continuity gives

$$\begin{aligned} \varvec{\nabla }\cdot {\varvec{u}}=0, \end{aligned}$$
(1)

where \({\varvec{u}}\) is the MNF velocity.

Following [3, 12], the equation of momentum, under the Boussinesq approximation, is given by the following equation

$$\begin{aligned} \rho _{f} \left( \frac{\partial {\varvec{u}}}{\partial t} +{\varvec{u}}\cdot \varvec{\nabla }{\varvec{u}}\right) =-\varvec{\nabla }p+\mu _{1}\nabla ^{2}{\varvec{u}}+\mu _{0}({\varvec{M}}\cdot \varvec{\nabla }){\varvec{H}} -\rho g{\varvec{k}}, \end{aligned}$$
(2)

where \(\rho _{f}, t, p, {\varvec{M}} , \mu _0\), and \(\phi \) are the fluid density, time, pressure, magnetization, magnetic permeability of the vacuum, and nanoparticle volume fraction, respectively. Here \(\rho \) is the total density of the nanofluid, which we assume to be given by

$$\begin{aligned} \rho = \rho _{p} \phi +\rho _{f} (1-\phi )\{1-\alpha (T-T_{c} )\}, \end{aligned}$$

where \(\rho _p\) is the nanoparticle density, \(T-T_c\) is the temperature difference, and \(\alpha \) is the coefficient of thermal expansion.

When thermophoresis is taken into account, the conservation equation for the MNF, in the absence of chemical reactions, takes the form [3, 23]

$$\begin{aligned} \frac{\partial \phi }{\partial t} +{\varvec{u}}\cdot \varvec{\nabla }\phi =-\frac{1}{\rho _{p} } \varvec{\nabla }\cdot {\varvec{j}}_{p}, \end{aligned}$$
(3)

where \({\varvec{j}}_{p} \) is the mass flux for the MNF, given by the sum of “diffusiophoresis,” thermophoresis, and “magnetophoresis” as

$$\begin{aligned} {\varvec{j}}_{p} ={\varvec{j}}_{pB} +{\varvec{j}}_{pT} +{\varvec{j}}_{pM} =-\rho _{p} D_{B} \varvec{\nabla }\phi -\rho _{p} D_{T} \frac{\varvec{\nabla }T}{T} +\rho _{p} D_{H} \varvec{\nabla }H, \end{aligned}$$
(4)

where \(D_{B} \) is the Brownian diffusion coefficient, \(D_{T} \) is the thermophoretic diffusion coefficient, and \(D_{H} \) is the magnetophoretic diffusion coefficient. Using Eq. (4), the conservation equation for MNF (3) becomes

$$\begin{aligned} \frac{\partial \phi }{\partial t} + {\varvec{u}}\cdot \varvec{\nabla }\phi =\varvec{\nabla }\cdot \left( D_{B} \varvec{\nabla }\phi +D_{T} \frac{\varvec{\nabla }T}{T} -D_{H} \varvec{\nabla }H\right) . \end{aligned}$$
(5)

The thermal energy equation for the MNF can be written

$$\begin{aligned} (\rho c)_{f}\left( \frac{\partial T}{\partial t} + {\varvec{u}}\cdot \varvec{\nabla }T\right) =-\varvec{\nabla }\cdot {{\varvec{V}}}+ h_{p} \varvec{\nabla }\cdot {\varvec{j}}_{p}, \end{aligned}$$
(6)

where \({c_{{} { f}}}\) is the MNF specific heat, T is the MNF temperature, \(h_{p}\) is the specific enthalpy of the MNF material, and \({\varvec{V}}\) is the energy flux with respect to a frame moving with the MNF velocity \({\varvec{u}}\), is given by the following equation

$$\begin{aligned} {\varvec{V}}=-k_{1} \varvec{\nabla }T+h_{p} {\varvec{j}}_{p}. \end{aligned}$$

Here \(k_{1} \) is the MNF thermal conductivity. Substituting the preceding expression for \({\varvec{V}}\) into Eq. (6) and using the vector identity \(\varvec{\nabla }h_{p} =c_{p} \varvec{\nabla }T\), we get

$$\begin{aligned} (\rho c)_{f}\left( \frac{\partial T}{\partial t} +{\varvec{u}}\cdot \varvec{\nabla }T\right) =\,&\varvec{\nabla }\cdot (k_{1} \varvec{\nabla }T)+\rho _{p} c_{p} \Big (D_{B} \varvec{\nabla }T\cdot \varvec{\nabla }\phi +D_{T} \frac{\varvec{\nabla }T\cdot \varvec{\nabla }T}{T} -D_{H} \varvec{\nabla }T\cdot \varvec{\nabla }H\Big ), \end{aligned}$$
(7)

where \(c_p\) is the specific heat of the nanoparticle material.

Maxwell’s equations in the magnetostatic limit are

$$\begin{aligned} \varvec{\nabla }\cdot {\varvec{B}}=0,\quad \varvec{\nabla }\times {\varvec{H}}=0,\quad {\varvec{B}}=\mu _{0} ({\varvec{M}}+{\varvec{H}}). \end{aligned}$$
(8)

In general, magnetization is a function of the magnetic field, particle concentration, and temperature. At equilibrium, it is aligned with the stationary magnetic field. It is assumed to be governed by Langevin’s formula [24]:

$$\begin{aligned} {\varvec{M}}_{eq} =\frac{{\varvec{H}}}{H} M_{s} \phi L(\alpha _{L} )=\frac{{\varvec{H}}}{H} M_{eq} (H,\phi ,T), \end{aligned}$$
(9)

where

$$\begin{aligned} L(\alpha _{L} )=\coth (\alpha _{L} )-\dfrac{1}{\alpha _{L}},\qquad \alpha _{L} =\dfrac{mH}{k_{B} T}, \end{aligned}$$

where \(k_B\) is Boltzmann’s constant and \(M_s\) is the magnetic saturation.

To obtain the steady-state solution, following [12], we first linearize the magnetization equation \(M_{eq}\) as follows:

$$\begin{aligned} M_{eq} (H,\phi ,T)=M_{0} +\chi (H-H_{0} )-K_{m} (T-T_{h} )+K_{p} (\phi -\phi _{0} ), \end{aligned}$$

where \(\chi \) is the tangent magnetic susceptibility, and \(K_m\) and \(K_p\) are the magnetic coefficients. The tangent and chord magnetic susceptibility \(\chi ,\chi _{2} \) can be estimated by Langevin’s formula (9) for a different Langevin parameter \(\alpha _{L}\) [25]:

$$\begin{aligned} \alpha _{L} =\frac{mH_{0} }{k_{B} T_{h} } =\left\{ \begin{array}{l} \ll 1,\quad \chi =\frac{M_{S} m}{3k_{B} T_{h} } , \quad \chi _{2} =\chi , \\ \simeq 1,\quad \chi =\frac{M_{S} m}{k_{B} T_{h} } L'(\alpha _{L} ),\quad \chi _{2} =\frac{M_{S} }{T_{h} } L(\alpha _{L}), \\ \gg 1,\quad \chi =\frac{M_{S} k_{B} T_{h} }{mH_{0}^{2} } ,\quad \chi _{2} =\frac{M_{S} }{H_{0} }\left( 1-\frac{1}{\alpha _{L} } \right) . \end{array}\right. \end{aligned}$$

We assume that the temperature and the volumetric fraction of the particles are constant at the boundaries. Thus the boundary conditions are

$$\begin{aligned} \left. \begin{array}{c} \displaystyle w=0,\quad T=T_h,\quad \phi =\phi _0 \quad \text {at} \quad z=0,\\ \displaystyle w=0,\quad T=T_c,\quad \phi =\phi _1 \quad \text {at} \quad z=d, \end{array} \right\} \end{aligned}$$
(10)

with \({\partial w}/{\partial z} =0\) on a rigid surface and \({\partial ^{2} w}/{\partial z^{2} } =0\) on a stress-free surface. We also assume that the normal component of magnetic induction and the tangential component of the magnetic field are continuous across the boundary.

Equations (1)–(9) are made dimensionless by scaling all lengths with d, time with \(d^2/\kappa \), pressure with \(\mu \kappa /d^2\), velocity with \(\kappa /d\), temperature with \(T_h-T_c\), concentration with \(\phi _0-\phi _1\), H with \(H_0\), and M with \(M_0\). Here, \(\kappa ={k_{1} }/{(\rho C)_{f} }\). Then Eqs. (1)–(9) take the form

$$\begin{aligned}&\varvec{\nabla }\cdot {\varvec{u}}=0,\end{aligned}$$
(11)
$$\begin{aligned}&\frac{1}{\mathrm {Pr}}\left( \frac{\partial {\varvec{u}}}{\partial t} +{\varvec{u}}\cdot \varvec{\nabla }{\varvec{u}}\right) =-\varvec{\nabla }p+\nabla ^{2}{\varvec{u}}+\{c_1(\varvec{\delta }\cdot {\varvec{M}})+c_2(\varvec{\delta }\cdot {\varvec{H}})\}\nabla ^2{\varvec{u}}+c_3({\varvec{M}}\cdot \varvec{\nabla }){\varvec{H}} -{\mathrm {Rn}}~\,\phi {\varvec{k}}\nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+\,{\mathrm {Ra}}\,T{\varvec{k}} -\mathrm {Ra}_{{ N}} {N}_{\phi } T\phi {\varvec{k}}-\rho _1{\varvec{k}}+\rho _2\phi {\varvec{k}},\end{aligned}$$
(12)
$$\begin{aligned}&\frac{\partial \phi }{\partial t} +{\varvec{u}}\cdot \varvec{\nabla }\phi =\frac{1}{\mathrm {Le}}\nabla ^2\phi +\frac{{ {N}_{\mathrm{A}}}}{{\mathrm {Le}}}\nabla ^2T-\frac{{ {N}'_{\mathrm{A}}}}{{\mathrm {Le}}}\nabla ^2 H,\end{aligned}$$
(13)
$$\begin{aligned}&\frac{\partial T }{\partial t}+{\varvec{u}}\cdot \varvec{\nabla }T = \nabla ^2 T+\frac{{ {N}_{\mathrm{B}}}}{{\mathrm {Le}}}(\varvec{\nabla }\phi \cdot \varvec{\nabla }T)+\frac{{ {N}_{\mathrm{A}} { N}_{\mathrm{B}}}}{{\mathrm {Le}}}(\varvec{\nabla }T\cdot \varvec{\nabla }T)-\frac{{ {N}'_{\mathrm{A}}{} { N}_{\mathrm{B}}}}{{\mathrm {Le}}}(\varvec{\nabla }H\cdot \varvec{\nabla }T),\end{aligned}$$
(14)
$$\begin{aligned}&\chi _2\varvec{\nabla }\cdot {\varvec{M}}+\varvec{\nabla }\cdot {\varvec{H}}=0,\end{aligned}$$
(15)
$$\begin{aligned}&{\varvec{M}}=\frac{{\varvec{H}}}{H}\frac{(1+\chi )}{\chi _2}\left\{ \frac{\chi }{1+\chi }H-\frac{{ {M}_1}}{{ {M}_3}}T+\frac{{ {M}'_1}}{{ {M}'_3}}\phi +c_4\right\} , \end{aligned}$$
(16)

where

$$\begin{aligned} c_1&=\mu _0M_0,\quad c_2=\mu _0H_0,\quad c_3=\dfrac{\mu _0M_0H_0d^2}{\kappa \mu },\quad \rho _1=\dfrac{d^3\rho _f}{\kappa \mu }(1+\alpha T_c)g,\nonumber \\ \chi _2&=\frac{M_0}{H_0},\quad c_4=\dfrac{M_0-\chi H_0+K_{m}T_h-K_{p}\phi _0}{H_0(1+\chi )},\quad \rho _2=\dfrac{d^3\rho _f}{\kappa \mu }(\phi _0-\phi _1)\alpha T_c g. \end{aligned}$$

\(K_{m} ={\chi H_{0} }/{T_{h} } \) is in general a function of the magnetic field and temperature and \(K_{p} ={\chi H_{0} }/{\phi _{0} } \) is a function of the magnetic field and particle concentration. Here, the following are the nondimensional parameters:

$$\begin{aligned}&{\mathrm {Le}}=\frac{\kappa }{D_B},\quad {\mathrm {Ra}}=\frac{\rho _f g\alpha d^3(T_h-T_c)}{\mu \kappa },\quad { {N}_{\mathrm{A}}} = \frac{D_T(T_h-T_c)}{D_B T_c (\phi _0-\phi _1)},\quad {\mathrm {Pr}} =\frac{\mu }{\rho _{f} \kappa },\nonumber \\&{N}_{\mathrm{A}}' =\frac{D_H H_0}{D_B(\phi _0-\phi _1)},\quad { {N}_{\mathrm{B}}} =\frac{(\rho C)_p(\phi _0-\phi _1)}{(\rho C)_{f}},\quad {\mathrm {Rn}}=\frac{(\rho _{p} -\rho _{f} )(\phi _{0} -\phi _{1} )gd^3}{\mu \kappa },\nonumber \\&{\mathrm {Ra}_{{N}}} = (1-\phi _0){\mathrm {Ra}}, \quad { {N}_{\phi }} =\dfrac{\phi _{0} -\phi _{1} }{1-\phi _{0}},\quad { {M}_\mathrm{{1}}} =\frac{\mu _{0} \chi ^{2} H_{0}^{2} (T_{h} -T_{c} )}{\rho _{f} g\alpha d(1+\chi )T_{{h} }^{2} },\nonumber \\&{ {M}_\mathrm{{3}}} =\frac{\mu _{0} \chi H_{0}^{2} }{\rho _{f} g\alpha dT_{h} }, \quad { {M}'_\mathrm{{3}}} =\frac{\mu _{0} \chi H_{0}^{2} }{\rho _{f} g\alpha d\phi _{0} }, \quad { {M}'_\mathrm{{1}}} =\frac{\mu _{0} \chi ^{2} H_{0}^{2} (\phi _{0} -\phi _{1} )}{\rho _{f} g\alpha d(1+\chi )\phi _{0}^{2} }, \end{aligned}$$

where \(\mathrm {Le}\) is the Lewis number, \(\mathrm {Ra}\) is the thermal Rayleigh number, \(\textit{N}_{\mathrm{A}}\) and \({ N}'_{\mathrm{A}}\) are the modified diffusivity ratios, \(\mathrm {Pr}\) is the Prandtl number, \(\textit{N}_{\mathrm{B}}\) is a modified particle-density increment, \(\mathrm {Rn}\) is the nanoparticle Rayleigh number, and \(\textit{M}_{1}, { M}_{1}', { M}_{3}\), and \(\textit{M}_{3}'\) are the magnetic parameters. The boundary conditions now become

$$\begin{aligned} \left. \begin{array}{c} \displaystyle w=0,\quad T=\frac{T_h}{T_h-T_c},\quad \phi =\frac{\phi _0}{\phi _0-\phi _1} \quad \text {at} \quad z=0\\ \displaystyle w=0,\quad T=\frac{T_c}{T_h-T_c},\quad \phi =\frac{\phi _1}{\phi _0-\phi _1} \quad \text {at} \quad z=1 \end{array} \right\} . \end{aligned}$$
(17)

3 Steady-state solution

Equations (11)–(16) possess a steady-state solution in which

$$\begin{aligned}&{\varvec{u}}_{b} = \mathbf 0 ,\qquad p=p_b (z),\qquad T=T_b(z), \nonumber \\&{\varvec{M}}={\varvec{M}}_{b} (z),\quad \phi =\phi _b(z),\quad {\varvec{H}}={\varvec{H}}_{b}(z). \end{aligned}$$
(18)

Equations (11)–(16) then reduce to

$$\begin{aligned}&-\frac{\mathrm{d}p_b}{\mathrm{{d}}z}+c_3M_b\frac{\mathrm{d}H_b}{\mathrm{{d}}z}-{\mathrm {Rn}}\;\phi _b+{\mathrm {Ra}}\; T_b-\mathrm {Ra}_{{ N}} \;\textit{N}_{\phi } T_b\phi _b-\rho _1+\rho _2\phi _b=0, \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\mathrm{d}^2\phi _b}{\mathrm{{d}}z^2}+{\textit{N}_{\mathrm{A}}} \frac{\mathrm{d}^2T_b}{\mathrm{{d}}z^{2} }-{\textit{N}'_{\mathrm{A}}}\frac{\mathrm{d}^2H_b}{\mathrm{{d}}z^2}=0,\end{aligned}$$
(20)
$$\begin{aligned}&\frac{\mathrm{d}^2T_b}{\mathrm{{d}}z^2}+ \frac{\mathrm{d}T_b}{\mathrm{{d}}z}\left\{ \frac{{\textit{N}_{\mathrm{B}}}}{{\mathrm {Le}}}\frac{\mathrm{d}\phi _b}{\mathrm{{d}}z}+ \frac{{\textit{N}_{\mathrm{A}} { N}_{\mathrm{B}}}}{{\mathrm {Le}}} \frac{\mathrm{d}T_b}{\mathrm{{d}}z} -\frac{{\textit{N}'_{\mathrm{A}}{} { N}_{\mathrm{B}}}}{{\mathrm {Le}}}\frac{\mathrm{d}H_b}{\mathrm{{d}}z}\right\} =0,\end{aligned}$$
(21)
$$\begin{aligned}&\chi _2\frac{\mathrm{d}M_b}{\mathrm{{d}}z}+\frac{\mathrm{d}H_b}{\mathrm{{d}}z}=0,\end{aligned}$$
(22)
$$\begin{aligned}&{} { M}_{b}=\frac{1+\chi }{\chi _{2}}\left\{ \frac{\chi }{1+\chi }H_b-\frac{{\textit{M}_1}}{{\textit{M}_3}}T_b+\frac{{\textit{M}'_1}}{{\textit{M}'_3}}\phi _b+c_4\right\} . \end{aligned}$$
(23)

Using the boundary conditions (17) and Eqs. (22), (23), Eq. (20) may be integrated to give

$$\begin{aligned}&\left( 1+{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}'_1}}{{\textit{M}'_3}}\right) \phi _b+\left( {\textit{N}_{\mathrm{A}}}-{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}_1}}{{\textit{M}_3}}\right) T_b\nonumber \\&\quad =-\left\{ \left( 1+{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}'_1}}{{\textit{M}'_3}}\right) +\left( {\textit{N}_{\mathrm{A}}}-{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}_1}}{{\textit{M}_3}}\right) \right\} z \left( 1+{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}'_1}}{{\textit{M}'_3}}\right) \left( \frac{\phi _0}{\phi _0-\phi _1}\right) +\left( {\textit{N}_{\mathrm{A}}}-{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}_1}}{{\textit{M}_3}}\right) \left( \frac{T_h}{T_h-T_c}\right) . \end{aligned}$$
(24)

Substituting the preceding value of \(\phi _b\) into Eq. (21) and again making use of Eqs. (22) and (23) gives

$$\begin{aligned} \frac{\mathrm{d}^2T_b}{\mathrm{{d}}z^2}+\frac{{\textit{N}_{\mathrm{B}}}}{{\mathrm {Le}}}\left\{ {\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}_1}}{{\textit{M}_3}}-\left( 1+{\textit{N}_{\mathrm{A}}}+{\textit{N}'_{\mathrm{A}}}\frac{{\textit{M}'_1}}{{\textit{M}'_3}}\right) \right\} \frac{\mathrm{d}T_b}{\mathrm{{d}}z}=0. \end{aligned}$$
(25)

The solution of Eq. (25) satisfying Eq. (17) is

$$\begin{aligned} T_b=\frac{T_h}{T_h-T_c}-\left\{ \frac{1-\mathrm{e}^{-Pz}}{1-\mathrm{e}^{-P}}\right\} , \end{aligned}$$
(26)

where

$$\begin{aligned} P=\dfrac{{\textit{N}_{\mathrm{B}}}}{{\mathrm {Le}}}\left\{ {\textit{N}'_{\mathrm{A}}}\dfrac{{\textit{M}_1}}{{\textit{M}_3}}-\left( 1+{\textit{N}_{\mathrm{A}}}+{\textit{N}'_{\mathrm{A}}}\dfrac{{\textit{M}'_1}}{{\textit{M}'_3}}\right) \right\} . \end{aligned}$$

According to Buongiorno [3], for a typical nanofluid, \(10^2\le {\mathrm {Le}}\le 10^6\), while \(1\le {\textit{N}_{\mathrm{A}}}\le 10,{\textit{N}'_{\mathrm{A}}}\approx 10^2\) and \({\textit{N}_{\mathrm{B}}}\approx 10^{-3}\). The ratios \({{\textit{M}_1}}/{{\textit{M}_3}}\) and \({{\textit{M}'_1}}/{{\textit{M}'_3}}\) are \(\approx 10^{-2}\) and \(\approx 10^{-3}\), respectively. If one takes the preceding approximations, then the exponents in Eq. (26) are small, so following [2], to a good approximation one has

$$\begin{aligned} T_b=\frac{T_h}{T_h-T_c}-z. \end{aligned}$$

Using this we obtain the steady-state solution of Eqs. (19)–(23):

$$\begin{aligned}&{\varvec{u}}_{b} =\mathbf 0 ,\quad p=p_{b}(z),\quad T_b=\frac{T_h}{T_h-T_c}-z,\end{aligned}$$
(27)
$$\begin{aligned}&\phi _b=\frac{\phi _0}{\phi _0-\phi _1}-z,\quad H_{b} =1 -{\frac{M_1}{{M}_3}}z+ {\frac{{M}'_1}{{M}'_3}}z,\end{aligned}$$
(28)
$$\begin{aligned}&M_{b} =1 +\frac{1}{\chi _2}\left( \frac{{\textit{M}_1}}{{\textit{M}_3}}\right) z-\frac{1}{\chi _2}\left( \frac{{\textit{M}'_1}}{{\textit{M}'_3}}\right) z. \end{aligned}$$
(29)

4 Linear stability problem

We consider a small perturbation of amplitude \(\epsilon ' \ (0<\epsilon '\ll 1)\) to the steady-state equation (18), so that

$$\begin{aligned}&{\varvec{u}} ={\varvec{u}}_{b}+\epsilon '{\varvec{u}}',\qquad p=p_{b}+\epsilon ' p',\qquad T=T_{b} +\epsilon '\theta ', \nonumber \\&{\varvec{M}}={\varvec{M}}_{b}+\epsilon '{\varvec{M}}',\qquad \phi =\phi _{b} +\epsilon '\phi ',\qquad {\varvec{H}}={\varvec{H}}_{b}+\epsilon '{\varvec{H}}'. \end{aligned}$$
(30)

Substituting the perturbed variables into Eqs. (11)–(16) and linearizing about the steady state by collecting the \(O(\epsilon ')\) terms and dropping the primes gives

$$\begin{aligned} \frac{1}{{\mathrm {Pr}}} \frac{\partial \nabla ^{2} w}{\partial t} =&\nabla ^{4} w+\delta ^{*} \nabla ^{4} w-\{ {\mathrm{{Ra}}M}_\mathrm{3} -{\mathrm {Ra}_{\mathrm{s}} { M}_{3}'}\}(\partial \nabla _{H}^{2} \psi /\partial z)\nonumber \\&+ \Bigg \{ {\mathrm{{Ra}}M}_\mathrm{1} -{\mathrm {Ra}}\frac{{\textit{M}_{3} { M}_{1}'}}{{\textit{M}_{3}'}}\,+\,{\mathrm {Ra}}_{ N} (1+\textit{N}_{\phi } z )\Bigg \}\nabla _{H}^{2} \theta \nonumber \\&- \Bigg \{{\mathrm {Ra}}\frac{{\textit{M}_{3} { M}_{1}' }}{{\textit{M}_{3}'}} -{{\mathrm{Ra}_{\mathrm{s}} { M}_{1}'}} +{\mathrm {Rn}}+{\mathrm{{Ra}_{ N} { N}_{\phi }}} (1-z )\Bigg \}\nabla _{H}^{2}\phi , \end{aligned}$$
(31)
$$\begin{aligned}&\frac{\partial \theta }{\partial t} = \nabla ^{2} \theta +w-\frac{{{ {N}_\mathrm{B}}}}{{\mathrm {Le}}} \frac{\partial \phi }{\partial z} +\frac{{{ {N}_\mathrm{B} { N}_\mathrm{A}' }}}{{\mathrm {Le}}} \frac{\partial ^{2} \psi }{\partial z^{2} } -\left\{ \frac{{{ {N}_\mathrm{B}}}}{{\mathrm {Le}}} +\frac{2{{ {N}_\mathrm{A} { N}_\mathrm{B}}}}{{\mathrm {Le}}} -\frac{{{{ N}_\mathrm{B} { N}_\mathrm{A}' M_{1}}}}{{\mathrm {Le}}{{{ M}_\mathrm{3}}}}\right. \left. +\frac{{{{ N}_\mathrm{B} { N}_\mathrm{A}' { M}_\mathrm{1}' }}}{{{\mathrm{Le}{} { M}_\mathrm{3}' }}}\right\} \frac{\partial \theta }{\partial z},\end{aligned}$$
(32)
$$\begin{aligned}&\frac{\partial \phi }{\partial t} = w+\frac{1}{{\mathrm {Le}}} \nabla ^{2} \phi +\frac{{{{ N}_\mathrm{A} }}}{{\mathrm {Le}}} \nabla ^{2} \theta -\frac{{{{ N}_\mathrm{A}' }}}{{\mathrm {Le}}} \frac{\nabla ^{2} \partial \psi }{\partial z},\end{aligned}$$
(33)
$$\begin{aligned}&\frac{\partial ^{2} \psi }{\partial z^{2} } = -\frac{ (1+\chi _{2} )}{ (1+\chi )} \nabla _{H}^{2} \psi +\frac{{{{ M}_\mathrm{1} }}}{{{ {M}_\mathrm{3} }}} \frac{\partial \theta }{\partial z} -\frac{{{{ M}_\mathrm{1}' }}}{{{{ M}_\mathrm{3}'}}} \frac{\partial \phi }{\partial z}, \end{aligned}$$
(34)

where

$$\begin{aligned} \nabla ^{2}_H=\dfrac{\partial ^2}{\partial x^2}+\dfrac{\partial ^2}{\partial y^2}, \ \ \delta ^{*}=\mu _{0}\delta H_{0}(1+\chi _{2}),\ \ \mathrm {Ng={ M}_{1} Ra}, \ \ \mathrm {Ra_{s}} =\dfrac{\rho _{_{f} } g\alpha d^3(\phi _{0} -\phi _{1} )}{\mu \kappa }. \end{aligned}$$

Here \(\mathrm {Ng}\) is the magnetic thermal Rayleigh number. Since \(\varvec{\nabla }\times {\varvec{H}}=0\), there exists a potential function \(\psi \) such that \({\varvec{H}}=\varvec{\nabla }\psi \). Here Eq. (31) was obtained by taking the vertical component of the double curl of the linearized momentum equation.

Equations (31)–(34) comprise a boundary value problem that will be solved by the Chebyshev pseudospectral–QZ method. To apply the Chebyshev pseudospectral–QZ method to the preceding boundary value problem, we transform the present domain from [0, 1] to \([-1,1]\) with the coordinate transformation z to 2z–1 in the equations. We assume that the variables \(w,\ \theta ,\ \phi ,\psi \) have the form

$$\begin{aligned}{}[w,\theta ,\phi ,\psi ]=[w(z),\theta (z),\phi (z),\psi (z)]\exp (\sigma t+\mathrm {i}(k_{x} x+k_{y} y)). \end{aligned}$$
(35)

Upon substituting these equations into Eqs. (31)–(34) in the new domain, we obtain

$$\begin{aligned} \frac{\sigma }{{\mathrm {Pr}}} (4D^{2} -k^{2} )w&= (4D^{2} -k^{2} )^2w+\delta ^{*}(4D^{2} -k^{2} )^2w\nonumber \\&\quad -\left\{ {{\mathrm{Ra}M_{1}}} -{\mathrm {Ra}}\frac{{{{ M}_{3} { M}_{1}' }}}{{{{ M}_{3}' }}}\right. \quad \left. +{{\mathrm{Ra}_{{ N}}}} \left\{ 1+ {N}_{\phi } \left( \frac{z+1}{2}\right) \right\} \right\} k^{2} \theta \nonumber \\&\quad +\left\{ {\mathrm {Ra}}\frac{{{{ M}_{3} { M}_{1}' }}}{{ {{ M}_{3}' }}}-{{\mathrm{Ra}_{\mathrm{s}} { M}_{1}'}} +{ {\mathrm{Rn} +\mathrm{Ra}_{{ N}} { N}_{\phi }}} \right. \times \left. \left( \frac{1-z}{2}\right) \right\} k^{2} \phi +2({{\mathrm{Ra}M_{3}}} -{{\mathrm{Ra}_{\mathrm{s}} { M}_{3}'}})k^{2} D\psi , \end{aligned}$$
(36)
$$\begin{aligned}&\sigma \theta = w+(4D^{2} -k^{2} )\theta -2\left\{ {{\frac{{ N}_{\mathrm{B}} }{\mathrm{Le}}}} + {{\frac{2{ N}_{\mathrm{A}} { N}_{\mathrm{B}} }{\mathrm{Le}}}} -{{\frac{{ N}_{\mathrm{B}} { N}_{\mathrm{A}}' { M}_{1} }{\mathrm{Le}M_{3} }}} +{{\frac{{ N}_{\mathrm{B}} { N}_{\mathrm{A}}' { M}_{1}' }{\mathrm{Le}M_{3}'}}}\right\} - {{\frac{2{ N}_{\mathrm{B}} }{\mathrm{Le}}}} D\phi + {{\frac{4{ N}_{\mathrm{B}} { N}_{\mathrm{A}}' }{\mathrm{Le}}}} D^{2} \psi ,\end{aligned}$$
(37)
$$\begin{aligned}&\sigma \phi = w+ {{\frac{1}{\mathrm{Le}}}} (4D^{2} -k^{2} )\phi + {{\frac{{ N}_{\mathrm{A}} }{\mathrm{Le}}}} (4D^{2} -k^{2} )\theta -{{\frac{2{ N}'_{\mathrm{A}}}{\mathrm{Le}}}} (4D^{2} -k^{2} )D\psi ,\end{aligned}$$
(38)
$$\begin{aligned}&4D^{2}\psi = \frac{k^{2} (1+\chi _{2} )}{(1+\chi )}\psi +{{\frac{2{ M}_{1} }{{ M}_{3} }}} D\theta -{{\frac{2{ M}_{1}' }{{ M}_{3}'}}} D\phi , \end{aligned}$$
(39)

with the boundary conditions

$$\begin{aligned} \left. \begin{array}{l} \displaystyle w=0,\quad \theta =0,\quad \phi =0 \quad \text {at} \quad z=\pm 1\\ \displaystyle Dw=0,\quad 2(1+\chi )D\psi -k\psi =0 \quad \text {at} \quad z=-1\\ \displaystyle D^2w=0,\quad 2(1+\chi )D\psi +k\psi =0 \quad \text {at} \quad z=1 \end{array} \right\} . \end{aligned}$$
(40)
Table 1 Values of physical quantities used [25, 27]
Full size table

5 Method of solution

The system of equations (36)–(39) with boundary conditions (40) comprise an eigenvalue problem. The Chebyshev pseudospectral method [26] is applied to solve this eigenvalue problem. We closely follow the algorithm of Kaloni and Lou [27]. The algorithm is as follows. For a given temperature gradient \(\beta \), \(H_{0}\), and other physical parameters, fix \(k=\sqrt{k_{x}^2+k_{y}^2}\) and the initial trial estimates for the Rayleigh number \(\mathrm {Ra}\). Then use the \({QZ}\)-algorithm, EIG function in MATLAB, to find the leading eigenvalue \(\sigma =\sigma _{r} +\mathrm {i}\sigma _{i}\) for k. Here we recall that the leading eigenvalue \(\sigma =\sigma _{r} +\mathrm {i}\sigma _{i} \) is the one for which \(\sigma _r\) is the largest among the whole set of eigenvalues of the preceding eigenvalue problem. If necessary, we adjust \(\beta \) by the secant method to obtain \(\beta \) when the real part \(\sigma _{r}\) approaches zero, where \(\sigma _r\) is the real part of the leading eigenvalue \(\sigma =\sigma _{r} +\mathrm {i}\sigma _{i} \). We repeat the preceding step until the solution with a predefined accuracy is found. The critical temperature gradient \(\beta _{c} \) with critical wave number \(k_{c} \) is defined as follows:

$$\begin{aligned} \beta _{c} =\mathop {\min }\limits _{k}\ \beta \left( \mathrm {Pr},\mathrm {Le},\ldots \ldots \right) . \end{aligned}$$
(41)

The function FMINBND in MATLAB was used to carry out a minimization in Eq. (41). If the imaginary part of the leading eigenvalue happens to be zero, and if \(\sigma _r\) approaches zero, then the instability is stationary; otherwise, it is oscillatory.

To test the accuracy of our method, we solved the Bénard problem for three types of boundary conditions, viz. rigid–rigid, rigid–free, and free–free in the absence of a magnetic field and particle concentration. The computations for the considered boundary conditions were benchmarked against Chandrasekhar’s results for the Bénard problem Table III, pp. 43 [28].

6 Results

The numerical results presented in this section are for water- and ester-based MNFs. The values of the physical quantities used are taken from the table given in [25, 27], which we reproduce here for the sake of completeness (Table 1).

The numerical results are provided for the nanoparticle concentration near the lower plate for a \(d=1\hbox { mm}\) thick layer of nanofluid. The calculations are based on 10 nm nanoparticle suspended in carrier fluid.

A neutral curve is defined as the locus of points where Re \((\sigma )=0\). If in addition Im \((\sigma ) = 0\) on such a curve, then the principle of exchange of instabilities is said to be valid.

6.1 Microgravity environment

A microgravity environment is one in which the value of acceleration due to gravity g is assumed to be negligible. In a microgravity environment we set the value of g equal to \(1\times 10^{-6}\ \text {m}\text {s}^{-2}\).

When a nanofluid is placed in an externally applied magnetic field in a microgravity environment, convection is driven owing to magnetic forces alone independent of the gravitational force. Owing to the temperature dependence of the magnetization of the magnetic fluid, a magnetization gradient will be established across the fluid layer. Magnetization of ferrofluids decreases with increasing temperature of the ferrofluid, so the direction of the magnetization gradient will be opposite to the direction of the temperature gradient. This will in turn give rise to an inner magnetic field gradient parallel to temperature gradient. A volume element displaced from the colder region with large magnetization will replace hotter ferrofluid with lower magnetization, resulting in a flow that will continue as long as the magnetic field and temperature field gradients are maintained [29].

The effects of the Langevin parameter \(\alpha _L\) on the neutral curves for water- and ester-based MNFs are shown in Fig. 2a, b, respectively. The critical magnetic Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) is finite for both types of MNF. The neutral curves show that the increase in the value of the Langevin parameter \(\alpha _L\) decreases the critical value of the magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) in the microgravity environment. This is because in the microgravity environment, as the value of \(\alpha _L\) increases, the strength of the inner magnetic field gradient \(\varvec{\nabla }H\) also increases. The volume element moves in the fluid at greater speed, producing strong disturbances and thus resulting in a lower value of the critical magnetic thermal Rayleigh number. Since the critical magnetic thermal Rayleigh number separates the turbulent regime from the laminar regime, the heat transfer coefficient remains higher in the turbulent regime than in the laminar regime [7]. Thus the effect of increase in the magnetic field strength in the microgravity environment is to enhance the heat transfer in the water- and ester-based MNFs. Figure 2c, d shows the effects of the volumetric fraction \({\Delta }\phi \) of the nanoparticles on the neutral curves for both types of MNF. The critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) increases as the value of \({\Delta }\phi \) increases. The temperature gradient produces an unstable, top-heavy configuration. As the particle concentration near the bottom of the fluid layer increases, the density distribution decreases with height; this has a stabilizing effect for natural convection in MNFs, which results in higher values of the critical magnetic thermal Rayleigh number. Thus increasing the value of the volumetric fraction \({\Delta }\phi \) of nanoparticles has a stabilizing effect on the system.

Figure 3a, b shows the variation of the critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) with \({\Delta }\phi \) at different values of the parameter \(\delta \). The figure clearly shows that \(\mathrm {Ng}_{\mathrm{c}}\) increases as \({\Delta }\phi \) increases.

Figure 3c, d shows that the critical magnetic thermal Rayleigh number decreases as the value of the nanoparticle Rayleigh number \(\mathrm {Rn}\) increases. Therefore, \(\mathrm {Rn}\) has a destabilizing effect on the system. This is because as the value of \(\mathrm {Rn}\) increases, the Brownian motion of the nanoparticles is promoted, which in turn facilitates the development of turbulence, leading to a lower value of \(\mathrm {Ng}_{\mathrm{c}}\). It is also worth noting that water-based MNFs are more resilient to convection than ester-based MNFs.

Figure 4a, b shows the variation of the critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) with the nanoparticle Rayleigh number \(\mathrm {Rn}\); as mentioned earlier, both of these panels clearly show that \(\mathrm {Ng}_{\mathrm{c}}\) decreases as the value of \(\mathrm {Rn}\) increases. Since \(\mu _{1}=\mu (1+\varvec{\delta }\cdot {\varvec{B}})\), at the higher value of \(\delta \), the nanoparticles in the fluid slow down owing to the high viscosity. This is manifested in the higher value of the critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\).

Fig. 2
figure 2

a, b Neutral curves for different values of Langevin parameter \(\alpha _L\); c, d neutral curves for different values of volumetric fraction \({\Delta }\phi \) of nanoparticles. Here a and c correspond to water-based MNFs and b and d to ester-based MNFs. The fixed parameter values are \(\delta =0.01,{\Delta }\phi =0.01, {N}_{\mathrm{A}}=\mathrm{{10}}, \mathrm {Le}=\mathrm{{200}}\), and \(d=0.001\)

Full size image
Fig. 3
figure 3

a, b Variation of critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) with \({\Delta }\phi \); c, d neutral curves for different values of nanoparticle Rayleigh number \(\mathrm {Rn}\). Here a and c correspond to water-based MNFs, b and d to ester-based MNFs. The fixed parameter values are \(\alpha _L=2,\delta =0.01\),\(N_{\mathrm{A}}=\mathrm{{10}},\mathrm {Le}=\mathrm{{200}}\), \({\Delta }\phi \) = 0.01, and \(d=0.001\)

Full size image
Fig. 4
figure 4

a, b Variation of critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) with nanoparticle Rayleigh number \(\mathrm {Rn}\); c, d) neutral curves for different values of depth of nanofluid layer d. Here a and c correspond to water-based MNFs, b and d to ester-based MNFs. The fixed parameter values are \(\delta =0.01\), \(N_{\mathrm{A}}\) = 10, \(\mathrm {Le}\) = 200, and \(d=0.001\)

Full size image
Fig. 5
figure 5

a, b Neutral curves for different values of nanoparticle Rayleigh number \(\mathrm {Rn}\); c, d variation of critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) with nanoparticle Rayleigh number \(\mathrm {Rn}\). Here a and c correspond to water-based MNFs, b and d to ester-based MNFs. The fixed parameter values are \(\alpha _L=2,\delta =0.01\), \(N_{\mathrm{A}}=\mathrm{{10}}, \mathrm {Le}=\mathrm{{200}}\), \({\Delta }\phi \) = 0.01, and \(d=0.001\)

Full size image

6.2 Gravity environment

The neutral curves associated with different values of d, the depth of the nanofluid layer, in a gravitational environment are plotted in Fig. 4c, d. The figure shows that the critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) increases as the value of d increases for both types of MNF. Since now both gravitational and magnetic forces are operational, as the depth of the nanofluid layer increases, the buoyancy force dominates the magnetic forces, which results in a higher value of \(\mathrm {Ra}_{\mathrm{c}}\).

Figure 5a, b shows the effects of the nanoparticle Rayleigh number \(\mathrm {Rn}\) on both types of MNF. The critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) decreases with an increasing value of \(\mathrm {Rn}\) in water- and ester-based MNFs. Thus increasing the depth of the nanofluid layer has a stabilizing effect, while increasing the value of \(\mathrm {Rn}\) has a destabilizing effect on the system.

Table 2 Values of critical thermal Rayleigh number and critical wavenumber in gravitational environment for water- and ester-based MNFs
Full size table
Table 3 Values of critical magnetic thermal Rayleigh number and critical wavenumber in microgravity environment for water- and ester-based MNFs
Full size table

Figure 6a, b shows the neutral curves for different values of \(\alpha _L\). The critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) increases with increases in the value of \(\alpha _L\), indicating that increasing \(\alpha _L\) has a stabilizing effect on the system. When only magnetic forces were in operation, i.e., in the microgravity environment, the effect of \(\alpha _L\) was to advance the onset of convection (Fig. 2a, b). Figure 6c, d shows the neutral curves associated with different values of modified particle density \(\mathrm {N}_{\mathrm{B}}\). The effect of increasing the value of \(\mathrm {N}_{\mathrm{B}}\) is to advance the onset of convection. This is because the movement of the heavier nanoparticles in the fluid produces strong disturbances, which results in the lower value of \(\mathrm {Ra}_{\mathrm{c}}\). Figure 7a, b shows the variation of the critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) with \( {N}_{\mathrm{B}}\) at different values of the parameter \(\delta \). As we just mentioned, the value of the critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) decreases as the value of \(\mathrm {N}_{\mathrm{B}}\) increases. There is a sudden change in behavior around the point 0.010; this is because some of the nanoparticles may amass near the bottom owing to sedimentation if we keep on increasing the value of \(\mathrm {N}_{\mathrm{B}}\).

Fig. 6
figure 6

a, b Neutral curves for different values of Langevin parameter \(\alpha _L\); c, d neutral curves for different values of modified particle density increment \( {N}_{\mathrm{B}}\). Here a and c correspond to water-based MNFs, b and d to ester-based MNFs. The fixed parameter values are \(\alpha _L=2,\delta =0.01\), \(N_{\mathrm{A}}=\mathrm{{10}},\mathrm {Le}=\mathrm{{200}}\), \({\Delta }\phi \) = 0.01, and \(d=0.001\)

Full size image
Fig. 7
figure 7

a, b Variation of critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) for different values of modified particle density increment \( {N}_{\mathrm{B}}\); c, d neutral curves for different values of \({\Delta }\phi \). Here a and c correspond to water-based MNFs, b and d to ester-based MNFs. The fixed parameter values are \(\alpha _L=2,\delta =0.01,\mathrm {N}_{\mathrm{A}}=\mathrm{{10}},\mathrm {Le}=\mathrm{{200}},{\Delta }\phi =0.01\), and \(d=0.001\)

Full size image

The effects of increasing the volumetric fraction \({\Delta }\phi \) of nanoparticles on neutral curves are shown in Fig. 7c, d. The critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) increases with increases in the value of \({\Delta }\phi \). Thus increasing the value of \({\Delta }\phi \) has a stabilizing effect on the system.

We have also solved the same problem for other combinations of boundary conditions, viz., when both upper and lower boundaries are rigid and when both upper and lower boundaries are free. The results for these combinations of boundary conditions are displayed in Table 2 in a gravity environment and in Table 3 in a microgravity environment. The results for these boundary conditions are qualitatively similar to the results discussed earlier; thus they are not included in the paper. Tables 2 and 3 display the critical wavenumber \(k_c\), critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\), and critical magnetic thermal Rayeligh numbers \(\mathrm {Ng}_{\mathrm{c}}\). Our first observation from these tables is that for any given value of the parameter \(\delta \), for a given MNF, and for a particular combination of boundary conditions, the value of the critical wavenumber \(k_c\) is the same in the gravity and microgravity environments. The value of the critical magnetic Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) in a microgravity environment is larger than that of \(\mathrm {Ra}_{\mathrm{c}}\) in gravity environment. Thus when only magnetic forces are operational, the convection gets delayed. We observe from Table 2 that the value of the critical thermal Rayleigh number \(\mathrm {Ra}_{\mathrm{c}}\) first decreases as \(\alpha _L\) increases from 1 to 2 and then starts increasing with further increases in the value of \(\alpha _L\). In Table 3 the value of the critical magnetic thermal Rayleigh number \(\mathrm {Ng}_{\mathrm{c}}\) first increases as \(\alpha _L\) increases from 1 to 3 and then starts decreasing with further increases in the value of \(\alpha _L\). Similar behavior was observed in [30] for water- and ester-based ferrofluids. This seems to be analogous to tight coupling between buoyancy and magnetic forces, as pointed out by Finlayson [12]. He proposed the following formula (using his notations) in the case of ferromagnetic fluids to make precise the aforementioned coupling:

$$\begin{aligned} {\frac{\mathrm{Rg}_{\mathrm{c}}}{\mathrm{Rg}_{0\mathrm{c}}}+\frac{{ N}_{\mathrm{c}}}{{ N}_{0\mathrm{c}}}=1}, \end{aligned}$$

where \(\mathrm {Rg}_{\mathrm{c}}\) and \( {N}_{\mathrm{c}}\) are critical Rayleigh numbers in gravity and microgravity environments, respectively, and \(\mathrm {Rg}_{0\mathrm{c}}=1708, {N}_{\mathrm{0c}}=\mathrm{2568.5}\). In our case, it is difficult to make precise this type of tight coupling.

7 Conclusions

Linear stability theory was used to study convective instability in a thin layer of MNF. The viscosity of the MNF is assumed to be dependent on the applied magnetic field. The effects of Brownian diffusion, thermophoresis, and magnetophoresis were incorporated in the mathematical model. The resulting eigenvalue problem was solved using the Chebyshev pseudospectral method. The effects of important parameters of the problem were observed at the onset of convection in microgravity and gravity environments. We draw the following conclusions:

  1. (i)

    In a microgravity environment, the effect of \({\Delta }\phi \) is to delay the onset of convection, while \(\alpha _L\) and \(\mathrm {Rn}\) advance the onset of convection.

  2. (ii)

    In a gravity environment, the effect of \(d,\alpha _L,{\Delta }\phi \) is to stabilize the system, while \(\mathrm {Rn}\) and \( {N}_{\mathrm{B}}\) destabilize the system.