A Dirichlet–Neumann cost functional approach for the Bernoulli problem

Abstract

The Bernoulli problem is rephrased into a shape optimization problem. In particular, the cost function, which turns out to be a constitutive law gap functional, is borrowed from inverse problem formulations. The shape derivative of the cost functional is explicitly determined. The gradient information is combined with the level set method in a steepest descent algorithm to solve the shape optimization problem. The efficiency of this approach is illustrated by numerical results for both interior and exterior Bernoulli problems.

1 Introduction

The Bernoulli problem can be considered as a prototype of a stationary free boundary problem. It arises in various physical situations, such as electrochemical machining [1], potential flow in fluid mechanics [2], heat flow [3], optimal insulation [4], and many more. It is also used as a model in various linear flow laws, such as Ohm’s law for electrical current, Fourier’s law for heat transfer, and Darcy’s law for fluid flow through a porous medium. In certain industrial problems such as shape optimization, painting, and galvanization, one seeks to find level lines of the potential function (i.e., streamlines) with prescribed pressure on them. The latter is given by Bernoulli’s law

$$\begin{aligned} |\nabla u| =c, \end{aligned}$$

where $c$ is a positive given constant and $u$ is the potential function. The linear flow law states that the flow vector $K$ is a linear function with respect to $\nabla u$, more precisely $K$ is given by the expression

$$\begin{aligned} K=-\gamma \nabla u, \end{aligned}$$

where $\gamma$ is the conductivity of the flow. For more details on the physical background and an exhaustive bibliography we refer the reader to [5, 6]. As another application in electrostatics we mention the problem of designing an annular condenser with one boundary component given, the other one to be determined (together with a potential function) such that the intensity of the electrostatic field is constant on it.

The last application is an example of the so-called exterior Bernoulli problem: given a bounded Lipschitz domain $A\subset \mathbb R ^2$, with boundary $\Upsilon _0$ and $\lambda <0$, the exterior Bernoulli problem, also known as the Alt–Caffarelli problem, consists in finding a bounded domain $B\supset \overline{A}$ with $C^{1,1}$ boundary $\Gamma$ and a function $u$ defined on $\Omega =B{\setminus }\overline{A}$ such that

$$\begin{aligned} \!\!\left\{ \begin{array}{l} \displaystyle \Delta u =0\quad \text{ in} \Omega ,\\ \displaystyle u = 1\quad \text{ on} \Upsilon _0,\\ \displaystyle u = 0 \quad \text{ on} \Gamma ,\\ \displaystyle \frac{\partial u}{\partial \nu } = \lambda \quad \text{ on} \Gamma , \end{array} \right. \end{aligned}$$

(1)

where $\nu$ is the outward unit normal to $\Gamma$.

The interior Bernoulli problem is similar; however, the free boundary component is interior to $\Upsilon _0$. We point out that the last two statements in (1) – $u=0$ and ${\partial u}/{\partial \nu } = \lambda$ – imply the Bernoulli condition $|\nabla u|=|\lambda |$, which corresponds to Bernoulli’s principle in fluid mechanics.

The existence of solutions of the exterior problem can be obtained in various ways, for example, by variational methods [7] or by the method of sub- and supersolutions [8]. In general, solutions of Bernoulli’s free boundary problem are not unique. However, uniqueness for the exterior problem was proven in the context of convex domains (see [9]). Uniqueness for the exterior problem is also proven in [10] for a given star-shaped domain, together with results on the star shapeness and convexity of the solution domain for the $p$-Laplacian. The interior problem, instead, need not have a solution for every domain $A$ and for every positive constant $\lambda >0$. However (see, in particular, [11]), when the known domain $A$ is convex (with $C^1$ boundary), for the more general case of the $p$-Laplacian there exists a positive constant $\lambda ^*(\Omega )$, called Bernoulli constant, such that the Bernoulli problem has no solution if $\lambda <\lambda ^*(\Omega )$, while it has at least one classic solution if $\lambda \ge \lambda ^*(\Omega )$ and the solution is a $C^2$ convex set. In [12] it is proven for the Laplacian that this solution is unique for $\lambda =\lambda ^*(\Omega )$. For the qualitative theory and stability of solutions in dimension two we refer the reader to [6] and [9].

We are aware of two different strategies for the numerical solution of such problems. First, a fixed-point-type approach can be used where a sequence of elliptic problems are solved in a sequence of converging domains that are updated using one of the redundant boundary conditions on $\Gamma$ in a sophisticated way [6, 13]. This approach does not require any gradient information. Second, an equivalent shape optimization problem can be considered [14, 15].

Shape optimization provides an efficient tool to solve free boundary problems (see [14–17]). Typically it leads to an optimization problem of the form

$$\begin{aligned} \left\{ \begin{array}{l} \min _\Omega J(\Omega , u_\Omega ),\\ \text{ subject} \text{ to} e(u_\Omega ) = 0, \end{array} \right. \end{aligned}$$

(2)

where $J$ denotes a suitable functional that depends on a domain $\Omega$ as well as on a function $u_\Omega$, which is the solution of a partial differential equation $e(u) =0$ posed on $\Omega$. For the numerical solution of such a shape optimization problem one can apply a steepest descent method, which requires the shape gradient of $J$. Alternatively, one could use a variant of Newton’s method that requires the shape Hessian of $J$, which is considerably more difficult to obtain and apply (see [18, 19], and references therein). One of the difficulties in shape optimization problems is that the topology of the optimal shape is unknown. Developing numerical techniques that can handle topology changes therefore becomes essential. The level set method introduced in [20] is well known for being able to handle topology changes such as breaking one component into two, merging two components into one, or forming sharp corners. Therefore, it is widely used for the numerical realization of shape optimization problems.

There are several ways to transform the Bernoulli problem into a shape optimization problem. In [14], the following variant was considered:

$$\begin{aligned} \min _\Omega J_D(\Omega )=\min _\Omega \frac{1}{2}\int _\Gamma \left( \frac{\partial u_D}{ \partial \nu }-\lambda \right) ^2, \end{aligned}$$

where $u_D$ is the solution of the Dirichlet problem

$$\begin{aligned} \!\!\left\{ \begin{array}{l} \Delta u_D =0\quad \text{ in} \Omega ,\\ u_D = 1\quad \text{ on} \Upsilon _0,\\ u_D = 0\quad \text{ on} \Gamma . \end{array}\right. \end{aligned}$$

(3)

In [15], this problem is also transformed into a shape optimization problem exploiting the Neumann boundary condition,

$$\begin{aligned} \min _\Omega J_N(\Omega )=\min _\Omega \frac{1}{2}\int _\Gamma u_N^2, \end{aligned}$$

where $u_N$ is the solution of the Neumann problem

$$\begin{aligned} \!\!\left\{ \begin{array}{l} \displaystyle \Delta u_N =0\quad \text{ in} \Omega ,\\ \displaystyle u_N = 1\quad \text{ on} \Upsilon _0,\\ \displaystyle \frac{\partial u_N}{\partial \nu } = \lambda \quad \text{ on} \Gamma . \end{array}\right. \end{aligned}$$

(4)

As in [14, 15], we are interested in formulating the Bernoulli problem as a shape optimization problem. The originality of the present approach relies on the use of an error functional that can be interpreted as a constitutive law error functional. This approach was introduced in [21] in the context of a posteriori error estimates for a finite element method. In this context, the minimization of the constitutive law error functional makes it possible to detect the reliability of the mesh without knowing the exact solution. Within the inverse problem community this functional was introduced in [22] in the context of parameter identification. It has also been used to recover Robin-type boundary conditions [23] and in the context of identifying geometrical flaws (see [24] and references therein). Here, the error functional depending on the domain $\Omega$ is defined by

$$\begin{aligned} J(\Omega ):=\frac{1}{2}\int _\Omega |\nabla u_D-\nabla u_N|^2. \end{aligned}$$

(5)

Let us consider the subspace $V$ of $H^1(\Omega )$,

$$\begin{aligned} V=\{v\in H^1(\Omega );\ v=0 \text{ on} \Upsilon _0\}, \end{aligned}$$

and define the seminorm on $H^1(\Omega )$,

$$\begin{aligned} |v|_{H^1(\Omega )} := \left( \int _{\Omega }|\nabla v|^2\right) ^{\frac{1}{2}}. \end{aligned}$$

We recall that $|.|_{H^1(\Omega )}$ is a norm on $H^1_0(\Omega )$ as well as on $V$, which by Poincaré’s inequality is equivalent to the norm of $H^1(\Omega )$.

If $(u,\Omega )$ is a solution of (1), then $u_D=u_N=u$; therefore, $J(\Omega )=0$. Conversely if $J(\Omega )=0$, since $u_D-u_N\in V, J(\Omega )=\frac{1}{2}|u_D-u_N|_{H^1(\Omega )}^2$ and $|.|_{H^1(\Omega )}$ is a norm on $V$, then $u_D=u_N$, and $u=u_D=u_N$ is a solution of problem (1). Therefore, $(u,\Omega )$ is a solution of (1) if and only if $J(\Omega )=0$. Thus problem (1) is equivalent to the following shape optimization problem: find $(u,\Omega )$ such that

$$\begin{aligned} J(\Omega )=\min _{\tilde{\Omega }} J(\tilde{\Omega })=0. \end{aligned}$$

(6)

The main contribution of the present paper is to numerically solve the shape optimization problem (6). We point out that the same cost functional $J$ was studied in [25]. The technique used in [25], which was inspired by [26, 27], restricts the results to starlike domains. Here we extend it to more general $C^{1,\alpha }$ domains as well as to the interior case. We also give some numerical tests with topology changes.

The remainder of this paper is organized as follows. In Sect. 2 we recall some basic concepts and results related to shape differentiation. In Sect. 3 we prove the existence of the Eulerian derivatives of the state functions $u_D$ and $u_N$ and give the variational formulae verified by them. In Sect. 4 we prove the existence of the shape derivative of the functional $J$ and give its analytical representation for the exterior Bernoulli problem together with the proof of this expression. In Sect. 5 we give a similar result for the interior Bernoulli problem without proof. In Sect. 6 we describe how the level set method is used in combination with the shape derivative to obtain numerical solutions for the Bernoulli problem and outline the algorithm to be implemented. In Sect. 7 some numerical results for the exterior and interior problems are given.

2 Shape derivative of functional $J$

Let us consider a domain $U$ such that $U\supset \overline{\Omega }$ and introduce the mapping $F_t$, which defines a perturbation of the domain $\Omega$ of the form

$$\begin{aligned} F_t=\text{ Id}+th, \end{aligned}$$

where Id is the identity operator, $h$ is a deformation field belonging to the space

$$\begin{aligned} Q=\{h\in \mathcal C ^{1,1}(\overline{U})^2;\ h=0 \text{ on} \Upsilon _0\}, \end{aligned}$$

and $t$ is sufficiently small such that $F_t$ is a diffeomorphism from $\Omega$ onto its image. The perturbations of $\Omega$ and $\Gamma$ are respectively defined by

$$\begin{aligned} \Omega _t:=F_t(\Omega ),\quad \Gamma _t:=F_t(\Gamma ). \end{aligned}$$

Since $h$ vanishes on $\Upsilon _0$ for $h\in Q$, $F_t(\Upsilon _0)=\Upsilon _0$. Thus, for all $t$, $\Upsilon _0$ is a part of the boundary of $\Omega _t$. We further note $\Omega _0=\Omega$ and $\Gamma _0=\Gamma$.

We consider the solutions $u_{Dt}:=u_D(\Omega _t)$ and $u_{Nt}:=u_N(\Omega _t)$ of (3) and (4) respectively formulated on the perturbed domain $\Omega _t$ instead of $\Omega$, i.e.,

$$\begin{aligned} \!\!\left\{ \begin{array}{l} \Delta u_{Dt} =0\quad \text{ in} \Omega _t,\\ u_{Dt} = 1\quad \text{ on} \Upsilon _0,\\ u_{Dt} = 0\quad \text{ on} \Gamma _t, \end{array}\right. \end{aligned}$$

(7)

$$\begin{aligned} \!\!\left\{ \begin{array}{l} \displaystyle \Delta u_{Nt} = 0\quad \text{ in} \Omega _t,\\ \displaystyle u_{Nt} = 1\quad \text{ on} \Upsilon _0,\\ \displaystyle \frac{\partial u_{Nt}}{\partial \nu _t}= \lambda \quad \text{ on} \Gamma _t, \end{array}\right. \end{aligned}$$

(8)

where $\nu _t$ is the outward unit normal vector to $\Gamma _t$.

We say that the functional $J$ has a directional Eulerian shape derivative to direction $h$ at $\Omega$ if the limit

$$\begin{aligned} \text{ d}J(\Omega ,h)=\lim _{t\rightarrow 0}\frac{J(\Omega _t)-J(\Omega )}{t} \end{aligned}$$

exists. If, furthermore, $\text{ d}J (\Omega ,h)$ is linear and continuous with respect to $h$, then we say that $J$ is shape differentiable at $\Omega$ and $\text{ d}J(\Omega ,.)$ is called the shape derivative of $J$ at $\Omega$. By the Hadamard–Zolesio structure theorem [28], $\text{ d}J (\Omega ,h)$ only depends on the normal component of $h$ on $\Gamma$.

In what follows, we prove the existence of the shape derivative of $J$ defined by (5) and show that, according to the Hadamard–Zolesio structure theorem, it can be written in the form

$$\begin{aligned} \mathrm{d}J(\Omega ,h)=\int _\Gamma G(h\cdot \nu ), \end{aligned}$$

(9)

where $G$ is a well-defined function on $\Gamma$. This part of our analysis exploits the smoothness of $\Omega$.

This structure of the shape derivative is advantageous because the gradient flow can be chosen to minimize the functional $J$. More precisely,

$$\begin{aligned} h\in Q\quad \text{ such} \text{ that} h_{|\Gamma } = -G\nu \end{aligned}$$

(10)

is a descent direction of the functional $J$. Thus, perturbing the domain in the direction defined by (10) decreases the value of $J$. In Sect. 5 we use this normal velocity and the level set method to numerically solve the shape optimization problem (6).

To prove existence and determine the shape derivative we first recall some transformation and differentiation formulae in the following two lemmas (see [17, 29]). In what follows, if $\varphi _t$ is a function defined on the perturbed domain $\Omega _t$ or interface $\Gamma _t$, then we write $\varphi ^t$ for the function $\varphi _t\circ F_t$, which is defined on the reference domain $\Omega$ or interface $\Gamma$, especially we consider the functions

$$\begin{aligned} u_N^t=u_{Nt}\circ F_t,\quad u_D^t=u_{Dt}\circ F_t. \end{aligned}$$

Lemma 1

(i) If $\varphi _t\in L^{1}(\Omega _t)$, then $\varphi ^t\in L^1(\Omega )$ and we have

$$\begin{aligned} \int _{\Omega _t}\varphi _t=\int _{\Omega }\delta _t\varphi ^t, \end{aligned}$$

(11)

where $\delta _t=\det (DF_t)=\det (I+t\,\nabla h^{\mathsf{T }})$ (${ DF}_t$ is the Jacobian matrix of $F_t$).

(ii) If $\varphi _t\in H^{1}(\Omega _t)$, then $\varphi ^t\in H^{1}(\Omega )$, and we have

$$\begin{aligned} (\nabla \varphi _t)\circ F_t=M_t\nabla \varphi ^t, \end{aligned}$$

(12)

with $M_t=DF_t^{-T}$.

(iii) If $\varphi _t\in L^{1}(\Gamma _t)$, then $\varphi ^t\in L^{1}(\Gamma )$ and we have

$$\begin{aligned} \int _{\Gamma _t}\varphi _t=\int _{\Gamma }\omega _t\varphi ^t, \end{aligned}$$

(13)

with $\omega _t=\delta _t\,|M_t \nu |$.

For a domain dependent function $u(\Omega )\in H^1(\Omega )$ one can now define the Eulerian derivative $\tilde{u}$ at $0$ in the direction $h$ by the limit

$$\begin{aligned} \widetilde{u}=\lim _{t\rightarrow 0}\frac{u(\Omega _t)\circ F_t-u(\Omega )}{t} \end{aligned}$$

if it exists in $H^1(\Omega )$.

Lemma 2

The mappings $t\mapsto \delta _t$, $t\mapsto M_t$, and $t\mapsto \omega _t$ with values in $\mathcal C (\Omega )$, $\mathcal C (\Omega )^{2\times 2}$, and $\mathcal C (\Gamma )$, respectively, are $\mathcal C ^1$ in a neighborhood of $0$, and we have

$$\begin{aligned} \begin{array}{l} \!\!\left. \dfrac{d\delta _t}{dt}\right| _{t=0} = \mathrm div{ h},\\ \!\!\left. \dfrac{dM_t}{dt}\right| _{t=0} = -\nabla h,\\ \!\!\left. \dfrac{d\omega _t}{dt}\right| _{t=0} = \mathrm div_\Gamma { h}, \end{array} \end{aligned}$$

where $\mathrm div_\Gamma { h}:=\mathrm div{ h}_{|\Gamma }-\nabla { h}\, \nu \cdot \nu$ is the surface divergence of $h$ on $\Gamma$.

Using (11) and (12) and the fact that the mapings $t\mapsto \delta _t$ and $t\mapsto M_t$ are $\mathcal C ^1$ in a neighborhood of $0$ (see Lemma 2), we get

$$\begin{aligned} J(\Omega _t)=\frac{1}{2}\int _\Omega \delta _t|M_t(\nabla u_D^t-\nabla u_N^t)|^2. \end{aligned}$$

In the remainder of this section $h$ is a fixed element of the space $Q$. In Theorem 1 we prove that the mappings $t\mapsto u_D^t$ and $t\mapsto u_N^t$ are $\mathcal C ^1$ in a neighborhood of  $0$, and we characterize their Eulerian derivatives at $0$ in the direction $h$. The same type of result will then be proved for $t\mapsto J(\Omega _t)$ in Theorem 2.

Theorem 1

The mappings $t\mapsto u_D^t$ and $t\mapsto u_N^t$ with values in $H^1(\Omega )$ are $\mathcal C ^1$ in a neighborhood of   $0$. Furthermore, their Eulerian derivatives at $0$, denoted by $\widetilde{u}_D$ and $\widetilde{u}_N$ respectively, satisfy the properties $\widetilde{u}_D\in H^1_0(\Omega ), \widetilde{u}_N\in V$ and are solutions of the following respective variational problems:

$$\begin{aligned}&\!\!\displaystyle \int _{\Omega }\nabla \widetilde{u}_D\cdot \nabla v = -\int _\Omega A\, \nabla u_D\cdot \nabla v \displaystyle \quad \forall \ v\in H_0^1(\Omega ),\ \ \end{aligned}$$

(14)

$$\begin{aligned}&\!\!\displaystyle \int _{\Omega }\nabla \widetilde{u}_N\cdot \nabla v = -\int _\Omega A\, \nabla u_N\cdot \nabla v + \lambda \int _{\Gamma }(\mathrm div_\Gamma { h})\,{ v}\displaystyle \quad \forall \ { v}\in { V},\ \ \end{aligned}$$

(15)

where $A=(\mathrm{div} h)\mathrm{I}-\nabla h-(\nabla h)^\mathsf{T }$.

3 Proof of Theorem 1

Proof of Theorem 1

The proof of Theorem 1 is based on the following two Lemmas.

Lemma 3

The bilinear form $a_t$ defined on $V\times V$ by

$$\begin{aligned} a_t(u,v)=\displaystyle \int _\Omega A_t\nabla u\cdot \nabla v\qquad \forall \ u,v\in V, \end{aligned}$$

with $A_t=\delta _t M_t^{\mathsf{T }}M_t$, is continuous and coercive on $V\times V$ for sufficiently small $t$.

Proof

For $u,v\in V$ and sufficiently small $t$ we have

$$\begin{aligned} |a_t(u,v)| \le \Vert A_t\Vert _\infty \, |u|_{H^1(\Omega )}\,|v|_{H^1(\Omega )}, \end{aligned}$$

where $\Vert \cdot \Vert _\infty$ is the $L^\infty (\Omega )$-norm. Therefore, $a_t$ is continuous. Let us prove the coerciveness of $a_t$. We have

$$\begin{aligned} a_t(u,u) = \int _\Omega A_t\nabla u\cdot \nabla u=\displaystyle \int _ \Omega |\nabla u|^2+\int _\Omega (A_t-I) \nabla u\cdot \nabla u. \end{aligned}$$

Since the mapping $t\mapsto A_t$ is continuous at $0$, there is a constant $C_0>0$ such that

$$\begin{aligned} a_t(u,u)\ge C_0|u|^2_{H^1(\Omega )} \end{aligned}$$

holds for sufficiently small $t$. Thanks to the previously mentioned equivalence of norms on $H^1_0(\Omega )$, we deduce the coerciveness of $a_t$ for $t$ small enough.$\square$

Lemma 4

The functions $u_N^{t}$ and $u_D^t$ are the unique solutions in $H^1(\Omega )$ of

$$\begin{aligned}&\!\!\!\left\{ \begin{array}{l} \displaystyle u_D^t=1\quad \text{ on} \ \Upsilon _0,\quad u_D^t=0\quad \text{ on} \ \Gamma ,\\ \displaystyle \int _{\Omega }A_t\nabla u_D^t\cdot \nabla v=0\qquad \forall \ v\in H_0^1(\Omega ), \end{array}\right. \end{aligned}$$

(16)

$$\begin{aligned}&\!\!\!\left\{ \begin{array}{l} \displaystyle u_N^t=1\quad \text{ on} \ \Upsilon _0,\\ \displaystyle \int _{\Omega }A_t\nabla u_N^t\cdot \nabla v=\lambda \int _{\Gamma } \omega _tv\qquad \forall \ v\in V, \end{array}\right. \end{aligned}$$

(17)

where $A_t=\delta _t M_t^{\mathsf{T }}M_t$ and $\omega _t=\delta _t|M_t\nu |$.

Proof

The function $u_{Nt}\in H^1(\Omega _t)$ is the solution of the variational problem

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle u_{Nt}=1\quad \text{ on} \Upsilon _0,\\ \displaystyle \int _{\Omega _t}\nabla u_{Nt}\cdot \nabla \varphi _t = \lambda \int _{\Gamma _t}\varphi _t \quad \forall \ \varphi _t\in V_t, \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} V_t=\{\varphi _t\in H^1(\Omega _t);\ \varphi _t=0 \text{ on} \Upsilon _0\}. \end{aligned}$$

Thus using (11) and (12) we have for all $\varphi _t\in V_t$

$$\begin{aligned} \begin{array}{rll} \displaystyle \int _{\Omega _t}\nabla u_{Nt}\cdot \nabla \varphi _t \, = \, \displaystyle \int _{\Omega }\delta _t M_t\nabla u_N^t\cdot M_t\nabla \varphi ^t \\ = \, \displaystyle \int _{\Omega }\delta _t M^{\mathsf{T }}_t M_t\nabla u_N^t\cdot \nabla \varphi ^t= \displaystyle \int _{\Omega }A_t\nabla u_N^t\cdot \nabla \varphi ^t. \end{array} \end{aligned}$$

We also have, using (13),

$$\begin{aligned} \int _{\Gamma _t}\varphi _t=\displaystyle \int _\Gamma \omega _t \varphi ^t. \end{aligned}$$

Therefore, taking $v=\varphi ^t$ we obtain (17). We have $u_N^t-1\in V$, and by (17),

$$\begin{aligned} \int _\Omega A_t\nabla (u_N^t-1)\cdot \nabla v=\int _\Gamma \omega _tv\quad \forall \,\, v\in V. \end{aligned}$$

Since the bilinear form $a_t$ is continuous and coercive on $V\times V$ by Lemma 3, and since the linear form $v\longmapsto \int _\Gamma \omega _t v$ is continuous on $V$, the Lax–Milgram theorem ensures that $u_N^t-1$ is the unique solution in $V$ of

$$\begin{aligned} \int _\Omega A_t\nabla (u_N^t-1)\cdot \nabla v=\int _\Gamma \omega _tv\,\,\forall \,\, v\in V. \end{aligned}$$

Hence, $u_N^t$ is the unique solution of the variational problem (17) in $H^1(\Omega )$.$\square$

Remark 1

Since the mappings $t\mapsto \delta _t$ and $t\mapsto M_t$ are $\mathcal C ^1$ in a neighborhood of $0$, the mapping $t\mapsto A_t$, with values in $\mathcal C (\Omega )^{2\times 2}$, is also $\mathcal C ^1$, and we have

$$\begin{aligned} \frac{\text{ d}A_t}{\text{ d}t}\Bigg |_{t=0}=A, \text{ with} A:=(\text{ div} h) \text{ I}-\nabla h-(\nabla h)^{\mathsf{T }}. \end{aligned}$$

Let us prove this result for the mapping $t\mapsto u_N^t$, the proof for $t\mapsto u_D^t$ being similar. We use the implicit function theorem. Using (17), we find that $u_N^t-u_N$ is the unique element of $V$ that satisfies

$$\begin{aligned} \int _\Omega A_t\nabla (u_N^t-u_N)\cdot \nabla v = -\int _\Omega A_t\nabla u_N\cdot \nabla v+\lambda \int _{\Gamma }\omega _t\, v\quad \forall \ v\in V. \end{aligned}$$

We consider the function $\Phi :\mathcal I \times V\rightarrow V^{\prime }$ defined by

$$\begin{aligned} \langle \Phi (t,w),v\rangle \ := \int _{\Omega }A_t\nabla (w+u_N)\cdot \nabla v-\lambda \int _{\Gamma }\omega _tv\qquad \forall \ v,w\in V, \end{aligned}$$

where $V^{\prime }$ is the dual space of $V, \mathcal I$ is a neighborhood of $0$ such that for each $t\in \mathcal I , F_t$ is a diffeomorphism of $\Omega$ onto $\Omega _t$, and the brackets $\langle \!\cdot \,,\cdot \!\rangle$ stand for the duality pairing of $V^{\prime }\times V$. Thus, $u_N^t-u_N$ is the unique element in $V$ such that $\Phi (t,u_N^t-u_N)=0$. Since the mappings $t\mapsto A_t$ and $t\mapsto \omega _t$ are $\mathcal C ^1$ in a neighborhood of $0, \Phi$ is $\mathcal C ^1$, and we have for all $v,w\in V$,

$$\begin{aligned} \langle D_w\Phi (0,0)\,w,v{\rangle }\ = \int _{\Omega }\nabla w\cdot \nabla v. \end{aligned}$$

(18)

Observing that the bilinear form on the right-hand side of (18) is continuous and coercive on $V$, we deduce from the Lax–Milgram theorem that $D_w\Phi (0,0)$ is an isomorphism from $V$ onto $V^{\prime }$. Using the implicit function theorem we conclude that the mapping $t\mapsto u_N^t-u_N$ is $\mathcal C ^1$ in a neighborhood of $0$. Let $\widetilde{u}_N\in V$ be its derivative at $0$. Differentiating the identity $\Phi (t,u_N^t-u_N)=0$ with respect to $t$ we obtain at $0$

$$\begin{aligned} {\langle }D_w\Phi (0,0)\,\widetilde{u}_N,v{\rangle }+{\langle }\frac{\partial \Phi }{\partial t}(0,0),v{\rangle }=0\qquad \forall \ v\in V, \end{aligned}$$

which results in (15).$\square$

Theorem 2

The mapping $t\mapsto J(\Omega _t)$ is $\mathcal C ^1$ in a neighborhood of $0$, and its derivative at $0$ is given by

$$\begin{aligned} J^{\prime }(\Omega ,h)=\int _\Gamma G(h\cdot \nu ), \end{aligned}$$

with

$$\begin{aligned} G=\frac{1}{2}\,\left( \lambda ^2-(\nabla u_D\cdot \nu )^2+2\lambda \kappa \, u_N-(\nabla u_N\cdot \tau )^2\right) , \end{aligned}$$

(19)

where $\tau$ is the unit tangent vector to $\Gamma$ and $\kappa$ is the curvature of $\Gamma$.

4 Proof of Theorem 2

To prove Theorem 2, we need the following lemma. The regularity of $\Omega$ implies $u_D$ and $u_N\in H^2(\Omega )$, which will be used subsequently without further notice.

Lemma 5

The solutions $u_D$ and $u_N$ of problems (3) and (4) respectively satisfy the identities

$$\begin{aligned}&\!\!\!\displaystyle \int _{\Omega }A\nabla u_D\cdot \nabla u_D \displaystyle = -\int _\Gamma (\nabla u_D\cdot \nu )^2h \cdot \nu ,\end{aligned}$$

(20)

$$\begin{aligned}&\!\!\!\displaystyle \int _{\Omega }A\nabla u_N\cdot \nabla u_N \displaystyle = \int _\Gamma |\nabla u_N|^2h\cdot \nu -2\lambda \int _\Gamma h\cdot \nabla u_N. \end{aligned}$$

(21)

Proof

Using Green’s formula and the fact that $h$ vanishes on $\Upsilon _0$, we have for all $u,v\in H^1(\Omega )$

$$\begin{aligned}&\!\!\!\displaystyle -\int _\Omega (\mathrm div{ h})\,(\nabla { u}\cdot \nabla { v}) \displaystyle = \int _\Omega (Hess({ u})\nabla { v} +Hess({ v})\nabla { u})\cdot { h} {\displaystyle \,-\int _\Gamma (\nabla { u}\cdot \nabla { v})\,{ h}\cdot \nu ,}\\&\!\!\!\displaystyle \int _\Omega (\nabla h)^{\mathsf{T }} \nabla v\cdot \nabla u \displaystyle = -\int _\Omega (\Delta v)\,h\cdot \nabla u-\int _\Omega \text{ Hess}(u)\nabla v\cdot h {\displaystyle \,+\int _\Gamma (\nabla v\cdot \nu )(h\cdot \nabla u),}\\&\!\!\!\displaystyle \int _\Omega \nabla h\,\nabla v\cdot \nabla u \displaystyle = \int _\Omega (\nabla h) ^{\mathsf{T }} \nabla u\cdot \nabla v \displaystyle = -\int _\Omega (\Delta u)\,h\cdot \nabla v-\int _\Omega \text{ Hess}(v)\nabla u\cdot h {\displaystyle \,+\int _\Gamma (\nabla u\cdot \nu )(h\cdot \nabla v),} \end{aligned}$$

where $\text{ Hess}(u)$ is the Hessian of $u$. From these identities, and using the fact that $A=(\text{ div} h) \ I-\nabla h-(\nabla h)^\mathsf{T }$, one obtains

$$\begin{aligned}&\!\!\!-\displaystyle \int _\Omega A\nabla u\cdot \nabla v \displaystyle = -\int _\Omega \Delta u\, (h\cdot \nabla v)-\int _\Omega \Delta v\,(h\cdot \nabla u)+\int _\Gamma \frac{\partial v}{\partial \nu }(h\cdot \nabla u) +\int _\Gamma \frac{\partial u}{\partial \nu }(h\cdot \nabla v) -\int _\Gamma (\nabla u\cdot \nabla v)\,h\cdot \nu . \end{aligned}$$

Therefore, we get (20) and (21) for $u=v=u_D$, then for $u=v=u_N$ by noting that

$$\begin{aligned} \nabla u_D=\left( \frac{\partial u_D}{\partial \nu }\right) \,\nu ,\quad \frac{\partial u_N}{\partial \nu }=\lambda , \quad \Delta u_D=\Delta u_N=0. \end{aligned}$$

$\square$

Proof of Theorem 2

We have

$$\begin{aligned} \begin{array}{rl} \displaystyle \!\!J(\Omega _t)&=\displaystyle \frac{1}{2}\int _\Omega \delta _t\,|M_t(\nabla u_D^t-\nabla u_N^t) |^2=\frac{1}{2}\int _\Omega A_t\,(\nabla u_D^t-\nabla u_N^t)\cdot (\nabla u_D^t- \nabla u_N^t). \end{array} \end{aligned}$$

Since the mappings $t\mapsto A_t$ and by Theorem 1 $t\mapsto u_N^t$ and $t\mapsto u_D^t$ with values in $H^1(\Omega )$ are $\mathcal C ^1$ in a neighborhood of $0$, then the mapping $t\mapsto J(\Omega _t)$ is $\mathcal C ^1$, and we have

$$\begin{aligned} J^{\prime }(\Omega ,h)=\frac{1}{2}\int _\Omega A\,(\nabla u_D-\nabla u_N)\cdot (\nabla u_D-\nabla u_N)+\int _{\Omega }(\nabla u_D-\nabla u_N)\cdot (\nabla \widetilde{u}_D-\nabla \widetilde{u}_N), \end{aligned}$$

where $\widetilde{u}_D$ and $\widetilde{u}_N$ are the solutions of (14) and (15), respectively.

Let us express $\int _{\Omega }(\nabla u_{D}-\nabla u_{N})\cdot (\nabla \widetilde{u}_{D}-\nabla \widetilde{u}_{N})$ by $u_D$ and $u_N$ only. As $\widetilde{u}_D\in H_0^1(\Omega )$, we have from the variational problems verified by $u_D$ and $u_N$

$$\begin{aligned} \int _{\Omega }\nabla u_{D}\cdot \nabla \widetilde{u}_D=0 \quad \text{ and}\quad \int _{\Omega }\nabla u_{N}\cdot \nabla \widetilde{u}_{D}=\lambda \int _\Gamma \widetilde{u}_D=0. \end{aligned}$$

Since $u_D-u_N\in V$, we have, using (15),

$$\begin{aligned} \int _{\Omega }(\nabla u_{D}-\nabla u_{N})\cdot \nabla \widetilde{u}_{N}=-\int _\Omega A\,\nabla u_N\cdot \nabla (u_D-u_N)+\lambda \int _{\Gamma }\mathrm div_\Gamma { h}({ u}_{ D}-{ u}_{ N}). \end{aligned}$$

Thus, since $u_D=0$ on $\Gamma$,

$$\begin{aligned} \int _{\Omega }(\nabla u_{D}-\nabla u_{N})\cdot (\nabla \widetilde{u}_{D}-\nabla \widetilde{u}_{N})=\int _\Omega A\,\nabla u_N\cdot \nabla (u_D-u_N)+\lambda \int _{\Gamma }\mathrm div_{\Gamma }{ h}\,{ u}_{ N}. \end{aligned}$$

Thus,

$$\begin{aligned} J^{\prime }(\Omega ,h)=\frac{1}{2}\int _{\Omega }A\,\nabla u_D\cdot \nabla u_D-\frac{1}{2}\int _{\Omega }A\,\nabla u_N\cdot \nabla u_N+\lambda \int _{\Gamma }\mathrm div_\Gamma { hu}_{ N}. \end{aligned}$$

Therefore, using Lemma 5 we have

$$\begin{aligned} J^{\prime }(\Omega ,h)=-\frac{1}{2}\int _\Gamma (\nabla u_D\cdot \nu )^2 h\cdot \nu + \lambda \int _\Gamma (h\cdot \nabla u_N+\mathrm div_\Gamma { h}\,{ u}_{ N})-\frac{1}{2} \int _\Gamma |\nabla { u}_{ N}|^2{ h} \cdot \nu . \end{aligned}$$

By the following formula, which is valid when $\Gamma$ is $\mathcal C ^{1,1}$,

$$\begin{aligned} \int _\Gamma (\nabla b\cdot V+b\mathrm div_\Gamma { V})=\int _\Gamma \left( \frac{\partial { b}}{\partial \nu }+ { b}\mathrm div_\Gamma \nu \right) \,{ V}\cdot \nu , \end{aligned}$$

we obtain

$$\begin{aligned} \int _\Gamma h\cdot \nabla u_N+\mathrm div_\Gamma { hu}_{ N}=\int _\Gamma \left( \lambda +{ u}_{ N} \mathrm div_\Gamma \nu \right) \,{ h}\cdot \nu . \end{aligned}$$

Recalling that $|\nabla u_N|^2=\lambda ^2+(\nabla u_N\cdot \tau )^2$ and $\mathrm div_\Gamma \nu =\kappa$, we eventually get

$$\begin{aligned} J^{\prime }(\Omega ,h)=\frac{1}{2}\int _\Gamma \left( \lambda ^2-(\nabla u_D\cdot \nu )^2 +2\lambda u_N \kappa -(\nabla u_N\cdot \tau )^2\right) \,h\cdot \nu . \end{aligned}$$

$\square$

Remark 2

The function $G$ introduced in Theorem 2 is given by

$$\begin{aligned} G= \frac{1}{2}\left( \lambda ^2-(\nabla u_D\cdot \nu )^2+2\lambda u_N \kappa -(\nabla u_N\cdot \tau )^2\right) . \end{aligned}$$

Since $\Omega$ is a $C^{1,1}$-domain, the curvature $\kappa$ is well defined almost everywhere and belongs to $L^\infty (\Gamma )$; hence $G$ is not just a distribution, it is actually an element in $L^2(\Gamma )$.

Remark 3

The proof of Theorem 2 is based on the Eulerian derivatives $\tilde{u}_D$ and $\tilde{u}_N$, which are rigorously justified in the proof of Theorem 1, which is included to make the paper self-contained. We point out that only the weak form of the Eulerian derivatives is utilized. Alternatively, Theorem 2 could be proven using the concept of the shape derivatives of $u_D$ and $u_N$ combined with the calculus for domain integral cost functionals; see, for instance, [17, 28, 30–32]. To obtain the shape gradient of $J$ in the form (9) according to the Hadamard–Zolesio structure theorem, one would use the strong form of the equation as well as the boundary conditions satisfied by the shape derivatives of $u_D$ as well as $u_N$. However, the derivation of the Neumann condition satisfied by the shape derivative of $u_N$ requires more regularity of the state; see, for example, Theorem 5.5.2 in [32]. Accepting this restriction and taking the shape differentiability of the states for the present configuration for granted, a more elegant and simpler proof could be given.

5 Interior Bernoulli problem

Given a bounded domain $A\subset \mathbb R ^2$, with boundary $\Upsilon _0$ and $\lambda >0$. The interior Bernoulli problem consists in finding a bounded domain $B\subset \overline{A}$ with boundary $\Gamma$ and a function $u$ defined on $\Omega =A{\setminus }\overline{B}$ such that

$$\begin{aligned} \!\!\!\left\{ \begin{array}{l} \displaystyle \Delta u =0\quad \text{ in} \Omega ,\\ \displaystyle u = 0\quad \text{ on} \Upsilon _0,\\ \displaystyle u = 1\quad \text{ on} \Gamma ,\\ \displaystyle \frac{\partial u}{\partial \nu } = \lambda \quad \text{ on} \Gamma , \end{array}\right. \end{aligned}$$

(22)

where $\nu$ is the interior unit normal to $\Gamma$.

As for the exterior problem we consider the functions $u_D$ and $u_N$ solutions of the following problems:

$$\begin{aligned} \!\!\!\left\{ \begin{array}{l} \Delta u_D =0\quad \text{ in} \Omega ,\\ u_D = 0\quad \text{ on} \Upsilon _0,\\ u_D = 1\quad \text{ on} \Gamma , \end{array}\right. \end{aligned}$$

(23)

$$\begin{aligned} \!\!\!\left\{ \begin{array}{l} \displaystyle \Delta u_N =0\quad \text{ in} \Omega ,\\ \displaystyle u_N = 0\quad \text{ on} \Upsilon _0,\\ \displaystyle \frac{\partial u_N}{\partial \nu } = \lambda \quad \text{ on} \Gamma , \end{array}\right. \end{aligned}$$

(24)

and the functional $J$ defined by

$$\begin{aligned} J(\Omega )=\frac{1}{2}\int _\Omega |\nabla u_D-\nabla u_N|^2. \end{aligned}$$

(25)

The shape derivative of the functional $J$ is given in the following theorem, whose proof will be skipped, because it is similar to that of Theorem 2.

Theorem 3

The mapping $t\mapsto J(t)$ is $\mathcal C ^1$ in a neighborhood of $0$, and its derivative at $0$ is given by

$$\begin{aligned} J^{\prime }(\Omega ,h) = \int _\Gamma G(h\cdot \nu ), \end{aligned}$$

with

$$\begin{aligned} G = \frac{1}{2}\left( \lambda ^2-(\nabla u_D\cdot \nu )^2+2\lambda \kappa \, (u_N-1)-(\nabla u_N\cdot \tau )^2\right) . \end{aligned}$$

(26)

6 Numerical approximation

The numerical solution of the Bernoulli problem is considered by adopting an iterative method that consists in decreasing the value of the cost functional $J$ at each iteration. Let $\Gamma ^k:=\Gamma$ be the free boundary at the $k$th iteration. We consider for $t\ge 0$ the deformation of $\Gamma$, as in Sect. 2,

$$\begin{aligned} \Gamma ^k_t:=\Gamma _t=\{x+th(x);\ x\in \Gamma \}, \end{aligned}$$

where $h_{\mid \Gamma }=-G\nu$ is a descent direction of the functional $J$. The expression of $G$ is given in (19) for the exterior Bernoulli problem and (26) for the interior Bernoulli problem. Therefore, we set

$$\begin{aligned} \Gamma ^{k+1}:=\Gamma _{\delta t} \end{aligned}$$

for a given “final time” $\delta t$ whose value will be made precise below. To numerically implement this iterative method, we use the level set method.

6.1 Level set formulation

Level set methods introduced by Osher and Sethian [20] are computational techniques for tracking moving interfaces under a variety of complex motions, which handle topology changes in an automatic way. They have been used with considerable success in a wide collection of models, including fluid mechanics, crystal growth, combustion, and medical imaging. For several optimization problems, the level set method has been successfully applied to compute optimal geometries [33, 34]. A general overview of the theory, numerical approximation, and range of applications may be found in [35, 36]. It consists in representing the interface $\Gamma _t$ as the zero level set of a time-dependent, implicit, and smooth function $\varphi (\cdot ,t)$ defined on a neighborhood of $\Gamma$, i.e.,

$$\begin{aligned} \Gamma _t=\{x;\ \varphi (x,t)=0\}, \end{aligned}$$

the function $\varphi (\cdot ,t)$ being negative inside $\Gamma _t$ and positive outside. An advantage of the level set method is that geometric properties of the interface, such as the curvature $\kappa$ and the normal vector $\nu$, are naturally obtained from the level set function $\varphi$ as follows:

$$\begin{aligned} \nu =\frac{\nabla \varphi }{|\nabla \varphi |},\quad \kappa =\nabla \cdot \frac{\nabla \varphi }{|\nabla \varphi |}. \end{aligned}$$

However, these formulae require an approximation of the first- and second-order derivatives of $\varphi$, which by itself is available only in discretized form. This may cause oscillations of the free boundary. As in [37], we therefore propose in Sect. 6.2 a different strategy to evaluate the curvature that follows the ideas of the mollified method of [6].

Since $x+th(x)\in \Gamma _t$ for $x\in \Gamma$, we have

$$\begin{aligned} \varphi (x+th(x),t)=0\qquad \forall \ (x,t)\in \Gamma \times [0,\delta t]. \end{aligned}$$

Differentiating this identity with respect to $t$ and taking into account that

$$\begin{aligned} h|_{\Gamma }=-G\,\nu =-G\,\frac{\nabla \varphi }{|\nabla \varphi |}, \end{aligned}$$

we obtain the level set equation

$$\begin{aligned} \left\{ \begin{array}{l} \partial _t\varphi - G\,|\nabla \varphi |=0\qquad t\in (0,\delta t],\\ \varphi (\cdot ,0)=\varphi _0, \end{array}\right. \end{aligned}$$

(27)

where $\varphi _0$ is a level set function corresponding to $\Gamma$. To solve this equation, the normal velocity $G$ needs to be extended in an appropriate way (explained below) into a function $G_{\text{ ext}}$ into a neighborhood of $\Gamma$.

6.2 Approximation of curvature and speed function $G$

For the numerical implementation we consider a square large enough to contain $\Upsilon _0$ and define a uniform mesh of size $\delta x$. The level set functions are characterized by their nodal values on this mesh. A point $P$, with coordinate $x_P$, located on the interface between two nodes $M$ and $N$ of the mesh, with respective coordinates $x_M$ and $x_N$, is approximated using linear interpolation, i.e.,

$$\begin{aligned} x_P = x_M+\frac{\varphi (x_M)}{\varphi (x_M)-\varphi (x_N)}\,(x_N-x_M). \end{aligned}$$

In a square cell intercepted by the interface, the interface is approximated by the segment linking the two points of the interface common with the boundary of this square cell (the segment $[PQ]$ in Fig. 1).

Fig. 1

Finite difference approximation stencil

We use the $P_1$–finite element method to compute $u_D$ and $u_N$. Note that as the boundary evolves, instabilities due to high ratios between the length of the edges (which could become very small) may occur. However, we did not encounter such a problem in any of our numerical tests.

For the approximation of the speed function $G$ on the interface $\Gamma$, the term $(\nabla u_D\cdot \nu )^2=|\nabla u_D|^2$ is directly deduced from the approximate $u_D$. The term $\nabla u_N\cdot \tau$ is approximated at $P$ by

$$\begin{aligned} |\nabla u_N\cdot \tau |\approx \frac{|u_N(x_P)-u_N(x_Q)|}{|x_P-x_Q|}. \end{aligned}$$

For the approximation of the curvature at $P$ (Fig. 2), we use the points $(x_i,y_i)$ on the boundary located in the square $[x_M-k\delta x,x_M+k\delta x]\times [y_M-k\delta x,y_M+k\delta x]$ centered at $M$, where $k$ is an integer that is taken to be equal to $4,5,{\ldots },$ or $10$. Then, we construct a polynomial $p$ of degree $4$ that fits the data $p(x_i)$ to $y_i$ [or $p(y_i)$ to $x_i$] in a least-squares sense (Fig. 2), and then we compute the local curvature using the classical formula

$$\begin{aligned} \kappa =\frac{-p^{\prime \prime }}{(1+p^{\prime 2})^{3/2}}. \end{aligned}$$

Once we have computed $G$ at all intersections of the boundary with the mesh, we approximate $G$ at a point $P$ by taking the average of the five nearest points to $P$ to regularize the computed curvature, as suggested in [6].

Fig. 2

The red marks $^{\prime }\circ ^{\prime }$ indicate the intersection of the boundary with the grid lines located in the square $[x_M-k\delta x,x_M+k\delta x]\times [y_M-k\delta x,y_M+k\delta x]$ centered on $M$ for $k=4$; the green solid line is the fitting polynomial

6.3 Extension of normal velocity

The extension $G_{\text{ ext}}$ of the normal velocity $G$ is designed such that the signed distance function is maintained as the interface moves. We use the fast marching method [38] to simultaneously determine the signed distance function $\widehat{\varphi }_0$ to $\Gamma$ by solving

$$\begin{aligned} \!\!\left\{ \begin{array}{l} |\nabla \widehat{\varphi }_0|=1, \\ \widehat{\varphi }_0=0\quad \text{ on}\ \Gamma , \end{array}\right. \end{aligned}$$

(28)

and we extend the normal velocity $G$ into $G_{\mathrm{ext}}$ on a neighborhood of $\Gamma$ by solving

$$\begin{aligned} \!\!\left\{ \!\begin{array}{l} \nabla G_{\mathrm{ext}}\cdot \nabla \widehat{\varphi }_0=0,\\ G_{\mathrm{ext}}=G\quad \text{ on}\ \Gamma . \end{array}\right. \end{aligned}$$

(29)

6.4 Updating the interface

Once the normal velocity is extended and the signed distance function $\widehat{\varphi }_0$ is determined, the level set equation (27) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \varphi _t-G_{\mathrm{ext}}|\nabla \varphi |=0,\,\,\, t\in [0,\delta t],\\ \varphi (\cdot ,0)=\widehat{\varphi }_0. \end{array}\right. \end{aligned}$$

(30)

As the extension of the normal velocity maintains the signed distance function, we have $|\nabla \varphi | \approx 1$; thus we approximate the level set function $\varphi (.,t)$ by

$$\begin{aligned} \varphi (.,t)\approx \widehat{\varphi }_0+t\,G_{\mathrm{ext}},\,\,\, t\in [0,\delta t], \end{aligned}$$

Thereafter we update the level set function by

$$\begin{aligned} \varphi =\widehat{\varphi }_0+\delta t\,G_{\mathrm{ext}}. \end{aligned}$$

(31)

We determine $\delta t$ according to the following heuristics, which is inspired by the Armijo–Goldstein line search strategy [15]:

$$\begin{aligned} J(\Omega _{\delta t}) = J(\Omega )-\Vert G\Vert ^2_{L^2(\Gamma )}\delta t + \mathcal O (\delta t^2) \approx J(\Omega )-\Vert G\Vert ^2_{L^2(\Gamma )}\delta t. \end{aligned}$$

Let us assume that $J(\Omega _{\delta t})=\alpha J(\Omega )$ for some $\alpha \in (0,1)$; then

$$\begin{aligned} \delta t=\frac{J(\Omega )(1-\alpha )}{\Vert G\Vert ^2_{L^2(\Gamma )}}. \end{aligned}$$

(32)

Note that, for $\alpha =0$, this would simply lead to

$$\begin{aligned} \delta t=\frac{J(\Omega )}{\Vert G\Vert ^2_{L^2(\Gamma )}} \end{aligned}$$

(33)

and $J(\Omega _{\delta t}) =\mathcal O (\delta t^2)$. However, it is known that the use of $\alpha =0$ may lead to instabilities. We use the value $\alpha =0.1$, which is reported in the literature (see [15]). Our numerical tests support this choice.

6.5 Stopping criterion

To define a stopping criterion, we consider the Hausdorff distance, which is defined for two sets $A,B\subset \mathbb R ^2$ by

$$\begin{aligned} d_H(A,B)=\max (\sup _{a\in A} d(a,B),\sup _{b\in B}d(b,A)), \end{aligned}$$

where $d(a,B)=\inf _{b\in B}|a-b|$, the distances $d(a,b)$ being available via the level set functions. The stopping criterion of the algorithm is $d_H(\Gamma ^k,\Gamma ^{k-1})<\delta x^2$.

6.6 Outline of algorithm

Let us now summarize the proposed algorithm for solving the Bernoulli problem. Assume that we know the interface $\Gamma ^k:=\Gamma$ and a level set function $\varphi ^k:=\varphi _0$ associated to $\Gamma ^k:=\Gamma$.

• 1. Compute the solutions $u_D$ and $u_N$ of problems (3) and (4), respectively, using the $P_1$ finite element method.

• 2. Compute the speed function $G$ on $\Gamma$.

• 3. Simultaneously determine from $\varphi _0$ the signed distance function $\widehat{\varphi }_0$ to $\Gamma$, and extend $G$ to $G_{\mathrm{ext}}$ in a neighborhood of $\Gamma$ using the fast marching method by solving (28) and (29).

• 4. Compute the final time $\delta t$ according to (32).

• 5. Update the level set function $\varphi$ by (31).

7 Numerical tests

We consider the square $[-1,1]\times [-1,1]$ as a computational domain for all the following numerical tests except in the topology change test where the computational domain is $[-1.5,1.5]\times [-1.5,1.5]$. The parameter $\alpha$ in (32) was set to $0.1$ as in [15].

7.1 Exterior case

In the first test for the exterior Bernoulli problem, we take

$$\begin{aligned} \Upsilon _0 = \{x;\;|x|=r\}, \quad \lambda =\frac{1}{R\,(\log r-\log R)}, \end{aligned}$$

with $R>r>0$. In this case, the only solution is the circle $C_{\mathrm{ex}}$ centered at the origin with radius $R$, and the explicit expression $u_{\mathrm{ex}}$ of $u$ is given by

$$\begin{aligned} u_{\mathrm{ex}}(x)=\frac{\log |x|-\log R}{\log r-\log R}. \end{aligned}$$

For $r<\rho$, let $\Gamma _\rho$ be the circle centered at the origin with radius $\rho$ and $\Omega _\rho$ the domain limited by $\Upsilon _0$ and $\Gamma _\rho$; then $u_D(\Omega _\rho )$ and $u_N(\Omega _\rho )$ are given by the following expressions:

$$\begin{aligned} \begin{array}{lll} &{}&{}\displaystyle \!\!u_D(\Omega _\rho )=\frac{\log |x|-\log \rho }{\log r-\log \rho },\\ &{}&{}\displaystyle \!\!u_N(\Omega _\rho )=\rho \lambda \log \left( \frac{|x|}{r}\right) +1. \end{array} \end{aligned}$$

Thus the exact values of the functionals $J$, $J_D$, and $J_N$ are given by the following expressions:

$$\begin{aligned} \begin{array}{l} \displaystyle \!J(\Omega _\rho )=\pi \log \left( \frac{\rho }{r}\right) \left( \lambda \rho + \frac{1}{\log (\frac{\rho }{r})}\right) ^2,\\ \displaystyle \!J_D(\Omega _\rho )=\pi \rho \left( \lambda -\frac{1}{\rho \log (\frac{\rho }{r})}\right) ^2,\\ \displaystyle \!J_N(\Omega _\rho )=\pi \rho \left( \lambda \rho \log \left( \frac{\rho }{r}\right) +1\right) ^2. \end{array} \end{aligned}$$

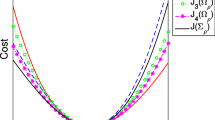
Figure 3 shows that the algorithms using $J$, $J_D$, and $J_N$ are not equivalent.

Fig. 3

Variation of functionals $J$, $J_D$, and $J_N$ with respect to $\rho$

We chose $r=0.3$ and $R=0.5$; thus $\lambda =-3.9152$. We take as an initial guess the circle centered at the origin with radius $0.6$. Table 1 shows the convergence test toward the exact solution. Figure 4 shows the convergence history of the algorithm in Sect. 6.6 for the functional $J$ for the $32\times 32$, $52\times 52$, and $102\times 102$ mesh grids.

Table 1 Convergence test toward exact solution

Fig. 4

Convergence history for $32\times 32$, $52\times 52$, and $102\times 102$ grids, top to bottom

In the second test $\Upsilon _0$ is an L-shaped domain and $\lambda =-9$. We take as an initial guess the circle centered at the origin of radius $0.8$. We have obtained convergence after $10$ iterations with $J (\Gamma ^{10})=0.0323$ for a $152\times 152$ mesh grid. Figure 5 shows the evolution of the free boundary $\Gamma ^k$ for a $152\times 152$ mesh grid, at different iterations.

Fig. 5

Position of $\Gamma ^k$ for $k=0,1,4,5,8,10$ (a–f); dashed line: $\Upsilon _0$; solid line: $\Gamma ^k$

The last test for the exterior Bernoulli problem is a topology change test. $\Upsilon _0$ is the union of two disjoint circles of radius $0.2$, one centered at $(-0.4,0)$ and the other at $(0.4,0)$. We take $\lambda =-1$; in this case the solution is connected, but we consider a disconnected initial guess: the union of the two disjoint circles of radius $0.3$, one centered at $(-0.4,0)$ and the other at $(0.4,0)$ (Fig. 6). We obtained convergence after $17$ iterations with $J(\Gamma ^{17}) =0.0005$ for a $152\times 152$ mesh grid. Figure 6 shows the evolution of the free boundary.

Fig. 6

Topology change test: dashed line: $\Upsilon _0$; evolution of free boundary (solid line) $\Gamma ^k$ for $k=0,1,2,3,4,17$ (b–g)

7.2 Interior case

In the first test for the interior Bernoulli problem, we take $\Upsilon _0$ as the circle

$$\begin{aligned} \Upsilon _0 = \{x;\;|x|=R\},\quad \lambda =\frac{1}{r\,(\log R-\log r)}, \end{aligned}$$

with $R/e<r<R$.

For this case there are two solutions for the interior Bernoulli problem, one (called the “elliptic”) solution is the circle $C_e=\{x;\;|x|=r\}$ and the other (called the “hyperbolic”) solution is the circle $C_h=\{x;\;|x|=r_h\}$, where $r_h$ is the unique real number such that

$$\begin{aligned} 0<r_h<R/e,\quad \frac{1}{r_h(\log R-\log r_h)}=\lambda . \end{aligned}$$

For $0<\rho <R$, let $\Gamma _\rho$ be the circle centered at the origin with radius $\rho$ and $\Omega _\rho$ the domain limited by $\Upsilon _0$ and $\Gamma _\rho$; then $u_D(\Omega _\rho )$ and $u_N(\Omega _\rho )$ are given by the following expressions:

$$\begin{aligned} \begin{array}{l} \displaystyle u_D(\Omega _\rho )=\frac{\log (|x|)-\log (R)}{\log (\rho )-\log (R)},\\ \displaystyle u_N(\Omega _\rho )=-\rho \lambda \log \left( \frac{|x|}{R}\right) . \end{array} \end{aligned}$$

The exact values of the functionals $J$, $J_D$, and $J_N$ are given by the following expressions:

$$\begin{aligned} \!\!\!&J\left( \Omega _\rho \right) =-\pi \log \left( \frac{\rho }{R}\right) \left( \lambda \rho +\frac{1}{ \log \left( \frac{\rho }{R}\right) }\right) ^2,\\ \!\!\!&J_D\left( \Omega _\rho \right) =\pi \rho \left( \lambda +\frac{1}{\rho \log \left( \frac{\rho }{R}\right) }\right) ^2,\\ \!\!\!&J_N(\Omega _\rho )=\pi \rho \left( 1+\lambda \rho \log \left( \frac{\rho }{R}\right) \right) ^2. \end{aligned}$$

As for the exterior case (Fig. 3), Fig. 7 shows that the convergence speed may be different using one or another cost functional.

Fig. 7

Variation of functionals $J$, $J_D$, and $J_N$ with respect to $\rho$

Convergence to the elliptic or hyperbolic solution depends on the initial guess. In our test, we are interested only in the elliptic solution. We take $R=0.9$ and $r=0.7$, so $\lambda =5.6844$. We take as an initial guess the circle centered at the origin of radius $0.4$. Table 2 shows the convergence toward the elliptic solution.

Table 2 Convergence test to elliptic solution

In the second test, $\Upsilon _0$ is L-shaped, the mesh grid is $202\times 202$, $\lambda =14$, and the initial guess is the circle centered at $(-0.15,0.15)$ of radius $0.25$. We obtained convergence after $48$ iterations with $J(\Gamma ^{48})=0.0339$. Figure  8 shows the position of $\Gamma ^k$ at some iterations.

Fig. 8

Convergence test where $\Upsilon _0$ (dashed line) is $L$-shaped: the solid line shows the position of $\Gamma ^k$ for $k=0,9,19,29,44,48$ (a–f)

8 Conclusion

We presented a new formulation of the Bernoulli problem: a shape optimization problem consisting in minimizing a constitutive error cost functional. We numerically solved this optimization problem by a steepest descent algorithm using the gradient information combined with the level set method. Numerical tests illustrated the efficiency of the proposed approach.