Abstract
This paper presents a new methodology for the optimal design of space–time hydraulic head monitoring networks and its application to the Valle de Querétaro aquifer in Mexico. The selection of the space–time monitoring points is done using a static Kalman filter combined with a sequential optimization method. The Kalman filter requires as input a space–time covariance matrix, which is derived from a geostatistical analysis. A sequential optimization method that selects the space–time point that minimizes a function of the variance, in each step, is used. We demonstrate the methodology applying it to the redesign of the hydraulic head monitoring network of the Valle de Querétaro aquifer with the objective of selecting from a set of monitoring positions and times, those that minimize the spatiotemporal redundancy. The database for the geostatistical space–time analysis corresponds to information of 273 wells located within the aquifer for the period 1970–2007. A total of 1,435 hydraulic head data were used to construct the experimental space–time variogram. The results show that from the existing monitoring program that consists of 418 space–time monitoring points, only 178 are not redundant. The implied reduction of monitoring costs was possible because the proposed method is successful in propagating information in space and time.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
The information collected by groundwater monitoring networks is extremely valuable in understanding the dynamics of aquifers. Since hydraulic head (HH) is a variable that depends not only on space but also on time, a space–time monitoring network design is necessary to capture HH evolution in aquifers. However, extensive monitoring in space and/or time may involve considerable costs. Therefore, in this paper, we present a new methodology for the optimal design of space–time hydraulic head monitoring networks and its application to redesign the monitoring network of the Valle de Querétaro aquifer in Mexico.
The following sections describe the state of the art of two closely related problems: hydraulic head estimation and its monitoring. These two problems are related because when designing a monitoring network, usually the objective involves estimating the variable of interest at sites and possibly at times, where no samples will be taken from the variable. Therefore, a method is required to interpolate or estimate the variable. On the other hand, once an estimation method is chosen, it can be used to determine the “best” sites and monitoring times to satisfy a given optimization criterion.
Hydraulic head estimation
Hydrogeologists need methodologies to better represent hydraulic heads and efficiently estimate this variable. Although hydraulic heads can be represented as a function of position and time, it is often difficult to carry out an analysis of HH evolution in aquifers, since databases are usually not consistent in space and/or time. Due to this, HH estimates are difficult to compare because its spatial uncertainty can be different for different years.
Geostatistical techniques for HH estimation have been employed since the 1970s (Delhomme 1978; Gambolati and Volpi 1979; Volpi et al. 1979). Many models have been proposed, validated, and corrected, but their application and implementation has not been exhausted (Kemal and Guney 2007; Ahmadi and Sedghamiz 2007; Ahmadi and Sedghamiz 2008). Although univariate and multivariate techniques have been used, space–time developments are relatively new, both in geostatistics and in hydrogeology applications. Rouhani and Hall (1989) were the first researchers that proposed to determine HH in aquifers using joint information in a space–time domain. In recent years, interest in applying space–time techniques for HH estimation has increased (Mendoza and Herrera 2007; Mendoza 2008; Ta’any and Tahboub 2009).
Hydraulic head and groundwater quality monitoring networks
According to Herrera and Pinder (2005), three approaches have greatly influenced the design of groundwater monitoring networks. In the first one, called hydrological framework (Loaiciga et al. 1992), the network and its monitoring program are defined by considering only the hydrological conditions of the site, without using advanced statistical or probabilistic techniques. The second, called statistical framework, proposes an analysis of data within a statistical framework and defines the monitoring network based on inferences obtained from data. In the last approach, the modeling framework, groundwater mathematical models are used to determine groundwater monitoring locations and frequencies.
In most methods for optimal monitoring network design, only space is taken into account, that is, only the positions of the monitoring wells are selected (Rouhani 1985; Rouhani and Hall 1988; Samper and Carrera 1990; Andricevic 1990; Storck et al. 1995; Ely et al. 2000; Hill et al. 2000; Lin and Rouhani 2001; Wu 2003; Herrera et al. 2004; Júnez-Ferreira 2005; Bravo 2005; Kumar et al. 2005; Mogheir et al. 2006; Faisal et al. 2007).
The review presented below focuses on space–time designs within the statistical framework since they are the most relevant to our study [For readers interested in space–time designs within the modeling framework, some examples are: Loaiciga (1989), Andricevic (1990), Van Geer et al. (1991), Yangxiao et al. (1991), Herrera (1998), Ely et al. (2000), Hill et al. (2000), Herrera et al. (2001), Herrera and Pinder (2005), and Zhang et al. (2005)]. In addition to the works that address the design of hydraulic head monitoring networks, we include works that propose methods for designing groundwater-quality monitoring networks because these methods, with some modifications, can also be used for designing networks that allow an adequate characterization of HH in aquifers.
Within the statistical framework, Cameron and Hunter (2000) proposed an optimization algorithm for groundwater monitoring networks, through the reduction of spatial and temporal redundancy. They employed two separate algorithms: one temporal and another spatial. The temporal algorithm combines time series of data from many wells to construct a composite temporal variogram, used to define sampling frequencies. In the spatial algorithm, numeric weights are assigned (denoted global kriging weights) to the well locations in the monitoring network to gauge their relative contribution to the contaminant plume map. The wells with the lowest influence in the variance of new estimates, obtained by kriging, are removed. In this manner, the contaminant estimate is obtained by kriging, the temporal optimization is obtained from the composite temporal variogram range, and the spatial optimization is also obtained by criteria derived from the kriging process. In this paper, the cross space–time correlation of the contaminant is not considered.
Nunes et al. (2004a) optimized groundwater monitoring networks considering a reduction in spatial and/or temporal redundancy. They proposed three optimization models to select the best subset of stations of a large groundwater monitoring network: (1) one that maximizes spatial accuracy, (2) one that minimizes temporal redundancy, and (3) a model that maximizes spatial accuracy and minimizes temporal redundancy. The proposed optimization models are solved with simulated annealing and a parametrization algorithm based on statistical entropy. The three models are derived from an equation that considers two terms: one spatial and another temporal. The employed models result from simplifications of the objective function. The estimation is done by kriging and the optimization method is simulated annealing. The model that uses the joint space–time information produces the best results. The general equation from which the models are derived contains a variance term and a term that considers time series. The time series are represented by common mathematical functions based on empirical judgment and experience.
Nunes et al. (2004b) proposed a methodology to determine the optimal subset of stations from an existing groundwater-level monitoring network. The method considers an optimization function that adds a spatial component (seeking to reduce estimate error variances), a temporal component (using time series to consider temporal redundancies), and two other terms that include sampling times and their costs (to visit all the chosen sites and measure at each station). Kriging is employed for estimation, and the optimization method is simulated annealing. Authors conclude that relative reduction in exploration costs compensates the relative loss of information in representative data. In this paper, the space and time are analyzed independently and later added in the objective function, so the estimation method does not include space and time jointly. Sampling frequencies are not determined. Time series are employed only to evaluate temporal redundancy of information acquired when sampling on a site, so the less time-redundant positions have preference for being chosen.
The methodology presented in this paper for the optimal design of hydraulic head monitoring networks falls in the statistical framework. It is based on the methodology proposed by Herrera (1998), but the space–time covariance matrix required to estimate by the Kalman filter (KF) is obtained from a space–time geostatistical analysis of data. The optimization method is also of successive inclusions, but, in contrast to Herrera (1998), the evaluation of possible monitoring space–time points is done by implementing a forward spatiotemporal filtering (the meaning of this will be explained in detail later).
This kind of methodology is very useful in designing new monitoring networks or in redesigning an existing one, including also its optimal monitoring calendar according to the objective function. The proposed methodology only requires historical data of the variable, regardless of whether or not the monitoring was constant in space and/or time.
To our knowledge, the proposed methodology is the first of its kind that selects monitoring positions and times to monitor HH using a space–time variogram obtained from a geostatistical analysis. A space–time estimation is employed, unlike most works based on geostatistics for the design of monitoring networks which consider only space or time.
Space–time estimation methods
Due to the variability of hydrogeological phenomena, it is necessary to consider HH measurements in different times to achieve a better understanding of the hydrodynamic behavior of an aquifer. In this sense, analysis of the spatial distributions and temporal evolution of the variable is needed for a proper decision making when managing an aquifer. On the other hand, HH information is usually scarce (in space and/or time), making it difficult to obtain accurate space–time estimates. One way to address this problem is to consider the variable as a space–time random function.
Usually, available hydrogeological information is multivariate, i.e., a variable is generally correlated with others so that measurements from those variables can be used as additional information to strengthen the variable estimate. In classical geostatistics, the correlation between two or more variables that vary in space has been studied; joint variation of two attributes is measured through a cross-variogram. The associated estimation technique is known as cokriging and is also referred to as multivariate geostatistical analysis. Ahmadi and Sedghamiz (2008) compared water level estimates in an aquifer using univariate and multivariate analysis, obtaining better results in the multivariate case. Rouhani and Hall (1989) proposed to determine HH using joint space–time information with a linear model; however, their model presents problems because the covariance matrix is singular in certain cases (Myers and Journel 1990; Rouhani and Myers 1990). De Iaco et al. (2001) and De Cesare et al. (2001) represented space–time correlation structures through the product–sum model. Mendoza and Herrera (2007) and Mendoza (2008) explored various methods for estimating HH; results obtained with multivariate (spatiotemporal) analysis using the techniques of cokriging and a product–sum model were better than univariate (spatial) analysis, using ordinary kriging.
Methodological framework
The first step of the proposed methodology is to define the monitoring design objective. In a space–time design, this objective involves estimating HH over an area of interest (such as areas of intensive exploitation, recharge or discharge areas, the entire aquifer, etc.) for a certain time period. In this work, a design is proposed for a predefined period; afterward, data can be collected for that period and a design for a new period can be obtained. That is, management periods can be defined, and a different design can be proposed for each period. In the example presented, the design is proposed for a single management period.
The selection of the monitoring positions and times that will define the monitoring network and its schedule for the period of interest is performed using a static Kalman filter (Herrera 1998) and an optimization method. The Kalman filter requires a prior space–time covariance matrix, which is calculated through a product–sum model (De Cesare et al. 2001). The optimization method is heuristic and sequential. It selects, one at a time, the space–time points that minimize an objective function. The objective function depends on the estimate error variance and may change according to the particular problem of implementation. The optimization procedure seeks to reduce the value of this function over a set of space–time points for which estimates are needed. This set can be denser over areas and times with higher priority, in order to assign them more weight in the optimization process.
Space–time geostatistical analysis
A geostatistical analysis is needed to determine the spatiotemporal correlation structure of the data. The result of this analysis is the space–time variogram model.
Space–time random functions
Consider a space domain D and a time domain T. A space–time random variable (RV) Z(x, t) is a variable that depends on both a space location \( {\bf x} = \left( {x,y} \right) \in D \) and a time t ∈ T. A space–time random function \( \left\{ {Z({\mathbf{x}},t),({\mathbf{x}},t) \in D \times T} \right\} \) is defined as a group of dependent RV Z(x, t). The RV Z(x, t) is fully characterized by knowing its distribution function, which gives the probability that the variable Z in a space position x and a time t is not greater than any given threshold z:
The space–time random function concept is analogous to that of a spatial random function, so the second-order stationarity and intrinsic hypothesis also apply to it (De Iaco et al. 2001).
Sample space–time variogram
The central tool of geostatistics is the variogram. In classical geostatistics, the covariance and the variogram are functions that describe the spatial structure of the property being studied. In the space–time conceptualization, this definition is extended to consider also the time correlation.
The sample variogram for the increments \( \Delta {\bf x} = \left( {\Delta x,\Delta y} \right) \) and Δt is based on the following expression:
where \( N\left( {\Delta {\bf x},\Delta t} \right) \) is the number of pairs \( \left( {Z\left( {{{\bf x}_k},{t_i}} \right),Z\left( {{{\bf x}_k} + \Delta {\bf x},{t_i} + \Delta t} \right)} \right) \) separated by a space–time increment (Δx, Δt). To capture the structure of sample space–time variograms, it is necessary to use authorized models.
Product–sum models
A very general geostatistical model for space–time covariances is the product sum (De Cesare et al. 2001; De Iaco et al. 2001). This model has the following structure:
Or equivalently, for space–time variograms:
where C s and C t are space and time covariance functions, respectively; γ s and γ t are their corresponding variogram functions. C st (0) is the variance of γ st , C s (0) is the variance of γ s , and C t (0) is the variance of γ t . By definition, \( {\gamma_{{st}}}\left( {0,0} \right) = {\gamma_s}(0) = {\gamma_t}(0) = 0 \).
The following condition is implicit in the covariance–variogram transformation of Eq. 4:
Evaluating Eq. 4 for h t = 0, the following equality is obtained,
and evaluating the same equation for h s = 0, we get
To estimate and model γ s (h s ) and γ t (h t ) through γ st (h s , 0) and γ st (0, h t ), respectively, it is assumed that
From Eq. 3, it is clear that k 1 > 0, k 2 ≥ 0, and k 3 ≥ 0 are sufficient conditions to obtain a positive definite covariance. From Eqs. 4 and 8, it is obtained:
To model separately the spatial and temporal variograms, it is necessary to ensure that variances are chosen so that k 1, k 2 and k 3 in Eq. 9 are positive (De Cesare et al. 2001).
A second-order stationary space–time random field must satisfy the following equation (De Iaco et al. 2001):
Trend
The expected value of a random function may depend on its coordinates. For a random function to satisfy the intrinsic hypothesis, the trend must be a constant value.
When the expected value of a space–time random function depends on the space location, on time or both, the random function does not satisfy the intrinsic hypothesis. In that case, it is possible to work with a modified variable called the residual, by rewriting the space–time random function Z(x, t) as:
where m(x, t) is a deterministic function (known as trend) of space–time coordinates x and t, and R(x, t), known as the residual, is a zero mean stationary spatiotemporal random function modeling the space–time fluctuations around m(x, t) (Kyriakidis and Journel 1999).
To represent the function m(x, t), a trend surface (typically polynomial functions for the spatial coordinates and periodic functions for time, although other functions can be used) can be obtained by a least-squares fit to the data. In this way, zero mean stationary data (residuals) are obtained and used to calculate the variogram. This technique is called residual kriging.
The Kalman filter
The KF is a set of mathematical equations that provide a minimum-variance unbiased linear estimate for the state of a system given noisy data (Jazwinski 1970). In its general form, the filter relies upon two equations, a dynamic and a measurement equation. In this paper, we use what we call the static KF, which only uses measurement equations and incorporates the time through space–time state vectors (Herrera 1998; Herrera and Pinder 2005).
The linear measurement equation of the discrete KF, which relates the state vector of the variable h in positions and times of interest with the sampled data z, is:
where \( \left\{ {{{{\bf z}}_j},j = 1,2, \ldots } \right\} \) is a sequence of HH measurements. The jth sampling matrix H j is a 1 × N matrix that is non-zero only at the space–time positions corresponding to the entry of h where the jth sample is taken and N is the dimension of the vector h. The space–time vector h = {h ip } with the HH values in the positions and times of interest (h ip is the HH in position x i and time t p ). The vectors \( \left\{ {{{{\bf v}}_j},j = 1,2, \ldots } \right\} \) represent measurement errors. They are a white Gaussian sequence, with zero mean and covariance r j . The measurement error sequence {v j } and the vector h are independent.
The estimate error covariance matrix is:
where \( {\widehat{{{\bf h}}}^n} = E\left\{ {{{\left( {{{{{\bf h}}} \left/ {{{{{\bf z}}_1}}} \right.},{{{\bf z}}_2}, \ldots, {{{\bf z}}_n}} \right)}}} \right\} \) is the expected value of h, given the measurements z 1, z 2,…z n . In this notation, the superscript identifies the number n of measurement vectors used to obtain the estimate.
To implement the filter, it is required a prior estimate of both h (named \( {\widehat{{{\bf h}}}^0} \)) and of the error covariance matrix (P 0). Note that P 0 is a space–time covariance matrix. Given these prior estimates, the minimum-variance linear estimate for h can be obtained sequentially through the following formulas:
There are many ways to estimate \( {\widehat{{{\bf h}}}^0} \); a particular one is presented in the application included in this paper. The prior estimate-error covariance matrix (P 0) is obtained through a geostatistical analysis by fitting a space–time variogram model to the sample variogram. Once the variogram model is selected, the elements of the space–time covariance matrix are calculated with Eq. 10.
Monitoring network optimization
Consider the sets of all possible monitoring positions \( \left\{ {{{\bf x}}_1^M,{{\bf x}}_2^M,...,{{\bf x}}_{{{N_{{mp}}}}}^M} \right\} \) and all possible monitoring times \( \left\{ {t_1^M < t_2^M < \ldots < t_{{{N_{{mt}}}}}^M} \right\} \), where N mp is the number of possible monitoring locations and N mt is the number of possible monitoring times. For the present application, we define the set of possible space–time monitoring points as \( M = \left\{ {\left( {{{\bf x}}_i^M,t_p^M} \right),i = 1, \ldots, {N_{{mp}}};p = 1, \ldots, {N_{{mt}}}} \right\} \) (but notice that the proposed methodology can be applied even if the monitoring times are not the same for each well). From this set, the points that minimize the estimate error variance on the space–time points for which estimates are needed, \( E = \left\{ {\left( {{{\bf x}}_j^E,t_q^E} \right),j = 1, \ldots, {N_{{ep}}};q = 1, \ldots, {N_{{et}}}} \right\} \), where N ep is the number of estimation locations and N et is the number of estimation times, will be selected.
In previous works, we have tried two options for the optimization objective function. The first, used by Herrera (1998), is the estimate error variance summed over all the space–time estimation points. This function is called the total variance of the estimate error and is calculated using the following formula:
where \( \sigma_{{j,q}}^2 \) is the variance of the estimate error \( e\left( {{{\bf x}}_j^E,t_q^E} \right) = h\left( {{{\bf x}}_j^E,t_q^E} \right) - \widehat{h}\left( {{{\bf x}}_j^E,t_q^E} \right) \) at the jth estimation location and at the qth estimation time, obtained from the diagonal of the KF covariance matrix. Note that when using this objective function, each monitoring point contributes to the reduction of the estimate error variance at all times considered. That is, each monitoring point contributes to reduce the estimate error variance in the past, present, and future. The formulas used to minimize the total variance are presented in Herrera (1998) and Herrera and Pinder (2005).
The second option is to consider the effect of each monitoring point \( \left( {{{\bf x}}_i^M,t_p^M} \right) \) in the estimate error variance only in present and future times. This objective function was used to optimize one of the groundwater quality monitoring networks presented in Herrera and Pinder (2005).
In the present work, the effect of data in the estimate error variance is also considered only in present and future times, but in addition, the covariance matrix is only updated in the present and future. This is when a monitoring point is selected to be part of the monitoring network, the covariance matrix is updated by the KF only in present and future times. The application of this procedure is what we call the forward spatiotemporal filtering (FSTF) optimization of the monitoring network.
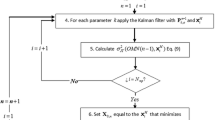
The problem is optimized sequentially, using a successive-inclusion method (Samper and Carrera 1990) as is explained next. Given an order of the spatiotemporal monitoring points \( {{\bf X}} = \left( {{{{\bf x}}^M},{t^M}} \right) \) in M, \( \left\{ {{{\bf X}}_1^M,{{\bf X}}_2^M, \ldots, {{\bf X}}_{{{N_{{mp}}} \times {N_{{mt}}}}}^M} \right\} \), for \( n = 1, 2, \ldots, {N_{{mp}}} \times {N_{{mt}}} \), choose the point X o,n that minimizes the function \( \sigma_{\text{FSTF}}^2\left( {{\text{OMP}}\left( {n - 1} \right),{{\bf X}}} \right) = \sum\limits_{{j = 1}}^{\text{Nep}} {\sum\limits_{{q = p}}^{\text{Net}} {\sigma_{{j,q}}^2\left( {{\text{OMP}}\left( {n - 1} \right),{{\bf X}}} \right)} } \)where \( \sigma_{{j,q}}^2\left( {{\text{OMP}}\left( {n - 1} \right),{{\bf X}}} \right) \) is the estimate error variance at the estimation point \( \left( {{{\bf x}}_j^E,t_q^E} \right) \), obtained using the n − 1 optimal monitoring program \( {\text{OMP}}\left( {n - 1} \right) = \left\{ {{{{\bf X}}_{{o,1}}},{{{\bf X}}_{{o,2}}}, \ldots, {{{\bf X}}_{{o,n - 1}}}} \right\} \) previously chosen and the spatiotemporal point X. Let \( {{\bf P}}_o^{{n - 1}} \) be the spatiotemporal covariance matrix obtained after applying Eqs. (15) and (16) of the KF to the \( {\text{OMP}}\left( {n - 1} \right) \). Then, to find X o,n , for each possible monitoring point that has not been chosen before, calculate the covariance matrix of the estimate error using Eqs. (15) and (16) of the KF with the covariance matrix \( {{\bf P}}_o^{{n - 1}} \) and the possible monitoring point; select the point that gives the minimum \( \sigma_{\text{FSTF}}^2\left( {{\text{OMP}}\left( {n - 1} \right),{{\bf X}}} \right) \). The selected point is then added to the set of optimal monitoring points, and the matrix \( {{\bf P}}_o^n \) is calculated again using the KF. The process starts with \({ \bf P}_o^0 = {{ \bf P}^0} \), the prior covariance matrix obtained from the space–time geostatistical analysis.
When applying a sequential optimization, it is necessary to determine where to stop the process, i.e., to determine the total number of space–time points to be included in the optimal monitoring network. There are several possible procedures to define this number; the criterion used in this work will be explained later in the context of the problem presented.
Results and discussions
We demonstrate the methodology applying it to the redesign of the hydraulic head monitoring network for the Valle de Querétaro aquifer. The objective is to select from a set of monitoring positions and times those that minimize the spatiotemporal redundancy, that is, to minimize the number of positions and times needed to obtain a HH estimate uncertainty close enough to the one obtained using the present monitoring network and monitoring schedule.
The Valle de Querétaro aquifer is located in the central part of Mexico. It is an unconfined aquifer that is locally confined in some regions (Geofísica de Exploraciones Guysa 1991). It covers an area of approximately 379 km2, and the deepest zones are about 600 m. This aquifer is located within the Mexican states of Querétaro and Guanajuato. We present the monitoring network design for the eastern part of the aquifer, located in the state of Querétaro (Fig. 1).
Study area and well locations with piezometric data
Data sets
The HH database for the space–time analysis includes information of 273 wells located in the Valle de Querétaro aquifer for the period between August 1970 and November 2007 (Fig. 1). There are not complete annual piezometric records for any of these wells during this period. Well 612-F has the maximum piezometric data (32). On the other hand, December 1995 is the month with more information (60 data). In total, we have 1,435 piezometric data.
The analysis was based on the construction of the sample space–time variogram with the piezometric data available (Fig. 2). To perform this analysis, we used a modified routine of GAMV (Deutsch and Journel 1997) by De Cesare et al. (2002) for modeling space–time variograms. We used 20 spatial lags, with 1,362.4 m of space lag separation and 37 temporal lags with a 1-year lag separation.
Hydraulic head sample space–time variogram
To better analyze the behavior of the space–time variogram, we present its projection on the variogram-spatial lags plane (Fig. 3) and on the variogram-temporal lags plane (Fig. 4). The spatial projection shows a curvature close to a quadratic function in the first part, which indicates the possible presence of drift (Journel and Huijbregts 1978). However, the variogram decreases in the 22,000-m lag. It can also be seen a more scattered behavior beginning in the 13,000-m lag. The temporal projection shows that higher variogram values have a much higher variability than small variogram values. To continue the space–time analysis, the trend was removed by fitting a polynomial function through least squares.
Projection of the sample space–time variogram of hydraulic head on the variogram-spatial lags plane
Projection of the sample space–time variogram of hydraulic head on the variogram-temporal lags plane
Trend removal
First- and second-order polynomials were tested. The first-order polynomial fit was chosen because the space–time variogram calculated with the residuals obtained is better defined (Fig. 5). The same number of spatial and temporal lags and lag separation as the HH analysis were used.
Sample space–time variogram of residuals from a first-order polynomial fit
Figure 6 shows the spatial projection. The quadratic function behavior is no longer present in the variogram, and it is bounded at 16,000 m. However, the decreasing behavior in the last part of the variogram is still present, but now occurs after the 17,000-m lag. Figure 7 shows the temporal projection. A more homogeneous behavior than before is found by removing the trend, although a higher variability is still present in high variogram values.
Projection of the sample space–time variogram of residuals from a first-order polynomial fit on the variogram-spatial lags plane (circles) and fitted variogram model (squares)
Projection of the sample space–time variogram of residuals from a first-order polynomial fit on the variogram-temporal lags plane (circles) and fitted variogram model (squares)
Fitting of the variogram model
For the variogram model fit, piezometric data from the last 10 years with information (December 1997–November 2007) were used. The aquifer conditions since that recent period have not changed drastically, and therefore, it is expected that a properly adjusted variogram for those years should model accurately the spatiotemporal correlation of HH after the year 2007.
Following De Iaco et al. (2002), a product–sum model was fitted to the space–time sample variogram manually (i.e., different models were proposed “by eye” and evaluated to choose the one with the best cross validation results). The parameters of the selected model are presented in Table 1.
Cross-validation results for the last 10 years of information are presented in Table 2; as it can be seen, maximum and minimum errors are large; however, we consider this an acceptable adjustment taking into account the high variability of the data.
Design of a hydraulic head space–time monitoring network
The monitoring network was designed for the period 2008–2018. Since for any period in the future it is impossible to use a geostatistical analysis of data, we used historical data to construct the variogram and validated it for the period 1997–2007. In what follows, we redesign the monitoring network, and then we use the data that would be gathered from the resulting monitoring network and sampling program to evaluate estimate errors for the 1997–2007 period. Júnez-Ferreira (2011) tested the proposed methodology using synthetic data from a numerical transient flow model that produces declining groundwater levels with time. He used “historical data” to find the best space–time variogram fit and “future data” to calculate the estimate errors. The model included groundwater extraction through wells that were kept with similar extraction rates in the “future period.” He found that estimate errors were similar to those obtained for the “historical period.” Therefore, we assume that if aquifer conditions do not change dramatically (for example, in cases where there are no significant changes in land use or in groundwater extraction), the analysis just explained gives an idea of future estimate errors for the period 2008–2018.
As was mentioned before, the objective of the design was to select locations and monitoring times needed to obtain a good estimate of the variable at different specified times for the whole aquifer. Since we use a discrete set \( \left\{ {{{\bf x}}_j^E,j = 1,...,{N_{{ep}}}} \right\} \) to represent the continuous area of the aquifer and in the objective function \( \sigma_{{FSTF}}^2(OMP(n - 1),{{\bf X}}) = \sum\limits_{{j = 1}}^{{{N_{{ep}}}}} {\sum\limits_{{q = p}}^{{{N_{{et}}}}} {\sigma_{{j,q}}^2(OMP(n - 1),{{\bf X}})} } \), the variances are added over those positions at the estimation times; if we want to give the same weight to the uncertainty in the whole aquifer, we need to define the estimation locations on a regular grid. We used a grid with square elements of 2 km side length, which results in a set of 82 nodes; we call this set the estimation grid (Fig. 8). One possible estimation time was selected at December of each year, with the exception of 2007, for which November was used because data are available only for that month. In this way, 82 estimation positions and 11 estimation times were included in the space–time estimation grid.
Estimation grid (squares) and possible spatial monitoring locations (dots)
Thirty-eight well positions were selected as possible spatial monitoring locations (Fig. 8). These wells were selected because they were monitored in the most recent groundwater level surveys on December 2006 and/or November 2007. Every December in the period 1997–2006 and November of 2007 were considered possible monitoring times.
Since the space–time variogram model was adjusted to residuals from a first-order polynomial fit, the KF was applied to estimate this variable. Once residuals were estimated, HH values at each space–time estimation node were obtained by adding its residual estimate and the value of the polynomial function at the corresponding space–time point. For each year, the KF prior estimate of the state vector was calculated with the average of residuals corresponding to positions with HH data measured in the field. Since there were no data for December 2001 and December 2002, the state vector prior estimates for those years were obtained by linear interpolation of the averages of adjacent years. The prior space–time covariance matrix was calculated from the space–time variogram model, applying Eq. 10. It was constructed for 82 (estimation positions) + 38 (monitoring positions) + 29 (additional support positions to estimate missing data) = 149 positions and 11 times, so its dimension was of 1,639 columns (149 × 11) by 1,639 rows.
Priority order
When the monitoring network optimization method is applied, at each round the point that reduces the most the variance (in other words, the point that gives maximum information) is selected. For this reason, the order in which the space–time points are selected represents a priority order in a natural way, so the selection order is an indicator of how important the data obtained at those points are in reducing the total variance. If the selection order is small, the priority is great. This can be seen clearly in Fig. 9; the total variance is greatly reduced when choosing the first space–time points, but as the number of selected points increases, the amount of reduction of the total variance decreases.
Total variance vs. number of space–time monitoring points
Criterion for determining the total number of monitoring points
As mentioned above, there are several criteria to determine the total number of space–time monitoring points in the monitoring network program. In this paper, we have implemented a criterion based on the results of the total variance.
It can be seen in Fig. 9 that after monitoring the 200 monitoring points with larger priority, the total variance remains almost constant (around 675,000 m2). This indicates that the 218 remaining points might be redundant, that is, they provide little information and do not contribute much in reducing the total variance.
To define the number of space–time points of the monitoring network, we propose using the \( \sqrt {{\frac{{Total\,Variance}}{N}}} \) value, where \( N = {N_{{ep}}}\; \times \;{N_{{et}}} \) is the number of space–time estimation points.
It can be shown that
for N ≥ 1 and \( \sum\limits_{{j = 1}}^{{{N_{\text{ep}}}}} {\sum\limits_{{q = 1}}^{{{N_{\text{et}}}}} {{\sigma_{{j,q}}} \geqslant 0} } \). In this way, the proposed statistic value is an upper bound for the average standard error in the space–time estimation grid, which can help us to consider a conservative design scenario. The calculated values of square root (total variance/space–time estimation points) versus number of space–time monitoring points are shown in Fig. 10.
Square root (total variance/space–time estimation positions) vs. number of space–time monitoring points
The criterion consists in selecting the space–time points where a 99 % of the maximum possible reduction (MPR) value is achieved:
This occurs when 178 space–time points are selected and an average estimate uncertainty of 27.53 m is expected in the space–time estimation grid. This value is high but it is extremely close to the one obtained using all the available space–time monitoring points (27.27 m). That means that the existing monitoring network cannot reduce the uncertainty in some zones enough and thus that it is necessary to monitor other positions as well.
Optimal monitoring network
In this example and according to the exposed before, 178 monitoring points were selected to constitute the optimal sampling program for the existing monitoring network. Figure 11 shows the number of samples to be taken in each monitoring time. It can be seen that the most intense monitoring campaign is proposed for the first year, which is consistent with the chosen optimization criterion. Positions in the first monitoring year have the highest priority order because there is not available information in previous years of the design period to reduce the variance in that year and also because every well chosen in the first year provides information for the entire period. When we advance in time, less wells are needed, but periodically a little increase occurs because the influence of previous monitored years decreases and more wells are needed to improve the estimates.
Number of sampling locations for every year
Figure 12 shows the number of monitoring times for each well. As it can be seen, locations that need to be measured with higher frequencies are located in poorly covered zones by the existing monitoring network spatial array.
Number of monitoring times in the optimal space–time monitoring program for each well (top) and well ID (bottom)
Estimation
As an illustration of the HH estimates that would be obtained using the proposed monitoring program for the analysis period, HH estimates were obtained on the estimation grid, for each one of the estimation times. Since for this case there are no information data in all monitoring locations for all the design period, it was necessary to estimate the missing information. Missing values were obtained by estimating them through the KF using the space–time variogram model selected previously and the residuals of existing data in the 38 monitoring locations and the support measurements in 29 additional wells (in total, 255 space–time data were used for the estimation). Residuals of HH data were then estimated in all the space–time monitoring points without information measured in the field. In this way, we had information in the 418 possible space–time monitoring points.
Hydraulic head estimation
Figures 13, 14, 15, and 16 show FSTF hydraulic head estimates obtained for four years with the proposed monitoring network. These figures show the estimated HH spatial and temporal changes in the aquifer. The recharge zones correspond to the zones with maximum level of HH, which coincide with the maximum topographic levels. In Fig. 13, we can see that for December 1997, the flow direction is northeast–southwest and the HH levels at the north entrance are higher than 1,860 m above sea level (asl); another entrance is located at the northeast, where the flow goes to the center of the aquifer. The minimum HH levels are present at the central and south zones of the aquifer (the levels are lower than 1,700 m asl). Over time, the cone of depression at the central zone becomes larger, and by December 2001 (Fig. 14), the lowest levels in this zone are below 1,680 m asl. In those years, levels are below than 1,670 m asl at the southwest zone. From this moment, levels start recovering in the zones with the most pronounced drawdowns, but from 2004, a very important cone of depression is formed in the south zone of the aquifer with levels below 1,670 m asl.
Hydraulic head estimate for December of 1997
Estimate error variances
Figures 17, 18, 19, and 20 show FSTF estimate error variances obtained for each year with the proposed monitoring network. The priority order is also included.
We can see that variances have almost the same spatial distribution for any monitoring time. The minimum values are located around the center of the aquifer, where most part of the wells is found and the maximum variances are located at the margin of the aquifer because just a few monitoring wells are found there. However, the variances have high values (between 300 and 1,700 m2). These values are close to the minimum possible values that can be obtained with the present position of the monitoring wells. These variance maps, together with practical criteria, can be very useful in choosing new monitoring locations in the zones with the maximum variances.
Hydraulic head estimate for December of 2001
Hydraulic head estimate for December of 2004
Hydraulic head estimate for November of 2007
Estimate error variances and priority order of wells for December of 1997
Estimate error variances and priority order of wells for December of 2001
Estimate error variances and priority order of wells for December of 2004
Estimate error variances and priority order of wells for November of 2007
Conclusions and recommendations
The proposed methodology incorporates spatiotemporal correlation between data, using a spatiotemporal variogram model obtained through a geostatistical analysis of historical data. An important advantage of the method is that the cross-correlation between hydraulic heads at different locations and times is accounted for, which allows for a more complete evaluation of redundant monitoring positions and/or monitoring times.
The results show that the average standard error in the study area when monitoring the 418 available space–time monitoring locations is less than 27.27 m and when monitoring the 178 locations with higher priority order is less than 27.53 m. This means that the last chosen 240 monitoring space–time locations are redundant, since the information they provide reduce very little the average standard error. These results show that the proposed method is successful in propagating information in space and time.
The most sampled date for the selected optimal monitoring network was the first one. This is due to three reasons: (1) The temporal variogram range is equal to 30 years, which is large in comparison with the analyzed period; (2) in the optimization process, the effect of each sample is considered only in present and future times, which makes the first monitoring time the one that can provide the largest information of HH in the design period; and (3) we did not condition the prior covariance matrix with historical data, something that we would do if we apply the method for consecutive management periods.
Large values of total variance after measuring all possible space–time monitoring points indicate that the present monitoring network is quite deficient in providing enough information to represent the space–time evolution of HH in the aquifer with certainty. This means that new wells should be added to the optimal monitoring network, in zones with the highest variance values. To propose new wells locations, practical and hydrogeological criteria should also be used.
An underlying hypothesis of the proposed methodology is that if aquifer conditions do not change dramatically (for example, in cases where there are no significant changes in land use or in groundwater extraction), then the spatiotemporal sampling networks obtained would be useful for a period in the future of the same length as the one used in the design. Júnez-Ferreira (2011) tested the proposed methodology using synthetic data from a numerical transient flow model that produces declining groundwater levels with time. He used “historical data” to find the best space–time variogram fit and “future data” to calculate the estimate errors. The model included groundwater extraction through wells that were kept with similar extraction rates in the “future period.” He found that estimate errors were similar to those obtained for the “historical period.” We will publish those results in a forthcoming paper.
Drift is usually present in hydraulic heads; in this work, as in many others before (Samper and Carrera 1990; Kumar et al. 2005; Ahmadi and Sedghamiz 2007; Mendoza and Herrera 2007; Mendoza 2008), the drift was removed through a technique called residual kriging. Some authors (see, for example, Webster and Oliver (2007)) argue that there are two disadvantages in using residual kriging. First, the trend is usually estimated by ordinary least squares, which gets unbiased estimates, although they have no minimum variance unless the sampling sites have been selected through a sampling plan. The second disadvantage is that semivariances calculated with the residuals are biased. In future work, an evaluation of the effect of this problem in the KF estimates has to be done, and if necessary, a different method to remove the drift from HH data could be used. Further work is also needed in the evaluation of the adjustment quality of space–time variogram models to represent the space–time dependence of the variable.
References
Ahmadi, S. H., & Sedghamiz, A. (2007). Geostatistical analysis of spatial and temporal variations of groundwater level. Environmental Monitoring and Assessment, 129, 277–294.
Ahmadi, S. H., & Sedghamiz, A. (2008). Application and evaluation of kriging and cokriging methods on groundwater depth mapping. Environmental Monitoring and Assessment, 138, 357–368.
Andricevic, R. (1990). A real-time approach to management and monitoring of groundwater hydraulics. Water Resources Research, 26(11), 2747–2755.
Bravo, J. A. (2005). Diseño de una red de monitoreo para evaluar el comportamiento del acuífero del Valle de Querétaro durante la operación de la presa Extoraz. Tesis de maestría, UNAM, México.
Cameron, K., & Hunter, P. (2000). Optimization of LTM networks using GTS: statistical approaches to spatial and temporal redundancy. Tech. Rep., Air Force Center for environmental excellence. TX: Brooks AFB.
De Cesare, L., Myers, D. E., & Posa, D. (2001). Estimating and modeling space–time correlation structures. Statistics and Probability Letters, 51, 9–14.
De Cesare, L., Myers, D. E., & Posa, D. (2002). Fortran programs for space–time modeling. Computers & Geosciences, 28, 205–212.
De Iaco, S., Myers, D. E., & Posa, D. (2001). Space–time analysis using a general product–sum model. Statistics & Probability Letters, 52, 21–28.
De Iaco, S., Myers, D. E., & Posa, D. (2002). Space–time variograms and a functional form of total air pollution measurements. Computational Statistics & Data Analysis, 41, 311–328.
Delhomme, J. P. (1978). Kriging in the hydrosciences. Advances in Water Resources, 1(5), 251–266.
Deutsch, C. V., & Journel, A. G. (1997). GSLIB: geostatistical software library and user’s guide (2nd ed.). New York: Oxford University Press.
Ely, D. M., Hill, M. C., Tiedeman, C. R., & O’Brien, G. M. (2000). Evaluating observations in the context of predictions for the Death Valley regional groundwater system. In Proceedings of the 2000 Joint Conference on Water Resources Engineering and Water Resources Planning and Management, Minneapolis, MN, compact disk, American Society of Civil Engineers, Washington, DC.
Faisal, K. Z., Ahmed, S., Dewandel, B., & Maréchal, J. (2007). Optimizing a piezometric network in the estimation of the groundwater budget: a case study from a crystalline-rock watershed in southern India. Hydrogeology Journal, 15(6), 1131–1145.
Gambolati, G., & Volpi, G. (1979). Groundwater contour mapping in Venice by stochastic interpolators: 1. Theory. Water Resources Research, 15(2), 281–290.
Geofísica de Exploraciones Guysa (1991). Estudio geohidrológico integral del Valle de Querétaro y sus alrededores para el manejo automatizado de los recursos hidráulicos subterráneos, technical report, Comisión Estatal de Aguas, Querétaro, August 1990 – September 1991.
Herrera, G. S. (1998). Cost effective groundwater quality sampling network design. Ph. D. Dissertation, University of Vermont.
Herrera, G. S., & Pinder, G. F. (2005). Space–time optimization of groundwater quality sampling networks. Water Resources Research, 41(W12407), 15.
Herrera, G. S., Guarnaccia, J., Pinder, G. F., & Simuta, R. (2001). Design of efficient space–time groundwater quality sampling networks. In Proceedings of the 2001 International Symposium on Environmental Hydraulics, ISEH.
Herrera, G. S., Júnez-Ferreira, H. E., González, L., & Cardona, A. (2004). Diseño de una red de monitoreo de la calidad del agua para el acuífero Irapuato-Valle, Guanajuato. Memorias del XVIII Congreso Nacional de Hidráulica, AMH, SLP, México.
Hill, M. C., Ely, M. D., Tiedeman, C. R., D’Agnese, F. A., Faunt, C. C., & O’Brien, B. A. (2000). Preliminary evaluation of the importance of existing hydraulic head observation locations to advective-transport prediction, Death Valley regional flow system, California and Nevada. U.S. Geological Survey Water-Resources Investigations Report 00-4282, http://pubs.usgs.gov/wri/wri004282/book/wri004282.pdf. Accessed 3 September 2009.
Jazwinski, A. H. (1970). Stochastic processes and filtering theory. London: Academic Press.
Journel, A. G., & Huijbregts, C. J. (1978). Mining geostatistics. London: Academic.
Júnez-Ferreira, H. E. (2005). Diseño de una red de monitoreo de la calidad del agua para el acuífero Irapuato-Valle, Guanajuato. Tesis de Maestría, UNAM, México. Online access http://132.248.9.195/ptd2012/anteriores/0339152/Index.html
Júnez-Ferreira, H. E. (2011). Optimización de redes de monitoreo de la carga hidráulica utilizando métodos geoestadísticos espacio-temporales. Tesis de Doctorado. UNAM, México. Online access: http://132.248.9.195/ptd2012/mayo/0679742/Index.html
Kemal, S. G., & Guney, I. (2007). Spatial analyses of groundwater levels using universal kriging. Journal of Earth System Science, 116(1), 49–55.
Kyriakidis, P. C., & Journel, A. G. (1999). Geostatistical space–time models: a review. Mathematical Geology, 31(6), 651–684.
Kumar, S., Sondhi, S. K., & Phogat, V. (2005). Network design for groundwater level monitoring in Upper Bari Doab canal tract, Punjab, India. Irrigation and Drainage, 54, 431–442.
Lin, Y., & Rouhani, S. (2001). Multiple-point variance analysis for optimal adjustment of a monitoring network. Environmental Monitoring and Assessment, 69, 239–266.
Loaiciga, H. A. (1989). An optimization approach for groundwater quality monitoring network design. Water Resources Research, 25(8), 1771–1782.
Loaiciga, H. A., Charbeneau, R. J., Everett, L. G., Fogg, G. E., & Hobbs, B. F. (1992). Review of groundwater quality monitoring network design. Journal of Hydraulic Engineering, 118(1), 11–32.
Mendoza, E. Y. (2008). Análisis de Alternativas para la Estimación de la Carga Hidráulica Utilizando Métodos Geoestadísticos en Espacio y Espacio-Tiempo. Tesis de doctorado, UNAM, México.
Mendoza, E. Y., & Herrera, G. S. (2007). Estimación multivariada espacio-tiempo de la carga hidráulica en el Valle de Querétaro-Obrajuelo. Ingeniería hidráulica en México, 22(1), 63–80.
Mogheir, Y., Singh, V. P., & de Lima, J. L. M. P. (2006). Spatial assessment and redesign of a groundwater quality monitoring network using entropy theory, Gaza Strip, Palestine. Hydrogeology Journal, 14, 700–712.
Myers, D. E., & Journel, A. (1990). Variograms with zonal anisotropies and noninvertible kriging sytems. Mathematical Geology, 22(7), 779–785.
Nunes, L. M., Cunha, M. C., & Ribeiro, L. (2004a). Groundwater monitoring network optimization with redundancy reduction. Journal of Water Resources Planning and Management, 1(33), 33–43.
Nunes, L. M., Cunha, M. C., & Ribeiro, L. (2004b). Optimal space–time coverage and exploration costs in groundwater monitoring networks. Environmental Monitoring and Assessment, 93, 103–124.
Rouhani, S. (1985). Variance reduction analysis. Water Resources Research, 21(6), 837–846.
Rouhani, S., & Hall, T. (1988). Geostatistical schemes for groundwater sampling. Journal of Hydrology, 103(1), 85–102.
Rouhani, S., & Hall, T. (1989). Space–time kriging of groundwater data. In: M. Armstrong (Ed.) Geostatistics, Vol. 2. Dordrecht: Kluwer Academic.
Rouhani, S., & Myers, D. E. (1990). Problems in space–time kriging of geohydrological data. Mathematical Geology, 22(5), 611–623.
Samper, F. J., & Carrera, J. (1990). Geoestadística, aplicaciones a la hidrogeología subterránea. Barcelona: Centro Internacional de Métodos Numéricos en Ingeniería, UPC.
Storck, P., Valocchi, A. J. & Eheart, J. W. (1995). Optimal location of monitoring wells for detection of groundwater contamination in three-dimensional heterogeneous aquifers. Models for Assessing and Monitoring Groundwater Quality (Proceedings of a Boulder Symposium. IAHS), 227, 39–47.
Ta’any, R. A., & Tahboub, A. B. (2009). Geostatistical analysis of spatiotemporal variability of groundwater level fluctuations in Amman-Zarqa basin, Jordan: a case study. Environmental Geology, 57, 525–535.
Van Geer, F. C., Te Stroet, C. B. M., & Yangxiao, Z. (1991). Using Kalman filtering to improve and quantify the uncertainty of numerical groundwater simulations: 1. The role of system noise and its calibration. Water Resources Research, 27(8), 1987–1994.
Volpi, G., Gambolati, G., Carbognin, L., & Mozzi, G. (1979). Groundwater contour mapping in Venice by stochastic interpolators: 2. Results. Water Resources Research, 15(2), 291–297.
Webster, R., & Oliver, M. (2007). Geostatistics for environmental scientists. UK: Wiley.
Wu, Y. (2003). Optimal design of a groundwater monitoring network in Daqing, China. Environmental Geology, 45, 527–535.
Yangxiao, Z., Te Stroet, C. B., & Van Geer, F. (1991). Using Kalman filtering to improve and quantify the uncertainty of numerical groundwater simulations: 2. Application to monitoring network design. Water Resources Research, 27(8), 1995–2006.
Zhang, Y., Pinder, G. F., & Herrera, G. S. (2005). Least cost design of groundwater quality monitoring networks. Water Resources Research, 41(W08412), 13.
Acknowledgments
H. E. Júnez-Ferreira greatly appreciates the support of the Consejo Nacional de Ciencia y Tecnología (CONACYT) for a scholarship grant from February 2009 to August 2010. We would also like to acknowledge the reviewers for their comments and suggestions which helped us to improve this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Júnez-Ferreira, H.E., Herrera, G.S. A geostatistical methodology for the optimal design of space–time hydraulic head monitoring networks and its application to the Valle de Querétaro aquifer. Environ Monit Assess 185, 3527–3549 (2013). https://doi.org/10.1007/s10661-012-2808-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10661-012-2808-5