Equilibrium and Stability of Anisotropic Hyperelastic Graphene Membranes

Abstract

The lack of experimental investigations on graphene fostered researchers to focus on its mechanical modeling. Being graphene a one-atom-thick sheet, many authors developed continuum membrane models to analyze its mechanical behavior. However, an entirely nonlinear approach in finite elasticity has not been presented so far. In this work, the equilibrium problem of anisotropic hyperelastic graphene membranes is addressed. Strain and stress measures are expressed under the hypothesis of homogeneous deformations and the boundary-value problem is formulated for a graphene membrane subjected to biaxial loads. The stability of the equilibrium configurations is assessed through an energy criterion. Explicit relations between stretches and stresses of the membrane are derived for the cases of uniaxial and equibiaxial loads. Unexpectedly, bifurcation and multiple equilibrium solutions are found when graphene is subjected to equibiaxial loads. A linearization of the finite theory is presented and the expressions of Young’s modulus and Poisson’s ratio of graphene are derived. The formulation proposed in this work may be the basis for accurate investigations of the mechanics of graphene subjected to large deformations.

1 Introduction

Graphene is a one-atom-thick sheet composed of carbon atoms arranged in a hexagonal lattice [37]. The remarkable mechanical, thermal and electrical properties of this material [15, 36] make it suitable for many applications in various research fields, such as micro- and nano-electronics [63], biomedicine [49], energy generation and storage [42, 44] and composite materials [38]. Experimental activities showed that a small amount of graphene added to a polymer matrix produces a significant enhancement of the mechanical properties [10, 45]. This is why in the recent years many new technologies, for instance in mechanical and aerospace engineering, involve the use of graphene to obtain strong, light and durable materials.

A deep understanding of the mechanical behavior of graphene is required in order to fully exploit its potentialities. However, due to the technical difficulties connected to the small scale of the problem, only a few experimental tests were carried out [12, 23, 28, 41]. For this reason, there is the necessity of reliable models for the mechanical behavior of graphene.

Graphene modeling can be done mainly with three different approaches: atomistic, equivalent continuum and molecular mechanics. Atomistic simulations, such as molecular dynamics (MD), density functional theory (DFT) and ab initio, are probably the ones that provide the most detailed description of the chemical interactions at the nanoscale. Molecular mechanics makes use of concepts of classical mechanics to analyze the hexagonal lattice as a structure composed of nodes (atoms) connected by continuum elements (chemical bonds). Both atomistic and molecular mechanics approaches require a large computational effort even for systems composed of a small number of atoms. Many parameters are involved in these simulations, therefore it is easy to find conflicting results in the literature (see, e.g., [6, 8, 14, 61, 62]). Hence, many authors often neglect the discrete nature of the lattice structure and develop continuum models [1, 11, 46]. This is the simplest approach from a computational point of view and also the most effective for practical engineering applications. Thus, simulations based on continuum mechanics are necessary for characterizing the mechanical properties and the mechanics of deformation of graphene [51].

Being graphene a two-dimensional material, continuum elastic models are generally developed using membrane or plate theories. Ansari et al. [4] and Shen et al. [50] evaluated the natural frequencies of graphene sheets using nonlocal plate models that take into account size effects. Gong et al. [19] considered a modified non-local plate model and demonstrated that good predictions can be obtained by fitting the model parameters to the numerical results deriving from atomistic models or experimental data. Caillerie et al. [7] developed an equivalent macroscopic membrane model by means of a discrete homogenization technique and Mianroodi et al. [33] developed a nonlinear membrane model for large amplitude vibrations of single layer graphene sheets. One of the most recent contributions regarding continuum graphene membranes is the work by Höller et al. [20]. In that contribution, the authors proposed a hyperelastic formulation governed by a polynomial stored energy function that takes into account for the anisotropy of graphene for large deformations. Their work was inspired by the first anisotropic hyperelastic model for graphene membranes proposed by Kumar and Parks [25]. The assumption of anisotropic behavior is due to the fact that graphene is isotropic only for small deformations [17, 21]. Therefore, an accurate description of the response of graphene when subjected to large deformations must take into account its anisotropy.

The behavior of membranes subjected to finite in-plane deformations has been investigated for a long time. Treloar [57] was the first to carry out experiments on rubber membranes subjected to equibiaxial loads. He discovered that, in some cases, for a critical value of the external load the membrane experiences asymmetric stable deformations. In other words, the membrane loses its square shape and assumes the shape of a rectangle. It was in fact demonstrated from a theoretical point of view that, depending on the stored energy function adopted for the material, bifurcation and stable asymmetric solutions may take place [22, 26, 53]. The surprising thing is that this behavior is observed for isotropic hyperelastic membranes. The nonlinearities of the boundary-value problem generate an unexpected lack of symmetry of the solution even in a completely symmetric layout.

Höller et al. [20] derived the expressions of strain and stress tensors for continuum graphene membranes and estimated the coefficients of the polynomial stored energy function by fitting the results of DFT simulations. However, a solution of the boundary-value problem was not given. Solving the boundary-value problem is the only way to investigate the mechanical response of graphene membranes and, eventually, discover unexpected multiple equilibrium solutions. In this regard, the expressions of strain and stress tensors are not enough. Therefore, in the present paper, we make use of equilibrium equations and boundary conditions to derive the general solution of the boundary-value problem. The expressions of the equilibrium solutions for the cases of uniaxial and equibiaxial loads are obtained. This allows to derive the relations between external loads and stretches and between stretches themselves. Such relations describe the equilibrium paths of graphene subjected to uniaxial and equibiaxial loads. Hence, the novelty of the present work is that we propose a fully nonlinear solution to the equilibrium problem of anisotropic hyperelastic graphene membranes. This solution allows to deeply understand the mechanics of deformation of graphene.

The paper is structured as follows. Section 2 introduces the basic notions of the theory of anisotropic hyperelastic graphene membranes. The general form of the stored energy function is given and the expressions of Piola-Kirchhoff and Cauchy stress tensors are derived. The boundary-value problem is formulated in Sect. 3 and its solutions for the cases of uniaxial loads and equibiaxial loads are given in Sects. 4 and 5, respectively. The stability of the equilibrium configurations is assessed through an energy criterion, which is outlined in Sect. 6. The nonlinear formulation of the equilibrium is linearized in Sect. 7 by introducing the hypothesis of small deformation field. The expressions of Young’s modulus and Poisson’s ratio are thus derived. Numerical results expressing the mechanical behavior of graphene sheets are presented in Sect. 8 and, as a consequence, a reparametrization of the stored energy function is proposed in Sect. 9. Conclusions are drawn in Sect. 10.

2 Anisotropic Hyperelasticity for Graphene

Graphene is considered as a two-dimensional membrane, which is defined by the closure $\overline{\mathcal{B}}$ of the domain ℬ of the two-dimensional Euclidean space $\mathfrak{E}$. The boundary $\partial \mathcal{B}$ is Lipschitz-continuous and the domain is non-empty, connected and bounded. The undeformed configuration $\overline{\mathcal{B}}$ is considered as reference configuration, while the deformed configuration is given by the deformation $\mathbf{\varphi } : \overline{\mathcal{B}} \rightarrow \mathcal{V}$, which is a smooth enough, injective and orientation-preserving vector field [27]. $\mathcal{V}$ denotes the vector space associated with $\mathfrak{E}$.

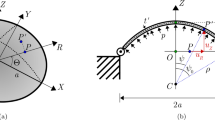
The Cartesian coordinate system in the graphene plane is defined by the orthonormal basis of vectors $\mathbf{n}_{x}$ and $\mathbf{n}_{y}$, which represent zigzag and armchair directions, respectively. The principal strain directions are identified by the unit vectors $\mathbf{n}_{1}$ and $\mathbf{n}_{2}$. The angle that direction 1 forms with zigzag direction is $\phi$, namely $\cos \phi = \mathbf{n}_{1} \cdot \mathbf{n}_{x}$ (Fig. 1). The representation of the Green-Lagrange strain tensor in the principal reference system is

$$ \mathbf{E} = E_{1} \mathbf{n}_{1} \otimes \mathbf{n}_{1} + E_{2} \mathbf{n}_{2} \otimes \mathbf{n}_{2}, $$

where ⊗ denotes the dyadic product.

Fig. 1

Graphene analyzed as a continuum membrane: Symmetry and periodicity of the graphene honeycomb lattice allows to investigate the material behavior considering only directions between zigzag and armchair directions ($\phi \in [0,\pi /6]$)

The isotropicization theorem [43] allows to express the strain energy density of an anisotropic hyperelastic material as a function of a set of invariants that take into account the material symmetry group. Given the particular symmetry and periodicity of the graphene honeycomb lattice, Kumar and Parks [25] introduced the following invariants of the Green-Lagrange strain tensor $\mathbf{E}$:

$$ \begin{aligned} & I_{1} = \text{tr}\mathbf{E} = E_{1} + E_{2}, \\ & I_{2} = \frac{1}{2} \left [ \left ( \text{tr}\mathbf{E} \right )^{2} - \text{tr}\left (\mathbf{E}^{2}\right ) \right ] = E_{1} E_{2}, \\ & I_{3} = \left (\mathbf{M}\cdot \mathbf{E}\right )^{3} - 3 \left ( \mathbf{M}\cdot \mathbf{E}\right ) \left (\mathbf{N}\cdot \mathbf{E} \right )^{2} = (E_{1} - E_{2})^{3} \cos \left (6 \phi \right ), \end{aligned} $$

(1)

where (⋅) denotes the second-order tensor contraction and the geometric tensors $\mathbf{M}$ and $\mathbf{N}$ are defined as

$$ \mathbf{M} = \mathbf{n}_{x} \otimes \mathbf{n}_{x} - \mathbf{n}_{y} \otimes \mathbf{n}_{y}, \quad \mathbf{N} = \mathbf{n}_{x} \otimes \mathbf{n}_{y} + \mathbf{n}_{y} \otimes \mathbf{n}_{x}. \quad $$

The invariants $I_{1}$ and $I_{2}$ expressed by (1) are the isotropic principal invariants of the Green-Lagrange strain tensor. The material anisotropy in the constitutive response of graphene is captured by the third invariant $I_{3}$. Note that anisotropy activates only at large deformations and when $E_{1} \neq E_{2}$.

In order to develop a stored energy function that includes higher order dependencies on the components of tensor $\mathbf{E}$, Höller et al. [20] introduced a set of so-called main invariants, which are defined as combinations of invariants $I_{1}$, $I_{2}$ and $I_{3}$ as follows:

$$ \begin{aligned} J_{1} & = I_{1}^{2} - 2 I_{2}, & J_{2} & = I_{1}^{3} - 3 I_{1} I_{2}, & J_{3} & = I_{1} I_{2}, & J_{4} & = I_{1}^{4} - 4 I_{1}^{2} I_{2} + 2 I_{2}^{2}, \\ J_{5} & = I_{2}^{2}, & J_{6} & = I_{1}^{2} I_{2} - 2 I_{2}^{2}, & J_{7} & = I_{1}^{5} - 5 I_{1}^{3} I_{2} + 5 I_{1} I_{2}^{2}, & J_{8} & = I_{1}^{3} I_{2} - 3 I_{1} I_{2}^{2}, \\ J_{9} & = I_{1} I_{2}^{2}, & J_{10} & = I_{3} I_{1}, & J_{11} & = I_{3} (I_{1}^{2} - 2 I_{2}). \end{aligned} $$

(2)

The first nine main invariants are associated with isotropic material behavior, while the contribution of anisotropy is involved only in invariants $J_{10}$ and $J_{11}$. Given relations (2), the stored energy function for graphene proposed in [20] is

$$ \omega (I_{1},I_{2},I_{3}) = \sum _{k=1}^{3} c_{k} I_{k} + \sum _{h=1}^{11} c_{h+3} J_{h} $$

(3)

where $c_{1}$–$c_{14}$ are polynomial fitting coefficients with dimension of energy per unit area. Note that, for three-dimensional solids, the stored energy function has dimension of energy per unit volume. However, being graphene a one-atom-thick layer, it is assumed to be a two-dimensional material. This explains the physical dimension of coefficients $c_{1}$–$c_{14}$.

The second Piola-Kirchhoff stress tensor is energetically conjugated to the Green-Lagrange strain tensor. Therefore, its expression (with dimension of force over length) read

$$ \boldsymbol{\Sigma } = \frac{\partial \omega }{\partial \mathbf{E}} (I_{1},I_{2},I_{3}) = \sum _{k=1}^{3} \frac{\partial \omega }{\partial I_{k}} \frac{\partial I_{k}}{\partial \mathbf{E}}. $$

(4)

The derivatives of the principal invariants with respect to the Green-Lagrange strain tensor are [20]

$$ \frac{\partial I_{1}}{\partial \mathbf{E}} = \mathbf{I}, \quad \frac{\partial I_{2}}{\partial \mathbf{E}} = I_{1} \mathbf{I} - \mathbf{E}, \quad \frac{\partial I_{3}}{\partial \mathbf{E}} = \mathbf{S}, $$

(5)

with

$$ \mathbf{S} = 3 \left [ \left (\mathbf{M}\cdot \mathbf{E}\right )^{2} - \left (\mathbf{N}\cdot \mathbf{E}\right )^{2} \right ] \mathbf{M} - 6 \left [ \left (\mathbf{M}\cdot \mathbf{E}\right ) \left (\mathbf{N} \cdot \mathbf{E}\right ) \right ] \mathbf{N}. $$

(6)

Using (5) and (6), the expression of the second Piola-Kirchhoff stress tensor (4) become

$$ \boldsymbol{\Sigma } = \beta _{1} \mathbf{I} + \beta _{2} \mathbf{E} + \beta _{3} \mathbf{S}, $$

(7)

where

$$ \begin{aligned} \beta _{1} = & \; c_{1} + c_{2} I_{1} -3 c_{5} I_{2} +c_{6} \left (I_{1}^{2}+I_{2}\right )-4 c_{7} I_{1} I_{2} + 2 c_{8} I_{1} I_{2} + c_{9} \left (I_{1}^{3} - 2 I_{1} I_{2}\right ) \\ & + 5 c_{10} \left (I_{2}^{2} -I_{1}^{2} I_{2}\right ) + c_{11} \left (I_{1}^{4} -3 I_{2}^{2} -3 I_{1}^{2} I_{2}\right ) + c_{12} \left (I_{2}^{2} + 2 I_{1}^{2} I_{2}\right ) +c_{13} I_{3}, \\ \beta _{2} = & - c_{2} +2 c_{4} +3 c_{5} I_{1} -c_{6} I_{1} +4 c_{7} \left (I_{1}^{2}-I_{2}\right )-2 c_{8} I_{2} +c_{9} \left (4 I_{2}-I_{1}^{2}\right ) \\ & + 5 c_{10} \left (I_{1}^{3}-2 I_{1} I_{2}\right )+c_{11} \left (6 I_{1} I_{2}-I_{1}^{3}\right )-2 c_{12} I_{1} I_{2} +2 c_{14} I_{3}, \\ \beta _{3} = & \; c_{3} + c_{13} I_{1}+c_{14} \left (I_{1}^{2}-2 I_{2}\right ). \end{aligned} $$

We assume that graphene in undeformed configuration relates to zero stresses. With this position, we immediately observe that $c_{1} = 0$.

Leaving out rigid rotations, the deformation gradient in the principal reference system is written in function of the principal stretches $\lambda _{1}$ and $\lambda _{2}$ with the diagonal form

$$ \mathbf{F} = \lambda _{1} \mathbf{n}_{1} \otimes \mathbf{n}_{1} + \lambda _{2} \mathbf{n}_{2} \otimes \mathbf{n}_{2}. $$

Introducing the right Cauchy-Green deformation tensor $\mathbf{C} = \mathbf{F}^{T}\mathbf{F}$, the following relation between Green-Lagrange strain tensor and deformation gradient holds

$$ \mathbf{E} = \frac{1}{2}\left (\mathbf{C} - \mathbf{I}\right ) = \frac{1}{2}\left (\mathbf{F}^{T}\mathbf{F} - \mathbf{I}\right ), $$

(8)

from which the second Piola-Kirchhoff stress tensor (7) assumes the form

$$ \boldsymbol{\Sigma } = \left (\beta _{1} - \frac{\beta _{2}}{2}\right ) \mathbf{I} + \frac{\beta _{2}}{2} \mathbf{C} + \beta _{3} \mathbf{S}, $$

with tensor $\mathbf{S}$ that is rewritten as

$$ \mathbf{S} = \frac{3}{4} \left [ \left (\mathbf{M}\cdot \mathbf{C}\right )^{2} - \left (\mathbf{N}\cdot \mathbf{C}\right )^{2} \right ] \mathbf{M} - \frac{3}{2} \left [ \left (\mathbf{M}\cdot \mathbf{C}\right ) \left (\mathbf{N}\cdot \mathbf{C}\right ) \right ] \mathbf{N}. $$

The first Piola-Kirchhoff stress tensor is then computed by applying the transformation

$$ \mathbf{T}_{R} = \mathbf{F} \boldsymbol{\Sigma } = \left (\beta _{1} - \frac{\beta _{2}}{2}\right ) \mathbf{F} + \frac{\beta _{2}}{2} \mathbf{F} \mathbf{F}^{T} \mathbf{F} + \beta _{3} \mathbf{F} \mathbf{S}. $$

(9)

The representation of $\mathbf{T}_{R}$ in the reference system identified by the principal strain directions, $\mathbf{n}_{1}$ and $\mathbf{n}_{2}$, is

$$ \begin{aligned} & T_{R_{11}} = \lambda _{1} \left [\beta _{1} +\frac{\beta _{2}}{2} \left (\lambda _{1}^{2}-1\right ) + \frac{3}{4} \beta _{3} \left ( \lambda _{1}^{2}-\lambda _{2}^{2}\right )^{2} \cos \left ( 6 \phi \right ) \right ], \\ & T_{R_{12}} = -\frac{3}{4} \beta _{3} \lambda _{1} \left (\lambda _{1}^{2}- \lambda _{2}^{2}\right )^{2} \sin (6 \phi ), \\ & T_{R_{21}} = -\frac{3}{4} \beta _{3} \lambda _{2} \left (\lambda _{1}^{2}- \lambda _{2}^{2}\right )^{2} \sin (6 \phi ), \\ & T_{R_{22}} = \lambda _{2} \left [\beta _{1}+\frac{\beta _{2}}{2} \left (\lambda _{2}^{2}-1\right )-\frac{3}{4} \beta _{3} \left ( \lambda _{1}^{2}-\lambda _{2}^{2}\right )^{2} \cos (6 \phi )\right ]. \end{aligned} $$

(9)

Note that, in general, in this reference system $\mathbf{T}_{R}$ is not diagonal. This means that the principal strain directions do not coincide with the principal stress directions. The only cases in which these directions coincide is when $\phi = n \pi /6$, $\forall n \in \mathbb{Z}$, for which $T_{R_{12}} = T_{R_{21}} = 0$. Hence, this happens only when the principal strain directions correspond to the zigzag and armchair directions.

The first Piola-Kirchhoff stress tensor can be written in terms of components with respect to the base frame $\mathbf{n}_{x}$–$\mathbf{n}_{y}$ according to $\mathbf{T}_{R} = \sum _{i=1}^{2} \sum _{j=1}^{2} T_{R_{\mathit{ij}}} \mathbf{n}_{i} \otimes \mathbf{n}_{j}$, yielding

$$ \begin{aligned} T_{R_{xx}} &= T_{R_{11}}\cos ^{2}(\phi )+ T_{R_{22}}\sin ^{2}(\phi ) - \left (T_{R_{12}}+T_{R_{21}}\right )\sin (\phi ) \cos (\phi ), \\ T_{R_{xy}} &= T_{R_{12}}\cos ^{2}(\phi )- T_{R_{21}}\sin ^{2}(\phi ) + \left (T_{R_{11}}-T_{R_{22}}\right )\sin (\phi ) \cos (\phi ), \\ T_{R_{yx}} &= T_{R_{21}}\cos ^{2}(\phi )- T_{R_{12}}\sin ^{2}(\phi ) + \left (T_{R_{11}}-T_{R_{22}}\right )\sin (\phi ) \cos (\phi ), \\ T_{R_{yy}} &= T_{R_{11}}\sin ^{2}(\phi )+ T_{R_{22}}\cos ^{2}(\phi ) + \left (T_{R_{12}}+T_{R_{21}}\right )\sin (\phi ) \cos (\phi ), \end{aligned} $$

(10)

where components $T_{R_{\mathit{ij}}}$ ($i = 1,2$ and $j = 1,2$) are given in (9).

The stress tensors described above represent measures of stress referred to the undeformed configuration of the membrane (Lagrangian analysis). An alternative way of investigating the elastic behavior of graphene is in terms of Eulerian quantities, which are associated with the deformed configuration. The measure of stress consistent with the deformed configuration is the Cauchy stress tensor, defined by the transformation

$$ \mathbf{T} = \frac{1}{\text{det} \mathbf{F}} \mathbf{T}_{R} \mathbf{F}^{T} = \frac{1}{\text{det} \mathbf{F}} \mathbf{F} \mathbf{F}^{T} \left [\beta _{1} \mathbf{I} + \frac{\beta _{2}}{2} \left (\mathbf{F} \mathbf{F}^{T} - \mathbf{I} \right ) \right ] + \frac{\beta _{3}}{\text{det} \mathbf{F}} \mathbf{F} \mathbf{S} \mathbf{F}^{T}. $$

(11)

The components of the Cauchy stress tensor in the principal strain system are

$$ \begin{aligned} & T_{11} = \frac{\lambda _{1}}{\lambda _{2}} \left [\beta _{1} + \frac{\beta _{2}}{2} \left (\lambda _{1}^{2}-1\right ) + \frac{3}{4} \beta _{3} \left (\lambda _{1}^{2}-\lambda _{2}^{2}\right )^{2} \cos \left ( 6 \phi \right ) \right ], \\ & T_{12} = T_{21} = -\frac{3}{4} \beta _{3} \left (\lambda _{1}^{2}- \lambda _{2}^{2}\right )^{2} \sin (6 \phi ), \\ & T_{22} = \frac{\lambda _{2}}{\lambda _{1}} \left [\beta _{1}+ \frac{\beta _{2}}{2} \left (\lambda _{2}^{2}-1\right )-\frac{3}{4} \beta _{3} \left (\lambda _{1}^{2}-\lambda _{2}^{2}\right )^{2} \cos (6 \phi )\right ]. \end{aligned} $$

(11)

3 Boundary-Value Problem

Graphene is regarded as a square membrane with side $l$, which is thus identified by the closure of region $\mathcal{B} = \left \{ \left ( x, y \right ): \left |x\right |< l/2, \left |y\right |< l/2 \right \}$. The membrane is stretched and maintained in equilibrium by tensile surface forces applied uniformly and orthogonally to the four edges. These forces are considered as dead load, namely not dependent on the deformation. Body forces are not taken into account. As required by the plane stress condition, the two faces of the membrane are traction-free. The boundary-value problem assumes thus the form of a pure traction problem [39, 40], which is governed by the following field equation and boundary conditions:

$$ \begin{gathered} \text{Div} \, \mathbf{T}_{R} = \mathbf{o}, \quad \forall \ x,y \in \mathcal{B}, \\ \mathbf{T}_{R} \mathbf{n}_{x} = s_{x} \mathbf{n}_{x}, \quad \text{for} \ x = \frac{l}{2} \ \text{and} \ \left |y\right |\leq \frac{l}{2}, \\ \mathbf{T}_{R} \mathbf{n}_{y} = s_{y} \mathbf{n}_{y}, \quad \text{for} \ y = \frac{l}{2} \ \text{and} \ \left |x\right |\leq \frac{l}{2}, \end{gathered} $$

(12)

where $s_{x}$ and $s_{y}$ are assigned positive constants that specify the intensity of the external loads, with dimension of force per unit length.

Solutions to the governing equations (12) are sought in the class of homogeneous deformations, namely in the set of deformations with constant deformation gradient. Note that this is an appropriate assumption when dealing with the equilibrium problem of membranes subjected to in-plane loads, as observed by other theoretical and experimental works (see, e.g., [22, 53, 57]). In this case, the solution of the equilibrium problem does not depend on the length of the side of the membrane [26].

Under the assumption of homogeneous deformations, the local equilibrium (12)₁ is trivially satisfied by a constant stress field, which must fulfill the remaining boundary conditions (12)₂ and (12)₃. Introducing (9) and (10) into (12)₂ and (12)₃ and operating a linear combination among the four equations, we derive the system

$$ \begin{aligned} &\frac{1}{8} \left [4 \delta _{1}+\eta _{1} \cos \left (6 \phi \right )\right ] \left (\lambda _{1}+\lambda _{2}\right ) = s_{x}+s_{y}, \\ &\frac{1}{16} \left [8 \delta _{2} \cos (2 \phi )+\eta _{2} \cos (4 \phi )+\kappa \cos (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2} \right ) = s_{x}-s_{y}, \\ & \left [8 \delta _{2} \sin (2 \phi )-\eta _{2} \sin (4 \phi )+ \kappa \sin (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2}\right ) = 0, \\ &\beta _{3} \sin (6 \phi ) \left (\lambda _{1}-\lambda _{2}\right )^{3} = 0, \end{aligned} $$

(13)

where, for the sake of clarity, the following quantities were introduced:

$$ \begin{aligned} &\kappa = \left (\lambda _{1}^{2}-\lambda _{2}^{2} \right )^{3} \left (c_{13}+\alpha _{2} c_{14}\right ), \\ &\eta _{1} = \left (\lambda _{1}-\lambda _{2}\right )^{3} \left ( \lambda _{1}+\lambda _{2}\right ) \left [\left (\lambda _{1}+\lambda _{2} \right )^{2} \left (c_{13}+\alpha _{1} c_{14}\right )+6 \beta _{3} \right ], \\ &\eta _{2} = \left (\lambda _{1}+\lambda _{2}\right )^{3} \left ( \lambda _{1}-\lambda _{2}\right ) \left [\left (\lambda _{1}-\lambda _{2} \right )^{2} \left (c_{13}+\alpha _{2} c_{14}\right )+12 \beta _{3} \right ], \\ &\delta _{1} = 2 \gamma _{1}+\alpha _{1} \gamma _{2}, \quad \delta _{2} = 2 \gamma _{1}+\alpha _{2} \gamma _{2}, \\ &\gamma _{1} = \beta _{1} - c_{13} I_{3}, \quad \gamma _{2} = \beta _{2} - 2 c_{14} I_{3}, \\ &\alpha _{1} = \lambda _{1}^{2}-\lambda _{1} \lambda _{2}+\lambda _{2}^{2}-1, \quad \alpha _{2} = \lambda _{1}^{2}+\lambda _{1} \lambda _{2}+ \lambda _{2}^{2}-1. \end{aligned} $$

System (13) describes the equilibrium of the graphene membrane. In the following sections, solutions will be investigated in the cases of uniaxial loads along zigzag and armchair directions and equibiaxial loads.

4 Equilibrium Solutions for Uniaxial Loads

4.1 Zigzag Load

When the load is applied along the zigzag direction ($s_{y} = 0$), the governing equations (13) of the boundary-value problem become

$$ \begin{aligned} &\frac{1}{8} \left [4 \delta _{1}+\eta _{1} \cos \left (6 \phi \right )\right ] \left (\lambda _{1}+\lambda _{2} \right ) = s_{x}, \\ &\frac{1}{16} \left [8 \delta _{2} \cos (2 \phi )+\eta _{2} \cos (4 \phi )+\kappa \cos (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2} \right ) = s_{x}, \\ & \left [8 \delta _{2} \sin (2 \phi )-\eta _{2} \sin (4 \phi )+ \kappa \sin (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2}\right ) = 0, \\ &\beta _{3} \sin (6 \phi ) \left (\lambda _{1}-\lambda _{2}\right )^{3} = 0. \end{aligned} $$

From the second equation, we notice that for symmetric solutions ($\lambda _{1} = \lambda _{2}$), the intensity of the external load $s_{x}$ is always equal to zero. This means that the only possible symmetric solution in this case is the undeformed configuration $\lambda _{1} = \lambda _{2} = 1$. Considering only asymmetric solutions ($\lambda _{1} \neq \lambda _{2}$), we obtain

$$ \begin{aligned} &\frac{1}{8} \left [4 \delta _{1}+\eta _{1} \cos \left (6 \phi \right )\right ] \left (\lambda _{1}+\lambda _{2}\right ) = s_{x}, \\ &\frac{1}{16} \left [8 \delta _{2} \cos (2 \phi )+\eta _{2} \cos (4 \phi )+\kappa \cos (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2} \right ) = s_{x}, \\ & 8 \delta _{2} \sin (2 \phi )-\eta _{2} \sin (4 \phi )+\kappa \sin (8 \phi ) = 0, \\ &\beta _{3} \sin (6 \phi ) = 0. \end{aligned} $$

(14)

Meaningful solutions to this system of equations can be found only with $\phi = 0$,¹ for which

$$ \begin{aligned} &s_{x} = \frac{1}{8} \left (4 \delta _{1}+\eta _{1} \right ) \left ( \lambda _{1}+\lambda _{2}\right ), \\ &\left (8 \delta _{2} +\eta _{2} +\kappa \right ) \left (\lambda _{1}- \lambda _{2}\right ) - 2 \left (4 \delta _{1}+\eta _{1} \right ) \left (\lambda _{1}+\lambda _{2}\right ) = 0. \end{aligned} $$

(16)

Equation (16)₁ gives the relation between stress and stretch along zigzag direction, while (16)₂ is the implicit relation between stretches along zigzag and armchair directions ($\lambda _{1}$ and $\lambda _{2}$, respectively).

4.2 Armchair Load

When the load is applied along the armchair direction ($s_{x} = 0$), the governing equations (13) of the boundary-value problem become

$$ \begin{aligned} &\frac{1}{8} \left [4 \delta _{1}+\eta _{1} \cos \left (6 \phi \right )\right ] \left (\lambda _{1}+\lambda _{2}\right ) = s_{y}, \\ &-\frac{1}{16} \left [8 \delta _{2} \cos (2 \phi )+\eta _{2} \cos (4 \phi )+\kappa \cos (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2} \right ) = s_{y}, \\ & \left [8 \delta _{2} \sin (2 \phi )-\eta _{2} \sin (4 \phi )+ \kappa \sin (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2}\right ) = 0, \\ &\beta _{3} \sin (6 \phi ) \left (\lambda _{1}-\lambda _{2}\right )^{3} = 0. \end{aligned} $$

(17)

Again, the only symmetric solution is the undeformed configuration $\lambda _{1} = \lambda _{2} = 1$, for which $s_{y} = 0$. Considering asymmetric solutions ($\lambda _{1} \neq \lambda _{2}$), as done in Sect. 4.1, we observe that meaningful solutions exist only for $\phi = 0$. Therefore, also for the case of armchair uniaxial load, the first principal direction is found to be the zigzag direction. In this case, system (17) reads

$$ \begin{aligned} &s_{y} = \frac{1}{8} \left (4 \delta _{1}+\eta _{1} \right ) \left ( \lambda _{1}+\lambda _{2}\right ), \\ &\left (8 \delta _{2} +\eta _{2} +\kappa \right ) \left (\lambda _{1}- \lambda _{2}\right ) + 2 \left (4 \delta _{1}+\eta _{1} \right ) \left (\lambda _{1}+\lambda _{2}\right ) = 0. \end{aligned} $$

(18)

Equation (18)₁ gives the relation between stress and stretch along armchair direction, while (18)₂ is the implicit relation between stretches along armchair and zigzag directions ($\lambda _{2}$ and $\lambda _{1}$, respectively).

5 Equilibrium Solutions for Equibiaxial Loads

The equibiaxial loading condition is defined by $s_{x} = s_{y} = s$. In this circumstance, system (13) becomes

$$ \begin{aligned} &\left [4 \delta _{1}+\eta _{1} \cos \left (6 \phi \right )\right ] \left (\lambda _{1}+\lambda _{2}\right ) = 16 s, \\ &\left [8 \delta _{2} \cos (2 \phi )+\eta _{2} \cos (4 \phi )+\kappa \cos (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2}\right ) = 0, \\ & \left [8 \delta _{2} \sin (2 \phi )-\eta _{2} \sin (4 \phi )+ \kappa \sin (8 \phi )\right ] \left (\lambda _{1}-\lambda _{2}\right ) = 0, \\ &\beta _{3} \sin (6 \phi ) \left (\lambda _{1}-\lambda _{2}\right )^{3} = 0. \end{aligned} $$

(19)

This set of equations provides two classes of solutions, which are discussed in the following.

5.1 Symmetric Solutions Under Equibiaxial Loads

Considering symmetric solutions, system (19) turns into

$$ \begin{aligned} & \lambda _{1} = \lambda _{2} = \lambda , \\ & s = \frac{1}{2} \left [2 \gamma _{1} + \gamma _{2} \left ( \lambda ^{2} - 1 \right )\right ] \lambda . \end{aligned} $$

(20)

The solutions of this class do not depend on angle $\phi$. Since the principal stretches are equal, the membrane undergoes a homothetic transformation, maintaining its square shape. The strain ellipse degenerates into a circle and every direction is principal.

5.2 Asymmetric Solutions Under Equibiaxial Loads

The graphene membrane subjected to equibiaxial loads may admit asymmetric solutions, characterized by $\lambda _{1} \neq \lambda _{2}$. Since $\phi \in [0,\pi /6]$, equation (19)₄ is satisfied only for $\phi = 0$ and $\phi = \pi /6$.² Asymmetric solutions to equibiaxial loads can be thus observed only when the first principal strain direction corresponds to the zigzag or the armchair direction. Two classes of solutions are derived:

$$ \phi = 0 \textstyle\begin{cases} s = \frac{1}{16} \left (4 \delta _{1} + \eta _{1} \right ) \left ( \lambda _{1}+\lambda _{2}\right ), \\ \kappa + 8 \delta _{2} + \eta _{2} = 0 \end{cases} $$

(21)

$$ \phi = \frac{\pi }{6} \textstyle\begin{cases} s = \frac{1}{16} \left (4 \delta _{1} - \eta _{1} \right ) \left ( \lambda _{1}+\lambda _{2}\right ), \\ \kappa - 8 \delta _{2} + \eta _{2} = 0 \end{cases} $$

(22)

When a certain intensity of the load is reached, bifurcation of the equilibrium path takes place and the membrane loses its square shape, becoming a rectangle that follows solutions (21) and (22).

This result shows that, adopting a stored energy function of the form expressed by (3), the boundary-value problem admits multiple solutions. This surprising behavior was also observed by other researches when dealing with rubber membranes subjected to equibiaxial loads (see, e.g., [22, 26, 53, 57]).

6 Stability of the Equilibrium Configurations

The stability of the equilibrium solutions is assessed through an energy criterion [54, 55]. An equilibrium configuration is stable if the Hessian matrix $\mathbf{K}$ of the total potential energy ℰ is positive definite [65]. The equilibrium solutions are said to be neutrally stable when $\mathbf{K}$ is positive semi-definite and unstable when $\mathbf{K}$ is indefinite. In other words, for stable equilibrium configurations all the eigenvalues of the Hessian matrix are positive, while if one eigenvalue is zero and the remaining are positive the equilibrium is neutrally stable. When at least one eigenvalue is negative the equilibrium is unstable [29]. Along the equilibrium paths, configurations where the equilibrium is neutrally stable correspond to critical points. A critical point can be classified as limit point, where the external load is stationary, or bifurcation point, where the equilibrium path is no longer unique and multiple branches of equilibrium appear [56].

The total potential energy of the graphene membrane is defined as

$$ \mathcal{E} \left (\mathbf{\varphi }\right ) = \int _{\mathcal{B}} \tilde{\omega }\left (\mathbf{F}\right ) da - \int _{\partial \mathcal{B}} \mathbf{s} \cdot \mathbf{\varphi } \, dl, $$

(23)

where $\mathbf{s}$ is the density of external force per unit length in undeformed configuration and $\tilde{\omega } \left (\mathbf{F}\right ) = \omega (I_{1},I_{2},I_{3})$. Recalling the boundary condition $\mathbf{T}_{R} \mathbf{n} = \mathbf{s}$ and applying the divergence theorem, equation (23) turns into

$$ \mathcal{E} \left (\mathbf{\varphi }\right ) = \int _{\mathcal{B}} \left ( \tilde{\omega }\left (\mathbf{F}\right ) - \mathbf{T}_{R} \cdot \mathbf{F} \right ) da, $$

(24)

where the dependence on $\mathbf{\varphi }$ appears through its gradient $\mathbf{F}$. Since the deformation field is assumed to be homogeneous, the integrand of (24) is constant. We can thus replace the total potential energy by its specific counterpart (energy per unit area in undeformed configuration):

$$ \tilde{e} \left (\mathbf{F}\right ) = \tilde{\omega } \left ( \mathbf{F}\right ) - \mathbf{T}_{R} \cdot \mathbf{F}. $$

(25)

The expression of the specific energy (25) in terms of principal stretches $\lambda _{1}$ and $\lambda _{2}$ is

$$ e \left (\lambda _{1},\lambda _{2}\right ) = \omega \left (I_{1},I_{2},I_{3} \right ) - \left (s_{1} \lambda _{1} + s_{2} \lambda _{2}\right ). $$

(26)

The principal invariants $I_{1}$, $I_{2}$ and $I_{3}$ in (26) are functions of stretches $\lambda _{1}$ and $\lambda _{2}$ through relations

$$ \begin{aligned} & I_{1} = \frac{1}{2} \left (\lambda _{1}^{2} + \lambda _{2}^{2} - 2 \right ), \\ & I_{2} = \frac{1}{4} \left (\lambda _{1}^{2} -1\right ) \left ( \lambda _{2}^{2} - 1 \right ), \\ & I_{3} = \frac{1}{8} \left (\lambda _{1}^{2} -\lambda _{2}^{2} \right )^{3} \cos \left (6 \phi \right ), \end{aligned} $$

(27)

which are obtained by introducing (8), that defines the link between $\mathbf{E}$ and $\mathbf{F}$, into (1).

The Hessian matrix of the specific potential energy reads

$$ \left [\mathbf{K}\right ] = \begin{bmatrix} \dfrac{\partial ^{2} e}{\partial \lambda _{1}^{2}} & \dfrac{\partial ^{2} e}{\partial \lambda _{1} \partial \lambda _{2}} \\ \dfrac{\partial ^{2} e}{\partial \lambda _{2} \partial \lambda _{1}} & \dfrac{\partial ^{2} e}{\partial \lambda _{2}^{2}} \end{bmatrix} . $$

Note that the contribution of loads to the specific potential energy $e$ is linear with respect to stretches $\lambda _{1}$ and $\lambda _{2}$ (see (26)). Thus, the Hessian matrix does not depend on vector $\mathbf{s}$. Therefore, although the equilibrium configurations are determined by the applied loads, their stability is not directly related to $\mathbf{s}$.

The second partial derivatives of the specific potential energy are computed by applying the chain rule

$$ \frac{\partial ^{2} e}{\partial \lambda _{i} \partial \lambda _{j}} = \sum _{h = 1}^{3} \sum _{k = 1}^{3} \frac{\partial ^{2} \omega }{\partial I_{h} \partial I_{k}} \frac{\partial I_{h}}{\partial \lambda _{i}} \frac{\partial I_{k}}{\partial \lambda _{j}} + \sum _{h = 1}^{3} \frac{\partial \omega }{\partial I_{h}} \frac{\partial ^{2} I_{h}}{\partial \lambda _{i} \partial \lambda _{j}}, \quad i,j = 1,2. $$

(28)

From the expression of the stored energy function (3), the following derivatives are computed:

$$\begin{aligned} \frac{\partial \omega }{\partial I_{1}} = & \; 2 I_{1} c_{4}+3 \left (I_{1}^{2}-I_{2} \right ) c_{5}+I_{2} c_{6}+4 \left (I_{1}^{3}-2 I_{1} I_{2}\right ) c_{7}+2 I_{1} I_{2} c_{9} \\ &+5 \left (I_{1}^{4}-3 I_{1}^{2} I_{2}+I_{2}^{2} \right ) c_{10} +3 \left (I_{1}^{2}-I_{2}\right ) I_{2} c_{11}+I_{2}^{2} c_{12}+I_{3} \left (c_{13}+2 I_{1} c_{14}\right ), \\ \frac{\partial \omega }{\partial I_{2}} = & \; c_{2}-2 c_{4}- I_{1} \left (3 c_{5}- c_{6}\right )+4 \left (-I_{1}^{2}+I_{2}\right ) c_{7}+2 I_{2} c_{8}+\left (I_{1}^{2}-4 I_{2}\right ) c_{9} \\ &-5 \left (I_{1}^{3}-2 I_{1} I_{2}\right ) c_{10} +\left (I_{1}^{3}-6 I_{1} I_{2}\right ) c_{11}+2 I_{1} I_{2} c_{12}-2 I_{3} c_{14}, \\ \frac{\partial \omega }{\partial I_{3}} = & \; c_{3}+I_{1} c_{13}+ \left (I_{1}^{2}-2 I_{2}\right ) c_{14}, \\ \frac{\partial ^{2} \omega }{\partial I_{1}^{2}} = & \; 2 \left \{ c_{4}+3 I_{1} c_{5}+\left (6 I_{1}^{2}-4 I_{2}\right ) c_{7}+10 I_{1}^{3} c_{10}+I_{2} \left [c_{9}+3 I_{1} \left (-5 c_{10}+c_{11}\right )\right ]+I_{3} c_{14} \right \} , \\ \frac{\partial ^{2} \omega }{\partial I_{2}^{2}} = & \; 2 \left [2 c_{7}+c_{8}-2 c_{9}+I_{1} \left (5 c_{10}-3 c_{11}+c_{12}\right )\right ], \\ \frac{\partial ^{2} \omega }{\partial I_{3}^{2}} = & \; 0, \\ \frac{\partial ^{2} \omega }{\partial I_{2} \partial I_{1}} = & \; \frac{\partial ^{2} \omega }{\partial I_{1} \partial I_{2}} = -3 c_{5}+c_{6}-8 I_{1} c_{7}+2 I_{1} c_{9}+5 \left (-3 I_{1}^{2}+2 I_{2}\right ) c_{10} \\ &+3 \left (I_{1}^{2}-2 I_{2}\right ) c_{11}+2 I_{2} c_{12}, \\ \frac{\partial ^{2} \omega }{\partial I_{3} \partial I_{1}} = & \; \frac{\partial ^{2} \omega }{\partial I_{1} \partial I_{3}} = c_{13}+2 I_{1} c_{14}, \\ \frac{\partial ^{2} \omega }{\partial I_{3} \partial I_{2}} = & \; \frac{\partial ^{2} \omega }{\partial I_{2} \partial I_{3}} = - 2 c_{14}. \end{aligned}$$

(29)

From the definition of the principal invariants given in (27), we derive

$$\begin{array}{rlrlrl}\frac{\partial I_1}{\partial {\lambda }_i}& ={\lambda }_i,& \frac{\partial I_2}{\partial {\lambda }_i}& =\frac{1}{2}{\lambda }_i({\lambda }_j^2-1),& \frac{\partial I_3}{\partial {\lambda }_i}& =\pm \frac{3}{4}{\lambda }_i{({\lambda }_i^2-{\lambda }_j^2)}^{2}cos\left(6\varphi \right),\\ \frac{{\partial }^2{I}_1}{\partial {\lambda }_i^2}& =1,& \frac{{\partial }^2{I}_2}{\partial {\lambda }_i^2}& =\frac{1}{2}({\lambda }_j^2-1),& \frac{{\partial }^2{I}_3}{\partial {\lambda }_i^2}& =\pm \frac{3}{4}(5{\lambda }_i^4-6{\lambda }_i^2{\lambda }_j^2+{\lambda }_j^4)cos\left(6\varphi \right),\\ \frac{{\partial }^2{I}_1}{\partial {\lambda }_i\partial {\lambda }_j}& =0,& \frac{{\partial }^2{I}_2}{\partial {\lambda }_i\partial {\lambda }_j}& ={\lambda }_1{\lambda }_2,& \frac{{\partial }^2{I}_3}{\partial {\lambda }_i\partial {\lambda }_j}& =-3{\lambda }_1{\lambda }_2({\lambda }_1^2-{\lambda }_2^2)cos\left(6\varphi \right),\end{array}$$

(30)

with $i,j = 1,2$ and $i \neq j$.³ Substituting (29), (30) and (27) into (28), we obtain the following expressions of the scalar components of the Hessian matrix in terms of principal stretches $\lambda _{1}$ and $\lambda _{2}$:

$$\begin{aligned} \frac{\partial ^{2} e}{\partial \lambda _{i}^{2}} = & \; \frac{1}{16} \left \{ 8 \left (-1+\lambda _{j}^{2}\right ) c_{2} \pm 12 \left (5 \lambda _{i}^{4}-6 \lambda _{i}^{2} \lambda _{j}^{2}+\lambda _{j}^{4} \right ) c_{3} \cos (6 \phi )\right . \\ & \left . +16 \left (-1+3 \lambda _{i}^{2}\right ) c_{4}+12 \left (1-6 \lambda _{i}^{2}+5 \lambda _{i}^{4}\right ) c_{5} \right . \\ & \left . + \; 4 \left (-1+\lambda _{j}^{2}\right ) \left (-3+6 \lambda _{i}^{2}+\lambda _{j}^{2}\right ) c_{6}+8 \left (-1+\lambda _{i}^{2} \right )^{2} \left (-1+7 \lambda _{i}^{2}\right ) c_{7}\right . \\ & \left .+4 \left (-1+3 \lambda _{i}^{2}\right ) \left (-1+\lambda _{j}^{2}\right )^{2} c_{8} \right . \\ & \left . +\; 2 \left (-1+\lambda _{j}^{2}\right ) \left (4-18 \lambda _{i}^{2}+15 \lambda _{i}^{4}-2 \lambda _{j}^{2}+\lambda _{j}^{4} \right ) c_{9}+5 \left (-1+\lambda _{i}^{2}\right )^{3} \left (-1+9 \lambda _{i}^{2}\right ) c_{10} \right . \\ & \left . +\left (-1+\lambda _{j}^{2}\right ) \left (-5+36 \lambda _{i}^{2}-60 \lambda _{i}^{4}+28 \lambda _{i}^{6}+3 \lambda _{j}^{2}-3 \lambda _{j}^{4}+ \lambda _{j}^{6}\right ) c_{11} \right . \\ & \left . +\left (-1+\lambda _{j}^{2}\right )^{2} \left [5+15 \lambda _{i}^{4}-2 \lambda _{j}^{2}+6 \lambda _{i}^{2} \left (-4+ \lambda _{j}^{2}\right )\right ] c_{12} \right . \\ & \left . \pm \; 4 \left [14 \lambda _{i}^{6}+18 \lambda _{i}^{2} \lambda _{j}^{2}+\lambda _{j}^{4} \left (-3+\lambda _{j}^{2}\right )-15 \lambda _{i}^{4} \left (1+\lambda _{j}^{2}\right )\right ] c_{13} \cos (6 \phi ) \right . \\ & \left . \pm \left [45 \lambda _{i}^{8}-28 \lambda _{i}^{6} \left (2+3 \lambda _{j}^{2}\right )-12 \lambda _{i}^{2} \lambda _{j}^{2} \left (3+2 \lambda _{j}^{4}\right )+\lambda _{j}^{4} \left (6-4 \lambda _{j}^{2}+3 \lambda _{j}^{4}\right ) \right .\right . \\ & \left .\left . + \; 30 \lambda _{i}^{4} \left (1+2 \lambda _{j}^{2}+ 2 \lambda _{j}^{4}\right )\right ] c_{14} \cos (6 \phi ) \right \} , \\ \frac{\partial ^{2} e}{\partial \lambda _{i} \partial \lambda _{j}} = & \; 4 c_{2}+12 \left (-\lambda _{i}^{2}+\lambda _{j}^{2}\right ) c_{3} \cos (6 \phi ) +4 \left (-2+\lambda _{i}^{2}+\lambda _{j}^{2}\right ) c_{6} \\ &+4 \left (-1+\lambda _{i}^{2}\right ) \left (-1+\lambda _{j}^{2}\right ) c_{8} + 3 \left (2-2 \lambda _{i}^{2}+\lambda _{i}^{4}-2 \lambda _{j}^{2}+ \lambda _{j}^{4}\right ) c_{9} \\ & +2 \left (-2+3 \lambda _{i}^{2}-3 \lambda _{i}^{4}+\lambda _{i}^{6}+3 \lambda _{j}^{2}-3 \lambda _{j}^{4}+ \lambda _{j}^{6}\right ) c_{11} \\ & + 3 \left (-1+\lambda _{i}^{2}\right ) \left (-1+\lambda _{j}^{2} \right ) \left (-2+\lambda _{i}^{2}+\lambda _{j}^{2}\right ) c_{12} \\ & -6 ( \lambda _{i}-\lambda _{j}) (\lambda _{i}+\lambda _{j}) \left (-2+ \lambda _{i}^{2}+\lambda _{j}^{2}\right ) c_{13} \cos (6 \phi ) \\ & - 6 (\lambda _{i}-\lambda _{j}) (\lambda _{i}+\lambda _{j}) \left [1+ \lambda _{i}^{4}-\lambda _{j}^{2}+\lambda _{j}^{4}-\lambda _{i}^{2} \left (1+\lambda _{j}^{2}\right )\right ] c_{14} \cos (6 \phi ) = \frac{\partial ^{2} e}{\partial \lambda _{j} \partial \lambda _{i}}, \end{aligned}$$

with $i,j = 1,2$ and $i \neq j$. The eigenvalue problem is then stated by writing the characteristic equation

$$ \det \left ( \mathbf{K} - \tau \mathbf{I} \right ) = \left (\tau - \frac{\partial ^{2} e}{\partial \lambda _{1}^{2}}\right ) \left ( \tau -\frac{\partial ^{2} e}{\partial \lambda _{2}^{2}}\right ) - \left ( \frac{\partial ^{2} e}{\partial \lambda _{1} \partial \lambda _{2}} \right )^{2} = 0, $$

whose solution provides the eigenvalues

$$ \tau _{1,2} = \frac{1}{2} \left \{ \frac{\partial ^{2} e}{\partial \lambda _{1}^{2}} + \frac{\partial ^{2} e}{\partial \lambda _{2}^{2}} \mp \left [4 \left ( \frac{\partial ^{2} e}{\partial \lambda _{1} \partial \lambda _{2}} \right )^{2} + \left ( \frac{\partial ^{2} e}{\partial \lambda _{1}^{2}}- \frac{\partial ^{2} e}{\partial \lambda _{2}^{2}}\right )^{2}\right ]^{\frac{1}{2}} \right \} . $$

(31)

An equilibrium configuration is stable if both eigenvalues $\tau _{1}$ and $\tau _{2}$ are positive. Neutrally stable configurations are found when $\tau _{1} = 0$ and $\tau _{2} > 0$. This condition marks the transition between stable and unstable regions.

7 Linearized Theory

In this section, the solutions derived for the finite elastic theory are linearized by introducing the hypothesis of small deformation field. Hereinafter, the components of the Green-Lagrange strain tensor $E_{1}$ and $E_{2}$ are replaced by symbols $\varepsilon _{1}$ and $\varepsilon _{2}$ respectively, while nominal stresses $s_{x}$ and $s_{y}$ with $\sigma _{x}$ and $\sigma _{y}$ respectively. This for the sole purpose of consistency with the common notation employed in linear elasticity.

From the definition of the Green-Lagrange strain tensor (8), the following relations between stretch and strain components are derived:

$$ \begin{aligned} \lambda _{1} = \sqrt{2 \varepsilon _{1} + 1}, \\ \lambda _{2} = \sqrt{2 \varepsilon _{2} + 1}, \end{aligned} $$

(32)

where we recall that $E_{1}$ and $E_{2}$ have been replaced by $\varepsilon _{1}$ and $\varepsilon _{2}$. The hypothesis of small deformation field allows to develop (32) in Taylor series in the variables $\varepsilon _{1}$ and $\varepsilon _{2}$, obtaining

$$ \begin{aligned} \lambda _{1} \simeq 1 + \varepsilon _{1}, \\ \lambda _{2} \simeq 1 + \varepsilon _{2}. \end{aligned} $$

(33)

Introducing (33) into (9) and (11), which give the expressions of the first Piola-Kirchhoff and the Cauchy stress tensors respectively, we obtain the following approximated form:

$$ \left [\mathbf{T}_{R}\right ] = \left [\mathbf{T}\right ] \simeq \begin{bmatrix} 2 c_{4} \varepsilon _{1} + c_{2} \varepsilon _{2} & 0 \\ 0 & c_{2} \varepsilon _{1} + 2 c_{4} \varepsilon _{2} \\ \end{bmatrix}. $$

This result shows that in the infinitesimal theory, as it is well known, the two stress measures coincide. Therefore, from now on in this section, tensor $\mathbf{T}$ is simply called stress tensor. Furthermore, we notice that the representation of the stress tensor in the principal strain system is diagonal. This indicates that in the linearized theory principal strain and stress directions coincide.

The linearization of boundary conditions (13) reduces to the following system of three scalar equations:⁴

$$ \begin{aligned} & \left (c_{2} + 2 c_{4}\right ) \left (\varepsilon _{1} + \varepsilon _{2}\right ) = \sigma _{x}+\sigma _{y}, \\ & \left (2 c_{4} - c_{2}\right ) \left (\varepsilon _{1} - \varepsilon _{2}\right ) \cos (2 \phi ) = \sigma _{x}-\sigma _{y}, \\ & 16 \sin (2 \phi ) \left (2 c_{4} - c_{2}\right ) \left ( \varepsilon _{1} - \varepsilon _{2}\right ) = 0, \end{aligned} $$

(34)

where we recall that $s_{x}$ and $s_{y}$ have been replaced by $\sigma _{x}$ and $\sigma _{y}$. With the intent of deriving expressions for the Young’s modulus and Poisson’s ratio of graphene, we consider the two uniaxial load cases along zigzag and armchair directions. In both cases, with the exception of the undeformed configuration, solutions exist only for $\varepsilon _{1} \neq \varepsilon _{2}$ and $\phi = 0$,⁵ which means that the first principal direction corresponds to the zigzag direction, allowing us to write $\varepsilon _{1} = \varepsilon _{x}$ and $\varepsilon _{2} = \varepsilon _{y}$. In light of the above, in case of zigzag uniaxial load ($\sigma _{y} = 0$), the solution of system (34) is

$$ \begin{aligned} \sigma _{x} & = \left (2 c_{4} - \frac{c_{2}^{2}}{2 c_{4}}\right ) \varepsilon _{x}, \\ \varepsilon _{y} & = - \frac{c_{2}}{2 c_{4}} \varepsilon _{x}. \end{aligned} $$

(35)

Considering, with $\sigma _{y} = 0$, the Navier’s inverse relationships $\sigma _{x} = E \varepsilon _{x}$ and $\varepsilon _{y} = - \nu \varepsilon _{x}$, the solution given in (35) allows us to write the expressions of Young’s modulus and Poisson’s ratio for graphene

$$ E = 2 c_{4} - \frac{c_{2}^{2}}{2 c_{4}}, \quad \nu = \frac{c_{2}}{2 c_{4}}. $$

(36)

The same result can be derived considering the case of armchair uniaxial load ($\sigma _{x} = 0$), for which the solution of system (34) is

$$ \begin{aligned} \sigma _{y} & = \left (2 c_{4} - \frac{c_{2}^{2}}{2 c_{4}}\right ) \varepsilon _{y}, \\ \varepsilon _{x} & = - \frac{c_{2}}{2 c_{4}} \varepsilon _{y}. \end{aligned} $$

(37)

Again, the Navier’s inverse relationships $\sigma _{y} = E \varepsilon _{y}$ and $\varepsilon _{x} = - \nu \varepsilon _{y}$ provide the expressions of Young’s modulus and Poisson’s ratio given in (36). The fact that both Young’s modulus and Poisson’s ratio along zigzag and armchair directions coincide demonstrates the isotropy of graphene for small deformations.

In case of equibiaxial loads $\sigma _{x} = \sigma _{y} = \sigma$, system (34) reduces to

$$ \begin{aligned} & \left (c_{2} + 2 c_{4}\right ) \left (\varepsilon _{1} + \varepsilon _{2}\right ) = 2 \sigma , \\ & \left (2 c_{4} - c_{2}\right ) \left (\varepsilon _{1} - \varepsilon _{2}\right ) \cos (2 \phi ) = 0, \\ & 16 \sin (2 \phi ) \left (2 c_{4} - c_{2}\right ) \left ( \varepsilon _{1} - \varepsilon _{2}\right ) = 0. \end{aligned} $$

(37)

Asymmetric solutions ($\varepsilon _{1} \neq \varepsilon _{2}$) are found only if $c_{2} = 2 c_{4}$, which obviously does not represent a general case, therefore it must not be considered. Hence, when the deformation is small, the case of equibiaxial loads admits only the symmetric solution ($\varepsilon _{x} = \varepsilon _{y} = \varepsilon$), for which system (37) gives

$$ \sigma = \left (c_{2} + 4 c_{4}\right ) \varepsilon . $$

(38)

Note that this solution corresponds to the classical linear elastic solution $\sigma = E \varepsilon /(1 - \nu )$ for membranes subjected to equibiaxial loads, with Young’s modulus $E$ and Poisson’s ratio $\nu$ given by (36).

8 Results

In this section, numerical solutions of the equilibrium equations are given for the cases of uniaxial loads (armchair and zigzag) and equibiaxial loads. Graphene is considered a two-dimensional material, thus the values of stress quantities are given with dimension of force over length. Coefficients $c_{1}$–$c_{14}$ of the stored energy function (3) were estimated in [20] by fitting the energy landscapes of graphene determined through DFT simulations for principal strains $E_{I}$ and $E_{II}$ ranging from −0.14 to 0.28 and for loading angles ranging from 0 to $\pi /6$. The resulting estimated parameters are listed in Table 1 and are considered in the present section.

Table 1 Fitting coefficients $c_{1}$–$c_{14}$ estimated by Höller et al. [20], which are valid for a Green-Lagrange strain range between −0.14 and $+0.28$. The physical unit of the coefficients is eV/Ų

8.1 Uniaxial Loads

The equilibrium equations for zigzag load, expressed by (16), and for armchair load, given by (18), are solved numerically with software Wolfram Mathematica [59] by increasing step by step a kinematic control parameter. In detail, for the case of zigzag uniaxial load, control parameter is $\lambda _{x}$ (or $\lambda _{1}$) with initial value 1 and final value 1.28, with an increasing step of $10^{-4}$. For each step, system (16) is solved using the FindRoot command, obtaining as solution the corresponding values of $\lambda _{y}$ and $s_{x}$. Likewise, $\lambda _{y}$ (or $\lambda _{2}$) is the control parameter of the armchair uniaxial load case, ranging from 1 to 1.28 with increasing step of $10^{-4}$. System (18) is solved with the same strategy and the solution is obtained in terms of $\lambda _{x}$ and $s_{y}$ values.

The resulting equilibrium paths along zigzag and armchair directions are depicted respectively in Figs. 2(a) and 2(b). In both cases we observe a softening behavior and we notice that for small deformations ($\lambda _{x} \simeq 1$ and $\lambda _{y} \simeq 1$) the two curves coincide, whereas for large deformations the effect of anisotropy arises. In fact, as already mentioned, anisotropy of graphene is contained in the third invariant of equation (1), which plays a role only when the deformation field is large. In particular, as also other authors reported (see, e.g., [14, 17, 35]), graphene is stronger along the zigzag direction.

Fig. 2

Equilibrium paths in terms of nominal stress vs. stretch for the uniaxial load cases (stable solutions: continuous lines, unstable solutions: dashed lines)

The stability of the equilibrium solutions is investigated by computing eigenvalues $\tau _{1}$ and $\tau _{2}$ from (31) with $\phi = 0$, because this is the only case for which equilibrium solutions for both the uniaxial load cases exist. A contour plot of the eigenvalues on $\lambda _{x}$–$\lambda _{y}$ plane is shown in Fig. 3. The green colored region satisfies the condition that both $\tau _{1}$ and $\tau _{2}$ are positive, therefore it represents the region of stability of the equilibrium configurations. The boundary of this region indicates the configurations of neutrally stable equilibrium, for which $\tau _{1} = 0$ and $\tau _{2} > 0$. The intersections of such boundary with the projection of the equilibrium paths on $\lambda _{x}$–$\lambda _{y}$ plane give the configurations at which the equilibrium loses its stability. These configurations are indicated in Figs. 3 and 2 with red and blue points for the zigzag and armchair uniaxial load cases, respectively.

Fig. 3

Projection of elastic stability region and equilibrium paths on $\lambda _{x}$–$\lambda _{y}$ plane for the uniaxial load cases. The boundary of the stable region represents the neutrally stable configurations and its intersections with the equilibrium paths (red and blue points) indicate the configurations at which the equilibrium loses its stability

The set of numerical solutions obtained for the uniaxial loads ($\lambda _{x}$, $\lambda _{y}$ and $s_{x}$ for zigzag load and $\lambda _{y}$, $\lambda _{x}$ and $s_{y}$ for armchair load) allows to compute the Poisson’s ratio of the graphene membrane as a function of the deformation, along both zigzag ($\nu _{xy}$) and armchair ($\nu _{yx}$) directions

$$ \nu _{xy} = \frac{1 - \lambda _{y}}{\lambda _{x} - 1}, \quad \nu _{yx} = \frac{1 - \lambda _{x}}{\lambda _{y} - 1}. $$

The trend of $\nu _{xy}$ and $\nu _{yx}$ with the increasing of uniaxial deformation are depicted in Figs. 4(a) and 4(b), respectively. The values of $\nu _{xy}$ and $\nu _{yx}$ in initial configuration coincide due to the isotropy of graphene for small deformations. The two curves deviate as the deformation increases. This is a consequence of the anisotropy for large deformations.

Fig. 4

Trend of Poisson’s ratio with the increasing of uniaxial deformation (stable solutions: continuous lines, unstable solutions: dashed lines)

Table 2 shows a comparison of the results presented in this work with other results available in the literature. The mechanical properties of graphene are usually given referring to the engineering strains $\epsilon _{x} = \lambda _{x} - 1$ and $\epsilon _{y} = \lambda _{y} - 1$. This notation is thus used in Table 2, with the purpose of providing a straightforward and comprehensible comparison.

Table 2 Uniaxial stress and strain at the limit configuration ($\epsilon _{x,\text{cr}} = \lambda _{x,\text{cr}} - 1$ and $\epsilon _{y,\text{cr}} = \lambda _{y,\text{cr}} - 1$) and comparison with other results available in the literature

The variability of the results given in Table 2 is due to different modeling strategies and interatomic potentials employed. As pointed out by Genoese et al. [16], the same potential with different sets of parameters may lead to sensible changes in the results. We observe that the values of $s_{x,\text{cr}}$ and $\epsilon _{x,\text{cr}}$ derived in this work are significantly underestimated with respect to the ones given in the experimental work of Lee et al. [28] and to many others in Table 2. Given the lack of experimental observation, it is hard to say which modeling strategy and potential are the best ones. However, we believe that the parametrization given in Table 1 can be adjusted in order to obtain a mechanical response of graphene that is more consistent with other works and especially with the experimental observation of [28]. A reparametrization of the stored energy function will be thus proposed in Sect. 9.

8.2 Equibiaxial Loads

The symmetric solution in case of equibiaxial loads is given in closed form by (20). Asymmetric solutions for $\phi = 0$ and $\phi = \pi /6$ are also admitted respectively as solutions of (21) and (22). These solutions are derived numerically with the same strategy described in the previous section. Namely, for $\phi = 0$ control parameter $\lambda _{1}$ is increased from initial value 1 to final value 1.28 with step $10^{-4}$, while for $\phi = \pi /6$ the same is done with control parameter $\lambda _{2}$. For each step, systems (21) and (22) are solved using the FindRoot command.

Figure 5 shows the projection of the equilibrium paths on $\lambda _{1}$–$\lambda _{2}$ plane. Only the symmetric solution is found until the critical configuration characterized by $\lambda _{\text{cr}} = 1.1808$ and $s_{\text{cr}} = 38.063$ nN/nm. At this point, bifurcation instability takes place and the two asymmetric solutions are observed.

Fig. 5

Projection of elastic stability regions with $\phi = 0$ and $\phi = \pi /6$ and equilibrium paths on $\lambda _{1}$–$\lambda _{2}$ plane for the case of equibiaxial loads. The symmetric solution loses its stability after the configuration indicated with the orange point and asymmetric solutions appear

The elastic stability regions of Fig. 5 are obtained by computing eigenvalues $\tau _{1}$ and $\tau _{2}$ from (31) for the limit cases of $\phi = 0$ and $\phi = \pi /6$. The boundaries of the two stable regions intersect in correspondence of the bifurcation point, after which the symmetric solution is unstable. Namely, when a perturbation is applied and $s > s_{\text{cr}}$, the square membrane abandons the symmetric path and it randomly transforms into one of the two possible asymmetric configurations, becoming a rectangle. As depicted in the zoom of Fig. 5, the asymmetric solutions with $\phi = 0$ and $\phi = \pi /6$ are stable only for a very small range of deformation. When the curves intersect the boundaries of the corresponding stability regions, the solutions become unstable, as represented by the red and blue points in Fig. 5. Given the very small region where such solutions are stable, it is hard to say if it is even possible to observe them in a real experiment.

The equilibrium path of the symmetric solution in the plane $\lambda$–$s$ is represented in Fig. 6. We notice that, when equibiaxial loads are applied to the graphene membrane, the limit value of load $s_{\text{max}} = 38.754$ nN/nm is not reached by the system because a bifurcation instability occurs at the critical load $s_{\text{cr}} = 38.063$ nN/nm. Asymmetric solutions appear in correspondence of the critical load, as shown in the three-dimensional representation of the equilibrium paths given in Fig. 7. The stretch corresponding to the critical configuration is $\lambda _{\text{cr}} = 1.1808$.

Fig. 6

Representation of the symmetric solution in case of equibiaxial loads in the plane $\lambda$–$s$ (stable solutions: continuous lines, unstable solutions: dashed lines)

Fig. 7

Three-dimensional view of the equilibrium paths for equibiaxial loads: after bifurcation, asymmetric solutions for $\phi = 0$ and $\phi = \pi /6$ are found (stable solutions: continuous lines, unstable solutions: dashed lines)

The solution of the boundary-value problem (19) allowed thus to conclude that, when equibiaxial loads are applied to graphene, the solution is unique and symmetric until the critical configuration ($\lambda _{\text{cr}}$, $s_{\text{cr}}$). Asymmetric solutions take place and they are stable only for a very small range of deformation. The most interesting result is that the strength of graphene subjected to equibiaxial loads is not given by the limit value $s_{\text{max}}$. The stability analysis revealed that this configuration is never observed, because bifurcation instability occurs at a previous critical configuration, where the equilibrium along the symmetric path loses its stability.

A final remark is related to the critical value $s_{\text{cr}} = 38.063$ nN/nm experienced by graphene under equibiaxial loads. As reported in the previous section, the critical configurations in case of uniaxial loads are characterized by $s_{x,{\text{cr}}} = 36.07$ nN/nm and $s_{y,{\text{cr}}} = 34.01$ nN/nm. We observe that $s_{\text{cr}}$ is higher than both $s_{x,{\text{cr}}}$ and $s_{y,{\text{cr}}}$. However, it is unlikely that the graphene membrane exhibits an ultimate strength $s_{\text{cr}}$ for equibiaxial loads that is higher than the uniaxial strength in zigzag direction $s_{x,{\text{cr}}}$, along which it is well known that graphene shows the highest strength. In fact, the case of equibiaxial loads was analyzed also by other authors through MM simulations (see, e.g, [13, 35]), obtaining a value of $s_{\text{cr}}$ always less than $s_{x,{\text{cr}}}$. It goes without saying that there is still lack of results and experiments for graphene subjected to equibiaxial loads, but the fact that the parametrization of Table 1 leads to this unlikely outcome points out once again the need for a reparametrization of the stored energy function.

8.3 Elastic Constants of Graphene

Numerical values of Young’s modulus and Poisson’s ratio are computed from (36) by using the values of coefficients $c_{2}$ and $c_{4}$ given in Table 1, obtaining $E = 341.81$ nN/nm and $\nu = 0.177$. A comparison with the elastic constants given by other studies is reported in Table 3. Although different methods and potentials are employed in the literature, the results show a quite good agreement.

Table 3 Comparison of Young’s modulus and Poisson’s ratio with previous studies in the literature

9 Reparametrization of the Stored Energy Function

As pointed out in Sect. 8.1, the limit values of $s_{x}$ and $\epsilon _{x}$ derived with the parametrization of Table 1 are significantly underestimated with respect to the experimental results given by Lee et al. [28]. In general, underestimation of the limit values of both $s_{x}$ and $s_{y}$ is also found with respect to other MM simulations (see Table 2). For this reason, in this section we propose a new parametrization of coefficients $c_{1}$–$c_{14}$, which gives results that are more consistent with experimental observation and other models found in the literature.

Firstly, parameters $c_{2}$ and $c_{4}$ are adjusted to obtain certain values of Young’s modulus and Poisson’s ratio. For the Young’s modulus we considered the value $E = 333.54$ nN/nm as the most reliable, which is given by the experiment carried out through atomic force microscope by Lee et al. [28]. For the Poisson’s ratio the value considered is $\nu = 0.159$, given by Chang and Gao [8]. This because it is obtained with a very effective stick-and-spring approach that makes use of simple harmonic potentials with parameters that have a clear physical meaning and, in linear elasticity, have been often considered reliable for predictions of elastic properties of graphene [32, 47, 60]. The coefficients $c_{2}$ and $c_{4}$ that give such values of $E$ and $\nu$ are computed using (36) and are reported in Table 4.

Table 4 Values of fitting coefficients $c_{1}$–$c_{14}$ after the reparametrization of the stored energy function. The physical unit of the coefficients is eV/Ų

The other parameters are collected into parameter vector $\mathbf{p} = [c_{3} \ c_{5} \ c_{6} \ c_{7} \ c_{8} \ c_{9} \ c_{10} \ c_{11} \ c_{12} \ c_{13} \ c_{14}]^{T}$ and their values are estimated by performing a nonlinear constrained optimization with function fmincon in the software MATLAB [9]. The optimization is performed in order to obtain critical configurations ($\epsilon _{x,\text{cr}}$, $s_{x, \text{cr}}$) and ($\epsilon _{y,\text{cr}}$, $s_{y,\text{cr}}$) that are as close as possible to the ones considered most reliable, on the basis of the information available from other works found in the literature. In particular, for the zigzag uniaxial load, the critical values assumed as goal of the optimization are the ones given by Lee et al. [28] through experimental tests ($\epsilon _{x, \text{cr}} = 0.25$ and $s_{x,\text{cr}} = 43.55$ nN/nm, see Table 2). For the armchair uniaxial load, reliable experimental results were not found. Thus, the goal of the optimization are the values computed by Genoese et al. [17] through MM simulations ($\epsilon _{y,\text{cr}} = 0.192$ and $s_{y,\text{cr}} = 34.80$ nN/nm, see Table 2). This because in the work by Genoese et al. [17] a modified Morse potential was employed, with a parametrization that was adjusted on the basis of a thorough analysis of the most recent atomistic simulations for graphene. It goes without saying that this is a decision based on the information available, which does not guarantee that this result is the most accurate. However, the reliability of MM simulations with modified Morse potential is supported by many authors (see, e.g., [5, 18, 35, 52]).

The optimization in MATLAB is performed as a single-objective optimization with nonlinear constraints. In detail, the relations between uniaxial stress and stretch for the cases of zigzag and armchair loads, expressed by (16)₁ and (18)₁ respectively, are written in a MATLAB function and will be refferred as $s_{x} (\lambda _{1}, \lambda _{2}, \mathbf{p})$ and $s_{y} (\lambda _{1}, \lambda _{2}, \mathbf{p})$. The following objective function is then defined:

$$ \text{obj}(\mathbf{p}) = \sqrt{\left ( s_{x,\text{cr}} - \max _{ \lambda _{1}} s_{x} (\lambda _{1}, \lambda _{2}, \mathbf{p}) \right )^{2} + \left ( s_{y,\text{cr}} - \max _{\lambda _{2}} s_{y} (\lambda _{1}, \lambda _{2}, \mathbf{p}) \right )^{2}}, $$

(38)

where $s_{x,\text{cr}} = 43.55$ nN/nm and $s_{y,\text{cr}} = 34.80$ nN/nm are the goal values. The implicit relations between stretches $\lambda _{1}$ and $\lambda _{2}$, expressed by (16)₂ and (18)₂, are introduced as nonlinear constraints in another MATLAB function. In order to achieve also the goal values of deformations $\epsilon _{x,\text{cr}} = 0.25$ $(\lambda _{x,\text{cr}} = 1.25)$ and $\epsilon _{y,\text{cr}} = 0.192$ $(\lambda _{y,\text{cr}} = 1.192)$, the following lower and upper bounds for the stretches are defined: $\lambda _{1} \in \left [ 1.24, 1.26 \right ]$ for zigzag load and $\lambda _{2} \in \left [ 1.18, 1.20 \right ]$ for armchair load. In this way, the objective function (38) allows to obtain the goal values of stress in correspondence of stretches that range in intervals close to $\epsilon _{x,\text{cr}}$ and $\epsilon _{y,\text{cr}}$. Meanwhile, the implicit relations between stretches are satisfied through the nonlinear constraints.

Parameter vector $\mathbf{p}$ contains eleven parameters to be optimized under only two nonlinear constraints. Therefore, the optimization problem described above does not admit a unique solution. The optimization was thus guided by defining as initial guess the coefficients given by Höller et al. [20] (see Table 1). As a result, the best fitting parameters estimated through optimization are listed in Table 4. The corresponding equilibrium paths along zigzag and armchair directions are depicted respectively in Figs. 8(a) and 8(b). We notice that, with the new set of coefficients $c_{1}$–$c_{14}$, the critical values of stress along both directions coincide with the goal values of the optimization. The stretch $\lambda _{x,\text{cr}} = 1.252$ is also very close to the one given by Lee et al. [28]. Larger gap is observed between $\lambda _{y,\text{cr}} = 1.200$ and the corresponding value 1.192 given by Genoese et al. [17]. However, as previously pointed out, it is not sure that such value is the most accurate, especially because it does not derive from experimental observation. Therefore, the results provided by the optimized set of coefficients are still considered reliable.

Fig. 8

Equilibrium paths for the uniaxial load cases after reparametrization of the stored energy function (stable solutions: continuous lines, unstable solutions: dashed lines)

The trend of Poisson’s ratio with the increasing of deformation is shown in Fig. 9. As expected, the initial value $\nu = 0.159$ provided by the new values of coefficients $c_{2}$ and $c_{4}$ corresponds to the one proposed by Chang and Gao [8].

Fig. 9

Poisson’s ratio with the increasing of uniaxial deformation after reparametrization of the stored energy function (stable solutions: continuous lines, unstable solutions: dashed lines)

The symmetric solution in case of equibiaxial loads obtained with the new parametrization of the stored energy function is shown in Fig. 10. We observe that the limit value of load $s_{\text{max}} = 44.297$ nN/nm can not be reached because a bifurcation instability occurs at the critical load $s_{\text{cr}} = 42.908$ nN/nm. The zoom of Fig. 11 shows that the asymmetric solutions with $\phi = 0$ and $\phi = \pi /6$ are stable for a small range of deformation.

Fig. 10

Representation of the symmetric solution in case of equibiaxial loads in the plane $\lambda$–$s$, obtained after reparametrization of the stored energy function (stable solutions: continuous lines, unstable solutions: dashed lines)

Fig. 11

Three-dimensional view of the equilibrium paths for equibiaxial loads after reparametrization of the stored energy function: after bifurcation, asymmetric solutions for $\phi = 0$ and $\phi = \pi /6$ are found (stable solutions: continuous lines, unstable solutions: dashed lines)

Compared to the result obtained with the parametrization proposed by Höller et al. [20] (Fig. 7), the asymmetric solutions are stable for a larger part of the equilibrium paths. This shows that the region of stability of the asymmetric solutions depends on the values of coefficients $c_{1}$–$c_{14}$ assumed for the stored energy function. As far as we know, there is still no experimental evidence of this behavior in case of graphene membranes subjected to equibiaxial loads. Hence, the information available do not allow to guarantee that such solutions can actually be observed. However, the results obtained for uniaxial loads with the new parametrization show good agreement with the ones found in the literature that are considered most reliable. A more thorough and comprehensive optimization of the parameters of the stored energy function can be carried out when new experimental data will be available.

10 Conclusions

This paper presented a formulation for equilibrium and stability of graphene membranes in the fully nonlinear context of finite elasticity. The solutions were derived under the assumption of homogeneous deformations. An anisotropic form of stored energy function was considered, from which the expressions of Piola-Kirchhoff and Cauchy stress tensors were obtained. Consequently, the boundary-value problem was formulated and the stability of the equilibrium configurations was investigated through an energy criterion. The finite theory was linearized by introducing the hypothesis of small deformation field. The expressions of Young’s modulus and Poisson’s ratio of graphene were obtained.

In previous works on hyperelastic graphene membranes [20, 25], the authors limited their analysis to the derivation of strain and stress quantities. However, a complete characterization of the mechanics of graphene requires a solution of the boundary-value problem. In fact, the solutions proposed in this work revealed unexpected behaviors that were not observed in previous works in the literature. Explicit relations between stretches and stresses of the membrane were derived for the cases of uniaxial loads along zigzag and armchair directions and for equibiaxial loads. It was discovered that graphene subjected to equibiaxial loads experiences bifurcation and asymmetric solutions appear other than the symmetric one.

The results were put in comparison with those given by other works found in the literature. In general, an underestimation of the mechanical properties was found. It was therefore decided to propose a reparametrization of the coefficients of the stored energy function. This allowed to obtain a mechanical behavior of graphene as close as possible to the one considered most reliable, with particular regard to the experimental investigation carried out by Lee et al. [28].

The formulation proposed in this work may be the basis for reliable models in the growing field of structural mechanics of graphene.