A Peridynamic Model of Fracture Mechanics with Bond-Breaking

Abstract

We present a new formulation of a peridynamic model for brittle fracture that incorporates a properly defined bond-breaking rule which leads to a dynamic system of time-dependent differential integral equations having both spatial nonlocal/nonlinear interactions and temporal memory/history dependence. The dynamic system is shown to be well-posed through rigorous mathematical analysis. Its effectiveness in simulating crack propagation in a two dimensional brittle material is also demonstrated.

1 Introduction

Peridynamic models initially proposed by Silling [1] are reformulations of classical continuum mechanics that allow a natural treatment of discontinuities by replacing spatial derivatives of stress tensors with integrals of force density functions. Although more refined models, such as [3, 9], have been proposed in the literature, the models proposed by Silling [1] are simple enough for the purpose of mathematical analysis in this work and are still physically meaningful. Many numerical simulations based on the peridynamic theory have been carried out thereafter [2, 4–8]. Some related mathematical analysis can be found [10–20].

While a large part of the existing mathematical work on peridynamics has been on linear models, a few recent studies have touched upon the rigorous mathematical theory of nonlinear models [17–19, 21]. In this paper, we present rigorous results on the existence, uniqueness and continuous dependence on the initial data of solutions to the nonlinear peridynamic model with a properly defined bond-breaking rule. The basic idea is to properly reformulate the model equation into a functional dynamic system and then apply the standard Picard type iterations well documented in, for example, [27–29]. Numerical simulations of crack propagation and convergence studies are also presented.

The peridynamic model studied here is a closely related variant of those studied numerically in [7] and [4, 22]. However, modifications are introduced to the original models to provide well-defined mathematical equations while preserving the necessary physics. From the dynamic system point of view, it is natural to make such modifications in order to have a coherent dependence of the bond forces on the history. Our work is new in terms of the following aspects. First, unlike earlier works [18, 19] where they consider small deformation, we do not impose such limitations in the model formulation. Secondly, rather than assuming the Lipschitz continuity of the pairwise force density function as in [17, 21], we attempt to work with the original nonlinear pairwise force density function in the peridynamic simulations presented by many authors in the literature and demonstrate how the Lipschitz continuity can be established with suitable modifications of the force factor. Thirdly, we explicitly incorporate the irreversibility of bond breaking, which has been mostly ignored in the mathematical analysis of peridynamic models except in [21]. We note that our treatment of bond-breaking rule is different from that used in [21] and requires minimal changes from the popular bond-breaking rule used in earlier numerical simulations of crack propagation [4, 7, 22]. The rigorous mathematical theorems on the well-posedness of resulting equations and the illustration of total energy decay are key contributions of this work. Meanwhile, numerical simulations are carried out and they serve several purposes. For example, they offer demonstrations on how to mathematically impose inhomogeneous traction loading conditions properly in the numerical simulations of nonlocal models like peridynamics, which is an interesting and important practical issue. Moreover, numerical convergence can be observed in the test cases and the simulations also illustrate the effectiveness of the well-posed peridynamic models for crack propagation. In particular, they are able to capture propagation and branching patterns that are consistent to those presented in earlier simulations.

The rest of the paper is organized as follows. In Sect. 2, we present a commonly used peridynamic model with a bond-breaking rule, and introduce some desirable modifications to retain the same essential physics while making the rule more adapted to careful mathematical analysis presented in Sect. 3. Section 4 presents simulation results, followed by further discussions in Sect. 5.

2 Peridynamic Models with Bond-Breaking

Studies on nonlocal peridynamic models that involve bond-breaking rules have been mostly limited to numerical simulations. Mathematically, they are nonlinear time-dependent integro-differential equations with both spatial nonlocal and nonlinear interactions and temporal memory and history dependence. Here, we describe the common practice in existing numerical simulations and explain our reformulation that allows us to demonstrate the well-posedness of the nonlinear dynamic models.

2.1 A Bond-Based Peridynamic Model for Prototype Microelastic Brittle Materials

We note first that the more recent development of peridynamics has largely been under the framework of state-based peridynamics. Nevertheless, bond-based peridynamic theory has played an important role in the historical development, in particular, on the earlier numerical studies of fracture and damage. Moreover, the study of bond-based peridynamic models offers valuable insight into the more general models. Let us briefly recall a common practice in formulating peridynamic models with bond-breaking rules for brittle fractures [4, 7]. For convenience, this has often been viewed as a model for prototype microelastic brittle (PMB) materials.

Let $\mathbf{u}=\mathbf{u}(t,\mathbf{x})$ denote the displacement field and $\rho$ be the constant density, the bond-based peridynamic equation of motion is given by an integro-differential equation of the form

$$ \rho \ddot{\mathbf{u}}(t,\mathbf{x})= \int_{B_{\delta }(\mathbf{x})} \mathbf{f}\bigl(t,\mathbf{u}(t, \hat{\mathbf{x}})- \mathbf{u}(t, \mathbf{x}), \hat{\mathbf{x}}-\mathbf{x}\bigr) d\hat{\mathbf{x}}+ \mathbf{b} (t, \mathbf{x}) , $$

(1)

where $\mathbf{b}=\mathbf{b} (t, \mathbf{x})$ denotes the body force, and $\mathbf{f}$ is the pairwise force density. When the bond-breaking rule is incorporated, the force density $\mathbf{f}$ also takes on history dependence, so the dynamic system is in fact a distributed system of spatially nonlocal functional differential equations. The constitutive model, previously used in the peridynamic model for PMB materials [23], is defined as follows:

$$ \mathbf{f}\bigl(t,\boldsymbol{\eta }(t),\boldsymbol{\xi }\bigr)= \left \{ \textstyle\begin{array}{l@{\quad }l} \omega_{\delta }(|\boldsymbol{\xi }|) \mathcal{S}(\boldsymbol{\eta }(t), \boldsymbol{\xi }) \mathbf{e}(\boldsymbol{\eta }(t),\boldsymbol{\xi }), & \text{if } \mathcal{S}( \boldsymbol{\eta }(s), \boldsymbol{\xi })< \mathcal{S}_{c} \text{ for all } 0\leq s \leq t , \\ 0, &\text{otherwise}, \end{array}\displaystyle \right . $$

(2)

where $\boldsymbol{\eta }(t)$ and $\boldsymbol{\xi }$ are used to denote $\mathbf{u}(t, \hat{\mathbf{x}})-\mathbf{u}(t,\mathbf{x})$ and $\hat{\mathbf{x}}- \mathbf{x}$ respectively (see Fig. 1), and $\mathcal{S}_{c}>0$ represents the critical value of bond breaking that is determined by the specific material under consideration. The unit vector $\mathbf{e}$ for bond direction and the bond relative elongation (stretch) $\mathcal{S}$ are given by

$$ \mathbf{e}(\boldsymbol{\eta },\boldsymbol{\xi })=\frac{\boldsymbol{\eta }+\boldsymbol{\xi }}{| \boldsymbol{\eta }+\boldsymbol{\xi }|} \quad \text{and }\quad \mathcal{S}( \boldsymbol{\eta }, \boldsymbol{\xi })= \frac{|\boldsymbol{\eta }+\boldsymbol{\xi }|- |\boldsymbol{\xi }|}{ |\boldsymbol{\xi }|} . $$

(3)

Fig. 1

Undeformed bond and deformed bond

The kernel function $\omega_{\delta }$ is assumed to be compactly supported. In particular,

$$ \omega_{\delta }(|\boldsymbol{\xi }|) =0 \quad \text{if } |\boldsymbol{\xi }|>\delta , $$

with the constant $\delta >0$ representing the horizon parameter measuring the range of nonlocal interaction. An additional assumption on $\omega_{\delta }$ used in this paper is that

$$ \int \frac{\omega_{\delta }(|\boldsymbol{\xi }|)}{|\boldsymbol{\xi }|} d\boldsymbol{\xi }< \infty . $$

(4)

Remark 1

Note that, for kernels with compact support, in order to have a consistent notion of elastic modulus for a small linear displacement field, a condition less stringent than (4) only requires $\omega_{\delta }(|\boldsymbol{\xi }|)|\boldsymbol{\xi }|$ being integrable. However, for all of the popular kernels used in the literature, (4) is always satisfied. The case involving more general kernels could be of mathematical interest and be studied in the future.

Remark 2

In this work, we either take $\delta$ as a finite constant or let $\delta =\infty$. The study of the limiting case as $\delta \to 0$ is also an interesting subject, which remains to be explored. We note similar studies on the linear models in [16, 24] and on a nonlinear model in [18].

2.2 A New Mathematical Formulation

For the peridynamic model of the PMB material discussed earlier, we reformulate the original form via a rigorously defined mathematical relation where the force density $\mathbf{f}$ is specified by a single scalar equation given by

$$ \mathbf{f}(t, \mathbf{x},\hat{\mathbf{x}},\mathbf{u})= \omega_{\delta }(|\boldsymbol{\xi }|) f( \mathcal{S}(t,\mathbf{x},\hat{ \mathbf{x}}, \mathbf{u}) \mu \bigl(\mathcal{S}^{\ast }(t,\mathbf{x},\hat{ \mathbf{x}}, \mathbf{u})\bigr) \mathbf{e}(t,\mathbf{x},\hat{\mathbf{x}}, \mathbf{u}) . $$

(5)

We note that in the notations $\mathbf{f}$, $\mathcal{S}$, $\mathcal{S}^{\ast }$ and $\mathbf{e}$ above, their arguments have been modified from the earlier ones involving $\boldsymbol{\eta }=\boldsymbol{\eta }(t)$ and $\boldsymbol{\xi }$ to show the explicit dependence on the time $t$, particle positions $\hat{\mathbf{x}}$ and $\mathbf{x}$ as well as the displacement field $\mathbf{u}$. It is important to note the dependence of $\mathbf{f}$ on the history of $\mathbf{u}$. Indeed, $\mathcal{S} ^{\ast }$ is defined as

$$ \mathcal{S}^{\ast }(t,\mathbf{x},\hat{\mathbf{x}},\mathbf{u})= \max _{0\leq s\leq t} \mathcal{S}(s,\mathbf{x},\hat{\mathbf{x}}, \mathbf{u}) . $$

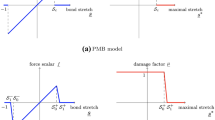
For this reason, several additional functions are introduced in the above force density formulation to make the definition more precise. In particular, $f$ and $\mu$ are two scalar functions associated with the specific types of constitutive relations. For example, in [25], $f$ is called the bond force or pairwise force function and $\mu$ is called the damage factor. For brevity, we name $f$ the force scalar. For the original peridynamic model of PMB materials studied in the literature, the forms of $f$ and $\mu$ are given by

$$ f(x)= \left \{ \textstyle\begin{array}{l@{\quad }l} x, & \text{if } x\in (-1,\mathcal{S}_{c}), \\ 0, & \text{elsewhere} \end{array}\displaystyle \right . \quad \text{and}\quad \mu (x)= \left \{ \textstyle\begin{array}{l@{\quad }l} 1, & \text{if } x\in (-\infty ,\mathcal{S}_{c}), \\ 0, & \text{if } x\in (\mathcal{S}_{c}, \infty ), \end{array}\displaystyle \right . $$

and they may be visualized in Fig. 2.

Fig. 2

Force scalar and damage factor in the original peridynamic model of PMB materials

Remark 3

The equation of motion presented in our simpler setting corresponds to the original PD system in the special case that the force scalar $f$ is given by $f(x)= \mu (x) x$ where $\mu (x)=\chi_{[-1, \mathcal{S}_{c})}(x)$. We note that neither $\mathcal{S}$ nor $\mathcal{S}^{\ast }$ is less than −1 by definition.

Remark 4

While we take $\mathcal{S}^{\ast }$ to be the maximum bond stretch before time $t$, [21] has adopted a different regularization where the damage factor is a function of the time integral of the positive part of $\mathcal{S}-\mathcal{S}_{c}$ so that a time-accumulated effect exists in the model. Following the studies in [4, 7], the new regularization adopted in this work does not introduce such accumulated effects over time.

We now introduce some modifications to $f$ and $\mu$ in order to have desired continuous history dependence of the force field, which could be a physically sensible feature as well. To this end, we define some constant parameters

$$ -1< \mathcal{S}^{-}_{1}< \mathcal{S}^{-}_{0} < 0\leq \mathcal{S}^{+} _{0}< \mathcal{S}^{+}_{1}< \infty , $$

and scalar functions $f, \mu \in C([-1,\infty ])$ such that

$$ f(x)= \left \{ \textstyle\begin{array}{l@{\quad }l} \mathcal{S}^{-}_{0} \frac{x-\mathcal{S}^{-}_{1}}{\mathcal{S}^{-}_{0}- \mathcal{S}^{-}_{1}}, &\text{if } x\in (\mathcal{S}^{-}_{1}, \mathcal{S}^{-}_{0}), \\ x, &\text{if } x\in [\mathcal{S}^{-} _{0}, \mathcal{S}^{+}_{0}], \\ \mathcal{S}^{+}_{0}\frac{\mathcal{S} ^{+}_{1}-x}{\mathcal{S}^{+}_{1}-\mathcal{S}^{+}_{0}}, &\text{if } x \in (\mathcal{S}^{+}_{0},\mathcal{S}^{+}_{1} ), \\ 0, & \text{elsewhere}, \end{array}\displaystyle \right . \quad \text{and}\quad \mu (x)=\left \{ \textstyle\begin{array}{l@{\quad }l} 1, &\text{if } x\in [-1,\mathcal{S}^{+}_{0}), \\ \frac{ \mathcal{S}^{+}_{1}-x}{\mathcal{S}^{+}_{1}-\mathcal{S}^{+}_{0}}, &\text{if } x\in [\mathcal{S}^{+}_{0}, \mathcal{S}^{+}_{1}], \\ 0, &\text{if } x\in (\mathcal{S}^{+}_{1}, \infty ). \end{array}\displaystyle \right . $$

(6)

A pictorial illustration of $f$ and $\mu$ is shown in Fig. 3. Physically speaking, the definition allows the weakening of force scalar within small ranges of excessive bond stretch values. Similarly, partial failure is also allowed when the bond stretch is very close to the critical value. An important observation is the following proposition whose proof is elementary and thus omitted.

Fig. 3

Modified force scalar and damage factor

Proposition 1

$f$ and $\mu$ are uniformly bounded and uniformly Lipschitz continuous.

Some remarks on the choices of the parameters $\mathcal{S}^{-}_{1}, \mathcal{S}^{-}_{0} , \mathcal{S}^{+}_{0}$ and $\mathcal{S}^{+}_{1}$ are given below.

Remark 5

$\mathcal{S}^{+}_{0}$ and $\mathcal{S}^{+}_{1}$ can be any two positive constants that satisfy $\mathcal{S}^{+}_{1}- \mathcal{S}^{+}_{0} >0$. The critical stretch value $\mathcal{S}_{c}$ is in the interval $[ \mathcal{S}^{+}_{0}, \mathcal{S}^{+}_{1}]$. The original relations in [4, 7] can be seen as a limiting case where $\mathcal{S}^{+}_{1}=\mathcal{S}_{c}=\mathcal{S}^{+}_{0}$.

Remark 6

$\mathcal{S}^{-}_{1}$ and $\mathcal{S}^{-}_{0}$ can be any two negative constants that are larger than −1 and $\mathcal{S}^{-}_{0}- \mathcal{S}^{-}_{1}>0$. These parameters are introduced to avoid the complication due to potential material penetration. Indeed, the use of the unit vector $\mathbf{e}$ for the force orientation can be problematic when it flips sign as two distinct material points collapse.

We note in addition that the modifications to the force scalar $f$ not only offer mathematical rigor and convenience but also make little impact on the application of peridynamic models. This is because that for simulations given here and most of the existing peridynamic based numerical simulations of crack initiation and growth for brittle materials, the set-up usually involves a tensile loading and the relative stretch never reaches a negative value close to −1. This means that the modifications made for $f$ close to −1 would never take effect so that the reformulated force field is in fact consistent with those employed in earlier experiments. In general, however, constitutive relations may need to be modified near −1 to incorporate contact forces with broken bonds, and to allow for either unbounded forces or kinematic condition as discussed in [26] when there is no broken bond. This remains an interesting issue to be studied further in future works.

3 Well-Posedness of the Peridynamic Model

We now develop the mathematical theory for the well-posedness of solutions to (7) in this section. Again, the force scalar and damage factor are given by (6) and the kernel $\omega_{\delta }$ satisfies (4). The main approach is to adopt a distributed (and spatially nonlocal) functional differential system formulation of (7). Then, the standard theory for abstract dynamic systems, such as that discussed in classical texts on the subject like [27–29], can be applied.

3.1 Problem Set-up

Assume that the material occupies an open domain $\Omega \subset \mathbb{R}^{d}$ and $T>0$ represents a terminal time of interest. Let $\Omega_{\mathcal{I}}$ be a nonlocal interaction domain, which is a notion introduced in [13] for nonlocal models to account for the nonlocal effect in the presence of physical boundary. Namely, any essential constraints on the displacement field would need to be imposed over the domain $\Omega_{\mathcal{I}}$. Without loss of generality, we let the constant density $\rho$ be normalized so that $\rho =1$ can be taken to simplify the notation. For the displacement field $\mathbf{u}$ defined on $\Omega \cup \Omega_{\mathcal{I}}$ and a given body force $\mathbf{b} =\mathbf{b}(t,\mathbf{x})$, we then consider the peridynamic equations defined on $\Omega$, namely, for $\mathbf{x}\in \Omega , \ t\in [0,T]$,

$$ \left \{ \begin{aligned} & \ddot{\mathbf{u}}(t, \mathbf{x})= \int_{\Omega \cup \Omega_{\mathcal{I}}} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| ) f\bigl( \mathcal{S}( t, \mathbf{x}, \hat{\mathbf{x}}, \mathbf{u})\bigr) \mu \bigl(\mathcal{S}^{\ast }(t, \mathbf{x}, \hat{\mathbf{x}}, \mathbf{u})\bigr) \mathbf{e}(t, \mathbf{x}, \hat{\mathbf{x}}, \mathbf{u})d\hat{\mathbf{x}}+ \mathbf{b} (t, \mathbf{x}) , \\ &\mathbf{u}(0,\mathbf{x})=\mathbf{w}(\mathbf{x}),\qquad \dot{\mathbf{u}}(0, \mathbf{x})=\mathbf{v}(\mathbf{x}),\qquad \mathbf{u}(t, \cdot )|_{\Omega_{\mathcal{I}}}=0 . \end{aligned} \right . $$

(7)

We note that both Cauchy problems (initial-value problems, or IVP) and initial-nonlocal-boundary value problems (InBVP) can be proposed for (7). Specifically, we let

$$ \Omega_{\delta }=\bigl\{ x\in \mathbb{R}^{d}\backslash \Omega , \text{dist}(x,\partial \Omega )< \delta \bigr\} $$

denote a layer around $\Omega$, and we list the different types of problems below with different choices of $\Omega$ and $\Omega_{\mathcal{I}}$ (see Fig. 4 for an illustration).

$$ \left \{ \textstyle\begin{array}{l@{\quad }l} \text{Cauchy problem:}& \Omega =\mathbb{R}^{d}, \Omega_{ \mathcal{I}}=\emptyset , \\ \text{Dirichlet InBVP:} & \Omega \text{ open and bounded}, \Omega_{\mathcal{I}}=\Omega_{\delta } , \\ \text{Neumann InBVP:} & \Omega \text{ open and bounded}, \Omega_{\mathcal{I}}=\emptyset , \\ \text{Mixed InBVP:} & \Omega \text{ open and bounded}, \emptyset \neq \Omega_{\mathcal{I}}\subsetneq \Omega_{\delta } . \end{array}\displaystyle \right . $$

Fig. 4

A domain $\Omega$ with different $\Omega _{\mathcal{I}}$: $\Omega _{\mathcal{I}}=\Omega _{\delta }$ (left), $\Omega _{\mathcal{I}}=\emptyset$ (center), $\emptyset \neq \Omega _{\mathcal{I}}\subsetneq \Omega _{\delta }$ (right)

Note that for notation simplicity, the nonlocal Dirichlet and Neumann boundary problems that we consider here are both given with homogenous boundary data. Nonlocal inhomogeneous boundary conditions are also possible and they do not cause essential difficulty in the mathematical proofs. In fact, we use nonlocal inhomogeneous Neumann boundary conditions in Sect. 4 when performing numerical simulations. Further discussions of inhomogeneous Neumann data are given in Sect. 5 since this is an important practical issue.

Now, let $X=(L^{\infty }_{0}(\Omega ))^{d}$, where $L^{\infty }_{0}( \Omega )$ denotes functions in $L^{\infty }(\Omega )$ with zero value outside $\Omega$. The well-posedness study is done for solutions that are in the space $C^{2}([0,T], X)$. First, we make a convention to extend functions defined on the time interval $[0, T)$ identically by their values at time 0 to the interval $[-T,0]$, i.e., it remains unchanged in time. Thus any solution at time less than zero is treated as the same as its definition at time zero. For any $\mathbf{u}\in C([0,T], X)$ and any $t\in [0,T]$, we denote by $\mathbf{u}_{t} \in C([-T,0], X)$ a time shift described by $\mathbf{u}_{t}(\theta , \cdot )=\mathbf{u}(t+\theta ,\cdot )$ for $\theta \in [-T,0]$. The notation $\mathbf{u}_{t}$ is a common usage in the context of functional differential equations [27, 28]. It should not be confused with the notion of differentiation in time. For derivatives with respect to time $t$, we adopt in this paper the dot notation $\dot{\mathbf{u}}$ as often the case in the mathematical formulations of equations in continuum mechanics.

3.2 A Nonlinear Map

We define a nonlinear map $\mathbf{F}: C([-T,0], X)\to X$ given by

$$ \mathbf{F}(\boldsymbol{\phi }) = \int_{B_{\delta }(x)} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| ) f\bigl( \mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi })\bigr) \mu \bigl(\mathcal{S}^{\ast }(0,\mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{ \phi })\bigr) \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi })d \hat{\mathbf{x}} , $$

(8)

where

$$ \left \{ \begin{aligned} \mathcal{S}(\tau , \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{ \psi }) &:=\frac{| \boldsymbol{\psi }(\tau ,\hat{\mathbf{x}})-\boldsymbol{\psi }(\tau ,\mathbf{x})+ \hat{\mathbf{x}}-\mathbf{x}|- |\hat{\mathbf{x}}-\mathbf{x}|}{| \hat{\mathbf{x}}-\mathbf{x}|} , \\ \mathcal{S}^{\ast }(\tau , \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })&:=\max_{\tau -T\leq t\leq \tau }\frac{|\boldsymbol{\psi }(t,\hat{\mathbf{x}})-\boldsymbol{\psi }(t,\mathbf{x})+ \hat{\mathbf{x}}-\mathbf{x}|- |\hat{\mathbf{x}}-\mathbf{x}|}{| \hat{\mathbf{x}}-\mathbf{x}|} , \\ \mathbf{e}(\tau , \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })&:= \frac{\boldsymbol{\psi }(\tau , \hat{\mathbf{x}})-\boldsymbol{\psi }(\tau ,\mathbf{x})+\hat{\mathbf{x}}- \mathbf{x}}{|\boldsymbol{\psi }(\tau ,\hat{\mathbf{x}})-\boldsymbol{\psi }(\tau , \mathbf{x})+\hat{\mathbf{x}}-\mathbf{x}|} . \end{aligned} \right . $$

(9)

Lemma 1

The nonlinear map $\mathbf{F}$ is uniformly bounded and uniformly Lipschitz continuous, namely, there exist positive constants $L$ and $\tilde{L}$, such that for any $\boldsymbol{\phi },\boldsymbol{\psi }\in C([-T,0], X)$, we have

$$\begin{aligned} & \| \mathbf{F}(\boldsymbol{\phi }) -\mathbf{F}(\boldsymbol{\psi }) \|_{X}\leq L \| \boldsymbol{\phi }-\boldsymbol{\psi }\|_{C([-T,0], X)} , \end{aligned}$$

(10)

$$\begin{aligned} &\| \mathbf{F}(\boldsymbol{\phi })\|_{X}\leq \tilde{L}\| \boldsymbol{\phi}\|_{C([-T,0],X)} . \end{aligned}$$

(11)

Proof

From the boundedness and Lipschitz continuity of $f$ and $\mu$, we immediately get (11) by using that the kernel $\omega_{\delta }$ is integrable due to its compact support and the assumption (4). Furthermore, we have

$$ \begin{aligned} &\big\| \mathbf{F}(\boldsymbol{\phi })-\mathbf{F}( \boldsymbol{\psi })\big\| _{X} \\ &\quad \leq \bigg\| \int_{B_{\delta }(\mathbf{x})} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| ) (f\bigl( \mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi }) \bigr)\\ &\quad \quad {}-f\bigl( \mathcal{S}(0,\mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) \bigr) \mu \bigl(\mathcal{S}^{\ast }(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi })\bigr) \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{ \phi }) d\hat{\mathbf{x}} \bigg\| _{X} \\ &\quad \quad {} + \bigg\| \int_{B_{\delta }(\mathbf{x})} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| )f\bigl(\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })\bigr) ( \mu \bigl( \mathcal{S}^{\ast }(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{ \phi })\bigr)\\ &\quad \quad {}-\mu \bigl( \mathcal{S}^{\ast }(0, \mathbf{x}, \hat{ \mathbf{x}}, \boldsymbol{\psi }) \bigr) \mathbf{e}( 0, \mathbf{x}, \hat{ \mathbf{x}}, \boldsymbol{\phi })d\hat{\mathbf{x}} \bigg\| _{X} \\ &\quad \quad {} + \bigg\| \int_{B_{\delta }(\mathbf{x})} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| )f\bigl(\mathcal{S}(0,\mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })\bigr)\mu ( \mathcal{S}^{\ast }(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) \bigl( \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi })\\ &\quad \quad {} - \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) \bigr) d\hat{ \mathbf{x}} \bigg\| _{X} \\ &\quad \leq C_{1} \bigg\| \int_{B_{\delta }(\mathbf{x})} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| ) |\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi })- \mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) | d\hat{ \mathbf{x}} \bigg\| _{L^{ \infty }(\Omega )} \\ &\quad \quad {}+ C_{2} \bigg\| \int_{B_{\delta }(\mathbf{x})} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| ) | \mathcal{S}^{\ast }(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi }) - \mathcal{S}^{\ast }(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) | d\hat{\mathbf{x}} \bigg\| _{L^{\infty }(\Omega )} \\ &\quad \quad {}+ \bigg\| \int_{B_{\delta }(\mathbf{x})} \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| ) f\bigl(\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })\bigr) | \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi }) - \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) | d\hat{\mathbf{x}} \bigg\| _{L^{ \infty }(\Omega )} \\ & \quad := \mathrm{I} + \mathrm{II} + \mathrm{III} . \end{aligned} $$

Now for the first term I in the above, since

$$ \begin{aligned} &|\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi })-\mathcal{S}(0, \mathbf{x},\hat{\mathbf{x}}, \boldsymbol{\psi }) | \\&\quad = \frac{ | |\boldsymbol{\phi }(0, \hat{\mathbf{x}})-\boldsymbol{\phi }(0,\mathbf{x})+\hat{\mathbf{x}}- \mathbf{x}|-|\boldsymbol{\psi }(0,\hat{\mathbf{x}})-\boldsymbol{\psi }(0,\mathbf{x})+ \hat{\mathbf{x}}-\mathbf{x}| |}{|\hat{\mathbf{x}}- \mathbf{x}|} \\ &\quad \leq \frac{ | \boldsymbol{\phi }(0,\hat{\mathbf{x}})-\boldsymbol{\phi }(0, \mathbf{x})-(\boldsymbol{\psi }(0,\hat{\mathbf{x}})-\boldsymbol{\psi }(0,\mathbf{x})) |}{|\hat{\mathbf{x}}- \mathbf{x}|} , \end{aligned} $$

we have

$$ \begin{aligned} \mathrm{I}&\leq C_{1} \mathop{\mathrm{ess sup}}_{\mathbf{x}\in \Omega } \int_{B_{\delta }(\mathbf{x})} \frac{\omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| )}{|\hat{\mathbf{x}}-\mathbf{x}|} | ( \boldsymbol{\phi }- \boldsymbol{\psi }) (0, \hat{\mathbf{x}})-(\boldsymbol{\phi }-\boldsymbol{\psi }) (0, \mathbf{x}) | d\hat{\mathbf{x}} \\ &\leq C_{1}\mathop{\mathrm{ess sup}}_{\mathbf{x}\in \Omega } \biggl\{ \mathop{ \mathrm{ess sup}}_{\mathbf{z}\in \Omega \cup \Omega_{ \delta }} |(\boldsymbol{\phi }-\boldsymbol{\psi }) (0, \mathbf{z})-(\boldsymbol{\phi }- \boldsymbol{\psi }) (0,\mathbf{x}) | \int_{B_{\delta }(\mathbf{x})}\frac{ \omega_{\delta }(|\hat{\mathbf{x}}-\mathbf{x}| )}{|\hat{\mathbf{x}}- \mathbf{x}|}d\hat{\mathbf{x}} \biggr\} \\ &\leq C \mathop{\mathrm{ess sup}}_{x\in \Omega } |(\boldsymbol{\phi }- \boldsymbol{\psi }) (0,\mathbf{x}) | \leq \tilde{C} \| \boldsymbol{\phi }- \boldsymbol{\psi }\|_{C([-T,0], X)} . \end{aligned} $$

The second term II can be estimated similarly by noticing that

$$ \begin{aligned} |\mathcal{S}^{\ast }(0, \mathbf{x}, \hat{ \mathbf{x}}, \boldsymbol{\phi })- \mathcal{S}^{\ast }(0, \mathbf{x},\hat{ \mathbf{x}}, \boldsymbol{\psi }) | &= \max_{-T\leq t\leq 0} \frac{ |(\boldsymbol{\phi }-\boldsymbol{\psi })(t, \hat{\mathbf{x}})-(\boldsymbol{\phi }-\boldsymbol{\psi })(t,\mathbf{x}) |}{| \hat{\mathbf{x}}- \mathbf{x}|} . \end{aligned} $$

Thus,

$$ \begin{aligned} \text{II}&\leq C_{2}\mathop{\mathrm{ess sup}}_{\mathbf{x}\in \Omega } \int_{B_{\delta }(x)} \frac{\omega_{\delta }(|\hat{\mathbf{x}}- \mathbf{x}| )}{|\hat{\mathbf{x}}-\mathbf{x}|} \max_{-T\leq t\leq 0} |( \boldsymbol{\phi }-\boldsymbol{\psi }) (t, \hat{\mathbf{x}})-(\boldsymbol{\phi }- \boldsymbol{\psi }) (t,\mathbf{x}) | d\hat{\mathbf{x}} \\ &\leq C_{2} \mathop{\mathrm{ess sup}}_{\mathbf{x}\in \Omega } \biggl\{ \mathop{ \mathrm{ess sup}}_{\mathbf{z}\in \Omega \cup \Omega_{\delta }} \max_{-T\leq t\leq 0} |(\boldsymbol{\phi }-\boldsymbol{\psi }) (t, \mathbf{z})-(\boldsymbol{\phi }-\boldsymbol{\psi }) (t, \mathbf{x}) | \int_{B_{\delta }(\mathbf{x})} \frac{\omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}| )}{|\hat{\mathbf{x}}-\mathbf{x}| } d \hat{\mathbf{x}} \biggr\} \\ & \leq C \mathop{\mathrm{ess sup}}_{\mathbf{x}\in \Omega } \max_{-T\leq t\leq 0} |(\boldsymbol{\phi }-\boldsymbol{\psi }) (t, \mathbf{x}) | = \tilde{C} \| \boldsymbol{\phi }-\boldsymbol{\psi }\|_{C([-T,0], X)} . \end{aligned} $$

Now we only need to estimate the term III. To do so, we note first that if $\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })< \mathcal{S}^{-}_{1}$, then by definition we have $f(\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }))=0$. Since in this case there is no contribution from $\text{III}$, we only need to focus on the case where $\mathcal{S}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi })\geq \mathcal{S}^{-}_{1}$, which implies that

$$ \frac{|\boldsymbol{\psi }(0,\hat{\mathbf{x}})-\boldsymbol{\psi }(0,\mathbf{x})+ \hat{\mathbf{x}}-\mathbf{x}|}{|\hat{\mathbf{x}}-\mathbf{x}|}\geq 1+ \mathcal{S}^{-}_{1}>0 . $$

Let $\boldsymbol{\alpha }=\boldsymbol{\phi }(0,\hat{\mathbf{x}})-\boldsymbol{\phi }(0, \mathbf{x})+\hat{\mathbf{x}}-\mathbf{x}$, $\boldsymbol{\beta }=\boldsymbol{\psi }(0, \hat{\mathbf{x}})-\boldsymbol{\psi }(0,\mathbf{x})+\hat{\mathbf{x}}- \mathbf{x}$, then,

$$ \begin{aligned} & | \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\phi }) - \mathbf{e}(0, \mathbf{x}, \hat{\mathbf{x}}, \boldsymbol{\psi }) | = \biggl\vert \frac{ \boldsymbol{\alpha }|\boldsymbol{\beta }|- \boldsymbol{\beta }|\boldsymbol{\alpha }|}{|\boldsymbol{\alpha }| | \boldsymbol{\beta }| } \biggr\vert \leq \biggl\vert \frac{\boldsymbol{\alpha }(|\boldsymbol{\beta }|-| \boldsymbol{\alpha }|)}{|\boldsymbol{\alpha }||\boldsymbol{\beta }|} \biggr\vert + \biggl\vert \frac{| \boldsymbol{\alpha }| (\boldsymbol{\alpha }-\boldsymbol{\beta })}{|\boldsymbol{\alpha }| |\boldsymbol{\beta }| } \biggr\vert \\ & \quad \leq 2\frac{|\boldsymbol{\alpha }-\boldsymbol{\beta }|}{|\boldsymbol{\beta }|} = 2\frac{|( \boldsymbol{\phi }-\boldsymbol{\psi })(0, \hat{\mathbf{x}})-(\boldsymbol{\phi }-\boldsymbol{\psi })(0, \mathbf{x})| }{|\boldsymbol{\psi }(0,\hat{\mathbf{x}})-\boldsymbol{\psi }(0, \mathbf{x})+\hat{\mathbf{x}}-\mathbf{x}|} \\ & \quad \leq \frac{2}{1+\mathcal{S}^{-}_{1}} \frac{|(\boldsymbol{\phi }-\boldsymbol{\psi })(0, \hat{\mathbf{x}})-(\boldsymbol{\phi }-\boldsymbol{\psi })(0,\mathbf{x})| }{| \hat{\mathbf{x}}-\mathbf{x}|} . \end{aligned} $$

Therefore, we get the estimate

$$ \text{III}\leq \tilde{C} \| \boldsymbol{\phi }-\boldsymbol{\psi } \|_{C([-T,0], X)} , $$

by using arguments similar to those made for the term $\text{I}$. Putting all the estimates together, we get the desired result (10). □

3.3 Well-Posedness Theorems

By the definition of $\mathbf{F}$, the equations of motion under consideration can be written as

$$ \ddot{\mathbf{u}}(t, \mathbf{x})=\mathbf{F}(\mathbf{u}_{t}) + \mathbf{b} (t, \mathbf{x}) . $$

We may transform the second-order-in-time equation to a first order system by denoting

$$ U= \begin{bmatrix} \mathbf{u} \\ \mathbf{v} \end{bmatrix} = \begin{bmatrix} \mathbf{u} \\ \dot{\mathbf{u}} \end{bmatrix} ,\qquad U_{t}= \begin{bmatrix} \mathbf{u}_{t} \\ \mathbf{v}_{t} \end{bmatrix} , \qquad G(t,U_{t}) = \begin{bmatrix} \mathbf{v}_{t}(0) \\ \mathbf{F}(\mathbf{u}_{t}) + \mathbf{b} (t, \mathbf{x}) \end{bmatrix} = \begin{bmatrix} \dot{\mathbf{u}} \\ \mathbf{F}(\mathbf{u}_{t}) +\mathbf{b} (t, \mathbf{x}) \end{bmatrix} , $$

where by convention $(\dot{\mathbf{u}})_{t} (\theta ,\cdot )= \dot{\mathbf{u}}(t+\theta ,\cdot )$ and in particular $( \dot{\mathbf{u}})_{t} (0)=\dot{\mathbf{u}}(t)$. Then the second-order-in-time equation is equivalent to the following first order distributed (and spatially nonlocal) dynamic system:

$$ \dot{U}=G(t, U_{t}) , $$

which, due to the history dependence, may be viewed as a functional differential system. The initial values of $\mathbf{u}$ may be translated into that of $U$, so do the nonlocal boundary conditions, if any.

Now let us denote the space $Y=(L^{\infty }_{0}(\Omega ))^{d\times 2}$. Similar to the result presented in Lemma 1, and with a given $\mathbf{b}(t,\mathbf{x})\in C([0,T],X)$, a simple exercise shows that for any $\Phi$ and $\Psi$ in $C([-T,0],Y)$,

$$ \| G(t, \Phi )-G(t,\Psi )\|_{Y}\leq L \| \Phi - \Psi \|_{C([-T,0],Y)} , \quad \mbox{and} \quad \| G(s, \Phi )\|_{Y}\leq \bar{L}+ \|\Phi \|_{C([-T,0],Y)} , $$

for some generic uniform constants $L>0$ and $\bar{L}>0$.

This leads to one of the key theorems of the paper.

Theorem 2

Well-posedness of the nonlocal dynamic system

Assume that $W\in Y$ and $\mathbf{b}(t,\mathbf{x})\in C([0,T],X)$, then there exists a unique solution $U\in C([0,T], Y)$ that satisfies the following integral form of the nonlocal dynamic system:

$$ \left \{ \begin{aligned} &U(t)= \int_{0}^{t} G(s, U_{s})ds+W , \\ & U_{0}(\theta )\equiv W \quad (-T\leq \theta \leq 0) . \end{aligned} \right . $$

(12)

Proof

Let us define an iteration in $C([0,T],X)$ by

$$ U^{0}(t)\equiv W, \qquad U^{n}(t)= \int_{0}^{t} G\bigl(s, U^{n-1}_{s} \bigr)ds+W . $$

Since $G$ is uniformly bounded and globally Lipschitz continuous, this then leads to the standard Picard iteration. Indeed, we easily see from the following estimates for any $t\in [0, T]$,

$$ \|U^{1}(t) - U^{0}(t)\|_{Y}\leq M t, \quad \mbox{and} \quad \|U^{n}(t) - U^{n-1}(t)\|_{Y}\leq M L^{n-1}\frac{t^{n}}{n!} ,\quad \forall n>1, $$

that $\{ U^{n}\}$ is a Cauchy sequence in $C([0,T], Y)$ with the limit $U$ satisfying the desired dynamic system. The uniqueness follows from standard comparison argument. We note that these arguments are exactly the same standard techniques presented in classical analysis of dynamic systems, see for instance, [27–29] for more discussions. □

Now we link the solutions to integral forms of the model with solutions to the more conventional functional differential equation form.

Lemma 2

Let $W\in Y$ and $\mathbf{b}(t,\mathbf{x})\in C([0,T],X)$. Then the solution $U\in C([0,T], Y)$ to the integral equation (12) is the solution to the following functional differential equation with $U\in C^{1}([0,T],Y)$.

$$ \left \{ \begin{aligned} &\frac{dU}{dt} =G(t,U_{t}), && t\in (0, T), \\ & U_{0}(\theta ) \equiv W, && (-T\leq \theta \leq 0). \end{aligned} \right . $$

(13)

Proof

By definition, we have

$$ \frac{U(t+h)-U(t)}{h} -G(t,U_{t})= \frac{1}{h} \int_{t}^{t+h} G(s, U _{s})-G(t,U_{t})ds . $$

Since

$$ \begin{aligned} \| G(s, U_{s})-G(t,U_{t}) \|_{Y} &\leq \| G(s, U_{s})-G(t,U_{s}) \|_{Y} + \| G(t, U_{s})-G(t,U_{t}) \|_{Y} \\ &\leq C_{1}+C_{2} \| U_{s}- U_{t} \|_{C([-T,0],Y)} \\ &\leq C_{1}+\tilde{C}_{2} \| U\|_{C([0,T], Y)}\leq C , \end{aligned} $$

then

$$ \lim_{h\to 0} \| \frac{U(t+h)-U(t)}{h} -G(t,U_{t}) \|_{Y} \to 0 . $$

So $\frac{dU}{dt}=G(t,U_{t})\in C([0,T],Y)$. □

Combing the above arguments, we arrive at the following theorem of the peridynamic system, which is our main theoretical result.

Theorem 3

With initial data $\mathbf{w}\in X, \mathbf{v}\in X$ and forcing term $\mathbf{b}(t,\mathbf{x})\in C([0,T], X)$, there exists a unique solution $\mathbf{u}\in C^{2}([0,T], X)$ to the system (7).

Proof

This follows immediately from Theorem 2 and Lemma 2. □

By the similar argument as in the uniqueness proof, one may also derive easily the continuous dependence of the solution on data (initial condition and body force). In summary, the well-posedness of the peridynamic model is established.

3.4 Energy Decay

Now let us assume that the external force does not change with respect to time, namely $\mathbf{b}(t,\mathbf{x})=\mathbf{b}(\mathbf{x})$, we define the total energy of the system (7) to be

$$\begin{aligned} E(t) =& \frac{1}{2} \int_{\Omega \cup \Omega_{\mathcal{I}}} \int_{\Omega \cup \Omega_{\mathcal{I}}} |\hat{\mathbf{x}}-\mathbf{x}| \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}|) p\bigl(\mathcal{S}(t, \mathbf{x},\hat{\mathbf{x}}, \mathbf{u})\bigr) \mu \bigl(\mathcal{S}^{\ast }(t, \mathbf{x},\hat{ \mathbf{x}},\mathbf{u})\bigr) d\hat{\mathbf{x}}d\mathbf{x} \\ &{} +\frac{1}{2} \int_{\Omega }|\dot{\mathbf{u}}(t, \mathbf{x})|^{2} d \mathbf{x}- \int_{\Omega }\boldsymbol{\mathbf{u}}(t,\mathbf{x})\cdot \mathbf{b}( \mathbf{x}) d\mathbf{x} , \end{aligned}$$

(14)

which consists of the contributions from the stored nonlocal elastic energy, kinetic energy and the work done by external force. Here $p$ is the antiderivative of the force scalar function $f$. More specifically, we can let $p(0)=0$ and $p^{\prime }(x)=f(x)$. By the definition of $f$ in (6), we can see that $p(x)\geq 0$ for any $x$. See Fig. 5 for a sketch of $p(x)$.

Fig. 5

Sketch of $p(x)$. $p^{\prime }(x)=f(x)$, $p(0)=0$

Then we have the following result on the non-increasing property of the total energy over time.

Theorem 4

(Energy decay)

The total energy of the system (7) is nonincreasing in time, namely,

$$ \frac{d E(t)}{dt}\leq 0 . $$

Proof

$$\begin{aligned} \frac{d E(t)}{dt} =& \int_{\Omega }\dot{\mathbf{u}}(t, \mathbf{x}) \cdot \ddot{ \mathbf{u}}(t, \mathbf{x}) \ d\mathbf{x}- \int_{\Omega } \dot{\mathbf{u}}(t, \mathbf{x}) \cdot \mathbf{b}( \mathbf{x}) \ d \mathbf{x} \\ &{}- \int_{\Omega \cup \Omega_{\mathcal{I}}} \int_{\Omega \cup \Omega_{\mathcal{I}}}\omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}|) f(\mathcal{S}) \mu \bigl(\mathcal{S}^{\ast }\bigr) \mathbf{e}\cdot \dot{ \mathbf{u}}(t,\mathbf{x})d\hat{\mathbf{x}}d \mathbf{x} \\ &{}+\frac{1}{2} \int_{\Omega \cup \Omega_{\mathcal{I}}} \int_{\Omega \cup \Omega_{\mathcal{I}}}|\hat{\mathbf{x}}-\mathbf{x}| \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}|) p\bigl(\mathcal{S}(t, \mathbf{x},\hat{\mathbf{x}}, \mathbf{u})\bigr) \frac{d \mu (\mathcal{S}^{ \ast }(t,\mathbf{x},\hat{\mathbf{x}},\mathbf{u})) }{dt}d \hat{\mathbf{x}}d\mathbf{x} \\ = &\frac{1}{2} \int_{\Omega \cup \Omega_{\mathcal{I}}} \int_{\Omega \cup \Omega_{\mathcal{I}}}|\hat{\mathbf{x}}-\mathbf{x}| \omega_{\delta }(| \hat{\mathbf{x}}-\mathbf{x}|) p\bigl(\mathcal{S}(t, \mathbf{x},\hat{\mathbf{x}}, \mathbf{u})\bigr) \frac{d \mu (\mathcal{S}^{ \ast }(t,\mathbf{x},\hat{\mathbf{x}},\mathbf{u})) }{dt}d \hat{\mathbf{x}}d\mathbf{x} . \end{aligned}$$

Now by the definition of $\mathcal{S}^{\ast }(t,\mathbf{x}, \hat{\mathbf{x}},\mathbf{u})$, the maximum value of all $\mathcal{S}(s, \mathbf{x},\hat{\mathbf{x}},\mathbf{u})$ for $s\in [0,t]$, we know that $\mathcal{S}^{\ast }$ is increasing with time. Since $\mu$ is a nonincreasing function, we have

$$ \frac{d \mu (\mathcal{S}^{\ast }(t,\mathbf{x},\hat{\mathbf{x}}, \mathbf{u})) }{dt} \leq 0, $$

in the weak sense. Thus the theorem is proved by noticing that $p(x)\geq 0$. □

The energy decay property provides some stability to the peridynamic equation and makes the dynamic system consistent with the laws of thermodynamics. We note that due to the presence of bond-breaking, it is not expected that the energy given by (14) remains constant. The energy naturally transfers to broken bonds when singularities develop.

4 Numerical Simulations

In this section, we present a set of numerical experiments to demonstrate the effectiveness of the new peridynamic model when applied to the numerical simulations of dynamic brittle fracture. For comparison purposes, we mainly focus on the crack branching process in a model of soda-lime glass as documented in [22].

4.1 Discretization

The numerical solution to nonlocal peridynamic models has been a popular research subject. Various methods have been implemented including particle/meshfree discretization, finite difference and finite element methods as well as Fourier spectral methods (for spatially periodic problems). We refer to [30] for a brief review. We note that in recent works on the numerical analysis of nonlocal models, the notion of asymptotically compatible schemes has played an important role so as to obtain a consistent and convergent discretization of the nonlocal continuum equations even in the local limit as the horizon approaches zero [31, 32]. However, in this work, we only focus on solving peridynamic models with a fixed horizon. We therefore adopt a more popular quadrature based discretization developed in [23, 33]. For the integrals in (1), the discretization uses a midpoint quadrature rule. We denote by $\mathbf{x}_{i}$ (the reference position of the node $i$) and $V_{i}$ (the nodal volume of the node $i$) the quadrature point and weight respectively. The spatially discrete dynamic systems are then given by

$$ \rho \ddot{\mathbf{u}}_{i}=\sum_{j\in \mathcal{F}_{i}} \mathbf{f}_{ij} V_{j}^{(i)} +\mathbf{b}_{i}, $$

where $\mathbf{f}_{ij}$ denotes the discrete pairwise force function as defined by (5) and (6). For time discretization of the dynamic system, we use the standard Velocity Verlet scheme. As in [22], we use the 2D conical micromodulus as the nonlocal interaction kernel:

$$ \omega_{\delta }(|\boldsymbol{\xi }|)=\frac{24E}{\pi \delta^{3}(1-\nu )} \biggl( 1- \frac{|\boldsymbol{\xi }|}{\delta } \biggr) , $$

where $E$ is Young’s modulus and $\nu$ is Poisson ratio (fixed to 1/3 in this 2D plane stress case). It is easy to see that in 2D, the above defined $\omega_{\delta }$ satisfies (4) so our mathematical theory does apply. For the conical micromodulus function, the critical relative elongation used in the original PMB model is given by

$$ \mathcal{S}_{c}=\sqrt{\frac{5\pi G_{0}}{9E\delta }} , $$

where $G_{0}$ is the material fracture energy. In our simulations, $\mathcal{S}_{1}^{-}$ and $\mathcal{S}_{0}^{-}$ are simply set to be −0.99 and −0.98 respectively, which are thought to be close enough to −1 so that it will not affect bond breaking when the bonds are in compression. Indeed, we see from the simulations that making them closer to −1 do not change the solution at all. Meanwhile, we consider several choices of $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$ as they get closer together and the results will be discussed in more details later. We also use the algorithms stated in [22] to approximate the nodal areas covered by the horizon and to compute the conical micromodulus function.

4.2 Modeling Dynamic Fracture of Soda-Lime Glass

Similar to the problem setup in [22], let us consider a central-crack thin rectangular plate of dimensions $10~\mbox{cm}\times 4~\mbox{cm}$ (see Fig. 6). Along the top and bottom edges a spatially uniform and constant-in-time tensile load $\sigma$ is applied. The implementation details for such a loading boundary condition will be given later. The material used here is the soda-lime glass with its elastic and fracture properties given in Table 1. Rather than the Poisson ratio 0.22, we note that the corresponding 2D bond-based peridynamic model takes on a Poisson ratio 1/3.

Fig. 6

Two-dimensional rectangular pre-cracked plate under traction loading

Table 1 Material and model parameters for the crack propagation simulation in Fig. 6

In [22], loading traction boundary conditions are imposed on a single layer of discrete nodal points by the upper and lower boundary edge, which is a practice that may lead to some issues as the mesh get refined, see [34] for more extensive discussions. The more suitable and mathematically rigorous approach, which is implemented in our experiments here, is to impose “Neumann”-type nonlocal boundary conditions through a body force $\mathbf{b}=\mathbf{b}(t, \mathbf{x})$ on a $\delta$-layer inside the boundary edges, or discretely, on $m$ layers of nodal points near the boundary where $m$ is the ratio between horizon and mesh size: $m=\delta /h$. In [34], it is demonstrated that this is a nonlocal analogue of local Neumann boundary conditions. Initially in discretization, if a node, indexed by $n_{i}$, is close to the upper boundary with a distance less than $\delta$, then the traction on this node is defined as

$$ \mathbf{b}(n_{i})=\frac{\sigma \cdot \Delta x}{m\cdot V(n_{i})}\boldsymbol{e} , $$

where $\boldsymbol{e}$ is the unit vector pointing up, i.e. $\boldsymbol{e}=(0,1)$, $\Delta x$ is the grid spacing in the $x$-direction and $V(n_{i})$ is the area of the node $n_{i}$ covered by the horizon of the current node. Similarly, if the node is close enough to the lower boundary, that traction on this node is computed by the same formula but in an opposite direction $-\boldsymbol{e}$.

4.3 Crack Branching in Soda-Lime Glass

We first perform an experiment to see how the cracks propagate subject to different loading amplitudes. A uniform grid spacing, namely $\Delta x=\Delta y=h$ is used. We choose the tensile load $\sigma$ to be 0.2 MPa, 2 MPa and 4 MPa respectively. The results in terms of the damage maps with a horizon of $\delta =1~\mbox{mm}$ and a sufficiently small time stepping $\Delta t=0.02~\upmu \mbox{s}$ are shown in Fig. 7. In this example we choose $\mathcal{S}_{0}^{+}=0.95 \mathcal{S}_{c}$ and $\mathcal{S}_{1}^{+}=1.05 \mathcal{S}_{c}$ first. To assure the numerical accuracy of all of our reported simulation results, we focus on the propagation of the pre-existing central crack and the first branching process. We stop the time evolution roughly around the time of a secondary crack branching. Reliable simulations after such a point in time are feasible but demand much higher numerical resolution, which is beyond the scope of this work.

Fig. 7

Damage index maps (or crack paths) computed with different amplitudes. From top to bottom: (a) $\sigma =0.2~\mbox{MPa}$ at 150 μs; (b) $\sigma =2~\mbox{MPa}$ at 43 μs; (c) $\sigma =4~\mbox{MPa}$ at 20 μs

The damage index $\phi$ for a node is a number between 0 and 1 whose definition is given by

$$ \phi (\boldsymbol{x},t)=1-\frac{ \int_{B_{\delta }(\mathbf{x})} \mu dV_{\hat{\mathbf{x}}} }{ \int_{B_{\delta }(\mathbf{x})} dV_{\hat{\mathbf{x}}} } , $$

where $\mu$ is the modified damage factor as defined by (6). We plot the damage index $\phi$ (using a threshold of 0.4 to highlight the damage area and crack path) in Fig. 7. By comparing the results in Fig. 7 with that in [22, Fig. 5], we can see that our new model does not alter the damage maps much for all the different loading amplitudes.

We now discuss the effect of the choice of $\mathcal{S}_{0}^{+}=0.95 \mathcal{S}_{c}$ and $\mathcal{S}_{1}^{+}=1.05 \mathcal{S}_{c}$ on the simulation results. In fact, the crack profile has little change when we make perturbations to values $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$. Figure 8 presents the damage index maps with three sets of values to demonstrate the numerical convergence as $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$ go to $\mathcal{S}_{c}$. In order to see the convergence more quantitatively, we look into the displacement fields and damage indices at the final time step. We compute the differences between the solutions of $\{\mathcal{S}_{0}^{+},\mathcal{S}_{1}^{+}\}=\{0.85\mathcal{S}_{c},1.15 \mathcal{S}_{c}\}$, $\{0.9\mathcal{S}_{c},1.1\mathcal{S}_{c}\}$ and $\{0.95\mathcal{S}_{c},1.05\mathcal{S}_{c}\}$ and the solution of $\{\mathcal{S}_{0}^{+},\mathcal{S}_{1}^{+}\}=\{0.98\mathcal{S}_{c},1.02 \mathcal{S}_{c}\}$ in the $L^{2}$ norm. We denote by $\{e_{i}^{x}, e _{i}^{y}, e_{i}^{p}, i=1, 2, 3\}$ these norms of the differences in the components of the displacement field in the $x$-direction and the $y$-direction, and the damage index respectively. In Table 2, we present the differences at the final time $t=43~\upmu \mbox{s}$. The results imply that the errors are relatively quite small and the convergence is evident as both $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$ go to $\mathcal{S}_{c}$. Based on this observation, in the remaining experiments, we retain the choice of $\mathcal{S}_{0}^{+}=0.95 \mathcal{S}_{c}$ and $\mathcal{S}_{1}^{+}=1.05 \mathcal{S}_{c}$.

Fig. 8

Damage index maps (or crack paths) computed with different $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$ for $\delta =1~\mbox{mm}$, $m=4$ and $\sigma =2~\mbox{MPa}$ at $43~\upmu \mbox{s}$. From top to bottom: (a) $\mathcal{S}_{0}^{+}=0.85 \mathcal{S}_{c}$ and $\mathcal{S}_{1}^{+}=1.15 \mathcal{S}_{c}$; (b) $\mathcal{S}_{0}^{+}=0.9 \mathcal{S}_{c}$ and $\mathcal{S}_{1}^{+}=1.1 \mathcal{S}_{c}$; (c) $\mathcal{S}_{0}^{+}=0.98 \mathcal{S}_{c}$ and $\mathcal{S}_{1}^{+}=1.02 \mathcal{S}_{c}$

Table 2 Differences between displacements and damage indices computed with different $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$ for $\delta=1~\mbox{mm}$, $m=4$ and $\sigma=42~\mbox{MPa}$ at 43 μs, showing convergence as $\mathcal{S}_{0}^{+}$ and $\mathcal{S}_{1}^{+}$ go to $\mathcal{S}_{c}$

Let us next conduct a numerical convergence test, which is important but has not been carefully performed in the literature especially for crack growth simulations. The convergence is checked by refining meshes with a fixed horizon ($\delta =1~\mbox{mm}$) and a constant loading amplitude ($\sigma =4~\mbox{MPa}$). We refine the spatial mesh by taking the ratio between horizon and mesh size to be $m=2$, 3, 6 and 12. The case $m=1$ is also performed but it produces nonphysical results and is thus discarded. We take a sufficiently small time step $\Delta t=0.02~\upmu \mbox{s}$ to assure that the time-integration error is negligible. Figure 9 shows the damage maps and plots of energies with different values of $m$, where Ep and Ek denote the potential and kinetic energy respectively, and Total ME is the total energy $E(t)$ defined in (14). From the figure we can see that the total energy is a nonincreasing function over time which has been shown in Theorem 4. Moreover, Fig. 10 also shows convergence results with mesh refinement where the plots of strain energy density (in logarithmic scale) are given at the final time. From Fig. 9 and Fig. 10, the convergence can be visually observed.

Fig. 9

Damage index maps (or crack paths) and energies computed with different $m$ for $\delta =1~\mbox{mm}$ and $\sigma =4~\mbox{MPa}$ at $20~\upmu \mbox{s}$. Left from top to bottom: damage maps of (a) $m=2$, (c) $m=3$, (e) $m=6$, and (g) $m=12$; Right from top to bottom: the plots of energies of (b) $m=2$, (d) $m=3$, (f) $m=6$, and (h) $m=12$

Fig. 10

Strain energy computed with different $m$ for $\delta =1~\mbox{mm}$ and $\sigma =4~\mbox{MPa}$ at $20~\upmu \mbox{s}$. From top to bottom: (a) $m=2$; (b) $m=3$; (c) $m=6$; (c) $m=12$

Moreover, in Fig. 11, the convergence can also be seen from the plots of the differences, between the coarse meshes ($m=2$, $m=3$ and $m=6$) and the finest mesh ($m=12$), of the potential energy, kinetic energy and total mechanical energy including the work done by the external body force (tensile loading). As time increases, the crack propagates and branches so that the increased complexity in the solutions and accumulations of errors generally leads to increases in the absolute differences. This is particularly evident in the plots of the total mechanical energy in Fig. 11. The plots of errors of potential energy and kinetic energy (differences between solutions on different meshes), however, show oscillations, which may be correlated with the variations in numerical resolutions of the different phases of the underlying process (including the growth of cracks, branching of cracks as well as effects of wave reflections from the boundary). More details on the different phases of crack evolution can be visualized in Fig. 12. Nevertheless, all of the results show diminishing differences between numerical solutions on different meshes as the mesh gets refined.

Fig. 11

Convergence of energy differences with different $m$ for $\delta =1~\mbox{mm}$ and $\sigma =4~\mbox{MPa}$. From top to bottom: (a) Potential energy; (b) Kinetic energy; (c) Total ME

Fig. 12

Different phases of crack propagation and branching for $\delta =1~\mbox{mm}$ and $\sigma =4~\mbox{MPa}$. From top to bottom: (a) $t=0~\upmu \mbox{s}$; (b) $t=6~\upmu \mbox{s}$; (c) $t=9~\upmu \mbox{s}$; (d) $t=15~\upmu \mbox{s}$

In order to see the convergence more quantitatively, we look into the displacement fields for different $m$. We interpolate displacement fields computed on coarse meshes ($m=2$, $m=3$ and $m=6$) to the finest mesh ($m=12$). Then we compute the differences between the interpolated solutions on the coarse meshes and the solution on the finest mesh in the $L^{2}$ norm. We denote by $\{\mathit{error}_{m}^{x}, \mathit{error}_{m}^{y}, m=2, 3, 6\}$ these norms for the components of the displacement field in the $x$-direction and $y$-direction respectively. In Table 3, we present $\{\mathit{error}_{m}^{x}, \mathit{error}_{m}^{y}, m=2, 3, 6\}$ at the final time $t=20~\upmu \mbox{s}$. We note that the relatively larger errors (differences) produced in the $\{\mathit{error}_{m}^{y}\}$ are consistent with the larger displacement fields in the $y$-direction.

Table 3 Differences between displacements computed with different $m$ for $\delta =1~\mbox{mm}$ and $\sigma =4~\mbox{MPa}$ at $20~\upmu \mbox{s}$

5 Discussions

The new peridynamic model given in this paper is not only mathematically rigorous but also able to effectively reproduce crack growth patterns observed in the literature and offer convergent numerical simulations. We have focused on a simple setting to illustrate our approach, but the results remain valid in more general situations. We discuss some of the possible extensions here. In addition, there are obviously many interesting questions remain to be investigated. Some examples are also discussed here.

Other boundary conditions. As we mentioned in Sect. 3, although the model equation (7) appears to only represent a Cauchy problem and homogeneous boundary condition, we can also treat inhomogeneous boundary conditions. First, with inhomogeneous Dirichlet boundary conditions, we just need to modify the solution space $X$ and the rest remains the same. Second, the (nonlocal) inhomogeneous Neumann boundary condition is equivalent to an extra body force around a $\delta$-layer of the domain $\Omega$ (see brief discussions in the numerical simulation section and more extensive studies in [34]). Such extra term added to the body force will not require significant changes to the proof of the well-posedness.

More general models. Our study has focused on a bond-based peridynamic model which has been a very popular choice in the literature. Nevertheless, the more general state-based models have demonstrated its superiority over the original bond-based models. Moreover, in more recent work on peridynamic models, the damage factor has been assigned as a dynamic equation of its own. Conditions are made to ensure the thermodynamic consistency. It will be interesting to extend our mathematical studies to these more general cases.

The various limiting cases. The mathematical analysis of this paper is based on abstract functional differential equation theories and the key relies on the Lipschitz continuity of the right-hand side defined in (8). To obtain the Lipschitz continuity (10), it is necessary to modify the original peridynamic bond-breaking model by adding four parameters $\mathcal{S}_{1}^{-},\mathcal{S}_{0}^{-},\mathcal{S}_{0}^{+}, \mathcal{S}_{1}^{+}$ that are used to smooth out the jumps. The original bond-breaking model then can be seen as the limit when $\mathcal{S} _{1}^{-}\to -1,\mathcal{S}_{0}^{-}\to -1$ and $\mathcal{S}_{0}^{+} \to \mathcal{S}_{c},\mathcal{S}_{1}^{+}\to \mathcal{S}_{c}$. However, the limiting model does not satisfy the Lipschitz continuity condition and the discussion is beyond the scope of this paper. As a subsequent work, we are working on the limiting model by means of theories of differential inclusion [35, 36], which are generalizations of differential equation theories to incorporate discontinuous right-hand side. The existence theory is possible to achieve by taking the right-hand side to be a multivalued map that satisfies certain continuity condition. The uniqueness theory, however, is a challenge for such model. In addition, as discussed before, the study of the local limit of our model (as $\delta \to 0$) is also an interesting subject. Similar numerical analysis concerning the discretization may also offer insights of the effective simulations of crack growth based on peridynamic models.