Abstract
We formulate a nonlocal cohesive model for calculating the deformation inside a cracking body. In this model a set of physical properties including elastic and softening behavior are assigned to each point in the medium. We work within the small deformation setting and use the peridynamic formulation. Here strains are calculated as difference quotients. The constitutive relation is given by a nonlocal cohesive law relating force to strain. At each instant of the evolution we identify a process zone where strains lie above a threshold value. Perturbation analysis shows that jump discontinuities within the process zone can become unstable and grow. We derive an explicit inequality that shows that the size of the process zone is controlled by the ratio given by the length scale of nonlocal interaction divided by the characteristic dimension of the sample. The process zone is shown to concentrate on a set of zero volume in the limit where the length scale of nonlocal interaction vanishes with respect to the size of the domain. In this limit the dynamic evolution is seen to have bounded linear elastic energy and Griffith surface energy. The limit dynamics corresponds to the simultaneous evolution of linear elastic displacement and the fracture set across which the displacement is discontinuous. We conclude illustrating how aspects of the approach developed here can be applied to limits of dynamics associated with other energies that \(\varGamma\)-converge to the Griffith fracture energy.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Dynamic brittle fracture is a multiscale phenomenon operating across a wide range of length and time scales. Contemporary approaches to brittle fracture modeling can be broadly characterized as bottom-up and top-down. Bottom-up approaches take into account the discreteness of fracture at the smallest length scales and are expressed through lattice models. This approach has provided insight into the dynamics of the fracture process [22, 48, 49, 66]. Complementary to the bottom-up approaches are top-down computational approaches using cohesive surface elements [23, 44, 58, 71]. In this formulation the details of the process zone are collapsed onto an interfacial element with a force traction law given by the cohesive zone model [7, 27]. Cohesive surfaces have been applied within the extended finite element method [11, 26, 54] to minimize the effects of mesh dependence on free crack paths. Higher order multi-scale cohesive surface models involving excess properties and differential momentum balance are developed in [57]. Comparisons between different cohesive surface models are given in [32]. More recently variational approaches to brittle fracture based on quasi-static evolutions of global minimizers of Grifffith’s fracture energy have been developed [16, 35, 36]. Phase field approaches have also been developed to model brittle fracture evolution from a continuum perspective [14, 16, 17, 53, 59, 69]. In the phase field approach a second field is introduced to interpolate between cracked and undamaged elastic material. The evolution of the phase field is used to capture the trajectory of the crack. A concurrent development is the emergence of the peridynamic formulation introduced in [60] and [64]. Peridynamics is a nonlocal formulation of continuum mechanics expressed in terms of displacement differences as opposed to spatial derivatives of the displacement field. These features provide the ability to simultaneously simulate kinematics involving both smooth displacements and defect evolution. Numerical simulations based on peridynamic modeling exhibit the formation and evolution of sharp interfaces associated with defects and fracture [13, 28, 34, 42, 61, 62, 68]. In an independent development nonlocal formulations have been introduced for modeling the passage from discrete to continuum limits of energies for quasistatic fracture models [2, 6, 19, 21], for smeared crack models [47] and for image processing [40] and [41]. A complete review of contemporary methods is beyond the scope of this paper however the reader is referred to [1, 8, 12, 15, 16, 18, 20] for a more complete guide to the literature.
In this paper we formulate a nonlocal, multi-scale, cohesive continuum model for assessing the deformation state inside a cracking body. This model is expressed using the peridynamic formulation introduced in [60, 64]. Here strains are calculated as difference quotients of displacements between two points \(x\) and \(y\). In this approach the force between two points \(x\) and \(y\) is related to the strain through a nonlinear cohesive law that depends upon the magnitude and direction of the strain. The forces are initially elastic for small strains and soften beyond a critical strain. We introduce the dimensionless length scale \(\epsilon\) given by the ratio of the length scale of nonlocal interaction to the characteristic length of the material sample \(D\). Working in the new rescaled coordinates the nonlocal interactions between \(x\) and its neighbors \(y\) occur within a horizon of radius \(\epsilon\) about \(x\) and the characteristic length of \(D\) is taken to be unity. This neighborhood of \(x\) is the ball of radius \(\epsilon\) with center \(x\) and is denoted by \(\mathcal {H}_{\epsilon}(x)\).
To define the potential energy we first assume the deformation \(z\) is given by \(z(x)=u(x)+x\) where \(u\) is the displacement field. The strain between two points \(x\) and \(y\) inside \(D\) is given by
In this treatment we assume small deformation kinematics and the displacements are small (infinitesimal) relative to the size of the body \(D\). Under this hypothesis (1.1) is linearized and the strain is given by
where \(e=\frac{y-x}{|y-x|}\). Both two and three dimensional problems will be considered and the dimension is denoted by \(d=2,3\). The cohesive model is characterized through a nonlocal potential
associated with points \(x\) and \(y\). The associated energy density is obtained on integrating over \(y\) for \(x\) fixed and is given by
where \(V_{d}=\epsilon^{d}\omega_{d}\) and \(\omega_{d}\) is the (area) volume of the unit ball in dimensions \(d=(2)3\). The potential energy of the body is given by
We introduce the class of potentials associated with a cohesive force that is initially elastic and then softens after a critical strain. These potentials are of the generic form given by
where \(\mathcal{W}^{\epsilon}(\mathcal{S},y-x)\) is the peridynamic potential per unit length associated with \(x\) and \(y\) given by
These potentials are of a general form and are associated with potential functions \(f:[0,\infty)\rightarrow\mathbb{R}\) that are positive, smooth and concave with the properties
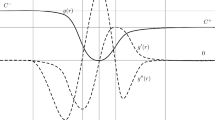
The composition of \(f\) with \(|y-x|\mathcal{S}^{2}\) given by (1.5) delivers the convex-concave dependence of \(\mathcal {W}^{\epsilon}(\mathcal{S},y-x)\) on \(\mathcal{S}\) for fixed values of \(x\) and \(y\), see Fig. 1. Here \(J^{\epsilon}(|y-x|)\) is used to prescribe the influence of separation length \(|y-x |\) on the force between \(x\) and \(y\) inside \(\mathcal{H}_{\epsilon}(x)\). \(J^{\epsilon}\) is defined by the rescaling \(J^{\epsilon}(|y-x|)=J(|y-x|/\epsilon)\) where we require \(0\leq J(|\xi|)< M\) for \(\xi\) in the unit ball \(\mathcal {H}_{1}(0)\) and \(J=0\) for \(|\xi|>1\). For fixed \(x\) and \(y\) the inflection point for the potential energy (1.5) with respect to the strain \(\mathcal{S}\) is given by \(\overline{r}/\sqrt{|y-x|}\), where \(\overline{r}\) is the inflection point for the function \(r:\rightarrow f(r^{2})\), see Fig. 1. This choice of potential delivers an initially elastic and then softening constitutive law for the force per unit length along the direction \(e\) given by
The force between points \(y\) and \(x\) begins to drop at the softening value where the strain \(\mathcal{S}\) exceeds the critical strain
see Fig. 2. The energy per unit length necessary to bring the force between two points \(x\) and \(y\) to its softening value is the area under the force strain curve (1.7) between \(\mathcal{S}=0\) and \(\mathcal{S}_{c}\) and is given by \(\mathcal {W}^{\epsilon}(\mathcal{S}_{c},y-x)\). The energy per unit length necessary to bring the force far into the softening phase of the force-strain relation is \(\mathcal{W}^{\epsilon}(\mathcal{S}_{c}^{+},y-x)\), where \(\mathcal {S}_{c}^{+}>\mathcal{S}_{c}\) and is \(\mathcal{S}_{c}^{+}=\overline {r}/|y-x|^{1/2+\delta}\), \(\delta>0\).
We prescribe boundary conditions for the displacement \(u\) on a layer of thickness \(\alpha=2\epsilon\) surrounding \(D\), see Fig. 4, and apply the principle of least action to recover the cohesive equation of motion describing the state of displacement inside the body \(D\subset\mathbb{R}^{d}\) given by
where \(\rho\) is the density and \(b(t,x)\) is the body force. This is a well posed formulation in that existence and uniqueness (within a suitable class of evolutions) can be shown, see Sect. 2 and Theorem 6.1 of Sect. 6.1.
In this model a more complete set of physical properties including elastic and softening behavior are assigned to each point in the medium. Here each point in the domain is connected to its neighbors by a cohesive law see Fig. 2. We define the process zone to be the collection of points \(x\) inside the body \(D\) associated with peridynamic neighborhoods \(\mathcal{H}_{\epsilon}(x)\) for which the strain \(\mathcal{S}\) between \(x\) and \(y\) exceeds a threshold value for a sufficiently large proportion of points \(y\) inside \(\mathcal {H}_{\epsilon}(x)\). Here the force vs. strain law departs from linear behavior when the strain exceeds the threshold value. The mathematically precise definition of the process zone is given in Sect. 4, see Definition 4.1. In this model the fracture set is associated with peridynamic neighborhoods \(\mathcal{H}_{\epsilon}(x)\) with strains beyond the threshold \(|\mathcal {S}|>\mathcal{S}_{c}^{+}\) for which the force vs. strain law is softenting and is defined in Sect. 4, see Definition 4.2. The nonlinear elastic-softening behavior put forth in this paper is similar to the ones used in cohesive zone models [7, 27]. However for this model the dynamics selects whether a material point lies inside or outside the process zone. The principal feature of the cohesive dynamics model introduced here is that the evolution of the process zone together with the fracture set is governed by an equation consistent with Newton’s second law given by (1.9). This is a characteristic feature of peridynamic models [60, 64] and lattice formulations for fracture evolution [22, 48, 49, 66].
The first goal of this paper is to characterize the size of the process zone for cohesive dynamics as a function of domain size and the length scale of the nonlocal forces. For the model introduced here the parameter that controls the size of the process zone is given by the radius of the horizon \(\epsilon\). We derive an explicit inequality that shows that the size of the process zone is controlled by the horizon radius. Perturbation analysis shows that jump discontinuities within the process zone can become unstable and grow. This analysis shows that the horizon radius \(\epsilon\) for cohesive dynamics is a modeling parameter that can be calibrated according to the size of the process zone obtained from experimental observations.
The second focus is to identify properties of the distinguished limit evolution for these models in the limit of vanishing non-locality as characterized by the \(\epsilon\rightarrow0\) limit. In order to anticipate the limiting behavior we introduce a notion of fracture toughness for the cohesive models developed here. The fracture toughness \(\mathcal{G}_{c}^{\epsilon}\) is defined to be the energy per unit length required to send the cohesive force between each point \(x\) and \(y\) on either side of a planar surface far into the softening phase of the force-strain relation associated with \(\mathcal{S}>\mathcal {S}_{c}^{+}\). Because of the finite length scale of interaction only the force between pairs of points within an \(\epsilon\) distance from the surface need to be considered. For this model we can proceed to calculate the fracture toughness \(\mathcal{G}_{c}^{\epsilon}\) as in [61]. The fracture toughness is given by the formula
where \(\zeta=|y-x|\), see Fig. 3. A similar computation can be carried out for two dimensional problems. Substitution of \(\mathcal {W}^{\epsilon}(\mathcal{S},y-x)\) given by (1.5) into (1.10) and calculation delivers the formulas
where \(\omega_{d}\) is the volume of the \(n\) dimensional unit ball, \(\omega_{1}=2,\omega_{2}=\pi,\omega_{3}=4\pi/3\).
Evaluation of fracture toughness \(\mathcal{G}_{c}^{\epsilon}\). For each point \(x\) along the dashed line, \(0\leq z\leq\epsilon\), the work required to break the interaction between \(x\) and \(y\) in the spherical cap is summed up in (1.10) using spherical coordinates centered at \(x\)
For small homogeneous strains the energy density for the cohesive model is related to the strain energy density of a linearly elastic material. For this case the energy density is described to leading order by shear and Lamé moduli \(\mu\) and \(\lambda\) when the strain field is uniform across \(\mathcal{H}_{\epsilon}(x)\) Consider the linear displacement associated with a constant strain tensor \(F\) given by \(u(x)=Fx\). A straight forward calculation provided in Sect. 6.6 reveals that \(\mu\) and \(\lambda\) defined by (5.7) describe the strain energy density to leading order for \(\mathcal{S}=Fe\cdot e<\mathcal{S}_{c}\), i.e.,
Further calculation shows that the volume of the process zone goes to zero with \(\epsilon\) in the limit of vanishing non-locality, \(\epsilon \rightarrow0\). Application of compactness arguments Theorem 6.2 and Theorem 6.4 shows the existence of distinguished \(\epsilon\rightarrow0\) limits of cohesive evolutions. For a suitable class of initial data the limit evolutions are found to lie in the space of special functions of bounded deformation and have both bounded linear elastic energy and Griffith surface energy, see Theorem 5.2. \(\varGamma\)-convergence arguments, see Theorems 6.4 and 6.5 show in an independent way that the fracture toughness characterizing the Griffith surface energy for the limit evolution (5.8) is precisely the one recovered from the cohesive model on sending \(\epsilon\rightarrow0\) in (1.11). The limit dynamics is shown to correspond to the simultaneous evolution of linear elastic displacement and a fracture set across which the displacement is discontinuous. Here the evolving fracture set is shown to be confined to a set of \(d-1\) dimensional Hausdorf measure. It is seen under suitable hypotheses the displacement field evolves elastodynamically for points away from the fracture set and is governed by the balance of linear momentum expressed by the Navier Lamé equations. The elastic moduli mediating the balance of linear momentum together with energy release rate of the fracture surface for the limit evolution are recovered directly from the cohesive model and given by (5.7) and (5.8). The results presented here are consistent with the asymptotic behavior seen in the convergence of solutions of the Barenblatt model to the Griffith model when cohesive forces are confined to a surface act over a sufficiently short range [50, 70].
Earlier work has shown that linear peridynamic formulations recover the classic linear elastic wave equation in the limit of vanishing non-locality see [30, 63]. The convergence of linear peridynamics to the Navier Lamé equations in the sense of solution operators is demonstrated in [52]. Recent work shows that analogous results can be found for dynamic problems and fully nonlinear peridynamics [46] in the context of antiplane shear. There distinguished \(\epsilon \rightarrow0\) limits of cohesive evolutions are identified and are found to have both bounded linear elastic energy and Griffith surface energy. It is shown that the limiting displacement evolves according to the linear elastic wave equation away from the crack set, see [46]. For large deformations, the connection between hyperelastic energies and the small horizon limits of nonlinear peridynamic energies is recently established in [10]. In the current paper both two and three dimensional problems involving multi-mode fracture are addressed. For these problems new methods are required to identify the existence of a limit dynamics as the length scale of nonlocal interaction \(\epsilon\) goes to zero. A crucial step is to establish a suitable notion of compactness for sequences of cohesive evolutions. The approach taken here employs nonlocal Korn inequalities introduced in [25]. This method is presented in Sect. 6.3. We conclude noting that the cohesive dynamics model introduced here does not have an irreversibility constraint and that the constitutive law (1.7) applies at all times in the fracture evolution. However with this caveat in mind, the nonlocal cohesive model offers new computational and analytical opportunities for understanding the effect of the process zone on fracture patterns.
In the next section we write down the Lagrangian formulation for the cohesive dynamics and apply the principle of least action to recover the equation of motion. In that section it is shown that the nonlinear-nonlocal cohesive evolution is a well posed initial boundary value problem. It is also shown that energy balance is satisfied by the cohesive dynamics. A formal stability analysis is carried out in Sect. 3 showing that jump discontinuities within the process zone can become unstable and grow, see Proposition 3.1. In Sect. 4 we provide a mathematically rigorous inequality explicitly showing how the volume of the process zone for the cohesive evolutions is controlled by the length scale of nonlocal interaction \(\epsilon\), see Theorem 4.1. In Sect. 5 we introduce suitable technical hypothesis and identify the distinguished limit of the cohesive evolutions as \(\epsilon \rightarrow0\), see Theorem 5.1. It is shown that the solution is elastodynamic and governed by the Navier Lamé equations away from the evolving crack set, see Theorem 5.4. These displacements are shown to have bounded bulk elastic and surface energy in the sense of Linear Elastic Fracture Mechanics (LEFM), see Theorem 5.2. In Sect. 6 we provide the mathematical underpinnings and proofs of the theorems. In Sect. 7 we apply the approach developed here to examine limits of dynamics associated with other energies that \(\varGamma\)-converge to the Griffith fracture energy. As an illustrative example we examine the Ambrosio-Tortorelli [4] approximation as applied to the dynamic problem in [17] and [45].
2 Cohesive Dynamics
We formulate the initial boundary value problem for the cohesive evolution. Since the problem is nonlocal we define a boundary layer surrounding \(D\) of thickness \(\alpha=2\epsilon\) and denote it by \(D_{c}\), see Fig. 4. The boundary condition for the displacement \(u\) is nonlocal and given by \(u(t,x)=0\) for \(x\) in \(D_{c}\). To incorporate nonlocal boundary conditions we introduce the space \(L^{2}_{0}(D;\mathbb {R}^{d})\), of displacements that are square integrable over \(D\) and zero in the layer \(D_{c}\). The initial conditions for the cohesive dynamics belong to \(L^{2}_{0}(D;\mathbb{R}^{d})\) and are given by
We will investigate the evolution of the deforming domain for general initial conditions. These can include an initially un-cracked body or one with a preexisting system of cracks. For two dimensional problems the cracks are given by a system of curves of finite total length, while for three dimensional problems the crack set is given by a system of surfaces of finite total surface area. Depending on the dimension of the problem the displacement suffers a finite jump discontinuity across each curve or surface. The initial condition is specified by a crack set \(K\) and displacement \(u_{0}\). The strain \(\mathcal{E}u_{0}=(\nabla u_{0}+\nabla u_{0}^{T})/2\) is defined off the crack set and the displacement \(u_{0}\) can suffer jumps across \(K\). Griffith’s theory of fracture asserts that the energy necessary to produce a crack \(K\) is proportional to the crack length (or surface area). For Linear Elastic Fracture Mechanics (LEFM) the total energy associated with bulk elastic and surface energy is given by
where \(\mu\), \(\lambda\) are the shear and Lamé moduli, \(\mathcal {G}_{c}\) is the critical energy release rate for the material, \(|\mathcal {E}u_{0}|^{2}=\sum_{i,j=1}^{d}(\mathcal{E}_{ij}u_{0})^{2}\), and \(\operatorname{div} u_{0}=\sum_{i=1}^{d}\mathcal{E}_{ii}u_{0}\). Here \(|K|\) denotes the length or surface area of the crack. In what follows we will assume that the bulk elastic energy and surface energy of the initial displacement are bounded as well as the initial velocity and displacement. In this work we consider a broad class of initial displacements \(u_{0}\) for which \(\mathit{LEFM}(u_{0})\) is well defined. This class is defined by the space of functions of bounded deformation \(\mathit{SBD}\) introduced in [9]. This space is appropriate for describing discontinuities associated with linear elastic fracture. To expedite the presentation we postpone the technical description of \(\mathit{SBD}\) functions until Sect. 5. We note here that \(\mathit{SBD}\) functions \(u\) belong to \(L^{1}(D;\mathbb{R}^{d})\) and the set of jump discontinuities \(J_{u}\) for elements of \(\mathit{SBD}\) is described by a countable number of components \(K_{1},K_{2},\ldots{}\), contained within smooth manifolds. Here the notion of arc length or (surface area) of the jump set is the \(d-1\) dimensional Hausdorff measure of \(J_{u}\) and \(\mathcal{H}^{d-1}(J_{u})=\sum_{i}\mathcal{H}^{d-1}(K_{i})\). The strain [5] of a displacement \(u\) belonging to \(\mathit{SBD}\), written as \(\mathcal{E}u\), is a generalization of the classic strain tensor and is related to the strain
introduced here by
for almost every \(x\in D\), with respect to \(d\)-dimensional Lebesgue measure \(\mathcal{L}^{d}\).
The energy of linear elastic fracture mechanics extended to the class of \(\mathit{SBD}\) functions is given by:
for \(u\) belonging to \(\mathit{SBD}\). Here the fracture surface is described by the jump set \(J_{u}\) of the displacement \(u\).
We state the following lemma that provides an inequality between the potential energy for cohesive dynamics and the free energy of Linear Elastic Fracture Mechanics.
Theorem 2.1
For any function \(u\) belonging to \(\mathit{SBD}\) the inequality between its peridynamic potential energy and its LEFM energy is given by
This theorem follows directly from the inequality for the cohesive potential between \(x\) and \(y\) given by
The upper bound (2.7) is a local Griffith dichotomy expressed as the minimum of two energies; one given by a quadratic elastic energy and the second given by the energy required to completely soften the force between \(x\) and \(y\). The proof of Theorem 2.1 is given in Sect. 6.8.
With these observations in mind we take the initial displacement \(u_{0}\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\) and require that it belong to the space \(\mathit{SBD}\) and make the following definition.
Definition 2.1
Initial data \(u_{0}\in L_{0}^{2}(D;\mathbb{R}^{d})\), \(v_{0}\in L_{0}^{2}(D;\mathbb {R}^{d})\) with \(u_{0}\) belonging to \(\mathit{SBD}\) that satisfy
are defined to be LEFM initial data.
In what follows we write \(u(t,x)\) as \(u(t)\) to expedite the presentation. The displacements \(u(t)\) considered here are twice differentiable in time and take values in \(L^{2}_{0}(D;\mathbb{R}^{d})\). The space of such functions is denoted by \(C^{2}([0,T];L^{2}_{0}(D;\mathbb{R}^{d}))\). The cohesive dynamics is described by the Lagrangian
with
where \(\rho\) is the mass density of the material and \(b(t,x)\) is the body force density. The \(\mathit{LEFM}\) initial data \(u(0,x)=u_{0}(x)\) and \(u_{t}(0,x)=v_{0}(x)\) are prescribed and the action integral for the peridynamic evolution is
The principle of least action delivers the evolution \(u^{\epsilon}(t)\) in \(C^{2}([0,T];L^{2}_{0}(D;\mathbb{R}^{d}))\) that satisfies the initial conditions and Euler Lagrange Equation for this system described by
where
and
The initial value problem for the peridynamic evolution (2.12) is seen to have a unique solution in \(C^{2}([0,T];L^{2}_{0}(D;\mathbb {R}^{d}))\), see Theorem 6.1 of Sect. 6.1. The cohesive evolution \(u^{\epsilon}(x,t)\) is uniformly bounded in the mean square norm over bounded time intervals \(0< t< T\), i.e.,
Here \(\Vert u^{\epsilon}(t,x)\Vert_{L^{2}(D;\mathbb{R}^{d})}= (\int _{D}|u^{\epsilon}(t,x)|^{2}\,dx )^{1/2}\) and the upper bound \(C\) is independent of \(\epsilon\) and depends only on the initial conditions and body force applied up to time \(T\), see Sect. 6.2.
The cohesive evolution has the following properties that are established in Sect. 6.2. The evolution has uniformly bounded kinetic and elastic potential energy
Theorem 2.2
(Bounds on Kinetic and Potential Energy for Cohesive Dynamics)
There exists a positive constant \(C\) depending only on \(T\) and independent of \(\epsilon\) for which
The evolution is uniformly continuous in time as measured by the mean square norm.
Theorem 2.3
(Continuous Cohesive Evolution in Mean Square Norm)
There is a positive constant \(K\) independent of \(t_{2} < t_{1}\) in \([0,T]\) and index \(\epsilon\) for which
The evolution satisfies energy balance. The total energy of the cohesive evolution at time \(t\) is given by
and the total energy of the system at time \(t=0\) is
The cohesive dynamics is seen to satisfy energy balance at every instant of the evolution.
Theorem 2.4
(Energy Balance for Cohesive Dynamics)
3 Dynamic Instability and Fracture Nucleation
In this section we present a fracture nucleation condition that arises from the unstable force law (1.7). This condition is manifested as a dynamic instability. In the following companion section we investigate the localization of dynamic instability as \(\epsilon _{k}\rightarrow0\) and define the notion of process zone for the cohesive evolution. Fracture nucleation conditions can be viewed as instabilities and have been identified for peridynamic evolutions in [65]. Fracture nucleation criteria formulated as instabilities for one dimensional peridynamic bars are developed in [68]. In this treatment we define a source for crack nucleation as jump discontinuity in the displacement field that can become unstable and grow in time. Here we establish a direct link between the growth of jump discontinuities and the appearance of strain concentrations inside the deforming body.
We proceed with a formal perturbation analysis and consider a time independent body force density \(b\) and a smooth equilibrium solution \(u\) of (2.12). Now perturb \(u\) in the neighborhood of a point \(x\) by adding a piecewise constant vector field \(\delta\). The perturbation takes the value zero on one side of a plane with normal vector \(\nu\) passing through \(x\) and on the other side of the plane takes the value \(\delta=\overline{u}s(t)\). Here \(s(t)\) is a scalar function of time and \(\overline{u}\) is a constant vector. Consider the neighborhood \(\mathcal{H}_{\epsilon}(x)\), then \(\delta(y)=0\) for \((y-x)\cdot\nu<0\) and \(\delta(y)=\overline{u}s(t)\) for \((y-x)\cdot\nu \geq0\), see Fig. 5. The half space on the side of the plane for which \((y-x)\cdot\nu<0\) is denoted by \(E^{-}_{\nu}\).
Write \(u^{p}=u+\delta\) and assume
We regard \(s(t)\) as a small perturbation and expand the integrand of \(\nabla PD^{\epsilon}(u^{p})\) in a Taylor series to recover the linearized evolution equation for the jump \(s=s(t)\). The evolution equation is given by
where the stability matrix \(\mathcal{A}_{\nu}(x)\) is a \(d\times d\) symmetric matrix with real eigenvalues and is defined by
and
Calculation shows that
where \(f'(|y|\mathcal{S}^{2})>0\) and \(f''(|y|\mathcal{S}^{2})<0\). On writing
we have that
and
Here \(\overline{r}\) is the inflection point for the function \(r:\rightarrow f(r^{2})\) and \(\overline{r}=\sqrt{\overline{x}}\) where \(\overline{x}\) is the root of the equation
Note that the critical strain \(\mathcal{S}_{c}\) for which the cohesive force between a pair of points \(y\) and \(x\) begins to soften is akin to the square root singularity seen at the crack tip in classical brittle fracture mechanics.
For eigenvectors \(\overline{u}\) in the eigenspace associated with positive eigenvalues \(\lambda\) of \(\mathcal{A}_{\nu}(x)\) one has
and the perturbation \(s(t)\) can grow exponentially. Observe from (3.7) that the quadratic form
will have at least one positive eigenvalue provided a sufficiently large proportion of bonds \(y-x\) inside the horizon have strains satisfying
for which the cohesive force is in the unstable phase. For this case we see that the jump can grow exponentially. The key feature here is that dynamic instability is explicitly linked to strain concentrations in this cohesive model as is seen from (3.7) together with (3.10). Collecting results we have the following proposition.
Proposition 3.1
(Fracture Nucleation Condition for Cohesive Dynamics)
A condition for crack nucleation at a point \(x\) is that there is at least one direction \(\nu\) for which \(\mathcal{A}_{\nu}(x)\) has at least one positive eigenvalue. This occurs if there is a square root strain concentration \(|\mathcal{S}(y,x)|>\mathcal{S}_{c}\) over a sufficiently large proportion of cohesive bonds inside the peridynamic horizon.
Proposition 3.1 together with (3.7) provide the explicit link between dynamic instability and the critical strain where the cohesive law begins to soften.
More generally we may postulate a condition for the direction along which the opposite faces of a nucleating fissure are oriented and the direction of the displacement jump across it. Recall that two symmetric matrices \(A\) and \(B\) satisfy \(A\geq B\) in the sense of quadratic forms if \(A\overline{w}\cdot\overline{w}\geq B\overline{w}\cdot\overline{w}\) for all \(\overline{w}\) in \(\mathbb{R}^{d}\). We say that a matrix \(A\) is the maximum of a collection of symmetric matrices if \(A\geq B\) for all matrices \(B\) in the collection.
We postulate that the faces of the nucleating fissure are perpendicular to the direction \(\nu^{*}\) associated with the matrix \(\mathcal {A}_{\nu^{*}}(x)\) for which
and that the orientation of the jump in displacement across opposite sides of the fissure lies in the eigenspace associated with the largest positive eigenvalue of \(\mathcal{A}_{\nu^{*}}\), i.e., the fissure is oriented along the most unstable orientation and the displacement jump across the nucleating fissure is along the most unstable direction.
4 The Process Zone for Cohesive Dynamics and Its Localization in the Small Horizon Limit
In this section it is shown that the collection of centers of peridynamic neighborhoods with strain exceeding a certain threshold concentrate on sets with zero volume in the limit of vanishing non-locality. In what follows we probe the dynamics to obtain mathematically rigorous and explicit estimates on the size of the process zone in terms of the radius of the peridynamic horizon \(0<\epsilon<1\).
We consider solutions \(u^{\epsilon}\) of (2.12) and define a mathematical notion of process zone based the strain exceeding threshold values associated with \(\mathcal{S}_{c}\). The process zone is best described in terms of the basic unit of peridynamic interaction: the peridynamic neighborhoods \(\mathcal {H}_{\epsilon}(x)\) of radius \(\epsilon>0\) with centers \(x\in D\). The strain between \(x\) and a point \(y\) inside the neighborhood is denoted by
The collection of points \(y\) inside \(\mathcal{H}_{\epsilon}(x)\) for which the strain \(|\mathcal{S}^{\epsilon}(y,x)|\) exceeds the threshold function \(\mathcal{S}_{c}=\overline{r}/\sqrt{|y-x|}\) is denoted by \(\{y \in \mathcal{H}_{\epsilon}(x): |\mathcal{S}^{\epsilon}(x,y)|>\mathcal{S}_{c}\}\). Recall for the cohesive model there is softening in the cohesive force-strain behavior given by (1.7) when \(|\mathcal{S}(y,x)|>\mathcal{S}_{c}\).
The fraction of points inside the neighborhood \(\mathcal{H}_{\epsilon}(x)\) with strains exceeding the threshold is written
where the weighted volume fraction for any subset \(B\) of \(\mathcal {H}_{\epsilon}(x)\) is defined as
with normalization constant
chosen so that \(P(\mathcal{H}_{\epsilon}(x))=1\).
Definition 4.1
(Process Zone)
Fix a volume fraction \(0<\overline{\theta}\leq1\), and with each time \(t\) in the interval \(0\leq t\leq T\), define the process zone \(PZ^{\epsilon}(\overline{\theta},t)\) to be the collection of centers of peridynamic neighborhoods for which the portion of points \(y\) with strain \(\mathcal{S}^{\epsilon}(t,y,x)\) exceeding the threshold \(\mathcal {S}_{c}\) is greater than \(\overline{\theta}\), i.e., \(P (\{y\in\mathcal {H}_{\epsilon}(x): |\mathcal{S}^{\epsilon}(t,y,x)|>\mathcal{S}_{c}\} )>\overline{\theta}\).
The fracture set lies within the process zone process zone and is the collection of neighborhoods with centers with strains exceed the threshold \(\mathcal{S}_{c}^{+}>\mathcal{S}_{c}\).
Definition 4.2
(Fracture Set)
The fracture set is defined to be the collection of centers of peridynamic neighborhoods for which the portion of points \(y\) with strain \(\mathcal{S}^{\epsilon}(t,y,x)\) exceeding the threshold \(\mathcal{S}_{c}^{+}\) is greater than \(1/2\), i.e., \(P (\{y\in\mathcal{H}_{\epsilon}(x): |\mathcal{S}^{\epsilon}(t,y,x)|>\mathcal{S}_{c}^{+}\} )>1/2\).
The definition of fracture set given here is consistent with the fracture toughness for this model and is different from the usual one which collapses material damage onto a surface across which the displacement jumps.
It follows from Proposition 3.1 that the process zone contains peridynamic neighborhoods associated with softening cohesive forces. Within this zone pre-existing jump discontinuities in the displacement field can grow.
Remark 4.1
Here we have described a range of process zones depending upon the choice of \(\overline{\theta}\). In what follows we show that for any choice of \(0<\overline{\theta}\leq1\) the volume of the process zone is explicitly controlled by the radius of the peridynamic horizon \(\epsilon\).
We consider problem formulations in two and three dimensions and the volume or area of a set is given by the \(d\) dimensional Lebesgue measure denoted by \(\mathcal{L}^{d}\), for \(d=2,3\). We let
and note that \(C(t)\leq C(T)\) for \(t< T\).
We now give the following bound on the size of the process zone.
Theorem 4.1
(Dependence of the Process Zone on the Radius of the Peridynamic Horizon)
where \(0\leq\beta<1\) and \(\beta=2\alpha-1\) and \(0\leq t\leq T\).
A straight forward calculation shows that the energy necessary to soften the force between \(x\) and a fraction \(\overline {\theta}\) of all points \(y\) inside the neighborhood is given by
The inequality (4.5) together with (4.6) shows in a quantitative way that the process zone scales inversely with the energy required to soften bonds. Theorem 4.1 explicitly shows that the size of the process zone is controlled by the radius \(\epsilon\) of the peridynamic horizon, uniformly in time. The calculation establishing theorem is 4.1 provided in Sect. 6.7.
Remark 4.2
This analysis shows that the horizon size \(\epsilon\) for cohesive dynamics is a modeling parameter that may be calibrated according to the size of the process zone obtained from experimental observations.
5 The Small Horizon Limit of Cohesive Dynamics
In this section we identify the distinguished small horizon \(\epsilon \rightarrow0\) limit for cohesive dynamics. It is shown here that the limit dynamics has bounded bulk linear elastic energy and Griffith surface energy characterized by the shear moduli \(\mu\), Lamé modulus \(\lambda\), and energy release rate \(\mathcal{G}_{c}\) respectively.
We consider a family of cohesive evolutions \(u^{\epsilon_{k}}\), each associated with a fixed potential \(W^{\epsilon_{k}}\) and horizon length \(\epsilon_{k}\), with \(k=1,2,\ldots\) and \(\epsilon_{k}\rightarrow0\). Each \(u^{\epsilon_{k}}(t,x)\) can be thought of as being the result of a perfectly accurate numerical simulation of a cohesive evolution associated with the potential \(W^{\epsilon_{k}}\). It is shown in this section that the cohesive dynamics \(u^{\epsilon_{k}}(t,x)\) converges to a limit evolution \(u^{0}(t,x)\) in the limit, \(\epsilon_{k}\rightarrow0\). The limit evolution describes the dynamics of the cracked body when the scale of nonlocality is infinitesimally small with respect to the material specimen. We show that the cohesive dynamics \(u^{\epsilon _{k}}(t,x)\) approaches the limit dynamics \(u^{0}(t,x)\) characterized by \(\mu \), \(\lambda\), and \(\mathcal{G}_{c}\) given by the formulas (5.7) and (5.8).
In what follows the sequence of cohesive dynamics described by \(u^{\epsilon_{k}}\) is shown to converge to the limiting free crack evolution \(u^{0}(t,x)\) in mean square, uniformly in time, see Theorem 5.1. The limit evolution is shown to have the following properties:
-
It has uniformly bounded energy in the sense of linear elastic fracture mechanics for \(0\leq t \leq T\).
-
It satisfies an energy inequality involving the kinetic energy of the motion together with the bulk elastic and surface energy associated with linear elastic fracture mechanics for \(0\leq t\leq T\).
-
It is elastodynamic away from the fracture set.
We provide explicit conditions under which these properties are realized for the limit dynamics.
Hypothesis 5.1
We suppose that the magnitudes of the displacements \(u^{\epsilon_{k}}\) for cohesive dynamics are bounded for \(0\leq t\leq T\) uniformly in \(\epsilon_{k}\), i.e., \(\sup_{\epsilon_{k}}{ \sup_{0\leq t\leq T}}\Vert u^{\epsilon_{k}}(t)\Vert_{L^{\infty}(D;\mathbb{R}^{d})}<\infty\).
The convergence of cohesive dynamics is given by the following theorem,
Theorem 5.1
(Convergence of Cohesive Dynamics)
For each \(\epsilon_{k}\) we prescribe identical LEFM initial data \(u_{0}(x)\) and \(v_{0}(x)\) and the solution to the cohesive dynamics initial value problem is denoted by \(u^{\epsilon_{k}}\). Now consider a sequence of solutions \(u^{\epsilon_{k}}\) associated with a vanishing peridynamic horizon \(\epsilon_{k}\rightarrow0\) and suppose Hypothesis 5.1 holds true. Then, on passing to a subsequence if necessary, the cohesive evolutions \(u^{\epsilon_{k}}\) converge in mean square uniformly in time to a limit evolution \(u^{0}\) belonging to \(C([0,T];L^{2}_{0}(D;\mathbb{R}^{d}))\) with the same LEFM initial data, i.e.,
and \(u^{0}(0,x)=u_{0}(x)\) and \(\partial_{t} u^{0}(0,x)=v_{0}(x)\).
It is shown in Theorem 6.6 of Sect. 6.4 that the limit evolution \(u^{0}(t,x)\) has a weak derivative \(u_{t}^{0}(t,x)\) belonging to \(L^{2}([0,T]\times D;\mathbb{R}^{d})\).
The limiting \(\epsilon_{k}\rightarrow0\) dynamics is given by displacements described by functions of bounded deformation \(\mathit{SBD}\). Functions \(u\in \mathit{SBD}\) belong to \(L^{1}(D;\mathbb{R}^{d})\) and are approximately continuous, i.e., have Lebesgue limits for almost every \(x\in D\) given by
where \(\mathcal{H}_{\epsilon}(x)\) is the ball of radius \(\epsilon\) centered at \(x\). The jump set \(J_{u}\) for elements of \(\mathit{SBD}\) is defined to be the set of points of discontinuity which have two different one sided Lebesgue limits. One sided Lebesgue limits of \(u\) with respect to a direction \(\nu_{u}(x)\) are denoted by \(u^{-}(x)\), \(u^{+}(x)\) and are given by
where \(\mathcal{H}^{-}_{\epsilon}(x)\) and \(\mathcal{H}^{+}_{\epsilon}(x)\) are given by the intersection of \(\mathcal{H}_{\epsilon}(x)\) with the half spaces \((y-x)\cdot\nu_{u}(x)<0\) and \((y-x)\cdot\nu_{u}(x)>0\) respectively. SBD functions have jump sets \(J_{u}\), described by a countable number of components \(K_{1},K_{2},\ldots{}\), contained within smooth manifolds, with the exception of a set \(K_{0}\) that has zero \(d-1\) dimensional Hausdorff measure [5]. Here the notion of arc length or (surface area) is the \(d-1\) dimensional Hausdorff measure of \(J_{u}\) and \(\mathcal{H}^{d-1}(J_{u})=\sum_{i}\mathcal{H}^{d-1}(K_{i})\). The strain [5] of a displacement \(u\) belonging to SBD, written as \(\mathcal{E}u\), is a generalization of the classic strain tensor and is related to the strain \(\mathcal{S}\) introduced here by
for almost every \(x\in D\), with respect to \(d\)-dimensional Lebesgue measure \(\mathcal{L}^{d}\). The symmetric part of the distributional derivative of \(u\), \(E u=1/2(\nabla u+\nabla u^{T})\) for \(\mathit{SBD}\) functions is a \(d\times d\) matrix valued Radon measure with absolutely continuous part described by the density \(\mathcal{E}u\) and singular part described by the jump set [5, 9] and
for every continuous, symmetric matrix valued test function \(\varPhi\).
We now describe the elastic energy for the limit dynamics associated with \(\mathit{LEFM}\) initial data.
Theorem 5.2
(The Limit Dynamics Has Bounded \(\mathit{LEFM}\) Energy)
For LEFM initial data and if the initial displacement \(u_{0}\in \mathit{SBD}\) and \(\Vert u_{0}\Vert_{L^{\infty}(D;\mathbb{R}^{d})}<\infty\) then the limit evolution \(u^{0}\) belongs to SBD for every \(t\in[0,T]\). Furthermore there exists a constant \(C\) depending only on \(T\) bounding the \(\mathit{LEFM}\) energy,
for \(0\leq t\leq T\) where \(J_{u^{0}(t)}\) denotes the evolving fracture surface and \(\mathcal{H}^{d-1}(J_{u^{0}(t)})\) is its \(d-1\) dimensional Hausdorff measure at time \(t\). Here \(\mu\), \(\lambda\) are given by the explicit formulas
and
where \(f_{\infty}\) is defined by (1.6) and \(\omega_{n}\) is the volume of the \(n\) dimensional unit ball, \(\omega_{1}=2\), \(\omega_{2}=\pi\), \(\omega_{3}=4\pi/3\). The potential \(f\) and influence function \(J\) can always be chosen to satisfy (5.7) and (5.8) for any \(\mu=\lambda >0\) corresponding to the Poisson ratio \(\nu=1/3\), for \(d=2\) and \(\nu =1/4\), for \(d=3\), and \(\mathcal{G}_{c}>0\).
Remark 5.1
The absolutely continuous part of the strain \(\mathcal{E}u^{0}\) is defined for points away from the fracture surface \(J_{u^{0}(t)}\) and the process zone for the limit evolution can be viewed as being confined to the evolving fracture surface \(J_{u^{0}(t)}\). Theorem 5.2 shows that the fracture set \(J_{u^{0}(t)}\) for the limit evolution \(u^{0}(t,x)\) is confined to a set of finite \(d-1\) dimensional Hausdorff measure.
We now present an energy inequality for the limit evolution. The sum of energy and work for the displacement \(u^{0}\) at time \(t\) is written
The sum of energy and work for the initial data \(u_{0},v_{0}\) is written
The energy inequality for the limit evolution \(u^{0}\) is given by,
Theorem 5.3
(Energy Inequality)
For almost every \(t\) in \([0, T]\),
We identify conditions for which the limit dynamics for \(u^{0}\) is elastodynamic away from the process zone.
Theorem 5.4
(Elastodynamics Away from the Process Zone)
Fix \(\delta>0\) and consider an open set \(D'\subset D\) for which points \(x\) in \(D'\) do not belong to the process zone for every evolution \(u^{\epsilon_{k}}(t,x)\) with \(\epsilon_{k}<\delta\) and \(0\leq t\leq T\), i.e.,
for every \(x\in D'\) and \(y\) for which \(|y-x|<\epsilon_{k}\). Then the limit evolution \(u^{0}(t,x)\) evolves elastodynamically on \(D'\) and is governed by the balance of linear momentum expressed by the Navier Lamé equations on the domain \([0,T]\times D'\) given by
where the stress tensor \(\sigma\) is given by,
where \(I_{d}\) is the identity on \(\mathbb{R}^{d}\) and \(\mathrm{Tr}(\mathcal{E} u^{0})\) is the trace of the strain. Here the second derivative \(u_{tt}^{0}\) is the time derivative in the sense of distributions of \(u^{0}_{t}\) and \(\operatorname{div}\sigma\) is the divergence of the stress tensor \(\sigma\) in the distributional sense.
Remark 5.2
The limiting evolution of the cohesive dynamics model is given by the displacement—crack set pair \(u^{0}(t,x)\), \(J_{u^{0}(t)}\). The Navier Lamé equations describes the dynamics of the body away from the evolving fracture path inside the media.
Remark 5.3
The equality \(\lambda=\mu\) appearing in Theorem 5.2 is a consequence of the central force nature of the local cohesive interaction mediated by (1.7). More general non-central interactions are proposed in Sect. 15 of [60] and in the state based peridynamic formulation [64]. The non-central formulations deliver a larger class of energy-volume-shape change relations for homogeneous deformations. Future work will address state based formulations that deliver general anisotropic elastic response for the bulk energy associated with the limiting dynamics.
Remark 5.4
We point out that the cohesive model addressed in this work does not have an irreversibility constraint and the constitutive law (1.7) applies at all times in the peridynamic evolution. Because of this the crack set at each time is given by \(J_{u^{0}(t)}\). For rapid monotonic loading we anticipate that crack growth is increasing for this model, i.e., \(J_{u^{0}(t')}\subset J_{u^{0}(t)}\) for \(t'< t\). For cyclic loading this is clearly not the case and the effects of irreversibility (damage) must be incorporated into in the cohesive model.
6 Mathematical Underpinnings and Analysis
In this section we provide the proofs of theorems stated in Sects. 2, 4 and 5. The first subsection asserts the Lipschitz continuity of \(\nabla PD^{\epsilon_{k}}(u)\) for \(u\) in \(L^{2}_{0}(D;\mathbb{R}^{d})\) and applies the theory of ODE to deduce existence of the cohesive dynamics, see Sect. 6.1. A Gronwall inequality is used to bound the cohesive potential energy and kinetic energy uniformly in time, see Sect. 6.2. Uniformly bounded sequences \(\{u^{\epsilon_{k}}\}_{k=1}^{\infty}\) of cohesive dynamics are shown to be compact in \(C([0,T]; L^{2}_{0}(D;\mathbb{R}^{d}))\), see Sect. 6.3. Any limit point \(u^{0}\) for the sequence \(u^{\epsilon_{k}}\) is shown to belong to SBD for every \(0\leq t\leq T\), see Theorem 6.4 of Sect. 6.3. The limit evolutions \(u^{0}\) are shown to have uniformly bounded elastic energy in the sense of linear elastic fracture mechanics for \(0\leq t\leq T\), see Sect. 6.3. In Sect. 6.4 we pass to the limit in the energy balance equation for cohesive dynamics (2.20) to recover an energy inequality for the limit flow. The balance of linear momentum satisfied by the limit flow is obtained on identifying the weak \(L^{2}\) limit of the sequence \(\{\nabla PD^{\epsilon_{k}}(u^{\epsilon_{k}})\}_{k=1}^{\infty}\) and passing to the limit in the weak formulation of (2.12), see Sect. 6.5. The small strain expansion of the cohesive potential energy (1.12) is derived in Sect. 6.6. We then provide the proof of Theorem 4.1 in Sect. 6.7 and conclude with the proofs of Theorem 2.1 in Sect. 6.8 and Theorem 6.4 in Sect. 6.9.
6.1 Existence of a Cohesive Evolution
The peridynamic equation (1.9) for cohesive dynamics is written as an equivalent first order system. We set \(y^{\epsilon _{k}}=(y^{\epsilon_{k}}_{1},y^{\epsilon_{k}}_{2})^{T}\) where \(y^{\epsilon _{k}}_{1}=u^{\epsilon_{k}}\) and \(y_{2}^{\epsilon_{k}}=u_{t}^{\epsilon_{k}}\). Set \(F^{\epsilon_{k}}(y^{\epsilon_{k}},t)=(F^{\epsilon_{k}}_{1}(y^{\epsilon _{k}},t),F^{\epsilon_{k}}_{2}(y^{\epsilon_{k}},t))^{T}\), where
The initial value problem for \(y^{\epsilon_{k}}\) given by the first order system is
with \(\mathit{LEFM}\) initial conditions \(y^{\epsilon_{k}}(0)=(u_{0},v_{0})^{T}\). In what follows we consider the more general class of initial data \((u_{0},v_{0})\) belonging to \(L^{2}_{0}(D;\mathbb{R}^{d})\times L^{2}_{0}(D;\mathbb{R}^{d})\).
Theorem 6.1
For \(0\leq t\leq T\) there exists unique solution in \(C^{1}([0,T];L^{2}_{0}(D;\mathbb{R}^{d}))\) for the mesoscopic dynamics described by (6.1) with initial data in \(L^{2}_{0}(D;\mathbb{R}^{d})\times L^{2}_{0}(D;\mathbb{R}^{d})\) and body force \(b(t,x)\) in \(C^{1}([0,T];L^{2}_{0}(D;\mathbb{R}^{d}))\).
It now follows that for \(\mathit{LEFM}\) initial data one has a unique solution \(u^{\epsilon_{k}}\) of (2.12) in Sect. 2 belonging to \(C^{2}([0,T];L^{2}_{0}(D;\mathbb{R}^{d}))\).
Proof of Theorem 6.1
A straight forward calculation shows that for a generic positive constant \(C\) independent of \(\mathcal{S}\), \(y-x\), and \(\epsilon_{k}\),
From this it easily follows from Hölder and Minkowski inequalities that \(\nabla PD^{\epsilon_{k}}\) is a Lipschitz continuous map from \(L^{2}_{0}(D;\mathbb{R}^{d})\) into \(L^{2}_{0}(D;\mathbb{R}^{d})\) and there is a positive constant \(C\) independent of \(0\leq t\leq T\), such that for any pair of vectors \(y=(y_{1},y_{2})^{T}\), \(z=(z_{1},z_{2})^{T}\) in \(L^{2}_{0}(D;\mathbb {R}^{d})\times L^{2}_{0}(D;\mathbb{R}^{d})\)
Here for any element \(w=(w_{1},w_{2})\) of \(L^{2}_{0}(D;\mathbb{R}^{d})\times L^{2}_{0}(D;\mathbb{R}^{d})\), \(\Vert w \Vert^{2}_{L^{2}(D;\mathbb{R}^{d})^{2}}= \Vert w_{1}\Vert_{L^{2}(D;\mathbb{R}^{d})}^{2}+\Vert w_{2}\Vert_{L^{2}(D;\mathbb{R}^{d})}^{2}\). Since (6.3) holds the theory of ODE in Banach space [24] shows that there exists a unique solution to the initial value problem (6.1) with \(y^{\epsilon_{k}}\) and \(\partial_{t} y^{\epsilon_{k}}\) belonging to \(C([0,T]; L^{2}_{0}(D;\mathbb{R}^{d}))\) and Theorem 6.1 is proved. In this context we point out the recent work of [29] where existence theory for peridynamic evolutions with Lipschitz continuous pairwise force functions are established. □
6.2 Bounds on Kinetic and Potential Energy for Solutions of PD
In this section we apply Gronwall’s inequality to obtain bounds on the kinetic and elastic energy for peridynamic flows described by Theorem 2.2. The bounds are used to show that the solutions of the PD initial value problem are Lipschitz continuous in time with values in \(L_{0}^{2}(D;\mathbb{R}^{d})\).
We now prove Theorem 2.2. Multiplying both sides of (2.12) by \(u_{t}^{\epsilon_{k}}(t)\) and integration together with a straight forward calculation gives
Set
and applying (6.4) gives
and
Hence
and
We now apply Theorem 2.1 to get the upper bound
where \(\mathit{LEFM}(u_{0},D)\) is the elastic potential energy for linear elastic fracture mechanics given by (2.2) or equivalently (2.5). Theorem 2.2 now follows from (6.9).
Theorem 2.2 implies that PD solutions are Lipschitz continuous in time; this is stated explicitly in Theorem 2.3 of Sect. 2. To prove Theorem 2.3 we write
where the third to last line follows from Jensen’s inequality, the second to last line from Fubini’s theorem and the last inequality follows from the upper bound for \(\Vert u_{t}^{\epsilon_{k}}(t)\Vert^{2}_{L^{2}(D;\mathbb{R}^{d})}\) given by Theorem 2.2.
6.3 Compactness and Convergence
In this section we prove Theorems 5.1 and 5.2. To proceed with the proof of Theorem 5.1 we require the compactness theorem.
Theorem 6.2
(Compactness)
Given a sequence of functions \(u^{\epsilon_{k}}\in L^{2}_{0}(D;\mathbb {R}^{d})\), \(\epsilon_{k}=1/k,k=1,2,\ldots\) such that
then there exists a subsequence \(u^{{\epsilon_{k}}'}\) and limit point \(u\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\cap L^{\infty}(D;\mathbb{R}^{d})\) for which
In what follows it is convenient to change variables \(y=x+\delta\xi\) for \(|\xi|<1\) and \(0<\delta<\alpha/2<1\), here the peridynamic neighborhood \(\mathcal{H}_{\delta}(x)\) transforms to \(\mathcal{H}_{1}(0)=\{ \xi\in\mathbb{R}^{d}; |\xi|<1\}\). The unit vector \(\xi/|\xi|\) is denoted by \(e\). To prove Theorem 6.2 we need the following upper bound given by the following theorem.
Theorem 6.3
(Upper Bound)
For any \(0<\delta<\alpha/2\) there exist positive constants \(\tilde {K}_{1}\) and \(\tilde{K}_{2}\) independent of \(u\in L^{2}_{0}(D;\mathbb{R}^{d})\cap L^{\infty}(D;\mathbb{R}^{d})\) such that
We establish the upper bound in two steps.
Lemma 6.1
(Coercivity)
There exists a positive constant \(C\) independent of \(u\in L^{2}_{0}(D;\mathbb{R}^{d})\) for which
Proof of Lemma 6.1
We prove by contradiction. Suppose for every positive integer \(N>0\) there is an element \(u^{N}\in L_{0}^{2}(D;\mathbb{R}^{d})\) for which
The Cauchy Schwartz inequality together with the triangle inequality deliver a constant \(\overline{K}>0\) independent of \(u\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\) for which
An application of the nonlocal Korn inequality [25, Lemma 6, App. 2] gives the existence of a constant \(\underline{K}>0\) independent of \(u\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\) for which
Applying the inequalities (6.16), (6.17), and (6.18) we discover that \(\overline{K}/N>\underline{K}\) for all integers \(N>0\) to conclude \(\underline{K}=0\) which is a contradiction and Lemma 6.1 is proved. □
Theorem 6.3 now follows from Lemma 6.1 and the upper bound given by
Lemma 6.2
(Upper Bound)
Proof of Lemma 6.2
Consider the concave potential function \(f\) described in the introduction, recall \(f(0)=0\) and given \(M>0\) set \(H_{M}=f(M)/M\). For \(0< r< M\) one has \(r< H_{M}^{-1}f(r)\) and set
so
Now \(f(r)>f(M)\) for \(r>M\) gives
and
Noting that
and collecting results, one has
Lemma 6.2 follows on multiplying both sides of (6.25) by \(J(|\xi|)\) and integration over \(\mathcal{H}_{1}(0)\). Theorem 6.3 follows from Lemmas 6.1 and 6.2. □
Arguing as in as in Lemma 5.4 of [41] we have the monotonicity given by
Lemma 6.3
(Monotonicity)
For any integer \(M\), \(\eta>0\) and \(u\in L^{\infty}(D;\mathbb{R}^{d})\) one has
Now choose the subsequence \(\epsilon_{k}=1/2^{k}\), \(i=1,2,\ldots\) and from Theorem 6.3 and Lemma 6.3 we have for any \(0< K< k\) with \(\delta=2^{-K}\), \(\epsilon_{k}=2^{-k}\),
Applying the hypothesis (6.12) to inequality (6.27) gives a finite constant \(B\) independent of \(\epsilon _{k}\) and \(\delta\) for which
for all \(\epsilon_{k}<\delta\). One can then apply (6.28) as in [41] (or alternatively apply (6.28) and arguments similar to the proof of the Kolomogorov-Riesz compactness theorem [43]) to show that the sequence \(\{u^{\epsilon_{k}}\}_{k=1}^{\infty}\) is a totally bounded subset of \(L^{2}_{0}(D;\mathbb{R}^{d})\) and Theorem 6.2 is proved.
Now it is shown that the family of evolutions \(\{u^{\epsilon_{k}}\} _{k=1}^{\infty}\) is relatively compact in \(C([0,T];L_{0}^{2}(D;\mathbb{R}^{d}))\). For each \(t\) in \([0,T]\) we apply Theorem 2.2 and Hypothesis 5.1 to obtain the bound
where \(C<\infty\) and is independent of \(\epsilon_{k}\), \(k=1,2,\ldots{}\), and \(0\leq t\leq T\). With this bound we apply Theorem 6.2 to assert that for each \(t\) the sequence \(\{u^{\epsilon_{k}}(t)\}_{k=1}^{\infty}\) is relatively compact in \(L^{2}(D;\mathbb{R}^{d})\). From Theorem 2.3 the sequence \(\{u^{\epsilon_{k}}\} _{k=1}^{\infty}\), is seen to be uniformly equi-continuous in \(t\) with respect to the \(L^{2}(D;\mathbb{R}^{d})\) norm and we immediately conclude from the Ascoli theorem that \(\{u^{\epsilon _{k}}\}_{k=1}^{\infty}\) is relatively compact in \(C([0,T];L^{2}(D;\mathbb{R}^{d}))\). Therefore we can pass to a subsequence also denoted by \(\{u^{\epsilon _{k}}(t)\}_{k=1}^{\infty}\) to assert the existence of a limit evolution \(u^{0}(t)\) in \(C([0,T];L^{2}(D;\mathbb{R}^{d}))\) for which
and Theorem 5.1 is proved.
We now prove Theorem 5.2. One has that limit points of sequences satisfying (6.12) enjoy higher regularity and that the \(\mathit{LEFM}\) energy for the limit point provides a lower bound on the sequence of energies.
Theorem 6.4
(Higher Regularity and Lower Bound)
Every limit point \(u^{0}\) of a sequence \(\{u^{\epsilon_{k}}\}_{k=1}^{\infty}\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\) satisfying (6.12) belongs to \(\mathit{SBD}\cap L^{\infty}(D,\mathbb {R}^{d})\) and we have the lower bound
We provide the proof of Theorem 6.4 in Sect. 6.9.
Since \(u^{0}(t)\) is a cluster point for the sequence \(\{u^{\epsilon _{k}}(t)\}\) we apply Theorem 6.4 to discover that the limit has bounded elastic energy in the sense of fracture mechanics, i.e.,
and Theorem 5.2 is proved.
We conclude this section by stating the following pointwise convergence of cohesive energies to the \(\mathit{LEFM}\) energy for \(u\in \mathit{SBD}\).
Theorem 6.5
(Point Wise Convergence of Peridynamic Energies for Cohesive Dynamics)
Suppose \(u\) belongs to \(L_{0}^{2}(D;\mathbb{R}^{d})\), then
Theorem 6.5 follows immediately from Theorems 2.1 and 6.4. Indeed given \(u\in \mathit{SBD}\cap L^{\infty}(D;\mathbb{R}^{d})\) and \(u\in L^{2}_{0}(D;\mathbb{R}^{d})\) we apply Theorem 2.1 and note that the choice \(u^{\epsilon _{k}}=u\) satisfies (6.12) and apply Theorem 6.4 to conclude that
6.4 Energy Inequality for the Limit Flow
In this section we prove Theorem 5.3. We begin by showing that the limit evolution \(u^{0}(t,x)\) has a weak derivative \(u_{t}^{0}(t,x)\) belonging to \(L^{2}([0,T]\times D;\mathbb{R}^{d})\). This is summarized in the following theorem.
Theorem 6.6
On passage to subsequences if necessary the sequence \(u_{t}^{\epsilon_{k}}\) weakly converges in \(L^{2}([0,T]\times D;\mathbb{R}^{d})\) to \(u^{0}_{t}\), where
for all compactly supported smooth test functions \(\psi\) on \([0,T]\times D\).
Proof
The bound on the kinetic energy given in Theorem 2.2 implies
Therefore the sequence \(u^{\epsilon_{k}}_{t}\) is bounded in \(L^{2}([0,T]\times D;\mathbb{R}^{d})\) and passing to a subsequence if necessary we conclude that there is a limit function \(\tilde{u}^{0}\) for which \(u_{t}^{\epsilon_{k}}\rightharpoonup\tilde{u}^{0}\) weakly in \(L^{2}([0,T]\times D;\mathbb{R}^{d})\). Observe also that the uniform convergence (6.30) implies that \(u^{\epsilon _{k}}\rightarrow u^{0}\) in \(L^{2}([0,T]\times D;\mathbb{R}^{d})\). On writing the identity
applying our observations and passing to the limit it is seen that \(\tilde{u}^{0}=u_{t}^{0}\) and the theorem follows. □
To establish Theorem 5.3 we require the following inequality.
Lemma 6.4
For almost every \(t\) in \([0,T]\) we have
Proof
We start with the identity
and for every non-negative bounded measurable function of time \(\psi (t)\) defined on \([0,T]\) we have
Together with the weak convergence given in Theorem 6.6 one easily sees that
Applying (6.36) and invoking the Lebesgue dominated convergence theorem we conclude
to recover the inequality given by
The lemma follows noting that (6.43) holds for every non-negative test function \(\psi\). □
Theorem 5.3 now follows immediately on taking the \(\epsilon_{k}\rightarrow0\) limit in the peridynamic energy balance equation (2.20) of Theorem 2.4 and Theorem 6.5, (6.32), and (6.38) of Lemma 6.4.
6.5 Stationarity Conditions for the Limit Flow
In this section we prove Theorem 5.4. The first subsection establishes Theorem 5.4 using Theorem 6.7. Theorem 6.7 is proved in the second subsection.
6.5.1 Proof of Theorem 5.4
To proceed we make the change of variables \(y=x+\epsilon\xi\) where \(\xi \) belongs to the unit disk \(\mathcal{H}_{1}(0)\) centered at the origin and the strain \(\mathcal{S}\) is of the form
where \(e={\xi}/{|\xi|}\). It is convenient for calculation to express the strain through the directional difference operator \(D_{e}^{\epsilon|\xi|}u\) defined by
One also has
and the integration by parts formula for functions \(u\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\), densities \(\phi\) in \(L_{0}^{2}(D;\mathbb{R})\) and \(\psi\) continuous on \(\mathcal{H}_{1}(0)\) given by
Note further for \(v\) in \(C^{\infty}_{0}(D;\mathbb{R}^{d})\) and \(\phi\) in \(C^{\infty}_{0}(D;\mathbb{R})\) one has
where the convergence is uniform in \(D\).
Taking the first variation of the action integral (2.11) gives the Euler equation in weak form
where the test function \(\delta=\delta(x,t)=\psi(t)\phi(x)\) is smooth and has compact support in \([0,T]\times D\). Next we make the change of function and write \(F_{s} (\mathcal{S})=\frac {1}{s}f(s\mathcal{S}^{2})\), \(F'_{s}(\mathcal{S})=2\mathcal{S}f'(s\mathcal {S}^{2})\), and \(s={\epsilon_{k}}|\xi|\) we transform (6.49) into
where
For future reference observe that \(F_{s}(r)\) is convex-concave in \(r\) with inflection point \(\overline{r}_{s}=\overline{r}/\sqrt{s}\) where \(\overline{r}\) is the inflection point of \(f(r^{2})=F_{1}(r)\). One also has the estimates
We send \(\epsilon_{k}\rightarrow0\) in (6.50) applying the weak convergence Theorem 6.6 to the first term to obtain
Theorem 5.4 follows once we identify the limit of the second term in (6.54) for smooth test functions \(\phi(x)\) with support contained in the set \(D'\subset D\) described in the hypothesis of Theorem 5.4. We state the following convergence theorem.
Theorem 6.7
Given any infinitely differentiable test function \(\phi\) with compact support in \(D'\), then
where \(\mathbb{C}\mathcal{E} u^{0}:\mathcal{E}\phi=\sum_{ijkl=1}^{d}\mathbb {C}_{ijkl}\mathcal{E}u^{0}_{ij}\mathcal{E}\phi_{kl}\), \(\mathbb{C}\mathcal {E}u^{0}=\lambda I_{d} \operatorname{Tr}(\mathcal{E}u^{0})+2\mu\mathcal{E}u^{0}\), and \(\lambda \) and \(\mu\) are given by (5.7).
Theorem 6.7 is proved in Sect. 6.5.2. The sequence of integrals on the left hand side of (6.55) are uniformly bounded in time, i.e.,
this is demonstrated in (6.75) of Lemma 6.7 in Sect. 6.5.2. Suppose \(\phi(x)\) has support contained in \(D'\) and applying the Lebesgue bounded convergence theorem together with Theorem 6.7 with \(\delta(t,x)=\psi(t)\phi(x)\) delivers the desired result
and we recover the identity
from which Theorem 5.4 follows.
6.5.2 Proof of Theorem 6.7
We decompose the difference \(D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e\) as
where
where \(\overline{r}\) is the inflection point for the function \(F_{1}(r)=f(r^{2})\). Here \((D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e)^{+}\) is defined so that (6.59) holds. We prove Theorem 6.7 by using the following two identities described in the lemmas below.
Lemma 6.5
For any \(\phi\) in \(C^{\infty}_{0}(D;\mathbb{R}^{d})\)
Lemma 6.6
Assume the hypothesis of Theorem 5.4 and define the weighted Lebesgue measure \(\nu\) by \(d\nu=|\xi|J(|\xi|)\,d\xi\, dx\) for any Lebesgue measurable set \(S\subset D'\times\mathcal{H}_{1}(0)\). Passing to subsequences if necessary \(\{(D_{e}^{\epsilon_{k} |\xi |}u^{\epsilon_{k}}\cdot e)\}_{k=1}^{\infty}\) converges weakly in \(L^{2}(D'\times\mathcal{H}_{1}(0);\nu)\) to \(\mathcal{E} u^{0} e\cdot e\), i.e.,
for any test function \(\psi(x,\xi)\) in \(L^{2}(D'\times\mathcal{H}_{1}(0);\nu)\).
We now apply the lemmas. Observing that \(D_{e}^{\epsilon_{k} |\xi|}\phi \cdot e \) converges strongly in \(L^{2}(D'\times\mathcal{H}_{1}(0):\nu)\) to \(\mathcal{E}\phi e\cdot e\) for test functions \(\phi\) in \(C^{\infty}_{0}(D';\mathbb{R}^{d})\) and from the weak \(L^{2}(D'\times \mathcal{H}_{1}(0):\nu )\) convergence of \((D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e)\) together with the hypothesis of Theorem 5.4 we deduce that
Now we show that
where \(\mu\) and \(\lambda\) are given by (5.7). To see this we write
and observe that \(\varGamma(e)\) is a totally symmetric tensor valued function defined for \(e\in S^{d-1}\) with the property
for every rotation \(Q\) in \(SO^{d}\). Here repeated indices indicate summation. We write
to see that for every \(Q\) in \(SO^{d}\)
Therefore we conclude that \(\int_{S^{d-1}}\varGamma_{ijkl}(e)\,de\) is an isotropic symmetric 4th order tensor and of the form
Here we evaluate \(a\) by contracting both sides of (6.69) with a trace free matrix and \(b\) by contracting both sides with the \(d\times d\) identity and calculation delivers (6.64). Theorem 6.7 now follows immediately from (6.63) and (6.61).
To establish Lemmas 6.5 and 6.6 we develop the following estimates for the sequences \((D_{e}^{\epsilon_{k} |\xi |}u^{\epsilon_{k}}\cdot e)^{-}\) and \((D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon _{k}}\cdot e)^{+}\). We define the set \(K^{+,\epsilon_{k}}\) by
We have the following string of estimates.
Lemma 6.7
We introduce the generic positive constant \(0< C<\infty\) independent of \(0<\epsilon_{k}<1\) and \(0\leq t\leq T\) and state the following inequalities that hold for all \(0<\epsilon_{k}<1\) and \(0\leq t\leq T\) and for \(C^{\infty}(D)\) test functions \(\phi\) with compact support on \(D\).
Proof
For \((x,\xi)\in K^{+,\epsilon_{k}}\) we apply (6.52) to get
and in addition since \(|\xi|\leq1\) we have
where Theorem 2.2 implies that the right most element of the sequence of inequalities is bounded and (6.71) follows noting that the inequality (6.77) is equivalent to (6.71). More generally, since \(|\xi|\leq1\) we may argue as above to conclude that
for \(0\leq p\). We apply (6.53) and (6.78) to find
and (6.72) follows.
A basic calculation shows there exists a positive constant independent of \(r\) and \(s\) for which
so
and
where Theorem 2.2 implies that the right most element of the sequence of inequalities is bounded and (6.73) follows.
To establish (6.74) we apply Hölder’s inequality to find that
and (6.74) follows from (6.71) and (6.73).
We establish (6.75). This bound follows from the basic features of the potential function \(f\). We will recall for subsequent use that \(f\) is smooth positive, concave and \(f'\) is a decreasing function with respect to its argument. So for \(A\) fixed and \(0\leq h\leq A^{2}\overline{r}^{2}\) we have
The bound (6.75) is now shown to be a consequence of the following upper bound valid for the parameter \(0< A<1\) given by
We postpone the proof of (6.85) until after it is used to establish (6.75). Set \(h_{\epsilon_{k}}= (D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e)^{-}\) to note
Applying Hölders inequality, (6.72), (6.73), (6.85), and (6.86) gives
and (6.75) follows.
We establish the inequality (6.85). Set \(h_{\epsilon _{k}}=(D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e)^{-}\) and for \(0< A<1\) introduce the set
To summarize \((x,\xi)\in K^{+,\epsilon_{k}}_{A}\) implies \(A^{2}\overline {r}^{2}\leq\epsilon_{k}|\xi||h_{\epsilon_{k}}|^{2}\leq\overline{r}^{2}\) and \((x,\xi)\notin K^{+,\epsilon_{k}}_{A}\) implies \(\epsilon_{k}|\xi||h_{\epsilon _{k}}|^{2}< A^{2}\overline{r}^{2}\) and \(|f'(\epsilon_{k}|\xi||h_{\epsilon _{k}}|^{2})-f'(0)|\leq|f'(A^{2}\overline{r}^{2})-f'(0)|\). Inequality (6.73) implies
the last inequality follows since \(1\geq|\xi|>0\). Hence
and it follows that
Collecting observations gives
and (6.85) follows. □
We now prove Lemma 6.5. Write
and from (6.72) it follows that
To finish the proof we identify the limit of the right hand side of (6.94). Set \(h_{\epsilon_{k}}=(D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e)^{-}\) and apply Hólder’s inequality to find
We estimate the first factor in (6.95) and apply (6.86), Hölder’s inequality, (6.73), and (6.85) to obtain
Lemma 6.5 follows on applying the bound (6.96) to (6.95) and passing to the \(\epsilon _{k}\) zero limit and noting that the choice of \(0< A<1\) is arbitrary.
We now prove Lemma 6.6. From the hypothesis of Theorem 5.4 we have for \(\phi\in C_{0}^{1}(D')\)
We form the test functions \(\phi(x)\psi(\xi)\), with \(\phi\in C_{0}^{1}(D')\) and \(\psi\in C(\mathcal{H}_{1}(0))\). From (6.73) we may pass to a subsequence to find that \((D_{e}^{\epsilon_{k} |\xi|}u^{\epsilon_{k}}\cdot e)^{-}\) weakly converges to the limit \(g(x,\xi)\) in \(L^{2}(D'\times\mathcal{H}_{1}(0);\nu)\). With this in mind we write
where we have integrated by parts using (6.47) in the last line of (6.98). Noting that \(D_{-e}^{\epsilon_{k} |\xi|}\phi(x)\) converges uniformly to \(-e\cdot\nabla\phi(x)\) and from the strong convergence of \(u^{\epsilon _{k}}\) to \(u^{0}\) in \(L^{2}\), we obtain
Collecting results we have
Application of Fubini’s theorem gives
for every test function \(\psi\in C(\mathcal{H}_{1}(0))\), and we conclude that
for every \(\phi\in C_{0}^{1}(D')\). Applying the definition of the distributional derivative in the context of SBD shows that \(Eu^{0}e\cdot e\lfloor D'=g(x,\xi)\mathcal{L}^{d}\lfloor D'=\mathcal{E} u^{0} e\cdot e\mathcal{L}^{d}\lfloor D'\) for \(\xi\in H_{1}(0)\), and we conclude that \(g(x,\xi)=\mathcal{E} u^{0}(x) e\cdot e\) on \(D\times\mathcal {H}_{1}(0)\) a.e. and Lemma 6.6 is proved.
6.6 Cohesive Energy Density for Homogeneous Strain
In this subsection we outline the calculation used to establish the identity (1.12) for the energy density. When the displacement is linear \(u(x)=Fx\) then the associated strain is given by \(\mathcal{S}=Fe\cdot e\). Here it is assumed that \(\mathcal {S}^{2}\ll \mathcal{S}_{c}^{2}\) so \(|y-x|\mathcal{S}^{2}\ll|y-x|\mathcal{S}_{c}^{2}\) and we expand \(f(|y-x|\mathcal{S}^{2})\) in a Taylor series about 0 in the small parameter \(|y-x|\mathcal{S}^{2}\) noting that \(f(0)=0\) to get
Substitution of (6.103) into (1.2) and the change of variables \(\xi=(y-x)/\epsilon\) gives
where \(\mathcal{H}_{1}(0)\) is the unit ball centered at the origin and \(\omega_{d}\) is its volume \(d=2,3\). Observe next that \((Fe\cdot e)^{2}=\sum{ijkl}F_{ij}F_{kl}e_{i}e_{j}e_{k}e_{l}\) and the leading order term in (6.104) is given by
where
The identity (1.12) now follows directly from (6.64).
6.7 Proof of Theorem 4.1
We begin with the proof on the upper bound on the size of the process zone given by Theorem 4.1. Recall the set \(K^{+,\epsilon_{k}}\) is defined by
and recall that the potential function \(f(r^{2})=F_{1}(r)\) is increasing to get
and we have
Rearranging factors in (6.109) gives
Introduce the characteristic function \(\chi^{+,\epsilon_{k}}(x,\xi)\) defined on \(D\times\mathcal{H}_{1}(0)\) taking the value 1 for \((x,\xi)\) in \(K^{+,\epsilon_{k}}\) and zero otherwise. Observe that
so
For \(0<\overline{\theta}\leq1\), Tchebyshev’s inequality delivers
and Theorem 4.1 follows on applying (6.9) and (6.10).
6.8 Proof of Theorem 2.1
Here and in the following section we apply a slicing decomposition [41] to the energies \(PD^{\epsilon_{k}}\) to reduce the analysis to the one dimensional case. The results of the one dimensional analyses on slices are extended to \(D\) using the structure theorem for \(\mathit{SBD}\) on slices and the appropriate integral geometric arguments. The slicing theorem and integralgeometric measure appropriate for this approach in the context of \(\mathit{SBD}\) are given by Theorems 4.5 and 4.10 of [5].
We introduce the unit ball \(\mathcal{H}_{1}(0)=\{\zeta\in\mathbb{R}^{d}: | \xi|\leq1\}\), \(d=2,3\) and define the \(d-1\) dimensional subspace \(\varPi ^{\xi}=\{y\in\mathbb{R}^{d}:y\cdot\xi=0\}\). In what follows we change coordinates and \(x\in D\) is written as \(x=y+t\xi\). We introduce
To proceed we set \(u^{\xi,y}=u(y+t\xi)\cdot\xi\) for \(t\in D_{y}^{\xi}\) and the space of special functions of bounded variation over the set \(D_{y}^{\xi}\) is denoted by \(\mathit{SBV}(D_{y}^{\xi})\). The distributional derivative of \(u^{\xi,y}\) is the Radon measure denoted by \(D u^{\xi,y}\) and its total variation on \(D_{y}^{\xi}\) is \(|D u^{\xi,y}|(D_{y}^{\xi})\), see [18]. We introduce the following structure theorem for \(\mathit{SBD}\) functions on slices [5].
Theorem 6.8
(One Dimensional Restrictions of \(\mathit{SBD}\) Functions)
Let \(u\in L^{1}(D;\mathbb{R}^{d})\) and let \(\{e_{1},e_{2},\ldots,e_{d}\}\) be a basis of \(\mathbb{R}^{d}\). Then the following two conditions are equivalent:
-
1.
For every \(\xi=e_{i}+e_{j}\), \(1\leq i\), \(j\leq d\):
-
(a)
\(u^{\xi,y}\in \mathit{SBV}(D_{y}^{\xi})\) for \(\mathcal{H}^{d-1}\), a.e. \(y\in D^{\xi}\),
-
(b)
\(\int_{\varPi^{\xi}}|D u^{\xi,y}|(D_{y}^{\xi})\,d\mathcal{H}^{d-1}<\infty\),
-
(a)
-
2.
\(u\in \mathit{SBD}\).
Moreover if \(u\in \mathit{SBD}\) and \(\xi\in\mathbb{R}^{d}\setminus\{0\}\) the following properties hold
-
1.
For \(\mathcal{H}^{d-1}\) a.e. \(y\in D^{\xi}\) one has \(\partial_{t} u^{\xi,y}(t)=\mathcal{E}u(y+t\xi) \xi\cdot\xi\) for \(\mathcal{L}^{1}\) a.e. \(t\in D_{y}^{\xi}\),
-
2.
\(J_{u^{\xi,y}}=(J_{u}^{\xi})_{y}^{\xi}\) for \(\mathcal{H}^{d-1}\) a.e. \(y\in D^{\xi}\) where \(J_{u}^{\xi}=\{x\in J_{u}:(u^{+}(x)-u^{-}(x))\cdot\xi\neq0\}\),
-
3.
\(\mathcal{H}^{d-1}(J_{u}\setminus J_{u}^{\xi})=0\) for a.e. \(\xi\in S^{d-1}\).
For any \(u\in L_{0}^{2}(D;\mathbb{R}^{d})\cap \mathit{SBD}\) we apply Fubini’s theorem and write
where
Recall here that \(D_{e}^{\epsilon_{k}|\xi|}u\cdot e\) is the strain defined by (6.45) and \(F_{s}(r)=\frac{1}{s}f(sr^{2})\). Introduce \(u^{e,y}(t)=u(y+te)\cdot e\), then
and on setting \(x=y+te\) and changing coordinates in (6.116) we have
where the functional defined over one dimensional sections \(D_{y}^{e}\) is given by
Theorem 6.8 asserts that the one dimensional restrictions \(u^{e,y}\) of \(u\in L^{2}_{0}(D;\mathbb{R}^{d})\cap \mathit{SBD}\) belong to \(\mathit{SBV}(D_{y}^{e})\) for a.e. \(y\in\varPi^{e}\) and let \(J_{u^{e,y}}\) denote the jump set of \(u^{e,y}(t)\) for \(t\in D_{y}^{e}\). The zero dimensional Hausdorff measure of the jump set \(\mathcal {H}^{0}(J_{u^{e,y}})\) counts the number of jumps of \(u^{e,y}(t)\) on \(D_{y}^{e}\). Define the one dimensional functional \(\mathcal{F}_{0}(u^{e,y},D_{y}^{e})\) by
The upper bound for one dimensional sections is given by the following theorem.
Theorem 6.9
Proof
If \(\mathcal{F}_{0}(u^{e,y},D_{y}^{e})=\infty\) the theorem holds automatically so we will assume that \(\mathcal {F}_{0}(u^{e,y},D_{y}^{e})<\infty\). Let \(A_{\epsilon_{k}}=\{t\in D_{y}^{e}: [t,t+\epsilon_{k}|\xi|]\cap J_{u^{e,y}}\neq\emptyset\}\) and note for \(F_{s}(r)=\frac{1}{s}f(sr^{2})\) that
We have
and below we provide an upper bound for each term. If \(t\notin A_{\epsilon_{k}}\) then \(u^{e,y}\) is absolutely continuous in \([t,t+\epsilon_{k}|\xi|]\) and by Hölder’s inequality
From (6.122) we see that the first term in (6.123) is bounded above by
Application of (6.122) to the second term of (6.123) delivers the upper bound
and the theorem follows. □
Applying Theorem 6.9 to (6.118) gives the estimate
We identify the first term on the righthand side of (6.127) using the structure theorem for SBD. From Theorem 6.8 we have \(\partial_{t} u^{e,y}(t)=\mathcal{E}u(y+te) e\cdot e\) for \(\mathcal{L}^{1}\) a.e. \(t\in D_{y}^{e}\) and \(\mathcal{H}^{d-1}\) \(y\in D^{e}\) and it follows that
To identify the second term we introduce the integralgeometric measure developed in [9]. The non-negative Borel measure \(\lambda _{u}\) on \(D\) is given by
and
for every \(e\in S^{d-1}\). We give the following theorem [5] relating integralgeometric measure to the Hausdorff measure of the jump set for \(u\in \mathit{SBD}\).
Theorem 6.10
Now observe that the second term on the righthand side of (6.127) is given by
and collecting results we write (6.127) as
and we obtain
Theorem 2.1 now follows on applying Fubini’s theorem to the first term and (6.64) and application of Theorem 6.10 to the second term.
6.9 Proof of Theorem 6.4
The higher regularity is established first on the one dimensional sections \(D_{y}^{e}\). Consider a limit point \(u^{0}\) described in Theorem 6.4 and write \(u^{e,y}(t)=u^{0}(y+te)\cdot e\) with \(t\in D_{y}^{e}\). We extend this function by zero for \(t\in\mathbb{R}\setminus D_{y}^{e}\). Now we construct piecewise affine approximations as in [41]. We start by defining a local Griffith free energy for \(u \in L^{\infty}(\mathbb{R})\). Given an interval \([a,b]\subset\mathbb{R}\), set \(J=|u(b)-u(a)|\) and define
Pick \(a\in\mathbb{R}\) for which \(a+q\) is a Lebesgue point for \(u^{e,y}\) for every rational number \(q\) and consider the intervals \(I_{j}^{z}=(a+z/j,a+(z+1)/j)\) for \(z\in\mathbb{Z}\) and \(J_{j}^{z}\) is the absolute value of the difference of the function \(u^{e,y}\) evaluated at the end points of \(I_{j}^{z}\). We construct the piecewise affine interpolations \(v_{j}(t)\) on each interval \(I_{j}^{z}\) according to the following energy minimizing criteria.
-
1.
If
$$\begin{aligned} f'(0) \biggl(\frac{J_{j}^{z}}{1/j} \biggr)^{2}< \frac{f_{\infty}}{1/j}, \end{aligned}$$(6.136)then
$$\begin{aligned} v_{j}(t)=u^{e,y}(a+z/j)+(t-a-z/j)\frac{u^{e,y}(a+(z+1)/j)-u^{e,y}(a+z/j) }{1/j}. \end{aligned}$$(6.137) -
2.
Otherwise \(v_{j}\) is chosen to be the piecewise constant function which agrees with \(u^{e,y}\) at the endpoints of \(I_{j}^{z}\) and has a single jump discontinuity at the mid point of \(I_{j}^{z}\).
The interpolants \(v_{j}\) satisfy the following properties:
-
1.
$$\begin{aligned} v_{j} \in L^{\infty}\bigl(D_{y}^{e} \bigr), \qquad\lim_{j\rightarrow\infty}v_{j}=u^{e,y} \hbox{ in $L^{1}\bigl(D_{y}^{e}\bigr)$}, \end{aligned}$$(6.138)
-
2.
$$\begin{aligned} \lambda\bigl(J_{j}^{z},I_{j}^{z} \bigr)=\mathcal{F}_{0}\bigl(v_{j},I_{j}^{z} \bigr)= \int_{I_{j}^{z}}f'(0)|\partial _{t} v_{j}|^{2}\,dt+f_{\infty}\mathcal{H}_{0} \bigl(J_{v_{j}}\cap I_{j}^{z}\bigr), \end{aligned}$$(6.139)
-
3.
$$\begin{aligned} \mathcal{F}_{0}\bigl(v_{j},D_{y}^{e} \bigr)= \int_{D_{y}^{e}}f'(0)|\partial_{t} v_{j}|^{2}\, dt+f_{\infty}\mathcal{H}_{0}(J_{v_{j}})= \sum_{z\in\mathbb{Z}}\lambda\bigl(J_{j}^{z},I_{j}^{z} \bigr). \end{aligned}$$(6.140)
Consider now any sequence \(\{\tilde{u}_{k}\}\) converging to \(u^{e,y}\) in \(L^{2}(D_{y}^{e})\). Application of Lemma 3.5 of [41] delivers the following lower bound:
Lemma 6.8
With these preliminaries we now state the following higher regularity property and lower bound on one dimensional sections.
Theorem 6.11
Suppose \(\tilde{u}_{k}\rightarrow u^{e,y}\) in \(L^{2}(D_{y}^{e})\) and
Then \(u^{e,y}\) belongs to \(\mathit{SBV}(D_{y}^{e})\cap L^{\infty}(D_{y}^{e})\) for \(\mathcal {H}^{d-1}\) \(a.e\). \(y\in D^{e}\) and
Proof
We have \(\Vert u^{e,y}\Vert_{L^{\infty}(D_{y}^{e})}<\infty\), \(\liminf_{j\rightarrow\infty}\Vert v_{j}\Vert_{L^{\infty}(D_{y}^{e})}<\infty\) and Lemma 6.8 together with (6.142) delivers the inequality
It follows from (6.144) that \(v_{j}\) belongs to \(\mathit{SBV}(D_{y}^{e})\) for all \(j\in\mathbb{N}\), the sequence \(\{|\partial_{t} v_{j}|\}\) is equi-integrable and \(\sup_{j\in\mathbb{N}}\mathcal{H}_{0}(J_{v_{j}})<\infty \), so by the SBV compactness theorem there exists \(v\) belonging to \(\mathit{SBV}(D_{y}^{e})\) and a subsequence also denoted by \(\{v_{j}\}\) converging to \(v\) in \(L^{1}(D_{y}^{e})\). Since \(\{v_{j}\}\) also converges to \(u^{e,y}\) in \(L^{1}(D_{y}^{e})\) we conclude that \(v=u^{e,y}\) and
follows from the weak convergence of \(\partial_{t} v_{j}\) to \(\partial_{t} u^{e,y}\) and \(\liminf_{j\rightarrow\infty}\mathcal{H}_{0}(J_{v_{j}})\geq \mathcal{H}_{0}(J_{u^{e,y}})\). □
Now we recover the higher regularity for \(u^{0}\). Assume the hypothesis of Theorem 6.4 and for \(u^{\epsilon_{k}}\rightarrow u^{0}\) in \(L_{0}^{2}(D;\mathbb{R}^{d})\) we have \(u^{0}\in L^{\infty}(D;\mathbb{R}^{d})\). The function \(u^{\epsilon_{k}}(y+te)\cdot e\) is written \(u^{\epsilon_{k},e,y}\) and \(u^{\epsilon_{k},e,y}\rightarrow u^{e,y}\) in \(L^{2}(D_{y}^{e})\) for \(a.e\). \(y\in D^{e}\), with \(\sup_{k}\{\Vert u^{\epsilon_{k},e.y}\Vert_{L^{\infty}(D_{y}^{e})<\infty}\}\). Then
where the first inequality follows from the Fatou Lemma and the second inequality follows from Theorem 6.11. Since \(\Vert u^{e,y}\Vert_{L^{\infty}(D_{y}^{e})}< C\), for \(\mathcal{H}^{d-1}\) \(a.e\). \(y\in D^{e}\), we have the upper estimate on the total variation given by
where \(K\) is a constant independent of \(y\) and \(e\). Since \(\liminf_{\epsilon_{k}\rightarrow0}PD^{\epsilon_{k}}(u^{\epsilon_{k}})<\infty\) it follows from (6.146) and (6.147) that
Therefore we can find a linear independent set of vectors \(e_{1},e_{2},\ldots, e_{d}\), such that parts 1(a) and (b) of Theorem 6.8 hold to conclude that \(u^{0}\in \mathit{SBD}\). Last we argue as in Sect. 6.8 to discover
7 Dynamics and Limits of Energies that \(\varGamma\)-Converge to Griffith Fracture Energies
In this section we first recall the definition of \(\varGamma\)-convergence and collect results to remark that the nonlocal cohesive energies introduced here \(\varGamma\)-converge to the energies of linear elastic fracture mechanics. The \(\varGamma\)-convergence follows immediately from the results of the previous sections.
Consider a sequence of functions \(\{F_{j}\}\) defined on a metric space \(\mathbb{M}\) with values in \(\overline{\mathbb{R}}\) together with a function \(F\) also defined on \(\mathbb{M}\) with values in \(\overline {\mathbb{R}}\). In what follows let \(X\) be a subset of \(\mathbb{M}\).
Definition 7.1
We say that \(F\) is the \(\varGamma\)-limit of the sequence \(\{F_{j}\}\) with respect to \(\mathbb{M}\) on \(X\) if the following two properties hold:
-
1.
for every \(x\) in \(X\) and every sequence \(\{x_{j}\}\) converging to \(x\), we have that
$$\begin{aligned} F(x)\leq\liminf_{j\rightarrow\infty} F_{j}(x_{j}), \end{aligned}$$(7.1) -
2.
for every \(x\) in \(X\) there exists a recovery sequence \(\{x_{j}\}\) converging to \(x\), for which
$$\begin{aligned} F(x)=\lim_{j\rightarrow\infty} F_{j}(x_{j}). \end{aligned}$$(7.2)
Now for \(u\) in \(L^{\infty}(D;\mathbb{R}^{d})\cap L_{0}^{2}(D;\mathbb{R}^{d})\) define the Griffith fracture energy \(PD^{0}\) by
where \(\mathit{LEFM}(u,D)\) is defined in (2.5). The \(\varGamma\)-convergence of cohesive peridynamic energies to the Griffith fracture energy is given by the following theorem.
Theorem 7.1
\(PD^{0}\) is the \(\varGamma\)-limit of \(PD^{\epsilon_{k}}\) with respect to \(L^{2}(D;\mathbb{R}^{d})\) convergence on \(L^{\infty}(D;\mathbb{R}^{d})\).
We now illustrate how the approach presented in the earlier sections can be used to examine limits of dynamics associated with other energies that \(\varGamma\)-converge to the Griffith fracture energy. As an example we consider the phase field approach based on the Ambrosio-Tortorelli approximation for dynamic brittle fracture calculations [17]. This model is seen to be a well posed formulation in the sense that existence of solutions can be shown [45]. To illustrate the ideas we focus on anti-plane shear and the model is described by an out of plane elastic displacement \(u^{\epsilon}(x,t)\) and phase field \(0\leq v^{\epsilon}(x,t)\leq1\) defined for points \(x\) belonging to the domain \(D\subset\mathbb{R}^{2}\). The potential energy associated with the cracking body is given by the Ambrosio-Tortorelli potential
with
and
Here \(a^{\epsilon}(t)=a^{\epsilon}(x,t)=(v^{\epsilon}(x,t))^{2}+\eta^{\epsilon}\), with \(0<\eta^{\epsilon}\ll \epsilon\). In this model the phase field \(v^{\epsilon}\), provides an approximate description of a freely propagating crack taking the value 1 for points \((x,t)\) away from the crack and zero on the crack. To formulate the problem we introduce the space \(H^{1}_{0}(D)\) defined to be displacements \(u\) in \(H^{1}(D)\) with zero Dirichlet data on \(\partial D\) and the set of functions \(H_{1}^{1}(D)\) defined to be functions \(v\) in \(H^{1}(D)\) for which \(v=1\) on \(\partial D\). The total energy is given by
The body force \(f(x,t)\) is prescribed and the displacement—phase field pair \((u^{\epsilon},v^{\epsilon})\) is a solution of the initial boundary value problem [45] given by:
for \(t\in(0,T]\) with initial conditions \(u^{\epsilon}(0)=u_{0}\), \(\partial _{t} u^{\epsilon}(0)=u_{1}\in H^{1}_{0}(D)\) and \(v_{0}\in H_{1}^{1}(D)\) with \(0\leq v_{0}\leq1\), a.e. in \(D\). In addition for each \(t\in[0,T]\) the pair is required to satisfy the crack stability condition
and energy balance
In this formulation the pair \(u^{\epsilon}(t)\), \(v^{\epsilon}(t)\) provides a regularized model for free crack propagation. Here the phase field tracks the evolution of the crack with \(v^{\epsilon}=1\) away from the crack and \(v^{\epsilon}=0\) in the crack set. This model includes a viscous dissipation term \(\nabla\partial_{t} u^{\epsilon}\). Here the viscosity is chosen to match the elasticity and is also given by the value \(a^{\epsilon}\).
For a body force \(f(x,t)\) in \(C^{1}([0,T];L^{2}(D))\) it is shown in [45] that there exists at least one trajectory \((u^{\epsilon},v^{\epsilon})\in H^{2}((0,T);L^{2}(D))\cap W^{1,\infty}((0,T); H^{1}_{0}(D))\times W^{1,\infty}((0,T); H_{1}^{1}(D))\) satisfying (7.8) in the weak sense, i.e.,
for all \(\varphi\) in \(H^{1}_{0}(D)\) for almost every \(t\) in \((0,T]\), with \(u^{\epsilon}(0)=u^{\epsilon}_{0}\), \(\partial_{t} u^{\epsilon}(0)=u^{\epsilon}_{1}\), \(v^{\epsilon}(0)=v^{\epsilon}_{0}\), and such that (7.9) and (7.10) are satisfied for all times \(0\leq t\leq T\). The problem is formulated in a simplified setting to illustrate the ideas and note that this type of evolution is shown to exist for evolutions with more general boundary conditions and for displacements in two and three dimensions, see [45]. For future reference the pair \((u^{\epsilon}(t),v^{\epsilon}(t))\) is referred to as a phase field fracture evolution.
In what follows we pass to the \(\epsilon\rightarrow0\) limit in the phase field evolutions to show existence of a limiting evolution with bounded linear elastic fracture energy. Here the limit evolution \(u^{0}(t)\) is shown to take values in the space of special functions of bounded variation \(\mathit{SBV}(D)\). This space is well known and for antiplane shear problems this space coincides with the space SBD introduced earlier in Sect. 5. For a treatment of SBV and its relation to fracture the reader is referred to [3].
Applying the techniques developed in previous sections it is possible to state and prove the following theorem on the dynamics associated with the phase field evolutions \((u^{\epsilon},v^{\epsilon})\) in the limit as \(\epsilon\rightarrow0\).
Theorem 7.2
(Sharp Interface Limit of Phase Field Fracture Evolutions)
Suppose for every \(\epsilon>0\) that: (a) the potential energy of the initial data \((u_{0}^{\epsilon},v_{0}^{\epsilon})\) is uniformly bounded, i.e., \(\sup_{\epsilon>0} \{P^{\epsilon}(u^{\epsilon}_{0},v_{0}^{\epsilon}) \}<\infty\), and that (b) \(\Vert u^{\epsilon}(t)\Vert_{L^{\infty}(D)}< C\) for all \(0<\epsilon\) and \(0\leq t\leq T\). Then on passing to a subsequence if necessary in the phase field fracture evolutions \((u^{\epsilon}, v^{\epsilon})\) there exists an anti-plane displacement field \(u^{0}(x,t)\) in \(\mathit{SBV}(D)\) for all \(t\in[0,T]\) such that \(u^{0}\in C([0,T];L^{2}(D))\) and
with
for \(0\leq t\leq T\).
For anti-plane shear deformations the energy \(\mathit{GF}\) is a special form of the energy \(\mathit{LEFM}\) introduced in Sect. 5.
The strategy we will use for proving Theorem 7.2 is the same as the one developed in the proofs of Theorems 5.1 and 5.2. This strategy can be made systematic and applied to evolutions associated with potential energies that \(\varGamma\)-converge to the Griffith fracture energy. It consists of four parts:
-
1.
Constructing upper bounds on the kinetic and potential energy of the evolutions that hold uniformly for \(0\leq t\leq T\) and \(0<\epsilon\).
-
2.
Showing compactness of the evolution \(u^{\epsilon}(t)\) in \(L^{2}(D)\) for each time \(0\leq t\leq T\).
-
3.
Showing limit points of the sequence \(\{u^{\epsilon}(t)\}\) belong to \(\mathit{SBD}(D)\) for each time \(0\leq t\leq T\).
-
4.
\(\varGamma\)-convergence of the potential energies to the Griffith energy \(\mathit{LEFM}\) (or \(\mathit{GF}\) as appropriate).
Assume first that Parts 1 through 4 hold for the phase field fracture evolution with potential energies \(P^{\epsilon}\) given by (7.4). These are used as follows to prove Theorem 7.2. Part 1 is applied as in (6.11) to show that the sequence of evolutions \(u^{\epsilon}(t)\) is uniformly Lipschitz continuous in time with respect to the \(L^{2}(D)\) norm, i.e.,
for \(K\) independent of \(\epsilon\) and for any \(0\leq t_{1}< t_{2}\leq T\). Part 2 together with (7.14) and the Ascoli theorem imply the existence of a subsequence and a limit \(u^{0}(x,t)\in C([0,T];L^{2}(D))\) such that the convergence (7.12) holds. Part 3 shows that \(u^{0}(x,t)\) belongs to \(\mathit{SBV}(D)\) for every time in \([0,T]\). Part 4 together with Part 1 and the lower bound property of \(\varGamma \)-convergence described by (7.1) shows that (7.13) holds and Theorem 7.2 follows.
We now establish Parts 1 through 4 for the dynamic phase field fracture evolution introduced in [45]. To obtain a uniform bound on the kinetic and potential energy differentiate both sides of the energy balance (7.10) with respect to time to get
Manipulation and application of the identity \(f\partial_{t} u^{\epsilon}=\partial_{t}(f u^{\epsilon})-\partial_{t} f u^{\epsilon}\) to (7.15) delivers the inequality
Now set
and proceed as in Sect. 6.2 to get
Part 1 easily follows from (7.18) noting that \(\sup_{\epsilon >0}\{W^{\epsilon}(0)\}<\infty\) is a consequence of hypothesis (a) of Theorem 7.2. For this example Parts 2 and 3 follow from the uniform bound of Part 1, hypothesis (b) of Theorem 7.2 and the well known compactness result for the Ambrosio Tortorelli functional, see for example the remark following Theorem 2.3 of [39]. Part 4 is given by the Ambrosio-Tortorelli \(\varGamma\)-convergence result [4] as expressed in Theorem 2.3 of [39].
8 Conclusions
The cohesive model for dynamic brittle fracture evolution presented in this paper does not require extra constitutive laws such as a kinetic relation between crack driving force and crack velocity or a crack branching condition. Instead the evolution of the process zone together with the fracture set is governed by one equation consistent with Newton’s second law given by (1.9). This is a characteristic feature of peridynamic models [60, 64]. This evolution is intrinsic to the formulation and encoded into the nonlocal cohesive constitutive law. Crack nucleation criteria although not necessary to the formulation follow from the dynamics and are recovered here by viewing nucleation as a dynamic instability, this is similar in spirit to [65] and the work of [28] for phase transitions. Theorem 4.1 explicitly shows how the size of the process zone is controlled by the radius of the horizon. This analysis shows that the horizon size \(\epsilon\) for cohesive dynamics is a modeling parameter that can be calibrated according to the size of the process zone obtained from experimental measurements. The process zone is seen to concentrate on a set of zero volume as the length scale of non-locality characterized by the radius of the horizon \(\epsilon\) goes to zero, see Theorem 4.1. In this limit the dynamics is shown to coincide with the simultaneous evolution of a displacement crack set pair. Here the evolution is elastodynamic for points in space-time away from the crack set. The shear and Lamé moduli together with the fracture toughness for the limit evolution are described explicitly by the nonlocal potentials and given by (5.7), and (5.8).
In closing we note that more generally the “time” variable appearing in peridynamics need not be the physical time, and that a “motion” may be regarded as any type of one-parameter evolution. In this way the theory need not be connected strictly to the presence of inertia.
References
Agwai, A., Guven, I., Madenci, E.: Predicting crack propagation with peridynamics: a comparative study. Int. J. Fract. 171, 65–78 (2011)
Alicandro, R., Focardi, M., Gelli, M.S.: Finite-difference approximation of energies in fracture mechanics. Ann. Sc. Norm. Super. Pisa, Cl. Sci. 23, 671–709 (2000)
Ambrosio, L., Brades, A.: Energies in SBV and variational models in fracture mechanics. In: Cioranescu, D., Damlamian, A., Donato, P. (eds.) Homogenization and Applications to Materials Science 9, pp. 1–22. Gakkotosho, Tokyo (1997)
Ambrosio, L., Tortorelli, V.M.: Approximation of functionals depending on jumps by elliptic functionals via \(\varGamma\)-convergence. Commun. Pure Appl. Math. XLIII, 999–1036 (1990)
Ambrosio, L., Coscia, A., Dal Maso, G.: Fine properties of functions with bounded deformation. Arch. Ration. Mech. Anal. 139, 201–238 (1997)
Attouch, H., Buttazzo, G., Michaille, G.: Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization. MPS-SIAM Series on Optimization. SIAM, Philadelphia (2006)
Barenblatt, G.I.: The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 7, 55–129 (1962)
Bažant, Z.P., Planas, J.: Fracture and Size Effect in Concrete and Other Quasibrittle Materials. CRC Press, Boca Raton (1998)
Bellettini, G., Coscia, A., Dal Maso, G.: Compactness and lower semicontinuity properties in SBD(\(\varOmega\)). Math. Z. 228, 337–351 (1998)
Bellido, J.C., Morra-Corral, C., Pedregal, P.: Hyperelasticity as a \(\varGamma\)-limit of peridynamics when the horizon goes to zero. Calc. Var. Partial Differ. Equ. 54, 1643–1670 (2015). doi:10.1007/s00526-015-0839-9
Belytschko, T., Black, T.: Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 45, 601–620 (1999)
Belytschko, T., Gracie, R., Ventura, G.: A review of the extended/generalized finite element methods for material modelling. Model. Simul. Mater. Sci. Eng. 17, 043001 (2009)
Bobaru, F., Hu, W.: The meaning, selection, and use of the Peridynamic horizon and its relation to crack branching in brittle materials. Int. J. Fract. 176, 215–222 (2012)
Borden, M., Verhoosel, C., Scott, M., Hughes, T., Landis, C.: A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 217–220, 77–95 (2012)
Bouchbinder, E., Fineberg, J., Marder, M.: Dynamics of simple cracks. Annu. Rev. Condens. Matter Phys. 1, 371–395 (2010)
Bourdin, B., Francfort, G., Marigo, J.-J.: The variational approach to fracture. J. Elast. 91, 5–148 (2008)
Bourdin, B., Larsen, C., Richardson, C.: A time-discrete model for dynamic fracture based on crack regularization. Int. J. Fract. 168, 133–143 (2011)
Braides, A.: Approximation of Free Discontinuity Problems. Lecture Notes in Mathematics, vol. 1694. Springer, Berlin (1998)
Braides, A.: Discrete approximation of functionals with jumps and creases. In: Homogenization. Naples, 2001. Gakuto Internat. Ser. Math. Sci. Appl., vol. 18, pp. 147–153. Gakkotosho, Tokyo (2003)
Braides, A.: Local Minimization, Variational Evolution and \(\varGamma\)-Convergence. Lecture Notes in Mathematics, vol. 2094. Springer, Berlin (2014)
Braides, A., Gelli, M.S.: Limits of discrete systems with long-range interactions. J. Convex Anal. 9, 363–399 (2002)
Buehler, M.J., Abraham, F.F., Gao, H.: Hyperelasticity governs dynamic fracture at a critical length scale. Nature 426, 141–146 (2003)
Cox, B.N., Yang, Q.D.: In quest of virtual tests for structural composites. Science 314, 1102–1107 (2006)
Driver, B.: Analysis Tools with Applications. Springer, Berlin (2003). E-book
Du, Q., Gunzburger, M., Lehoucq, R., Zhou, K.: Analysis of the volume-constrained peridynamic Navier equation of linear elasticity. J. Elast. 113, 193–217 (2013)
Duarte, C.A., Hamzeh, O.N., Liszka, T.J., Tworzydlo, W.W.: A generalized finite element method for the simulation of three-dimensional dynamic crack propagation. Comput. Methods Appl. Mech. Eng. 190, 2227–2262 (2001)
Dugdale, D.: Yielding of steel sheets containing slits. J. Mech. Phys. Solids 8, 100–104 (1960)
Dyal, K., Bhattacharya, K.: Kinetics of phase transformations in the peridynamic formulation of continuum mechanics. J. Mech. Phys. Solids 54, 1811–1842 (2006)
Emmrich, E., Puhst, D.: Well-posedness of the peridynamic model with Lipschitz continuous pairwise force function. Commun. Math. Sci. 11, 1039–1049 (2013)
Emmrich, E., Weckner, O.: On the well-posedness of the linear peridynamic model and its convergence towards the Navier equation of linear elasticity. Commun. Math. Sci. 5, 851–864 (2007)
Evans, L.C.: Partial Differential Equations. Graduate Studies in Mathematics, vol. 19. Am. Math. Soc., Providence (2010)
Falk, M., Needleman, A., Rice, J.R.: A critical evaluation of cohesive zone models of dynamic fracture. J. Phys. IV 11, 43–50 (2001)
Federer, H.: Geometric Measure Theory. Springer, Berlin (1969)
Foster, J., Silling, S.A., Chen, W.: An energy based failure criterion for use with peridynamic states. Int. J. Multiscale Comput. Eng. 9, 675–688 (2011)
Francfort, G., Larsen, C.: Existence and convergence for quasi-static evolution in brittle fracture. Commun. Pure Appl. Math. 56, 1465–1500 (2003)
Francfort, G., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46, 1319–1342 (1998)
Freund, L.B.: Dynamic Fracture Mechanics. Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press, Cambridge (1998)
Gerstle, W., Sau, N., Silling, S.: Peridynamic modeling of concrete structures. Nucl. Eng. Des. 237, 1250–1258 (2007)
Giacomini, A.: Ambrosio-Tortorelli approximation of quasi-static evolution of brittle fractures. Calc. Var. Partial Differ. Equ. 22, 129–172 (2005)
Gobbino, M.: Finite difference approximation of the Mumford-Shah functional. Commun. Pure Appl. Math. 51, 197–228 (1998)
Gobbino, M., Mora, M.G.: Finite difference approximation of free discontinuity problems. Proc. R. Soc. Edinb., Sect. A, Math. 131, 567–595 (2001)
Ha, Y.D., Bobaru, F.: Studies of dynamic crack propagation and crack branching with peridynamics. Int. J. Fract. 162, 229–244 (2010)
Hanche-Olsen, B., Holden, H.: The Kolomogorov-Riesz compactness theorem. Expo. Math. 28, 385–394 (2010)
Hillerborg, A., Modeer, M., Petersson, P.E.: Analysis of crack formation and crack growth by means of fracture mechanics and finite elements. Cem. Concr. Res. 6, 731–781 (1976)
Larsen, C.J., Ortner, C., Suli, E.: Existence of solutions to a regularized model of dynamic fracture. Math. Models Methods Appl. Sci. 20, 1021–1048 (2010)
Lipton, R.: Dynamic brittle fracture as a small horizon limit of peridynamics. J. Elast. 117, 21–50 (2014). doi:10.1007/s10659-013-9463-0
Lussardi, L., Negri, M.: Convergence of nonlocal finite element energies for fracture mechanics. Numer. Funct. Anal. Optim. 28, 83–109 (2007)
Marder, M.: Supersonic rupture of rubber. J. Mech. Phys. Solids 54, 491–532 (2006)
Marder, M., Gross, S.: Origin of crack tip instabilities. J. Mech. Phys. Solids 43, 1–48 (1995)
Marigo, J.-J., Truskinovsky, L.: Initiation and propagation of fracture in the models of Griffith and Barenblatt. Contin. Mech. Thermodyn. 16, 391–409 (2004)
Matthies, H., Strang, G., Christiansen, E.: The saddle point of a differential program. In: Energy Methods in Finite Element Analysis. Wiley, New York (1979)
Mengesha, T., Du, Q.: Nonlocal constrained value problems for a linear peridynamic Navier equation. J. Elast. 116, 27–51 (2014). doi:10.1007/s10659-013-9456-z
Miehe, C., Hofacker, M., Welschinger, F.: A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 199, 2765–2778 (2010)
Möes, N., Delbow, J., Belytschko, T.: A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46, 131–150 (1999)
Morgan, F.: Geometric Measure Theory, a Beginner’s Guide. Academic Press, San Diego (1995)
Mumford, D., Shah, J.: Optimal approximation by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 17, 577–685 (1989)
Oh, E.S., Walton, J.R., Slattery, J.C.: A theory of fracture based upon an extension of continuum mechanics to the nanoscale. J. Appl. Mech. 73, 792–798 (2006)
Remmers, J.J.C., de Borst, R., Needleman, A.: The simulation of dynamic crack propagation using the cohesive segments method. J. Mech. Phys. Solids 56, 70–92 (2008)
Schmidt, B., Fraternali, F., Ortiz, M.: Eigenfracture: an eigendeformation approach to variational fracture. Multiscale Model. Simul. 7, 1237–1266 (2009)
Silling, S.A.: Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 48, 175–209 (2000)
Silling, S.A., Askari, E.: A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 83, 1526–1535 (2005)
Silling, S.A., Bobaru, F.: Peridynamic modeling of membranes and fibers. Int. J. Non-Linear Mech. 40, 395–409 (2005)
Silling, S.A., Lehoucq, R.: Convergence of peridynamics to classical elasticity theory. J. Elast. 93, 13–37 (2008)
Silling, S.A., Epton, M., Weckner, O., Xu, J., Askari, E.: Peridynamic states and constitutive modeling. J. Elast. 88, 151–184 (2007)
Silling, S., Weckner, O., Askari, E., Bobaru, F.: Crack nucleation in a peridynamic solid. Int. J. Fract. 162, 219–227 (2010)
Slepyan, L.I.: Models and Phenomena in Fracture Mechanics. Springer, Berlin (2002)
Suquet, P.M.: Un espace fonctionnel pour les équations de la plasticité. Ann. Fac. Sci. Toulouse 1, 77–87 (1979)
Weckner, O., Abeyaratne, R.: The effect of long-range forces on the dynamics of a bar. J. Mech. Phys. Solids 53, 705–728 (2005)
Wheeler, M.F., Wick, T., Wollner, W.: An augmented-Lagrangian method for the phase-field approach for pressurized fractures. Comput. Methods Appl. Mech. Eng. 271, 69–85 (2014)
Willis, J.R.: A comparison of the fracture criteria of Griffith and Barenblatt. J. Mech. Phys. Solids 15, 152–162 (1967)
Xu, X.P., Needleman, A.: Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 42, 1397–1434 (1994)
Acknowledgements
The author would like to thank Stewart Silling, Richard Lehoucq and Florin Bobaru for stimulating and fruitful discussions. This research is supported by NSF grant DMS-1211066, AFOSR grant FA9550-05-0008, and NSF EPSCOR Cooperative Agreement No. EPS-1003897 with additional support from the Louisiana Board of Regents.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lipton, R. Cohesive Dynamics and Brittle Fracture. J Elast 124, 143–191 (2016). https://doi.org/10.1007/s10659-015-9564-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-015-9564-z