1 Introduction

There has been significant recent renewed interest in the mechanics of anisotropic non-linear hyperelastic materials motivated by applications in the modeling of soft biological tissue. As is often the case in the physical sciences, the theory has outpaced both the gathering of reliable experimental data and the efficient interpretation of such data. The second of these deficiencies will be addressed here for extension-torsion experiments of transversely isotropic materials. Transversely isotropic materials will be considered here because of their wide use in biomechanics (see, e.g., the books of Humphrey [9] and Taber [19]) and because transverse isotropy is the simplest form of anisotropy. Extension-torsion experiments are important material characterization tests, given that the associated deformation is inhomogeneous and combines both volumetric and deviatoric modes of deformation. Their importance were recognized in the seminal work of Rivlin and Saunders [18] where these tests were crucial in obtaining useful explicit forms of the isotropic strain-energy function to model rubbers.

The main obstacle in the general analysis of the deformation of transversely isotropic hyperelastic materials is the inherent complexity of the underlying system of equations of equilibrium and boundary conditions. This is the case even when the simplifying assumptions of homogeneity and incompressibility are assumed. The problem of torsion superimposed on extension of a circular cylinder is a classic problem that has received considerable attention in the literature on nonlinear elasticity for homogeneous incompressible isotropic materials. A recent review has been carried out by Kanner and Horgan [11]. See also Horgan and Murphy [6]. The corresponding problem for transversely isotropic materials is considerably more complicated (see, e.g., Horgan and Murphy [8]). However, when the direction of transverse anisotropy is aligned along the axis of the cylinder, it was shown by Humphrey et al. [10] that major simplifications occur. The purpose of the present paper is to show that further analytic progress can be made due to the presence of a naturally occurring small dimensionless parameter \(\hat{\tau}\) that suggests a simple asymptotic approach. Although the analysis presented here is standard, it will be shown that expanding the basic equations in a Maclaurin series in \(\hat{\tau}\) enables a large subclass of constitutive models to be included in the modeling process. Thus one does not have to specify ab initio a particular form of the strain-energy function. The usefulness of adopting this asymptotic approach does not seem to have been recognized previously in the literature, even for isotropic materials. It will be shown that small values of this parameter can be interpreted as describing twisting through moderate angles of slender cylinders. Since physiological strains are themselves moderate (for example, Pearson et al. [15] measured the diastolic diameter of the descending aorta in normotensive men to be 2.11 cm and the systolic diameter to be 2.29 cm) and experimental testing in extension-torsion tests typically requires slender specimens, the regime of small values for \(\hat{\tau}\) will be valid for the typical extension-torsion experiments for soft biological tissue.

This is indeed the case for the experimental data considered here, which are data for rabbit papillary muscles obtained by Criscione et al. [3]. Papillary muscles are approximately cylindrical extensions of the ventricle and play an essential role in the operation of both the mitral and tricuspid valves in the heart. As noted in [3], papillary muscles are composite structures comprised of a hyperelastic myocardial core and endocardial sheath. A commonly used model for the mechanical behavior of papillary muscles is based on their being modeled as incompressible homogeneous nonlinearly hyperelastic materials. The orientation of the collagen fibres in papillary muscles is aligned with the longitudinal axis of the muscle, which will be modeled here as a circular cylinder. This morphology of the muscles naturally motivates the assumption of transverse isotropy. Particularly elegant expositions of this type of modeling can be found in the books of Humphrey [9] and of Taber [19] and in the work of Humphrey et al. [10]. These studies provided motivation for the approach presented here. To demonstrate a predictive capability of the modeling process proposed here, a specific form of the strain-energy function is adopted. The simplest specification is a truncated Taylor series in the appropriate invariants. It will be shown that a good fit is obtained between the data of Criscione et al. [3] and a four-term polynomial constitutive model.

Poynting [17] noted that under a pure torsional couple a solid cylinder of copper wire experiences an elongation. It can be shown that under reasonable constitutive assumptions, all homogeneous incompressible isotropic nonlinearly elastic materials display this classic Poynting effect. An excellent discussion of the Poynting effect within the context of rubber elasticity can be found in [1] and within the context of the passive response of papillary muscles in [19]. It was shown recently by Horgan and Murphy [7] that the classic Poynting effect is not necessarily observed for transversely isotropic cylinders. In fact, for sufficiently large anisotropy, a reverse Poynting effect was predicted to occur where the cylinder shortens on twisting. In the present paper we develop an approximate theory for the problem of torsion superimposed on extension of long slender cylinders for moderate angles of twist. The leading-order term in the average axial stress required to maintain a constant stretch in such cylinders is shown to be of \(O(\hat{\tau}^{2})\). The sign of this term determines whether the stretched cylinder tends to elongate or shorten on twisting and an explicit condition on the strain-energy density is obtained that determines which behavior occurs. For the special case of pure torsion where no extension is allowed, this condition determines whether the classical or reverse Poynting effect occurs. For the rabbit papillary muscles, the theoretical results predict and the experimental results confirm that a reverse Poynting-type effect occurs where the stretched rabbit muscle tends to shorten on twisting.

2 Extension and Torsion of Transversely Isotropic Cylinders

The mechanical properties of elastomeric materials are described in continuum mechanics in terms of a strain-energy density function W per unit undeformed volume. For our purposes here, it is sufficient to consider the subclass of incompressible transversely-isotropic materials for which W=W(I 1,I 4) where I 1=tr B=tr FF T and F is the gradient of the deformation. On denoting the unit vector defining the direction of anisotropy in the undeformed configuration by A, we have I 4=FA⋅FA and the Cauchy stress T is given by

$$\boldsymbol{T}=-p\boldsymbol{I}+2W_1\boldsymbol{B}+2W_4\boldsymbol{a}\otimes \boldsymbol{a}, $$
(2.1)

where a=FA, W i ≡∂W/∂I i (i=1,4), ⊗ denotes the tensor product with Cartesian components a i a j and p is a hydrostatic pressure term associated with the incompressibility constraint det B=1. For detailed accounts of the theory of hyperelasticity for anisotropic materials see, e.g., Holzapfel [5] and Ogden [12].

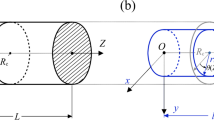
Consider a long solid circular cylinder of radius A and length L composed of an incompressible transversely-isotropic hyperelastic material subjected to a stretch in the axial direction and then to a twist at its ends. On using cylindrical coordinates (R,Θ,Z) in the undeformed configuration and (r,θ,z) in the current configuration, we may thus write

$$r=\gamma^{-1/2}R, \qquad \theta=\Theta+\tau\gamma Z, \qquad z=\gamma Z, $$
(2.2)

where τ denotes the twist per unit length of the stretched rod and γ denotes the given axial stretch. The coefficient γ −1/2 appears in (2.2)1 in order to maintain incompressibility, so that for extension (γ>1), the cylinder necessarily contracts laterally. The deformed radius a is given by a=γ −1/2 A. Corresponding to (2.2), one has the left Cauchy-Green tensor B

$$\boldsymbol{B}=\left[\begin{array}{c@{\quad}c@{\quad}c}\gamma^{-1} & 0 & 0\\0 & \gamma^{-1}+\gamma\tau^2R^2 & \gamma^{3/2}\tau R\\0 & \gamma^{3/2}\tau R & \gamma^2\end{array}\right], $$
(2.3)

and so the relevant invariants are

$$I_{1} = \gamma^{2} + 2\gamma^{-1} + \gamma\tau^{2}R^{2},\qquad I_{3}=1. $$
(2.4)

To describe the anisotropy of concern here, we write the unit vector A in the undeformed configuration as A=(0,cosψ,sinψ) where ψ denotes a pitch angle. Thus the fibers are considered to be helically wound throughout the cylinder. On using the notation c≡cosψ, s≡sinψ, we find that

$$I_{4} = \gamma^{ - 1}c^{2} + 2\tau Rsc + \bigl( 1 + \gamma^{ -1}\tau^{2}R^{2} \bigr)\gamma^{2}s^{2}. $$
(2.5)

General expressions for the physical components of the Cauchy stresses for the case where W=W(I 1,I 4) are given in [9] and [10]. We confine attention here to the resultant applied moment M and the average axial stress N necessary to maintain the deformation. On using the results of [10] and on converting to the notation of the present paper we obtain

$$M \equiv\int_{0}^{2\pi} \int_{0}^{a} T_{z\theta} r^{2}drd\theta =4\pi\int_{0}^{A} \bigl[ \tau RW_{1} + \bigl( \gamma^{ - 1}sc + s^{2}\tau R \bigr)W_{4}\bigr]R^{2}dR, $$
(2.6)

and

(2.7)

respectively, where the subscript on W denotes differentiation with respect to the corresponding invariant and these derivatives are evaluated at (2.4), (2.5).

The purpose of this paper is to exploit the simplicity in the analysis of the foregoing problem when the intrinsic non-dimensional parameter \(\hat{\tau} = \tau A\) is small. This simplicity is especially enhanced if the resultant moment and force are either even or odd in \(\hat{\tau}\). In general this is not the case. However in the important special case of transverse isotropy along the longitudinal axis of the cylinder where ψ=π/2, equations (2.6), (2.7) simplify to

(2.8)
(2.9)

with I 4 now given by

$$I_4=\gamma^2+\gamma\tau^2R^2. $$
(2.10)

It follows immediately that in this special case, the quantities M, N are odd and even functions of \(\hat{\tau}\) respectively. Consequently attention will be focused on this special case.

Note that on setting τ=0 in (2.2) we have the deformation of simple extension. It follows immediately from (2.8), (2.9) on setting τ=0 that

$$M = 0,\qquad N_{0} \equiv N |_{\tau = 0} = 2\bigl( \gamma - \gamma^{ - 2} \bigr)W_{1}^{0} + 2\gamma W_{4}^{0}, $$
(2.11)

where the superscript ‘0’ attached to partial derivatives of the strain-energy function denote evaluation when their arguments have the values

$$I_1=\gamma^2+2\gamma^{-1},\qquad I_4=\gamma^2. $$
(2.12)

Therefore

(2.13)

and, in particular,

$$\left.\frac{dN_{0}}{d\gamma} \right|_{\gamma = 1} = 6W_{1}( 3{,}1 ) + 2W_{4}( 3{,}1 )+ 4W_{44}( 3{,}1 ). $$
(2.14)

It will be required that N 0=0 when γ=1 and hence from (2.11) we obtain

$$W_4(3{,}1)=0. $$
(2.15)

We note that this restriction can also be motivated more generally from (2.1) on assuming that the stress be purely hydrostatic in the undeformed state (cf. [16]). On using (2.15), (2.14) thus simplifies to

$$\left. \frac{dN_{0}}{d\gamma} \right|_{\gamma = 1} = 6W_{1}( 3{,}1 ) + 4W_{44}( 3{,}1). $$
(2.16)

On physical grounds, one expects the axial force required to produce a simple extension to be a monotone increasing function of γ and so we require that

$$3W_{1}( 3{,}1 ) + 2W_{44}( 3{,}1 ) > 0. $$
(2.17)

3 The Resultant Boundary Conditions

The resultants (2.8), (2.9) can be rewritten in a non-dimensional form on using the following non-dimensional variables:

$$\rho = \frac{R}{A},\qquad \hat{\tau} = \tau A. $$
(3.1)

The quantity \(\hat{\tau}\) is the total angle of twist. In terms of these variables, (2.9) becomes

$$N = 2\int_{0}^{1} \bigl[ \bigl( 2\bigl( \gamma - \gamma^{ - 2} \bigr) - \hat{\tau}^{2}\rho^{2} \bigr) W_{1} + \bigl( 2\gamma - \hat{\tau} ^{2}\rho^{2} \bigr) W_{4} \bigr]\rho d\rho, $$
(3.2)

where now

$$I_{1} = \gamma^{2} + 2\gamma^{ - 1} + \gamma\hat{\tau} ^{2}\rho^{2},\qquad I_{4} = \gamma^{2} + \gamma\hat{\tau} ^{2}\rho^{2}. $$
(3.3)

This relation will next be expanded in a Maclaurin series about \(\hat{\tau} = 0\) and truncated after a finite number of terms. This should yield good fits with experimental data when \(\hat{\tau} \ll 1\). It is worthwhile noting that \(\hat{\tau}\) is not an easily measured physical parameter and consequently, it is not immediately obvious when these asymptotic forms apply. However

$$\hat{\tau} = \tau A = \tau L\cdot\frac{A}{L} \equiv\tilde{\tau} \Omega. $$
(3.4)

Both of the quantities \(\tilde{\tau}\), Ω have an obvious physical interpretation: \(\tilde{\tau}\) is the relative twist of the planar ends of the cylinder and is the strain measure typically measured in torsion experiments and Ω is the aspect ratio of the cylinder. Thus infinitesimal values of \(\hat{\tau}\) can be identified with the twisting of slender cylinders, provided, of course, that the relative twist is not too large. This is the interpretation adopted here although we note that the asymptotic forms obtained in the sequel are likely to be valid in other contexts such as moderate relative twists and moderate aspect ratios whose product is infinitesimal. In particular, we note that the asymptotic forms obtained here are likely to be valid for the testing of biological soft tissue since the range of strains of physiological interest is small. This view is validated in the next section where it is shown that experimental data for the twisting of papillary muscles from rabbits are matched extremely well by such expansions. This match is facilitated by the fact that papillary muscles from rabbits were found by Pagani and Julian [14] to have aspect ratios of the order of 0.1, which will be assumed typical.

On expanding \(N( \hat{\tau} )\) in a Maclaurin series, and exploiting the fact that \(N( \hat{\tau} )\) is an even function in \(\hat{\tau}\), we obtain

$$N( \hat{\tau} ) = N_{0} + N_{2}\hat{\tau} ^{2} + O( \hat{\tau} ^{4} ), $$
(3.5)

where N 0 is defined in (2.11) and

$$N_{2} = - \frac{1}{2}\bigl( W_{1}^{0} + W_{4}^{0} \bigr) + \bigl( \gamma^{2} -\gamma^{ - 1} \bigr) W_{11}^{0} + \bigl( 2\gamma^{2} - \gamma^{ - 1} \bigr) W_{14}^{0}+ \gamma^{2}W_{44}^{0}. $$
(3.6)

From a modeling perspective, the advantage of this expansion is that truncation after just two terms yields an expression that is valid up to \(O( \hat{\tau} ^{4} )\) and is therefore likely to be valid for even moderate values of the parameter \(\hat{\tau}\). For pure torsion, the coefficient of the second-order term, henceforth denoted by \(N_{2}^{PT}\), is therefore given by

$$N_{2}^{PT} = - \frac{1}{2}W_{1}( 3{,}1 ) + W_{14}( 3{,}1) + W_{44}( 3{,}1 ), $$
(3.7)

where we have used (2.15).

If the axial stretch is held constant, it follows from (3.5) that the sign of \(dN / d\hat{\tau}\) up to \(O( \hat{\tau} ^{3} )\) is determined by the sign of (3.6). Thus we have shown that \(dN / d\hat{\tau} < 0\) if and only if

$$2\bigl(\gamma^2-\gamma^{-1}\bigr)W_{11}^0+2\bigl(2\gamma^2-\gamma^{-1}\bigr)W_{14}^0+2\gamma^2W_{44}^0<W_1^0+W_4^0. $$
(3.8)

Thus in order to keep the length of the cylinder constant upon twisting, the axial force needs to be decreased with increasing twist. For the important special case of pure torsion for which no extension is allowed, (3.8) simplifies to

$$2( W_{14}( 3{,}1 ) + W_{44}( 3{,}1 ) ) <W_{1}( 3{,}1 ), $$
(3.9)

where again we have used (2.15). Thus the condition (3.9) ensures that the axial force required to maintain pure torsion is compressive. In the absence of such a force, the cylinder would elongate on twisting reflecting the classic Poynting effect. However, if the inequality sign in (3.9) is reversed, then the leading term in (3.5) given by (3.7) is positive and so to within the order of \(\hat{\tau}\) under consideration the axial force is tensile and in the absence of such a force, the cylinder would shorten on twisting. This reverse-Poynting effect has been discussed recently by Horgan and Murphy [7] for the exact theory of pure torsion for transversely isotropic materials modeled by (2.1).

In terms of the non-dimensional variables defined in (3.1), the resultant moment relation (2.8) becomes

$$M = 4\pi A^{3}\hat{\tau} \int_{0}^{1} ( W_{1} + W_{4} )\rho^{3}d\rho, $$
(3.10)

where the invariants have the form (3.3). Expanding in a Maclaurin series in \(\hat{\tau}\) yields

$$M = M_{1}\hat{\tau} + M_{3}\hat{\tau} ^{3} + O\bigl( \hat{\tau} ^{5} \bigr), $$
(3.11)

where

$$M_{1} \equiv\pi A^{3}\bigl( W_{1}^{0} + W_{4}^{0} \bigr),\qquad M_{3} \equiv\frac{2\pi A^{3}\gamma}{3}\bigl( W_{11}^{0} + 2W_{14}^{0} + W_{44}^{0} \bigr). $$
(3.12)

For pure torsion, these coefficients simplify to

$$M_{1}^{PT} = \pi A^{3}W_{1}( 3{,}1 ),\qquad M_{3}^{PT} = \frac{2\pi A^{3}}{3}[W_{11}( 3{,}1 ) + 2W_{14}( 3{,}1 ) + W_{44}( 3{,}1 ) ]. $$
(3.13)

It is now proposed that the two relations (3.5) and (3.11) should be sufficient to model experiments where slender transversely isotropic cylinders with the direction of anisotropy aligned along the longitudinal axis are first axially stretched and then moderately twisted while maintaining the length of the cylinder. Note that this theory is essentially a five-constant theory: four of the constants are coefficients of the powers of \(\hat{\tau}\) in (3.5), (3.11) and the fifth is necessary to satisfy (2.15). Once again, we would like to emphasise the fact that (3.5) and (3.11) are valid for all forms of the strain-energy function W=W(I 1,I 4). In order to obtain a predictive capability, a specific form of the strain-energy function must be specified.

The simplest five-constant strain-energy density of the form W=W(I 1,I 4) is the following five-term polynomial expansion in I 1−3, I 4−1:

(3.14)

Polynomial forms of this type have been used to model myocardial tissue (see, e.g. Humphrey [9] and references cited therein). Of course, another well-known alternative is to use exponential forms. The restriction (2.15) is satisfied if and only if c 01=0. Thus the strain-energy is actually a four-parameter model of the form

$$W^{4c} = c_{10}( I_{1} - 3 ) + c_{20}( I_{1} - 3 )^{2} + c_{02}( I_{4}- 1 )^{2} + c_{11}( I_{1} - 3 )( I_{4} - 1 ). $$
(3.15)

The restriction (2.17) requires that

$$3c_{10}+4c_{02}>0. $$
(3.16)

The general Poynting criterion (3.8) for this material model reduces to

$$2\gamma^{3}( c_{20} + c_{02} + c_{11} ) + \gamma( 6c_{20} + 2c_{02} +4c_{11} - c_{10} ) - 4( c_{11} + 2c_{20} ) < 0, $$
(3.17)

which simplifies in the case of pure torsion to

$$4c_{02} + 2c_{11} - c_{10} < 0. $$
(3.18)

For this quadratic model, the coefficients in (3.5) and (3.11) are given by

(3.19)

In the important special case of pure torsion, these coefficients simplify to

(3.20)

It will be shown in the next section that (3.5), (3.11) fit the data from torsion superimposed on extension experiments on rabbit papillary muscles extremely well and the least squares fit of the constitutive model (3.15) with this data will be obtained.

4 Experimental Data for Rabbit Papillary Muscles

The passive response of intact papillary muscles was carefully measured in a series of elegant experiments by Criscione et al. [3]. Five right ventricular papillary muscles from New Zealand white rabbits were selected, with care taken to ensure that the specimens had an essentially cylindrical geometry. The muscles were first extended in the axial direction with γ=1.04 and then twisted while maintaining their lengths constant. The required moment and axial forces necessary to sustain the deformation at different levels of twist, both positive and negative, were measured. Only the results from one muscle were given, with A=0.6 mm, these being representative of all five tests. The results were reported in graphical form. These data points were digitized and the results are given in the Appendix.

The central thesis of this paper is that, for moderate twisting of slender cylinders, the response in torsion superimposed on extension of transversely isotopic cylinders, with the direction of anisotropy along the axis of the cylinder, is essentially described by the following relations for the applied average axial stress and moment respectively:

$$N = N_{0} + N_{2}\tau^{2}A^{2},\qquad M = M_{1}\tau A + M_{3}\tau^{3}A^{3}, $$
(4.1)

where N 0, N 2, M 1, M 3 are given by (2.11), (3.6), (3.12), A is the initial radius of the cylinder and τ is the twist per unit deformed length. To test this hypothesis, experimental data for papillary muscles from rabbits will be compared to the predictions from (4.1).

The average axial stress data, given in Table 2 in the Appendix, are modeled first. Note that when the twist is zero, the average axial stress is 0.21 mN mm−2 and so, motivated by (4.1)1, an empirical model of the form N=0.21+cτ 2 (constant c) is fitted to the data on using a least-squares error minimization technique. The units for τ are rad/mm. The result is

$$N = 0.21 + 1.54\tau^{2}. $$
(4.2)

The predictions from this empirical model are plotted together with the experimental data in Fig. 1. An excellent fit of the model with the data is obtained.

Fig. 1
figure 1

Fit of model (4.2) with the experimental data from Table 2. The units for the average stress are mN mm−2 while the units for τ are rad mm−1

Full size image

Similarly, motivated by (4.1)2, on fitting the empirical model M=c 1 τ+c 3 τ 3,c 1,c 2 constants, with the data from Table 1 using a least-squares approach we obtain

$$M = 0.08\tau + 0.45\tau^{3}. $$
(4.3)

The fit of this model with the corresponding experimental data from Table 1 is shown in Fig. 2.

Fig. 2
figure 2

Comparison of model predictions and experimental data from Table 1. The units for the resultant moment are mN mm

Full size image
Table 1 Digitized data for the intact muscle from the upper Fig. 3 of [3]
Full size table

Although still quite good, the same excellent fit as previously achieved is not obtained. From a pure model-fitting perspective, the problem is that the experimental data is not an odd function of the twist. Physically, this is because the symmetry assumptions that are the basis of models of the form (4.1)2 are idealizations that are never likely to be valid in practice and certainly do not seem to hold here. The main symmetry assumptions used as the basis of the mathematical model are that the papillary muscle is perfectly cylindrical, the muscle is homogeneous and that the transverse isotropy is aligned perfectly in the axial direction. Despite the fact that the experimental data are not perfectly odd in the twist, nonetheless expressions of the form (4.1)2 yield predictions that agree at least qualitatively with the experimental data and, indeed, for one direction of twist, there is also excellent quantitative agreement. These observations and the excellent fit achieved with the average axial stress data suggest that expansions of the form (4.1) show considerable promise for the modeling of papillary muscles and are likely to be useful also in the modeling of moderate twisting of other nonlinearly elastic slender cylindrical bodies. Of course, to carry out a complete analysis of the accuracy of the above models to match experimental data, it would be desirable to obtain estimates for the relative errors introduced in the fitting process (cf. the work of Ogden et al. [13] for isotropic natural rubber) but we shall not pursue this here.

The determination of the constants in the strain-energy density (3.15) is now straightforward. On comparing the first of (4.1) with (4.2) and using the first of (3.19) we get

$$0.21 = 0.23c_{10} + 0.34c_{02} + 0.03c_{11}, $$
(4.4)

where we recall that γ=1.04 and this and subsequent calculations are rounded to two decimal places. It also follows from (4.1)1 and (4.2) that A 2 N 2=1.54. Since A=0.6, we find from (3.19)2 that

$$4.28 = - 0.5c_{10} + 0.24c_{20} + 2.08c_{02} + 1.16c_{11}. $$
(4.5)

Similarly, on comparing (4.1)2 with (4.3) and using the last two of (3.19) we obtain

$$0.20 = c_{10} + 0.01c_{20} + 0.16c_{02} + 0.08c_{11},\qquad 2.21 = c_{20} +c_{02} + c_{11}. $$
(4.6)

On solving the four linear equations (4.4)–(4.6) we find that

$$c_{10} = 0.06,\qquad c_{20} = - 1.44,\qquad c_{02} = 0.43,\qquad c_{11} = 3.22, $$
(4.7)

where the units are mN mm−2 or kPa. These are the values of the constants in the strain-energy (3.15).

It is easily verified that the restriction (3.16) is satisfied for this choice of material parameters. Since we also have 4c 02+2c 11−c 10>0, it follows from (3.18) that for the pure torsion of the rabbit papillary muscles a reverse Poynting effect is predicted to hold with a tensile axial force necessary to maintain γ=1. Indeed, it follows easily from (3.17) that this reverse Poynting-type effect is predicted to hold for all γ≥1 for the material modeled by (3.15) with constants given in (4.7). This is reflected by both the experimental and theoretical results shown in Fig. 1 where the extension ratio is held constant (γ=1.04) and the average axial stress is seen to be monotonic increasing in the twist. The torsion experiments of Criscione et al. [3] were performed while maintaining a stretch of γ=1.04. We suspect that this very small pre-stretch was implemented to keep the muscle taut and thus the results shown in Fig. 1 should be very close to those that occur for pure torsion.

5 Concluding Remarks

For the problem of torsion superimposed on extension of incompressible nonlinearly elastic transversely isotropic cylinders, an asymptotic analysis has been carried out on using a small parameter that reflects the moderate twisting of slender cylinders. On using a four-parameter polynomial expression for the strain-energy density in terms of classical invariants, this analysis has been shown to be in excellent agreement with experimental data of Criscione et al. [3] for rabbit papillary muscles. The theoretical results predict and the experimental results confirm that a reverse Poynting-type effect occurs where the stretched rabbit muscle tends to shorten on twisting.

It has been pointed out by Criscione [2] that the classical invariants give rise to a covariance between the response functions in the constitutive law for the stresses. An alternative set of invariants which form an orthogonal invariant basis has been proposed in [2]. For the case of biaxial testing of incompressible materials, the new invariants have been shown to have some advantages over the usual invariants. It remains to be seen, however, whether such invariants will attract widespread use. For example, it has been shown by Ogden et al. [13] in a study of fitting isotropic hyperelastic models to experimental data for natural rubber that strain-energy functions of the type proposed in [2] for incompressible materials do not always lead to smaller residual error than classical strain-energies. While it would be of interest to investigate the use of alternative invariants for the transversely isotropic materials of concern here, such a study is beyond the scope of the present work. Yet another alternative to modeling soft biological tissues would be to employ a theory of weakly nonlinear elasticity involving third or fourth-order elastic constants (see, e.g., Destrade et al. [4] for a discussion) but we prefer to use the exact nonlinear theory presented here.