Scalar mixing in an urban canyon

Abstract

The scalar dynamics within a unit-aspect-ratio street canyon are studied using large-eddy simulation. The key processes of ventilation and mixing are analysed with the canyon-averaged concentration, mean tracer age and variance. The results are sensitive to the source location and can be classified according to the streamline geometry. The canyon-averaged concentrations for the corner vortices, vortex sea and central vortex do not converge to the same value at large times, though the mean decay rates do. The variance measured with respect to the canyon average shows two distinct decay regimes: the early regime reflects large-scale straining and enhanced diffusion across streamlines, while the late regime is associated with escape from the canyon, i.e., ventilation. Analytical predictions for the variance-decay or mixing time scales are verified for the early regime. It is argued that the presence of an open boundary at the roof level suppresses rapid mixing of the scalar field and is responsible for differences with respect to scalar dynamics within closed domains.

1 Introduction

The evolution of a passive scalar, c, is governed by the advection–diffusion equation

$$\begin{aligned} \frac{\partial c}{\partial t} + \overrightarrow{u} \cdot \overrightarrow{\nabla }c = \kappa \nabla ^2c + S, \end{aligned}$$

(1)

where $\overrightarrow{u}(\mathbf {x})$ is the velocity, $\kappa$ is the (turbulent) diffusivity, and $S(\mathbf {x})$ is the source flux. Physically the scalar distribution is the product of transport or ventilation, the coherent movement from one location to another, and mixing, the elimination of concentration gradients. These processes may also depend on the initial conditions, or more concretely, the source locations.

Scalar dynamics are especially complicated in the urban context. First, the presence of buildings and other obstacles introduces strong spatial inhomogeneity. Many studies have shown that the urban geometry exerts a significant influence on both winds and pollutant fields [7]. On the one hand, urban geometry varies from one neighbourhood to another; on the other, the flow around a single building is inhomogeneous on account of boundary layers, wakes and vortices. Second, sources and boundary conditions are time-dependent and difficult to implement or define (see e.g. [16]). The complexity of urban flow and dispersion has led to simplifying assumptions, most notably steady flow and a ground-level source.

The assumption of steady flow has often been made in urban computational fluid dynamics (CFD). Traditionally it was invoked in models based on the Reynolds-averaged Navier–Stokes equations [5]. With the increasing popularity of large-eddy simulation, the restriction to steady flow has been made in the diagnostics rather than the dynamics. Diagnostics based on time-averaged concentrations, such as the local age of air [24] and pollutant exchange rate [35], have proven valuable for forced ventilation problems, but they are less appropriate for initial-value problems or applications such as emergency response modelling and air-quality forecasting. Furthermore, time-averaged Eulerian statistics do not provide much insight into the underlying physical mechanism for flows that are strongly inhomogeneous.

The use of ground-level line [53] or area [12] sources with constant amplitude is also standard. Although ground-level sources are representative of vehicle exhaust, other sources exist as well: kitchen exhaust is emitted from walls or rooftops [58]; secondary pollutant species are generated at different heights; biogenic volatile organic compounds are emitted by trees and vegetation [20], which may extend to the middle of a canyon or higher [9]; regional pollutants originating, for example, from factories [54] or fires [29], may enter the urban canopy.

Ventilation and mixing in urban areas are characterised more accurately without invoking these assumptions about the time dependence and initial conditions. This has been done for ventilation [36]. Objective ventilation diagnostics can be derived by adapting age diagnostics from atmospheric science [62], in which fluid parcels are tracked within an Eulerian framework. A comparable analysis has not been performed for mixing. In fact, apart from the well-known review paper by Belcher [3], mixing has received little attention in the urban pollutant dispersion literature. This is somewhat surprising because mixing is an important subject in theoretical fluid dynamics [60]. From a practical perspective, chemical reactions depend on the rate at which species are brought into contact with each other or mixed [18, 50], while atmospheric winds, humidity and chemical constituents are affected by the mixing of dynamical and passive scalars.

The analysis of ventilation and mixing is greatly simplified for idealised urban flows that avoid some of the complexities posed by the real urban environment. An urban street canyon is a simple yet non-trivial configuration that is often considered the basic unit of cities [48]. An infinite (two-dimensional) canyon represents a severe approximation because the spanwise flow is statistically homogeneous when the mean (streamwise) flow is perpendicular to the canyon axis. Nevertheless it still captures key aspects of scalar dispersion in more realistic flows, notably the influence of the spatial structure of the velocity field or streamlines. In the skimming flow regime, flow within a street canyon is dominated by the presence of a large central vortex and smaller corner vortices [33]. The phenomenon of topological dispersion at intersections [3], which is associated with the “branching” of streamlines, cannot be captured, but the change in streamline topology from the primary or secondary vortices to the turbulent “vortex sea” between them is retained.

This paper analyses mixing within a street canyon. Following the analysis of streamline topology by Belcher [3], the influence of the streamline geometry is examined. In the fluid dynamics literature, essentially kinematic approaches have been developed. For large-scale spatially smooth velocity fields in which the integral or eddy turnaround time is independent of scale, the mixing or variance decay rate [55] is determined by the Lagrangian strain rate (or largest Lyapunov exponent) when the domain is periodic and of comparable size to the flow scale [25]. For vortical flows with closed streamlines, the mixing rate is determined by an effective diffusivity that depends on the Péclet number [26]. The preceding kinematic theories are rather idealised and their applicability to urban turbulence is not guaranteed. Nonetheless, the strong spatial organisation of flow within a street canyon and the relatively weak turbulence away from the roof level [56] give reason to believe that kinematic theories may be applicable. Indeed it is shown that the predicted mixing rates agree with the kinematic theories at early times (of the order of the mean canyon circulation time scale). However, the inhomogeneous nature of the flow and the presence of an open boundary are responsible for significant departures from the behaviour of idealised kinematic flows. At late times (of the order of 10 canyon circulation times), mixing is largely suppressed and the scalar dynamics are driven by ventilation.

The objectives of this study are to (1) quantify mixing; (2) relate mixing to the more intensively studied phenomenon of ventilation; and (3) test the applicability of idealised mixing theories. Sect. 2 reviews the methodology, viz., the numerical model, initial conditions and diagnostics. Qualitative aspects of the time evolution and sensitivity to initial conditions are described in Sect. 3. Ventilation and mixing are quantified in Sects. 4 and 5. The extension to conventional ground-level sources is considered in Sect. 6. Implications of the results are discussed in Sect. 7.

2 Methodology

2.1 Numerical model

The flow and scalar transport are simulated using the parallelized large-eddy simulation model, PALM [40], which is based on the implicitly filtered non-hydrostatic, incompressible Boussinesq equations and the Deardorff subgrid-scale (SGS) scheme [14]. PALM has been successfully applied to street canyons [31, 45], building arrays [51] and realistic urban areas [52]. Third-order Runge–Kutta time-stepping [66] is combined with spatial finite differences and a fifth-order scheme for momentum and scalar advection [64]. The Poisson equation for the pressure is solved with the multigrid method. The SGS eddy viscosity and diffusivity are calculated from the SGS turbulent kinetic energy (SGS-TKE).

Fig. 1

Schematic diagram of the computational domain

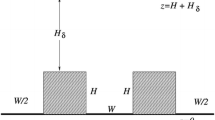
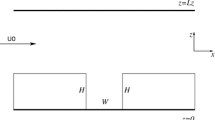
A street canyon of unit aspect ratio $AR\equiv H/W=1$ is located in the centre of the computational domain; see Fig. 1 for a schematic illustration. The grid spacing is uniform in the streamwise, x, spanwise, y, and vertical, z, directions, i.e. $\varDelta x=\varDelta y=\varDelta z=1\,{\text {m}}$, which meets the recommendation that the canyon walls be separated by at least 10 gridpoints [19]. The domain parameters are summarised in Table 1.

Table 1 Computational domain parameters corresponding to Fig. 1

The model configuration is standard [31]. Identical boundary conditions are adopted for the velocity and scalar fields at the edges of the computational domain: periodic in the spanwise, Neumann at the top, Dirichlet at the inlet, and radiation at the outlet. The streamwise boundary conditions ensure that the scalar cannot re-enter the domain after exiting at the outlet. At solid surfaces, there is no-slip for the velocity and Neumann for the scalar; in place of an explicit wall function, the near-wall boundary conditions are parameterised, following Monin–Obukhov similarity theory, using a roughness length, $z_0=0.1\,{\text {m}}$, and a constant-flux layer between the wall and the first gridpoint.

Turbulence at the inflow is maintained using the turbulence recycling technique [28, 39], wherein turbulence near the outlet of the main run is fed back to the inlet and superimposed on an inflow velocity profile generated from a precursor run that is allowed to reach statistical equilibrium. The precursor run has periodic boundary conditions and is forced by an external pressure gradient, $dp/dx=-6\times 10^{-4}\,{\text {Pa}}\,{\text {m}}^{-1}$. Thermal effects are neglected.

The passive scalar or nominal pollutant was released at time $t=t_0$, where $t_0={1000}\,{\text {s}}$ corresponds to the initial spin-up from the end of the precursor run. More precisely, an impulse source, viz.

$$\begin{aligned} S = C_0\delta (t-t_0)\mathcal {R}(\mathbf {x}), \end{aligned}$$

(2)

with arbitrary amplitude, $C_0$, was applied over a source region,

$$\begin{aligned} \mathcal {R}(\mathbf {x}) = {\left\{ \begin{array}{ll} 1, \quad &{}\mathbf {x}\in {\mathcal{R}}_i, \\ 0, \quad &{}\mathbf {x}\notin {\mathcal{R}}_i. \\ \end{array}\right. } \end{aligned}$$

(3)

This is an initial-value problem: the $\mathcal{R}_i$ represent initial conditions (see Sect. 2.3) and each $\mathcal{R}_i$ is associated with a separate realisation or simulation. Concentration statistics are collected over a time $t_f-t_0=5000\,\mathrm{s}$ using an output interval of $\varDelta t={10}\,{\text {s}}$.

2.2 Validation

Simulated velocity and scalar fields are validated against wind-tunnel measurements. Figure 2 shows that the LES velocity profiles, represented by the temporal and spanwise average $\langle \overline{\cdot }\rangle$, are in good agreement with the wind-tunnel measurements. The shear close to the bottom boundary is slightly underestimated by the model for $x/W=-0.25$ and $x/W=0$. Similar behaviour was also noticed in previous validation studies [12, 13]. This may be related to the treatment of the wall layer: the value of the roughness length, $z_0=0.1\,{\text {m}}$, which has been used in previous street-canyon studies [31], is representative of very rough walls [32] and may not yield an optimal validation. Statistical performance measures [10] also indicate a successful validation [16, 17]: the normalised mean square error ${NMSE}\sim 0.01{-}0.03$, fractional bias ${FB}\sim 0.01{-}0.13$, correlation coefficient ${R}\sim 0.99$ and hit rate ${q}\sim 68\%$.

Fig. 2

Normalised mean streamwise velocity profiles, $\langle \overline{u}\rangle /\langle \overline{U}_s\rangle$, for the current LES (solid blue curve) and the wind-tunnel measurements of Brown et al. [8] (black circles). a$x/W=-0.4$; b$x/W=-0.25$; c$x/W=0$; d$x/W=0.25$; e$x/W=0.4$. $\langle \overline{U}_s\rangle$ denotes the shear-layer average, $1\le z/H\le 1.5$, of the streamwise velocity

Time-averaged concentration statistics are compared against wind-tunnel measurements by introducing a continuous ground-level line source along the centreline of the canyon. Figure 3 shows vertical profiles of the normalised mean concentrations. The overall trend is well-captured, though the concentrations are slightly overpredicted. Similar behaviour was reported in LES validations [34, 43, 44], albeit at lower resolution, but the discrepancy is smaller in the present LES. The overprediction may be a consequence of the spanwise periodic boundary conditions, which function as a “pseudo-source” that enhances the effective source strength. Concentration fluctuations (not shown) also show better agreement with experimental data [42, 53] than do previous LES validations [43].

In addition to the validation, the sensitivity to the lid height was assessed by performing simulations with $L_z=3H,\ 4H,\ 5H$ and periodic boundary conditions in the horizontal. The mean streamlines almost coincide and the standard deviation of the TKE (among the three simulations) is around $1\%$. The scalar fields also show identical spatial structures (not shown).

Fig. 3

Vertical profiles of the normalised mean concentration, $\langle \overline{C}\rangle U_{2.5H}HL/Q$, evaluated at a$x/W=-0.5$; b$x/W=0$; c$x/W=0.5$. Wind-tunnel data from Pavageau and Schatzmann [53] (filled triangles) and Meroney et al. [42] (filled circles) are compared with LES data from the present validation (solid line) and Michioka et al. [43] (open circles). $U_{2.5H}$ is the temporal and spatial average of the streamwise velocity at $z/H = {2.5}\,\text{and}\,Q$ is the source flux

2.3 Initial conditions

The sensitivity of ventilation and mixing to the source location (or initial conditions) is analysed using different source regions, $\mathcal{R}_i$. Since urban air quality depends on primary and secondary pollutants, as well as on emission from buildings or factories, the pollutant sources do not necessarily lie at ground level. Furthermore, they need not span the entire domain, as with the large-scale initial conditions favoured in idealised studies [55]. The choice of the $\mathcal{R}_i$ is guided by the structure of the velocity field. The scalar dynamics are strongly influenced by the streamline geometry in 2-D [50, 65] and flow within an infinitely long street canyon (or one with periodic boundary conditions in the spanwise direction) is effectively two-dimensional. Mixing tends to occur more rapidly between vortices, where the strain is stronger, while dispersion is partially constrained by the vortices.

Fig. 4

Spatial structure of the (spanwise and temporally averaged) mean flow in the $x-z$ plane. a Streamlines; b spanwise vorticity, $\langle \overline{\omega _y} \rangle$. The locations of the source regions (Fig. 5) are superimposed on top of the streamlines

Fig. 5

Schematic illustration of the source regions, $\mathcal{R}_i$, which represent effective initial conditions. The pollutant blocks are identical in height and width, i.e. $l=h=w=6.0\,{\text {m}}$, and are labelled as $\alpha \beta$ with $\alpha \in \{\mathrm {T,C,B}\}$ and $\beta \in \{{\mathrm{L}},{\mathrm{C}},{\mathrm{R}}\}$ denoting the locations of the $\mathcal{R}_i$, i.e. top, centre, bottom, left and right. The colours identify the sets defined in Eq. (19): Set A (yellow, corner vortices); Set B (green, vortex sea); Set C (purple, central vortex)

Streamlines are plotted in Fig. 4a. As in many other studies [33], there are small corner vortices (at the bottom right, bottom left and top left) and a large central vortex composed of closed streamlines. Note that a corner vortex is absent from the top right, which is where the turbulence is strongest (cf. Fig. 8; [13]). The spanwise vorticity, $\omega _y \equiv u_z-w_x$ (Fig. 4b), confirms the existence of the vortices. Several distinct regions may be identified, namely the three corner vortices, the central canyon vortex and the “vortex sea” lying between them. They are used to define the $\mathcal{R}_i$ (Fig. 5). Cubic “pollutant blocks” with size $l=6.0\,{\text {m}}$ in the $x-z$ plane and length $L_y$ in the spanwise direction are adopted in the first instance; other choices are examined as well. The pollutant blocks are labelled as $\alpha \beta$, where $\alpha \in \{\mathrm {T,C,B}\}$ and $\beta \in {\{ \mathrm{L,C,R}\}}$ stand for top, centre, bottom, left and right. Referring to the streamlines (Fig. 4a) and vorticity contours (Fig. 4b), BR, BL and TL coincide with the corner vortices; CC lies inside the central vortex; and the remaining blocks, BC, CL, CR, TC and TR, belong to the vortex sea.

2.4 Scalar diagnostics

Ventilation and mixing diagnostics are calculated for each set of initial conditions. The initial concentrations are uniform within the source region, $\mathcal{R}_i$; the sensitivity to a non-constant source is examined in Sect. 5.2.4.

2.4.1 Ventilation

A standard ventilation diagnostic is the mean concentration. The spatial average within an open domain may decrease with time. The definition of the ventilation diagnostic depends on the choice of receptor. Taking the receptor to be identical to the source $\mathcal{R}_i$,

$$\begin{aligned} {\langle C \rangle }_{\mathcal {R}_i} = \frac{1}{V_i} \int \limits _{\mathcal {R}_i}{C(\mathbf {x})}d\mathbf {x}, \end{aligned}$$

(4)

where the volume $V_i = \int \limits _{\mathcal {R}_i} d\mathbf {x}$. Assuming the receptor coincides with the canyon yields the canyon average,

$$\begin{aligned} \langle C \rangle _{\mathcal {R}_c} = \frac{1}{V_{c}} \int \limits _{\mathcal {R}_c}C(\mathbf {x}) d\mathbf {x}, \end{aligned}$$

(5)

where $V_c = \int \limits _{\mathcal {R}_c} d\mathbf {x}$ and $\mathcal{R}_c$ denotes the entire canyon (i.e. the space between the ground and the roof level).

A ventilation time scale can be estimated from the mean concentration, $\hat{C}\equiv \langle C \rangle _{\mathcal {R}_c}$. Assuming that the concentration decays exponentially in time, one may define an inverse ventilation rate or retention time, $T_r$, from the e-folding time scale [15], viz.

$$\begin{aligned} \hat{C}(t)/\hat{C}(t=0) \sim \exp (-t/T_r). \end{aligned}$$

(6)

The existence of a well-defined $T_r$ implies that ventilation is controlled by a single time scale. Although it has proven useful in applications [67], the retention time neglects statistical variability and prioritises the behaviour at long times.

Alternatively one may calculate the tracer age [23, 27], which is the time elapsed from the release of a passive tracer at the source, $\mathbf {x}_0$, to its arrival at the receptor, $\mathbf {x}$. Following Lo and Ngan [36], the age spectrum is given by

$$\begin{aligned} {Z}(\mathbf {x},\xi |S) = \frac{\int \limits _{{\mathcal{D}}} d\mathbf {x}_0 {G}(\mathbf {x},\xi |\mathbf {x}_0){S}(\mathbf {x}_0) }{c(\mathbf {x},t)}, \end{aligned}$$

(7)

where the Green’s function, G, is obtained by integrating a delta-function source, Eq. (2). $Z(\xi )$ is a probability distribution of tracer ages, $\xi$, i.e. it characterises the statistical distribution of transit times between source and receptor. The age spectrum has an exponential tail for skimming flow within a single street canyon, in accord with the retention time and pure diffusion; more generally, however, ventilation cannot be characterised by a single time scale. A convenient diagnostic is the mean tracer age (MTA) or first moment of the age spectrum,

$$\begin{aligned} \tau _{a}(\mathbf {x}) = \int \limits _{t_0}^{t_f}\xi Z(\mathbf {x},\xi |S)d\xi . \end{aligned}$$

(8)

The canyon average is denoted by $\hat{\tau }_a\equiv \langle \tau _a\rangle _{\mathcal{R}_c}$. Unlike the retention time, $\tau _a$ explicitly measures transit times between source and receptor; nonetheless, $\hat{\tau }_a$ and $T_r$ are comparable for skimming flow within a street canyon, the deviation of ${\sim }20\%$ reflecting differences between the age and retention time [38]. The MTA does not necessarily equate low concentrations with improved ventilation, as is the case with diagnostics that assume spatial homogeneity.

2.4.2 Mixing

A popular mixing diagnostic is the variance of the scalar field [55]. The variance vanishes when the field has been homogenised or mixed completely, irrespective of the physical mechanism. The variance within a closed domain approaches zero after initial transients have subsided.

The appropriate definition of the variance depends on the domain. For a closed domain $\mathcal{D}$, it can be assumed without loss of generality that the mean concentration vanishes, i.e., $\int \limits _{\mathcal{D}} C d\mathbf {x}=0$. For an open, inhomogeneous domain, a reference baseline should be retained. To measure mixing throughout the canyon, the canyon average, ${\langle C \rangle }_{\mathcal {R}_c}$, is used as the baseline, i.e

$$\begin{aligned} \langle \sigma ^{2} \rangle _{\mathcal{R}_i}&= \frac{1}{V_i}\int \limits _{\mathcal{R}_i} {\left( C(t,\mathbf {x})-\langle C \rangle _{\mathcal{R}_c}\right) ^2} d\mathbf {x}, \end{aligned}$$

(9a)

$$\begin{aligned} \langle \sigma ^{2} \rangle _{\mathcal{R}_c}&= \frac{1}{V_c} \int \limits _{\mathcal{R}_c} {\left( C(t,\mathbf {x})-\langle C \rangle _{\mathcal{R}_c}\right) ^2} d\mathbf {x}. \end{aligned}$$

(9b)

While both $\langle \sigma ^2 \rangle _{\mathcal{R}_i}$ and $\langle \sigma ^2 \rangle _{\mathcal{R}_c}$ quantify convergence towards the canyon average, the former describes variations within the source region only. Alternatively the variance may be defined using a local average, $\langle C \rangle _{\mathcal{R}_i}$, as the baseline:

$$\begin{aligned} \langle {\sigma _{{\rm loc}}^2} \rangle _{\mathcal{R}_i}= \frac{1}{V_i} \int \limits _{\mathcal{R}_i} {\left( C(t,\mathbf {x})-\langle C \rangle _{\mathcal{R}_i}\right) ^2} d\mathbf {x}, \end{aligned}$$

(10)

which measures relaxation towards the local average. Roughly speaking, $\langle \sigma ^2 \rangle _{\mathcal{R}_i}$ and $\langle \sigma ^2 \rangle _{\mathcal{R}_c}$ are associated with the canyon-scale variance, and $\langle \sigma _{\mathrm loc}^2 \rangle _{\mathcal{R}_i}$ with the local one. It is shown below that the definitions are not necessarily equivalent.

The variance decay rate, $\gamma$, characterises the rapidity of the mixing. It can be calculated for any definition of the variance, $\langle \sigma ^2 \rangle$. Assuming exponential decay

$$\begin{aligned} \langle \sigma ^2 \rangle \sim e^{-\gamma t}, \end{aligned}$$

(11)

$\gamma$ may be determined from a least-squares fit, whence

$$\begin{aligned} \tau \equiv \frac{1}{\gamma }. \end{aligned}$$

(12)

The interpretation of $\tau$ as a mixing time scale is discussed below. Subscripts (i.e., ‘$\mathcal{R}_i$’, ‘$\mathcal{R}_c$’ and ‘$\mathrm {loc}$’), label the $\tau$ for Eqs. (9a), (9b) and (10). The propagation of errors from $\gamma$ to the derived quantity $\tau$ is calculated according to,

$$\begin{aligned} SD[\tau ]=SD\left[ \frac{1}{\gamma }\right] \approx \frac{1}{E[\gamma ]^2}\times SD[\gamma ], \end{aligned}$$

(13)

where SD and E are the standard deviation and expectation.

Efficient mixing requires the rapid creation of small scales [18, 50]. To see this, imagine that the scalar field has a characteristic scale, $\varLambda$. Mixing by molecular diffusion will become important when $\varLambda \lesssim L_d$, where $L_d$ is a diffusive length scale. Alternatively mixing in a coarse-grained sense may occur, in the absence of diffusive processes, when $\varLambda \lesssim \varLambda _0$ for some arbitrary scale $\varLambda _0$ (e.g., a grid scale). There are various means by which small scales can be created. First, strong 3-D turbulence is the most obvious, though it may not be present throughout the entire domain. Second, repeated stretching-and-folding within a closed domain leads to elongation and filamentation, with the separation between filaments decreasing with the number of filaments. This process, which is the essence of chaotic advection [50, 65], is associated with the large-scale strain field. Third, diffusion could be enhanced through the synergistic interaction with the shear. An important example of this is the effective diffusivity for so-called cellular flows with closed streamlines [26].

The decay rate, $\gamma$, can be predicted theoretically for the second case [25]. For a random velocity field with (i) mean velocity gradient independent of scale; (ii) characteristic scale comparable to the domain size; and (iii) periodic boundary conditions, $\gamma$ is given to leading order in the (inverse) Péclet number

$$\begin{aligned} Pe = UL/\kappa , \end{aligned}$$

(14)

where U and L are the characteristic velocity and length scales and $\kappa$ is the diffusivity, by the largest Lyapunov exponent, $\lambda _1$, which measures the exponential divergence of particle trajectories in the infinite-time limit [49]. The theory is summarised in Ngan and Vanneste [46]. Although mixing may have a macroscopic or microscopic origin [18], for the preceding class of flows it is driven by the large-scale strain (when the diffusivity is small). A velocity field with the required properties can be realised by a randomised area-preserving sine map [55], a (statistically) homogeneous vortex, or a turbulent flow with a steep energy spectrum, i.e. $E\sim k^{-n}$ with $n\ge 3$ [4]. One-dimensional energy spectra inside a single street canyon suggest that $n\approx 5/3$ on scales large compared to the dissipation scale [37].

The Lyapunov exponents, $\lambda$, are estimated in the Eulerian frame and spatially averaged over $\mathcal{R}_i$ (see Appendix 1 for details). The resulting “pseudo-Lyapunov exponents”, which do not require the use of a Lagrangian model [38, 63], assume that the Eulerian evolution does not differ significantly from the Lagrangian evolution. This approximation is acceptable for the local variance decay since the blocks are relatively small; indeed an average over a larger area may be less appropriate. Henceforth the qualifier is omitted. The associated Lyapunov time scale is given by

$$\begin{aligned} \tau _L \equiv \frac{1}{\lambda _1}. \end{aligned}$$

(15)

Fig. 6

Normalised, spanwise-averaged scalar fields, $\langle C \rangle /C_0$, at $t=250\,{\text {s}}$. The panels are organised according to the locations of the associated initial conditions (Fig. 5): the top-left panel corresponds to source location TL, the bottom right to BR, etc. The canyon-averaged concentrations are indicated above the associated panels. The structure of the early-time scalar fields depends on the source location

Fig. 7

As in Fig. 6, but for $t=5000\,{\text {s}}$. Large relative differences among the scalar fields are maintained at late times

3 Scalar fields

Snapshots of the normalised spanwise-averaged concentrations, $\langle C \rangle /C_0$ are plotted at two different times, $t=250\,\mathrm{s}$ (Fig. 6) and $t=5000\,\mathrm{s}$ (Fig. 7). The former is associated with early times, the latter with late times. The time scale of the mean circulation may be defined as

$$\begin{aligned} T_c \equiv 2\left( \frac{H}{W_\mathrm{1}} + \frac{W}{U_\mathrm{1}}\right) \approx 521\,\mathrm{s}, \end{aligned}$$

(16)

where the characteristic velocities, $U_\mathrm{1}$ and $W_\mathrm{1}$, are ${L}^1$ norms (absolute values) of the streamwise and vertical velocities. The preceding definition has a straightforward physical interpretation and has been used for other problems [16].

The scalar fields reflect the streamline geometry. A central “vortex” is seen for all initial conditions. Furthermore, concentrations are largest for the $\mathrm {CC}$ initial conditions, though the structure of the scalar field near the roof level and upper half of the downwind wall follows the TKE rather than the streamlines (Fig. 8). The TKE is defined as $\mathrm {TKE}\equiv {\frac{1}{2} ({u^\prime }^2 + {v^\prime }^2 + {w^\prime }^2)}$, where $u'$, $v'$ and $w'$ denote departures from the time averages of the streamwise (u), spanwise (v) and vertical (w) velocity components. Strong turbulence within the shear layer enhances dispersion and weakens the influence of the streamline geometry.

Fig. 8

Time- and spanwise-averaged turbulent kinetic energy, $\langle \overline{\mathrm {TKE}}\rangle$. $U_{2.5H}$ is the temporal and spatial average of the streamwise velocity at $z/H=2.5$, a level within the inertial layer

The scalar fields also depend on the initial conditions. Each set of scalar initial conditions yields a qualitatively distinct scalar field at the early time, $t=250\,\mathrm{s}$, as may be expected for a turbulent flow. More interestingly, the sensitivity is maintained at the late time, $t=5000\,\mathrm{s}$. Relative differences persist despite the decay in mean concentration. Using the canyon-averaged concentrations for the ensemble of initial conditions, the ratio of the standard deviation to the mean increases from 0.23 to 0.42 over the course of the simulation. Memory of the initial conditions is lost after the scalar field is completely mixed, but this does not happen here. A plausible explanation is that the open boundary precludes efficient dynamical mixing in the long-time limit. This is confirmed in Sect. 5. Lagrangian calculations also indicate that only $\sim 25\%$ of particle trajectories experience re-entrainment while the return coefficient defined from a normalised re-entrainment timescale is similar [38].

Despite the quantitative differences, the scalar fields appear to share a common spatial structure. The similarities are highlighted by plotting the normalised concentration,

$$\begin{aligned} \phi = \frac{C - \langle C \rangle _{\mathcal{R}_c}}{\langle \sigma ^2 \rangle _{\mathcal{R}_c} ^\frac{1}{2}} \end{aligned}$$

(17)

at the late time. The spatial structure of the spanwise average, $\langle \phi \rangle$, is rather similar for the different initial conditions (Fig. 9), albeit with some differences in the central vortex. This is notable because the CC scalar field looks rather different in Fig. 7. If the scalar dynamics were controlled by the same physical mechanism, the scalar fields for the different initial conditions would converge towards the same spatial structure at large times. This is reminiscent of the “strange eigenmode”, a statistical structure that emerges from the scalar decay in a large-scale velocity field [55]. Nonetheless, quantitative differences in the mean concentration and standard deviation persist.

Fig. 9

Spanwise-averaged normalised concentrations, $\langle \phi \rangle$, at $t=5000\,\mathrm{s}$ for a BR (Set A); b CC (Set C). Similar results are obtained with the other initial conditions

The mixing seen in Figs. 6 and 7 cannot be obviously related to strong 3-D turbulence throughout the canyon. The TKE decays rapidly away from the roof level (Fig. 8) and the scalar fields exhibit large-scale filamentary structures. Furthermore, the mixing cannot be explained solely by turbulent diffusion. Defining the diffusive time scale as

$$\begin{aligned} t_d \equiv \frac{L_d^2}{\kappa _T}, \end{aligned}$$

(18)

where $\kappa _T$ is the turbulent diffusivity, $t_d\sim 10^{5}\,\mathrm{s}$ for $L_d=H=50\,\mathrm{m}$ and $\kappa _T\sim 0.025 \,\mathrm{m}^2\,\mathrm{s}^{-1}$. Alternative mechanisms are examined in Sect. 5 for each set of initial conditions.

Table 2 Canyon-averaged statistics of the mean tracer age, $\hat{\tau }_a$, for the different initial conditions, $\mathcal{R}_i$

4 Ventilation

4.1 Mean concentration

The normalised canyon-averaged concentrations, ${\langle C \rangle }_{\mathcal {R}_c}/C_0$, are plotted in Fig. 10a. After an initial adjustment period, the slopes or ventilation rates are approximately independent of initial conditions. In all cases, the asymptotic slope is achieved for $t\gtrsim T_c/2\approx 260\,\mathrm{s}$, the time scale required for fluid parcels to be transported from the ground to the open boundary at the roof level [16]. The ensemble average over the 9 initial conditions has mean ventilation time scale $T_{r}={910}\,{\text {s}}$ (with standard error less than $1\,\mathrm{s}$). An identical ventilation rate causes mean concentrations to decrease in step, but does not eliminate differences among the $\mathcal{R}_i$ (that may be generated during the initial stage).

The picture changes somewhat when the spatial average is taken over the source regions rather than the canyon. The normalised local concentrations (Fig. 10b), ${\langle C \rangle }_{\mathcal {R}_i}/C_0$, decay faster at early times ($t\lesssim 1000\,\mathrm{s}$ for CC, $t\lesssim 500\,\mathrm{s}$ for the other initial conditions), but differences with respect to ${\langle C \rangle }_{\mathcal {R}_c}/C_0$ are much smaller at later times. The slopes in Fig. 10a, b converge for large t: the $T_r$ differ by less than $10\,\mathrm{s}$ (or $1\%$) and ventilation is insensitive to the definition.

Fig. 10

Decay of the mean concentrations. a${\langle C \rangle }_{\mathcal {R}_c}$; b${\langle C \rangle }_{\mathcal {R}_i}$. The colours correspond to the sets summarised in Eq. (19) (green: Set A; red: set B; blue: set C). There is exponential decay for all initial conditions

4.2 Mean tracer age

The MTA is plotted in Fig. 11 for the different $\mathcal{R}_i$. The lowest values (youngest air) are found near the source regions. Values increase away from the sources following the preferred ventilation pathways for the different initial conditions. For initial conditions within the central vortex (CC), the MTA increases away from the centre and is approximately axisymmetric. For the corner vortices (BL, BR and TL), the age increases between the corner and roof level, roughly following the mean circulation (Fig. 4a). For the vortex sea (BC, CL, CR, TC and TR), the structure of the age fields resembles that for the corner vortices, but there is less localisation within the source regions. It will be shown below that this has implications for mixing at early times.

The MTA and scalar fields are obviously similar, but the former provides additional information on the nature of ventilation because it is based on the Lagrangian evolution. In particular, the MTA highlights the effects of the vortices. For initial conditions outside the central vortex, penetration into it is delayed, while for initial conditions inside the central vortex, escape from it to the outside is also delayed. In both cases the MTA is extremal within the central vortex (i.e., it contains the youngest or oldest air). The effect of the corner vortices is much less noticeable. These results are likely related to the Prandtl–Batchelor theorem [1], which states that diffusion across closed streamlines controls the scalar dynamics for steady 2-D flow. Presumably the corner vortices are less persistent and do not trap (or block) scalars as effectively. The MTA also shows that ventilation of specific source regions is not determined solely by the (local) turbulence intensity. While the TKE is maximised near the roof level, the MTA may not be dramatically lower in this region.

The sensitivity to initial conditions can be characterised with the canyon-averaged MTA, $\hat{\tau }_a$. Whereas the retention time, $T_r$, shows little sensitivity to the initial conditions, $\hat{\tau }_a$ varies by almost 40% (Table 2). (i) $\hat{\tau }_a=960\pm 14\,\mathrm{s}$ inside the corner vortices; (ii) $\hat{\tau }_a=898\pm 3\,\mathrm{s}$ inside the vortex sea; (iii) $\hat{\tau }_a=1200\,\mathrm{s}$ inside the central vortex. The classification introduced above is used to organise the mixing results (Sect. 5). Henceforth we refer to

$$\begin{aligned} {\mathrm {Set A}} \equiv \{\mathrm {BR,BL,TL}\}, \quad {\mathrm {Set B}} \equiv \{\mathrm {BC,CL,CR,TC,TR}\}, \quad {\mathrm {Set C}} \equiv \{\mathrm {CC}\}. \end{aligned}$$

(19)

Each set of initial conditions undergoes a qualitatively distinct time history.

Fig. 11

Contour fields of the mean tracer age, $\hat{\tau }_a$; the organisation of the subfigures follows Fig. 6. The ventilation pathways reflect the source locations and mean circulation (cf. Eq. (19))

5 Mixing

For a single-scale (random) velocity field and large-scale initial conditions,¹ the large-scale strain creates small scales and mixes scalar throughout the domain. This yields essentially uniform exponential decay [55]. This behaviour does not carry over to the street-canyon configuration (Sect. 2), for which there is inhomogeneous, multiscale flow and localised source regions, $\mathcal{R}_i$. The canyon-scale variance averaged over $\mathcal{R}_i$, $\langle \sigma ^2 \rangle _{\mathcal{R}_i}$, decreases as pollutant disperses from the source region (Fig. 12), but uniform exponential decay is not observed. Instead there is a clear distinction between early and late regimes. Similar behaviour is obtained for $\langle \sigma ^2 \rangle _{\mathcal{R}_c}$, the canyon-scale variance averaged over $\mathcal{R}_c$, and $\langle \sigma _{\mathrm loc}^2 \rangle _{\mathcal{R}_i}$, the local variance (not shown). All three definitions of the variance, Eqs. (9)–(10), show abrupt changes in the decay rates or slopes between 400$\,\mathrm{s}$ and 1000$\,\mathrm{s}$; for simplicity, $t=1000\,\mathrm{s}$ is taken to define the onset of the late regime. The decay rates for either regime are broadly similar for the three sets, Eq. (19). At late times, the decay rates are nearly indistinguishable (Appendix 2, Table 3); however, there is greater variability at early times (Appendix 2, Table 4).

Non-uniform variance decay has been previously noted. Salman and Haynes [57] observed four distinct stages for the scalar evolution driven by a large-scale, spatially smooth velocity field within a 2-D domain with no-slip boundaries. They found that exponential decay is preceded by a strain-induced adjustment stage and that boundary effects are important only during the final two stages. This sequence does not apply to street-canyon flow, for which the boundary conditions differ. Nonetheless a comparable analysis, in which the late and early regimes are explained in terms of distinct physical processes, is performed below.

Fig. 12

Time series of $\langle \sigma ^2 \rangle _{\mathcal{R}_i}/C_0^2$, the canyon-scale variance normalised against the initial concentration, $C_0$. a Set A (corner vortices); b Set B (vortex sea); c Set C (central vortex); d combined plot (green: Set A; red: Set B; blue: Set C). For Set B, the early-time decay is highlighted in the inset of b. In all cases, there is a clear contrast between early and late regimes

Fig. 13

As in Fig. 12, but for $\langle \sigma ^2 \rangle _{\mathcal{R}_i}/{\langle C \rangle }^2_{\mathcal {R}_c}$, the canyon-scale variance normalised by the square of the canyon-averaged concentration, ${\langle C \rangle }_{\mathcal {R}_c}$. The normalised variance is essentially constant for $t\gtrsim 1000\,\mathrm{s}$

5.1 Late stage

Ventilation of the subregions at late times is controlled by escape of scalar from the canyon (Sect. 4.1). It is plausible that the variance decay obeys a similar mechanism on these time scales, implying that the variance decay should follow the mean concentration. In fact, normalising the canyon-scale variance, by the (square of the) time-dependent canyon-averaged concentration (Fig. 13), eliminates the variance decay for $t\gtrsim 1000\,\mathrm{s}$. This implies that the variance decay at late times is a byproduct of the simultaneous decay of ${\langle C \rangle }_{\mathcal {R}_i}$ and ${\langle C \rangle }_{\mathcal {R}_c}$. Although the magnitude of scalar gradients decreases, we do not ascribe this to mixing because the normalised gradients are largely maintained. The scalar field is not homogenised in a meaningful way.

To confirm that the late-time variance decay is driven by ventilation rather than mixing, the variance-decay time scales are compared to the ventilation decay rates. Assuming mixing is determined solely by ventilation, and equating the variance, $\langle \sigma ^2 \rangle _{\mathcal{R}_i}$, with ${\langle C \rangle }^2_{\mathcal {R}_c}\sim \exp (-2t/T_r)$, it follows from Eq. (6) that

$$\begin{aligned} \tau _v\sim \frac{T_r}{2}=455\,\mathrm{s}, \end{aligned}$$

(20)

where $\tau _v$ is the time scale implied by ventilation. The actual time scales, $\tau _{\mathcal {R}_i}$, are around $400\,\mathrm{s}$ for CC and $458\,\mathrm{s}$ for the remaining initial conditions (Appendix 2, Table 3). This suggests that ventilation and the open boundary, which are not relevant to scalar dynamics within a closed domain, are responsible for differences from the evolution described by Salman and Haynes [57]: there is no evidence that boundary-layer effects control the long-time evolution. Multiscale effects associated with the shallow energy spectrum are probably small. The agreement between $\tau _v$ and $\tau _{\mathcal {R}_i}$ is not as good for CC, possibly because trapping within the central vortex delays the establishment of the late regime; from Fig. 13, it is not fully established until $t\sim 4000\,\mathrm{s}$.

5.2 Early stage

During the early stage, $t\lesssim 1000\,\mathrm{s}$, the variance decay is not controlled by ventilation or escape from the canyon (cf. Fig. 13). Hence we associate it with mixing. The nature of the mixing depends on the initial conditions (Fig. 12). While there is a single regime for Sets A (corner vortices) and C (central vortex), there are multiple subregimes for Set B (vortex sea).

5.2.1 Set A (corner vortices)

Scalar initially located inside the corner vortices escapes into the vortex sea and spreads throughout the canyon interior (Figs. 6, 7). This is a strongly inhomogeneous process. The influence of the vortices and the sensitivity to scale (or variance definition) are assessed below.

Time series of the canyon-scale variance $\langle \sigma ^2 \rangle _{\mathcal{R}_i}$ (Fig. 12a) show essentially uniform exponential decay for $t<400\,\mathrm{s}$. The errors are small, indicating that the assumption of a single decay time scale holds to a good approximation (Table 4). The mixing time scales, $\tau _{\mathcal {R}_i}$, $\tau _{\mathcal {R}_c}$ and $\tau _{\mathrm {loc}}$, are not identical for the different initial conditions. Memory of the initial conditions persists during the early stage and the mixing is incomplete.

The decay of $\langle \sigma ^2 \rangle _{\mathcal{R}_i}$, Eq. (9a) can arise from (i) the simultaneous decay of C, the concentration within $\mathcal{R}_i$, and ${\langle C \rangle }_{\mathcal {R}_c}$, the canyon mean, or (ii) a decrease in $|C-{\langle C \rangle }_{\mathcal {R}_c}|$, the canyon-scale difference between C and ${\langle C \rangle }_{\mathcal {R}_c}$. The first process (ventilation) has already been discussed in connection with mixing during the late regime of Sect. 5.1. The relevance of the second of these processes (mixing) is now discussed.

A single exponential decay stage is observed for all three definitions of the variance. The associated time scales, $\tau _{\mathcal {R}_i}$, $\tau _{\mathcal {R}_c}$ and $\tau _{\mathrm {loc}}$, are not identical, but the differences are not statistically significant. This suggests that the early-stage mixing is largely independent of definition or scale, as in mixing by a large-scale strain field. To assess the importance of large-scale straining, the mixing time scales are compared to the Lyapunov time scales, $\tau _L$ (Appendix 2, Table 5). Analytical predictions of the variance-decay rate in terms of the Lyapunov exponents have been well-verified numerically in 2-D [25] and 3-D [46] for idealised single-scale velocity fields. Although turbulent flow in a street canyon does not satisfy the requirements of a homogeneous velocity or periodic boundary conditions,² agreement in an order-of-magnitude sense may be assessed by comparing $\tau _L$ to $\tau _{L,\mathrm {lower}},\ \tau _{L,\mathrm {upper}}$, where $\tau _{L,\mathrm {upper}}/\tau _{L,\mathrm {lower}}=10$, e.g.

$$\begin{aligned} \tau _{L,\mathrm {lower}}= 1/\sqrt{10}\tau _L, \quad \tau _{L,\mathrm {upper}}= \sqrt{10}\tau _L. \end{aligned}$$

(21)

Figure 14 confirms order-of-magnitude agreement between $\tau _{\mathcal {R}_i}$, $\tau _{\mathcal {R}_c}, \tau _{\mathrm {loc}}$ and $\tau _L$.

We conclude that early-time mixing is strongly influenced by the large-scale strain. Evidently the scale dependence of the velocity field, which cannot be captured by the Lyapunov exponents, does not play an important role. This is difficult to predict a priori, but consistent with relatively weak turbulence inside the canyon (cf. [38]). According to the analytical theory [25], diffusive contributions to the variance-decay rate, which enter at higher order in 1 / Pe, vanish for $Pe\rightarrow \infty$; in the present simulation, they may be taken to be relatively small away from the inner wall layers. Incorporating Lagrangian variations through a proper calculation of the Lyapunov exponents could improve agreement. The Eulerian approximation holds only for a small averaging area, though $\tau _{\mathrm {loc}}$, which is also defined over a small area, does not show significantly better agreement with $\tau _L$. The effective strain would likely decrease with a Lagrangian calculation. Since the rotation of the local strain axes, which partially suppresses stretching [30, 47], would be included with a Lagrangian trajectory, $\tau _L$ should increase.

Fig. 14

Comparison of the mixing time scales against the Lyapunov time scales (in seconds) for Sets A and B. a$\tau _{\mathcal {R}_i}$; b$\tau _{\mathcal {R}_c}$; c$\tau _{\mathrm {loc}}$. The dotted lines correspond to upper and lower bounds (Eq. (21)). There is good order-of-magnitude agreement for $\tau _{\mathcal {R}_c}$ and $\tau _{\mathrm {loc}}$

The sensitivity to the size of the $\mathcal{R}_i$ is examined for a single source location, BL. Over a wide range of source sizes, $l\in [4\,\mathrm{m},16\,\mathrm{m}]$, $\tau _{\mathcal {R}_i}$ varies from $30\,\mathrm{s}$ to $46\,\mathrm{s}$; the variation of $\tau _L$ is smaller, from $25\,\mathrm{s}$ to $29\,\mathrm{s}$, but still consistent with order-of-magnitude agreement. The results do not depend qualitatively on the size of the source region.

5.2.2 Set B (vortex sea)

Set B evolves similarly to Set A. For initial locations inside the vortex sea and the corner vortices, the scalar is stretched and folded by the canyon circulation (Fig. 6). Indeed the prediction of $\tau _{\mathrm {loc}}$ and $\tau _{\mathcal {R}_c}$ from $\tau _L$ shows comparable errors for both sets (Fig. 14), suggesting that mixing is driven by the same physical mechanism outside the central vortex. Nevertheless, the MTA indicates that the Lagrangian evolution is not identical for the two sets. Differences in the early-time mixing are analysed below.

The evolution for source locations inside the vortex sea is distinguished by the existence of three distinct subregimes (see the inset in Fig. 12b), a steep drop, plateau and roughly exponential decay. These subregimes may be interpreted, following the MTA field (Fig. 11) and the analysis of Sect. 5.2.1, as (i) rapid advection of scalar out of the source region (cf. Fig. 10); (ii) an intermediate stage in which neither C nor ${\langle C \rangle }_{\mathcal {R}_c}$ decreases significantly; (iii) the onset of mixing. As these processes occur sequentially, they are associated with distinct time scales. A single decay stage is obtained for the canyon-scale variance averaged over the entire canyon, $\langle \sigma ^2 \rangle _{\mathcal{R}_c}$ (not shown).

Mixing is relevant only to the final stage of the initial evolution. The associated mixing time scales are listed in Appendix 2, Table 4. The ensemble averages depend on the variance definition: $\tau _{\mathcal {R}_i}=127\pm 92\,{\text {s}}$, $\tau _{\mathrm {loc}}=41\pm 8\,{\text {s}}$ and $\tau _{\mathcal {R}_c}=50\pm 3\,{\text {s}}$.³ The average for $\tau _{\mathcal {R}_i}$ is biased by the very large value for TR, $\tau _{\mathcal {R}_i}|_{TR}=307\pm 47\,\mathrm{s}$; omitting this value yields $\tau _{\mathcal {R}_i}=82\pm 23\,\mathrm{s}$. Nonetheless there is some evidence that the mixing is approximately independent of scale: $\tau _{\mathrm {loc}}$ and $\tau _{\mathcal {R}_c}$ agree well, as with Set A. These time scales show order-of-magnitude agreement with $\tau _L$; the agreement between $\tau _{\mathcal {R}_i}$ and $\tau _L$ is poorer (Fig. 14).

The anomalous behaviour identified above is related to the source location and averaging region. The agreement among the ensemble-averaged mixing time scales is improved when TR is omitted from the ensemble. This location is special because strong turbulence near the leading edge of the windward wall, where the TKE is maximised, increases dispersion (Fig. 6) and $\tau _{\mathcal {R}_i}|_{TR}$. The other definitions, $\tau _{\mathrm {loc}}$ and $\tau _{\mathcal {R}_c}$, are less susceptible to transient behaviour related to the choice of localised initial conditions. It is plausible that agreement worsens for $\tau _{\mathcal {R}_i}$ since it represents an average of the canyon-scale variance over the source region (Eq. (9a)).

The subregimes disappear with a spatially distributed “ring source”, in which the scalar is initially confined to the region, $R_i \le r \le R_o$, with r(x, z) defined with respect to the origin, $(x/W=0,z/H=0.5)$. The thickness of the ring $dR\equiv R_o-R_i=l$, the spatial dimension of the block sources in Fig. 5. The cases (i) $R_i=16\,{\text {m}}, R_o=22\,{\text {m}}$ (which excludes the corner vortices) and (ii) $R_i=19\,{\text {m}}, R_o=25\,{\text {m}}$ (which includes the largest R that can be inscribed within the canyon) have been tested. In agreement with $\tau _{\mathcal {R}_c}$ and $\tau _{\mathrm {loc}}$ for the vortex sea (Set B), there is uniform exponential decay for $t\lesssim 200\,\mathrm{s}$ with $\tau _{\mathcal {R}_i}|_{\mathrm {ring,i}}=34\pm 1\,{\text {s}}$ and $\tau _{\mathcal {R}_i}|_{\mathrm {ring,ii}}=38\pm 1\,{\text {s}}$.

5.2.3 Set C (central vortex)

The evolution of scalar initially located inside the canyon vortex differs qualitatively from Sets A and B. The scalar fields have an axisymmetric appearance and show less evidence of large-scale straining (Fig. 6). Indeed the variance-decay time scales are about 5–6 times longer than $\tau _L$: averaging over the three definitions, $\tau _{\mathrm {avg}(\mathcal{R}_i,\mathcal{R}_c,\mathrm {loc})}=149\pm 15\,\mathrm{s}$. Furthermore, mixing is slow compared to Sets A and B.

A likely explanation is that mixing inside the central vortex obeys a different physical mechanism. Since turbulence is weaker near the canyon midplane [13, 56], the central vortex is more persistent than the corner vortices. It is tempting to estimate the mixing time scale as the diffusive time scale across a vortex of prescribed radius. However, Eq. (18) gives $t_d\sim 10^4\,\mathrm{s}\gg \tau _{\mathrm {avg}}$ for a radius $L_d=17\,\mathrm{m}$, which is the largest radius that excludes the corner vortices within the present configuration [16]. This estimate is inconsistent with the observed variance decay.

The motion along streamlines increases the effective diffusion across streamlines [59]. Analytical estimates of the effective diffusivity, $\kappa _{\mathrm {eff}}$, come from the theory of cellular flow for closed, spatially periodic flows [26]. A well-known estimate gives

$$\begin{aligned} \kappa _{\mathrm {eff}}= \kappa {Pe}^{1/2}, \end{aligned}$$

(22)

where $\kappa$ is the molecular or turbulent diffusivity. The Péclet number, ${Pe}=RV/\kappa$, depends on the tangential velocity V at radius R (see Appendix 3). The average turbulent diffusivity, $\langle \overline{\kappa }_T\rangle$, taken over the region bounded by R, is substituted for $\kappa$. The associated diffusive or mixing time scale is then given by

$$\begin{aligned} \tau _{\mathrm {eff}}= \frac{R^2}{\kappa _{\mathrm {eff}}}. \end{aligned}$$

(23)

The choice of R is somewhat arbitrary because the vortex does not have a distinct boundary. A reasonable choice is $R=9\,\mathrm{m}$, within which approximately 74% of the vorticity is concentrated [16]: this yields $\tau _{\mathrm {eff}}= 222\pm 6\,\mathrm{s}$, where the errors reflect the variability in mean tangential speed, and $\tau _{\mathcal {R}_i}|_{R=9\,\mathrm{m}}=167\pm 2 \,\mathrm{s}$. The prediction shows rough agreement with the actual variance decay. For $R\in [4\,\mathrm{m}, 17\,\mathrm{m}]$, $\tau _{\mathcal {R}_i}$ ranges between $93\,\mathrm{s}$ and $561\,\mathrm{s}$ while the variation in $\tau _{\mathrm {eff}}$ is much smaller (not shown). Exact agreement between the analytical estimate (Eq. (22)) and the numerical results is unlikely even if the “true” value of R could be determined: the canyon vortex is not steady and the theory assumes spatially periodic flow with a separatrix dividing each cell [59]. Nonetheless there is agreement within an order of magnitude.

5.2.4 Non-constant initial concentrations

The preceding results were obtained with constant initial concentration, $C_0$. Following Pierrehumbert [55], non-constant initial conditions have been tested:

$$\begin{aligned} C_0^\prime (\mathbf {x},0)=C_0 \left| \sin \left[ \frac{2\pi (x-x_0)}{l} \right] \sin \left[ \frac{2\pi (y-y_0)}{L_y} \right] \sin \left[ \frac{2\pi (z-z_0)}{l} \right] \right| , \end{aligned}$$

(24)

where l is the spatial dimension of the source block (see Fig. 5) and $(x_0,y_0,z_0)$ are the coordinates of the lower-left corner. Without loss of generality, one $\mathcal{R}_i$ is selected from each of the three sets: BL from Set A; CL from Set B; CC from Set C.

The variance decay of the three non-constant $C_0^\prime$’s is plotted in Fig. 15. There is minimal sensitivity to $C_0'$: $\tau _{\mathcal{R}_i}|_{BL}=32\pm 1\,{\text {s}}$, $\tau _{\mathcal{R}_i}|_{CL}=61\pm 5\,{\text {s}}$ and $\tau _{\mathcal{R}_i}|_{CC}=143\pm 2\,{\text {s}}$ compared to $32\pm 1, 62\pm 5, 147\pm 2$ respectively (Appendix 2, Table 4).

Fig. 15

As in Fig. 12 but for BL, CL and CC and non-constant initial conditions, Eq. (24). The early and late regimes persist

6 Ground-level sources

Ground-level sources are of particular relevance to urban air quality. Since qualitatively similar behaviour is obtained for initial conditions outside the central vortex (Sects. 5.2.1 and 5.2.2), ground-level area and line sources should be well-approximated by Sets A and B. This is tested using results from ground-level area and line sources (Fig. 16)

Fig. 16

Schematic illustrations of the ground-level a area; b line sources. The configuration of the line source follows Gromke and Ruck [22]

Fig. 17

Scalar fields at $t=250\,\mathrm{s}$ for the ground-level a area; b line sources. There are qualitative similarities with the results for localised initial conditions (see the bottom row of Fig. 6)

Snapshots of the scalar fields are shown at $t=250\,\mathrm{s}$ for the line and area sources (Fig. 17). In both cases, the effects of large-scale straining by the canyon circulation are obvious. The similarity between them probably arises from their symmetric arrangement about $x/W=0$: the results resemble a composite of those for the ground-level pollutant blocks, BL, BC and BR (Fig. 6).

More generally, line and area sources show good quantitative agreement with the earlier results. The mean concentration decays almost exponentially from the outset with $T_r|_{{\mathrm{line}\,\mathrm{and}\,\mathrm{area}}}=909\pm 1\,\mathrm{s}$ versus $T_r=910\,\mathrm{s}$ for the nine $\mathcal{R}_i$. The MTA’s, $\hat{\tau }_a|_\mathrm{line}=924\,{\text {s}}$ and $\hat{\tau }_a|_\mathrm{area}=921\,{\text {s}}$, lie within the range spanned by BL, BC and BR (Table 2). The variance decay is divided into an early and late regime and the time scales are consistent with the values for Set B (Table 4). For the late regime, $\tau _{\mathcal {R}_i}|_\mathrm{area~ and~line}=457\pm 2 \,\mathrm{s}$, while for the early regime, $\tau _{\mathcal {R}_i}|_\mathrm{area}=58\pm 2\,\mathrm{s}$ and $\tau _{\mathcal {R}_i}|_\mathrm{line}=52\pm 2\,\mathrm{s}$. As with the ring source (see Sect. 5.2.2), there is minimal sensitivity to the variance definition.

7 Conclusions

This paper has shown that the scalar dynamics within a street canyon depend sensitively on initial conditions. It was found that differences in the scalar fields persist even after $\sim 10$ large-scale circulation times. Analyses of ventilation and mixing confirmed the importance of the open boundary. The canyon-averaged concentrations for initial conditions defined by cubic “pollutant blocks” arranged in a $3\times 3$ grid within the canyon do not converge to the same value, though the decay rates are essentially identical at large times. The canyon-averaged variance decayed in two distinct regimes: the early regime reflects large-scale straining and diffusion across streamlines but the late regime is associated with escape from the canyon, i.e., ventilation. The variance decay rates may be classified into three sets defined by the location of the pollutant blocks relative to the central or corner vortices.

Given the idealised setting of this study, e.g. the restriction to a 2-D street canyon with unit aspect ratio and perpendicular incident flow, the main findings are somewhat theoretical in nature. First, it is demonstrated that the open roof-level boundary of a street canyon leads to profound differences compared to mixing within closed domains. Since fluid parcels that leave the domain by crossing the roof level do not necessarily return, significant mixing occurs only at early times, i.e. on the time scale of the canyon circulation. Memory of the initial conditions is maintained because the scalar fields are not homogenised over the entire canyon. In the language of dynamical systems theory, the dynamics reflect transient chaos or scattering [49] rather than the stationary chaotic dynamics of chaotic advection [50]. Second, it is shown that analytical predictions for chaotic advection [25] and effective diffusion across closed streamlines [59] apply to the variance decay rates. Although the agreement is quite rough, it is still notable insofar as the theories invoke many assumptions (e.g. spatial homogeneity or exactly 2-D flow) that are not satisfied by turbulent flow inside a street canyon; indeed there is no guarantee that the theories should apply at all.

Despite the inherent limitations of this study, there are several ways in which this work could be applied more generally. With respect to practical urban design, the present street-canyon results indicate that a ground-level source located at the centre of the canyon yields improved air quality compared to sources at the upwind and downwind corners (e.g. the canyon-averaged concentration is approximately 20–30% lower, with a similar effect for the pedestrian level). The level of improvement would obviously depend on the details of the flow, but there is reason to believe that the phenomenon may be more general. Neither escape of fluid parcels from the urban canopy nor a spatially inhomogeneous circulation, which are the key ingredients responsible for the sensitivity to initial conditions, is exclusive to street-canyon flow. With respect to implications for modelling, parameterisations of mixing based on the variance decay rate could be developed for more realistic flows. This would be a natural extension of network models of urban pollutant dispersion [2, 61], which assume uniform concentration or perfect mixing within a box (e.g., a street canyon). Application to pollutant dispersion aside, quantification of the (inhomogeneous) mixing rate could prove useful for urban canopy parameterisations (UCPs), which seek to represent the effects of the urban environment on larger scales [11, 41]. Mixing on urban scales would still need to be related to mixing on larger scales, e.g., the mesoscale; one possibility would be to “embed” a highly reduced urban model, based on the mixing and ventilation rates, inside each mesoscale grid box. Such an approach is similar in spirit to UCPs and existing atmospheric parameterisations, e.g., multiscale cloud parameterisation schemes [21]. The relevance of the analytical predictions to more realistic settings is unclear and would need to be investigated on a case-by-case basis.

Appendices

Appendix 1: Lyapunov exponents

The stretching of fluid trajectories or the divergence of particles trajectories is governed by the velocity-gradient tensor. It has elements $J_{ij}= \partial u_i/\partial x_j$. After discretising in time, (vector) perturbations evolve according to the map

$$\begin{aligned} dX_{n+1} = (J(\mathbf {U})\varDelta t)_n dX_n. \end{aligned}$$

(25)

For simplicity, $dX_0={\varvec{I}}$. The Lyapunov exponents are calculated following the algorithm of von Bremen et al. [6]. Applying QR-factorization to the matrix product $J_nJ_{n-1}\cdots J_1$ yields $R=\{R_0,\ R_1,\ \ldots \ ,\ R_{n-1},\ R_n\}$ where $n\in [0,n]$ and $R_i$ denotes the upper triangular matrix from the $i^\mathrm{{th}}$ QR-factorization. The Lyapunov exponents follow from

$$\begin{aligned} \lambda = \frac{1}{n\varDelta t}\sum \limits _{i=0}^n \log {(\varLambda R_i)}, \end{aligned}$$

(26)

where $\varLambda$ denotes the diagonal elements of $R_i$ and $\lambda$ is a row vector, i.e. $\lambda = \lambda (\lambda _0,\lambda _1,\lambda _2)$ with $\lambda _0$ representing the maximum Lyapunov exponent. The associated time scale is just the reciprocal of $\lambda _0$. For initial conditions within $\mathcal {R}_i$ (cf. Fig. 5),

$$\begin{aligned} \tau _L=1/\langle \lambda _0 \rangle _{\mathcal {R}_i}, \end{aligned}$$

(27)

where $\langle \cdot \rangle _{\mathcal {R}_i}$ denotes the spatial average over $\mathcal {R}_i$.

Appendix 2: Variance-decay and Lyapunov time scales

Variance-decay time scales for the early and late regimes are listed in Tables 3 and 4, respectively. The corresponding Lyapunov time scales are shown in Table 5.

Table 3 Variance-decay time scales (s) for the late regime, $t\in [1000\,\mathrm{s}, 5000\,\mathrm{s}]$

Table 4 Variance-decay time scales (s) for the early regime (Fig. 12)

Table 5 Lypaunov time scales (s)

Appendix 3: Tangential velocity of the central vortex

The tangential velocity, $V(x,z)=\sqrt{u(x,z)^2+w(x,z)^2}$, is calculated by assuming that the vortex is circular and centred at the centre of the canyon O(0, H / 2) (see Fig. 5 of Duan and Ngan [16]). The coordinates of a particle are defined by

$$\begin{aligned} x = R\cos \theta , \quad z = R\sin \theta , \end{aligned}$$

(28)

where R is the radius of the nominal vortex. Averaging in space and time

$$\begin{aligned} \langle \overline{V} \rangle = \frac{1}{A_{\ell }} \int \limits _{-L_y/2}^{L_y/2}dy \int \limits _{-\pi }^{\pi }Rd\theta \ \overline{{V}}(x,z), \end{aligned}$$

(29)

where $L_y$ is the canyon length in the spanwise direction and $A_{\ell }=2.0\pi RL_y$ is the surface area of the cylindrical vortex. For brevity, $\langle \overline{\cdot }\rangle$, is omitted from the text.