1 Introduction

Understanding wave breaking is fundamental for many coastal engineering problems. It is well known that turbulence and undertow currents in the breaking zone are key factors in the mixing and transport processes. Experimental studies on breaking waves are particularly difficult to carry out. The breakers which most commonly occur are the spilling breaking waves, which occur mostly in deep ocean waters. Spilling type breaking flows can be those generated by wind waves (known as white caps), in contrast with plunging type breaking. These spilling breakers are responsible for most of the air-sea interactions, and consequently for the air entrainment which is important for underwater life [3]. Also, one can easily observe wave breaking phenomena in shallow-water hydraulic jumps or bow and stern waves of boats. In the spilling type breaking category, Tulin and Cointe [47] showed a distinction between spilling type breaking in shallow water (bore) and spilling type breaking in deep water. Several investigators have contributed to our basic understanding of spilling breaking waves. Elementary models describe breaking as a roller residing over the front face of a non-breaking wave. Later studies [3, 41] have shown that the flow just below the breaker is not a roller, but a thin turbulent region beneath the spilling breaker. The turbulent layer extends downstream at the free surface, and decays with increasing distance from the breaker. Battjes and Sakai [5] used a hydrofoil to induce spilling breakers, and obtained velocity profiles at various stations downstream of the hydrofoil. They determined that the turbulent wake downstream of the separation at the surface is self-preserving, indicating the possible existence of a shear layer.

Tulin and Cointe [47] and Cointe and Tulin [7] present a detailed and comprehensive theory of steady wave breaking. Their results were compared with the experiments by Duncan [16, 17] and were found to agree quite well with them. In their work, Duncan and Philomin [18] showed some of the features associated with the development of spilling breaking waves.

Using the Particle Image Velocimetry (PIV) technique, Lin and Rockwell [26] were able to map the flow field directly beneath the spilling breaker, and were therefore able to show the existence of a shear layer beneath the breaking wave. Through further studies, they were also able to characterize the evolution of wave breaking [27]. An interesting approach to the studying of ship-generated wave breaking is given by Miyata and Inui [32], where the authors suggest that the proper Froude number necessary to describe these breakers should be based on the ship draught rather than its length.

Experimental techniques and grid-based numerical methods suffer from certain limitations and difficulties when they are employed in the study of such violent free surface flows (for further details see [23, 42]. On the other hand, particle methods have the potential to provide a comprehensive description of the full processes associated with wave breaking, whilst they can accurately capture the water surface profile during such processes.

Smoothed Particle Hydrodynamics (SPH), developed since 1977 to simulate astrophysical problems [21, 30], is presently one of the most popular mesh-free methods for numerical simulations in solid and fluid mechanics. The basics of the methodology are described in review papers and textbooks [28, 33, 35, 48]. The method is fully Lagrangian and obtains, through a discrete kernel approximation, the solution of the equations of motion for each of the fluid particles in which the flowing volume is discretized. The free surface requires, therefore, no special approach, such as in the case of the Volume-of-Fluid method or of Lagrangian surface tracking techniques. Furthermore, the method can easily treat rotational flows with vorticity and turbulence.

The purpose of this paper is using SPH to study the connection between the breaking process and the near-surface turbulence and vorticity fields generated just below the breaker. A comparison between 2D SPH solutions and experimental Laser Doppler Anemometer (LDA) results on the spilling type breaking generated by a hydrofoil in a free surface current is first shown to validate the use of the numerical solution in the understanding of the physical features of the flow. In particular, the comparison regards the velocity profiles obtained at different locations downstream of the trailing edge, the turbulence intensities (measured in terms of the fluctuating velocity components \(u^{\prime}\) and \(v^{\prime}\)), the turbulent shear stresses \(\left( {\overline{{u^{\prime}v^{\prime}}} } \right)\) along the channel and the velocity and vorticity fields.

2 Experimental set up

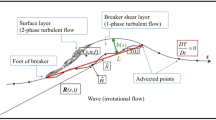
Experimental investigations were carried out in the hydraulic laboratory of Department of Civil, Environmental Building Engineering and Chemistry of Bari Technical University (Italy), in the 0.40 m wide, 24.4 m long Plexiglas channel shown in Fig. 1, which has a sidewall height of 0.5 m. Discharges were measured by a triangular sharp-crested weir. Measurements of the upstream and downstream water depths were carried out with electric hydrometer-type point gauges, supplied with electronic integrators which yielded the estimation of the time-averaged flow depth. The hydrometers were supplied with verniers, allowing us to obtain a measurement accuracy of ±0.1 mm. Water discharge and hydrodynamic conditions were regulated by two gates placed at the upstream and downstream ends of the channel. The velocity field was measured in the mid-plane of the channel by using a backscattered, two-component, four-beam fiber-optic LDA system. A 5 W watercooled argon-ion laser, a transmitter, a 85 mm probe (having a focal length of 310 mm and a beam spacing of 60 mm) and a Dantec 58N40FVA enhanced signal processor were used. The laser wave lengths were 488.0 and 514.5 nm. The wave elevation downstream of the hydrofoil was also measured in the mid-plane of the channel by a resistance wave gauge. A rigid Plexiglas hydrofoil NACA 0024, characterized by a chord of 0.2 m and spanning the entire width of the flume, was fixed to the channel side walls at an attack angle of 10°, as shown in Fig. 2. The leading edge of the hydrofoil was positioned 15.13 m downstream of the inlet gate, at a height of 0.1 m from the bottom of the channel (i.e. equal to half of the hydrofoil chord). During the experiments, the discharge was kept fixed to a value of 76.07 ls−1, resulting in a mean velocity of 0.79 ms−1 upstream of the hydrofoil (measured in a cross section positioned 14 m downstream of the inlet, i.e. more than 5 chords upstream of the hydrofoil) and of 0.93 ms−1 in the cross section B8 (see Table 2), where the wave elevation profile was already negligible. In the aforementioned sections, the corresponding Froude numbers were 0.51 and 0.65, with a tailwater level in the channel of 0.24 m and 0.205 m, respectively. The flow Reynolds number Re = V c h/ν, where V c is the mean velocity in the cross section, h is the upstream water depth and ν is the water kinematic viscosity at the mean temperature of 14.7 °C, was 165000. The measured wave breaking height H b was equal to 0.075 m (Fig. 1). For further details see Mossa [39].

Fig. 1
figure 1

Experimental set-up and sections where LDA measurements were obtained

Full size image
Fig. 2
figure 2

NACA 0024 hydrofoil: a geometry at an angle of attack of 10°; b installation of the hydrofoil model in the flume

Full size image

3 SPH numerical method

In SPH, any continuous vector function a(x,t) characterizing the flow is approximated by a discrete vector function a i (t) = a(x i , t), defined in a suitable number of discrete moving points. Each discrete point is associated to an elementary fluid volume (or particle) i, which has position x i and constant mass m i .

The values of \(a({\bar{\varvec{X}}},t)\) at a generic point \({\bar{\varvec{X}}}\) can then be interpolated from the nodal values a i (t) through a kernel function \(W(\varvec{X}-{\bar{\varvec{X}}},\eta)\) which is continuous, non-zero only inside a sphere \(\varvec{X}-{\bar{\varvec{X}}}\; < \;2\eta\) and tends to the Dirac delta function when η (defined as the smoothing length) tends to zero.

Among the different available kernel functions, the SPH computations discussed in the present paper were based on the cubic-spline function [37]. Although it has been shown [14] that the Wendland kernel function [49] can be more computationally convenient than the B-spline function, allowing better numerical convergence, and that the quintic-spline function [38] can be more effective [29] in interpolating the second-order derivatives (which are however computed here by a renormalization of the kernel function, as explained in the following), the cubic-spline kernel proved nevertheless to be effective in the simulation of several different hydraulic flows, such as those involving jets [19], hydraulic jumps [13] or interactions with deformable elastic walls [1] or with granular beds [31]. The approximated value of the function a becomes therefore:

$${\mathbf{a}}({\bar{\mathbf{x}}},t) \approx \; < {\mathbf{a}}({\bar{\mathbf{x}}},t) > \, = \sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}} \,{\mathbf{a}}({\mathbf{x}}_{j} ,t)\,W({\mathbf{x}}_{j} - {\bar{\mathbf{x}}},\eta )$$
(1)

where ρ is the fluid density and the summation is extended to all of the N particles located inside the sphere of radius 2η centred on \({\bar{\mathbf{x}}}\).

Accordingly, any differential operator applied to \({\mathbf{a}}({\mathbf{x}},t)\) can be approximated by making use of the gradient of the kernel function. For instance, the divergence \(\nabla \cdot {\mathbf{a}}({\mathbf{x}},t)\) can be approximated by:

$$\nabla \cdot {\mathbf{a}}({\bar{\mathbf{x}}},t) \approx \; < \nabla \cdot {\mathbf{a}}({\bar{\mathbf{x}}},t) > \, = \sum\limits_{j = 1}^{N} {\frac{{m_{j} }}{{\rho_{j} }}} \,\left[ {{\mathbf{a}}({\bar{\mathbf{x}}},t) - {\mathbf{a}}({\mathbf{x}}_{j} ,t)} \right]\,\nabla \,W({\mathbf{x}}_{j} - {\bar{\mathbf{x}}},\eta )$$
(2)

Equation (2) has the property of vanishing exactly for a constant vector field. The reader is referred to general descriptions of the SPH method for further details on the different methods for SPH approximations of all the vector operators [22, 28, 33, 35, 48]. The spilling breaker generated by a NACA 0024 hydrofoil is here modelled by use of the Reynolds-averaged Navier–Stokes equations for a weakly compressible fluid. In a Lagrangian frame, the full system of the equations of continuity, momentum, state and turbulent closure takes the following form:

$$\left\{ {\begin{array}{lll} {\frac{{{\text{D}}\rho }}{{{\text{D}}t}} + \rho \nabla \cdot {\mathbf{v}} = 0} \\ {\frac{{{\text{D}}{\mathbf{v}}}}{{{\text{D}}t}} = - \frac{1}{\rho }\nabla p + \frac{1}{\rho }\nabla \cdot \text{T} + {\mathbf{g}}} \\ {p - p_{0} = c^{2} (\rho - \rho_{0} )} \\ {\text{T} = \mu_{T} \text{S}} \\ \end{array} } \right.$$
(3)

where v = (u, v) is the velocity vector, p is pressure, g is the gravity acceleration vector, T is the turbulent shear stress tensor, c is the speed of sound in the weakly compressible fluid, μ T is the dynamic eddy viscosity, S is rate-of-strain tensor and the subscript 0 denotes a reference state for pressure computation. All the variables in Eq. (3) are assumed to be Reynolds-averaged.

The Weakly Compressible SPH (WCSPH) here followed consists in adopting the weakly compressible formulation (3) with a reduced value of the speed of sound, which takes therefore the role of a numerical parameter. Monaghan [33] demonstrated that the error associated with the adoption of a compressible formulation for the incompressible free-surface water flow is bounded to 1 %, provided the local numerical Mach number \(M_{i} = \left| {{\mathbf{v}}_{i} } \right|/c_{i}\) be everywhere lower than 0.1. After applying the SPH space-discretization, Eq. (3) become:

$$\left\{ {\begin{array}{lll} {\left\langle {\frac{{{\text{D}}\rho_{i} }}{{{\text{D}}t}}} \right\rangle = \sum\limits_{j} {m_{j} \left( {{\mathbf{v}}_{i} - {\mathbf{v}}_{j} } \right)\nabla W_{ij} } } \\ {\left\langle {\frac{{{\text{D}}{\mathbf{v}}_{i} }}{{{\text{D}}t}}} \right\rangle = - \sum\limits_{j} {m_{j} \left( {\frac{{p_{i} }}{{\rho_{i}^{2} }} + \frac{{p_{j} }}{{\rho_{j}^{2} }}} \right)\nabla W_{ij} } + \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {\text{T}_{i} - \text{T}_{j} } \right) \cdot \nabla W_{ij} } + {\mathbf{g}}} \\ {p_{i} - p_{0} = c_{i}^{2} (\rho_{i} - \rho_{0} )} \\ {\text{T}_{i} = \mu_{{T_{i} }} \text{S}_{i} } \\ \end{array} } \right.$$
(4)

where W ij is a shorthand notation for \(W({\mathbf{x}}_{i} - {\mathbf{x}}_{j} ,\eta )\), while the local rate-of-strain tensor for each particle is obtained from the velocity gradient, evaluated through the solution, at each time step, of the following renormalization condition:

$$\sum\limits_{j} {m_{j} \left( {{\mathbf{v}}_{i} - {\mathbf{v}}_{j} } \right)\,\nabla W_{ij} } = \left\langle {\nabla {\mathbf{v}}} \right\rangle_{i} \cdot \left( {\sum\limits_{j} {m_{j} \left( {{\mathbf{r}}_{i} - {\mathbf{r}}_{j} } \right)\nabla W_{ij} } } \right)$$
(5)

which enforces 1st-order consistency on the first derivatives of the velocity function [6].

The semi-discretized system (4) is then integrated in time by a 2nd order two-step XSPH explicit algorithm [33], where the velocity field at the previous step is firstly used to compute the velocity gradient (5) and hence the turbulent stress tensor. The momentum equation is then solved to yield an intermediate velocity field \({\hat{\mathbf{v}}}\), which is then corrected through a smoothing procedure based on the values of the neighbouring fluid particles:

$${\mathbf{v}}_{i} \, = (1 - \phi_{v} )\,{\hat{\mathbf{v}}}_{i} + \,\phi_{v} \frac{{\sum\nolimits_{j} {\frac{{m_{j} }}{{\rho_{j} }}{\hat{\mathbf{v}}}_{j} W_{ij} } }}{{\sum\nolimits_{j} {\frac{{m_{j} }}{{\rho_{j} }}W_{ij} } }}$$
(6)

through the use of a velocity smoothing coefficient φ v . The corrected velocity value is then used to update the particle position and to solve the continuity equation. The new density values are finally used to compute pressure, according to the equation of state.

A smoothing procedure similar to (6) is applied also to pressure values [45] in order to reduce the numerical noise in pressure evaluation which is present, in particular in WCSPH, owing to high frequency acoustic signals [2]. Integral interpolations [8] give good results but do not properly conserve the total volume of the particle system for long time simulations owing to improper filtering of the hydrostatic component of pressure. The present method is therefore applied only to the difference between the intermediate pressure field \(\hat{p}\) and the hydrostatic pressure gradient, resulting in:

$$p_{i} = \frac{{\sum\nolimits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left[ {\hat{p}_{j} + \rho_{i} g\,(y_{j} - y_{i} )} \right]\;W_{ij} } }}{{\sum\nolimits_{j} {\frac{{m_{j} }}{{\rho_{j} }}W_{ij} } }}$$
(7)

where y is the vertical coordinate. This approach is alternative to other methods proposed to reduce pressure oscillations, such as the one by Antuono et al. [2], where a numerical diffusive term for density is added to the continuity equation.

The eddy viscosity coefficient in Eq. (4) was evaluated either through a mixing-length model, as suggested by Gallati and Braschi [20], or through a k-ε model. In the adopted mixing-length model, the time scale is obtained from the norm \(\left\| \text{S} \right\| = \sqrt {(\text{S}:\text{S}^{T} )}\) of the rate-of-strain tensor S, while the mixing-length for each particle is evaluated as:

$$\ell_{i} = f_{i}\; \hbox{min}\left[{\mathbf{\upkappa}}(z),\ell_{\hbox{max}}\right]$$
(8)

where κ = 0.41 is the Von Kármán constant, z is the distance from the wall, ℓ max is a cutoff maximum value and:

$$f_{i} = { \hbox{min} }\left[ {1,\left| {\sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\nabla W_{ij} } } \right|^{ - 3} } \right]$$
(9)

is a damping function which assumes values lower than unity only near the free-surface and avoids a non-physical growth of ℓ which may lead to numerical instabilities [11, 12]. According to the sensitivity analysis shown by De Padova et al. [13], the simulation of the spilling type breaking flow field produced by a NACA 0024 hydrofoil, was performed by adopting a velocity smoothing coefficient in the XSPH scheme scheme φ = 0.02 and a mixing length turbulence model with l max  = 0.5 h 2 . The two-equation model is a SPH version of the standard k-ε turbulence model by Launder and Spalding [25]:

$$\begin{aligned} \frac{{Dk_{i} }}{Dt} = P_{{k_{i} }} + \frac{1}{{\sigma_{k} }}\mathop \sum \limits_{j} m_{j} \frac{{\nu_{{T_{i} }} + \nu_{{T_{j} }} }}{{\rho_{i} + \rho_{j} }}\frac{{k_{i} - k_{j} }}{{r_{ij}^{2} + 0.01h^{2} }}\vec{r}_{ij} \cdot \vec{\nabla }{\text{W}}_{ij} - \varepsilon_{i} \hfill \\ \frac{{D\varepsilon_{i} }}{Dt} = \frac{1}{{\sigma_{\varepsilon } }}\mathop \sum \limits_{j} m_{j} \frac{{\nu_{{T_{i} }} + \nu_{{T_{j} }} }}{{\rho_{i} + \rho_{j} }}\frac{{\varepsilon_{i} - \varepsilon_{j} }}{{r_{ij}^{2} + 0.01h^{2} }}\vec{r}_{ij} \cdot \vec{\nabla }{\text{W}}_{ij} \;+ \hfill \\ \; + C_{{\varepsilon_{1} }} \frac{{\varepsilon_{i} }}{{k_{i} }}P_{{k_{i} }} + C_{{\varepsilon_{2} }} \frac{{\varepsilon_{i} }}{{k_{i} }}\mathop {\,\sum }\limits_{j} \frac{{m_{j} }}{{\rho_{j} }}\varepsilon_{j} {\text{W}}_{ij} \; \hfill \\ \end{aligned}$$
(10)

where Pk is the production of turbulent kinetic energy depending on the local rate of deformation, ν T is the eddy viscosity and σ k  = 1, σε = 1.3, C ε1  = 1.44 and C e2  = 1.92 are model constants whose values are those proposed for the standard k-ε formulation.

It must be noted that aeration plays an important role in the dynamics of a turbulent spilling breaker and that a multi-phase analysis, which can be ordinarily tackled through SPH [36] should be in general preferred. However, air entrainment in spilling breakers can give rise to a dispersed bubbly flow: the SPH modeling of bubble flows can be at present performed efficiently in many cases of bubble raising or merging [24], but its application to a general, dispersed bubbly flow can be still questionable and excessively demanding on the computational ground. A reliable validation of a model for air entrainment in a spilling breaker would be therefore outside the scope of the present paper.

On the other hand, the fact that the production of the sub-surface vorticity layer, which is later entrained in the breaker (and whose analysis is one of the main topics in our paper), occurs where air entrainment is still absent, allows us to obtain a consistent simulation of the flow also by using a single-phase description. In our experience, this approach proved to be effective in other cases, like hydraulic jumps [11], where air entrainment plays an important role but consistent results can be obtained also through a single-phase analysis.

The boundary conditions are imposed by using the ghost particle technique [41]. However, to avoid superposition of ghost particles in the trailing edge region, the width of the layer of boundary particles has been limited to half of the thickness of the hydrofoil. Although particle penetration inside the solid wall is not completely guaranteed in this case, it did not occur owing to the prevalent tangential direction of the flow.

This solution, which proved to work satisfactorily in the present case, might not be of general applicability, especially in case of flows around hydrofoils at higher angles of attack. In these cases, a more accurate approach, such as semi-analytic boundary integrals [15] or Multiple Boundary Tangents [42], may be more appropriate.

The inflow condition is enforced through the introduction of a 2 h-wide layer of fluid particles with constant velocity and head along the water depth. In this way the boundary condition guarantees a completely irrotational uniform flow and vorticity at the inlet is exactly zero.

4 Numerical tests and results

The 2D simulations reported in Table 1 were performed in a physical domain consisting in a rectangle 4 m long and 0.3 m high, shorter than the real channel in the test facility. The shorter domain was chosen in order to reduce the computational cost without influencing the quality of the numerical solution. Therefore, it was extended to those stations where the upstream and downstream influence of the hydrofoil on the measured flow was negligible.

Table 1 Principal characteristics of SPH simulations
Full size table

The upstream flow depth h 1 and the downstream flow depth h 2 were therefore set to 0.24 and 0.205 m, respectively. Particles were initially placed on a Cartesian grid with zero initial velocity. The choice of the initial particle spacing Σ depends on the physical process of the problem and on the desired computational accuracy and efficiency.

The accuracy of particle methods is influenced by the initial particle spacing Σ, as well as by the smoothing length η. Both parameters must be taken into account when attempting to improve the resolution of the numerical simulation. It has been shown that the efficiency of the SPH kernel function depends also on the choice of the η/Σ ratio [14] and that a value η/Σ ≥ 1.2 should be preferred [10]. Here, a constant the value of the ratio, i.e. η/Σ = 1.5, was maintained, the effect of particle resolution on the quality of the numerical results was investigated and a convergence analysis was carried out on the test case T1. Simulations were performed by decreasing progressively the initial particle spacing Σ, approximately doubling each time the particle number.

In particular, the 2D flow was simulated by discretizing the computational domain through a value of an initial particle spacing Σ varying from 0.007 to 0.015 m: the related number of SPH particles Np in the computational domain ranged from about 4000 to 18,000, respectively.

The comparison of the free-surface profiles along the channel predicted at the different particle resolutions (Fig. 3) shows that position and height of the standing wave downstream of the hydrofoil are correctly predicted if Np ≥ 9000: this choice appears therefore to guarantee the independence of the SPH result from the resolution. All the remaining SPH simulations have been then performed with Np = 9000 (Table 1).

Fig. 3
figure 3

Effect of the resolution on the free-surface profile in the SPH simulation of Test T1

Full size image

The results of the SPH simulations were compared with the experimental data in terms of: (1) velocity profiles obtained at different locations downstream of the trailing edge for both tests T1 and T2; (2) turbulence intensities, measured in terms of the rms values of the fluctuating velocity components and the turbulent shear stresses along the channel (for test T1 only); (3) the velocity and vorticity fields (for test T1 only).

The analysis of turbulence properties is based on the Reynolds decomposition \(v = V + v^{\prime}\) or, in terms of velocity components, \(\left( {u,v} \right) = \left( {U,V} \right) + \left( {u^{\prime},v^{\prime}} \right)\), where capital letters indicate time-averaged velocities and the prime indicates velocity fluctuations. It must be underlined that, in the flow around the hydrofoil, the velocity fluctuations around the mean flow depend both on the small-scale turbulent eddies and on the large-scale unsteady vortical motions induced by the presence of the hydrofoil itself. In the experiments, no difference can be made on the different origin of these fluctuations and the measurement includes globally all the effects. In the time-dependent SPH simulation, however, the large-scale vortical motions are directly simulated, while small-scale turbulence is modelled: in this case, the fluctuations of velocity with respect to the steady-state conditions can only be referred to large-scale motions.

In the discussion which follows, therefore, it will be assumed that turbulence intensities are evaluated as:

$$\begin{aligned} u^{\prime}_{rms} = \sqrt {\frac{1}{{N_{T} }}\sum\limits_{n = 1}^{{N_{T} }} {(u_{n} - U)^{2} } } \hfill \\ v^{\prime}_{rms} = \sqrt {\frac{1}{{N_{T} }}\sum\limits_{n = 1}^{{N_{T} }} {(v_{n} - V)^{2} } } \hfill \\ \end{aligned}$$
(11)

where N T is the number of recorded values at steady state, while the turbulent shear stress takes into account also the effect of the modelled small-scale turbulent eddies and is evaluated as:

$$\overline{{u^{\prime}v^{\prime}}} = \frac{1}{{N_{T} }}\sum\limits_{n = 1}^{{N_{T} }} {(u_{n} - U)(v_{n} - V)} + \frac{{\mu_{T} }}{{\rho N_{T} }}\sum\limits_{n = 1}^{{N_{T} }} {{\text{S}}_{{xy_{n} }} }$$
(12)

Table 2 indicates the flow sections where the measurement points were located. In detail, these velocity profiles represent the initial development of the hydrofoil wake (section B0), the supercritical flow at maximum Froude number (B1), the development of the standing wave (B2) and the spilling type breaking (B3–B4), as indicated in the velocity vector field shown in Fig. 4. In general, the velocity profiles computed in tests T1 and T2 compare satisfactorily with the experiments, both in the wake and wave regions and in the far field downstream (Fig. 5). The hydrofoil wake is correctly reproduced in section B0 with its downward flow near the free surface; the sudden reduction of the vertical velocity component V near the spilling type breaking is section B4 is also well represented.

Table 2 Location of measurement points
Full size table
Fig. 4
figure 4

Instantaneous SPH velocity field in the SPH simulation of Test T1 a particle distribution and velocity magnitude b velocity vector field downstream of the hydrofoil, with indication of the sections where the velocity was measured

Full size image
Fig. 5
figure 5

Diagrams of a horizontal (U) and b vertical (V) time-averaged velocity components: numerical solution versus laboratory experiments in Tests T1 and T2 in the wake region and below the standing wave (Sections B0–B4) and in the far field (Sections B5–B8)

Full size image

Indeed, separation in the numerical simulation occurs on the upper surface just upstream of the trailing edge, as it is evident, for instance, in the instantaneous vector field in Fig. 4b. The extension of the separated region appears to be limited and affects only the velocity profile in section B0: this influence appears also on the vorticity field, which shows a negative (counterclockwise) peak just downstream of the hydrofoil. It must be noted that the behaviour of this symmetric NACA airfoils at an angle of attack of 10° is not linear and separation is prone to occur at the trailing edge. Existing wind tunnel data for the NACA 0025 airfoil [44] show that the lift coefficient curve departs from linearity at 9° (indicating possible trailing edge separation) even at Re = 5 106, while it approaches its maximum (indicating complete separation on the upper surface) at Re = 160,000 (Fig. 6). In the present case, the undisturbed upstream Re for the hydrofoil is 158,000: even if the flow just upstream of the hydrofoil is not exactly uniform (as shown in Fig. 3), it is then reasonable to assume that the flow around the hydrofoil is in an unstable regime where separation is prone to occur and a discrepancy between numerical simulation and experiment is therefore not surprising.

Fig. 6
figure 6

Lift coefficient C L versus angle of attack α for a NACA 0025airfoil at different Upstream Reynols numbers. Data from [44]

Full size image

A global evaluation of the can be obtained by computing the index proposed by Wilmott [50]:

$$I_{W} = 1 - \frac{{{}_{k = 1}^{N} \left( {Xc_{k} - Xm_{k} } \right)^{2} }}{{{}_{k = 1}^{N} \left[ {\left| {Xc_{k} - \overline{Xm} } \right| + \left| {Xm_{k} - \overline{Xm} } \right|} \right]^{2} \, }}$$
(13)

a statistical parameter in which X c and X m are the modelled and measured values respectively, while the bar denotes an average of the modelled and measured values.

I W assumes a value of 1, when a perfect agreement exists between the measured and modelled values, while a value of I W close to 0 denotes a complete discrepancy between the numerical and the experimental results. The computed values of I W (which is equal to 0.90 and 0.88 for the horizontal velocity component and to 0.99 and 0.97 for the vertical component in test T1 and test T2, respectively) confirm the good agreement between simulations and experiments.

It is therefore not surprising that the SPH simulation does not appear to be strongly sensitive to the adopted turbulence model: actually, both the mixing-length model and the k-ε model yield similar results, although the detailed comparison of the velocity fields shows that the mixing-length results prove to be closer to the experimental data than the k-ε ones, which seem instead to underpredict slightly the time-averaged longitudinal velocity component U.

Figure 7 shows the values of turbulence intensities u′ rms and v′ rms and of the cross-correlation between the turbulent velocity components \(\left( {u^{\prime},v^{\prime}} \right)\) in all the measurement points. The comparison between the numerical results (T1) and laboratory measurements is satisfactory, with a value of I W equal to 0.75, 0.85 and 0.80 being found for the turbulence intensities u′, v′ and the turbulent velocity components \(\left( {u^{\prime},v^{\prime}} \right)\), respectively.

Fig. 7
figure 7

Diagrams of a \(u^{\prime}_{rms}\); b \(v^{\prime}_{rms}\) and c \(\overline{{u^{\prime}v^{\prime}}}\): numerical solution versus laboratory experiments in Tests T1

Full size image

From the analysis of Fig. 7c it is clear that the cross-correlation \(\overline{{u^{\prime}v^{\prime}}}\) presents values which are strongly different from zero only in the flow region downstream of the hydrofoil and closest to the free surface, whereas they are considerably reduced downstream of section B8.

Figures 5 and 7 highlight the existence of a velocity deficit similar to that which can be found in a wake, where the following similarity conditions hold [46]:

$$l\,\propto\,x^{{*^{1/2} }}$$
(14)
$$\tilde{u^{\prime}}\,\,\propto\,\,x^{{*^{ - 1/2} }}$$
(15)
$$U_{\text{d}} \,\propto\, x^{{*^{ - 1/2} }}$$
(16)

where l is the wake transversal length scale, \(\tilde{u^{\prime}}\) is the turbulence velocity scale and U d is the velocity defect.

As proposed by Battjes and Sakai [5], the velocity defect is calculated as U d = U l−U f , where U l is estimated as the flow velocity outside the bottom boundary layer, i.e. where the experimental velocity profile is approximately constant, while U f is the time-averaged value near the free surface. The way in which U 1 is estimated is shown in Fig. 5a for section B4 (as an example for the other measurement locations) while U f is assumed to be equal to the value in the monitoring point closest to the free-surface velocity.

The characteristic turbulence scale \(\tilde{u^{\prime}}\) is defined as the maximum value of the longitudinal turbulence intensity in each section; apart from section B0, where turbulence in the hydrofoil wake is intense, this maximum value is found in the sub-surface layer (Fig. 7a). The wake transversal length scale l is defined as the depth from which a sharp reduction of the cross-correlations \(\overline{{u^{\prime}v^{\prime}}}\), if compared with their maximum value found in the sub-surface layer, is present; the way in which l is estimated is shown in Fig. 7c for section B4 (as an example for the other measurement locations). The virtual origin of the wake is obtained by plotting \(U_{d}^{ - 2}\) as a function of the distance x, as shown in Fig. 8a. The intercept of the interpolating line with the abscissa axis enables us to estimate the origin x 0 . The trend of l, \(\tilde{u^{\prime}}\) and U d as a function of the distance x ∗ = x−x 0 in the transversal sections B3÷B7 (Fig. 8b–d) enables us to observe that the theoretical velocity-defect law (16) and, to a minor extent, the wake-scale law (15), are satisfied; less accordance is found between the theoretical turbulence intensity law (14) and the observed behavior, possibly because the flow field is affected by the free-surface fluctuations. Nevertheless, the existence of similarity conditions for the analyzed phenomenon can be substantially confirmed.

Fig. 8
figure 8

Self-similarity conditions of the wake function: a \(U_{d}^{ - 2}\), b l, c \(\tilde{u^{\prime}}\), d U d

Full size image

The analysis of the vorticity fields has been performed in detail in the three reaches shown in Fig. 9 and has been based on the results of test T1. The three analysed reaches overlap partially: reach 1 is located just after the hydrofoil trailing edge, reach 2 lays in the middle of the high-speed region at minimal water height while reach 3 includes the free-surface rise and the spilling breaker.

Fig. 9
figure 9

Sketch of the flow region where the breaking occurs, with indications of the flow reaches where the vorticity field was investigated in detail

Full size image

The vectors within the velocity fields show the magnitude and direction of the velocity vectors throughout each of the three reaches. For the vorticity plots, positive contours are shown by dashed lines, while negative contours are shown by solid lines (Figs. 10, 11, 12). The velocity and vorticity fields in reach 1 are plotted in Fig. 10a, b, respectively. The velocity field shows high velocities, except for a small region just downstream of the trailing edge, where the nearly separated flow on the upper surface of the hydrofoil at high angle of attack results in a thick wake.

Fig. 10
figure 10

Detail of the flow-field in reach 1 (case T1) a vorticity contour lines; the increment for each negative (solid lines) and positive (dashed lines) contour line is 5 s−1; b velocity vector field

Full size image
Fig. 11
figure 11

Detail of the flow-field in reach 2 (case T1) a vorticity contour lines; the increment for each negative (solid lines) and positive (dashed lines) contour line is 5 s−1; b velocity vector field

Full size image
Fig. 12
figure 12

Detail of the flow-field in reach 3 (case T1) a vorticity contour lines; the increment for each negative (solid lines) and positive (dashed lines) contour line is 5 s−1; b velocity vector field

Full size image

The vorticity field shows the high negative vorticity peak in the upper part of the hydrofoil wake; a small positive vorticity region, which can be related to the fact that the maximum velocity occurs below the free-surface, appears instead near the surface, between 0.22 and 0.25 m downstream of the leading edge.

Upstream from this positive vorticity region, the fluid directly beneath the free surface (approximately in a layer 0.023 m deep) is relatively vorticity-free (Fig. 10a).

The negative vorticity layer extends further downstream, while the near-surface positive vorticity layer tends to disappear. A second positive vorticity layer, located 0.05 m below the free surface and having a thickness of 0.04 m, is also present immediately downstream of the trailing edge and is due to the shear layer originating at the interface between the high-speed water flowing along the lower hydrofoil surface and the slow water in the hydrofoil wake. Figure 11 shows the velocity and vorticity fields in reach 2. The velocity vector plots show that the high-speed layer just below the free surface persists, as well as the negative vorticity layer below it.

Finally, Fig. 12 shows the velocity and vorticity fields associated with reach 3. The velocity plot in Fig. 12b shows that the higher-velocity free-surface layer rapidly decelerates beneath the breaker, leading to the formation of a positive vorticity layer on the wave front.

On the other hand, the negative vorticity layer due to the hydrofoil decays, indicating that the wake of the hydrofoil used to generate the standing wave also decays almost completely and that the shear layer connected with the wake itself are not entrained in the spilling breaker and do not influence directly the vorticity field in the wave. Finally, a small negative vorticity peak, possibly connected with flow circulation near the spilling region, can be also noticed.

The velocity and vorticity plots in Fig. 10a, b, show that the higher-velocity free-surface layer, decelerates at 0.24 m and, immediately downstream, positive vorticity appears. This process occurs at the free surface and seems to be independent from the flow beneath it, since the negative vorticity layer below the free-surface high-speed layer and the positive vorticity shear layer isolate that region from the bulk of the flow.

Consequently, as suggested by Dabiri and Gharib [9], the flow region laying directly below the free surface (and above the negative vorticity shear layer) can be analysed as an independent supercritical flow leading to a hydraulic jump. In this respect, the appropriate Froude number should be based on the velocity within the free-surface higher-velocity layer and on the thickness of this layer. For this case, the corresponding velocity and layer thickness were evaluated from the plots in Fig. 10 and are approximately equal to 1.62 ms−1 and 0.023 m respectively, resulting in a Froude number of 3.45. In a hydraulic jump, the upstream and downstream heights h 1 and h 2 are linked by the Boussinesq equation:

$$\frac{{h_{2} }}{{h_{1} }} = \frac{1}{2}\left[ { - 1 + \left( {1 + 8Fr_{1}^{2} } \right)^{1/2} } \right]$$
(17)

where Fr 1 is the upstream Froude number. If the previously mentioned values h 1  = 0.023 m and Fr 1  = 3.45 are introduced in (17), a downstream height h 2  = 0.1013 m is obtained. The resulting breaker height h 2  − h 1  = 0.078 m, agrees quite nicely with the measured value of 0.075 m.

In order to better understand the behaviour of the vorticity field, one may examine the behaviour of the surface velocity in terms of deceleration and the gravity terms. Actually, as shown for instance by [9], the flux of vorticity through the free surface can be approximated as:

$$\nu \left( {\frac{\partial \omega }{\partial r}} \right)_{r = 0} \cong - g\cos \theta - U_{s} \frac{{\partial U_{s} }}{\partial s}$$
(18)

where r and s are the directions normal and parallel to the free-surface, respectively, while θ is the angle between the unit vector in direction s and the gravity acceleration. Hence the vorticity flux at the free surface depends on a gravity and a deceleration term.

The analysis of the vorticity flux in the case of test T1 was therefore performed in detail in the three reaches, as shown in Fig. 13a–c, where the deceleration term is compared—being negligible the contribution of the gravity term in Eq. (18)—with the vorticity flux through the free surface, directly computed from the flow field obtained from the SPH simulation. The substantial agreement of the two plots is a further proof of the accuracy of the SPH results.

Fig. 13
figure 13

Free-surface velocity, deceleration term and vorticity flux in Eq. (18) for reach a 1, b 2 and c 3. The vorticity flux scale is shown on the left-hand axis, while the velocity scale is shown on the right-hand axis

Full size image

Figure 13a shows the deceleration term and the surface velocity along reach 1. The deceleration term shows a peak at 0.23 m from the origin. This coincides with the strong generation of positive vorticity seen in Fig. 10a. The plot of the deceleration term and the surface velocity along reach 2 (Fig. 13b) does not show instead any of the strong peaks seen in the previous figures, since no new vorticity is generated.

Finally, Fig. 13c shows that, along reach 3, the deceleration term shows a strong peak at 0.65 m from the origin. This is again coincident with the strong generation of positive vorticity seen in Fig. 12a. The velocity plot shows that the free-surface velocity rapidly decreases after 0.60 m from the origin and the fluid tends to reach a stagnation point (b) at 0.68, 0.03 m downstream of the vorticity flux peak.

This again confirms the experimental findings by Dabiri and Gharib [9] on a spilling breaker generated by an upstream honeycomb, showing that positive vorticity generation occurs upstream of stagnation and that the initiation of wave breaking does not contribute to it. It must be noted that given Eq. (18), the dominant term contributing to the velocity flux is the deceleration term, which is of the order of 200,000 cm s−2, while the gravity term, which can be no greater than 980 cm s−2, is negligible with respect to the deceleration term.

The vorticity production at the surface was related by [9] to the sharp deceleration of the surface fluid which causes the sub-surface velocity gradient which is evident in Fig. 5 (section B2), just upstream of the standing wave. The resulting surface shear layer is then entrained into the fluid and gives rise to the positive vorticity layer which is clearly evident in Fig. 12a.

5 Conclusions

A 2D SPH scheme was applied to model numerically the spilling type breaking flow field produced by a NACA 0024 hydrofoil positioned in a uniform current, based on the laboratory experiments. The agreement between the numerical results and laboratory measurements in the wake region downstream of the hydrofoil is satisfactory and confirms the validity of the numerical tools to yield a deeper insight in the flow mechanisms associated with the generation of the breaker.

The SPH model provides in particular a good prediction in terms of time-averaged longitudinal velocity components and reproduces correctly the formation of the spilling type breaking flow, in accordance with the laboratory experiences.

Small-scale turbulence was modelled either by a mixing-length or by a k-ε turbulence model: although some differences arise when the length of the computational domain is not sufficient, the basically good agreement of both models with the reference experiments infers that large-scale vortical motions (which are directly simulated by the time-dependent SPH model) are more relevant in the flow dynamics than small-scale turbulence effects.

Given the key role of vortical motions in the generation of the spilling breaker, the sources of vorticity were then examined in detail. The present results confirm the findings by Dabiri and Gharib [9] that the vorticity injection due to the free-surface deceleration dominates over the gravity-generated vorticity flux. Their study showed that the source of the viscous vorticity flux for a steady spilling wave is due to the deceleration of the surface fluid, rather than to the sharp free-surface curvature at the toe: the use of a NACA 0024 hydrofoil to induce spilling breakers allows us to obtain a sufficiently gradual deceleration along the free surface, in order that the location of maximum deceleration, and therefore the flux of vorticity into the flow, are clearly distinguishable.

Finally, the analysis of the vorticity field shows that the strong generation of vorticity represented by the deceleration of the free-surface fluid results in the appearance of a strong positive vorticity layer just below the free surface and upstream of the spilling breaker.