Characterization of turbulence statistics on the non-aerated skimming flow over stepped spillways: a numerical study

Abstract

In this work we address the mean flow and turbulence statistics in the non-aerated region of a stepped spillway by using two different numerical strategies in two dimensions. First, we present results regarding the flow in a large portion of the spillway, simulated with a volume of fluid (VoF) method to capture the position of the free surface (case A). Numerically-obtained data are in very good agreement with particle image velocimetry (PIV) data; further, results suggest that profiles of mean velocity, turbulent kinetic energy (TKE) and dissipation rate of TKE at the step edges are approximately self-similar. It was also found that values of TKE and dissipation rate of TKE in the boundary layer development region follow universal similarity laws which are valid for open-channel flows. In addition, the field of simulated dimensionless pressure and pressure distributions at the step edges are qualitatively similar to those reported in a recent experimental work. Second, additional simulations were developed as a pressure-driven flow for only a portion of the spillway (case B). This was possible due to prior knowledge of the water depths. We show that, despite the fact that the pressure field can not be interpreted as in case A, the numerical simulations closely reproduce the experimental data regarding averaged velocity, vorticity, and the turbulence statistics. It was also found that turbulence intensity profiles in the intermediate region are consistent with published experimental results for open-channel flows. These numerical results offer new avenues for the simulation of portions of stepped spillways to assess the physics at the inception point of air entrainment with more sophisticated turbulence closures.

1 Introduction

Stepped spillways are extensively used around the world to dissipate larger amounts of flow kinetic energy downstream of dams as opposed to smooth counterparts, thus allowing for the reduction of size (and cost) of the associated stilling basins. Other characteristics of the flow over stepped spillways include a lower risk of cavitation and the presence of larger concentrations of oxygen downstream of the structure [5, 9, 13, 14, 35, 36, 44].

Most experimental research on stepped spillways has focused on the skimming flow regime, perhaps the most common condition in practice. Under skimming conditions, the flow becomes aerated when both the thickness of the boundary layer reaches the free surface, and eddies possess enough energy to distort the free surface and to entrain air [3, 36], thus determining the so-called inception point of air entrainment [12]. However, in many practical applications where the specific discharge is large, the aerated region can start very late in the extension of the spillway, or not start at all if the spillway is relatively short. Meireles et al. [35] showed that in some built roller compacted concrete (RCC) dams such as De Mistkraal in South Africa, Randleman in the United States, Shuidong in China, or Pedrógão in Portugal, the inception point of air entrainment will not take place at the toe. This indicates conclusively that the non-aerated region possesses a tremendous importance in some major spillways in different continents, since the non-aerated portion of the flow will determine the flow depths, the flow velocities and the turbulent kinetic energy (TKE)—crucial variables for the design of the spillway.

In addition to its intrinsic importance, understanding what occurs in the non-aerated region is essential for an accurate prediction of the location of the inception point of air entrainment in cases it exists, and hence for the determination of the flow features that lead to the distributions of air concentrations downstream. Meireles et al. [36] discussed a particular model for the prediction of the location of the inception point of air entrainment (among others), in which the amount of air being entrained increases with increasing TKE close to the free surface (keeping other factors constant). Furthermore, new knowledge regarding the flow vorticity could yield evidence on the potential distortion of the free surface, which is responsible for the air entrainment.

The majority of studies on skimming flows have been devoted to the analysis of the aerated region (i.e., downstream of the inception point), addressing issues such as distribution of void fraction, profile of time-averaged velocity, distance from the spillway crest to the inception point of air entrainment, pressure field on the steps, and gas transfer through the free surface. An exhaustive list of previous experimental studies on this topic can be found in Matos and Meireles [32]. (to the best of our knowledge, there is no comprehensive study reporting accurate numerical simulations of flow statistics and air concentrations in the entire stepped spillway).

Conversely, only a few studies have focused on the flow properties of the non-aerated region [1, 2, 11, 33–36, 56–58]. Even scarcer are the discussions about the statistics of turbulence in that non-aerated region, and the comparison among numerical-model and experimental results. Most previous numerical studies of stepped spillways have employed finite-volume techniques in the solution of the flow equations, but a couple of works have used finite elements in two dimensions (2D). Most works have captured the position of the free surface adopting variations of the volume of fluid (VoF) technique originally developed by Hirt and Nichols [27], and have simulated the flow as a gravity flow (see Bombardelli et al. [6], for a discussion on the nature and variants of the VoF method). In particular, a partial VoF technique was used by Chen et al. [14], Cheng et al. [15, 16], Simoes et al. [49], and Arantes [4], in which both air and water flows were considered [6]. Tabbara et al. [50] updated the free-surface each time step and re-meshed, in a general finite-element code. In Bombardelli et al. [9] and Meireles [34], the TruVOF method embedded in the commercial code FLOW-3D ^® was used to address time-averaged flow velocities, water depths, boundary-layer growth and turbulence statistics. Tongkratoke et al. [51] presented numerical results for the full stepped spillway where diverse turbulence closures were used. Qian et al. [43] obtained numerical results of mean velocity, span-wise vorticity, and growth of boundary-layer thickness, employing four different turbulence models. Very recently, Cheng et al. [17] applied the commercial code FLUENT to study time-averaged flow velocities and water depths, and discussed purported air concentrations in the aerated portion (without comparing against data). Regarding turbulence closures, the k − ε, and the RNG (renormalization group) k − ε models have been employed; these are models in which an isotropic-eddy-viscosity tensor (i.e., with a unique eddy-viscosity coefficient) is specified [42], and in which a quasi-steady-state solution is obtained [9]. Further, turbulence closures including non-isotropic or non-linear eddy viscosity [51] or explicit simulation of the Reynolds stresses (i.e., Reynolds Stress Models, RSM) [4] have been rarely employed in the published papers related to stepped spillways. This latter type of closures is important when the flow is highly anisotropic, and has been found to provide better results in rotating and swirling flows, and secondary flows in channels [26, 42]. In Table 1 (updated from Bombardelli et al. [9]) we detail the main differences among our work and previous numerical simulations on stepped spillways.

Table 1 Summary of features of previous numerical investigations on stepped spillways (expanded from Bombardelli et al. [9])

In recent years and in other fields of fluid mechanics, “hydrid,” large-eddy simulation (LES)-type turbulence models have been developed; these closures have been employed in water resources in the last decade [40, 45]. These simulations, which need to be developed in three dimensions (3D), are highly-intensive computationally, but they provide unsteady descriptions of the flow which could be of tremendous importance in two-phase flows [7]. However, they have not been employed to solve the flow in stepped spillways, to the best of our knowledge.

The above-mentioned numerical works included the region located upstream of the face of the spillway in order to ensure a proper development of the flow over the stepped spillway. If accurate experimental data were available over the steps, that region would not be needed, reducing in this way the computational time in 2D, and allowing a 3D simulation of the flow. Frizell et al. [24] very recently developed experiments on the flow in a stepped spillway assuming it is driven by a pressure difference, to study the cavitation tendency within the steps. This experimental analysis of the flow as a pressurized chamber suggested to us the idea of developing a computer simulation of the stepped spillway as a pressurized flow. This approach has the advantage that significant computational resources are saved, since the evolution of the free surface and the air flow do not need to be calculated. Overall, simulating the flow as a pressurized chamber saves computational time allowing for numerical simulations of the LES type.

Based on the above state of the art, we address in this paper the following specific issues:

• (a) Can the skimming flow be adequately simulated as a pressure-driven flow? In other words, is the simulation of the free surface a sine qua non requirement for a successful modeling of stepped spillways?

• (b) What are the distributions of pressure at the steps and inside the cavities?

• (c) How important is to incorporate turbulence models with detailed anisotropy (i.e., models which solve explicitly the components of the Reynolds Stress tensor) in the simulation of this kind of flows? Since the flow in stepped spillways is non-isotropic and non-homogeneous, there is a natural need to ascertain to what extent detailed anisotropy affects the results.

• (d) What is the shape of the profiles of TKE, turbulence intensity and vorticity for the skimming flow in the non-aerated region? How do those profiles vary close to the inception point of air entrainment? Is it there any self-similarity in the profiles of TKE and dissipation rate of TKE? Does the flow vorticity remain important far away from the pseudo-bottom (the line passing through the edges of the steps)? To the best of our knowledge, only the papers by Cheng et al. [15, 16] and Bombardelli et al. [9] have presented contours of TKE obtained via numerical simulation, but without comparison against data. Likewise, Qian et al. [43] were the only authors presenting plots of vorticity in flows on stepped spillways but without rigorously comparing against data.

The paper is then organized as follows. In Sect. 2, the used theoretical models are introduced; in Sect. 3 we present the selected experimental data and then we describe the two variants for the implementation of the numerical models in OpenFOAM, the code employed. We performed our analysis with two configurations: a case A where the flow is simulated as a free-surface flow, and a case B where we treat it as a pressurized flow. In case A, we solve for the location of the free surface (as done in Bombardelli et al. [9]), while in case B the position of the free surface is fixed as obtained from experiments. To the best of our knowledge, this last methodology has not been implemented previously for this type of flow. The main reason for using OpenFOAM is that, in contrast to FLOW-3D ^®, it is open-source software allowing us to add our own pieces of code. Although we did not modify the code in the present work, the modeling of air entrainment through the water surface (which is part of our near future research) requires adding some code to existing tools. Furthermore, we are also currently using a hybrid turbulence method (detached eddy simulation) which is not available in FLOW-3D ^®. In Sect. 4, we compare numerical results in 2D of the classical k − ε and RNG k − ε models with those of the Launder-Gibson Reynolds Stress Model. Numerical results are compared with the experimental data obtained by Amador [1]. Concluding remarks are given in Sect. 5.

2 Theoretical model

We used the Reynolds-averaged Navier–Stokes (RANS) equations for an incompressible flow in all our simulations. The equations representing the conservation laws of mass and momentum are, respectively:

$$\frac{{\partial \overline{{u_{j} }} }}{{\partial x_{j} }} = 0$$

(1)

$$\rho \frac{{\partial \overline{{u_{i} }} }}{{\partial t}} + \rho \overline{{u_{j} }} \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} = - \frac{{\partial \bar{p}}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\bar{\tau }_{{ij}} + \tau _{{ij}} ^{R} } \right)$$

(2)

where $\overline{{u_{i} }}$ denotes the turbulence-averaged flow velocity, $\rho$ is the density of the fluid, $\bar{p}$ is the mean pressure, $\bar{\tau }_{ij}$ represents the time-averaged stresses associated with viscosity, $\tau_{ij}^{R}$ are the Reynolds stresses, and $i$ goes from 1 to 2; further, the Einstein convention is implied in repeated indices. Since the focus of the research is the non-aerated region, we did not include any reference to a disperse phase as it was done in Bombardelli et al. [9] (For possible disperse-phase models, see Bombardelli [7]; Buscaglia et al. [10]; Bombardelli and Jha [8]).

The $k - \varepsilon$ [29], the RNG $k - \varepsilon$ [53, 54] and Launder-Gibson Reynolds Stress [31] models were employed to close the problem stated by Eqs. (1) and (2). The $k - \varepsilon$ and RNG $k - \varepsilon$ models utilize the concept of eddy viscosity $\left( {\nu_{T} } \right)$, and assume that the Reynolds stresses and the mean strain rate $\left( {\overline{S}_{ij} } \right)$ are linearly related according to the Boussinesq’s assumption, as follows [20]:

$$\tau_{ij}^{R} = - \rho \overline{{u_{i}^{\prime} u_{j}^{\prime} }} = 2\rho \nu_{T} \overline{S}_{ij} - \frac{\rho }{3}\left( {\overline{{u_{k}^{\prime} u_{k}^{\prime} }} } \right)\delta_{ij}$$

(3)

where the primes indicate turbulent fluctuations (such that the instantaneous velocities are given by $u_{i} = \overline{{u_{i} }} + u_{i}^{\prime}$) and $\delta_{ij}$ is the Kronecker delta. The mean strain rate is given by:

$$\overline{S}_{ij} = \frac{1}{2}\left( {\frac{{\partial \bar{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \bar{u}_{j} }}{{\partial x_{i} }}} \right)$$

(4)

The transport equations of the standard $k - \varepsilon$ and $k - \varepsilon$ models are provided in the Appendix. So far, this is exactly the same theoretical model as used in Bombardelli et al. [9].

Differently from Bombardelli et al. [9], we use here the Launder-Gibson RSM, not included in the code used in the 2011 work. The Launder-Gibson RSM is a second-moment turbulence model, and hence it does not use the concept of eddy viscosity; instead, it directly estimates the Reynolds stresses by solving a system of transport equations for the stress tensor components, as [20]:

$$\frac{{\partial \tau_{ij}^{R} }}{\partial t} + \overline{{u_{j} }} \frac{{\partial \tau_{ij}^{R} }}{{\partial x_{j} }} = - 2\overline{{p^{\prime} S_{ij}^{\prime} }} + \left( {\tau_{ik}^{R} \frac{{\partial \overline{{u_{j} }} }}{{\partial x_{k} }} + \tau_{jk}^{R} \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{k} }}} \right) - \rho \varepsilon_{ij} + \frac{\partial }{{\partial x_{k} }}\left( {H_{ijk} } \right)$$

(5)

where $p^{\prime}$ refers to the pressure fluctuations, and $\varepsilon_{ij}$ expresses the tensor of the rate of dissipation of TKE. Finally,

$$H_{ijk} = \rho \overline{{u_{i}^{\prime} u_{j}^{\prime} u_{k} }} + \overline{{p^{\prime} \left( {u_{i}^{\prime} \delta_{jk} + u_{j}^{\prime} \delta_{ik} } \right)}}$$

(6)

The terms on the right side in (5) represent the stress redistribution due to fluctuating pressure (also called “pressure strain;” Gibson and Rodi [25]), production by mean-flow deformation, dissipation, and diffusive transport, respectively [26]. In order to close the above system of equations, $\varepsilon_{ij}$ is approximated by assuming local isotropy, as follows:

$$\varepsilon_{ij} = \frac{2}{3}\varepsilon \delta_{ij} , \quad \varepsilon = \nu \overline{{\frac{{\partial u_{l}^{\prime} }}{{\partial x_{k} }}\frac{{\partial u_{l}^{\prime} }}{{\partial x_{k} }}}}$$

(7)

The model equation for $\varepsilon$, in turn, is similar to Eq. (A.2); however, the terms $\left( {\nu + \nu_{T} /\sigma_{\varepsilon } } \right)$ are replaced by the anisotropic diffusivity $(C_{\varepsilon } k/\varepsilon )\tau_{ij}^{R}$, where the coefficient $C_{\varepsilon }$ is taken to be 0.15:

$$\frac{\partial \varepsilon }{\partial t} + \overline{{u_{j} }} \frac{\partial \varepsilon }{{\partial x_{j} }} = \frac{\partial }{{\partial x_{i} }}\left[ {C_{\varepsilon } \frac{k}{\varepsilon }\tau_{ij}^{R} \frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + c_{1\varepsilon } \frac{\varepsilon }{k}\left( {\frac{{\tau_{ij}^{R} }}{\rho }} \right){\mathop {{\overline{S}_{\!ij}}}} - c_{2\varepsilon } \frac{{\varepsilon^{2} }}{k}$$

(8)

The pressure strain term is modeled as the sum of a “slow term” [22, 46] containing turbulence quantities and a “rapid term,” containing the mean rate of strain (see the “Isotropization of Production” model of Naot et al. [37]), as follows:

$$2\overline{{p^{\prime} S_{ij}^{\prime} }} = - \rho C_{R} \frac{\varepsilon }{k}\left[ {\left( {\overline{{u_{i}^{\prime} u_{j}^{\prime} }} } \right) - \frac{2}{3}\delta_{ij} k} \right] - \rho \hat{C}_{R} \left[ {P_{ij} - \frac{2}{3}G\delta_{ij} } \right]$$

(9)

where $G = - \overline{{u_{i}^{\prime} u_{j}^{\prime} }} \, \overline{S}_{ij} = 0.5P_{ii}$ and

$$\rho P_{ij} = \tau_{ik}^{R} \frac{{\partial \bar{u}_{j} }}{{\partial x_{k} }} + \tau_{jk}^{R} \frac{{\partial \bar{u}_{i} }}{{\partial x_{k} }}$$

(10)

The turbulence and pressure diffusion terms are modeled together by using a gradient-type diffusion expression [48], as follows:

$$\frac{\partial }{{\partial x_{k} }}\left( {H_{ijk} } \right) = \frac{\partial }{{\partial x_{k} }}\left( {C_{S} \frac{{k^{2} }}{\varepsilon }\frac{{\partial \tau_{ij}^{R} }}{{\partial x_{k} }}} \right)$$

(11)

The coefficients $C_{R}$, $\hat{C}_{R}$, and $C_{S}$ are considered to be 1.8, 0.6 and 0.11, respectively. More details about this model can be found in Hanjalic and Jakirlic [26], Davidson [20] and Durbin and Pettersson Reif [22].

For case A, the free surface was obtained by using a Partial VoF algorithm (Bombardelli et al. [6]), which solves a modified conservation equation for $\alpha_{w}$ (i.e., the volume fraction contained in each computational cell) as follows:

$$\frac{{\partial \alpha_{w} }}{\partial t} + \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{w} \overline{{u_{j} }} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\overline{{u_{r} }}_{j} \alpha_{w} \left( {1 - \alpha_{w} } \right)} \right) = 0$$

(12)

The last term in Eq. (12) is an artificial compression term [47], which uses the relative velocity field between air and water ($\overline{{u_{r} }}$) to reduce numerical diffusion at the interface, and to allow $\alpha_{w}$ to be bounded between zero and one [21].

3 Implementation of the numerical models: geometry and boundary conditions. Numerical approach

3.1 Experiments selected for the study

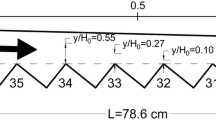
The experimental stepped chute at the Laboratory of Hydraulics at the University of A Coruña [1, 2] was composed by 37 steps of 5 cm of height and 4 cm of length, which corresponds to a pseudo-bottom inclination of 51.3^o. In addition, 3 steps having variable dimensions were added close to the crest, in order to emulate the geometry of a Waterways Experimental Station crest profile [1]. The height of the stepped chute from crest to toe was 2 m, and the stepped flume was 0.5 m wide. The flowrate per unit width ($q$) was 0.11 m²/s and the Reynolds number ($Re = q/\nu$) was approximately 10⁵. Measurements of the instantaneous velocity field were taken every 1 s for 500 s, by using the PIV technique. In Table 2 we present the accuracy of the computed mean velocity for the analyzed steps (34, 33, 31 and 29, see Fig. 1), while in Table 3 the measured values of the water depths are shown. To the best of our knowledge, this dataset is the only PIV dataset containing turbulence statistics in the non-aerated region of stepped spillways. More details about the measurements can be found in Amador [1] and Amador et al. [2].

Table 2 Error interval for experimental mean velocity (from Amador et al. [2])

Fig. 1

Simulation domain employed for case A. Dark color indicates the water-flow domain and light color represents the air-flow domain. Numbers follow the step numbering by Amador [1]

Table 3 Water depth (cm) in the experimental tests by Amador [1]

3.2 OpenFOAM

OpenFOAM is a general-purpose, free-distribution, open-source C++ library for solving complex problems of fluid mechanics. OpenFOAM offers a large library of turbulence models including RANS, Unsteady RANS (URANS), LES, and hybrid RANS/LES methods such as detached eddy simulation (DES) or scale adaptive simulation (SAS). Other tools include utilities for mesh generation, conversion and manipulation; boundary conditions; wall functions; and pre and post-processing utilities. One of the major strengths of OpenFOAM is that, based on the aforementioned existing tools, new solvers and utilities can be developed by the user with relative ease.

As many of the computational fluid dynamics (CFD) codes (e.g., FLOW-3D ^®, as an example), the conservation laws of flow variables are solved through the use of finite-volume method in OpenFOAM. We used the solver pimpleFoam, which combines the original, steady-state SIMPLE (semi-implicit method for pressure-linked equations) and the transient pressure implicit with splitting of operators (PISO) algorithms originally developed by Patankar and Spalding [41], and Issa [28], respectively. Using the Courant number criterion, the solver varies the time step to ensure better performance [39].

First step in SIMPLE method provides an intermediate velocity field based on an initial guess for pressure. Second, the continuity equation is used in order to obtain a correction for pressure, which is then used to update the velocity field; finally, convergence of the iterations is checked. PISO is similar to SIMPLE, but includes an additional corrector step, which makes the method more robust. Scalar variables (e.g., pressure) are evaluated at ordinary nodal points, but velocity nodes are staggered with respect to pressure nodes. By doing that, pressure is properly represented and mass is conserved [19]. The convective terms were discretized using a second-order total variation diminishing (TVD) scheme.

In all the numerical simulations, the mesh was generated using the BlockMesh tool, which reads the geometry declared in a file named blockMeshDict and decomposes such geometry into hexahedral blocks. For 2D simulations, as the ones presented herein, the geometry is still generated in 3D, but using a unit width in the transverse (Z) direction (perpendicular to the page). The mesh is then refined using the SnappyHexMesh tool. For further details about OpenFOAM, the reader is referred to the OpenFOAM Documentation [39].

3.3 Case A: 2D model using VoF technique

The 2D geometry shown in Fig. 1 was created in AutoCAD, using the same dimensions of the experimental set-up. A very short length of 0.5 m upstream of the crest of the spillway (0.455 m from the face of the spillway) was found to be large enough to allow the flow to be properly developed over the stepped spillway; a discussion on this issue can be found in Bombardelli et al. [9]. The outlet corresponds to step 25, where according to some pictures and visual observations [1] the air entrainment begins to occur. A 3D object was then obtained by extruding the geometry along the Z axis, and subsequently exported into OpenFOAM as an STL file.

As detailed in Table 4, three mesh sizes were utilized to assess grid-independent results. Similar mesh sizes have been used in previous studies on spillways [9]. In Sect. 4, we show that three meshes led to practically the same results for the velocity profiles and turbulence statistics, and therefore we only present results associated with Run 2. Except for the volumes located near the crest and near the extruded area at the air boundary, the mesh included volumes of uniform size.

Table 4 Meshes utilized for the RNG $k - \varepsilon$ model in case A and average values of $y_{1}^{ + }$ over the step walls

For case A, null velocity components in the horizontal and vertical directions ($u = v = 0$) were considered at the walls (no-slip conditions). At the inlet (of 0.43 m total height), the volume fraction of water was initialized as follows:

$$\begin{array}{*{20}l} {\alpha_{w} = 1 \quad 0 \le h \le 0.40} \\ {\alpha_{w} = 0 \quad 0.4 < h \le 0.43 } \\ \end{array}$$

Also, a uniform water velocity profile of 0.275 m/s was imposed over the fixed height of 0.4 m, while air velocity at the inlet (of 3 cm thickness therein) was considered to be zero (Fig. 1). At the outlet, the pressure Inlet Outlet Velocity boundary condition for velocity was used [39]. The fluxes of air were assumed to enter (or exit) normal to the air boundaries (except the upstream counterpart where it is zero), based on the values of pressure. The total pressure boundary condition was employed to set pressure values at the air boundaries [39]. For the variables $k$ and $\varepsilon$, a zero gradient boundary condition was used at air boundaries and the outlet. The TKE in the first node $\left( {k_{1} } \right)$ above the wall was estimated by iteratively computing the shear velocity $\left( {u_{*} } \right)$ from the semi-logarithmic law of the wall. Standard wall functions [23, 52] were then employed to relate $k_{1}$ and $\varepsilon_{1}$ (the value of dissipation rate of TKE in the first node) in the logarithmic region as follows:

$$\varepsilon_{1} = \frac{{C_{\mu }^{0.75} k_{1}^{1.5} }}{{\kappa y_{1} }}$$

(13)

where $y_{1}$ is the distance between the wall surface and the first interior node, and equal to ${{\Delta }}y/2$; $\kappa$ is the von-Kármán constant [30]. For the first node, the normalized distance from the wall can be written as:

$$y_{1}^{ + } = \frac{{\rho u_{*} y_{1} }}{\mu }$$

(14)

where $\nu = \mu /\rho$ is the kinematic viscosity, considered to be $1.15 \times 10^{ - 6} \, {\rm m^{2}/s}$ (at about 15 °C). The distribution of $y_{1}^{ + }$ was found to be non-uniform throughout the walls of the steps, as expected. The average values of $y_{1}^{ + }$ for the first node are presented in Table 4; all the cases include average values of $y_{1}^{ + }$ greater than 20, which is considered adequate in cases when the wall-function formulation of Eq. (13) is utilized [52].

3.4 Case B: 2D model as a pressurized flow

In case B, a much smaller portion of the physical domain was employed (44.8 cm long by approximately 4 cm height). As stated above, based on the experimental results of Frizell et al. [24], the flow was simulated as a pressure-driven flow. The 2D geometry (Fig. 2) was created similarly to case A; here the free surface was made coincident with data coming from PIV measurements. In addition, given that the X coordinate is in this case aligned with the streamwise direction, the volumes located near the step walls were of variable size. It is important to remark that the same resolution as in case A was used here, given the small domain size. The outlet corresponded to step 27, before the actual aeration inception point and, as in case A, only the non-aerated portion of the spillway was simulated. In Sect. 4, we show that three different meshes led to practically the same results for the velocity profiles and turbulence statistics, and therefore we only present results associated with Run 2.

Fig. 2

Schematic of channel geometry for case B, including the numbers of the steps. Numbers follow the step numbering by Amador [1]

Given that PIV measurements were available at the edge of step 34, the inlet boundary conditions were set up on that step edge based on the existing data. A zero-gradient boundary condition for the pressure was set at the free surface. A reference value for the pressure was utilized at the outlet boundary. Null velocity components in the stream-wise and pseudo-bottom-normal directions ($u = v = 0$) were considered at step walls, whereas at the inlet we used the velocity profile obtained with the PIV technique (Fig. 3a). For the free surface, a free-slip boundary condition was imposed; in other words, a zero normal velocity component, with zero tangential-velocity derivatives, was used. At the outlet boundary, the velocity gradient of the longitudinal velocity was assumed to be zero.

Fig. 3

a Measured mean velocity profile at the inlet boundary (at the edge of step 34). Filled symbols indicate experimental values obtained with the PIV technique; unfilled symbols correspond to values of water velocity outside of the boundary layer, which were not measured but rather computed by Amador [1]. b Computed values of 2D TKE from PIV measurements at the edge of step 34 (shown on a scale of 0 to 0.4 m²/s², which is used herein for all the steps)

Based on the experimental data on the components of the velocity fluctuations in the streamwise ($u^{\prime}$) and vertical ($v^{\prime}$) directions to the flow, a profile for TKE was obtained at the inlet boundary (Fig. 3b). In turn, the values for the dissipation rate of TKE were not determined from the observations due to the lack of accuracy of possible evaluation procedures (please recall the definition of $\varepsilon$). Instead, they were initially approximated from the values of TKE, as follows [52]:

$$\varepsilon \approx \frac{{k^{1.5} }}{l}; \quad l = \left\{ \begin{array}{l} {0.07h \quad y > l} \\ y \quad\quad\;\;\; y < l \\ \end{array} \right.$$

(15)

in which l indicates the “large-eddy” scale. Since the evaluation of l is approximate, we developed an iterative procedure. By trial and error of upstream distributions of $\varepsilon$, the upstream profile of ɛ was finally determined by successive comparisons of simulated values of $\varepsilon$ at other step edges among themselves. Only a few iterations were needed to achieve this result.

Similarly to case A, wall functions were employed at step walls. The distribution of $y_{1}^{ + }$ using the three numerical models is shown in Table 5.

Table 5 Meshes utilized in case B and average values of $y_{1}^{ + }$ over the step walls

Since no data on the velocity fluctuations in the transverse (Z) direction were available, there is an uncertainty as to which expression of TKE should be used in stepped spillways. Initially, the values of TKE presented in Fig. 3b were estimated by using $k = 0.5( {\overline{{u^{\prime2} }} + \overline{{v^{\prime2} }} } )$. Values of TKE are representative of the 3D nature of the physical flow phenomenon; thus, a new estimate for TKE at the inlet was assessed, which includes the velocity fluctuations in the transverse ($w^{\prime}$) direction by using an expression in Nezu and Nakagawa [38], which was obtained for open-channel flows:

$$\frac{{\overline{{w^{\prime 2}}} }}{2k} = 0.28$$

(16)

Using the above expression, the new estimate for TKE at the inlet is $k = 0.694( {\overline{{u^{\prime2} }} + \overline{{v^{\prime2} }} } )$, which is equivalent to stretch our original 2D TKE profile at the inlet by 38.8 %. It was found that, by using this procedure, results at other cross sections did not change significantly (maximum values of TKE increase less than 8 %).

For the Launder-Gibson RSM, we applied boundary conditions for the Reynolds stress tensor components at the inlet by using the Boussinesq’s assumption (Eq. 3) and the results already obtained with the $k - \varepsilon$ model. Only five components of the Reynolds stress tensor were considered to be different from zeros as follows:

$$\tau_{ij}^{R} = \left[ {\begin{array}{*{20}c} {\tau_{xx}^{R} } & {\tau_{xy}^{R} } & 0 \\ {\tau_{xy}^{R} } & {\tau_{yy}^{R} } & 0 \\ 0 & 0 & {\tau_{zz}^{R} } \\ \end{array} } \right]$$

(17a)

$$\frac{{\tau_{xx}^{R} }}{\rho } = - \overline{{u^{\prime} u^{\prime} }} = 2\nu_{T} \frac{{\partial \bar{u}}}{\partial x} - \frac{2}{3}k; \quad \frac{{\tau_{yy}^{R} }}{\rho } = - \overline{{v^{\prime} v^{\prime} }} = 2\nu_{T} \frac{{\partial \bar{v}}}{\partial y} - \frac{2}{3}k$$

(17b)

$$\frac{{\tau_{xy}^{R} }}{\rho } = - \overline{{u^{\prime} v^{\prime} }} = \nu_{T} \left( {\frac{{\partial \bar{u}}}{\partial x} + \frac{{\partial \bar{v}}}{\partial y}} \right); \quad \frac{{\tau_{zz}^{R} }}{\rho } = - \overline{{w^{\prime} w^{\prime} }} = - \frac{2}{3}k$$

(17c)

4 Results and discussion

4.1 Case A

First, in order to check grid independence of the numerical results, we show in Fig. 4a that virtually the same velocity profiles were obtained at the edges of steps 34 and 29 with the use of the three meshes of Table 4, regardless of the mesh size employed. For the mesh size of 1.5 mm, the normalized root-mean-square error (NRMSE) of streamwise velocity against the experimental data, was 6.8 and 6.6 % at the edges of steps 34 and 29, respectively, which is considered to be very good. In terms of turbulence statistics, we noted basically the same results, except that maximum values of TKE, $\nu_{T}$ and $\varepsilon$ at the pseudo-bottom increase when mesh is reduced, as expected; this tendency was even stronger at the step edges, where turbulence quantities were overpredicted (Fig. 4b).

Fig. 4

Mesh-convergence results: a comparison of water velocities at the edges of steps 34 and 29 using three meshes. b Comparison of TKE for profiles at 33.5 and 30.5 using three meshes (fractional numbers indicate locations in between steps)

Simulated water flow depths ($d$), for which the volume fraction of water $\alpha_{w}$ was considered to be equal to 0.5—as customarily done-, are shown in Fig. 5. The agreement among the PIV data and numerical results is excellent.

Fig. 5

Comparison among water flow depths obtained with the RNG $k - \varepsilon$ model and PIV data

We found that the computed velocity profiles at the edges of steps 34, 33, 31 and 29 were approximately self-similar, with a power-law velocity profile given by:

$$\frac{V}{{V_{max} }} = \left( {\frac{y}{\delta }} \right)^{{\frac{1}{N}}}$$

(18)

where $V_{max}$ is the free-stream velocity, $y$ is the distance normal to the pseudo-bottom, and $\delta$ is the boundary-layer thickness. This is a result which agrees with previous empirical and numerical evidence [9, 35].

From Table 6, it is concluded that a global $N = 2.8$ well represents the obtained numerical values, which is in excellent agreement with $N = 3.0$ calculated from the experimental results [1]. These values are smaller than those obtained in Bombardelli et al. [9], equal to 3.4 and 5.4 for experimental and numerical data, respectively. This difference of values is within ranges published in previous works [35].

Table 6 Comparison among simulated and experimental exponent $N$

Meireles [34] suggested that turbulence statistics should undergo self-similarity as in regular open channels; the non-dimensionalization was undertaken using $V_{max}$ and $\delta$, the boundary layer thickness. Here, vertical distributions of TKE ($k$) and dissipation rate of TKE ($\varepsilon$) at step edges were analyzed to determine the existence of self-similarity. From Fig. 6a, it can be observed that profiles of TKE obtained via numerical simulations collapse into one single curve. Similarly, from Fig. 6b, it is concluded that profiles of $\varepsilon$ show approximate self-similarity and are in excellent agreement with a universal equation for $\varepsilon$ in open-channel flows [38]:

Fig. 6

Approximate self-similar distributions of turbulence statistics: a TKE. b Dissipation rate of TKE at step edges

$$\frac{\varepsilon \delta }{{V_{max}^{3} }} = 7.77 \times 10^{ - 3} \left( {\frac{y}{\delta }} \right)^{{ - \frac{1}{2}}} exp\left( { - 3\frac{y}{\delta }} \right)\quad 0.1\delta \le y \le \delta$$

(19)

In Fig. 7 we present the nondimensional field of pressure obtained with the RNG $k - \varepsilon$ model, where values have been normalized with the hydrostatic pressure $p^{*}$. It is evident that areas of maximum pressure are located immediately upstream of the step edges, and values are approximately four times larger than the hydrostatic pressure. In the intermediate region between two consecutive steps, an area of low pressure is observed, where values of pressure fall below the hydrostatic counterpart. In Fig. 8, we compare profiles of pressure distributions at two distinct locations, namely at the step edges and the intermediate region between two consecutive steps. As illustrated in Fig. 8a, the pressure distribution at step edges is clearly non hydrostatic, although it follows a quasi-linear relationship in the flow region close to the free surface. Maximum values of pressure at step edges are located at a certain small distance from the pseudo-bottom. These numerical results are qualitatively similar to those presented very recently by Zhang and Chanson [56, 58] from an experimental study of the non-aerated flow region of a large-size stepped spillway model.

Fig. 7

Field of dimensionless pressure ($p^{*} = p/\rho ghcos\left( \theta \right)$) obtained with the RNG $k - \varepsilon$ model, where $h$ is the characteristic water depth (equal to 4 cm), and $\theta$ is the angle of the spillway

Fig. 8

Dimensionless pressure distributions: a at step edges. b Between two consecutive steps

4.2 Case B

In order to check grid independence of the numerical results, the same procedure as in case A was followed, using three different meshes (Table 5). In Fig. 9 it is shown that nearly the same velocity profiles were obtained at profile 30.5, regardless of the mesh size. Similarly as in case A, it was noticed that maximum values of TKE, $\nu_{T}$ and $\varepsilon$ at the pseudo-bottom increase when mesh is reduced. Turbulence quantities were again overpredicted in that region, except that for the current methodology this tendency was even much stronger (not shown herein).

Fig. 9

Mesh-convergence results for case B: comparison of water velocities at profile 30.5 using three meshes and two numerical models. a $k - \varepsilon$ model. b Launder-Gibson RSM

We discuss herein results associated with the intermediate mesh (cells of 1.5 mm) for which a mesh-converged solution is obtained in terms of velocity and turbulence statistics. In particular, mean velocity profiles in the developing flow region on the stepped spillway are shown in Fig. 10, where Y is the normal distance measured from the pseudo-bottom of the stepped spillway. Numerical results with different turbulence closures provide almost the same predictions for the mean flow with no significant differences among them (on average, differences are smaller than 2.5 %); further, the agreement between those numerical values and experimental data is very good. For instance, the NRMSE of mean velocity at step 29 was 4.4, 4.7, and 4.8 %, for the $k - \varepsilon$, RNG $k - \varepsilon$ and Launder-Gibson Reynolds Stress models, respectively. This indicates that the result is virtually the same regardless whether we use isotropic eddy-viscosity or more elaborated turbulence closures. A deviation from the PIV measurements is observed over step 29 (Fig. 10b), where the boundary-layer thickness is smaller on the simulations. Over that step, “free-stream” velocity is underestimated by the numerical results by approximately 5 %, which is considered to be very good. Maximum values of $k$, $\varepsilon$ and $\nu_{T}$ are located close to the pseudo-bottom, and continuously increase in the downstream direction for a given fixed distance from it (as an example, Fig. 11 shows the evolution of $\varepsilon$).

Fig. 10

Numerical and experimental mean velocity profiles: a at the edge of step 31; b at the edge of step 29. Filled symbols indicate experimental measurements obtained with the PIV technique; unfilled symbols correspond to values of water velocity outside of the boundary layer

Fig. 11

Field of dissipation rate of TKE (in m²/s³) obtained with the RNG $k - \varepsilon$ model (case B)

In Fig. 12 we present profiles of streamwise velocity and TKE at profile 30.5, which is equidistant from the inlet and outlet boundaries; the comparison addresses a significant portion of the cavity. Numerical simulations predictions are very close to the experimental values. The maximum values of $k$ obtained with the $k - \varepsilon$ model are approximately 9 % higher than those obtained with the RNG $k - \varepsilon$ model (whose maximum value of $k$ is in turn 5 % smaller than the experimental value). In general, numerical predictions for $k$ obtained with the RNG $k - \varepsilon$ model are slightly different than those obtained with the $k - \varepsilon$ model. These small differences could be in principle attributed to the production term in the $\varepsilon$ equation. Simulation results show that the width of the shear layer is slightly thicker in the data than in the numerical results.

Fig. 12

Mean velocity a and TKE b at profile 30.5 (fractional number indicates location in between steps 30 and 31)

In Fig. 13 we developed a comparison among time-averaged values of span-wise vorticity component computed from measurements and counterparts coming from numerical results, showing that the pseudo-bottom corresponds to an area with a highly defined peak of vorticity (a representative value of $\left| {\omega_{z} } \right| = 300 \,{\rm s^{ - 1}}$ is observed close to the step edges). The time-averaged vorticity outside of the boundary layer is very small throughout the whole domain, and there is no clear increase of time-averaged vorticity towards the point of air entrainment. Numerical results of vorticity in Fig. 14 are in good agreement with the experimental values, especially results obtained with k − ε and RNG k − ε models. Although the peak values of vorticity predicted by the Launder-Gibson Reynolds Stress model might at first sight be considered erroneous, that overestimation is in fact explained by small differences in the velocities obtained with the Launder-Gibson Reynolds Stress model, in comparison with those of the other two models employed. As such, differences as relatively small as 5 % in velocities, may explain differences as large as 70 % in the predicted values of vorticity. Inside the step cavities, there are some more important differences which can be explained by the same reasons. Near the step walls, numerical values of vorticity are much larger than counterparts coming from data.

Fig. 13

Contours of span-wise vorticity component (1/s). a Numerical results using RNG $k - \varepsilon$ model. b Experimental values

Fig. 14

Experimental and numerical values for vorticity at profile 30.5 (fractional number indicates location in between steps 30 and 31)

The computed pressures, on the other hand, are very different from those obtained in case A (not shown herein), as expected. This means that the pressure field cannot be interpreted as in case A.

The turbulence intensity $T_{i}$ is the root mean square of the velocity fluctuations divided by a reference mean flow velocity, $U_{ref}$ [52]:

$$T_{i} \equiv \frac{{\sqrt {\left( {\overline{{u^{\prime 2} }} + \overline{{v^{\prime 2} }} + \overline{{w^{\prime 2} }} } \right)/3} }}{{U_{ref} }} = \frac{{\sqrt {2/3k} }}{{U_{ref} }}$$

(20)

Based on the fact that no data on velocity fluctuations in the transverse direction were available, the average experimental turbulence intensity $T_{ei}$ was estimated by using the following 2D representation:

$$T_{ei} \approx \frac{{\sqrt {\left( {\overline{{u^{\prime 2} }} + \overline{{v^{\prime 2} }} } \right)/2} }}{U\left( y \right)} = \frac{\sqrt k }{U\left( y \right)}$$

(21)

where $U\left( y \right)$ is the average streamwise velocity. For the numerical results, the average RMS values of velocity fluctuations were also estimated as $\sqrt k$. In Fig. 15, a good agreement between numerical results and observations is observed. The turbulence intensity profiles presented in Fig. 15 also follow the same shape as the values of turbulence intensity presented by Nezu and Nakagawa [38] for open-channel flows (see Figs. 4.4 and 4.5 on pp. 54, 55 of the monograph). Basically, for the intermediate region ($0.1 < Y/h < 0.6$), the turbulence intensity profile follows an exponential law. Close to the step edge ($Y/h < 0.05$), the values of $T_{i}$ sharply increase (values are not shown here) and the exponential fit is not valid. The exponential distribution of turbulence intensity has also been observed in numerical simulations over smooth spillways [18].

Fig. 15

Turbulence intensity at the edge of step 31

5 Conclusions

We have presented a thorough numerical investigation on the flow over the non-aerated region of a stepped spillway, with a special emphasis on the turbulence statistics. To the best of our knowledge, this is the first time that profiles of TKE, vorticity and turbulence intensity are rigorously compared against experimental data for this kind of flow in a consistent way. In addition, we developed for the first time, pressure-driven simulations of the flow in stepped spillways, using the experimentally-determined free surface. Based on the analysis undertaken, and addressing the scientific questions made explicit in the Introduction, the following conclusions can be extracted:

• (a) The simulation of the flow over a stepped spillway as a pressure-driven flow (case B), intended to save time, offers results as good as those of the free-surface computations (case A) in terms of the mean flow as well as the turbulence statistics. In particular, velocity profiles and TKE obtained with the $k - \varepsilon$, RNG $k - \varepsilon$, and Launder-Gibson Reynolds Stress models agree very well with the PIV experimental results. This approach can now be used in 3D simulations using standard RANS or DES, without excessive requirements of computational resources. This is encouraging in order to simulate the aerated zone of those spillways.

• (b) In case A, pressure distributions were found to be consistent with recent experimental data and very different from the hydrostatic distribution observed in standard open-channel flows. Since the flow is driven by gravity, pressure distributions in case B can not be interpreted as in case A.

• (c) More elaborated turbulence closures do not appear to be dramatically important in predicting averaged water flow velocities and the overall effect of turbulence (e.g., TKE, and rate of dissipation of TKE); in other words, numerical results obtained with the Launder-Gibson RSM are very similar to those obtained with $k - \varepsilon$ and RNG $k - \varepsilon$ models. This means that, for the purpose of estimating averaged properties of the flow, there is no clear need to go beyond the classical two-equation models to obtain good results.

• (d) The numerical results of TKE at step edges show approximate self-similarity. We found that profiles of rate of dissipation of TKE show approximate self-similarity as well, following similar patterns as in open-channel flows.

Future work on skimming flow over stepped spillways will focus on resolving turbulent flow structures in 3D via hybrid RANS/LES models (e.g., DES, scale-adaptive simulations). When these techniques are used, requirements for grid spacing must be analyzed in order to obtain a solution consistent with existing data. Such work will also focus on the three dimensionality of the flow within the cavity under different geometrical configurations.

Appendix

The transport equation for the TKE $\left( k \right)$ corresponds to a modified energy equation and can be written as:

$$\frac{\partial k}{\partial t} + \overline{{u_{j} }} \frac{\partial k}{{\partial x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\nu + \frac{{\nu_{T} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right] - \varepsilon + \left( {\frac{{\tau_{ij}^{R} }}{\rho }} \right)\overline{S}_{ij}$$

(A.1)

where $k = 0.5 \left( {\overline{{u_{k}^{\prime} u_{k}^{\prime} }} } \right)$, and $\nu$ is the molecular kinematic viscosity. The last term in (A.1) is the production term ($G$) and can be written in compact form as $\underline{\underline{\tau }}^{R} : \underline{\underline{{\bar{S}}}}$.

The rate of dissipation of TKE $\left( \varepsilon \right)$ and the eddy viscosity $\left( {\nu_{T} } \right)$ are obtained as follows:

$$\frac{\partial \varepsilon }{\partial t} + \overline{{u_{j} }} \frac{\partial \varepsilon }{{\partial x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\nu + \frac{{\nu_{T} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + c_{1\varepsilon } \frac{\varepsilon }{k}\left( {\frac{{\tau_{ij}^{R} }}{\rho }} \right)\overline{S}_{ij} - c_{2\varepsilon } \frac{{\varepsilon^{2} }}{k}$$

(A.2)

$$\nu_{T} = C_{\mu } k^{2} /\varepsilon$$

(A.3)

with $\varepsilon = 2\nu \overline{{S_{ij}^{\prime} S_{ij}^{\prime} }}$ and $S_{ij} \prime = \frac{1}{2}\left( {\frac{{\partial u_{i}^{\prime } }}{{\partial x_{j} }} + \frac{{\partial u_{j}^{\prime } }}{{\partial x_{i} }}} \right)$. The values of the coefficients $\sigma_{k}$, $\sigma_{\varepsilon }$, $c_{1\varepsilon }$, $c_{2\varepsilon }$, and $C_{\mu }$ in the $k - \varepsilon$ model are usually taken equal to 1.0; 1.3; 1.44; 1.92; 0.09, respectively [52]. The RNG $k - \varepsilon$ model utilizes Eqs. (3), (4), (A.1) and (A.3), but employs a modified form of Eq. (A.2) that includes an additional term $R$, which is a function of the parameter $\eta$, which in turn is the ratio of the turbulent to mean strain time scale, as follows:

$$\frac{\partial \varepsilon }{\partial t} + \overline{{u_{j} }} \frac{\partial \varepsilon }{{\partial x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\nu + \frac{{\nu_{T} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + \left( {c_{1\varepsilon } - R} \right)\frac{\varepsilon }{k}\left( {\frac{{\tau_{ij}^{R} }}{\rho }} \right)\mathop {\overline{S} }\limits^{{}}_{ij}\, -\, c_{2\varepsilon } \frac{{\varepsilon^{2} }}{k}$$

(A.4)

where

$$R = \eta \left( { - \eta /\eta_{0} + 1} \right)/\left( {\beta \eta^{3} + 1} \right); \quad \eta = Sk/\varepsilon; \quad S = \left( {2\overline{S}_{ij} \overline{S}_{ij} } \right)^{1/2}$$

(A.5)

The constants ${{\upsigma }}_{\text{k}}$, ${{\upsigma }}_{{{\varepsilon }}}$, ${\text{c}}_{{1{{\varepsilon }}}}$, ${\text{c}}_{{2{{\varepsilon }}}}$, ${\text{C}}_{{{\upmu }}}$, ${{\upeta }}_{0}$, and ${{\upbeta }}$ are usually taken equal to 0.71942; 0.71942; 1.42; 1.68; 0.0845; 4.38; 0.012, respectively [54].