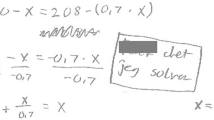1 Introduction

With the introduction of computer algebra systems (CAS) in the everyday teaching and learning of mathematics, much of the usual paper-and-pencil mathematics that our students previously had to do is now outsourced to CAS and other digital tools (Buchberger, 2002; Grønbæk, 2017; Shaffer & Kaput, 1998; Trouche, 2005a). The reader may be familiar with the “solve” and “desolve” procedures of CAS, which in a flash take care of all the otherwise cumbersome, intermediate calculations and reductions that previously had to be done “by hand.” Of course, if a student is familiar with the traditional techniques behind these CAS procedures, then everything in the garden is lovely. But what if the student is not? It is a well-known fact that the calculations and procedures performed by mathematics students can heavily influence their concept development (e.g., Tall, 1994; Zandieh, 2000). Therefore, a change in typical procedures deserves to be studied from a conceptual perspective.

In Denmark, CAS entered heavily in the upper secondary school mathematics program with a reform of 2005 (see, e.g., Jankvist, Misfeldt, & Marcussen, 2016)—and not only in teaching, but also in written assessments. One unintended consequence of the high reliance on “solve” and “desolve” in Danish upper secondary school appears to be that these CAS procedures themselves become “pieces of mathematics” for the students, e.g., “just as we are able to differentiate and integrate, we can also solve and desolve.” Danish upper secondary mathematics teachers explain that the word “solve” has become an integrated part of the students’ mathematical vocabulary.Footnote 1 In Danish, “to solve” is “at løse” and “I solve” is “jeg løser,” but since CAS entered the mathematics program, students now say “jeg solver,” i.e., adopting the English word “solve” and adding an “r” when conjugating the verb. For Danish upper secondary school students, “jeg solver” means something like “I solve the problem by applying the solve command.” Furthermore, the ways in which Danish upper secondary students apply the “solve” command have changed. According to the teachers, it is not uncommon to observe students using it even when at the blackboard: upon reaching a point in their algebraic reductions where they know CAS can do the rest, some students simply bracket the expression and write “solve” in front of the first bracket, convinced that they are now done with the problem.

Considering the way CAS procedures may give rise to specific—and perhaps problematic—cognitive constructs in students’ minds is in a sense a peculiar task to undertake. But the current Danish situation suggests the relevance of doing exactly so, since CAS are used to an extreme extent and the didactical consequences remain largely undealt with: students are required to use CAS in their mathematical work, but only small transformations of the curriculum and negotiation of renewed pedagogies have been done. These issues have been described in four (empirical) articles on learning difficulties and CAS use (Jankvist & Misfeldt, 2015); CAS’ role on classroom interaction (Jankvist et al., 2016); textbooks’ use of CAS (Misfeldt & Jankvist, 2018); and instrumental mediation and students’ identities (Iversen, Misfeldt, & Jankvist, 2018). This specific Danish situation obviously calls for further empirical investigation. However, it also calls for a clearer theoretical understanding, not least in relation to conceptualization—and that is the intention of this article.

We start out by describing the existing state of the art regarding the use of technology in mathematics education (mainly the instrumental approach and the anthropological approach). Then we present our research questions and the approach we have taken in addressing these. This approach partly builds on looking back and reusing selected theoretical constructs previously used to discuss mathematical conceptions and underlying procedures. Following this, we describe and analyze two examples of CAS procedures (“solve” and “desolve”). Finally, we discuss conceptual consequences of relying increasingly on CAS procedures in the teaching and learning of mathematics.

2 Previous research on technology and conceptualization

We are not the first to consider CAS’ effects on mathematical learning and concept formation. Already with the introduction of advanced calculators, this was discussed. One of the original hopes of introducing CAS in mathematics education was that it was deemed able to connect the mathematical representations to concepts better than other digital technologies (Tall, 1994), and has a potential positive influence on concept formation (Dreyfus, 1994). Often studies were building specifically on constructivist theories of learning, e.g., the work of Dubinsky (1991), who focused on how students could use digital technologies and programming languages to support mathematical concept formation. Such visionary approaches to the use of CAS for developing mathematical conceptualization have in the new millennium been replaced by a more realistic attitude, since “no one would claim that the expectations expressed at the time of the first study have been fulfilled” (Artigue, 2010, p. 464). In addition, the focus seems to have shifted towards descriptive approaches of the actual influences of technology on teacher and classroom practices (Hoyles & Lagrange, 2010). A paradigmatic contribution to this development comes from the two theories known as the instrumental approach to mathematics education, focusing on cognition and artifacts, and the Anthropological Theory of the Didactics (ATD), focusing on the institutional nature of mathematical knowledge as well as on the interaction between practical and theoretical knowledge in the learning of mathematics.

The instrumental approach takes its departure in the challenges that digital technologies pose to the existing practices of mathematics education, since “the appearance of more and more complex tools in mathematics classes is not a response to an institutional need” (Trouche, 2005a, p. 9). The approach was developed in France in the late 1990s as an answer to “a contrast between the idealistic discourse of the experts [...] and what was revealed by observations” that were present when looking at students’ use of CAS (Artigue, 2010, p. 466). To better understand this gap, researchers deliberately left the constructivist discourse behind and looked for new ways to conceptualize students’ CAS-related work. Even more, they saw the use of constructivism as an unhealthy attempt “to caution [...] the technical-conceptual cut” and thus “felt the need to take some distance” from the constructivist approaches (Artigue, 2002, p. 247). The instrumental approach marks a shift in focus away from only capitalizing the didactical potentials of CAS towards also describing how teachers and students adopt these technologies into their existing practices, in a process of instrumental genesis:

[A]n artifact is a material or abstract object, aiming to sustain human activity in performing a type of task [...]; it is given to a subject; an instrument is what the subject builds from the artifact. This building [...], the so called instrumental genesis, is a complex process, linked to characteristics of the artifact (its potentialities and constraints) and to the subject’s activity, her/his knowledge and former work methods. (Trouche, 2005b, p. 144)

The instrumental genesis may be described as consisting of three dualities (Drijvers, Godino, Font, & Trouche, 2013). The first is the duality between artifact and instrument (Verillon & Rabardel, 1995); the subject develops the artifact into a personal instrument by using it. The second is the duality between instrumentalization, i.e., that the subject shapes and modifies the artifact; and instrumentation, i.e., that the artifact shapes and influences the subject. The third is the duality between scheme and technique. When students are using CAS to do mathematics, they are developing instrumented action schemes (Drijvers et al., 2013).

The concept of technique stems from ATD, which was developed by Chevallard to characterize mathematical knowledge and its institutional framing (Bosch & Gascón, 2014). In particular, ATD focuses on what characterizes mathematical knowledge in the school system and other places in society in order to further understand the didactical transposition of mathematical knowledge into the classroom. Central to the theory is the interplay between theoretical and practical aspects of knowledge, where the latter consist of specific explicit solution strategies, and the former on how these strategies fit into a larger mathematical landscape of concepts and practices. The concept of technique mediates between these epistemic and pragmatic aspects of mathematical knowledge and has been used in the development of the concept of instrumented technique within the instrumental approach, as described by Artigue:

First, the anthropological approach helped us overcome the problem posed by the conceptual/technical dichotomy by making clear that mathematical techniques have both an epistemic value and a pragmatic value. As a consequence, we were obliged to seriously consider the change in the balance between these two values induced by the use of CAS, which was especially insightful. (Artigue, 2010, p. 467)

A positive focus is not unusual in the technology literature, even though the importance of the influence of CAS on the formation of mathematical concepts is acknowledged (e.g., Weigand, 2014). Still, when reviewing the literature on the use of CAS for mathematics teaching and learning, one realizes that it has undergone a change in focus from describing potentials in terms of concept formations towards a focus on understanding the developing work practices of students. This development marks a move from vision to reality, in the sense that the central book edited by Guin, Ruthven, and Trouche (2005) takes its outset in symbolic calculators, not as a gift to the formation of mathematical concepts, but as a challenge to the practices of teaching and learning mathematics:

[P]aper-and-pencil techniques tend to become obsolete because of the ease of using CAS commands. This obsolescence is a problem because traditional techniques can no longer play their role in conceptualization and ‘push button’ techniques cannot take over this role directly. (Lagrange, 2005, p. 118)

Yet, what happens if “push button” techniques actually do take over the role of conceptualization from traditional techniques? This appears to be the case for many Danish upper secondary students, where “solve” and “desolve” are the associated techniques per se with the concepts of equation and differential equation, respectively (Jankvist & Misfeldt, 2015). In the following section, we address this problem by revisiting some of the theories of mathematical conceptualization that predate the current discussion of technologies in mathematics education.

3 Questions, approach, and theoretical constructs applied

Digging into the rich literature on mathematical conceptualization, the overall purpose of the present article is to address the following two questions from a theoretical standpoint:

  1. 1.

    What happens when CAS procedures are objectified in the minds of our students?

  2. 2.

    What is the nature of the resulting “objects” that the CAS procedures may give rise to?

Our notion of objectification and objects is grounded in a psychological (Piagetian) understanding of abstract objects as results of empirical and reflective abstractions on performed actions. Dubinsky (1991) expresses this: “Reflective abstraction interiorizes and coordinates these actions to form new actions and, ultimately new objects” (p. 98). Hence, when we talk about the process of objectification and the resulting objects, we refer to the result of reflective abstraction (in a Piagetian understanding) and reification processes, as also described by Sfard (1991). An assumption of Sfard is that once a procedure is reified into an object, this object becomes itself the input to a higher-order mathematical concept. Still, what if the underlying procedure is not truly reified and students still attempt to work with the associated higher-order objects? Observing students’ work in algebra, Sfard realized this shortcoming of her original model and introduced the notion of pseudostructural conceptions (e.g., Sfard & Linchevski, 1994). According to Zandieh (2000), a pseudostructural conception usually has the form of a gestalt, i.e., an object with no internal structure, a whole without parts—referred to as a pseudo-object. But what of CAS procedures that take over a bundle of underlying mathematical processes with one push of a button? Jankvist and Misfeldt (2015) argue that reification of a given mathematical concept will be challenged, if its underlying processes are only rarely performed due to extensive outsourcing to CAS, and that this will lead to a variation of Sfard’s vicious circle—i.e., that reification of a lower level mathematical object can only happen when this object serves as input for an interiorization of a higher level object—referred to as a vicious spiral, where “more and more abstract concepts are built from processes acting on lower level objects that have not been reified” (p. 18). Yet, what if a CAS procedure does not lead to a mathematical object—or even a pseudo-object—in our usual understanding of such? We cannot know this a priori. Sfard’s (1991) original model of concept formation (interiorization, condensation, and reification) does not seem able to predict this, mainly due to its hierarchical nature. Hence, for the sake of our theoretical investigation, we augment the notion of pseudo-objects to Dubinsky and colleagues’ APOS framework (e.g., Asiala et al., 1996), in order to use the insights from Sfard and Dubinsky when trying to shed light on the consequences of increasingly adopting instrumented techniques when trying to develop abstract mathematical concepts with the students. This is a feasible strategy because APOS recognizes the existence of different levels of internalization involving impoverished or partial mathematical concepts in a student’s mind. We also use Vinner and colleagues’ notion of concept definition and concept image (e.g., Tall & Vinner, 1981), not least due to its articulation of cognitive conflicts. It should be noted that these theoretical constructs do not take the institutional level into account in the same way that ATD does. Still, we are very aware that the analysis we are conducting, despite its theoretical nature, is framed by the institutional setting of Danish upper secondary school. Here the combination of heavy implementation of CAS tools and a slightly conservative mathematical curriculum focusing on high-level procedures (e.g., solutions to equations and differential equations) constitute a specific institutional setting (Jankvist et al., 2016) that will influence the outcome of the analysis.

4 A theoretical analysis of two CAS procedures

We begin by introducing a recurring example based on which we continuously present and apply the selected theoretical constructs mentioned above. We choose a well-described problemFootnote 2 from Bodin (1993), i.e., solve the linear equation:

$$ 7x-3=13x+15. $$
(1)

From a procedural point of view, what we are interested in is to first collect the terms involving x on one side of the equal sign and those not on the other side, e.g.:

$$ 7x-3+3-13x=13x+15+3-13x. $$
(2)
$$ 7x-13x=15+3. $$
(3)

Secondly, performing arithmetic operations on both sides of the equal sign, we obtain:

$$ -6x=18, $$
(4)
$$ x=18/-6, $$
(5)
$$ x=-3. $$
(6)

Several studies have shown that students may be able to perform operations resulting in the expression x =  − 3, without actually possessing any relational understanding of why these operations are allowed or lead to a correct result (e.g., Kieran, 2007; Rhine, Harrington, & Starr, 2018). Bodin (1993) finds that students, upon arriving at x =  − 3, are not able to answer the question of whether or not x = 10 could also be a solution to the original equation. From a conceptual point of view, these students have not understood that −3 is a solution—and the only solution. Despite potentially possessing sufficient procedural abilities, they lack conceptual understanding of the concept of equation. In a CAS environment, the same scenario is possible as well, but here the number of procedural steps is reduced to only one, namely:

$$ \left(\ast \right)\ \mathrm{solve}\left(7x-3=13x+15,x\right). $$

That is to say, CAS reduces the procedural knowledge needed to the ability of writing up the above expression and then “pushing a button,” thus obtaining the result, x =  − 3.

According to Dubinsky and colleagues “…understanding a mathematical concept begins with manipulating previously constructed mental or physical objects to form actions; actions are then interiorized to form processes which are then encapsulated to form objects. Objects can be de-encapsulated back to the processes from which they were formed. Finally, processes and objects can be organized in schemas” (Asiala et al., 1996, p. 9). This quote refers to the key mental structures constituting the APOS framework: Action, Process, Object, and Schema. Solving the linear Eq. (1), the Actions could consist of trying out whether specific numbers satisfy the equation, or in playing with specific algebraic manipulations. When the student is beginning to perform the necessary algebraic transformations in order to isolate x and find its value, the actions are taking the first step towards being internalized to a Process of solving equations. This internalization happens when the student repeatedly performs actions on a mathematical entity and reflects on these; e.g., this means that the student will know the procedures involved in solving the equation to an extent where there is less need for step by step instructions in the process. For instance, a student might be able to go from (1) to (4) without realizing the intermediate steps of the algebraic transformation, and even without being able to reverse those steps. The act of internalizing an action is known as a Process. However, actions can also be applied to processes; this happens when the student interprets the process as a whole, i.e., as an entity to which transformations can be applied. When a student is able to do so, (s)he has encapsulated the process into a mathematical Object. In the case of solving Eq. (1), the student must encapsulate the process of solving an equation of this type into a mathematical object. A coherent set of actions, processes, and mathematical objects, e.g., in relation to the concept of linear equation, may be collected into the structure of a Schema, which are the forms in which concepts exist in the mind of a student. A built-in tenet of Dubinsky’s theoretical construction is the possibility to shift from an object back to a process, as required in many mathematical situations. This is done by “de-encapsulating the object, that is, to go back to the process which was encapsulated in order to construct the object in the first place” (Dubinsky, Dautermann, Leron, & Zazkis, 1994, p. 271).

The application of the “solve” command to our linear Eq. (1) may be regarded as an action on a mathematical entity. However, a feature of this action is that it leads to the solution of the equation in a single step. This of course frees the student of the need to perform the intermediate steps of the solution process. Yet, at the same time, it reduces considerably the number of actions to be applied (Fig. 1). Using the APOS framework, the Action is simply applying the solve command. When a student is comfortable with the command, it can be interiorized as a Process and later encapsulated when the student refers to the solution as an independent Object. The broader Schema will be concerned with the structure of the relation between equations, the commands applied, and the output that the CAS tool delivers (solutions, error messages, etc.).

Fig. 1
figure 1

Screenshot of the solution of the linear Eq. (1) in a CAS tool (Wolfram Alpha)

Full size image

One may argue that a student could repeatedly apply the “solve” command to different linear equations until the command might become internalized and conceptualized as a “process” in itself. Still, within the CAS environment, the space of actions is reduced. Of course, there are a number of actions that potentially could be performed, e.g., “simplify.” However, as we also know from the Danish situation, students soon realize that the space of actions which leads to good—or acceptable to the teacher—solutions is rather limited. In a traditional setting, one characteristic of the interiorization process is that a student is able to reverse all steps performed during, say, an algebraic transformation. Clearly, this is not the situation when using CAS’ “solve” command. In that sense, CAS solutions of equations are built on irreversible actions. Hence, at least two characteristic features of the APOS framework are not present when relying on the CAS procedure “solve”: that encapsulated processes are reversible; and that the students do several actions on the object(s). Also, the intensive use of the “solve” command in the solving of equations may indeed represent a stumbling block with respect to conceptualization, particularly in the students’ transition from actions to processes. In her study of elementary school students’ learning of fractions, Arnon (1998) identified levels within the progression from the action stage to the process stage among which the interiorization of improper actions (i.e., actions that are incomplete or incorrect) is considered. Thus, the transition from action to process requires an interiorization mechanism, but this mechanism is a developmental continuum with levels in between that may include the interiorization of an incorrect action or the interiorization of a partially incorrect action.

The execution of CAS procedures, such as the “solve” command, may be considered as an implementation of “incomplete” or “improper” actions, in the sense that their operational underpinnings remain hidden from the student (Buchberger, 2002). However, such actions, although incomplete, may be internalized by the student; in fact, the students’ verbal manifestations of “jeg solver” and their use of the command “solve” at the blackboard can be considered as evidence of such an interiorization mechanism having taken place. Nevertheless, as Arnon, Nesher, and Nirenburg (2001) warn us, the interiorization of incomplete or improper actions leads to a pre-concept level of conceptualization—in this case a pre-concept of solution of an equation—that is manifested by an impoverished knowledge of the concept. So, while Sfard and colleagues acknowledge the possibility of not fully interiorizing a process that gives rise to an abstract object, i.e., a pseudo-object, the APOS researchers’ suggestion is different, because the transition happens between action and process and is conceptualized as a developmental continuum. Or in other words: Sfard and colleagues’ pseudo-object may be considered as the potential outcome of going from the mental structure of Process to that of Object in the APOS framework, while Arnon and colleagues’ consider the potential outcome of going from Action to Process, i.e., what might be referred to as a “pseudo-process.”

Another consequence related to conceptualization of having only one action, i.e., pushing the “solve” button, may be illuminated through Vinner and colleagues’ “distinction between the mathematical concepts as formally defined and the cognitive processes by which they are conceived” (Tall & Vinner, 1981, p. 151). This they achieve by considering concept image, which is “the total cognitive structure that is associated with the concept, including all the mental pictures and associated properties and processes,” and concept definition, which is “a form of words” used to specify or define a concept (p. 152). Part of a concept image may be in conflict with other parts of the image or with the concept definition, which constitutes a potential conflict factor. Only if potential conflict factors are evoked simultaneously will they result in a cognitive conflict. Students who have a concept image of linear equations as something having one and only one solution may find themselves in a cognitive conflict, when encountering equations with either no solutions or all real numbers as solutions. To some extent, such cognitive conflicts may still be potentially possible when applying the CAS procedure of “solve.” For instance, when CAS provides the answers “false” and “true” to equations with no or all real numbers as solutions. Still, by outsourcing the solution procedure to CAS, students may miss many other potential cognitive conflicts concerning the lower level mathematical objects of the equation, e.g., the concepts of equality, variable, and number.

In Danish upper secondary school, differential equations are one of the more advanced topics that students will encounter. While the “solve” command may be said to encompass only “fairly simple” actions, mathematically speaking, CAS procedures may potentially “encapsulate” a variety of arbitrarily complex mathematical techniques. The “desolve” command that solves differential equations illuminates this. As an illustrative topic, let us take first-order differential equations. Depending on the equation, the solution procedure of course varies quite a bit. Even if we have a differential equation on the apparently simple (antiderivative) form y’ = f(t), a student may need to choose from an arsenal of procedures to solve this, e.g., applying various rules of differentiation, known antiderivatives, methods of substitution, and partial integration. If, however, we have a linear first-order differential equation, i.e., of the form y’ + f(t) ∙ y = g(t), then, upon recognizing this form, the student will need to know that such a differential equation has an exact solution, and how to arrive at this. Something similar will happen for separable first-order differential equations, i.e., of the form y’ ∙ g(y) = f(t), where the solution procedure relies heavily on integration techniques.

In relation to CAS and conceptualization, solving an arbitrary first-order differential equation is once again reduced to a single action, “desolve.” As for “solve,” the encapsulated processes of “desolve” are also not reversible from an APOS point of view. Here too, the students do not perform actions on objects in our usual understanding of such. Furthermore, for “desolve,” the amount of potentially encapsulated processes is much larger than for “solve,” which reduces a much larger space of potential actions for the students. This limits the students’ possibilities to create new sound concept images related to differential equations and their solutions. For example, Rasmussen (2001, p. 64) found that “the notion that a solution is a function is likely a new idea for many students since much of their past experience with ‘solving’ resulted in a number (or numbers).” Hence, the limited space of potentially many more actions causes students to miss a much larger number of potential cognitive conflicts. In relation to numerical solutions to differential equations, Rasmussen (2001) further states that students’ “mental picture may not be specific to Euler’s method but rather be indicative of students’ concept image about approximations in general” (p. 76). Also, CAS may impose superficial similarities between different procedures which essentially operate on very diverse mathematical objects. Most evident is the apparent similarity between “solve” and “desolve” procedures. This blurriness occasionally leads students to regard “desolve” as a special case of “solve” (Jankvist & Misfeldt, 2015). Rasmussen’s (2001) observation that the “switch from conceptualizing solutions as numbers to conceptualizing solutions as functions is nontrivial for students” (p. 67) further indicates that the superficial similarities between “solve” and “desolve” most likely do not improve the situation.

5 Discussion of arising phenomena

The fact that in particular the “desolve” command, but also the “solve” command, cover such a vast domain of mathematical concepts and techniques, seems to lead to the emergence of new classifications of objects—classifications which are very different from those we usually operate with within the discipline of mathematics. In the case of “desolve,” students need no longer pay much attention to whether the first-order differential equations are of the separable, the linear, or of the simple antiderivative type. Nor do they need to pay attention to whether the differential equations are homogeneous or inhomogeneous, if they are of first order or second order, if they form a system of differential equations, or even if they are to be solved analytically or numerically. CAS encapsulate all these types into being handled by one and the same command, “desolve.” The same is the case for “solve”; not much attention on the student’s behalf is necessary in relation to whether we are dealing with linear equations, quadratic equations, third- or fourth-degree equations, a system of three equations with two unknowns, etc. To say it more bluntly, it is simply a different way of “chunking up” the mathematical objects; a reclassification based on the CAS output. From the perspective of a student, who is not familiar with the usual mathematical classifications of equations and differential equations as well as the associated techniques for solving these, there may only be two kinds of CAS outputs: solutions and non-solutions. A few examples of outputs in the case of “desolve” could be “?,” “illegal input,” “undefined,” “syntax error,” etc., or even full sentences such as “Supplied equations are not differential equations of the given functions,” if for instance entering desolve(y’ = 2y, x, t) instead of desolve(y’ = 2y, x, y), where the latter would reveal the actual mathematical solution. Whether or not a student perceives such output as a solution or a non-solution is of course individual; one student might regard the full sentence above as an acceptable solution and the output “undefined” as a non-solution, whereas it would be different for another student. Although such solutions and non-solutions may be considered as gestalts, i.e., wholes without internal parts and structures, they are not necessarily mathematical pseudo-objects in the usual sense. The usual classification of the objects, according to their mathematical qualities, is in competition with a classification based on the relevance of the CAS output in relation to value as solutions to be provided for the teacher. It is not a matter of whether an equation/differential equation has a solution or not; the answer “false,” i.e., no solutions, is in itself a solution. Rather it is a matter of if CAS can or cannot “solve” an equation or “desolve” a differential equation. Surely, some engaged students may wonder why we sometimes get solutions and sometimes not, and then potentially dig into the mathematical theories behind this. But based on experiences from the Danish upper secondary school mathematics program, students are often quite content with presenting a “non-solution” as a solution to a question, if this is what CAS display.Footnote 3

In a sense, the usual classifications of mathematical objects cease to exist when CAS is used, and this CAS cessation has potential cognitive consequences. As debated above, cognitive theories within the field indicate that actions related to mathematical entities lead to the objectification of such actions, thus forming concepts in people’s minds. Hence, when students’ mathematical activity develops in a setting where their actions on abstract concepts are predominantly CAS procedures, students are likely to interiorize those procedures, thus generating some kind of CAS objects. Since the constitution of CAS objects is based on few and generic actions, their input to concept formation is coarse. Students will lose access to algorithmic specificities that are critical to the constitution of mathematical objects; a process that we believe will result in the impairment of students’ concept images. Of course, there will be a basis of actions and outcomes of these actions on which a classification of mathematical objects could be constructed, but this classification would be rudimentary and impoverished.

A special feature of these CAS objects of solutions is that they are unstable. CAS introduce an instability of solutions in the sense that the same mathematical situation can be interpreted and solved differently due to features that are contingent from a mathematical perspective, at least in the eyes of the students. Due to the ongoing improvements of the user interfaces of CAS, these tools are increasingly taking part in supporting mathematical interpretations (including mathematical problem solving and modeling). This situation potentially changes the CAS objects of solutions. Different CAS tools might make different choices when interpreting the same input. Furthermore, two inputs with the same mathematical meaning but with different wording might be processed differently.

That CAS tools are interpreting and mathematizing input is a fact, which not least is due to the rapid development in language technologies. Dreyøe, Schewitsch, and Hansen (2017) describe how certain tasks from the Danish national grade 9 examination can be typed more or less directly into Wolfram Alpha. For example, a task where students are to find out how much water is used in an 8-min and 30-s long shower with 14 liters of water used per minute. By entering “14 L per min 8 min and 30 sec” into Wolfram Alpha, the tool gives you the answer “119 L”. There is no longer the need for students to perform the mathematization, i.e., write up: 14 L/ min  ∙ 8.5 min. Moreover, nor do they have to perform the de-mathematization of providing the unit L to the answer 119. Of course the actual solution algorithm that a system applies might also differ and thus lead to different solutions, in particular in the case of numerical solutions (for simplicity, say, e.g., the number of iterations CAS carry out of Euler’s method or Runge-Kutta’s method).

In the students’ investigative processes, the instability poses a problem. It leads to what might be termed “the mathematician’s regress”Footnote 4 in the sense that it is not possible for students to describe the origin of unexpected or instable results experienced in a CAS environment. Most important, they are not able to see what part of the instability comes from an unclear formulation of the problem, from a mathematical phenomenon (e.g., two solutions to a quadratic equation), or from specific (e.g., numerical) methods hardwired into the software. A student who relies on CAS to solve a linear equation and receives a strange output—e.g., solving an equation with no solutions and getting the output “false” (cf. earlier)—cannot know, if (s)he is looking at a mathematical phenomenon, if (s)he is using CAS in an incorrect manner, or if the CAS tool is relying on an insecure numerical method. The cognitive consequences of such a less stable concept of solution may be several. However, introducing a regress, where it ceases to be (even in principle) within the reach of students to clarify such situations, runs a risk of students losing a clear concept of the “solution” to a mathematical problem—an issue which is known to be important. Niss (2010), for instance, refers to the ability to conduct mathematical work on solutions that have not yet been obtained as the result of a pending mathematization. He refers to this as implemented anticipation and suggests that a stable concept of solution is necessary in order for mathematical work to be successful. Hence, a weak concept of mathematical solution can have negative consequences on students’ ability to conduct mathematical problem solving work, because students can anticipate neither the solutions nor the processes leading to them.

Instead, students may increasingly attempt to find solutions by trial-and-error experiments. However, such reasoning process is fundamentally different from the a priori reasoning process usually identified with mathematical thinking and working. Of course, experimental mathematics has existed as an accepted mathematical practice for many years. However, the interesting consequence in the present case is not the augmentation of mathematical reasoning with a posteriori elements, but rather the transformation of mathematical reasoning away from being mainly a priori. CAS procedures not only free the student from the algorithmic burden that may be associated with the resolution of mathematical problem, they also minimize the need to exert an a priori analytic reasoning about the structure of a problem or the nature of a mathematical situation before deciding on specific algorithmic procedures. Students need only know the syntax that allows them to enter, say, a differential equation into the CAS tool, choose appropriate variables as part of that syntax, and then push the “desolve” button. Clearly, in this new scenario, the need for an a priori reasoning fades away. This means that many mathematical tasks can be solved with one or two instrumented techniques—and the students may already be well aware of this, i.e., that there is no real need to try to understand the underlying mathematics.

Even in less restricted situations, where several instrumented techniques are available to the student, an a priori reasoning may remain an element that, from the point of view of the student, makes no or little sense. If a number of methods are available, and if they, with almost no cognitive effort, can lead to different outputs, then the easiest approach to solve a mathematical problem would be to look for the most trustworthy output from the CAS. The reasoning that students apply in order to perform this task will often be far from mathematical. This type of behavior is similar to the working random method (e.g., Guin & Trouche, 1998). However, more often than not, the choice between different CAS procedures and outputs will not be exactly random, but rather based on superficial recognition of what type of output seems credible and relevant as a solution to the problem. This process, from mathematical reasoning to superficial recognition, characterizes one of the major problems with heavy introduction of CAS tools in the teaching and learning of mathematics.

6 Conclusion: the dawn of “instrumatics”

In the Danish context, it is often articulated that CAS have changed the school subject of mathematics into something else (e.g., Grønbæk, 2017). With this article, we have identified four phenomena that may provide some illumination of what this “something else” might involve. Firstly, the development of mathematical concepts is affected because the actions and processes involved in doing mathematics are changed. We suggest that the resulting concepts are coarser, because one command can handle a number of mathematical phenomena. Secondly, the involved processes are not reversible and transparent, and this means that the concepts are weaker. Thirdly, we have argued that the use of CAS challenge students’ conception of mathematical solution. Fourthly, the a priori reasoning process that characterizes the mathematical way of working will be in competition with more superficial trial and error strategies. CAS make trial and error ways of working much more efficient for students, which cause the students to lose the ability to acknowledge the necessary nature of mathematical solutions. This provides a narrowing down of potential answers to our two initial research questions, since it tells us what does not happen when CAS procedures take over. The two phenomena of reclassification of mathematical objects and the prevailing of a posteriori reasoning to some extent make up our answers to the first research question, i.e., what might happen when CAS procedures are objectified in the minds of our students. As for the second research question, i.e., what is the nature of the resulting objects that CAS procedures give rise to, we have pointed to the fact that in the case of resulting objects (CAS objects), these will be a different kind of cognitive (non-mathematical) objects in the sense that they are coarser and by nature possess an embedded instability.

From the perspective of any experienced Danish upper secondary school mathematics teacher, who usually holds a master’s degree in mathematics proper, it is understandable if (s)he thinks that “it’s the end of mathematics as we know it”Footnote 5 once CAS enter the classroom. Some might even go so far as to state that what is taking place is no longer mathematics.Footnote 6 But if not mathematics, what then? Perhaps what we are witnessing the beginning of in our present day CAS heavy environments is a kind of “instrumatics.” That is to say, a subject where CAS are used for solving mathematical problems—but not for learning mathematics—and where the mathematical work is undoable for the students without a CAS tool. In such a subject, mathematical problems and situations would be classified more in relation to the CAS technique for addressing them and less by internal mathematical relationships. In that sense, mathematics would cease to be a genuine subject to be studied.

Summing up, we find ourselves in a situation today where the classical theories of the psychological formation of mathematical concepts and objects all suggest that CAS can have significant and non-intended influences on students’ concept formation. The literature on technology, and especially the instrumental approach and ATD, in many ways have the necessary machinery to study the developmental results of using CAS in this manner and to this extent. However, in order to do so, we might need to focus more specifically on the unintended consequences of heavy CAS use. We suggest that it will be beneficial to “network” the instrumental approach and ATD with the same psychological and constructivist theories that these approaches initially turned away from partly due to a disappointment about the hopes of positive effects on students’ learning with technology. Perhaps therefore, this has so far not been done in a way where the focus is on long-term negative cognitive consequences of the use of CAS. For the two CAS procedures “solve” and “desolve,” this article offers an attempt at doing just that.