1 Introduction

The analysis conducted in this study dates back to Brownell (1942, 1947), who states the importance of understanding-related learning phenomena through the analysis of arithmetic problem-solving processes. Since then, much progress has been made towards a profound understanding of what it means to learn meaningful arithmetic (Bednarz & Janvier, 1996; Vergnaud, 1990; Verschaffel & De Corte, 1996) characterizing an arithmetic thinking. Didactic research centered, on the one hand, on the role of mathematical error when solving algebraic tasks (e.g., Booth, 1984, 1988) and, on the other, on how pupils learn algebra, focusing on the paradigm related to the transition from arithmetic to algebra. Many studies have followed this line of thinking, with Vergnaud (1988, p. 189, p. 195), for example, positing that algebra is “an important epistemological rupture with arithmetic” for pupils. Like other authors (Filloy & Rojano, 1989; Herscovics & Linchevski, 1994), Vergnaud thinks that this rupture merits detailed analysis, as many pupils do not come easily to the symbolic manipulation game. These authors, implicitly and/or explicitly, introduce algebra as the main tool for resolving equations and/or mathematical problems that are not easily solvable only using arithmetic.

Verschaffel and De Corte (1996), analysing worldwide curriculum, characterized number and arithmetic as involving: number concepts and number sense; the meaning of arithmetic operations; control of basic arithmetic facts; mental and written arithmetic; word problems using digital literacy and arithmetic skills. On the other hand, Kieran’s algebraic thinking model (2007) outlines the following: G) Generational activities, such as the formation of expressions and equations that are objects of algebra; T) Transformational activities such as factoring, expanding, substituting; and, Gm) Global/meta-level mathematical activities, such as problem solving, predicting, conjecturing, and modelling.

Research on a rupture approach has mainly focused on algebra in the context of the transformational activities specified in Kieran’s model of algebraic thinking.

Kaput’s publications (1995, 2000) have had a major impact on the didactic community, and have created a new paradigm for teaching algebra:

…algebraic reasoning is a complex composite of five interrelated forms of reasoning. The first two of these underlie all the others, the next two constitute topic strands in the curriculum, and the last reflects algebra as a web of languages - its linguistic side. All five richly interact conceptually as well as in activity…

  1. 1.

    (Kernel) Algebra as generalizing and formalizing patterns, …

  2. 2.

    (Kernel) Algebra as syntactically-guided manipulations of formalisms,

  3. 3.

    (Topic-strand) Algebra as the study of structures and systems abstracted from computations and relations,

  4. 4.

    (Topic-strand) Algebra as the study of functions, relations and joint variation,

  5. 5.

    (Language aspect) Algebra as a cluster of (a) modelling and (b) Phenomena-controlling languages. (2000, p. 2–3)

Looking at Kaput’s first and second points, it is clear that he had in mind a continuous approach to learning algebra rather than a rupture. Generalization processes related to patterns and the formalization of those processes was, for him, the beginning (the kernel) of an introduction to the other three points related to advanced algebraic thinking. This view on the transition from arithmetic to algebra as a continuum rather than rupture was supported by others; for example, Lee and Wheeler (1989, p. 41) said that, while introducing algebra to beginner pupils as “generalised arithmetic” may be a sensible strategy, there are distinct pedagogical obstacles for its adoption. Lee (1996) continued to search for a generalised arithmetic approach to teaching algebra. All this became the impetus for the Early Algebra movement (see Cai & Knuth, 2011). The Early Algebra paradigm comprises two major components:

  1. a)

    An early years introduction to algebraic thinking (elementary school)

  2. b)

    A characterization of arithmetic and algebraic thinking

Discord among the followers of the Early Algebra movement began to emerge. While some researchers agree with the introduction of some kind of algebraic reasoning in elementary school, they see the panorama as still too hazy to make a clear distinction between arithmetic thinking and algebraic thinking (e.g., Radford, 2011).

2 The general opinion on the early algebra movement and others

Recent opinion on the Early Algebra movement is summed up by Lins and Kaput (2012), they state:

Early algebra is that an algebrafied elementary mathematics would empower students, particularly by fostering a greater degree of generality in their thinking and an increased ability to communicate that generality. (p. 58)

They continue, stating that the Early Algebra group agrees on:

…two characteristics of algebraic thinking. First, it involves acts of deliberate generalization and expression of generality. Second, it involves, usually as a separate endeavour, reasoning based on the forms of syntactically-structured generalisations, including syntactically and semantically guided actions. (p.48)

Taking into account the literature on the Early Algebra movement, two tendencies can, roughly, be distinguished:

  1. a)

    Some researchers focus on mathematical content and skills development that direct the student toward algebraic thinking (e.g., Britt & Irwin, 2011; Carraher, Schliemann, & Brizuela, 2000; Carraher, Schliemann, Brizuela, & Earnest, 2006). For example, Schliemann, Carraher, and Brizuela (2012) state, that: “The 5th grade lessons focused on algebraic notation for representing word problems, leading to linear equations with a single variable or with variables on both sides of equals sign.” (p. 115)

  2. b)

    Researchers such as Carpenter, Ansell, Franke, Fennema, and Weisbeck (1993), Carpenter and Franke (2001); Davydov and J. Kilpatrick (1972/1990), and Radford (2011) among others approach algebraic thinking through the strengthening of a “meaningful arithmetic” that focuses on concepts, relationships and structure.

Researchers allied to the first tendency criticize authors who center their research on cognitive obstacles, arguing that this approach hides the ‘natural way’ of learning algebra (e.g., Britt & Irwin, 2011, p. 139). However, at the same time, recent research shows that dismissing the “transition” from arithmetic to algebra and proposing the teaching of algebraic content in primary school presents problems, as has been described in the past with regard to cognitive obstacles. For example, Cooper and Warren (2011) state that:

The results have shown the negative effect of closure on generalisation in symbolic representations, the predominance of single variance generalisation over covariant generalisation in tabular representations, and the reduced ability to readily identify commonalities and relationships in enactive and iconic representations.” (p. 187)

Taking into account all these results, this study sought to present research centered around the second tendency described above, which seeks to strengthen meaningful arithmetic as related to algebraic thinking. Specifically, this research focused on arithmetico-algebraic thinking.

3 Arithmetico-algebraic thinking in terms of a modelling process

3.1 Theoretical aspects featured in this research

Vergnaud (1988) takes a position allied to the traditional curriculum, where algebra is first introduced through solving equations and is then taught through algebraic manipulation. The literature shows a great deal of research focusing on epistemological ruptures. Indeed, the Early Algebra movement challenges these ruptures and forces (as noted by Artigue, 2012; or Radford, 2011) an improved analysis to be performed in order to ascertain whether these cognitive problems are linked to the manner in which arithmetic and algebra are taught. This study is closely aligned to this perspective.

Additionally, in the past, communication among individuals was not an essential issue in the mathematics classroom. On the contrary, the approach employed here considers communication in the classroom as the predominant factor in the evolution of pupils’ spontaneous representations (Hitt & González-Martín, 2015). Hence, a specific teaching method and task design are necessary in order to promote communication in the solving of a mathematical problem. This method and corresponding task design (see the structure of the activity) must take into account both the individual and teamwork aspects, where communication among pupils generates conjectures and enables validation processes, sensitivity to a contradiction, and the evolution of spontaneous representations.

It is precisely the notion proposed by Voloshinov (1973) on the construction of the sign on which this study focuses, in terms of the evolution of pupils’ spontaneous representations: “The reality of the sign is wholly a matter determined by that communication. After all, the existence of the sign is nothing but the materialization of that communication…” (p. 13). Moreover, as noted by Eco (1988, 1992), of foremost importance is the process of objectification in the construction of the sign and not the sign itself. Particularly in the context of learning mathematics, Radford (2003) constructed the “Semiotic means of objectification”:

These objects, tools, linguistic devices, and signs that individuals intentionally use in social meaning-making processes to achieve a stable form of awareness, to make apparent their intentions, and to carry out their actions to attain the goal of their activities, I call semiotic means of objectification. (p.41)

From this, the focus must be on mathematics instruction, task design, communication in the classroom, and the processes of objectification as a unified entity. Thus, this study proposes a process of instruction in a sociocultural approach. This means we are taking into account the activity theory under a Vygotskian perspective (see next section).

The first step in this process is to prepare the pupil for significant communication with others. As some pupils are often quicker than others to develop ideas, the intention is to promote reflexion before interacting with teammates:

  1. 1)

    Individual work based on a sociocultural approach to building knowledge in the mathematics classroom

    A classical approach to collaborative learning is to take into account:

  2. 2)

    Teamwork based on a sociocultural approach to constructing knowledge

  3. 3)

    Debate (with the possibility of promoting scientific debate)

    As highlighted by Hitt and González-Martín (2015), “consensus is usually ephemeral in the mathematics classroom” (p. 206). This drove the conception of the important 4th step in the instructional approach employed in this study, comprising self-reflection in a process of reconstruction as related to what was conceived and discussed in the three previous steps. Indeed, before the fourth step, teachers must take all the pupils’ productions, and give new handouts to the pupils.

  4. 4)

    Self-reflection (reconstruction of what was done in the classroom)

    Finally, step five requires the teacher to take into account the evolution of pupils’ ideas and promote an institutional approach.

  5. 5)

    The process of institutionalisation

    We named this five-step teaching approach ACODESA (from French: Apprentissage Collaboratif, scientifique Debate, Auto-réflexion).

3.2 Research goal

This research project began with an analysis of the literature on the Early Algebra movement and the controversy that has emerged among its followers. This study follows a different approach, based on the construction of signs through an objectification process (Eco, 1988, 1992; Radford, 2003; and, Voloshinov, 1973) which, rather than considering the gap between arithmetic and algebra, is based on the need to construct arithmetico-algebraic thinking through an objectification process immersed in collaborative learning. This requires task design that promotes reflection on the unknown, the variable and co-variation between variables as concepts that must be developed in a generalization process as part of this arithmetic-algebraic thinking.

4 Methodological approach

Since this study centres on a problem-solving environment, and a post-Vygotskian theory of activity (5th generation), Engeström’s theoretical framework (1999) is proposed along with the ACODESA teaching method (Hitt, 2007, 2013; Hitt & González-Martín, 2015). This study contends that this approach precisely accounts for the individual and teamwork aspects that must be considered when organising the teaching process in the mathematics classroom:

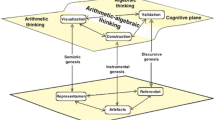
Figure 1 (left) summarises the 5 steps of the ACODESA method, and Fig. 1 (right) presents the organisation of the community using Engeström’s model immersed in an activity theory approach (activity system as culturally mediated human activity). Under this organisation, this study sought to promote in pupils an articulation among different content:

Fig. 1
figure 1

ACODESA and activity theory following Engeström’s model (taken from Hitt & Gonzalez-Martin 2015)

Full size image

  • Mathematical. Related to visualization skills (with patterns), the unknown, the variable, co-variation between variables, conversion among representations and modelling,

  • Cognitive. Construction of the sign in an objectification process. Special attention is given to spontaneous representations that usually do not correspond to institutional ones.

Thus, according to the theoretical framework used here, arithmetico-algebraic thinking can be characterised by pupils’ ability to work with:

  1. a)

    Generalisation processes supported by the evolution of spontaneous representation, visualisation and arithmetic calculation. In accordance with ACODESA, pupils change their first approach to the problem during discussions with teammates and the whole class, and consolidate their learning using the two other steps.

  2. b)

    Covariation between variables (e.g., Hitt & González-Martín, 2015; Thompson & Carlson, 2016). The unknown, the variable and covariation between variable concepts are regulated by a task, working first with smaller numbers in a paper and pencil setting in order to begin developing some arithmetic and visual strategies necessary for dealing with larger numbers.

  3. c)

    Generation of expressions that make sense within the context, this can be a mixture of natural language and ideas related to generalisation in a process of objectification when communicating with others.

  4. d)

    Construction of a cognitive control structure, related to: anticipation, verification, sensitivity to contradictions, thoughtful commitment, discernment / informed choice (see Saboya, Bednarz, & Hitt, 2015) that consistently integrates those validation processes that emerged in the group discussions.

  5. e)

    Integration of algebraic knowledge into a reversible process, to enable the possibility of metacognitive processes that promote articulation between algebra and arithmetic. Davis, Jokusch, and McKnight (1978) about pupils’ algebraic performance that rarely considers checking with numbers.

Taking into consideration a careful task design (Prusak, Hershkowits, & Schwarz, 2013) in a paper and pencil environment and technology (as in Hitt & Kieran, 2009), a task was designed with the intention of promoting the construction of a cognitive structure that enables the articulation of arithmetic and algebraic ideas.

5 Revisiting the introduction to algebraic thinking using polygonal numbers in technological environments

Healy and Sutherland (1990) conducted research on an activity involving the calculation of polygonal numbers using EXCEL during the second year of secondary school. The authors report that a couple of pupils formulated the expression: “trig. ∆n = na before + position”. Spontaneous representation linked to an iterative process in an Excel environment. This representation does not reflect an institutional representation. In textbooks, the n th triangular number is usually proposed as \( {T}_n=\frac{n\left(n+1\right)}{2} \).

From a different perspective, Hitt (1994) (on the issue of polygonal numbers) states that, by using solely an Excel environment, pupils could be anchored to the idea of iteration if no other activity is proposed that would provoke them to move on to an alternative.

Researchers took into account the activities studied by Healy and Sutherland (1990) and Hitt (1994) to propose a new task, structured in order to analyse the construction of concepts such as the unknown, the variable and covariation between variables in a process of modelling using ACODESA. In this case, the variables are the position of the Triangular number (TN will hereafter denote a Triangular number) and the number of balls associated to the TN.

The hypothesis posited here is that technology can play a significant role in the way that pupil conjecture can be tested in isolation (at 7th grade level, pupils are not introduced to the concept of proof) and, in this way, can promote an articulation between arithmetic and algebra. This hypothesis states that activities immersed in a technological environment (using Excel and the POLY applet) play a crucial role in this articulation.

The POLY applet is able to give the first six polygonal numbers and a particular polygonal number in numerical and figurative form if screen limitation permits (if not, only a numerical result is given, see Fig. 2).

Fig. 2
figure 2

Screens from the POLY applet

Full size image

6 The experimental setting

6.1 The population

Our idea, in this research, was to test our research hypothesis and the methodological approach with two different populations:

  • 13 pupils in the first grade of secondary school in Quebec, Canada

  • 14 pupils in the third grade of secondary school in Michoacán, Mexico

The activities, as described below, were used with both populations. Although the results for the Mexican population are of interest with regard to visualisation and the methodology used, this paper focuses on the Quebec population on the construction of arithmetico-algebraic thinking.

Two sessions of an hour and fifteen minutes were planned for the Quebec population in accordance with the teachers’ suggestions (each team was allocated one computer with which they were to use Excel and Poly). Three teams were formed with 3 persons and one team with four persons. A process of reconstructing the activity involving triangular and pentagonal numbers was also planned (self-reflexion step in ACODESA), and was to be performed 45 days after the first two sessions. Due to the unexpected result of the experiment, an interview with a pupil was added that related to a special case identified by researchers during the experiment.

The two first activities were filmed with two cameras and each teamwork discussion was recorded. All the handouts were collected at the end of each activity as recommended by ACODESA.

6.2 Activities – overview

  • The pupils were first asked to solve two arithmetic word problems with paper and pencil, after which an Excel solution was discussed. The teacher had used Excel before, and this activity was designed to help the pupils recall the environment.

  • Pupils were then immediately given a short historical introduction to polygonal numbers, followed by five questions on the triangular numbers activity to be resolved using paper and pencil. They then answered some questions in an Excel environment. Finally, they were asked to respond to some questions which had arisen when conjecturing and validating using the POLY applet.

  • Approximately two weeks later, an individual interview (not part of the original organisational plan) was conducted.

  • The final activity involved the reconstruction of triangular numbers 45 days after the first two sessions, along with a challenge undertaken by one of the pupils, which involved pentagonal numbers.

6.3 Activities – specific description

Researcher 1 (hereafter R1) asked pupils to solve the two arithmetic word problems with paper and pencil. R1 then looked at the pupils’ solutions and they were worked out using Excel.

Researcher 2 (hereafter R2) began the activity with a historical introduction to polygonal numbers. The handouts were then distributed, pupils first were asked to begin the task individually, and after to work in teams (in accordance with ACODESA), see Fig. 3.

Fig. 3
figure 3

First five questions of the activity in paper and pencil setting

Full size image

7 Description and interpretation of selected results

Following the ACODESA methodology, this experiment began by requesting individual work followed by teamwork. Three team groups (G1, G2 & G4) presented their results in the general discussion, with team G3 stating that they did the same as one of the other groups.

Figure 4 shows the different strategies proposed by each team. G1 progressed from visual to an arithmetic expression. The strategy followed by G2 is different in that they associated the position of a TN with the number of balls on one side and could thus visually represent “any TN”. When R2 was summarising each strategy, one pupil (denoted as G4-1) went to the blackboard showing an iterative process using “jumps”. In the middle of his explanation, G4-1 changed to another spontaneous notation also related to an iterative process (see Fig. 4).

Fig. 4
figure 4

Representations and strategies used by the three teams (G1, G2 & G4)

Full size image

This confirms the importance of objectification processes in communication among individuals, as identified by Voloshinov, Eco and Radford.

7.1 First step in an objectification process

First step in the process of objectification was made when working in teams and with the whole group (Fig. 4). They progressed from iconic representation to an arithmetic representation involving anticipation, and did not need to develop an iconic representation of the 11th TN to provide an arithmetic representation or an iterative process.

Pupils were immediately asked to return to work in teams, with R2 clarifying the task for G4 (comprising a boy - G4-1, and two girls - G4-2 and G4-3).

R2. Well, here we do not tell you the number of....

G4-1. Is this number related to the diagonal?

G4-2. The number on the side?

G4-1. I take 83 on the side or on the diagonal and then you can count 1, 2, and 3 up to 83.

R2. It’s interesting, you have two different strategies.

From this excerpt, it is clear that G4-2 sees the “position of the TN” on one side, and G4-1 on the diagonal, and associates this with the process involving jumps (see Fig. 5).

Fig. 5
figure 5

Visualising the process and associating it with a process involving jumps

Full size image

G4-1 visualised the series of TNs by adding balls on the diagonal according to the position of the nth TN, and then transformed this process of visualisation by proposing jumps when balls were added on the diagonal.

7.1.1 Second stage teamwork activity involving triangular numbers

As discussed in relation to Fig. 6, G4-1 had visualised each TN, associating the number with the diagonal - a visualization process that allowed him to add that number to the previous TN. When using Excel (see Fig. 6), rather than following the instructions to work horizontally, he wrote the numbers vertically in Excel, constructing the two first lines, and then, copying the formula until line 84. Also, in Fig. 6, we can see that, while the two girls wanted to draw balls to continue calculating TNs, G4-1 tried to persuade them to use a better strategy, which the girls finally agreed to follow.

Fig. 6
figure 6

Teamwork (G4 discussion)

Full size image

R2 made a summary and questioned the whole group on how to calculate any TN. The pupils answered that this was achieved by the calculation 1 plus 2 plus 3 and so on, up to “your number”. R2 asked “but I do not know my number, what can I write at the end of the addition?” G4-1 then proposed that a question mark should be put at the end: “1 + 2 + 3 + … + ?”.

For the pupils, it was natural to put a question mark as the unknown. A girl immediately mentioned that “we” could place a “question mark or a letter”, which provoked the rest of the pupils to mention “x and y”, in response to which the researcher asked “Can I put a heart instead?” The pupils answered that he could use that sign, and that it did not matter.

R2 sought to continue the task in teams using Excel, at the end challenging the children by adding: “I can calculate any triangular number with three operations. Can you?” This was a significant challenge for the pupils, as described below.

A few minutes later, G4-1 informed R1 that they (G4) already had a general strategy to calculate any TN.

On the questionnaire, G4-1 wrote the calculations “(83 + 1) / 2 = 42” and, immediately after, “42 × 83 = 3486” (see Fig. 7). G4-1 then said to take any number, for example the 101st TN, on which R1 interrupted and said that it was better to use the 100th TN. G4-1 replied by stating that it could be any number, describing the calculation 100 plus one divided by two. At this point he stopped, turned to his companions and asked G4-2 whether they thought that a decimal number made sense. R1 told them to discuss it in their team in order to clarify their strategy and verify this conjecture with the POLY applet. R1 noted that this pupil had used Excel to make a table up to the 84th TN.

Fig. 7
figure 7

G4-1 showed R1 what he had achieved using Excel and some operations written on the right-hand side of the questionnaire, later adding what is shown in the middle of Fig. 8

Full size image

7.2 Second step in the objectification process

  • Students proposed to write 1 + 2 + 3 + … + ?, which expressed one plus two plus three “until your triangular number” is reached.

  • G4-1 took the 100th TN as a problem with the process (see Fig. 7). A generic number (83 first, 100 later) is noted on the left hand side of the questionnaire. The letter “x” plays the role of the variable associated with the generic number: “I am dividing by two and later multiplying by an even number, finally obtaining a whole number”.

  • Here we can see some traces of the idea of calculating a TN with “three operations”.

When interviewed two weeks later, the pupil who found this relationship (Fig. 7), mentioned that it came from the POLY applet. However, before this, R1 saw that this pupil had calculated up to the 84th TN with Excel.

Among the pupils that wanted to show what their team has done, G4-1 was asked to approach the blackboard, whereupon he showed his strategy with a generic example, the 46th TN, and mentioned that the strategy worked for any TN, (see Fig. 8).

Fig. 8
figure 8

G4-1 at the blackboard and his teammates verifying his calculations with POLY

Full size image

7.3 Third step in an objectification process

  • Pupil G4-1 showed a generic example to the whole group, and asked his teammates to verify his results with POLY.

    When the bell had rung ending the session and R2 had informed the class that the course had come to an end, a girl asked for R2’s strategy relating to three operations. G4-1 at the blackboard said he knew what the strategy was, on which he was encouraged to write it down. While the pupils began to gather their things in order to go to their next class, he wrote:

7.4 Fourth step in an objectification process

  • The algebraic expression written by G4-1 shows the use of the variable and co-variation between variables.

In accordance with the ACODESA methodology used here, at the end of the class, researchers collected the handouts used by the pupils.

8 Interview with G4-1 (two weeks later of the original lessons)

Due to the unexpected result obtained by G4-1 who had found a general rule using the variables x and y (Fig. 9) while working at the blackboard, he was interviewed two weeks after the original lessons. One part of the interview is presented below:

Fig. 9
figure 9

G4-1’s spontaneous representation in an objectification process

Full size image

R2. What I want to know is how you found it… What was your reasoning?

G4-1. I remember you told me with the number 83, for example.

R2. OK.

G4-1. So there we used the software you gave us on the Mac.

R2. POLY? This gives you the triangular number.

G4-1. Yes, that’s right.

R2. I’ll show you the formula you found: (x + 1) / 2 = y and x . y =

G4-1. Yes that’s right.

R2. Here I would like you to explain how you did this, I do not know what you’ve done. I wish I could figure it out.

G4-1. I started by taking 83. Then I asked POLY to “see” [to show the result on the screen using POLY], and it gave me 3486. Then I tried to [pause] then I tried with 84, not with 85. I asked to “see”, and it gave me 3655. Then I noticed [pause] I did [pause] Yes, it was [pause] I divided that number there, 3486 by 83.

G4-1. 3486 divided by 83, like that. It gave me 42, then I tried to find the ratio of 42 to 83. I noticed that 83 plus 1 gave 84 and 84 divided into 2 gave 42 which multiplied by 83…

They continued to discuss the 100th triangular number.

R2. …what did you think about writing “x” and “y”? Did you use these symbols like this?

G4-1. Yes, my mother showed me algebra and then I thought - I’m going to use algebra to solve [the task].

R2. Ok, and what is algebra, what is algebra, what does that mean?

G4-1. Ben, it is a kind of mathematics - a way to solve any problem. It can be done with algebra - it is not trial and error - we can find anything.

The interview with G4-1 confirms that he found the strategy by applying a reverse process, as shown in Fig. 10 (interpretation of the last answer given by G4-1).

Fig. 10
figure 10

Interpretation of a reverse process applied to the result obtained with Excel and POLY

Full size image

G4-1 seems to have an idea about algebra as some kind of mathematics that can be used to solve “any” problem. G4-1 expresses that “trial and error” is not compatible with algebra.

9 Reconstruction process 45 days after the original lessons

During the process as part of the ACODESA self-reflection stage, pupils were asked to perform a reconstruction of the same activity 45 days after the experiment had taken place. Researchers also added a specific challenge regarding pentagonal numbers (PN hereafter) especially for G4-1.

While pupils were not allowed to use Excel or Poly, they could use a calculator if they wanted.

Three weeks after the interview, G4-1 used an incorrect “formula” when calculating the 11th TN (see Fig. 11).

Fig. 11
figure 11

G4-1’s error when calculating the 11th TN, 45 days after the experiment

Full size image

Related to the pentagonal numbers challenge designed especially for G4-1, he used the strategy involving jumps that had first been constructed 45 days previously, which helped him find the 5th pentagonal number (equal to 35 in Fig. 12), where he realised that +3 needed to be added to the “jump before”.

Fig. 12
figure 12

G4-1 used his strategy involving jumps to calculate the 5th PN

Full size image

Taking into account the result shown in Fig. 12 and, possibly, the fact that the position of every TN played a fundamental role in finding the general rule, G4-1 followed the same strategy by dividing the result of every PN by the position. Although the position was not given, as you can see in Fig. 12, he added it. In Fig. 13, he began directly with the 4th PN, which is 22, and then divided 22 by its position (4), giving 5.5. Again, G4-1 wanted to relate 5.5 to the position, finding the relationship 4 + (4/2 – 0.5), that is Pentagonal number/position = result and result = position + (position/2 – 0.5). Again, by following a reverse process, he found a general formula. What is interesting here is that he named it with the letter “y”: Position * (Position + (Position * 0.5 - 0.5) = pentagonal number. It is clear that he was trying to find something similar to the expressions related to TNs in that he wrote: position * y = Pentagonal number × (Rang × y = nombre pentagonal). This way, he calculated the 34th PN. It is not clear how he realized that he had done something wrong. Returning to his expression, he removed both the letter “y” and the second expression. Finally, he gave the right expression using the position as a variable.

Fig. 13
figure 13

G4-1’s final formula to calculate any PN. Formula: Position × (Position × 0.5 – 0.5)) = pentagonal number

Full size image

9.1 Fifth step in an objectification process

  • The formula obtained in Fig. 13 expresses a spontaneous representation that differs completely from the institutional one: P n  = n (3n – 1) / 2.

Even though G4-1 forgot the formula for TNs, the pupil followed the same strategy for calculating the PNs. It is interesting to note here that although this pupil proposed x and y to give a general formula to calculate any TN, 45 days later, he returned to using “an algebraic representation using words instead of letters”.

10 What was the influence, if any, of the pupil’s presentation to the entire group 45 days previously?

The entire population performed as shown in Table 1. We listed the pupils from 1 to 13 (who were present in the original lessons). We put an arrow showing the change of performance if any of the 8 pupils that were present after 45 days. Only the pupil G4-1 (13 in the table) was asked to resolve the challenge.

Table 1 Results of the experiment (global approach)
Full size table

In general, Table 1 shows that some pupils returned to their initial strategy of drawing balls, which is the case, for example, with pupil 8 (G4-2), the girl discussing her strategy with G4-1. However, others achieved a major advance 45 days after the experiment. A special case is pupil 11 (G3-1), a girl in a team with 3 boys, whose first strategy was to draw balls. During the reconstruction process, she abandoned her strategy of drawing balls changing this for a similar strategy to the one used by G4-1 involving jumps (see Fig. 14).

Fig. 14
figure 14

G3-1’s strategy to calculate the 11th TN. Answer: The 11th triangular number is 66

Full size image

10.1 Sixth step in an objectification process

During the process of individual reconstruction, this pupil (G3-1) not only reconstructed what had been achieved with the strategy involving jumps, but also building a single expression different to the one given by G4-1 (see Fig. 15). This shows considerable evolution from her first experience in class 45 days earlier. It should be mentioned that she could not overcome the problem of division by 2. G3-1 said that her formula functions to odd TNs (see Fig. 15). Indeed, her formula works for any TN, surely, she was avoiding decimal numbers when dividing by 2 the firs term of her formula.

Fig. 15
figure 15

G3-1’s final formula to any odd TN. Formula: (position + 1) ÷ 2 × position = triangular number

Full size image

11 Conclusions

As can be seen, this study opted for a natural approach to building arithmetico–algebraic thinking and avoided the “rupture model” of introducing algebra through the solving of equations as a first approach. Instead, the activity was designed to tackle the notions of the unknown, the variable and covariation between variables in a natural way, through a modelling process. Our aim is to promote in the pupils a construction of a cognitive structure taking into account objectification processes in a sociocultural setting (Eco, 1988, 1992; Radford, 2003; and, Voloshinov 1973). Taking this theoretical approach, researchers paid attention to the spontaneous representations pupils could use when solving a mathematical task (Hitt & González-Martín, 2015). The task was conceived using a methodological approach (ACODESA), paper and pencil, and technology.

Particularly, following the theoretical framework used here, the task design favoured the emergence of spontaneous representations and the construction of a sign in a long process of objectification comprising several steps regulated by both the activity and methodology.

Outlined below is work undertaken by team G4, focusing on both the productions by pupil G4-1 and the overall performance of the group as related to the different steps of the objectification process.

  1. 1.

    Teams G1, G2 and G4 showed different results during a whole group discussion: Drawing balls and the relationship with an arithmetic operation; the abstraction of the drawing and its relationship with an arithmetic operation; and, a strategy involving jumps and associated notation as an iterative process.

  2. 2.

    Question mark used as an unknown, which promoted the use of letters “x” and “y”.

  3. 3.

    Team G4 used the iterative process with Excel and discovered a relationship with calculating “any TN”. Disturbed by the result when calculating the 100th TN, they validated their result using the POLY applet. G4-1 showed a generic example (the 46th TN) of how to calculate any TN.

  4. 4.

    When a girl asked R2 what her strategy was for using 3 operations to calculate any TN, G4-1 wrote a formula (x + 1)/2 = y and x * y = to calculate any TN with three operations.

  5. 5.

    While, during the process of auto-reflection without the use of technology, G4-1 forgot his formula for calculating TNs, on the contrary, he was able to construct a general formula to calculate any PN.

  6. 6.

    The only girl of team G3, under the collaborative work, she obtained the correct formula naming with words the variables and using the jumps strategy and solely one expression “only for the odd triangular numbers”.

It is important to highlight that this entire objectification process is based on an activity developed in a sociocultural setting where communication plays a principal role, and is regulated by careful task design which equilibrates paper and pencil and technology. The results of this experiment with polygonal numbers show the importance of building arithmetic–algebraic thinking, wherein:

  1. a)

    Natural language appears in the formulation of expressions in the process of generalising patterns that are linked to pupils’ production of spontaneous representations.

  2. b)

    The evolution of these representations is framed in an objectification process where communication is essential.

  3. c)

    For this experiment, the teacher/researcher serves as a guide. The difficulties and contradictions that pupils face are discussed and then validated or discarded by them, with technological environments serving to validate their conjectures, as in this experiment.

  4. d)

    The aim of forming arithmetico–algebraic thinking that articulates both arithmetic and also algebraic ideas is much more complex than expected, and meant that experimental questions could not be fully addressed.

  5. e)

    The fact that the most advanced pupil forgot the formula that he had found 45 days previously only confirms what the literature has shown for many years – namely that the knowledge retention process is fragile, and that even advanced pupils are not used to verifying their processes.

  6. f)

    The results in Table 1 shown the importance of promoting the construction of the sign in a sociocultural setting (ACODESA), taking into account the task-design variable to deal with the fragility of knowledge retention.

These results show a way to articulate arithmetic and algebra to promote an arithmetico-algebraic thinking. The results also show the importance of paying attention to the spontaneous representations pupils are able to generate in an objectification process, and, therefore, the importance of equilibrating a task using paper and pencil and technology. The institutional representation of a TN (Tn = n (n + 1) /2) did not appear in the pupil production obtained in this study.

To conclude, this study highlights the importance of creating arithmetico-algebraic thinking as a prelude to algebraic thinking.