An arithmetic-algebraic work space for the promotion of arithmetic and algebraic thinking: triangular numbers

Abstract

This paper presents an experiment that attempts to mobilise an arithmetic-algebraic way of thinking in order to articulate between arithmetic thinking and the early algebraic thinking, which is considered a prelude to algebraic thinking. In the process of building this latter way of thinking, researchers analysed pupils’ spontaneous production using a triangular numbers activity. Based on a specific collaborative learning methodology, this study explores the possibility of constructing an Arithmetic-Algebraic Work Space around the process of constructing signs as framed by both activity theory and a technological approach, showing the spontaneous representations produced by seventh grade pupils and their evolution in a socio-cultural environment.

1 Introduction

The Twentieth Century can be characterised by a didactic approach to pupil error (see Goupille & Thérien, proceedings CIEAEM39 1987) and a perspective that views some errors as consequences of epistemological obstacles (Brousseau 1997). Since then, some researchers have treated the transition from arithmetic to algebra as a cognitive obstacle, promoting a characterisation, on the one hand, of arithmetic thinking (e.g., Verschaffel & De Corte 1996) and algebraic thinking (e.g., Kieran 2007) on the other. In order to move from one type of thinking to another, a cognitive obstacle, a didactic cut, must be surpassed (Filloy & Rojano 1989; Herscovics & Linchevski 1994; Vergnaud 1988). This passage from one type of thinking to another was thus characterised as problematic.

Some researchers have thought that characterising the structure of arithmetic problems and proposing a better approach to problem solving would produce a better approach to teaching and learning algebra. Thus, Vergnaud (1990), with his “theory of conceptual fields”, focused strictly on pupils’ problem-solving performance, with the work of Bednarz and Janvier (1996) also aligned with the same line of thought.

By the early 1990s, an alternative approach had been suggested, with Lee and Wheeler (1989) reporting that “introducing algebra to beginning pupils as ‘generalised arithmetic’ may be a sensible strategy, but there are distinct pedagogical difficulties to be faced if it is adopted” (p. 41). Some years later, two chapters were included in the book “Approaches to Algebra” by Bednarz, Kieran and Lee (Eds. 1996), as part of a discussion of the importance of addressing the generalisation of arithmetic to tackling algebra (Mason 1996; Lee 1996). The clarification in Radford’s analysis (1996) of these two chapters enables a better understanding of a generalisation process:

The above discussion suggests that the algebraic concepts of unknowns and equations appear to be intrinsically bound to the problem-solving approach, and that the concepts of variable and formula appear to be intrinsically bound to the pattern generalization approach. Thus generalization and problem solving approaches appear to be mutual complementary fields in teaching algebra. How can we connect these approaches in the classroom? I think this is an open question. (p. 111)

Following this train of thought, Wille (2008) stresses the important work undertaken in Germany by Malle (1993) with respect to the notion of the variable.

In summary, three trends were emerging at that time:

• 1. Researchers wish to create in pupils a cognitive structure related to stronger mathematical thinking based on problem solving (Carpenter, Ansell, Franke, Fennema & Weisbeck 1993; Vergnaud 1990; Verschaffel, & De Corte 1996). Their work is rooted in a tradition established from the work of Brownell (1942, 1947) onwards that is based on solving arithmetic word problems.

• 2. Researchers focus on the paradigm of the cognitive obstacle related to solving equations (Filloy & Rojano 1989; Herscovics & Linchevski 1994; Kieran 2007; Vergnaud 1988), an approach which leads to a clear distinction between arithmetic and algebraic thinking.

• 3. Researchers opt for an approach around a generalised arithmetic that permits an approach to algebraic thinking (Kaput 1995; Lee & Wheeler 1989; Lee 1996; Mason 1996).

In his seminal work, Kaput (1995, 1998, 2000) proposes a new paradigm consisting of the 5 components that characterise algebraic thinking, stressing the important role of the first two components as the core of this new approach:

• 1. (Kernel) Algebra as generalising and formalising patterns and constraints, especially, but not exclusively, Algebra as Generalised Arithmetic Reasoning and Algebra as Generalised Quantitative Reasoning,

• 2. (Kernel) Algebra as syntactically-guided manipulations of formalisms,

• 3. (Topic-strand) Algebra as the study of structures and systems, abstracted from computations and relations,

• 4. (Topic-strand) Algebra as the study of functions, relations and joint variation,

• 5. (Language aspect) Algebra as a cluster of (a) modelling and (b) Phenomena-controlling languages (2000, p. 3).

This new paradigm emerged in the late Twentieth Century in the United States is characterised by the Early Algebra movement which centred, from a pragmatic point of view, on the algebraic tasks that can be undertaken in an elementary school math class. Given the weight of contemporary research conducted on this approach, perspectives on this subject began to differentiate (see Cai & Knuth 2011). Regarding arithmetic and algebraic thinking, Radford (2011, p. 304) states that “…the idea of introducing algebra in the early years remains clouded by the lack of clear distinction between what is arithmetic and what is algebraic”. On the other hand, Lins and Kaput (2004), as spokesmen for the Early Algebra group, characterise their movement as:

Early algebra is that an algebrafied elementary mathematics would empower students, particularly by fostering a greater degree of generality in their thinking and an increased ability to communicate that generality. (p. 58)

As part of an ICME working group (2004), these researchers began to oppose other researchers by saying that, in the past, “sad stories” were told about pupil performance (centred on error analysis and cognitive obstacles). They go on to say that we can now speak of “happy stories” by presenting the results of what primary school pupils are able to achieve (e.g., Carpenter & Franke 2001; Blanton & Kaput 2011; Britt & Irwin 2011; Schliemann, Carraher & Brizuela 2012), and these results demonstrate the boundless enthusiasm of this group. Carpenter et al. (1993) report that pupils are capable of solving complex word problems. However, research by the Early Algebra Group that followed the learning path to functions (Schliemann, Carraher & Brizuela 2012) show some precipitation by introducing algebraic notation in elementary school in order to develop mathematical content. They conclude: “The 5th grade lessons focused on algebraic notation for representing word problems, leading to linear equations with a single variable or with variables on both sides of the equal sign” (p. 115). Thus, researchers such as Cooper and Warren (2011) argue that:

The results have shown the negative effect of closure on generalisation in symbolic representations, the predominance of single variance generalisation over covariant generalisation in tabular representations, and the reduced ability to readily identify commonalities and relationships in enactive and iconic representations. (p. 187)

The position taken by this study is different from that described above. Instead of separating arithmetic from algebraic thinking and focusing on that which distinguishes them, this study proposes the construction of a cognitive structure that enables an articulation between these two kinds of thinking. For example, knowing that pattern-related generalised thinking has proven fruitful in elementary school (Radford 2011), this study relies on generalised arithmetic. This acts as a driver for the construction of the sign that is specific to mathematical thinking, and can help in the construction of algebraic thinking. This study proposes the development of a type of thinking, named here as arithmetic-algebraic thinking.

Eco (1992) argues that it is the process of constructing the sign that matters, not the sign per se. In terms of learning mathematics, Radford’s theoretical approach (2003) proposes the process of objectification in the construction of the sign. This process specifies the concept of the “semiotic means of objectification” and gives importance to the manipulation of objects, drawings, gestures, and the use of linguistic categories, analogies, metaphors, etc. as a part of the objectification process.

From this perspective, and taking into account the notion of Mathematical Work Space (MWS) proposed by Kuzniak (2011), this study seeks to stress the importance of characterising what could be called arithmetic-algebraic thinking (A-AT). This may shed light on the arithmetic process, as well as the visual-arithmetic, visual-algebraic, and purely algebraic approaches and, most important here, their interactions. Taking a socio-cultural approach to learning mathematics (Hitt 2013), this study proposes an analysis of 7th grade pupils’ production in an A-AWS when solving a mathematical task.

From this new perspective, this study seeks to explore the possibility of building a cognitive structure that allows the articulation between arithmetic and algebra. This articulation should enable naturalistic actions related to arithmetic and visual-arithmetic processes, their transformation into algebra, and vice versa. The choice explored here is thus based on a natural approach, rather than a “cut” or “cognitive obstacle” approach, as has been the case in the past.

This study uses paper and pencil (Saboya, Bednardz & Hitt 2015; Hitt & González-Martín 2015), follows task design (Prusak, Hershkowits & Schwarz 2013), and takes a technological approach to the task (see Hitt & Kieran 2009). It therefore, makes equal use of paper/pencil and technology.

2 The use of MWS as a frame to organise the construction of arithmetic-algebraic thinking (A-AT) in an A-AWS

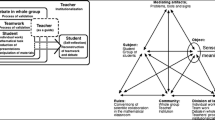
Since Kuzniak presented his theoretical foundations for the building of an MWS in 2011, his model has been evolving over time, and has been applied to subjects other than geometry. This study focuses on both the construction of the sign and functional representations (Hitt 2013) in both mathematical activity and the construction of an A-AT. Researchers chose an approach that, rather than trying to impose the sign as in Carraher et al. (2006) and Schliemann et al. (2012), focuses on building a rich cognitive structure (A-AT) which intersects broadly with arithmetic and algebraic thinking (see Fig. 1). From a classical point of view, it would be possible to have two cognitive planes, one related to arithmetic thinking and the other to algebraic thinking, and, in general, focus on one learning direction—from arithmetic to algebra. The hypothetical cognitive plane in this study demands an articulation between arithmetic and algebraic thinking (see Fig. 1). Moreover, this approach uses Duval’s concept of visualisation (2003):

Fig. 1

The A-AWS after the adaptation of Kuzniak’s model (2011)

Visualize is to produce a representation that, in the absence of any visual perception of the objects, allows to look as if they were really in front of your eyes… (p. 49).

This adaptation of Kuzniak’s model (2011) takes the following into consideration:

• A semiotic genesis related to visualisation and the production of representations;

• An instrumental genesis related to the constructions determined by the instruments used (paper, pencil, Excel, the Poly applet, etc.);

• A discursive genesis determined by the pupils’ anticipations, verifications, error perceptions, sensibility to contradictions, reflected commitment, and a clear strategic choice (discernment).

Previous studies (Saboya 2010; Saboya et al. 2015) focused on those aspects mentioned in the third part of the previous paragraph, regarding what is known as cognitive control when related to validation processes.

The structure of the A-AWS enables an analysis of pupils’ production and provides an explanation of progress made in building an A-AT. Thus, in the 1st stage of the experiment, semiotic genesis occurs based on visual and numerical representations (construction of operational schemas related to the representations) in a pencil and paper environment. It is in the 2nd stage where the processes of instrumental genesis (construction of schemas related to the work with Excel, Poly, and paper and pencil environments) is able to help with the activity of generalization and the connection to early algebraic thinking linked to the notion of the variable (unknown) and the possibility of constructing algebraic expressions, again under the process of objectification that does not necessarily produce institutional algebraic representations. According to the A-AWS model in the context of this collaborative learning project, discursive genesis related to validation (pupils at this school level do not know about proof) is mainly promoted via team members and large group discussions.

Another important aspect is that, in this research, pencil/paper and technological artefacts are essential (Excel and the Poly applet), as the use of these artefacts strongly depend on the development of activities that include technology. The notions of institutional representation and functional representation are introduced here. These are concepts which, at first glance, could be confused with the “idoine ETG” (Appropriate Geometrical Working Space, or GWS) and “personnel ETG” (personal GWS) notions proposed by Houdement and Kuzniak (2006), but are in fact very different (see below).

Kuzniak (2011) refers to Duval’s theoretical framework on the notion of the register of representation, which gives priority to institutional representations (Hitt 2006). In this document, one of ours goals is to show the importance of the spontaneous representations in the mathematical activity. Spontaneous representations are not necessarily institutional representations, and may not belong to a register. Therefore, under this approach, the work carried out by a pupil or group of pupils based on spontaneous representations could be set aside as unimportant.

This paper seeks to present an alternative approach based on the role of spontaneous and institutional representations as defined by Hitt (2013):

• Institutional representation: “representations found in textbooks or on computer screens, etc.” (p. 10)

• Functional representation: “… mental representation that emerges when facing a non-routine mathematical activity, which is expressed by a representation [spontaneously] linked to action.” (p. 13)

This study posits that non-institutional representations emerge naturally in the process of solving a complex mathematical task. Thus, researchers sought to follow the path through which pupils use icons, arguments, and arithmetic representations mixed with algebraic representations in the process of building the sign-function before arriving at the symbols in one or more register of representations—the construction of the sign in a process of objectification, as in Radford’s (2011) work.

Another aspect of our research, as noted above, is related to the use of technology. In this sense, in the MWS, artefacts and the notion of instrumental genesis are taken into account (Kuzniak 2011, p. 21) in the design of the task (Hitt & Kieran 2009; Prusak et al. 2013). Finally, as the study is also interested in the problem of the fragility of knowledge (Thompson 2002; Karsenty 2003) in the construction of mathematical thinking, researchers considered it important to use a collaborative learning-teaching methodology named ACODESA (Hitt 2013; Hitt & González-Martín 2015) with the intention of enhancing the knowledge built into the resolution of these activities.

3 Research questions

The general research question for this study is how to develop a cognitive A-AT structure as an articulation between arithmetic thinking (AT) and algebraic thinking (AT). More specifically, the study looks at promoting another view about the transition from arithmetic to algebra and to ascertain the contribution of technology to the development of A-AT structure. As an intermediate goal, we are promoting spontaneous representations that will support the transition from visual to the construction of the sign related to generalization and algebraic representations that permit pupils to calculate any triangular number and any pentagonal number.

4 Methodology

The methodological approach employed in this study is based on activity theory (see Hitt 2013; Hitt & González-Martín 2015), which integrates such aspects of a mathematics class as collaborative learning, debate and self-reflection (ACODESA). The methodology is comprised of 5 stages:

• 1. Individual work. Individual work initially aims to provide pupils with the opportunity to represent the problem or problem situation themselves, on an individual basis, before moving on to the team discussion (see Fig. 2). The functional representations (most likely unrelated to the institutional representations) often appear at this stage, and, through them, pupils produce an external representation that allows them to take action.

  Fig. 2

  

  ACODESA based on Engeström’s activity theory model

• 2. Teamwork. The interaction between pupils has the purpose of enriching the individual approach developed in the first stage. Usually, it is here where the process of validation begins (Fig. 2), as does the work of refining the functional representations in a process of communication which must be materialized in the productions of institutional representations via this process of communication.

• 3. Debate (with the possibility of promoting scientific debate). The results achieved by different teams are weighed and discussed by these teams in order to arrive at conviction and consensus. Again, a non-institutional representation refinement process appears regularly at this stage. It is common for pupils to express their agreement during a large group discussion.

• 4. Self-reflection. The individual reconstruction of knowledge that emerged in team and large group discussion is an essential step in the promotion of abstraction in the pupils. Researchers took into account the fact that, as consensus in mathematics class can be ephemeral for some pupils, it is therefore important to return and rebuild what had been undertaken in class.

• 5. Institutionalisation of knowledge. At this point, the teacher summarizes what the pupils have produced and oversees the efficient use of institutional representations (see Fig. 2).

This methodology was applied to two populations (this paper is restricted to the Quebec population):

• A. In Quebec, with 13 pupils from the 7th grade at secondary school. Two researchers conducted the experiment, and

• B. In Mexico, with 14 pupils from the 9th grade at secondary school. The teacher and a researcher conducted the experiment.

From the Quebec population, only 13 pupils agreed to participate in the experiment, which comprised two sessions in an extra class (2 and a half hours), an interview and one session dealing with individual reconstruction (for 1 h, 45 days after the experiment). The pupils knew how to use Excel. In the first session, an introduction to Excel related to the resolution of two word-based arithmetic problems was planned. One of the researchers conducted the presentation, and the other filmed it, while, in the second part of the experiment, the researchers swapped roles. Only one computer was permitted to be used by each team.

5 A priori analysis

In the past, research was conducted on activities dealing with polygonal numbers in technological environments at different levels in secondary schools, and with teachers. Healy and Sutherland (1990), in a technological approach activity related to Excel and polygonal numbers, report 7th grade pupils’ production related to the expression “trig. Δn = na before + position”, and explain that, in order to find a triangular number, one simply has to add their position to the previous triangular number. This production can be classified as a spontaneous representation that emerges from a nonordinary activity. Hitt (1994) criticises this approach, saying that pupils will not “move” to algebra if they remain in a purely technological environment such as Excel. In both studies, a tendency to move as quickly as possible to the algebraic representations can be observed.

This study focuses on the mathematical task, as defined by Prusak et al. (2013) and Hitt and Kieran (2009), that prioritises a sociocultural approach to the co-construction of knowledge, the production of functional representations, and external production (spontaneous representation) associated with the task.

The experiment conducted in Quebec (for the Mexican experiment, see Cortés, Hitt & Saboya 2014) presented two preliminary word problems—first in a paper–pencil environment, and then using Excel, in order to familiarise pupils with the use of the program. The second part of the experiment consists of the main activity with triangular numbers, beginning with a brief history to present the origin of polygonal numbers. The five first questions were designed to promote the development of spontaneous representations by the pupils and the evolution, through collaborative work, into institutional representations related to triangular numbers, for example T _n  = n(n + 1)/2. At the time of the experiment, the pupils had not yet discussed with their teacher the chapter on generalisation activities based on number series. The following section focuses on the analysis of the second part of the activity, which is related to triangular numbers.

6 Presentation of the activity

After a brief explanation of the discovery of polygonal numbers, a triangular numbers activity was suggested to the pupils, first with paper and pencil (see Fig. 3), in accordance with the ACODESA methodology (Fig. 2), and then, using technology (see Figs. 4, 5).

Fig. 3

The first five questions about the activity (paper and pencil)

Fig. 4

Teamwork task for using technology

Fig. 5

Task for teamwork using paper/pencil and technology (optional)

7 A posteriori analysis (Quebec population)

7.1 Individual work (step 1 ACODESA)

As mentioned in the previous section, before pupils completed this activity, two verbal problems were presented in the pencil/paper and Excel environment. The purpose of this first step was to remind pupils how to use Excel (researcher R₁). By the beginning of the second part of the activity, the pupils were already well familiar with the Excel environment. To solve the first two problems (see Fig. 3), researcher R₂ asked pupils to work individually using paper and pencil. Figure 6 shows an example of the work of a pupil who demonstrates and explains how she proceeded to find the fifth triangular number (Question 1, see Fig. 3).

Fig. 6

Individual work, visual representation of “T₅ = 15”

It can be seen that the pupil lacks cognitive control (Saboya 2010; Saboya et al. 2015) over the passage from an institutional representation to the visual production of T₅. Indeed, in the representation of it, each of the three columns from the center is represented by four “rounds” (in the pupil’s own words) when they should be constituted, respectively, by four, three, two and one “round”. However, the pupil’s verbal representation explains a general procedure, giving a generic explanation referring to any triangular number (an example of early algebraic thinking). Furthermore, there is a mismatch between the procedure related to natural language and the action when drawing the representation, this lack of control over figural representations was present in others copies.

At this stage, this pupil (as well than others) has not constructed a cognitive structure that would enable him/her to articulate the different representations related to the task, or to use the arithmetic approach as a temporary cognitive structure and as a step to construct an algebraic approach to the situation.

Three aspects, then, are noteworthy for the construction of A-AT (Arithmetic-Algebraic Thinking), which this study seeks to promote:

• (a) An evolution of his/her spontaneous representations to the institutional representations, taking into account a learning approach in a socio-cultural milieu.

• (b) Development of a cognitive control schema, as described in the theoretical section, based on the mathematical visualisation process and the discovery of relationships between numbers associated with each triangular number.

• (c) A generalisation process. The task design of the activity was intended to promote different kinds of generalisations: visual, verbal, arithmetic, and algebraic, and most importantly, the articulations among them.

The first question (see Fig. 3) sought to force pupils to undertake a task analysis from a visual perspective and to undertake a figural production, that is, to continue the series that began with the first four triangular numbers that were presented. However, the intention behind asking them to build T₁₁ (the 11th triangular number, see Fig. 3, Question 3) was to provoke a change in the register of representation. The idea is that pupils should not continue to draw; instead, they should change the register in order to consider generalisation in an arithmetic or algebraic register, or with their own spontaneous representations. The spontaneous pupil representations obtained were surprising. With regard to the second stage of the methodology, pupils were placed in teams, and there were four teams in total. The pupils’ productions on the blackboard are presented below. The G3 group reported that they made similar representations to the G1 group.

7.2 First case: group 1 (G1)

To calculate T₁₁, the G1 group used their iconic representations for the first three triangular numbers and, in a semiotic genesis, they switched to the arithmetic register. This approach can be classified as a visual arithmetic promoted by a semiotic genesis (see the A-AWS model in Fig. 1). In the given arithmetic expression, we can see that the pupils were visualizing a relationship between each triangular number, which is bound to increase by one (“the number of balls”) in the vertical column or horizontal row from the previous triangular number (Fig. 7).

Fig. 7

Visualisation process and arithmetic production

7.3 Second case: group 2 (G2)

In this group (G2), a double abstraction process was put in place based on a visual-arithmetic strategy (Fig. 8). There is “one generic abstract triangle” that is applicable to “any triangular number” (semiotic genesis, following the A-AWS model). The construction of the previous triangles has not been used in this strategy. Researchers began with the number related to the side of the triangle associated with the requested triangular number and then decreased by one each time, thus generating an arithmetic expression.

Fig. 8

Visual process, abstraction and arithmetic production

7.4 Third case: group 4 (G4)

A pupil in the G4 group (to whom we refer as pupil G4-1) said that the representation on the left-hand side was produced in his group (Fig. 9). While giving his explanation, he suddenly changed his approach, presenting a more convenient notation based on a process of iteration. In fact, this pupil produced a visualisation process and a transformation of the sign-function, in accordance with Voloshinov (1973), Eco (1992) and Radford (2003). Moreover, if we take these two representations into account, one next to the other, we are faced with a non-institutional spontaneous representation, as described by Hitt (2006).

Fig. 9

Visualisation process, visual production and symbolic notation related to an iterative processs

Once T₁₁ was found, the researcher (R₂) asked all the pupils to explain how to calculate T₈₃ (Fig. 10).

Fig. 10

Construction of sign in a communication process in the mathematics classroom

In this dialogue, we believe that the intervention of R₂ is fundamental. Pupils with a strategy that can work to calculate any triangular number were asked to designate “until your number.” The “question mark” seems natural for pupils. R₂ then asked if everyone agreed, a question which led pupils to propose the use of the letter “x” and then “y”. The researcher finally asked if she can use a heart (see Fig. 11). It should be noted that these pupils had used an empty box to denote missing terms in equalities in primary school. At the end of his speech, R₂ asked pupils how to write the “penultimate number” and “before the penultimate number”. Pupils then selected the question mark as a symbol and declared “question mark minus one” and “question mark minus two” (Fig. 11).

Fig. 11

Different stages in a sociocultural learning environment in the construction of a symbol

At this early stage of the experiment, it can be seen that classroom communication is promoting semiotic genesis (see Fig. 1) and visualisation processes. Moreover, communication in the mathematics classroom promoted the evolution of the pupils’ spontaneous representations in a process of meaning as described by Radford (ibid.). As mentioned above, the work conducted so far is based on pencil and paper.

Subsequently, R₂ announced that she is able to calculate any triangular number by carrying out three operations:

[…] I tell you that in three shots, I give you your number. Whatever number you want, in three operations I can find it for you…

This assertion, as we shall see, challenged the pupils. They returned to work individually and in teams (following ACODESA), but this time using technology.

In our methodology, collaborative work is very important. The evolution of the functional representations related to spontaneous representations and their products follow a natural path with institutional representations not imposed by the teacher. This approach shows that following ACODESA (see Fig. 2) promotes the construction of signs through semiotic, instrumental and discursive genesis in accordance with Kuzniak (2011) and Voloshinov (1973), in a process linked to Eco’s notion of sign-function (1992) and Radford’s (2003) process of meaning. As noted above, pupil G4-1 convinced the two girls on his team to drop their drawing process and move to a more efficient representation. There was a “consensus” within the team, even if the girls had difficulties articulating the visual with the iterative process (see Fig. 12).

Fig. 12

Lack of control over the drawing process, but effective use of the iterative process proposed by one G4 team member

This research focuses on building a stable consensus that should be converted into knowledge. According to Thompson (2002) and Hitt and González-Martín (2015), the consensus is ephemeral for some pupils, a point to which this paper will return.

7.5 Teamwork—second and third stage of the activity with technology

During the resolution of this second stage of the activity, a G4 pupil asked R₁ whether to wait for the group to continue, as his team were further ahead in their reflections (see Fig. 13). In response, R₁ encouraged him to continue with the third part of the activity (see Fig. 5).

Fig. 13

Teamwork and “consensus” about the “jumps” and its transformations with Excel

A few minutes later, the pupil completed his questionnaire with an arithmetic approach (see Fig. 14). This relates to the calculation of T₈₃: adding 1 to 83, dividing by 2 and multiplying the result by 83 to get 3486.

Fig. 14

Production by reading from right to left: a generic example to find any triangular number

Several minutes later, pupil G4-1 said he found a strategy and described the strategy by giving an example, T₁₀₁ (a “generic example” as described by Balacheff 1987), which he obtained by adding 1 to 101, dividing the sum by 2 and multiplying the result by 101. R₁ told him to try his strategy with T₁₀₀, to which the pupil replied: “Whatever you want!” Then he added 1 to 100 and divided the sum by 2. The pupil stopped suddenly, saying: “Oh, we arrive at a ‘decimal number’!” He then headed towards a girl (a team member) and asked, “Does it make sense with a decimal number?” R₁ then asked them to discuss this whole strategy and to check using POLY. It was after this discussion that pupil G4-1 added the part on the left-hand side of Fig. 14. The steps produced by the pupil in order to calculate T₁₀₀ can be observed, where he added 1 to 100, divided the sum by 2, and designated the result as “x”, which was then subsequently multiplied by 100 in order to find T₁₀₀. This last expression is the product of the three-fold genesis, according to the A-AWS model.

When R₁ asked the pupil to find T₁₀₀, he reached a decimal result (100 + 1)/2 and stopped, thinking that something was wrong. Subsequently, pupils used Poly to check his conjecture and realized that his strategy had worked (Fig. 15).

Fig. 15

Examples of the use of the Poly applet (Cortés & Hitt 2012) with triangular numbers

7.6 Large group discussion

This point in the activity took place just minutes before the end of the period allotted for the experimentation. R₂ then began a large group discussion and pointed to pupil G4-1, who raised his hand to indicate his desire to approach the blackboard (Fig. 16).

Fig. 16

Explanation to the group on how to calculate “any triangular number”

When the pupil was at the blackboard, he chose T₄₆ and found the result. He was convinced that his strategy worked. When R₂ asked him to explain how he found the algorithm, he mentioned that it was with T₈₃ and T₈₄ (results he found using Excel). He did not specify to the other pupils in the large discussion group that he had checked his conjecture using Poly. Fifteen days later, in a separate interview, the boy said that it was the Poly applet that enabled him to find the relationship.

In summary, we can say the following:

• The pupil, using a semiotic, instrumental and discursive genesis, found an arithmetic relationship with Excel,

• The pupil was motivated to seek a relationship between a triangular number and its term (which G4-1 mentioned in an interview). When G4-1 divided T₈₃ = 3486 by 83, he obtained 42, and realised that the result was half of 84. Surprisingly, in a reverse process, he arrived at (83 + 1)/2 = 42 and 42 × 83 = 3486 = T₈₃. We can say that the pupil has articulated arithmetic, with early algebra promoting a process of thinking (A-AT) in accordance with our model (Fig. 1).

• From this expression (generic example), the pupil mentioned that he had a strategy to compute “any” triangular number (odd triangular numbers).

• R₁ asked the pupil to calculate T₁₀₀. The pupil was surprised when he obtained a decimal number when he divided the sum of 100 and 1 by two.

• The pupil used the Poly applet to verify their conjecture. The instrumental and discursive genesis promoted validation processes.

• The pupil wrote in his copy of the questionnaire: (100 + 1) ÷ 2 = x and x × 100 = (see Fig. 14). In the interview, the pupil said that obtaining a decimal number bothered him.

7.7 The bell rang when R₂ was engaged in the large group discussion

It can be seen that the pupils’ curiosity was piqued when the researcher mentioned the possibility of calculating any triangular number with only three operations, about which they wanted to know more when the session finished. At this very moment, G4-1 spoke to the whole group on how to calculate any triangular number (Fig. 17) using various symbols, which demonstrated fluency regarding the notion of the variable. From the theoretical approach, this showed a final process of an A-AT related to the model.

Fig. 17

Construction of an algebraic representation through a communication process related to the calculation of any triangular number

7.8 Step 4: self-reflection

Before the self-reflection stage, it was decided to conduct an interview with G4-1 (15 days after the experiment) to better understand how he had been able to calculate any triangular number. Then, 45 days after the experiment, a further challenge was made to him: the calculation of any pentagonal number (see “Appendix”).

Eight of the thirteen pupils who worked on the experiment were present at the self-reflection stage.

• (a) Two pupils (one from the G4 team) used the dot pattern to answer questions (see Fig. 18), forgetting what was established in the “consensus”.

  Fig. 18

  

  An ephemeral consensus for some pupils after 45 days

• (b) Five pupils used an arithmetic addition approach and jumps. It should be noted that those pupils have appropriated G4-1’s strategy. One of the pupils even used: The sum of the previous figure + the triangular number [position] (similar to the result found by Healy & Sutherland). In addition, a pupil from another team wrote the expression: (rank + 1) ÷ 2 × row = triangular number. Moreover, she added that the formula can only be used for the odd triangular numbers. This result is, in the opinion of researchers, the product of working in a socio-cultural environment. It can be seen that this pupil retained the result for 6 weeks and, after a process of self-reflection (commognition, according to Sfard 2008), she was able to rebuild and improve the results detailed in the large group discussion (see Fig. 19).

  Fig. 19

  

  Individual work in the first stage (gauche) and self-reflection (reconstruction) stage 45 days later (the intermediate stages of his work as related to collaborative learning)

• (c) While pupil G4-1 gave the wrong result for T₁₁ by using the incorrect formula, his spontaneous expression was correct for the challenge related to pentagonal numbers.

To calculate the pentagonal number 34 (see “Appendix”), G4-1 wrote as shown in Fig. 20.

Fig. 20

G4-1’s production from the pentagonal numbers activity

Figure 20 shows how G4-1 managed to find a general expression for calculating any pentagonal number (see “Appendix”). Taking into account the examples, the pupils arrived at P₄ = 22, then P₄/4 = 5.5. So, position + (position/0.5 − 1.5) = 5.5. The pupil checked other examples and calculated P₅ = 35 to check his procedure (a validation process without technology). First, G4-1 wrote (probably following the strategy used on the blackboard):

$$rang*(rang + (rang * 0.5 - 0.5)) \; = \;y,\;{\text{and}}\;rang*y \; = \; nombre \, pentagonal.$$

After crossing out one part (see Fig. 20), which we do not know the reason behind his actions, he finally gave a correct expression.

The process of self-reflection is an important phase in ACODESA. On the one hand, we can see that some pupils went back to their initial position and, indeed, returned to the process of drawing balls to respond to questions rather than using a more elaborate strategy. On the other hand, there were more pupils who adopted the strategy that used jumps to calculate the requested triangular numbers.

In summary, the results of the experiment in the self-reflection phase show the following:

• Consensus is ephemeral. After 45 days some pupils returned to their initial strategy;

• Pupil’s knowledge is fragile (pupil G4-1 wrote a formula for triangular numbers which he “remembered” but had not checked and therefore did not realize it was wrong);

• Pupils learn to structure their actions (a habitus) as described by Bourdieu (1980); and

• Researchers found that the pupils’ representations are far from the institutional representations as taught in a classic lecture-style maths class.

8 Conclusions

The Early Algebra movement has generated two trends—one which is related to the construction of a path that could lead pupils to algebra as quickly as possible, and the other which enables a better understanding of this different kind of thinking. This study sought to present another trend, a new discussion-based approach centred on “strengthening the intersection between arithmetic and algebra”, proposing that the following must be taken into account for A-AT and also the A-AWS:

• I. Semiotic and instrumental genesis related to the production of representations:

  • Pattern-recognition,

  • Visualisation associated with an arithmetic algorithm or an arithmetic–geometric process,

  • Visualisation of a general arithmetic-algebraic algorithm.

• II. Instrumental and discursive genesis:

  • Activities with technology (e.g. Excel and applets) to promote conjecture and validation processes.

• III. Discursive and semiotic genesis:

  • Activities that promote validation processes in a paper and pencil environment.

• IV. Cognitive control structure related to an A-AWS model:

  • The activity should be presented so that pupils’ conjecture can be corroborated, while teachers must take into account the cognitive process mentioned in this document that relates to anticipation, verifications, error perceptions, sensibility to contradictions and validation.

  • Arithmetic as a permanent feedback environment. It is thus necessary to promote a reversible process between algebra and arithmetic.

This is a limited study whose results are restricted to triangular and polygonal numbers with a small group of pupils from Quebec (for the Mexican experiment, which is still in process, see Cortés, Hitt and Saboya 2014). Literature shows that the patterns are important for use in the mathematics classroom to promote generalization processes, as highlighted by both Mason (1996) and Lee (1996). It would be useful, at this point, to consider how these research results can be used to generate large-scale arithmetic-algebraic thinking and to build a cognitive structure linked to a mathematical control activity in which the use of technology could play a key role in promoting conjecture and validation.

Finally, the approach presented in this paper seeks to enable pupils to take ownership of the concept of building symbolism before constructing the notion of indeterminate or unknown parameters, thus generalising mathematics and, at the same time, developing a control structure (Saboya 2010) for the mathematical activity involved, and helping to develop sensitivity to a contradiction when solving a mathematical task. Significantly, this study also suggests the fragility of knowledge, with its results showing that, while there was progress in some pupils, in others there was a setback 45 days after the experiment. These results pose the question as to how to promote the strongest consensus.

Appendix: Pentagonal numbers