1 Introduction

In this paper, we present a cognitive analysis of the relationship between the argumentation process leading to the construction of a conjecture and its algebraic proof. Specifically, this analysis aims to fill the gap for the case when the argumentation process is inductive and is constructed in the field of arithmetic and the proof is deductive and in the algebraic domain. Theoretically, this type of relationship would pose students two sources of potential difficulties: the shift from using arithmetic in the argumentation to using algebra in the proof and the shift from an inductive argument towards a deductive proof. Thus, the aim of this article is to empirically examine such a relationship by studying students’ resolution process including difficulties that emerge while solving each one of three Calendar Algebra problems (Martinez, 2011). These problems were intended to promote the construction of conjectures studying regularities in the calendar and its corresponding proof.

In addition, since we look at students solving a sequence of three related problems, we compare the corresponding argumentations across the three problems paying attention to potential changes in the nature of the argument (e.g., type of warrant, type of backing, etc.).

Consequently, in this report, our overarching research questions are:

  • (1) To what extent does the cognitive distance between inductive arithmetic argumentation and deductive algebraic proof become a challenge for students in the construction of a proof?

  • (2) How do students learn to overcome this distance during the solutions of the three problems?

Methodologically, we compare students’ problem solving process corresponding to three problems presented in the first four lessons of a teaching experiment. The analysis and comparison between these three resolution processes is performed using Toulmin’s model.

2 Relationship between argumentation and proof

The relationship between argumentation and proof is complex as reported in previous studies. Some researchers highlighted the epistemological (Balacheff, 1988) and cognitive (Duval, 1995) distance between argumentation and proof. In contrast, researchers in the Italian tradition focused on the continuity, called cognitive unity, that exists between argumentation, as a process of production of statements, and the construction of its proof (Boero, Garuti, & Mariotti, 1996; Garuti, Boero, & Lemut, 1998). Trying to clarify these different research results, Pedemonte (2007) pointed out that in general, the comparison between argumentation and proof should be carried out considering two complementary dimensions: the referential system and the structure.

The referential system includes the representational system (e.g., language, heuristics, drawing etc.) and the knowledge system (conceptions, theorems) of argumentation and proof (Pedemonte, 2005). For example, there is continuity between argumentation and proof in the referential system (or cognitive unity) if some words, drawing and theorems used in the proof have been used in the argumentation process. On the contrary, for instance, if argumentation and proof are constructed using elements from different mathematical domains (e.g., arithmetic in the argumentation and algebra in the proof), then there is discontinuity between argumentation and proof taking into account the referential system.

The structure of either the argumentation or the proof is the logical cognitive connection between statements (i.e., abduction, induction or deduction). It is relevant to include the notion of structural continuity/discontinuity between argumentation and proof since it has the potential to explain some of students’ difficulties when constructing a proof. As highlighted in previously reported results (Pedemonte, 2007), when solving open geometrical problems, students are often unable to construct a proof because they are not able to transform the abductive structure of the argumentation into the deductive structure of the proof (e.g., some students often construct an “abductive proof” if they have previously produced an abductive argumentation). This happened even in the case of continuity in the referential system between argumentation and proof, that is to say, when all “elements” necessary to construct a proof are present (Pedemonte, 2007).

However, according to Pedemonte (2008), the structural continuity/discontinuity between argumentation and proof does not always pose a challenge for students. Indeed, in solving open problems requiring the construction of an algebraic proof, it seems that even if students produce abductive steps in the argumentation phase, they do not use them in the proof because the deductive structure is very strong inside an algebraic proof. In this specific case, it seems that the abductive steps in the argumentation can be useful for the construction of proof because they can favour continuity between argumentation and proof in the referential system (Pedemonte, 2008).

Some other studies in geometry (Pedemonte, 2007) analyzed the relationship between inductive argumentation and mathematical induction. The results of this study showed that the construction of the mathematical induction strongly depended on the kind of generalisation used in the inductive argumentation. Students constructed mathematical induction only when they were able to generalize the process leading to the solution of the problem in inductive argumentation.

Given that this research program calls for attention to both structure and referential system, it is essential to study the case in which the argumentation is inductive in arithmetic and the proof is deductive in algebra in order to have an exhaustive empirical examination of this relationship. In particular, we would like to investigate if it is possible to extend research results obtained comparing inductive argumentation and mathematical induction when the comparison is made between inductive argumentation and deductive proof. Even if we already know there is a structural distance between inductive argumentation and deductive proof (that can probably be considered as a difficulty for the construction of the proof), we want to analyze if the cognitive distance between them depends on the kind of generalisation used. We need to do this study because some unexpected results could be found; we have seen that research results obtained in geometry do not necessary correspond to research results obtained in algebra. In fact, because deductive structure in algebra is strong, it could be that structural distance between argumentation and proof is not a challenge for students. In the next section, we describe the tool of our analysis–Toulmin’s model–and how we can accomplish this analysis from the referential system and the structural points of view.

2.1 Toulmin’s model

Toulmin’s (1958/1993) model has been used by several researchers in mathematics education (e.g., Hollebrands, Conner, & Smith, 2010; Inglis, Mejia-Ramos, & Simpson, 2007; Knipping, 2008; Lavy, 2006; Stephan & Rasmussen, 2002) to examine students’ mathematical arguments. In this report, Toulmin’s model is used to analyze argumentation and proof from a cognitive point of view.

The comparison between argumentation supporting a conjecture and its proof is based on the hypothesis that proof can be considered as a specific kind of argumentation in mathematics (Pedemonte, 2005, 2007). For this reason, we use Toulmin’s (1958/1993) model to identify and analyze the argumentation process that supports the production of conjectures and proofs. In this model, both argumentation and proof can be represented and compared from the structural point of view and from the referential point of view.

In Toulmin’s (1958/1993) model, an argument is represented by an assertion referred to as the claim (C) and data (D) supporting the claim and by a warrant (W) that provides the justification for using the data conceived as a support for the data–claim relationships. The warrant, which can be expressed by a principle, or a rule, acts as a bridge between the data and the claim.

Three other elements may be necessary to describe an argument: qualifier, rebuttal, and backing (Toulmin, 1958/1993). The qualifier (Q) represents the strength, the soundness of an argument. The force of the warrant would be weakened if there were exceptions to the rule; in that case, conditions of exceptions or rebuttal (Re) should be inserted. A backing (B) is required if the authority of the warrant is not accepted straight away. Thus, Toulmin’s model of argumentation may contain six related elements (Fig. 1).

Fig. 1
figure 1

Toulmin’s comprehensive model

Full size image

In this report, Toulmin’s (1958/1993) model is used to map out students’ arguments as part of their argumentation and proof. In addition, both their corresponding referential system and structure will be compared. This is done for each of three consecutive problems. In doing so, we hope to identify difficulties students may have in the construction of the proof as well as ways in which these difficulties were overcome.

As reported elsewhere (Pedemonte, 2005, 2007, 2008), Toulmin’s (1958/1993) model can be used to analyze and to compare argumentation and proof from two points of view: the referential system and the structure. In what follows, we present how we can accomplish this analysis.

2.2 Comparing argumentation and proof taking into account the referential system

To compare the referential system of both argumentation and proof, the corresponding warrants and backings need to be taken into account as part of the analysis. The warrant in an argument within the proof may be an axiom, definition, or theorem. The backing is the theoretical system which justifies the warrant. Thus, in solving Calendar Algebra problems, we probably observe that the backing in the proof is algebra while the backing in argumentation is arithmetic, similarly in the case of warrants.

We are interested in analysing whether the cognitive distance in the referential system between argumentation and proof runs as an obstacle in the construction of the proof. Moreover, we try to detect “elements” that seem to be meaningful to shorten the cognitive distance in the referential system, when students are able to construct a proof.

2.3 Comparing argumentation and proof taking into account the structure

As mentioned earlier, in this report we focus on inductive argumentation and deductive algebraic proof. In creating an algebraic proof, students would generate a chain of equivalent expressions. Each expression is generated using properties that hold in the set of the Real Numbers such as the distributive property, inverse element, and so forth. Because of the way in which equivalent expressions are generated, the resulting chain is a chain of deductions. In a similar way, we can consider a chain of deductions given by equivalent propositions (i.e., equations). This is the case when a proposition is generated from another proposition through the use of a specific rule (i.e., equation solving rules).

In Toulmin’s (1958/1993) model, each step appears as a deductive step: data (e.g., an expression or proposition) and warrants (e.g., Real Numbers properties) lead to the claim (e.g., an equivalent expression or proposition). Nevertheless, Pedemonte (2007) has shown how other argumentative structures can be represented using this model. In this paper, the focus is on induction, which is an inference that allows the construction of a claim generalising from particular cases (Fann, 1970; Polya, 1954, 1958). Harel (2001) distinguishes two inductive generalisation processes: result pattern generalisation and process pattern generalisation.

Result pattern generalisation focuses on the regularity of the results, and it can be visualized as: E1, E2, E3… where E is a property generalized on cases 1, 2, 3 and so on. Process pattern generalisation focuses on the regularity of the process, and it can be visualized as E1 → E2, E2 → E3,… The resulting generalisation is given by the inference connecting one case to the next one (Figs. 2 and 3).

Fig. 2
figure 2

Representation of result pattern generalisation (induction) using Toulmin’s model

Full size image
Fig. 3
figure 3

Representation of process pattern generalisation (induction) using Toulmin’s model

Full size image

We are interested in analysing whether the structural distance between inductive argumentation and deductive proof may function as an obstacle for the construction of an algebraic proof in solving Calendar Algebra problems. In addition, we analyze the role that the type of generalisation (following Harel’s distinction, i.e., result pattern and process pattern) that students produced may play in overcoming this discontinuity.

3 Methodology

3.1 Teaching experiment

In this paper, we describe and analyze the work of three ninth/tenth grade students (i.e., Abbie, Desiree, and Grace) who participated in the Calendar Algebra teaching experiment, led by one of the authors of this paper (i.e., Martinez), in which a total of nine ninth/tenth graders took part, at a public school in the Boston area, Massachusetts, in the USA.

3.1.1 Lessons

Fifteen 1-h lessons were held once a week. These lessons were part of the regular school schedule but not part of the students’ regular mathematics classes. All students were interviewed individually (mid-way through and at the end of the teaching experiment). During these lessons, 17 problems were proposed. In this paper, we report on data collected during the first four lessons. During lessons 1 and 2, the three students Abbie, Desiree, and Grace worked on problem 1 (Fig. 4). During lesson 3, students worked on problem 2 (Fig. 5) while during lesson 4 they worked on problem 3 (Fig. 6). We chose to analyze this group and these particular lessons because of the contrasting nature of their work. As mentioned earlier, students faced many obstacles when solving problem 1, while when solving problems 2 and 3, students’ problem solving process went smoothly. The three problems considered in the analysis are in Figs. 4, 5 and 6.

Fig. 4
figure 4

Problem 1 from the Calendar Algebra teaching experiment

Full size image
Fig. 5
figure 5

Problem 2 from the Calendar Algebra teaching experiment

Full size image
Fig. 6
figure 6

Problem 3 from the Calendar Algebra teaching experiment

Full size image

Students were provided with calendars corresponding to years 2005–2008 accompanying problem 1—part 1 (see Fig. 4). As a result of students’ work on part 1, they implicitly had to analyze the nature of the outcome of the described calculation (subtraction of the cross product). It was expected that students would anticipate some kinds of variation in the outcome in relation to the set of days where the operator is applied. It was also expected that students would find out, through exploration, that the same outcome is always obtained (i.e., −7), no matter where (square location within a month, across months, and across years) they apply the operator. The ultimate educational goal of part 1 of problem 1 was to get students to produce conjectures about the behaviour of the outcome (of the subtraction of the cross product) as it relates to the square’s location in the calendar. After each group of students produced their conjectures, as part of part 1 of problem 1, students had to gather evidence to show that their conjecture is true. The challenge for the students was to find out why this happens and whether this is “always” going to be the case. At this stage in the problem, from a mathematical point of view, algebra becomes a tool to solve the problem. Thus, one of the challenges in problem 1 is to show the limitations of using a non-exhaustive finite set of examples to prove that proposition is true and to encourage students to use algebra as a tool that allows them to express all cases using a unique expression. Data collected during lessons 1 and 2 on three students (Abbie, Desiree, and Grace) solving problem 1 are analyzed in problem 1. Problems 2 and 3 (Figs. 5 and 6) were purposely designed as variations of problem 1 in order to provide students multiple opportunities to encounter similar situations and consolidate their understanding. For a detailed description about task design, framework, and results, see Martinez, Brizuela, & Superfine (2011); Martinez & Superfine (2012).

3.2 The cognitive distance between argumentation and proof in solving Calendar Algebra problems

In solving Calendar Algebra problems, students need to shift from an inductive argumentation constructed in arithmetic to a deductive proof constructed in algebra. So they need to shift from one kind of structure in the argumentation (i.e., inductive) to another (i.e., deductive) in the proof. Previous research (Pedemonte, 2007) has shown that in geometry, the construction of mathematical induction strongly depends on the kind of generalisation used in the inductive argumentation: only when generalisation is based on the process (Harel, 2001) were students able to construct a mathematical induction. The structural distance between inductive argumentation and deductive proof is apparently greater than the distance between inductive argumentation and mathematical induction. Thus, we need to investigate if generalisation on the process can also function as a bridge in the relationship between inductive argumentation and deductive proof. Some studies (Ellis, 2007; Lannin, 2005) have shown that there is a close connection between generalisation and deductive proof; thus, our hypothesis is that the generalisation on the process probably affects the construction of a deductive proof, at least in the case of Calendar Algebra problems.

In addition, in solving these problems, students need to prove in algebra a conjecture grounded in arithmetic. The distance between these two domains (i.e., arithmetic and algebra) might function as an obstacle in the construction of the proof. Many studies have devoted their attention to the relationship between arithmetic and algebra. In particular, some highlight the “cognitive gap” between the two fields (Herscovics & Linchevski, 1994; Linchevsky & Livneh, 1999). To grasp meanings in algebra, students use numerical examples to make sense of letters. They use the language of arithmetic to understand the algebraic language. Although procedural aspects reflect those of arithmetic, in algebra they have a completely different meaning. Students are often unable to apply basic algebraic concepts and skills and to understand the underlying structure (Linchevski & Herscovics, 1996). However, many other researchers have shown how students connect arithmetic and algebra, drawing meaning from their work with numbers (e.g., Barallobres, 2004; Bell, 1995; Mason, 1996). Following these research results, we make the hypothesis that to decrease the cognitive gap between arithmetic argumentation and algebraic proof, the warrant in the argumentation should be transformed into a warrant in the proof. In other words, the warrant should “live” both in arithmetic and in algebra. Only in this way is it likely that the continuity in the referential system between argumentation and proof can be maintained.

3.2.1 Data analysis

To perform the analysis, we have to present the “indicators” that allow us to determine the kind of argumentation students construct. In particular, we have to recognize if the argumentation is in arithmetic or in algebra and which kind of generalisation is used in inductive argumentation. In the table that follows (Table 1), we describe how warrants and backing were coded correspondingly, taking into account the referential system and the way the generalisation was produced.

Table 1 Coding scheme
Full size table

4 Results

4.1 Problem 1

These students consider examples as part of their first exploration of the problem. The argument is constructed inductively in arithmetic. Indeed, they first observe the regularities among elements in the square (i.e., difference of six and eight) and through a process pattern generalisation in arithmetic they arrive at C2 (i.e., “…there’s always going to be a difference of eight between the diagonal from the top left, bottom right and a difference of six from the top right to the bottom left”).

A: There’s always going to be a difference of 8 between this one and this one, 1, 2, 3, 4, 5, 6, and a difference of 6 between this one and this one

Students calculate the outcome considering several numerical examples. In doing so, they observe certain regularities.

D: In every single one of them or just that square?

A: In every single one because it’s the difference of 1 more than a week here and 1 less than a week here....

[…]

A: We know that there’s always going to be a difference of 8 between the diagonal from the top left, bottom right and a difference of 6 from the top right to the bottom left, so

Using more examples, students arrive at a claim like the previous argument (i.e., D 1  -> C 1 ) through a process pattern generalisation (right below).

So far, students have observed and generalized the relationships among relevant elements within the square. They continue to observe the invariance of the outcome (i.e., −7) across several numerical examples. Students do so generalising the result inductively (i.e., result pattern generalisation) and arriving at the fourth claim (i.e., C4).

Students calculate the outcome considering some squares.

D: It’s still negative 7, I think it’s always going to be negative 7

A: So like on May

D: Cause July it’s on well first it’s on a Saturday, so the number combinations are different, but it still turns out to be negative 7

A: Yeah and on May the first day of the month is on Monday which is the same as the one that’s on our problem sheet and they end up to be the same, negative 7

Students inductively generalize the result they obtained across cases producing the fourth claim.

D: Yeah I started to do that one out and then I realized, wait a minute that’s the example

A: They’re always going to be the same

In what follows, students are aware that a finite set of numerical examples is not enough to prove their claim; consequently, students shift from arithmetic to algebra. At this point, they are focused on expressing in a general way the relationships among variables and the subtraction of the cross product. The first expression they produce (i.e., C5) only takes into account the relationship between the elements of the diagonal, as opposed to considering also the relationships among elements in the same row. Thus, the expression contains two “independent” variables. However, soon after, students become aware of the dependence between elements in neighbouring rows. As a consequence, they rewrite the expression in terms of just one independent variable (C6).

This is a crucial step in bridging argumentation and proof from the point of view of the referential system. Indeed, the shift from arithmetic to algebra is necessary to construct a proof. Note that in the backing of the following two arguments, arithmetic and algebra co-exist, as this is the modelling stage. In modelling the situation, there is interplay between the algebraic and the arithmetic domains.

A: All right so this is what I have ‘x’ times ‘x’ minus 8, minus ‘y’ times ‘y’ minus 6 that’s basically what we’re doing. Yes?

G: Say that again

D: Could you walk us through it?

A: We’re subtracting the product of these two, times, wait, we’re subtracting the product of these two from the product of these two. And the product of these two is this number times 8 less than this number. So ‘x’ times ‘x’ minus 8, minus ‘y’ times ‘y’ minus 6.

....

.....

Considering a specific square students observe that there is a relationship between x and y, and proceed to modify the previous expression.

A: 12 times 12 minus 8 minus, oh wait but ‘y’ and ‘x’ also are related because ‘x’ is one less than ‘y’ ok so we can go ‘x’ minus 1 times ‘x’ minus 1 minus 6

D: Ok, what?

A: So ‘y’ and ‘x’ aren’t like random numbers cause like this wouldn’t be 17 and that wouldn’t be 2, that’s always going to be 1 less than that, so we can say everything in terms of this number right here

.....

D: Ok you’ve just made this a lot harder to write, but it’d be a different formula if we wrote it differently so

....

A: So ‘x’ times ‘x minus 8’ minus ‘x minus 1’ times ‘x minus 7’

In what follows, students generate an equation linking the subtraction of the cross product with −7. As shown in arguments 3 and 4, the outcome (i.e., −7) is inductively obtained by generalising the result across cases (i.e., result pattern generalisation) in arithmetic. In contrast, the algebraic expression representing the subtraction of the cross product is obtained via induction based on a process pattern generalisation in an interplay between arithmetic and algebra. When students equate x(x − 8) − (x − 1)(x − 7) with −7, they are linking two objects of different natures in regards to the field in which the generalisation is carried out (i.e., arithmetic versus arithmetic/algebra) and the type of inductive generalisation (i.e., result versus process). The cognitive distance between argumentation and proof in the referential system and in the structure functions as an obstacle in the construction of proof.

A: So ‘x’ times ‘x minus 8‘minus ‘x minus 1’ times ‘x minus 7’

A: Equals negative 7

…

A: What we still have to prove is that it does in fact it does always equal negative 7

 

In the backing two different fields (arithmetic and algebra) are present because for students −7 is grounded in arithmetic while the expression in algebra.

 

Note that the qualifier Q 7 is in arithmetic where students know that the expression is equal to −7.

Once students have the expression x(x − 8) − (x − 1)(x − 7) = −7, the notion of equation is triggered and they proceed to apply traditional equation solving procedures (i.e., moving terms from one side of the equal sign to the other one). Therefore, students’ initial proving strategy is that of equation solving. It is at this moment that the connection with the argumentation is lost. The continuity in the referential system is broken.

A: Ok, so I don’t know how to prove things like this

....

A: All right, let’s just try moving things around

…

A: ‘x’ minus 1 times ‘x minus 7’ equals negative 7 plus ‘x’, I mean

D: Oh Abbie

Students apply equation-solving rules in their first attempt to transform the expression.

A: Times ‘x minus 8’, ok

Here the qualifier Q 8 is still not true. Students are reasoning in algebra now where they have to prove that the formula is true, as described by Abbie.

…

A: Well it’s always sort of, this is backwards for me because usually I’m like doing something and working towards making a formula now I like have a formula and I have to like prove that it’s true

A: Well I just don’t really like understand I mean we’re trying to prove that, that equals negative 7 but like I don’t know, I don’t know how we’re going to go about doing that, like… I understand what we did here but I don’t know how that works towards negative 7… Like it just feels like we sort of re-arranged it

The discontinuity in the referential system between argumentation and proof is evident because the rules used in the argumentation (i.e., calculations) are essentially different (i.e., properties of the real numbers such as distributive property) than the rules of equation solving used at the beginning of their attempt to prove. Students transform the first expression into the equation (x − 1)(x − 7) = −7 + x(x − 8), but as highlighted by Abbie’s comment, it seems as if they lose sight of the connection to the meaning constructed in the argumentation process.

There is also structural distance between argumentation and proof. Argumentation is inductively developed by students using process pattern generalisation (while constructing the expression) and result pattern generalisation (while constructing the outcome). Students need to shift from an inductive argumentation to a deductive proof: this offers resistance in the construction of a proof.

At this moment, students stumbled upon an obstacle and were not able to continue constructing a proof by themselves. Abbie was not sure how to get from the initial equality to what they wanted to prove (i.e., outcome equals −7). The intervention of the teacher was necessary to help students move forward; she suggested rearranging the elements on one side of the equation to see whether they could cancel something. After trying the teacher’s suggestion and re-arranging what they had, students were able to cancel things out until finally obtaining −7 = −7. This was students’ first experience in proving deductively using algebra.

4.2 Problem 2

Students start working on the problem by trying examples, as was the case in problem 1. The argumentation process is predominantly inductive based on both result pattern and process pattern generalisations. As a result, not only do students conclude that the outcome will be zero but also they are certain of the invariance of the relationships among numbers in the square. This double conclusion enables reducing the distance between the argumentation and the proving processes, in terms of the referential system (i.e., algebra and arithmetic).

figure afigure a

In what follows, students continue to model the problem using algebra in order ultimately to prove their conjecture. Abbie first proposes a not so efficient model of the situation. Abbie uses four variables and even though she is aware of the relationships among variables, she does not express three variables as a function of the same independent variable.

A: I made this little thing where I called this one x, this one y, and this one N, and this one Q… So x minus 16 = y because it's 2 weeks and 2 days away, that’s 16 days… N minus 12 is Q, because it’s 2 less than 2 weeks… And then x minus 2 is N, because it’s 2 days less than 2 weeks

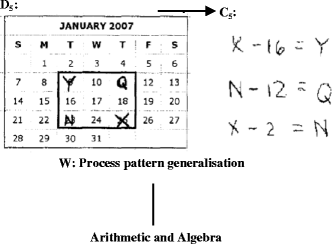
Abbie represents the relationships among numbers in the square using algebraic notation and through a process pattern generalisation. In doing so, Abbie engages in an interplay between arithmetic and algebra.

Even though the proposed model is not instrumental in helping her to prove the conjecture, the interplay between algebra and arithmetic is a crucial step forward in reducing the distance between argumentation and proof. The co-existence of both fields at this stage is conducive to the production of a proof. It is in this respect that there is cognitive continuity in the referential system between argumentation and proof.

Arguments 3 and 5 are crucial to reduce the cognitive distance between argumentation and proof, both from the referential point of view and the structural point of view. As a result of arguments 3 and 5, students produced an algebraic model of the problem. Let us consider in particular argument 5. Here Abbie replaces the numbers in the calendar with algebraic symbols. This seems important to reconstruct the continuity in the referential system because the student uses the problem description simultaneously to represent a physical calendar and algebra. The insertion of the letter in the calendar runs as a “pivot” element to reduce the distance between argumentation and proof in the referential system. Having a single representation for arithmetic and algebra allows students to have a bridge between them. The qualifier of these arguments lives in arithmetic where students have constructed the conjecture, but also in algebra because the expression is constituted by letters that are for students a generalisation of numbers.

Furthermore, the inductive structure based on a process pattern generalisation, which expresses the relationship between the corners of each square runs as a connection between argumentation and proof. The argument 6, which expresses the solution of the problem as an algebraic expression, is directly constructed by arguments 3 and 5.

Below, Desiree suggests to Abbie she should re-consider her model by using only one independent variable (i.e., x) and expressing the others as a function of it.

D: Aren’t they kind of hard to simplify because we have different variables?

The intervention of Desiree works as a restriction in Abbie’s argument. Following Desiree’s idea, the resulting modelisation is completely different.

A: Ok what are your variables?

D: x

A: Just x?

A: Well I have for the same one, I just added other ones too

The previous argument allows students to construct the equality to be proved:

G: The other ones are just gonna be x minus the other ones

A: Yeah ok

A: It’s basically the same thing, it’s just x minus 16

A: Alright so I’m just going to write it the same way you guys are writing it

D: Ok, do we wanna try it out?

A: Ok basically we need to prove that x + x − 16 = x − 2 + x − 14

Abbie writes the equality generalising the third argument. Its backing is grounded in the arithmetic field as well as the algebraic field. The algebraic domain allows students to model the outcome in a general way. The arithmetic field is the domain of validity of the equality since students are certain of its plausibility on the basis of numerical examples.

Still, students are aware that proving the assertion remains to be done. Abbies states ‘we need to prove that x + x − 16 = x − 2 + x – 14’ even if she is aware that the equality is true.

This last step in students’ mathematical process, as just illustrated above, is crucial in linking argumentation and proof. The assertion to be proved is resulting knowledge produced by students as part of the argumentation process. In this way, this statement is one of the shared elements between the argumentation and proof. It is in this way that the distance between them is overcome. This is one more example of an element that works towards the continuity in the referential system between argumentation and proof.

Abbie and Desiree are in agreement in terms of what needs to be proved (i.e., x + x − 16 = x − 2 + x − 14). However, this is not the case for Grace. She thinks that they need to prove a different statement, as illustrated below.

Abbie transforms the equation to an equivalent equation in which the two expressions are equal

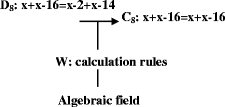
She writes

x + x − 16 = x − 2 + x − 14

x + x − 16 = x + x − 16

Grace is not convinced it is correct

G: This isn’t what we’re doing… we need to prove that what we’re doing is always going to be zero

Grace thinks that they have not proved the problem because they should obtain zero.

A: This is what we’re doing..

G: No, we’re doing x + x − 16 MINUS x − 2 + x − 14

A: Wait, it’s always going to equal zero, if this plus that equals this plus that

G: Yeah, but I just think that it’s confusing if we…

D: Well it makes sense to prove those two equalling each other first… And then prove that those two minus each other equals zero, is that what you’re trying to say?

A: Yeah, if they’re the same then we know they’re going to be zero

Attending to Grace’s concern, students end up re-writing the expression in order explicitly to show that the outcome always comes to zero.

G: Okay, that makes more sense

Then Abbie writes

The backing in argument 9 can be considered as a theorem in action (Vergnaud, 1991 ): ‘If two quantities are equal, then their difference is equal to zero’. The theorems in actions are implicit mathematical theorems which act as invariants and lead the action.

x + (x − 16) can be rearranged as x + x − 16

x − 2 + x − 14 can be rearranged as x + x − 16 also

x + x − 16 − (x + x − 16) = 0

If the expressions are equivalent, then their difference will always be 0

Abbie uses this theorem explicitly but she probably is not aware this is a theorem. This theorem is used by Abbie to transform the equation to an equivalent version, in which it is probably easier to explain that the result is 0.

Grace brings back to the proving phase an element from the argumentation to show that the outcome will always be zero. In this way, these students give closure to the proving process.

4.3 Problem 3

In this case, students again start by trying with numerical examples (C1); after that, they conjecture that the outcome is −63 always (C2).

D: Wait; so which one did we do first again? Let me see, the upper left times the bottom right, minus the bottom right times the upper left

A: That one, times that one minus that one times that one I think

D: Yes, that’s what I said… okay

A: So, yes… okay

G: That one, times that one, times that one…

A: Or is it the other way around?

Students generalize the previous argument and construct the resulting conjecture. It is grounded in both domains: algebraic and arithmetic. Abbie appeals to the notion of variable as a generalized number by stating that the conclusion holds for ‘any number’.

G: If I did the upper left times lower right, then the other two… it comes out

D: So these times these, right?

G: I did those two, and those two, and it came out to negative 63

D: Yeah

D: Negative 63

A: I got negative 63 too

D: It’s always going to turn out as negative 63

A: Yes the outcome will always be negative 63 for any number

In this exchange, Abbie generalizes the invariance of the outcome across cases. As evidenced in claim C2, Abbie explicitly connects the numerical value of the outcome with “any number”. The fact that she uses the expression “any number” indicates a conceptualization of the variable as generalized number. As can be observed, the backing for the second arguments rests upon arithmetic and algebra simultaneously. Again, this is a bridging element between argumentation and proof in terms of the referential system. Moreover, the qualifier of this argument, Q2, lives only in arithmetic and algebra because students already know that the result −63 will be found by manipulating the expression they are constructing in algebra, as can be observed in the first statement of the following extract.

In what follows, Abbie proceeds to express three of the variables as a function of x (i.e., number in the lower right corner) as well as the relationships among them using algebraic notation (C3). We can observe that in solving this problem, Abbie does not struggle with using multiple independent variables as she did in problem 2.

figure b

We can observe that Abbie replaces numbers with letters in the calendar. There is a difference with respect to the previous example: Here there are no numbers in Abbie’s square; she used algebraic notation right away to represent the variables involved in the problem. The same can be said for Grace and Desiree. This might be related to their work on previous problems; it seems as if their recent experience works as implicit backing in their arguments.

Starting in the third argument, everything is in the algebraic domain. Students are able to construct the proof transforming the expression (x − 24)x − (x − 3)(x − 21) into −63 using several properties as shown in the table below.

figure c

In contrast to the first example, the students focus on the transformation of the expression on the left-hand side of the equal sign, purposely moving to the background the numerical value of the outcome. In other words, they do not engage the numerical value of the outcome in any kind of transformation.

From the point of view of the referential system, we can observe that there is only one argument in which the backing is arithmetic (i.e., first argument). The rest are either an interplay of arithmetic and algebra or solely algebra. As a consequence, the distance between argumentation and proof is considerably diminished in comparison to the first case. As shown in the table, the students are able to construct a deductive proof even though the structure of the argument is inductive. The students seem to have learned to manage the two kinds of complexity that characterize this kind of problem: the cognitive distance in the referential system (i.e., algebra and arithmetic) and the cognitive distance in the structure between argumentation and proof (i.e., inductive and deductive). With respect to the first of these last two cases (problem 2 and problem 3), the students insert letters in the calendar: in the first case, Abbie replaces numbers in the calendar with algebraic symbols; in the second case, she does not use any number. The insertion of the algebraic symbol in the calendar seems to construct a bridge between arithmetic and algebra: in both cases, the continuity in the referential system is reconstructed.

4.4 Discussion of results

The Calendar Algebra problems provided the opportunity for students to produce a conjecture by inductive argumentation using specific numeric examples and to construct an algebraic deductive proof. Thus, a distance both in the referential system and in the structure between argumentation and proof has been observed in the students’ resolution process.

Even though for the analysis we presented data corresponding to three students in the same group, we have analyzed the work by a total of nine students. All of them produced a correct conjecture through an inductive argumentation in the arithmetic field for the three problems. For problem 1, all students were unable to produce a proof without the teacher’s careful scaffolding. For problems 2 and 3, we have observed an “evolution” in terms of the solution of the problems. All students learned to overcome the cognitive distance between argumentation and proof for these specific problems. Therefore, the group presented in this report is representative of students’ strategies.

By looking across all three problems, we can observe that all three argumentations are inductively constructed with a strong presence of the arithmetic field. In other words, the conjecture is constructed in arithmetic using numerical examples. In all three cases, the qualifier of the argument strengthens the argument: students know that the conjecture is true because they have verified the results through different numerical examples. All three proofs are deductively constructed, grounded on algebra. Given that argumentation and proof from a cognitive perspective are different (i.e., inductive vs. deductive and arithmetic vs. algebra), we wonder what makes it possible for students to overcome these distances. In problem 1, the teacher’s intervention (i.e., re-arranging) was a crucial stepping stone in transitioning from the argumentation process to the proving process. However, there is more. Results show that: (1) In all three problems, students start the argument purely in arithmetic, going through steps that integrate both arithmetic and algebra, bridging to the last steps when they use only algebra; (2) arguments became shorter in subsequent problems (i.e., argument in problem 3 has seven steps while argument in problem 1 has ten steps); (3) algebra becomes a central part of the argument earlier in subsequent problems (i.e., step 3 in problem 3 in contrast to step 8 in problem 1); (4) numbers in the calendar are replaced with letters to connect the real numbers to algebra; and (5) the construction of the deductive proof is performed only when inductive argumentation is based on a process pattern generalisation (problems 2 and 3).

Thus, the bridging element between inductive argumentation in arithmetic and deductive proof in algebra is the co-existence of arithmetic and algebra in the backing of the arguments within the argumentation. Indeed, this co-existence allows modelling the problem (Table 2 in Appendix). This is particularly important since it is through modelling that both referential systems (i.e., arithmetic and algebra, respectively) corresponding to argumentation and proof become inter-connected. This inter-connection is realized only when students place the algebraic symbols over the numerical symbols on the calendar (episode 2) or when they directly insert letters in the calendar (episode 3). In the first episode, students do not place letters in the calendar. The continuity in the referential system is not reconstructed in the first case while we can observe it in the other two cases. However, the co-existence of arithmetic and algebra is not sufficient to guarantee the construction of a proof. It is also important to note that the inductive argumentation is grounded in a process pattern generalisation. In problem 1, we have observed a structural distance between argumentation and the attempted proof. Argumentation was constituted by two kinds of induction: one based on a process pattern generalisation (i.e., constructing the expression) and one based on a result pattern generalisation (i.e., constructing the outcome). Students were not able to transition into a deduction previous to the teacher’s intervention. In fact, the different structures in argumentation (i.e., inductive) and in the proof (i.e., deductive) offer resistance in the construction of the proof. As shown in problem 1, when students constructed the proof, they lost sight of the link with argumentation. Thus, the connection and permanence in meaning between algebraic letters and arithmetic numbers is important to enable the algebraic manipulation as needed in the algebraic proof. Only when students produce inductive argumentation grounded in process pattern generalisation they are able to construct a deductive proof, as shown in problems 2 and 3.

As a consequence, in solving Calendar Algebra, the process pattern generalisation in inductive argumentation functions as a bridge between argumentation and deductive proof like in the geometrical case where mathematical induction was constructed only if generalisation in inductive argumentation was grounded in the process (Pedemonte, 2007). In addition, it is important that this generalisation could be made both in arithmetic and in algebra in order to decrease the cognitive distance in the referential system between argumentation and proof. The co-existence of arithmetic and algebra in the backing of the arguments allows the warrant to live in both fields. This co-existence is strongly supported by the fact that the numbers in the calendar are replaced with letters that cover the numbers in the calendar without eliminating them. It is this fact that supports the continuity in the referential system between arithmetic argumentation and algebraic proof.