Making sense by measuring arcs: a teaching experiment in angle measure

Abstract

I discuss a teaching experiment that sought to characterize precalculus students’ angle measure understandings. The study’s findings indicate that the students initially conceived angle measures in terms of geometric objects. As the study progressed, the students formed more robust understandings of degree and radian measures by constructing an arc length image of angle measures; the students’ quantification of angle measure entailed measuring arcs and conceiving multiplicative relationships between a subtended arc, a circle’s circumference, and a circle’s radius. The students leveraged these quantitative relationships to transition between units with a fixed magnitude (e.g., an arc length’s measure in feet) and various angle measure units, while maintaining invariant meanings for angle measures in different units. These results suggest that quantifying angle measure, regardless of unit, through processes that involve measuring arc lengths can support coherent angle measure understandings.

1 Introduction

Angle measure and trigonometric functions have been high school and undergraduate mathematics topics for well over a century. In addition to their deep-rooted place in mathematics, both topics are frequently used in physics, engineering, and applied mathematics. The results of several research studies have indicated, however, that students and teachers have difficulty understanding and reasoning about trigonometric functions (Brown, 2005; Fi, 2003; Thompson, Carlson, & Silverman, 2007; Weber, 2005). Other studies have reported that teachers’ and students’ fragmented understandings of angle measure lead to disconnected understandings of trigonometric functions (Akkoc, 2008; Topçu, Kertil, Akkoc, Kamil, & Osman, 2006). Complicating the issue, few research studies have addressed how students come to understand angle measure in the particular ways in which they do.

The present study examines two undergraduate precalculus students’ evolving angle measure understandings¹ as they participated in a teaching experiment (Steffe & Thompson, 2000). Thompson’s (1990) theory of quantitative reasoning, research on the teaching and learning of trigonometry and angle measure, and the historical roots of angle measure inform the study. In the present work, I develop hypotheses of the students’ angle measure understandings with a focus on the students’ quantification of angle measure. I also discuss the students’ angle measure understandings in terms of several ideas of quantitative reasoning.

2 Research literature on angle measure

Previous research on students’ angle measure understandings has mainly focused on elementary students’ angle conceptions (Clements & Burns, 2000; Kieran, 1986; Mitchelmore & White, 2000). These studies have identified the important role of physical experience in students’ construction of angle (Mitchelmore & White, 2000), including their ability to coordinate turn as a physical action and turn as a number (Clements & Burns, 2000; Kieran, 1986). Such findings offer valuable insights into elementary students’ development of angle conceptions, but leave much to uncover about students’ angle measure concept past the elementary level.

Research literature on trigonometric functions (Akkoc, 2008; Brown, 2005; Fi, 2003; Thompson et al., 2007; Topçu et al., 2006; Weber, 2005) also generates a need to better understand students’ angle measure conceptions. Two studies (Akkoc, 2008; Topçu et al., 2006) characterized preservice and in-service mathematics teachers in Turkey as holding understandings of radian angle measures dominated by degree measure; when given radian measures, the teachers converted these measures into a number of degrees in order to attribute a meaning to the measures.² Not one of the four teachers interviewed by Topçu and colleagues defined radian measures as a ratio of lengths. As Akkoc (2008) reported and compatible with previous findings (Fi, 2003), preservice teachers also claimed that radian measures are only given in terms of π, leading teachers to interpret 30 as a number of degrees in expressions such as sin(30). In light of his findings, Akkoc suggested that impoverished radian angle measure understandings likely contribute to teacher and student difficulties in trigonometry.

Collectively, the aforementioned research has revealed that students and teachers construct shallow and fragmented angle measure understandings that inhibit their ability to construct flexible trigonometric function understandings. Of particular relevance to the present study, the research suggests that teachers’ and students’ angle measure understanding often lacks meaningful connections to arcs. These observations illustrate a need to gain better insight into students’ ways of thinking about angle measure that support connected³ angle measure understandings.

3 An arc approach to angle measure

USA and international textbooks provide many different characterizations of angle measure. In a survey of 30 elementary and secondary textbooks, I found angle measures defined as an amount of a rotation, a number obtained by using a protractor, and a measurement of an arc length, to name a few. The roots of each definition can be linked to various points in the historical development of angle measure. Matos (1990) and Bressoud (2010) have provided summaries of the history of angle and the history of trigonometry, respectively, while highlighting critical angle measure developments.

Of relevance to the present article, Matos’s (1990) and Bressoud’s (2010) historical accounts illustrate that the majority of angle measure developments occurred in the context of measuring arcs. For instance, the Babylonians measured the circular movement of celestial bodies using 360 whole parts for the sky (Matos, 1990). Despite the rich historical focus on measuring arcs, an educator can be, depending on her or his country, hard pressed to find curricula that relate degree measure to the length of an arc. A textbook might use an arc to label an angle and its measure, but it is not necessarily the case that degree angle measure is presented as a process of partitioning an arc using a specified unit length.

Consider an approach to angle measure that defines degrees as the standard unit of angle measure and asks students to use a protractor to assign degree measures to angles. The approach then defines right angles, supplementary angles, obtuse angles, etc., and students execute calculations using angle measures and these definitions. Such an approach, which is customary in the USA, might facilitate relating angle measures through calculations, but it fails to address the quantitative structure behind the process of determining an angle’s measure. In contrast to such an approach, radian angle measures are typically introduced in terms of measuring an intersected or subtended arc using a circle’s radius as a unit; the measure is defined in terms of a quantitative relationship with an explicit connection to a subtended arc. Such a definition for radian measures fundamentally differs from more common approaches to degree angle measure.

One approach that avoids a divide in angle measure meanings is to develop angle measures, regardless of unit, as representative of the same quantitative relationship. This can be accomplished by conceiving angle measure as the process of determining the fractional amount of a circle’s circumference subtended by an angle, provided that the circle is centered at the vertex of the angle (Thompson, 2008). An angle that measures 1° subtends 1/360 of the circumference of any circle centered at the vertex of the angle and an angle that measures 1 rad subtends 1/2π of the circumference of any circle centered at the vertex of the angle; radians and degrees measure the same quantity and are thus scaled versions of one another (Thompson, 2008).

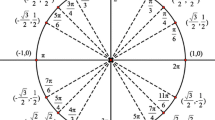
With angle measure understandings that foreground relationships between quantities, students should interpret an arc used to denote an angle measure as more than a label; they should understand the arc as denoting an equivalence class involving arc lengths (including the given arc length) and circles. For instance, an angle measure of 2 rad conveys that the angle subtends two radii on all circles centered at the vertex and that same angle subtends 2/2π of each circle’s circumference (Fig. 1). A benefit of radian angle measures is that, once a circle is specified, the unit magnitude is more explicit than the magnitude associated with 1°. Also, by understanding radian measures as equivalence classes grounded in measuring in radii, a foundation is in place for students to understand the values associated with the unit circle in terms of equivalence classes. If students are to connect the unit circle—an arbitrary circle of radius 1—to all circles and radian angle measures, it is important that they connect the unit circle to measuring in radii (Moore, LaForest, & Kim, 2012).

Fig. 1

An arc length image of angle measure that involves equivalence of arcs

4 Theoretical perspective

Principles of quantitative reasoning (Smith & Thompson, 2008; Thompson, 1990), which call attention to the importance of students constructing quantities and relationships between quantities when learning mathematics, provide a foundation for the present investigation into student thinking. Quantitative reasoning involves an individual’s mental actions when conceiving of a situation, constructing measurable attributes of the situation (which are called quantities) and constructing about relationships between conceived quantities. These mental actions create a (quantitative) structure that forms a foundation for constructing mathematical understandings.

A quantity is defined as a conceived attribute of something that admits a measurement process (Thompson, 1990). Relative to the focus of this research, two intersecting rays in relation to each other form an object (the something) that has a measurable attribute of openness. Quantifying the openness of an angle entails conceiving a quantitative relationship—specifically, a multiplicative relationship—between a subtended arc and a unit length (e.g., the radius). Also, as described previously, quantifying angle measure involves coming to understand a unit in terms of a multiplicative relationship between a class of subtended arcs and the corresponding circles’ circumferences.

I adopt Thompson’s (1990) definition of value to refer to a number that reflects the result of a measurement process. I use number to refer to a number that does not reflect the result of a measurement process.⁴ As an example of the difference between a number and a value, consider a student solving a problem in which they use a ratio between an arc length that subtends an angle and the circumference of the corresponding circle. When calculating the ratio, the student might conceive the ratio only as a call to execute a calculation (e.g., ratio as a number) or the student might interpret the ratio as representing a measure of the fractional amount of the circle’s circumference that is subtended by the angle (e.g., ratio as a value). In the case of ratio as a value, the student’s subsequent actions might stem from reasoning about the ratio as a value (e.g., I multiply the ratio by the total number of angle measure units in a circle to determine the angle measure that is the equivalent fractional amount of the total angle measure units).

It is important to note that a quantity is a cognitive object. Quantities can and will differ from individual to individual; an individual’s quantification of an angle’s openness may or may not include a subtended arc as inherent to the measurement process. As Thompson described, quantifying a quantity “is a process of settling what it means to measure a quantity, what one measures to do so, and what a measure means after getting one” (Thompson, 2011, p. 38).

5 Methodology of the study

One purpose of education research is building models of students’ mathematics that provide a viable explanation of the schemes and operations driving the students’ behaviors (Steffe & Thompson, 2000). I conducted the present study in order to develop such models in the context of the students’ quantification of angle measure over the course of a teaching experiment (Steffe & Thompson, 2000).

5.1 Subjects and setting

Three full-time students from an undergraduate precalculus course at a large public university in the Southwest USA participated in the teaching experiment. The three students were chosen out of necessity, as they were the only volunteers from the class who had schedules that aligned with my schedule. Two students (Judy and Zac) are the focus of the present study.⁵ Judy was a female in her mid-twenties and a biochemistry student. Zac was a male in his early twenties and an ethnomusicology/audio technology major. Judy received an “A” for her final course grade, and Zac received a “B” for his final course grade. The students were monetarily compensated for their time. I chose precalculus students because precalculus is typically the course that introduces trigonometric functions and radian angle measure.

The aforementioned precalculus classroom was part of a design research study informed by literature on covariational reasoning (Carlson, Jacobs, Coe, Larsen, & Hsu, 2002) and quantitative reasoning. An observer to the teaching experiment and I served as teaching assistants in the course. Course topics included quantity, rate of change, linear functions, function, exponential functions, and rational functions. Angle measure and trigonometric functions formed the last module of the course. The participants did not attend the angle measure and trigonometry class sessions, instead participating in the teaching experiment.

Students who take precalculus at the students’ university (and peer institutions) represent a wide range of majors, and a majority of these students are not mathematics majors. Research with undergraduate students in precalculus suggests that they encounter difficulties similar to those of their secondary level counterparts when reasoning about quantities and relationships between quantities (Moore & Carlson, 2012). Also, undergraduate precalculus students’ performance on a research-based precalculus assessment (Carlson, Oehrtman, & Engelke, 2010) is comparable to that of their secondary school counterparts. Thus, although the participants in the present study represent a convenience sample, undergraduate and secondary precalculus populations are not dissimilar and the students were not atypical relative to their peers.

5.2 Data collection and analysis methods

The angle measure portion of the teaching experiment involved two 75-min teaching sessions occurring within a span of 4 days. Each teaching session included Judy, Zac, an observer, a third student, and myself. In an attempt to gain insights into the students’ angle measure conceptions upon entering the study, I conducted preinterviews with each student that followed the design of a clinical interview (Clement, 2000) and Goldin’s (2000) principles of structured, task-based interviews. The preinterviews occurred 1 week prior to the first teaching session.

Following two teaching sessions on trigonometric functions,⁶ the teaching experiment included a 2-h researcher–student teaching session with each student. The one-on-one sessions occurred 2 weeks after the second teaching session (Fig. 2) and followed the teaching experiment principles. I use teaching sessions and interview sessions to distinguish between the sessions that included more than one student and the sessions that included only one student, respectively.

Fig. 2

The progression of the teaching experiment, with solid frame boxes indicating the focus of the present work

Teaching experiments (Steffe & Thompson, 2000) adhere to the stance that students are in a constant mode of construction, a stance that is in line with the principles of quantitative reasoning. During a teaching experiment, a researcher aims to build viable models of students’ mathematical understandings and document shifts in these understandings. These models may become more precise over time, but the models are never to be interpreted as one-to-one representations of the students’ thinking. The researcher’s mathematical understandings, the perspective that the researcher uses during the study (e.g., quantitative reasoning), and the researcher’s learning goals for the students shape his models (Steffe & Thompson, 2000). Relative to the present study, I was involved (both in teaching and design) in the aforementioned precalculus design research study. Hence, I was aware the materials addressed research-established student difficulties and needs for calculus. My previous teaching experiences and understanding of the project goals thus influenced the design of the study and my models. For instance, I was aware that students often face difficulty conceiving calculations in terms of quantitative relationships, and many of my decisions during the study revolved around determining students’ meanings for calculations.

All sessions during the teaching experiment were videotaped and I digitized all student work. The sessions included two cameras, one for the students’ table and one for work produced on a whiteboard, and a computer feed capture. Following the teaching experiment methodology (Steffe & Thompson, 2000), data analysis included both ongoing and retrospective elements that included documenting decisions during the teaching experiment and revisiting these decisions during a retrospective analysis of the data. Upon completion of data collection, a retrospective analysis of the data occurred. After transcribing all sessions, I conducted an open coding (Strauss & Corbin, 1998) of the data that involved identifying episodes that offered insights into the students’ thinking. Consistent with Thompson’s (2008) description of a conceptual analysis, I analyzed the identified instances in an attempt to create hypotheses of the students’ schemes and operations of thought. I tested these tentative models by searching and analyzing the data for evidence that either contradicted or supported the generated models. Such analyses led to modifications of these hypothesized models of each student’s mathematics, as well as documenting shifts in the students’ thinking. Additionally, the students’ ways of thinking were compared and contrasted.

6 Results

I first provide an overview of the preinterview findings. I then characterize the students’ quantification of angle measure during the teaching sessions. To further illustrate the outcomes of the students’ quantification of angle measure, I summarize their activity during the post-teaching interview sessions.

6.1 Preinterviews

Initially, I asked the students to describe their meanings for various angle measures (e.g., 1°, 34°, and 90°). The students predominantly described angle measures as properties of familiar geometric objects (e.g., a line has 180°, two perpendicular segments have 90°, and a circle has 360°) and had difficulty describing angle measures that did not correspond to such geometric objects (e.g., an angle measure of 1°). The students often drew a circle or an arc when measures did not relate to a familiar geometric object, but the students treated arcs as labels and not as measurable attributes (e.g., a subtended arc and a circumference). To illustrate, when tasked with describing 1°, Judy claimed, “Wow…I really don’t know what an angle is outside of formulas,” and explained that the angle is supplementary to an angle of measure 179°. When asked to provide another meaning for 1°, she stated that she could only think about it in terms of a line having a measure of 180°.

I also asked the students to measure an angle using a compass, waxed string, and a ruler (Fig. 3). Both students constructed a circle centered at the vertex of the angle, but neither student completed the task. After drawing a circle, Zac stated, “they have…a [protractor] that’s already designed out, shows you where all the angles are.” Yet, he did not relate the protractor to the circle. Judy determined the circumference of the circle, the arc length subtended by the angle, and divided the arc length by the circumference (obtaining 0.087). Yet, she was unable to provide a meaning for her calculation or solve the problem. To Judy, 0.087 was a number; the calculation did not reflect a multiplicative comparison between the arc length and circumference.

Fig. 3

Measuring an angle with tools

To conclude the interview, I tasked the students with the traversed arc problem (Fig. 4), which provided specified values for an arc length and radius. Despite their difficulties during the previous problems, both students obtained a correct solution by using an equation with two ratios (e.g., $\left( {32/\left( {102\pi } \right)} \right)=\left( {x/360} \right)$ or $\left( {90/80.1} \right)=\left( {x/32} \right)$).

Fig. 4

The traversed arc problem

The students justified their solutions by comparing the units of each value and using the calculational⁷ strategy of cross-multiplication. As an example, after Zac determined the arc length (80.1 ft) that corresponded to 90°, he described that the equation $\left( {90/80.1} \right)=\left( {x/32} \right)$ is appropriate for solving a problem in which there are three known numbers and an unknown number (Excerpt 1).

Excerpt 1

	Zac:	Well it’s just, if you’re given three variables and you just need one more. Well, you, uh, ‘cause you’re given degrees and feet and degrees and feet…And it just, it gives you three of the four you need. It’s a very easy equation to find a fourth…
	Int:	OK, and so, and how do you know how, which way to set up the proportion?
	Zac:	Well you could do it either way. I could do eighty point one over ninety is thirty two, as long as the top’s are both the same unit, they're both degrees, and these are both feet (writing units by the measurements).

I asked Zac to provide a meaning of the ratio 90/80.1 independent of the calculations he used to solve the problem, but he only focused on the calculations he performed. Zac conceived 90/80.1 as a number. As an alternative conception, 90/80.1 can be thought of as representing the number of degrees per foot of arc length for that circle.

I took the students’ actions during the preinterview to imply that they had not quantified angle measure in a way that entailed quantitative relationships. Instead, they predominantly conceived angle measures as intrinsic properties of geometric objects or in terms of calculations with corresponding angle measures (e.g., supplementary angles).⁸ The students did draw arcs, but their arcs were not a component of a measurement scheme. I also noted that neither student mentioned the radian (or radius) as a unit of angle measure during the preinterview. This observation aligns with research (Akkoc, 2008; Brown, 2005; Fi, 2003; Topçu et al., 2006) that has identified degree angle measure as dominating individuals’ angle measure conceptions.

6.2 Connecting angle measure and arc length

I designed the first teaching session to challenge the students to determine a process to create a protractor (the protractor problem; Fig. 5), with each student using a different-sized blank protractor. I expected that the students’ angle measure understandings, as inferred from the preinterview, would not support solving the problem. Thus, I hoped that the students would face a perturbation that caused them to consider what one quantifies when measuring an angle.

Fig. 5

The protractor problem. (*I chose the word circle to be intentionally vague. I did not wish to point the students directly to a measurable attribute of the circle (e.g., area or circumference) in the hopes of determining which imagery was more natural forthe students)

When working on task 1, Judy first used the waxed string to measure the circumference of the protractor.⁹ The students quickly discarded the measure and relied on folding the protractor to create the equal areas (Excerpt 2).

Excerpt 2

	Zac:	Well, I already figured out what two gips is by just dividing it in half.
	Int:	So dividing what in half?
	Zac:	The protractor. I just drew a line down the middle (waving hand over the protractor) and that gives me two gips. And then I just need to figure out how to find…(pause)
	Int:	So how’d you know how to draw the line?
	Zac:	Uh, I figure out that the diameter is four inches, and just found out where two inches is, marked it (referring to the midpoint of the diameter), and found my best two inches this way (waving pen tip from the bottom to the top of the protractor) and drew it up.

Despite Judy’s initial act of determining the circumference, Zac did not attempt to measure or discuss the circumference. Instead, Zac reasoned about dividing the entire protractor into equal pieces (e.g., areas). After creating the two-gip mark, both students divided the protractor into four equal areas by folding the protractor. Believing the students were reasoning about areas, I modified task 1 so that a folding method does not produce integer measures (task 2). The students immediately claimed they needed to determine 7.5 equal areas and started folding the protractor. They then realized that folding the protractor into successive halves did not yield 7.5 equal areas and explained that they could only approximate the partitioning of equal areas.

To support a shift in the students’ thinking, I asked them for a second method to decide, as precisely as possible, the placement of the quip marks with the stipulation that they could not fold the protractor. Zac grabbed the waxed string and claimed, “Measure out the whole thing…measure out the perimeter.” Zac and Judy used the waxed string to measure the circumferences of their protractors, and then divided their circumferences by the total number of quips (e.g., 7.5 for the half-circle or 15 for the entire circle). They explained that the value represented the arc length corresponding to one quip on their circle (approximately 1.885 cm/quip and 1.6336 cm/quip); their calculations emerged from reasoning about partitioning the circumference of the protractor into equal arc lengths (e.g., ratio as a value). This moment marked the first instance of the students generating and relating measurable arc lengths to angle measures, which appeared to be fostered by facing a situation in which their area image of angle measure did not support solving the task.

To continue exploring relationships between angle measure and arc lengths, I drew the students’ attention to a diagram (Fig. 6) of their two protractors. Just prior to drawing the diagram, the students observed that the arc length per unit of angle measure varied between their protractors, yet there was something “the same” about the arc lengths. In an attempt to build on their observation, I posed ratios comparing the unit arc lengths to the total circumference of the corresponding circle (1.885/28.2744 and 1.6336/24.5044), as well as the ratio of 1/15.

Fig. 6

Two protractors of different size (figure not to scale)

After the students calculated each ratio (approximately 0.067), I emphasized that I wanted a meaning for the ratios in terms of the quantities of the situation and not just the numerical value. Zac claimed, “It’s just taking the full circumference and then a fifteenth of a full circumference…It’s the exact same. You’re taking one-fifteenth of the full circumference and dividing it by the full circumference.” Zac conceived each ratio as a value representing an arc length’s fraction of a circle’s circumference, which supported him in identifying that the angle cut off an equivalent fraction of each circle’s circumference. The students then generalized this relationship to conclude that quip measures convey a fractional amount of a circle’s circumference cut off by the angle that holds for all circles centered at the vertex of the angle.

6.3 Extending to degree measure

The protractor problem occurred over 45 min, a period during which the students conceived of an arc length as a measurable attribute related to angle measure in two ways. First, they reasoned about an arc length per unit of angle measure that can be iterated along the circumference of a circle. Second, they conceived angle measures in quips (and gips) in terms of the fractional amount of any circle’s circumference cut off by the corresponding angle.

I hypothesized that their meanings for degree angle measure shifted accordingly, and thus asked the students to respond to a question from the preinterview: “What does it mean for an angle to have an openness of one degree?” Zac claimed, “[The angle cuts off] one three-hundred and sixtieth of a circle’s circumference.” Judy further described that an angle of 10° subtends 10/360 of a circle’s circumference and she used a calculator to determine that the subtended arc is approximately 2.7 % of the circumference for any circle centered at the vertex of the angle.

I took the students’ actions to imply that they had quantified angle measure such that they had an invariant meaning for different units. Specifically, they interpreted angle measures, regardless of unit, as a multiplicative comparison between an arc length and a circle’s circumference that is not dependent on the size of the circle used to make this comparison. I hypothesized that a method for converting between angle measures might emerge as a consequence of giving an invariant meaning to angle measures of different units. In an attempt to test this conjecture, I asked them to determine the angle measure in quips that is equivalent to 10°.

Judy suggested using the equation $\left( {10/360} \right) = \left( {x/15} \right)$ to solve for the number of quips that are equivalent to 10°, and the students claimed that each ratio represented an equivalent percentage (2.7 %) of the total number of angle measure units. Recall that Judy and Zac used a similar equation and calculations to determine an angle measure during the preinterview, but their explanations conveyed that their solution stemmed from a calculational strategy (Excerpt 1); the ratios did not represent the measure of a quantity formed by making a multiplicative comparison between two other quantities. In the present case, their ratios represented an equivalent percentage (e.g., a multiplicative relationship) of the total number of angle measure units (e.g., ratio as value).

To conclude the first teaching session, I implemented the protractor applet (Fig. 7). I designed the applet so that the user can increase/decrease the radius of the circle or the angle’s openness, with the displayed measures varying correspondingly. I used the applet to formalize the prior outcomes and continue promoting a focus on expressions and calculations as representative of quantities’ values.

Fig. 7

The protractor applet

As I posed either a varying radius or a varying openness of the angle, both students correctly predicted how the measures change or stay constant. For instance, Zac predicted that, for a decreasing radius, “The arc length of A B and the circumference will get smaller, but the angle [measure] and percent will stay the same.” It is important to note that the students’ ability to correctly predict how the measures change reveal a capacity to reason about indeterminate values. That is, they were able to imagine the measures of the various quantities varying and justify these variations using their angle measure understandings without reasoning about specified values and performing calculations to determine these comparisons. The students also spoke with extreme precision when describing the values on the applet. As opposed to referencing “the circle” or using ambiguous referents (e.g., it), the students explicitly mentioned “the circumference” and “the arc length” and discussed the beginning and ending points for all identified lengths. Although using such specific terms might seem of little consequence, previous research (Moore & Carlson, 2012) has revealed that precalculus students frequently reason about lengths in ambiguous ways and thus do not construct precise quantitative structures of problem situations that support products (e.g., calculations, formulas, and graphs) correctly relating quantities’ values.

6.4 Creating circles and measuring in radii

During the second teaching session, I transitioned the instruction to radian angle measure. The circumference problem (Fig. 8) prompted the students to create a circle with a radius having the length of a piece of waxed string and then measure various string (radii) lengths along the circle’s circumference. During the task and in line with their actions during the protractor problem, I intended that the students develop a scheme for radian angle measure involving partitioning an arc length into a number of unit lengths (e.g., radii).

Fig. 8

The circumference problem

I intended that the circumference problem support the students in leveraging several facets of their reasoning from the first teaching session. First, I hoped to engage the students in measuring along a circle’s circumference to partition the circumference into equal lengths. Second, a major outcome of the first teaching session was that an angle measure conveys a fractional amount of a circle’s circumference cut off by the angle that is not dependent on the size of the circle. Building off of this outcome, Judy’s and Zac’s strings were of different lengths with the hope that the students realize that the size of the circle used to create an angle subtending a particular number of radii is inconsequential.

At the outset of the circumference problem, Zac recalled the formula relating the circumference and radius of a circle (C = 2πr), yet neither student was able to clarify how the task relates to this formula. After creating circles and using the waxed strings to determine that approximately the same number of string lengths (2π) marked off the circles’ circumferences, they conjectured that, if an individual measures an equivalent number of string lengths along her circumference, then the resulting arc lengths correspond to angles with an equivalent amount of openness. Following their observation, I asked the students to discuss using a unit of angle measure based on a circle’s radius (Excerpt 3).

Excerpt 3

	Zac:	Is it a useful unit of measure, well yes or no, what do you think? We could use quips, but is it useful?
	Judy:	I don’t know.
	Zac:	It simplifies the circle, you know, the circumference of the circle is equal to two pi r. The radius is the unit, not inches or centimeters or anything like that.
	Judy:	Oh, you mean, oh! OK. So you mean, OK. I think I’m thinking in terms of the length of the radius.
	Zac:	We’re using it as an actual unit… One radius, and then six point two eight radius, or radians.

While Zac appeared to conceive the radius as a unit that “simplified a circle” to a radius of “one radius” and a circumference of “six point two eight radius,” Judy’s response to Zac suggests that she was initially considering measuring the length of the radius and not considering the length of the radius as a unit to measure other lengths. As the discussion continued, Judy claimed, “OK, yeah, in that sense, you don’t have to bother with length numbers,” using “length numbers” to refer to measures of the radius in a unit other than radii.

I returned the discussion to the number of 6.28. The students’ responses suggest that both were considering the radius as a unit of measure that could be used for any circle (Excerpt 4).

Excerpt 4

Int.:	So what measurement does that represent, six point two eight?
Zac:	That’s always the circumference on every circle.
Int.:	That’s always the circumference measured in what units?
Judy:	Radiuses.

At this point in the lesson, we defined the term radian ¹⁰ as a measure that stems from the process of measuring in radii and subsequently asked the students to describe the meaning of various radian angle measures, including 1.5, 3.5, and π radians. In each case, the students described the measures in terms of an angle subtending an arc of that number of radii. Zac explained that an angle with a measure of 1.5 rad subtends “one and a half radiuses,” regardless of the circle used to measure the angle. As another example, Judy stated that multiplying π radians by the length of a circle’s radius determines the arc length subtended by an angle that measures π radians, “Because π is just an amount of, um, radiuses along the circumference. So you would just need to multiply by the radius length.”

6.5 Post-interviews

By the completion of the second teaching session, the students had exhibited multiple ways of thinking about angle measure that stemmed from measuring (e.g., an act of partitioning) along arc lengths in various units (e.g., radii, degrees, and conventional length units) and coordinating these measures. Of particular importance, the students reasoned about (a) multiplicative comparisons between arc lengths and circles’ circumferences and (b) multiplicative comparisons between arc lengths and circles’ radii. The teaching sessions did not fully explore connections between these ways of thinking and I questioned if the students would continue to use such reasoning after the teaching sessions. I conducted an interview session with each student 2 weeks after the second teaching session to gain deeper insights into their thinking.

I first tasked Zac with the arc length problem (Fig. 9). Zac explained his solution previous to executing calculations (Excerpt 5).

Given that the following angle measurement θ is 35 degrees, determine the length of each arc cut off by the

angle. Consider the circles to have radius lengths of 2 inches, 2.4 inches, and 2.9 inches (figure not to scale).

Fig. 9

The arc length problem

Excerpt 5

Zac:

So what I plan on doing for this one is converting thirty-five degrees into radians. And a very easy way of doing that is putting thirty-five over three sixty is equal to x over two pi (writing corresponding equation)…And then with that all I have do is just multiply the answer (pointing to x) by two inches, two point four inches, and two point nine inches (pointing to each value in the problem statement) to get the different arc lengths (identifying each arc length with his pen tip) right there, because radians is just a percentage of a radius.

Stemming from understanding radian measures as a multiplicative relationship between a set of arcs and corresponding radius lengths, Zac anticipated using the radian measure to determine each arc length. That is, his understanding of radian angle measures was such that he was able to give meaning to calculations involving these measures without executing the calculations. Likewise, Zac anticipated converting the angle measure by conceiving angle measures as a fractional amount of a circle’s circumference. Zac explained, “Well what you’re doing is just technically finding a percentage. Like thirty-five over three sixty is (using calculator), is nine point seven percent of the full circumference.”

Differing from Zac, Judy did not first convert the angle measures to a number of radians. Instead, Judy used the equation $\left( {35/360} \right)=\left( {x/\left( {2\pi r} \right)} \right)$ for each radius. Judy claimed, “if you have your first circle and you increase the radius then even though the percentage of the entire circle is the same, you have to compensate with a larger arc length in inches.” Compatible with Zac’s conversion method, Judy’s solution came as a consequence of understanding angle measures as conveying a fractional amount of a circle’s circumference.

At various points in the interviews, I also asked the students to describe radian angle measures. When explaining the meaning of an angle measure of 0.61 rad, Zac fluently transitioned between reasoning about a radian angle measure as a multiplicative relationship between a subtended arc and a radius of a circle and as a multiplicative relationship between a subtended arc and the circumference of a circle. Moreover, understanding angle measures as a fraction of a circle’s circumference subtended by the angle enabled Zac to give an invariant meaning to degree and radian angle measures (Excerpt 6).

Excerpt 6

	Zac:	That means that this arc length right here (tracing the arc length on the smallest circle) is point six one, or sixty one percent of the radius.
	Int:	OK. Now (pause), and then so why times…with the point six one (pointing to 0.61(x), the calculation Zac used to solve the problem).
	Zac:	Well because I couldn’t just leave it as radians, so I have to get it in inches, or you know, an actual distance measure. So knowing that it’s sixty one percent, or it’s equal to sixty one percent of the radius, all I have to do is just multiply it by the radius and I know what it is.
	Int:	OK, so one last question. So we have all these different lengthed arcs right (tracing the three arcs)…but yet that angle measurement doesn’t change?
	Zac:	Well, because it’s always the same percent of the circle it’s cutting out for each different circle…
	Int:	OK…so what’s the same percent there you said?
	Zac:	The, well, the degrees or radians is showing a chunk of the circle being cut out, and that’s a certain percent of the circle being cut out. It’s always the same no matter what, as long as you’re using that same degree or radian length, then you’re always going to have that same amount, or same percent of the circle, or circumference being cutout no matter what size the radius is, or the circumference of the circle is (making circular motion with hand).

Like Zac, Judy also reasoned about measures in radians as conveying a multiplicative relationship between a subtended arc and the radius. Specifically, she described that she thought of radian measures as a “function,” meaning that the measures described a relationship between two quantities that holds for all circles. In Excerpt 7, she describes measures of 5.27 and 1.2π radians in the context of a circle with a radius of 3.5 in. (Fig. 10).

Fig. 10

Judy’s diagram for angle measures

Excerpt 7

	Judy:	It means that if you travel from your starting point here, and you travel counterclockwise (tracing arc length), you travel five point two seven times your radius length along the circumference (moving her pen tip in the shape of a circle).
	Int:	OK, what about the one point two pi radians? What’s that mean…
	Judy:	Um, I guess one point two pi times the radius length, which is, (using calculator) um, about three point seven seven radius lengths.
	Int:	OK, so what role does pi play in that?
	Judy:	Just a number. Oh, and then the arc length is, um, I just multiplied the radians times the radius length (3.5 inches) to get the arc length, which is eighteen point four four five.
	Int:	So why does that operation work, why does that give you the arc length?
	Judy:	Um, because, uh, I kind of look at the radians like a function almost, so I always look at it as five point two seven times whatever the radius length is, is the linear arc length ‘cause um, that’s how it translates to any other circle you use. So if it was a larger one where the radius was five, then I’d multiply it by five instead.

I note that Judy’s description suggests that she imagined traveling along an arc. Zac also exhibited behaviors throughout his interview suggestive of this imagery. I conjecture that their image of traveling along an arc stemmed from repeatedly measuring along a subtended arc length during previous tasks.

As the study progressed, there was a noticeable shift in the students’ thinking from reasoning about numbers and calculations to reasoning about quantitative relationships independent of specified values. During the teaching sessions, we had not focused on developing formulas, but I expected that their thinking about quantitative relationships involving indeterminate values would support the use of formulas to represent relationships. To test this conjecture, I gave each student the arc problem (Fig. 11). Both students’ formulas emerged as representative of a multiplicative relationship between a subtended arc and corresponding radius (Excerpts 8 and 9).

Fig. 11

The arc problem

Excerpt 8

Judy:

Oh, um, then, theta is equal to s over r…because radians is, it calculates the number of radius lengths that have passed along the circumference.

Excerpt 9

Zac:

We’ll say theta equals radians (writing θ = rad), very very simple then. r theta is equal to s (writing rθ = s). ‘Cause theta is in radians, that means a percentage of the radius. Which would then be equal to this length (tracing arc length). So you multiply the percentage of the radius by the radius, you’ll get the arc length.

7 Discussion

Returning to Thompson’s characterization of quantification, quantifying a quantity involves “a process of settling what it means to measure a quantity, what one measures to do so, and what a measure means after getting one” (Thompson, 2011, p. 38). In other words, one’s understanding of a quantity inherently involves her quantifying of that quantity. I discuss the students’ quantification of angle measure in two parts. First, I discuss critical operations involved in the students’ quantification of angle measure. I then highlight other central aspects of quantitative reasoning that emerged as critical for their quantification process, such as their capacity to reason about indeterminate values.

7.1 The students’ quantification of angle measure

Upon entering the study, Judy and Zac’s thinking about angle measure was constrained to situations in which they were given angle measures or numbers with which to execute calculational strategies to obtain angle measures. Angle measures, to Judy and Zac, were intrinsic properties of geometric objects and relatable to other angle measures through calculations (e.g., supplementary or complementary angles). They appeared to have no discernible scheme of what one measures when measuring an angle, nor did their angle measure understandings include a quantitative meaning for the units used to measure the openness of an angle. Without a robust understanding of the process of measuring an angle and how the structure of the unit relates to this process, it made little sense for them to discuss the meaning of angle measures independent of other angle measures and geometric objects.

As the study progressed, the students conceived situations in ways that supported their constructing specific quantitative meanings for angle measure. More pointedly, by encountering situations in which they engaged in the partitioning of subtended arc lengths and reflecting on these actions, the students conceived degree and radian angle measures (as well as other informal units like quips) as one in the same: both units convey the fractional amount of a circle’s circumference that is subtended by an angle with that measure. To quantify angle measure as such required that the students conceive a subtended arc length as a property of an angle’s openness to be partitioned into unit lengths, where each unit length is a fractional amount of a circle’s circumference. Encountering multiple situations in which these actions were purposeful likely supported such quantification acts, leading to their abstracting angle measure as representative of quantitative relationships. For instance, their connecting angle measure to the subtended fractional amount of any circle’s circumference stemmed from identifying and comparing arc lengths per unit of angle measure on multiple circles. Similarly, the students came to understand radian angle measures as a multiplicative relationship that holds for any circle by comparing radii measures on multiple circles.

Judy and Zac’s capacity to reason about multiplicative relationships, which included interpreting expressions as representing multiplicative relationships, played a critical role in their quantification of angle measure. During the preinterview, the students used ratios during their solutions, but these ratios did not represent multiplicative relationships. A critical transition in their thinking occurred when they conceived several ratios between arc lengths and circumferences as representing the same multiplicative relationships. As the students reflected on different arc lengths on different circles corresponding to the same angle measure, the students reasoned that the ratio a/b conveys that a is a/b times as large as b. In turn, they concluded that an angle measure conveys the fractional amount of any circle’s circumference that is subtended by the angle. Likewise, Judy and Zac concluded that a measure in radians conveys that the subtended arc is so many times as large as the corresponding circle’s radius. Without such multiplicative reasoning schemes available, the students likely would have quantified angle measures in an entirely different manner.

7.2 Quantitative reasoning and indeterminate values

The students came to understand angle measure as the process of (a) constructing a circle centered at the vertex of the angle, (b) measuring the circle’s circumference and subtended arc length, (c) determining the fractional amount of the circumference subtended by the angle, and (d) determining the number of angle measure units that correspond to that fractional amount.¹¹ It is important to note that the end product of the students’ quantification of angle measure was such that they were not constrained to carrying out these actions. That is, they reasoned about such actions and relationships without having to physically carry them out, execute calculations, or determine specified values.

In principle, quantitative reasoning is based on constructing relationships between quantities such that specified values are inconsequential to the conceived relationships (Smith & Thompson, 2008). Specified values come into play when attempting to determine particular quantities’ values, but they are not required to reason about quantities and relationships between these quantities. Thus, quantitative reasoning rests on the capacity to reason about indeterminate values. As evidence of reasoning based on quantitative relationships, during the latter parts of the study, the students anticipated calculations during their solutions by reasoning about indeterminate values. The students also produced formulas and equations that stemmed from quantitative relationships between indeterminate values. The students’ tendency to reason about indeterminate values and quantitative relationships, as opposed to numbers and calculations, was most apparent during the post-interview sessions (Excerpts 5–9). For instance, both students determined the standard formulas of s = rθ and θ = s/r by reasoning about unspecified radian angle measures as measures of arcs in radii. The fluency by which they produced these formulas and the reasoning that supported this fluency stand in stark contrast with previous research on students’ and teachers’ understandings of radian angle measure (Akkoc, 2008; Topçu et al., 2006).

In their description of quantitative reasoning, Smith and Thompson (2008) argued, “If students are eventually to use algebraic notation and techniques to express their ideas and reasoning productively, then their ideas and reasoning must become sufficiently sophisticated to warrant such tools” (p. 98). In the present study, the students’ reasoning indicates that paying particular attention to students’ quantification of a quantity can support the productive use of algebraic notation and techniques. By developing understandings rooted in quantities and relationships between these quantities, the students’ understandings afforded the use of formulas, equations, and calculations to represent relationships between quantities and indeterminate values.

8 Concluding remarks

The results of this study contribute to the growing body of research (e.g., Castillo-Garsow, 2010; Ellis, 2007; Johnson, 2012; Thompson, 1994) that reveals the critical role of quantitative reasoning in learning mathematics. Specifically, the students’ progress was contingent on ideas of measurement, multiplicative reasoning, and reasoning about indeterminate values, all central strands of quantitative reasoning. How students who lack critical measurement and multiplicative reasoning schemes would progress during a similar instructional sequence remains a question open for investigation. Studies that pursue students’ progress under these circumstances have the potential to contribute to the body of knowledge on students’ angle measure understandings, including how various reasoning abilities, or the lack thereof, influence their angle measure understandings.

In addition to being of interest to teachers and researchers of undergraduate precalculus students, the findings are also pertinent to those involved in the teaching and learning of secondary students. Research has identified that quantitative reasoning can support middle and secondary school students' learning of precalculus ideas, including exponential (Castillo-Garsow, 2010) and quadratic (Ellis, 2007) functions. The students of the present study also showed performance in their precalculus course comparable to that of secondary precalculus students. Thus, secondary students might also benefit from an approach to angle measure that is based on principles of quantitative reasoning. Future studies that investigate secondary students’ quantification of angle measure are needed, the results of which will likely produce additional insights into the role of quantitative reasoning in secondary students’ learning.

While the study’s findings suggest that an arc approach to angle measure can foster coherent experiences for students, I caution the reader to conclude that all arc approaches to angle measure will produce such experiences. Instead, the students’ actions emphasize that an arc approach to angle measure is beneficial when the approach foregrounds quantitative reasoning, and namely, the quantification of angle measure. Quantification is not a passive activity; it is a cognitive process. As Thompson (2011) described, the quantification process is a critical and complex part of conceiving a quantity and this process takes time (sometimes years). If we, as educators, expect students to understand angle measure (and other quantities), then we must take seriously their quantification of angle measure, which includes creating a need and giving time for students’ quantification acts. Introducing angle measures (and using arcs) without taking seriously the quantification of angle measure likely sends students the message: use these numbers to perform calculations and find other numbers, but do not worry about what the numbers, arcs, and calculations mean. Likewise, giving students a protractor without addressing how to measure an angle in the absence of a protractor likely sends the message: use this protractor to measure an angle, but do not worry about the structure behind the protractor. In contrast, placing quantification at the forefront of the teaching of angle measure positions students to conceive quantities and relationships between quantities as inherent to the process of measuring an angle.