Upper bound of the length of truncated impossible differentials for AES

Abstract

On the provable security of a block cipher against impossible differential cryptanalysis, the maximal length of impossible differentials is an essential aspect. Most previous work on finding impossible differentials for AES, omits the non-linear component (S-box), which is important for the security. In EUROCRYPT 2016, Sun et al. showed how to bound the length of impossible differentials of a SPN “structure” using the primitive index of its linear layer. They proved that there do not exist impossible differentials longer than four rounds for the AES “structure”, instead of the AES cipher. Since they do not consider the details of the S-box, their bound is not feasible for a concrete cipher. With their result, the upper bound of the length of impossible differentials for AES, is still unknown. We fill this gap in our paper. By revealing some important properties of the AES S-box, we further prove that even though the details of the S-box are considered, there do not exist truncated impossible differentials covering more than four rounds for AES, under the assumption that round keys are independent and uniformly random. Specially, even though the details of the S-box and key schedule are both considered, there do not exist truncated impossible differentials covering more than four rounds for AES-256.

1 Introduction

Since Rijndael was selected as the Advanced Encryption Standard (AES) [8], its security has been widely studied by many cryptanalysts. Differential cryptanalysis [5] and linear cryptanalysis [19] are among the most powerful cryptanalysis tools, against which the AES adopts “wide trail strategy [9]” to provide elegant provable security. Differential attack makes use of differential characteristics with high probability to sieve right keys. By counting the number of differential active S-boxes (S-box with non-zero input difference) in a differential characteristic covering several rounds, we could give upper bound on the differential probability of this differential characteristic. Things are similar for the linear attack.

Unlike differential attack, impossible differential attack [3, 15] utilizes impossible differentials, namely differentials with probability 0, to discard wrong keys. Among these impossible differentials, truncated impossible differentials [13, 16] attract much attention. For AES, there are many four-round truncated impossible differentials being constructed [1, 4, 6, 22]. In [1, 4, 6, 22], some four-round truncated impossible differentials, which are the longest truncated impossible differentials found so far for AES, are used to mount impossible differential attack on (seven-round) AES-128. Therefore, the maximal length of impossible differentials for a cipher, are estimated to evaluate the resistance of this cipher against impossible differential cryptanalysis.

Although many approaches (like U-method [14], UID-method [18], WW-method [26] and Cui-method [7]) have been proposed to find impossible differentials for SPN block ciphers, they do not take advantage of the properties of the non-linear substitution layer (e.g., S-box), which might result in tighter bound on the length of impossible differentials.

In EUROCRYPT 2016, Sun et al. [24] utilized the “primitive index” [7, 24] of the linear layer of SPN “structure”, to bound the length of impossible differentials. They proved that there do not exist impossible differentials covering more than four rounds for AES “structure”. Their target is not the concrete cipher, but the “structure” [24, 25]:

Definition 1

[24] Let $E:F_{2}^{n}\rightarrow F_{2}^{n}$ be a block cipher with bijective S-boxes as the basic non-linear components.

• 1. A structure ${{\varepsilon }^{E}}$ on $F_{2}^{n}$ is defined as a set of block ciphers ${E}'$ which is exactly the same as E except that the S-boxes can take all possible bijective transformations on the corresponding domains.

• 2. Let $a,b\in F_{2}^{n}$. If for any ${E}'\in {{\varepsilon }^{E}}$, $a\rightarrow b$ is an impossible differential of ${E}'$, $a\rightarrow b$ is called an impossible differential of ${{\varepsilon }^{E}}$.

With their method, we are able to get the upper bound of the length of impossible differentials for a “structure”. However, the concept of “structure” is far from practical cipher, since S-boxes are often fixed, or varying within a much small subspace of the space of all bijective S-boxes (when viewing AddRoundKey transformation and fixed S-boxes into variable S-boxes controlled by keys) in a concrete cipher. Their method cannot prove that there do not exist impossible differentials covering more than four rounds for AES.

These existing methods do not exploit the properties of the non-linear S-box transformation. Therefore, finding a method, that exploits the properties of the S-boxes and gives practical maximal length of impossible differentials for SPN ciphers (such as AES and AES-like ciphers), is a problem worth further investigating.

Relation to the five-round impossible differential distinguisher proposed by Grassi et al. [11]. As we mentioned before, four-round “key-independent” impossible differentials are used to mount impossible differential attack on round-reduced AES (typically on seven-round AES-128). Such a four-round key-independent impossible differentials can be used to mount key-recovery attacks on five-round AES, namely, five-round AES can be distinguished from a random permutation on knowing some key bytes of the first or last round. In [23], a five-round “key-dependent” zero-correlation linear hull (it can also be seen as an impossible differential) was derived from a four-round “key-independent” zero-correlation linear hull, on knowing the difference of two key bytes. This “key-dependent” distinguishing property (in other words, five-round key-recovery attack) was further turn into a five-round integral distinguisher on AES by Sun et al. [23]. Later, such five-round “key-dependent” distinguisher property was further explained with “subspace trails” notation and greatly improved by Grassi et al. [11]. In [11], Grassi et al. set up an impossible differential attack on five rounds of AES to recover the difference of two key bytes, based on a four-round “key-independent” impossible differential. Furthermore, they turned this five-round key recovery attack into a five-round (subspace) impossible differential distinguisher for AES. Therefore, both the five-round zero-correlation linear hull in [23] and five-round impossible differential in [11] are much different from the usual “key-independent” zero-correlation linear hulls or impossible differentials that are used in the zero-correlation linear attack or the impossible differential attack. In our paper, we consider the maximal length of the core “key-independent” impossible differentials, that are used in the impossible differential attacks and their [11, 23] five-round distinguisher on AES.

Our contributions By revealing some important properties of the AES S-box, we prove that there do not exist truncated impossible differentials covering more than four rounds for AES with the details of S-boxes considered (stronger than the ”structure” as [24]), under practical assumption that round keys are independent and uniformly random. Specially, for AES-256, even though the S-boxes and the key schedule are both taken into consideration, there do not exist truncated impossible differentials covering more than four rounds.

Outline In Sect. 2, we give some preliminaries to make our representation clear and understandable. In Sect. 3, we reveal an important property of the AES S-box, and then attain the longest rounds of truncated impossible differentials for AES. Whole paper is concluded in Sect. 4.

2 Preliminaries

2.1 Notations

• $\oplus$ : bitwise XOR (it is coincided with the addition in the finite field ${F}_{2^8}$ in our representation).

• $a{\mathop {\vee }}b$ : bitwise OR of binary vectors a and b.

• |A| or $\#\{A\}$: the number of elements in the set A.

• X : matrix defined over a finite field, $X={{({{x}_{i,j}})}_{4\times 4}}$, ${{x}_{i,j}}\in F_{2^8}$.

• ${{x}_{\centerdot ,j}}$ : the jth column of the state matrix X.

• $\varDelta X$ : the difference of X.

• $\varDelta \tilde{X}$ : the truncated difference of X.

• $\circ$ : composition of transformations.

• $f,{f}^{-1}$ : transformation f and its inverse.

2.2 Some definitions

AES is an SPN block cipher with block size 128 bits. These 128 bits are organized as a $4\times 4$ matrix of bytes, denoted by $X={{({{x}_{i,j}})}_{4\times 4}},{{x}_{i,j}}\in {F}_{2^8}$, as Fig. 1.

Fig. 1

AES state

The round function of AES is composed of four transformations [8, 20]:

• 1. SubBytes (SB): apply the same 8-bit invertible S-box to 16 bytes in parallel. The S-box is composed of the multiplicative inverse function in ${F}_{2^8}$ and an invertible affine transformation, denoted by $s(x)=A\cdot {{x}^{-1}}\oplus b$.

• 2. ShiftRows (SR): shift the ith row by i bytes to the left circularly.

• 3. MixColumns (MC): left multiplication by a $4\times 4$ MDS matrix with elements in ${F}_{2^8}$. This matrix and its inverse are defined as:

  $$\begin{aligned} C=\left[ \begin{matrix} 2 &{} 3 &{} 1 &{} 1 \\ 1 &{} 2 &{} 3 &{} 1 \\ 1 &{} 1 &{} 2 &{} 3 \\ 3 &{} 1 &{} 1 &{} 2 \\ \end{matrix} \right] , {{C}^{-1}}=\left[ \begin{matrix} e &{} b &{} d &{} 9 \\ 9 &{} e &{} b &{} d \\ d &{} 9 &{} e &{} b \\ b &{} d &{} 9 &{} e \\ \end{matrix} \right] . \end{aligned}$$

• 4. AddRoundKey (${AK}_{K^i}$): bitwise exclusive-or with 128-bit round key $K^i$. $K^i$ denotes the subkey of the ith round, and $K^0$ denotes the whiten key before the first round.

The ith full round transformation of AES can be written as ${{AK}_{K^i}} \circ MC \circ SR \circ SB$. Since SR and MC are linear, we could change the order of SR, MC and ${AK}_{K^i}$ by XORing equivalent subkeys before MC or SR, denoted by $MC \circ {{AK}_{{{MC}^{-1}} (K^i)}} \circ SR \circ SB$ and $MC \circ SR \circ {{AK}_{{{SR}^{-1}} \circ {{MC}^{-1}} (K^i)}} \circ SB$ respectively. Here, ${{MC}^{-1}}(K^i)$ and ${{SR}^{-1}} \circ {{MC}^{-1}} (K^i)$ denote the equivalent subkeys at differential places respectively.

We wouldn’t introduce the details of the key schedule of AES, since our main result is under the assumption that its round keys are independent and uniformly random.

Definition 2

For function $f:F_{2}^{n}\mapsto F_{2}^{n}$, its differential probability for the differential $\varDelta x\rightarrow \varDelta y$ is defined as:

$$\begin{aligned} P(\varDelta x\xrightarrow {f}\varDelta y)=\frac{\#\left\{ x|f(x\oplus \varDelta x)\oplus f(x)=\varDelta y\right\} }{{{2}^{n}}}. \end{aligned}$$

Definition 3

For a keyed function ${{f}_{k}}:F_{2}^{n}\mapsto F_{2}^{n},k\in K$, its differential probability for differential $\varDelta x\rightarrow \varDelta y$ is defined as:

$$\begin{aligned} P(\varDelta x\rightarrow \varDelta y)=\frac{\text {1}}{\left| K \right| }\sum \limits _{k\in K}{P\left( \varDelta x\xrightarrow {{{f}_{k}}}\varDelta y\right) }. \end{aligned}$$

Definition 4

(Pattern) Let $X=({{x}_{1}},{{x}_{2}},\ldots ,{{x}_{n}})\in {F_{2^m}^n}$, then the pattern of X is defined as:

$$\begin{aligned} \chi (X)=({{y}_{1}},{{y}_{2}},\ldots ,{{y}_{n}})\in {F_2^n}, \end{aligned}$$

where ${{y}_{i}}=0$ if ${{x}_{i}}=0$, and ${{y}_{i}}=1$ otherwise.

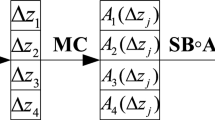
To characterize the diffusion of differences through the MixColumns transformation, we define the operation of MC on the difference patterns (truncated differences) as:

Definition 5

For the MixColumns transformation MC of AES, its operation on the state pattern (or truncated difference) $\tilde{X}=({\tilde{x}}_{i,j})_{4\times 4}$, is defined as: let state pattern $\tilde{Y}=MC (\tilde{X})$, then the $j^{th}(0\le j\le 3)$ column of $\tilde{Y}$ is calculated as ${{\tilde{y}}_{\centerdot ,j}}=MC ({{\tilde{x}}_{\centerdot ,j}})=({{\tilde{x}}_{0,j}}{{\tilde{c}}_{\centerdot ,0}}){\mathop {\vee }} ({{\tilde{x}}_{1,j}}{{\tilde{c}}_{\centerdot ,1}}){\mathop {\vee }} ({{\tilde{x}}_{2,j}}{{\tilde{c}}_{\centerdot ,2}}){\mathop {\vee }} ({{\tilde{x}}_{3,j}}{{\tilde{c}}_{\centerdot ,3}})$, where ${{\tilde{c}}_{\centerdot ,i}}=\chi (c_{\centerdot , i})$ and $c_{\centerdot , i}$ denotes the $i^{th}(0\le i\le 3)$ column of the MixColumns matrix C. Similar for ${{MC }^{-1}}$.

Definition 6

[13] For function $f:{F_{2^m}^n}\mapsto {F_{2^m}^n}$, its truncated differential probability for truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Y}$ is defined as:

$$\begin{aligned} P(\varDelta \tilde{X}\xrightarrow {f}\varDelta \tilde{Y})=\frac{\sum \limits _{\chi (\varDelta X)=\varDelta \tilde{X},\chi (\varDelta Y)=\varDelta \tilde{Y}}{P(\varDelta X\xrightarrow {f}\varDelta Y)}}{\#\left\{ \varDelta X|\chi (\varDelta X)=\varDelta \tilde{X}\right\} }. \end{aligned}$$

Definition 7

For a keyed function ${{f}_{k}}:{F_{2^m}^n}\mapsto {F_{2^m}^n},k\in K$, its truncated differential probability for truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Y}$ is defined as:

$$\begin{aligned} P(\varDelta \tilde{X}\xrightarrow {{{f}_{k}},K}\varDelta \tilde{Y})=\frac{1}{\left| K \right| }\sum \limits _{k\in K}{P(\varDelta \tilde{X}\xrightarrow {{{f}_{k}}}\varDelta \tilde{Y})}. \end{aligned}$$

Then for a cipher ${{E}_{k}}$ with key space K, a truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Y}$ is impossible if $P(\varDelta \tilde{X}\xrightarrow {{{E}_{k}},K}\varDelta \tilde{Y})=0$, which means that for any $k\in K$ and any differential $\varDelta X \rightarrow \varDelta Y$ such that $\chi (\varDelta X)=\varDelta \tilde{X}$ and $\chi (\varDelta Y)=\varDelta \tilde{Y}$, we have $P(\varDelta X \xrightarrow {{{E}_{k}}}\varDelta Y)=0$. However, $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Y}$ is possible if for some $k\in K$ and differential $\varDelta X \rightarrow \varDelta Y$ such that $\chi (\varDelta X)=\varDelta \tilde{X}$ and $\chi (\varDelta Y)=\varDelta \tilde{Y}$, we have $P(\varDelta X \xrightarrow {{{E}_{k}}}\varDelta Y)\ne 0$.

3 Our claims on AES

To prove that the upper bound of the length of truncated impossible differentials for AES is four rounds, we would show that any nontrivial truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Y}$ is possible for five-round AES (without MixColumns in the last round). As stated at the end of the Section 2.1, we aim to construct a concrete differential $\varDelta X \rightarrow \varDelta Y$ such that $\chi (\varDelta X)=\varDelta \tilde{X}$ and $\chi (\varDelta Y)=\varDelta \tilde{Y}$, as well as a series of round keys (we make the assumption that round keys are independent and uniformly random), which make that $P(\varDelta X\xrightarrow {5\_round\_AES}\varDelta Y)\ne 0$.

Firstly, we need to investigate some details about the AES S-box in Sect. 3.1.

3.1 Some properties of the AES S-box

In this section, we investigate the properties of the AES S-box. The AES S-box is composed of two functions: the multiplicative inverse function in ${F}_{2^8}$, denoted by $x^{-1}$, and an invertible affine transformation, denoted by $L(x)=A\cdot x \oplus b$. Then, the AES S-box is described as:

$$\begin{aligned} s(x)=L(x^{-1})=A\cdot x^{-1} \oplus b,\text { }with\text { }0^{-1}=0, \end{aligned}$$

here,

$$\begin{aligned} A=\left[ \begin{matrix} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{matrix} \right] ,b=\left[ \begin{matrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ \end{matrix} \right] . \end{aligned}$$

We mainly focus on the properties of the multiplicative inverse function in ${F}_{2^8}$. Then, a nontrivial differential $\alpha \rightarrow \beta$ is possible for this function if for some x,

$$\begin{aligned} (x\oplus \alpha )^{-1} \oplus x^{-1}=\beta . \end{aligned}$$

(1)

For Eq. (1), when the output difference $\beta$ is fixed, the set of all the possible input difference $\alpha$ possesses a special property, deduced by Daemen et al. [10]. This property can be expressed as the following lemma:

Lemma 1

For any nonzero output difference $\beta$ of the multiplicative inverse function in ${F}_{2^8}$, the set of the multiplicative inverse elements of all the possible input differences $\alpha$ (add 0 element) forms a 7-dimensional linear space over $F_2$. Namely, ${{V}_{\beta }}=\{{{\alpha }^{-1}}|{{(x\oplus \alpha )}^{-1}}\oplus {{(x)}^{-1}}=\beta ,x\in {F}_{2^8}\}\bigcup \{0\}$ is a 7-dimensional linear space over $F_2$.

Proof

This fact has been proved by Daemen et al. [10]. $\square$

Based on the linear property of the multiplicative inverse function in Lemma 1, we can get the following essential property of the AES S-box, which plays an important role in the construction of our differential trails.

Theorem 1

For all $({{\beta }_{0}},{{\beta }_{1}},{{\beta }_{2}},{{\beta }_{3}})\in {{[{F}_{2^8}^{*}]}^{4}},({{c}_{0}},{{c}_{1}},{{c}_{2}},{{c}_{3}})\in {{[{F}_{2^8}^{*}]}^{4}}$, there exist $({{k}_{0}},{{k}_{1}},{{k}_{2}},{{k}_{3}})\in {{F}_{2^8}^{4}}$ and $\alpha \in {{F}_{2^8}^{*}}$, satisfying the following system of equations:

where s denotes the AES S-box, $s(x)=A\cdot {{x}^{-1}}\oplus b$ and ${{0}^{-1}}=0$.

Proof

By peeling off the bijective affine transformation in AES S-box s, we get that the system (*) is equivalent to the following one

By Lemma 1, we know that ${{V}_{{{c}_{i}}({{A}^{-1}}{{\beta }_{i}})}}(0\le i \le 3)$ are all 7-dimensional linear space over $F_2$. Since ${F}_{2^8}$ is an 8-dimensional linear space over $F_2$, we have $\left| {{V}_{{{c}_{0}}({{A}^{-1}}{{\beta }_{0}})}}\bigcap {{V}_{{{c}_{1}}({{A}^{-1}}{{\beta }_{1}})}}\bigcap {{V}_{{{c}_{2}}({{A}^{-1}}{{\beta }_{2}})}}\bigcap {{V}_{{{c}_{3}}({{A}^{-1}}{{\beta }_{3}})}} \right| \ge {{2}^{4}}$. Take nonzero ${{\alpha }^{-1}}\in {{V}_{{{c}_{0}}({{A}^{-1}}{{\beta }_{0}})}}\bigcap {{V}_{{{c}_{1}}({{A}^{-1}}{{\beta }_{1}})}}$ $\bigcap {{V}_{{{c}_{2}}({{A}^{-1}}{{\beta }_{2}})}}$ $\bigcap {{V}_{{{c}_{3}}({{A}^{-1}}{{\beta }_{3}})}}$, then there exists corresponding ${{x}_{i}}(0\le i \le 3)$ such that ${{c}_{i}}({{A}^{-1}}{{\beta }_{i}})={{(\alpha \oplus {{x}_{i}})}^{-1}}\oplus {{({{x}_{i}})}^{-1}}(0\le i \le 3)$. Take ${{k}_{i}}={{c}_{i}}{{x}_{i}}(0\le i \le 3)$. Thus, resulting $\alpha \in {{F}_{2^8}^{*}}$ and $({{k}_{0}},{{k}_{1}},{{k}_{2}},{{k}_{3}})\in {{F}_{2^8}^{4}}$ satisfy the system (**), also the system (*). $\square$

3.2 Bound the length of truncated impossible differentials for AES

To prove that any nontrivial truncated differential $\varDelta \tilde{X}^0\rightarrow \varDelta \tilde{X}^5$ is possible for five-round AES (without MixColumns in the last round), the main idea of our proof is: for any nontrivial truncated differential $\varDelta \tilde{X}^0\rightarrow \varDelta \tilde{X}^5$, construct a five-round truncated differential trail, $\varDelta \tilde{X}^0 \rightarrow \varDelta \tilde{X}^1 \rightarrow \varDelta \tilde{X}^2 \rightarrow \varDelta \tilde{X}^3 \rightarrow \varDelta \tilde{X}^4 \rightarrow \varDelta \tilde{X}^5$, following from Sun’s idea “meet-in-the-middle” in [24] (this procedure is shown with a special example in Fig. 2); along with the construction of this truncated differential trail, a concrete differential trail, $\varDelta X^0 \rightarrow \varDelta X^1 \rightarrow \varDelta X^2 \rightarrow \varDelta X^3 \rightarrow \varDelta X^4 \rightarrow \varDelta X^5$ such that $\chi (\varDelta X^i)=\varDelta \tilde{X}^i$, is constructed, whose existence heavily depends on the algebraic property of the AES S-box in Theorem 1.

To construct the differential trail as we want, we need to have a good knowledge of the difference propagation of the AES round function. Combining the properties of the AES S-box and its linear layer, we get the following lemmas on the differential properties of the AES round function.

Lemma 2

For any nonzero truncated difference $\varDelta \tilde{X}$ and concrete difference $\varDelta Y$ of the AES state such that $\chi (\varDelta Y)=MC(\varDelta \tilde{X})$, there exist $\varDelta X$ and X, such that $\chi (\varDelta X )=\varDelta \tilde{X}$, satisfying $SB\circ MC(X\oplus \varDelta X)\oplus SB\circ MC(X)=\varDelta Y$.

Proof

Let $\varDelta {{Y}^{1}}=MC(\varDelta X)$ and ${{Y}^{1}}=MC(X)$. Then the ${j}^{th}(0\le j \le 3)$ column of $\varDelta {{Y}^{1}}$ is represented as

$$\begin{aligned} \left\{ \begin{matrix} \varDelta y_{0,j}^{1}=2\varDelta {{x}_{0,j}}\oplus 3\varDelta {{x}_{1,j}}\oplus \varDelta {{x}_{2,j}}\oplus \varDelta {{x}_{3,j}} \\ \varDelta y_{1,j}^{1}=\varDelta {{x}_{0,j}}\oplus 2\varDelta {{x}_{1,j}}\oplus 3\varDelta {{x}_{2,j}}\oplus \varDelta {{x}_{3,j}} \\ \varDelta y_{2,j}^{1}=\varDelta {{x}_{0,j}}\oplus \varDelta {{x}_{1,j}}\oplus 2\varDelta {{x}_{2,j}}\oplus 3\varDelta {{x}_{3,j}} \\ \varDelta y_{3,j}^{1}=3\varDelta {{x}_{0,j}}\oplus \varDelta {{x}_{1,j}}\oplus \varDelta {{x}_{2,j}}\oplus 2\varDelta {{x}_{3,j}} \\ \end{matrix} \right. \end{aligned}$$

If $\varDelta {{\tilde{x}}_{\cdot ,j}}=0$, then $\varDelta {x}_{\cdot ,j}=0$ and $\varDelta {y}_{\cdot ,j}=MC(\varDelta {x}_{\cdot ,j})=0$. Naturally, ${x}_{\cdot ,j}$ can be arbitrary.

Therefore, we only need to consider those nonzero columns of $\varDelta {\tilde{x}}$, i.e. those $\varDelta {{\tilde{x}}_{\cdot ,j}}\ne 0$. Suppose that $\varDelta {{x}_{i,j}}={{c}_{i,j}}{{\alpha }_{j}} (0 \le i \le 3)$. Here, ${{c}_{i,j}} (0 \le i \le 3)$ are taken as the following steps:

• 1. If $\varDelta {{\tilde{x}}_{0,j}} \ne 0$, take nonzero ${{c}_{0,j}}$ then $(2{{c}_{0,j}},{{c}_{0,j}},{{c}_{0,j}},3{{c}_{0,j}})$ is all-nonzero, else take ${{c}_{0,j}}=0$;

• 2. If $\varDelta {{\tilde{x}}_{1,j}} \ne 0$, take nonzero ${{c}_{1,j}}$ such that $(2{{c}_{0,j}} \oplus 3{{c}_{1,j}},{{c}_{0,j}} \oplus 2{{c}_{1,j}},{{c}_{0,j}} \oplus {{c}_{1,j}},3{{c}_{0,j}} \oplus {{c}_{1,j}})$ is all-nonzero, else take ${{c}_{1,j}}=0$;

• 3. If $\varDelta {{\tilde{x}}_{2,j}} \ne 0$, take nonzero ${{c}_{2,j}}$ such that $(2{{c}_{0,j}} \oplus 3{{c}_{1,j}} \oplus {{c}_{2,j}},{{c}_{0,j}} \oplus 2{{c}_{1,j}} \oplus 3{{c}_{2,j}},{{c}_{0,j}} \oplus {{c}_{1,j}} \oplus 2{{c}_{2,j}},3{{c}_{0,j}} \oplus {{c}_{1,j}} \oplus {{c}_{2,j}})$ is all-nonzero, else take ${{c}_{2,j}}=0$;

• 4. If $\varDelta {{\tilde{x}}_{3,j}} \ne 0$, take nonzero ${{c}_{3,j}}$ such that $(2{{c}_{0,j}} \oplus 3{{c}_{1,j}} \oplus {{c}_{2,j}} \oplus {{c}_{3,j}},{{c}_{0,j}} \oplus 2{{c}_{1,j}} \oplus 3{{c}_{2,j}} \oplus {{c}_{3,j}},{{c}_{0,j}} \oplus {{c}_{1,j}} \oplus 2{{c}_{2,j}} \oplus 3{{c}_{3,j}},3{{c}_{0,j}} \oplus {{c}_{1,j}} \oplus {{c}_{2,j}} \oplus 2{{c}_{3,j}})$ is all-nonzero, else take ${{c}_{3,j}}=0$.

With above values of ${{c}_{0,j}}$, ${{c}_{1,j}}$, ${{c}_{2,j}}$ and ${{c}_{3,j}}$, we can get

$$\begin{aligned} \left\{ \begin{matrix} \varDelta y_{0,j}^{1}=(2{{c}_{0,j}} \oplus 3{{c}_{1,j}} \oplus {{c}_{2,j}} \oplus {{c}_{3,j}}) {{\alpha }_{j}}={{{{c}'}}_{0,j}} {{\alpha }_{j}} \\ \varDelta y_{1,j}^{1}=({{c}_{0,j}} \oplus 2{{c}_{1,j}} \oplus 3{{c}_{2,j}} \oplus {{c}_{3,j}}) {{\alpha }_{j}}={{{{c}'}}_{1,j}} {{\alpha }_{j}} \\ \varDelta y_{2,j}^{1}=({{c}_{0,j}} \oplus {{c}_{1,j}} \oplus 2{{c}_{2,j}} \oplus 3{{c}_{3,j}}) {{\alpha }_{j}}={{{{c}'}}_{2,j}} {{\alpha }_{j}} \\ \varDelta y_{3,j}^{1}=(3{{c}_{0,j}} \oplus {{c}_{1,j}} \oplus {{c}_{2,j}} \oplus 2{{c}_{3,j}}) {{\alpha }_{j}}={{{{c}'}}_{3,j}} {{\alpha }_{j}} \\ \end{matrix} \right. ,\text { }where\text { }{{{c}'}_{i,j}}\ne 0(0\le i\le 3). \end{aligned}$$

Since $\varDelta Y=SB(\varDelta {{Y}^{1}})\oplus SB(\varDelta {{Y}^{1}}\oplus {{Y}^{1}})$,

$$\begin{aligned} \left\{ \begin{matrix} \varDelta {{y}_{0,j}}=s\left( {{{{c}'}}_{0,j}} {{\alpha }_{j}}\oplus y_{0,j}^{1}\right) \oplus s\left( y_{0,j}^{1}\right) \\ \varDelta {{y}_{1,j}}=s\left( {{{{c}'}}_{1,j}} {{\alpha }_{j}}\oplus y_{1,j}^{1}\right) \oplus s\left( y_{1,j}^{1}\right) \\ \varDelta {{y}_{2,j}}=s\left( {{{{c}'}}_{2,j}} {{\alpha }_{j}}\oplus y_{2,j}^{1}\right) \oplus s\left( y_{2,j}^{1}\right) \\ \varDelta {{y}_{3,j}}=s\left( {{{{c}'}}_{3,j}} {{\alpha }_{j}}\oplus y_{3,j}^{1}\right) \oplus s\left( y_{3,j}^{1}\right) \\ \end{matrix} \right. . \end{aligned}$$

By Theorem 1, we know that for all $(\varDelta {{y}_{0,0}},\varDelta {{y}_{1,0}},\varDelta {{y}_{2,0}},\varDelta {{y}_{3,0}})\in {{[{F}_{2^8}^{*}]}^{4}}$, above system has solutions on variables ${{\alpha }_{j}}$ and $y_{\cdot ,j}^{1}$. We get the jth column of $\varDelta X$ by taking $\varDelta {{x}_{0,j}}={{c}_{0,j}} {{\alpha }_{j}}$, $\varDelta {{x}_{1,j}}={{c}_{1,j}} {{\alpha }_{j}}$, $\varDelta {{x}_{2,j}}={{c}_{2,j}} {{\alpha }_{j}}$, $\varDelta {{x}_{3,j}}={{c}_{3,j}} {{\alpha }_{j}}$, and get the jth column of X by $X=M{{C}^{-1}}({{Y}^{1}})$. Other nonzero columns of $\varDelta X$ and corresponding columns of X are similarly calculated.

Then, resulting $\varDelta X$ and X satisfies $SB\circ MC(X\oplus \varDelta X)\oplus SB\circ MC(X)=\varDelta Y$. $\square$

Lemma 3

For any nonzero concrete difference $\varDelta X$ and truncated difference $\varDelta \tilde{Y}$ of the AES state such that $\varDelta \tilde{Y}={{MC}^{-1}}(\chi (\varDelta X))$, there exist $\varDelta Y$ and X, such that $\chi (\varDelta Y )=\varDelta \tilde{Y}$, satisfying ${{MC}^{-1}}\circ {{SB}^{-1}}(\varDelta X)\oplus {{MC}^{-1}}\circ {{SB}^{-1}}(\varDelta X\oplus X)=\varDelta Y$.

Proof

Let $\varDelta {{X}^{1}}={{SB}^{-1}}(X)\oplus {{SB}^{-1}}(X\oplus \varDelta X)$. Suppose that $\varDelta {{x}_{\cdot ,j}}\ne 0$, then the jth column of $\varDelta Y$ is represented as:

$$\begin{aligned} \left\{ \begin{matrix} \varDelta {{y}_{0,j}}=e\varDelta x_{0,j}^{1}\oplus b\varDelta x_{1,j}^{1}\oplus d\varDelta x_{2,j}^{1}\oplus 9\varDelta x_{3,j}^{1} \\ \varDelta {{y}_{1,j}}=9\varDelta x_{0,j}^{1}\oplus e\varDelta x_{1,j}^{1}\oplus b\varDelta x_{2,j}^{1}\oplus d\varDelta x_{3,j}^{1} \\ \varDelta {{y}_{2,j}}=d\varDelta x_{0,j}^{1}\oplus 9\varDelta x_{1,j}^{1}\oplus e\varDelta x_{2,j}^{1}\oplus b\varDelta x_{3,j}^{1} \\ \varDelta {{y}_{3,j}}=b\varDelta x_{0,j}^{1}\oplus d\varDelta x_{1,j}^{1}\oplus 9\varDelta x_{2,j}^{1}\oplus e\varDelta x_{3,j}^{1} \\ \end{matrix} \right. , \end{aligned}$$

where $\varDelta x_{i,j}^{1}={{s}^{-1}}({{x}_{i,j}})\oplus {{s}^{-1}}({{x}_{i,j}}\oplus \varDelta {{x}_{i,j}})$, $0\le i \le 3$.

For nonzero $\varDelta {{x}_{i,j}}$, resulting $\varDelta x_{i,j}^{1}$ can take ${{2}^{7}}-1$ different nonzero values when ${{x}_{i,j}}$ runs through ${F}_{2^8}$ [10]. For $\varDelta {{x}_{i,j}}$ equal to 0, resulting $\varDelta x_{i,j}^{1}=0$ obviously. Then, we are able to construct $(\varDelta x_{0,j}^{1},\varDelta x_{1,j}^{1},\varDelta x_{2,j}^{1},\varDelta x_{3,j}^{1})$ such that $(\varDelta {{y}_{0,j}},\varDelta {{y}_{1,j}},\varDelta {{y}_{2,j}},\varDelta {{y}_{3,j}})$ is all-nonzero, by changing $({{x}_{0,j}},{{x}_{1,j}},{{x}_{2,j}},{{x}_{3,j}})$ as the following steps:

• 1. If $\varDelta {{x}_{0,j}}\ne 0$, take arbitrary ${x}_{0,j}$ then $\varDelta x_{0,j}^{1}\ne 0$ and $(e\varDelta x_{0,j}^{1},9\varDelta x_{0,j}^{1},d\varDelta x_{0,j}^{1},b\varDelta x_{0,j}^{1})$ is all-nonzero. If $\varDelta {{x}_{0,j}}= 0$, then $\varDelta x_{0,j}^{1}= 0$ and take ${x}_{0,j}$ arbitrarily.

• 2. If $\varDelta {{x}_{1,j}}\ne 0$, there are at most 4 values of $\varDelta x_{1,j}^{1}$ which make that there is zero in $(e\varDelta x_{0,j}^{1}\oplus b\varDelta x_{1,j}^{1},9\varDelta x_{0,j}^{1}\oplus e\varDelta x_{1,j}^{1},d\varDelta x_{0,j}^{1}\oplus 9\varDelta x_{1,j}^{1},b\varDelta x_{0,j}^{1}\oplus d\varDelta x_{1,j}^{1})$. Since $\varDelta x_{1,j}^{1}$ can take ${{2}^{7}}-1$ different nonzero values, we can easily avoid those 4 values of $\varDelta x_{1,j}^{1}$ by changing ${{x}_{1,j}}$. Take ${{x}_{1,j}}$ such that $(e\varDelta x_{0,j}^{1}\oplus b\varDelta x_{1,j}^{1},9\varDelta x_{0,j}^{1}\oplus e\varDelta x_{1,j}^{1},d\varDelta x_{0,j}^{1}\oplus 9\varDelta x_{1,j}^{1},b\varDelta x_{0,j}^{1}\oplus d\varDelta x_{1,j}^{1})$ is all-nonzero. If $\varDelta {{x}_{1,j}}=0$, then $\varDelta x_{1,j}^{1}= 0$ and take ${{x}_{1,j}}$ arbitrarily.

  ......

• 3. Step by step. Things are similar for ${{x}_{2,j}}$ and ${{x}_{3,j}}$. Eventually, we construct $({{x}_{0,j}},{{x}_{1,j}},{{x}_{2,j}},{{x}_{3,j}})$ such that $(\varDelta {{y}_{0,j}},\varDelta {{y}_{1,j}},\varDelta {{y}_{2,j}},\varDelta {{y}_{3,j}})$ is all-nonzero.

For other nonzero columns of $\varDelta X$, corresponding columns of X and $\varDelta Y$ are similarly calculated.

For zero columns of $\varDelta X$, corresponding columns of X are arbitrary and $\varDelta Y$ are all-zero.

Then, resulting X and $\varDelta Y$ satisfying ${{MC}^{-1}}\circ {{SB}^{-1}}(\varDelta X)\oplus {{MC}^{-1}}\circ {{SB}^{-1}}(\varDelta X\oplus X)=\varDelta Y$. $\square$

Lemma 4

Let ${{R}_{1}}=SB\circ MC\circ SR\circ {{AK}_{K}}\circ SB\circ MC$. For any nonzero truncated difference $\varDelta \tilde{X}$ and all-nonzero concrete difference $\varDelta Y$ of the AES state, there exist $\varDelta X$, K and X, such that $\chi (\varDelta X )=\varDelta \tilde{X}$, satisfying ${{R}_{1}}(X\oplus \varDelta X)\oplus {{R}_{1}}(X)=\varDelta Y$.

Proof

Let ${{Y}^{1}}=SB\circ MC(X)$, $\varDelta {{Y}^{1}}=SB\circ MC(X)\oplus SB\circ MC(\varDelta X\oplus X)$ and ${{Y}^{2}}=SR\circ {{AK}_{K}}({{Y}^{1}})$.

Take $\varDelta {{\tilde{Y}}^{1}}=MC(\varDelta {\tilde{X}})$, then $\varDelta {{\tilde{Y}}^{1}}$ has at least one all-nonzero column by the definition of MC on a truncated difference (see Definition 5), and every column of $\varDelta {{\tilde{Y}}^{2}}=SR(\varDelta {{\tilde{Y}}^{1}})$ is nonzero.

For $\varDelta {{\tilde{Y}}^{2}}\xrightarrow {SB\circ MC}\varDelta Y$, since every column of $\varDelta {{\tilde{Y}}^{2}}$ is nonzero, we know that $MC(\varDelta {{\tilde{Y}}^{2}})$ is all-nonzero (namely, $MC(\varDelta {{\tilde{Y}}^{2}})=\chi (\varDelta Y)$). By Lemma 2, there exist corresponding $\varDelta {{Y}^{2}}$ and ${{Y}^{2}}$, such that $\chi (\varDelta {{Y}^{2}})=\varDelta {{\tilde{Y}}^{2}}$, satisfying $\varDelta Y=SB\circ MC({{Y}^{2}})\oplus SB\circ MC({{Y}^{2}}\oplus \varDelta {{Y}^{2}})$. Then ${\varDelta Y}^{1}={SR}^{-1}({\varDelta Y}^{2})$ and $\chi ({\varDelta Y}^{1})=\varDelta {{\tilde{Y}}^{1}}$.

For $\varDelta \tilde{X}\xrightarrow {SB\circ MC}\varDelta {{Y}^{1}}$, since $\chi (\varDelta {{Y}^{1}})=\varDelta {{\tilde{Y}}^{1}}=MC(\varDelta {\tilde{X}})$ as we take, by Lemma 2, there exist corresponding $\varDelta X$ and X, such that $\chi (\varDelta X )=\varDelta \tilde{X}$, satisfying $\varDelta {{Y}^{1}}=SB\circ MC(X)\oplus SB\circ MC(\varDelta X\oplus X)$. Take $K={{Y}^{1}}\oplus {{SR}^{-1}}({{Y}^{2}})$.

Therefore, resulting $\varDelta X$, K and X satisfying ${{R}_{1}}(X\oplus \varDelta X)\oplus {{R}_{1}}(X)=\varDelta Y$. $\square$

Lemma 5

Let ${{R}_{2}}={{MC}^{-1}}\circ {{SB}^{-1}}\circ {{SR}^{-1}}\circ {{MC}^{-1}}$. For any nonzero truncated difference $\varDelta \tilde{X}$ and all-nonzero truncated difference $\varDelta \tilde{Y}$ of the AES state, there exist $\varDelta X$, $\varDelta Y$ and X, such that $\chi (\varDelta X )=\varDelta \tilde{X}$ and $\chi (\varDelta Y )=\varDelta \tilde{Y}$, satisfying ${{R}_{2}}(X\oplus \varDelta X)\oplus {{R}_{2}}(X)=\varDelta Y$.

Proof

According to the proof of Lemma 3, we could take nonzero bytes of $\varDelta X$ such that corresponding columns of the ${{MC}^{-1}}(\varDelta X)$ are all-nonzero. Then, every column of the $\varDelta {{X}^{1}}={{SR}^{-1}}\circ {{MC}^{-1}}(\varDelta X)$ is nonzero.

For $\varDelta {{X}^{1}}\xrightarrow {{{MC}^{-1}}\circ {{SB}^{-1}}}\varDelta \tilde{Y}$, since every column of the $\varDelta {{X}^{1}}$ is nonzero, we know that ${{MC}^{-1}}(\chi (\varDelta {{X}^{1}}))$ is all-nonzero (namely, ${{MC}^{-1}}(\chi (\varDelta {{X}^{1}}))=\varDelta \tilde{Y}$). By Lemma 3, there exist corresponding $\varDelta Y$ and $X^1$, such that $\chi (\varDelta Y)=\varDelta \tilde{Y}$, satisfying $\varDelta Y={{MC}^{-1}}\circ {{SB}^{-1}}({{X}^{1}})\oplus {{MC}^{-1}}\circ {{SB}^{-1}}({{X}^{1}}\oplus \varDelta {{X}^{1}})$. Take $X=MC\circ SR({{X}^{1}})$.

Therefore, resulting $\varDelta X$, $\varDelta Y$ and X satisfying ${{R}_{2}}(X\oplus \varDelta X)\oplus {{R}_{2}}(X)=\varDelta Y$. $\square$

Based on above preparation, we are able to give our claims on AES. Note that Sun et al. [24] didn’t consider the S-box, therefore, their bound is not suitable for AES (cipher). Our Theorem 2 is stronger than it, since our bound is built on the details of the AES S-box.

Fig. 2

Five-round AES (Note that this figure only shows the ”meet-in-the-middle” of a special truncated differential which is only nonzero at one byte of the input difference and one byte of the output difference, but our proof considers all possible truncated differentials)

Theorem 2

There do not exist truncated impossible differentials covering more than four rounds for AES with S-box considered and under the assumption that round keys are independent and uniformly random. Longer truncated impossible differentials might exist only if the key schedule is considered.

Proof

We will prove this by showing that any nontrivial truncated differential is possible for five-round AES (without MixColumns transformation in the last round, as shown in Fig. 2).

Write the five-round AES transformation (without MixColumns transformation in the last round) as: $5\_round\_AES={{AK}_{{{K}^{5}}}}\circ SR\circ SB\circ {{AK}_{{{K}^{4}}}}\circ R\circ {{AK}_{{{MC}^{-1}}({{K}^{1}})}}\circ SR\circ SB\circ {{AK}_{{{K}^{0}}}}$, here $R=MC\circ SR\circ SB\circ MC\circ SR\circ {{AK}_{{{SR}^{-1}}\circ {{MC}^{-1}}({{K}^{3}})}}\circ SB\circ MC\circ {{AK}_{{{MC}^{-1}}({{K}^{2}})}}\circ SR\circ SB\circ MC$.

Since transformations ${{AK}_{{{MC}^{-1}}({{K}^{1}})}}\circ SR\circ SB\circ {{AK}_{{{K}^{0}}}}$ before the R and ${{AK}_{{{K}^{5}}}}\circ SR\circ SB\circ {{AK}_{{{K}^{4}}}}$ after the R, are “transparent”¹ with truncated differences, we only need to prove that for any nontrivial truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Z}$, $P(\varDelta \tilde{X}\xrightarrow {R}\varDelta \tilde{Z})\ne 0$.

We prove this by showing that there exists concrete differential $\varDelta X\rightarrow \varDelta Z$, such that $\chi (\varDelta X)=\varDelta \tilde{X}$ and $\chi (\varDelta Z)=\varDelta \tilde{Z}$, satisfying $P(\varDelta X\xrightarrow {R}\varDelta Z)\ne 0$. That is to say, there exist corresponding $\varDelta X$, $\varDelta Z$, X, ${{K}^{2}}$ and ${{K}^{3}}$ satisfying $R(X)\oplus R(X\oplus \varDelta X)=\varDelta Z$.

We write the R as: $R={{R}_{2}}\circ {{AK}_{{{MC}^{-1}}({{K}^{3}})}}\circ SR\circ {{R}_{1}}$, here ${{R}_{1}}=SB\circ MC\circ SR\circ {{AK}_{{{SR}^{-1}}\circ {{MC}^{-1}}({{K}^{2}})}}\circ SB\circ MC$, ${{R}_{2}}=MC\circ SR\circ SB\circ MC$. Note that $R_1$ is key-dependent, and $R_2$ is key-independent.

For any nontrivial truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Z}$, we construct one corresponding concrete differential following from “meet-in-the-middle” idea, as following steps:

• 1. By Lemma 5, for any nonzero $\varDelta \tilde{Z}$, there exist $\varDelta Z$ and Z, such that $\chi (\varDelta Z)=\varDelta \tilde{Z}$, satisfying $\varDelta Y=R_{2}^{-1}(Z)\oplus R_{2}^{-1}(Z\oplus \varDelta Z)$ is all-nonzero. Then ${{SR}^{-1}}(\varDelta Y)$ is all-nonzero obviously.

• 2. By Lemma 4, for ${{SR}^{-1}}(\varDelta Y)$ and any nonzero $\varDelta \tilde{X}$, there exist $\varDelta X$, X and ${{K}^{2}}$, such that $\chi (\varDelta X)=\varDelta \tilde{X}$, satisfying ${{SR}^{-1}}(\varDelta Y)={{R}_{1}}(X)\oplus {{R}_{1}}(X\oplus \varDelta X)$.

• 3. Take ${{K}^{3}}=MC(SR\circ {{R}_{1}}(X)\oplus R_{2}^{-1}(Z))$.

Therefore, resulting $\varDelta X$, $\varDelta Z$, X, ${{K}^{2}}$ and ${{K}^{3}}$ satisfying $R(X\oplus \varDelta X)\oplus R(X)=\varDelta Z$. $\square$

3.3 Special case for AES-256

Notice following property of the AES-256 key schedule:

Property 1

[8] On knowing 256-bit round keys of any consecutive two rounds for AES-256, the key schedule of AES-256 would allow to uniquely regenerate all the other round keys.

For AES-256, the assumption that round keys are independent and uniformly random can be removed. We have following theorem:

Theorem 3

Even though the key schedule is considered, there do not exist truncated impossible differentials covering more than four rounds for AES-256 with S-box considered.

Proof

In the proof of Theorem 2, we prove that any truncated differential $\varDelta \tilde{X}\rightarrow \varDelta \tilde{Z}$ for the R is possible, by elaborately choosing consecutive two-round keys ${{K}^{2}}$ and ${{K}^{3}}$, input X and output Z of the R. By Property 1, “choosing consecutive two-round keys: ${{K}^{2}}$ and ${{K}^{3}}$” is feasible in the key schedule of AES-256. Therefore, proof of Theorem 2 is also suitable for AES-256 with key schedule. $\square$

4 Conclusion

In this paper, we investigate the provable security of AES against impossible differential cryptanalysis, by giving the maximal length of truncated impossible differentials. From a more practical point than previous work, we dive into the non-linear S-box, which is always “structured [24]” or “idealized [7]” by other researchers, but significant for the practical maximal length of impossible differentials of SPN block ciphers. After revealing several essential properties of the AES S-box, we prove that there do not exist truncated impossible differentials longer than four rounds for AES with S-box considered and under the assumption that round keys are independent and uniformly random. Specially, for AES-256, even though the S-box and the key schedule are both considered, there do not exist truncated impossible differentials longer than four rounds.

On the security of the AES, impossible differentials covering more than four rounds might be constructed only if the key schedule is considered (exclude AES-256), or the differential is concrete (not truncated differential). These investigation may shed light on how to design block ciphers with provable security against impossible differential attack.