Improved, black-box, non-malleable encryption from semantic security

Abstract

We give a new black-box transformation from any semantically secure encryption scheme into a non-malleable one which has a better rate than the best previous work of Coretti et al. (in: Kushilevitz and Malkin (eds) TCC 2016-A, Part I, Springer, Heidelberg, 2016). We achieve a better rate by departing from the “matrix encoding” methodology used by previous constructions, and working directly with a single codeword. We also use a Shamir secret-share packing technique to improve the rate of the underlying error-correcting code.

1 Introduction

The basic security requirement for public key encryption (PKE) schemes, known as semantic security or IND-CPA (indistinguishability under chosen plaintext attack), is that an eavesdropping adversary learns nothing about the plaintext underlying a communicated ciphertext (equivalently, cannot distinguish an encryption of one plaintext from another). Often, however, this indistinguishability guarantee is not sufficient, and a PKE satisfying stronger properties is required.

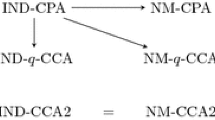
IND-CCA2 from semantic security. A strong level of PKE security, which is sufficient for most applications, is indistinguishability under chosen-ciphertext attacks (IND-CCA2), wherein the adversary may ask adaptive queries to a decryption oracle (as long as it does not query the “challenge ciphertext” itself).

A natural question is whether one can achieve IND-CCA2 security only from IND-CPA security; however, this question still remains a big open problem. On one hand, the various known constructions of IND-CCA2 secure encryption either rely on IND-CPA security and some additional properties that computational hardness assumptions from number theory provide [11, 18, 24, 25, 29, 30, 40] or use generic assumptions seemingly stronger than IND-CPA secure encryption, e.g., non-interactive zero knowledge, identity-based encryption, or lossy trapdoor functions [6, 16, 35]. On the other hand, there has been only a partial black-box separation result [19] between IND-CPA and IND-CCA2. Therefore, researchers have proposed and studied various intermediate notions of security.

Non-malleable encryption from semantic security. In this work, we consider the notion of non-malleability under chosen-plaintext attacks (NM-CPA), initially put forward by Dolev, Dwork and Naor [16]. Roughly, non-malleability requires that it is infeasible for an adversary to modify a ciphertext into one, or many, other ciphertexts of messages related to the original plaintext. It was shown by Bellare and Sahai [3] and by Pass, shelat and Vaikuntanathan [34] that NM-CPA is equivalent to security against adversaries with access to a non-adaptive decryption oracle, meaning that the adversary can only ask one “parallel” CCA2 decryption query. We also consider the notion of non-malleability under bounded-CCA2 attacks (NM-q-CCA2) [12], where we allow the adversary to adaptively query the decryption oracle at most q times (in contrast, NM-CCA2 allows an unbounded number of queries, and is equivalent to IND-CCA2 [16]).

Besides being a “stepping stone” between semantically secure and CCA2 secure encryption, non-malleability (or NM-CPA security) is an important notion in its own right. As one motivating example, consider the use of PKE in auctions. Buyers place their bids for an item to a seller, encrypted under the seller’s public key, and the seller sells the item to the buyer with the highest bid. We certainly want to rule out adversaries who consistently bid exactly one dollar more than the previous bidders.

Table 1 The ciphertext lengths of various NM-CPA encryption schemes

Previous work on achieving NM-CPA from IND-CPA. Interestingly, although NM-CPA appears closer to IND-CCA2 than IND-CPA security, a sequence of results (i.e., a non-black-box construction by [34] followed by a black-box construction by [9]) showed that NM-CPA schemes (and even NM-q-CCA2 schemes) can be constructed from any IND-CPA scheme.

In a recent work, Coretti et al. [10] revisited the work of [9], and investigated (among other results) the question of how efficient the black-box transformation can be. The measure of efficiency they consider is the rate of the resulting NM-CPA encryption scheme, defined as $\frac{n}{c(n)}$, where n is the message length and c(n) is the length of the corresponding ciphertext.¹

The transformation of [9] gives an n-bit NM-CPA scheme such that its encryption algorithm calls the underlying n-bit IND-CPA scheme $\varTheta (k^2)$ times, where k is the security parameter.² For example, assuming a constant-rate IND-CPA encryption, the transformation gives a $\varTheta (k)$-bit NM-CPA scheme with the ciphertext length of $\varTheta (k^3)$.

Coretti et al. [10] give an improved transformation by replacing the error-correcting code used in [9] with one having a better rate, although the transformation still invokes the same number $\varTheta (k^2)$ of calls to the underlying IND-CPA encryption. In particular, this allows $\varTheta (k^3)$-bit ciphertexts to encrypt $\varTheta (k^2)$-bit messages. See Table 1 for more detailed comparison.

1.1 Our results

In this work, we give a black-box transformation from IND-CPA encryption to NM-CPA encryption with better efficiency.

Conceptual contribution. Our main conceptual contribution is that we no longer follow the framework of [16] (and all subsequent constructions) of creating k encryptions of the same message or codeword.

In particular, as we elaborate on in the next section, previous constructions rely on a “matrix encoding” of the plaintext as a $k \times \ell$ matrix of elements, where each row in the matrix is an encoding of the plaintext message via an appropriate code (the message itself in [16], or more sophisticated encodings in subsequent works). The rows of the matrix are indexed by a one-time signature, so we need at least k (security parameter) rows. It follows that using this methodology incurs a ciphertext expansion of at least a factor of k, regardless of the underlying code used. In this sense, [10] have achieved the best possible rate within this construction framework.

We depart from this “matrix encoding” methodology and work directly with a single codeword. This allows us to achieve the first black-box transformation that invokes $\varTheta (k)$ calls to the underlying IND-CPA encryption algorithm; previous black-box constructions need $\varTheta (k^2)$ calls.

Main theorem (informal) There exists a (fully) black-box construction of a non-malleable encryption scheme from any IND-CPA encryption scheme, in which the encryption algorithm calls the underlying IND-CPA encryption algorithm $\varTheta (k)$ times.

We also extend the theorem to provide a black-box construction of NM-q-CCA2 secure encryption [12] from any semantically secure encryption, calling the IND-CPA encryption algorithm $\varTheta (k+q)$ times.

NM-CPA encryption with a better rate. Applying the aforementioned transformation, we achieve an NM-CPA encryption scheme with a better rate. For this, we use a Shamir secret-share packing technique to improve the rate of the underlying error-correcting code to encode the plaintext in the transformation. In particular, we achieve a constant-rate NM-CPA encryption for messages of length $\varOmega (k^2)$. We compare our results with the previous work in Table 1.

We note that one can achieve a better rate for long messages by using hybrid encryption. In particular, Herranz et al. [23] showed that NM-CPA KEM plus IND-CCA2 DEM implies NM-CPA PKE. (For shorter messages, the ciphertext length is dominated by the KEM part of encrypting the $\varTheta (k)$-long encapsulated key, since for the DEM part, we have a constant-rate IND-CCA2 secure symmetric encryption scheme [2].) Even considering the hybrid encryption framework, our scheme achieves better efficiency: Our scheme achieves a constant rate for messages of length $\varOmega (k^2)$, rather than for messages of length $\varOmega (k^3)$ in the previous schemes.

Potential applications to other related work. The original techniques of [9] (in particular, the properties of the matrix encoding scheme and its use for verifying consistency) have been used implicitly or explicitly in several works for different purposes. For example, there have been black-box constructions of non-malleable commitments [33], set intersection protocols from homomorphic encryptions [14], and a CCA2-secure encryption scheme for strings starting from one for bits [32]. The works of [26, 27, 31, 39] used these techniques in the context of black-box, round-efficient secure computation. The works of [21, 22] extended the ideas to provide consistency relations beyond equality using VSS and the paradigm of MPC-in-the-head.

We hope that our improved efficiency, constant rate transformation can be used to improve efficiency in some of these or other application domains. In fact, a very recent work [1] has already used our results to construct their non-malleble codes resilient against local tampering functions and bounded-depth circuits. Indeed, their results instantiated with the previous matrix encoding techniques would yield non-malleable codes resilient against functions with locality up to $n^c$ for some specific $c<1$ (roughly $c=1/3$). However, using our results as an ingredient, they were able to achieve resilience against locality $n^{1-\epsilon }$ for any constant $\epsilon <1$ (and even $\frac{n}{\log n}$ with inefficient codes), and much better rate even in lower locality ranges.

2 Techniques

2.1 Overview of previous techniques

We begin with an overview of previous techniques of [9, 10, 16, 34], which we will refer to below as DDN, PSV, CDMW and CDTV, respectively. We focus on the details that will be helpful towards understanding our techniques.

Non-black-box transformations by DDN and PSV. Let k be the security parameter. The key generation algorithm generates 2k independent keys for the underlying semantically-secure public key encryption scheme $\textsc {pk}_i^b$ for $i = 1, \ldots , k$, and $b \in \{0,1\}$ (and the corresponding secret keys). Encryption of message m proceeds as follows:

• (a) Generate a $(\textsc {vksig}, \textsc {sksig})$ pair for a one-time signature (where $|\textsc {vksig}|=k$).

• (b) Generate k encryptions of the message m. In particular, use keys $\textsc {pk}_{i}^{\textsc {vksig}_i}$ for $i=1, \ldots , k$ for encryptions.

• (c) Give a non-interactive zero-knowledge proof (or the relaxed “designated verifier” version) proving that all resulting ciphertexts are encryptions of the same message.

• (d) Sign the entire bundle with a one-time signature.

It is in step (c) that a general $\mathsf {NP}$-reduction is used, which in return makes the construction non-black-box (and inefficient). In the proof of security, we exploit the fact that for a well-formed ciphertext, we can recover the message if we know the secret key for any of the k encryptions.

Black-box transformations by CDMW. Let k be the security parameter, and let $\ell =O(k)$ (or any superlogarithmic function in k). The key generation algorithm generates $2k\ell$ independent keys for the underlying semantically-secure PKE scheme $\textsc {pk}_{i,j}^b$ for $i=1,\ldots ,k$, $j=1,\ldots ,\ell$, and $b\in \{0,1\}$ (and the corresponding secret keys). The encryption algorithm utilizes a Reed–Solomon (RS) error correcting code (ECC) with encoding algorithm $\mathsf {E}$ (see Appendix 1.1). Now, the encryption algorithm has the following form:

• (a) Generate a $(\textsc {vksig}, \textsc {sksig})$ pair for a one-time signature (where $|\textsc {vksig}|=k$).

• (b) Obtain an encoding w of a message m by computing $w \leftarrow \mathsf {E}(m)$. Generate k encryptions of the same codeword w, using $\ell$ public keys per each of the k encryptions in a way that we explain below.

• (d) Sign the entire bundle with a one-time signature.

Obviously, the scheme should provide some mechanism for checking the consistency of k encryptions, corresponding to step (c) in DDN and PSV (i.e., the non-interactive zero-knowledge proof). That way, even if the simulated decryption in the proof of security decrypts any of the k ciphertexts, the decryption should be correct with overwhelming probability. CDMW achieved this by using a codeword w consisting of $\ell$ elements, and encrypting each element with a different public key, for a total of $k\ell$ encryptions. The decryption algorithm checks consistency of the k encryptions of w by checking consistency of a random subset of columns (where the randomness is determined by its secret key). Then, the decryption algorithm decrypts and error-corrects the first row, and checks that in that same subset of locations, this codeword is not corrupted. If both these column-check and codeword-check pass, output the decoded message.

We next describe the details of how the above outline is implemented, and the intuition behind its security and parameter choices. Recall that a RS codeword consisting of $\ell$ output symbols is simply a polynomial p of degree $d=O(\ell )$ over a finite field, evaluated at $\ell$ points (say $1, \ldots , \ell$). The way CDMW encode a message m is via Shamir secret-sharing, which can be viewed as an instantiation of a RS code. Specifically, set $p(0) = m$, choose the values of $p(1), \ldots , p(d)$ at random, and interpolate to obtain the unique degree d polynomial p. Let the final encoding $w \leftarrow \mathsf {E}(m)$ consist of $w_1=p(1),\ldots ,w_\ell =p(\ell )$. The encryptions now proceed as follows:

Construct a $k \times \ell$ matrix M, where $M_{i,j} = w_j$ and k is the number of bits in $\textsc {vksig}= \textsc {vksig}_1, \ldots , \textsc {vksig}_k$. Each entry of $M_{i,j}$ is then encrypted under a one of two public keys $(\textsc {pk}^0_{i,j}, \textsc {pk}^1_{i,j})$, depending on whether $\textsc {vksig}_i$ is 0 or 1.

In the actual decryption algorithm, the first row of the encrypted matrix is always decrypted and decoded, whereas in the security proof, the decrypted row will be chosen based on which secret keys are available to the reduction, and it is ensured that in each submitted ciphertext there is some row for which the reduction knows all the secret keys. The key challenge is to ensure that decrypting and decoding any one of the k rows of the encrypted matrix will yield the same message $\widetilde{m}$ (possibly $\bot$) as the decrypting and decoding the first row. This is where the “column check” and “codeword check” come in. In the column check, we decrypt a random subset of $t=O(\ell )$ columns, and check that all the entries in each of these columns are the same; the random subset is chosen in key generation and embedded into the private key. Intuitively, this ensures that the encoding in each row is “close” to the encoding in the first row. In the codeword check, we decrypt and decode the first row and then check the resulting codeword against the received word in the first row. Specifically, we check that $t=O(\ell )$ random positions of the first row (the same ones that were opened during the column check) agree with the corresponding t positions in the decoded codeword. Intuitively, this is a type of a cut-and-choose check which ensures that the encoding in the first row is “close” to a valid codeword. If either of the checks fails, we output $\bot$. Put together, the two checks ensure that with overwhelming probability, all rows must decode to the same message (or to $\bot$), and thus provide the desired consistency.

The reason CDMW needs $\ell$ to be superlogarithmic, is that for the codeword check, we need the number of random positions $t=O(\ell )$ to satisfy $2^{-t} = \mathsf {negl}(k)$ so that a codeword that is far from valid will pass the check with negligible probability. Thus, the RS code used for each row is not constant rate.

More efficient black-box transformation by CDTV. The general insight of CDTV (and also the full version of CDMW [8]) is that the above construction can be generalized to work for a larger class of encoding schemes $\mathsf {E}$, beyond just RS codes. Specifically, Coretti et al. [10] note that using a LECSS (linear error-correcting secret sharing scheme) [7, 13] is sufficient, whereas [8] introduced a notion of reconstructable probabilistic encoding scheme (building on [15]). Using these insights, the above works were able to replace the RS code described above with a constant-rate encoding scheme (for long enough messages). Specifically, each row with $\ell$ elements can in fact encode a message of length $O(\ell )$ elements, resulting in a constant rate code for each row (while still maintaining k rows).

2.2 Our techniques

Our encryption scheme also utilizes reconstructable probabilistic encoding (RPE) schemes. RPE schemes are, informally, error-correcting codes (ECCs) with additional secrecy and reconstruction properties. The secrecy property guarantees that the symbols at any not-too-large subset of positions in the codeword are distributed uniformly and independently of the encoded message. The reconstruction property says that furthermore, any assignment of symbols to such a subset of positions, can be completed to a (correctly distributed) codeword for any given message. The parameter regime we will be interested in is the standard one, where the error-correction is with respect to a constant fraction of errors, and the secrecy and reconstruction are also with respect to a (smaller) constant fraction of positions.

From k encryptions to a single encryption. Our first technical contribution is identifying a property of RPE schemes and showing how it can be leveraged to eliminate the need for the “repetition” encoding in previous works. The property we use is that error-correction and decoding can be performed given any large enough (constant-fraction) sized subset $\lambda \cdot \ell$ of positions of the corrupted codeword (here $0<\lambda <1$ is a constant). We call this property the “decoding from partial views” property. Crucially, we would like this property to hold in a strong way, so that for any such subset, we always decode to the same codeword/message (possibly $\bot$), even for arbitrarily corrupt codewords, with overwhelming probability (taken over the random choice of the secret key).

We have already discussed a similar property as underlying, at least implicitly, the previous works relying on matrix encoding. However, in those works the property applied to decoding from any one of the k rows (which constitute a repetition code), and was unrelated to the use of RPE for the encoding within each row. Our novel observation is that in fact a similar property can apply directly to RPE (with appropriate parameters). A single RPE codeword could then allow decoding from any partial view subset, and by correctly adapting a codeword check and another layer of (standard) encoding on the signature, we can achieve the strong version guaranteeing consistency with overwhelming probability.

Thus, encryption of a message m proceeds as follows:

• (a) Generate a $(\textsc {vksig}, \textsc {sksig})$ pair for a one-time signature.

• (b) Let $\mathsf {E}$ be the encoding algorithm of a RPE with the output length $\ell$. Let C be a linear code with relative distance $\lambda < 1$, encoding the length-k $\textsc {vksig}$ to a length-$\ell$ string (note that C does not have to be efficiently error correctable). Set $\mathbf {s} \leftarrow \mathsf {E}(m)$, where $\mathbf {s}$ is a vector of length $\ell$. Let $v_1 \cdots v_\ell$ be the output of $C(\textsc {vksig})$. For $j=1, \ldots , \ell$, encrypt each entry $s_{j}$ under public key $\textsc {pk}^{v_j}_{j}$, yielding a vector of ciphertexts.

• (c) Sign the entire bundle with a one-time signature.

In the actual decryption algorithm, the first $\lambda \cdot \ell$ positions of the ciphertext vector are always decrypted and decoded, whereas in the security proof, a specific subset of size $\lambda \cdot \ell$ will be chosen based on which secret keys are available to the reduction. In the proof, we use the fact that, due to unforgeability of the signature scheme, the $\textsc {vksig}$ for each submitted ciphertext must be different than the $\textsc {vksig}$ of the challenge ciphertext, and the fact that C has distance $\lambda \cdot \ell$ to ensure that there is always some sufficiently large subset for which the reduction knows all the secret keys.

To ensure that decoding any of subset of size $\lambda \cdot \ell$ positions yields the same message $\widetilde{m}$ as the first subset (or both will give $\bot$), we require an analogue of the codeword check only (but no column check). As before, in the codeword check we compare the codeword obtained by decrypting and decoding the first $\lambda \cdot \ell$ positions with the received word. Specifically, we check that t random positions throughout the entire received word agree with the corresponding t positions in the decoded codeword.

Constant-rate RPE. Our second contribution is to show that the above framework is implementable with a constant rate RPE: we show that using RS codes with packed Shamir secret sharing yields a constant rate RPE with appropriate parameters. Compared with the RS based encodings used by [9] for k rows, here our encoding has a single row (of length a constant times larger), and a longer message is encoded in each codeword via the packing technique [17]. That is, the polynomial is taken to be of a larger degree, and the message is encoded in several evaluation points of the polynomial.

3 Preliminaries and definitions

We use [n] to denote $\{1,2,\ldots ,n\}$. If A is a probabilistic polynomial time (hereafter, ppt) algorithm that runs on input x, A(x) denotes the random variable according to the distribution of the output of A on input x. We denote by A(x; r) the output of A on input x and random coins r. A function $\mu$ from the natural numbers to the non-negative real numbers is negligible if for every positive polynomial $p(\cdot )$ there is an N such that for all integers $k > N$, $\mu (k) < \frac{1}{p(k)}$. We use $\mathsf {negl}(k)$ to denote some arbitrary negligible function.

Definition 1

(Statistical Indistinguishability) Two probability ensembles $A = \{A_k\}_{k \in \mathbb {N}}$ and $B = \{B_k\}_{k \in \mathbb {N}}$ are statistically indistinguishable if it holds that

$$\begin{aligned} \sum _\alpha \Big |\Pr [X_k = \alpha ] - \Pr [Y_k = \alpha ] \Big | \le \mathsf {negl}(k). \end{aligned}$$

Statistical indistinguishability between two ensembles A and B is denoted by $A \mathop {\approx }\limits ^{s} B$.

Definition 2

(Computational Indistinguishability) Two probability ensembles $A = \{A_k\}_{k \in \mathbb {N}}$ and $B = \{B_k\}_{k \in \mathbb {N}}$ are computationally indistinguishable if for every ppt distinguisher D, it holds that

$$\begin{aligned} \left| \Pr _{a \leftarrow A_k}[D(1^k, a) = 1] - \Pr _{b \leftarrow B_k}[D(1^k,b)=1] \right| \le \mathsf {negl}(k). \end{aligned}$$

Computational indistinguishability between two ensembles A and B is denoted by $A \mathop {\approx }\limits ^{c}B$.

Distance of two strings. Given two strings v, w of length $\ell$ over an alphabet $\varSigma$, we say that v and w are $\delta$-far if they disagree in more than $\delta \cdot \ell$ positions, where $0 \le \delta \le 1$; we say that v and w are $\delta$-close if they agree in more than $\delta \cdot \ell$ positions.

3.1 Semantically secure encryption

In the following we define the syntax of a PKE scheme and the standard security notion, semantic security. We then present the two stronger security notions of non-malleability and bounded-CCA2 non-malleability.

Definition 3

(Encryption scheme) A triple $(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ is an encryption scheme, if $\mathsf {Gen}$ and $\mathsf {Enc}$ are ppt algorithms and $\mathsf {Dec}$ is a deterministic polynomial-time algorithm which satisfies the following property:

Correctness. With probability $1-\mathsf {negl}(k)$ over $(\textsc {pk},\textsc {sk}) \leftarrow \mathsf {Gen}(1^k)$: for all m, $\Pr [\mathsf {Dec}_\textsc {sk}(\mathsf {Enc}_\textsc {pk}(m)) = m] = 1$.

Definition 4

(Semantic security) Let $\Uppi = (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ be an encryption scheme and let the random variable $\mathsf {IND}_b(\Uppi , A, k)$, where $b \in \{0,1\}$, $A = (A_1, A_2)$ are ppt algorithms and $k \in \mathbb {N}$, denote the result of the following probabilistic experiment:

$\mathsf {IND}_b(\Uppi , A, k):$

    $(\textsc {pk}, \textsc {sk}) \leftarrow \mathsf {Gen}(1^k)$

    $(m_0, m_1, \textsc {state}_A) \leftarrow A_1(\textsc {pk})$ s.t. $|m_0| = |m_1|$

    $y \leftarrow \mathsf {Enc}_{\textsc {pk}}(m_b)$

    $D \leftarrow A_2(y, \textsc {state}_A)$

    Output D

$(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ is indistinguishable under a chosen-plaintext (CPA) attack, or semantically secure, if for any ppt algorithms $A = (A_1, A_2)$ the following two ensembles are computationally indistinguishable:

$$\begin{aligned} \Big \{ \mathsf {IND}_0(\Uppi , A, k) \Big \}_{k \in \mathbb {N}} \mathop {\approx }\limits ^{c}~ \Big \{ \mathsf {IND}_1(\Uppi , A, k) \Big \}_{k \in \mathbb {N}}. \end{aligned}$$

It follows from a straight-forward hybrid argument that semantic security implies indistinguishability of multiple encryptions under independently chosen keys:

Proposition 1

Let $\Uppi = (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ be a semantically secure encryption scheme and let the random variable $\mathsf {mIND}_b(\Uppi , A, k, \ell )$, where $b \in \{0,1\}$, $A = (A_1, A_2)$ are ppt algorithms and $k \in \mathbb {N}$, denote the result of the following probabilistic experiment:

$\mathsf {mIND}_b(\Uppi , A, k, \ell ):$

    For $i=1, \ldots , \ell$: $(\textsc {pk}_i, \textsc {sk}_i) \leftarrow \mathsf {Gen}(1^k)$

    $( \langle m_0^1, \ldots , m_0^{\ell } \rangle , \langle m_1^1, \ldots , m_1^{\ell } \rangle , \textsc {state}_A) \leftarrow A_1( \langle \textsc {pk}_1, \ldots , \textsc {pk}_{\ell } \rangle )$

        s.t. $|m_0^1| = |m_1^1|, \ldots , |m_0^\ell | = |m_1^\ell |$

    For $i=1,\dots ,\ell$: $y_i \leftarrow \mathsf {Enc}_{\textsc {pk}_i}(m_b^i)$

    $D \leftarrow A_2(y_1,\dots ,y_\ell , \textsc {state}_A)$

    Output D

then for any ppt algorithms $A = (A_1, A_2)$ and for any polynomial p(k) the following two ensembles are computationally indistinguishable:

$$\begin{aligned} \Big \{ \mathsf {mIND}_0(\Uppi , A, k, p(k)) \Big \}_{k \in N} \mathop {\approx }\limits ^{c}~ \Big \{ \mathsf {mIND}_1(\Uppi , A, k, p(k)) \Big \}_{k \in N}. \end{aligned}$$

3.2 Non-malleable encryption

We next define the notion of non-malleability for PKE. Recall that, intuitively, non-malleability says that upon receiving the challenge ciphertext, which encrypts the message $m_b$, $b \in \{0,1\}$, the decryptions of the set of ciphertexts produced by the adversary for $b=0$ and $b=1$ are computationally indistinguishable.

Definition 5

(Non-malleable encryption [34]) Let $\Uppi = (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ be an encryption scheme and let the random variable $\mathsf {NME}_b(\Uppi , A, k, \ell )$ where $b \in \{0,1\}$, $A = (A_1, A_2)$ are ppt algorithms and $k, \ell \in \mathbb {N}$ denote the result of the following probabilistic experiment:

$\mathsf {NME}_b(\Uppi , A, k, \ell ):$

    $(\textsc {pk}, \textsc {sk}) \leftarrow \mathsf {Gen}(1^k)$

    $(m_0, m_1, \textsc {state}_A) \leftarrow A_1(\textsc {pk})$ s.t. $|m_0| = |m_1|$

    $y \leftarrow \mathsf {Enc}_{\textsc {pk}}(m_b)$

    $(\psi _1, \ldots , \psi _{\ell }) \leftarrow A_2(y, \textsc {state}_A)$

    Output $(d_1, \ldots , d_{\ell })$ where $d_i = {\left\{ \begin{array}{ll} \bot &{} \text{ if } \psi _i = y \\ \mathsf {Dec}_{\textsc {sk}}(\psi _i) &{} \text{ otherwise } \end{array}\right. }$

$(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ is non-malleable under a chosen plaintext (CPA) attack if for any ppt algorithms $A = (A_1, A_2)$ and for any polynomial p(k), the following two ensembles are computationally indistinguishable:

$$\begin{aligned} \Big \{ \mathsf {NME}_0(\Uppi , A, k, p(k)) \Big \}_{k \in \mathbb {N}} \mathop {\approx }\limits ^{c}~ \Big \{ \mathsf {NME}_1(\Uppi , A, k, p(k)) \Big \}_{k \in \mathbb {N}}. \end{aligned}$$

It was shown in [34] that an encryption that is non-malleable (under Definition 5) remains non-malleable even if the adversary $A_2$ receives several encryptions under many different public keys (the formal experiment is the analogue of $\mathsf {mIND}$ for non-malleability).

3.3 Bounded-CCA2 non-malleability

The definition of bounded-CCA2 non-malleability is almost identical to the definition of Non-Malleability except here, we allow the adversary to query $\mathsf {Dec}$ at most q times in the non-malleability experiment (but it must not query $\mathsf {Dec}$ on the challenge ciphertext).

Definition 6

(Bounded-CCA2 non-malleable encryption [12]) Let $\Uppi = (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ be an encryption scheme and let the random variable $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b(\Uppi , A, k, \ell )$ where $b \in \{0,1\}$, $A = (A_1, A_2)$ are ppt algorithms and $k, \ell \in \mathbb {N}$ denote the result of the following probabilistic experiment:

$\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b(\Uppi , A, k, \ell ):$

    $(\textsc {pk}, \textsc {sk}) \leftarrow \mathsf {Gen}(1^k)$

    $(m_0, m_1, \textsc {state}_A) \leftarrow A_1^{O_1}(\textsc {pk})$ s.t. $|m_0| = |m_1|$

    $y \leftarrow \mathsf {Enc}_{\textsc {pk}}(m_b)$

    $(\psi _1, \ldots , \psi _{\ell }) \leftarrow A_2^{O_2}(y, \textsc {state}_A)$

    Output $(d_1, \ldots , d_{\ell })$ where $d_i = {\left\{ \begin{array}{ll} \bot &{} \text{ if } \psi _i = y \\ \mathsf {Dec}_{\textsc {sk}}(\psi _i) &{} \text{ otherwise } \end{array}\right. }$

$(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ is non-malleable under a bounded-CCA2 attack for a function $q(k) : \mathbb {N}\rightarrow \mathbb {N}$ if $\forall$ ppt algorithms $A = (A_1, A_2)$ which make q(k) total queries to the oracles and for any polynomial p(k), the following two ensembles are computationally indistinguishable:

$$\begin{aligned} \Big \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_0(\Uppi , A, k, p(k)) \Big \}_{k \in \mathbb {N}} \mathop {\approx }\limits ^{c}~ \Big \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_1(\Uppi , A, k, p(k)) \Big \}_{k \in \mathbb {N}}. \end{aligned}$$

The oracle $O_1 = \mathsf {Dec}_{\textsc {sk}}(\cdot )$ is the decryption oracle. $O_2 = \mathsf {Dec}_{\textsc {sk}}^y(\cdot )$ is the decryption oracle except that $O_2$ returns $\perp$ when queried on y.

3.4 (Strong) One-time signature schemes

Informally, a (strong) one-time signature scheme $(\mathsf {GenSig},\mathsf {Sign},\mathsf {VerSig})$ is an existentially unforgeable signature scheme, with the restriction that the signer signs at most one message with any key. This means that an efficient adversary, upon seeing a signature on a message m of his choice, cannot generate a valid signature on a different message, or a different valid signature on the same message m. Such schemes can be constructed in a black-box way from one-way functions [28, 36], and thus from any semantically secure encryption scheme $(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})$ using black-box access only to $\mathsf {Gen}$. We next present the formal definition.

Definition 7

((Digital) signature scheme) A triple $(\mathsf {GenSig},\mathsf {Sign},\mathsf {VerSig})$ is a (digital) signature scheme, if $\mathsf {GenSig}$ and $\mathsf {Sign}$ are ppt algorithms and $\mathsf {VerSig}$ is a deterministic polynomial-time algorithm which satisfies the following property:

Correctness. With probability $1-\mathsf {negl}(k)$ over $(\textsc {vksig},\textsc {sksig}) \leftarrow \mathsf {GenSig}(1^k)$: for all m, $\Pr [\mathsf {VerSig}_\textsc {vksig}(m, \mathsf {Sign}_\textsc {sksig}(m)) = 1] = 1$.

Definition 8

(Strong, existential unforgeability for a single message) Let $\Uppi = (\mathsf {GenSig},\mathsf {Sign},\mathsf {VerSig})$ be a signature scheme. For a pair of ppt algorithms $A = (A_1, A_2)$ and $k \in \mathbb {N}$, let the random variable $\mathsf {Forge}(\Uppi , A, k)$ denote the result of the following probabilistic experiment:

$\mathsf {Forge}(\Uppi , A, k):$

    $(\textsc {vksig},\textsc {sksig}) \leftarrow \mathsf {GenSig}(1^k)$

    $(m, \textsc {state}_A) \leftarrow A_1(\textsc {vksig})$

    $\sigma \leftarrow \mathsf {Sign}_{\textsc {sksig}}(m)$

    $(m', \sigma ') \leftarrow A_2(\sigma , \textsc {state}_A)$

    Output 1 iff $\sigma ' \ne \sigma$ and $\mathsf {VerSig}_\textsc {vksig}(m', \sigma ') = 1$

$\Uppi = (\mathsf {GenSig},\mathsf {Sign},\mathsf {VerSig})$ is strongly existentially unforgeable for a single message if any ppt algorithms $A = (A_1, A_2)$:

$$\begin{aligned} \Pr [\mathsf {Forge}(\Uppi , A, k) = 1] \le \mathsf {negl}(k). \end{aligned}$$

In this paper, signature/verification key pairs are sometimes represented as strings over a non-binary alphabet; this technique has also been used in [37]. This augmented version can simply be cast into the version over the binary alphabet by trivially encoding such keys into a binary string.

4 Reconstructable probabilistic encoding scheme (RPE)

4.1 RPE definition

We assume that the readers are familiar with basic notions of error correcting codes and RS codes (Appendix 1.1 gives a brief overview of the notions). We define a reconstructable probabilistic encoding (RPE) below. The secrecy property of an RPE implies that short partial codewords are not bound to any message. The reconstruction property implies that one can later bind such a short partial codeword to any target message and reconstruct the whole consistent codeword. Jumping ahead, this reconstruction procedure will be used to create two different messages sharing the same partial codeword in the reduction step of the proof.

There are several parameters in RPE schemes. A message is represented as a binary string, and the parameter n specifies the length of a message (in bits). A codeword is represented as a string over alphabet $\varSigma$, and the parameter $\ell$ specifies the length of a codeword in the codeword space. The parameter $\delta$ is used to specify the relative distance between codewords. The parameter t is used to specify a threshold to determine whether a partial codeword is short; every codeword of length at most t is considered short.

Definition 9

(Reconstructable probabilistic encoding) We say a triple $(\mathsf {E}, \mathsf {D}, \mathsf {R})$ is a reconstructable probabilistic encoding scheme with parameters $(n, \ell , \delta , t, \varSigma )$, where $n, \ell , t \in \mathbb {N}$, $0< \delta < 1$, $t < \ell$, and $\varSigma$ is an alphabet.

• The encoding algorithm $\mathsf {E}$ is an efficient probabilistic procedure, which takes a message $m \in \{0,1\}^n$ as input and outputs a codeword w over $\varSigma ^\ell$. We let the code $\mathcal {W}$ be the support of $\mathsf {E}$.

• The decoding algorithm $\mathsf {D}$ is an efficient procedure that takes a string $w' \in \varSigma ^\ell$ as input and outputs a codeword w and a message m (or $(\bot , \bot )$ if it fails).

• The reconstruction algorithm $\mathsf {R}$ is an efficient procedure that takes input a set $S \subset [\ell ]$ of size t, a partial codeword $(\alpha _1,\ldots ,\alpha _t) \in \varSigma ^t$, and a message $m \in \{0,1\}^n$, and outputs a complete codeword $w \in \mathcal {W}$ consistent with the given partial codeword $(\alpha _1, \ldots , \alpha _t)$ and message m.

The three algorithms should satisfy the following requirements:

• (1) Error correction: Any two strings in $\mathcal {W}$ are $\delta$-far. For any string $w'$ that is $(1-\delta /2)$-close to some codeword w in $\mathcal {W}$, it holds that $D(w')$ outputs w along with a message m consistent with w.

• (2) Secrecy of partial views: For all $m \in \{0,1\}^n$ and all sets $S \subset [\ell ]$ of size t, the projection of $\mathsf {E}(m)$ onto the coordinates in S, as denoted by $\mathsf {E}(m)|_S$, is identically distributed to the uniform distribution over $\varSigma ^t$.

• (3) Reconstruction from partial views: For any set $S \subset [\ell ]$ of size t, any $(\alpha _1,\ldots ,\alpha _t) \in \varSigma ^t$, and any $m \in \{0,1\}^n$, it holds that $\mathsf {R}(S, (\alpha _1, \ldots , \alpha _t), m)$ is identically distributed to $\mathsf {E}(m)$ with the constraint $\mathsf {E}(m)|_S = (\alpha _1,\ldots ,\alpha _t)$.

We note that similar properties have been exploited already in the early work on secure multi-party computation of Ben-Or et al. [4], with encoding via low-degree polynomials (or RS codes or Shamir secret sharing with Berlekamp–Welch correction). The above notion of RPE was explicitly defined in [8], extending a definition given by Decatur et al. [15], who only required error-correction and secrecy, but not reconstruction.

4.2 Decoding from partial views

The following property will be useful for our construction of non-malleable encryption. Informally, the following lemma states that for any RPE as above, given a sufficiently large “partial view” (i.e. subset of positions), decoding with error correction can be successfully performed on this partial view.

Lemma 1

Let $(\mathsf {E}, \mathsf {D}, \mathsf {R})$ be a reconstructable probabilistic encoding scheme with parameters $(n, \ell , \delta , t, \varSigma )$, and let $\lambda := (1-\delta /4)$ and $\delta ' := \delta /2$. Then, there is an efficient procedure $\mathsf {D}'$ satisfying the following:

For any set $S \in [\ell ]$ with size $s:=\lambda \cdot \ell$, for any $w \in \mathcal {W}$, and for any $w' \in \varSigma ^{s}$ that is $(1-\delta '/2)$-close to $w |_S$, it holds that $D'(S, w')$ outputs w along with a consistent m.

Proof

Let $S = \{i_1, \ldots , i_{s}\}$, where $s = \lambda \cdot \ell$. The decoding from partial views procedure $\mathsf {D}'(S, w')$ does the following. Define the string $\widetilde{w} = \widetilde{w}_1, \ldots , \widetilde{w}_\ell \in \varSigma ^\ell$ in the following way: For $j \in [s], \widetilde{w}_{i_j} := w'_j$ and for $v \in [\ell ]\setminus S$, $\widetilde{w}_v = \sigma$, where $\sigma$ is an arbitrary symbol in $\varSigma$. Note that if $w'$ is $(1-\delta '/2)$-close to $w |_S$ for some w in $\mathcal {W}$, then $\widetilde{w}$ is $(1-\delta /2)$-close to w for some string w in $\mathcal {W}$. Therefore, running the regular decode procedure, $\mathsf {D}(\widetilde{w})$ is guaranteed to output (w, m), where $w \in \mathcal {W}$ is the corrected codeword, and m is the original message. $\square$

4.3 RPE from Reed–Solomon codes

In this section, we construct such a constant-rate RPE scheme with a RS code and packed secret-sharing [17]. We note this is a simple construction; similar constructions were given in different contexts.

Construction 1

(RS-based RPE) For any $n, t, \gamma \in \mathbb {N}$, and for any $\delta$ with $0< \delta < 1$, we construct an RPE scheme with parameters $(n, \ell , \delta , t, \varSigma )$, where $\ell$ is an integer such that $\ell \ge \frac{t+u-1}{1-\delta }$ with $u = \lceil n/\gamma \rceil$ and $\varSigma = \mathrm {GF}(2^{\gamma })$.

We implicitly associate a string $m \in \{0,1\}^{n}$ with a vector $(m_1, m_2, \ldots , m_{u})$ where each $m_i \in \mathrm {GF}(2^{\gamma })$; an integer i with $0 \le i < 2^{\gamma }$ will also be implicitly encoded into a field element in $\mathrm {GF}(2^{\gamma })$. We construct an RPE scheme $(\mathsf {E}, \mathsf {D}, \mathsf {R})$ as follows:

• $\mathsf {E}(m)$: Let $d=t+u-1$. Choose a random degree-d polynomial q over $\varSigma$ such that $q(\ell +1) = m_1$, ..., $q(\ell +u) = m_u$ and output $w = (q(1), q(2), \ldots , q(\ell ))$.

• $\mathsf {D}(w')$: Decode $w'$ using the Berlekamp–Welch algorithm (see Appendix 1.1) and output (w, m), where w is the corrected codeword, and m is the original message.

• $\mathsf {R}(S, (\alpha _1,\ldots ,\alpha _{t}), m)$: Let $S = \{i_1, \ldots , i_{t}\}$. Compute the degree-d polynomial q such that $q(i_1) = \alpha _1, \ldots , q(i_t) = \alpha _t$ and $q(\ell +1) = m_1, \ldots , q(\ell +u) = m_u$ by using Lagrange interpolation polynomial (see Appendix 1.2). Output $(q(1), \ldots , q(\ell ))$.

The error correction property holds since we simply use the RS code with set of codewords $\mathcal {W}$ in encoding and decoding, where

$$\begin{aligned} \mathcal {W}= \{(q(1),\ldots ,q(\ell )) \mid q\hbox { is a degree-}d\hbox { polynomial}\}. \end{aligned}$$

Note that $\mathcal {W}$ is a code over the alphabet $\varSigma$ with minimum relative distance $\frac{\ell - d + 1}{\ell } > \delta$, which means we may efficiently correct up to a $\delta /2$ fraction of errors. Secrecy and reconstruction properties hold since the codeword $(q(1), \ldots , q(\ell ))$ is a $(t+u)$-out-of-$\ell$ secret-sharing of m using Shamir’s secret-sharing scheme, and $(\alpha _1, \ldots , \alpha _t, m_1, \ldots , m_u)$ allows the reconstruction of the (one and only) degree-d polynomial.

Decoding from partial views with better parameters. By using the property of RS codes, we can obtain better parameters in terms of decoding from partial views. In particular, Lemma 2 will allow us to decode from partial views of size $s < \ell /2$, whereas Lemma 1 only allows decoding from partial views of size $s > 3\ell /4$. We illustrate concretely the improvements gained by using the specialized Lemma 2 below for RS codes, as opposed to using the generic Lemma 1 for any RPE, in Example instantiations 1 and 2.

Lemma 2

Let $(\mathsf {E}, \mathsf {D}, \mathsf {R})$ be an RPE scheme with parameters $(n, \ell , \delta , t, \varSigma )$ according to Construction 1; recall $\gamma = \log |\varSigma |$, $u = \lceil n/\gamma \rceil$, and $\ell \ge \frac{t+u-1}{1-\delta }$. Let $\lambda$ be an arbitrary number such that $\frac{t+u}{\ell } < \lambda \le 1$ and $\delta ' = \frac{s-(t+u-1)}{s}$. Then, there is an efficient procedure $\mathsf {D}'$ satisfying the following:

For any set $V \subseteq [\ell ]$ with size $s= \lambda \ell$, for any $w \in \mathcal {W}$, and for any $w' \in \varSigma ^{s}$ that is $(1 - \delta '/2)$-close to $w |_V$ where, it holds that $\mathsf {D}'(V, w')$ outputs w along with a consistent m.

Proof

Let $V = \{i_1, \ldots , i_{s}\}$. Then,

$$\begin{aligned} \mathcal {W}' = \{ (q(i_1),\ldots ,q(i_s)) \mid q\hbox { is a degree-}d \hbox { polynomial}\} \end{aligned}$$

forms another RS code, where $d = t+u-1$. Note that $\mathcal {W}'$ is a code over the alphabet $\mathrm {GF}(2^\gamma )$ with minimum relative distance $\frac{s - d + 1}{s} > \delta '$, which means we can decode $w'$ using the Berlekamp–Welch algorithm, correcting up to a $\delta '/2$ fraction of errors. $\square$

Example instantiation 1. By applying Construction 1 with $\delta = 0.9$ and $\gamma = n$, we obtain an RPE with parameters $(n, 10t, 0.9, t, \mathrm {GF}(2^n))$. According to Lemma 2 with $\lambda =0.3$, the scheme can decode a partial codeword of length 3t, correcting up to $\delta '/2 = 1/3$ fraction of errors. On the other hand, applying the generic Lemma 1, we would only be able to decode a partial codeword of length 8t, correcting up to $\delta '/2 \approx 0.2$-fraction of errors.

Example instantiation 2 (constant-rate RPE). By applying Construction 1 with $\delta = 0.9$ and $\gamma = n/t$, we obtain an RPE with parameters $(n, 20t, 0.9, t, \mathrm {GF}(2^\gamma ))$ with rate 0.05. According to Lemma 2 with $\lambda =0.3$, the scheme can decode a partial codeword of length 6t, correcting up to $\delta '/2 = 1/3$ fraction of errors. On the other hand, applying the generic Lemma 1, we would only be able to decode a partial codeword of length 16t, correcting up to $\delta '/2 \approx 0.2$-fraction of errors.

5 Non-malleable encryption from semantic security

5.1 Generic construction using any RPE

Given a semantically secure encryption scheme $\mathcal{E} = (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ and an RPE, we construct a non-malleable encryption scheme $\Uppi = (\mathsf {NMGen}^\mathsf {Gen}, \mathsf {NMEnc}^{\mathsf {Gen},\mathsf {Enc}}, \mathsf {NMDec}^{\mathsf {Gen},\mathsf {Dec}})$, summarized in Fig. 1 and described as follows. We remark that $\mathsf {NMEnc}$ and $\mathsf {NMDec}$ has black-box access to $\mathsf {Gen}$ (as a one-way function) in order to use one-time signatures; recall that one-time signature schemes can be constructed in a black-box way from one-way functions [28, 36].

Key generation. Let k be the security parameter. Let $(\mathsf {E}, \mathsf {D}, \mathsf {R})$ be an RPE scheme with parameters $(n, \ell , \delta , t, \varSigma )$ and let $\lambda$ and $\delta '$ be the parameter associated with decoding the partial views. In addition, set $t = k$.

The public key contains an error correcting code $C:\varGamma ^t \rightarrow \varGamma ^{\ell }$ with distance $\lambda \ell$, where $\varGamma$ is an appropriately chosen finite alphabet in order to satisfy the distance condition. Let $g = |\varGamma |$ and we will implicitly associate $\varGamma = [g]$. According to the Gilbert–Varshamov bound [20, 38], for any $\lambda < 1 - 1/g$ and for any $R = t/\ell$ with $R < 1 - H_g(\lambda )$, there is an error correcting code with rate R and relative distance $\lambda$, where $H_g(\lambda ) = \lambda \log _g (g-1) - \lambda \log _g \lambda - (1 - \lambda ) \log _g (1 - \lambda )$. We note this technique was used in [37]. In addition, there are $g \cdot \ell$ public keys from $\mathsf {Gen}$ indexed by a pair $(j,b)\in [\ell ] \times [g]$, that is, $\{ \textsc {pk}^b_{j} \mid (j, b) \in [\ell ] \times [g] \}$.

The secret key contains the decryption keys $\textsc {sk}^b_{j}$ and a random subset S of $[\ell ]$ with size t to be used in decryption for consistency checks (described below).

Encryption. Encryption of a message $m \in \{0,1\}^{n}$ proceeds as follows:

• 1. Generate $(\textsc {sksig},\textsc {vksig})$ for a one-time signature where $\textsc {vksig}\in \varGamma ^t$, and compute $(v_1, \ldots , v_{\ell }) \leftarrow C(\textsc {vksig})$.

• 2. Compute $(s_1,\ldots ,s_{\ell }) \leftarrow \mathsf {E}(m)$ and compute an $\ell$-long vector $\mathbf {c} = (c_1, \ldots , c_{\ell })$ of ciphertexts where $c_{j} = \mathsf {Enc}_{\textsc {pk}_{j}^{v_j}}(s_j)$:

  $$\begin{aligned} \mathbf {c} = \left( \mathsf {Enc}_{\textsc {pk}_{1}^{v_1}}(s_1), \mathsf {Enc}_{\textsc {pk}_{2}^{v_2}}(s_2), \ldots , \mathsf {Enc}_{\textsc {pk}_{\ell }^{v_{\ell }}}(s_{\ell }) \right) \end{aligned}$$

• 3. Create a signature $\sigma$ on $\mathbf {c}$ using $\textsc {sksig}$. The ciphertext is $[\textsc {vksig}, \mathbf {c}, \sigma ]$.

Fig. 1

The non-malleable encryption scheme $\Uppi$. We annotate the construction with specific parameters when the message length is $\omega (k)$ and our RS-based RPE is used

Decryption. To decrypt, we verify the signature and perform consistency checks. A valid ciphertext in $\Uppi$ is an encryption of a codeword in $\mathcal {W}$. We want to design consistency checks that reject ciphertexts that are “far” from being valid ciphertexts under $\Uppi$. For simplicity, we will describe the consistency checks as applied to the underlying vector of plaintexts. The checks depend on a random subset S of t columns chosen during key generation.

decoding-check::

Let $I = \{1, \ldots , \lambda \ell \}$. We find a codeword w such that $w |_I$ is $(1-\frac{\delta '}{2})$-close to the first $\lambda \ell$ elements of the vector $(s_1, \ldots , s_\ell )$; the check fails if no such w exists. Recall that according to Lemma 1, it can correct up to a $\delta '/2$ fraction of errors in $(s_1, \ldots , s_{\lambda \ell })$.

codeword-check::

We check that the vector $(s_1, \ldots , s_\ell )$ agrees with w at the positions indexed by S.

Finally, if all the checks accept, decode the codeword w and output the result; otherwise output $\perp$.

We note that we only need a partial set of the decryption keys, in particular for I and S, in order to complete the decryption procedure.

5.2 Using construction 1 for RPE

By plugging our RS-based RPE in Construction 1, using parameters $(n,20k,0.9,k,\mathrm {GF}(2^{n/k}))$, into the above generic NM-CPA construction, we obtain an NM-CPA encryption scheme for messages of length $\omega (k)$. In Fig. 1, we briefly annotate the generic construction with the parameters for this RPE, in order to provide a better sense of how the actual NM-CPA scheme would look. The underlying IND-CPA scheme encrypts an element of $\mathrm {GF}(2^{n/k})$, and there are 20k of them in the overall NM-CPA ciphertext; if the underlying IND-CPA encryption is constant rate, the overall NM-CPA also achieves a constant rate. Note we can use the binary alphabet for the error correcting code C, since it has a relative distance of $\lambda = 0.3$ and a rate of 0.05; the Gilbert–Varshamov bound [20, 38] guarantees the existence of a linear code satisfying such distance and rate conditions.

When the message is of length O(k), we can instantiate an NM-CPA encryption scheme by using an RPE with parameters $(n,10k,0.9,k,\mathrm {GF}(2^n))$. Note the overall NM-CPA ciphertext length becomes $\varTheta (k^2)$. The underlying IND-CPA scheme encrypts an element of $\mathrm {GF}(2^n)$, and there are 10k of them in the overall NM-CPA ciphertext.

6 Analysis

Theorem 1

If $\mathcal{E} = (\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ is a semantically secure PKE, then the PKE scheme $\Uppi = (\mathsf {NMGen}^\mathsf {Gen}, \mathsf {NMEnc}^{\mathsf {Gen},\mathsf {Enc}}, \mathsf {NMDec}^{\mathsf {Gen},\mathsf {Dec}})$ described in Fig. 1 is non-malleable under a chosen plaintext attack.

6.1 Proof of main theorem

In the hybrid argument, we consider the following variants of $\mathsf {NME}_b$ as applied to $\Uppi$, where $\textsc {vksig}^*= (v_1^*, \ldots , v_\ell ^*)$ denotes the verification key in the ciphertext $y = \mathsf {NMEnc}_\textsc {pk}(m_b)$:

Experiment $\mathsf {NME}^{(1)}_b$: $\mathsf {NME}^{(1)}_b$ proceeds exactly like $\mathsf {NME}_b$, except we replace sig-check in $\mathsf {NMDec}$ with sig-check $^*$:

(sig-check $^*$) Verify the signature with $\mathsf {VerSig}_\textsc {vksig}[\mathbf {c},\sigma ]$. Output $\perp$ if the signature fails to verify or if $\textsc {vksig}= \textsc {vksig}^*$.

Experiment $\mathsf {NME}^{(2)}_b$: $\mathsf {NME}^{(2)}_b$ proceeds exactly like $\mathsf {NME}_b^{(1)}$ except we replace $\mathsf {NMDec}$ with $\mathsf {NMDec}^*$:

$\mathsf {NMDec}^*_\textsc {sk}([\mathbf {c}, \textsc {vksig}, \sigma ])$:

• 1. (sig-check $^*$) Verify the signature with $\mathsf {VerSig}_\textsc {vksig}[\mathbf {c},\sigma ]$. Output $\perp$ if the signature fails to verify or if $\textsc {vksig}= \textsc {vksig}^*$.

• 2. (decoding-check $^*$) Let $\mathbf {c} = (c_{j})$ and $C(\textsc {vksig}) = (v_1,\ldots ,v_\ell )$. Let $X = (x_1, \ldots , x_{\lambda \ell })$ be the smallest distinct values such that $v_{x_i} \ne v^*_{x_i}$. Note there must be these values since C is an encoding with minimum distance $\lambda$. Compute $s_{x_i} = \mathsf {Dec}_{\textsc {sk}^{v_{x_i}}_{x_i}}(c_{x_i})$, $i = 1,\ldots ,\lambda \ell$. Compute $w = (w_1,\ldots ,w_{\ell }) \in \mathcal {W}$ such that $(w_{x_1}, \ldots , w_{x_{\lambda \ell }})$ is least $(1-\frac{\delta '}{2} )$-close to $(s_{x_1},\ldots ,s_{x_{\lambda \ell }})$ by running $\mathsf {D}'(X, (s_{x_1}, \ldots , s_{x_{\lambda \ell }}))$ based on the property of decoding from the partial view. If no such codeword exists, output $\perp$.

• 3. (codeword-check $^*$) For all $j \in S$, check that $\mathsf {Dec}_{\textsc {sk}^{v_j}_{j}}(c_{j}) = w_{j}$.

If all the checks accept, output the message m corresponding to the codeword w; else, output $\perp$.

Claim 6.1

For $b \in \{0,1\}$, $\Bigl \{ \mathsf {NME}_b(\Uppi ,A,k,p(k)) \Bigr \} \mathop {\approx }\limits ^{c} \Bigl \{ \mathsf {NME}_b^{(1)}(\Uppi ,A,k,p(k)) \Bigr \}.$

Proof

Assume towards contradiction that there is a ppt machine A that distinguishes $\mathsf {NME}_b(\Uppi ,A,k,p(k))$ and $\mathsf {NME}_b^{(1)}(\Uppi ,A,k,p(k))$ with non-negligible probability. We construct a ppt machine B that breaks the security of the strong, one-time signature scheme, $\Uppi ' := (\mathsf {GenSig},\mathsf {Sign},\mathsf {VerSig})$.

First, note that since A may not query the decryption oracle on the challenge ciphertext itself, experiments $\mathsf {NME}_b$ and $\mathsf {NME}_b^{(1)}$ can only differ (due to the difference between sig-check and sig-check $^*$) if the following event takes place:

A outputs a ciphertext $[\mathbf {c},\textsc {vksig},\sigma ]$ such that the signature correctly verifies and $\textsc {vksig}= \textsc {vksig}^*$.

Thus, the above event must occur with non-negligible probability. We are now ready to describe the adversary B. B participates externally in a $\mathsf {Forge}(\Uppi ', B, k)$ experiment with verification key $\textsc {vksig}^*$, while internally playing the role of challenger in the $\mathsf {NME}_b(\Uppi , A, k, p(k))$ experiment. B runs $(\textsc {pk}, \textsc {sk}) \leftarrow \mathsf {NMGen}(1^k)$, instantiates $A_1(\textsc {pk})$ and waits for $A_1$ to submit $(m_0, m_1, \textsc {state}_A)$. B then chooses $b \leftarrow \{0,1\}$, sets the verification key to $\textsc {vksig}^*$, computes the first part of the challenge ciphertext, $\mathbf {c}^*$ honestly, and queries its signing oracle on $\mathbf {c}^*$ to obtain $\sigma ^*$. B then instantiates $A_2(y:=[\mathbf {c}^*,\textsc {vksig}^*,\sigma ^*], \textsc {state}_A)$ and waits for $A_2$ to output $(\psi _1, \ldots , \psi _{p(k)})$. Upon receiving $(\psi _1, \ldots , \psi _{p(k)})$, B checks whether for any $\psi _i := [\mathbf {c}_i,\textsc {vksig}_i,\sigma _i], i \in [p(k)]$, it is the case that the signature correctly verifies and $\textsc {vksig}_i = \textsc {vksig}^*$. If yes, B forwards $(\mathbf {c}_i, \sigma _i)$ to its external challenger. Recall that this event occurs with non-negligible probability, and so B succeeds in forging with non-negligible probability, resulting in a contradiction to the security of $\Uppi '$. $\square$

Claim 6.2

For $b \in \{0,1\}$, $\Bigl \{ \mathsf {NME}_b^{(1)}(\Uppi ,A,k,p(k)) \Bigr \} \mathop {\approx }\limits ^{s} \Bigl \{ \mathsf {NME}_b^{(2)}(\Uppi ,A,k,p(k)) \Bigr \}.$

Proof

We will show that both distributions are statistically close for all possible coin tosses in both experiments (specifically, those of $\mathsf {NMGen}, A$ and $\mathsf {NMEnc}$) except for the choice of S in $\mathsf {NMGen}$. Once we fix all the coin tosses apart from the choice of S, the output $(\psi _1,\ldots ,\psi _{p(k)})$ of $A_2$ are completely determined and identical in both experiments $\mathsf {NME}_b^{(1)}$ and $\mathsf {NME}_b^{(2)}$.

Recall the guarantees we would like from $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$:

• On input a ciphertext that is an encryption of a message m under $\Uppi$, both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ will output m with probability 1.

• On input a ciphertext that is “close” to an encryption of a message m under $\Uppi$, both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ will output m with the same probability (the exact probability is immaterial) and $\perp$ otherwise.

• On input a ciphertext that is “far” from any encryption, then both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ output $\perp$ with high probability.

To quantify and establish these guarantees, we consider the following promise problem $(\Uppi _Y, \Uppi _N)$ that again refers to the underlying vector of plaintexts. An instance is a vector of $\ell$ entries each of which lies in $\{0,1\}^n \,\cup \perp$.

$\Uppi _Y$ :

(yes instances)—for some $w \in \mathcal {W}$, the instance equals w.

$\Uppi _N$ :

(no instances)—either the first $\lambda \ell$ elements of the instance is $\delta '/2$-far from the first $\lambda \ell$ elements of every codeword in $\mathcal {W}$ or the entire instance is $\frac{\lambda \delta '}{2}$-far from every codeword in $\mathcal {W}$.

Valid encryptions correspond to the yes instances, while no instances will correspond to “far” ciphertexts. To analyze the success probability of an adversary, we examine each ciphertext $\psi$ it outputs with some underlying vector $\mathbf {M}$ of plaintexts (which may be a yes or a no instance or neither) and show that both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ agree on $\psi$ with high probability. To facilitate the analysis, we consider two cases:

• If $\mathbf {M} \in \Uppi _N$, then it fails the codeword checks in both decryption algorithms with high probability, in which case both decryption algorithms output $\perp$.

  Specifically, if the first $\lambda \ell$ elements of $\mathbf {M}$ is $\delta '/2$-far from the first $\lambda \ell$ elements of every codeword in $\mathcal {W}$ then the decoding check in $\mathsf {NMDec}$ rejects $\mathbf {M}$ with probability 1. Moreover, being $\delta '/2$-far from the first $\lambda \ell$ elements for every codeword implies that $\mathbf {M}$ have at least $(\delta '/2)\cdot \lambda \ell$ different positions, where c is some constant. Therefore, the codeword check in $\mathsf {NMDec}^*$ rejects $\mathbf {M}$ with probability at least $1 - \left( 1 - \frac{\delta ' \lambda }{2} \right) ^t$, since the condition implies that $\mathbf {M}$ is $\frac{\delta ' \lambda }{2}$-far from every codeword. From Lemma 1, both $\delta '$ and $\lambda$ are constant, and therefore with overwhelming probability in t, $\mathsf {NMDec}^*$ will reject $\mathbf {M}$ as well.

  On the other hand, if $\mathbf {M}$ is $\lambda \delta '/2$-far from every codeword, both codeword checks in $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ rejects $\mathbf {M}$ with probability $1-(1 - \frac{\delta ' \lambda }{2})^t$.

  Therefore, both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ reject $\mathbf {M}$ with with probability at least $1- 2 \cdot (1 - \frac{\delta ' \lambda }{2})^k$, since we have $t = k$.

• If $\mathbf {M} \notin \Uppi _N$, then both decryption algorithms always output the same answer for all choices of the set S, provided there is no forgery. Fix $\mathbf {M} \notin \Uppi _N$ and a set S. Note that the decoding check in both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ will be successful. This is because $\mathbf {M}$ is $(1-\lambda \delta '/2)$-close to w, and there are at most $(\lambda \delta '/2) \cdot \ell$ erroneous positions compared with some codeword in $\mathcal {W}$. This implies that any $\lambda \ell$ elements of $\mathbf {M}$ has at most $\frac{(\lambda \delta '/2) \cdot \ell }{\lambda \ell } = \frac{\delta '}{2}$ fraction of errors. Moreover, the codeword check is the same in both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$. As such, both decryption algorithms output $\perp$ with exactly the same probability, and whenever they do not output $\perp$, they output the same message m.

From the above analysis, the two hybrids are statistically close. $\square$

Claim 6.3

Let $(n, \ell , \delta , t, \varSigma )$ be the parameters of an RPE scheme that $\Uppi$ uses in Fig. 1. Then, for every ppt machine A and for any polynomial p, there exists a ppt machine B such that for $b \in \{0,1\}$, it holds

$$\begin{aligned}\Bigl \{ \mathsf {NME}_b^{(2)}(\Uppi ,A,k,p(k)) \Bigr \} \equiv \Bigl \{ \mathsf {mIND}_b(\mathcal{E},B,k,\ell -t) \Bigr \}.\end{aligned}$$

Recall that the value p(k) in the various $\mathsf {NME}$ experiments corresponds to the number of (mauled) ciphertexts that the adversary would come up with, after given the challenge ciphertext.

Proof

The machine B is constructed as follows: B participates in the experiment $\mathsf {mIND}_b$ (the “outside”) while internally simulating $A = (A_1,A_2)$ in the experiment $\mathsf {NME}^{(2)}_b$.

• (pre-processing) Pick a random subset $S = \{u_1,\ldots ,u_t\}$ of $[\ell ]$. Choose an ECC C, and run $\mathsf {GenSig}(1^k)$ to generate $(\textsc {sksig}^*,\textsc {vksig}^*)$ and set $(v^*_1,\ldots ,v^*_\ell ) = C(\textsc {vksig}^*)$. Let $\phi : \{ j \mid j \in [\ell ]\setminus S \} \rightarrow [\ell -t]$ be a bijection.

• (key generation) B receives $\langle \textsc {pk}_1,\ldots ,\textsc {pk}_{\ell -t} \rangle$ from $\mathsf {mIND}_b$ and simulates $\mathsf {NMGen}$ as follows: for all $j \in [\ell ], \beta \in [g]$,

  $$\begin{aligned} (\textsc {pk}^\beta _{j}, \textsc {sk}^\beta _{j}) = {\left\{ \begin{array}{ll} (\textsc {pk}_{\phi (j)},\perp ) &{} \text{ if } \beta = v^*_j \text{ and } j \notin S\\ \mathsf {Gen}(1^k) &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

• (message selection) Let $(m^0, m^1)$ be the pair of messages $A_1$ returns. B chooses $(\alpha _1, \ldots , \alpha _t) \leftarrow \varSigma ^t$ uniformly at random and then computes

  $$\begin{aligned} (w^0_1, \ldots , w^0_\ell ) \leftarrow \mathsf {R}(S, (\alpha _1, \ldots , \alpha _t), m^0),~~ (w^1_1, \ldots , w^1_\ell ) \leftarrow \mathsf {R}(S, (\alpha _1, \ldots , \alpha _t), m^1). \end{aligned}$$

  Recall that $\mathsf {R}$ is the reconstruction algorithm of the underlying RPE scheme. For $j \in S$, let $\gamma _j = w^0_j = w^1_j$. B forwards $(\langle m^0_1, \ldots , m^0_{\ell -t} \rangle , \langle m^1_1, \ldots , m^1_{\ell -t} \rangle )$ to $\mathsf {mIND}_b$, where $m^b_{\phi (j)} = w^b_j$, for $j \in [\ell ] \setminus S$.

• (ciphertext generation) B receives $\langle y_1,\ldots ,y_{\ell -t} \rangle$ from $\mathsf {mIND}_b$ (according to the distribution $\mathsf {Enc}_{\textsc {pk}_1}(m^b_1),\ldots ,\mathsf {Enc}_{\textsc {pk}_{\ell -t}}(m^b_{\ell -t})$) and generates a ciphertext $[\mathbf {c}, \textsc {vksig}^*, \sigma ]$ as follows:

  $$\begin{aligned} c_{i,j} = {\left\{ \begin{array}{ll} y_{\phi (j)} &{} \hbox {if }j \notin S\\ \mathsf {Enc}_{\textsc {pk}^{v^*_j}_j}(\gamma _{j}) &{} \hbox {otherwise} \end{array}\right. } \end{aligned}$$

  B then computes the signature $\sigma \leftarrow \mathsf {Sign}_{\textsc {sksig}^*}(\mathbf {c})$ and forwards $[\mathbf {c}, \textsc {vksig}^*, \sigma ]$ to $A_2$. It is straight-forward to verify that $[\mathbf {c}, \textsc {vksig}^*, \sigma ]$ is indeed a random encryption of $m_b$ under $\Uppi$.

• (decryption) Upon receiving a sequence of ciphertexts $(\psi _1,\ldots ,\psi _{p(k)})$ from $A_2$, B decrypts these ciphertexts using $\mathsf {NMDec}^*$ as in $\mathsf {NME}^{(2)}_b$.

Note that the view of A in the original experiment is identically distributed to the one that B simulates. We conclude the proof by pointing out that B perfectly simulates $\mathsf {NMDec}^*$, since it has the secret keys $\{ \textsc {sk}^\beta _{j} \mid \beta \ne v^*_j \text { or } j \in S \}$, which B generated by itself. $\square$

Combining the three claims, we conclude that for every ppt adversary A, there is a ppt adversary B such that for $b \in \{0,1\}$,

$$\begin{aligned}&\Bigl \{ \mathsf {NME}_b(\Uppi ,A,k,p(k)) \Bigr \} \mathop {\approx }\limits ^{c} \Bigl \{ \mathsf {NME}_b^{(1)}(\Uppi ,A,k,p(k)) \Bigr \} \\&\quad \mathop {\approx }\limits ^{s} \Bigl \{ \mathsf {NME}_b^{(2)}(\Uppi ,A,k,p(k)) \Bigr \} \equiv \Bigl \{\mathsf {mIND}_b(\mathcal{E},B,k, \ell - t) \Bigr \} \end{aligned}$$

We have $\mathsf {mIND}_0(\mathcal{E},B,k,\ell -t) \mathop {\approx }\limits ^{c} \mathsf {mIND}_1(\mathcal{E},B,k, \ell -t)$, due to semantic security of the underlying encryption scheme, which concludes the proof.

7 Achieving bounded-CCA2 non-malleability

We describe how our scheme may be modified to achieve non-malleability under a bounded-CCA2 attack. Recall that, informally, an encryption scheme is non-malleable against a q-bounded CCA2 attack if the adversary is allowed to query $\mathsf {Dec}$ adaptively at most q(k) times in the non-malleability experiment. Our modification is the straight-forward analogue of the [12] modification of the [34] scheme: We change the parameter $(n, \ell , \delta , t, \varSigma )$ of the underlying RPE scheme such that $t = a \cdot (k + q(k))$, where a is a constant such that $\left( 1 - \frac{\lambda \delta '}{2} \right) ^a \le \frac{1}{2}$. See Fig. 1 for more details.

We analyze the security of the encryption scheme using a similar hybrid argument. We define the following hybrid experiments as before.

• Experiment $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}^{(1)}_b$: This experiment proceeds exactly like $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b$, except we replace sig-check in $\mathsf {NMDec}$ with sig-check $^*$ as described in Sect. 6.

• Experiment $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}^{(2)}_b$: This experiment proceeds exactly like $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(1)}$ except we replace $\mathsf {NMDec}$ with $\mathsf {NMDec}^*$ as described in Sect. 6.

We note that $\Bigl \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b(\Uppi ,A,k,p(k)) \Bigr \}$ and $\Bigl \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(1)}(\Uppi ,A,k,p(k)) \Bigr \}$ are computationally indistinguishable for each $b \in \{0,1\}$, which can be argued based on security of the signature scheme as in Claim 6.1. Moreover, it holds that $\Bigl \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(2)}(\Uppi ,A,k,p(k)) \Bigr \}$ and $\Bigl \{ \mathsf {mIND}_b(\mathcal{E},B,k, \ell - t) \Bigr \}$ are identically distributed for each $b \in \{0,1\}$, which can be shown using the reduction in the proof of Claim 6.3. (Recall that the value p(k) in the various $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}$ experiments corresponds to the number of (mauled) ciphertexts that the adversary would come up with, after given the challenge ciphertext.) Therefore, we are only left to show the following claim to conclude the analysis.

Claim 7.1

For $b \in \{0,1\}$, we have

$$\begin{aligned} \Bigl \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(1)}(\Uppi ,A,k,p(k)) \Bigr \} \mathop {\approx }\limits ^{s} \Bigl \{ \mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(2)}(\Uppi ,A,k,p(k)) \Bigr \} \end{aligned}$$

Proof

Let $q = q(k)$ and for a ciphertext c, let $\mathbf {M}_c$ denote the underlying plaintext vector of c.

As before, we will show that both distributions are statistically close for all possible coin tosses in both experiments (specifically, those of $\mathsf {NMGen}, A$ and $\mathsf {NMEnc}$) except for the choice of S in $\mathsf {NMGen}$. Fix all the coin tosses apart from the choice of S. Here, however, unlike the case of chosen plaintext attacks, we cannot immediately deduce that the outputs of $A_2$ in both experiments are completely determined and identical, since they depend on the adaptively chosen queries to $\mathsf {NMDec}$, and the answers depend on S. Still, the choice of S only affects whether the consistency checks accept or not; therefore, for each query, the number of possible responses of $\mathsf {NMDec}/\mathsf {NMDec}^*$ is at most two (since we fixed all the coin tosses except S). Moreover, if a query c is such that $\mathbf {M}_c \in \Uppi _N$, $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ will both give only one response of $\perp$ with overwhelming probability, according to the analysis in Claim 6.2.

This leads us to consider a binary tree of depth q that corresponds informally to “unrolling” the q adaptive queries that A makes to $\mathsf {NMDec}/\mathsf {NMDec}^*$ in the experiments $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(1)}/\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(2)}$. The root node of the tree corresponds to the first query A makes to $\mathsf {NMDec}/\mathsf {NMDec}^*$, and each edge from a node to its child is labeled with the answer of $\mathsf {NMDec}/\mathsf {NMDec}^*$ to the node’s query. In particular, the tree is inductively built as follows:

• When A makes a query c with $\mathbf {M}_c \in \Uppi _N$, we only consider the computation path corresponding to $\mathsf {NMDec}/\mathsf {NMDec}^*$ responding with $\perp$.

• When A makes a query c with $\mathbf {M}_c \not \in \Uppi _N$, we consider two computation paths, that is, one case of $\mathsf {NMDec}/\mathsf {NMDec}^*$ responding with a valid decryption (in which case the value returned is independent of S) and the other case of responding with $\perp$.

• The query at an internal node (except the root) corresponds to the query that A makes when following the computation path from the root to the node while $\mathsf {NMDec}/\mathsf {NMDec}^*$’s answers correspond to the labels of the edges in the path. Each leaf node contains p(k) ciphertexts output by A at the end of the experiment.

Observe that the construction of the computation tree is completely deterministic and independent of the choice of S. Moreover, since $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ behave identically for queries c with $\mathbf {M}_c \not \in \Uppi _N$ as shown in Claim 6.2, the computation tree is $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(1)}$ is identical to that in $\mathsf {NME}\textsf {-}q\textsf {-}\mathsf {CCA}_b^{(2)}$. Note also that A makes at most q adaptive queries to $\mathsf {NMDec}$, and therefore the total number of ciphertexts in the tree is at most $2^{q+1} p(k)$. The claim follows from combining the following two observations:

• Let $\mathsf{good}(S)$ be an event in which given the choice S, for every ciphertext c in the tree such that $\mathbf {M}_c \in \Uppi _N$, both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ output $\perp$. We have

  $$\begin{aligned} \Pr _S[\mathsf{good}(S)] \ge 1 - 2 \cdot \big (2^{q+1} p(k) \big ) \cdot \Big (1 - \frac{\lambda \delta '}{2}\Big )^t \ge 1 - 2 \cdot \big ( 2^{q+1} p(k) \big ) \cdot \frac{1}{2^{k + q}} = 1 - \mathsf {negl}(k). \end{aligned}$$

  This follows from a union bound over these ciphertexts in the tree and the analysis in Claim 6.2.

• For every S such that $\mathsf{good}(S)$ is true, the outputs in both experiments are the same. This follows readily by induction on the queries made by A, and using the fact both $\mathsf {NMDec}$ and $\mathsf {NMDec}^*$ always output the same answer for any $\mathbf {M} \not \in \Uppi _N$ as explained in the analysis in Claim 6.2. $\square$

Appendix 1: Background

1.1 Appendix 1.1: Error-correcting codes

For integers $\ell , n$, $0< \delta < 1$ and a collection of symbols $\varSigma$, an $[\ell ,n,\delta ]$-code over $\varSigma$ is a collection $\mathcal {W}\subset \varSigma ^\ell$ of $\ell$-letter words over the alphabet $\varSigma$ with $|\mathcal {W}| = 2^n$ and the property that any two strings in $\mathcal {W}$ differ in at least $\delta \cdot \ell$ locations. Note that given any string $s \in \varSigma ^\ell$, there is at most one string $w \in \mathcal {W}$ which is within distance $\frac{\delta \ell -1 }{2}$ from s.

Reed–Solomon codes. For a finite field F of size $2^n$, a set $S = \{i_0, i_1, \ldots , i_\ell \} \subseteq F$, and parameter d, where $\ell \ge d + 1$, the Reed Solomon Code is an $[\ell , n, (\ell -d)/\ell ]$-code over alphabet $\varSigma := F$, whose codewords are the strings $\{(p(i_1), p(i_2), \ldots , p(i_\ell )\}$, where p ranges over all polynomials of degree at most d over F.

For purposes of this work, to encode a message m:

• Choose a random degree-d polynomial p subject to $p(i_0) := m$.

• Output $\{(p(i_1), p(i_2), \ldots , p(i_n)\}$.

The Berlekamp–Welch algorithm. The decoding algorithm for RS codes can be efficiently implemented using the Berlekamp–Welch algorithm [5]. Specifically, this algorithm can be used to efficiently recover the nearest codeword—i.e. the nearest degree-d polynomial p—given a corrupted codeword $\{(f(i_1), f(i_2), \ldots , f(i_\ell )\}$, as long as there exists some set $S' \subseteq S$ of size at least $(n-d)/2$, such that $f(i_j) = p(i_j)$, for all $i_j \in S'$. Once such a polynomial p is found, the message can be recovered by outputting $p(i_0)$.

1.2 Appendix 1.2: Lagrange interpolation polynomial

For a given set of distinct points $\{(a_1, b_1), \ldots , (a_{d+1}, b_{d+1})\}$, the Lagrange interpolation polynomial is a degree-d polynomial q such that $q(a_1) = b_1, \ldots q(a_{d+1}) = b_{d+1}$, which can be computed as follows:

$$\begin{aligned} q(x) = \sum _{i=1}^{d+1} b_i L_i(x), \end{aligned}$$

where Lagrangian $L_i$ is a degree-d polynomial such that $L_i(x) = 1$ if $x = a_i$ and $L_i(x) = 0$ if $x \in \{a_1, \ldots , a_{d+1}\}$ but $x \ne a_i$. In particular, we have

$$\begin{aligned} L_i(x) = \prod _{j \in [d+1]\setminus \{i\}} \frac{x - a_j}{a_i - a_j}. \end{aligned}$$