Separating invertible key derivations from non-invertible ones: sequential indifferentiability of 3-round Even–Mansour

Abstract

Iterated Even–Mansour (IEM) scheme consists of a small number r of fixed n-bit permutations separated by $r+1$ round-key additions. When the permutations are public, independent and random, and a common round key derived from the master key by an idealized non-invertible key derivation (KD) function is used, 5 rounds was proved sufficient to obtain (full) indifferentiability from ideal ciphers by Andreeva et al. (CRYPTO 2013). The KD can be a random oracle, or a Davies-Meyer construction from a random permutation. This work considers such IEM with non-invertible KD in the sequential indifferentiability model of Mandal et al. (TCC 2012). As results, this work shows that in both cases mentioned before, 3 rounds yields sequential indifferentiability from ideal ciphers. As Andreeva et al. has proved 3-round IEM with idealized invertible key derivations not sequentially indifferentiable (by exhibiting an attack), a definitive separation between IEM with invertible key derivations and IEM with non-invertible key derivations is established. This is the most important implication of the results in this work.

1 Introduction

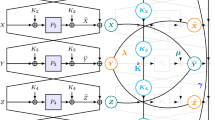
Even–Mansour scheme (EM) was proposed in 1991 [21] in an attempt to build the simplest possible blockcipher, using a single permutation and two whitening keys. Generalizing EM by iterating multiple rounds, the iterated Even–Mansour cipher (IEM) is obtained. More clearly, the r-round iterated Even–Mansour $\text {IEM}_r$ consists of r fixed n-bit permutations $P_1,\ldots ,P_r$ separated by round-key addition:

$$\begin{aligned} \text {IEM}_r(K,m)=k_r\oplus P_r(\ldots k_2\oplus P_2(k_1\oplus P_1(k_0\oplus m))\ldots ). \end{aligned}$$

IEM is also known as key-alternating cipher, which is the basic structure of the popular substitution-permutation network (SPN) blockciphers such as AES [15], Serpent [1], and PRESENT [7].

The provable security of IEM is analyzed in the Random Permutation Model (RPM), in which the underlying permutations are modeled as public random ones, and the adversary is only given black-box oracle access to them. Such proofs are viewed as evidence for the non-existence of generic attacks, although idealized models are actually uninstantiable: please see Canetti, Goldreich, Halevi (CGH) [9], Maurer, Renner, and Holenstein (MRH) [30] on random oracle model (ROM), Black [6] on ideal cipher model (ICM). In RPM, Even and Mansour [22] proved the basic EM secure up to $O(2^{n/2})$ queries when the keys are secret, and this bound was later proved tight (Daemen [14], Biryukov and Wagner [4], and finally Dunkelman et al. [20]). Since then, the community has witnessed a soar of studies on IEM—especially in the recent half decade. Such studies cover minimization (Dunkelman et al. [20] and Chen et al. [11]), pseudorandomness (Bogdanov et al. [8], Steinberger [31], Lampe et al. [28], and finally Chen and Steinberger [10]), related-key security (Farshim and Procter [23] and Cogliati and Seurin [12]), and attacks (for example, a series of works of Dinur, Dunkelman, etc. [16–18, 20]).

Indifferentiability of IEM Several recent works considered IEM in MRH’s indifferentiability model [30] and Mandal et al.’s sequential-indifferentiability model [29] (seq-indifferentiability; please see Sect. 2 for the formal definition) of IEM. The motivation is to prove security against known-key attacks (due to Knudsen and Rijmen [25]) and chosen-key attacks (due to Biryukov et al. [5]), in which the adversary knows and chooses keys and tries to exhibit non-randomness. Briefly speaking, indifferentiability of IEM means that IEM can be as secure as an ideal cipher. Whereas seq-indifferentiability of IEM means that IEM is correlation intractable [9],¹ so that any attack (even a chosen-key one) that exploits relations between the inputs and outputs of IEM cannot succeed. Here the ideal cipher ${\mathbf {IC}}[\kappa ,n]:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^n$ is taken randomly from the set of $(2^{n}!)^{2^{\kappa }}$ blockciphers with key space $\{0,1\}^{\kappa }$ and plaintext and ciphertext space $\{0,1\}^n$.

In this field, Andreeva et al. [2] showed that $\text {IEM}_5$ is indifferentiable from ${\mathbf {IC}}[\kappa ,n]$, if a common round key derived by a $\kappa$-to-n-bit random oracle is used (we denote this combination of EM with a Random oracle by $\text {EMR}$). $\text {IEM}_5$ without random oracle was also considered, and the conclusion was that instantiating the key derivation (KD) by a Davies-Meyer construction $KD(K)=P(K)\oplus K$ (denote by $\text {EMDP}$ such entirely Permutation-based Even–Mansour) preserves indifferentiability. On the other hand, Lampe, Seurin [26] and Cogliati, Seurin [12] concentrated on single-key Even–Mansour ($\text {SEM}$) in which the user-provided n-bit master key is directly used at each round. They two respectively proved that $\text {SEM}_{12}$ is indifferentiable, and $\text {SEM}_{4}$ is seq-indifferentiable. Results on $\text {SEM}$ can be easily generalized to the case where each round key is derived by an efficiently invertible permutation, so that they are closer to most of the concrete designs.

1.1 The problem, and our motivation

With the results mentioned above, a natural question is whether IEM really benefits from cryptographically strong assumptions about the KD. It seems like that the result on $\text {SEM}$ [26] is worse than the result on $\text {EMR}$ [2] in the sense that the former worked with more rounds, used a simulator which has a worse complexity, while achieved looser security bounds—so that stronger KDs are really beneficial. But it should be noted that there is no evidence for the tightness of the two results.² The (full) indifferentiability analyses of idealized blockciphers are usually very complicated and (possibly) not tight. Hence there is no definitive separation.

In related-key setting, Cogliati and Seurin [12] showed that for IEM with linear KDs, 3 rounds are needed to resist xor-induced related-key attacks, whereas for IEM with non-linear KDs, 1 round is already secure. This sheds light on the importance of KD, but this did not address the problem in the chosen-key setting. Moreover, in the indifferentiability setting, it seems like that IEM with non-linear KD does not deviate from IEM with no KD, if the non-linear KD is invertible [26]. Therefore, whether KDs are important in the context of chosen-key attacks or even indifferentiability remains unclear.

Turn to seq-indifferentiability In a departure from full indifferentiability, we note that for $\text {IEM}_3$, if the KD is invertible, then there is a sequential distinguisher³ exhibited by Andreeva et al. [2] even if the KD is idealized (please see Appendix 2). [2] also exhibited a distinguisher against a large range of simulators for $\text {EMR}_3$—but this distinguisher is not sequential. By this, it seems like that $\text {EMR}_3$ is seq-indifferentiable; if this can be proved, then the knowledge above definitively separates invertible KDs from non-invertible ones in the context of Even–Mansour. So we have the question:

$$\begin{aligned} Is \,EMR _3~{ seq}{\text {-}} { indifferentiable} ? \end{aligned}$$

1.2 Our contributions

We positively answer the question, i.e. we prove that $\text {EMR}_3$ is seq-indifferentiable from ${\mathbf {IC}}[\kappa ,n]$. As a sequential distinguisher on $\text {EMR}_2$ has been exhibited by Andreeva et al. [2], the number of rounds is optimal. As discussed before, together with a distinguisher in [2], this work successfully establishes the first definitive separation between invertible and non-invertible KDs. We view this as the most important implication of this work.

We note that sequential indifferentiability is much easier to handle than the full indifferentiability. Additionally, the studies on sequential indifferentiability usually lead to optimal results (with respect to the number of rounds required; e.g. Feistel [29], SEM [12]); this helps a lot in establishing the separation.

The problem of replacing the random oracle in $\text {EMR}$ is attractive, for two reasons: theoretically speaking, such schemes are entirely permutation-based (and are “natural”, compared to the transition chain ${\mathbf {RP}}\xrightarrow {\text {(possibly) by Sponge [3]}}{\mathbf {RO}}\xrightarrow {\text {by Feistel [13]}}{\mathbf {IC}}$); in practice, non-invertible primitives with good cryptographic properties are usually harder to design than their invertible counterparts. This is why $\text {EMDP}$ was considered by Andreeva et al. [2]. With these in mind, we also consider $\text {EMDP}$ in seq-indifferentiability model. Unfortunately, the un-keyed Davies-Meyer construction $KD(K)=P(K)\oplus K$ is not seq-indifferentiable from a random function. This forces us to prove from scratch. Fortunately, most part of the proof for $\text {EMR}_3$ can be retained, and we only have to do a few modifications. By this, we prove the second main result of this work: $\text {EMDP}_3$ is seq-indifferentiable from ${\mathbf {IC}}[n,n]$.

1.3 Related works

Strong KD is crucial for some kind of Feistel ciphers: due to the complementation property, in Feistel ciphers, if each round key is xored before each round function (named key-alternating Feistel ciphers by Lampe and Seurin [27]), then the round keys have to be derived in some very complicated ways (which is still unknown at current time, cf. [24]) to obtain indifferentiability. Moderately strong KD is also crucial for Even–Mansour in single-key setting: Chen et al. [11] showed that for $\text {IEM}_2$ from a single random permutation, if all the three round keys are common, then it is only pseudorandom up to $O(2^{n/2})$ queries; whereas if the first and third round keys are common while the second round key is derived from the first round key by a linear orthomorphism, then it is pseudorandom up to $O(2^{2n/3})$ queries. Finally, we already mentioned the three results on (seq-)indifferentiability of IEM [2, 12, 26]. Cogliati and Seurin’s presentation [12] is very simple and clean, therefore we follow [12] in our presentation to improve the quality.

1.4 Organization

Section 2 supplies necessary preliminaries and notations. Then Sects. 3 and 4 presents the seq-indifferentiability proofs for $\text {EMR}_3$ (3-round Even–Mansour with a Random oracle key schedule) and $\text {EMDP}_3$ (3-round Even–Mansour which takes a Davies-Meyer construction from a random Permutation as key schedule) respectively. Finally, Sect. 5 concludes. To make the main section simpler and clearer, when the proof of a lemma is obtained by standard techniques and does not reveal the features of $\text {EMR}$, then it will be deferred to the Appendix.

2 Preliminaries

2.1 Notation for master/round keys

Throughout this paper, all the master keys are denoted by the capital letter K, while all the round keys are denoted by the lower-case letter k (with superscripts or subscripts, whenever necessary).

2.2 Ideal primitives and their interfaces

A random oracle is an ideal primitive which returns a random fixed-length string if x was never queried, or the same answer as before if x was previously queried. The random oracles considered in this work map $\kappa$-bit inputs to n-bit outputs, and is denoted by ${\mathbf {H}}$. We assume that the interface of ${\mathbf {H}}$ is ${\mathbf {H}}.\text {H}(K):=\{0,1\}^{\kappa }\rightarrow \{0,1\}^{n}$.

An n-bit random permutation is a permutation that is uniformly selected from all $(2^n)!$ possible choices. In this work, the notations ${\mathbf {P}}$ and ${\varvec{\Pi }}$ are used to denote tuple of independent random permutations. More clearly, ${\mathbf {P}}=({\mathbf {P}}_1,{\mathbf {P}}_2,{\mathbf {P}}_3)$ is to be used by $\text {EMR}_3$, while ${{\varvec{\Pi }}}=({{\varvec{\Pi }}}_0,{{\varvec{\Pi }}}_1,{{\varvec{\Pi }}}_2,{{\varvec{\Pi }}}_3)$ is to be used by $\text {EMDP}_3$. We let such tuples provide unified interfaces, i.e. ${\mathbf {P}}$ provides ${\mathbf {P}}.\text {P}(i,\delta ,z):=\{1,2,3\}\times \{+,-\}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$, and ${{\varvec{\Pi }}}$ provides ${{\varvec{\Pi }}}.{\Pi }(i,\delta ,z):=\{0,1,2,3\}\times \{+,-\}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ (i is the index, $\delta \in \{+,-\}$ indicates direct query or inverse query, and $z\in \{0,1\}^n$ is the queried value).

Ideal ciphers have been mentioned before. In the rest part, depending on the context, the notation ${\mathbf {E}}$ has two different meanings: in Sect. 3, ${\mathbf {E}}$ refers to ${\mathbf {IC}}[\kappa ,n]$, and the interface is ${\mathbf {E}}.\text {E}(\delta ,K,z):=\{+,-\}\times \{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$; in Sect. 4, ${\mathbf {E}}$ refers to ${\mathbf {IC}}[n,n]$, and the interface is ${\mathbf {E}}.\text {E}(\delta ,K,z):=\{+,-\}\times \{0,1\}^{n}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$.

2.3 Sequential indifferentiability, and correlation intractability

To formally define seq-indifferentiability, we first specify a restricted distinguisher class, namely the sequential distinguishers (seq-distinguisher) [29]. For concreteness, consider the idealized blockcipher $\text {EMR}^{{\mathbf {H}},{\mathbf {P}}}$ from ${\mathbf {H}}$ and ${\mathbf {P}}$. A distinguisher $D^{\text {EMR}^{{\mathbf {H}},{\mathbf {P}}},({\mathbf {H}},{\mathbf {P}})}$ with oracle access to the cipher and the underlying primitives is trying to distinguish $\text {EMR}^{{\mathbf {H}},{\mathbf {P}}}$ from ${\mathbf {IC}}$. Then, D is sequential if it issues queries in a strict order; more clearly, D works in the following steps: (1) queries the underlying primitive $({\mathbf {H}},{\mathbf {P}})$ as it wishes; (2) queries the cipher $\text {EMR}^{{\mathbf {H}},{\mathbf {P}}}$ as it wishes; (3) outputs, and cannot query $({\mathbf {H}},{\mathbf {P}})$ again in this phase. This order is illustrated by the red numbers in Fig. 2. In this setting, if there is a simulator ${\mathbf {S}}^{{\mathbf {IC}}}$ that has access to ${\mathbf {IC}}$ and can “mimic” $({\mathbf {H}},{\mathbf {P}})$ such that in the view of any sequential distinguisher D, the system $({\mathbf {IC}},{\mathbf {S}}^{{\mathbf {IC}}})$ is indistinguishable from the system $(\text {EMR}^{{\mathbf {H}},{\mathbf {P}}},({\mathbf {H}},{\mathbf {P}}))$, then $\text {EMR}^{{\mathbf {H}},{\mathbf {P}}}$ is sequentially indifferentiable (seq-indifferentiable) from ${\mathbf {IC}}$.

To give a formal definition, we first define a notion total oracle query cost of D, which refers to the total number of queries received by $({\mathbf {H}},{\mathbf {P}})$ (from D or $\text {EMR}^{{\mathbf {H}},{\mathbf {P}}}$) when D interacts with $(\text {EMR}^{{\mathbf {H}},{\mathbf {P}}},({\mathbf {H}},{\mathbf {P}}))$ [29]. Then, a definition of seq-indifferentiability due to Cogliati and Seurin [12] is as follows.

Definition 1

(Seq-indifferentiability) An idealized blockcipher ${EMR }^{{\mathbf {H}},{\mathbf {P}}}$ with oracle access to ideal primitives $({\mathbf {H}},{\mathbf {P}})$ is said to be statistically and strongly $(q,\sigma ,t,\varepsilon )$-seq-indifferentiable from an ideal cipher ${\mathbf {IC}}$ if there exists a simulator ${\mathbf {S}}^{{\mathbf {IC}}}$ such that for any sequential distinguisher D of total oracle query cost at most q, ${\mathbf {S}}^{{\mathbf {IC}}}$ issues at most $\sigma$ queries to ${\mathbf {IC}}$ and runs in time at most t and it holds

$$\begin{aligned} \left| Pr_{{\mathbf {H}},{\mathbf {P}}}[ D ^{{EMR }^{{\mathbf {H}},{\mathbf {P}}}, ({\mathbf {H}},{\mathbf {P}})} = 1] - Pr_{{\mathbf {IC}}}[ D ^{{\mathbf {IC}}, {\mathbf {S}}^{{\mathbf {IC}}}} = 1] \right| \le \varepsilon \end{aligned}$$

If D makes $q'$ queries, then its total oracle query cost is poly$(q')$. As a concrete example, the cipher $\text {EMR}_3^{{\mathbf {H}},{\mathbf {P}}}$ makes $c=4$ queries to $({\mathbf {H}},{\mathbf {P}})$ to answer any query it receives, and if D makes $q_e$ queries to $\text {EMR}_3^{{\mathbf {H}},{\mathbf {P}}}$ and $q_p$ queries to $({\mathbf {H}},{\mathbf {P}})$, then the total oracle query cost of D is $q_p+4q_e=\text {poly}(q_p+q_e)=\text {poly}(q')$.

Seq-indifferentiability—although weaker than indifferentiability [30]—is already sufficient to imply correlation intractability in the idealized model (proved in [29] and [12]). The notion correlation intractability was introduced by Canetti et al. [9] to capture the feature that there is no exploitable relation between the inputs and outputs of the function ensembles in question. It was transposed to idealized models to guarantee similar feature on idealized constructions (e.g. $\text {EMR}^{{\mathbf {H}},{\mathbf {P}}}$). To formally define this notion, we first give the definition (from [12]) of evasive relation.

Definition 2

(Evasive Relation) A relation ${\mathcal {R}}$ over pairs of binary sequences is said $(q,\epsilon )$-evasive with respect to an ideal cipher ${\mathbf {IC}}$ with n-bit blocks, if for any oracle Turing machine ${\mathcal {M}}$ issuing at most q oracle queries, it holds

$$\begin{aligned} Pr[ (x_1,\ldots ,x_m)\leftarrow {\mathcal {M}}^{{\mathbf {IC}}}(1^n) : ((x_1,\ldots ,x_m),({\mathbf {IC}}(x_1),\ldots ,{\mathbf {IC}}(x_m)))\in {\mathcal {R}} ] \le \epsilon . \end{aligned}$$

We then define correlation intractability itself.

Definition 3

(Correlation Intractability) Let ${\mathcal {R}}$ be an m-ary relation. Then, an idealized blockcipher ${EMR }^{{\mathbf {H}},{\mathbf {P}}}$ with oracle access to ideal primitives $({\mathbf {H}},{\mathbf {P}})$ is said to be $(q,\epsilon )$-correlation intractable with respect to ${\mathcal {R}}$, if for any oracle Turing machine ${\mathcal {M}}$ issuing at most q oracle queries, it holds

$$\begin{aligned} Pr[ (x_1,\ldots ,x_m)&\leftarrow {\mathcal {M}}^{{\mathbf {H}},{\mathbf {P}}}(1^n) \\&: \left( (x_1,\ldots ,x_m),\left( {EMR }^{{\mathbf {H}}, {\mathbf {P}}}(x_1),\ldots ,{EMR }^{{\mathbf {H}}, {\mathbf {P}}}(x_m)\right) \right) \in {\mathcal {R}} ] \le \epsilon . \end{aligned}$$

Seq-indifferentiability implies correlation intractability:

Theorem 1

(Theorem 4 in [12]) For an idealized blockcipher ${EMR }^{{\mathbf {H}},{\mathbf {P}}}$ which has oracle access to ideal primitives $({\mathbf {H}},{\mathbf {P}})$ and makes at most c queries to ${\mathbf {H}}$ and ${\mathbf {P}}$ in total on any input, if ${EMR }^{{\mathbf {H}},{\mathbf {P}}}$ is $(q+cm,\sigma ,\epsilon )$-seq-indifferentiable from ${\mathbf {IC}}$, then for any m-ary relation ${\mathcal {R}}$ which is $(\sigma +m,\epsilon _{{\mathcal {R}}})$-evasive with respect to ${\mathbf {IC}}$, ${EMR }^{{\mathbf {H}},{\mathbf {P}}}$ is $(q,\epsilon +\epsilon _{{\mathcal {R}}})$-correlation intractable with respect to ${\mathcal {R}}$.

When the primitive implemented by the seq-indifferentiable construction is stateless, seq-indifferentiability implies public indifferentiability—indifferentiability from the target primitive in the setting where all the queries to it are public (a notion due to Yoneyama et al. [32] and Dodis et al. [19]).

3 Sequential indifferentiability of $\text {EMR}_3$

The first main result of this work is formally stated as follows.

Theorem 2

Assuming that ${\mathbf {P}}=({\mathbf {P}}_1,{\mathbf {P}}_2,{\mathbf {P}}_3)$ is a tuple of three independent random permutations and ${\mathbf {H}}$ is a $\kappa$-to-n-bit random oracle, then for any integer q such that $q^2\le {2^n}/{4}$, the 3-round Even–Mansour with n-bit blocks and $\kappa$-bit keys

$$\begin{aligned} {EMR }_3(K,m)=k\oplus {\mathbf {P}}_3(k\oplus {\mathbf {P}}_2(k\oplus {\mathbf {P}}_1(k\oplus m))) \end{aligned}$$

where $k={\mathbf {H}}(K)$ is strongly and statistically $(q,\sigma ,t,\varepsilon )$-seq-indifferentiable from an ideal cipher ${\mathbf {IC}}[\kappa ,n]$, where $\sigma =q^{2}$, $t=O(q^2),\text { and }\varepsilon \le \frac{18q^{4}}{2^{n}}=O(\frac{q^{4}}{2^n}).$

Note that Cogliati and Seurin’s proof showed that $\text {SEM}_4$ is $(q,q^2,O(q^2),\frac{68q^{4}}{2^{n}})$-seq-indifferentiable from ${\mathbf {IC}}[n,n]$ ([12], Theorem 5). The two tuples of bounds (Cogliati and Seurin’s and ours) are of the same order of magnitude.

To prove it, we: (1) build a simulator (Sect. 3.1); (2) introduce an intermediate system used in the proof (Sect. 3.2); (3) bound the complexity of the simulator (Sect. 3.3); (4) prove that the simulator simulates well (Sect. 3.4); and (5) briefly discuss the interpretation (Sect. 3.5).

3.1 Simulator for $\text {EMR}_3$

Randomness and interfaces We borrow a variant of Holenstein et al.’s explicit randomness technique [13] from [12], that is, letting the simulator ${\mathbf {S}}$ have explicit access to ${\mathbf {H}}$ and ${\mathbf {P}}$ and query them to obtain necessary random values. We denote by ${\mathbf {S}}^{{\mathbf {H}},{\mathbf {P}}}$ the simulator for $\text {EMR}_3$ which accesses ${\mathbf {H}}$ and ${\mathbf {P}}$. ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$ provides exactly the same interfaces as ${\mathbf {H}}$ and ${\mathbf {P}}$, i.e. ${\mathbf {S}}.\text {H}(K)$, and ${\mathbf {S}}.\text {P}(i,\delta ,z)$. As argued [12], using such explicit randomness is actually equivalent to lazily sampling it before the experiments.

Maintaining history Internally, ${\mathbf {S}}$ maintains three sets $P_1$, $P_2$ and $P_3$ that have entries in the form of (x, y) for $x,y\in \{0,1\}^n$, to keep track of previously answered permutation queries; and another set KSet that has entries in the form of (K, k) for $K\in \{0,1\}^{\kappa }$ and $k\in \{0,1\}^n$, to keep track of the key derivation queries. Additionally, ${\mathbf {S}}$ will ensure that for any $z\in \{0,1\}^n$ and $i\in \{1,2,3\}$, there is at most one $z'\in \{0,1\}^n$ such that $(z,z')\in P_i$, and vice versa; also, for any $k\in \{0,1\}^n$, there is at most one $K\in \{0,1\}^{\kappa }$ such that $(K,k)\in KSet$.⁴ If such consistency cannot be kept at some point, ${\mathbf {S}}$ aborts (will be further discussed). By this, the sets $\{P\}=\{P_1,P_2,P_3\}$ are expected to define three partial permutations, and we denote by $P_i^{+}$ ($P_i^{-}$, resp.) the (time-dependent) set of all n-bit values x (y, resp.) satisfying that $\exists z\in \{0,1\}^n$ s.t. $(x,z)\in P_i$ ($(z,y)\in P_i$, resp.); denote by $P_i^{+}(x)$ ($P_i^{-}(y)$, resp.) the corresponding value of z. Similarly for KSet: $KSet^{+}$ is the set of all $\kappa$-bit values K such that $\exists k\in \{0,1\}^n$ s.t. $(K,k)\in KSet$, and $KSet^{+}(K)$ is the corresponding value of k; $KSet^{-}$ is the set of all n-bit values k such that $\exists K\in \{0,1\}^{\kappa }$ s.t. $(K,k)\in KSet$, and $KSet^{-}(k)$ the corresponding value of K.

To simplify some arguments, we let ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$ maintain a set ESet that has entries in the form of (K, x, y) for $K\in \{0,1\}^{\kappa }$, and $x,y\in \{0,1\}^{n}$ to keep track of the queries it has issued to ${\mathbf {E}}$. Similarly to the 4 sets mentioned before, the notation $ESet^{+}$ ($ESet^{-}$, resp.) is used to denote the sets $(K,x)\in \{0,1\}^{\kappa }\times \{0,1\}^{n}$ ($(K,y)\in \{0,1\}^{\kappa }\times \{0,1\}^{n}$ resp.) such that $\exists y\in \{0,1\}^n$ ($\exists x\in \{0,1\}^n$, resp.) s.t. $(K,x,y)\in ESet$. Finally, for any set $Set\in \{P_1,P_2,P_3,KSet,ESet\}$, denote by |Set| the number of entries in Set.

For $\delta \in \{+,-\}$, we denote $\overline{\delta }$ the opposite of $\delta$. For example, when $\delta =+$, $P_i^{\overline{\delta }}$ is $P_i^{-}$.

Simulation strategy, and pseudocode The basic idea is Coron et al.’s simulation via chain completion technique [13], which has achieved success in (weaker) indifferentiability proofs of a variety of idealized blockciphers. It requires the simulator ${\mathbf {S}}$ to detect “partial” computation chains formed by the queries of the distinguisher, and completes the chains in advance by querying the ideal cipher ${\mathbf {E}}$, so that ${\mathbf {S}}$ is ready for answering queries in the future. To simulate answers that are consistent with ${\mathbf {E}}$, ${\mathbf {S}}$ has to use the answer from ${\mathbf {E}}$ to define some simulated answers; this action is called adaptation.

It may be expected that we will reuse the tripwire paradigm introduced by Andreeva et al. [2] for proving indifferentiability of $\text {EMR}_5$.⁵ since we analyze $\text {EMR}_3$ exactly as they did. But this is not the case. In fact, our simulator is (surprisingly) closer to Cogliati and Seurin’s simulator for $\text {SEM}_4$ [12]. We actually take the round key k as if it is an additional state value (besides the input and output of the three permutations $(x_1,y_1),(x_2,y_2),(x_3,y_3)$), and detect partial chains formed by $k\in KSet^{-}$ and $x_2\in P_2^{+}$; upon any query, ${\mathbf {S}}$ will immediately complete all newly formed partial chains, and “adapt” by adding consistent values to $P_1$ or $P_3$. More clearly, upon a new query $\text {P}(2,+,z)$ or $\text {H}$ (queries that have never appeared in the history), besides querying ${\mathbf {P}}$ or ${\mathbf {H}}$ to obtain a random answer $z'$ or k, ${\mathbf {S}}$ considers all pairs $(k,x_2)$ formed by this query and entries in the sets, and completes them by computing $y_1:=z\oplus k$, $y_0:={\mathbf {S}}.\text {P}(1,-,y_1)\oplus k$, querying ${\mathbf {E}}$ to obtain $x_4$, computing $x_3:=z'\oplus k$, $y_3:=x_4\oplus k$, and adding $(x_3,y_3)$ to $P_3$ if $x_3\notin P_3^{+}$ and $y_3\notin P_3^{-}$. Upon a new query $\text {P}(2,-,z)$, ${\mathbf {S}}$ completes all such new pairs $(k,x_2)$ by a process symmetric to that upon $\text {P}(2,+,z)$ or ${\mathbf {H}}$, and adapts on $P_1$. The chain completion strategy is illustrated in Fig. 1. Queries $\text {P}(1,\delta ,z)$ and $\text {P}(3,\delta ,z)$ do not form new partial chains, and are simply answered by relaying those of ${\mathbf {P}}$.

Fig. 1

The strategy of the simulator

${\mathbf {S}}$ may abort, when a random answer obtained from ${\mathbf {P}}$ or a pair of input and output obtained during adaptation collides with the entries in $\{P\}$. For instance, during an adaptation on $P_3$, if $x_3\in P_3^{+}$ or $y_3\in P_3^{-}$, ${\mathbf {S}}$ aborts. ${\mathbf {S}}$ also aborts if ${\mathbf {H}}$ maps two different master keys to the same round key.

With all the thoughts above, ${\mathbf {S}}$ is formally described by code as follows.

3.2 Systems involved in this proof

For any random primitives ${\mathbf {E}}$, ${\mathbf {H}}$, and ${\mathbf {P}}$, denote by $\varSigma _1({\mathbf {E}},{\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}})$ ($\varSigma _1({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$, or even $\varSigma _1$ for short) the simulated system, and denote by $\varSigma _3(\text {EMR}_3^{{\mathbf {H}},{\mathbf {P}}},({\mathbf {H}},{\mathbf {P}}))$ ($\varSigma _3({\mathbf {H}},{\mathbf {P}})$ and $\varSigma _3$ for short) the real system. We use an intermediate system $\varSigma _2(\text {EMR}_3^{{\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}},{\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}})$ ($\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and $\varSigma _2$ for short), which consists of the simulator ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$ and the cipher $\text {EMR}_3$, and $\text {EMR}_3$ computes by calling the interface $\text {H}$ and $\text {P}$ provided by ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$ rather than those provided by the random primitives. Note that this intermediate system is very close to those used in [29] and [12].⁶ The systems are depicted in Fig. 2. Further note that in $\varSigma _1({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and $\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$, all the randomness is captured by the three primitives $({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$; while in $\varSigma _3({\mathbf {H}},{\mathbf {P}})$, the randomness is captured by $({\mathbf {H}},{\mathbf {P}})$.

Fig. 2

Systems used in the sequential indifferentiability proof for $\text {EMR}_3$. The number in red illustrates the order of the queries/actions (of the sequential distinguisher)

3.3 Bounding the complexity of ${\mathbf {S}}$

In $\varSigma _1$, the complexity of ${\mathbf {S}}$ is polynomial. The idea is quite simple: the number of partial chains $(k,x_2)$ completed by ${\mathbf {S}}$ is $|KSet|\cdot |P_2|$, which is at most the square of the total oracle query cost of D.

Lemma 1

For any tuple of primitives $({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and any sequential distinguisher D of total oracle query cost at most q, the following hold:

• (i) At the end of the $\varSigma _2$ execution $D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$, with respect to the sets of ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$, it holds $|KSet|\le q$, $|P_2|\le q$, $|P_1|\le 2q^2$, $|P_3|\le 2q^2$;

• (ii) ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$ issues at most $q^2$ queries to ${\mathbf {E}}$ during the $\varSigma _2$ execution $D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$;

• (iii) During the $\varSigma _1$ execution $D^{\varSigma _1({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$, ${\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}$ issues at most $q^2$ queries to ${\mathbf {E}}$, and runs in time $O(q^2)$.

Proof

Note that in $D^{\varSigma _2}$, the total number of queries received by ${\mathbf {S}}$ (from D or $\text {EMR}_3$) is exactly the total oracle query cost q of D. With this in mind, we start by bounding |KSet|, which can only be enlarged by at most 1 when ${\mathbf {S}}$ receives a query of the form $\text {H}(K)$. As the number of such queries is at most q, we have $|KSet|\le q$. Since $|P_2|$ is similarly enlarged only upon a query $\text {P}(2,\delta ,z)$, we also get $|P_2|\le q$.

Then, consider $|P_1|$: $|P_1|$ can by enlarged by at most 1 when ${\mathbf {S}}$ executes $\text {Complete}(k,x_2,y_2,\delta )$, or when ${\mathbf {S}}$ receives a query of the form $\text {P}(1,\delta ,z)$ (at most q times). As $|KSet|\le q$ and $|P_2|\le q$, $\text {Complete}$ is executed at most $q^2$ times, so that $|P_1|\le q+q^2\le 2q^2$. The same for $|P_3|$.

For proposition (ii), note that ${\mathbf {S}}$ queries ${\mathbf {E}}$ only during an execution of $\text {Complete}$, so that the bound is $|KSet|\cdot |P_2|\le q^2$.

Finally, the two variables |KSet| and $|P_2|$ standing at the end of $D^{\varSigma _1({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$ are clearly not larger than those standing at the end of $D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$. Also note that the most time-costing procedure of ${\mathbf {S}}$ is clearly $\text {Complete}$. These along with proposition (ii) establish proposition (iii). $\square$

3.4 Indistinguishability of $\varSigma _1$ and $\varSigma _3$

To prove the indistinguishability, we will reach the following two goals:

• (i) ${\mathbf {S}}$ is unlikely to abort. More precisely, during $\varSigma _2$ executions, ${\mathbf {S}}$ aborts with only negligible probability;

• (ii) the intuition that if ${\mathbf {S}}$ does not abort then it simulates the primitives well (i.e. $({\mathbf {E}},{\mathbf {S}})$ and $(\text {EMR}_3,({\mathbf {H}},{\mathbf {P}}))$ are indistinguishable) does hold.

The first goal is reached in the next paragraph, by analyzing each possibility. On the other hand, the second goal is reached in the last paragraph of this subsection, by a variant of Holenstein et al.’s randomness mapping argument [13], which has been a quite standard step in indifferentiability proof. However, as the reader will see, by slightly tweaking the argument of Cogliati and Seurin [12], we even do not explicitly define any map.

Note that when proving the non-abortion of ${\mathbf {S}}$, we indeed focus on $\varSigma _2$ executions rather than $\varSigma _1$ executions. The reason is that only if ${\mathbf {S}}$ does not abort in a $\varSigma _2$ execution will we be able to find a $\varSigma _1$ execution and a $\varSigma _3$ execution such that the distinguisher D gives the same output in the three executions (and further establish the second goal as above). For a technical illustration, the reader could see Lemma 8, which indeed considers the $\varSigma _2$ executions during which ${\mathbf {S}}$ does not abort.

3.4.1 The abort probability of ${\mathbf {S}}$ in $\varSigma _2$ is negligible

We sketch the idea first. Roughly speaking, the abortion of ${\mathbf {S}}$ is due to some values unexpectedly colliding with entries in the sets. Such values are usually random, so that the probability of such collisions is negligible. For this, we have to show that the answers obtained from ${\mathbf {E}}$ are really random in the view of ${\mathbf {S}}$.

${\mathbf {E}}$’s Answers are Random This is because each query to ${\mathbf {E}}$ issued by ${\mathbf {S}}$ cannot have appeared in the history of such queries.

Lemma 2

Assume that ${\mathbf {S}}$ does not abort up to some point in the execution $D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$, and issues a query ${\mathbf {E}}.\text {E}(+,K,z)$ (${\mathbf {E}}.\text {E}(-,K,z)$, resp.) right after this point. Then $(K,z)\notin ESet^{+}$ ($(K,z)\notin ESet^{-}$, resp.) before this point.

Proof

${\mathbf {S}}$ queries ${\mathbf {E}}$ only during an execution of $\text {Complete}(k,x_2,y_2,\cdot )$, and any two queries to ${\mathbf {E}}$ in two different such executions must be different. Otherwise since the contents of the sets are never overwritten, it can be easily deduced that the two chains corresponding to the two queries share the same k and $x_2$ values and they are the same chain, which is not possible by construction. $\square$

Abort probability The bound can now be obtained with the help of Lemma 2. To calculate the bound, we prove individual upper bounds on the probability of various types of abortions, and then apply a union bound.⁷ All the following abort probabilities assume that in $D^{\varSigma _2}$, the total oracle query cost of D is at most q.

Lemma 3

During a call to ${H }(K)$, the probability that ${\mathbf {S}}$ aborts at line 8 is at most $\frac{q}{2^n}$.

Proof

Directly follows from $|KSet|\le q$ (Lemma 1). $\square$

Lemma 4

During a call to $\text {P}(1,\delta ,z)$ or $\text {P}(3,\delta ,z)$, the probability that ${\mathbf {S}}$ aborts at line 18 is at most $\frac{q^2}{2^n-2q^2}$.

Proof

For $\text {P}(1,\delta ,z)$, if the abort condition at line 17 holds, then it is necessarily due to the random value ${\mathbf {P}}.\text {P}(1,\delta ,z)$ colliding with a value in $P^{\overline{\delta }}_1$ added by previous adaptations (line 62). Since ${\mathbf {S}}$ completes at most $q^2$ chains (Lemma 1), the number of values added by adaptation is at most $q^2$, so that the bound is at most $\frac{q^2}{2^n-|P_1|}\le \frac{q^2}{2^n-2q^2}$. Similarly for $\text {P}(3,\delta ,z)$. $\square$

Lemma 5

During an execution $\text {Complete}(k,x_2,y_2,-)$, the probability that ${\mathbf {S}}$ aborts at line 59 or line 61 is at most $\frac{4q^2}{2^n-q^2}$.

Proof

Such an execution must be triggered by a call $\text {P}(2,-,y_2)$, inside which $x_2$ was assigned a random value ${\mathbf {P}}.\text {P}(2,-,y_2)$. Let $y_1=x_2\oplus k$, then right after this assignment, $Pr[y_1\in P_1^{-}]\le \frac{|P_1|}{2^n-|P_2|}\le \frac{2q^2}{2^n-q}$. If $y_1\notin P_1^{-}$ right after this assignment, then from the point this assignment happens till the call $\text {Complete}(k,x_2,y_2,-)$, it is not possible that $y_1\in P_1^{-}$: because the chains that are completed during this period are of the form $(k',x_2)$ where $k'\ne k$, so that $k'\oplus x_2\ne y_1$. Therefore, the probability that the abort condition at line 60 holds is at most $\frac{2q^2}{2^n-q}$. On the other hand, by Lemma 2, $Pr[x_1\in P_1^{+}]\le \frac{|P_1|}{2^n-|ESet|}\le \frac{2q^2}{2^n-q^2}$. In total the bound is $\frac{4q^2}{2^n-q^2}$. $\square$

Lemma 6

During an execution $\text {Complete}(k,x_2,y_2,+)$, the probability that ${\mathbf {S}}$ aborts at line 45 or line 47 is at most $\frac{4q^2}{2^n-q^2}$.

Proof

Such forward completions may be triggered by queries $\text {P}(2,+,x_2)$ or $\text {H}(K)$. The analysis of the former case is similar to Lemma 5 by symmetry, and results in the same bound $\frac{2q^2}{2^n-q}+\frac{2q^2}{2^n-q^2}$. For the latter, let $x_3=y_2\oplus k$. Conditioned on that ${\mathbf {S}}$ did not abort at line 8 in $\text {H}(K)$, the value assigned to k is uniformly picked from a pool of size at least $2^n-q$, so that right after the assignment inside $\text {H}(K)$, $Pr[x_3\in P_3^{+}]\le \frac{2q^2}{2^n-q}$. Then, similarly to Lemma 5, if $x_3\notin P_3^{+}$ right after this assignment, then it won’t be added to $P_3^{+}$ until the call to $\text {Complete}(k,x_2,y_2,+)$. Hence the bound is $\frac{2q^2}{2^n-q}$. On the other hand, the probability that the corresponding value $y_3$ hits values in $P_3^{-}$ is at most $\frac{2q^2}{2^n-q^2}$ which is similar to those obtained before. $\square$

All the above yield the overall probability.

Lemma 7

When $q^2\le \frac{2^n}{4}$, $Pr_{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}[{\mathbf {S}}\text { aborts during }D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}] \le \frac{17q^4}{2^n}$.

Proof

By Lemma 1, line 7 is executed at most q times, line 18 is executed at most $2\times 2q^2$ times in total, while line 58, 60, 44, and 46 are executed at most $q^2$ times in total. Therefore, when $q^2\le \frac{2^n}{4}$, the overall abort probability is at most $q\cdot \frac{q}{2^n}+ 4q^2\cdot \frac{q^2}{2^n-2q^2} + q^2\cdot \frac{4q^2}{2^n-q^2}\le \frac{17q^4}{2^n}$. $\square$

3.4.2 Non-abortion implies indistinguishability of answers

As mentioned, this paragraph presents the reduction from indistinguishability to non-abortion. To this end, we focus on a fixed and deterministic seq-distinguisher D rather than an arbitrary one, since the advantage of a probabilistic distinguisher cannot exceed the corresponding deterministic version with the best random coins. With respect to D, we introduce some terminology first (these notions are due to Andreeva et al. [2] and Cogliati, Seurin [12]).

First, a tuple of primitives $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ is called a good $\varSigma _2$ -tuple if ${\mathbf {S}}^{\alpha }$ does not abort during the $\varSigma _2$ execution $D^{\varSigma _2(\alpha )}$.

Second, for a good $\varSigma _2$-tuple $\alpha$, consider the tuple of sets $\gamma =\{KSet,\{P\}\}$ of ${\mathbf {S}}^{\alpha }$ standing at the end of $D^{\varSigma _2(\alpha )}$. Denote by ${\mathcal {T}}$ the set of all such set-tuples that can be generated by ${\mathbf {S}}$ when running with good $\varSigma _2$-tuples. For a good $\varSigma _2$-tuple $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$, if the sets of ${\mathbf {S}}^{\alpha }$ standing at the end of $D^{\varSigma _2(\alpha )}$ share exactly the same contents with $\gamma \in {\mathcal {T}}$, then denote by $D^{\varSigma _2(\alpha )}\rightarrow \gamma$.

Third, consider a set-tuple $\gamma =\{KSet,\{P\}\}\in {\mathcal {T}}$. For a random oracle ${\mathbf {H}}$, if for any $K\in KSet^{+}$, it holds ${\mathbf {H}}.\text {H}(K)=KSet^{+}(K)$, then we said that ${\mathbf {H}}$ extends KSet, and denote ${\mathbf {H}}\cong KSet$; for a tuple of random permutations ${\mathbf {P}}$, if for any $z\in P_i^{\delta }$, it holds ${\mathbf {P}}.\text {P}(i,\delta ,z)=P_i^{\delta }(z)$, then we said that ${\mathbf {P}}$ extends $\{P\}=\{P_1,P_2,P_3\}$, and denote ${\mathbf {P}}\cong \{P\}$. Finally, a tuple of primitives $\beta =({\mathbf {H}},{\mathbf {P}})$ extends $\gamma$ (denoted $\beta \cong \gamma$), if ${\mathbf {H}}\cong KSet\wedge {\mathbf {P}}\cong \{P\}$.

Then, we have the following lemma: the $\varSigma _1$, $\varSigma _2$, and $\varSigma _3$ executions that are “linked” by the sets of ${\mathbf {S}}$ behave the same in the view of D, i.e. they are indistinguishable.

Lemma 8

Let $\alpha =({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })$ be a good $\varSigma _2$-tuple, and denote by $\gamma =\{KSet,\{P\}\}$ the sets of ${\mathbf {S}}^{\alpha }$ standing at the end of $D^{\varSigma _2(\alpha )}$. Then for any tuple $\beta =({\mathbf {H}}^{\beta },{\mathbf {P}}^{\beta })$ such that $\beta \cong \gamma$, the transcripts of queries and answers of D in $D^{\varSigma _1(\alpha )}$, $D^{\varSigma _2(\alpha )}$, and $D^{\varSigma _3(\beta )}$ are the same; and $D^{\varSigma _1(\alpha )}=D^{\varSigma _2(\alpha )}=D^{\varSigma _3(\beta )}$.

Proof

The idea is that the random values used during the three executions are consistent. See “Proof of Lemma 8” of Appendix 1 for the formal proof, which is quite standard. $\square$

For any $\gamma \in {\mathcal {T}}$, the probabilities of the following two events are close:

• (i) a $\varSigma _2$ execution with a random tuple $({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ generates $\gamma$;

• (ii) a random tuple $({\mathbf {H}},{\mathbf {P}})$ extends $\gamma$.

Lemma 9

With respect to a fixed distinguisher D of total oracle query cost at most q, for any $\gamma \in {\mathcal {T}}$, it holds

$$\begin{aligned} \frac{Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ]}{Pr_{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma ]} \ge 1-\frac{q^4}{2^n}. \end{aligned}$$

Proof

See Appendix “Proof of Lemma 9” of Appendix 1. $\square$

Then the following lemma completes the transition from $\varSigma _1$ to $\varSigma _3$ (and the seq-indifferentiability proof for $\text {EMR}_3$). We do not transit from $\varSigma _1$ to $\varSigma _3$ “step by step” (as done in many previous such proofs); instead, we make a single-step leap. This helps achieving a slightly better hidden constant, since it allows counting $Pr[{\mathbf {S}}\text { aborts}]$ only once.

Lemma 10

For any seq-distinguisher D of total oracle query cost at most q, when $q^2\le {2^n}/{4}$, it holds

$$\begin{aligned} \left| Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3(\text {EMR}_3^{{\mathbf {H}},{\mathbf {P}}},({\mathbf {H}},{\mathbf {P}}))}=1] - Pr_{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _1({\mathbf {E}},{\mathbf {S}}^{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}})}=1] \right| \le \frac{18q^4}{2^n}. \end{aligned}$$

Proof

The bound $\frac{q^4}{2^n}+\frac{17q^4}{2^n}=\frac{18q^4}{2^n}$ follows from the bound $1-\frac{q^4}{2^n}$ in Lemma 9 (the ratio of the probabilities of the executions linked by $\gamma \in {\mathcal {T}}$ is close to 1) and the bound $\frac{17q^4}{2^n}$ in Lemma 7 (most of the $\varSigma _2$ executions result in member of ${\mathcal {T}}$). The full proof is deferred to Appendix “Proof of Lemma 10” of Appendix 1. $\square$

3.5 Interpretation

By Theorem 1, Theorem 2 implies that for any $(q^2,\varepsilon )$-evasive relation ${\mathcal {R}}$, $\text {EMR}_3$ is $(q,\varepsilon +O(q^4/2^n))$-correlation intractable with respect to ${\mathcal {R}}$ (very similar to [12]). Whereas as mentioned in Introduction, in our view, the most important implication of Theorem 2 is the definitive separation between the two kinds of KD.

4 Eliminating the random oracle: the case of $\text {EMDP}_3$

The second main result of this work is formally presented as follows.

Theorem 3

Assuming that ${{\varvec{\Pi }}}=({{\varvec{\Pi }}}_0,{{\varvec{\Pi }}}_1,{{\varvec{\Pi }}}_2,{{\varvec{\Pi }}}_3)$ is a tuple of four independent random permutations, then for any integer q such that $q^2\le {2^n}/{4}$, the 3-round Even–Mansour

$$\begin{aligned} {EMDP }_3(K,m)=k\oplus {{\varvec{\Pi }}}_3(k\oplus {{\varvec{\Pi }}}_2(k\oplus {{\varvec{\Pi }}}_1(k\oplus m))) \end{aligned}$$

where $k={{\varvec{\Pi }}}_0(K)\oplus K$ is strongly and statistically $(q,\sigma ,t,\varepsilon )$-seq-indifferentiable from an ideal cipher ${\mathbf {IC}}[n,n]$, where $\sigma =q^{2}$, $t=O(q^{2}),\text { and }\varepsilon \le \frac{ 19 \cdot q^{4}}{2^{n}}=O(\frac{q^{4}}{2^n}).$

Proof

As mentioned in Introduction, the un-keyed Davies-Meyer $KD(K)={{\varvec{\Pi }}}_0(K)\oplus K$ is not seq-indifferentiable from a random function, so that we have to do from scratch; but, fortunately, we can follow the line of the proof for $\text {EMR}_3$ to save many pages (as done by Andreeva et al. [2]). We first build the simulator.

4.1 Modified simulator ${\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}}$

To make a distinction from the notations in the last section, we denote the simulator for $\text {EMDP}_3$ by ${\mathcal {S}}$, and let it have access to ${{\varvec{\Pi }}}$. The interface provided by ${\mathcal {S}}$ is exactly the same as ${{\varvec{\Pi }}}$. The overall strategy of ${\mathcal {S}}$ is very close to that of ${\mathbf {S}}$ – except for replacing the procedure $\text {H}$ by ${\Pi }(0,\delta ,z)$. With these in mind, the code of ${\mathcal {S}}$ is as follows.

With ${\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}}$ at hand, the three systems are $\varSigma _1'({\mathbf {E}},{\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}})$, $\varSigma _2'(\text {EMDP}_3^{{\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}}},{\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}})$, and $\varSigma _3'(\text {EMDP}_3^{{{\varvec{\Pi }}}},{{\varvec{\Pi }}})$. Then, consider a fixed sequential distinguisher D of total oracle query cost at most q: the modified key points are as follows.

4.2 Complexity of ${\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}}$

This point is very close to Lemma 1. At the end of the $\varSigma '_2$ execution $D^{\varSigma _2'({\mathbf {E}},{{\varvec{\Pi }}})}$ it holds: (i) $|P_0|=|KSet|$, $|P_0|\le q$, and $|P_2|\le q$, since $|P_0|$ and $|P_2|$ can only be enlarged (by at most 1) by a query to $\text {P}(0,\delta ,z)$ and $\text {P}(2,\delta ,z)$ respectively; (ii) the number of calls to $\text {Complete}$ is at most $|P_0|\cdot |P_2|\le q^2$; (iii) $|P_1|$, $|P_3|\le 2q^2$, since they can be enlarged when ${\mathcal {S}}$ completes a chain besides a query to $\text {P}(1,\delta ,z)$ and $\text {P}(3,\delta ,z)$. Then, during the $\varSigma '_1$ execution $D^{\varSigma '_1({\mathbf {E}},{{\varvec{\Pi }}})}$, both the number of calls to $\text {Complete}$ and the number of queries of ${\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}}$ to ${\mathbf {E}}$ are at most $q^2$, so that the time complexity of ${\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}}$ is also $O(q^2)$.

4.3 Modified non-abortion Lemma: $Pr[{\mathcal {S}}\text { aborts during }\varSigma _2'({\mathbf {E}},{{\varvec{\Pi }}})] \le \frac{18q^4}{2^n}$

The types of abortions that are different from the context of $\text {EMR}$ are the abortion actions relevant to the simulated ${{\varvec{\Pi }}}_0$. More clearly, they are:

Sub-claim 1: during a call ${\Pi }(0,\delta ,z)$, the probability that ${\mathcal {S}}$ aborts at line 10 is at most $\frac{q}{2^n-q}$. Since $|P_0|\le q$, the bound is $\frac{|P_0|}{2^n-|P_0|}\le \frac{q}{2^n-q}$. This is similar to Lemma 3 albeit different.

Sub-claim 2: during an execution $\text {Complete}(k,x_2,y_2,+)$ , the probability that ${\mathcal {S}}$ aborts due to adaptation is at most $\frac{4q^2}{2^n-2q^2}$. The case that the execution $\text {Complete}(k,x_2,y_2,+)$ is triggered by a query of the form ${\Pi }(2,+,y_2)$ is exactly the same as analyzed in Lemma 6. The case that the execution is triggered by a call ${\Pi }(0,\delta ,z)$ is slightly different. Wlog assume that it is triggered by a call ${\Pi }(0,+,z)$ and $z'={{\varvec{\Pi }}}.{\Pi }(0,+,z)$. Conditioned on $z\oplus z'\notin KSet^{-}$, $z'$ is picked from a pool with size at least $2^n-2|P_0|\ge 2^n-2q$, so that for any $(x_2,y_2)\in P_2$, $Pr[y_2\oplus (z\oplus z')\in P_3^{+}]\le \frac{2q^2}{2^n-2q}$. The argument on the other side ($Pr[y_3\in P_3^{-}]$) is exactly the same as Lemma 6, leading to the same bound $\frac{2q^2}{2^n-q^2}$, so that in total it is $\frac{2q^2}{2^n-2q}+\frac{2q^2}{2^n-q^2}\le \frac{4q^2}{2^n-2q^2}$.

The almost unchanged ones are Lemmas 4 and 5, as follows:

Sub-claim 3: during a call to ${\Pi }(1,\delta ,z)$ or ${\Pi }(3,\delta ,z)$ , the probability that ${\mathbf {S}}$ aborts due to the random answer colliding with previous adapted values is at most $\frac{q^2}{2^n-2q^2}$ ; during an execution $\text {Complete}(k,x_2,y_2,-)$ , the probability that ${\mathbf {S}}$ aborts due to adaptation is at most $\frac{4q^2}{2^n-q^2}$.

The above yield the upper bound on the overall abort probability: $q\cdot \frac{q}{2^n-q}+ 4q^2\cdot \frac{q^2}{2^n-2q^2} + q^2\cdot \frac{4q^2}{2^n-2q^2}\le \frac{18q^4}{2^n}$ (when $q^2\le \frac{2^n}{4}$).

4.4 The randomness mapping argument

Let $\{P\}=(P_0,P_1,P_2,P_3)$ be an arbitrary set-tuple that can be generated during a good $\varSigma _2'$ execution. Then we have the following probability ratio:

$$\begin{aligned} \frac{Pr_{{{\varvec{\Pi }}}}[{{\varvec{\Pi }}}\cong \{P\}]}{Pr_{{\mathbf {E}},{{\varvec{\Pi }}}}[D^{\varSigma _2'({\mathbf {E}},{{\varvec{\Pi }}})}\rightarrow \{P\}]} \ge 1-\frac{q^4}{2^n}. \end{aligned}$$

The argument is similar to the proof of Lemma 9: first, (trivially) $Pr_{{{\varvec{\Pi }}}}[{{\varvec{\Pi }}}\cong \{P\}] = (\prod _{j=0}^{|P_0|-1}\frac{1}{2^n-j})\cdot (\prod _{j=0}^{|P_1|-1}\frac{1}{2^n-j}) \cdot (\prod _{j=0}^{|P_2|-1}\frac{1}{2^n-j}) \cdot (\prod _{j=0}^{|P_3|-1}\frac{1}{2^n-j})$; second, let the number of entries in $P_1$ and $P_3$ that are set to values from ${{\varvec{\Pi }}}$ be u and v respectively, and let $w=|ESet|$, then

$$\begin{aligned} Pr[D^{\varSigma _2'({\mathbf {E}},{{\varvec{\Pi }}})}\rightarrow \{P\}] \le&\left( \prod _{j=0}^{|P_0|-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{u-1}\frac{1}{2^n-j}\right) \\&\cdot \left( \prod _{j=0}^{|P_2|-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{v-1}\frac{1}{2^n-j}\right) \cdot \left( \frac{1}{2^n-w}\right) ^w, \end{aligned}$$

so that

$$\begin{aligned} \frac{Pr_{{{\varvec{\Pi }}}}[{{\varvec{\Pi }}}\cong \{P\}]}{Pr_{{\mathbf {E}},{{\varvec{\Pi }}}}[D^{\varSigma _2'({\mathbf {E}},{{\varvec{\Pi }}})}\rightarrow \{P\}]} \ge 1-\frac{w^2}{2^n} \ge 1-\frac{q^4}{2^n}. \end{aligned}$$

Then, following the same line as the proof of Lemma 10, it yields

$$\begin{aligned} \left| Pr_{{{\varvec{\Pi }}}}[D^{\varSigma '_3(\text {EMDP}_3^{{{\varvec{\Pi }}}},{{\varvec{\Pi }}})}=1] - Pr_{{\mathbf {E}},{{\varvec{\Pi }}}}[D^{\varSigma '_1({\mathbf {E}},{\mathcal {S}}^{{\mathbf {E}},{{\varvec{\Pi }}}})}=1] \right| \le \frac{18q^4}{2^n} + \frac{q^4}{2^n} \le \frac{19q^4}{2^n}. \end{aligned}$$

These completes the key points of the proof of Theorem 3. $\square$

5 Conclusion

This work proves that $\text {EMR}_3$ and $\text {EMDP}_3$, two types of 3-round Even–Mansour with non-invertible KD, are seq-indifferentiable. Besides complementing existing indifferentiability results, it establishes a definitive separation between invertible KDs and non-invertible ones in the context of Even–Mansour.

At the end of this paper, recall the comparison between $\text {EMR}$ and $\text {SEM}$ (single-key Even–Mansour). To achieve seq-indifferentiability, $\text {SEM}$ requires exactly 4 rounds [12], which is one round more than $\text {EMR}$. However, the proved security bounds on the two constructions are the same: this work proves $\text {EMR}_3$ $(q,q^{2},O(q^2),O(\frac{q^{4}}{2^n}))$-seq-indifferentiable, while Cogliati and Seurin proved $\text {SEM}_4$ $(q,q^{2},O(q^2),O(\frac{q^{4}}{2^n}))$-seq-indifferentiable.

A problem left open in [12] is whether the bound $(q,q^{2},O(q^2),O(\frac{q^{4}}{2^n}))$ on $\text {SEM}_4$ is tight. This work does not consider this problem (as the main goal is to seek for the separation), while raises a new problem: whether the bound $(q,q^{2},O(q^2),O(\frac{q^{4}}{2^n}))$ on $\text {EMR}_3$ is tight? These are left as future work.

Appendices

Appendix 1: Deferred proofs for $\text {EMR}_3$

1.1 Two other helper lemmas

The first helper lemma claims that the simulator really gives answers consistent with ${\mathbf {E}}$.

Lemma 11

For any good $\varSigma _2$-tuple $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$, D obtains the same answer for any query to ${\mathbf {E}}$/${EMR }_3^{{\mathbf {S}}^{\alpha }}$ in the two executions $D^{\varSigma _1(\alpha )}$ and $D^{\varSigma _2(\alpha )}$.

Proof

In $D^{\varSigma _2(\alpha )}$, each time D issues a query $(K,y_0)$ to $\text {EMR}_3$, $\text {EMR}_3$ will query ${\mathbf {S}}^{\alpha }.\text {H}(K)$ and ${\mathbf {S}}^{\alpha }.\text {P}(2,+,x_2)$ (for the corresponding $x_2$), so that after $\text {EMR}_3$ answers this query, it holds $(K,k)\in KSet$ and $(x_2,y_2)\in P_2$. By this, the query ${\mathbf {S}}.\text {H}(K)$ and the query ${\mathbf {S}}.\text {P}(2,\delta ,x_2)$ must have appeared during $D^{\varSigma _2(\alpha )}$, and the one appeared later would trigger a call to ${\mathbf {S}}.\text {Complete}$, after which the answer of $\text {EMR}_3$ (computed from the tables $\{P\}$ of ${\mathbf {S}}$) would have been consistent with ${\mathbf {E}}$. This establishes the claim, since the answer in $D^{\varSigma _1(\alpha )}$ is directly given by ${\mathbf {E}}$. $\square$

The second one is an inequality. It uses a new notation $\varTheta _1$, which is based on a corollary of Lemma 8. For this, consider a tuple of sets $\gamma \in {\mathcal {T}}$, and assume that the following hold for a tuple of primitives $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$:

• $D^{\varSigma _2(\alpha )}\rightarrow \gamma$;

• D outputs 1 in $D^{\varSigma _2(\alpha )}$, say, $D^{\varSigma _2(\alpha )}=1$.

Then by Lemma 8, for any tuple $\alpha '=({\mathbf {E}}',{\mathbf {H}}',{\mathbf {P}}')$, once $D^{\varSigma _2(\alpha ')}\rightarrow \gamma$, $D^{\varSigma _2(\alpha ')}=1$ – to this end, consider a tuple $\beta =({\mathbf {H}},{\mathbf {P}})\cong \gamma$, then $1=D^{\varSigma _2(\alpha )}=D^{\varSigma _3(\beta )}=D^{\varSigma _2(\alpha ')}$. With this in mind, the notation $\varTheta _1$ is used to denote the subset of ${\mathcal {T}}$ such that for any $\alpha$ such that $D^{\varSigma _2(\alpha )}\rightarrow \gamma \in \varTheta _1$ it holds $D^{\varSigma _2(\alpha )}=1$.

Lemma 12

$Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3({\mathbf {H}},{\mathbf {P}})}=1]\ge \sum _{\gamma \in \varTheta _1} Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ]$.

Proof

We show that for any tuple $({\mathbf {H}}^{*},{\mathbf {P}}^{*})$, there exists at most one $\gamma \in {\mathcal {T}}$ s.t. $({\mathbf {H}}^{*},{\mathbf {P}}^{*})\cong \gamma$. Assume otherwise, i.e. $\exists \gamma '\in {\mathcal {T}}$ s.t. $\gamma \ne \gamma '\wedge ({\mathbf {H}}^{*},{\mathbf {P}}^{*})\cong \gamma \wedge ({\mathbf {H}}^{*},{\mathbf {P}}^{*})\cong \gamma '$. Assume that for two good tuples $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and $\alpha '=({\mathbf {E}}',{\mathbf {H}}',{\mathbf {P}}')$, it holds $D^{\varSigma _2(\alpha )}\rightarrow \gamma$ and $D^{\varSigma _2(\alpha ')}\rightarrow \gamma '$. Then, consider any query of the combination $(D,{\mathbf {S}})$ in the two executions $D^{\varSigma _2(\alpha )}$ and $D^{\varSigma _2(\alpha ')}$: (i) the answers to the query to ${\mathbf {H}}$/${\mathbf {H'}}$ are the same, since ${\mathbf {H}}.\text {H}(K)={\mathbf {H}}^{*}.\text {H}(K)={\mathbf {H}}'.\text {H}(K)$; (ii) similarly, the answers to the query to ${\mathbf {P}}$/${\mathbf {P'}}$ are the same; (iii) the answers to the query to ${\mathbf {E}}$/${\mathbf {E'}}$ are also the same. For this, first, by Lemma 11, the answers of ${\mathbf {E}}$/${\mathbf {E'}}$ equal the answers of $\text {EMR}_3$ in the two $\varSigma _2$ executions; second, the answers of $\text {EMR}_3$ are computed from the sets $\gamma$ and $\gamma '$ respectively; third, the corresponding entries in $\gamma$ and $\gamma '$ have the same contents, since both of them coincide with the contents of $({\mathbf {H}}^{*},{\mathbf {P}}^{*})$. Then, following the same line as the proof of Lemma 8, we have that the transcripts of the combination $(D,{\mathbf {S}})$ in the two executions $D^{\varSigma _2(\alpha )}$ and $D^{\varSigma _2(\alpha ')}$ are the same, so that the two set-tuples $\gamma$ and $\gamma '$ should be the same, a contradiction. After this, we have

$$\begin{aligned} Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3({\mathbf {H}},{\mathbf {P}})}=1]&\ge Pr_{{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _3({\mathbf {H}},{\mathbf {P}})}=1 \wedge \exists \gamma \in {\mathcal {T}}\text { s.t. }({\mathbf {H}},{\mathbf {P}})\cong \gamma ] \\&= \sum _{\gamma \in \varTheta _1} Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ] \text { (by Lemma 8)}. \end{aligned}$$

as claimed. $\square$

The (analogues of) the two helper lemmas also hold in the context of $\text {EMDP}_3$. The proofs can be obtained by make very little modifications on the two proofs above, thus omitted.

1.2 Proof of Lemma 8

By an induction, assume that the transcripts obtained by D are the same up to some point in the three executions, and consider the next query of D. Since D is deterministic, the next query in the three executions are the same. We argue that the answers obtained in the three executions are the same. Depending on the type of this query, we distinguish three cases:

• (i) the query is to $\text {H}$: then since ${\mathbf {S}}$ only relays the answers of ${\mathbf {H}}^{\alpha }$, the answers obtained in $D^{\varSigma _1({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ and $D^{\varSigma _2({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ are the same; and since ${\mathbf {H}}^{\beta }$ extends the set KSet of ${\mathbf {S}}^{\alpha }$, the answers obtained in $D^{\varSigma _2({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ and $D^{\varSigma _3({\mathbf {H}}^{\beta },{\mathbf {P}}^{\beta })}$ are also the same;

• (ii) the query is to $\text {P}$: then in $D^{\varSigma _1(\alpha )}$ and $D^{\varSigma _2(\alpha )}$, the query must be made during the first phase (in which D only queries $\text {H}$ and $\text {P}$). It can be easily seen that this part of $D^{\varSigma _1(\alpha )}$ is exactly the same as that of $D^{\varSigma _2(\alpha )}$, so that the answers obtained are the same. On the other hand, the answers obtained in $D^{\varSigma _2({\mathbf {E}}^{\alpha },{\mathbf {H}}^{\alpha },{\mathbf {P}}^{\alpha })}$ and $D^{\varSigma _3({\mathbf {H}}^{\beta },{\mathbf {P}}^{\beta })}$ are also the same since ${\mathbf {P}}^{\beta }$ extends the set $\{P\}$ of ${\mathbf {S}}^{\alpha }$;

• (iii) the query is to $\text {E}$: then due to Lemma 11, the answers obtained in $D^{\varSigma _1(\alpha )}$ and $D^{\varSigma _2(\alpha )}$ are the same. Also, the answers obtained in $D^{\varSigma _2(\alpha )}$ and $D^{\varSigma _3(\beta )}$ are the same, since the function/permutation values used by $\text {EMR}_3$ to compute the answers are the same.

Therefore, the three transcripts of D are the same. Since D is deterministic, the three outputs of D are also the same.

1.3 Proof of Lemma 9

Let $\gamma =\{KSet,\{P\}\}$ and $\{P\}=\{P_1,P_2,P_3\}$. Then clearly $Pr_{{\mathbf {H}},{\mathbf {P}}}[({\mathbf {H}},{\mathbf {P}})\cong \gamma ]= (\frac{1}{2^n})^{|KSet|} \cdot (\prod _{j=0}^{|P_1|-1}\frac{1}{2^n-j}) \cdot (\prod _{j=0}^{|P_2|-1}\frac{1}{2^n-j}) \cdot (\prod _{j=0}^{|P_3|-1}\frac{1}{2^n-j})$.

As to $Pr[D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma ]$, consider a good tuple $\alpha =({\mathbf {E}}',{\mathbf {H}}',{\mathbf {P}}')$ which satisfies $D^{\varSigma _2(\alpha )}\rightarrow \gamma$. It can be easily checked that $D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma$ if and only if the transcripts of the combination $(D,{\mathbf {S}})$ in ${D}^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$ and ${D}^{\varSigma _2(\alpha )}$ are the same,⁸ i.e. the random values accessed during ${D}^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}$ are exactly the same as those accessed during ${D}^{\varSigma _2(\alpha )}$. Assume that during $D^{\varSigma _2(\alpha )}$, there are u (v, resp.) entries in $P_1$ ($P_3$, resp.) that are defined by calling ${\mathbf {P}}'$, and let $w=|ESet|$. Then we have

$$\begin{aligned}&Pr[D^{\varSigma _2({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})}\rightarrow \gamma ] \\&\quad \le (\frac{1}{2^n})^{|KSet|} \cdot \left( \prod _{j=0}^{u-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{|P_2|-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{v-1}\frac{1}{2^n-j}\right) \cdot \left( \frac{1}{2^n-w}\right) ^w. \end{aligned}$$

Since each adaptation (either in $P_1$ or in $P_3$) uniquely corresponds to an execution of $\text {Complete}$ (by construction) and the latter uniquely corresponds to an entry in ESet (by Lemma 2), we have $u+v+w=|P_1|+|P_3|$. Moreover we have $|P_1|\ge u$, $|P_3|\ge v$, and $w\le q^2$ (Lemma 1), hence

$$\begin{aligned} \frac{Pr_{{\mathbf {H}},{\mathbf {P}}}[\left( {\mathbf {H}},{\mathbf {P}}\right) \cong \gamma ]}{Pr_{{\mathbf {E}},{\mathbf {H}},{\mathbf {P}}}[D^{\varSigma _2\left( {\mathbf {E}},{\mathbf {H}},{\mathbf {P}}\right) }\rightarrow \gamma ]}&\ge \frac{\left( \prod _{j=0}^{|P_1|-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{|P_3|-1}\frac{1}{2^n-j}\right) }{\left( \prod _{j=0}^{u-1}\frac{1}{2^n-j}\right) \cdot \left( \prod _{j=0}^{v-1}\frac{1}{2^n-j}\right) \cdot \left( \frac{1}{2^n-w}\right) ^w} \\&\ge \frac{\left( \frac{1}{2^n}\right) ^{w}}{\left( \frac{1}{2^n-w}\right) ^{w}} \ge 1-\frac{w^2}{2^n} \ge 1-\frac{q^4}{2^n}. \end{aligned}$$

as claimed.

1.4 Proof of Lemma 10

Let $\alpha =({\mathbf {E}},{\mathbf {H}},{\mathbf {P}})$ and $\beta =({\mathbf {H}},{\mathbf {P}})$. Recall from Sect. 3.4.2 that the event “$\alpha$ bad” means that ${\mathbf {S}}^{\alpha }$ aborts during the $\varSigma _2$ execution $D^{\varSigma _2(\alpha )}$, while “$\alpha$ good” means otherwise. Furthermore, let $\varTheta _1$ be the subset of ${\mathcal {T}}$ such that for any $\alpha$ such that $D^{\varSigma _2(\alpha )}\rightarrow \gamma \in \varTheta _1$ it holds $D^{\varSigma _2(\alpha )}=1$ (same as Appendix 1). Then, wlog assume that $Pr_{\alpha }[D^{\varSigma _1(\alpha )}=1]\ge Pr_{\beta }[D^{\varSigma _3(\beta )}=1]$, it holds

$$\begin{aligned}&\left| Pr_{\beta } [D^{\varSigma _3(\beta )}=1] - Pr_{\alpha }[D^{\varSigma _1(\alpha )}=1] \right| \\&\quad = \underbrace{Pr_{\alpha }[\alpha \text { bad}\wedge D^{\varSigma _1(\alpha )}=1]}_{\le Pr[\alpha \text { bad}]\le \frac{17q^4}{2^n}\text { (Lemma 7)}} + Pr_{\alpha }[\alpha \text { good}\wedge D^{\varSigma _1(\alpha )}=1] - \underbrace{Pr_{\beta }[D^{\varSigma _3(\beta )}=1].}_{\ge \sum _{\gamma \in \varTheta _1}Pr_{\beta }[\beta \cong \gamma ]\text { (Lemma 12)}} \end{aligned}$$

By Lemma 8, when $\alpha$ is good, $D^{\varSigma _1(\alpha )}=D^{\varSigma _2(\alpha )}$. Hence we have

$$\begin{aligned}&Pr_{\alpha }[\alpha \text { good}\wedge D^{\varSigma _1(\alpha )}=1] = Pr_{\alpha }[\alpha \text { good}\wedge D^{\varSigma _2(\alpha )}=1] = \sum _{\gamma \in \varTheta _1} Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ], \end{aligned}$$

and

$$\begin{aligned}&\left| Pr_{\beta } [D^{\varSigma _3(\beta )}=1] - Pr_{\alpha }[D^{\varSigma _1(\alpha )}=1] \right| \\&\quad \le \frac{17q^4}{2^n} + \sum _{\gamma \in \varTheta _1} \left( Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ] - \underbrace{Pr_{\beta }[\beta \cong \gamma ]}_{\ge (1-\frac{q^4}{2^n})Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ] \text { (Lemma 9)} } \right) \\&\quad \le \frac{17q^4}{2^n} + \sum _{\gamma \in \varTheta _1} \frac{q^4}{2^n} \cdot Pr_{\alpha } [D^{\varSigma _2(\alpha )}\rightarrow \gamma ] \le \frac{18q^4}{2^n} \end{aligned}$$

as claimed.

Appendix 2: Andreeva et al.’s seq-distinguisher on 3-round Even–Mansour with invertible KD [2]

Consider the 3-round Even–Mansour with an invertible KD function ${\mathbf {IKD}}$:

$$\begin{aligned} \text {EMIKD}_{3}(K,m)={\mathbf {IKD}}(K)\oplus {\mathbf {P}}_{3}({\mathbf {IKD}}(K)\oplus {\mathbf {P}}_{2}({\mathbf {IKD}}(K)\oplus {\mathbf {P}}_{1}({\mathbf {IKD}}(K)\oplus m))), \end{aligned}$$

the (seq-)distinguisher D works as follows (the notations have been adapted to the convention used in this paper):

• (1) D queries ${\mathbf {P}}_1$ on some arbitrary $x_1$: $y_1:={\mathbf {P}}_1(x_1)$.

• (2) For two distinct, arbitrarily chosen keys $K_1$ and $K_2$, D queries $k_1:={\mathbf {IKD}}(K_1)$ and $k_2:={\mathbf {IKD}}(K_2)$.

• (3) D queries ${\mathbf {P}}_2$: $x_2:=y_1\oplus k_1$, $y_2:={\mathbf {P}}_2(x_2)$, and $x_2':=y_1\oplus k_2$, $y_2':={\mathbf {P}}_2(x_2')$; queries ${\mathbf {P}}_3$: $x_3:=y_2\oplus k_1$, $y_3:={\mathbf {P}}_3(x_3)$, and $x_3':=y_2'\oplus k_2$, $y_3':={\mathbf {P}}_3(x_3')$ (notice that D’s objective is to compute two distinct values $y_3$ and $y_3'$, namely two diverging paths connected only under the ${\mathbf {P}}_1$ evaluation).

• (4) D sets $k_3:=y_2\oplus x_3'$ and $k_4:=y_2'\oplus x_3$, and queries ${\mathbf {IKD}}$: $K_3:={\mathbf {IKD}}^{-1}(k_3)$ and $K_4:={\mathbf {IKD}}^{-1}(k_4)$.

• (5) D computes using inverse queries to $E(-,\cdot ,\cdot )$: $x_1':=E(-,K_3,y_3'\oplus k_3)\oplus k_3$ and $x_1'':=E(-,K_4,y_3\oplus k_4)\oplus k_4$.

• (6) If $x_1'=x_1''$, then D guesses the real world and otherwise the simulated.

A (seq-)distinguisher based on the same principle was exhibited by Lampe and Seurin [26], which finds an evasive relation between the inputs and outputs of $\text {SEM}_{3}$.