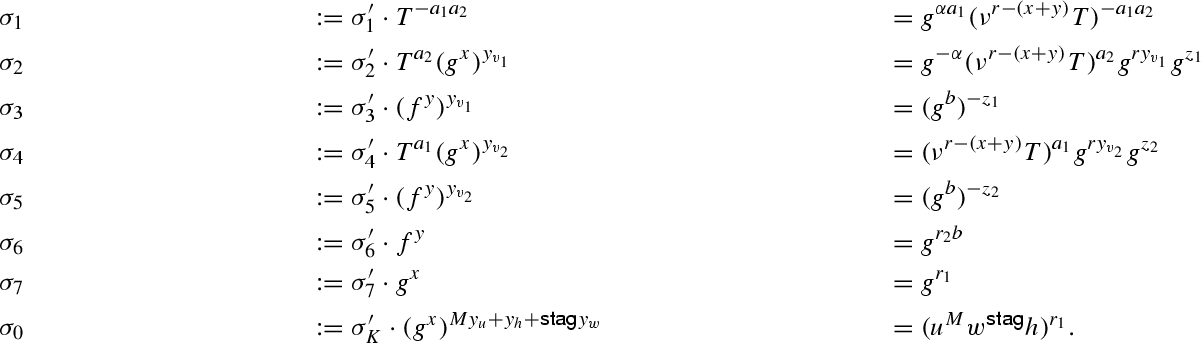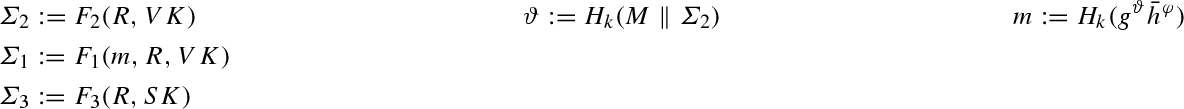Verifiably encrypted signatures with short keys based on the decisional linear problem and obfuscation for encrypted VES

Abstract

Verifiably encrypted signatures (VES) are encrypted signatures under a public key of a trusted third party. We can verify their validity without decryption. VES has useful applications such as online contract signing and optimistic fair exchange. We propose a VES scheme that is secure under the decisional linear (DLIN) assumption in the standard model. We also propose new obfuscators for encrypted signatures (ES) and encrypted VES (EVES) that are secure under the DLIN assumption. All previous VES schemes in the standard model are either secure under standard assumptions (such as the computational Diffie–Hellman assumption) with large verification (or secret) keys or secure under non-standard dynamic $q$-type assumptions (such as the $q$-strong Diffie–Hellman extraction assumption) with short verification keys. Our scheme is the first VES scheme with short verification (and secret) keys secure under the DLIN assumption (standard assumption). We construct new obfuscators for ES/EVES as byproducts of our new VES scheme. They are more efficient than previous obfuscators with respect to public key size. Previous obfuscators for EVES are secure under non-standard assumption and use zero-knowledge (ZK) proof systems and Fiat–Shamir heuristics to obtain non-interactive ZK, i.e., its security is considered in the random oracle model. Thus, our scheme also has an advantage with respect to assumptions and the security model. Our new obfuscator for ES is obtained from our new obfuscator for EVES.

1 Introduction

1.1 Background

In verifiably encrypted signature (VES) schemes, we consider signers, verifiers, and a trusted third party, called the adjudicator. A signer generates a signature, encrypts it under the public key of the adjudicator, and adds extra content to make it verifiable without decryption. The adjudicator can recover ordinary signatures from encrypted ones by using its decryption key.

The concept of VES was introduced by Boneh et al. [12], who proposed the first VES scheme based on the Boneh-Lynn-Shacham signature scheme in the random oracle model (ROM) [10]. VES schemes have useful and important applications such as online contract signing and optimistic fair exchange [2, 3]. Suppose a user, Alice, wants to buy digital goods from a company online. Alice gives the company her VES for a contract instead of paying money and the company returns the requested digital goods if it received a valid VES. Alice sends an ordinary signature to the company if she receives the goods. If a malicious company does not return the requested goods when it receives the VES, Alice can claim that the VES is of no use for the contract since it is encrypted. If malicious Alice does not return an ordinary signature when she receives the goods, the company sends the encrypted signature together with the transcript to the adjudicator and the adjudicator extracts an ordinary signature from the VES by using the secret key of the adjudicator and returns it to the company. The adjudicator is offline, that is, it should be active only when malicious Alice cheats the company. Fuchsbauer used a certain kind of VES to construct delegatable anonymous credentials [30]. Anonymous credentials are useful for access control [5]. In some systems with access control, users must prove having the required credentials issued by an authority to use the system. The authority may want to delegate its right to other entities to avoid centralization of power.

Lu et al. [45] proposed a VES scheme that is secure under the computational Diffie–Hellman (CDH) assumption in the standard model, but the verification key is quite long. Rückert and Schröder [48] proposed a VES scheme with short verification keys, but its security relies on a non-standard $q$-type assumption, called the $q$-strong Diffie–Hellman ($q$-SDH) extraction assumption. They did not prove its hardness in the generic group model [50]. Thus, there is no VES scheme that achieves a constant size verification key and signature based on standard assumptions.

Program obfuscation and encrypted signature/VES. An Encrypted VES (EVES) is an extension of an encrypted signature (ES) proposed by Hada [41]. The ES/EVES functionalities output an encryption of a signature/VES. They do not encrypt messages, but can be used as building blocks of signcryption functionalities, as pointed out by Hada [41]. In order to show this application, Hada proposed the notion of Encrypted-Signature-then-Encryption (EStE). In it, we first compute a signature for a message, then encrypt the signature. Finally, we encrypt both the message and the encrypted signature. The combination of the first and second steps is the ES functionality, so Hada claims that the ES functionality is useful for signcryption although the situation is somewhat different (In EStE, a signature is doubly encrypted).

We explain how to use obfuscators (explained below) for ES/EVES functionalities in a realistic scenario in this paragraph. If Alice uses free web-mail services to send mail to Bob on low computational power devices, such as smart-phones, and her web browsers do not have enough resources to sign messages and encrypt them with Bob’s public key, then she would want web-mail providers to carry out its process instead of her. However, she does not want to reveal her signing key. The obfuscation for ES/EVES will provide a solution. A program obfuscator is an algorithm that transforms a program into a completely unintelligible program whose functionality is the same as the original one [4, 40]. Informally speaking, obfuscators should guarantee that what is efficiently computed given an obfuscated program is nothing more than what is computed given black-box access to the original program. This means that no adversary can obtain non-trivial information about the original program. If Alice provides an obfuscated program for ES/EVES functionality, then she can securely delegate her signing capability to web-mail providers. Moreover, in a situation in which president Alice is on vacation wants to have vice president Carol sign contracts for Bob (only Alice to Bob) instead of her, Alice can provide Carol an obfuscated program for EVES functionality. In this scenario, Carol cannot obtain any information about the secret key of Alice due to the property of obfuscation. This is a strong motivation of obfuscation for the ES/EVES functionalities.

In Hada’s obfuscator for an ES, if a malicious party has access to Bob’s decryption key, then Alice’s signing key is extracted from the obfuscated program [41]. However, in our obfuscator for an EVES, even such a malicious party cannot extract Alice’s key due to the existence of the adjudicator’s key. Thus, obfuscators for an EVES have useful applications.

The problem of program obfuscation is very attractive in the area of cryptology from both the theoretical and practical points of view since program obfuscators completely hide non-trivial information encoded into programs (for example, signing keys of signature/VES) and have many cryptographic applications as pointed out in [4]. A few positive results are shown for cryptographic functionalities [22, 41–43].

Unfortunately, in the seminal work by Barak et al. [4], they showed the impossibility result for general-purpose obfuscation. Many other impossibility results have been shown in various settings [6, 21, 38–40, 42, 54]. There are a few positive results for very simple functionalities, such as point functions [16–19, 46, 54], proximity testing [27], testing hyperplane membership [20]. In order to sidestep broad impossibility results, Hohenberger et al. [43] and Hofheinz et al. [42] independently proposed a new definition of secure obfuscation for cryptographic purposes, average-case secure obfuscation of randomized functionalities. Moreover, Hohenberger et al. [43] proposed the first (average-case secure) obfuscator for a complicated cryptographic functionality, re-encryption functionality and Chandran et al. [22] proposed an obfuscator for functional re-encryption functionality.

Hada [41] proposed a secure obfuscator for an ES functionality and its application to signcryption. His scheme is secure under the decisional linear (DLIN) assumption in the standard model, but the verification key size is quite large. Cheng et al. [23] proposed a secure obfuscator for an EVES functionality at ProvSec’11. Their VES scheme and obfuscator for EVES use zero-knowledge (ZK) proofs and Fiat–Shamir heuristics to crash the ZK proofs into non-interactive zero-knowledge (NIZK) proofs. That is, their scheme and obfuscator are secure in the ROM. Furthermore, they used a non-standard assumption, called exponent 3-weak DH assumption, to prove the unforgeability of their scheme and did not prove the opacity (explained in the next section), which is required for secure VES schemes, of their scheme.

In general, obfuscators for ES/EVES can be obtained from fully homomorphic encryption (FHE) schemes [33]. However, current FHE schemes are still inefficient, though many improvements have been proposed [13–15, 24, 26, 34–37, 51]. Therefore we do not rely on expensive FHE schemes but directly construct obfuscators for ES/EVES.

Very recently, Garg et al. [32] proposed an indistinguishability obfuscator for all polynomial-sized circuits by using multilinear maps [31]. The notion of indistinguishability obfuscation was proposed by Barak et al. [4] and is a weaker notion than the black-box obfuscation. Their construction is quite elegant, but it is a generic construction and uses multilinear maps and an ad hoc non-standard assumption. Thus, their obfuscator is not efficient.

1.2 Our contributions and constructions

We propose a VES scheme based on the DLIN assumption in the standard model. The main advantages over previous VES schemes are as follows.

• 1. It is secure under a standard (i.e., not $q$-type) assumption in the standard model.

• 2. The verification key and signature size are small (constant).

As a by-product of our VES scheme, we construct secure obfuscators for an ES/EVES functionality based on the DLIN assumption in the standard model. Main advantages of our obfuscators for an ES/EVES over previous obfuscators for an ES/EVES are as follows. They are secure under the DLIN assumption in the standard model with short verification keys.

Comparison and related work. Comparisons of our results with previous results of VES schemes and obfuscators for a ES/EVES are shown in Tables 1 and 2, respectively. Let $\lambda$ denote the security parameter. The CDH assumption stands for the CDH assumption in bilinear groups. There has been no VES scheme and obfuscator for ES/EVES that are secure under standard assumptions in the standard model with short verification keys prior to ours. The VES scheme by Lu et al. requires a large verification key but its signature size is small and its security is based on a standard CDH assumption, so one may believe that the scheme of Lu et al. is better than ours in terms of signature size. However, we believe it is incomparable with our new scheme and we showed a tradeoff between the verification key size and signature size. Rückert proposed a VES scheme based on the full-domain hash RSA signature, but it is secure in the ROM [47]. Rückert et al. [49] proposed generic constructions for a VES without NIZKs, pairings, and ROM. Their construction is very insightful, but their schemes use an extra adjudication setup phase and Merkle trees, so they need to set-up large parameters and have large keys (non-constant size).

Table 1 Summary of previous schemes and ours for VES

Table 2 Summary of previous obfuscators for encrypted ES/EVES

Our construction technique. Loosely speaking, a VES scheme consists of a signature scheme and an encryption scheme as Lu et al. and Rückert and Schröder stated [45, 48]. We use Waters’ signature scheme presented at CRYPTO’09 [53] as an underlying signature scheme. We call it Waters’ dual signature in this paper to distinguish it from Waters’ signature at Eurocrypt’05 [52]. Someone may believe that a combination of Waters’ dual signature and ElGamal encryption easily yields a secure VES scheme under the DLIN assumption, but this is not the case. The reason is as follows. We can prove unforgeability of a VES scheme by relying on the unforgeability of the underlying signature scheme as in previous schemes [12, 45, 48], but the opacity is non-trivial. The opacity means that it is difficult to extract an ordinary signature from a VES, i.e., decrypt a VES. Moreover, it is highly non-trivial whether we can prove opacity from standard assumptions. The reason is as follows. The VES scheme of Lu et al. is a combination of Waters’ signature (Eurocrypt’05) [52] and ElGamal encryption scheme, and they proved its opacity from the aggregate extraction assumption [12] (fortunately, it is equivalent to the CDH assumption [25]). On the other hand, the VES scheme of Rückert and Schröder [48] is a combination of the Boneh–Boyen signature [7] and ElGamal encryption schemes, but they proved its opacity from the $q$-strong DH extraction assumption, which is a stronger assumption than that of the underlying Boneh–Boyen signature scheme.

Our construction is a combination of Waters’ dual signature and ElGamal encryption schemes. We encrypt only signature elements related to signing keys. The security proof of Waters’ dual signature is somewhat different from that of many known secure signature schemes, such as Boneh–Boyen [7], and Waters [52], so we must use a somewhat different proof strategy from that of Lu et al. and Rückert and Schröder. Waters’ dual signature has two types of signatures, standard signature (Type A) and semi-functional signature (Type B). Semi-functional signatures also pass the verification algorithm as standard ones and are indistinguishable from them [53]. We extend the proof strategy of this dual form signature technique to prove opacity. First, we use Type B signatures as normal signatures generated by a normal signing algorithm and Type A signatures are used for simulation. Both Type A and B signatures are valid signatures and there is no essential difference in terms of functionality as long as a normal verification algorithm is used. We use this swapping of roles since we do not know how to prove that an adversary cannot extract a valid Type A signature from a given VES when the oracle answers Type A signatures.

In the experiment of the opacity explained in Sect. 2.4, an adversary can output a signature and message pair such that the message is queried to an oracle which returns a VES for the queried message. This causes the main difficulty in proving the opacity since the adversary may output a re-randomized signature obtained using valid signatures from oracles. Unfortunately, Waters’ dual signature is re-randomizable. Thus, we modify Waters’ dual signature scheme and make it strongly unforgeable. Strong unforgeability guarantees that an adversary cannot output a forgery even for a queried message, so it must hold that if the adversary output valid signature for a queried message in the experiment of opacity, then the signature is identical to the signature generated by the VES creation oracle (otherwise, contradict to strong unforgeability). This fact can be used to prove the opacity of our scheme.

In the proof of opacity, we must simulate two oracles. One is the creation oracle, which answers VESs for queried messages. The other is the adjudication oracle, which extracts ordinary signatures from queried messages and VESs and returns them. When we answer only the encryption of Type B signature for VES creation queries of the adversary, we can prove that the adversary cannot extract Type B signature from a VES under the aggregate extraction assumption. This is why we swap the roles of Type A signatures for that of Type B signatures. We have no way to prove that when we answer only the encryption of a Type A signature for VES creation queries of an adversary, the adversary cannot extract a Type A signature from a VES.

Thus, we can prove that no adversary can output a valid signature for a queried message to the VES creation oracle. For non-queried messages, we can use the proof technique for the unforgeability of dual form signatures. We prove that no adversary can output a Type A signature when the oracle returns Type B signatures (VESs).

Next, we change the type of signatures used to generate VESs, which are answered by the VES creation oracle. Answers from the adjudication oracle depend on the type of the VES creation oracle. Thus, we prove that the view of the adversary is indistinguishable even if the type of each answer is changed from Type B to Type A for each query. This order of change is reverse to the original proof, but it is not a major difference. Finally, we prove that no adversary can output a Type B signature when the oracle returns Type A signatures (VESs).

Secure obfuscations for ES and EVES based on Waters’ dual signature scheme are also non-trivial because the signing keys of this scheme consist of multiple group elements, and the signing algorithm computes exponentiation of the signing keys with randomness in contrast to Waters’ signature presented at Eurocrypt’05, whose signing key is only one group element and signing algorithm only multiplies it by other group elements [52]. We overcome this hurdle by using the homomorphic property of the ElGamal and linear encryption schemes [9]. Cheng et al. use the linear encryption scheme for not only encryption of a VES but also the construction of the VES, so their VES scheme cannot check the validity of ciphertext by using only the pairing technique and they need (NI)ZK. We do not need (NI)ZK because our VES scheme uses the ElGamal encryption scheme and can verify the validity of VES by using only pairings.

2 Preliminaries

Notations and conventions. For any $n\in \mathbb {N}{\setminus } \{0\}$, let $[n]$ be the set $\{1,\ldots ,n\}$. When $D$ is a random variable or distribution, $y \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}D$ denotes that $y$ is randomly selected from $D$ according to its distribution. If $S$ is a set, then $x \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}S$ denotes that $x$ is uniformly selected from $S$. We denote $y$ is a set, defined or substituted by $z$ by $y :=z$. When $b$ is a fixed value, $A(x) \rightarrow b$ (e.g., $A(x) \rightarrow 1$) denotes the event in which machine (or algorithm) $A$ outputs $b$ on input $x$. We say that positive function $f:\mathbb {N}\rightarrow \mathbb {R}$ is negligible in $\lambda \in \mathbb {N}$ if for every constant $c \in \mathbb {N}$ there exists $k_{c} \in \mathbb {N}$ such that $f(\lambda )<\lambda ^{-c}$ for any $\lambda > k_{c}$. Let $\mathcal {X}=\{X_{\lambda }\}_{\lambda \in \mathbb {N}}$ and $\mathcal {Y}=\{Y_{\lambda }\}_{\lambda \in \mathbb {N}}$ denote two ensembles of random variables indexed by $\lambda$.

Definition 1

We say that $\mathcal {X}$ and $\mathcal {Y}$ are computationally indistinguishable if for every non-uniform probabilistic polynomial-time (PPT) algorithm $D$,

$$\begin{aligned} \left| \Pr [D(X_{\lambda })=1]-\Pr [D(Y_{\lambda })=1]\right| \end{aligned}$$

is negligible in $\lambda$.

We write $\mathcal {X}\mathop {\approx }\limits ^{\mathsf {c}}\mathcal {Y}$ to denote that $\mathcal {X}$ and $\mathcal {Y}$ are computationally indistinguishable.

2.1 Cryptographic bilinear maps (or pairings)

We consider cyclic groups $\mathbb {G}$ and $\mathbb {G}_{T}$ of prime order $p$. A bilinear map is an efficient mapping $e: \mathbb {G}\times \mathbb {G}\rightarrow \mathbb {G}_{T}$ satisfying the following properties:

• bilinearity: For all $g\in \mathbb {G}$ and $a,b\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, $e(g^{a},g^{b})= e(g,g)^{ab}$.

• non-degeneracy: If $g$ generates $\mathbb {G}$, then $e(g,g)\ne 1$.

Let $\mathcal {G}_\mathsf {bmp}$ be a standard parameter generation algorithm that takes security parameter $\lambda$ as input and outputs parameters $(p,\mathbb {G},\mathbb {G}_{T},e,g)$. That is, $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},e,g) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$ and $\varGamma$ is a description of groups $\mathbb {G}$ and $\mathbb {G}_{T}$ of prime order $p$ equipped with efficient bilinear map $e: \mathbb {G}\times \mathbb {G}\rightarrow \mathbb {G}_{T}$. Here, $g$ is a generator in $\mathbb {G}$. We often omit common parameters $\varGamma$.

2.2 Complexity assumptions

We review several complexity assumptions that are used to prove the security of cryptographic primitives.

Definition 2

(Discrete Logarithm (DL) assumption) The DL problem in bilinear groups is to compute $x$, given $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},e,g) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$ and $g^x$ for $x \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$. The advantage is defined as follows.

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {dl}}(\lambda ) :=\Pr [z= x \mid \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda }); x \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p; z \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}(\varGamma ,g^{x})]. \end{aligned}$$

We say that the DL assumption holds in bilinear groups if the DL problem in bilinear groups is hard, that is, for any PPT $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {dl}}(\lambda )$ is negligible in $\lambda$.

Definition 3

(CDH assumption) The CDH problem in bilinear groups is to compute $g^{x y}$, given $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},e,g) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$ and $(g^x,g^y)$ for $x,y \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$. The advantage is defined as follows.

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {cdh}}(\lambda ) :=\Pr [z=g^{x y} \mid \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda }); x,y \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p;z \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}(\varGamma ,g^{x},g^{y})]. \end{aligned}$$

We say that the CDH assumption holds in bilinear groups if the CDH problem in bilinear groups is hard, that is, for any PPT $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {cdh}}(\lambda )$ is negligible in $\lambda$.

Definition 4

(DLIN assumption) The DLIN problem in bilinear groups is to guess $\beta \in \{0,1\}^{}$, given $(\varGamma , g,f,\nu ,g^x , f^y , Q_{\beta }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_{\beta }^{\mathsf {dlin}}(1^\lambda )$, where $\mathcal {G}_{\beta }^{\mathsf {dlin}}(1^{\lambda })$: $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},e,g) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$, $f,\nu \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, $x,y \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, $Q_0 :=\nu ^{x+y}$, $Q_1 \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, return $(\varGamma , g,f,\nu ,g^{x},f^{y},Q_{\beta })$. The advantage is defined as follows.

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {dlin}}(\lambda ) :=\left| \Pr \left[ {\mathcal {A}}(\mathcal {I}) \rightarrow 1 \mid \mathcal {I}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_{0}^{\mathsf {dlin}}(1^{\lambda }) \right] - \Pr \left[ \mathcal {A}(\mathcal {I}) \rightarrow 1 \mid \mathcal {I}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_{1}^{\mathsf {dlin}}(1^{\lambda }) \right] \right| . \end{aligned}$$

We say that the DLIN assumption holds if the DLIN problem is hard, that is, for any PPT $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {dlin}}(\lambda )$ is negligible in $\lambda$.

Definition 5

(Aggregate Extraction (AgExt) assumption) The AgExt problem in bilinear groups is to compute $g^{x y}$, given $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},e,g) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$ and $(g^{x},g^{y},g^{\beta },g^{\delta },g^{x y + \beta \delta })$ for $x,y,\beta ,\delta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$ [12, 25]. The advantage is defined as follows.

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {agext}}(\lambda ) :=\Pr \left[ \begin{array}{l} z=g^{x y} \end{array} \left| \begin{array}{l} \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda });x, y,\beta ,\delta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}; \\ z \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}(\varGamma ,g^{x},g^{y},g^{\beta },g^{\delta },g^{x y + \beta \delta }) \end{array} \right. \right] . \end{aligned}$$

We say that the AgExt assumption holds in bilinear groups if the AgExt problem in bilinear groups is hard, that is, for any PPT $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {agext}}(\lambda )$ is negligible in $\lambda$.

The AgExt assumption is equivalent to the CDH assumption, which is implied by the DLIN assumption.

Theorem 1

(The CDH and AgExt are equivalent [25]) The AgExt and CDH problems are Karp reducible to each other with $O(1)$ computation.

2.3 Cryptographic primitives

Signature. Signature scheme ${\mathsf {SIG}}$ consists of three PPT algorithms ${\mathsf {SIG}}={\mathsf {SIG}}.\{\mathsf {Gen},\mathsf {Sign}, \mathsf {Vrfy}\}$ satisfying the following properties.

• Key Generation: ${\mathsf {SIG}}.\mathsf {Gen}$ takes as input security parameter $1^{\lambda }$ and outputs a pair of keys, that is, $(vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}}.\mathsf {Gen}(1^{\lambda })$. They are called the (public) verification key and the (private) signing key, respectively.

• Sign: ${\mathsf {SIG}}.\mathsf {Sign}{}$ takes as input a signing key and a message and outputs signature $\sigma$. That is, $\sigma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}}.\mathsf {Sign}{}(sk,m)$, where $m\in \mathcal {M}_{vk}$ and $\mathcal {M}_{vk}$ is a message space defined by the verification key.

• Verification: ${\mathsf {SIG}}.\mathsf {Vrfy}{}$ is deterministic, takes as input a verification key, a message, and a signature, and outputs bit $b$. If $b=1$, then the signature is valid. Else, it is invalid. That is, ${\mathsf {SIG}}.\mathsf {Vrfy}{}(vk,\sigma ,m) \rightarrow b$.

It is required that $\forall \lambda \ \forall (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}}.\mathsf {Gen}(1^{\lambda }) \ \forall m\in \mathcal {M}_{vk} \$ ${\mathsf {SIG}}.\mathsf {Vrfy}{}(vk,{\mathsf {SIG}}.\mathsf {Sign}{}(sk,m),m)\rightarrow 1$. Signature scheme ${\mathsf {SIG}}={\mathsf {SIG}}.\{ \mathsf {Gen}, \mathsf {Sign}{}, \mathsf {Vrfy}{} \}$ is said to be existentially unforgeable under adaptive chosen message attacks (EUF-CMA) if the advantage of the following game is negligible.

• 1. Setup: A challenger generates $(vk,sk) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}.\mathsf {Gen}}(1^{\lambda })$ and sends $vk$ to an adversary.

• 2. Queries: The adversary sends message $M_{i} \in \mathcal {M}_{vk}$ to the challenger and answers $\sigma _{i}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}}.\mathsf {Sign}{}(sk,M_{i})$. These queries are sent adaptively for $i=1$ to $n$. Let $Q$ be the set of messages $M_{1},\ldots , M_{k}\in \mathcal {M}_{vk}$ queried by the adversary.

• 3. Output: The adversary outputs $(m^{*},\sigma ^{*})$. If it holds that ${\mathsf {SIG}}.\mathsf {Vrfy}{}(vk,\sigma ^{*},m^{*}) \rightarrow 1$ and $m^{*} \notin Q$, then it is said that the adversary wins the game.

We define $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {euf} \text{- } \mathsf {cma}}(\lambda )$ to be the probability that an adversary $\mathcal {A}$ wins in the game.

Definition 6

(Existentially Unforgeable against Adaptive Chosen Message Attacks) Signature scheme ${\mathsf {SIG}}$ is existentially unforgeable against adaptive chosen message attacks if for any PPT $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {euf} \text{- } \mathsf {cma}}(\lambda )$ is negligible in $\lambda$.

In the game of EUF-CMA, if we replace condition $m^{*} \notin Q$ with $(m^{*},\sigma ^{*}) \ne (\mathrm{M}_{i},\sigma _{i})$ for any $i$, then we say that the security is strongly existentially unforgeable (sEUF). We define $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {seuf} \text{- } \mathsf {cma}}(\lambda )$ to be the probability that $\mathcal {A}$ wins in the modified game.

Public key encryption. A public key encryption (PKE) scheme consists of three PPT algorithms ${\mathsf {PKE}}.\{\mathsf {Gen},\mathsf {Enc},\mathsf {Dec}\}$ satisfying the following properties.

• Key Generation: ${\mathsf {PKE}}.\mathsf {Gen}$ takes as input security parameter $1^{\lambda }$ and outputs a pair of keys, that is, $(pk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}}.\mathsf {Gen}(1^{\lambda })$. They are called the public key and secret (decryption) key, respectively.

• Encryption: ${\mathsf {PKE}}.\mathsf {Enc}$ takes as input $pk$ and plaintext $m$ and outputs ciphertext $c$. That is, $c \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}}.\mathsf {Enc}(pk,m)$. If we express that we explicitly use randomness $r$, then we use notation $c :=\mathsf {Enc}(pk,m;r)$.

• Decryption: ${\mathsf {PKE}}.\mathsf {Dec}$ is deterministic, takes as input $sk$ and $c$, and outputs plaintext $m^{\prime }$. That is, $m^{\prime } :={\mathsf {PKE}}.\mathsf {Dec}(sk,c)$.

It is required $\forall \lambda \ \forall (pk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}}.\mathsf {Gen}(1^{\lambda }) \ \forall m \$ $m = {\mathsf {PKE}}.\mathsf {Dec}(sk,{\mathsf {PKE}}.\mathsf {Enc}(pk,m))$.

We present indistinguishability against chosen plaintext attacks (IND-CPA), that is the basic security of PKE.

Definition 7

(IND-CPA security) The model for proving the IND-CPA security of PKE against $\mathcal {A}$ is given as follows.

• 1. ${\mathsf {PKE}.}\mathsf {Gen}$ is run with input $1^{\lambda }$ to generate keys $pk$ and $sk$, and $pk$ is given to $\mathcal {A}$.

• 2. $\mathcal {A}$ outputs challenge plaintexts $(m_0,m_1)$ such that $\left| m_0\right| = \left| m_1\right|$.

• 3. Uniformly random bit $b$ is chosen. $\mathcal {A}$ is given $c^{*} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Enc}(pk,m_{b})$.

• 4. $\mathcal {A}$ outputs a bit $b^{\prime }$ and wins if $b^{\prime }= b$.

The advantage of $\mathcal {A}$ in the above game is defined as $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {ind} \text{- } \mathsf {cpa}} (\lambda ) :=\left| 2 \Pr [b^{\prime } = b] - 1\right|$ for any security parameter $\lambda$. A PKE scheme is IND-CPA secure if for any PPT adversary $\mathcal {A}$, it holds that $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {ind} \text{- } \mathsf {cpa}} (\lambda )$ is negligible in $\lambda$.

Collision resistant hash functions (CRHF). Let $\mathcal {H}:=\left\{ H_{k}\right\}$ be a keyed hash family of functions $H_{k} : \{0,1\}^{*} \rightarrow \{0,1\}^{n}$ indexed by $k \in \mathcal {K}_{\lambda }$ where $\lambda$ is a security parameter.

Definition 8

We say that $\mathcal {H}$ is $(t,\epsilon )$-collision-resistant if for any $\mathcal {A}$ running in time $t$, we have that $\mathsf {Adv}_{\mathcal {A},\mathcal {H}}^{\mathsf {crhf}} (\lambda ) :=\Pr [m_0 \ne m_1 \wedge H_{k}(m_0) = H_{k} (m_1) \mid (m_0,m_1) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}(k) ] < \epsilon$, where the probability is over the random choice of $k \in \mathcal {K}_{\lambda }$ and random coins of $\mathcal {A}$.

2.4 Verifiably encrypted signature (VES)

A VES scheme consists of seven PPT algorithms, $\{\mathsf {AdjGen}, \mathsf {Gen},\mathsf {Sign}, \mathsf {Vrfy}, \mathsf {Create}, \mathsf {VesVrfy}, \mathsf {Adj}\}$, satisfying the following properties.

• Adjudicator Key Generation: $\mathsf {AdjGen}$ takes as input security parameter $1^{\lambda }$ and outputs a pair of keys for an adjudicator, that is, $(apk,ask) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(1^{\lambda })$.

• Key Generation: $\mathsf {Gen}$ takes as input $1^{\lambda }$ and outputs a pair of keys for a signer, that is, $(vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(1^{\lambda })$. They are called the verification key and the signing key, respectively.

• Signing: $\mathsf {Sign}$ takes as input a signing key and a message and outputs signature $\sigma$. That is, $\sigma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Sign}(sk,M)$, where $M\in \mathcal {M}_{vk}$ and $\mathcal {M}_{vk}$ is a message space defined by $vk$.

• Verification: $\mathsf {Vrfy}$ is deterministic, takes as input $vk$, $M$, and $\sigma$, and outputs bit $b$. If $b=1$ then the signature is valid. Else, it is invalid. That is, $\mathsf {Vrfy}{}(vk,\sigma ,m) \rightarrow b$.

• VES Creation: $\mathsf {Create}$ takes as input $sk$, $apk$, and $M$ and outputs VES $\omega$ on $M$. That is, $\omega \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Create}(sk,apk,M)$.

• VES Verification: $\mathsf {VesVrfy}$ is deterministic, takes as input $apk$, $vk$, $\omega$, and $M$, and outputs bit $b$, that is, $\mathsf {VesVrfy}(apk,vk,\omega ,M) \rightarrow b$.

• Adjudication: $\mathsf {Adj}$ takes as input $ask,apk,vk,\omega$, and $M$. If $\omega$ is valid, it extracts an plain signature $\sigma$ on $M$ and returns $\sigma$, that is $\sigma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Adj}(ask,apk,vk,\omega ,M)$ if $\mathsf {VesVrfy}(apk,vk, \omega ,M) \rightarrow 1$.

It is required that $\forall \lambda \ \forall (apk,ask)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(1^\lambda ) \ \forall (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(1^{\lambda }) \ \forall m\in \mathcal {M}_{vk} \$ $\mathsf {VesVrfy}(apk,pk,\mathsf {Create}(sk,apk,M),M)\rightarrow 1$ and $\mathsf {Vrfy}(vk,\mathsf {Adj}(ask,apk,vk,\mathsf {Create} (sk,apk,M),M),M)\rightarrow 1$.

A VES scheme is secure if it satisfies the unforgeability and the opacity [12]. In experiments defined below, oracle $\mathcal {C}\mathcal {O}(sk,apk,\cdot )$ returns VESs for queried messages, oracle $\mathcal {A}\mathcal {O}(ask,apk,vk,\cdot ,\cdot )$ extracts and returns signature for queried message/VES pairs, and $Q_{\mathsf {C}}$ and $Q_{\mathsf {A}}$ are sets of messages queried by the adversary to $\mathcal {C}\mathcal {O}$ and $\mathcal {A}\mathcal {O}$, respectively.

Definition 9

(Unforgeability) Experiments $\mathsf {Forge}^{\mathsf {ves}}_{\mathcal {A}}(\lambda )$ is defined as follows.

We say that a VES scheme is unforgeable if for any PPT adversary $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {ves}\mathrm - \mathsf {uf}}(\lambda ) :=\Pr [\mathsf {Forge}^{\mathsf {ves}}_{\mathcal {A}}(\lambda ) \rightarrow 1]$ is negligible in $\lambda$.

Definition 10

(Opacity) Experiment ${\mathsf {Opac}}_{\mathcal {A}}(\lambda )$ is defined as follows.

We say that a VES scheme is opaque if for any PPT $\mathcal {A}$, $\mathsf {Adv}_{\mathcal {A}}^{\mathsf {opac}}(\lambda ) :=\Pr [{\mathsf {Opac}}_{\mathcal {A}}(\lambda ) \rightarrow 1]$ is negligible in $\lambda$.

More properties of VES. Rückert and Schröder [48] proposed several properties of a VES to achieve a modular analysis for it. Rückert and Schröder [48, 49] defined key-independence and extractability of a VES to prove its unforgeability and collusion-resistance. Key-independence means that a VES creation algorithm consists of a signature generation part and a transformation (into a VES) part and they are independent. Extractability means that if VES $\omega$ is valid, then the adjudicator can extract a valid (ordinary) signature $\sigma$ except with negligible probability. Collusion-resistance means that no adversary can forge a VES even if the adjudicator is corrupted, i.e., the adversary obtains the secret decryption key of the adjudicator. Formal definitions are as follows.

Definition 11

(Key-Independence of VES [48]) Let a signer’s private key $sk$ consist of two independent elements $sk = (kisk,ssk)$ and let $vk = (kivk,svk)$ be the corresponding verification key pair. A VES scheme is key-independent if there exists an efficient (encryption) algorithm ${\mathsf {KIEnc}}$ such that the distribution of ${\mathsf {KIEnc}}(apk,kivk,kisk,\mathsf {Sign}(ssk,M),M)$ is perfectly indistinguishable from that of $\mathsf {Create}(sk,apk,M)$ for all $M\in \mathcal {M}_{vk}$.

Definition 12

(Extractability of VES [48]) Experiment ${\mathsf {Extract}}_{\mathcal {A}}^{\mathsf {ves}}$ is as follows.

A VES scheme is extractable if for any PPT $\mathcal {A}$, $\Pr [{\mathsf {Extract}}_{\mathcal {A}}^{\mathsf {ves}}(\lambda ) \rightarrow 1]$ is negligible in $\lambda$.

Definition 13

(Collusion-Resistance [48, 49]) Experiment ${\mathsf {Collusion}}_{\mathcal {A}}^{\mathsf {ves}}$ is as follows.

A VES scheme is collusion-resistant if for any PPT $\mathcal {A}$, $\Pr [{\mathsf {Collusion}}_{\mathcal {A}}^{\mathsf {ves}}(\lambda ) \rightarrow 1]$ is negligible in $\lambda$.

Rückert and Schröder [48] called this notion “abuse-freeness”, but later Rückert, Schneider, and Schröder [49] renamed it “collusion-resistance” to avoid confusion. If $\mathcal {A}$ is allowed to select the public key in the above game, then we call it strong collusion-resistance.

Rückert and Schröder showed the following theorems.

Theorem 2

([48]) Let a VES scheme be an extractable and key-independent verifiably encrypted signature scheme. The VES scheme is unforgeable if and only if the underlying signature scheme is unforgeable.

Theorem 3

([48]) A key-independent, extractable, and secure VES scheme is collusion-resistance if the underlying signature scheme is unforgeable.

In fact, we can prove strong collusion-resistance in the above theorem since adversaries cannot forge VESs due to the unforgeability of underlying signature schemes even if an adjudicator public key is adversarially selected. Dodis, Lee, and Yum consider strong collusion-resistance (though they did not use the name) to construct optimistic fair exchange protocols [28], thus our VES scheme can be used to construct optimistic fair exchange protocols.

3 Strongly unforgeable Waters’ dual signature

In this section, we propose a strongly secure version of Waters’ dual signature scheme since we use it as a building block of our VES scheme.

Waters’ dual signature scheme. We review a signature scheme proposed by Waters [53] since we use it as an essential building block. However, we add a few minor changes to fit the scheme to our VES scheme. We explain the differences between the original scheme and ours.

• $\mathsf {Wd.Gen}(1^{\lambda },\varGamma )$: On input security parameter $\lambda$ and $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},e, g) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$ (hereafter we often omit input $1^{\lambda }$), it selects generators $v,v_1,v_2,w,u,h \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$ and exponents $a_1,a_2,b,\alpha \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, computes $\tau _1 :=v v_{1}^{a_1}, \tau _2 :=v v_{2}^{a_2}$, and outputs

  $$\begin{aligned} VK&:=(\varGamma ,g^b,g^{a_1},g^{a_2},g^{b a_1},g^{b a_2},v,v_1,v_2,\tau _1,\tau _2, \tau _{1}^{b},\tau _{2}^{b},w,u,h,e(g,g)^{\alpha a_{1}b}) \\ SK&:=(VK,g^{\alpha },g^{\alpha a_{1}},g^{a_1 a_2}). \end{aligned}$$

• $\mathsf {Wd.Sign}(SK,M)$: On input message $M\in \mathbb {Z}_{p}$, it selects $r_1, r_2, z_1, z_2, \gamma ,\mathsf {stag}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, sets $r :=r_1 + r_2$, computes

  

  and outputs $\mathsf {sig}:=(\sigma _0,\sigma _1 ,\ldots , \sigma _{7}, \mathsf {stag})$.

• $\mathsf {Wd.Vrfy}(VK,\mathsf {sig}, M)$: On input $VK,M$, and $\mathsf {sig}$, it outputs $1$ if and only if it holds that

  $$\begin{aligned} e( u^{M} w^{\mathsf {stag}} h,\sigma _7)&= e(g, \sigma _0) \\ e(g^b,\sigma _1)\, e(g^{b a_{1}},\sigma _2) e( g^{ a_{1}},\sigma _3)&= e(\tau _1,\sigma _6)\, e(\tau _{1}^{b},\sigma _7) \\ e(g^{b},\sigma _1)\, e(g^{b a_{2}},\sigma _4)\, e(g^{a_{2}},\sigma _5)&= e(\tau _2,\sigma _6)\, e(\tau _{2}^{b},\sigma _7)\, e(g,g)^{\alpha a_{1} b}. \end{aligned}$$

The differences from the original scheme are as follows. In original Waters’ dual signature scheme,

• 1. The verification equation is only one equation and probabilistic.

• 2. Values $v,v_1,v_2$ are included in secret keys.

• 3. Value $g^{a_1 a_2}$ is not included in the signing key.

• 4. The (normal) signing algorithm does not multiply $g^{-a_{1} a_{2} \gamma }$, $g^{a_{2} \gamma }$, $g^{a_{1}\gamma }$ in $\sigma _{1}$, $\sigma _{2}$, $\sigma _{4}$, respectively, that is, the signing algorithm outputs Type A signatures, as explained below.

First, note that there are two types of signatures in Waters’ dual signature scheme, type A (if $\gamma = 0$) and Type B (if $\gamma \ne 0$). Both types are valid signatures. The modified verification equations were introduced by Abe et al. [1]. They proved that if a signature passes the equations, then the signature is either Type A or B, so we use the modified equations.

The original verification equations use ciphertexts and the decryption procedure of Waters’ dual encryption scheme, so it is probabilistic and has a semi-functional verification algorithm that uses semi-functional ciphertexts [53]. Type A signatures are signatures with $\gamma = 0$ and pass both the normal and semi-functional verification equations. Type B signatures are signatures with $\gamma \ne 0$ and cannot pass the semi-functional verification equations.

As long as the verification equations are normal, both Type A and Type B signatures are valid signatures and there is no essential difference. Thus, we use Type B signatures in the normal signing algorithm.

Even if $v,v_1,v_2$ are disclosed, the adversary cannot compute $v_{2}^{b}$ (and semi-functional ciphertexts of Waters’ dual system encryption [53]). Thus, we add $(v,v_1,v_2)$ to the verification key, which does not affect its security since $g^{\alpha }$ and $g^{\alpha a_1}$ (and $v_{2}^b$) are kept secret and are essential secret signing keys. This was observed by Abe et al. [1].

For the slightly changed version above, the following theorem holds.

Theorem 4

([53]) If the DLIN assumption holds, then $\mathsf {WdSig} :=\mathsf {Wd.}\{\mathsf {Gen},\mathsf {Sign}{},\mathsf {Vrfy}{} \}$ is existentially unforgeable against adaptive chosen message attacks.

Waters proposed the signature scheme at CRYPTO’09, but he presented only an outline of the proof and did not write a full proof. We present a full proof for confirmation since we slightly modified the scheme as explained above.

Proof

There are two types of signature in Waters’ dual signature scheme [53].

• Type A: $\gamma = 0$ for $( \sigma _{0},\sigma _1 ,\ldots ,\sigma _7, \mathsf {stag}) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Wd.Sign}(SK,M)$.

• Type B: $\gamma \ne 0$. We can generate a Type B signature if we have the secret key and $g^{a_{1}a_{2}}$.

Both types of signatures pass the verification algorithm (we can check this by simple calculation). Type B signatures correspond to semi-functional private keys of the dual system encryption [53]. We can use the following lemma proved by Abe et al. in this proof.

Lemma 1

([1]) Any signature that is accepted by the verification algorithm must be formed either as a Type A or Type B signature.

To show that Waters’ dual signature scheme satisfies unforgeability, we introduce the following games.

• 1. We denote a game where the signing oracle answers Type A signatures for all signing queries by $\mathsf {Game}\mathrm - {0}$. If adversary $\mathcal {A}$ outputs a forgery of a Type B signature, then we can construct algorithm $\mathcal {B}_{1}$ (simulator for $\mathcal {A}$), which solves the DLIN problem (Lemma 2). In this case, $\mathcal {B}_{1}$ generates a Type A signature for simulation of the signing oracle. Thus, in the following games, we consider adversary $\mathcal {A}$ which outputs a forgery of a Type A signature only.

• 2. We consider $\mathsf {Game}\mathrm - {i}$ where the signing oracle returns a Type B signature for the first $i$ signing queries and Type A signature for the remaining $q-i$ queries ($i \in [q]$). If $\mathcal {A}$ detects the change (from Type A to Type B answer), we can construct algorithm $\mathcal {B}$ (simulator for $\mathcal {A}$) that solves the DLIN problem (Lemma 3). Thus, we can return a Type B signature for all signing queries in $\mathsf {Game}\mathrm - {q}$.

• 3. Now, all answers for signing queries of $\mathcal {A}$ are Type B signatures. We show that $\mathcal {A}$ cannot forge a Type A signature in this game ($\mathsf {Game}\mathrm - {q}$). If $\mathcal {A}$ outputs a forgery of a Type A signature, then we can construct algorithm $\mathcal {B}_{2}$ that solves the CDH problem (Lemma 4). Thus, if the DLIN assumption holds, the signature scheme is unforgeable (the CDH assumption is implied by the DLIN assumption).

We can reverse the order of the game transitions, so we can use either type of signatures as a signature generated by a normal signing algorithm. We denote $\mathsf {Adv}_{i}^{\mathsf {Type} \text{- } \mathsf {A}}$ as the advantage of the adversary which outputs a Type A forgery in $\mathsf {Game}\mathrm - {i}$ (similarly $\mathsf {Adv}_{i}^{\mathsf {Type} \text{- } \mathsf {B}}$). It holds that

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {euf}\mathrm - \mathsf {cma}}(\lambda )&= \mathsf {Adv}_{0}^{\mathsf {Type} \text{- } \mathsf {A}} + \mathsf {Adv}_{0}^{\mathsf {Type} \text{- } \mathsf {B}} \\&\le \mathsf {Adv}_{0}^{\mathsf {Type} \text{- } \mathsf {A}} + \mathsf {Adv}_{\mathcal {B}_{1}}^{\mathsf {DLIN}} \\&\le q \mathsf {Adv}_{\mathcal {B}}^{\mathsf {DLIN}} + \mathsf {Adv}_{q}^{\mathsf {Type} \text{- } \mathsf {A}} + \mathsf {Adv}_{\mathcal {B}_{1}}^{\mathsf {DLIN}} \\&\le q \mathsf {Adv}_{\mathcal {B}}^{\mathsf {DLIN}} + \mathsf {Adv}_{\mathcal {B}_{2}}^{\mathsf {CDH}} + \mathsf {Adv}_{\mathcal {B}_{1}}^{\mathsf {DLIN}} \end{aligned}$$

by Lemmas 2, 3, and 4.$\square$

Lemma 2

If there exists adversary $\mathcal {A}$ that outputs a Type B forgery, then we can construct algorithm $\mathcal {B}_{1}$ that solves the DLIN problem.

Proof of lemma

Algorithm $\mathcal {B}_1$ is given instance $(\varGamma ,g,f=g^{a_1},\nu = g^{a_2},g^x,f^y,T)$ of the DLIN problem and simulates the verification key and the signing oracle for the signature scheme ($\mathcal {B}_1$ does not have value $a_{1},a_{2},x,y$).

$\mathcal {B}_1$ generates the verification key as follows. It selects exponents $b,\alpha ,y_v,y_{v_{1}},y_{v_{2}} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$ and generators $u,w,h \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, computes

and sets $VK :=(\varGamma ,g^b,f,\nu ,f^b,\nu ^b,\tau _{1},\tau _{2},\tau _{1}^{b},\tau _{2}^{b},w,u,h,e(g,f)^{\alpha b})$ and $SK :=(VK,g^{\alpha }, f^{\alpha },v,v_{1},v_{2})$. $\mathcal {B}_1$ can generate Type A signatures by using the (normal) signing algorithm since $\mathcal {B}_1$ has $\alpha$ and $g^{a_1}$.

If adversary $\mathcal {A}$ outputs a Type B forgery $\sigma _1 :=(g^{\alpha a_1}v^r)\cdot g^{-a_{1}a_{2}\gamma }$, $\sigma _2 :=(g^{-\alpha }v_{1}^{r}g^{z_1})\cdot g^{a_{2}\gamma }$, $\sigma _3 :=(g^b)^{-z_1}$, $\sigma _4 :=(v_{2}^{r}g^{z_2})\cdot g^{a_{1}\gamma }$, $\sigma _5 :=(g^b)^{-z_2}$, $\sigma _6 :=(g^b)^{r_2}$, $\sigma _7 :=g^{r_1}$, and $\sigma _{0} :=(u^{M}w^{\mathsf {stag}}h)^{r_1}$ for some $r_1,r_2,z_1,z_2,\gamma \in \mathbb {Z}_{p}$ ($r = r_1 + r_2$), then $\mathcal {B}_1$ can compute $(g^{-a_{1}a_{2}\gamma },g^{a_{1}\gamma },g^{a_{2}\gamma })$ from $\sigma _1,\sigma _4,\sigma _2$, respectively. The reason is as follows.

$\mathcal {B}_1$ has $b$, so can compute $g^{z_{1}}$, $g^{z_{2}}$, $g^{r_{1}}$, $g^{r_{2}}$ from $\sigma _3 = g^{-b z_{1}}$, $\sigma _5 = g^{-b z_{2}}$, $\sigma _7 = g^{r_{1}}$, $\sigma _6 = g^{b r_{2}}$, respectively, and obtains $g^r = g^{r_{1}+r_{2}}$, $v^r = g^{r y_{v}}$, $v_{1}^{r} = g^{r y_{v_1}}$, $v_{2}^{r} = g^{r y_{v_2}}$ ($\mathcal {B}_1$ has $y_v,y_{v_1},y_{v_2}$). Thus, $\mathcal {B}_1$ can extract $(g^{-a_{1}a_{2}\gamma },g^{a_{1}\gamma },g^{a_{2}\gamma })$ from $\sigma _1,\sigma _2,\sigma _4$ and solve the DLIN problem by checking whether $e(g^x , g^{-a_{1}a_{2}\gamma })^{-1} \cdot e(f^y,g^{a_{2}\gamma }) = e(g^{a_{1}\gamma },T)$ because $e(g^x , g^{-a_{1}a_{2}\gamma })^{-1} \cdot e(g^{a_{1}y},g^{a_{2}\gamma }) = e(g,g)^{a_{1}a_{2}\gamma x + a_{1}a_{2}\gamma y} = e(g,g)^{a_{1}a_{2}\gamma (x+y)}$. If $T= g^{a_{2}(x+y)} = \nu ^{x+y}$, then the equation holds. Thus, $\mathcal {B}_1$ can solve the DLIN problem if the adversary outputs a Type B forgery. $\square$

Lemma 3

If there exists adversary $\mathcal {A}$ that makes at most $q$ queries and it holds that for some $k \in [q]$, $\left| \mathsf {Adv}_{k-1}^{\mathsf {Type} \text{- } \mathsf {A}} - \mathsf {Adv}_{k}^{\mathsf {Type} \text{- } \mathsf {A}}\right| = \varepsilon$, then we can construct algorithm $\mathcal {B}$ that solves the DLIN problem with advantage $\varepsilon$.

Proof of lemma

$\mathcal {B}$ is given instance $(\Gamma ,g,f=g^b,\nu ,g^x,f^y,T)$ of the DLIN problem. $\mathcal {B}$ generates the verification key as follows. It selects exponents $\alpha ,a_{1},a_{2},y_{v_1},y_{v_2},y_{w},y_{u},y_{h}, A, B \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, computes

and $e(g,g)^{\alpha a_{1}b} :=e(f,g)^{\alpha a_{1}}$, and sets $VK :=(\varGamma ,f,g^{a_1},g^{a_2},f^{a_1},f^{a_2},v,v_1,v_2,\tau _{1},\tau _{2},\tau _{1}^{b},\tau _{2}^{b},w,u,h,e(f,g)^{\alpha a_1})$ and $SK :=(VK,g^{\alpha },g^{\alpha a_1})$. $\mathcal {B}$ has $g^{a_1 a_2}$ since it has $(a_1,a_2)$. Thus, $\mathcal {B}$ can generate Type B signatures.

We define $\mathcal {F}(M) :=AM + B$. If $\mathsf {vtag}:=\mathcal {F}(M)$, then it holds $(u^M w^{\mathsf {vtag}}h) = f^{\mathsf {vtag}-AM-B}\cdot g^{My_{u} + \mathsf {vtag}y_{w}+ y_{h}} = g^{My_{u} + \mathsf {vtag}y_{w}+ y_{h}}$.

$\mathcal {B}$ answers signing queries as follows. For the $i$-th signing query,

• Case $i>k$: Returns Type A signatures by using $SK = (VK,g^{\alpha },g^{\alpha a_1})$.

• Case $i<k$: Returns Type B signatures by using $SK$ and $g^{a_1 a_2}$.

• Case $i=k$: Embeds the instance as follows. For the $k$-th query $M$, $\mathcal {B}$ first generates a Type A signature $(\sigma _{1}^{\prime },\sigma _{2}^{\prime },\sigma _{3}^{\prime },\sigma _{4}^{\prime },\sigma _{5}^{\prime },\sigma _{6}^{\prime }, \sigma _{7}^{\prime },\sigma _{0}^{\prime })$ by using tag $\mathsf {stag}:=\mathcal {F}(M)$ (with randomness $r_{1}^{\prime },r_{2}^{\prime },z_{1}^{\prime },z_{2}^{\prime } \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, $r^{\prime } :=r_{1}^{\prime } + r_{2}^{\prime }$). Next, it computes

  

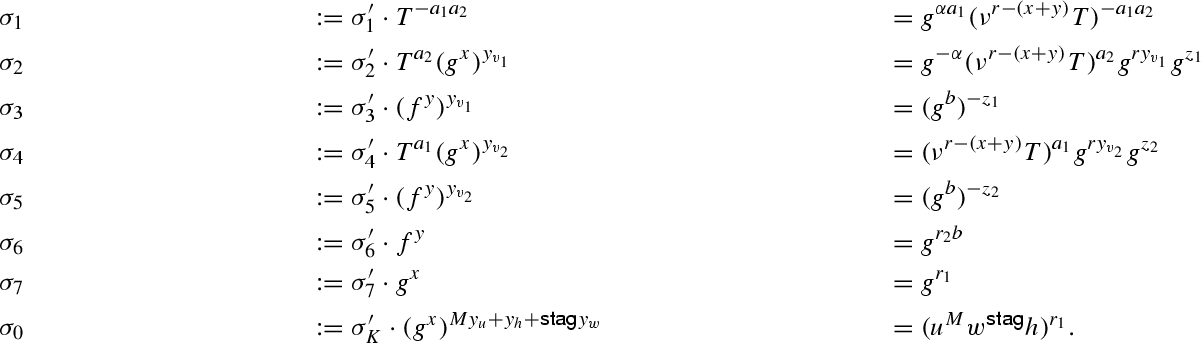
  In this case, it implicitly holds that $z_{1} :=z_{1}^{\prime } - y_{v_1}y$, $z_{2} :=z_{2}^{\prime } - y_{v_2}y$, $r_{1} :=r_{1}^{\prime } + x$, $r_{2} :=r_{2}^{\prime } + y$. $\mathcal {B}$ can generate $\sigma _K$ correctly since $\mathcal {B}$ set $\mathsf {stag}:=\mathcal {F}(M)$.

• If $T = \nu ^{x + y}$, the above signature is a Type A with randomness $r_{1} :=r_{1}^{\prime } + x$, $r_{2} :=r_{2}^{\prime } + y$.

• If $T \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, the above signature is a Type B since $T =\nu ^{x + y}g^{\gamma }$ for some $\gamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$.

At some point, $\mathcal {A}$ outputs a signature $\sigma ^{*} = (\sigma _{0}^{*},\ldots , \sigma _{7}^{*},\mathsf {stag}^{*})$ and message $M^{*}$. $\mathcal {B}_{2}$ verifies

$$\begin{aligned}&e(\sigma _{0}^{*}, \nu ) e(\nu ^{\mathsf {stag}^{*} - A M^* -B},\sigma _{6}^{*}) \\&\quad = e((\sigma _{1}^{*}/ g^{\alpha a_{1}} )^{- \frac{1}{a_{1}a_{2}}}, f^{\mathsf {stag}^{*} - A M^* -B}) e(\sigma _{7}^{*},\nu ^{M^* y_{u} + \mathsf {stag}^{*} y_{w} + y_{h}}). \end{aligned}$$

It holds that $\sigma _{0}^{*} = (f^{\mathsf {stag}^{*} - A M^* - B} g^{M^* y_{u} + \mathsf {stag}^{*}y_{w} + y_{h}})^{r_{1}^{*}}$, $\sigma _{1}^{*} = g^{\alpha a_{1}} \nu ^{- a_{1}a_{2} r^{*}}g^{- a_{1}a_{2}\gamma ^{*}}$, $\sigma _{6}^{*} = g^{b r_{2}^{*}}$, and $\sigma _{7}^{*} = g^{r_{1}^{*}}$. Thus, the left-hand side is

$$\begin{aligned} e(f,\nu )^{r_{1}^{*} (\mathsf {stag}^{*} - A M^* -B)} e(g,\nu )^{r_{1}^{*} (M^* y_{u} + \mathsf {stag}^{*}y_{w} + y_{h})} e(\nu ,f)^{r_{2}^{*}(\mathsf {stag}^{*} - A M^* -B )}, \end{aligned}$$

and the right-hand side is

$$\begin{aligned} e(\nu ,f)^{{r}^{*} (\mathsf {stag}^{*} - A M^* -B)} e(g,f)^{\gamma ^{*} (\mathsf {stag}^{*} - A M^* -B)} e(g,\nu )^{r_{1}^{*}(M^* y_{u} + \mathsf {stag}^{*}y_{w} + y_{h} )}. \end{aligned}$$

A simplified equation is

$$\begin{aligned} 1 = e(g,f)^{\gamma ^{*}(\mathsf {stag}^{*} - A M^* - B)}. \end{aligned}$$

It holds that $\mathsf {stag}^{*} \ne A M^* + B$ without negligible probability because $M^{*} \ne M_{i}$ for all $i \in [q]$ and $A$ and $B$ are information theoretically hidden from the adversary.

If signature $\sigma ^{*}$ is Type A, then the above equation holds and $\mathcal {B}_{2}$ outputs $1$. On the other hand, if $\sigma ^{*}$ is Type B, then it does not hold and $\mathcal {B}_{2}$ outputs $0$.

Thus, if $\mathcal {A}$ can distinguish the two games, then $\mathcal {B}_{2}$ can solve the DLIN problem with the same advantage. $\square$

Lemma 4

If there exists adversary $\mathcal {A}$ that outputs a Type A forgery when all answers to signing queries are Type B signatures, then we can construct algorithm $\mathcal {B}_2$ that solves the CDH problem.

Proof of lemma

$\mathcal {B}_2$ is given instance $(\varGamma ,g,g^x,g^y)$ of the CDH problem. $\mathcal {B}_2$ generates the verification key as follows. It selects exponents $a_1,b,y_v,y_{v_1},y_{v_2},y_w,y_h,y_u \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, computes

and $e(g,g)^{\alpha a_{1}b} :=e(g^x,g^y)^{a_{1}\cdot b}$ (it implicitly holds $\alpha = x y$ though $\mathcal {B}_2$ does not have $\alpha$), and sets $VK :=(\varGamma ,g^b,g^{a_1},g^{a_2},g^{b a_{1}},g^{b a_{2}},\tau _1,\tau _2,\tau _{1}^{b},\tau _{2}^{b},w,u,h,e(g,g)^{\alpha a_{1}b})$. Note that $\mathcal {B}_2$ does not have $g^{\alpha } = g^{x y}$, so $\mathcal {B}_2$ cannot compute a Type A signature. $\mathcal {B}_2$ outputs Type B signatures for signing query $M$ as follows. It selects $r_1,r_2,z_1,z_2,\gamma ^{\prime },\mathsf {stag}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, sets $r :=r_1 + r_2$ (we want to set $\gamma :=x + \gamma ^{\prime }$), computes

and outputs signature $(\sigma _1,\ldots , \sigma _{0},\mathsf {stag})$ for $M$.

At some point, $\mathcal {A}$ outputs a Type A forgery, $\sigma _{1}^{*} = g^{\alpha a_1}v^{r_{1}^{*}}$, $\sigma _{2}^{*} = g^{-\alpha }v_{1}^{r^{*}}g^{z_{1}^{*}}$, $\sigma _{3}^{*} = (g^b)^{-z_{1}^{*}}$, $\sigma _{4}^{*} = v_{2}^{r^{*}}g^{z_{2}^{*}}$, $\sigma _{5}^{*} = (g^b)^{-z_{2}^{*}}$, $\sigma _{6}^{*} = g^{r_{2}^{*}b}$, $\sigma _{7}^{*} = g^{r_{1}^{*}}$, and $\sigma _{0}^{*} = (u^{M^{*}}w^{\mathsf {stag}^{*}}h)^{r_{1}^{*}}$ for some $r_{1}^{*},r_{2}^{*},z_{1}^{*},z_{2}^{*},\mathsf {stag}^{*} \in \mathbb {Z}_{p}$.

By using these values, $\mathcal {B}_2$ can compute $g^{r_{2}^{*}} = (\sigma _{6}^{*})^{1/b}$, $g^{r_{1}^{*}} = \sigma _{7}^{*}$, $g^{z_{1}^{*}}= (\sigma _{3}^{*})^{-1/b}$, $v_{1}^{r^{*}} = (g^{r_{1}^{*}}\cdot g^{r_{2}^{*}})^{y_{v_1}}$ since $v_1 = g^{y_{v_1}}$. Thus, $\mathcal {B}_2$ can compute $g^{z_{1}^{*}}\cdot v_{1}^{r^{*}}/\sigma _{2}^{*} = g^{\alpha } = g^{x y}$. That is, $\mathcal {B}_2$ can solve the CDH problem.$\square$

Original Waters’ dual signature is not strongly unforgeable since it is re-randomizable. “Strong” means that the adversary cannot forge a signature even for a queried message to the signing oracle. To make our VES scheme satisfy opacity, we extend the technique by Boneh, Shen, and Waters [11] and modify Waters’ dual signature. They introduced a property called $2$-partitioned to convert unforgeable signature schemes into strongly unforgeable signature schemes. We extend $2$-partitioned to $3$-partitioned.

Definition 14

A signature scheme is $3$-partitioned if it satisfies the following two properties.

• The signing algorithm consists of three deterministic algorithms $F_1$, $F_2$, and $F_3$.

  • 1. It selects random $R \in \mathcal {R}$ ($\mathcal {R}$ is a space for randomness).

  • 2. It computes $\varSigma _1 :=F_{1}(M,R,VK)$, $\varSigma _2 :=F_{2} (R,VK)$, $\varSigma _3 :=F_{3}(R,SK)$.

  • 3. It outputs signature $\sigma :=(\varSigma _1,\varSigma _2,\varSigma _3)$.

• Given $M$ and $\varSigma _2$, there is at most one $(\varSigma _1, \varSigma _3)$ such that $(\varSigma _1,\varSigma _2,\varSigma _3)$ is a valid signature on $M$ under $VK$.

A $2$-partitioned signature is $\sigma = (\varSigma ^{\prime }_{1},\varSigma ^{\prime }_{2})$ where $\varSigma ^{\prime }_{1} = F^{\prime }_{1}(M,R,SK)$ and $\varSigma ^{\prime }_{2} = F^{\prime }_{2}(R,SK)$ [11]. Value $\varSigma ^{\prime }_{2}$ binds all randomness $R$, so $M$ and $R$ fully determine $\varSigma ^{\prime }_{1}$. For a VES, signature elements related to the secret signing key (i.e., $\varSigma _{3}$) should be encrypted, so we cannot use such elements as inputs to hash functions (we will use hash functions to obtain strongly secure signature) and want to isolate the secret signing key from $\varSigma ^{\prime }_{2}$. Otherwise, encrypted signatures are not verifiable. If $\varSigma _{3}$ is not used as an input of a hash function, then hash values are not changed even if $\varSigma _{3}$ is encrypted. This is the reason we introduced $3$-partitioned and $\varSigma _{1}$ and $\varSigma _{2}$ do not depend on the secret signing key.

Let $\varPi :=(\mathsf {Gen},\mathsf {Sign},\mathsf {Vrfy})$ be an existentially unforgeable signature scheme. The new signature scheme $\varPi ^{\prime } :=(\mathsf {Gen}^{\prime },\mathsf {Sign}^{\prime },\mathsf {Vrfy}^{\prime })$ is as follows.

• $\mathsf {Gen}^{\prime }(1^{\lambda })$: It generates $(VK,SK) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(1^{\lambda })$, selects $\bar{h} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$ and random hash key $k\in \mathcal {K}$, and sets $(VK^{\prime },SK^{\prime }) :=((VK,\bar{h},k),SK)$.

• $\mathsf {Sign}^{\prime } (SK^{\prime },M)$: On input message $M\in \{0,1\}^{\ell }$, it selects exponent $\varphi \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$ and randomness $R\in \mathcal {R}$, computes

  

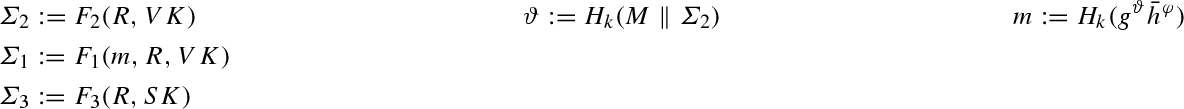
  (we consider $\vartheta$ as an element in $\mathbb {Z}_p$), and outputs $\mathsf {sig}:=(\varSigma _1 ,\varSigma _{2},\varSigma _{3},\varphi )$ as a signature.

• $\mathsf {Vrfy}^{\prime }(VK^{\prime },\mathsf {sig}, M)$: On input $VK^{\prime },M$, and signature $\mathsf {sig}= (\varSigma _1,\varSigma _2,\varSigma _3,\varphi )$, it computes $\vartheta ^{\prime } :=H_{k}(M \parallel \varSigma _2)$ (view $\vartheta ^{\prime }$ as an element in $\mathbb {Z}_p$), $m^{\prime } :=H_{k} (g^{\vartheta ^{\prime }} \bar{h}^{\varphi })$, It outputs $1$ if and only if $\mathsf {Vrfy}(VK,(\varSigma _1,\varSigma _2,\varSigma _3), m^{\prime }) \rightarrow 1$.

Theorem 5

Signature scheme $\varPi ^{\prime }$ is strongly existentially unforgeable if $\varPi$ is existentially unforgeable, the DL assumption holds in $\mathbb {G}$, and $H$ is collision-resistant. Specifically,

$$\begin{aligned} \mathsf {Adv}_{\mathcal {F}^{\prime }}^{\mathsf {seuf}\mathrm - \mathsf {cma}} \le \frac{1}{3}\mathsf {Adv}_{\mathcal {F}}^{\mathsf {euf}\mathrm - \mathsf {cma}} + \frac{1}{3}\mathsf {Adv}_{\mathcal {B}}^{\mathsf {dl}} + \frac{1}{3}\mathsf {Adv}_{\mathcal {C}}^{\mathsf {crhf}}. \end{aligned}$$

This is easily proved by extending the proof of Boneh et al. [11]. The essential point is that given message $M$ and partial signature $\varSigma _2$, the randomness that is used to generate the whole signature is determined and there is at most one $(\varSigma _1, \varSigma _3)$ such that $(\varSigma _1,\varSigma _2,\varSigma _3)$ is a valid signature on $M$ under $VK$. Intuitively, in the construction of $\varPi ^{\prime }$, we sign not only message $M$ but also randomness $R$ to bind the randomness and prevent re-randomization. Moreover, to prevent message $m$, which will be signed depending on randomness $R$, new randomness $\varphi$ is introduced and chameleon hash functions, $g^{\vartheta }\bar{h}^{\varphi }$, are used.

Proof

We assume that there is adversary $\mathcal {A}$ that breaks strong unforgeability of $\varPi ^{\prime }$. $\mathcal {A}$ is given $(VK,g,\bar{h},k)$, queries $M_1,\ldots ,M_{q}$, and obtains $(\varSigma _{i,1},\varSigma _{i,2},\varSigma _{i,3},\varphi _{i})$ for $i = 1,\ldots ,q$, $\vartheta _{i} :=H_{k}(M_{i}\parallel \varSigma _{i,2})$ and $m_{i} :=H_{k}(g^{\vartheta _{i}}\bar{h}^{\varphi _{i}})$. At some point, $\mathcal {A}$ outputs forgery $(M^{*},(\varSigma _{1}^{*},\varSigma _{2}^{*},\varSigma _{3}^{*},\varphi ^{*}))$ such that $\vartheta ^{*} :=H_{k} (M^{*}\parallel \varSigma _{2}^{*})$ and $m^{*} :=H_{k}(g^{\vartheta ^{*}}\bar{h}^{\varphi ^{*}})$. The forgery is one of the following three types.

• Type 1: For some $i \in [q]$, $m^{*} = m_{i}$ and $\vartheta ^{*}= \vartheta _{i}$.

• Type 2: For some $i \in [q]$, $m^{*} = m_{i}$ and $\vartheta ^{*} \ne \vartheta _{i}$.

• Type 3: For all $i \in [q]$, $m^{*} \ne m_{i}$.

Type 1 breaks the collision-resistance of the hash function, Type 2 breaks the DL assumption, and Type 3 breaks the existential unforgeability of the underlying signature scheme $\Pi$. We construct a simulator that breaks the one of them by using $\mathcal {A}$. First, we randomly guess which type of forgery $\mathcal {A}$ outputs.

Type 1 case. If $\mathcal {A}$ is a Type 1 forger, then we can construct algorithm $\mathcal {B}$ that breaks the collision-resistance of $\mathcal {H}$. $\mathcal {B}$ is given random key $k$, generates $(VK,SK) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(1^{\lambda })$, selects $g,\bar{h} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, and gives $(VK,g,\bar{h},k)$ to $\mathcal {A}$. If $\mathcal {A}$ queries $M_{i}$, then $\mathcal {B}$ generates $\mathsf {sig}_{i} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Sign}^{\prime }(SK,M_{i})$ and returns $\mathsf {sig}_{i}$. If $\mathcal {A}$ outputs $(M^{*},\mathsf {sig}^{*} :=(\varSigma _{1}^{*},\varSigma _{2}^{*},\varSigma _{3}^{*}))$ such that $(M^{*},\mathsf {sig}^{*}) \notin \{(M_{1},\mathsf {sig}_{1}),\ldots , (M_{q},\mathsf {sig}_{q})\}$, $m^{*} = m_{i}$, and $\vartheta ^{*} = \vartheta _{i}$ for some $i \in [q]$, then $\mathcal {B}$ outputs $(M^{*}\parallel \varSigma _{2}^{*}, M_{i}\parallel \varSigma _{i,2})$ as a collision on $H_{k}$. $\vartheta ^{*}= \vartheta _{i}$ means that $H_{k}(M^{*}\parallel \varSigma _{2}^{*}) = H_{k}(M_{i}\parallel \varSigma _{i,2})$ and $m^{*} = m_{i}$ means that $H_{k}(g^{\vartheta ^{*}} \bar{h}^{\varphi ^{*}}) = H_{k}(g^{\vartheta _{i}} \bar{h}^{\varphi _{i}})$ If $M^{*}\parallel \varSigma _{2}^{*} \ne M_{i}\parallel \varSigma _{i,2}$, then the output of $\mathcal {B}$ is a valid collision. Assume that $M^{*} = M_{i}$ and $\varSigma _{2}^{*} = \varSigma _{i,2}$ for a contradiction. If $\varphi ^{*} \ne \varphi _{i}$, then $\mathcal {B}$ outputs $(g^{\vartheta ^{*}} \bar{h}^{\varphi ^{*}},g^{\vartheta _{i}} \bar{h}^{\varphi _{i}})$ as a collision on $H_{k}$ since $\vartheta ^* =\vartheta _i$ in this case. Else if it holds that $\varphi ^{*} = \varphi _{i}$, then $m^{*} = m_{i}$ since $\vartheta ^{*} = \vartheta _{i}$. Due to the second property of 3-partitioned signatures $m^{*} = m_{i}$ and $\varSigma _{2}^{*} = \varSigma _{i,2}$ implies that $\varSigma _{1}^{*} = \varSigma _{i,1}$ and $\varSigma _{3}^{*} = \varSigma _{i,3}$. Such $(M^{*},(\varSigma _{1}^{*},\varSigma _{2}^{*},\varSigma _{3}^{*}))$ is not a valid forgery of $\Pi ^{\prime }$. Thus, it should hold that $M^{*}\parallel \varSigma _{2}^{*} \ne M_{i}\parallel \varSigma _{i,2}$ and $\mathcal {B}$ can output a valid collision.

Type 2 case. If $\mathcal {A}$ is a Type 2 forger, then we can construct algorithm $\mathcal {B}$ that breaks the DL assumption. $\mathcal {B}$ is given $(g,\bar{h})$ (Implicitly it holds $\bar{h} = g^{\eta }$), generates $(VK,SK) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(1^{\lambda })$, selects random $k \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {K}$, and gives $(VK,g,\bar{h},k)$ to $\mathcal {A}$. If $\mathcal {A}$ queries $M_{i}$, then $\mathcal {B}$ generates $\mathsf {sig}_{i} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Sign}(SK,M_{i})$ and returns $\mathsf {sig}_{i}$. If $\mathcal {A}$ outputs $(M^{*},\mathsf {sig}^{*}= (\varSigma _{1}^{*},\varSigma _{2}^{*},\varSigma _{3}^{*}))$ such that $H_{k} (g^{\vartheta ^{*}}\bar{h}^{\varphi ^{*}}) = H_{k}( g^{\vartheta _{i}}\bar{h}^{\varphi _{i}})$ and $\vartheta ^{*} \ne \vartheta _{i}$ for some $i \in [q]$, then it holds that $H_{k}(g^{\vartheta ^{*}}(g^{\eta })^{\varphi ^{*}}) = H_{k}( g^{\vartheta _{i}}(g^{\eta })^{\varphi _{i}})$. $\mathcal {B}$ computes $\eta :=(\vartheta _{i} - \vartheta ^{*})/(\varphi ^{*} - \varphi _{i})$ and outputs it as a solution of the DL problem. It holds that $\varphi ^{*} \ne \varphi _{i}$ since if $\varphi ^{*} = \varphi _{i}$ (here, we assume that $\vartheta ^{*} \ne \vartheta _{i}$), then we can output $(g^{\vartheta ^{*}}\bar{h}^{\varphi ^{*}},g^{\vartheta _{i}}\bar{h}^{\varphi _{i}})$ as a collision of $H_{k}$. Thus, $\eta$ is a valid solution.

Type 3 case. If $\mathcal {A}$ is a Type 3 forger, then we can construct algorithm $\mathcal {B}$ that breaks the unforgeability of $\Pi$. $\mathcal {B}$ is given $VK$, selects generator $g \in \mathbb {G}$, exponent $\eta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, random key $k \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {K}$, and sets $\bar{h} :=g^{\eta }$. It gives $(VK,g,\bar{h},k)$ to $\mathcal {A}$ as a verification key. If $\mathcal {A}$ queries $M_{i}$, then $\mathcal {B}$ selects $w \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, sets $m_{i} :=H_{k}(g^{w})$, queries $m_{i}$ to the signing oracle of $\Pi$, and obtains signature $\mathsf {sig}_{i} = (\varSigma _1,\varSigma _2, \varSigma _3)$. It computes $\vartheta _{i} :=H_{k}(M_{i}\parallel \varSigma _2)$, sets $\varphi _{i} :=(w - \vartheta _{i})/\eta$, and returns $(\varSigma _1,\varSigma _2,\varSigma _3,\varphi _{i})$. Note that it holds that $m = H_{k}(g^{w}) = H_{k}(g^{\eta \varphi _{i} + \vartheta _{i}}) =H_{k}(g^{\vartheta _{i}}\bar{h}^{\varphi _{i}})$. If $\mathcal {A}$ outputs a Type 3 forgery $(M^{*},(\varSigma _{1}^{*},\varSigma _{2}^{*},\varSigma _{3}^{*},\varphi ^{*}))$, then $\mathcal {B}$ computes $\vartheta ^{*} :=H_{k}(M^{*}\parallel \varSigma _{2}^{*})$, sets $m^{*} :=H_{k}(g^{\vartheta ^{*}}\bar{h}^{\varphi ^{*}})$, and outputs $(m^{*},(\varSigma _{1}^{*},\varSigma _{2}^{*},\varSigma _{3}^{*}))$. Now, $\mathcal {A}$ is a Type 3 forgery, so $m^{*} \notin \{m_1,\ldots ,m_{q}\}$ and $\mathcal {B}$ succeeded in outputting a new signature for $m^{*}$. This breaks the security of $\Pi$.$\square$

Theorem 6

Waters’ dual signature is $3$-partitioned.

Proof

Let $\mathcal {R}:=\left\{ (r_1,r_2,z_1,z_2,\mathsf {stag},\gamma ) \vert \ r_1,r_2,z_1,z_2,\mathsf {stag},\gamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p\right\}$, then functions $F_1$, $F_2$, and $F_3$ are defined as follows:

where $R \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathcal {R}$. Here, $\gamma$ is selected for Type B signatures. If the signature is Type A, then $\gamma :=0$. We can interpret $\sigma _3, \sigma _5, \sigma _6, \sigma _7$ (these are outputs of $F_{2}$) as $g^{-b z_{1}}, g^{-b z_{2}},g^{b r_{2}}, g^{r_{1}}$, respectively and it follows $\sigma _0 = (u^{M}w^{\mathsf {stag}}h)^{r_{1}}$ from the first verification equation, that is, the output of $F_{1}$ is fixed. If we interpret $\sigma _4$ as $v_{2}^{r} g^{z_{2}} \cdot g^{a_{1}\gamma }$, then by the second and third equations, two unknowns $\sigma _1$ and $\sigma _2$ are fixed to $g^{\alpha a_{1}}v^{r}\cdot g^{- a_{1}a_{2}\gamma }$ and $g^{-\alpha }v_{1}^{r}g^{z_{1}}$, respectively, that is, the output of $F_{3}$ is fixed. Therefore, if the output of $F_{2}$, $(\sigma _3,\ldots ,\sigma _{7},\mathsf {stag})$, and $M$ are fixed, then the outputs of $F_{1}$ and $F_{3}$ are also fixed. $\square$

We can see that even if $(\sigma _1,\sigma _2)$ is encrypted by the ElGamal encryption, hash value $\vartheta = H_{k} (M\parallel (\sigma _{3},\ldots ,\sigma _{7},\mathsf {stag}))$ is not changed, so it can be fitted to VES schemes. Note that we assume that each element $g \in \mathbb {G}$ has a unique encoding. We can obtain a strongly secure scheme $\mathsf {sWdSig}$ as follows:

• $\mathsf {sWd.Gen}(1^{\lambda },\varGamma )$: It generates $(VK^{\prime },SK^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Wd.Gen}(1^{\lambda },\varGamma )$, selects $\bar{h} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$ and random hash key $k\in \mathcal {K}$, and outputs $(VK,SK) :=((VK^{\prime },\bar{h},k),SK^{\prime })$.

• $\mathsf {sWd.Sign}(SK,M)$: On input message $M\in \mathbb {Z}_p$, it selects $r_1, r_2, z_1, z_2, \gamma , \mathsf {stag}, \varphi \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, sets $r :=r_1 + r_2$, computes

  

  and outputs $\mathsf {sig}:=(\sigma _{0},\sigma _1 ,\ldots , \sigma _7 , \mathsf {stag},\varphi )$.

• $\mathsf {sWd.Vrfy}(VK,\mathsf {sig}, M)$: On input $VK,M$, and signature $\mathsf {sig}= (\sigma _0,\sigma _1,\ldots , \sigma _7,\mathsf {stag},\varphi )$, it computes $\vartheta ^{\prime } :=H_{k}(M \parallel (\sigma _3,\ldots ,\sigma _7,\mathsf {stag}))$, $m^{\prime } :=H_{k} (g^{\vartheta ^{\prime }} \bar{h}^{\varphi })$, and $\mathsf {Wd.Vrfy}(VK^{\prime }, \mathsf {sig}^{\prime },m^{\prime }) \rightarrow b$ where $\mathsf {sig}^{\prime } :=(\sigma _{0},\ldots ,\sigma _{7},\mathsf {stag})$, and outputs $b$.

Corollary 1

The scheme above is strongly unforgeable against adaptive chosen message attacks if the DLIN assumption holds. That is, $\mathsf {Adv}_{\mathcal {F}^{\prime },\mathsf {sWdSig}}^{\mathsf {seuf}\mathrm - \mathsf {cma}} (\lambda ) \le 1/3 (\mathsf {Adv}_{\mathcal {F}, \mathsf {WdSig}}^{\mathsf {euf}\mathrm - \mathsf {cma}}(\lambda ) + \mathsf {Adv}_{\mathcal {C},\mathcal {H}}^{\mathsf {crhf}}(\lambda ) + \mathsf {Adv}_{\mathcal {B}}^{\mathsf {dl}}(\lambda )) \le \{(q + 3)/3 \} \mathsf {Adv}_{\mathcal {B}^{\prime }}^{\mathsf {dlin}} + (1/3 )\mathsf {Adv}_{\mathcal {C},\mathcal {H}}^{\mathsf {crhf}}$. (The DL assumption is implied by the DLIN assumption).

4 Construction of our VES

In this section, we present our VES scheme, $\mathsf {sWdVES}$, based on the strongly secure version of Waters’ dual signature scheme. The proposed scheme is essentially the same as strongly unforgeable Waters’ dual signature scheme explained in Sect. 3 except that we encrypt signature elements that include secret keys $(g^{\alpha },g^{\alpha a_1},g^{a_{1} a_{2}})$ by using the ElGamal encryption scheme. That is, in our creation algorithm, only $\sigma _{1}$ and $\sigma _{2}$ are encrypted. To verify an encrypted signature, we add extra elements and cancel out group elements that are generated by pairing computation of encrypted signature elements in the verification equations. Our scheme, $\mathsf {sWdVES}$, is as follows.

• $\mathsf {AdjGen}(1^\lambda )$: It selects $\beta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p^{\times }$ and sets $apk :=\zeta :=g^{\beta }$ and $ask :=\beta$.

• $\mathsf {Gen}(1^{\lambda })$: It generates key pair $(VK^{\prime },SK^{\prime })$ by using $\mathsf {sWd.Gen}(1^\lambda )$, that is,

  $$\begin{aligned} VK^{\prime }&:=(g,g^b,g^{a_1},g^{a_2},g^{b a_1},g^{b a_2}, \tau _1,\tau _2,\tau _{1}^{b},\tau _{2}^{b},v,v_1,v_2,w,u,h,\bar{h},k,e(g,g)^{\alpha a_1 b})\\ SK^{\prime }&:=(g^{\alpha }, g^{\alpha a_1}, g^{a_{1} a_{2}}) \end{aligned}$$

  and outputs $vk :=VK^{\prime }$ and $sk :=(VK^{\prime },SK^{\prime })$.

• $\mathsf {Sign}$ and $\mathsf {Vrfy}$: These are the same as $\mathsf {sWd.Sign}$ and $\mathsf {sWd.Vrfy}$ explained in Sect. 3, respectively.

• $\mathsf {Create}(sk,apk,M)$: It generates $(\sigma _0, \sigma _1 , \ldots ,\sigma _7, \mathsf {stag},\varphi ) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {sWd.Sign}(SK^{\prime },M)$, selects $\rho _1,\rho _2 \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, sets

  

  and outputs $\omega :=(K_0,\ldots ,K_7, K_{1}^{\prime },K_{2}^{\prime }, \hat{K}_{1},\hat{K}_{2} ,\mathsf {stag},\varphi )$.

• $\mathsf {VesVrfy}(apk,vk,\omega ,M)$: It parses $\omega = (K_0,\ldots ,K_7,K_{1}^{\prime },K_{2}^{\prime },\hat{K}_{1},\hat{K}_{2},\mathsf {stag},\varphi )$ and computes $\vartheta ^{\prime } :=H_{k}(M \parallel (K_3,\ldots , K_7, \mathsf {stag}))$ and $m^{\prime } :=H_{k} (g^{\vartheta ^{\prime }} \bar{h}^{\varphi })$. It outputs $1$ if and only if it holds that

  $$\begin{aligned} e( u^{m^{\prime }} w^{\mathsf {stag}} h,K_7)&= e(g, K_0) \\ \frac{e(g^b,K_1)}{e(\zeta ,\hat{K}_{1})} \cdot \frac{e(g^{b a_{1}},K_2) }{e(\zeta , \hat{K}_{2})} \cdot e( g^{ a_{1}},K_3)&= e(\tau _1,K_6)\, e(\tau _{1}^{b},K_7) \\ \frac{e(g^{b},K_1)}{e(\zeta , \hat{K}_{1})} \cdot e(g^{b a_{2}},K_4)\, e(g^{a_{2}},K_5)&= e(\tau _2,K_6)\, e(\tau _{2}^{b},K_7)\, e(g,g)^{\alpha a_{1} b}\\ e(K_{1}^{\prime },g^b)&= e(g,\hat{K}_{1}) \\ e(K_{2}^{\prime },g^{b a_1})&= e(g,\hat{K}_{2}). \end{aligned}$$

• $\mathsf {Adj}(ask,apk,vk,\omega ,M)$: It parses $\omega = (K_0,\ldots , K_7,\mathsf {stag},\varphi )$ and computes $\sigma _1 :=K_1 \cdot (K_{1}^{\prime })^{-\beta }$, $\sigma _2 :=K_2 \cdot (K_{2}^{\prime })^{-\beta }$, $\sigma _3 :=K_3$, $\sigma _4 :=K_4$, $\sigma _5 :=K_5$, $\sigma _6 :=K_6$, $\sigma _7 :=K_7$, $\sigma _{0} :=K_0$. If $\mathsf {VesVrfy}(apk,vk,\omega ,M) \rightarrow 1$, then it outputs $(\sigma _{0}^{},\ldots ,\sigma _{7}^{},\mathsf {stag},\varphi )$.

Intuitively, the scheme above is secure because the underlying signature scheme is strongly unforgeable. The adversary has no choice but to decrypt a valid VES given by oracles to output a valid signature, but it contradicts the one-wayness of the ElGamal encryption scheme.

As a corollary of Theorem 2, $\mathsf {sWdVES}$ is unforgeable under the DLIN assumption since we can easily show that $\mathsf {sWdVES}$ based on $\mathsf {sWdSig}$ is key-independent and extractable. See Sect. 2.4 for the definitions and Theorem 2.

Key-independence. For $\mathsf {sWdVES}$, we can set $kisk = \emptyset$, $ssk = (g^{\alpha },g^{\alpha a_1},g^{a_1 a_2})$, $kivk = (g^b,g^{b a_1},g^{b a_2})$, and $svk = VK^{\prime }$. Thus, $\mathsf {sWdVES}$ is key-independent.

Extractability.

Proof

From $\mathsf {VesVrfy}$, we have

$$\begin{aligned} e(u^{m^{\prime }}w^{\mathsf {stag}}h,K_{7}) = e(g,K_{0}) \end{aligned}$$

(V1)

$$\begin{aligned} \frac{e(g^{b},K_1)}{e(\zeta ,\hat{K}_{1})} \cdot \frac{e(g^{b a_{1}},K_2)}{e(\zeta ,\hat{K}_2)} \cdot e(g^{a_{1}},K_3) = e(\tau _1,K_{6}) e(\tau _{1}^{b},K_{7}) \end{aligned}$$

(V2)

$$\begin{aligned} \frac{e(g^{b},K_1)}{e(\zeta ,\hat{K}_{1})} \cdot e(g^{b a_{2}},K_4) \cdot e(g^{a_{2}},K_5) = e(\tau _2,K_{6}) e(\tau _{2}^{b},K_{7}) e(g,g)^{\alpha a_{1} b} \end{aligned}$$

(V3)

$$\begin{aligned} e(K_{1}^{\prime },g^{b}) = e(g,\hat{K}_1) \end{aligned}$$

(V4)

$$\begin{aligned} e(K_{2}^{\prime },g^{b a_1}) = e(g,\hat{K}_2). \end{aligned}$$

(V5)

For $j = 0, 3,4,5,6,7$, it holds that $K_j = \sigma _j$. For an extracted signature from $\omega$ by $\mathsf {Adj}$, it holds that (in the following calculation, we use the number of equations above.)

$$\begin{aligned}&e(u^{m^{\prime }}w^{\mathsf {stag}}h,\sigma _{7}) = e(g,\sigma _{0})&\hbox { (V1)}, \end{aligned}$$

and

$$\begin{aligned}&e(g^{b},K_1 \cdot (K_{1}^{\prime })^{-\beta }) \cdot e(g^{b a_{1}},K_2 \cdot (K_{2}^{\prime })^{-\beta }) \cdot e(g^{a_{1}},K_{3})&\\&\quad = e(g^{b},K_{1}) e(g^{b a_{1}},K_{2}) e(g^{a_{1}},K_{3}) \cdot e(g^{b}, (K_{1}^{\prime })^{-\beta }) \cdot e(g^{b a_{1}}, (K_{2}^{\prime })^{-\beta })&\\&\quad = e(\tau _1,\sigma _{6}) e(\tau _{1}^{b},\sigma _{7}) \cdot e(\zeta ,\hat{K}_{1}) \cdot e(\zeta ,\hat{K}_2) \cdot e(g^{b}, K_{1}^{\prime })^{-\beta } e(g^{b a_{1}}, K_{2}^{\prime })^{-\beta }&\hbox {(V2)}\\&\quad = e(\tau _1,\sigma _{6}) e(\tau _{1}^{b},\sigma _{7}) \cdot e(g^b,K_{1}^{\prime })^{\beta } \cdot e(g^{b a_1},K_{2}^{\prime })^{\beta } \cdot e(g^{b}, K_{1}^{\prime })^{-\beta } e(g^{b a_{1}}, K_{2}^{\prime })^{-\beta }&\hbox {(V4, V5)}\\&\quad = e(\tau _1,\sigma _{6}) e(\tau _{1}^{b},\sigma _{7}),&\end{aligned}$$

and

$$\begin{aligned}&e(g^{b},K_1 \cdot (K_{1}^{\prime })^{-\beta }) \cdot e(g^{b a_{2}},K_4)\cdot e(g^{a_{2}},K_{5})&\\&\quad = e(g^{b},K_{1}) e(g^{b a_{2}},K_{4}) e(g^{a_{2}},K_{5}) \cdot e(g^{b}, (K_{1}^{\prime })^{-\beta })&\\&\quad = e(\tau _2,\sigma _{6}) e(\tau _{2}^{b},\sigma _{7}) \cdot e(g,g)^{\alpha a_{1} b } \cdot e(\zeta ,\hat{K}_{1}) \cdot e(g^{b}, K_{1}^{\prime })^{-\beta }&\hbox {(V3)}\\&\quad = e(\tau _2,\sigma _{6}) e(\tau _{2}^{b},\sigma _{7}) \cdot e(g,g)^{\alpha a_{1} b } \cdot e(g^b,K_{1}^{\prime })^{\beta } \cdot e(g^{b}, K_{1}^{\prime })^{-\beta }&\hbox {(V4)}\\&\quad = e(\tau _2,\sigma _{6}) e(\tau _{2}^{b},\sigma _{7})e(g,g)^{\alpha a_{1} b}.&\end{aligned}$$

This means that the extracted signature passes the verification algorithm of the underlying signature scheme, $\mathsf {Wd.}\mathsf {Vrfy}$. $\square$

As a corollary, $\mathsf {sWdVES}$ is unforgeable since $\mathsf {sWdVES}$ is key-independent and extractable due to Theorem 2.

Corollary 2

$\mathsf {sWdVES}$ is unforgeable.

By Theorem 3, $\mathsf {sWdVES}$ is collusion-resistant under the DLIN assumption.

Next, we prove the opacity of our scheme.

Theorem 7

$\mathsf {sWdVES}$ is opaque if the DLIN assumption holds and there exists CRHF.

Proof

If $\mathcal {A}$ outputs forgery $\sigma ^{*} =(\sigma _{0}^{*},\ldots , \sigma _{7}^{*},\mathsf {stag}^{*},\varphi ^{*})$ and $M^{*}$ such that $M^{*}$ is not queried to $\mathcal {A}\mathcal {O}$, then it means that $\mathcal {A}$ breaks the opacity of $\mathsf {sWdVES}$. $\mathcal {A}$ directly forges a signature of the underlying $\mathsf {sWdSig}$ or extracts a signature by breaking the one-wayness of the ElGamal encryption scheme. To show that $\mathsf {sWdVES}$ satisfies opacity, we introduce the following games. Let $\mathsf {Game}\mathrm - {(i)}$ denote a game where the VES creation oracle answers encrypted signatures of Type A signatures for the first $i$ ($i \in [q_{\mathsf {C}}]$ and $q_{\mathsf {C}}$ is the number of creation queries by $\mathcal {A}$) and queries and encrypted signatures of Type B signatures for the remaining $q_{\mathsf {C}}-i$ queries, and the adjudication oracle answers signatures extracted from the queried VES for all $q_{\mathsf {A}}$ (the number of adjudication queries) queries. Let $\mathsf {Adv}_{i}^{\mathsf {forge} \text{- } \mathsf {A}}$ (resp. $\mathsf {Adv}_{i}^{\mathsf {forge} \text{- } \mathsf {B}}$) denote the advantage of the adversary in $\mathsf {Game}\mathrm - {(i)}$ for outputting a Type A (resp. B) forgery for a non-queried message (a message that is not queried to $\mathcal {C}\mathcal {O}$). Let $\mathsf {Adv}_{0}^{\mathsf {extract} \text{- } \mathsf {B}}$ denote the advantage of the adversary in $\mathsf {Game}\mathrm - {0}$ for extracting a signature from a VES for a queried message (a message that is queried to $\mathcal {C}\mathcal {O}$).

• 1. In $\mathsf {Game}\mathrm - {(0)}$, the VES creation oracle returns encrypted signatures of Type B signatures and the adjudication oracle returns Type B signatures. First, we show Lemma 5: If $\mathcal {A}$ outputs a valid Type B signature for message $M_i$ that has been already queried to the VES creation oracle, $\mathcal {C}\mathcal {O}$ in $\mathsf {Game}\mathrm - {(0)}$, then we can construct algorithm $\mathcal {E}$ that solves the AgExt problem. Thus, in the remaining games, we only consider $\mathcal {A}$ which outputs a forgery for message $M^{*}$ such that $M^{*} \ne M_{i}$ for all $i \in [q]$. We can show Lemma 6: If $\mathcal {A}$ outputs a forgery of a Type A signature in $\mathsf {Game}\mathrm - {(0)}$, then we can construct algorithm $\mathcal {B}_{1}$ (simulator for $\mathcal {A}$), which solves the CDH problem.

• 2. Next, we consider $\mathsf {Game}\mathrm - {(i)}$. We can show Lemma 7: If $\mathcal {A}$ detects the change of answers by the VES creation oracle (from Type B answer to Type A answer), we can construct algorithm $\mathcal {B}_{2}$ (simulator for $\mathcal {A}$) that solves the DLIN problem.

• 3. Finally, we consider $\mathsf {Game}\mathrm - {(q_{\mathsf {C}})}$, where all answers for VES queries of $\mathcal {A}$ are encrypted signatures of Type A signatures. We can show Lemma 8: If $\mathcal {A}$ outputs a forgery of a Type B signature in $\mathsf {Game}\mathrm - {(q_\mathsf {C})}$, then we can construct algorithm $\mathcal {B}_{3}$ that solves the DLIN problem.

Thus, if the DLIN assumption holds, the signature scheme is opaque since the AgExt assumption is equivalent to the CDH assumption and the CDH assumption is implied by the DLIN assumption. The core part is Lemma 5. By Lemmas 5, 6, 7, and 8, we can show

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {Opac}}(\lambda )&= \mathsf {Adv}_{0}^{\mathsf {forge} \text{- } \mathsf {A}} + \mathsf {Adv}_{0}^{\mathsf {extract} \text{- } \mathsf {B}} + \mathsf {Adv}_{0}^{\mathsf {forge} \text{- } \mathsf {B}} \\&\le \mathsf {Adv}_{0}^{\mathsf {extract} \text{- } \mathsf {B}} + \mathsf {Adv}_{\mathcal {F},\mathsf {WdSig}}^{\mathsf {euf} \text{- } \mathsf {cma}} \\&\le q_{\mathsf {C}} \mathsf {Adv}_{\mathcal {E}}^{\mathsf {AgExt}} + \mathsf {Adv}_{\mathcal {F}^{\prime },\mathsf {sWdSig}}^{\mathsf {seuf} \text{- } \mathsf {cma}} + \mathsf {Adv}_{\mathcal {C}}^{\mathsf {crhf}} + \mathsf {Adv}_{\mathcal {F},\mathsf {WdSig}}^{\mathsf {euf} \text{- } \mathsf {cma}} \\&\le ((7/3)q_{\mathsf {C}} + 3) \mathsf {Adv}_{\mathcal {B}}^{\mathsf {dlin}} + (4/3)\mathsf {Adv}_{\mathcal {C}}^{\mathsf {crhf}}. \end{aligned}$$

Lemma 5

If there exists adversary $\mathcal {A}$ that outputs a Type B forgery for a queried message $M_{i}$ in $\mathsf {Game}\mathrm - {0}$, then we can construct algorithm $\mathcal {E}$ that solves the AgExt problem.

Proof of lemma

$\mathcal {E}$ is given instance $(\varGamma ,g^x,g^y,g^{\beta },g^{\delta },g^{x y + \beta \delta })$ of the AgExt problem and generates the verification key as follows. It selects exponents $a_1,b,y_v,y_{v_1},y_{v_2},y_w,y_h,y_u,\eta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, and hash key $k \in \mathcal {K}$, computes

and $e(g,g)^{\alpha a_{1}b} :=e(g^x,g^y)^{a_{1}\cdot b}$ (it implicitly holds $\alpha = x y$ though $\mathcal {E}$ does not have $\alpha$), and sets $VK :=(g,g^b,g^{a_1},g^{a_2},g^{b a_{1}}, g^{b a_{2}},\tau _1,\tau _2,\tau _{1}^{b},\tau _{2}^{b},w,u,h,\bar{h},k,e(g,g)^{\alpha a_{1}b})$ and $apk :=\zeta = g^{\beta }$. Note that $\mathcal {E}$ does not have $g^{\alpha } = g^{x y}$, so $\mathcal {E}$ cannot directly compute a Type B signature.

Simulation of creation oracle: $\mathcal {E}$ initializes list $\mathsf {QList} :=\emptyset$, selects random index $j \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}[q_{\mathsf {C}}]$, i.e., guesses which VES $\mathcal {A}$ selects and outputs its extraction, and outputs encrypted signatures of Type B signatures for the $i$-th VES creation query $M_{i}$ as follows. If $i \ne j$, $\mathcal {E}$ then selects $r_1,r_2,z_1,z_2,\gamma ^{\prime },\mathsf {stag},\varphi _{i}, \rho _{1},\rho _{2} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, sets $r :=r_1 + r_2$ (we want to set $\gamma :=x + \gamma ^{\prime }$), computes

$$\begin{aligned}&\sigma _{i,1} :=(g^y)^{-\gamma ^{\prime }a_1} \cdot v^r = (g^{\alpha a_1}v^{r})\cdot g^{-a_1a_2\gamma } \\&(\text{ where } a_2 = y \text{ and } x y =\alpha ) \\&\sigma _{i,2} :=(g^y)^{\gamma ^{\prime }}v_{1}^{r}g^{z_1} = (g^{\alpha }v_{1}^{r}g^{z_1})\cdot g^{a_2 \gamma } \\&K_{1} :=\sigma _{i,1} \cdot \zeta ^{\rho _{1}}, \ K_{1}^{\prime } :=g^{\rho _{1}}, \ \hat{K}_{1} :=(g^{b})^{\rho _1} \\&K_{2} :=\sigma _{i,2} \cdot \zeta ^{\rho _{2}},\ K_{2}^{\prime } :=g^{\rho _{2}},\ \hat{K}_{2} :=(g^{b a_1})^{\rho _2} \\&K_{3} :=\sigma _{i,3} :=(g^b)^{-z_1} \\&K_{4} :=\sigma _{i,4} :=(g^x)^{a_1}g^{a_1 \gamma ^{\prime }}v_{2}^{r}g^{z_2} = (v_{2}^{r}g^{z_2})\cdot g^{a_1\gamma } \\&K_{5} :=\sigma _{i,5} :=(g^b)^{-z_2},\ K_{6} :=\sigma _{i,6} :=g^{r_2 b},\ K_{7} :=\sigma _{i,7} :=g^{r_1} \\&\vartheta _{i} :=H_{k}(M_{i}\parallel \Sigma _{i,2}) \text{ where } \Sigma _{i,2} :=(\sigma _{i,3},\ldots , \sigma _{i,7}) \\&m_{i} :=H_{k}(g^{\vartheta _{i}}\bar{h}^{\varphi _{i}}),\ K_{0} :=\sigma _{i,0} :=(u^{m_{i}} w^{\mathsf {stag}}h)^{r_1}, \end{aligned}$$

stores $(M_i , \sigma _{i}, R_{i} :=(r_1,r_2,z_1,z_2, \mathsf {stag}, \gamma _{i} :=\gamma ^{\prime }) )$ in $\mathsf {QList}$ where $\sigma _{i} :=(\sigma _{i,0},\ldots ,\sigma _{i,7},\mathsf {stag},\varphi _{i})$, and outputs $\omega :=(K_0,\ldots , K_7,K_{1}^{\prime },K_{2}^{\prime } ,\hat{K}_{1},\hat{K}_{2},\mathsf {stag},\varphi _{i})$ for $M_{i}$. We can verify $\sigma _{i}$ is a correct Type B signature.

Embedding the instance: If $i = j$, then $\mathcal {E}$ selects $r^{*}_1,r^{*}_2,z^{*}_1,z^{*}_2,\gamma ^{*},\mathsf {stag}^{*},\varphi ^{*},\rho _{1},\rho _{2} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, sets $r^{*} = r^{*}_1 + r^{*}_2$, answers

$$\begin{aligned}&K^{*}_1 :=(g^{x y + \beta \delta })^{a_1} v^{r^{*}} (g^{y})^{- a_1 \gamma ^{*}} \zeta ^{\rho _{1}} = (g^{\alpha a_1}v^{r^{*}}) g^{-a_1 a_2\gamma ^{*}}\zeta ^{\rho _{1}^{\prime }} \\&(\text{ where } a_2 = y , x y =\alpha , \rho _{1}^{\prime } :=a_1 \delta + \rho _1) \\&K_{1}^{*\prime } :=(g^{\delta })^{a_1}g^{\rho _1} = g^{\rho _{1}^{\prime }} \\&\hat{K}^{*}_{1} :=(g^\delta )^{b a_1}g^{b \rho _1} = (g^b)^{\rho _{1}^{\prime }} \\&K^{*}_2 :=(g^{x y + \beta \delta })^{-1}v_{1}^{r^{*}}g^{z^{*}_1}\cdot (g^{a_2})^{\gamma ^{*}}(g^{\beta })^{\rho _2} = (g^{- \alpha }v_{1}^{r^{*}}g^{z^{*}_1})\cdot g^{a_2 \gamma ^{*}} \zeta ^{\rho _{2}^{\prime }} \\&(\text{ where } \rho _{2}^{\prime } :=-\delta + \rho _2) \\&K_{2}^{*\prime } :=(g^{\delta })^{-1}g^{\rho _2} = g^{\rho _{2}^{\prime }} \\&\hat{K}^{*}_{2} :=(g^\delta )^{- b a_1}g^{b a_1 \rho _2} = (g^{b a_1})^{\rho _{2}^{\prime }} \\&K^{*}_3 :=(g^b)^{-z^{*}_1}, \ K^{*}_4 :=v_{2}^{r^{*}}g^{z^{*}_2} g^{a_1 \gamma ^{*}}, \ K^{*}_5 :=(g^b)^{-z^{*}_2},\ K^{*}_6 :=g^{r^{*}_2 b},\ K^{*}_7 :=g^{r^{*}_1} \\&\vartheta ^{*} :=H_{k}(K_{3}^{*},\ldots , K_{7}^{*},\mathsf {stag}^{*}),\ m^{*} :=H_{k}(g^{\vartheta ^{*}}\bar{h}^{\varphi ^{*}}),\ K^{*}_0 :=(u^{m^{*}} w^{\mathsf {stag}^{*}}h)^{r^{*}_1}, \end{aligned}$$

and records $(M_{j} , \omega ^{*}:=(K_{0}^{*},\ldots ,\varphi ^{*}),j,\gamma ^{*})$ as the challenge instance. It can be verified that $\omega ^{*}$ is a correct encrypted signature of a Type B signature.

Simulation of adjudication oracle: When $\mathcal {A}$ makes the $\ell$-th adjudication query $(M_{\ell },\omega _{\ell })$, we know that $\mathcal {A}$ must have queried $M_{\ell }$ to $\mathcal {C}\mathcal {O}$ by the theorem of Rückert and Schröder (Otherwise, it is a forgery. This is the same argument by Rückert and Schröder in [48]). First, $\mathcal {E}$ verifies the query and returns $\bot$ if it is invalid. Otherwise, $\mathcal {E}$ acts as follows. If $M_{\ell } = M_{j}$, that is, the guessed index ($(M_{j},\ldots ) \notin \mathsf {QList}$), then $\mathcal {E}$ aborts. Otherwise, there exists $(M_{i},\sigma _{i},R_{i}) \in \mathsf {QList}$ for some $i \ne j$ such that $M_{\ell } = M_{i}$ and the signature is Type B. In this case ($M_{\ell } =M_{i}$), for query $(M_{\ell },\omega = (K_0,\ldots ,K_7,K_{1}^{\prime },K_{2}^{\prime },\hat{K}_{1},\hat{K}_{2},\mathsf {stag},\varphi ))$, if $\varphi \ne \varphi _{i}$, then $\mathcal {A}$ breaks the strong unforgeability of our modified Waters’ dual signature. We consider an intermediate game where if $\varphi \ne \varphi _{i}$, then $\mathcal {E}$ aborts. The probability of $\mathcal {E}$ aborting under this condition is at most the success probability of breaking the strong unforgeability of $\mathsf {sWdSig}$. That is, it holds that $\varphi = \varphi _{i}$ without negligible probability. If $\varphi = \varphi _{i}$, then it holds that $K_3 = \sigma _{i,3}$, $K_{4} = \sigma _{i,4}$, $K_{5} = \sigma _{i,5}$, $K_6 = \sigma _{i,6}$, $K_7 = \sigma _{i,7}$, and $\mathsf {stag}= \mathsf {stag}_{i}$ since otherwise it means $\mathcal {A}$ outputs $(K_3, \ldots , K_7,\mathsf {stag})$ such that $H_{k}(\sigma _{i,3},\ldots ,\sigma _{i,7},\mathsf {stag}_{i}) = \varphi _{i} = \varphi = H_{k}(K_{3},\ldots ,K_{7},\mathsf {stag})$ and $(K_3, \ldots , K_7,\mathsf {stag}) \ne (\sigma _{i,3},\ldots , \sigma _{i,7},\mathsf {stag}_{i})$. This is a collision of the hash function and contradicts the collision-resistant property. We consider an intermediate game where if $H_{k}(\sigma _{i,3},\ldots ,\sigma _{i,7},\mathsf {stag}_{i}) = \varphi _{i} = \varphi = H_{k}(K_{3},\ldots ,K_{7},\mathsf {stag})$ and $(K_3, \ldots , K_7,\mathsf {stag}) \ne (\sigma _{i,3},\ldots , \sigma _{i,7},\mathsf {stag}_{i})$, then $\mathcal {E}$ aborts. The probability of $\mathcal {E}$ aborting under this condition is less than the success probability of breaking the CRHF. That is, the randomness of $(K_3,\ldots , K_7,\mathsf {stag})$ is the same as that of $(\sigma _{i,3},\ldots ,\sigma _{i,7},\mathsf {stag}_{i})$ without negligible probability.

By using $K_3 = g^{- b z_1}$, $K_5 = g^{-b z_2}$, $K_6 = g^{b r_2}$, and $K_7 = g^{r_1}$, $\mathcal {E}$ can compute $g^{r_{2}^{}} = (K_{6}^{})^{1/b}$, $g^{r_{1}^{}} = K_{7}^{}$, $g^{z_{1}^{}}= (K_{3}^{})^{-1/b}$, $g^{z_{2}^{}}= (K_{5}^{})^{-1/b}$, $v^{r^{}} = (g^{r_{1}^{}}\cdot g^{r_{2}^{}})^{y_{v}}$, $v_{1}^{r^{}} = (g^{r_{1}^{}}\cdot g^{r_{2}^{}})^{y_{v_1}}$, and $v_{2}^{r^{}} = (g^{r_{1}^{}}\cdot g^{r_{2}^{}})^{y_{v_2}}$ since $\mathcal {E}$ has $b,y_{v},y_{v_1},y_{v_2}$ and it holds that $v = g^{y_{v}}$ $v_1 = g^{y_{v_1}}$ $v_2 = g^{y_{v_2}}$. $\mathcal {E}$ can use the same computation procedure in the simulation of the VES creation oracle above by using $\gamma _{i}$ stored in $\mathsf {QList}$. Therefore, $\mathcal {E}$ can return a valid Type B signature $(\sigma _0,\ldots ,\sigma _{7},\mathsf {stag},\varphi )$ such that the randomness $r$ in $\sigma _1$, $\sigma _2$ is the same as that in $K_1$, $K_2$ by using stored information $\sigma _{i}$. That is, the adjudication oracle is perfectly simulated by $\mathcal {E}$.

Solving the problem: At some point, $\mathcal {A}$ outputs a Type B extraction, $M^{*} = M_{j}$, $\mathsf {stag}^{*}$, $\sigma _{1}^{*} = g^{\alpha a_1}v^{r^{*}} g^{- a_1 a_2 \gamma ^{*}}$, $\sigma _{2}^{*} = g^{-\alpha }v_{1}^{r^{*}}g^{z_{1}^{*}} g^{a_2 \gamma ^{*}}$, $\sigma _{3}^{*} = (g^b)^{-z_{1}^{*}}$, $\sigma _{4}^{*} = v_{2}^{r^{*}}g^{z_{2}^{*}} g^{a_{1} \gamma ^{*}}$, $\sigma _{5}^{*} = (g^b)^{-z_{2}^{*}}$, $\sigma _{6}^{*} = g^{r_{2}^{*}b}$, $\sigma _{7}^{*} = g^{r_{1}^{*}}$, $\vartheta ^{*} = H_{k}(\sigma _{3},\ldots , \sigma _{7},\mathsf {stag}^{*})$, $m^{*} = H_{k}(g^{\vartheta ^{*}}\bar{h}^{\varphi })$, and $\sigma _{0}^{*} = (u^{m^{*}}w^{\mathsf {stag}^{*}}h)^{r_{1}^{*}}$ (not queried to $\mathcal {A}\mathcal {O}$ but $\mathcal {C}\mathcal {O}$) such that randomnesses are the same as those used when $\mathcal {B}$ embedded the problem instance at the j-th query and $(M_{j},\omega ^{*},j,\gamma ^{*})$ is recorded as the challenge instance. This is guaranteed by the strong unforgeability and collision-resistant property we discussed above. By using these values, $\mathcal {E}$ can compute $g^{r_{2}^{*}} = (\sigma _{6}^{*})^{1/b}$, $g^{r_{1}^{*}} = \sigma _{7}^{*}$, $g^{z_{1}^{*}}= (\sigma _{3}^{*})^{-1/b}$, $g^{z_{2}^{*}}= (\sigma _{5}^{*})^{-1/b}$, $v^{r^{*}} = (g^{r_{1}^{*}}\cdot g^{r_{2}^{*}})^{y_{v}}$, $v_{1}^{r^{*}} = (g^{r_{1}^{*}}\cdot g^{r_{2}^{*}})^{y_{v_1}}$, $v_{2}^{r^{*}} = (g^{r_{1}^{*}}\cdot g^{r_{2}^{*}})^{y_{v_2}}$ since $\mathcal {E}$ has $b,y_{v},y_{v_1},y_{v_2}$ and it holds that $v = g^{y_{v}}$ $v_1 = g^{y_{v_1}}$ $v_2 = g^{y_{v_2}}$. Thus, $\mathcal {E}$ can compute $g^{z_{1}^{*}}\cdot v_{1}^{r^{*}} g^{a_2 \gamma ^{*}}/\sigma _{2}^{*} = g^{\alpha } = g^{x y}$ (where $g^{a_2} = g^y$) since $\mathcal {E}$ has $a_1$ and $\gamma ^{*}$ is recorded. That is, $\mathcal {E}$ can output solution $g^{x y}$ of the AgExt problem if the adversary outputs a Type A extraction for queried message $M_j$ to $\mathcal {C}\mathcal {O}$. $\mathcal {E}$ guesses index $j$, so its success probability is degraded by a factor of $1/q_{\mathsf {C}}$. However, it still breaks the AgExt problem with non-negligible probability $\epsilon /q_{\mathsf {C}}$, where $\epsilon$ is the success probability of $\mathcal {A}$. $\square$

Lemma 6

If there exists adversary $\mathcal {A}$ that outputs a Type A forgery when all answers to signing queries are Type B signatures, then we can construct algorithm $\mathcal {B}_1$ that solves the CDH problem.

Proof of lemma

$\mathcal {B}_1$ is given instance $(\varGamma ,g,g^x,g^y)$ of the CDH problem and generates the verification key as follows: It selects exponents $a_1,b,y_v,y_{v_1},y_{v_2},y_w,y_h,y_u, \eta ,\zeta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, computes

and $e(g,g)^{\alpha a_{1}b} :=e(g^x,g^y)^{a_{1}\cdot b}$ (implicitly $\alpha = x y$ though $\mathcal {B}_1$ does not have $\alpha$), and sets $VK :=(\varGamma ,g^b,g^{a_1},g^{a_2}, g^{b a_{1}}, g^{b a_{2}}, v,v_1,v_2, \tau _1,\tau _2,\tau _{1}^{b},\tau _{2}^{b},w,u,h,\bar{h},k,e(g,g)^{\alpha a_{1}b})$ and $apk :=g^{\beta }$. Note that $\mathcal {B}_1$ does not have $g^{\alpha } = g^{x y}$, so $\mathcal {B}_1$ cannot directly compute a Type A signature. $\mathcal {B}_1$ outputs encrypted signatures of Type B signatures for creation query $M$ as follows. It selects $r_1,r_2,z_1,z_2,\gamma ^{\prime },\mathsf {stag},\varphi \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, sets $r :=r_1 + r_2$ (we want to set $\gamma :=x + \gamma ^{\prime }$), and computes

$\mathcal {B}_1$ outputs VES for $M$ by using signature $(\sigma _{0},\ldots , \sigma _{7},\mathsf {stag},\varphi )$ for $M$ and algorithm $\mathsf {Create}$ with $apk = \beta$. For an adjudication query, $\mathcal {B}_1$ verifies its validity and returns the decrypted value by using $\beta$ if it is valid.

At some point, $\mathcal {A}$ outputs a Type A forgery $\mathsf {sig}^{*} = (\sigma ^{*}_{0},\ldots , \sigma ^{*}_{7},\mathsf {stag}^{*},\varphi ^{*})$. If $\mathsf {sig}^{*}$ is a valid Type A forgery, then it passes the verification equations and it should hold that $\sigma _{1}^{*} = g^{\alpha a_1}v^{r_{1}^{*}}$, $\sigma _{2}^{*} = g^{-\alpha }v_{1}^{r^{*}}g^{z_{1}^{*}}$, $\sigma _{3}^{*} = (g^b)^{-z_{1}^{*}}$, $\sigma _{4}^{*} = v_{2}^{r^{*}}g^{z_{2}^{*}}$, $\sigma _{5}^{*} = (g^b)^{-z_{2}^{*}}$, $\sigma _{6}^{*} = g^{r_{2}^{*}b}$, $\sigma _{7}^{*} = g^{r_{1}^{*}}$, $\vartheta ^{*} = H_{k}(M^{*}\parallel \sigma _{3}^{*},\ldots \sigma _{7}^{*},\mathsf {stag}^{*})$, $m^{*} = H_{k}(g^{\vartheta ^{*}}\bar{h}^{\varphi ^{*}})$, and $\sigma _{0}^{*} = (u^{m^{*}}w^{\mathsf {stag}^{*}}h)^{r_{1}^{*}}$, for some $r_{1}^{*},r_{2}^{*},z_{1}^{*},z_{2}^{*},\mathsf {stag}^{*} \in \mathbb {Z}_{p}$.

By using these values, $\mathcal {B}_1$ can compute $g^{r_{2}^{*}} = (\sigma _{6}^{*})^{1/b}$, $g^{r_{1}^{*}} = \sigma _{7}^{*}$, $g^{z_{1}^{*}}= (\sigma _{3}^{*})^{-1/b}$, $v_{1}^{r^{*}} = (g^{r_{1}^{*}}\cdot g^{r_{2}^{*}})^{y_{v_1}}$ since $v_1 = g^{y_{v_1}}$. Thus, $\mathcal {B}_1$ can compute $g^{z_{1}^{*}}\cdot v_{1}^{r^{*}}/\sigma _{2}^{*} = g^{\alpha } = g^{x y}$. That is, $\mathcal {B}_1$ can solve the CDH problem.$\square$

Lemma 7

If there exists $\mathcal {A}$ that makes at most $q_{\mathsf {C}}$ creation and $q_{\mathsf {A}}$ adjudication queries and it holds $\left| \mathsf {Adv}_{k-1}^{\mathsf {forge} \text{- } \mathsf {B}} - \mathsf {Adv}_{k}^{\mathsf {forge} \text{- } \mathsf {B}}\right| = \varepsilon$ for some $k \in [q_{\mathsf {C}}]$, then we can construct algorithm $\mathcal {B}_2$ that solves the DLIN problem with advantage $\varepsilon$.

Proof of lemma

$\mathcal {B}_2$ is given instance $(\Gamma ,g,f=g^b,\nu ,g^x,f^y,T)$ of the DLIN problem and generates the verification key as follows. It selects exponents $\alpha ,a_{1},a_{2},y_{v_1},y_{v_2},y_{w},y_{u},y_{h}, \eta , A, B,\beta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, computes

and sets $VK :=(\varGamma ,f,g^{a_1},g^{a_2},f^{a_1},f^{a_2},\tau _{1},\tau _{2},\tau _{1}^{b},\tau _{2}^{b},v,v_1,v_2,w,u,h,\bar{h},k, e(f,g)^{\alpha a_1})$, $SK :=(VK,g^{\alpha },g^{\alpha a_1},g^{a_{1} a_{2}})$, and $apk :=\zeta$. $\mathcal {B}_{2}$ has $g^{a_1 a_2}$ since it has $(a_1,a_2)$, thus, it can generate a Type B signature. We define $\mathcal {F}(M) :=AM + B$. If $\mathsf {stag}:=\mathcal {F}(M)$, then $(u^M w^{\mathsf {stag}} h) = f^{\mathsf {stag}- A M - B}\cdot g^{M y_{u} + \mathsf {stag}y_{w}+ y_{h}} = g^{M y_{u} + \mathsf {stag}y_{w}+ y_{h}}$. $\mathcal {B}_{2}$ generates signatures as follows. For the $i$-th creation query,

• Case $i>k$: Returns encrypted signatures of Type B signatures by using $SK$, $g^{a_1 a_2}$ and $\zeta$.

• Case $i<k$: Returns encrypted signatures of Type A signatures by using $SK = (g^{\alpha },g^{\alpha a_1})$ and $\zeta$.

• Case $i=k$: Embeds the instance as follows. For the $k$-th creation query $M$, $\mathcal {B}_{2}$ first generates a Type A signature as follows. It selects $m_{0} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, sets $m :=H_{k}(g^{m_0})$ and $\mathsf {stag}:=\mathcal {F}(m)$, and generates a Type A signature $(\sigma _{0}^{\prime },\sigma _{1}^{\prime },\sigma _{2}^{\prime },\sigma _{3}^{\prime },\sigma _{4}^{\prime },\sigma _{5}^{\prime },\sigma _{6}^{\prime }, \sigma _{7}^{\prime })$ for $m$ by using tag $\mathsf {stag}$ (with randomness $r_{1}^{\prime },r_{2}^{\prime },z_{1}^{\prime },z_{2}^{\prime } \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, $r^{\prime } :=r_{1}^{\prime } + r_{2}^{\prime }$). Next, it computes

  

In this case, it implicitly holds that $z_{1} :=z_{1}^{\prime } - y_{v_1}y$, $z_{2} :=z_{2}^{\prime } - y_{v_2}y$, $r_{1} :=r_{1}^{\prime } + x$, $r_{2} :=r_{2}^{\prime } + y$. $\mathcal {B}_{2}$ can generate $\sigma _{0}$ correctly since $\mathcal {B}_{2}$ sets $\mathsf {stag}:=\mathcal {F}(m)$.

• If $T = \nu ^{x + y}$, the above signature is Type A with randomness $r_{1} :=r_{1}^{\prime } + x$, $r_{2} :=r_{2}^{\prime } + y$.

• If $T \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, the above signature is Type B since $T =\nu ^{x + y}g^{\gamma }$ for some $\gamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$.

For VES creation query $M$, $\mathcal {B}_{2}$ returns an encrypted signature of the above signature for $M$ by using $\zeta$. For adjudication query $(M,\omega )$, if it is a valid VES, then $\mathcal {B}_{2}$ decrypts it by using $\beta$ and returns extracted signatures for $M$. That is, if $T = \nu ^{x+y}$ (linear), then $\mathcal {A}$ is in $\mathsf {Game}\mathrm - {(k-1)}$, otherwise $\mathcal {A}$ is in $\mathsf {Game}\mathrm - {(k)}$.

At some point, $\mathcal {A}$ outputs a signature $\sigma ^{*} = (\sigma _{0}^{*},\ldots , \sigma _{7}^{*},\mathsf {stag}^{*},\varphi ^{*})$ and message $M^{*}$. Note that in this game, $M^{*}$ is not queried to $\mathcal {C}\mathcal {O}$. $\mathcal {B}_{2}$ computes $\vartheta ^{\prime } :=H_{k}(M^{*}\parallel (\sigma _{3}^{*},\ldots ,\sigma _{7}^{*},\mathsf {stag}^{*}))$, $m^{\prime } :=H_{k}(g^{\vartheta ^{\prime }}\bar{h}^{\varphi ^{*}})$ and verifies

$$\begin{aligned}&e(\sigma _{0}^{*}, \nu ) e(\nu ^{\mathsf {stag}^{*} - A m^{\prime } -B},\sigma _{6}^{*}) \\&\quad = e((\sigma _{1}^{*}/ g^{\alpha a_{1}} )^{- \frac{1}{a_{1}a_{2}}}, f^{\mathsf {stag}^{*} - A m^{\prime } -B}) e(\sigma _{7}^{*},\nu ^{m^{\prime } y_{u} + \mathsf {stag}^{*} y_{w} + y_{h}}). \end{aligned}$$

It holds that $\sigma _{0}^{*} = (f^{\mathsf {stag}^{*} - A m^{\prime } - B} g^{m^{\prime }y_{u} + \mathsf {stag}^{*}y_{w} + y_{h}})^{r_{1}^{*}}$, $\sigma _{1}^{*} = g^{\alpha a_{1}} \nu ^{- a_{1}a_{2} r^{*}}g^{- a_{1}a_{2}\gamma ^{*}}$, $\sigma _{6}^{*} = g^{b r_{2}^{*}}$, and $\sigma _{7}^{*} = g^{r_{1}^{*}}$. Thus, the left-hand side is

$$\begin{aligned} e(f,\nu )^{r_{1}^{*} (\mathsf {stag}^{*} - A m^{\prime } -B)} e(g,\nu )^{r_{1}^{*} (m^{\prime } y_{u} + \mathsf {stag}^{*}y_{w} + y_{h})} e(\nu ,f)^{r_{2}^{*}(\mathsf {stag}^{*} - A m^{\prime } -B )}, \end{aligned}$$

and the right-hand side is

$$\begin{aligned} e(\nu ,f)^{{r}^{*} (\mathsf {stag}^{*} - A m^{\prime } -B)} e(g,f)^{\gamma ^{*} (\mathsf {stag}^{*} - A m^{\prime } -B)} e(g,\nu )^{r_{1}^{*}(m^{\prime } y_{u} + \mathsf {stag}^{*}y_{w} + y_{h} )}. \end{aligned}$$

A simplified equation is

$$\begin{aligned} 1 = e(g,f)^{\gamma ^{*}(\mathsf {stag}^{*} - A m^{\prime } - B)}. \end{aligned}$$

It holds that $\mathsf {stag}^{*} \ne A m^{\prime } + B$ without negligible probability because $M^{*} \ne M_{i}$ for all $i \in [q_{\mathsf {C}}]$ and $A$ and $B$ are information theoretically hidden from the adversary. If signature $\sigma ^{*}$ is Type A, then the above equation holds and $\mathcal {B}_{2}$ outputs $1$. On the other hand, if $\sigma ^{*}$ is Type B, then it does not hold and $\mathcal {B}_{2}$ outputs $0$.

Thus, if $\mathcal {A}$ can distinguish the two games, then $\mathcal {B}_{2}$ can solve the DLIN problem with the same advantage. $\square$

Lemma 8

If $\mathcal {A}$ outputs a Type B forgery, then we can construct algorithm $\mathcal {B}_{3}$ that solves the DLIN problem.

Proof of lemma

Algorithm $\mathcal {B}_{3}$ is given instance $(\varGamma ,g,f=g^{a_1},\nu = g^{a_2},g^x,f^y,T)$ of the DLIN problem and simulates the verification key and the signing oracle for the signature scheme ($\mathcal {B}_{3}$ does not have values $a_{1},a_{2},x,y$).

$\mathcal {B}_{3}$ generates the verification key as follows. It selects exponents $b,\alpha ,y_v,y_{v_{1}},y_{v_{2}},\beta ,\eta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$ and generators $u,w,h \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, computes

and sets $VK :=(\varGamma ,g^b,f,\nu ,f^b,\nu ^b,\tau _{1},\tau _{2},\tau _{1}^{b},\tau _{2}^{b},w,u,h,\bar{h},k,e(g,f)^{\alpha b})$, $SK :=(VK,g^{\alpha },f^{\alpha },v,v_{1},v_{2})$, and $apk :=\zeta$. $\mathcal {B}_{3}$ can generate a Type A signature by using the (normal) signing algorithm since it has $\alpha$ and $g^{a_1}$. Thus, $\mathcal {B}_{3}$ can return valid encrypted signatures under $apk = \zeta$ for queries to $\mathcal {C}\mathcal {O}$. It also has $\beta$, so it can decrypt all valid VESs and perfectly simulate all queries to $\mathcal {A}\mathcal {O}$.

If adversary $\mathcal {A}$ outputs a Type B forgery $\sigma _1 :=(g^{\alpha a_1}v^r)\cdot g^{-a_{1}a_{2}\gamma }$, $\sigma _2 :=(g^{-\alpha }v_{1}^{r}g^{z_1})\cdot g^{a_{2}\gamma }$, $\sigma _3 :=(g^b)^{-z_1}$, $\sigma _4 :=(v_{2}^{r}g^{z_2})\cdot g^{a_{1}\gamma }$, $\sigma _5 :=(g^b)^{-z_2}$, $\sigma _6 :=(g^b)^{r_2}$, $\sigma _7 :=g^{r_1}$, $\vartheta :=H_{k}(M\parallel \sigma _{3},\ldots ,\sigma _{7})$, $m :=H_{k}(g^{\vartheta }\bar{h}^{\varphi })$, $\varphi$, and $\sigma _{0} :=(u^{m}w^{\mathsf {stag}}h)^{r_1}$ for some $r_1,r_2,z_1,z_2,\gamma \in \mathbb {Z}_{p}$ ($r = r_1 + r_2$), then $\mathcal {B}_{3}$ can compute $(g^{-a_{1}a_{2}\gamma },g^{a_{1}\gamma },g^{a_{2}\gamma })$ from $\sigma _1,\sigma _4,\sigma _2$, respectively. The reason is as follows.

$\mathcal {B}_{3}$ has $b$, so it can compute $g^{z_{1}}$, $g^{z_{2}}$, $g^{r_{1}}$, $g^{r_{2}}$ from $\sigma _3 = g^{-b z_{1}}$, $\sigma _5 = g^{-b z_{2}}$, $\sigma _7 = g^{r_{1}}$, $\sigma _6 = g^{b r_{2}}$, respectively, and obtain $g^r = g^{r_{1}+r_{2}}$, $v^r = g^{r y_{v}}$, $v_{1}^{r} = g^{r y_{v_1}}$, $v_{2}^{r} = g^{r y_{v_2}}$ ($\mathcal {B}_{3}$ has $y_v,y_{v_1},y_{v_2}$). Thus, $\mathcal {B}_{3}$ can extract $(g^{-a_{1}a_{2}\gamma },g^{a_{1}\gamma },g^{a_{2}\gamma })$ from $\sigma _1,\sigma _2,\sigma _4$ and can solve the DLIN problem by checking whether $e(g^x , g^{-a_{1}a_{2}\gamma })^{-1} \cdot e(f^y,g^{a_{2}\gamma }) = e(g^{a_{1}\gamma },T)$ because $e(g^x , g^{-a_{1}a_{2}\gamma })^{-1} \cdot e(g^{a_{1}y},g^{a_{2}\gamma }) = e(g,g)^{a_{1}a_{2}\gamma x + a_{1}a_{2}\gamma y} = e(g,g)^{a_{1}a_{2}\gamma (x+y)}$. If $T= g^{a_{2}(x+y)} = \nu ^{x+y}$, then the equation holds. Thus, $\mathcal {B}_{3}$ can solve the DLIN problem if $\mathcal {A}$ outputs a Type B forgery. Note that in this game, $\mathcal {A}$ outputs $M^{*} \ne M_{i}$ for all $i \in [q_{\mathsf {C}}]$. $\square$

We complete the proof of Theorem 7 by using Lemmas 5, 6, 7, and 8. $\square$

5 Application to obfuscators for ES and EVES

$\mathsf {sWdVES}$ can be used to construct new obfuscators for an ES and EVES. Hada [41] constructed an obfuscator for an ES by combining Waters’ signature [52] and the linear encryption scheme. The linear encryption scheme proposed by Boneh et al. [9] is as follows.

• ${\mathsf {L.Gen}} (1^\lambda )$: On input security parameter $\lambda$, it generates $\varGamma :=(p,\mathbb {G},\mathbb {G}_{T},g,e) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda })$, selects exponents $x_e, y_e\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$, and outputs $pk :=(f_e,h_e) :=(g^{x_e},g^{y_e})$, $dk :=(x_e,y_e)$.

• $\mathsf {L.Enc}(pk_e,m)$: On input $m \in \mathbb {G}$ and $pk=(f_e,h_e)$ it selects $r,s \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_{p}$ and outputs $c:=(f_{e}^{r},h_{e}^{s},g^{r+s}m)$.

• $\mathsf {L.Dec}(dk,c)$: On input $c=(c_1,c_2,c_3)$ and $dk$, it outputs $m :=c_3/ (c_{1}^{1/x_e}c_{2}^{1/y_e})$.

Hada’s idea is as follows. Suppose that signature $\sigma$ is computed as $\sigma = sk \cdot G(m)$ where $sk \in \mathbb {G}$ is the signing key, $m \in \mathbb {Z}_p$ is the message and $G: \mathbb {Z}_p\rightarrow \mathbb {G}$ is an efficiently computable function. Then, for ciphertext $c = \mathsf {L.Enc}(pk_e,sk)$, we can compute $\tilde{c} :=c \cdot G(m) = \mathsf {L.Enc}(pk_e, sk \cdot G(m))$ by the homomorphic property of the linear encryption scheme. This is exactly an encrypted signature. The ciphertext of $sk$ can be seen as an obfuscated circuit for encrypted signatures since the linear encryption scheme is semantically secure and no information about $sk$ is revealed. We extend Hada’s construction, that is, we combine $\mathsf {sWdVES}$ based on strongly unforgeable Waters’ dual signature and the linear encryption scheme. However, Waters’ dual signature is more complex than Waters’ signature at Eurocrypt’05, so it is non-trivial whether we can directly use Hada’s technique. In Waters’ signature at Eurocrypt’05, the signing algorithm does not exponentiate $sk$, but in Waters’ dual signature, it does. However, we can resolve this problem by using multiplicatively homomorphic property of the linear encryption scheme, that is, we can compute $c^{r} \cdot G(m) = \mathsf {L.Enc}(pk, sk^{r} \cdot G(m))$. Therefore, if we encrypt $sk = (g^{\alpha },g^{\alpha a_{1}},g^{a_{1}a_{2}})$ by linear encryption, then we can construct an obfuscator for an ES/EVES. We propose secure obfuscators for an ES and EVES in the section.

5.1 Secure obfuscation

We review some definitions for secure obfuscators for ESs/EVESs.

Average-case secure obfuscation. We review an extended notion of the average-case virtual black-box property (ACVBP) by Hohenberger et al. [43]. They proposed the definition to overcome the impossibility results by Barak et al. [4].

Definition 15

(Average-Case Secure Obfuscation [43]) An efficient algorithm $\mathsf {Obf}$ that takes as input a (probabilistic) circuit and outputs a new (probabilistic) circuit, is an average-case secure obfuscator for the family $\mathcal {C}=\{\mathcal {C}_{\lambda }\}$ where $\mathcal {C}_{\lambda }$ are the circuits in $\mathcal {C}$ with input length $\lambda$ if it satisfies the following properties:

• Preserving Functionality: For any input length $\lambda$ and $C\in \mathcal {C}_{\lambda }$, it holds that

  $$\begin{aligned} \Pr _{\text{ coins } \text{ of } \mathsf {Obf}}[\exists x\in \{0,1\}^{\lambda } : \Delta (\mathsf {Obf}(C)(x),C(x)) \text{ is } \text{ not } \text{ negligible } \text{ in } \lambda ] \end{aligned}$$

  is negligible in $\lambda$. The distributions $\mathsf {Obf}(C)(x)$ and $C(x)$ are taken over $\mathsf {Obf}(C)$’s and $C$’s random coins, respectively. $\Delta$ denotes statistical distance.

• Polynomial Blowup: There exists a polynomial $p$ such that for sufficiently large input length $\lambda$ and any $C\in \mathcal {C}_{\lambda }$, $\left| \mathsf {Obf}(C)\right| \le p(\left| C\right| )$.

• Average-Case Secure Virtual Black-Box: For any efficient adversary $\mathcal {A}$, there exists an efficient simulator $\mathcal {S}$ such that for every efficient distinguisher $\mathcal {D}$ and every auxiliary input $\mathsf {z}\in {\mathsf {poly}}(\lambda )$ (where ${\mathsf {poly}}$ is any polynomial),

  $$\begin{aligned} \left| \Pr \left[ \begin{array}{l}\mathcal {D}^{C}(\mathcal {A}(\mathsf {Obf}(C),\mathsf {z}),\mathsf {z})\rightarrow 1 \mid \\ C\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {C}_{\lambda } \end{array}\right] - \Pr \left[ \begin{array}{l}\mathcal {D}^{C}(\mathcal {S}^{C}(1^{\lambda },\mathsf {z}),\mathsf {z}) \rightarrow 1 \mid \\ C\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {C}_{\lambda } \end{array}\right] \right| \end{aligned}$$

  is negligible in $\lambda$. The probability is over the selection of a random circuit $C$ from $\mathcal {C}_{\lambda }$, and the coins of the distinguisher, simulator, oracle and obfuscator. Note that entities with black-box access to $C$ cannot set $C$’s random tape.

We review the ACVBP with respect to dependent oracles introduced by Hada [41] since our obfuscator is secure in this sense. Hada proposed the definition to consider the security of obfuscators for ES functionality. In the setting of ES functionalities, the adversary can access a signing oracle and is given a public-key used for encrypted signatures. However, the setting is not sufficient for meaningful security and a stronger security is required. That is, the adversary should be given not only the public-key but also an obfuscated circuit of an ES functionality (not black-box access). Hada showed that if an ES scheme satisfies the weaker security requirement (the adversary is given only a public-key) and its obfuscator satisfies ACVBP with respect to dependent oracles, then it also satisfies the stronger security requirement (the adversary is given an obfuscated circuit).

Definition 16

(Average-Case Secure Obfuscation w.r.t. Dependent Oracles [41]) An efficient algorithm $\mathsf {Obf}$ that takes as input a (probabilistic) circuit and outputs a new (probabilistic) circuit, is an average-case secure obfuscator for the family $\mathcal {C}=\{\mathcal {C}_{\lambda }\}$ if it satisfies the following properties:

• Preserving Functionality: This is the same as Definition 15.

• Polynomial Blowup: This is the same as Definition 15.

• Average Case Virtual Black-Box Property w.r.t. Dependent Oracles: Let $T(C)$ be a set of oracles dependent on the circuit $C$. A circuit obfuscator $\mathsf {Obf}$ for $\mathcal {C}$ satisfies the ACVBP w.r.t. dependent oracle set $T$ if the following condition holds. For any PPT $\mathcal {A}$, there exists a PPT $\mathcal {S}$ such that for any PPT $\mathcal {D}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

  $$\begin{aligned} \left| \Pr \left[ \begin{array}{l}\mathcal {D}^{C,T(C)}(\mathcal {A}(\mathsf {Obf}(C),\mathsf {z}),\mathsf {z})\rightarrow 1 \mid \\ C\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {C}_{\lambda } \end{array}\right] - \Pr \left[ \begin{array}{l}\mathcal {D}^{C,T(C)}(\mathcal {S}^{C}(1^{\lambda },\mathsf {z}),\mathsf {z}) \rightarrow 1 \mid \\ C\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {C}_{\lambda } \end{array}\right] \right| \end{aligned}$$

  is negligible in $\lambda$. Note that entities with black-box access to $C$ and $T(C)$ cannot set $C$’s and $T(C)$’s random tapes, respectively.

5.2 Security of ES and EVES

We review the definitions proposed by Hada [41]. In the following definitions, $\mathcal {SO}$ is a signing oracle, that is, if a message $M$ is queried by the adversary, then $\mathcal {SO}$ returns a valid signature for $M$ by using the secret key. First, we consider a weak security game where the adversary can access the signing oracle and is given a public key for encrypted signature.

Definition 17

(Existential Unforgeability w.r.t. ES Functionality) Let ${\mathsf {PKE}}$ and ${\mathsf {SIG}}$ be a pair of PKE and SIG schemes. ${\mathsf {SIG}}$ is existentially unforgeable w.r.t. ES functionality if the following condition holds. For every PPT $\mathcal {A}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

$$\begin{aligned} \Pr \left[ \begin{array}{l} {\mathsf {SIG}.}\mathsf {Vrfy}(vk,M^{*},\sigma ^{*})\rightarrow 1 \\ \wedge M^{*} \notin Q \end{array} \left| \begin{array}{l} \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Setup}(1^{\lambda }); \\ (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}.}\mathsf {Gen}(\varGamma ) ; \\ (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) ;\\ (M^{*},\sigma ^{*},Q) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}^{\mathcal {SO}(sk,\cdot )}(\varGamma ,vk,pk_e,\mathsf {z}) \end{array}\right. \right] \end{aligned}$$

is negligible in $\lambda$.

Next, we consider a strong security game where the adversary is given an obfuscated circuit of an ES functionality.

Definition 18

(Existential Unforgeability w.r.t. ES Obfuscator) Let ${\mathsf {PKE}}$ and ${\mathsf {SIG}}$ be a pair of PKE and SIG schemes. Let ${\mathsf {Obf}}_{\mathsf {ES}}$ be a circuit obfuscator for ${\mathsf {ES}}_{\lambda }$. ${\mathsf {SIG}}$ is existentially unforgeable w.r.t. $\mathsf {Obf}_{\mathsf {ES}}$ if the following condition holds. For any PPT $\mathcal {A}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

$$\begin{aligned} \Pr \left[ \begin{array}{l} {\mathsf {SIG}.}\mathsf {Vrfy}(vk,M^{*},\sigma ^{*})\rightarrow 1 \\ \wedge M^{*} \notin Q \end{array} \left| \begin{array}{l} \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Setup}(1^{\lambda });\\ (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}.}\mathsf {Gen}(\varGamma );\\ (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) ;\\ C^{\prime } \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Obf}_{\mathsf {ES}}(C_{sk,pk_e}) ;\\ (M^{*},\sigma ^{*},Q) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}^{\mathcal {SO}(sk,\cdot )}(\varGamma ,vk,pk_e,C^{\prime },\mathsf {z}) \end{array}\right. \right] \end{aligned}$$

is negligible in $\lambda$.

We extend these definitions to consider EVES functionalities. We can easily achieve this by adding a public-key of an adjudicator as input to $\mathcal {A}$ and giving the creation and adjudication oracles (the signing oracle in the security game for ES functionality is replaced with a oracle set that consists of those two oracles).

Definition 19

(Existential Unforgeability w.r.t. EVES Functionality) Let ${\mathsf {PKE}}$ and ${\mathsf {VES}}$ be a pair of PKE and VES schemes. ${\mathsf {VES}}$ is existentially unforgeable w.r.t. EVES functionality if the following condition holds. For any PPT $\mathcal {A}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

$$\begin{aligned} \Pr \left[ \begin{array}{l} \mathsf {VesVrfy}(apk,vk,\omega ^{*},M^{*})\rightarrow 1 \wedge M^{*} \notin Q_{\mathsf {C}} \wedge M^{*} \notin Q_{\mathsf {A}} \mid \\ \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Setup}(1^{\lambda }); \\ (apk,ask) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(\varGamma );(vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(\varGamma ) ; (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) ;\\ (M^{*},\omega ^{*},Q_{\mathsf {C}},Q_{\mathsf {A}}) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}^{\mathcal {CO}(sk,apk,\cdot ),\mathcal {AO}(ask,apk,vk,\cdot ,\cdot )}(\varGamma , vk,pk_e,apk,\mathsf {z}) \end{array} \right] \end{aligned}$$

is negligible in $\lambda$.

Definition 20

(Opacity w.r.t. EVES Functionality) Let ${\mathsf {PKE}}$ and ${\mathsf {VES}}$ be a pair of PKE and VES schemes. ${\mathsf {VES}}$ is opaque w.r.t. EVES functionality if the following condition holds. For any PPT $\mathcal {A}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

$$\begin{aligned} \Pr \left[ \begin{array}{l} \mathsf {Vrfy}(vk,\sigma ^{*},M^{*})\rightarrow 1 \wedge M^{*} \notin Q_{\mathsf {A}} \mid \\ \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Setup}(1^{\lambda }); \\ (apk,ask) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(\varGamma );(vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(\varGamma ) ; (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) ;\\ \! (M^{*},\sigma ^{*},Q_{\mathsf {C}},Q_{\mathsf {A}}) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}^{\mathcal {C O}(sk,apk,\cdot ),\mathcal {A O}(ask,apk,vk,\cdot ,\cdot )}(\varGamma , vk,pk_e,apk,\mathsf {z}) \end{array} \right] \end{aligned}$$

is negligible in $\lambda$.

Definition 21

(Existential Unforgeability w.r.t. EVES Obfuscator) Let ${\mathsf {PKE}}$ and ${\mathsf {VES}}$ be a pair of PKE and VES schemes. Let ${\mathsf {Obf}}_{\mathsf {EVES}}$ be a circuit obfuscator for ${\mathsf {EVES}}_{\lambda }$. ${\mathsf {VES}}$ is unforgeability w.r.t. $\mathsf {Obf}_{\mathsf {EVES}}$ if the following condition holds. For any PPT $\mathcal {A}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

$$\begin{aligned} \Pr \left[ \begin{array}{l} \mathsf {VesVrfy}(apk,vk,\omega ^{*},M^{*})\rightarrow 1 \wedge M^{*} \notin Q_{\mathsf {C}} \wedge M^{*} \notin Q_{\mathsf {A}} \mid \\ \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Setup}(1^{\lambda });\\ (apk,ask) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(\varGamma ); (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(\varGamma ) ; (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) ;\\ C^{\prime } \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Obf}_{\mathsf {EVES}}(C_{sk,pk_e,apk}) ;\\ (M^{*},\omega ^{*},Q_{\mathsf {C}},Q_{\mathsf {A}}) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}^{\mathcal {C O}l(sk,apk,\cdot ) ,\mathcal {A O}(ask,apk,vk,\cdot ,\cdot )} (\varGamma , vk,pk_e,apk,C^{\prime },\mathsf {z}) \end{array} \right] \end{aligned}$$

is negligible in $\lambda$.

Definition 22

(Opacity w.r.t. EVES Obfuscator) Let ${\mathsf {PKE}}$ and ${\mathsf {VES}}$ be a pair of PKE and VES schemes. Let ${\mathsf {Obf}}_{\mathsf {EVES}}$ be a circuit obfuscator for ${\mathsf {EVES}}_{\lambda }$. ${\mathsf {VES}}$ is opaque w.r.t. $\mathsf {Obf}_{\mathsf {EVES}}$ if the following condition holds. For any PPT $\mathcal {A}$ and every auxiliary input $\mathsf {z}\in \{0,1\}^{{\mathsf {poly}}(\lambda )}$,

$$\begin{aligned} \Pr \left[ \begin{array}{l} \mathsf {Vrfy}(vk,\sigma ^{*},M^{*})\rightarrow 1 \wedge M^{*} \notin Q_{\mathsf {A}} \mid \\ \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Setup}(1^{\lambda }); \\ (apk,ask) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(\varGamma );(vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(\varGamma ) ; (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) ;\\ C^{\prime } \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Obf}_{\mathsf {EVES}}(C_{sk,pk_e,apk}) ;\\ (M^{*},\sigma ^{*},Q_{\mathsf {C}},Q_{\mathsf {A}}) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {A}^{\mathcal {CO}(sk,apk,\cdot ),\mathcal {AO}(ask,apk,vk,\cdot ,\cdot )}(\varGamma , vk,pk_e,apk,C^{\prime },\mathsf {z}) \end{array} \right] \end{aligned}$$

is negligible in $\lambda$.

Theorem 8

Let oracle set $T(C_{\varGamma ,sk,apk,pk_e})$ be $\{\mathcal {C}\mathcal {O}(sk,apk,\cdot ), \mathcal {A}\mathcal {O}(ask,apk,vk,\cdot ,\cdot )\}$ where $C_{\varGamma , sk,apk,pk_e}$ is a circuit for the EVES functionality. If $\mathsf {Obf}$ for EVES satisfies the ACVBP w.r.t. dependent oracle set $T$, then the existential-unforgeability/opacity w.r.t. EVES functionality implies existential-unforgeability/opacity w.r.t. the EVES obfuscator, respectively.

The proof of this theorem is almost the same as that of Hada [41], but we write it for confirmation.

Proof

We show that if we assume that the existential-unforgeability/opacity w.r.t. an EVES functionality is satisfied but there exists $\mathcal {A}$ that breaks existential-unforgeability/opacity w.r.t. the EVES obfuscator, then $\mathsf {Obf}$ does not satisfy the ACVBP w.r.t. dependent oracle set $T$, that is, there exists a distinguisher $\mathcal {D}$ for ACVBP w.r.t. dependent oracle set $T$. We construct $\mathcal {D}$ as follows.

• 1. It is given an auxiliary-input $\mathsf {z}$ and a target circuit $\hat{C}$ that is either a real obfuscated circuit or a simulated circuit by a simulator.

• 2. It obtains keys $(\varGamma ,vk,apk,pk_e)$ by oracle access to $C_{\varGamma ,sk,apk,pk_e}$ with input $\mathsf {keys}$.

• 3. It gives keys $(\varGamma ,vk,apk,pk_e)$, $\hat{C}$ and auxiliary input $\mathsf {z}$ to $\mathcal {A}$ as inputs.

• 4. It simulates the creation and adjudication oracles by using oracle access to oracle set $T(C_{\varGamma ,sk,apk,pk_e})$.

• 5. It outputs $1$ if and only if the winning condition of the existential-unforgeability/opacity w.r.t. the EVES obfuscator holds, respectively.

It holds that $T(C_{\varGamma ,sk,apk,pk_e}) = \{\mathcal {C}\mathcal {O}(sk,apk,\cdot ), \mathcal {A}\mathcal {O}(ask,apk,vk,\cdot ,\cdot )\}$, so the oracle simulation above is perfect. If the target circuit is the real obfuscated circuit, then the simulation above perfectly simulates the experiment of existential-unforgeability/opacity w.r.t. the EVES obfuscator and $\mathcal {A}$ has a non-negligible advantage. If the target circuit is the simulated one, then the distribution of inputs to $\mathcal {A}$ is not correct and it does not have a non-negligible advantage. Therefore, $\mathcal {D}$ can distinguish two circuits by using $\mathcal {A}$. $\square$

5.3 Constructions of obfuscator for ES/EVES

To satisfy the virtual black-box property, we must construct simulator $\mathcal {S}$ that outputs an indistinguishable view from the real one. $\mathcal {S}$ does not have $sk$, so it encrypts random dummy elements over $\mathbb {G}$ instead of $sk$ and sets them as an obfuscated circuit. Encrypted signatures/VESs under semantic secure PKE are indistinguishable from ciphertexts of dummy messages. By semantic security of the linear encryption, the view by $\mathcal {S}$ is indistinguishable from the real one. Thus, we can achieve obfuscators for ESs/EVESs.

5.3.1 Obfuscator for EVES

A naive construction of an EVES is the sequential composition of the VES scheme discussed in Sect. 4 and the linear encryption scheme (create-then-encrypt). We define the family of circuits as

$$\begin{aligned} {\mathsf {EVES}}_{\lambda } :=\left\{ \begin{array}{l}C_{\varGamma ,sk,apk,pk_e} \end{array} \left| \begin{array}{l} (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Gen}(\varGamma ), \\ (apk,ask)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {AdjGen}(\varGamma ),\\ (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Gen}(\varGamma )\end{array} \right. \right\} , \end{aligned}$$

where each circuit $C_{\varGamma ,sk,apk,pk_e} \in {\mathsf {EVES}}_{\lambda }$ (for notational convention, we often omit $\varGamma ,sk,apk,pk_e$ and use just $C$ if it is clear from the context) is a probabilistic circuit that consists of the following two algorithms. ${\mathsf {EVES}}_{sk,apk,pk_e}(M)$ takes $M$ as input, generates $\omega \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Create}(sk,apk,M)$, and computes $C_{\omega } :=\mathsf {L.Enc}(pk,\omega )$; $\mathsf {Keys}_{sk,apk,pk_e}(\mathsf {keys})$ takes $\mathsf {keys}$ as input and outputs $(\varGamma ,vk,apk,pk_e)$.

We introduce a re-randomization algorithm for the linear encryption $\mathsf {ReRand}(pk_e,c_1,c_2,c_3)$ that takes as inputs $pk_e = (f_e,h_e)$ and a ciphertext of the linear encryption, selects $r^{\prime } , s^{\prime }\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, and outputs $(c_1 \cdot f_{e}^{r^{\prime }},c_{2}\cdot h_{e}^{s^{\prime }},c_3 \cdot g^{r^{\prime }+s^{\prime }})$.

Our obfuscator for an EVES is described in Fig. 1. We can see $ct _{sk}$ as a ciphertext of signing key $sk$. It is encrypted by $pk_e$ and $apk = \zeta$. If we set $\rho _{1}^{\prime } :=\varrho _{2} + \gamma \varrho _{3} + \rho _1$ and $\rho _{2}^{\prime } :=\varrho _{1}+ \rho _2$, then, by using the homomorphic property of the linear and ElGamal encryption schemes, we can write

$$\begin{aligned} (c_{1,1},c_{1,2},\Psi _1)&\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e, g^{\alpha a_1} v^r g^{- a_{1} a_{2} \gamma } \cdot \zeta ^{\rho _{1}^{\prime }} = K_1), \\ (K_{1}^{\prime },\hat{K}_{1})&= (g^{\varrho _{2}+ \varrho _{3} \gamma + \rho _1}, (g^b)^{\varrho _{2}+ \varrho _{3} \gamma + \rho _1}) = (g^{\rho _{1}^{\prime }},(g^b)^{\rho _{1}^{\prime }}), \\ (c_{2,1},c_{2,2},\Psi _2)&\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e, g^{-\alpha } v_{1}^{r} g^{z_1} g^{a_{2} \gamma } \cdot \zeta ^{\rho _{2}^{\prime }} = K_2), \\ (K_{2}^{\prime },\hat{K}_{2})&= (g^{\varrho _{1}+ \rho _2}, (g^{b a_1})^{\varrho _{1}+ \rho _2}) = (g^{\rho _{2}^{\prime }},(g^{b a_1})^{\rho _{2}^{\prime }}) \end{aligned}$$

by simple calculation. That is, we can write $C_{i} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {Enc}(pk_e,K_{i})$ for not only $i = 0,3,4,5,6,7$ but also $i =1,2$. Thus, we can verify that the output of $\mathsf {Obf}_{\mathsf {EVES}}(M)$ is identically distributed to the output of $C_{sk,apk,pk_e}(M)$. We need the re-randomization procedure of the linear and ElGamal encryption schemes to prove the security.

Fig. 1

Obfuscator for EVES

Remark

The proposed obfuscator encrypts elements in $\mathbb {Z}_p$ by using the linear encryption scheme. The message space of the linear encryption scheme is $\mathbb {G}$, so if we do not have an encoding between $\mathbb {Z}_p$ and $\mathbb {G}$, then we cannot use the linear encryption scheme. If we use a special elliptic curve defined by equation $y^2 = x^3 + b$, then we have such an encoding [8] and our construction works. Moreover, if we encrypt elements in $\mathbb {Z}_{p^{\prime }}$ such that $p^{\prime } < p$, then we can use an injective encoding proposed by Fouque, Joux, and Tibouchi [29].

Theorem 9

Let $T(C_{sk,apk,pk_e})$ be $\{\mathcal {CO}(sk,apk,\cdot ), \mathcal {AO}(ask,apk,vk,\cdot ,\cdot )\}$. If the DLIN assumption holds, then $\mathsf {Obf}_{\mathsf {EVES}}$ satisfies ACVBP w.r.t. dependent oracle set $T$.

Proof

We construct a simulator, $\mathcal {S}$. It does not have secret signing key $sk$, so it acts as follows.

• 1. Queries oracle $C$ on $\mathtt keys$ to obtain $(\varGamma ,vk,pk_e,apk)$.

• 2. Parses $vk = (g,g^b,g^{a_1},g^{a_2},g^{b a_1},g^{b a_2}, \tau _1, \tau _2, \tau _{1}^{b}, \tau _{2}^{b},w,u,h,\bar{h},k,e(g,g)^{\alpha a_1 b})$ and $apk = \zeta$.

• 3. Samples dummy elements $J_{\alpha },J_{\alpha a_1}, J_{a_{1}a_{2}}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$ and exponents $\varrho _{1},\varrho _{2}, \varrho _{3} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$.

• 4. Generates $(c_{\alpha ,1}^{\prime },c_{\alpha ,2}^{\prime },c_{\alpha ,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{\alpha })$.

• 5. Sets $c_{\alpha } :=(c_{\alpha ,1}^{\prime },c_{\alpha ,2}^{\prime },c_{\alpha ,3}^{\prime }\cdot \zeta ^{\varrho _{1}},g^{\varrho _{1}},g^{b a_1 \varrho _{1}})$.

• 6. Generates $(c_{\alpha a_1,1}^{\prime },c_{\alpha a_1,2}^{\prime },c_{\alpha a_1,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{\alpha a_1})$.

• 7. Sets $c_{\alpha a_1} :=(c_{\alpha a_1,1}^{\prime },c_{\alpha a_1,2}^{\prime },c_{\alpha a_1,3}^{\prime }\cdot \zeta ^{\varrho _{2}},g^{\varrho _{2}},g^{b \varrho _{2}})$.

• 8. Generates $(c_{ a_{1} a_{2},1}^{\prime },c_{ a_{1} a_{2}, 2}^{\prime },c_{ a_{1} a_{2},3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{ a_{1} a_{2}})$.

• 9. Sets $c_{ a_1 a_{2}} :=(c_{ a_1 a_{2},1}^{\prime },c_{ a_1 a_{2},2}^{\prime },c_{ a_1 a_{2},3}^{\prime }\cdot \zeta ^{\varrho _{3}},g^{\varrho _{3}},g^{b \varrho _{3}})$.

• 10. Sets $ct _{J} :=(c_{\alpha },c_{\alpha a_1},c_{a_{1} a_{2}})$.

• 11. Outputs circuit $(\varGamma ,vk,apk,pk_e,\mathsf {Ct}_{J})$.

We consider the following distributions.

$$\begin{aligned}&\quad \mathsf {Real}^{}\mathrm - \mathsf {C} (\mathcal {D},\lambda ,\mathsf {z}): \\&\quad \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda }); (pk_e,dk) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Gen}(\varGamma ); (vk,sk) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {W.Gen}(\varGamma ); \\&\quad \beta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p; (apk,ask) :=(g^{\beta },\beta ); \\&\quad (c_{\alpha ,1}^{\prime },c_{\alpha ,2}^{\prime },c_{\alpha ,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,g^{-\alpha });\ c_{\alpha } :=(c_{\alpha ,1}^{\prime },c_{\alpha ,2}^{\prime },c_{\alpha ,3}^{\prime }\cdot \zeta ^{\varrho _{1}},g^{\varrho _{2}},g^{b a_1 \varrho _{1}});\\&\quad (c_{\alpha a_1,1}^{\prime },c_{\alpha a_1,2}^{\prime },c_{\alpha a_1,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,g^{\alpha a_1}); \\&\quad c_{\alpha a_1} :=(c_{\alpha a_1,1}^{\prime },c_{\alpha a_1,2}^{\prime },c_{\alpha a_1,3}^{\prime }\cdot \zeta ^{\varrho _{2}},g^{\varrho _{2}},g^{b \varrho _{2}}) ;\\&\quad (c_{ a_1 a_{2},1}^{\prime },c_{ a_1 a_{2},2}^{\prime },c_{ a_1 a_{2},3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,g^{- a_1 a_{2}}); \\&\quad c_{ a_1 a_{2}} :=(c_{ a_1 a_{2},1}^{\prime },c_{a_1 a_{2},2}^{\prime },c_{ a_1 a_{2},3}^{\prime }\cdot \zeta ^{\varrho _{3}},g^{\varrho _{3}},g^{b \varrho _{3}}); \\&\quad ct _{sk} :=(c_{\alpha },c_{\alpha a_1},c_{a_{1} a_{2}}); \\&\quad b \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {D}^{C}(\varGamma , vk,pk_e,apk, ct _{sk},\mathsf {z}).\\&\quad \mathsf {Sim}^{}\mathrm - \mathsf {C} (\mathcal {D},\lambda ,\mathsf {z}):\\&\quad \varGamma \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {G}_\mathsf {bmp}(1^{\lambda }); \ (pk_e,dk) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Gen}(\varGamma );\ (vk,sk) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {W.Gen}(\varGamma ); \\&\quad \beta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p;\ (apk,ask) :=(g^{\beta },\beta ); \\&\quad (c_{\alpha ,1}^{\prime },c_{\alpha ,2}^{\prime },c_{\alpha ,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{\alpha }); \ c_{\alpha } :=(c_{\alpha ,1}^{\prime },c_{\alpha ,2}^{\prime },c_{\alpha ,3}^{\prime }\cdot \zeta ^{\varrho _{1}},g^{\varrho _{1}},g^{b a_1 \varrho _{1}});\\&\quad (c_{\alpha a_1,1}^{\prime },c_{\alpha a_1,2}^{\prime },c_{\alpha a_1,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{\alpha a_1}); \\&\quad c_{\alpha a_1} :=(c_{\alpha a_1,1}^{\prime },c_{\alpha a_1,2}^{\prime },c_{\alpha a_1,3}^{\prime }\cdot \zeta ^{\varrho _{2}},g^{\varrho _{2}},g^{b \varrho _{2}}); \\&\quad (c_{ a_1 a_{2},1}^{\prime },c_{a_1 a_{2},2}^{\prime },c_{a_1 a_{2},3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{ a_1 a_{2}}); \\&\quad c_{ a_1 a_{2}} :=(c_{ a_1 a_{2},1}^{\prime },c_{ a_1 a_{2},2}^{\prime },c_{ a_1 a_{2},3}^{\prime }\cdot \zeta ^{\varrho _{3}},g^{\varrho _{3}},g^{b \varrho _{3}}); \\&\quad ct _{J} :=(c_{\alpha },c_{\alpha a_1},c_{a_{1} a_{2}}); \\&\quad b \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathcal {D}^{C}(\varGamma , vk,pk_e,apk, ct _{J},\mathsf {z}). \end{aligned}$$

It holds that $\mathsf {Real}^{}\mathrm - \mathsf {C} (\mathcal {D},\lambda ,\mathsf {z}) = \mathcal {D}^{C}(\mathsf {Obf}(C),\mathsf {z})$ and $\mathsf {Sim}^{}\mathrm - \mathsf {C} (\mathcal {D},\lambda ,\mathsf {z}) = \mathcal {D}^{C}(\mathcal {S}^{C}(1^\lambda , \mathsf {z}),\mathsf {z})$. We let $J_{1} :=J_{\alpha }, J_{2} :=J_{\alpha a_{1}}, J_{3} :=J_{a_{1}a_{2}}$. We consider hybrid experiments $\mathsf {Hyb}_{i}^{C}$, where $i \in [3]$ for $j=1,\ldots ,i$, $(c_{1,1}^{\prime },c_{1,2}^{\prime },c_{1,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_{j})$, and for $j= i+1 ,\ldots ,3$, $(c_{1,1}^{\prime },c_{1,2}^{\prime },c_{1,3}^{\prime }) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,sk[j])$, where $(sk[1],sk[2], sk[3]) :=(g^{-\alpha },g^{\alpha a_1}, g^{- a_{1} a_{2}})$. It holds that $\mathsf {Hyb}_{0}^{C} = \mathsf {Real}^{}\mathrm - \mathsf {C}(\mathcal {D},\lambda ,\varvec{v},\mathsf {z}) = \mathcal {D}^{C}(\mathsf {Obf}(C),\mathsf {z})$ and $\mathsf {Hyb}_{3}^{C} = \mathsf {Sim}^{}\mathrm - \mathsf {C} (\mathcal {D},\lambda ,\mathsf {z}) = \mathcal {D}^{C}(\mathcal {S}^{C}(1^\lambda , \mathsf {z}),\mathsf {z})$. We can show $\mathsf {Hyb}_{i-1}^{C} \mathop {\approx }\limits ^{\mathsf {c}}\mathsf {Hyb}_{i}^{C}$. If there exists distinguisher $\mathcal {D}$ that can distinguish these two variables, then we can construct adversary $\mathcal {A}$ which breaks IND-CPA security of the linear encryption scheme. $\mathcal {A}$ takes as input common parameter $\varGamma$, public key $pk_e$, and auxiliary input $\mathsf {z}$. It selects $\beta \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$, sets $apk :=g^{\beta }$ and $ask:=\beta$, generates $(vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {sWd.Gen}(1^{\lambda })$, selects $J_{i}\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {G}$, sets $m_0 :=sk[i]$ and $m_1 :=J_{i}$, and returns $(m_0,m_1,vk)$. If $\mathcal {A}$ receives target ciphertext $c^{*}$, then $\mathcal {A}$ uses $\mathcal {D}$ as follows.

• 1. Parses $c^{*} = (c_{1}^{*},c_{2}^{*},c_{3}^{*})$.

• 2. For $j=1,\ldots ,i-1$, selects $\varrho _j \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$ and sets $(c_{i,1}^{\prime },c_{i,2}^{\prime },c_{i,3}^{\prime })\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,J_j)$ and $c_{sk[j]} :=(c_{i,1}^{\prime },c_{i,2}^{\prime },c_{i,3}^{\prime }\cdot \zeta ^{\varrho _j},g^{\varrho _j},\tilde{g}_{j}^{\varrho _j})$.

• 3. For $j=i$, selects $\varrho \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$ and sets $c_{sk[j]} :=(c_{1}^{*},c_{2}^{*},c_{3}^{*}\cdot \zeta ^{\varrho },g^{\varrho },\tilde{g}_{j}^{\varrho })$.

• 4. For $j=i+1,\ldots ,3$, selects $\varrho _j \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {U}}\mathbb {Z}_p$ and sets $(c_{i,1}^{\prime },c_{i,2}^{\prime },c_{i,3}^{\prime })\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,sk[j])$ and $c_{sk[j]} :=(c_{i,1}^{\prime },c_{i,2}^{\prime },c_{i,3}^{\prime }\cdot \zeta ^{\varrho _j},g^{\varrho _j},\tilde{g}_{j}^{\varrho _j})$.

• 5. Sets $ct _{sk} :=(c_{sk[1]} ,c_{sk[2]}, c_{sk[3]})$.

• 6. Gives $(\varGamma ,vk,pk_e,apk, ct _{sk})$ as inputs.

• 7. Simulates $\mathcal {D}^\mathcal {O}(\varGamma ,vk,pk_e,apk, ct _{sk},\mathsf {z})$, where oracle queries can be perfectly simulated by using $sk = (g^{\alpha },g^{\alpha a_1},g^{a_{1} a_{2}})$, $apk =\zeta$, and $pk_e$.

• 8. Outputs the output of $\mathcal {D}$.

Here, we set $\tilde{g}_{1} :=g^{b a_1}$, $\tilde{g}_{2} :=g^{b }$, $\tilde{g}_{3} :=g^b$.

If $c^{*}$ is an encryption of $m_0 = sk[i]$, then the distribution is the same as $\mathsf {Hyb}_{i-1}^{C}$. If $c^{*}$ is an encryption of $m_1 = J_{i}$, then the distribution is the same as $\mathsf {Hyb}_{i}^{C}$. Thus, if $\mathcal {D}$ can distinguish $\mathsf {Hyb}_{i-1}^{C}$ from $\mathsf {Hyb}_{i}^{C}$, then $\mathcal {A}$ can break semantic security of the linear encryption scheme. By transitivity, it holds that $\mathsf {Real}^{}\mathrm - \mathsf {C}(\mathcal {D},\lambda ,\mathsf {z}) = \mathsf {Hyb}_{1}^{C} \mathop {\approx }\limits ^{\mathsf {c}}\mathsf {Hyb}_{3}^{C} =\mathsf {Sim}^{}\mathrm - \mathsf {C} (\mathcal {D},\lambda ,\mathsf {z})$ and the theorem follows.$\square$

5.3.2 Obfuscator for ES

A naive construction of an ES is the sequential composition of a signature scheme and a encryption scheme (sign-then-encrypt), as Hada proposed [41]. We define the family of circuits as

$$\begin{aligned} {\mathsf {ES}}_{\lambda } :=\{C_{\varGamma ,sk,pk_e} | (vk,sk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {SIG}.}\mathsf {Gen}(\varGamma ), (pk_e,dk)\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}{\mathsf {PKE}.}\mathsf {Gen}(\varGamma ) \}, \end{aligned}$$

where each circuit $C_{sk,pk_e} \in {\mathsf {ES}}_{\lambda }$ is a probabilistic circuit that consists of the following two algorithms: ${\mathsf {ES}}_{sk,pk_e}(M)$ takes $M$ as input, generates $(\sigma _{0},\sigma _1,\ldots ,\sigma _{7}, \mathsf {stag},\varphi ) \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {sWd.Sign}(sk,M)$, computes $C_{i} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,\sigma _i)$, $C_{t} \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,\mathsf {stag})$, $C_{\varphi } \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,\varphi )$, and outputs $C_{\sigma } :=(C_0, \ldots , C_7 ,C_{t},C_{\varphi })$; $\mathsf {Keys}_{sk,pk_e}(\mathsf {keys})$ takes $\mathsf {keys}$ as input and outputs $(\varGamma ,vk,pk_e)$.

Our obfuscator for ES is easily obtained from our obfuscator for EVES and descried in Fig. 2.

Fig. 2

Obfuscator for ES

It holds that

$$\begin{aligned} (c_{1,1},c_{1,2},\Psi _1)&\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e, g^{\alpha a_1}\cdot v^r \cdot g^{- a_{1} a_{2} \gamma }) \\ (c_{2,1},c_{2,2},\Psi _2)&\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e, g^{-\alpha }\cdot v_{1}^{r}\cdot g^{z_1} \cdot g^{a_{2} \gamma }) \end{aligned}$$

by simple calculation. Thus, we can write $C_i \mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathsf {R}}\mathsf {L.Enc}(pk_e,\sigma _i)$ for not only $i =0, 3,4,5,6,7$ but also $i =1,2$. We can easily verify that ${\mathsf {ES}}_{sk,pk_e}(M)$ and $\mathsf {Obf}_{\mathsf {ES}}(M)$ are identically distributed.

Theorem 10

Let $T(C_{sk,pk_e})$ be $\mathcal {SO}(sk,\cdot )$. If the DLIN assumption holds, then $\mathsf {Obf}_{\mathsf {ES}}$ satisfies the ACVBP w.r.t. dependent oracle set $T$.

We can prove Theorem 10 by using the same proof technique as that of Theorem 9.