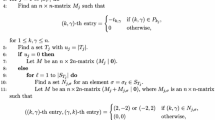An upper bound of the value of $t$ of the support $t$-designs of extremal binary doubly even self-dual codes

Abstract

Let $C$ be an extremal binary doubly even self-dual code of length $n$ and $D_{w}$ be the support design of $C$ for a weight $w$. We introduce the two numbers $\delta (C)$ and $s(C)$: $\delta (C)$ is the largest integer $t$ such that, for all wight, $D_{w}$ is a $t$-design; $s(C)$ denotes the largest integer $t$ such that there exists a $w$ such that $D_{w}$ is a $t$-design. In this paper, we consider the possible values of $\delta (C)$ and $s(C)$.

1 Introduction

Let $C$ be an extremal binary doubly even self-dual code (Type II code) of length $n$. Mallows et al. [10] showed that $C$ does not exist for all sufficiently large $n$. In 1999, it was shown by Zhang [11] that $C$ does not exist if $n=24m$ ($m \ge 154)$, $24m+8$ ($m \ge 159$), $24m+16$ ($m \ge 164$). A $t$-$(v,k,{\lambda })$ design is a pair $\mathcal {D}=(X,\mathcal {B})$, where $X$ is a set of points of cardinality $v$, and $\mathcal {B}$ a collection of $k$-element subsets of $X$ called blocks, with the property that any $t$ points are contained in precisely $\lambda$ blocks. It follows that every $i$-subset of points $(i \le t)$ is contained in exactly $\lambda _{i}= \lambda \left( {\begin{array}{c}v-i\\ t-i\end{array}}\right) / \left( {\begin{array}{c}k-i\\ t-i\end{array}}\right)$ blocks. The support $\text{ supp } (c)$ of a codeword $c=(c_{1}, \ldots , c_{n}) \in C$ is the set of indices of its nonzero coordinates: $\text{ supp } (c) = \{ i : c_{i} \ne 0 \}$. The support design of $C$ for a given nonzero weight $w$ ($w \equiv 0 \pmod 4$ and $4 \lfloor n/24 \rfloor +4 \le w \le n-(4 \lfloor n/24 \rfloor +4)$) is the design for which the points are the $n$ coordinate indices, and the blocks are the supports of all codewords of weight $w$. Let $D_{w}$ be the support design of $C$ for a weight $w$. Then it is known from the Assmus–Mattson theorem [2] that, for all $w$, $D_{w}$ is a $5$-, $3$- and $1$-design for $n=24m$, $24m+8$ and $24m+16$, respectively.

Let

$$\begin{aligned} \delta (C)&:=\max \{t\in \mathbb {N}\mid \forall w; D_{w} \text{ is } \text{ a } t\text{-design }\!\!\},\\ s(C)&:=\max \{t\in \mathbb {N}\mid \exists w; \text{ s.t. } D_{w} \text{ is } \text{ a } t\text{-design }\!\!\}. \end{aligned}$$

Note that $\delta (C) \le s(C)$.

In this paper, we consider the possible values of $\delta (C)$ and $s(C)$. Our motivations are the following problems.

Problem 1.1

Find an upper bound of $s(C)$.

Problem 1.2

Does the case occur for $\delta (C) < s(C)$ ?

First, we provide some known results for $\delta (C)$ and $s(C)$. The following theorem gives the lower bound of $\delta (C)$ due to Janusz [9].

Theorem 1.3

Let $C$ be an extremal binary doubly even self-dual code of length $n=24m+8r$, $r=0,1$ or $2$. Then either $\delta (C) \ge 7-2r$, or $\delta (C)= 5-2r$ and there is no nontrivial weight $w$ such that $D_{w}$ holds a $(1+ \delta (C))$-design.

We collect some known results for the support $t$-design of the minimum weight. Let $D_{4m+4}^{24m}$ be the support $t$-design of the minimum weight of an extremal binary doubly even self-dual $[24m,12m,4m+4]$ code. By the Assmus–Mattson theorem, $D_{4m+4}^{24m}$ is a $5$-$\left( 24m,4m+4,\left( {\begin{array}{c}5m-2\\ m-1\end{array}}\right) \right)$ design. Suppose that $D_{4m+4}^{24m}$ is a $t$-$(24m,4m+4,\lambda _{t})$ design with $t \ge 6$. Then $\lambda _{t}= \left( {\begin{array}{c}5m-2\\ m-1\end{array}}\right) \left( {\begin{array}{c}4m-1\\ t-5\end{array}}\right) /\left( {\begin{array}{c}24m-5\\ t-5\end{array}}\right)$ is a nonnegative integer. It is known that if $D_{4m+4}^{24m}$ is a $6$-design, then it is a $7$-design by a strengthening of the Assmus–Mattson theorem [5]. In 2006, Bannai et al. [4] showed that $D_{4m+4}^{24m}$ is never a $9$-design. In [7, 8], we showed that $D_{4m+4}^{24m}$ is never an $8$-design.

We investigate the support designs of the non minimum weights and as a corollary, we have an upper bound of $s(C)$. This paper is organized as follows. In Sect. 2, we recall the definition and some properties of the harmonic weight enumerators, which were introduced in [3], and which will be our main tool to study the support designs for the non minimum weights. In particular, we will use the fact that the harmonic weight enumerators of Type II codes are related to the invariant rings of some finite subgroups of $GL(2,{\mathbb {C}})$. By using these facts, we extend the methods of Bachoc [3] and Bannai et al. [4].

In Sect. 3, a proof of our result is given for each cases of lengths $24m$, $24m+8$ and $24m+16$. By using the methods of the harmonic weight enumerators, we give the results of the support designs for any weights in Propositions 3.1, 3.3 and 3.6. Then, by using these propositions, we apply our previous results [7, 8] of the minimum weight to the non minimum weights. Thus our result is the following theorem.

Theorem 1.4

Let $C$ be an extremal binary doubly even self-dual code of length $n$.

$(1)$ :

If $n=24m$, then $\delta (C)=s(C)=5$ or $\delta (C)=s(C)=7$.

$(2)$ :

If $n=24m+8$, then $\delta (C)=s(C)=3$ or $5 \le \delta (C) \le s(C) \le 7$.

$(3)$ :

If $n=24m+16$, then $\delta (C)=s(C)=1$ or $3 \le \delta (C) \le s(C) \le 5$.

It is still unknown whether $\delta (C)=s(C)=7$ (in case (1)) or $5\le \delta (C)\le s(C)\le 7$ (in case (2)) or $3\le \delta (C)\le s(C)\le 5$ (in case (3)), actually occurs or not. It is an interesting open problem to determine the existence of such examples. We give the details for each $m$ of the above theorem in Sects. 3.1, 3.2 and 3.3.

For Problem 1.1, we conclude that $s(C) \le 7$ for any extremal Type II code $C$. For Problem 1.2, if $n=24m$, we see that $\delta (C)<s(C)$ does not occur by (1) of Theorem 1.4. There is no known example of $\delta (C)<s(C)$. In the process of proving Theorem 1.4, we will see that, if $\delta (C)<s(C)$ occurs, it can only happen in a limited number of cases listed in the following proposition.

Proposition 1.5

If the case $\delta (C) < s(C)$ occurs, then one of the following holds:

$(1)$ :

$n=24m+8,\, m=58,\, \delta (C)=6$ and $s(C)= 7$ with $w=n/2$;

$(2)$ :

$n=24m+16,\, m \in \{10,\, 23,\, 79,\, 93,\, 118, \,120,\, 123,\, 125,\, 142\},\, \delta (C)=4$ and $s(C)= 5$ with $w=n/2$.

2 Harmonic weight enumerators

2.1 Harmonic weight enumerators

In this section, we extend a method of the harmonic weight enumerators which were used by Bachoc [3] and Bannai et al. [4]. For the reader’s convenience we quote the definitions and properties of discrete harmonic functions from [3, 6] (for more information the reader is referred to [3, 6]).

Let $\Omega =\{1, 2,\ldots ,n\}$ be a finite set (which will be the set of coordinates of the code) and let $X$ be the set of its subsets, while, for all $k= 0,1, \ldots , n$, $X_{k}$ is the set of its $k$-subsets. We denote by ${\mathbb {R}}X$, ${\mathbb {R}}X_k$ the free real vector spaces spanned by respectively the elements of $X$, $X_{k}$. An element of ${\mathbb {R}}X_k$ is denoted by

$$\begin{aligned} f=\sum _{z\in X_k}f(z)z \end{aligned}$$

and is identified with the real-valued function on $X_{k}$ given by $z \mapsto f(z)$.

Such an element $f\in {\mathbb {R}}X_k$ can be extended to an element $\tilde{f}\in {\mathbb {R}}X$ by setting, for all $u \in X$,

$$\begin{aligned} \tilde{f}(u)=\sum _{z\in X_k, z\subset u}f(z). \end{aligned}$$

If an element $g \in {\mathbb {R}}X$ is equal to some $\tilde{f}$, for $f \in {\mathbb {R}}X_{k}$, we say that $g$ has degree $k$. The differentiation $\gamma$ is the operator defined by linearity from

$$\begin{aligned} \gamma (z) =\sum _{y\in X_{k-1},y\subset z}y \end{aligned}$$

for all $z\in X_k$ and for all $k=0,1, \ldots n$, and ${{\mathrm{Harm}}}_{k}$ is the kernel of $\gamma$:

$$\begin{aligned} {{\mathrm{Harm}}}_k =\ker (\gamma |_{{\mathbb {R}}X_k}). \end{aligned}$$

Theorem 2.1

([6]). A set $\mathcal {B} \subset X_{k}$ of blocks is a $t$-design if and only if $\sum _{b\in \mathcal {B}}\tilde{f}(b)=0$ for all $f\in {{\mathrm{Harm}}}_k$, $1\le k\le t$.

In [3], the harmonic weight enumerator associated to a binary linear code $C$ was defined as follows:

Definition 2.2

Let $C$ be a binary code of length $n$ and let $f\in {{\mathrm{Harm}}}_{k}$. The harmonic weight enumerator associated to $C$ and $f$ is

$$\begin{aligned} W_{C,f}(x,y)=\sum _{c\in C}\tilde{f}(c)x^{n-\mathrm{wt}(c)}y^{\mathrm{wt}(c)}. \end{aligned}$$

Let $G$ be the subgroup of $\mathrm{GL}(2,{\mathbb {C}})$ generated by elements

$$\begin{aligned} T_{1}= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 &{} 1 \\ 1 &{} -1 \end{pmatrix}, \ T_{2}= \begin{pmatrix} 1 &{} \quad 0 \\ 0 &{} \quad i \end{pmatrix}. \end{aligned}$$

We consider the group $G= \langle T_{1}, T_{2} \rangle$ together with the characters $\chi _{k}$ defined by

$$\begin{aligned} \chi _{k}(T_{1})=(-1)^{k},\ \chi _{k}(T_{2})=i^{-k}. \end{aligned}$$

We denote by $I_{G}= {\mathbb {C}}[x,y]^{G}$ the ring of polynomial invariants of $G$ and by $I_{G,\chi _{k}}$ the ring of relative invariants of $G$ with respect to the character $\chi _{k}$. Let $P_{8}=x^8+14x^4y^4+y^8$, $P_{12}=x^2y^2(x^4-y^4)^2$, $P_{18}=xy(x^8-y^8)(x^8-34x^4y^4+y^8)$, $P_{24}=x^4y^4(x^4-y^4)^4$, $P_{30}=P_{12}P_{18}$ and

$$\begin{aligned} I_{G,\chi _{k}}= \left\{ \begin{array}{ll} \langle P_8,P_{24}\rangle &{}\quad \text{ if } k \equiv 0\pmod {4}\\ P_{12}\langle P_8,P_{24}\rangle &{}\quad \text{ if } k \equiv 2\pmod {4}\\ P_{18}\langle P_8,P_{24}\rangle &{}\quad \text{ if } k \equiv 3\pmod {4}\\ P_{30}\langle P_8,P_{24}\rangle &{}\quad \text{ if } k \equiv 1\pmod {4} \end{array}. \right. \end{aligned}$$

Then the structure of these invariant rings is described as follows:

Theorem 2.3

([3]). Let $C$ be an extremal binary doubly even self-dual code of length $n$, and let $f \in {{\mathrm{Harm}}}_{k}$. Then we have $W_{C,f}(x,y) =(xy)^{k} Z_{C,f} (x,y)$. Moreover, the polynomial $Z_{C,f} (x,y)$ is of degree $n-2k$ and is in $I_{G, \chi _{k}}$, the space of the relative invariants of $G$ with respect to the character $\chi _{k}$.

We recall the slightly more general definition of the notion of a $T$-design, for a subset $T$ of $\{ 1,2, \ldots , n \}$: a set $\mathcal {B}$ of blocks is called a $T$-design if and only if $\sum _{b\in \mathcal {B}}\tilde{f}(b)=0$ for all $f\in {{\mathrm{Harm}}}_k$ and for all $k \in T$. By Theorem 2.1, a $t$-design is a $T= \{1, \ldots , t \}$-design. Let $W_{C,f}=\sum _{i=0}^{n}c_f(i)x^{n-i}y^i$. Then we note that $D_w$ is a $T$-design if and only if $c_f(w)=0$ for all $f\in \text{ Harm }_j$ with $j\in T$. The following theorem is called a strengthening of the Assmus–Mattson theorem.

Theorem 2.4

([5]). Let $D_{w}$ be the support design of an extremal binary doubly even self-dual code of length $n$.

• If $n \equiv 0 \pmod {24}$, $D_{w}$ is a $\{1, 2, 3, 4, 5, 7\}$-design.

• If $n \equiv 8 \pmod {24}$, $D_{w}$ is a $\{1, 2, 3, 5\}$-design.

• If $n \equiv 16 \pmod {24}$, $D_{w}$ is a $\{1, 3\}$-design.

We remark that Bachoc gave an alternative proof of a strengthening of the Assmus–Mattson theorem in [3, Theorem 4.2].

2.2 Harmonic weight enumerators of extremal Type II codes

In this section, we give the explicit description of the harmonic weight enumerators of extremal Type II codes for the particular cases, which will be needed in the proof of our theorems in Sect. 3. We set $n=24m+8r$ the length of a code $C$.

Case t = 4 and r = 2 Let us assume that $t=4$, and $C$ is an extremal binary doubly even self-dual code of length $n=24m+16$. Then by the Theorem 2.3 we have $W_{C,f}(x,y) =c(f) (xy)^{4} Z_{C,f} (x,y)$, where $c(f)$ is a linear function from Harm$_{t}$ to ${\mathbb {R}}$ and $Z_{C,f} (x,y) \in I_{G,\chi _{0}}$. By Theorem 2.3, $Z_{C,f} (x,y)$ can be written in the following form:

$$\begin{aligned} Z_{C,f}(x,y) = \sum _{i=0}^{m}a_{i}P_{8}^{3(m-i)+1} P_{24}^{i}. \end{aligned}$$

Since the minimum weight of $C$ is $4m+4$, we have $a_{i}=0$ for $i \ne m$. Therefore, $W_{C,f}(x,y)$ can be written in the following form:

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{4} P_{8} P_{24}^{m} \nonumber \\&=c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m} (x^{8}+14x^{4}y^{4}+y^{8}). \end{aligned}$$

(2.1)

The other cases are as follows.

Case t = 5 and r = 2 $W_{C,f}(x,y)$ can be written in the following form:

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{5} Z_{C,f} (x,y) \nonumber \\&=c(f) (xy)^{5} P_{30} \sum _{i=0}^{m-1}a_{i}P_{8}^{3(m-i)-3} P_{24}^{i}. \end{aligned}$$

If $C$ is extremal, then

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{5} P_{30} P_{24}^{m-1} \nonumber \\&=c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-1}(x^{4}+y^{4}) \quad (x^{8}-34x^{4}y^{4}+y^{8}). \end{aligned}$$

(2.2)

Case t = 6 and r = 1, 2 $W_{C,f}(x,y)$ can be written in the following form:

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{6} Z_{C,f} (x,y) \nonumber \\&=c(f) (xy)^{6} P_{12} \sum _{i=0}^{m-1}a_{i}P_{8}^{3(m-i)-3+r} P_{24}^{i}. \end{aligned}$$

If $C$ is extremal, then

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{6} P_{12} P_{8}^{r} P_{24}^{m-1} \nonumber \\&=c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-2} (x^{8}+14x^{4}y^{4}+y^{8})^{r}. \end{aligned}$$

(2.3)

Case t = 7 and r = 1 $W_{C,f}(x,y)$ can be written in the following form:

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{7} Z_{C,f} (x,y) \nonumber \\&=c(f) (xy)^{7} P_{18} \sum _{i=0}^{m-1}a_{i}P_{8}^{3(m-i)-3} P_{24}^{i}. \end{aligned}$$

If $C$ is extremal, then

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{7} P_{18} P_{24}^{m-1}\nonumber \\&=c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-3}(x^{4}+y^{4}) \quad (x^{8}-34x^{4}y^{4}+y^{8}). \end{aligned}$$

(2.4)

Case t = 8 and r = 0, 1 $W_{C,f}(x,y)$ can be written in the following form:

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{8} Z_{C,f} (x,y) \nonumber \\&=c(f) (xy)^{8} \sum _{i=0}^{m-1}a_{i}P_{8}^{3(m-i)-2+r} P_{24}^{i}. \end{aligned}$$

If $C$ is extremal, then

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{8} P_{8}^{r+1} P_{24}^{m-1} \nonumber \\&=c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-4} (x^{8}+14x^{4}y^{4}+y^{8})^{r+1}. \end{aligned}$$

(2.5)

2.3 Coefficients of the harmonic weight enumerators of extremal Type II codes

As we mentioned in Sect. 2.1, it is important for the support designs of a code $C$ whether the coefficients of $W_{C,f}(x,y)$ are zero or not. Therefore, we investigate it and show the following lemmas.

Lemma 2.5

Let $Q=(x^{4}-y^{4})^{\alpha } (x^{8}+14x^{4}y^{4}+y^{8})^{\beta }$ with $0\le \alpha \le 652$ and $\beta = 1 ,2$.

$(1)$ :

In the case $\beta =1$, if the coefficients of $(x^{4})^{\alpha +2-i}(-y^{4})^{i}$ in $Q$ are equal to $0$ for $0 \le i \le \frac{\alpha +2}{2}$, then $(\alpha , i)=(14,1)$, $(223,15)$.

$(2)$ :

In the case $\beta =2$, the coefficients of $(x^{4})^{\alpha +4-i}(-y^{4})^{i}$ in $Q$ are equal to $0$ for $0 \le i \le \frac{\alpha +4}{2}$, then $(\alpha , i)=(28,1)$.

Proof

We have checked numerically using computer.

We note that $C$ does not exist if $n=24m$ ($m \ge 154)$, $24m+8$ ($m \ge 159$), $24m+16$ ($m \ge 164$). Then $0\le \alpha \le 652$ satisfy the condition for $m \le 163$ in Eqs. 2.1–2.5. $\square$

Lemma 2.6

Let $R=(x^{4}-y^{4})^{\alpha }(x^{4}+y^{4})(x^{8}-34x^{4}y^{4}+y^{8})$ with $1 \le \alpha \le 652$. If the coefficients of $(x^{4})^{\alpha +3-i}(-y^{4})^{i}$ in $R$ are equal to $0$ for $0 \le i \le \frac{\alpha +3}{2}$, then $\alpha =2i-3$.

Proof

We have checked numerically using computer. $\square$

3 Proof of Theorems

3.1 Case for $n=24m$

In this section, we consider the case of length $n=24m$. Let $D_{w}^{24m}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual $[24m,12m,4m+4]$ code $(m \le 153)$. By Theorem 1.3 and [7, 8, Theorem 1.1], we remark that if there exists $w'$ such that $D_{w'}^{24m}$ becomes a $6$-design, then $D_{w}^{24m}$ is a $7$-design for any $w$, and $m$ must be in the set $\{15,\,52,\, 55,\, 57,\, 59,\, 60,\, 63,\, 90,\, 93,\, 104, \,105,\, 107,\, 118,\, 125,\, 127,\, 135,\, 143,\, 151 \}$.

For $t \ge 8$, we give the following proposition.

Proposition 3.1

Let $D_{w}^{24m}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual code of length $n=24m$. Then all $D_{w}^{24m}$ are $8$-designs simultaneously, or none of $D_{w}^{24m}$ is an $8$-design.

Proof

If $r=0$ in the Eq. 2.5, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-4} (x^{8}+14x^{4}y^{4}+y^{8}). \end{aligned}$$

We recall that $C$ does not exist if $n=24m$ ($m \ge 154)$ [10, 11]. By Lemma 2.5 (1), the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero if $c(f)\ne 0$ or zero if $c(f)=0$ for $m\le 153$. Therefore, all $D_{w}^{24m}$ are $8$-designs simultaneously, or none of $D_{w}^{24m}$ is an $8$-design. $\square$

We apply [7, 8, Theorem 1.1] to Proposition 3.1. In [7, 8, Theorem 1.1], we showed that $D_{4m+4}^{24m}$ cannot be an $8$-design, so we obtain the following theorem.

Theorem 3.2

$D_{w}^{24m}$ is never an $8$-design for any $w$.

Thus the proof of Theorem 1.4 (1) is completed.

3.2 Case for $24m+8$

In this section, we state the cases of length $n=24m+8$. Let $D_{w}^{24m+8}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual $[24m+8,12m+4,4m+4]$ code ($m \le 158$). By Theorem 1.3 and [7, 8, Theorem 4.3(1)], we remark that if there exists $w'$ such that $D_{w'}^{24m+8}$ becomes a $4$-design, then $D_{w}^{24m+8}$ is a $5$-design for any $w$, and $m$ must be in the set $\{15,\,35,\, 45,\, 58,\, 75,\, 85,\, 90,\, 95,\, 113, \,115,\, 120,\, 125 \}$.

For $t \ge 6$, we give the following proposition. We call $w$ the middle weight if $w= n / 2$.

Proposition 3.3

Let $D_{w}^{24m+8}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual code of length $n=24m+8$.

$(1)$ :

(i):

Assume that $m \ne 4$. Then all $D_{w}^{24m+8}$ are $6$-designs simultaneously, or none of $D_{w}^{24m+8}$ is a $6$-design.

(ii):

Assume that $m= 4$. Then $D_{w}^{104}$ is a ${\left\{ \begin{array}{ll} \{1,2,3,5 \}\text {-design} &{} \text {if}\ w \ne 24 \\ \{1,2,3,5,6 \}\text {-design} &{} \text {if}\ w= 24. \end{array}\right. }$

$(2)$ :

(i):

Assume that $w \ne 12m+4$. Then all $D_{w}^{24m+8}$ are $7$-designs simultaneously, or none of $D_{w}^{24m+8}$ is a $7$-design.

(ii):

$D_{12m+4}^{24m+8}$ is a $\{1,2,3,5,7 \}$-design.

$(3)$ :

(i):

Assume that $m \ne 8$. Then all $D_{w}^{24m+8}$ are $8$-designs simultaneously, or none of $D_{w}^{24m+8}$ is an $8$-design.

(ii):

Assume that $m= 8$. Then $D_{w}^{200}$ is a ${\left\{ \begin{array}{ll} \{1,2,3,5 \}\text {-design} &{} \text {if}\ w \ne 40 \\ \{1,2,3,5,8 \}\text {-design} &{} \text {if}\ w= 40. \end{array}\right. }$

Proof

$(1)$ If $r=1$ in the Eq. 2.3, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-2} (x^{8}+14x^{4}y^{4}+y^{8}). \end{aligned}$$

By Lemma 2.5 (1), if $m \ne 4$, the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero or zero at the same time. Therefore, if $m \ne 4$, all $D_{w}^{24m+8}$ are $6$-designs simultaneously, or none of $D_{w}^{24m+8}$ is a $6$-design.

Let $m=4$. By Lemma 2.5 (1), if $i \ne 24$, the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $20 \le i \le 84$ are all nonzero or zero at the same time. Also, the coefficient of $x^{24}$ is equals to $0$. Therefore, if $w \ne 24$, $D_{w}^{104}$ is a $\{1,2,3,5 \}$-design. Also, $D_{24}^{104}$ is a $\{1,2,3,5,6 \}$-design.

$(2)$ By the Eq. 2.4, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-3}(x^{4}+y^{4})(x^{8}-34x^{4}y^{4}+y^{8}). \end{aligned}$$

By Lemma 2.6, if $i \ne 12m+4$, the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero or zero at the same time. Therefore, if $w \ne 12m+4$, then all $D_{w}^{24m+8}$ are $7$-designs simultaneously, or none of $D_{w}^{24m+8}$ is a $7$-design.

We consider the case that $w$ is the middle weight. By Lemma 2.6, the coefficient of $x^{12m+4}$ is equals to 0. Hence $D_{12m+4}^{24m+8}$ is a $\{1,2,3,5,7 \}$-design.

$(3)$ If $r=1$ in the Eq. 2.5, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-4} (x^{8}+14x^{4}y^{4}+y^{8})^{2}. \end{aligned}$$

By Lemma 2.5 (2), if $m \ne 8$, the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero or zero at the same time. Therefore, if $m \ne 8$, then all $D_{w}^{24m+8}$ are $8$-designs simultaneously, or none of $D_{w}^{24m+8}$ is an $8$-design.

Let $m=8$. By Lemma 2.5 (2), if $i \ne 40$, the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $36 \le i \le 164$ are all nonzero or zero at the same time. Also, the coefficient of $x^{40}$ is equals to $0$. Therefore, if $w \ne 40$, $D_{w}^{200}$ is a $\{1,2,3,5 \}$-design. Also, $D_{40}^{200}$ is a $\{1,2,3,5,8 \}$-design.

$\square$

Remark 3.4

In Lemma 2.5 (1), the solution $(\alpha ,i)=(223,15)$ corresponds to the polynomial $Q=(x^{4}-y^{4})^{223} (x^{8}+14x^{4}y^{4}+y^{8})$. In the case $t=9$ and $r=1$, if $C$ is extremal, then the harmonic weight enumerator is

$$\begin{aligned} W_{C,f}(x,y)&=c(f) (xy)^{9} P_{30}P_{8} P_{24}^{m-2}\nonumber \\&=c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-5}(x^{4}+y^{4})\nonumber \\&\quad \times \,(x^{8}+14x^{4}y^{4}+y^{8})(x^{8}-34x^{4}y^{4}+y^{8}). \end{aligned}$$

(3.1)

The polynomial $Q$ is contained in the case of $m=57$ in the Eq. 3.1. By a computation, the coefficients of $x^{i}$ in the Eq. 3.1 with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are not equal to $0$. Thus the solution $(\alpha ,i)=(223,15)$ does not give a design.

We apply [7, 8, Theorem 4.3(1)] to Proposition 3.3. In [7, 8, Theorem 4.3(1)], we showed the following: if $D_{4m+4}^{24m+8}$ becomes a $6$-design, then $m$ must be $58$; if $D_{4m+4}^{24m+8}$ becomes a $7$-design, then $m$ must be $58$; $D_{4m+4}^{24m+8}$ cannot be an $8$-design, so we obtain the following theorem.

Theorem 3.5

Let $D_{w}^{24m+8}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual $[24m+8,12m+4,4m+4]$ code $(m \le 158)$.

$(1)$ :

(i):

In the case $w \ne 12m+4$. If $D_{w}^{24m+8}$ becomes a $6$-design, then $m$ must be $58$. If $D_{w}^{24m+8}$ becomes a $7$-design, then $m$ must be $58$.

(ii):

In the case $w = 12m+4$. If $D_{12m+4}^{24m+8}$ becomes a $6$-design, then $D_{12m+4}^{24m+8}$ becomes a $7$-design and $m$ must be $58$.

$(2)$ :

$D_{w}^{24m+8}$ is never an $8$-design for any $w$.

Thus the proof of Theorem 1.4 (2) is completed.

3.3 Case for $24m+16$

In this section, we state the cases of length $n=24m+16$. Let $D_{w}^{24m+16}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual $[24m+16,12m+8,4m+4]$ code ($m \le 163$). By Theorem 1.3 and [7, 8, Theorem 4.3 (2)], we remark that if there exists $w'$ such that $D_{w'}^{24m+16}$ becomes a 2-design, then $D_{w}^{24m+16}$ is a $3$-design for any $w$, and $m$ must be in the set {5, 10, 20, 23, 25, 35, 44, 45, 50, 55, 60, 70, 72, 75, 79, 80, 85, 93, 95, 110, 118, 120, 121, 123, 125, 130, 142, 144, 145, 149, 150, 155, 156, 157, 160, 163}.

For $t \ge 4$, we give the following proposition.

Proposition 3.6

Let $D_{w}^{24m+16}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual code of length $n=24m+16$.

$(1)$ :

All $D_{w}^{24m+16}$ are $4$-designs simultaneously, or none of $D_{w}^{24m+16}$ is a $4$-design.

$(2)$ :

(i):

Assume that $w \ne 12m+8$. Then all $D_{w}^{24m+16}$ are $5$-designs simultaneously, or none of $D_{w}^{24m+16}$ is a $5$-design.

(ii):

$D_{12m+8}^{24m+16}$ is a $\{1,2,3,5 \}$-design.

$(3)$ :

All $D_{w}^{24m+16}$ are $6$-designs simultaneously, or none of $D_{w}^{24m+16}$ is a $6$-design.

Proof

$(1)$ If $r=2$ in the Eq. 2.1, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m} (x^{8}+14x^{4}y^{4}+y^{8}). \end{aligned}$$

By Lemma 2.5 (1), the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero or zero at the same time. Therefore, all $D_{w}^{24m+16}$ are $4$-designs simultaneously, or none of $D_{w}^{24m+16}$ is a $4$-design.

$(2)$ By the Eq. 2.2, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-1}(x^{4}+y^{4})(x^{8}-34x^{4}y^{4}+y^{8}). \end{aligned}$$

By Lemma 2.6, if $i \ne 12m+8$, the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero or zero at the same time. Therefore, if $w \ne 12m+8$, then all $D_{w}^{24m+16}$ are $5$-designs simultaneously, or none of $D_{w}^{24m+16}$ is a $5$-design.

We consider the case that $w$ is the middle weight. By Lemma 2.6, the coefficient of $x^{12m+8}$ is equals to $0$. Hence $D_{12m+8}^{24m+16}$ is a $\{1,2,3,5 \}$-design.

$(3)$ If $r=2$ in the Eq. 2.3, we have

$$\begin{aligned} W_{C,f}(x,y) =c(f) x^{4m+4}y^{4m+4} (x^{4}-y^{4})^{4m-2} (x^{8}+14x^{4}y^{4}+y^{8})^{2}. \end{aligned}$$

By Lemma 2.5 (2), the coefficients of $x^{i}$ with $i \equiv 0 \pmod {4}$ and $4m+4 \le i \le n-(4m+4)$ are all nonzero or zero at the same time. Therefore, all $D_{w}^{24m+16}$ are $6$-designs simultaneously, or none of $D_{w}^{24m+16}$ is a $6$-design. $\square$

We apply [7, 8, Theorem 4.3 (2)] to Proposition 3.6. In [7, 8, Theorem 4.3 (2)], we showed the following: if $D_{4m+4}^{24m+16}$ becomes a $4$-design, then $m$ must be in the set $\{10,\, 23,\, 79,\, 93,\, 118,\, 120,\, 123, \,125,\, 142\}$; if $D_{4m+4}^{24m+16}$ becomes a $5$-design, then $m$ must be in the set $\{23,\, 79,\, 93,\, 118,\, 120,\, 123, \,125,\, 142\}$; $D_{4m+4}^{24m+16}$ cannot be a $6$-design, so we obtain the following theorem.

Theorem 3.7

Let $D_{w}^{24m+16}$ be the support $t$-design of weight $w$ of an extremal binary doubly even self-dual $[24m+16,12m+8,4m+4]$ code $(m \le 163)$.

$(1)$ :

(i):

In the case $w \ne 12m+8$. If $D_{w}^{24m+16}$ becomes a $4$-design, then $m$ must be in the set $\{10,\, 23,\, 79,\, 93,\, 118,\, 120,\, 123,\, 125,\, 142\}$. If $D_{w}^{24m+16}$ becomes a $5$-design, then $m$ must be in the set $\{23,\, 79,\, 93,\, 118,\, 120,\, 123,\, 125,\, 142\}$.

(ii):

In the case $w = 12m+8$. If $D_{12m+8}^{24m+16}$ becomes a $4$-design, then $D_{12m+8}^{24m+16}$ becomes a $5$-design and $m$ must be in the set $\{10,\, 23,\, 79,\, 93,\, 118,\, 120,\, 123,\, 125,\, 142\}$.

$(2)$ :

$D_{w}^{24m+16}$ is never a $6$-design for any $w$.

Thus the proof of Theorem 1.4 (3) is completed.

Remark 3.8

Let $\mathcal {D}=(X, \mathcal {B})$ be a $t$-design. The complementary design of $\mathcal {D}$ is $\bar{\mathcal {D}}=(X, \bar{\mathcal {B}})$, where $\bar{\mathcal {B}}= \{ X \setminus B : B \in \mathcal {B} \}$. If $\mathcal {D}= \bar{\mathcal {D}}$, $\mathcal {D}$ is called a self-complementary design. Let $D_{n/2}$ be the support $t$-design of the middle weight of an extremal binary doubly even self-dual code of length $n$. It is easily seen that $D_{n/2}$ is self-complement.

Alltop [1] proved that if $\mathcal {D}$ is a $t$-design with an even integer $t$ and self-complementary, then $\mathcal {D}$ is also a $(t+1)$-design. Hence $D_{n/2}$ is a $\{ 1,3,5, \ldots , 2s+1 \}$-design. Thus Alltop’s theorem gives an alternative proof of Propositions 3.3 (2) (ii) and 3.6 (2) (ii).