Combining CPU and GPU architectures for fast similarity search

Abstract

The Signature Quadratic Form Distance on feature signatures represents a flexible distance-based similarity model for effective content-based multimedia retrieval. Although metric indexing approaches are able to speed up query processing by two orders of magnitude, their applicability to large-scale multimedia databases containing billions of images is still a challenging issue. In this paper, we propose a parallel approach that balances the utilization of CPU and many-core GPUs for efficient similarity search with the Signature Quadratic Form Distance. In particular, we show how to process multiple distance computations and other parts of the search procedure in parallel, achieving maximal performance of the combined CPU/GPU system. The experimental evaluation demonstrates that our approach implemented on a common workstation with 2 GPU cards outperforms traditional parallel implementation on a high-end 48-core NUMA server in terms of efficiency almost by an order of magnitude. If we consider also the price of the high-end server that is ten times higher than that of the GPU workstation then, based on price/performance ratio, the GPU-based similarity search beats the CPU-based solution by almost two orders of magnitude. Although proposed for the SQFD, our approach of fast GPU-based similarity search is applicable for any distance function that is efficiently parallelizable in the SIMT execution model.

1 Introduction

Multimedia retrieval systems frequently store billions of images and provide users with different ways of searching and browsing (e.g., catalog-based or keyword-based search). However, effective yet efficient techniques for content-based similarity search are still a hot research topic. To this end, multimedia retrieval systems are designed based on advanced similarity models consisting of image representations and similarity/distance measures.

A flexible way to represent the content of an image is by means of feature signatures [28]. In general, a feature signature of an image is a set consisting of multiple local image features, where the length of a feature signature is not fixed (to distinguish images of different complexities). However, the comparison of feature signatures requires more sophisticated and computationally expensive adaptive distance measures [4], such as the Earth Mover’s Distance (EMD) [28] or the Signature Quadratic Form Distance (SQFD) [3, 5]. In this paper, we focus on the latter, as the SQFD shows higher retrieval quality [4], higher stability [2], and lower time complexity compared to the EMD ($\mathcal{O}(n^{2})$ vs. $\mathcal {O}(n^{4})$). Nevertheless, the quadratic complexity is still too high to use the SQFD for a sequential search of a large database. In order to reduce the computational effort, indexing [31] approaches have been applied to the SQFD. It has been shown that metric indexing [1] and ptolemaic indexing [19] reach a speed-up of more than two orders of magnitude with respect to the sequential scan. However, even when using indexing approaches, the speed-up is generally limited due to the high intrinsic dimensionality [31]. Thus, in order to use the SQFD for large-scale image retrieval, we propose to parallelize the SQFD query processing.

Parallelization of data retrieval problems on many-core architectures has already been addressed from many perspectives. For instance the kNN query algorithm which is used in almost every data retrieval system has been successfully parallelized on GPUs by Bustos et al. [7] and later by Garcia et al. [10]. Pan et al. [26] showed that the solution can be improved even further using a hashing approach to compute the approximate kNN on GPUs. Other similarity-based operations can benefit from parallelization aswell. Lieberman et al. [18] suggested using GPUs for similarity joining operations. All these solutions exploited the parallel nature of GPUs to achieve significant speedup over CPU. However, the potential of the GPU lies especially in numeric computations, thus we can utilize its power even more efficiently to compute expensive distance functions that offer higher precision of the similarity search.

In this paper, we consider the combination of many-core GPU devices and multicore CPU processors for parallel SQFD query processing. While parallel CPU processing is straightforward and supported by many development tools, designing efficient algorithms for GPUs is a challenging task for content-based retrieval purposes. Although GPUs generally contain more cores than CPUs, they suffer from slow data transfer rates and code execution restrictions. We discuss GPU processing limitations and introduce two new schemes for efficient similarity search utilizing the combination of indexing approaches and the computational power of CPUs+GPUs.

The paper is organized as follows. Section 2 introduces the task of similarity search, the motivation and definition of the SQFD, and also the indexing techniques used for fast similarity search by the SQFD. Section 3 discusses the most important aspects of GPU architectures. The contribution of the paper are two algorithms addressing the implementation of similarity search on CPU and GPUs, described in Sects. 4 and 5. The first algorithm (SQFD-only) utilizes the GPUs only to compute the SQFD, leaving the other processing on CPU, while the second algorithm (SQFD+LB) utilizes the GPUs also to compute lower bound distances used in index pre-filtering. Section 6 presents the experimental results, and Sect. 7 concludes this paper.

2 Similarity search in multimedia databases

When searching multimedia databases by content, users issue similarity queries by selecting multimedia objects or by sketching the intended object contents. Given an example multimedia object or sketch q, the multimedia database $\mathbb{S} \subset\mathbb{U}$ (where $\mathbb{U}$ is the object universe) is searched for the most related objects with respect to the query by measuring the similarity between the query and each database object by means of a distance function δ. As a result, the multimedia objects with the lowest distance to the query are returned to the user. In particular, a range query (q,r), $q \in\mathbb{U}$, r∈ℝ⁺, reports all objects in $\mathbb{S}$ that are within a distance r to q, that is, $(q,r)=\{x \in\mathbb{S} \mid \delta(x,q) \leq r\}$. The subspace defined by q and r is called the query ball. Another popular similarity query is the k nearest neighbors query (kNN). It reports the k objects from $\mathbb{S}$ closest to q. That is, it returns the set $\mathbb{C} \subseteq\mathbb{S}$ such that |ℂ|=k and $\forall x \in\mathbb{C}, y \in\mathbb{S}-\mathbb{C}, \delta(x,q) \leq\delta(y,q)$. The kNN query also defines a query ball (q,r), but the distance r to the kth NN is not known in advance.

2.1 Model representation

When determining content-based similarity between two multimedia objects, the distance is evaluated on feature descriptors which aggregate the inherent properties of the multimedia objects. The conventional feature descriptors aggregate and store these properties in feature histograms, which can be compared by vectorial distances [15, 27].

2.1.1 Feature signatures

Unlike conventional feature histograms, feature signatures are frequently obtained by clustering the objects’ properties, such as color, texture, or other more complex features [9, 23], within a feature space and storing the cluster representatives and weights. Thus, given a feature space $\mathbb{F}$, the feature signature S ^o of a multimedia object o is defined as a set of tuples from $\mathbb {F}\times\mathbb{R}^{+}$ consisting of representatives $r^{o} \in \mathbb{F}$ and weights w ^o∈ℝ⁺.

We depict an example of image feature signatures according to a feature space comprising position, color and texture information, i.e. $\mathbb{F} \subseteq\mathbb{R}^{7}$, in Fig. 1. For this purpose we applied the k-means clustering algorithm where each representative $r^{o}_{i} \in\mathbb{F}$ corresponds to the centroid of the cluster $\mathcal {C}^{o}_{i} \subseteq\mathbb{F}$, i.e., $r^{o}_{i} = \frac{\sum_{f \in \mathcal {C}^{o}_{i}} f}{|\mathcal{C}^{o}_{i}|}$, with relative frequency $w^{o}_{i} = \frac {|\mathcal{C}^{o}_{i}|}{\sum_{i} |\mathcal{C}^{o}_{i}|}$. We depict the feature signatures’ representatives by circles in the corresponding color. The weights are reflected by the diameter of the circles. As can be seen in this example, feature signatures adjust to individual image contents by aggregating the features according to their appearance in the underlying feature space.

Fig. 1

Three example images with their corresponding feature signature visualizations

2.1.2 Signature quadratic form distance

The Signature Quadratic Form Distance (SQFD) [3, 5] is an adaptive distance-based similarity measure for the comparison of feature signatures, generalizing the classic vectorial Quadratic Form Distance (QFD) [12]. It is defined as follows.

Definition 1

(SQFD)

Given two feature signatures $S^{q}=\{\langle r^{q}_{i}, w^{q}_{i}\rangle\} _{i=1}^{n}$ and $S^{o}=\{\langle r^{o}_{i}, w^{o}_{i}\rangle\}_{i=1}^{m}$ and a similarity function $f_{s}: {\mathbb{F}} \times{\mathbb{F}} \rightarrow {\mathbb{R}}$ over a feature space ${\mathbb{F}}$, the signature quadratic form distance $\mathrm{SQFD}_{f_{s}}$ between S ^q and S ^o is defined as:

$$\mathrm{SQFD}_{f_s}\bigl(S^q,S^o\bigr) = \sqrt{ (w_q \mid-w_o ) \cdot A_{f_s} \cdot(w_q \mid-w_o )^T }\,, $$

where $A_{f_{s}} \in{\mathbb{R}}^{(n+m) \times(n+m)}$ is the similarity matrix arising from applying the similarity function f _s to the corresponding feature representatives, i.e., a _ij =f _s (r _i ,r _j ). Furthermore, $w_{q} = (w^{q}_{1},\ldots,w^{q}_{n})$ and $w_{o} = (w^{o}_{1},\ldots ,w^{o}_{m})$ form weight vectors, and $(w_{q} \mid-w_{o} ) = (w^{q}_{1},\ldots ,w^{q}_{n},-w^{o}_{1},\ldots,-w^{o}_{m})$ denotes the concatenation of weights w _q and −w _o .

The similarity function f _s is used to determine similarity values between all pairs of representatives from the feature signatures. In our implementation we use the similarity function $f_{s}(r_{i},r_{j}) = e^{-\alpha L_{2}(r_{i},r_{j})^{2}}$, where α is a constant for controlling the precision-indexability tradeoff, as investigated in our previous works [1, 19], and L ₂ denotes the Euclidean distance. In particular, lower values of the parameter α lead to better indexability, that is, to a smaller intrinsic dimensionality (iDIM) [8]. However, lower values of the parameter α also decrease the retrieval effectiveness (frequently measured in terms of mean average precision values), as can be seen in Fig. 2 for the ALOI [11] and MIR Flickr [16] databases as examples. On the contrary, the best mean average precision values can be reached using a large value of the parameter α making the SQFD space no longer indexable. In such cases a parallel query processing approach could be one feasible solution to significantly speedup the search process. Nevertheless, before we proceed to the parallel implementation of the SQFD query processing, we briefly summarize available indexing methods.

Fig. 2

The impact of α on the intrinsic dimensionality and mean average precision

2.2 Indexing

When processing content-based similarity queries by the naïve sequential scan, the computation of the SQFD has to be carried out for each database object individually. Unlike the cheap L _p distances, the SQFD is of more than quadratic time complexity (w.r.t. dimension), so the sequential scan, sometimes acceptable for L _p distances, is impractical for the SQFD even on a moderately sized database. Although it has been shown that the SQFD is a generalization [5] of the well-known Quadratic Form Distance [12], recent approaches indexing the data by a homeomorphic mapping into the Euclidean space [30] can not be applied to the SQFD, as the similarity matrix changes from computation to computation.

Nevertheless, recent papers showed that SQFD can be indexed by metric access methods [1] and ptolemaic indexing [19], achieving a speed-up of up to two orders of magnitude with respect to the sequential scan. In this section we review both approaches and detail the simplest and most intuitive metric/ptolemaic index: the pivot tables.

2.2.1 Metric indexing

A metric space $(\mathbb{U}, \delta)$ consists of a feature descriptor domain $\mathbb{U}$ (in this paper, the set of all possible signatures) and a distance function δ which has to satisfy the metric postulates: identity, non-negativity, symmetry, and triangle inequality. In this way, metric spaces allow domain experts to model their notion of content-based similarity by an appropriate feature representation and distance function serving as similarity measure. At the same time, this approach allows database experts to design index structures, so-called metric access methods (or metric indexes) [8, 13, 29, 31], for efficient query processing of content-based similarity queries in a database $\mathbb{S} \subset \mathbb{U}$. These methods rely on the distance function δ only, i.e., they do not necessarily know the structure of the feature representation of the objects.

Metric access methods (or metric indexes) organize database objects $o_{i} \in\mathbb{S}$ by grouping them based on their distances, with the aim of minimizing not only traditional database costs like I/O but also the number of costly distance function δ evaluations—in our case the number of SQFD evaluations. For this purpose, nearly all metric access methods apply some form of filtering based on cheap computation of lower bounds LB _Δ (δ(q,o)). These bounds are based on the fact that exact pivot–object distances are precomputed, where pivot is a suitable reference object selected from the database $\mathbb{S}$.

We illustrate this fundamental principle in Fig. 3 where we depict the query object $q \in\mathbb{U}$, some pivot object $p \in\mathbb{S}$, and a database object $o \in\mathbb{S}$ in some metric space. Given a range query (q,r), we wish to estimate the distance δ(q,o) by making use of δ(q,p) and δ(o,p), with the latter already stored in the metric index. Because of the triangle inequality, we can safely filter object o without needing to compute the (costly) distance δ(q,o) if the triangular lower bound

$$ \mathrm{LB}_\varDelta\bigl(\delta(q,o)\bigr) =\bigl| \delta(q, p) - \delta(o, p)\bigr|, $$

(1)

also known as the inverse triangle inequality, is greater than the query radius r. The SQFD has been proved [19] to be a metric distance, so metric indexing can be applied for efficient similarity search using SQFD.

Fig. 3

Lower-bound distance computed using triangle inequality and a single pivot

2.2.2 Ptolemaic indexing

In metric indexes, the triangle inequality is used to construct lower bounds for the distance. Analogously, in Ptolemaic indexing [14, 19], Ptolemy’s inequality is used to construct such lower bounds as well. A distance function is called a Ptolemaic distance if it has the properties of identity, non-negativity, and symmetry, and satisfies Ptolemy’s inequality. If a Ptolemaic distance also satisfies the triangle inequality, it is a Ptolemaic metric.

Ptolemy’s inequality states that for any quadrilateral, the pairwise products of opposing sides sum to more than the product of the diagonals. In other words, for any four points x, y, u, $v \in \mathbb{U}$, we have the following:

$$ \delta(x,v)\cdot\delta(y,u) \leq\delta(x,y)\cdot \delta(u,v) + \delta(x,u)\cdot\delta(y,v) $$

(2)

One of the ways the inequality can be used for indexing is in constructing a pivot-based lower bound. For a query q, object o, and pivots p and s, we get the candidate bound:

$$ \delta_\mathrm{C}(q,o,p,s) = \frac{|\delta(q,p)\cdot\delta (o,s)-\delta(q,s)\cdot\delta (o,p)|}{\delta (p,s)} $$

(3)

For simplicity, we let δ _C(q,o,p,s)=0 if δ(p,s)=0. As for triangular lower-bounding, one would normally have a set of pivots ℙ, and the bound can then be maximized over all (ordered) pairs of distinct pivots drawn from this set, giving us the final Ptolemaic bound [14, 19]:

$$ \delta(q,o)\geq\mathrm{LB}_{\mathrm{ptol}}\bigl(\delta(q,o)\bigr ) = \max_{p,s\, \in\,\mathbb{P}} \delta_\mathrm{C}(q,o,p,s) $$

(4)

As for the triangular case, the Ptolemaic lower bound LB_ptol could be used to filter objects not contained in the query ball, i.e., exclude those $o_{i} \in\mathbb{S}$ from search for which LB_ptol(δ(q,o _i ))>r.

Figure 4 illustrates a comparison (in two-dimensional Euclidean space) showing that ptolemaic indexing could provide much tighter lower bounds. Having two pivots s,p, both lower bounds constructed using triangle inequality would not filter the object o from search, as the value is lower than a radius of the range query r. On the other hand, the lower bound obtained using the ptolemaic approach leads to very tight distance approximation, and so filtering the object o from search.

Fig. 4

Comparison of triangle/Ptolemy’s lower-bound distances computed for two pivots

Luckily, the SQFD has been proved [19] to be both a metric and a ptolemaic distance, so ptolemaic indexing can be applied for efficient similarity search using SQFD.

2.3 Pivot tables

One of the most efficient (yet simple) indexes for similarity search is the pivot table [24], originally introduced as LAESA [22]. Basically, the structure of a pivot table is a simple matrix of distances δ(o _i ,p _j ) between the database objects $o_{i} \in \mathbb{S}$ and a pre-selected static set of m pivots $p_{j} \in \mathbb {P} \subset\mathbb{S}$. For querying, pivot tables allow us to perform cheap lower-bound filtering by computing the maximum lower bound to δ(q,o) using all the pivots. Moreover, the lowerbounding could be coupled with the querying more tightly because of the monotonous increase of the lower bound during its computation (i.e., usage of an additional pivot leads to possibly tighter/greater value). In particular, if the actual value of the lower bound being computed exceeds the radius of a query, the computation of the lower bound can be safely terminated and the object filtered out from further processing (so-called early termination optimization).

Although pivot tables have been introduced as a metric index, they could be used beyond the context of the metric space model. In fact, the data structure is just a distance matrix, so there is no metric-specific aggregate information stored (unlike in hierarchical metric indexes) that would prevent from usage elsewhere. In consequence, the original filtering based on triangular lower bounds (1) can be easily extended to the ptolemaic case using (4), or even combined. This extension was already presented as ptolemaic pivot tables [14, 19]. Because in the ptolemaic case there are pairs of pivots used in the lowerbounding, the quadratic size could lead to a large internal overhead when filtering. Therefore, there were also heuristics proposed for reduction of the set of pivot pairs yet preserving their filtering power [19]. It was experimentally confirmed that ptolemaic indexing could speedup the SQFD similarity search up to 4 times with respect to the metric case and up to 300 times with respect to the sequential scan [19].

2.4 Motivation for parallel indexing

The feature signatures and SQFD have been proved as an elegant and effective model for similarity search allowing to compare multimedia descriptors based on local features. There was also substantial effort spent on speeding up the SQFD search using the metric and ptolemaic indexing. However, despite these advances the SQFD similarity search is still not prepared for large-scale applications. Let us now analyze the empirical evidence. Depending on the parameter α of the internal SQFD’s similarity function f _s , where higher α lead to more precise but slower search, the single-core query times on Intel Xeon X5660 using a 25,000 database range from 150 ms to 1 s per query (see [19]). Obviously, even when the search complexity was heavily reduced by the ptolemaic indexing (two orders of magnitude), the practical performance is still not sufficient. In order to achieve competitive performance, it seems necessary to parallelize the approach and reduce the real times by another two orders of magnitude, yet keeping the hardware platform cheap (using common GPU cards). Accomplishing this goal would enable searching databases comprising millions of multimedia objects in real time.

In the rest of the paper we propose two algorithms. The SQFD-only algorithm parallelizes only the SQFD computation on GPU, leaving the other processing on CPU (work dispatching, pivot table filtering, results aggregation). This approach is efficient in case the workloads of SQFD computations and index filtering are balanced, so that GPU need not to wait for CPU. However, advanced filtering techniques (e.g., ptolemaic indexing) reduce the workload of SQFD computations by pruning a number of candidates, thus shifting the workload from GPU to CPU. For such cases we propose the SQFD+LB algorithm that precomputes on GPU the lower-bound values used by candidate pre-filtering, reducing thus the workload of CPU.

3 GPU fundamentals

GPU architectures [25] differ from CPU architectures in multiple ways. In the remainder of this section, we describe the GPU device architecture and its two major aspects, the thread execution and the memory organization, which have direct impact on the design of our framework and the SQFD implementation. The following description may be incomplete or simplified as we focus mainly on details important for GPU programming.

3.1 GPU architecture

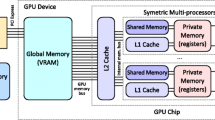
A GPU card is a peripheral device connected to the host system via the PCI-Express (PCIe) bus. The device consist of a GPU processor and on-board memory modules. The device also consists of other parts related to image processing, but they are out of scope of our method.

The GPU processor (Fig. 5) consists of several symmetric multiprocessing units (SMPs), while the SMPs share only the main memory bus and the L2 cache, otherwise they are completely independent. Each SMP consists of multiple GPU cores, single instruction decoder, L1 cache, and local memory. The GPU cores are tightly coupled since they share SMP resources, even the instruction decoder. As a result, all cores execute the same instruction at the same time. Each core has its own arithmetical units for integer and float operations and a private set of registers.

Fig. 5

GPU processor architecture

The most significant differences from the classic CPU architecture is the specific instruction execution by multiple cores in SMP and also multiple types of memory. Therefore, we address these issues in more detail in the following.

3.2 Thread execution

When it comes to parallel execution, we usually distinguish between two types of parallelism—task parallelism and data parallelism. The task parallelism is usually employed by CPUs as each core executes different code. In case of data parallelism, all cores execute the same code but on different portions of data. The GPUs are tailored to data parallelism since their original graphic-acceleration design is aimed at processing large number of geometric vertices or image fragments using the same algorithm.

The portions of code that are executed on the GPU are called kernels. A kernel is a procedure that is invoked multiple times simultaneously, thus spawning multiple threads that execute the same code. Each spawned thread gets the same set of calling arguments and a unique identifier which is used to select the proper parts of the parallel work. The threads are organized into one-, two-, or three-dimensional array and the thread identifier is an index into this array. The thread managing and context switching capabilities of the GPU are very advanced. Thus, it is usually better to create a multitude of threads, even if they execute only a few instructions each, in order to optimize the load balancing. In addition, fast context switching capabilities of the GPU are used to inhibit the latency of global memory transactions.

Threads are aggregated into small bundles called groups (Fig. 6). A group usually contains tens to hundreds of threads which are mapped to one SMP unit, thus executing the kernel code in SIMT (Single Instruction Multiple Threads) or virtual SIMT fashion. Usually, there are many more thread groups than SMPs, where the groups are planned sequentially and non-preemptively on available multiprocessors. When a group is assigned to an SMP, it must finish its execution before another group can be assigned to that SMP. Therefore, threads in one group must not wait for results of another group, because such behavior could easily lead to a deadlock.

Fig. 6

Example of thread allocation and grouping

Threads in a group are divided into subgroups called warps (NVIDIA) or wavefronts (ATI/AMD). The number of threads in these subgroups is equal to the number of GPU cores in SMPs, so threads in a subgroup run in real SIMT mode. Exactly one subgroup is actually running while others are waiting. When a subgroup is forced to wait (e.g., when transferring data from memory), SMP performs a fast context switch so that another subgroup may compute meanwhile.

The SIMT execution suffers from branching problems. When different threads in the group choose different branches—for instance when executing ‘if’ statements—all branches must be executed by all threads. Each thread masks instruction execution according to local result of the condition to ensure correct results. Therefore, heavily branched code or ‘while’ loops with highly different number of iterations will not perform well on GPUs. On the other hand, the SIMT approach simplifies synchronization within the group and allows threads to communicate and collaborate through SMP’s shared local memory.

3.3 Memory organization

The second difference is the memory organization which is depicted in Fig. 7. As we can observe, there are four types of memory:

• host memory (RAM),

• global memory (VRAM),

• local memory,

• and private memory (GPU core registers).

Fig. 7

Memory organization scheme of host and GPU device

The host memory is the operational memory of the computer. It is directly accessible by the CPU, but it cannot be accessed by any peripheral devices such as the GPU. Input data needs to be transferred from the host memory (RAM) to the graphic device global memory (VRAM), and the results need to be transferred back when the kernel execution finishes. For the transfer the PCI-Express bus is used, which is rather slow (8 GB/s) when compared to the internal memory buses.

The global memory is directly accessible from GPU cores, while input data and the results computed by a kernel are stored here. The global memory bus shows both high latency and high bandwidth. In order to access the global memory optimally, threads in one group are encouraged to use coalesced loads. A coalesced load is performed when all threads of a group load or store a contiguous memory area, so that each thread transfers a single 4-byte word of this block.

The local memory is shared among threads within one group. It is very small (tens of kB) but almost as fast as the GPU registers. The local memory can play the role of a program-managed cache for global memory, or the threads may share intermediate results in here while they cooperate on a task. The memory is divided into several (usually 16 or 32) banks. Two subsequent 4-byte words are stored in two subsequent banks (modulo number of banks). When two threads access the same bank (except if they read the same address), the memory operations are serialized which creates undesirable delay for all threads due to the SIMT execution model.

Finally, the private memory belongs exclusively to a single thread and corresponds to the GPU core registers. Private memory size is very limited (tens to hundreds of words), therefore it is suitable just for a few local variables.

3.4 Summary

Finally, we would like to summarize the implications for our implementation.

• The latency of data transfers between the host system and the GPU devices needs to be inhibited. The best way is to form a pipeline so that one block of data is being transferred to GPU, one block of data is being processed and one block of results is being transferred from GPU at the same time. Furthermore, the processing of a data block should take at least as much time as its transfer.

• Each algorithm being adapted for GPU must be carefully analyzed and its data transfers must be planned according to memory limitations of the GPU. The utilized data structures need to be designed with respect to the memory architecture, so that data can be fetched by coalesced loads from global memory and bank conflicts do not occur when accessing data in local memory by individual threads.

• Furthermore, the algorithm must embrace the SIMT execution model, at least for the parts of the work processed by one thread group. Usually, it is not feasible to parallelize an algorithm by simply assigning its inner loop to every spawned thread as the resources of the threads are limited. In such cases the algorithm must be redesigned so that threads of one group collaborate more closely and share their resources.

• Multitude of threads (at least thousands) needs to be spawned in order to utilize all available cores and balance the load efficiently.

4 Similarity search using GPU

The most time consuming operation in a search engine employing SQFD for similarity search is the computation of a distance between two signatures. This operation takes $\mathcal{O}((m+n)^{2})$ time, where m,n are the sizes of signatures being compared. Even when using indexing techniques that massively reduce the number of SQFD computations needed to compute, such as the pivot tables, there still remains a set of candidate database signatures that has to be filtered using direct SQFD computations.

Therefore, our primary objective is to utilize the computational power of GPU to calculate distances between query and database signatures in parallel. In our approach, we consider both the parallel execution of multiple SQFD computations during the query evaluation as well as the parallel computation of a single SQFD between two feature signatures.

4.1 Computing multiple distances in parallel

Since the SQFD is computed between the query signature and many database signatures, it would be inefficient to execute each computation separately on the GPU due to high latencies caused by data transfer and kernel executions. Therefore, we perform a block-wise computation of multiple SQFDs in parallel. Each block contains N+1 feature signatures. The first feature signature is the query signature and remaining N feature signatures are the database signatures, thus each block yields a vector of N distances as a result. The choice of N is essential for good performance. In general, a large number of N performs better.

The query processor treats the GPU implementation of the SQFD as an asynchronous operation that does not block the CPU when started, so the system can wait for its termination. The system may start as many operations as required, while the operations are queued and distributed over available GPU devices equally.¹ Since the architecture is flexible and leaves the CPU relatively low-utilized, it could be easily used with a distance-based index implemented in the CPU part of the system.

4.2 Computing each distance in parallel

In case of multi-core CPUs, computing multiple distances in parallel would be sufficient to achieve optimal speedup, since the number of distances computed vastly exceeds the number of available cores. Unfortunately, the same approach is not feasible on GPUs. The signatures need to be cached in local memory of the SMP, which is very limited, so they are able to accommodate just a few signatures. Furthermore, it would produce very imbalanced tasks for the threads in one group, which are running in SIMT fashion on one SMP. Hence, to efficiently utilize all the cores on the SMP unit we need to compute each distance in parallel as well.

Each SQFD is computed by a group of 256 threads, thus 256×N threads are spawned for one block. The constant 256 was selected based on current hardware capabilities. We have assigned one thread group to compute a single SQFD in a block, because these threads benefit from shared local memory, as the group does cache the input data from global memory and keeps intermediate results. Using multiple groups to compute one SQFD would be problematic as the groups do not have any effective means of communication. The opposite approach (using one group to compute multiple SQFDs) is feasible. However, in case of sufficient signature lengths, the parallelism would not be exploited any further and many technical complications would arise due to the limited size of local memory.

The SQFD between two feature signatures has been defined in Definition 1. For the sake of parallelism, we compute the elements of the similarity matrix $A_{f_{s}}$ concurrently by available threads in the group. Each element of the matrix is multiplied with the corresponding weights of $\overline{w} = (w_{q} \mid-w_{o})$, so that new matrix $\overline{A}$ is created, where $\overline{A}_{(i,j)} = \overline{w}_{(j)} A_{f_{s}(i,j)} \overline {w}_{(i)}$. Finally, we compute a sum of every element in the matrix $\overline{A}$ and we find its square root. These modifications are direct applications of distributivity and associativity laws, thus the result will not be affected in any way. The SQFD GPU implementation has the following phases:

• 1. Load feature signatures into local memory.

• 2. Compute the similarity matrix $A_{f_{s}}$ and multiply its elements by corresponding elements in the weight vectors (creating $\overline{A}$).

• 3. Sum up elements in the matrix $\overline{A}$ and yield the square root.

In the first phase, data are loaded into local memory as they are required multiple times and it would be ineffective to load them from global memory each time. Furthermore, the loading is more efficient when all threads cooperate in coalesced loads. The similarity matrix has (m+n)×(m+n) entries, where m and n are the numbers of feature representatives in S ^q and S ^o, respectively. Since m+n is usually smaller than 256 and varies for each pair of feature signatures, we use an irregular mapping of similarity matrix elements to threads. Figure 8 depicts the mapping scheme, where each area represents elements being computed in parallel. The numbers indicate consecutive (serial) steps in which the element areas are processed. In the last step the remaining area of the similarity matrix could be smaller than the total number of threads. In such case some threads remain idle.

Fig. 8

Work decomposition when computing the similarity matrix $A_{f_{s}}$ and $\overline{A}$

In the second phase the matrices are not stored in memory but rather computed on-the-fly since only a sum of elements in $\overline{A}$ is required. When a thread computes a new element in the similarity matrix, its value is added to a partial sum and the element itself is discarded. Even though this method requires significantly less memory, it creates a synchronization problem as multiple elements are being computed and added to the partial sum concurrently. To avoid explicit synchronization, every thread is provided with its own instance of the partial sum.

When the second phase terminates, the total sum of the partial sums of each thread is computed as the third phase of the algorithm. The total sum is only computed by the first thread in the group, which is also responsible for determining the square root and for writing the computed distance into the global memory. The total sum can also be computed cooperatively by all threads using reduction tree of logarithmic depth. However, such improvement has no measurable impact on the performance as the time required by the second phase dominates significantly the time required by the final summation.

4.3 The SQFD-only algorithm

The above described parallel computation of (multiple) SQFDs could be utilized in query processing, either directly in sequential scan of the entire database, or with the pivot table index. The SQFD-only algorithm utilizing the pivot table is depicted in Fig. 9.² When a query is started, the algorithm computes the SQFD distances between query and pivot objects (signatures). These distances are used by the pivot table for construction of lower bounds. Then, the pre-filtering based on the lower bounds takes place, resulting in a set of remaining candidate objects that have to be filtered using the expensively computed SQFDs. As depicted in the figure, only the SQFD computations take place on the GPU, while the lower bound construction, pre-filtering and filtering steps are performed on CPU. Since the computation of SQFDs is assumed as the most expensive operation, the rest of the functionality is left to the CPU. Moreover, because both the construction of lower bounds and the pre-filtering steps are implemented together on CPU, the lower bound computation can benefit from the early termination optimization (see Sect. 2.3).

Fig. 9

Workflow of the SQFD-only algorithm

In summary, the CPU iterates over the entire database, pre-filters the all the objects using the pivot table, and asynchronously dispatches blocks of candidate objects (signatures) to the GPU. The GPU computes the distances for each block and sends them back to CPU. Finally, the CPU compares the distances against the query range and forms the results set of objects.

4.4 Integration to indexing and query processor

We have described how to compute distances between a query signature and a block of database signatures on the GPU and also how to integrate such parallel computation of SQFD into a query algorithm using the pivot table index. In the remainder of this section we detail how to integrate the SQFD-only algorithm into a database indexer and query processor that evaluates range and kNN queries.

4.4.1 Computing pivot table

When a database of signatures is being indexed, a pivot table needs to be computed. The pivot table consists of distances from selected pivots to all objects in the database. Even though these distances are computed only when new objects are inserted, we can easily modify the SQFD-only algorithm to construct the pivot table in parallel as well. In order to do so, we disable the lower bound construction and pre-filtering steps and execute a query for each pivot object. Moreover, no result set is formed in the filtering step but the distances are saved into the pivot table instead.

4.4.2 Range query

The sequential range query algorithm (i.e., without an index) is easy to implement by the SQFD-only algorithm. The database is divided into blocks of appropriate size³ and all blocks are enqueued for GPU processing. The system waits for all SQFD computations to complete, and the computed distances are filtered on the CPU to exclude objects outside of the query range. Hence, the lower bound construction and pre-filtering steps are just omitted (all database objects are candidates).

When using the pivot table index (either metric or ptolemaic variant), the SQFD-only algorithm is used as described. In the pre-filtering and filtering steps the actual radius of the range query is used. Concerning the blocks of signatures that are dispatched to GPU, block size of 128–256 for α=0.01 and 1024–2048 for α=0.2 were observed as empirically optimal (see Sect. 6.5.1).

4.4.3 kNN query

The kNN query evaluation is slightly more complicated. When no indexing is used, it works very much like sequential range query. When the pivot table indexing is employed, some additional modifications are required. The problem is that the kNN query has no fixed query range for the pivot table pre-filtering, as this range is dynamically refined during the kNN query processing using heuristics. In order to adapt to the heuristics, we limit the block size to a value between 64 and 512 (depending on index type and α value). Also, there are at most as many blocks pending as there are the GPU devices available. These constants have been chosen empirically⁴ (see Sect. 6.5.2). When the limit of pending blocks is reached, the system waits for the first enqueued block to finish, its results are taken, and the query range is refined. This way a pipeline effect is achieved, so that the CPU pre-filters the database objects and refines the resulting kNN set while the GPU computes the SQFD.

5 Moving the index to GPU

The design of the basic SQFD-only algorithm assumes that implementing SQFD computation as an asynchronous operation performed on GPU leaves the CPU rather low-utilized and so capable of performing other tasks like lower bound construction, pre-filtering, and filtering. Although this holds true for the metric version of pivot table, the lower bound construction step becomes quite expensive when using the ptolemaic version (or combined ptolemaic and metric version). Instead of taking the maximum value over the p lower bounds, in the ptolemaic case we need to maximize over up to $\mathcal{O}(p^{2})$ bounds (see Sect. 2.3 for details). The SQFD-only algorithm, when applied on the ptolemaic pivot table, cannot fully utilize the GPUs due to the CPU, which is overloaded by the lower bound construction. In consequence, the CPU cannot timely dispatch the blocks of signatures to GPUs and these must wait (see the experiments for empirical evidence). To overcome this bottleneck, in this section we propose the SQFD+LB algorithm that moves the lower bound construction to GPU, thus reducing the computational load of CPU.

5.1 The SQFD+LB algorithm

The SQFD+LB algorithm is depicted in Fig. 10. The main difference is that the query evaluation is divided into two stages. In the first (new) stage, the lower bound construction step is moved to GPU. The second stage works as the original SQFD-only algorithm, except that the CPU has much less work due to the lower bounds constructed in the first stage.

Fig. 10

Workflow of the SQFD+LB algorithm

Despite the improvement in the GPUs/CPU load balance, moving the lower bound construction to GPU brings also an unpleasant side effect. Because now the lower bound construction and pre-filtering steps run separately and asynchronously (the former on GPUs, the latter on CPU), the lower bound construction cannot benefit from the early termination optimization anymore (Sect. 2.3), which makes the whole computation less efficient. However, the sacrifice is worth the overall gain in better utilized GPUs (as shown in the experiments). We must note that moving both of the steps to GPU (also the pre-filtering) cannot help, because the CPU still has to dispatch the blocks of candidate signatures to GPU (which is done together with pre-filtering).

Computing lower bounds for all the database objects on GPUs means the pivot table as well as the query-to-pivot distances must be transferred to global memory of the GPU (VRAM). In case the pivot table cannot fit the memory or in case we have multiple GPU devices available, the table is divided into blocks which are as large as possible.⁵ The lower bound construction is then performed in block-wise fashion the same way as SQFD computation is performed on the blocks of signatures. In the following we take more detailed look at the parallel lower bounds construction on GPU.

5.2 Pivot table representation

The most delicate issue of the lower bound construction is the memory representation of the pivot table. A pivot table is two dimensional array that holds distances between a small number of pivots to every object in the database. There are many ways how to represent two-dimensional array in linear memory. However, both direct approaches (row-wise or column-wise concatenation) are not suitable in our case. We need to consider the following requirements:

• The pivot table must be divisible (with acceptable granularity) to blocks in case it does not fit the VRAM or there are multiple GPU devices available.

• Pivot table fragment being processed by one thread group must be organized so that the data transfers are performed in coalesced loads.

• Data required by threads of one group at the same time should be distributed into the local memory banks as evenly as possible.

In order to meet these requirements, we have chosen a memory representation as depicted in Fig. 11. The pivot table is divided into blocks of equal size. Each block is assigned to one thread group so its size is determined accordingly. In our case the block spans over 256 columns of the pivot table as we use 256 threads per group.

Fig. 11

Pivot table memory representation

Each pivot table block is stored in a contiguous part of the memory, where distances to each particular pivot are stored consecutively. This representation is suitable for a model where one thread computes lower bound value for one database object. When a thread iterates over pivots, all threads in a group process distances to one pivot at the same time. Therefore, the data loaded by the threads lie in aligned continuous range of memory. Furthermore, distances are evenly distributed over memory banks as each distance is represented by one float value.

5.3 Computing lower bounds on the GPU

Given the pivot table memory representation described above, the GPU-based lower bound construction is much simpler than the GPU-based SQFD computation. Each thread computes the lower bound of one database object and each thread group operates on one pivot table block. To compute a lower bound for a database object, a vector of query-to-pivot distances and the matrix of pivot-to-pivot distances is additionally required to be transferred and stored in the memory of GPUs.

In particular, the query-to-pivot distances are computed and stored into a buffer on every GPU device available. It is cached in the local memory when the computation starts. The pivot-to-pivot matrix could be extracted from pivot table, but for the sake of simplicity and faster loading the data are duplicated so that all pivot-to-pivot distances are in one compact block. Also this matrix is cached in the local memory. The corresponding pivot table block may be cached in the local memory too; however, on the state-of-the-art GPUs we need not to cache it implicitly as the data is accessed in such manner that they are cached in L1 and L2 automatically.

6 Experiments

In this section we evaluate the efficiency of parallel similarity search using the SQFD. We have compared the performance of high-end multi-core CPU server with a common workstation that used one or two GPU cards. In the experiments we have observed the behavior of the two proposed query algorithms under various parameters, like the α used in SQFD computation, the type of lowerbounding used by pivot table indexes, and the size of the blocks dispatched for parallel processing. The last one in the list was especially important for the evaluation, as the block size heavily determined the throughput of the system and the load balancing between CPU and GPU. In all the experiments we measured just the real times, because other types of cost, like the number of distance computations, were not affected by the parallel processing.

6.1 Methodology and hardware setup

Each test was performed using 100 query signatures with different numbers of centroids, while each query was measured five times and then the mean value was determined by computing arithmetic average of the measured values. If any of the time values deviated from the average more than 15 %, the value was discarded and the test was repeated. In the results we show the mean value of the average times of all 100 queries.

Tests conducted on the GPU platform are denoted GPU1 and GPU2 in the figures, where the number refers to either on one or two GPU used. The workstation was based on Intel Core i7 870 CPU clocked at 2.93 GHz, and was equipped with 16 GB of RAM and two NVIDIA GTX 580 GPU cards with 512 CUDA cores and 1.5 GB of RAM each. Tests conducted on the multi-core CPU server platform are denoted CPU48 in the figures. We used Dell M910 server with four six-core Intel Xeon E7540 processors with hyper-threading (i.e., 48 logical cores) clocked at 2.0 GHz. The server was equipped with 128 GB of RAM organized as 4-node cache coherent NUMA. A RedHat Enterprise Linux 6 was used as operating system on both machines.

In order to compare the proposed algorithms to the multi-core CPU platform (CPU48), we have also modified the SQFD-only algorithm for pure CPU system by utilizing all available cores. Its architecture mimics the original SQFD-only algorithm, where one CPU core performs the pre-filtering, block dispatching, and final filtering, while the remaining cores compute SQFD distances in parallel instead of the GPU.

6.2 Datasets

The experiments were conducted on one synthetic dataset representing clouds of points and one real dataset consisting of feature signatures extracted from images.

A synthetic Clouds database was generated [20], namely 2,097,152 clouds (sets) of 100–140 5-dimensional points (embedded in a unitary 5D cube). This database was chosen as a set analogy to synthetic vector datasets when evaluating vectorial similarity search. Moreover, the cloud of points is a common representation for simplified representations of complex objects or objects consisting of multiple observations [21]. Each point has assigned a weight where the sum of all weights in the cloud was 10,000. For each cloud, its center was generated at random, while another 10,000 points were generated under normal distribution around the center (the mean and variance in each dimension were adjusted to not generate points outside the unitary cube). Then an adaptive variant of the k-means clustering [17] was used to create 100–139 centroids representing the original data. The weight of each centroid corresponded to the number of points assigned to the centroid in the last iteration of the k-means clustering. On average, a feature signature consisted of 120 representatives (centroids), i.e., 720 numbers per signature. The distribution of the number of representatives for Clouds is depicted on Fig. 12a.

Fig. 12

Distribution of the number of signature centroids for (a) Clouds and (b) CoPhIR databases

As a dataset from the real world, we have extracted feature signatures from 950,000 images from the CoPhIR database [6]. The extraction was based on seven-dimensional features (L; a; b; x; y; c; e)—color (L; a; b), position (x; y), contrast c, and entropy e. These features were extracted for a randomly selected subset of pixels for each image and then again aggregated by applying the adaptive variant of the k-means clustering algorithm. Thus, we have obtained one feature signature for each single image. These signatures vary in size between 15 and 215 feature representatives (for more details about the size distribution see Fig. 12b). On average, a feature signature consists of 75 representatives (i.e., 600 numbers per signature).

6.3 Index setup

For both the hardware platforms we have used a parallel implementation of the pivot table index (see Sect. 2.3). In order to observe the difference between SQFD-Only and SQFD+LB algorithm, we have used three types of lowerbounding in the pivot table, the metric type using triangle inequality (denoted Tri in the figures), ptolemaic type using Ptolemy’s inequality (denoted Pto), and both metric+ptolemaic type (denoted TriPto). In all experiments we used 32 pivots. Actually, we used as many pivots as possible with respect to memory and cache sizes available on present hardware. The limited number of pivots, however, is not crucial when using the ptolemaic pivot tables, because ptolemaic filtering exploits every distinct pair of pivots (e.g., the number of pivots squared).

6.4 Sequential search and indexing

In the first set of tests we performed similarity search without the aid of an index, that is, sequential search over the database, however, parallelized for both CPU48 and GPU platforms. The overhead of particular query result construction is negligible, thus we do not distinguish between range queries or kNN queries in sequential search. Furthermore, all tests were conducted only for α=0.2 as different alpha values affect only the efficiency of pivot table pre-filtering, but they have no measurable impact on the speed of SQFD evaluation. Besides query processing, these tests can also be interpreted as parallel construction of the pivot table, since the sequential search/pivot table construction procedures are similar.

First, we will examine how the performance is affected by different block size (Fig. 13). As there is no pre-filtering, this graph helps us determine the overhead of block dispatching. The experimental results show that dispatching distance computations in blocks of at least 1024 signatures is sufficient for optimal performance. However, this predicament holds only in case the CPU is capable of supplying GPU steadily with data blocks.

Fig. 13

The impact of the varying block size

Next, we compare the best possible result on GPU (using block size of 8,192 signatures) against our CPU implementation running on 48 logical cores (Fig. 14). The best speedup was achieved for Clouds database on 2 GPUs (1024 cores total)—10.08× w.r.t. to CPU 48 version. The Clouds dataset with signatures formed on average by 120 centroids shows better speedup than CoPhIR containing signatures formed on average by 75 centroids. Furthermore, we have observed that the CPU version has rather higher variance of measured times since the SQFD computation depends heavily on signature length which differs amongst the test queries. On the other hand, this effect is considerably reduced on GPU, where better speedup on larger signatures and stronger resistance to length variance were observed, because the GPU utilized the parallelism better on large signatures.

Fig. 14

Comparison of total GPU speedup over multi-core CPU server

6.5 Index search

In the second set of tests, we executed queries on pivot table indexes. Three types of pre-filtering were used in pivot table: the metric filter with triangular inequality (Tri), Ptolemaic filter (Pto) and combination of both (TriPto). We were testing both SQFD-only and SQFD+LB algorithms. The results are shown for α=0.01, which gave us the best indexability, and for α=0.2, which gave us the best tradeoff between performance and retrieval precision. Larger α values (such as α=3 which gave us the best precision but worst indexability) did not benefit much from indexing, so the results were similar to sequential search.

Furthermore, the SQFD+LB algorithm had preloaded the pivot table into the GPU memory and the table was kept in the memory during the whole test so all queries could use it. In our case the pivot table was small enough to not affect SQFD computations in any way. The upload of the pivot table to GPU memory took 54 ms for CoPhIR database and 118 ms for Clouds database.

6.5.1 Range queries

In order to normalize sizes of query results, the range queries were designed to have always the same selectivity (0.1 % of the database size). The results of tests performed to determine the optimal block size for each method are shown in Fig. 15.

Fig. 15

The impact of the varying block size for range queries

All results exhibit the same behavior. Unlike the sequential search, all methods were parameterized by an optimal block size where the CPU workload, GPU workload, and overhead were in balance. Increasing the block size beyond the optimal value did not help the performance, since it increased time periods when GPU waits for CPU or vice versa.

On single GPU the SQFD+LB algorithm is slower than (α=0.01) or approximately as fast as (α=0.2) the SQFD-only algorithm. This result is caused by fact that in case of single GPU, the CPU-GPU workload is almost in balance and the parallel lower bound construction does not completely make up for sacrifice of the early termination optimization. However, as we can see from 2 GPU tests, the SQFD+LB scales much better than SQFD-only algorithm and gives better results. In case of α=0.2, the SQFD+LB using TriPto index is by 21 % faster than SQFD-only algorithm with the same parameters. We believe that on more GPUs the difference between these two algorithms would be even greater.

Finally, we present comparison of best results for both algorithms employing TriPto index and choosing optimal block size on GPU 1, GPU 2 and CPU 48 (Fig. 16). The CPU version ran solely the SQFD-only algorithm as the SQFD+LB algorithm is not suitable for CPUs.

Fig. 16

Comparison of the best results on different architectures

6.5.2 kNN queries

For the kNN queries we used k=100, so that 100 nearest neighbors of the query object were selected. The kNN query differs from range query in fact that the query radius, which was also used for the pre-filtering step, was refined during the computation. Therefore, selecting appropriate block size was even more delicate than in sequential search or range queries (Fig. 17).

Fig. 17

The impact of the varying block size for kNN queries

The results indicate that even smaller blocks are required in order to achieve optimal performance, especially for α=0.01. For most algorithms, the optimal block size is 64–128 for α=0.01 and about 256 for α=0.2.

As shown in range queries tests, the SQFD+LB algorithm was slightly slower in case of α=0.01 on single GPU and slightly faster for α=0.2. But most importantly, it exhibits better speedup when comparing GPU1 and GPU2 results, thus provides much better opportunities for scalability.

The overall comparison of kNN results is reviewed in the remaining set of graphs (Fig. 18).

Fig. 18

Comparison of the best results on different architectures

6.6 Summary

We have experimentally proved that our GPU-based algorithms are significantly faster than multi-core CPU implementation in every type of query processing and also in indexing. Furthermore, the SQFD+LB algorithm demonstrates great scalability potential and offers better performance in case there is more GPU computational power available.

7 Conclusion

We have proposed a parallel approach to fast similarity search using the Signature Quadratic Form Distance (SQFD) on combined CPU and GPU architectures. In particular, we proposed two algorithms that adopt metric/ptolemaic indexing within a parallel architecture, such that the query processing workload is split between the CPU and multiple GPUs. The first algorithm utilizes the GPUs just by computation of SQFDs batches, leaving the other processing on CPU. The second algorithm utilizes the GPUs additionally by construction of lower-bound distances used in the index pre-filtering, leading to better balance of workload between the CPU and GPUs when expensive lower bound construction is used (such as the ptolemaic lowerbounding). In experimental evaluation we have shown that our implementation on a common workstation with just 2 GPU cards outperforms the traditional parallel implementation on a high-end 48-core server by up to an order of magnitude. If we consider also the price of the high-end server which is ten times higher than the GPU workstation, then based on price/performance ratio, the GPU-based similarity search beats the CPU-based solution by almost two orders of magnitude.