Time series joins, motifs, discords and shapelets: a unifying view that exploits the matrix profile

Abstract

The last decade has seen a flurry of research on all-pairs-similarity-search (or similarity joins) for text, DNA and a handful of other datatypes, and these systems have been applied to many diverse data mining problems. However, there has been surprisingly little progress made on similarity joins for time series subsequences. The lack of progress probably stems from the daunting nature of the problem. For even modest sized datasets the obvious nested-loop algorithm can take months, and the typical speed-up techniques in this domain (i.e., indexing, lower-bounding, triangular-inequality pruning and early abandoning) at best produce only one or two orders of magnitude speedup. In this work we introduce a novel scalable algorithm for time series subsequence all-pairs-similarity-search. For exceptionally large datasets, the algorithm can be trivially cast as an anytime algorithm and produce high-quality approximate solutions in reasonable time and/or be accelerated by a trivial porting to a GPU framework. The exact similarity join algorithm computes the answer to the time series motif and time series discord problem as a side-effect, and our algorithm incidentally provides the fastest known algorithm for both these extensively-studied problems. We demonstrate the utility of our ideas for many time series data mining problems, including motif discovery, novelty discovery, shapelet discovery, semantic segmentation, density estimation, and contrast set mining. Moreover, we demonstrate the utility of our ideas on domains as diverse as seismology, music processing, bioinformatics, human activity monitoring, electrical power-demand monitoring and medicine.

1 Introduction

The basic problem statement for all-pairs-similarity-search (also known as similarity join) problem is this: Given a collection of data objects, retrieve the nearest neighbor for every object. In the text domain, the dozens of algorithms which have been developed to solve the similarity join problem (and its variants) have been applied to an increasingly diverse set of tasks, such as community discovery, duplicate detection, collaborative filtering, clustering, and query refinement (Agrawr et al. 1993). However, while virtually all text processing algorithms have analogues in time series data mining (Mueen et al. 2009), there has been surprisingly little progress on Time Series subsequences All-Pairs-Similarity-Search (TSAPSS).

It is clear that a scalable TSAPSS algorithm would be a versatile building block for developing algorithms for many time series data mining tasks (e.g., motif discovery, shapelet discovery, semantic segmentation and clustering). As such, the lack of progress on TSAPSS stems not from a lack of interest, but from the daunting nature of the problem. Consider the following example that reflects the needs of an industrial collaborator: A boiler at a chemical refinery reports pressure once a minute. After a year, we have a time series of length 525,600. A plant manager may wish to do a similarity self-join on this data with week-long subsequences (10,080) to discover operating regimes (summer vs. winter or light-distillate vs. heavy-distillate etc.) The obvious nested loop algorithm requires 132,880,692,960 Euclidean distance computations. If we assume each one takes 0.0001 s, then the join will take 153.8 days. The core contribution of this work is to show that we can reduce this time to 1.2 hours, using an off-the-shelf desktop computer. Moreover, we show that this join can be computed and/or updated incrementally. Thus, we could maintain this join essentially forever on a standard desktop, even if the data arrival frequency was much faster than once a minute.

Our algorithm uses an ultra-fast similarity search algorithm under z-normalized Euclidean distance as a subroutine, exploiting the redundancies between overlapping subsequences to achieve its dramatic speedup and low space overhead.

Our method has the following advantages/features:

• It is exact: Our method provides no false positives or false dismissals. This is an important feature in many domains. For example, a recent paper has addressed the TSAPSS problem in the special case of earthquake telemetry (Yoon et al. 2015). The method does achieve speedup over brute force, but allows false dismissals. A single high-quality seismometer can cost $10,000 to $20,000 (Alibaba.com 2017), and the installation of a seismological network can cost many millions. Given that cost and effort, users may not be willing to miss a single nugget of exploitable information, especially in a domain with implications for human life.

• It is simple and parameter-free: In contrast, the more general metric space APSS algorithms typically require building and tuning spatial access methods and/or hash functions (Luo et al. 2012; Ma et al. 2016; Yoon et al. 2015).

• It is space efficient: Our algorithm requires an inconsequential space overhead, just O(n) with a small constant factor. In particular, we avoid the need to actually extract the individual subsequences (Luo et al. 2012; Ma et al. 2016) something that would increase the space complexity by two or three orders of magnitude, and as such, force us to use a disk-based algorithm, further reducing time performance.

• It is an anytime algorithm: While our exact algorithm is extremely scalable, for extremely large datasets we can compute the results in an anytime fashion (Ueno et al. 2006; Assent et al. 2012), allowing ultra-fast approximate solutions.

• It is incrementally maintainable: Having computed the similarity join for a dataset, we can incrementally update it very efficiently. In many domains this means we can effectively maintain exact joins on streaming data forever.

• It does not require the user to set a similarity/distance threshold: Our method provides full joins, eliminating the need to specify a similarity threshold, which as we will show, is a near impossible task in this domain.

• It can leverage hardware: Our algorithm is embarrassingly parallelizable, both on multicore processors and in distributed systems.

• It has time complexity that is constant in subsequence length: This is a very unusual and desirable property; virtually all time series algorithms scale poorly as the subsequence length grows (Ding et al. 2008; Mueen et al. 2009).

• It takes deterministic time: This is also unusual and desirable property for an algorithm in this domain. For example, even for a fixed time series length, and a fixed subsequence length, all other algorithms we are aware of can radically different times to finish on two (even slightly) different datasets. In contrast, given only the length of the time series, we can predict precisely how long it will take our finish in advance.

Given all these features, our algorithm may have implications for many time series data mining tasks (Chandola et al. 2009; Hao et al. 2012; Mueen et al. 2009; Yoon et al. 2015).

In series of recent works, we have introduced several TSAPSS algorithms and shown applications in various domains (Yeh et al. 2016a, b; Zhu et al. 2016). However, this work we provided (1) holistic analysis that summarizes and significantly expands on those efforts and (2) a description on incremental variant of STOMP algorithm (Zhu et al. 2016) (i.e., $\hbox {STOMP}I$).

The rest of the paper is organized as follows. Sections 2 and 3 review related work and introduces the necessary background materials and definitions. In Sect. 4 we introduce our algorithm and its anytime and incremental variants. Additionally, we further show that if we need to address truly massive datasets, and we are willing to forgo the anytime algorithm property, we can further speed up our algorithm, and in fact create the provably optimally fast algorithm. Section 5 sees a detailed empirical evaluation of our algorithm and shows its implications for many data mining tasks. Finally, in Sect. 6 we offer conclusions and directions for future work.

2 General related work and background

The particular variant of similarity join problem we wish to solve is: Given a collection of data objects, retrieve the nearest neighbor for every object. We believe this is the most basic version of the problem, and any solution for this problem can be easily extended to other variants of similarity join problem.

Other common variants include retrieving the top-K nearest neighbors or the nearest neighbor for each object if that neighbor is within a user-supplied threshold, $\tau$. (Such variations are trivial generalizations of our proposed algorithm, so we omit them from further discussion). The latter variant results in a much easier problem, provided that the threshold is reasonably small. For example, Agrawal et al. notes that virtually all research efforts “exploit a similarity threshold more aggressively in order to limit the set of candidate pairs that are considered.. [or] ...to reduce the amount of information indexed in the first place.” (1993).

This critical dependence on $\tau$ is a major issue for text joins, as it is known that “join size can change dramatically depending on the input similarity threshold” (Lee et al. 2011). However, this issue is even more critical for time series for two reasons. First, unlike similarity (which is bounded between zero and one), the Euclidean distance is effectively unbounded, and generally not intuitive. For example, if two heartbeats have a Euclidean distance of 17.1, are they similar? Even if you are a domain expert and know the sampling rate and the noise level of the data, this is not obvious. Second, a single threshold can produce radically different output sizes, even for datasets that are very similar to the human eye. Consider Fig.  1 which shows the output size versus threshold setting for the first and second halves of a ten-day period monitoring data center chillers (Patnaik et al. 2009). For the first five days a threshold of 0.6 would return zero items, but for the second five days the same setting would return 108 items. This shows the difficulty in selecting an appropriate threshold. Our solution is to have no threshold and do a full join. After the join is computed, the user may then use any ad-hoc filtering rule to give the result set she desires. For example, the top-fifty matches, or all matches in the top-two-percent. Moreover, as we show in Sects. 5.4.3, 5.5.2 and 5.5.3, we may be interested in the bottom-fifty matches, or all matches in the bottom-two-percent. To the best of our knowledge, no research effort in time series joins can support such primitives, as all techniques explicitly exploit pruning strategies based on “nearness” (Luo et al. 2012; Ma et al. 2016).

Fig. 1

Output size versus threshold for data center chillers (Patnaik et al. 2009). Values beyond 2.0 are truncated for clarity (but archived at Supporting Page 2017). For a large range of thresholds (from 0 to 0.65) the difference in the selectivity is enormous, from zero to one-hundred and eight

A handful of efforts have considered joins on time series, achieving speedup by (in addition to the use of MapReduce) converting the data to lower-dimensional representations such as PAA (Luo et al. 2012) or SAX (Ma et al. 2016) and exploiting lower bounds and/or Locality Sensitive Hashing (LSH) to prune some calculations. However, the methods are very complex, with many (10-plus) parameters to adjust. As Luo acknowledges with admirable candor, “Reasoning about the optimal settings is not trivial” (2012). In contrast, our proposed algorithm has zero parameters to set.

A very recent research effort (Yoon et al. 2015) has tackled the scalability issue by converting the real-valued time series into discrete “fingerprints” before using a LSH approach, much like the text retrieval community (Agrawr et al. 1993). They produced impressive speedup, but they also experienced false negatives. Moreover, the approach has several parameters that need to be set; for example, they set the threshold to a very precise 0.818. In passing, we note that one experiment they performed offers confirmation of the pessimistic “153.8 days” example we gave in the introduction. A brute-force experiment they conducted with slightly longer time series but much shorter subsequences took 229 hours, suggesting a value of about 0.0002 s per comparison, just twice our estimate (see Supporting Page 2017 for analysis). We will revisit this work in Sect. 5.3.

As we shall show, our algorithm allows both anytime and incremental (i.e. streaming) versions. While a streaming join algorithm for text was recently introduced (Morales and Gionis 2016) we are not aware of any such algorithms for time series data or general metric spaces. More generally, there is a huge volume of literature on joins for text and DNA processing (Agrawr et al. 1993). Such work is interesting, but of little direct utility given our constraints, data type and problem setting. We are working with real-valued data, not discrete data. We require full joins, not threshold joins, and we are unwilling to allow the possibility, no matter how rare, of false negatives.

2.1 Definitions and notation

We begin by defining the data type of interest, time series:

Definition 1

A time series T is a sequence of real-valued numbers $t_{i}: T=t_{1}$, $t_{2}, \ldots , t_{\mathrm{n}}$ where n is the length of T.

We are not interested in the global properties of time series, but in the similarity between local regions, known as subsequences:

Definition 2

A subsequence $T_{i,m}$ of a T is a continuous subset of the values from T of length m starting from position i. Formally, $T_{i,m}=t_{i}$, $t_{i+1}, {\ldots }, t_{i+m-1}$, where 1 $\le i \le n-m+1$.

We can take any subsequence from a time series and compute its distance to all sequences. We call an ordered vector of such distances a distance profile:

Definition 3

A distance profile D is a vector of the Euclidean distances between a given query and each subsequence in an all-subsequences set (see Definition 4).

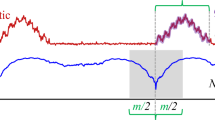
Note that we are assuming that the distance is measured using the Euclidean distance between the z-normalized subsequences, that is to say, the subsequences have a mean of zero, and a standard deviation of one (Agrawr et al. 1993). The distance profile can be considered a meta time series that annotates the time series T that was used to generate it. The first three definitions are illustrated in Fig. 2.

Fig. 2

A subsequence Q extracted from a time series T is used as a query to every subsequence in T. The vector of all distances is a distance profile

Note that by definition, if the query and all-subsequences set belong to the same time series, the distance profile must be zero at the location of the query, and close to zero just before and just after. Such matches are called trivial matches in the literature (Mueel et al. 2009), and are avoided by ignoring an exclusion zone (shown as a gray region) of m / 2 before and after the location of the query.

We are interested in similarity join of all subsequences of a given time series. We define an all-subsequences set of a given time series as a set that contains all possible subsequences from the time series. The notion of all-subsequences set is purely for notational purposes. In our implementation, we do not actually extract the subsequences in this form as it would require significant time overhead, and explode the memory requirements.

Definition 4

An all-subsequences set A of a time series T is an ordered set of all possible subsequences of T obtained by sliding a window of length m across $T: {{\varvec{A}}} =\{T_{1,m,}, T_{2,m},{\ldots }, T_{n-m+1,m}\}$, where m is a user-defined subsequence length. We use ${{\varvec{A}}}[i]$ to denote $T_{i,m}$.

We are interested in the nearest neighbor (i.e., 1NN) relation between subsequences; therefore, we define a 1NN-join function which indicates the nearest neighbor relation between the two input subsequences.

Definition 5

1NN-join function: given two all-subsequence sets ${{\varvec{ A}}}$ and ${{\varvec{B}}}$ and two subsequences ${{\varvec{A}}}[i]$ and ${{\varvec{B}}}[j]$, a 1NN-join function  $\uptheta _{\mathrm{1nn}}\, ({{\varvec{A}}}[i], {{\varvec{B}}}[j])$ is a Boolean function which returns “true” only if ${{\varvec{B}}}[j]$ is the nearest neighbor of ${{\varvec{A}}}[i]$ in the set ${{\varvec{B}}}$.

With the defined join function, a similarity join set can be generated by applying the similarity join operator on two input all-subsequence sets.

Definition 6

Similarity join set: given all-subsequence sets ${{\varvec{A}}}$ and ${{\varvec{B}}}$, a similarity join set ${{\varvec{J}}}_{{\varvec{AB}}}$ of ${{\varvec{A}}}$ and ${{\varvec{B}}}$ is a set containing pairs of each subsequence in ${{\varvec{A}}}$ with its nearest neighbor in ${{\varvec{B}}}: {{\varvec{J}}}_{{\varvec{AB}}}=\{\langle {{\varvec{A}}}[i], {{\varvec{B}}}[j] \rangle {\vert }\uptheta _{\mathrm{1nn}} ({{\varvec{A}}}[i], {{\varvec{B}}}[j])\}$. We denote this formally as ${{\varvec{J}}}_{{\varvec{AB}}} = {{\varvec{A}}}\bowtie _{\uptheta \mathrm{1nn}}{{\varvec{B}}}$.

We measure the Euclidean distance between each pair within a similarity join set and store the resultants into an ordered vector. We call the result vector matrix profile.

Definition 7

A matrix profile (or just profile) $P_{AB}$ is a vector of the Euclidean distances between each pair in ${{\varvec{J}}}_{{\varvec{AB}}}$ where $P_{AB}[i]$ contains the distance between ${{\varvec{A}}}[i]$ and its nearest neighbor in ${{\varvec{B}}}$.

We call this vector the matrix profile because one (inefficient) way to compute it would be to compute the full distance matrix of all the subsequences in one time series with all the subsequence in another time series and extract the smallest value in each row (the smallest non-diagonal value for the self-join case). In Fig. 3 we show the matrix profile of our running example.

Fig. 3

A time series T, and its self-join matrix profile P

Like the distance profile, the matrix profile can be considered a meta time series annotating the time series T if the matrix profile is generated by joining T with itself. The profile has a host of interesting and exploitable properties. For example, the highest point on the profile corresponds to the time series discord (Chandola et al. 2009), the (tying) lowest points correspond to the locations of the best time series motif pair (Mueen et al. 2009), and the variance can be seen as a measure of the T’s complexity. Moreover, the histogram of the values in the matrix profile is the exact answer to the one version of the time series density estimation problem (Bouezmarni and Rombouts 2010).

We name this special case of the similarity join set ( Definition 6) as self-similarity join set, and the corresponding profile as self-similarity join profile.

Definition 8

A self-similarity join set ${{\varvec{J}}}_{{\varvec{AA}}}$ is a result of similarity join of the set ${{\varvec{A}}}$ with itself . We denote this formally as ${{\varvec{J}}}_{{\varvec{AA}}} = {{\varvec{A}}}\bowtie _{\uptheta \mathrm{1nn}} {{\varvec{A}}}$. We denote the corresponding matrix profile or self-similarity join profile as $P_{AA}$.

Note that we exclude trivial matches when self-similarity join is performed, i.e., if ${{\varvec{A}}}[i]$ and ${{\varvec{A}}}[j]$ are subsequences from the same all-subsequences set ${{\varvec{A}}}$, $\uptheta _{\mathrm{1nn}} ({{\varvec{A}}}[i]$, ${{\varvec{B}}}[j])$ is “false” when ${{\varvec{A}}}[i]$ and ${{\varvec{A}}}[j]$ are trivially matched pair.

The $i{\mathrm{th}}$ element in the matrix profile tells us the Euclidean distance to the nearest neighbor of the subsequence of T, starting at i. However, it does not tell us where that neighbor is located. This information is recorded in the matrix profile index.

Definition 9

A matrix profile index $I_{{ AB}}$ of a similarity join set ${{\varvec{J}}}_{{\varvec{AB}}}$ is a vector of integers where $I_{AB}[i] = j$ if $\{{{\varvec{A}}}[i], {{\varvec{B}}}[j]\} \in {{\varvec{J}}}_{{\varvec{AB}}}$.

By storing the neighboring information this way, we can efficiently retrieve the nearest neighbor of ${{\varvec{A}}}[i]$ by accessing the $i^{th}$ element in the matrix profile index.

Note that the function which computes the similarity join set of two input time series is not symmetric; therefore, ${{\varvec{J}}}_{{\varvec{AB}}} \ne {{\varvec{J}}}_{{\varvec{BA}}}$, $P_{AB} \ne P_{BA}$, and $I_{AB} \ne I_{BA}$.

For clarity of presentation, we have confined this work to the single dimensional case; however, nothing about our work intrinsically precludes generalizations to multidimensional data. In the multidimensional data, we would still have a single matrix profile, and a single matrix profile index; the only change needed is to replace the 1D Euclidean Distance with the b D Euclidean Distance, where b is the number of dimensions the user wants to consider. The only issue here is that it may be unwise to us all the dimensions in a high dimensional problem. This issue is explained in detail (in a slightly different context) in Hu et al. (2013).

Summary of the Previous Section

The previous section was rather dense, so before moving on we summarize the main takeaway points. We can create two meta time series, the matrix profile and the matrix profile index, to annotate a time series $T_{A}$ with the distance and location of all its subsequences nearest neighbors in itself or another time series $T_{B}$. These two data objects explicitly or implicitly contain the answers to many time series data mining tasks. However, they appear to be too expensive to compute to be practical. In the next section we will show an algorithm that can compute these efficiently.

3 Related work in similarity search

We reviewed general related work in a previous section. Here we consider just related work in similarity search. In essence, our solution to the task-at-hand is almost exclusively comprised of similarity searches, thus having highly optimized searches is critical for scalability. There is a huge body of work on time series similarity search; see Ding et al. (2008) and the references therein. Most of the work is focused on efficiency in accessing disk resident data (Agrawr et al. 1993; Ding et al. 2008; Rakthanmanon et al. 2012, 2013a)

Unlike most other kinds of data, time series is unusual in that the atomic objects “overlap” with each other. It is possible to ignore this by explicitly extracting all subsequences. However, this makes the memory requirements explode. Recent work by Mueen and colleagues has focused on processing the subsequences in situ. In Rakthanmanon et al. (2012) overlap invariant z-normalization is achieved while calculating the distances in the old-fashioned single loop sum-of-squared-error manner. Efficient overlap invariance has been achieved in distance computation for Shapelet discovery in Mueen et al. (2011) by caching computation in the quadratic search space. The MASS algorithm exploits overlap in calculating z-normalized distances by using convolution and provides the worst-case time complexity of $\hbox {O}(n\hbox {log}n)$. This is optimally fast, assuming only (as is universally believed) that the Fast Fourier transform is optimal. In recent years MASS has emerged as significant development in subsequence similarity search for many similarity based pattern mining algorithms (Yeh et al. 2016a, b; Zhu et al. 2016).

Up to this point, the use of DFT (Discrete Fourier Transform) has mostly been to produce a lower dimensional representations of time series to index time series (Agrawr et al. 1993), to identify periodicities (Vlachos et al. 2004) to accelerate pair-wise distance computation (Mueen et al. 2010) and to achieve rotation/phase invariance (Vlachos et al. 2005). In contrast, we use DFT to perform convolution which operates at full resolution (as opposed to reduced dimensionality). Convolution is a century’s-old technique [The earliest use of convolution in English appears in Wintner (1934)]. MASS allows convolution for time series similarity search under z-normalized Euclidean distance for the first time.

We discuss more explicit rival algorithms to STAMP/STOMP in the relevant sections below.

4 Algorithms

We are finally in a position to explain our algorithms. We begin by stating the fundamental intuition, which stems from the relationship between distance profiles and the matrix profile. As Figs. 2 and 3 visually suggest, all distance profiles (excluding the trivial match region) are upper bound approximations to the matrix profile. More critically, if we compute all the distance profiles, and take the minimum value at each location, the result is the matrix profile.

This tells us that if we have a fast way to compute the distance profiles, then we also have a fast way to compute the matrix profile. As we shall show in the next section, we do have such an ultra-fast way to compute the distance profiles.

4.1 Ultra-fast similarity search

We begin by introducing a novel ultra-fast Euclidean distance similarity search algorithm called MASS (Mueen’s Algorithm for Similarity Search) for time series data. The algorithm does not just find the nearest neighbor to a query and return its distance; it returns the distance to every subsequence. In particular, it computes the distance profile, as shown in Fig. 2. The algorithm requires just $\hbox {O}(n\hbox {log}n)$ time by exploiting the fast Fourier transform (FFT) to calculate the dot products between the query and all subsequences of the time series.

We need to carefully qualify the claim of “ultra-fast”. There are dozens of algorithms for time series similarity search that utilize index structures to efficiently locate neighbors (Ding et al. 2008) While such algorithms can be faster in the best case, all of these algorithms degenerate to brute force search in the worst case¹ (actually, much worse than brute force search due to the overhead of the index). Likewise, there are index-free methods that achieve speed-up using various early abandoning tricks (Rakthanmanon et al. 2012) but they too degrade to brute force search in the worst case. In contrast, the performance of the algorithms outlined in Tables 1 and reft2 is completely independent of the data.

Table 1 Calculation of sliding dot products

Line 1 determines the length of both the time series T and the query Q. In line 2, we use that information to append T with an equal number of zeros. In line 3, we obtain the mirror image (i.e. Reverse) of the original query. Reverse of a sequence $\hbox {x}_{1, }\hbox {x}_{2}, \hbox {x}_{3}, {\ldots } \hbox {x}_{\mathrm{n}}$ is $\hbox {x}_{\mathrm{n}}, \hbox {x}_{\mathrm{n-1}}, \hbox {x}_{\mathrm{n-2}},\ldots \hbox {x}_{1}$. Reversing a sequence takes only linear time. Typically, the query time series is small, and the cost of reversing is so small it is difficult to reliably measure. This reversing ensures that a convolution (i.e. “crisscrossed” multiplication) essentially produces in-order alignment. Because we require both vectors to be the same length, in line 4 we append enough zeros to the (now reversed) query so that, like $T_{a}$, it is also of length 2n. In line 5, the algorithm calculates Fourier transforms of the appended-reversed query ($Q_{{ ra}}$) and the appended time series $T_{a}$. Note that we use FFT algorithm which is an $\hbox {O}(n\hbox {log}n)$ algorithm. The $Q_{{ raf}}$ and the $T_{{ af}}$ produced in line 5 are vectors of complex numbers representing frequency components of the two time series. The algorithm calculates the element-wise multiplication of the two complex vectors and performs inverse FFT on the product. Lines 5–6 are the classic convolution operation on two vectors (Convolution 2016). Figure 4 shows a toy example of the sliding dot product function in work. Note that the algorithm time complexity does not depend on the length of the query (m).

Fig. 4

A toy example of convolution operation being used to calculate sliding dot products for time series data. Note the reverse and append operation on T and q in the input. Fifteen dot products are calculated for every slide. The cells $m = 2$ to $n = 4$ from left (red/bold arrows) contain valid products. Table 2 takes this subroutine and uses it to create a distance profile (see Definition 3) (Color figure online)

In line 1 of Table 2, we invoke the dot products code outlined in Table 1. The formula to calculate the z-normalized Euclidean distance D[i] between two time series subsequence Q and $T_{i,m}$ using their dot product, QT[i], is (see Supporting Page 2017 for derivation):

$$\begin{aligned} D\left[ i \right] =\sqrt{2m\left( {1-\frac{QT\left[ i \right] -m\mu _Q M_T \left[ i \right] }{m\sigma _Q \Sigma _T \left[ i \right] }} \right) } \end{aligned}$$

(1)

where m is the subsequence length, $\mu _{Q}$ is the mean of Q, $M_{T}[i]$ is the mean of $T_{i,m}$, $\sigma _{Q}$ is the standard deviation of Q, and $\Sigma _{T}[i]$ is the standard deviation of $T_{i,m}$. Normally, it takes O(m) time to calculate the mean and standard deviation for every subsequence of a long time series. However, here we exploit a technique noted in Rakthanmanon et al. (2012) in a different context. We cache cumulative sums of the values and square of the values in the time series. At any stage the two cumulative sum vectors are sufficient to calculate the mean and the standard deviation of any subsequence of any length.

Table 2 The MASS algorithm

Unlike the dozens of time series KNN search algorithms in the literature (Ding et al. 2008), this algorithm calculates the distance to every subsequence, i.e. the distance profile of time series T. Alternatively, in join nomenclature, the algorithm produces one full row of the all-pair similarity matrix. Thus, as we show in the next section, our join algorithm is little more than a loop that computes each full row of the all-pair similarity matrix and updates the current “best-so-far” matrix profile when warranted.

4.2 The STAMP algorithm

We call our join algorithm STAMP, Scalable Time series Anytime Matrix Profile. The algorithm is outlined in Table 3. In line 1, we extract the length of $T_{B}$. In line 2, we allocate memory and initial matrix profile $P_{AB}$ and matrix profile index $I_{AB}$. From lines 3 to line 6, we calculate the distance profiles D using each subsequence ${{\varvec{B}}}[{ idx}]$ in the time series $T_{B}$ and the time series $T_{A}$. Then, we perform pairwise minimum for each element in D with the paired element in $P_{AB}$ (i.e., min(D[i], $P_{AB}[i]$) for $i=0$ to length($D)-1$.) We also update $I_{AB}[i]$ with idx when $D[i]\le P_{AB}[i]$ as we perform the pairwise minimum operation. Finally, we return the result $P_{AB}$ and $I_{AB}$ in line 7.

Note that the algorithm presented in Table 3 computes the matrix profile for the general similarity join. To modify the current algorithm to compute the self-similarity join matrix profile of a time series $T_{A}$, we simply replace $T_{B}$ in line 1 with $T_{A}$, replace ${{\varvec{B}}}$ with ${{\varvec{A}}}$ in line 4, and ignore trivial matches in D when performing ElementWiseMin in line 5.

Table 3 The STAMP algorithm

To parallelize the STAMP algorithm for multicore machines, we simply distribute the indexes to secondary process run in each core, and the secondary processes use the indexes they received to update their own $P_{{ AB}}$ and $I_{{ AB}}$. Once the main process returns from all secondary processes, we use a function similar to ElementWiseMin to merge the received $P_{{ AB}}$ and $I_{{ AB}}$.

4.3 An anytime algorithm for TSAPSS

While the exact algorithm introduced in the previous section is extremely scalable, there will always be datasets for which time needed for an exact solution is untenable. We can mitigate this by computing the results in an anytime fashion, allowing fast approximate solutions (Zilberstein and Russell 1995). To add the anytime nature to the STAMP algorithm, all we need to do are to ensure a randomized order when we select subsequences from $T_{B}$ in line 2 of Table 3.

We can compute a (post-hoc) measurement of the quality of an anytime solution by measuring the Root-Mean-Squared-Error (RMSE) between the true matrix profile and the current best-so-far matrix profile. As Fig. 5 suggests, with an experiment on random walk data, the algorithm converges very quickly.

Fig. 5

(Main) The decrease in RMSE as the STAMP algorithm updates matrix profile with the distance profile calculated at each iteration. (Inset) The approximate matrix profile at the 10% mark is visually indistinguishable from the final matrix profile

Zilberstein and Russell (1995) give a number of desirable properties of anytime algorithms, including Low Overhead, Interruptibility, Monotonicity, Recognizable Quality, Diminishing Returns and Preemptability (the meanings of these properties are mostly obvious from their names, but full definitions are at Zilberstein and Russell 1995).

Because each subsequence’s distance profile is bounded below by the exact matrix profile, updating an approximate matrix profile with a distance profile with pairwise minimum operation either drives the approximate solution closer the exact solution or retains the current approximate solution. Thus, we have guaranteed Monotonicity. From Fig. 5, the approximate matrix profile converges to the exact matrix profile superlinearly; therefore, we have strong Diminishing Returns. We can easily achieve Interruptibility and Preemptability by simply inserting a few lines of code between lines 5 and 6 of Table 3 that read:

The space and time overhead for the anytime property is effectively zero; thus, we have Low Overhead. This leaves only the property of Recognizable Quality. Here we must resort to a probabilistic argument. The convergence curve shown in Fig. 5 is very typical, so we could use past convergence curves to predict the quality of solution when interrupted on similar data.

4.4 Time and space complexity

The overall complexity of the algorithm is $\hbox {O}(n^{2}\hbox {log}n)$ where n is the length of the time series. However, our experiments (see Sect. 4.1) empirically suggest the running time of STAMP’s growth rate is roughly $\hbox {O}(n^{2})$ instead of $\hbox {O}(n^{2}\hbox {log}n)$. One possible explanation for this is that the $n\hbox {log}n$ factor comes from the FFT subroutine. Because FFT is so important in many applications, it is extraordinarily well optimized. Thus, the empirical runtime is very close to linear. This suggests that the running time can be further reduced by exploiting recent results in the Sparse Fourier Transform (Hassanieh et al. 2012) or by availing of hardware specialized for FFT. We leave such considerations for future work.

In contrast to the above, the brute force nested loop approach has a time complexity of $\hbox {O}(n^{2}m)$. Recall the industrial example in the introduction section. We have $m = 10{,}080$, but log(n) $=$ 5.7, so we would expect our approach to be about 1768 times faster. In fact, we are empirically even faster. The complexity analysis downplays the details of important constant factors. The nested loop algorithm must also z-normalize the subsequences. This either requires O(nm) time, but with an untenable O(nm) space overhead, or an $\hbox {O}(n^{2}m)$ time overhead. Recall that this is before a single Euclidean distance calculation is performed.

Finally, we mention one quirk of our algorithm which we inherit from using the highly optimized FFT subroutine. Our algorithm is fastest when n is an integer power of two, slower for non-power of two but composite numbers, and slowest when n is prime. The difference (for otherwise similar values of n) can approach a factor of 1.6x. Thus, where possible, it is worth contriving the best case by truncation or zero-padding to the nearest power of two.

4.5 From STAMP to STOMP, an optimally fast algorithm

As impressive as STAMP’s time efficiency is, we can create an even faster algorithm if we are willing to sacrifice one of STAMP’s features: its anytime nature. This is a compromise that many users may be willing to make. Because this variant of STAMP performs an ordered (not random) search, we call it STOMP, Scalable Time series Ordered-search Matrix Profile.

As we will see, the STOMP algorithm is very similar to STAMP, and at least in principle it is still an anytime algorithm. However, because STOMP must compute the distance curves in a left-to-right order, it is vulnerable to an “adversarial” time series dataset which has motifs only towards the right side, and random data on the left side. For such a dataset, the convergence curve for STOMP will similar to Fig. 5, but the best motifs will not be discovered until the final iterations of the algorithm. This is important because we expect the most common use of the matrix profile will be in supporting motif discovery, given that motif discovery has emerged as one of the most commonly used time series analysis tools in recent years (Brown et al. 2013; Mueen et al. 2009; Shao et al. 2013; Yoon et al. 2015). In contrast, STAMP is not vulnerable to such an “adversarial arrangement of motifs” argument as it computes the distance profiles in random order (Table 3, line 3). With this background stated, we are now in a position to explain how STOMP works.

In Sect. 4.1 we introduced a formula to calculate the z-normalized Euclidean distance of two time series subsequences Q and $T_{i,m}$ using their dot product. Note that the query Q is also a subsequence of a time series; let us call this time series the Query Time Series, and denote it $T^{Q}\, (T^{Q }=T$ if we are calculating self-join). To better explain the STOMP algorithm, here we denote query Q as $T^{Q}_{j,m}$, where j is the starting position of Q in $T^{Q}$. We denote the z-normalized Euclidean distance between $T^{Q}_{j,m}$ and $T_{i,m}$ as $D_{j,i}$, and their dot product as ${ QT}_{j,i}$. Equation (1) in Sect. 4.1 can then be rewritten as:

$$\begin{aligned} D_{j,i} =\sqrt{2m\left( {1-\frac{QT_{j,i} -m\mu _j \mu _i }{m\sigma _j \sigma _i }} \right) } \end{aligned}$$

(2)

where m is the subsequence length, $\mu _{j}$ is the mean of $T^{Q}_{j,m}$, $\mu _{i}$ is the mean of $T_{i,m}$, $\sigma _{j}$ is the standard deviation of $T^{Q}_{j,m}$, and $\sigma _{i}$ is the standard deviation of $T_{i,m}$.

The technique introduced in Rakthanmanon et al. (2012) allows us to obtain the means and standard deviations with O(1) time complexity; thus, the time required to compute $D_{j,i}$ depends mainly on the time required to compute $QT_{j,i}$. Here we claim that ${QT}_{j,i}$ can also be computed in O(1) time, once ${QT}_{j-1,i-1}$ is known.

Note that ${ QT}_{j-1,i-1}$ can be decomposed as:

$$\begin{aligned} QT_{j-1,i-1} =\mathop \sum \limits _{k=0}^{m-1} T_{j-1+k}^Q T_{i-1+k} \end{aligned}$$

(3)

and ${ QT}_{j,i}$ can be decomposed as:

$$\begin{aligned} QT_{j,i} =\mathop \sum \limits _{k=0}^{m-1} T_{j+k}^Q T_{i+k} \end{aligned}$$

(4)

Thus we have

$$\begin{aligned} QT_{j,i} =QT_{j-1,i-1} -T_{j-1}^Q T_{i-1} +T_{j+m-1}^Q T_{i+m-1} \end{aligned}$$

(5)

Our claim is thereby proved.

The relationship between ${ QT}_{j,i}$ and ${ QT}_{j-1,i-1}$ indicates that once we have the distance profile of time series T with regard to $T^{Q}_{j-1,m}$, we can obtain the distance profile with regard to $T^{Q}_{j,m}$ in just O(n) time, which removes an $\hbox {O}(\hbox {log}n)$ complexity factor from the MASS algorithm in Table 2.

However, we will not be able to benefit from the relationship between ${ QT}_{j,i}$ and ${ QT}_{j-1,i-1}$ when $j=1$ or $i=1$. This problem is easy to solve: we can simply pre-compute the dot product values in these two special cases with MASS algorithm in Table 2. Concretely, we use $\hbox {MASS}(T^{Q}_{1,\mathrm{m}}, T)$ to obtain the dot product vector when $j=1,$ and we use $\hbox {MASS}(T_{1,\mathrm{m}}, T^{Q})$ to obtain the dot product vector when $i=1$. The two dot product vectors are stored in memory and used when needed.

We call this algorithm the STOMP algorithm, as it exploits the fact that we evaluate the distance profiles in-Order. The algorithm is outlined in Table 4.

Table 4 The STOMP algorithm

The algorithm begins in Line 1 by evaluating the matrix profile length l. Lines 2 calculates the first distance profile and stores the corresponding dot product in vector QT. In Line 3 the algorithm pre-calculates the dot product vector ${ QT}_{B}$ for later use. Note that in lines 2 and 3, we require the similarity search algorithm in Table 2 to not only return the distance profile D, but also the vector QT in its first line. Line 4 initializes the matrix profile and matrix profile index. The loop in lines 5–13 evaluates the distance profiles of the subsequences of B in sequential order, with lines 6–8 updating QT according to the mathematical formula in Equation (5). Line 9 updates ${ QT}[i]$ with the pre-computed result from line 3. Finally, lines 10–12 evaluate distance profile and update matrix profile.

The time complexity of STOMP is $\hbox {O}(n^{2})$; thus, we have an achieved a $\hbox {O}(\hbox {log}n)$ factor speedup over STAMP. Moreover, it is clear that $\hbox {O}(n^{2})$ is optimal for any full-join algorithm in the general case. The $\hbox {O}(\hbox {log}n)$ speedup clearly make little difference for small datasets, for instance those with just a few tens of thousands of datapoints. However, as we tackle the datasets with millions of datapoints, something on the wish list of seismologists for example Beroza (2016) and Yoon et al. (2015) this $\hbox {O}(\hbox {log}n)$ factor begins to produce a very useful order-of-magnitude speedup.

As noted above, unlike the STAMP algorithm, STOMP is not really a good anytime algorithm, even though in principle we could interrupt it at any time and examine the current best-so-far matrix profile. The problem is that closest pairs (i.e. the motifs) we are interested in might be clustered at the end of the ordered search, defying the critical diminishing returns property (Zilberstein and Russell 1995) In contrast, STAMP’s random search policy will, with very high probability, stumble on these motifs early in the search.

In fact, it may be possible to obtain the best of both worlds in meta-algorithm by interleaving periods of STAMP’s random search with periods of STOMP’s faster ordered search. This meta-algorithm would be slightly slower than pure STOMP, but would have the anytime properties of STAMP. For brevity we leave a fuller discussion of this issue to future work.

4.6 Incrementally maintaining TSAPSS

Up to this point we have discussed the batch version of TSAPSS. By batch, we mean that the STAMP/STOMP algorithms need to see the entire time series $T_{A}$ and $T_{B}$ (or just $T_{A}$ if we are calculating the self-similarity join matrix profile) before creating the matrix profile. However, in many situations it would be advantageous to build the matrix profile incrementally. Given that we have performed a batch construction of matrix profile, when new data arrives, it would clearly be preferable to incrementally adjust the current profile, rather than starting from scratch.

Because the matrix profile solves both the times series motif and the time series discord problems, an incremental version of STAMP/STOMP would automatically provide the first incremental versions of both these algorithms. In this section, we demonstrate that we can create such an incremental algorithm.

By definition, an incremental algorithm sees data points arriving one-by-one in sequential order, which makes STOMP a better starting point than STAMP. Therefore we name the incremental algorithm STOMP I (STOMP Incremental). For simplicity and brevity, Table 5 only shows the algorithm to incrementally maintain the self-similarity join. The generalization to general similarity joins is obvious.

Table 5 The STOMPI algorithm

As a new data point t arrives, the size of the original time series $T_{A}$ increases by one. We denote the new time series as $T_{A,{ new}}$, and we need to update the matrix profile $P_{AA,{ new}}$ and its associated matrix profile index $I_{AA,{ new} }$ corresponding to $T_{A,{ new}}$. For clarity, note that the input variables ${ QT}$, ${M}_{T}$ and $\Sigma _{T}$ are all vectors, where ${ QT}[i]$ is the dot product of the $i{\mathrm{th}}$ and last subsequences of $T_{A}$; $M_{T}[i]$ and $\Sigma _{T}[i]$ are, respectively, the mean and standard deviation of the $i^{\mathrm{th}}$ subsequence of $T_{A}$.

In line 1, S is a new subsequence generated at the end of $T_{A,{ new}}$. Lines 2–5 evaluate the new dot product vector ${ QT}_{{ new}}$ according to Equation (5), where ${ QT}_{{ new}}[i]$ is the dot product of S and the $i^{\mathrm{th}}$ subsequence of $T_{A,{ new}}$. Note that the length of ${ QT}_{{ new}}$ is one item longer than that of QT. The first dot product ${ QT}_{{ new}}[1]$ is a special case where Equation (5) is not applicable, so lines 6–9 calculate with simple brute-force. In lines 10–12 we evaluate the mean and standard deviation of the new subsequence S, and update the vectors ${ {M}}_{T,{ new}}$ and $\Sigma _{T,{ new}}$. After that we calculate the distance profile D with regard to S and $T_{A,{ new}}$ in line 13. Then, similar to STAMP/STOMP, line 14 performs a pairwise comparison between every element in D and the corresponding element in $P_{{ AA}}$ to see if the corresponding element in $P_{{ AA}}$ needs to be updated. Note that we only compare the first l elements of D here, since the length of D is one item longer than that of $P_{{ AA}}$. Line 15 finds the nearest neighbor of S by evaluating the minimum value of D. Finally, in line 16, we obtain the new matrix profile and associated matrix profile index by concatenating the results in line 14 and line 15.

The time complexity of the STOMPI algorithm is $\hbox {O}(n)$ where n is the length of size of the current time series $T_{{ A}}$. Note that as we maintain the profile, each incremental call of STOMPI deals with a one-item longer time series, thus it gets very slightly slower at each time step. Therefore, the best way to measure the performance is to compute the Maximum Time Horizon (MTH), in essence the answer to this question: “Given this arrival rate, how long can we maintain the profile before we can no longer update fast enough?”

Note that the subsequence length m is not considered in the MTH evaluation, as the overall time complexity of the algorithm is $\hbox {O}(n)$, which is independent of m. We have computed the MTH for two common scenarios of interest to the community.

• House Electrical Demand (Murray et al. 2015): This dataset is updated every 8 s. By iteratively calling the STOMPI algorithm, we can maintain the profile for at least twenty-five years.

• Oil Refinery: Most telemetry in oil refineries and chemical plants is sampled at once a minute (Tucker and Liu 2004). The relatively low sampling rate reflects the “inertia” of massive boilers/condensers. Even if we maintain the profile for 40 years, the update time is only around 1.36 s. Moreover, the raw data, matrix profile and index would only require 0.5 gigabytes of main memory. Thus the MTH here is forty-plus years.

For both these situations, given projected improvements in hardware, these numbers effectively mean we can maintain the matrix profile forever.

As impressive as these numbers are, they are actually quite pessimistic. For simplicity we assume that every value in the matrix profile index will be updated at each time step. However, empirically, much less than 0.1% of them need to be updated. If it is possible to prove an upper bound on the number of changes to the matrix profile index per update, then we could greatly extend the MTH, or, more usefully, handle much faster sampling rates. We leave such considerations for future work.

4.7 GPU-STAMP

As we will show in the next section, both STAMP/STOMP are extremely efficient, much faster than real time for many tasks of interest in music processing or motion capture processing. Nevertheless, there are some domains that have a boundless desire for larger and larger joins. For example, seismologists would like to do cross correlation (i.e. joins) on datasets containing tens of millions of data point (Beroza 2016; Yoon et al. 2015). For such problems, it may be worth the investment in specialized hardware. Because our algorithms, unlike most join algorithms, do not require complex data structures, indexes or random access, they are particularly amiable to porting to GPUs.

To show this, we implemented STAMP in CUDA C++, which allows for massively parallel execution on NVIDIA GPUs. STOMP can also be ported to GPU, but we only focus on GPU STAMP due to the page limits. The GPU implementation of STOMP is left for future work. As we will show in Sect. 5, we can run STAMP on a GPU up to thirty times faster than a CPU implementation. We do this by exploiting highly optimized CUDA libraries that execute each of the STAMP’s subroutines such as FFT and distance calculation in parallel on a GPU. For example, to evaluate the distance profile, we assign a thread to calculate each single element in the profile. As these elements are independent of each other, we can launch as many threads as possible to compute the distance profile in parallel. Assuming that we have $\tau$ concurrent threads, it is possible to remove a constant factor of $\tau$ from the time complexity of the distance profile calculation as well as many of the other STAMP subproblems.

4.8 STAMP and STOMP allow a perfect “progress bar”

Both the STAMP and STOMP algorithms have an interesting property for a motif discovery/join algorithm, in that they both take deterministic and predicable time. This is very unusual and desirable property for an algorithm in this domain. In contrast, the two most cited algorithms for motif discovery (Li et al. 2015; Mueen et al. 2009), while they can be fast on average, take an unpredictable amount of time to finish. For example, suppose we observe that either of these algorithms takes exactly one hour to find the best motif on a particular dataset with $m = 500$ and $n = 100{,}000$. Then the following are all possible:

• Setting m to be a single data point shorter (i.e. $m = 499$), could increase or decrease the time needed by over an order of magnitude.

• Decreasing the length of the dataset searched by a single point (that is to say, a change of just 0.001%), could increase or decrease the time needed by over an order of magnitude.

• Changing a single value in the time series (again, changing only 0.001% of the data), could increase or decrease the time needed by over an order of magnitude (see “Appendix” for more details on these unintuitive observations).

Moreover, if we actually made the above changes, we would have no way to know in advance how our change would impact the time needed.

In contrast, for both STAMP and STOMP (assuming that $m \ll n)$, given only n, we can predict how long the algorithm will take to terminate, completely independent of the value of m and the data itself.

To do this we need to do one calibration run on the machine in question. With a time series of length n, we measure $\delta$, the time taken to compute the matrix profile. Then, for any new length $n_{\mathrm{new}}$, we can compute $\delta _{\mathrm{required}}$ the time needed as:

$$\begin{aligned} \delta _{{ required}} =\frac{\delta }{n^{2}}\times n_{{ new}}^2 \end{aligned}$$

So long as we avoid trivial cases, such as that $m \sim n$ or $n_{\mathrm{new}}$ and/or n are very small, this formula will predict the time needed with an error of less than 5%.

5 Experimental evaluation

We begin by stating our experimental philosophy. We have designed all experiments such that they are easily reproducible. To this end, we have built a webpage (Supporting Page 2017) which contains all datasets and code used in this work, together with spreadsheets which contain the raw numbers and some supporting videos.

Given page limits and the utility of our algorithm for a host of existing and new data mining tasks, we have chosen to include exceptionally broad but shallow experiments. We have conducted such deep detailed experiments and placed them at Supporting Page (2017). Unless otherwise stated we measure wall clock time on an Intel i7@4GHz with 4 cores.

This section is organized as follows. Section 5.1 analyzes the scalability of our algorithms. In Sect. 5.2 we compare our algorithms with two state-of-the-art methods. Section 5.3 shows how the anytime property of STAMP can be exploited to quickly provide an approximate solution to motif discovery problems. In Sect. 5.4 we show the application of our algorithms in comparing multiple time series, and in Sect. 5.5 we show how our algorithms can be used to discover motifs/discords, or to do semantic segmentation within a single time series.

5.1 Scalability of profile-based self-join

Because the time performance of STAMP is independent of the data quality or any user inputs (there are none except the choice of m, which does not affect the speed), our scalability experiments are unusually brief; for example, we do not need to show how different noise levels or different types of data can affect the results.

In Fig. 6 we show the time required for a self-join with m fixed to 256, for increasing long time series.

Fig. 6

Time required for both STAMP and STOMP self-join with $m = 256$, varying n

In Fig. 7, we show the time required for a self-join with n fixed to $2^{17}$, for increasing long m. Again recall that unlike virtually all other time series data mining algorithms in the literature whose performance degrades for longer subsequences (Ding et al. 2008; Mueen et al. 2009) the running time of both STAMP and STOMP does not depend on m.

Fig. 7

Time required for both STAMP and STOMP self-join with $n= 2^{17}$, varying m

Note that the time required for the longer subsequences is slightly shorter. This is because the number of pairs that must be considered for a time series join is ($n-m)/2$, so as m is becomes larger, the number of comparisons becomes slightly smaller.

We can further exploit the simple parallelizability of the algorithm by using four 16-core virtual machines on Microsoft Azure to redo the two-million join ($n = 2^{21}$ and $m = 256$) experiment. By scaling up the computational power, we have reduced the running time from 4.2 days to just 14.1 hours. This use of cloud computing required writing just few dozen lines of simple additional code (Supporting Page 2017).

In order to see the improvements of STOMP over STAMP, we repeated the last two sets of experiments. In Fig. 6 we also show the time required for a self-join with m fixed to 256, for increasing long time series. As expected, the improvements are modest for smaller datasets, but much greater for the larger datasets, culminating in a 4.7$\times$ speedup for the $\sim 2$ million length time series.

In Fig. 7, we show the time required for a self-join with n fixed to $2^{17}$, for increasing long m. Once again note that the running time of STOMP does not depend on m.

As we noted in Sect. 4.7, instead of abandoning the anytime property of STAMP to gain speedup with STOMP, we can instead gain speedup by exploiting GPUs. Once again we repeated the two experiments shown in Figs. 6 and 7, this time considering the performance of GPU-STAMP. We used an NVIDIA Tesla K40 GPU with 2880 cores and 12GB memory. In Table 6 we show the time required for a self-join with m fixed to 256, for increasing long time series.

Table 6 Time required for GPU-STAMP self-join with m = 256, varying n

In Table 7, we show the time required for a self-join with n fixed to $2^{17}$, for increasing long m, using GPU-STAMP.

Table 7 Time required for GPU-STAMP self-join with $n= 2^{17}$, varying m

By comparing the values in Table 6 to STAMP’s values in Fig. 6, we see that GPU-STAMP achieved a 30$\times$ speedup over original STAMP for large datasets.

Note that the parallelized version of MASS (Table 2) is a basic component of GPU-STAMP (see Table 3). To further investigate the scalability of GPU-STAMP, here in Table 8, we show how the average runtime of the parallelized version of MASS changes as n increases. To obtain this average runtime, we measured the runtime for GPU-STOMP, then divided it by $n-m+1$ (number of iterative calls of MASS).

Table 8 Time required for the parallelized version of MASS with $m= 256$, varying n

Note that to achieve maximum speedup for MASS, the number of threads we assign on the GPU is always equal to the time series length n. We can see that up to $n = 2^{16}$, the average runtime does not change much; this is because the GPU resources are not fully used and all n threads can be executed in parallel. When n becomes larger than $2^{16}$, the runtime grows linearly as n increases; this is because the kernel has utilized the maximum computing throughput of the GPU, and the work needs to be partially serialized.

Given that we can improve STAMP, both by using the STOMP variant and by using GPU-STAMP, it is natural to ask if a GPU accelerated version of STOMP would further speed up the time needed to compute the matrix profile. The answer is yes; however, we defer such experiments for another venue, in order to do justice to the careful optimizations required when porting STOMP to a GPU framework.

5.2 Comparisons to rival methods

Unlike all algorithms we are aware of, our timing results are independent of the data. In contrast, most traditional algorithms depend very critically on the data. For example, Luo explains how they contrived a dataset to have some relatively close pairs (“We add another group of vectors acting as the near-duplicates of the vectors”) to give reasonable speed-up numbers (2012). Against such algorithms, even if they were competitive to ours “out-of-the-box,” we could just add noise to the time series and force those algorithms to perform drastically slower, as our algorithm’s time was unaffected. Indeed, Fig. 18 right can be seen as a special case of this.

In addition, STAMP/STOMP time requirements are also independent of the dimensionality (i.e. m, the length of the subsequences). For example, in the following section we have a query length m of 60,000. While the “break-even” point depends on the intrinsic (not actual) dimensionality of the data, no metric indexing technique outperforms brute force search for dimensionalities of much greater than a few hundred, much less sixty thousand. For this dimensionality issue, Fig. 18 left can be seen as a special case of this problem.

To empirically show these two advantages of STOMP/STOMP over traditional methods, we compare it to the recently introduced Quick-Motif framework (Li et al. 2015), and the more widely known MK algorithm (Mueen et al. 2009). The Quick-Motif method was the first technique to do exact motif search on one million subsequences.

To be fair to our rival methods, we do not avail of GPU acceleration (we compare the rival methods with the CPU version of STOMP, not GPU-STAMP), but use the identical hardware (a PC with Intel i7-2600@3.40GHz) and programming language for all algorithms. We use the original author’s executables (Quick Motif 2015) to evaluate the runtime of both MK and Quick-Motif, and we measure the runtime of STOMP based on its C++ implementation.

In choosing the dataset to experiment on, we noticed that the memory footprint for Quick-Motif tends to be very large for noisy data. For example, for a seismology data with $m = 200$, $n = 2^{18}$, we measured the Quick-Motif memory footprint as large as 1.42 GB, while STOMP requires only 14MB memory for the same data, which is less than 1/100 the size. The huge memory requirement for complex and noisy datasets makes it impossible to compare the STOMP algorithm with Quick-Motif and MK, since Quick-Motif and MK often crashed with an out-of-memory error as we varied the value of m. Therefore, instead of comparing performance of the algorithms on noisy datasets such as seismology data, here we experimented on the much smoother ECG dataset (used in Rakthanmanon et al. 2013a), which is an ideal dataset for both MK and Quick-Motif to achieve their best performance (in both time and space). Figure 8 shows the time cost and memory footprint of the three algorithms for the ECG dataset with a fixed length $n=2^{18}$ and varying subsequence length m.

Fig. 8

(Left) Speed comparison of STOMP, MK and Quick-Motif for the ECG data, varying m (right) Memory footprint of the three methods, varying m

We can see that both the runtime and memory footprint for STOMP are independent of the subsequence length. In contrast, Quick-Motif and MK both scale poorly in subsequence length in both runtime and memory usage. The reason that we are unable to show the runtime and memory consumption for MK for $m=1024$, 2048 and 4096 is that it runs out of memory in these cases. The memory footprint for Quick-Motif is relatively smaller than MK; however, note that for Quick-Motif the memory footprint is not monotonic in m, as reducing m from 4096 to 2048 requires three times as much memory. This is not a flaw in implementation (we used the author’s own code) but a property of the algorithm itself. Both algorithms can be fast in ideal situations, with smooth data, short subsequence lengths, and “tight” motifs in the data. But both can, and do, require very large memory space and degenerate to brute-force search in less ideal situations (see “Appendix”).

Note that because the space overhead of our algorithm is extremely small, just $\hbox {O}(n)$, we can comfortably fit everything we need into main memory. For example, for the $n = 2^{21}$ experiments, the raw data, the matrix profile and the matrix profile index together require just 50.3 megabytes of memory. In contrast, the handful of attempts to do time series joins that we are aware of all use indices (Lian and Chen 2009; Luo et al. 2012; Ma et al. 2016) and as such have a space overhead of O(nD), where D is the reduced dimensionally used to index the data, a number typically between eight and twenty. In fact, even this bloated O(nD) hides large constants in the overhead for the index structure. As a result, even for datasets smaller than $2^{21}$, these approaches are condemned to be disk-based. It is hard to imagine any disk-based algorithm being competitive with a main memory algorithm, even if you ignore the time required to build the index and write the data to disk, and even if you only consider threshold joins with a very conservative threshold.

Having said all that, and adding a further disclaimer that it is dubious to compare CPU times across papers that use different machines, we note the following. All existing TSAPSS methods require data transformations, the building of indexes and the creation of data structures before actually attempting the joins. As best as we can determine, our index-free STAMP or STOMP would finish well before the rival methods had even finished building the indexes and performed other required preprocessing needed before comparing a single pair of subsequences (Luo et al. 2012; Ma et al. 2016).

In the rest of the experimental section we concentrate on showing multiple examples of the utility of matrix joins, both for multiple tasks and on multiple domains.

5.3 The utility of anytime STAMP

In the early 1980s it was discovered that in telemetry of seismic data recorded by the same instrument from sources in given region there will be many similar seismograms (Geller and Mueller 1980). Geller and Mueller suggested that “The physical basis of this clustering is that the earthquakes represent repeated stress release at the same asperity, or stress concentration, along the fault surface” (1980). These repeated patterns are call “doublets” in seismology, and exactly correspond to the more general term “time series motifs”. Figure 9 shows an example of doublets from seismic data. A more recent paper notes that many fundamental problems in seismology can be solved by joining seismometer telemetry in search of these doublets (Yoon et al. 2015), including the discovery of foreshocks, aftershocks, triggered earthquakes, swarms, volcanic activity and induced seismicity (we refer the interested reader to the original paper for details). However, the paper notes a join with a query length of 200 on a data stream of length 604,781 requires 9.5 days. Their solution, a clever transformation of the data to allow LSH based techniques, does achieve significant speedup, but at the cost of false negatives and the need for significant parameter tuning.

Fig. 9

A set of doublets extracts from the seismic data recorded at a station near Mammoth Lakes on February 17th, 2016. One occurrence (fine/blue) is overlaid on top of another occurrence (bold/orange) that happened about 45 min later (Color figure online)

The authors kindly shared their data and, as we hint at in Fig.  10, confirmed that our STOMP approach does not have false negatives.

Fig. 10

(Top) An excerpt of a seismic time series aligned with its matrix profile (bottom). The ground truth provided by the authors of Yoon et al. (2015) requires that the events occurring at time 4050 and 7800 match

We repeated the $n = 604{,}781$, $m = 200$ experiment and found it took just 1.7 hours to finish. As impressive as this is, we would like to claim that we can do even better.

The seismology dataset offers an excellent opportunity to demonstrate the utility of the anytime version of our algorithm. The authors of Yoon et al. (2015) revealed their long-term ambition of mining even larger datasets (Beroza 2016). In Fig. 11 we repeated the experiment with the snippet shown in Fig.  10, this time reporting the best-so-far matrix profile reported by the STAMP algorithm at various milestones. Even with just 0.25% of the distances computed (that is to say, 400 times faster), the correct answer has emerged.

Fig. 11

(Top) An excerpt of the seismic data that is also shown in Fig. 10. (Top-to-bottom) The approximations of the matrix profile for increasing interrupt times. By the time we have computed just 0.25% of the calculations required for the full algorithm, the minimum of the matrix profile points to the ground truth

Thus, we can provide the correct answers to the seismologists in just minutes, rather than the 9.5 days originally reported.

To show the generality of this anytime feature of STAMP, we consider a very different dataset. As shown in Table 9, it is possible to convert DNA to a time series (Rakthanmanon et al. 2012) We converted the Y-chromosome of the Chimpanzee (Pan troglodytes) this way.

Table 9 An algorithm for converting DNA string sequence to DNA time series (Color table online)

While the original string is of length 25,994,497, we downsampled by a factor of twenty-five to produce a time series that is little over one-million in length. We performed a self-join with $m = 60{,}000$. Figure 12 bottom shows the best motif is so well conserved (ignoring the first 20%), that it must correspond to a recent (in evolutionary time) gene duplication event. In fact, in a subsequent analysis we discovered that “much of the Y (Chimp chromosome) consists of lengthy, highly similar repeat units, or ‘amplicons’” (Hughes et al. 2010).

Fig. 12

(Top) The Y-chromosome of the Chimp in time series space with its matrix profile. (Bottom) A zoom-in of the top motif discovered using anytime STAMP, we believe it to be an amplicon (Hughes et al. 2010)

Fig. 13

Two songs represented by just the 2nd MFCC at 100 Hz. We recognize that it is difficult to see any structure in these times series; however, this difficulty is the motivation for this experiment

This demanding join would take just over a day of CPU time (see Fig. 6). However, using anytime STAMP we have the result shown above after doing just 0.021% of the computations, in about 18 s. At Supporting Page (2017) we have videos that intuitively show the rapid convergence of the anytime variant of STAMP.

5.4 Profile-based similarity join of multiple time series

In this section we show the usage of Matrix Profile-based similarity join on the comparison of multiple time series. The first and second examples are more familiar to APSS users, quantifying what is similar between two time series. The third example, quantifying what is different between two time series (similar to contrast sets), is novel and can only be supported by threshold-free algorithms that report the nearest neighbor for all objects. The fourth example shows how the common characteristic among a set of time series, the time series shapelet, can be extracted with our method.

5.4.1 Time series set similarity: case study in music processing

Given two (or more) time series collected under different conditions or treatments, a data analyst may wish to know what patterns (if any) are conserved between the two time series. To the best of our knowledge there is no existing tool that can do this, beyond interfaces that aid in a manual visual search (Hao et al. 2012). To demonstrate the utility of automating this, we consider a simple but intuitive example. Figure 13 shows the raw audio of two popular songs converted to Mel Frequency Cepstral Coefficients (MFCCs). Specifically, the songs used in this example are “Under Pressure” by Queen and David Bowie and “Ice Ice Baby,” by the American rapper Vanilla Ice. Normally, there are 13 MFCCs; here, we consider just one for simplicity.

Even for these two relatively short time series, visual inspection does not offer immediate answers. The problem here is compounded by the size reproduction, but is not significantly easier with large-scale (Supporting Page 2017) or even interactive graphic tools (Hao et al. 2012).

We ran ${{\varvec{J}}}_{{ AB}}$ (Queen-Bowie, Vanilla Ice) on these datasets with $m = 500$ (5 s), the best match, corresponding the minimum value of the matrix profile $P_{{ AB}}$, is shown in Fig. 14.

Fig. 14

The result of ${{\varvec{J}}}_{{ AB}}$ (Queen-Bowie (red/bold), Vanilla-Ice (green/fine)) produces a strongly conserved five second region (Color figure online)

Readers may know the cause for this highly conserved subsequence. It corresponds to the famous baseline of “Under Pressure,” which was sampled (plagiarized) by Vanilla Ice in his song. The join took 2.67 s. While this particular example is only of interest to the music processing community (Dittmar et al. 2012), the ability to find conserved structure in apparently disparate time series could open many avenues of research in medicine and industry.

5.4.2 Time series set similarity: DNA joins revisited

In Fig. 12 we showed the utility of STAMP for self-joins of DNA. We now revisit this domain, this time considering AB-joins. Here we use AB-joins to aid in the hunt for inversions between the genomic sequences of related organisms. Inversions are chromosome rearrangements in which a segment of a chromosome is reversed end to end. We consider two of the 180 known strains of Legionella, L. pneumophila Paris and L. pneumophila Lens, which consist of 3,503,504 and 3,345,567 bp respectively (Gomez-Valero et al. 2011). After conversion to time series of the same lengths, we ran ${{\varvec{J}}}_{{ AB}}$ (Paris, Lens) with a subsequence length of 100,000. We discovered that most the matrix profile had very low values, unsurprising given the relatedness of the two strains. However, one region of the matrix profile, almost exactly in the middle, reported a much larger difference. To see if this greater distance was the result of an inversion, we simply flipped one of the sequences left-to-right, performing ${{\varvec{J}}}_{{ AB}}$ (reverse(Paris), Lens). Gratifyingly, as shown in Fig. 15 bottom, this time the best matching section corresponded exactly to the previously poor matching section.

Fig. 15

(Top) The entire genomes of L. pneumophila Paris (red/fine) and L. pneumophila Lens (green/bold) after conversion to time series. (Bottom) A region of approximately 100,000 bp is strongly conserved, after reversing one of the sequences. (Inset) A dot-plot alignment of the two organisms created by more conventional analysis (Gomez-Valero et al. 2011) confirm the locations and length of the inversion discovered (Color figure online)

As before, we are not claiming any particular biological significance or utility of this finding. What is remarkable is the scalability of the approach. We joined two time series, both over three million data points long, and we did this for a subsequence length of 100,000. By exploiting the anytime property of STAMP, and stopping the algorithm after it had completed just 0.1% of the operations, we were able to obtain these results in under 10 min.

5.4.3 Time series difference

We introduce the Time Series Diff (TSD) operator, which informally asks “What happens in time series $T_{A}$ that does not happen in time series $T_{B}$?” Here $T_{A}/T_{B}$ could be an ECG before a drug is administered/after a drug is administered, telemetry before a successful launch/before a catastrophic launch, etc. The TSD is simply the subsequence referred to by the maximum value of the ${{\varvec{J}}}_{{ AB}}$ join’s profile $P_{{ AB}}$.

We begin with a simple intuitive example. The UK and US versions of the Harry Potter audiobook series are performed by different narrators, and have a handful of differences in the text. For example, the UK version contains:

Harry was passionate about Quidditch. He had played as Seeker on the Gryffindor house Quidditch team ever since his first year at Hogwarts and owned a Firebolt, one of the best racing brooms in the world...

But the corresponding USA version has:

Harry had been on the Gryffindor House Quidditch team ever since his first year at Hogwarts and owned one of the best racing brooms in the world, a Firebolt.

As shown in Fig. 16, we can convert the audio corresponding to these snippets into MFCCs and invoke a ${{\varvec{J}}}_{{ AB}}$ join set to produce a matrix profile $P_{AB}$ that represents the differences between them. As Fig. 16 left shows, the low values of this profile correspond to identical spoken phrases (in spite of having two different narrators). However, here we are interested in the differences, the maximum value of the profile. As we can see in Fig. 16 right, here the profile corresponds to a phrase unique to the USA edition.

Fig. 16

The 2nd MFCC of snippets from the USA (pink/bold) and UK (green/fine) Harry Potter audiobooks. The ${{\varvec{J}}}_{{ AB}}$ join of the two longer sections in the main text produces mostly small values in the profile correspond to the same phrase (left), the largest value in the profile corresponds to a phrase unique to the USA edition (right) (Color figure online)

The time required to do this is just 0.044 s, much faster than real time given the audio length. While this demonstration is trivial, in Supporting Page (2017) we show an example applied to ECG telemetry.

5.4.4 Time series shapelet discovery

Shapelets are time series subsequences which are in some sense maximally representative of a class (Rakthanmanon and Keogh 2013b; Ye and Keogh 2009). Shapelets can be used to classify time series (essentially, the nearest shapelet algorithm), offering the benefits of speed, intuitiveness and at least on some domains, significantly improved accuracy (Rakthanmanon and Keogh 2013b). However, these advantages come at the cost of a very expensive training phase, with $\hbox {O}(n^{2}m^{4})$ time complexity, where m is the length of the longest time series object in the dataset, and n is the number of objects in the training set. In order to mitigate this high time complexity, researchers have proposed various distance pruning techniques and candidate ranking approaches for both the admissible (Ye and Keogh 2009) and approximate (Rakthanmanon and Keogh 2013b) shapelet discovery. Nevertheless, scalability remains the bottleneck.

Because shapelets are essentially supervised motifs, and we have shown that STOMP can find motifs very quickly, it is natural to ask if STOMP has implications for shapelet discovery. While space limitations prohibit a detailed consideration of this question, we briefly sketch out and test this possibility as follows.

As shown in Fig. 17, we can use matrix profile to heuristically “suggest” candidate shapelets. We consider two time series $T_{A}$ (green/bold) and $T_{B}$ (pink/light) with class 1 and class 0 being their corresponding class label, and we take ${{\varvec{J}}}_{{\varvec{AB}}}$, ${{\varvec{J}}}_{{\varvec{AA}}}$, ${{\varvec{J}}}_{{\varvec{BA}}}$ and ${{\varvec{J}}}_{{\varvec{BB}}}$. Our claim is the differences in the heights of $P_{{ AB}}$, $P_{AA}$ (or $P_{BA}$, $P_{BB})$ are strong indicators of good candidate shapelets. The intuition is that if a discriminative pattern is present in, say, class 1 but not class 0, then we expect to see a “bump” in the $P_{AB}$ (the intuition holds if the order of the classes are reversed). A significant difference (quantified by a threshold shown in dashed line) between the heights of $P_{AA}$ and $P_{AB}$ curves therefore indicates the occurrence of good candidate shapelets, patterns that only occur in one of the two classes.

Fig. 17

(Top left) Two time series $T_{A}$ and $T_{B}$ formed by concatenating instances of class 1 and 0 respectively of the ArrowHead dataset (Chen et al. 2015). (Bottom) The height difference between $P_{{ AB}}$ (or $P_{{ BA}})$ and $P_{{ AA}}$ (or $P_{{ BB}})$ are suggestive of good shapelets. (Top right) An example of good shapelet extracted from class 1

The time taken to compute all four matrix profiles is 0.28 s and further evaluation of the two twelve candidates selected takes 1.65 s. On the same machine, the brute force shapelet classifier takes 4 min with 2364 candidates. Note that, in this toy demonstration, the speedup is 124$\times$; however, for larger datasets, the speedup is much greater (Supporting Page 2017).

5.5 Profile-based similarity self-join

In the previous section we showed how Matrix Profile-based similarity join can be used to discover the relationship between multiple time series. Here we will show the utility of Matrix Profile-based similarity self-join on the analysis of a single time series in various aspects, including motif discovery, discord discovery and semantic segmentation.

5.5.1 Profile-based motif discovery

Since their introduction in 2003, time series motifs have become one of the most frequently used primitives in time series data mining, with applications in dozens of domains (Begum and Keogh 2014). There are several proposed definitions for time series motifs, but in Mueen et al. (2009) it is argued that if you can solve the most basic variant, the closest (non-trivial) pair of subsequences, then all other variants only require some minor additional calculations. Note that the locations of the two (tying) minimum values of the matrix profile are exactly the locations of the closest (non-trivial) motif pair.

The fastest known exact algorithm for computing time series motifs is the MK algorithm (Mueen et al. 2009). Note, however, that this algorithm’s time performance depends on the time series itself. In contrast, the Profile-Based Motif Discovery (PBMD) takes time independent of the data. To see this, we compared the two approaches on an electrocardiogram of length 65,536. In Fig. 18 left we ask what happens as we search for longer and longer motifs. In Fig. 18 right we ask what happens if the motif length is fixed to $m = 512$, but the data becomes increasing noisy.

While PBMD is better able to take advantage of parallelism, for fairness we use a single processor for both approaches.

Fig. 18

The time required to find the top-motif pairs in a time series of length 65,536 for increasingly long motif lengths (left), and for a length fixed to 512, but in the face of increasing noise levels (right). The two algorithms being compared are MK (Mueen et al. 2009), the current state-of-the-art, and STOMP (PBMD)

These results show that even in the best case for MK, PBMD is competitive, but as we have longer queries and/or noisier data, its advantage becomes unassailable. Moreover, PBMD inherits STOMP’s parallelizability and incremental computability. Given these features, we expect PBMD to become the state-of-the-art for motif discovery.

5.5.2 Profile-based discord discovery

A time series discord is the subsequence that has the maximum distance to its nearest neighbor. While this is a simple definition, time series discords are known to be very competitive as novelty/anomaly detectors. For example, Vipin Kumar performed an extensive empirical evaluation and noted that “on 19 different publicly available data sets, comparing 9 different techniques (time series discords) is the best overall technique” (Chandola et al. 2009).

Note that as shown in Fig. 19, the time series discord is encoded as the maximum value in a matrix profile.

Fig. 19

(Top) An excerpt from an ECG incorporating a premature ventricular contraction (red/bold). (Bottom) The time series profile peaks exactly at the beginning of the PVC (Color figure online)

The time taken to compute the discord is obviously just the time needed to compute the matrix profile (0.09 s in the above case).

A recent paper proposes to speed up discord discovery using Parallel Discord Discovery (PDD), which “divides the discord discovery problem in a combinable manner and solves its subproblems in parallel” (Huang et al. 2016). By using a Spark cluster consisting of 10 computing nodes, they can find the top discord in a dataset of length 1,000,000 in just 10.2 hours. However, using our single machine, STOMP takes us 4.5 hours (If we use GPU-STAMP we can further reduce this to 45 min). Note that the PDD algorithm is only finding the top discord, whereas our approach finds the exact discord score for all 1,000,000 subsequences.

There are a few dozen other discord discovery algorithms in the literature (Huang et al. 2016). Some of them may be competitive in the best case, but just like motif-discovery algorithms they all degenerate to brute force search in the worst case.

Moreover, recently researchers have noted the utility of anytime algorithms for finding outliers in truly massive data archives (Assent et al. 2012), and the utility of supporting online algorithms for finding outliers in streaming data (Assent et al. 2012). In both cases, researchers have created sophisticated indexing structures to support these tasks (Assent et al. 2012; Seidl et al. 2009). However, because we can do discord discovery using only the matrix profile, we automatically inherit the ability to do both anytime and incremental outlier detection, essentially “for free”. For example, the PDD framework can exploit multiple nodes to gain speedup, but it does not have any kind of answer until the last instant (Huang et al. 2016). In contrast, in most datasets STAMP has an approximate answer that can be viewed almost instantly. Likewise, PDD is only defined as a batch algorithm, where as our algorithms can compute discords incrementally. We show an example of this incremental computation ability in the next section.

5.5.3 Incrementally maintaining motifs and discords

We have demonstrated the ability to detect time series motifs and discords using the matrix profile in the previous two sections. However, we assumed that the entire time series was available beforehand. Here we remove this assumption and show how STOMPI allows us to incrementally maintain time series motifs and discords in an online fashion. There are many attempts at one (Niennattrakul et al. 2010; Begum and Keogh 2014) or both (Truong and Anh 2015) of these tasks in the literature, but they are all approximate and allow false dismissals.

In Sect. 4.6, we introduced the STOMPI algorithm. The ability to incrementally maintain the matrix profile implies the ability to exactly maintain the time series motif (Mueen et al. 2009) and/or time series discord (Chandola et al. 2009) in streaming data. We simply need to keep track of the extreme values of the incrementally-growing matrix profile, report a new pair of motifs when a new minimum value is detected, and report a new discord when we see a new maximum value.

We demonstrate the utility of these ideas on the AMPds dataset (Makonin 2013). While this is a real dataset, it lacks ground truth annotation so we slightly contrived it such that we can check the plausibility of the outcomes. For simplicity, we assume that the kitchen fridge and the heat pump are both plugged into a single metered power supply. For the first week, only the refrigerator is running. At the end of the week, the weather gets cold and the heat pump is turned on. The sampling rate is one sample/minute, and the subsequence length is 100 (i.e. 1 h and 40 min). We apply the STOMP algorithm to the first three days of data, then invoke the STOMPI algorithm to handle newly arriving data. Whenever we detect a new extreme value, we report an event.

Our first event occurs at the 9864th minute (6 day 20 h 24 min). As shown in Fig. 20, a new minimum value is detected, which indicates a new time series motif. The just-arrived 100-min-long pattern looks very similar to another pattern that occurred five hours earlier. While there is a lot of regularity in the fridge data in general, the exceptional similarity observed here suggested some underlying physical mechanism that caused such a perfectly-conserved pattern, perhaps a mechanical ice-making “subroutine.”

Fig. 20

(Top) The matrix profile of the first 9864  min of data. (Bottom) The minimum value of the matrix profile corresponds to a pair of time series motifs in the power usage data. (Right) The time series motif detected (best viewed in color) (Color figure online)

Our second event occurs at the 10,473th minute (7 day 6 h 33 min). As shown in Fig. 21, a new maximum value is detected, which indicates a new time series discord. The time series discord corresponds to the first occurrence of a heat pump pattern in the power usage data.

Fig. 21

(Top) The matrix profile for the first 10,473  min. (Bottom) The maximum value of the matrix profile corresponds to a time series discord. (Right) The time series discord detected is the first heat pump pattern occurrence in the dataset

The maximum time needed to process a single data point with STOMPI in this dataset is 0.0003 s, which is less than 0.004% of the data sampling rate. Thus, on this dataset we could continue monitoring with the STOMPI algorithm for several decades before running out of time or memory.

5.5.4 Profile-based semantic segmentation

The goal of time series semantic segmentation is to partition a dataset containing multiple activities/regimes into atomic behaviors or conditions. For example, for human activity data the regimes might later be mapped to {eating, working, commuting,...}(Zhou et al. 2008), whereas for sleep physiology the discovered regimes might later be mapped to {REM, NREM, Unknown} 0As these examples suggest, most work in this area is highly domain-dependent. In contrast, here we show how the matrix profile index can be employed for domain agnostic time series segmentation.

The intuition of our approach is as follows. Within a single regime we might expect that most subsequences will have a nearest neighbor close by (in time). For example, consider the toy problem shown in Fig. 22, which shows two obvious regimes. We would expect that the nearest neighbor to the first run gait cycle is the second or third or fourth run cycle, but it will almost certainly not be one of the walk cycles. In general, this tendency for nearest neighbor pointers not to cross the boundaries corresponding to regime changes may be sufficient to discover these boundaries, and of course, this is precisely the information that is encoded in the matrix profile index.

Thus, for each point we count how many “arcs” connecting two nearest neighbors cross it if we connect each subsequence to its nearest neighbor as shown in Fig. 22. The time complexity of this arc counting segmentation algorithm is $\hbox {O}(n)$, which is negligible compared to the $\hbox {O}(n^{2})$ time complexity of STOMP.

Fig. 22

(Top) A (toy) time series (in red) and nearest neighbor locations for each subsequence. (Bottom) The number of arcs crossing above each of the points of time series (Color figure online)

For experimental evaluation, we applied the procedure described above to a heavily studied activity segmentation problem (Zhou et al. 2008) derived from CMU Motion Capture Database (2017). The recordings are represented as multi-dimensional time series, and most research efforts carefully select the best subset for the segmentation task. For example, Zhou et al. (2008) states that “we only consider the 14 most informative joints out of 29.” In contrast, we shall attempt to do this with a single dimension and without any preprocessing of the time series (e.g., down sampling or smoothing). The only parameter we need to set is sliding window size. We found the result is not sensitive to the sliding window size as long as it is within the range of average gait length, and we set it to be 200 points. In Fig. 23 we show the segmenting results obtained using our approach. The total runtime for this matrix profile based segmentation algorithm, including the time to run STOMP and to count the arcs, is 0.74 s. The human annotations are taken Zhou et al. (2008) and placed here for comparison.

Fig. 23

(Top) A matrix profile (in blue) obtained for the time series (red) and number of arcs crossing each point (green). Low values of this green curve correspond to candidate split points. (Bottom) Human annotations of the activities: w walking, s stretching, p punching, c chopping, t turning, d drinking (Color figure online)

Much of the evaluation in this community lacks formal metrics, preferring instead visual sanity tests like the one in Fig.  23. Given this, we can say that our approach is very competitive on this dataset, in spite of the fact that we handicapped ourselves to only consider one dimension.

We conducted experiments on another activity dataset: PAMAP (Physical Activity Monitoring for Aging People) (Reiss et al. 2011). Here the recordings are much longer, in order of hundreds thousands of data points. Each of the recordings consists of 45 dimensions, and again we randomly picked just one of the dimensions containing some representation of performed activity. We set the sliding window size to 1500. The results are presented in Fig. 24. As the reader can clearly see, the ground truth human annotations again correspond to the segmentation results provided by our algorithm. Note, than the data here is weakly labeled which means the regions marked as “other (transient activities)” may contain some variability within depending on what the subject was doing during the break. The total runtime of our segmentation algorithm for this recording of length 228,000 (38 min of data sampled at 100 Hz) took only 829.8 s (about 14 min).

Fig. 24

(Top) A matrix profile (in blue) obtained for the time series (red) and number of arcs crossing each point (green). Low values of this green curve correspond to candidate split points. (Bottom) Human annotations of the activities: w walking, nw Nordic walking, r running, c cycling, s playing soccer, o other (Color figure online)

Moreover, because we make no domain-specific assumptions, the same algorithm works well in other vastly different domains. Figure 25 shows the segmentation of a Photoplethysmogram (PPG) signal, where our algorithm again agrees the annotation kindly provided by noted Pulsus paradoxus expert, Dr. John Criley (UCLA School of Medicine). The runtime for segmenting the PPG signal shown in Fig. 25 with our approach is just 0.31 s, which is about two orders of magnitude faster than the data recording time (25 s of data recorded at 240 Hz).

Fig. 25

(Top) The $m = 450$ matrix profile (in blue) obtained for the time series (red) of PPG signal and number of arcs crossing each point (green). (Bottom) Human annotations: severe pulsus and pulsus (Color figure online)

Finally, our algorithm as outlined above does have a potential weakness. Consider a longer version of the times series shown in Fig. 25 that has a walk regime, followed by a run regime, followed by another walk regime, etc. Here the nearest neighbor to a walk subsequence could “jump” a walk regime to a distant walk subsequence. In fact, this actually happens a little in Fig. 23, and we imposed a kind of temporal constrain to mitigate this: in particular, we take into account only those nearest neighbors whose distance is less or equal to the median of the nearest neighbor distances.

6 Conclusion

We have introduced a scalable algorithm for creating time series subsequences joins. Moreover, we show that as a “side-effect” of computing all-pairs exact joins, we also obtain the motifs and discords, which are important time series primitives (Chandola et al. 2009; Hao et al. 2012).

Our algorithm is simple, fast, parallelizable and parameter-free, and can be incrementally updated for moderately fast data arrival rates. For domains where massive scalability is required, we have demonstrated that we can port our ideas to GPUs and avail of hardware to gain further speedups or push the computation into the cloud. We have shown that our algorithm has implications for many existing tasks, such as motif discovery, discord discovery, shapelet discovery and semantic segmentation, and may open up new avenues for research, including computing various definitions of time series set difference, a contrast set-like operation. Our code, including MATLAB interactive tools, a C++ version, and the GPU version, are freely available for community to confirm, extend and exploit our ideas.

There are many avenues for future work, and we suspect that the research community will find many uses for, and properties of, the matrix profile that did not occur to us.

Appendix: On the unpredictable time needed for state-of-the-art algorithms

In Section 4.8 we made some unintuitive observations about all known rival motif discovery/time series join algorithms. In essence, by making the problem apparently slightly easier, by either reducing the dimensionality or time series length, the time needed can get actually much worse (and vice versa). Here we sketch out an explanation for this fact.

The key observation is that these algorithms all use some form of pruning. The utility of pruning depends on two things; the distance between the discovered motifs (relative to all pairwise distances), and how quickly the algorithm can find these best motifs (or some good best-so-far motif) to enable the pruning strategy to extract the most benefit. Note that the former factor is a property of the data, not the algorithm.

Imagine we construct a dataset of length 100,000, and search for motifs of length 100. If our data is just random numbers, this is the worst case for both Li et al. (2015) and Mueen et al. (2009), as the intrinsic dimensionality is the same as the actual dimensionality. In MATLAB, we could create such a dataset with:

$$\begin{aligned}>> \mathtt{data1} = \mathtt{[rand(100000,1)]}; \end{aligned}$$

As this is the worst case for Li et al. (2015) and Mueen et al. (2009), both degenerate to brute force search and will take several hours to finish. Naturally the “motif” they discover will only be slightly closer than any randomly chosen pair of subsequences.

Now let us create a near identical dataset, but one which has a critical difference, this dataset has a perfect motif embedded at the beginning and at the end of the time series:

$$\begin{aligned}>> \mathtt{pattern}= & {} \mathtt{rand(100,1)};\\>> \mathtt{data2}= & {} \mathtt{[pattern; rand(99800,1); pattern]}; \end{aligned}$$

If we run motif discovery on this dataset, both Li et al. (2015) and Mueen et al. (2009) terminate much faster, in just seconds. This is because both will find the embedded motif early on, and this will allow very aggressive pruning.

Finally, suppose we consider a new dataset, which is simply data2 with the last point truncated:

$$\begin{aligned}>> \mathtt{data3} = \mathtt{data2(1:end-1)}; \end{aligned}$$

It is clear that although this dataset is very slightly smaller than data2, the time needed by either Li et al. (2015) or Mueen et al. (2009) will return to the many hours needed for than data1. This is because the best motif in data3 will once again be a time series pair that is only be slightly closer than any randomly chosen pair of subsequences, and the pruning will thus be ineffective. By similar reasoning we can construct the two other cases noted in Section 4.8.

Finally, we note that although the examples above are contrived and “worst case”, in practice both Li et al. (2015) and Mueen et al. (2009) do vary greatly in the time require to terminate, on real datasets that appear essentially identical to human inspection.