Time series motifs discovery under DTW allows more robust discovery of conserved structure

Abstract

In recent years, time series motif discovery has emerged as perhaps the most important primitive for many analytical tasks, including clustering, classification, rule discovery, segmentation, and summarization. In parallel, it has long been known that Dynamic Time Warping (DTW) is superior to other similarity measures such as Euclidean Distance under most settings. However, due to the computational complexity of both DTW and motif discovery, virtually no research efforts have been directed at combining these two ideas. The current best mechanisms to address their lethargy appear to be mutually incompatible. In this work, we present the first efficient, scalable and exact method to find time series motifs under DTW. Our method automatically performs the best trade-off of time-to-compute versus tightness-of-lower-bounds for a novel hierarchy of lower bounds that we introduce. As we shall show through extensive experiments, our algorithm prunes up to 99.99% of the DTW computations under realistic settings and is up to three to four orders of magnitude faster than the brute force search, and two orders of magnitude faster than the only other competitor algorithm. This allows us to discover DTW motifs in massive datasets for the first time. As we will show, in many domains, DTW-based motifs represent semantically meaningful conserved behavior that would escape our attention using all existing Euclidean distance-based methods.

1 Introduction

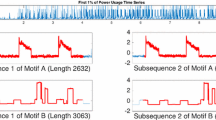
Time series motif discovery—the unearthing of locally conserved behavior in a long time series—has emerged as one of the most important time series primitives in the last decade (Bagnall et al. 2017; Chiu et al. 2003). In recent years, there has been significant progress in the scalability of motif discovery, but essentially all algorithms use the Euclidean Distance (ED) (Dau and Keogh 2017; Mueen et al. 2009). This is somewhat surprising, because in parallel, the community seems to have converged on the understanding that the Dynamic Time Warping (DTW) is superior in most domains, at least for the tasks of clustering, classification, and similarity search (Keogh and Ratanamahatana 2005; Rakthanmanon et al. 2013; Ratanamahatana and Keogh 2005; Tan et al. 2019). Could DTW also be superior to ED for motif discovery? To preview our answer to this question, consider Fig. 1, which shows the top-1 motif discovered in a household electrical power demand dataset, using the Euclidean distance (Murray et al. 2017).

Fig. 1

The top-1 Euclidean distance motif discovered in a one-month long electrical power demand dataset

We have no obvious reasons to discount this motif. It clearly shows the highly conserved behavior of relatively low demand for power for about ¾ of an hour, followed by a high sustained demand. Note that the Euclidean distance is robust to the short “blip” that appears in just the blue time series (from the duration, shape and watts drawn, this pattern almost certainly represents an electrical kettle).

However, now let us consider Fig. 2, which shows a different pair of subsequences from the same dataset.

Fig. 2

A pair of subsequences from household electrical power demand data. The pattern corresponds to (A) short run of discharge pump to empty any liquid in the machine, (B) pumping water into reservoir, (C) spraying water over dishes, (D) pumping out water

In retrospect, we would surely have preferred to have discovered this pair of motifs as the top-1 motif. The complexity of the pattern that is conserved points to a common mechanism. In fact, this is the case. This pattern corresponds to a particular program from a dishwasher. Why was this pattern not discovered by the classic motif discovery algorithm? Fig. 3 offers a visual explanation.

Fig. 3

The four subsequences shown in Figs. 1 and 2 clustered using single-linkage with the Euclidean distance and the DTW distance. DTW does not greatly change this distance between the two “boring” motifs, merely reducing the distance from 4.08 to 3.84. In contrast, DTW reduces the distance between the dishwasher patterns from 9.79 to just 2.78

As shown with the gray hatch-lines between the bottom pair of subsequences in Fig. 3, DTW’s ability to non-linearly match features that may be out of phase allows it to report a much smaller distance for subsequences that are semantically similar, but have local regions that are out-of-phase (Keogh and Ratanamahatana 2005; Minnen et al. 2007; Tanaka et al. 2005).

As we will show, given the ability to find motifs under DTW, examples like the one above are replete in diverse domains such as industry, medicine, and human/animal behavior. Given that there is a large body of literature on both motif discovery (Bagnall et al. 2017; Dau and Keogh 2017; Lagun et al. 2014; Minnen et al. 2007; Mueen et al. 2009; Silva and Batista 2018; Tanaka et al. 2005; Truong and Anh 2015; Zhu et al. 2016, 2018) and Dynamic Time Warping (and its variants) (Geler et al. 2019; Keogh et al. 2009; Rabiner 1993; Rakthanmanon et al. 2013; Ratanamahatana and Keogh 2005; Sakoe and Chiba 1978; Sankoff 1983; Shokoohi-Yekta et al. 2015; Silva et al. 2016; Tan et al. 2019), why are there essentially no DTW-based motif discovery tools?

We believe that the following explains this omission. Both motif discovery and DTW comparisons are famously computationally demanding (Bagnall et al. 2017; Keogh and Ratanamahatana 2005; Ratanamahatana and Keogh 2005; Chiu et al. 2003). Recent years have seen significant progress for both, especially the Matrix Profile for the former (Zhu et al. 2016), but the main speed-up techniques for each are not obviously combinable.

In this work we introduce a novel algorithm that makes DTW motif discovery tenable for large datasets for the first time. We call our algorithm SWAMP, Scalable Warping Aware Matrix Profile. This is something of a misnomer, since we attempt to avoid computing most of the true DTW Matrix Profile by instead computing much cheaper upper/lower bounding Matrix Profiles.

We claim the following contributions for our work:

• 1. We show, for the first time, that there exists conserved structure in real-world time series that can be found with DTW motifs, but not with classic Euclidean distance motifs (Mueen et al. 2009; Truong and Anh 2015). It was not clear that this had to be the case, as Mueen et al. (2009) and others had argued for the diminished utility of DTW for motif discovery (all-to-all search), relative to its known utility for similarity search (one-to-all search).¹

• 2. We introduce SWAMP, the first exact algorithm for DTW motif discovery that significantly outperforms brute force search by two or more orders of magnitude.

• 3. Our algorithmic approach uses a novel “adaptive hierarchy of lower bounds” methodology that may be useful for other problems.

The rest of the paper is organized as follows. In Sect. 2, we present the formal definitions and background, before outlining our approach in Sect. 3. Section 4 contains an extensive experimental evaluation. Section 5 provides a case study on using SWAMP in classification. Section 6 introduces discord discovery algorithm using SWAMP. Finally, we offer conclusions and directions for future work in Sect. 7.

2 Background and related work

2.1 Time series notation

We begin by introducing the necessary definitions and fundamental concepts, beginning with the definition of a Time Series:

Definition 1

A Time Series T = t₁, t₂, …, t_n is a sequence of n real values.

Our distance measures quantify the distance between two time series based on local subsections called subsequences:

Definition 2

A subsequence ${\mathbf{T}}_{i,m}$ is a contiguous subset of values with length m starting from position i in time series T; the subsequence ${\mathbf{T}}_{i,m}$ is in form ${\mathbf{T}}_{i,m}$ = t_i, t_i+1, …, t_i+m-1 where ($1 \le i \le n {-}m + 1$) and m is a user-defined subsequence length with value in range of 4 $\le m \le \left| {\mathbf{T}} \right|$.

Here we allow m to be as short as four, although that value is pathologically short for almost any domain (Rakthanmanon et al. 2013).

The nearest neighbor of a subsequence is the subsequence that has the smallest distance to it. The closest pairs of these neighbors are called the time series motifs.

Definition 3

A motif is the most similar subsequence pair of a time series. Formally, ${\mathbf{T}}_{a,m}$ and ${\mathbf{T}}_{b,m}$ is the motif pair iff $dist\left( {{\mathbf{T}}_{a,m} ,{\mathbf{T}}_{b,m} } \right) \le dist\left( {{\mathbf{T}}_{i,m} ,{\mathbf{T}}_{j,m} } \right) \forall i,j \in \left[ {1,2, \ldots ,n - m + 1} \right]$, where a ≠ b and i ≠ j, and $dist$ is a distance measure.

One can observe that the potential best matches to a subsequence (other than itself) tend to be the subsequences beginning immediately before or after the subsequence. However, we clearly want to exclude such redundant “near self matches”. Intuitively, any definition of motif should exclude the possibility of counting such trivial matches.

Definition 4

Given a time series T, containing a subsequence ${\mathbf{T}}_{i,m}$ beginning at position i and a subsequence ${\mathbf{T}}_{j,m}$ beginning at j, we say that ${\mathbf{T}}_{j,m}$ is a trivial match to ${\mathbf{T}}_{i,m}$ if $j \le i + m - 1$.

Following Dau and Keogh (2017) we use a vector called the Matrix Profile (MP) to represent the distances between all subsequences and their nearest neighbors.

Definition 5

A Matrix Profile (MP) of time series T is a vector of distances between each subsequence ${\mathbf{T}}_{i,m}$ and its nearest neighbor (closest match) in time series T.

The classic Matrix Profile definition assumes Euclidean distance measure which computes the distance between the ith point in one subsequence with the ith point in the other (see Fig. 4.left). However, as shown in Fig. 4.center, the non-linear DTW alignment allows a more intuitive distance that matches similar shapes even if they are locally out of phase. For brevity, we omit a formal definition of the (increasingly well-known) DTW, instead referring the interested reader to Ratanamahatana and Keogh (2005), Keogh and Ratanamahatana (2005) and Rakthanmanon et al. (2013).

Fig. 4

For two time series Q and T: (left) Their Euclidean Distance. (Center) Their DTW distance. (Right) Their LB_Keogh distance

Similarity search under DTW can be demanding in terms of CPU time. One way to address this problem is to use a lower bound to help prune sequences that could not possibly be a best match (Rakthanmanon et al. 2013). While there exist dozens of lower bounds in the literature, in our work we use a generalization of the LB_Keogh (Keogh and Ratanamahatana 2005; Rakthanmanon et al. 2013).

Definition 6

The LB_Keogh lower bound between a time series Q and another time series T, given a warping window size w, is defined as the distance from the closest of the upper and lower envelopes around T, to Q. Formally:

$$ LB_{{Keogh}} \left( {Q,T} \right) = \sqrt {\mathop \sum \limits_{{i = 1}}^{n} \left\{ {\begin{array}{*{20}l} {\left( {q_{i} - U_{i} } \right)^{2} } \hfill & {if\,~q_{i} > U_{i} } \hfill \\ {\left( {q_{i} - L_{i} } \right)^{2} } \hfill & {if\,~q_{i} < L_{i} } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.} $$

(1)

where the upper envelope ($U_{i}$) and lower envelope ($L_{i}$) of T are defined as:

$$ \begin{aligned} U_{i} & = \max \left( {t_{i - w} , t_{i - w + 1} , \ldots , t_{i + w} } \right) \\ L_{i} & = \min \left( {t_{i - w} , t_{i - w + 1} , \ldots , t_{i + w} } \right) \\ \end{aligned} $$

(2)

Figure 4 illustrates this definition.

For computationally demanding tasks, even the lower bound computation may take a lot of time. Thus, we plan to exploit a “spectrum” of lower bounds as we explain in Sect. 3.1, each of which makes a different compromise of fidelity versus tightness.

To create this spectrum, we exploit our ability to perform various computations on the reduced dimensionality data. More concretely, we can perform downsampling using the Piecewise Aggregate Approximation (PAA).

Definition 7

The PAA of time series T of length n can be calculated by dividing T into k equal-sized windows and computing the mean value of data within each window. More specifically, for each window i, the approximate value is calculated by the following equation:

$$ \overline{\varvec{t}}_{{\varvec{i}}} = \frac{{\varvec{k}}}{{\varvec{n}}}\mathop \sum \limits_{{{\varvec{j}} = \frac{{\varvec{n}}}{{\varvec{k}}}\left( {{\varvec{i}} - 1} \right) + 1}}^{{\frac{{\varvec{n}}}{{\varvec{k}}}.{\varvec{i}}}} {\varvec{t}}_{{\varvec{j}}} $$

(3)

The vector of these values is the PAA representation of the time series. $PAA\left( {T, k} \right) = \overline{t}_{1} , \overline{t}_{2} , \ldots , \overline{t}_{k}$.

It is convenient to express the compression rate of a PAA approximation as “D to 1”, or $D:1$, where ${\text{D}} = {\text{n}}/{\text{k}}$. This notation can be visualized as shown in Fig. 5.

Fig. 5

A time series Q, downsampled using PAA to two different compression rates. (Left) 4:1 (right) 16:1

Given that we can downsample time series, we can also generalize LB_Keogh to such downsampled data, with LB_KeoghD:1 ($D \ge 1$):

Definition 8

The downsampled lowerbound LB_KeoghD:1(Q,T) between a time series Q and another time series T is defined as the distance from the closest of the downsampled upper and lower envelopes around T, to the downsampled Q. Formally:

$$ LB_{{Keogh}} D:1\left( {Q,T} \right) = ~\sqrt {\mathop \sum \limits_{{i = 1}}^{n} \left\{ {\begin{array}{*{20}l} {\left( {\bar{q}_{i} - \bar{u}_{i} } \right)^{2} } \hfill & {if~\,\bar{q}_{i} > \bar{u}_{i} } \hfill \\ {\left( {\bar{q}_{i} - \bar{l}_{i} } \right)^{2} } \hfill & {if\,~\bar{q}_{i} < \bar{l}_{i} } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.} $$

(4)

where $\overline{Q} = PAA\left( {Q, k} \right),\overline{U} = PAA\left( {U_{T} ,k} \right), and \overline{L} = PAA\left( {L_{T} ,k} \right)$.

Figure 6 illustrates this definition.

Fig. 6

An illustration of parametrized LB_Keogh. Three possible settings that make different trade-offs on the spectrum of time-to-compute vs. tightness of lower bound. The special case of LB_Keogh1:1 is the classic lower bound also shown in Fig. 4, and used extensively in the community (Keogh and Ratanamahatana 2005; Rakthanmanon et al. 2013; Ratanamahatana and Keogh 2005)

Given these downsampled lower bounds, we can still use the LB_Keogh distance, but we need to scale the distance by $\surd {\text{n}}/D$ to generate a tighter, yet still admissible lower bound. The proof of this variation of the lower bound appears in a slightly different context in (Zhu and Shasha 2003). To see why it is needed, refer to Fig. 6.right. Here each gray hatch-line represents the aggregate distance for 16 datapoints. If we only counted each line once, we would have a very weak lower bound. It seems that we could scale each line’s contribution by 16 (or more generally, D), but then we would not have an admissible bound. It can be shown that $\surd {\text{n}}/D$ is the optimally tight admissible scaling factor (Yi and Faloutsos 2000; Zhu and Shasha 2003).

To see how the parameterization affects the tightness of the lower bound, we selected 256 random pairs from the electrical demand dataset (see Fig. 14) and computed both their true distance and the lower bound distances at the dimensionalities shown in Fig. 6. The results are shown in Fig. 7.

Fig. 7

An illustration of the tightness of the parametrized LB_Keogh. The tightness for each pair is inversely proportional to orthogonal distance to the diagonal line. For one randomly selected point, we show how this changes (inset)

Note that while our examples use powers of two for both the original and reduced dimensionality, PAA and our parametrized lower bounds are defined in the more general case.

2.2 Related work

There is a huge body of literature on DTW (Rakthanmanon et al. 2013) and on motif discovery (Bagnall et al. 2017; Minnen et al. 2007; Mueen et al. 2009; Tanaka et al 2005). However, there are very few papers on the intersection of these ideas.

In Truong and Anh (2015) the authors introduce “A fast method for motif discovery in large time series database under dynamic time warping”. However, this method does not produce the top motifs as we have defined them in Definition 3. It is perhaps better seen as a clustering algorithm that produces centroids that could be considered “motifs”. Likewise, Lagun et al. (2014) created an algorithm to explore cursor movement data. The algorithm discovers “common motifs” and does use the DTW distance, but once again, it is better seen as a clustering algorithm that produces centroids that could be considered motifs. These papers speak to the utility of both motif discovery and to the use of DTW. However, these works do not offer us actionable insights for the task-at-hand.

Finally, a recent paper uses DTW and reports results for “Motif Discovery” (Ziehn et al. 2019). However, this paper is simply doing what the community commonly calls “range queries”, not motif discovery.

To the best of our knowledge, there is only one research effort that finds exact motifs under DTW (Silva and Batista 2018). This method creates a full DTW Matrix Profile but optimizes its creation by exploiting many of the techniques used by the UCR-Suite (Rakthanmanon et al. 2013), including the lower-bounding and early abandoning tricks techniques that we will exploit. However, they only consider a single-resolution representation of the data, as we will show, working on a multi-resolution data representation allows at least two further orders of magnitude speed-up. These optimizations used by Silva and Batista (2018) do produce a ten-fold improvement over a naïve brute force implementation. We also achieve a much more dramatic speed up by not computing the full DTW Matrix Profile, but rather computing as little of it as possible, in order to admissibly discover just the top DTW motifs.

The reader may wonder if we could replace exact DTW with one of the “fast approximations” to it, such as FastDTW (Salvador and Chan 2007). Recent works suggest that these approximations are actually not faster than the carefully optimized exact DTW (Wu and Keogh 2020). Moreover, all such work is empirical, there are no bounds on how bad the approximation can be (Wu and Keogh 2020). Thus, we do not see this as a promising avenue for acceleration.

3 Observations and algorithms

Before introducing our algorithm in detail, we will take the time to outline the intuition behind our approach. In Fig. 8 we show a time series and its DTW MP.

Fig. 8

A time series and its DTW MP. The lowest points of the DTW MP are the locations of the top-1 DTW motifs

The two lowest points [they must have tied values by definition (Zhu et al. 2016)] correspond to the top-1 DTW motif. Thus, while we have solved our task-at-hand, this brute force computation of the DTW MP required $O\left( {n^{2} m^{2} } \right)$ time. (n is the length of the time series and m is the subsequence length as shown in Fig. 8).

There are some optimizations (which we use) including early abandoning, using the squared distance, etc. (see Murray et al 2017; Rakthanmanon et al. 2013). However, these only shave off small constant factors. It is possible to index DTW. However, that only helps to accelerate future ad-hoc similarity search queries. Here, the time required to build the index would only dramatically increase the time above.

Note that the Euclidean distance is an upper bound for the DTW. Moreover, there are perhaps a few dozen known lower bounds to DTW, including the LB_Keogh (Keogh and Ratanamahatana 2005). In Fig. 9 we revisit the data shown in Fig. 8 to include the MPs for these two additional measures. Note that they “squeeze” the DTW MP from above and below.

Fig. 9

A time series and its ED MP, its DTW MP and its LB_Keogh1:1MP. Note that the lowest values in the ED MP (denoted with the horizontal dashed line) are an upper bound on the values of the top DTW motif

This figure suggests an immediate improvement to the brute force algorithm. The lowest value of the ED MP is an upper bound on the value of the top-1 DTW motif. Thus, before we compute the DTW MP, we could first compute the ED MP and use its smallest value to initialize the best-so-far value for the DTW MP search algorithm. This has two exploitable consequences. It would speed up the brute force algorithm, because the effectiveness of early abandoning is improved if you can find a good best-so-far early on. However, there is a much more consequential observation. Any region in the time series for which the lower bound is greater than the best-so-far can be admissibly pruned from the search space.

Note that this pruning can dramatically accelerate our search. For example, suppose that the fraction p of the time series is pruned from consideration as the location of the best motif. We then only have to compute $(1 - p)^{2}$ of the possible pairs of subsequences. Moreover, this ratio can only get better, as we find good matches that further drive the best-so-far down.

In fact, as we shall see, on real datasets this pruning can be so effective that instead of doing $O\left( {n^{2} } \right)$ invocations of DTW, we only need to do a small constant number. This reduces the time complexity to find the top-1 DTW motifs from $O\left( {n^{2} m^{2} } \right)$, to the $O\left( {n^{2} m} \right)$ time required to compute the lower bound. Because m can be in the range, of say, one hundred to ten thousand (see the insect example in Fig. 12), this offers a significant speedup. Nevertheless, it is natural to ask if we can further improve on this.

Let us revisit Fig. 9. Note that in some locations, the lower bound is much greater than the best-so-far. This suggests an opportunity. In general, it is often the case that there are multiple lower bounds for a distance measure, which produce different tradeoffs on the spectrum of time-to-compute versus average tightness. Thus, instead of always using the tightest lower bound available to us everywhere, it would be better to use faster “just tight enough” lower bounds wherever possible. As we shall see, this is exactly what SWAMP does.

3.1 Creating a spectrum of lower bounds

As noted above, our SWAMP algorithm depends on the availability of multiple lower bounds that make different tradeoffs on the spectrum of tightness versus speed of execution.

It is not meaningful to measure the tightness of lower bounds on a single pair of time series, as the idiosyncrasies of the particular pair of subsequences may favor different lower bounds. Instead, it is common to measure the tightness of a lower bound by averaging over many pairs of randomly chosen time series (Ratanamahatana and Keogh 2005).

$$ tightness\left( {A,B} \right) = \frac{{LB\left( {A,B} \right)}}{{DTW\left( {A,B} \right)}} $$

(5)

In Fig. 10 we average over six million pairs of random-walk for each setting.

Fig. 10

A spectrum of lower bounds for DTW plotted with time (note the log scale) versus tightness. Recall that DTW is a lower bound to itself, thus occupies the top right corner

It is important to ward off a possible misunderstanding. If we computed the entire LB_Keogh1:1 and found that it aggressively pruned off all but one pair of subsequences (the true top-1 motif), then we would achieve a speedup of about 28.6 μs/1.84 μs = 15.5. This 15-fold speed would be impressive, but it appears to be the upper bound on speed-up. However, as hinted at above, we hope to prune off many of the LB_Keogh1:1 computations themselves, with the much cheaper LB_Keogh2:1 calculations. Moreover, we plan to do this iteratively, using cheaper (but weaker) lower bounds to prune off as many as possible more expensive (but stronger) lower bounds.

Note that the red dashed line in Fig. 10 forms a Pareto frontier. If there is any lower bound that is above the red line at any point, we should use it. We have investigated the dozens of alternative lower bounds, but we did not discover better performing bounds. There are two main classes of lower bounds:

• Lower bounds such as LB_KimFL that are $O\left( 1 \right)$ should in principle be on the Pareto frontier to the right of LB_Keogh32:1. However, their $O\left( 1 \right)$ time complexity assumes that the two time series are already normalized. If we are forced to normalize, these bounds are pushed to the interior of the frontier (however, as we will later show, the LB_KimFL can be used in a later phase of the algorithm, when the normalization is “free”, because it is computed for another purpose).

• There are at least a dozen lower bounds that are variants of the LB_Keogh, including LB_Improved, LB_Enhanced, LB_New, LB_Rotation, LB_Hust, LB_En, etc. (Junkui et al. 2006; Rakthanmanon et al. 2013; Gong et al. 2015). All of these exploit LB_Keogh, plus some additional information to produce a tighter lower bound. However, in all cases we found that the additional time required to exploit the “additional information” did not pay for itself. We would have been better off spending that extra time to compute the LB_Keogh at a higher level. However, we note that in some cases a clever implementation insight might fix this overhead.

Note that while we did not discover any other lower bounds to help for the task at hand, this does not say anything about the utility of these bounds for other tasks. LB_KimFL has been shown to be useful for in-memory similarity search (Rakthanmanon et al. 2013), and the more expensive lower bounds are useful for disk-based indexing (Keogh and Ratanamahatana 2005).

3.2 Introducing SWAMP

For notational simplicity we consider the task of finding the top-1 motif under DTW for a given value of w. The generalizations to top-K motifs or range motifs are trivial (Zhu et al. 2016).

We can best think of SWAMP as a two-phase algorithm. In Phase I it uses a single upper bound, and an adaptive hierarchy of lower bounds to prune off as many of the candidate time series subsequences as possible (candidate for being one of the best DTW motif pairs). Then, in Phase II, any surviving pairs of subsequences are searched with a highly optimized “brute force” search algorithm. The algorithm in Table 3 formalizes SWAMP which includes subroutines that compute Phase I and Phase II.

3.2.1 Phase I of SWAMP

We start by reviewing the two exploitable facts that we previewed in Fig. 9.

• The ED MP is the upper bound for LB_KeoghMP.

• The LB_KeoghMP is the lower bound for DTW MP.

Based on these observations, we know that any section of LB_KeoghMP (i.e. LB_Keogh1:1MP) that is greater than the minimum of ED MP (we consider that as the best-so-far), could not contain the best motif and can therefore be pruned. We can compute the DTW score for the region suggested by the lowest value of the pruned LB_Keogh1:1MP. If the score is lower than the minimum of ED MP, we can further lower the best-so-far. In this case, we can further reduce the number of DTW tests.

This basic strategy gains speedup, replacing most of the expensive DTW calculations with cheaper lower bound calculations. However, while computing LB_Keogh1:1MP is much faster than full DTW, it is still computationally expensive. Nevertheless, as we discussed in the previous section, we may not need to compute the full LB_Keogh1:1MP to find the best motifs. Instead, we can apply the above strategy on a hierarchy of cheaper downsampled LB_KeoghMP. The algorithm in Table 1 formalizes this process.

Table 1 ComputeDSMP: hierarchically computes the downsampled lower bound Matrix Profile and prunes off the unpromising locations

In line 1 we compute the classic Matrix Profile for the time series T with the given subsequence length m. This is needed to provide the upper bound of the distance between the DTW motifs we will discover. Using this Matrix Profile, we find the ED motifs, i.e. the pair of lowest values (Zhu et al. 2016, 2018). We then measure the distance between those motifs using the DTW distance rather than the ED distance, in order to initialize the best-so-far distance (lines 2–3).

Starting with a downsampling factor equal to the subsequence length (line 4), we first compute a very cheap lower bound for the entire time series using the algorithm in Table 2. If the DTW distance for the region suggested by the lowest value of this lower bound is smaller than the best-so-far, we update the best-so-far. For regions where it is too weak to prune, we selectively compute a tighter bound and repeat the same process. The algorithm ends after it has explored the highest resolution (i.e. D = 1) (lines 6–12).

Table 2 LB_KeoghDSMP: computes the LB_KeoghMP for the downsampled time series

Note that when computing lower bounds at any resolution level, we take the pruned-off locations at the lower levels into account, meaning that we do not compute a lower bound for those regions. The lower bound computation process is described Table 2.

Lines 1 and 2 downsample both the time series and the Boolean vector specifying the pruned and non-pruned locations. Line 3 scales downs the subsequence length relative to the downsampling rate. Lines 4–6 compute the downsampled lower bound LB_KeoghD:1, expand it to the size of the complete lower bound and scale up the result by the downsampling factor.

3.2.2 Phase II of SWAMP

Let us review the situation at the end of Phase I. From the original set of $n {-}m + 1$ candidate time series subsequences that might have contained the top-1 motif, we pruned many (hopefully the vast majority) of them into a much smaller set c, of remaining candidates.

Globally, we know:

• 1. A best-so-far value, which is an upper bound on the value of the top-1 motif. We also know which pair from c is responsible for producing that low value.

Locally, for each subsequence, we know:

• 2. A DTW lower bound value on its distance to its nearest neighbor.

• 3. The location of its nearest neighbor in the lower bound space, which may or may not also be its DTW nearest neighbor.

We now need to process the set of candidates c to find the true top-1 motif, or if the current best-so-far refers to the top-1 motif, confirm that fact by pruning every other possible candidate.

Note that even if we processed all $O\left( {c^{2} } \right)$ pairwise comparisons randomly, there is still the possibility of pruning more candidates. In particular, every time the best-so-far value decreases, we can use the information in ‘3’ above to prune additional candidates in c, whose lower bounds now exceed the newly decreased best-so-far value.

As shown in Table 3 we can see this search as a classic nested loop, in which the outer loop considers each candidate in c, finding its DTW nearest neighbor (non-trivial match) in c.

Table 3 SWAMP: discovers the top-1 DTW motifs

Given our stated strategy of trying to drive the best-so-far down as fast as possible, the optimal ordering for our search is obvious. In the outer loop we should start with a candidate that is one of the true DTW motif pair, and in the inner loop we should start with the other subsequence of that motif pair. Clearly, we cannot do this, since that assumes we already know what we are actually trying to compute. However, we can approximate this optimal ordering quite well. On average, the true DTW distance is highly correlated with its lower bound (see Fig. 9). Thus, we should order the outer loop in increasing order of the lower bounds provided by LB_Keogh1:1 in the last iteration of Phase I (line 2).

For the inner loop, for the very first iteration we consider the candidate’s nearest neighbor in lower bound space and replace it with its immediate neighbor (4–7). After this first comparison, the subsequent iterations can be done in any order. The algorithm in Table 3 formalizes these observations.

Note that we have added four further optimizations into the inner loop. We use a cheap but weak lower bound LB_KimFL to prune some subsequences (line 12). For those pairs that survive, we use a tighter but more expensive lower bound LB_Keogh1:1 (line 13). Moreover, we use the early abandoning version of LB_Keogh, as introduced in (Rakthanmanon et al. 2013). Finally, if all previous attempts at pruning fail, and we are forced to do DTW, we compute the early abandoning version of DTW, which was also introduced in Rakthanmanon et al. (2013) (line 14). If any candidates survive that step, we update the best-so-far and prune the remaining unpromising subsequences (line 15–18).

Revisiting LB_Keogh1:1 in this phase is worth clarifying. We do already know the LB_Keogh1:1 distance to each candidate’s nearest neighbor (from Phase I), but not to all its neighbors. Therefore, it is possible that with another round of lower bound computation for the remaining pairs, we can potentially have more prunings.

3.3 A visual intuition of SWAMP

We conclude our introduction of SWAMP with a visual intuition and review. In a test that previews the experiment shown later in Fig. 14, we searched for the top DTW motif of length 400, in an electrical demand dataset of length 20,000, using a warping window of 16. We carefully recorded what elements of the SWAMP algorithm are responsible for processing (pruning or computing) what fraction of the candidate pairs of subsequences. Figure 11 shows the results.

Fig. 11

For the power demand dataset (see Fig. 14), there are 184,348,801 pairwise subsequences that could be the top motif, which need to be pruned or compared. From top to bottom we see the progress of SWAMP in processing these candidate pairs. Numbers may not sum exactly to 100%, due to rounding for presentation

This trace shows that at least in this case, only a vanishing small percentage of candidates survive to Phase II, where increasingly expensive computations are used to prune them, except for just 0.0204% of the candidates, which actually need full DTW.

The figure also shows the utility of our hierarchy of lower bounds approach. For example, LB_Keogh2:1 pruned 65.71% of the candidates. Had we not used our hierarchical approach, then LB_Keogh1:1 would also have pruned them, but would have taken about four times longer. In general, this figure suggests that every element of our algorithm is responsible for some speedup.

3.4 Complexity analysis

The Euclidean distance MP algorithms such as SCRIMP (Zhu et al. 2018) have identical best-case and worst-case times, independent of the data. In contrast, the performance of SWAMP does depend on the data. For example, suppose we are given pure random data (not random-walk, which is actually an ideal case). Here we mean independent random samples; in Matlab these can be obtained by >  > worse_case = randn(1,10000);. And further suppose we are given a large value for w. In such cases, the lower bounds become very weak. In essence, they report a lower bound of zero for almost all comparisons. In this case, the time complexity of SWAMP is the same as brute force search, $O\left( {n^{2} m^{2} } \right)$ time (recall: n is the length of the time series and m is the subsequence length). This is because after no pruning in Phase I, it will be forced to do $O\left( {n^{2} } \right)$ comparisons that take $O\left( {m^{2} } \right)$ time.

Of course, such a dataset is unlikely to yield interesting motifs anyway. It is reasonable to ask what the time complexity is for datasets that are likely to yield semantically meaningful motifs, such as those shown in Sect. 4. For those datasets, we were able to prune at least 99.9% of all DTW calculations in Phase I alone. If we pessimistically assume that only the finest level of pruning (that is, LB_Keogh1:1) in Phase I actually did any pruning, then we have reduced the complexity to $O\left( {n^{2} m} \right)$. This is the same as the best time complexity known for Euclidean distance motif discovery before 2016 (Mueen et al. 2009) (since then a further factor of $O\left( m \right)$ has been shaved off this time (Zhu et al. 2018). However, let us revisit our pessimistic assumption. Suppose that 99% of the pruning came from a coarser lower bound, let us say LB_KeoghD:1, then the time complexity reduces to $O(n^{2} m/D^{2} )$. In real word datasets it is often the case that a coarser lower bound can prune the majority of DTW calculations. For example, for the dataset shown in Fig. 16, when D is 4 it still prunes off 82.7% of the DTW calculations. Because m is often approximately $D^{2}$, this means that the time complexity can be effectively $O\left( {n^{2} } \right)$, which is the same time complexity of SCRIMP (Zhu et al. 2018) and the other state-of-the-art Euclidean motif discovery algorithms. This may seem unintuitive but recall that in order to find the closest pair of subsequences, SCRIMP computes the exact distance of every pair of subsequences. In contrast, SWAMP tries to compute as few exact distances as possible, preferring to prune virtually everything if possible.

In terms of space complexity, SWAMP only requires an inconsequential $O\left( n \right)$ space overhead.

4 Empirical evaluation

We begin by stating our experimental philosophy. We have designed all experiments such that they are easily reproducible. To this end, we have built a webpage that contains all datasets, code and random number seeds used in this work, together with spreadsheets which contain the raw numbers (Alaee 2020). This philosophy extends to all the examples in the previous section.

4.1 Examples of DTW motifs

Before conducting more formal experiments, we will take the time to show some examples of DTW motifs we have discovered in various datasets, in order to sharpen the readers’ appreciation of the utility of DTW in motif discovery.

Entomologists use an apparatus called an Electrical Penetration Graph (EPG) to study the behavior of sap-sucking insects (Willett et al. 2016). It is known anecdotally (Willett et al. 2016), and by the use of classic motif discovery (Mueen et al. 2009), that such behaviors are often highly conserved at a time scale of 1 to 5 s. However, is there any behavior conserved at a longer time scale? As shown in Fig. 12.bottom.left, if we used the Euclidean distance, we might say “no”. While the two patterns in the motif are vaguely similar, we might attribute this to random chance.

Fig. 12

(Top) About 34 min of EPG data collected from an Asian citrus psyllid (ACP) that was feeding on a Troyer citrange (Sweet Orange) (Willett et al. 2016). (Bottom) The top-1 ED motif (left) and the top-1 DTW motif (right)

However, if we simply use the DTW distance, we discover an unexpectedly well-conserved long motif, corresponding to feeding behavior known as phloem ingestion (Willett et al. 2016).

Exploring such datasets rapidly gives one an appreciation as to how brittle the Euclidean distance can be. Consider the experiment on a different individual from the same insect species shown in Fig. 13.

Fig. 13

(Top) The top-1 ED and DTW motifs discovered in seven-hour segment EPG data collected from an ACP (Willett et al. 2016). (Bottom) A zoom-in of the DTW motif visually explains why ED has difficulty finding the same motif as DTW

As before, we cannot directly fault the ED. It does return a pair of subsequences that are similar, although somewhat “boring and degenerate”. However, an entomologist would surely prefer to see the DTW motif, which contains examples of a probing behavior (Willett et al. 2016). To understand why ED could not discover these, in Fig. 13.bottom we show the alignment both methods have on the sections corresponding to the behavior. ED, with its one-to-one alignment, cannot avoid mapping some peaks to valleys, incurring a large distance. In contrast, the flexibility of DTW allows it to map peak-to-peak and valley-to-valley, allowing the discovery of these semantically identical behaviors.

In Fig. 2 we showed a motif we discovered in consumer electrical-demand telemetry. However, for visual clarity we chose a very simple example, the data was from a single outlet that was attached to the dishwasher. In Fig. 14 we consider a much more complex and difficult example; we examine the entire household demand, which includes the combination of refrigeration, cooking devices, laundry machines, entertainment devices, etc.

Fig. 14

(Top) The electrical power demand of a UK house over 18.5 days (Murray et al. 2017). (Bottom) The top-1 ED motif (left) and the top-1 DTW motif (right) for an eight-hour query length

As before, it is hard to fault the ED motif. It tells us that sometimes there is a relatively long lull in demand, followed by a sharp increase. However, the DTW motif tells us much more. There is a highly conserved pattern, that surely has some semantic meaning. Based on its timing (in the middle of the night) we suspect the following. Most power providers in England use a differential tariff to encourage users to shift power-hungry processes to run during the night, using off-peak electricity. For many people, there are few options, unless they have high thermal mass heaters (i.e. underfloor heating). However, many modern European washing machines support the use of programable timers, so many people run their machines at night. The DTW motif is surely a wash cycle.

One of the most common uses of motif discovery is in analyzing human behavior. It is natural to ask if DTW motifs are helpful in that context. To avoid the conflict of interest of producing our own new datasets to test this, we simply examined the human behavior datasets in the UCI machine learning repository (Dua and Graff 2017). Figure 15 shows one sample experiment.

Fig. 15

(Top) A time series created by tracking the left-hand of a volunteer, using the Kinect system (Feitosa et al. 2018). (Bottom) The top-1 ED motif (left) and the top-1 DTW motif (right) are very different. The ED motif corresponds to the rest position before two different gestures; however, the DTW motif is a repeated gesture

As this figure hints at, DTW is often able to find repeated structure that defeats the Euclidean distance.

In Fig. 16 we performed a similar experiment using a different sensor (gyroscope), physically mounted on the body. Note that the amount of warping visible in Fig. 16.bottom.left is very small, but once again, it is enough to defeat the Euclidean distance.

Fig. 16

(Top) A time series created by a hip-worn gyroscope (Dua and Graff 2017). (Bottom) The top-1 ED motif (left) and the top-1 DTW motif (right) are very different. The ED motif corresponds to two transitions (lie-to-sit and sit-to-stand), the DTW motif corresponds to periods of walking-downstairs

Note that if we review the motifs discovered by ED in Figs. 1, 14, 15 and 16 they are all very similar, in spite of coming from different domains. Moreover, they are all “simple”.

This “simplicity bias” was observed in Dau and Keogh (2017), which suggests a technique to bias the results away from simple motifs. However, it is not clear we can bias towards warped patterns.

4.2 An example of DTW motif join

One of the useful implications of framing our hunt for DTW motifs as a Matrix Profile problem is that we can avail ourselves of the wealth of expanded definitions for the Matrix Profile (Zhu et al. 2016, 2018; Dau and Keogh 2017). In particular, here we show the utility of conducting time series joins. The Matrix Profile is defined for all types of joins. For example, classic motif discovery can be seen as a self-join. Here we are interested in a full-outer-join, equivalent to simply concatenating the two time series of interest, and running SWAMP on the result.

To demonstrate the utility of motif joins, we consider a dataset of cricket umpire signals. A carefully processed and contrived version of this dataset appears in the UCR Archive (Dau et al. 2019). However, the dataset shown in Fig. 17 was recorded in the same session, but in natural uninterrupted sequences. We took the full Z-axis right-hand acceleration time series from two participants and joined them. Because this is a full-outer-join, it is possible that subsequences from one person could join with themselves. That is exactly what happened with the ED motif, joining Graeme’s sign for “noball” with his (only superficially similar) sign for “six”. In contrast, the DTW motif joins examples of the sign for a “six”, in spite of the fact that Alex signs it more leisurely than Graeme.

Fig. 17

(Top) A dataset consisting of Graeme signaling, followed by Alex signaling cricket umpire signs. (Bottom.left) The top-1 ED motif joins the sign for “noball” with the sign for “six”. (Bottom.right) the top-1 DTW motif joins two signs for “six”, one each performed by Alex and Graeme

In passing, we foreshadow the scalability results in Sect. 4.4 by noting that for this experiment, 99.8562% of all candidate motif pairs were pruned in Phase I, and that by the end of Phase II, 99.999692% of all candidate motif pairs were pruned. Thus, only 0.000308% of the possible DTW comparisons needed to be made.

4.3 DTW motifs create testable hypotheses

We continue our examples with a case study that hints at one of the major uses of motif discovery, i.e. finding interesting hypotheses to explore. In Fig. 18 we show the results of DTW motif discovery on a dataset obtained by attaching a sensor to a wild penguin. The discovered motif is highly conserved (except for a little warping that defeats the ED), suggesting that it has some semantic meaning. However, what is that meaning? We do not know. However, if we plot the data with the simultaneous pressure reading, we see that this behavior seems to happen just as the swimming bird returns to the surface for a brief gulp of air before diving again. Testing this hypothesis on other datasets reveals it to be almost always true. However, understating the meaning/mechanism is ongoing work.

Fig. 18

(Top) Telemetry from a wild penguin hunting at sea. (Bottom) A zoom-in of the region that happens to contain the top-1 DTW motif [the ED motif is shown at Alaee (2020)] and is not obviously interesting). By aligning the motifs with a recording of pressure (red line) we find tentative meaning of the motifs (Color figure online)

4.4 Scalability of SWAMP

To demonstrate the scalability of SWAMP we revisited the experiments shown in Figs. 12, 14 and 16. We computed the time needed for brute force search. We measured the time needed for SWAMP. Finally, we also computed the time needed to find the best Euclidean motif, using the highly optimized state-of-the-art SCRIMP algorithm (Zhu et al. 2018). This comparison is unfair to us, as SCRIMP is returning a different, and much easier-to-compute answer than our algorithm. However, it offers what is surely an upper bound on the speedup that can be obtained. Figure 19 shows the results.

Fig. 19

The times required by three algorithms to find motifs in the three examples shown in Figs. 12, 14, and 16. Note that the bars are normalized by the slowest performing algorithm, i.e. brute force search

The results can be summarized as follows. SWAMP is two to three orders of magnitude faster than brute force search, and an order of magnitude slower than the fastest Euclidean motif algorithm.

These experiments also offer us a chance to do a lesion study. We spent considerable effort motivating the need for a spectrum of lower bounds in Phase I of our algorithm (Table 1, lines 6–14). Suppose instead we only use the highest resolution, LB_Keogh1:1. The returned answer would clearly be the same, but how would this affect speed? We tested this, discovering that the time needed increased by 187%, 1,028% and 113% respectively, showing that the “use the cheapest lower bound you can” approach really does help.

Finally, we compared to Silva and Batista (2018), which is the only other exact algorithm for finding DTW motifs. On the three datasets above this algorithm was slower by 17,274%, 185,511% and 13,857% respectively.

Given the utility of our algorithm for several data mining tasks, we chose to conduct additional detailed experiments which we discuss in the following. Figure 20 shows the time to compute and pruning rate for motif discovery with fixed subsequence length 400, fixed warping window size 16 and increasingly long time series. The time series in question is an extended version of the household electrical power demand dataset we used in Sect. 4.1.

Fig. 20

(Left) Time to compute SWAMP increases linearly as we increase the length of the time series (note the log scale). (Right) However, since we have pruning rate of almost 100% in every case, the increase would be tolerable for very large datasets

Clearly, the time to compute SWAMP would increase as we increase the length of the time series. However, as shown in Fig. 20.right, the pruning rate remains close to 1 for all lengths, meaning that we avoid computing most of the true DTW Matrix Profile even for very large datasets. With a dataset as large as 1,000,000 data points, the time to compute SWAMP is about 9 h as shown in Fig. 20.left. Here, the brute force algorithm would simply be untenable.

4.5 Objective evidence of the superiority of DTW over Euclidean distance

As shown in previous sections, DTW motif discovery can be used to spot conserved patterns in real datasets. However, the comparison to Euclidean distance was mostly anecdotal. In this section, we will compare the utility of DTW over Euclidean distance on a large-scale experiment with real and complex data.

In Fig. 21, we show an example of a “sentence” created by concatenating words spelled out by the eye movements of an individual modeling Locked-In Syndrome (Fang and Shinozaki 2018). The participants learn a code to translate words into a sequence of eye-movements, in which the eye traces along the eight cardinal directions of the compass (and “blinking” as a special character). For example, the word “moth” (ガ) can be communicated as the sequence: “left right down left upper-right lower-left blinking”. These eye movements can be tracked with an inexpensive apparatus and can then be used to transcribe movement-to-text.

Fig. 21

A time series corresponding to a sentence (in Japanese) spelled out by the eye movements of an individual modeling Locked-In Syndrome. Only vertical axis is shown. Each colored box shows one word. All words have been rescaled to exactly the same length, to facilitate comparison to Euclidean distance (Color figure online)

To compare the accuracy of DTW and Euclidean distance on the task of discovering conserved structure, we propose the following experiment. From a vocabulary of 150 words, each of which was performed three times by a single individual, we randomly create a sentence that has exactly one repeated word. As shown in Fig. 21, because the default position of the eye at the beginning and end of word is straight ahead, we can concatenate words without producing any obvious artifacts in-between them.

We generated sentences consisting of 8, 16, 32 and 64 words. We performed one hundred runs of motif discovery on these time series using both ED (using the Matrix Profile Zhu et al. 2016, 2018) and DTW (using SWAMP with w = 24). While all words are of length 600 (possible including a relatively constant prefix and suffix, because the participant was in a relaxed state of looking straight ahead), we wanted to avoid giving the algorithm this exact value. So, for every experiment we gave both ED and DTW a random subsequence length between 540 and 660. Figure 22 shows the motif discovery success rates for different algorithms.

Fig. 22

SWAMP (red) with a warping window size 24 performs better than both ED MP (blue) and the default rate (yellow) in finding the correct motifs on different settings (Color figure online)

Both ED and DTW work much better than the default rate (random guessing in proportion to the prior probability of events). However, DTW is clearly superior to both.

Let use briefly consider the sources of error. Because each time series is generated by concatenating words without any pause or noises in between, we might create “artificial” repeated words. For example, suppose the unique words we embedded happened to include “wombat”, “mangos” and “batman”. When embedded into a sentence they could form: …wombatmangosbatman…, making an accidental motif of “batman”, which really has only one occurrence. This issue is more likely in the domain under consideration, which has a cardinality of just nine distinct symbols. Figure 23 shows one such example of a spurious word we discovered.

Fig. 23

The suffix and prefix of two words concatenated to each other (red) is similar to the suffix and prefix of two other words concatenated to each other (green). These two words have been mistaken with the semantic motifs (the red circles) (Color figure online)

As shown in Fig. 24, another reason why SWAMP can fail here is simply because we are only using the X-axis time series. This motivates the need for multidimensional DTW motif discovery. The issues in generalizing to multidimensional DTW are subtle (should we allow each dimension to warp independently, or force them to warp in synchronicity? See Shokoohi-Yekta et al. (2015)), however they are orthogonal to SWAMP’s speed-up mechanisms.

Fig. 24

Two different words that are more similar (red and green) than the embedded motifs (the red circles) when considering only the vertical axis (Color figure online)

Finally, we should note that even the research effort that produced this dataset, and introduced a custom classification model that included information from the shape of the time series, and linguistic information (which we ignore), only manage to achieve a 81.2% classification accuracy. Therefore, some error seems intrinsic to this domain.

We provide another example to demonstrate that DTW can discover motifs that would evade classic ED motif discovery. We embedded real patterns extracted from Bhattacharjee et al. (2018) into a smoothed random walk. The embedded data consists of motion capture data where a fork was used to feed a dummy. The original data contains X, Y, Z components. Here we only use the X component. From a single class, we take an exemplar and concatenate it with an exemplar from a different class, to produce a higher-level semantic eating event “eating-carrotnoodle”. Carrot noodle is a popular dish in Thai restaurants. Figure 25 shows an example of a dataset with the motif “eating carrots and noodles” embedded in otherwise unstructured data.

Fig. 25

An example of a dataset with a pair of motifs “eating carrot and noodle” embedded in otherwise unstructured data. One pair is highlighted and shown with a zoom-in version

In order to compare DTW motif discovery algorithm with the classic motif discovery algorithm, we performed a similar experiment to the one suggested by Imani and Keogh (2019). We created 100 random walks, of four different lengths and embedded pairs of examples of the eating-carrot-noodles behavior as shown in Fig. 25. We then ran motif discovery on these time series using both ED and DTW (SWAMP with w = 8), to see if we could recover the embedded motif. Figure 26 shows the motif discovery success rates for different algorithms.

Fig. 26

SWAMP (red) with a warping window size 8 performs better than both ED MP (blue) and the default rate (yellow) in finding the correct motifs on different settings (Color figure online)

This is an intrinsically hard problem. As hinted at in Fig. 25, random walk can produce any possible shaped time series, including a pair of subsequences that are similar enough to be the motif. However, as shown in Fig. 26, both ED and DTW work much better than the default rate, but DTW is clearly superior to both.

5 Discussion

We conclude with a discussion that will help practitioners decide if they should use DTW or ED when searching for motifs, and also help them decide on a warping window size. Note that the second question really subsumes the first, as in the special case of w = 0, DTW is logically identical to ED.

In some domains there is aZeitgeber,² an external stimulus that synchronizes processes. In nature, this can be daily, lunar or annual cycles. In culture, this can include the weekly cycles of the typical nine-to-five constraints of the western workday. For example, Fig. 27.left shows pedestrian traffic outside a train station in Melbourne for two randomly chosen weeks. There are differences between two weeks, but they can mostly be explained by changes in volume at a given time. For example, a school holiday reducing lunch time traffic on Monday. Likewise, some physical devices (mostly solid state) can produce highly regular outputs. Of course, these distinctions may not be hard and fast. A pacemaker may give an otherwise erratic pulse rate a metronome-like regularity. Such “Zeitgeber time series” will rarely benefit from DTW.

Fig. 27

Two pairs of time series subsequences with seven peaks, aligned with DTW. For the foot traffic dataset, the DTW alignment is almost linear, essentially the Euclidean Distance. In contrast, respiration data has highly non-linear alignment

In contrast, as Fig. 27.right hints at, many biological signals can have similar shapes but develop at varying rates of time. This is also true of many physical processes. For example, the motif shown in Fig. 14.bottom.right was created by an integrated circuit (IC) controlling a device. One might imagine that the IC would produce perfect timing. However, it is at the mercy of the varying water pressure and water temperature in the house.

5.1 SWAMP variants

In the last forty years there have been many modifications or extensions of DTW proposed. A twenty year old classic reference lists dozens of variants (Sankoff 1983), and the pace of research has greatly accelerated since then (Geler et al. 2019; Keogh and Ratanamahatana 2005; Shokoohi-Yekta et al. 2015; Silva et al. 2016). We believe that the SWAMP algorithm can support most or all variants of DTW. Moreover, there may be reasons to use some of these variants, at least because they may be faster. In the following section we discuss this idea.

5.2 Itakura constraint on warping path

Virtually all works on DTW define a global constraint which determines how far the warping path is allowed to deviate from the diagonal. Up to this point, we have used the Sakoe-Chiba constraint (Rabiner 1993), which is the most commonly used variant by the data mining community (Dau et al. 2019; Keogh and Ratanamahatana 2005; Rakthanmanon et al. 2013; Silva and Batista 2018; Silva et al. 2016; Tan et al 2019). However, there exists other constraints including the Itakura parallelogram (Sakoe and Chiba 1978). Figure 28 illustrates the two schemes.

Fig. 28

Global constraints limit the scope of the warping path to the grey areas. The two most common constraints are (left) Sakoe-Chiba band, and (right) Itakura parallelogram. w is a term defining allowed range of warping for a given point in a sequence

As we will show below, there are two reasons to expect that the Itakura parallelogram could be faster than Sakoe-Chiba band for motif discovery. However, if we are to advocate the Itakura parallelogram, we must first address the quality of results it can return. It seems to be generally believed by the data mining community that the Itakura constraint is inferior to the Sakoe-Chiba band. For example, a recent head-to-head comparison of the two methods on eighty-five datasets finds “…although the Itakura parallelogram is generally inferior to the Sakoe-Chiba band…” The clustering experiment shown in Fig. 29.top.panel seems to confirm this.

Fig. 29

(Top.panel) Three data objects, A, B and C, clustered using either the Sakoe-Chiba band or the Itakura constraint produce essentially identical results. However, if we replace C with D, which is almost identical, but just slightly circularly shifted (see bottom.panel) the Sakoe-Chiba band is largely unaffected, but the Itakura constraint produces an unintuitive clustering, grouping C and A together, and considering D as the outlier

However, these results are based solely upon data from the UCR archive (Dau et al. 2019). Most of these datasets consist of individual exemplars extracted from a longer time series. For example, individual heartbeats extracted from an electrocardiogram. Sometimes, these individual heartbeats, gait cycles or gestures are not perfectly extracted, and may have small artifacts at their beginning or end. This is modeled by the data object D shown in Fig. 29.

This issue is compounded by the fact that most heartbeats extraction algorithms, and gait-cycle extraction algorithms tend to define the beginning point of a cycle at the most dynamic locations of the cycle. For heartbeats this is the peak of the R-wave, and for gait it is (typically) the heel strike. Both warping methods can tolerate differences between two time series that happen towards the middle of the time series, but as we get closer to either of the ends, the narrowing apex of the parallelogram mean that any differences are more keenly felt by the Itakura approach. The issues caused by these small artifacts at the Prefix and Suffix of a time series have been noted before in a classification context (Silva et al. 2016), and techniques have been suggested to solve this problem. However, this issue is largely irrelevant if we generalize from the (somewhat unnatural) UCR-contrived classification setting and consider subsequence similarity search or motif discovery. In such case we are implicitly or explicitly “sliding the subsequences against each other” and reporting the smallest distance. Thus, global misalignment of patterns (as opposed to local misalignments addressed by DTW itself) are not an issue.

To summarize, while the community may be correct to (slightly) prefer Sakoe-Chiba band over the Itakura constraint for classification of extracted time series snippets (Geler et al. 2019) this preference does not seem to have implications for motif discovery from long streams. Moreover, as we explain below, the Itakura approach can produce tighter lower bounds, hence speeding up our algorithm.

5.3 Exploiting the Itakura speed up part I: tighter lower bounds

Recall that we defined the upper and lower envelopes enclosing a time series Q in Eq. (2). In this equation w is the band or the maximum allowed range of warping. In the case of Sakoe-Chiba, w is independent of the index i of the time series. However, for Itakura it is a function of i. Figure 30 shows the envelopes created for the time series Q using the two schemes.

Fig. 30

An illustration of the envelopes U and L, created for time series Q (shown in red), using (left) the Sakoe-Chiba band and (right) the Itakura parallelogram (Color figure online)

We defined the lower bounding function between the time series T and Q, i.e. LB_Keogh(T,Q), in Eq. (1). The example in Fig. 4 shows the lower bound generated using the Sakoe-Chiba band. Figure 31 illustrates the lower bounds generated using the Sakoe-Chiba and Itakura for the same time series in Fig. 4.

Fig. 31

An illustration of the lower bounding function LB_Keogh(Q,T). Time series Q (shown in red), is enclosed in the bounding envelope of U and L using (left) the Sakoe-Chiba band and (right) the Itakura parallelogram (Color figure online)

Since the tightness of the bounds is proportional to the area filled with the gray hatch lines, we can see that in this example the Itakura parallelogram provides a tighter bound than the Sakoe-Chiba band.

The reader will appreciate that with equal w in these two cases, the parallelogram always produces a tighter lower bound. It is suggestive of a significant speed up. However, it is not necessarily the case. Recall that for the SWAMP algorithm, the speed depends upon both tightness of lower bounds and the value best-so-far. If the best-so-far is small, the algorithm can prune more efficiently. While the Itakura parallelogram has a tighter lower bound, the motif distance under the Itakura parallelogram can be higher, if there is significant warping near the beginning or end of the motif. If that is the case, the final best-so-far will not be as low as in the Sakoe-Chiba case. It is not obvious how these competing factors will affect the final result, but a brief review of some previous results gives us hope. Consider again the DTW motifs discovered in Figs. 2, 13, 14 and 15. In each case the warping variability is concentrated in the center of the subsequence. This means that the Itakura and Sakoe-Chiba distances will be almost identical, but as noted above, the Itakura parallelogram will have a much tighter lower bound. To compare the speed-up using the Itakura band against the Sakoe-Chiba for our algorithm, we repeated our experiments for three datasets described in Fig. 19, this time using Itakura constraint. The discovered motifs in every case remained essentially the same. However, the time needed to compute SWAMP changed as follows: On the three datasets in Figs. 12, 14 and 16 and the Itakura parallelogram was faster by 80%, 9% and 80%.

5.4 Exploiting the Itakura speed up part II: earlier early-abandoning

While the results in the previous section suggest that Itakura is more efficient than Sakoe-Chiba in some datasets, there is still another observation that we can exploit.

Normally when we want to compute the lower bound LB_Keogh, we do it in a left-to-right order. However, if we want to early abandon as early as possible, we should do it in order of the largest (in expectation) value first. This way, the incrementality computed error grows as fast as possible, and as soon as it exceeds the best-so-far we can abandon.

For the Sakoe-Chiba, every point on the subsequences has the same expected contribution, hence our use of simple left to right. However, as Fig. 31 shows, Itakura parallelogram tends to have most of its lower bound contribution at either end, where the envelopes are thinner. This suggests the following heuristic: sort the indices in the ascending order of their distance between lower and upper envelopes and compute the lower bound in that order. This means visiting the endpoints of the sequence first and then moving towards the middle points. To be clear, instead of scanning the indices of Eq. (4) in the order 1, 2, 3,…,m − 1, m, we visit them in the order 1, m, 2, m − 1, 3, m − 2, …, m/2. As before, as soon as the distance between the endpoints of two sequences is higher than the best-so-far, we can stop the lower bound calculation as shown in Fig. 32.

Fig. 32

An illustration of early abandoning of LB_Keogh using Itakura constraint. We have a best-so-far value of bsf. After incrementally summing the first fourteen (of sixty four) individual contributions to the lower bound (seven on each endpoint) we have exceeded bsf, thus it is pointless to continue the calculation (Keogh et al. 2009)

To see what difference this optimization makes, without regard to implementation dependent details of a language, we revisited Phase II of the experiment shown in Fig. 14. We measured at what point the early abandoning could actually abandon for all comparisons in Phase II. Figure 33 shows the results.

Fig. 33

The distribution of early abandoning offsets for all comparisons in Phase II of the experiment in Fig. 14. The distribution is spread out over the whole range of values with the left to right ordering (red), while it is mostly skewed to the beginning offsets with the optimized ordering (blue) (Color figure online)

Note that in the act of sorting the indices we have been able to shift the early abandoning to the most beginning offsets, cutting the number of all point-wise comparisons to almost half the length of the sequence, as shown in Fig. 33. However, without the optimized ordering, the distribution would be spread out over the whole range of values from zero to the full length of the sequence.

We refer the interested readers to the companion website (Alaee 2020) where we have made available all the source codes for this algorithm to download and execute.

6 A case study in using swamp to support a classification task

We conclude this work by showing how SWAMP can be used to help build a time series classification algorithm. There are literally hundreds of time series classification algorithms in the literature (Bagnall et al. 2017). However, the vast majority of them only consider the UCR archive datasets or similar data sources, which have had individual examples carefully extracted, normalized and processed. As Dau et al. (2019) and others have recently noted, these works largely bypass the real difficulty of creating a practical time series classifier. We argue that the key question is how we can extract high quality exemplars from noisy and weakly labeled data and estimate a distance threshold. The latter issue is typically glossed over by researchers that rely on the UCR archive datasets to motivate and test their contributions. For example, one of the most famous datasets in the UCR archive is Gun/Point, which tasks us with the problem of discriminating between aiming a gun, and merely pointing with a finger. It is obvious that in any practical situation, most of the time, an individual is doing neither action. This suggests that there should be a third, highly polymorphic class, neither, with a very high prior probability. It is not clear how most proposed methods would generalize to this more realistic setting.

Here we present an end-to-end example of how SWAMP can be used to build a classifier. This is meant to be a demonstration; a more rigorous evaluation is beyond the scope of this paper. For simplicity, we will confine our attention to a single time series, the Z-axis gyroscope on the right wrist. However, generalization to multidimensional data is straightforward.

We consider the OPPORTUNITY Activity Recognition Dataset (Chavarriaga et al. 2013). This activity recognition environment and scenario has been designed to generate many activity primitives in a realistic setting. Subjects operated in a room simulating a studio flat with furniture and kitchen. The subjects were monitored using body-worn sensors. In addition, various items and utensils also had sensors, some binary (such as door open/closed) and some real-valued acceleration values (including the cup). It can be helpful to transform these real-valued data into binary data, equivalent to “cup was moved”.

The data creators “instructed users to follow a high-level script but leaving them free interpretation as how to achieve the high-level goals.” In one experiment they asked the user to perform a drill comprising of the following actions:

• 1. Open then close the fridge.

• 2. Open then close the dishwasher.

• 3. Open then close 3 drawers (at different heights).

• 4. Open then close door 1.

• 5. Open then close door 2.

• 6. Toggle the lights on then off.

• 7. Clean the table.

• 8. Drink while standing.

• 9. Drink while seated.

As Fig. 34 shows, even if we know this script, it can be difficult to semantically segment this data. Fortunately, we can use the sensors on the implements to at least weakly label this data. For example, if there is significant acceleration of the cup, this is suggestive of either the Drink-while-standing or Drink-while-seated class. However, there are two reasons why this does not completely solve our problem at hand. First, it is possible that the cup could move during other behaviors, especially Clean-the-table. Second, even if we are sure that the motion of the utensils is associated with a particular class, we cannot be sure exactly what part of the behavior is conserved. For example, it may be the case that some motion before the cup is lifted is conserved (as the user reaches for it). It may also be the case that some motion during drinking is not well conserved. For example, perhaps the path from the table to the user’s lip is well conserved, but once at the lip, the level of the liquid in the cup specifies the amount of rotation needed to imbibe. Thus, that part of the behavior is not well conserved. To be clear, this is pure speculation on our part. However, most classification tasks surely have similar uncertainties.

Fig. 34

A sequence of nine activities performed by the user in OPPORTUNITY Activity dataset

This motivates our approach. Even in this most familiar domain, we cannot tell from prior knowledge what part of a behavior is conserved. However, SWAMP can find the most conserved patterns in the time series. If these motifs happen to approximately line up with a weak label for a behavior, we can assume that the motif is likely to be a good prototype to recognize future occurrences of that behavior. Moreover, even if we have only two weak labels, we have at least a starting point to produce a threshold. The motif distance reflects the smallest match between two instances; as such it is clearly a lower bound to a good threshold value, but clearly it is at least the correct order of magnitude.

Our experiments consist of two parts. The first part demonstrates use of SWAMP for intra-subject activity classification. We chose the motion data corresponding to the Right Wrist Inertial Measurement (RLA) Gyroscopic Z. Training was done on the first ten repetitions of the activity set. The first test was done on the remaining ten repetitions in the same Drill 1 session. Figure 35 shows the top motifs discovered from the training data. The input time series was of length 28,330 with a subsequence length of 300 (chosen to reflect the approximate length of Drink-while-standing) and a warping window of 4.

Fig. 35

About sixteen minutes of the activity sequence associated with the first Drill session of the OPPORTUNITY dataset. The top DTW motif was the pair [20102, 25575] and corresponds to Drink-while-standing, with a distance of 4.41. The best Euclidean distance motif was the pair [3867, 20098] with a distance of 6.93, which also corresponds to Drink-while-standing

To classify the test data, we computed the DTW distance between the first top motif in the train data and each test subsequence as shown in Fig. 36. We then validated the matches against the weak labels associated with the time series as shown in Fig. 37. The weak labels were pre-processed before the classification. First, we z-normalized Gyroscope Z-axis. The results were set to binary values by using a threshold value of 2.0. There are two events of drinking from cup in the dataset, Drinking-while-standing and Drinking-while-seated. We manually removed activity for Drinking-while-seated which is visually straightforward. Finally, we activated all points within 2 s of activity (i.e. 60 samples). All locations where the distance is minimum on Fig. 36 correspond to the activity of Drink-while-standing which have been correctly classified using DTW as shown in Fig. 37. Here the default rate is just 9.8%.

Fig. 36

DTW query distances (red) between the training set’s first top motif (blue) and the first test set (grey) (Color figure online)

Fig. 37

The intra-subject variability of the Drink-while-standing activity is well captured by both ED and DTW. However, DTW outperforms ED with no false positives. The reason that ED has some false positives so close to true positives in some cases is that it is matching with Drink-while-sitting rather than Drink-while standing

This test demonstrates that even though an activity may be the top-1 motif for both DTW and ED, DTW outperforms ED when querying for all instances of such an activity. If there is a phase variation in this activity, ED will have difficulty, especially if the motif is complex. In this first test, ED performs closely to DTW, but we speculate that intra-subject phase variations are minimal when performing a monotonized task like repeating a set of activities twenty times.

The second experiment uses the same training data as the first (i.e. the first ten activity set repetitions of the right wrist time series in Drill 1), but now we consider inter-subject variability. The test data from the Drill 2 session also corresponds to the right wrist motion. Figure 38 shows the test data and the DTW distances between the first top-1 motif in the train data and each test subsequence. Figure 39 illustrates the classification results for this time series.

Fig. 38

DTW query distances (red) between the training set’s first top motif and the second test set (grey) (Color figure online)

Fig. 39

DTW correctly finds seventeen instances of the Drink-while-standing activity out of twenty events. However, ED discovered only nine correct instances

As Fig. 39 shows, the inter-subject variability of the Drink-while-standing activity is well captured by DTW. Out of twenty events on this time series, seventeen events have been correctly classified (i.e. true positives) while three events have been missed (i.e. false negatives). Compare it to the results from ED where only nine have been correctly classified. Note that here the default rate is just 11%. This test demonstrates that DTW queries using a motif of motion data can effectively be used as an activity classifier despite inter-subject variability.

Without motif discovery, a reasonable idea would have been to assume that the beginning of the cup activation indicated the beginning of the pattern to extract in the Gyroscopic Z axis. We also tried this, using the same length query. Since there are twenty such locations in the training data, we tried all of them. The average result is 15.7 true positives and 4.3 false positives. Recall that using SWAMP gave us seventeen true positives and three false positives. This suggests that the simple heuristic of using the most conserved pattern is a promising idea.

While the above results are limited, they clearly show the utility of using motifs as a starting point in any attempt to build a time series classifier from the ground up.

7 Discord discovery using swamp

We have shown that SWAMP can find DTW motifs efficiently by using the Matrix Profile framework. Instead of computing the entire DTW Matrix Profile, we gain scalability by only computing the smallest values in it (i.e. the motifs themselves), plus some other values that we could not prune. However, there are several other interesting properties of the Matrix Profile (Zhu et al. 2016, 2018). In particular, the highest value in the Matrix Profile coincides with the definition of time series discords, a primitive introduced in Keogh et al. (2005). Since their introduction, time series discords have emerged as a competitive approach for discovering anomalies. For example, a team led by Vipin Kumar conducted an extensive empirical comparison and concluded “on 19 different publicly available data sets comparing 9 different techniques, time series discords is the best overall technique among all techniques.” (Chandola et al. 2009). We attribute much of this success to the simplicity of the definition. Time series discords are intuitively defined as the subsequences of a time series that are maximally far away from their nearest neighbors. This definition only requires a single user specified parameter, the subsequence length. With only a single parameter to set, it is harder to overfit the anomaly definition, and overfitting seems to be the major source of false positives (Chandola et al. 2009). The first algorithm to find time series discords, Heuristically Order Time series using Symbolic Aggregate Approximation (HOTSAX), required a worst-case $O\left( {n^{2} } \right)$ distance comparisons but was efficient in the average case. A later algorithm was discovered that required only worst-case $O\left( n \right)$ distance comparisons (albeit, with a high constant factor (Yankov et al. 2008)). Unfortunately, that algorithm requires the triangular inequality property, which is not satisfied by the DTW distance.

The reader will appreciate that an “inversion” of the SWAMP algorithm may help here. We can quickly compute the ED Matrix Profile, which is an upper bound to the DTW Matrix Profile. We can then find the highest value and compute its DTW nearest neighbor with any fast DTW subsequence search method (we use the UCR suite (Rakthanmanon et al. 2013)). This reduced distance is our best-so-far (higher the better, the reverse of motif discovery). If this value is greater than all other locations in the ED Matrix Profile, then we have discovered the top-1 DTW discord. If not, we can examine the next highest value in the ED Matrix Profile and prune all locations on the ED MP that are below the current best-so-far. We repeat this process until there are no more qualifying candidates, at which point we are assured that we have found the true DTW discord. The algorithm in Table 4 formalizes this process.

Table 4 DTWDiscordDiscovery: finds the top-1 discord using DTW

In line 1 we compute the classic Matrix Profile for the time series T with the given subsequence length m. At this moment, the value of the best-so-far is initialized to zero. Using this Matrix Profile, we find the highest values, i.e. ED discord (line 6). We then measure the distance between the discord and its nearest neighbor under Dynamic Time Warping (DTW) (line 9) and prune all locations in the ED Matrix Profile that are above this value (line 10). If the DTW distance for the region indicated by the highest value of Matrix Profile is greater than the best-so-far, we update the best-so-far. We repeat the same process with the next highest value in ED Matrix Profile (line 15). The algorithm ends when there are no regions in the ED Matrix Profile that have higher values than the best-so-far (lines 16–18).

To demonstrate the utility of this algorithm, we created a toy problem as shown in Fig. 40. This time series is a good model for the walking or running gait cycle; it is periodic, but not exactly so. There is an embedded anomaly inside the time series at location 1990 (highlighted in green). The anomaly is simply a dropped value. We can say it is a “true” anomaly in the sense that if we assume the time series was a gait cycle, the abrupt change would correspond to an acceleration that could not be achieved by a bullet, much less a human limb. The classic Matrix Profile does not find the induced anomaly as the top discord. According to the ED, the top discord is at 1261 (highlighted in red). However, the DTW discord discovery algorithm finds the discord to be in top place.

Fig. 40

(Top) The discord at location 1990 (shown in green) was discovered by DTW. However, ED finds the discord to be at location 1261 (shown in red). (Bottom) A zoom-in of the region that happens to contain the top-1 DTW motif and ED motif (Color figure online)

This tells us that if we have a fast way to discover the top DTW discord, same as the top DTW motif, then we also have a superior algorithm to ED in finding the discords. As we shall show in Fig. 41 our DTW discord discovery algorithm allows such fast computations.

Fig. 41

Only a tiny fraction of the pairs need to be compared using DTW before finding the discord. For all warping window sizes, the DTW calculation rate is below 10%

As Fig. 41 shows, for different sizes of the warping window, less than 10% of the pairs need to be compared using DTW, i.e. more than 90% of the pairs can be pruned from the search space. The maximum time needed to calculate DTW distance between a pair of subsequences with UCR suite in this dataset is 0.0001 s. The maximum time needed to calculate the ED Matrix Profile is 0.28 s. Overall, the maximum time needed to find the top discord is about 0.62 s on average which is about 143.2 speed up over the time to compute the brute force DTW Matrix Profile.

7.1 Respiratory data exploration with discords

We consider the problem of finding anomalies in respiration data. We investigated a time series showing a patient’s respiration (measured by thorax extension), as they wake up. We chose a discord length of 256. In Fig. 42, we see the outcome of the experiment.

Fig. 42

The top-1 discords found in a time series of a patient’s respiration as they wake up, using both ED (red) and DTW (green) (Color figure online)

As Fig. 42 shows, using only a small warping window (of size 2), we are able to find a meaningful discord in this time series. The discord found by DTW (highlighted in green) corresponds to shallow breaths that indicated the transition of sleeping states. However, the discord found by ED (highlighted in red) does not correspond to any anomalies.

8 Conclusion and future work

We have introduced SWAMP, the first practical tool to find DTW-based motifs in large datasets. Moreover, we have shown that on many real datasets, DTW returns more meaningful motifs than Euclidian distance-based motifs.

SWAMP offers many avenues for improvement. The time the classic Matrix Profile algorithms takes depends only on n, thus it is possible to know how long it will take to find the motifs and build a perfectly accurate progress bar for an interactive tool. In contrast, the time required for SWAMP depends on m, w and the data itself. We would like to be able to tell the user (at least approximately) how long our algorithm will take to finish.

The time for brute force DTW motif discovery is completely dominated by the cost of computing DTW. However, SWAMP is dominated by the time computation of the lower bounds. There has been little effort to optimize the time needed to compute these bounds, because they are most commonly used for disk-based indexing, which is itself dominated by I/O costs. Thus, we suspect that lower bounds computation may be amiable to many further algorithmic and implementation optimizations. Such optimizations could be trivially plugged into SWAMP to improve its performance. We also plan to explore the possibility of framing SWAMP as an anytime algorithm (Zhu et al. 2018).

Appendix

1.1 Reproducibility

We have taken extraordinary steps to make sure that every experiment (including the figures and samples that proceed the official experimental section) are easy to reproduce. To this end:

• For experiments that have a stochastic element, we initialize with the same random number generator seed before each iteration. This ensures that a reader can exactly reproduce our output, independent of their platform.

• Every data used in each figure or table is explicitly labeled with the name of the figure/table and archived at Alaee (2020) in a universally readable ASCII plain text format, in addition to the.mat format that we use internally.

• We have created a presentation that gives additional information about anything we did to create our final figures. For example, purely for aesthetic reasons, we “flipped” one of the dendrograms shown in Fig. 3 upside down (without changing its topology or distances). The presentation reconciles the slight differences between the output of the code, and the final figures.

• In addition to the main code, we have included all the minor code, including the code to produce dendrograms, etc.

For many experiments we choose to use time series and query lengths that are powers of two. This is not required for SWAMP but is a consideration for future researchers who may try to improve on our results with either DFT or DWT methods, both of which have their best cases when the data lengths are powers of two.

As noted in the paper but reiterated here, in many works, the size of the warping window is often given as a percentage of the length of the time series (Keogh and Ratanamahatana 2005; Ratanamahatana and Keogh 2005), in this work we give it as an absolute number. One reason for this is because a given percentage may not evenly divide a time series length, and different rounding policies may affect the results.

Where warranted, we presented some details in the paper very tersely. For example, we noted in the main text:

Finally, we compared to Silva and Batista (2018), which is the only other exact algorithm for finding DTW motifs. On the three datasets above this algorithm was 17,274%, 185,511% and 13,857% respectively.

The details are a little sparse in that text. However:

• The differences are so large that we hope the reader will understand our decision not to spend too much of the page limits here.

• The full detailed results are available at Alaee (2020), together with the full code and data needed to reproduce the results.

Here we note that this comparison was completely fair. We used the exact same computer, same datasets, and same implementations of all common subroutines, including the various lower bounds, ED and DTW comparison algorithms, etc. Moreover, we further optimized the original algorithm extensively. The original algorithm finds both discords and motifs under DTW, but we made it faster by removing the need to find discords, and only requiring it to find the top-1 motif.

Likewise, our comparison to brute-force search was rigorously fair. There are many ways to make a DTW-based algorithm perform poorly. For example, one could implement the rival method using the recursive version of DTW instead of the iterative version. The recursive version of DTW is one to two orders of magnitude slower than the iterative version. However, here we again used the exact same computer, same datasets, and most importantly same implementations of all common subroutines, including the various lower bounds, ED and DTW comparison algorithms.

1.1.1 A reproducibility “ROSETTA STONE”

As noted above, we have made all our code publicly available in perpetuity (Alaee 2020). However, a reader may wish to implement and test our ideas on another platform. If we both agree on all distance measures, including the Euclidean distance, cDTW distance and parametrized lower bounds, then we can be virtually assured that all other steps will be in agreement. It may seem unlikely that we could disagree on such matters. However, our experience suggests otherwise. For example, we have seen the w parameter in cDTW interpreted as the total freedom to wander off the diagonal. In essence, that (mis)understanding will give only half the w value that we mean to communicate (and is more commonly understood (Rakthanmanon et al. 2013)). Likewise, by default, some DTW programs normalize the distance by the path length. This makes only a very subtle difference when w is small, nevertheless it could cause our lower bounds to no longer be admissible. Thus, in order to make sure we agree on all measures, in Table 5 we will create a pair of time series that the interested reader can literally cut-and-paste into their framework and compare results on all measures.

Table 5 A pair of calibration time series

Note that after we z-normalized these time series, we rounded them to have just two significant digits, in order to further facilitate a detailed forensic tracing of the computation. However, this rounding means that the two time series are no longer exactly z-normalized. All subsequent analysis assumes the exact values in Table 5.

In Fig. 43 we show a visual intuition for the various measures that are key to this work. The Euclidean distance ED(Q,T) is 7.88098.

Fig. 43

(Top to bottom) For the two time series listed in Table 1, a visual intuition that shows: the Euclidean distance, the cDTW, the classic LB_Keogh lower bound, and the reduced dimensionality LB_Keogh lower bound

Recall that in our implementation we perform the optimization of not using the squared root function (see Sect. 4.1.1 of Rakthanmanon et al. 2013). However, we ignore that optimization here. Using a value of eight for the warping parameter w, cDTW(Q,T) is 2.4240. The value of Keogh’s classic lower bound, in our notation LB_Keogh1:1(Q,T), is 1.5865. It is important to recall that this function is not symmetric, in general LB_Keogh1:1(Q,T) ≠ LB_Keogh1:1(T,Q). Finally, Fig. 43.bottom illustrates the four-fold reduced lower bound, LB_Keogh4:1(Q,T), which has a value of 0.4999.

Note that LB_Keogh4:1(Q,T) ≤ LB_Keogh1:1(Q,T) ≤ cDTW(Q,T) ≤ ED(Q,T) as we should expect.