Discovering outlying aspects in large datasets

Abstract

We address the problem of outlying aspects mining: given a query object and a reference multidimensional data set, how can we discover what aspects (i.e., subsets of features or subspaces) make the query object most outlying? Outlying aspects mining can be used to explain any data point of interest, which itself might be an inlier or outlier. In this paper, we investigate several open challenges faced by existing outlying aspects mining techniques and propose novel solutions, including (a) how to design effective scoring functions that are unbiased with respect to dimensionality and yet being computationally efficient, and (b) how to efficiently search through the exponentially large search space of all possible subspaces. We formalize the concept of dimensionality unbiasedness, a desirable property of outlyingness measures. We then characterize existing scoring measures as well as our novel proposed ones in terms of efficiency, dimensionality unbiasedness and interpretability. Finally, we evaluate the effectiveness of different methods for outlying aspects discovery and demonstrate the utility of our proposed approach on both large real and synthetic data sets.

1 Introduction

In this paper, we address the problem of investigating, for a particular query object, the sets of features (a.k.a. attributes, dimensions) that make it most unusual compared to the rest of the data. Such a set of features is termed a subspace or an aspect. In recent works, this problem was also named outlying subspaces detection (Zhang et al. 2004), promotion analysis (Wu et al. 2009), outlying aspects mining (Duan et al. 2015), outlier explanation (Micenkova et al. 2013), outlier interpretation (Dang et al. 2014), or object explanation (Vinh et al. 2014b). It is worth noting, however, that this task is not limited to query objects being outliers, as in Zhang et al. (2004), Micenkova et al. (2013). Also, the outlying aspects need not be restricted to ‘good’ (i.e., favorable) characteristics, as in promotion analysis (Wu et al. 2009). Indeed, it has many other practical applications where the query can be just any regular object, with outlying aspects being potentially ‘bad’ (i.e., unfavorable) characteristics. For example, a sports commentator may want to highlight some interesting aspects of a player or a team in the most recent seasons, e.g., Alice scored many goals compared to the other defenders. A selection panel may be interested in finding out the most distinguishing merits of a particular candidate compared to the rest of the applicant pool, for instance, among other students with a similar GPA, Bob has far more volunteering activities. An insurance specialist may want to find out the most suspicious aspects of a particular claim, for example, the claim comes from Carol, a customer who made many more claims among all those who possess the same type of vehicle. A doctor may want to examine, for a cancer patient, the symptoms that make him/her most different from other cancer patients, thus potentially identifying the correct cancer sub-type and coming up with the most appropriate medical treatment. A home buyer will be very interested in features that differentiate a particular suburb of interest from the rest of a city.

Although having a close relationship with the traditional task of outlier detection, outlying aspects mining has subtle but crucial differences. Here, we only focus on the query object, which itself may or may not be an outlier with respect to the reference dataset. In contrast, outlier detection scans the whole dataset for all possible unusual objects, most often in the full space of all attributes. Current outlier detection techniques do not usually offer an explanation as to why the outliers are considered as such, or in other words, pointing out their outlying aspects. As discussed, outlier explanation could be used, in principle, to explain any object of interest to find any outlying characteristic (not necessarily just ‘good’ characteristics). Thus, in our opinion, the term outlying aspects mining as proposed in Duan et al. (2015) is more general. Outlying aspects mining can be considered as a task that is complementary to, but distinct from, outlier detection. More discussion on the differences between the current work on outlier detection and the novel task of outlying aspects mining can be found in Duan et al. (2015).

The latest work on outlying aspects mining tackles the problem from two different angles, which we refer to as the feature selection based approach and the score-and-search approach. In the feature selection based approach, the problem of outlying aspects mining is transformed into the classical problem of feature selection for classification. In score-and-search, it is first necessary to define a measure of the outlyingness degree for an object in any specified subspace. The outlyingness degree of the query object will be compared across all possible subspaces, and the subspaces that score the best will be selected for user further inspection.

While progress has been made in the area of outlying aspects mining, in our observation, there are still significant challenges to be solved:

• For feature selection based approaches existing black-box feature selection methods, as employed in Micenkova et al. (2013), are often not flexible enough to generate multiple outlying subspaces if requested by the user. Similarly, feature extraction approaches, as in Dang et al. (2014), generally suffer from reduced interpretability, nor do they offer multiple alternative explanatory subspaces.

• For score-and-search approaches the question of how to design scoring functions that are effective for comparing the outlyingness degree across subspaces without dimensionality bias remains open. In the next section we show that the existing scoring functions may not be always effective nor efficient in evaluating outlyingness. Furthermore, the question of how to efficiently search through the exponentially large sets of all possible subspaces is a long-standing challenge shared by other problems involving subspace search, such as feature subset selection (Vinh et al. 2014b, a), subspace outlier detection (Aggarwal and Yu 2001; Kriegel et al. 2009; Keller et al. 2012) and contrast subspace mining (Nguyen et al. 2013; Duan et al. 2014).

In this paper, we make several contributions to advancing the outlying aspects mining area. We formalize the concept of dimensionality-unbiasedness and characterize this property of existing measures. We propose two novel scoring functions that are proven to be dimensionally unbiased, suitable for comparing subspaces of different dimensionalities. The first metric, named the Z-score, is a novel and effective strategy to standardize outlyingness measures to make them dimensionally unbiased. The second metric, named the isolation path score, is computationally very efficient, making it highly suitable for applications on large datasets. To tackle the exponentially large search space, we propose an efficient beam search strategy. We demonstrate the effectiveness and efficiency of our approach on both synthetic and real datasets.

2 Related work

In this section, we first give a broad overview on the topic of outlier explanation, which is a special case of outlying aspects mining. Next, we look deeper into several recent works that are closely related to ours.

2.1 Overview on outlier explanation

The vast majority of research in the outlier detection community has focused on the detection part, with much less attention on outlier explanation. Though there are also outlier detection methods that provide implicit or explicit explanations for outliers, such explanations are commonly a by-product of the outlier detection process.

A line of methods that offer implicit explanation involves identifying outliers in subspaces. Subspace outlier detection identifies outliers in low dimensional projections of the data (Aggarwal and Yu 2001), which can otherwise be masked by the extreme sparsity of the high-dimensional full space. High Contrast Subspace (HiCS) (Keller et al. 2012) and CMI (Nguyen et al. 2013) identify high contrast subspaces where non-trivial outliers are more likely to exist.

Another line of methods offer explicit explanation for each outlier. The work of Micenkova et al. (2013) is such an example, which identifies subspaces in which the outlier is well separated from its neighborhood using techniques from supervised feature selection. Similarly, the subspace outlier degree (SOD) method proposed by Kriegel et al. (2009) analyze how far each data point deviate from the subspace that is spanned by a set of reference points. Local outliers with graph projection (LOGP) finds outliers using a feature transformation approach and offers an explanation in terms of the feature weights in its linear transformation (Dang et al. 2014). Similarly, the local outlier detection with interpretation (LODI) method proposed by Dang et al. (2013) seeks an optimal subspace in which an outlier is maximally separated from its neighbors.

All the above works focus on the numerical domain. For nominal or mixed database, frequent pattern based outlier detection methods such as that proposed by He et al. (2005) can offer interpretability, as the outliers are defined as the data transactions that contain less frequent patterns in their itemsets. Wu et al. (2009) developed a technique to find the desirable characteristics of a product for effective marketing purposes. More recently, Smets and Vreeken (2011) proposed a method for identifying and characterizing abnormal records in binary or transaction data using the Minimum Description Length principle.

It is noted that most of the above mentioned methods do not offer explicit mechanisms to handle a particular query. Furthermore, the subspaces are sometimes found using all possible outliers, and thus the explanation may not be tailored for the object of interest.

2.2 An in-depth review of recent works

In this section, we review several recent works on outlying aspects mining in greater detail and discuss their relative strengths and weaknesses, which will serve as motivation for our work in the subsequent sections. The notation we use in this paper is as follows. Let $\mathbf {q}$ be a query object and $\mathbf {O}$ be a background dataset of n objects $\{\mathbf {o}_1,\ldots ,\mathbf {o}_n\}$, $\mathbf {o}_i\in \mathbb {R}^d$. Let $\mathcal {D}=\{D_1,\ldots ,D_d\}$ be a set of d features. In this work we focus on numeric features. A subspace $\mathcal {S}$ is a subset of features in $\mathcal {D}$.

2.2.1 Score-and-search methods

The earliest work to the best of our knowledge that defines the problem of detecting outlying subspaces is HOS-Miner (HOS for High-dimensional Outlying Subspaces) by Zhang et al. (2004). Therein, the authors employed a distance based measure termed the outlying degree (OD), defined as the sum of distances between the query and its k nearest neighbors:

$$\begin{aligned} OD _\mathcal {S}(\mathbf {q})\triangleq \sum _{i=1}^k Dist _\mathcal {S}(\mathbf {q},\mathbf {o}_i),\ \mathbf {o}_i \in kNN _\mathcal {S}(\mathbf {q}) \end{aligned}$$

(1)

where $Dist _\mathcal {S}(\mathbf {q},\mathbf {o}_i)$ is the Euclidean distance between two points in subspace $\mathcal {S}$, and $kNN _\mathcal {S}(\mathbf {q})$ is the set of k nearest neighbors of $\mathbf {q}$ in $\mathcal {S}$. HOS-Miner then searches for subspaces in which the $OD$ score of $\mathbf {q}$ is higher than a distance threshold $\delta$, i.e., significantly deviating from its neighbors. HOS-Miner exploits a monotonicity property of the $OD$ score, namely $OD _{\mathcal {S}_1}(\mathbf {q})\le OD _{\mathcal {S}_2}(\mathbf {q})$ if $\mathcal {S}_1 \subset \mathcal {S}_2$, to prune the search space. More specifically, this monotonicity implies that if the query is not an outlier in a subspace $\mathcal {S}$, i.e., $OD _\mathcal {S}(\mathbf {q})<\delta$, then it cannot be an outlier in any subset of $\mathcal {S}$–and so we can exclude all subspaces of $\mathcal {S}$ from the search. On the other hand, if the query is an outlier in the subspace $\mathcal {S}$, i.e., $OD _\mathcal {S}(\mathbf {q})>\delta$, then it will remain an outlier in any subspace that is a superset of $\mathcal {S}$–and so we can exclude all subspaces that are a superset of $\mathcal {S}$ from the search. Although the monotonicity property of the distance measure with regards to the number of dimensions is desirable in designing efficient search algorithms, it is unfortunately the property one wants to avoid when subspaces of different dimensionalities are to be compared. The reason is because there is a bias towards subspaces of higher dimensionality, as distance monotonically increases when more dimensions are added.

In a recent work, Duan et al. (2015) propose OAMiner (for Outlying Aspects Miner), which employs a kernel density measure for quantifying outlyingness degree:

$$\begin{aligned} f_\mathcal {S}(\mathbf {q})\triangleq \frac{1}{|\mathbf {O}|(2\pi )^{|\mathcal {S}|/2} \prod _{D_i\in \mathcal {S}} h_{D_i} } \sum _{\mathbf {o}\in \mathbf {O}} e^{-\sum _{D_i\in \mathcal {S}} \frac{(\mathbf {q}.D_i-\mathbf {o}.D_i)^2 }{2h^2_{D_i}} } \end{aligned}$$

(2)

Here, the scoring metric $f _\mathcal {S}(\mathbf {q})$ is a kernel density estimate of $\mathbf {q}$ in $\mathcal {S}$ using a product of univariate Gaussian kernels (which is equivalent to a $|\mathcal {S}|$-dimensional kernel with a diagonal covariance matrix), with $h_{D_i}$ being the kernel bandwidth and $\mathbf {q}.D_i$ being the value of $\mathbf {q}$ in feature $D_i$. They stated that the density tends to decrease as dimensionality increases, thus higher dimensional subspaces might be preferred. To eliminate this dimensionality bias, they propose to use the density rank of the query as a quality measure. That is, for each subspace, the density of every data point needs to be computed from which a ranking will be tabulated. Subspaces in which the query has the best rank are then reported.

The density rank exhibits no systematic bias w.r.t. dimensionality, i.e., adding more attributes to an existing subspace can either increase or decrease the ranking of the query. This desirable property comes with two fundamental challenges: (i) the density rank is a much more computationally expensive measure, as the density of every point in the data set needs to be computed for the global ranking to be established, resulting in a complexity of $O(n^2d)$, (ii) because of the non-monotonicity of the quality measure, there is no efficient way to prune the search space, thus an expensive exhaustive search is necessary. Duan et al. (2015) overcome these difficulties by (a) introducing a bounding method where the density rank of the query can be computed without exhaustively computing the density rank of all other points, and (b) only exhaustively searching the subspaces up to a user-defined maximum dimensionality. Despite these improvements, scaling up OAMiner is still a major challenge. Apart from computational inefficiency, another probably more fundamental concern with the density rank is whether the rank statistic is always the appropriate outlyingness measure for comparing different subspaces, as illustrated in the following example.

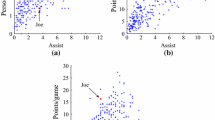
Example 1

Ranking does not preserve absolute degree of deviation Although in subspace {$D_1,D_2$} (Fig. 1a), the query point (red square) is ranked the first in terms of kernel density measure in equation (2), users could possibly be more interested in subspace {$D_3,D_4$} (Fig. 1b), where the query point only ranks the 5th, but deviates markedly from the norm. Thus, while the rank provides a normalized measure for comparing densities across subspaces, important information regarding the absolute degree of deviation is lost.

Fig. 1

Is the rank statistic most appropriate for comparing subspaces?. a Subspace {$D_1,D_2$}. b Subspace {$D_3,D_4$}

2.2.2 Feature selection/transformation approaches

The first feature selection based approach for mining outlying aspects was introduced in Micenkova et al. (2013). Outlying aspects mining, or the outlier explanation problem as termed therein, is cast as a two-class feature selection problem. More specifically, for each outlier (query point) $\mathbf {q}$, a positive class is constructed with synthetic samples drawn from a Gaussian $\mathcal {N}(\mathbf {q},\lambda ^2\mathbf {I})$ distribution, where $\lambda =\alpha \cdot \frac{1}{\sqrt{d}}\cdot k\text{-distance }(\mathbf {q})$, with $k\text{-distance }(\mathbf {q})$ being the distance from $\mathbf {q}$ to its k-th nearest neighbor. Here, each feature is assumed to be normalized to [0, 1], hence $\sqrt{d}$ is the upper bound on the distance between any two points. The parameter $\alpha$ controls the spread of the positive population while normalization by $\sqrt{d}$ is intended to ensure that $\alpha$ has the same effect in subspaces of different dimensionality. In their experiments, Micenkova et al. (2013) found $k=35$ and $\alpha =0.35$ to work well. The negative class is formed by a sub-sample formed by the k nearest neighbors of $\mathbf {q}$ in the full feature space, plus another k random samples from the rest of the data, for a total of 2k points. The number of positive and negative samples are matched, so that the classification problem is balanced.

While the feature selection based approach was shown to work well, two remarks are in order. First, the k-nearest neighbors in the full space may be significantly different, or even totally different, from the k-nearest neighbors in the subspace. This is especially true when the full space is of high dimensionality while the subspace has low dimensionality, which is the case in outlying aspect mining—we are more interested in low-dimensional subspaces for better interpretability. In Fig. 2a we plot the average percentage of common k nearest neighbors ($k=35$) between the full space and random subspaces of 3 dimensions, with the queries being randomly chosen from a standard Gaussian population of 1000 points. As expected, the proportion of shared nearest neighbors steadily decreases as the dimensionality of the full space increases. Thus, the k-nearest neighbors in the full space are not necessarily representative of the locality around the query in the subspaces. There could be situations where the query appears to be well separated from its k-nearest full-space neighbors, while in fact not being well separated from its subspace neighborhood. Following the same feature selection approach, Vinh et al. (2014b) instead chose to keep the whole dataset as the negative class, while over-sampling the synthetic positive class. The disadvantage of this approach is reduced scalability compared to the sampling approach adopted by Micenkova et al. (2013).

Fig. 2

Pitfalls of nearest neighbors and synthetic samples. a Subspace kNN and full-space kNN become less similar as the dimensionality of the full space increases. b The synthetic positive population heavily overlaps with the nearby cluster of inliers in this subspace

The second potential drawback of a feature selection based approach is with regard to the spread of the positive synthetic distribution. As proposed in Micenkova et al. (2013), the variance of the positive distribution is the same in every dimension and is determined based on $k\text{-distance }(\mathbf {q})$—the distance from $\mathbf {q}$ to its k-th nearest neighbor—in the full space. This choice is expected to affect all subspaces equally. However, in our opinion, some subspaces may be affected by this setting more than others, for example, subspaces in which the query is a local outlier with respect to its neighborhood, as in Fig. 2b. The spread of the positive population is determined based on a statistic in the full-space irrespective of the characteristics of the subspace. As such, although the subspace in Fig. 2b is a good explaining subspace (for the query clearly being a local outlier), the feature selection approach may eventually rule out this subspace as the positive synthetic examples (of which the standard deviation is represented by the red circle) heavily overlap with the negative examples.

Dang et al. (2014) recently introduced Local Outliers with Graph Projection (LOGP). LOGP is an outlier detection method that offers outlier explanation at the same time. More specifically, for each data point, LOGP seeks a linear transformation in which that point is maximally separated from its nearest full-space neighbors. Then, in that transformed space, an outlier score is computed for that point as the statistical distance from the point to its neighbors. Finally, the outlier scores for all objects are sorted to identify the outliers. As for outlier explanation, the weight vector in the linear transformation can be employed to sort the features according to their degree of contribution to the outlyingness of the point. Dang et al. (2014) suggested taking the features corresponding to the largest absolute weight values accounting for $80\,\%$ of the total absolute weight. LOGP can be straightforwardly applied in the context of outlying aspects mining for finding the most outlying subspace of the query. A critical observation regarding LOGP is that, similar to the feature selection approach, LOGP also attempts to separate the query from its full-space neighborhood. Again, we note that the neighborhood in the full space can be significantly different to the neighborhood in the subspace (cf. the example in Fig. 2a). In such cases, using the full space as a ‘reference point’ to predict what will happen in subspaces can be misleading.

Compared to score-and-search based methods, the major advantage of feature transformation/selection approaches is that they often do not perform an explicit search over the space of all subspaces, thus are generally faster. However, this also entails a major drawback in that such methods generally cannot provide alternative solutions, i.e., a list of high-ranked subspaces, if requested by the user. Furthermore, we point out that the issue of feature redundancy should be handled differently in the two paradigms: feature selection for classification versus feature selection for outlying aspects mining. In the former, feature redundancy can reduce classification accuracy (Peng et al. 2005), while in the latter, feature redundancy does not necessarily reduce interpretability. None of the previous feature selection approaches considers this issue.

3 Problem definition

Before developing new measures and algorithms for outlying aspects mining, we formalize the problem, by defining the following concepts.

Definition 1

Top k-outlying subspaces: Let $\rho _\mathcal {S}(\mathbf {q})$ denote an outlyingness scoring function that quantifies the outlyingness degree of the query $\mathbf {q}$ in a subspace $\mathcal {S}$. The top k-outlying subspaces are the k subspaces in which the query deviates most from the rest of the data, as ranked by the scoring function $\rho (\cdot )$.

Note that in this definition, the ranking is carried out on the subspaces. The degree of deviation might be either sufficient or insufficient to declare the query to be a subspace outlier. Such a declaration is not our main interest, however. It is our focus to identify the top k-outlying subspaces, ranked by the degree of deviation of the query for user inspection. Further, we categorize the features into 3 non-overlapping groups as follows:

Definition 2

Feature classification: Given an outlyingness scoring function $\rho (\cdot )$ and a percentile ranking threshold $\epsilon \in [0,1]$,

• 1. A trivial outlying feature $D_i$ is an individual feature in which the query $\mathbf {q}$’s outlyingness score is ranked within the top $(\epsilon \times 100)$% among all the data points according to $\rho _{D_i}(\cdot )$.

• 2. The top-k non-trivial outlying subspaces are subspaces which (a) comprise no trivial outlying features and (b) have the top-k highest outlyingness score, as ranked by $\rho (\cdot )$, amongst all the possible subspaces. A feature is called a non-trivial outlying feature if it forms part of at least one top-k non-trivial outlying subspace.

• 3. Inlying features are features that are not trivial outlying features, nor do they form part of any top-k non-trivial outlying subspace.

This explicit categorization will be helpful in guiding our subsequent approaches. Indeed, we now propose that trivial outlying features should be discovered first (using a likely straightforward approach), then taken out of the data, leaving only non-trivial outlying features and inlying features. The rationale for this proposal is as follows. First, trivial outlying features by themselves have high explanatory value for the users, as they can be easily visualized and interpreted. In a trivial outlying feature, the query either has an extreme value, or lies deep within the data but far away from any nearby clusters. Coupling trivial outlying features with other features can potentially increase confusion and false discoveries. An illustration is in Fig. 3a. The feature $D_1$ is a trivial outlying aspect w.r.t. the query. This can be seen by observing the histogram of $D_1$ alone. When coupled with another (either non-trivial outlying or inlying) feature $D_{10}$, the resulting subspace will still likely have a good outlyingness score for the query, but this does not offer any additional insight. Second, when a trivial outlying feature exists, the top scoring subspace list can be swamped with different combinations of that trivial feature with other features, thus preventing the discovery of other interesting subspaces.

Example 2

Effect of trivial outlying features We take the UCI Vowel data set with $n=990$ objects in $d=10$ features (data details given in Sect. 7.4). We then linearly scale and shift all features to the range [0,1] and pick a random data point as the query. For the query, we artificially increase its value in feature $D_1$ to 1.1 (i.e., outside the [0,1] range). Thus, it can be seen that $D_1$ is a trivial outlying feature for the query. We then employ the density rank measure (Duan et al. 2015) and carry out an exhaustive search over all subspaces of up to 5 features. The top-10 outlying subspaces for the query are $\{D_1\}$, $\{D_1,D_{10}\}, \{D_1,D_9\}, \{D_1,D_7\}, \{D_1,D_6\}, \{D_1,D_2, D_3\}, \{D_1,D_4\},\{D_1,D_3\}$ and $\{D_1,D_2\}$, which are all combinations of $D_1$ and other features. When $D_1$ is explicitly identified and removed, using the same search procedure, other outlying subspaces can be revealed, for example, $\{D_3, D_6, D_9\}$ in Figure 3b.

Fig. 3

Trivial outlying features can hinder the discovery of interesting outlying subspaces. a Combination of a trivial outlying feature and other features likely results in highly-scored subspaces. b A non-trivial outlying subspace for the query discovered after $D_1$ is removed

4 Outlyingness scores

As measures for outlyingness, one can consider a variety of scoring metrics in the current outlier detection literature. Before considering several such measures, we discuss several desiderata that a measure should possess in the context of outlying aspects mining.

4.1 Desiderata

• (i) Dimensionality unbiasedness As outlyingness measures are used to compare subspaces of potentially different dimensionalities, an ideal measure should have no bias towards any dimensionality. An example of a dimensionally biased measure is the Outlying Degree (OD) score built upon the Euclidean distance employed in Zhang et al. (2004), which monotonically increases as dimensionality increases, thus it is biased towards higher dimensional subspaces.

Definition 3

Monotonic scoring function: An outlyingness scoring function $\rho (\cdot )$ is monotonically increasing (decreasing) w.r.t. dimensionality if $\rho _{\mathcal {S}_1}(\mathbf {q})\ge \rho _{\mathcal {S}_2}(\mathbf {q})$ (respectively $\rho _{\mathcal {S}_1}(\mathbf {q})\le \rho _{\mathcal {S}_2}(\mathbf {q})$), where $\mathcal {S}_1\supset \mathcal {S}_2$, for all queries.

Theorem 1

The outlying degree defined in equation (1) using the Euclidean distance is a monotonically increasing scoring function.

This result is straightforward, given that the Euclidean distance is a monotonic measure, in the sense that $Dist _{\mathcal {S}_1}(\mathbf {q},\mathbf {o})\ge Dist _{\mathcal {S}_2}(\mathbf {q},\mathbf {o})$ if $\mathcal {S}_1\supset \mathcal {S}_2$. The kernel density measure defined in (2), on the other hand, is not a monotonic measure. Despite the common belief that the density tends to decrease as dimensionality increases, the kernel density measure can actually increase with dimensionality. To see this, we note that the kernel density in (2) can be rewritten as a sum of distance-like terms:

$$\begin{aligned} f_{\mathcal {S}}(\mathbf {q})=\frac{1}{n}\sum _{\mathbf {o}\in \mathbf {O}}\left( \frac{ e^{-\sum _{D_i\in \mathcal {S}} \frac{(\mathbf {q}.D_i-\mathbf {o}.D_i)^2 }{2h^2_{D_i}} }}{(2\pi )^{|\mathcal {S}|/2} \prod _{D_i\in \mathcal {S}}h_{D_i} }\right) \end{aligned}$$

(3)

where the kernel density values in the parentheses can be considered as the ‘distances’ between $\mathbf {o}_i$’s and $\mathbf {q}$. Now note that

$$\begin{aligned} f_{\mathcal {S}\cup D_j } (\mathbf {q})=\frac{1}{n}\sum _{\mathbf {o}\in \mathbf {O}}\left( \frac{ e^{-\sum _{D_i\in \mathcal {S}} \frac{(\mathbf {q}.D_i-\mathbf {o}.D_i)^2 }{2h^2_{D_i}} }}{(2\pi )^{|\mathcal {S}|/2} \prod _{D_i\in \mathcal {S}}h_{D_i} }\right) \cdot \frac{e^{\frac{-(\mathbf {q}.D_i-\mathbf {o}.D_i)^2}{2h^2_{D_j}}}}{ (2\pi )^{1/2} h_{D_j}} \end{aligned}$$

(4)

is a weighted sum of ‘distances’. Note further that the kernel density value in the newly added dimension $D_j$, i.e., $(\sqrt{2\pi } h_{D_j})^{-1}e^{\frac{-(\mathbf {q}.D_i-\mathbf {o}.D_i)^2}{2h^2_{D_j}}}$, unlike probability mass, is not restricted to lie within [0, 1] and in fact can be much larger than 1, hence increasing the density value. While the kernel density is not a monotonic function w.r.t. dimensionality, its values can be orders of magnitude different in scale at different dimensionalities. To demonstrate this point, let us consider the following example.

Fig. 4

Dimensionality bias: the OD and density measure tend to be biased towards higher dimensionalities. a Mean outlyingness score b Top outlying subspace dimension distribution

Example 3

Effect of dimensionality We generate a 10-dimensional data set of 1000 points, with 10 equal-sized spherical Gaussian clusters with random mean in $[0,1]^{10}$ and diagonal covariance matrix $\sigma \mathbf {I}_{10~\times ~10}$ with $\sigma \in [0,1]$. We randomly choose 10 d-dimensional subspaces for d from 1 to 10. For each subspace, we compute the average OD score and log kernel density score for all data points. The mean average scores over 10 subspaces at different dimensionalities are presented in Figure 4a, where the outlying degree is monotonically increasing while the kernel density is monotonically decreasing. Next, using the Outlying Degree, kernel density and density rank as the scoring functions, for each data point in turn being designated as the query, we carried out an exhaustive search on subspaces of up to 5 dimensions to find out the top outlying subspace for each query. The dimensionality distribution of the top subspaces according to each scoring function is presented in Figure 4b, where it can be observed that both the outlying degree and kernel density exhibit a bias towards higher-dimensional subspaces. The density rank measure, on the other hand, shows a more balanced result set, with top-scoring subspaces being present in considerable number at each dimensionality.

• (ii) Efficiency As search algorithms will likely have to search through a large number of subspaces, it is desirable for the scoring function to be evaluated efficiently. It is worth noting that certain normalization strategies, such as ranking, require computing the raw outlyingness values of all data points, and thus can be computationally expensive.

• (iii) Effectiveness The scoring metric should be effective for ranking subspaces in terms of the outlierness degree of the query.

• (iv) Interpretability The numeric score given by a measure should be interpretive and easily understood. In this respect, rank-based measures, such as the density rank, are arguably the most interpretable measures. The main drawback of rank-based measures is that the absolute degree of outlierness is lost.

Of these desiderata, efficiency can be formally analyzed in terms of time and space complexity. Effectiveness can be quantitatively assessed when some ground truth is known. Interpretability is arguably a semantic concept that is notoriously evasive to formal analysis and quantification. Thus, we will only be discussing this desideratum qualitatively. Dimensionality unbiasedness is a novel and important concept that was either totally neglected (Zhang et al. 2004) or only casually mentioned in previous work (Duan et al. 2015). We provide a formal description of dimensionality unbiasedness in Sect. 5.

4.2 Existing scoring measures

We next consider several scoring metrics. One of the most popular outlyingness measures is the local outlier factor (LOF) (Breunig et al. 2000). As the name implies, LOF was designed to detect local outliers, i.e., points that deviate significantly from their neighborhood. LOF is built upon the concept of local density: points that have a substantially lower density than their neighbors are considered to be outliers. Since the exact technical definition of LOF is quite intricate, we do not give its definition here. Interested readers are referred to the original work of Breunig et al. (2000).

In the context of outlying aspects mining, LOF has several desired features. First, points lying deep within a cluster, i.e., inliers, have a baseline value of approximately 1 regardless of the subspace dimensionality. This suggests that a normalization scheme such as converting a raw score to ranking, which requires computing the scores for all data points, might not be needed. Second, the LOF for a query can be efficiently computed in $O((nd+n\log n)\cdot (MinPtsUB) ^2)$ time where $MinPtsUB$ is the maximum neighborhood size parameter in LOF. This is the time required to compute the distances from $\mathbf {q}$ to its $MinPtsUB$ neighbors, and the distance from each of these neighbors to their own $MinPtsUB$ neighbors, and also the time required to sort the distances to answer kNN queries. When LOFs for all data points in the data set need to be computed, one can consider some data indexing structure that helps to reduce the computational complexity of kNN queries. However, when the LOF of a single query point is to be computed on demand as in outlying aspects mining, one must also take into account the overhead of building indexing structures. LOF can detect local outliers, i.e., points that deviate significantly from their neighborhood but need not deviate significantly from the whole data set. For high-dimensional data sets, Kriegel et al. (2008) recently introduced the Angle-Based Outlier Detection (ABOD) score. In the context of outlying aspects mining, we focus mainly on subspaces of lower dimensions (for improved interpretability), thus we do not consider ABOD further.

We have already discussed the density rank measure in the previous section. The drawback of the density rank is that while it might be a good measure for comparing different objects in the same subspace, it might not be always relevant for comparing the outlyingness of the same object in different subspaces (c.f. example in Fig. 1). As an alternative for the density rank, we introduce the density Z-score in the next section. We then introduce another novel measure that we term the isolation path score.

4.3 Density Z-score

We propose the density Z-score, defined as:

$$\begin{aligned} Z(f_\mathcal {S}(\mathbf {q}))\triangleq \frac{ {f_\mathcal {S}}(\mathbf {q})-\mu _{f_\mathcal {S}}}{\sigma _{f_\mathcal {S}}} \end{aligned}$$

(5)

where $\mu _{f_\mathcal {S}}$ and $\sigma _{f_\mathcal {S}}$ are, respectively, the mean and standard deviation of the density of all data points in subspace $\mathcal {S}$. A larger negative Z-score corresponds to a lower density, i.e., a possible outlier. As observed in Fig. 1, the density Z-score correctly points out that subspace {$D_3,D_4$} is more interesting than subspace {$D_1,D_2$}. Compared to the density rank, the density Z-score retains some information on the absolute degree of deviation while still being dimensionally-unbiased, with the latter point being demonstrated later in the experiments. The density Z-score is, however, an expensive statistic with $O(n^2d)$ time complexity, requiring the density of every data point to be computed. For the density rank, certain computational shortcuts can be applied to compute the correct ranking just for the query without computing the density (and rank) for all other data points (Duan et al. 2015). This is because the rank is a coarse-grained statistic that does not require precise values for the raw density, but just their relative ordering. However, for the density Z-score it is unlikely that a similar computational shortcut exists.

4.4 The isolation path score

We now introduce a novel scoring function named the isolation path score. This score is inspired by the isolation forest method for outlier detection (Liu et al. 2008). The isolation forest method is built upon the observation that outliers are few and different, and as such they are more susceptible to being isolated. In Liu et al. (2008), an isolation tree is a binary tree with each inner node having a random feature and a random splitting point, and leaf nodes having only a single data point (or identical points). Outliers tend to lie closer to the root, thus having a shorter path length from the root. The isolation forest does not rely on distance computation, thus it is fast. Also, it employs sub-sampling quite aggressively with each tree being suggested to use only 256 examples, which makes it highly scalable. In the context of outlying aspects mining, the motivation for the isolation path score is as follows: in an outlying subspace, it should be easier to isolate the query from the rest of the data (or a data sub-sample). When employing random binary trees as the isolation mechanism, the expected path length from the root should be small. The difference here is that in this context, since we only care about the path length of the query, we focus on building only the path leading to that query point while ignoring other parts of the tree, hence the name isolation path.

The procedure for computing the isolation path length of the query point with respect to a random sub-sample of the data is given in Algorithm 1. This algorithm isolates the query by a series of random binary splits, each divides the data space into two half-spaces, until the query is isolated, or until all the remaining data points, including the query, have the same value in the random feature selected at that stage. In the latter case, the path length is adjusted by an amount of $\zeta (|\mathbf {X}|) =2(\ln |\mathbf {X}| +\gamma ) -2$, where $\gamma \simeq 0.5772$ is the Euler constant. This is the average tree height of a random sample of the same size as the remaining data points (c.f. Sec. 5 Theorem 4). This adjustment takes into account the fact that the more points there are with the same value as the query, the less outlying it is. In order to have an accurate estimation of the path length, we employ an ensemble approach using multiple sub-samples of the original data set and compute the average. This final statistic is called the isolation path score.

Fig. 5

Isolation path illustration. The query is the red square. a A random isolation path for an outlier. b A random isolation path for an inlier (Color figure online)

The working mechanism of the isolation path is illustrated in Fig. 5. In Fig. 5a, the query (red square) is an outlying point in a 2D space $\{x,y\}$. Each split is illustrated as a numbered vertical or horizontal line (corresponding to an x-split or y-split). Each split divides the space into two half-spaces. The half-space that does not contains the query point is discarded, and the process repeats until the query is isolated. The series of splitting operations for Fig. 5a are, {horizontal split-retaining bottom half-space} $\rightarrow$ {vertical split-retaining right half-space} $\rightarrow$ {vertical split-retaining right half-space}. The number of splits is 3. Similarly, in Fig. 5b, 7 splits are needed to isolate a random inlier.

The proposed isolation path score possesses several desired characteristics:

Dimensionality unbiasedness We give a theoretical analysis on dimensionality unbiasedness for the isolation path score in the next section. Dimensionality unbiasedness implies that an expensive standardization scheme such as converting raw scores to a ranking or Z-score is not necessary.

Efficiency the isolation path score is computationally very fast as it requires no distance computation.

Theorem 2

The average-case time complexity of iPath$(\mathbf {X},\mathbf {q})$ on a subsample $\mathbf {X}$ of $n_s$ records is $O(n_s)$, while its worst-case time complexity is $O(n_s^2)$.

Proof

We can define the following recurrence for the average case computational complexity of building a isolation path on $n_s$ samples:

$$\begin{aligned} T(n_s)={\left\{ \begin{array}{ll} 0, &{} \text {if }n_s = 1.\\ n_s + T(\frac{n_s}{2}), &{} \text {if }n_s > 1. \end{array}\right. } \end{aligned}$$

(6)

where we have employed the assumption that by choosing a random data point as a split point, the sample size reduces on average by a factor of 1 / 2 after each split, and in order to realize a split over $n_s$ data points, we need to make $n_s$ comparisons. This is the 3rd case of the master theorem (Cormen et al. 2009), where $a = 1$, $b=2$ and $f(n_s) = n_s$. According to the master theorem, if $T(n_s) = a T(\frac{n}{b}) + f(n)$, $f(n) = \varOmega (n^c)$, $c> \log _b{a}$ and $\exists k < 1$ such as $f(\frac{n}{b}) \le k f(n)$, then $T(n) = O(f(n))$. In our case, $f(n_s) = \varOmega (n_s^c) = \varOmega (n_s)$, $c=1 > \log _b{a} = \log _2{1} = 0$, and $f(\frac{n_s}{b}) = f(\frac{n_s}{2}) = \frac{n_s}{2} = k f(n_s)$, with $k=0.5<1$. Therefore, $T(n_s) = O(n_s)$.

In the worst case, each split separates only 1 data point while the query is the last point to be separated in that sequence. This requires $2+3+\ldots +n=O(n^2)$ comparisons. $\square$

The average time complexity of building an ensemble of T paths is $O(Tn_s)$, while the space complexity is $O(n_s)$. The isolation path score admits a fixed time and space complexity that is independent of the data size and dimensionality.

5 Dimensionality unbiasedness

In this section, we make the first attempt, to the best of our knowledge, to formally capture the concept of dimensionality unbiasedness for outlying aspects mining measures. At a high level, we require unbiased measures to have a baseline value that is independent of dimensionality, or in other words, remaining constant w.r.t. dimensionality. So what constitutes a baseline value?

Before answering this question, we shall briefly digress and consider a similar problem: the problem of adjusting clustering comparison measures for cardinality bias, i.e., bias towards clusterings with more clusters (Vinh et al. 2010). Clustering is a fundamental task in data mining, which aims to group the data into groups (clusters) of similar objects. In order to evaluate the quality of a clustering algorithm, its clustering result can be compared with a ground-truth clustering. For the clustering comparison problem, numerous measures exist. One issue faced by many measures, such as the well-known Rand index, is that their baseline value for the case of no similarity between two clusterings is not a constant. Further, this baseline tends to increase when one or both clusterings have a higher number of clusters. As a result, these measures are biased towards clusterings with higher numbers of clusters. In order to correct different measures for this cardinality bias, several adjusted measures have been introduced, such as the adjusted Rand index, adjusted mutual information (Vinh et al. 2010) and more recently, standardized mutual information (Romano et al. 2014). The commonly adopted methodology for adjustment is by making these measures have a constant baseline value, by subtracting their expected value obtained under a baseline scenario (also termed the null hypothesis) of no similarity between two clusterings. In the baseline scenario, it is assumed that the two clusterings are generated randomly subject to having a fixed number of clusters and number of points in each cluster. As there is clearly no correlation between the two clusterings, an unbiased clusterison comparing measure should have a constant baseline value, independent of the number of clusters.

Similar to the clustering comparison problem, we shall also consider a baseline case in which the data distributes in such a way that there is no greater outlyingness behaviour in higher dimensional spaces. The average value of a measure over all data points in a baseline case is called the baseline value. We require an unbiased score to have a constant baseline w.r.t. the subspace dimensionality. A possible baseline case is when the data is bounded and uniformly distributed. In such a case, it is reasonable to expect that (i) no data point is significantly outlying and (ii) the average outlyingness degree should not increase/decrease as dimensionality increases.

Definition 4

Dimensionality unbiasedness: A dimensionally unbiased outlyingness measure is a measure of which the baseline value, i.e., average value for any data sample $\mathbf {O}=\{\mathbf {o}_1,\ldots ,\mathbf {o}_n\}$ drawn from a uniform distribution, is a quantity independent of the dimension of the subspace $\mathcal {S}$, i.e.,

$$\begin{aligned} E[\rho _\mathcal {S}(\mathbf {q})|\mathbf {q}\in \mathbf {O}]\triangleq \frac{1}{n}\sum _{\mathbf {q}\in \mathbf {O}} \rho _\mathcal {S}(\mathbf {q}) =const.\ w.r.t.\ |\mathcal {S}| \end{aligned}$$

We now prove some dimensionality-unbiasedness results for existing measures. First, we show that the rank and Z-score normalization can turn any measure into a strictly dimensionally-unbiased measure as per Definition 4.

Definition 5

The Rank of an outlyingness scoring metric $\rho$ is defined as

$$\begin{aligned} R(\rho _\mathcal {S}(\mathbf {q}))\triangleq |\{\mathbf {o}_i\in \mathbf {O}, \rho _\mathcal {S}(\mathbf {o}_i) \prec \rho _\mathcal {S}(\mathbf {q})\}| + 1 \end{aligned}$$

(7)

Here, we employ the notation $\rho _\mathcal {S}(\mathbf a ) \prec \rho _\mathcal {S}(\mathbf b )$ to denote object $\mathbf a$ being more outlying than object $\mathbf b$ according to $\rho$ in subspace $\mathcal {S}$, with ties broken arbitrarily.

Definition 6

The Z-score of an outlyingness scoring metric $\rho$ is defined as:

$$\begin{aligned} Z(\rho _\mathcal {S}(\mathbf {q}))\triangleq \frac{ {\rho _\mathcal {S}}(\mathbf {q})-\mu _{\rho _\mathcal {S}}}{\sigma _{\rho _\mathcal {S}}} \end{aligned}$$

(8)

where $\mu _{\rho _\mathcal {S}}$ and $\sigma _{\rho _\mathcal {S}}$ are, respectively, the mean and standard deviation of the $\rho$-score of all data points in subspace $\mathcal {S}$.

The density rank and density Z-score that we have discussed in the previous section are specific instantiations of these normalizations.

Theorem 3

Given an arbitrary scoring metric $\rho$, then $Z(\rho )$ and $R(\rho )$ are dimensionally-unbiased as per Definition 4.

Proof

Given a data set $\mathbf {O}$ of n objects, we can show that

$$\begin{aligned} E[R(\rho _\mathcal {S}(\mathbf {q}))|\mathbf {q}\in \mathbf {O}]= \frac{1+2+\cdots +n}{n}=\frac{n+1}{2}, \end{aligned}$$

which is independent of the dimensionality of the subspace $\mathcal {S}$. Similarly,

$$\begin{aligned} {\small E[Z(\rho _\mathcal {S}(\mathbf {q}))|\mathbf {q}\in \mathbf {O}]= \frac{1}{n}\sum _{i=1}^n Z(\rho _\mathcal {S}(\mathbf {o}_i)) = \frac{1}{n}\sum _{i=1}^n \frac{ \rho _\mathcal {S}(\mathbf {o}_i) - \mu _{\rho _\mathcal {S}}}{\sigma _{\rho _\mathcal {S}}} =0} \end{aligned}$$

(9)

$\square$

Note that for the Rank and Z-score normalization, not only the mean of the normalized measures is a constant, but also the variance of the normalized measures is also a constant w.r.t dimensionality. Indeed, it is easily seen that $\text{ Var }[Z(\rho _\mathcal {S}(\mathbf {q}))|\mathbf {q}\in \mathbf {O}]=1$ and $\text{ Var }[R(\rho _\mathcal {S}(\mathbf {q}))|\mathbf {q}\in \mathbf {O}]=\frac{1}{3}n(n^2-1)$. Also, we note that the proof of Theorem 3 did not make use of the uniform distribution assumption. In fact, the Z-score and Rank normalization hold their constant average value for any data set under any distribution. This raises the question whether these normalizations are overly strong normalization schemes. Indeed, if the data was deliberately generated in such a way that there are more outliers in higher dimensional subspaces, then the average outlyingness degree should in fact increase w.r.t. dimensionality to reflect this.

Next, we prove that the isolation path score is intrinsically dimensionally unbiased under Definition 4, without the need for normalization.

Theorem 4

The isolation path score is dimensionally unbiased under Definition 4.

Proof

First, it is noted that for computing the average isolation path within a data set, we simply build a full isolation tree (since no point is designated as the query). Since an isolation tree is built recursively, the average path length of its leaf nodes can also be computed recursively as:

$$\begin{aligned} L(n)={\left\{ \begin{array}{ll} 0, &{} \text {if }n = 1.\\ 1 + \sum _{\mathbf {split}} P(\mathbf {split}) \Big ( P( < \mathbf {split}) L( < \mathbf {split}) + P(\ge \mathbf {split}) L(\ge \mathbf {split}) \Big ), &{} \text {if }n > 1. \end{array}\right. } \end{aligned}$$

(10)

where L(n) denotes the average path length of a random tree built based on n samples. Note that for a data set of n distinct points in any splitting attribute, there are in fact at most $n-1$ distinct split intervals that will result in non-empty subtrees, and within any interval, all split points produce identical subtrees. $P(\mathbf {split})$ is the probability that a split interval is chosen. $P(<\mathbf {split})$ and $P( \ge \mathbf {split})$ denote the fraction of points falling on each side of the split point, while $L( < \mathbf {split})$ and $L(\ge \mathbf {split})$ denote the average path length of the left and right sub-tree respectively. Using the baseline-case assumption of the uniform data distribution, if the split point is uniformly chosen at random, then it has equi-probability to be in the interval between any two consecutive data points, thus $P(\mathbf {split})=\frac{1}{n-1}$. Let $1 \le i < N$ be the index of split points such that $\mathbf {split}_i \le \mathbf {split}_{i'}, \forall i < i'$, then $P( < \mathbf {split}_i) = \frac{i}{n}$ and $L( < \mathbf {split}_i) = L(i)$, and similarly $P(\ge \mathbf {split}_i) = \frac{n-i}{n}$ and $L(\ge \mathbf {split}_i) = L(n-i)$. We therefore arrive at the following recurrence:

$$\begin{aligned} L(n)={\left\{ \begin{array}{ll} 0, &{} \text {if }n = 1.\\ 1 + \frac{1}{n-1}\sum _{i=1}^{n-1} \left( \frac{i}{n} L(i) + \frac{n-i}{n} L(n-i)\right) , &{} \text {if }n > 1. \end{array}\right. } \end{aligned}$$

(11)

Due to the symmetry of the terms in the sum and by multiplying by $n(n-1)$:

$$\begin{aligned} n(n-1)L(n) = n(n-1) + 2\sum _{i=1}^{n-1}iL(i) \end{aligned}$$

(12)

By subtracting equation (12) for $L(n-1)$ from equation (12) for L(n), we obtain a simplified closed form:

$$\begin{aligned} L(n) = L(n-1) + \frac{2}{n} = 2 \sum _{i=2}^{n} \frac{1}{i} = 2H_n - 2 \end{aligned}$$

where $H_{n}$ is n-th harmonic number, which can be estimated by $\ln (n)+\gamma$, with $\gamma$ being the Euler’s constant. Since L(n) is independent of dimensionality, the isolation path score is dimensionally unbiased under Definition 4. $\square$

Of the remaining outlyingness measures, LOF (Breunig et al. 2000) in its raw form appears to also approximately satisfy our definition of dimensionality unbiasedness. More specifically, in Breunig et al. (2000, Lemma 1), it has been proven that for a compact cluster of points, most points have an LOF value of approximately 1 within a small multiplicative factor independent of the space dimensionality. The distribution of data in Definition 4 satisfies this requirement (a single uniform cluster).

5.1 Summary of desiderata for scoring measures

In Table 1, we give a brief summary for the desiderata of scoring measures. In terms of interpretability, ranking is arguably the easiest-to-understand measure, followed by the Z-score, which can be interpreted as the number of standard deviations from the mean raw score. The other scores are generally less comprehensible to the average user. Subjectively, we found LOF the least interpretable measure due to its rather intricate technical definition. We experimentally evaluate the effectiveness of various measures in Sect. 7.

Table 1 Summary of desiderata for scoring measures (n = data size; d = #dimensions; T = #random paths; $n_s$ = sample size)

6 The beam search procedure

For score-and-search approaches, after a scoring function has been determined, it remains to use this score to guide the search within the set of all possible subspaces. There are $2^d-1$ such subspaces. When the maximum dimensionality $d_ max$ is specified, the number of subspaces to search through is in the order of $O(d^{d_ max })$, i.e., still exponential in $d_ max$. While we have not attempted to formally prove the hardness of the score-and-search problem using the proposed scoring metrics, it is reasonable to assume that those problems are “hard”. In fact, the problem of searching for the best outlying subspace using the raw kernel density score is a special case of the MAX SNP-hard contrast subspace mining problem (Duan et al. 2015), where the positive class reduces to a single query point. A heuristic approach is thus essential.

In this work, we propose a beam search strategy. Beam search is a breadth-first-search method that avoids exponential explosion by restricting the number of nodes to expand to a fixed size (i.e., the beam width) while discarding all other nodes (Russell and Norvig 2003). The effectiveness of beam search depends mostly on the quality of the heuristic pruning procedure. In this work, we design the heuristic rule based on the following speculation: a highly-scored subspace will also exhibit good scores in some of its lower dimensional projections. Of course, there are exceptions to this speculation. Take the example in Fig. 6a for example. Consider a point close to the center of the circle, it is an outlier in the 2D space, yet does not exhibit any outlying behaviour in its 1D projections. We can further generalize this example to the case where the data distribute uniformly on the surface of a high dimensional hypersphere, and the query lies at the center of the sphere. In this setting, in any lower dimensional projection, the query will appear to be an inlier, thus that subspace will have a low score. While this example shows that our speculation does not always hold true, we point out that such an exception requires a careful and somewhat artificial setting.

In reality, it is reasonable to expect that a good outlying subspace will show some telltale sign in at least one of its lower dimensional projections. For this reason, we propose to build the subspaces incrementally in a stage-wise manner.

The overall search procedure is described as follows. In the first stage, all subspaces of 1 dimension are inspected to screen out trivial outlying features for user inspection. The user might then decide whether to take these trivial outlying features out of the data. In the second stage, we perform an exhaustive search on all possible 2D subspaces. The subsequent stages implement a beam search strategy: at the l-th stage, we keep only the W top-scoring subspaces (the beam width) from the previous $(l-1)$-th stage. Each of these subspaces is then expanded by adding one more attribute and then scored. The search proceeds until a user-defined maximum set size has been reached. The framework is presented in Algorithm 2. The number of subspaces considered by beam search is therefore in the order of $O(d^2 + Wd\cdot d_{max})$ where W is the beam width and $d_{max}$ is the maximum subspace dimension.

6.1 Filtering trivial outlying aspects

We now discuss possible approaches for filtering out trivial outlying aspects. This problem is not a challenging one, both computationally and methodologically. Given that there are only d univariate variables to be screened, the computational requirement is modest. Furthermore, most outlyingness scoring metrics work well on univariate variables. Here, given a scoring metric, we propose to use a parameter $\epsilon \in [0,1]$ to specify the percentile ranking threshold for the query. Any attribute in which the query’s outlierness score is within the top $(\epsilon \times 100)\%$ is deemed a trivial outlying attribute.

7 Experimental evaluation

In this section, we design a series of experiments to assess the effectiveness and efficiency of the proposed method and scoring metrics against the state of the art. For scoring metrics, we compare with LOF (Breunig et al. 2000), with the $MinPtsLB$ and $MinPtsUB$ parameters set to 10 and 30 respectively, and the density rank in Duan et al. (2015). For outlying subspaces mining methods, we compare our framework with the projection based approach LOGP (Dang et al. 2014) and the feature selection based approach GlobalFS (Vinh et al. 2014b), with all parameters set as recommended in the respective papers. For the isolation path, we have found that 500 paths on subsamples of size 256 generally work well, thus we employ this setting unless otherwise stated. In this work we focus on large datasets with the number of data points $n\gg 256$. However, in case n is not substantially larger or even smaller than 256, we have found that setting the subsample size to $\sim$ $\lfloor n/4\rfloor$ yields reasonable results. All experiments were performed on an i7 quad-core desktop PC with 16 GB of main memory. We implemented the isolation path score, LOF, density rank and density Z-score in C++/Matlab. The Beam search framework was implemented in Matlab. All source code will be made available on our web site. Implementations of LOGP (Matlab) and GlobalFS (C++) were kindly provided by the respective authors (Dang et al. 2014; Vinh et al. 2014b).

7.1 Basic properties

We first design several experiments on synthetic datasets to verify the basic properties of different scoring functions.

$\bullet$ Experiment 1—Convergence of isolation path score The convergence property of isolation forests was comprehensively established in Liu et al. (2008, 2012). Herein, we briefly confirm this convergence in the context of isolation path. We generate 1000 random data points uniformly distributed on a circle with a small amount of Gaussian noise as in Fig. 6. The query is at the center of the circle. In the first experiment, we fix the subsample size for the isolation path algorithm to 256 while the number of paths in the ensemble is varied from 1 to 10,000. In Fig. 6b it can be observed that the average path length converges quickly using just approximately 100 paths. It is also noted that the path length of the query $\mathbf {q}$ is significantly smaller than the average path length of a random inlier $\mathbf {o}$. This demonstrates that the isolation path length score is able to characterize non-trivial outliers, i.e., outliers that cannot be characterized by inspecting each feature separately. In the next experiment, we fix the number of paths to 500, but vary the size of the subsample from 50 to 500. The average path length grows as expected, approximately in the order of $O(\log n_s)$ where $n_s$ is the subsample size. Nevertheless, the average path length of $\mathbf {q}$ is consistently smaller than that of the inlier $\mathbf {o}$.

Fig. 6

Convergence of isolation path score. a Data on a circle; query q (red square), a random inlier o (green square). b Average path length convergence (fixing subsample size to 256). c Effect of subsample size (fixing the number of paths to 500) (Color figure online)

$\bullet$ Experiment 2—Dimensionality unbiasedness We generate 10 data sets, each consisting of 1000 points from a uniform distribution $\mathcal {U}([0,1]^d)$. The space dimension is varied within [2, 20]. We then compute the average mean isolation path score, density Z-score LOF, outlying degree score and log density of all data points. In addition, we also compute the average mean subspace size of the outlying subspace returned by LOGP for all data points. In Fig. 7b, we note that the LOF score and isolation path score shows a flat profile as the number of dimensions increases. For the Isolation path score, note that the average isolation path score coincides with $2H_n-2$, as dictated by Theorem 4. On the other hand, the outlying degree, log density score and LOGP all exhibit clear bias towards subspaces of higher dimensionalities.

An interesting question to ask is how the scoring functions behave under an arbitrary data distribution. Towards this end, we generate 10 data sets, each consisting of 1000 points from 10 equal-sized spherical Gaussian clusters with random mean in [0, 1] and diagonal covariance matrix $\sigma \mathbf {I}_{d\times d}$ with $\sigma \in [0,1]$. The space dimension is varied within [2, 20]. The result is presented in Fig. 7a. Under an arbitrary data distribution, it is not possible to predict whether the average outlyingness score should increase or decrease as dimensionality increase. Nevertheless, the density Z-score, by construction, has zero-mean across all dimensionalities. The LOF score and isolation path score both show a slight tendency to increase as the number of dimensions increases, but this variation is minor, compared to the outlying degree, log density score and LOGP, which all exhibit a strong bias towards subspaces of higher dimensionalities.

Fig. 7

Dimensionality unbiasedness (best viewed in color). a Dimensionality unbiasedness: baseline value. b Average value under Gaussian mixture distribution (Color figure online)

$\bullet$ Experiment 3—Scalability In this experiment, we test the scalability of the isolation path score in comparison with the next most scalable metric, namely LOF, with respect to the number of data points. Note that we do not test scalability w.r.t. the number of dimensions, as scoring metrics are often used for scoring low dimensional spaces (i.e., $d\le 5$) in the context of outlying aspects mining. Higher dimensional outlying subspaces are hard to interpret. We generate n data points in a 5-dimension space where the number of data points n ranges from $10^3$ to $10^6$ points (LOF) and $10^7$ points (isolation path score). The data distribution is a mixture of 100 equal-sized spherical Gaussian clusters with random mean and covariance. For each n value, we randomly take 100 points as queries and record the average time required for computing the LOF and isolation path score for these queries. For LOF, we also test the KD-tree based version for fast KNN queries. It is observed that the time for building the KD-tree is negligible compared to the time for KNN queries when the data size is sufficiently large. The result is presented in Fig. 8. It can be observed that the average cost for computing the isolation path score is very small and does not increase appreciably w.r.t. the data set size, thus making it suitable for mining very large data sets.

Fig. 8

Scalability w.r.t. dataset size

7.2 Identifying trivial outlying features

We demonstrate the usefulness of mining trivial outlying features. For this experiment, we employ the KDD Cup’99 data set. This benchmark data set is used commonly in the anomaly detection community. Though it has been criticized for not reflecting real-life conditions, we employ this data set since our primary goal is not about anomaly detection. This data set was also analyzed by Micenkova et al. (2013) where the authors extracted a small subset of 3500 records, and found a number of outlying aspects for the anomalies. Here, we extract 100,000 normal records and 18,049 outliers of 40 types of attacks from both the training and testing datasets. Each record is described by 38 attributes. We demonstrate that it is an easy yet meaningful task to explicitly identify trivial outlying aspects. We employ the LOF and isolation path score with the rank threshold parameter set to $0.5~\%$, i.e., attributes in which the query’s score lies within the top $0.5~\%$ are deemed trivial outlying features. Note that the density rank and Z-score are too expensive for data sets of this size. We search for trivial outlying features for each of the total 118,049 records.

Fig. 9

Trivial outlying aspects on KDD Cup’99 data set–shading scales indicate the proportion of points sharing the same trivial outlying attributes in each attack type (best viewed in color). a Isolation path score. b LOF (Color figure online)

For the isolation path score, the results are summarized as follows: amongst 18,049 outliers, 6166 records are found to possess some trivial outlying features, i.e., $34.3~\%$. This is in good contrast to only $4.1~\%$ of normal records having trivial outlying features. Note again that here we do not attempt to declare whether any record is an anomaly. In Fig. 9a we present the proportion of records in each type of attack sharing the same trivial outlying features. Several intuitive insights can readily be extracted from this table. For example, most land attacks share the trivial outlying feature named land. Most guess password attacks (guess_passw) have an extreme number of failed logins (num_failed_logins), as expected.

Explanations for other types of attacks require deeper domain knowledge. Take the processtable DoS attack for example. The attack is launched against network services, which allocate a new process for each incoming TCP/IP connection. Though the standard UNIX operating system places limits on the number of processes that a user may launch, there are no limits on the number of processes that the superuser can create. Since servers that run as root usually handle incoming TCP/IP connections, it is possible to completely fill a target machine’s process table with multiple instantiations of network servers. To launch a process table attack, a client needs to open a connection to the server and not send any information. As long as the client holds the connection open, the server’s process will occupy a slot in the server’s process table (Garfinkel et al. 2003). Most processtable attacks thus have extremely high connection times, as seen in Fig. 9a.

Another example is the warezmaster/warezclient attacks. Warezmaster exploits a system bug associated with file transfer protocol (FTP) servers on which guest users are typically not allowed write permissions. Most public domain FTP servers have guest accounts for downloading data. The warezmaster attack takes place when an FTP server has mistakenly given write permissions to guest users on the system, hence any user can login and upload files. The attacker then creates a hidden directory and uploads “warez” (copies of illegal software) onto the server for other users to download (Sabhnani and Serpen 2003). A warezclient attack can be launched after a warezmaster attack has been executed: users download the illegal “warez” software that was posted earlier through a successful warezmaster attack. The only feature that can be observed to detect this attack is downloading files from hidden directories or directories that are not normally accessible to guest users on the FTP server. The feature “hot” can be utilized to detect whether such suspicious activities took place: if many hot indicators are being observed in a small duration of time during the FTP session, it can be concluded that warezclient attack is being executed on the target machine (Sabhnani and Serpen 2003). In Fig. 9a it can be observed that many warezclient attacks share the “hot” and “is_guest_login” trivial outlying features.

For LOF, using the same $0.5\,\%$ rank threshold, $29.6\,\%$ of outliers were identified as having trivial outlying features (compared to $34.3\,\%$ when using the isolation path score), while $13.6\,\%$ of inliers were deemed to have trivial outlying features (which is significantly higher compared to $4.1\,\%$ when using the isolation path score). On this data set, it took LOF 2524 s to score all 118,049 points in all features, compared to 120 s when the isolation path score was used. Fig. 9b presents the proportion of records in each type of attack sharing the same trivial outlying features. While LOF also detects a number of ‘highlighted’ cells where a large proportion of attacks of the same type share the same outlying features, somewhat surprisingly, several intuitive pairs, such as land–land, guess_passw–num_failed_logins, and warezclient–hot, warezclient–is_guest_login were not detected. A closer inspection reveals that, as LOF is designed to detect local outliers, it is not sensitive towards groups of global outliers, as in the above cases. When an anomaly cluster becomes large and dense, the inner part of that cluster will be treated by LOF as inliers. This is known as the masking effect (Liu et al. 2012). The isolation path score, on the other hand, deals effectively with masking, since subsampling will thin out the anomaly cluster for easier detection.

The consensus index In order to quantitatively assess the results, we propose the Consensus Index (CI). It assesses the generalization performance of a method from the query point to other data points of the same class. More specifically, if a set of outlying features for a query point is good, then many other data points of the same class should also share such features, i.e., distinguishing features of the class. Thus, for each class, we count the number of times each feature is ‘voted’ as an outlying feature by some query points in that class, and form the consensus matrix C, where $C_{ij}$ represents the number of times the j-th feature is selected as an outlying feature by all query points in the i-th class. Normalizing each row of C by the number of query points in the respective class gives the heatmap visualization in Fig. 9. For each class, a small number of ‘highly-voted’ cells indicates better generalization. To quantify this consensus between members of the same class, we employ an entropy-based measure: for each class (i.e., row of C), we first add 1 to each cell (a Laplacian smoothing factor) to prevent degenerate distributions, then we compute the entropy for the row distribution as follows:

$$\begin{aligned} H(i)= \sum _{j=1}^d -\frac{C_{ij}+1}{N_i } \log \frac{C_{ij}+1}{N_i } \end{aligned}$$

where $N_i= \sum _{j=1}^d (C_{ij}+1)$. The consensus index is computed as the averaged normalized row entropy

$$\begin{aligned} CI \triangleq \frac{\sum _{i=1}^{n_C} H(i)}{n_C\log d} \end{aligned}$$

where $n_C$ is the number of classes. CI ranges within (0, 1], with smaller values indicating better consensus amongst queries of the same class, i.e., better generalization. For the KDD Cup’99 data set, the CI of LOF is 0.90 while for the isolation path score, the CI is 0.75. Thus the isolation path score appears to also return better results quantitatively. Note that, while these CI values seem high, i.e., close to 1, the minimally achievable consensus (i.e., normalized entropy) for a class is $-[(d-1)/(n_i+d)\log (1/(n_i+d)) - (n_i+1)/(n_i+d)\log ((n_i+1)/(n_i+d))]/\log (d)$, which is achieved when all $n_i$ queries of the i-th class vote for the same feature. This baseline minimum value can be high, e.g., 0.44 when $d=40, n_i=100$, and approaches zero when $n_i\rightarrow \infty$.

7.3 Identifying non-trivial outlying high dimensional subspaces

We employ a collection of data sets proposed by Keller et al. (2012) for benchmarking subspace outlier detection algorithms. This collection contains data sets of 10, 20, 30, 40, 50, 75 and 100 dimensions, each consisting of 1000 data points and 19 to 136 outliers. These outliers are challenging to detect, as they are only observed in subspaces of 2 to 5 dimensions but not in any lower dimensional projection. Note our task here is not outlier detection, but to explain why the annotated outliers are designated as such. These data sets were also employed in several previous studies in outlying aspects mining (Micenkova et al. 2013; Duan et al. 2015; Vinh et al. 2014b). Since the data size is relatively small, here we employ a range of different approaches, namely LOF score (including rank and Z-score variants), Outlying Degree (including rank and Z-score variants), density score rank and density Z-score, the isolation path score, GlobalFS (Vinh et al. 2014b) and LOGP (Dang et al. 2014).

For this data set, since the ground-truth (i.e., the annotated outlying subspace for each outlier) is available, we can objectively evaluate the performance of all approaches. Let the true outlying subspace be T and the retrieved subspace be P. To evaluate the effectiveness of the algorithms, we employ the sensitivity, $sen \triangleq |T\cap P|/|T|$ and the precision, $prec \triangleq |T\cap P|/|P|$. The average sensitivity and precision over all outliers for different approaches on all datasets are reported in Fig. 10. Note that since there are many methods being tested, we report the results for each metric on two separate subplots.

Fig. 10

Performance on identifying non-trivial outlying high-dimensional subspaces (best viewed in color). a Precision. b Precision. c Sensitivity. d Sensitivity (Color figure online)

On these data sets, the density Z-score performs competitively overall, and works better than the density rank variant. The isolation path score also performs competitively and is observed to work better than several previous approaches, including GlobalFS, density rank and LOGP. Of the two feature selection based approaches, GlobalFS’s performance is close to the isolation path score and is significantly better than LOGP. Again, we note that LOGP seeks a transformation that distinguishes the query from its full-space neighbors. In this case, it appears that full-space neighbors are not a relevant source of information to guide the search. To verify this hypothesis, we test to see how similar the full-space neighborhood of the query is, compared to its outlying-subspace neighborhood. It turns out that the average proportion of common neighbors drops steadily as the number of dimensions increases, from 22 % (10 dimensions) to just above 16 % (100 dimensions), similar to the trend observed in Fig. 2a. Thus, the topology of the data in the full space needs not be similar to that in the outlying subspaces. This observation can shed light on the poor performance of LOGP. While GlobalFS also being a method in the feature transformation/selection category, it does not rely on any statistic of the full space when building its synthetic data. It therefore exhibits better performance.

The outlying degree performs competitively, and albeit being a biased score, it outperforms LOF on these data sets. This is because all the artificial outliers are designed to be global outliers. LOF appears to discover many ’local’ outlying aspects, in which the query appear to be locally outlying. Unfortunately, these findings cannot be verified using the ground truth. While the OD has high precision, its dimensionality bias is also clearly exposed: for every query, the top subspace found by the OD always comprises 5 features, which is the maximum cardinality allowed, whereas the ground-truth subspace sometime comprises only 2-3 features. For this reason, the sensitivity of the OD is low. Of the normalized variants, only the OD Z-score improves upon OD, while the OD Rank degrades the results. We are also interested in seeing whether normalizing the LOF (to rank or Z-score) could improve the performance, but the answer appears to be negative in both cases: normalizing the LOF decreases the performance significantly, especially at higher dimensionalities. A possible explanation could be since LOF is already dimensionally-unbiased, normalizing LOF does not offer any additional benefit but instead disrupting its values. It is observed, however, that the LOF Z-score performs better than the LOF Rank.

Parameter sensitivity We test the performance of the beam search procedure w.r.t. the beam width parameter on the 75-dimension data set of this benchmark. The results are presented in Fig. 11, with the beam width ranges from 10 to 200. For most scoring metrics, the performance improves gradually and stabilizes after the beam width reaches 100. Note that increasing the bandwidth is guaranteed to return better solutions in terms of the chosen scoring metric, but not necessary better performance w.r.t. the ground-truth. Apparently, the performance of the density rank decreases slightly as the beam width increases.

Fig. 11

Parameter sensitivity: performance w.r.t. beam width parameter (best viewed in color) (Color figure online)

Execution time The wall clock execution time for various methods is presented in Fig. 12. The two feature transformation/selection approaches GlobalFS and LOGP are significantly faster than score-and-search approaches overall. Among the score-and-search methods, the isolation path score based approach is the most efficient.

Fig. 12

Execution time (best viewed in color) (Color figure online)

Table 2 Summary of UCI data sets

7.4 Other data

We have tested the methods on several real data sets from the UCI machine learning repository (Bache and Lichman 2013), as summarized in Table 2. These are data sets for classification. We select a subset of the data points to act as queries. For each query, we exclude all data points of the same class except the query, and mine the outlying features for the query. For these data sets, since the annotated ground-truth outlying subspace for each data point is not available, we employ the Consensus Index as a measure of generalization performance. For all search and score methods, the parameters for the beam search were set as $d_{max}=3$ (maximum subspace dimension) and $W=100$ (beam width), and the top scoring subspace was reported. For feature selection (GlobalFS) and transformation (LOGP) approaches, we also extract an explaining subspace of a maximum of 3 features. Note that for this experiment, whenever it takes an excessive amount of time for a method to complete (e.g., several days or weeks) based on an estimation from the first query, then we exclude that method from the experiment (marked as ‘*’ in Table 3). Also, since other proposed methods do not have any strategy for handling trivial outlying features, we did not filter out trivial outlying features in this experiment.

Table 3 Performance on UCI data sets: Consensus Index (lower the better) and average execution time (s)

A brief description for the data and the respective testing protocol is as follows: (1) The pen digit data set consists of 10,992 samples of 16 features for the 10 digits 0–9, i.e., 10 classes. We randomly picked 100 samples from each class as query points. (2) The vowel data set contains 990 samples of 10 features in 11 classes. We took all the data points as queries. (3) The English letter data set contains 20,000 samples of 16 features for the 26 letters A–Z. We took 2291 samples corresponding to three random letters as queries. (4) The forest cover type dataset consists of 581,012 samples of 54 features in 7 classes. We randomly took 100 data points in each class as queries. (5) The Ionosphere dataset comprises 351 samples of 33 attributes. We took all data points as queries. (6) The breast cancer data set consists of 569 instances of two classes: malignant and benign, and 30 features. We took all data points as queries. (7) The satellite dataset consists of 6435 data points of 36 features. We randomly took 100 data points from each class as queries. (8) The Shuttle data set contains 58,000 samples of 9 features in 7 classes. We randomly took 100 samples from each class as queries (or all samples if a class contains less than 100 data points). (9) The image segmentation data set consists of 2310 data points of 19 features in 7 classes. We randomly took 100 data points from each class as queries.

Table 4 % Cross-validation error on UCI data sets using top-5 ‘voted’ features

Note that in this experiment, we are more interested in ‘long’ data sets (i.e., $n\gg d$) rather than ‘wide’ data sets (i.e., $n\ll d$). The reason is that, when we have a relatively small number of samples and extremely large number of dimensions, such as a microarray data set comprising a few hundreds patients (samples) and a few tens of thousands of genes (features), it is often the case that each sample will exhibit many trivial outlying features, just by chance. That is because the data is so sparse. On the other hand, it is much more meaningful and challenging to discover outlying features when the data is dense. From the performance summary in Table 3, it can be observed that the proposed density Z-score measure achieves good results whenever applicable, but it is not very scalable, along with LOF and the density rank measures. For large datasets, the isolation path score consistently achieves better results than the other two scalable alternatives, namely LOGP and GlobalFS. Note that GlobalFS complexity is exponential in $\log n$, i.e., $O(d^{\log n})$, thus it is generally applicable up to medium-sized data, but becomes infeasible when the data size becomes large, e.g., on the Forest cover type data set.

We note that there is an important assumption underlying the Consensus Index as a quantitative performance measure that deserves some discussion. The assumption is that the classes are homogeneous, i.e., each class can be characterized by a relatively compact set of features. It is useful to discuss the notion of ‘natural clusters’ here. A natural cluster is a set of tightly coupled data objects in some subspace, ideally of a small cardinality. A homogeneous class comprises a single natural cluster, or several natural clusters all characterized by the same subspace. In the traditional context of feature selection for classification, the goal is to identify this set of features that characterize each class. Of course, it may also happen that some class is heterogeneous, i.e., comprising several natural clusters, each characterized by a different subset of features. The Consensus Index works best when the classes are homogeneous. In such cases, we can draw meaningful conclusions about the generalization performance of different methods, from individual queries to the whole class. Studies on class homogeneity are a challenging problem and fall outside the scope of this paper. It is also worth noting that the Consensus Index on its own as a performance measure can be misled by a malicious method which assigns the same feature to all queries, in such case the CI is maximized. Such a solution, however, will be poor in distinguishing different classes of queries. To this end, we take the top 5 ‘voted’ features across all queries and test the 10-fold cross validation error using a k-NN classifier (with k = 10). The result is presented in Table 4 where it can be observed that the isolation path, LOGP and GlobalFS are the methods that perform better in terms of the cross validation error rate.

8 Discussion and conclusion

In this paper, we have discussed the fundamental issues of outlying aspects mining. We formalized the concept of dimensionality unbiasedness, and established this property for several existing measures. We have also proposed two novel outlyingness scoring metrics. The density Z-score exhibits good performance, but is computationally expensive, thus is only applicable for small numeric data sets. On the other hand, the isolation path score is an efficient measure that also exhibits good performance, making it suitable for mining very large data sets.

While exhibiting desirable characteristics with respect to effectiveness and efficiency, the methods presented herein is not without limitations. Most notably, the isolation path, which is built upon the foundation of isolation forest, is not designed to detect local outlying subspaces, i.e. subspaces in which the query is only a local outlier w.r.t. its neighborhood. Second, scalability to both large and high dimensional data set remain a significant challenge. This is true especially for the rank or Z-score normalization, since the outlying score for all data points in all subspaces must be calculated. Example application scenarios include text corpus of millions of documents in tens to hundreds of thousands of words. Such large scale applications is currently beyond the scope of many methods investigated herein.

The above limitations suggest several exciting avenues for future research. First, a local version of the isolation path can be developed for local outlying subspaces. Second, it is interesting to develop hybrid frameworks that combine the efficiency of feature selection/transformation based approaches and the versatility and effectiveness of score-and-search based methods, capable of generating multiple alternative explanations and scalable to much larger high dimensional datasets. Third, in the spirit of the no-free-lunch theorem, it is likely that no measure is optimal in all settings. Therefore, an ensemble approach to outlying aspects mining, leveraging the strengths of multiple scoring metrics and methods would likely be more effective.