1 Introduction

For nonlinear, nonparametric, and time-varying financial markets across the world, understanding the temporal dynamics for deeper analysis is an extremely arduous task. The volatility in stock markets largely influences capital flow, which affects investors (Cipollini et al. 2015; Abounoori et al. 2016; Tiwari et al. 2019). Hence, it is essential to analyze different financial assets at a microscopic level for trading, portfolio management, and resource allocation. Globalization and rapid growth in information and communication technology have given impetus to continuous interaction and volatility contagion among financial markets. Empirical investigations for examining the efficient market hypothesis and predictability of equity markets have garnered a lot of attention (Zhang et al. 2015; Mensi et al. 2017). The literature reports usage of the variety of conventional econometric methods for accomplishing the objectives (Panda and Deo 2014; Ghosh and Kanjilal 2016). However, the major shortcoming such as inability to deal with the nonlinear pattern and conducting granular level inspection have spurred the active utilization of nonconventional frameworks ranging from Econophysics (Mantegna and Stanley 1999), machine learning (Wang et al. 2011; Kao et al. 2013; Ghosh et al. 2019), wavelet analysis (Sharif et al. 2017; Jammazi et al. 2017), and deep learning (Zhao et al. 2017) in modelling the financial time series. Global market uncertainty and the financial crisis have surged researchers worldwide to come up with different strategies for portfolio management and realignment (Das et al. 2019). The proper discovery of dynamic association among heterogeneous financial assets plays a pivotal role in risk mitigation. Recently, the dynamic conditional correlation (DCC) based analysis of the return series has emerged as an attractive approach to meet the goal (Basher and Sadorsky 2016; Creti et al. 2014; Jones and Olson 2013; Kim et al. 2016).

Crude oil and natural gas have significant impacts on socio-economic development and social stability (Jones and Kaul 1996; Henriques and Sadorsky 2008). The causal nexus between crude oil prices and energy has been observed as well (Reboredo et al. 2017). Due to their inherent chaotic characteristics and sensitiveness to outside shocks, forecasting future figures requires robust predictive frameworks capable of mining uncertain and nonlinear patterns. It is essential to assess the association among these highly volatile markets and stock markets at the short and long runs time intervals for effective strategic investment.

The objectives of this research are threefold. The first objective is to analyze the underlying evolutionary dynamics of individual markets using nonlinear dynamics tools. It is critical to detect the occurrence of the random walk in the time series. The predictive analytic models are of no use for financial markets exhibiting complete Brownian motion. We classify the time series into a random walk and biased random walk models by estimating the fractal dimensional index and the Hurst exponent. The second objective is to assess the dynamic associations among the said assets over different time intervals by employing the continuous wavelet transformation-based wavelet coherence analysis. For portfolio diversification and hedging, these findings are important.

The third objective is to estimate the dynamic association among the selected return time series for estimating hedging ratios for portfolio diversification. For this purpose, maximal overlap discrete wavelet transformation (MODWT) is used to decompose a time series into a set of time-varying linear and nonlinear components. Then the dynamic conditional correlation-generalized autoregressive conditional heteroscedasticity (DCC-GARCH) is applied on disentangled components to uncover the dynamic correlation to estimate hedge ratios. This paper presents a neoteric framework of nonlinear dynamics, wavelet analysis, and DCC-GARCH to accomplish research endeavors. The outcome of the fractal modeling sets the platform for wavelet coherence analysis to identify the dynamic dependence among the energy, crude oil, and equity market. It justifies the deployment of DCC-GARCH for obtaining hedge ratios.

The rest of the article is structured as follows. Section 2 presents the previous literature. Section 3 emphasizes the key statistical properties of the dataset and ascertains the nature of key properties. Section 4 explicitly elucidates the research models utilized in this paper. Section 5 discusses the overall findings of the study in terms of behavioral characteristics of temporal dynamics of assets, association, and dynamic conditional correlation among the said assets for obtaining hedge ratios. Finally, Sect. 6 provides conclusions.

2 Previous Research

A growing section of literature has actively discussed the empirical analysis and causal analysis of different financial markets. We highlight the findings of some major research work using nonlinear methodologies in allied areas.

2.1 Studies on Nonlinear Dynamics Based Empirical Inspection

Wang and Ma (2011) analyzed the non-linear dynamics of gold prices by utilizing fractal dimension analysis and Hurst exponent. For forecasting gold prices, they designed a variant of artificial neural network techniques. Priyadarshini and Babu (2012) used a conventional rescaled range based fractal modeling to test the random walk hypothesis for mutual funds and stock markets. They observed that the fractional Brownian motion governs the said markets. Yin et al. (2013) examined the fractal behavioral of the gold market of China and proposed a forecasting approach to predict future figures. Ghosh et al. (2017) presented an integrated framework of fractal inspection for examining the temporal dynamics of NIFTY 50, Hang Seng, NIKKEI, and NASDAQ indexes.

2.2 Studies on Dynamic Dependence

Fink and Fink (2013) have shown the upward revisions of major tropical storms positively influenced the returns of an index of petroleum firms in the northwest Gulf of Mexico. Khalfaoui et al. (2015) have analyzed the volatility spillover and hedging between the stock markets of G-7 countries and crude oil by applying the wavelet-based multi-resolution analysis and GARCH-BEKK model. Liu et al. (2015) have demonstrated the importance of indicators of the oil market in forecasting the excess return of the S&P 500 index. Genc (2017) have modeled the dynamic effect of oil price movements on-demand before and post-global financial crisis. Liu et al. (2017) have explored the volatility spillover between the oil and stock market by applying the GARCH-BEKK model in conjugation with wavelet analysis. The results indicated that the linkage between the oil and S&P 500 index weakens in the long term. The relationship is completely reverse for the MICEX index and the oil market.

Reboredo et al. (2017) have studied the association and causal inter-relationship between oil prices and renewable energy stock through wavelet-based econometric modeling. Their study revealed different types of causality at different time intervals between the assets. Mensi et al. (2017) have investigated the dynamic dependence in a pairwise manner by applying a wavelet-based copula method. Sharif et al. (2017) have examined the relationship between economic growth and electricity generation in Singapore based on wavelet analysis and econometric methods. Jammazi et al. (2017) have explored the time-varying causality between stock returns and oil price change of six oil-importing countries using wavelet-based multi-resolution analysis. Significant causal links appeared at the high frequencies and in periods of financial turmoil. Basher and Sadorsky (2016) applied DCC, asymmetric DCC (ADCC), and generalized OGARCH (GO-GARCH) approaches to unveil the conditional correlation between VIX, gold, and oil bonds with stock prices. The findings of these three approaches were applied separately to estimate hedge ratios. Pan et al. (2014) used the regime-switching ADCC (RS-ADCC) tool to examine the effect of hedging among gasoline, heating oil, and crude oil.

A review of existing research dedicated to testing random walk models suggests the usage of traditional econometric techniques, fractal modeling, recurrence analysis, etc. separately. It is hard to find studies reporting nonparametric frameworks combine multiple research methods to test the randomness of financial markets. Fractal Modelling can capture the presence of long or short-range dependence in time series. On the contrary, a large segment of literature dealing with causal interactions do not address any practical implications from empirical findings. In this paper, we utilize nonlinear dynamics for inspecting the evolutionary dynamics. We apply wavelet coherence analysis and wavelet-based DCC-GARCH to discover causal interactions and estimate hedge ratios for portfolio diversification. Most of the above studies focused on exploring the causal interrelationships among heterogeneous financial assets confined to equity and commodity markets, ignoring the country-specific sectoral index. We try to bridge this gap by assessing the role of country-specific Energy Index on overall interaction among considered markets.

3 Data and Key Statistical Properties

We collect the daily closing price of BSE Energy Index, Brent Crude Oil, DJIA Index, Natural Gas, and NIFTY Index from January 2012 to March 2017 from the ‘Metastock’ database for financial markets. DJIA and NIFTY act as proxies for the equity market of the USA and India, respectively. The BSE Energy Index represents the sectoral level energy index of the Indian energy market, reflecting sentiments of companies classified as members of the energy sector. Brent Crude Oil, primarily refined in Northwest Europe, is a benchmark for the worldwide crude oil price. It is comparatively lighter and sweeter than WTI. Table 1 presents the key statistical parameters of the said financial time series.

Table 1 Descriptive statistics
Full size table

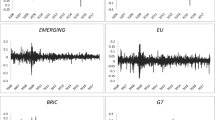
The results of Jarque–Bera, Shapiro–Wilk, and Hegazy–Green tests reject the normality assumption of the considered time series. Augmented Dickey–Fuller (ADF) and Philips Peron (PP) tests further reveal that none of the time series are stationary. To assess the presence of nonlinearity, we have used Terasvirta’s and White’s neural network tests. Both the test statistics indicate the presence of nonlinear trends at different significant levels except for the closing prices of Natural Gas. Terasvirta’s test suggests the existence of nonlinear behavioral movement in the closing price of Natural Gas, while White’s test rejects this hypothesis. Therefore, most of the considered time series exhibit complex nonstationary patterns, which entail the usage of sophisticated research methodologies for gaining insights. Figure 1 portrays the temporal movements.

Fig. 1
figure 1

Plots of a BSE Energy, b Crude Oil, c DJIA, d Natural Gas price, and e NIFTY

Full size image

4 Research Methods

This section enumerates the utilized research models. For fractal modeling and wavelet coherence analysis, we consider the original daily closing price series of respective assets. For DCGARCH, we consider the daily return series. Section 4.3 explains the process of estimating the return series. We test the Brownian motion hypothesis on each series through fractal modeling.

4.1 Fractal Modeling

We use fractal modeling for inspecting the efficient market hypothesis of various financial assets. In most of the cases of long duration, markets behave inefficiently. We use the Fractal Dimensional Index (D) and rescaled range (R/S) analysis to estimate the Hurst Exponent (H) for detecting the occurrence of short or long memory structure.

R/S analysis Hurst (1951) proposed this nonparametric approach. Mandelbrot and Wallis (1968) have improved the approach later. The R/S analysis is carried out in the following way:

  • Step 1 Segment the time series RN of length N into d subseries of length n.

  • Step 2 Compute the expected value (Ed) of individual subseries Rk,d.

  • Step 3 Find the sum of deviation of each element of the respective subseries from their mean as follows:

    $$ X_{k, d} = \mathop \sum \limits_{i = 1}^{k} \left( {R_{i, a} - E_{d} } \right) $$
    (1)

  • Step 4 Find the range as

    $$ R_{d} = max\left( {X_{k,d} } \right) - min\left( {X_{k,d} } \right) $$
    (2)

  • Step 5 Find the s.d. of each subseries as

    $$ S_{d} = \sqrt {\left( {1/n} \right)\mathop \sum \limits_{k = 1}^{n} \left( {R_{k,d} - E_{d} } \right)^{2} } $$
    (3)

  • Step 6 The average rescaled range value comprising all sub-series is

    $$ \left( {R/S} \right)_{n} = \left( {1/A} \right)\mathop \sum \limits_{d = 1}^{D} \left( {R_{d} /S_{d} } \right) $$
    (4)

Hurst exponent (H) The relationship between the Hurst coefficient (H) and the estimated R/S statistic is as follows:

$$ \left( {R/S} \right)_{n} = C*n^{H} $$
(5)

The magnitude of H is given by

$$ \log \left( {\frac{R}{S}} \right)_{n} = H\log n + \log C . $$
(6)

The magnitude of H can vary from 0 to 1. For a given sequence, an estimated value of 0.5 of H infers that the sequence purely follows an i.i.d. random walk process; otherwise, it is governed by fractional Brownian motion. The short and long memory trends correspond to H < 0.5 and H > 0.5, respectively.

Fractal dimensional index (D) It is a non-integer dimension that can characterize all chaotic systems and provide a detailed representation of how objects take up space. Now, D and H have the following relationship:

$$ D = 2 - H . $$
(7)

As H varies between 0 to 1, D varies between 1 to 2. D = 1.5 indicates a pure random walk. For \( 1 < D < 1.5 \), the time series shows a long memory trend and for \( 1.5 < D < 2 \), short memory trend. The value of \( D \approx 1 \) indicates ‘JOSEPH’S EFFECT,’ and \( D \approx 2 \) indicates ‘NOAH’S EFFECT’ in the time series.

Correlation between periods (CN) \( C_{N} \) represents the magnitude of persistence or anti-persistence trends.

$$ C_{N} = 2^{{\left( {2H - 1} \right)}} - 1 . $$
(8)

For \( C_{N} = 0 \), the time series is perfectly random, for \( C_{N} < 0 \), the time series is anti-persistent and for \( C_{N} > 0 \), the time series is persistent. If \( C_{N} = 0.8 \), say, then 80% of the dataset is influenced by its historical information.

Next, we present the wavelet-based inspection framework incorporating wavelet coherence analysis for evaluating the degree of the association at different timescales.

4.2 Continuous Wavelet Transformation Based Wavelet Coherence Analysis

Wavelet analysis is a powerful quantitative modeling tool that enables carrying out multi-resolution analysis of the nonstationary time series. It has been widely used for studying dynamic interactions and making predictions on a scale by sale manner (Han and Ge 2017; Das et al. 2018; Singh et al. 2018). We outline the continuous wavelets, cross wavelet transformation, and wavelet coherence processes and report the major findings.

Wavelet transformation generates father (\( \varphi \left( t \right) \)) and mother (\( \psi \left( t \right) \)) wavelets on a scale-wise manner by translating and dilating the original function (\( f\left( t \right) \)). The mother wavelet is a square-integrable function that generates a family of daughter wavelets. Its mathematical for is as follows:

$$ \psi_{\tau , s} \left( t \right) = \frac{1}{\sqrt s }\psi \left( {\frac{t - \tau }{s}} \right) $$
(9)

where \( s \) is the scaling parameter, and \( \tau \) is the location parameter. The ‘WaveletComp’ package in R helps in performing the analyses. The package uses ‘Morlet’ wavelet for analyses as follows:

$$ \psi \left( t \right) = \pi^{{ - \frac{1}{4}}} e^{{iw_{0} t}} e^{{ - \frac{{t^{2} }}{2}}} $$
(10)

Continuous wavelet transform (CWT) CWT provides a detailed assessment of the temporal evolution of frequency components. Its mathematical form is:

$$ W_{x} \left( s \right) = \mathop \int \limits_{ - \infty }^{\infty } f\left( t \right)\frac{1}{\sqrt s }\psi^{*} \left( {\frac{t}{s}} \right) $$
(11)

where \( * \) represents the operation of the complex conjugate.

Wavelet Coherence To assess the dynamic dependence among the financial time series at the microscopic level, cross wavelet transform, wavelet coherence, and wavelet power spectrum are applied. The cross wavelet of two-time series \( a\left( t \right) \) and \( b\left( t \right) \) having CWT, \( W_{n}^{a} \left( s \right) \) and \( W_{n}^{b} \left( s \right) \) is determined as:

$$ W_{n}^{ab} \left( s \right) = W_{n}^{a} \left( s \right)W_{n}^{b*} \left( s \right) $$
(12)

The wavelet coherence coefficient (\( R_{n}^{2} \left( s \right) \)) used to measure co-movements between two series across frequencies over time can be computed as (Torrence and Webster 1999):

$$ R_{n}^{2} \left( s \right) = \frac{{\left| {\left( {s^{ - 1} W_{n}^{ab} \left( s \right)} \right)} \right|^{2} }}{{\left( {s^{ - 1} \left| {W_{n}^{a} \left( s \right)} \right|^{2} } \right)\left( {s^{ - 1} \left| {W_{n}^{b} \left( s \right)} \right|^{2} } \right)}} $$
(13)

The wavelet coherence coefficient ranges from 0 to 1. If the value is close to 0, then there exists a weak dependence. If the value close to 1, then there exists a strong dependence. The wavelet coherence phase difference is calculated to understand the nature of the association, and the lead-lag relationship (Torrence and Webster 1999):

$$ \theta_{xy} \left( s \right) = tan^{ - 1} \left( {\frac{{{\Im }\left( {s^{ - 1} W_{s}^{ab} \left( s \right)} \right)}}{{{\Re }\left( {s^{ - 1} W_{s}^{ab} \left( s \right)} \right)}}} \right) $$
(14)

where \( {\Im } \) and \( {\Re } \) represent the imaginary and real components of the power spectrum.

Arrows indicate phase relationships in the coherence phase. The right arrows indicate a positive correlation, whereas the left arrows indicate a negative correlation and out of phase of the series. For in-phase case, downward pointed arrows signify the second series leads the first series by \( \pi /2 \) while upward-directed arrows are evidence of the first series leads the second by \( \pi /2 \). The exact opposite phenomenon is evident for out of the phase case.

4.3 Wavelet Based Dynamic Conditional Correlation and Hedging

To ascertain the dynamic correlation and subsequently delve into portfolio management, the study first uses wavelet-based multi-resolution analysis to capture the sort and long-run temporal dynamics. The DCC-GARCH technique is then applied on time-varying components to comprehend the dynamic association among returns of BSE Energy, Crude Oil, DJIA, Natural Gas, and NIFTY.

Wavelet decomposition It is used to conduct the multi-resolution analysis through the decomposition of the original time series \( y\left( t \right) \) into different time scales as follows:

$$ y\left( t \right) = \mathop \sum \limits_{k} s_{j,k} \varphi_{j,k} \left( t \right) + \mathop \sum \limits_{k} d_{j,k} \psi_{j,k} \left( t \right) + \mathop \sum \limits_{k} d_{j - 1,k} \psi_{j - 1,k} \left( t \right) + \cdots + \mathop \sum \limits_{k} d_{1,k} \psi_{1,k} \left( t \right) $$
(15)

where the father (\( \varphi ) \) and mother (\( \psi \)) wavelets account for the low and high-frequency components of the series; \( s_{j,k} \), \( d_{j,k} \),…, \( d_{1,k} \) are wavelet coefficients. Now, \( y\left( t \right) \) can be approximated by a J-level multi-resolution decomposition analysis as:

$$ y\left( t \right) = S_{j} \left( t \right) + D_{j} \left( t \right) + D_{j - 1} \left( t \right) + \cdots + D_{1} \left( t \right) $$
(16)

where frequency components \( D_{j} \) (detailed scales) account for short, medium or long-lived variations at \( 2^{j} \) time scale, \( S_{j} \) (approximation level) denote the determined residual after removing the detailed components from the original signal. The components of the lower frequency range prevail for longer periods, while higher frequency components prevail for shorter durations. We consider the multi-resolution analysis of 6 levels for decomposition, thus generating one approximation and six detailed components. The MODWT technique has been used to compute the respective coefficients. The decomposition has been carried out through the Daubechies least asymmetric filter of length eight (LA8), which outperforms traditional ‘Haar’ wavelet filters for obtaining smoother and uncorrelated coefficients across scales (Gencay et al. 2002; Cornish et al. 2006). Table 2 presents the time scale resolution of decomposition.

Table 2 Time interpretation of wavelet scales
Full size table

MODWT based time series decomposition has been carried out initially to enable the DCC-GARCH approach for critically delving the conditional correlation dynamically in a time-varying multiscale manner. The wavelet framework generates the decomposed time series. Table 2 shows them. DCC-GARCH is applied separately on the respective decomposed series to gain deeper insights. The DCC-GARCH requires the return series of the respective financial time series. So, it is necessary to compute the daily returns of the selected five assets beforehand.

The steps of enabling the DCC-GARCH to explore the dynamic association and performing in a time-varying manner are as follows:

  • Step 1 Estimate the daily return series as

    $$ R_{t} = \frac{{P_{t} - P_{t - 1} }}{{P_{t - 1} }} $$
    (17)

    where \( R_{t} \) denotes the return at time t while \( P_{t - 1} \) and \( P_{t} \) represent closing prices at time (t-1) and t, respectively.

  • Step 2 Decompose the original daily return series of BSE Energy, Crude Oil, DJIA, Natural Gas, and NIFTY into six levels (d1, d2, …, d6) using the MODWT framework applying LA8 filter.

  • Step 3 Apply the DCC-GARCH on three levels—d1, d3, and d6 to gain insights about the granular dynamic correlation existing between the return series of considered assets. Among the decomposed components, d1 and d3 represent the short-run dynamics, while d6 represents the long-run dynamics. Thus, the outcome of DCC-GARCH on the three levels of decomposed return series of the respective assets would reflect the nature of association in the long and short-run effectively.

  • Step 4 Estimate the hedge ratios on decomposed components—d1, d3, and d6 to identify hedging opportunities.

DCC-GARCH DCC-GARCH technique (Engle and Sheppard 2001; Engle 2002) helps in assessing the conventional conditional correlation among the financial time series through estimation of historical correlations and conditional volatilities. It decomposes the conditional covariance into two dynamic components, a conditional standard deviation matrix, and a standard deviation, as shown below:

$$ D_{t} = \left[ {\begin{array}{*{20}c} {\sqrt {h_{1t} } } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {\sqrt {h_{nt} } } \\ \end{array} } \right] $$
(18)

\( R_{t} \) accounts for time-varying conditional correlation of standardized innovations \( \left( {\varepsilon_{t} } \right) \).

$$ R_{t} = \left[ {\begin{array}{*{20}c} 1 & {\rho_{12,t} } & {\rho_{1n,t} } \\ {\begin{array}{*{20}c} {\rho_{12,t} } \\ \vdots \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ \vdots \\ \end{array} } & \vdots \\ {\rho_{1n,t} } & \cdots & 1 \\ \end{array} } \right] $$
(19)

For the DCC-GARCH model, \( H_{t} \) should be a positive definite matrix. As \( D_{t} \) follows the structure of a positive definite matrix in its positive diagonal entries, \( R_{t} \) must adhere to the typical properties of a positive definite matrix having elements less than or equal to one. \( R_{t} \) can be decomposed as follows:

$$ R_{t} = V_{t}^{* - 1} V_{t} V_{t}^{* - 1} $$
(20)
$$ V_{t} = \left( {1 - \alpha - \beta } \right)\bar{V} + \alpha \varepsilon_{t - 1} \varepsilon_{t - 1}^{T} + \beta V_{t - 1} $$
(21)

\( V_{t}^{*} \) is a diagonal matrix given by

$$ V_{t}^{*} = \left[ {\begin{array}{*{20}c} {\sqrt {q_{11,t} } } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {\sqrt {q_{nn,t} } } \\ \end{array} } \right] $$
(22)

\( V_{t}^{*} \) transforms the elements of \( V_{t} \) so that the following equation holds:

$$ \left| {\rho_{ij} } \right| = \left| {\frac{{q_{ij,t} }}{{\sqrt {q_{ii,t} q_{jj,t} } }}} \right| \le 1 $$
(23)

Lastly, \( \bar{V} = Cov\left[ {\varepsilon_{t} \varepsilon_{t}^{T} } \right] = E\left[ {\varepsilon_{t} \varepsilon_{t}^{T} } \right] \) and is estimated as

$$ \bar{V} = \frac{1}{T}\mathop \sum \limits_{t = 1}^{T} \varepsilon_{t} \varepsilon_{t}^{T} . $$
(24)

The parameters (\( \alpha \), \( \beta \)) are nonnegative and estimated to represent the DCC. The model exhibits mean-reverting behavior if \( \alpha + \beta < 1 \), where \( \alpha \) and \( \beta \) represent short-run and long-run persistence, respectively.

Hedge Ratio Proposed by Kroner and Sultan (1993), literature reports the successful usage of conditional volatility in the construction of a hedge ratio. An asset () on a long position can hedge with an asset () considering a short position, as shown below:

$$ \beta_{xy,t} = \frac{{h_{xy,t} }}{{h_{yy,t} }} $$
(25)

where \( h_{xy,t} \) and \( h_{yy,t} \) represent the conditional covariance between asset and, and the conditional variance of asset.

Wavelet coherence analysis-based CWT delves into the interrelationship measured in terms of the degree of association in time-varying frequency scales. Findings of the coherency analysis can effectively evaluate the magnitude of prevailing association and dependence in short, medium, and long-run scales. DCC-GARCH examines the DCC by critically evaluating historical correlation and conditional volatility. Unlike the wavelet coherence approach, it cannot extract the time-varying scale-wise nature of dynamic correlation. Thus, the present study conjugates DCC-GARCH with the MODWT framework for accomplishing the task. Both frameworks can deal with time series exhibiting non-parametric and non-stationary behavior.

5 Results and Discussions

The findings of the respective research models have been outlined here with adequate discussions.

5.1 Findings of Fractal Inspection

Table 3 shows the findings of the fractal analysis of the considered five-time series.

Table 3 Results of fractal inspection
Full size table

From Table 3, we see that all the five-time series exhibit fractional Brownian motion, which rejects the efficient market hypothesis. The H and D values justify the attempt to forecast future values. The value of H closer to 1 reflects the supremacy of the trend component that may not necessarily be linear. High figures of CN imply dependence of the present state on the historical information. Hence, the existence of long memory dependence entrenched in temporal dynamics of the global financial and energy market is apparent as manifested through fractional Brownian motion.

The presence of a strong persistence pattern entrenched in the evolutionary dynamics of daily closing prices of the time series can be ascertained based on the findings of the empirical assessment through fractal modeling. The findings instigate to delve into the dynamics of time-varying components through wavelet analysis. The inefficiency of the markets justifies the uncovering of causal inter-relationship for portfolio diversification.

5.2 Evidence from CWT Based Analysis

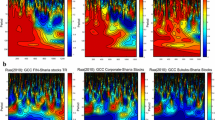
Figure 2 represents the cross-wavelet transformation between two time series in a pairwise manner. The covariance for all such pairs has increased with scale. The vertical axis shows the dynamic relationship between the two time series that are affected by medium to long-duration changes than short term shocks. Information related to phase infers that the interplay has not been homogeneous across the scales as they point out to all directions.

Fig. 2
figure 2figure 2

Cross wavelet transforms plots of a BSE Energy and Crude Oil, b BSE Energy and DJIA, c BSE Energy and NIFTY, d BSE Energy and Natural Gas, e Crude Oil and DJIA, f Crude Oil and Natural Gas, g Crude Oil and NIFTY, h DJIA and NIFTY, i DJIA and Natural Gas and j NIFTY and Natural Gas

Full size image

Figure 3 depicts the phase difference and wavelet coherence among the series under consideration. The plot displays evidence of varying dependence across time and frequency (period) scales among the financial markets. A solid-curved line marked a significant local correlation in the time–frequency domain. The wavelet coherence analysis identifies the portions and plots them with warmer colors. In this process, fewer dependence zones get cooler colors. The findings are extremely helpful in building and realignment of portfolios as coherence analysis can provide the exact time duration of high association phases.

Fig. 3
figure 3

Wavelet coherence plots of a BSE Energy and Crude Oil, b BSE Energy and DJIA, c BSE Energy and NIFTY, d BSE Energy and Natural Gas, e Crude Oil and DJIA, f Crude Oil and Natural Gas, g Crude Oil and NIFTY, h DJIA and NIFTY, i DJIA and Natural Gas and j NIFTY and Natural Gas

Full size image

From the two sets of plots accounting for dynamic co-movement, we see that the propensity of high association predominantly emerges in low frequency. Short interrelationships between the selected time series are not as intense as of medium and long-run dynamics. Cross wavelet transformation plots indicate that the BSE Energy index having the strongest co-movement with Crude Oil than others. Crude Oil exhibits stronger interaction with natural gas than DJIA and NIFTY. DJIA and NIFTY have been found to display a stronger bond between them than with energy markets. This implies that the units of energy markets are strongly associated among themselves, while financial markets follow the same traits. Directions of arrows have not been uniform across the plots for respective time series pairs. Hence, the presence of in-phase and anti-phase associations representing positive and negative correlation is apparent. Such behaviors suggest the scope for portfolio diversification and hedging appropriately.

Applications of wavelet coherence to evaluate nexus among heterogeneous financial assets on absolute prices are reported in the literature (Khalfaoui et al. 2015; Karatas et al. 2017; Phillips and Gorse 2018). The findings are used for various practical implications, including delving interaction, measuring spillovers, forecasting, etc. The proposed approach suggests the presence of significant association in price series. So, it becomes imperative to test the dynamic association among the selected market proxies in their return dynamics. The presence of conditional correlation in return series can help for effective hedging. Hence, the overall insights gained through wavelet coherence analysis prompt to apply of the wavelet-based DCC-GARCH model for discovering dynamic association.

5.3 Findings of Granular DCC-GARCH Model

The model inspects the dynamic correlation on decomposed components of time series. Unlike other approaches, the time-varying DCC-GARCH has been applied to return series of selected assets. We report the outcome and elucidate the implications on d1, d3, and d6 scales. The following tables furnish the magnitudes of key parameters (Tables 4, 5, 6).

Table 4 DCC parameters estimates at d1 level
Full size table
Table 5 DCC parameters estimates at d3 level
Full size table
Table 6 DCC parameters estimates at d6 level
Full size table

Scale wise estimated parameters are found to be significant in all the cases. Scales, d1 and d3 act as proxies for the short run, while d6 acts as the proxy for the long run. In short-run dynamics, values of beta are greater than alpha. Hence, a clear dominance of long-run persistence over the short run persistence is evident in the said time. The significance of DCC parameters specifies the existence of volatility clustering. The sum of alpha and beta less than one infers the evidence of the mean-reverting process. In the long run, both the parameters are statistically significant. However, in the case of Natural Gas and NIFTY, the alpha value is greater than the beta value. It indicates the dominance of short-run persistence over long-run persistence.

The following figures present the graphical illustration of DCC among BSE Energy, Crude Oil, DJIA, Natural Gas, and NIFTY in a pairwise manner at the d1 scale.

Graphical representations of DCC display that pairwise correlation between two return series fluctuates between negative and positive values. They move in cluster structures that hint at opportunities for portfolio diversification. It becomes a bit difficult to estimate the maximum and minimum values of DCC from mere visualization as heavy fluctuations are entrenched. To identify the range and to gain deeper insights, the maximum and minimum values of the DCC for the respective pairs for all three scales d1, d3, and d6 have been estimated and summarized in Table 7. The DCC value between BSE Energy and Crude Oil is maximum, and between BSE Energy and DJIA is minimum at the d1 scale. Overall, the DCC values range from (−) 0.75 to 0.75 at the d1 scale, which implies that in the short duration, the DCC displays high volatile characteristics. It happens in high return and high-risk situations. The d3 scale shows almost a similar behavioral pattern. In the d6 scale, the magnitude of dynamic correlation increases significantly from (− 0.91) to 1.00 almost. The degree of volatility in this scale increases. As observed earlier in Table 6, in the long duration, dominance in short-run persistence is apparent. Therefore, there exists ample opportunity for effective hedging on this scale too.

Table 7 Range of DCC
Full size table

The range of the DCC suggests the existence of ample scopes for portfolio formation at different time horizons. Figures 4, 5, 6 and 7 and Table 7 indicate that the probability of higher returns is substantially higher in long-run periods. On the other hand, a comparatively higher possibility of more risk cannot be ruled out in the long run as well. As mentioned in Table, d6 scale, a proxy for the long run corresponds to 64–128 weeks while d1 and d3 scales, representing the short-run, correspond to 2–4 and 8–16 weeks. Therefore, risk-averse players may get benefit from diversification of assets for up to 16 weeks. The players willing to take a risk for achieving excess profit may target diversification in the long run-up to 64–128 weeks. The horizontal axes of the figures show the time.

Fig. 4
figure 4

DCC between BSE Energy and other series at d1

Full size image
Fig. 5
figure 5

DCC between Crude Oil and other series at d1

Full size image
Fig. 6
figure 6

DCC between DJIA and other series at d1

Full size image
Fig. 7
figure 7

DCC between Natural Gas and NIFTY at d1

Full size image

However, the choice of constituents in the portfolio plays a critical role in the overall risk mitigation. Table 8 shows the mean and median values of the DCC at different time horizons.

Table 8 Average measures of DCC
Full size table

The dynamic association between any two assets can be observed to exhibit significant fluctuations between the negative and positive values as apparent from Figs. 4, 5, 6 and 7 and the range statistics summarized in Table 7. The negative and negligible correlations imply an ideal opportunity for portfolio diversifications. For example, the negative interplay between Crude Oil and NIFTY at a specific time scale signifies that the Crude Oil price tends to fall when the equity market resides in the bullish state. Such insights can effectively be utilized for risk mitigation as it prevails clear diversification opportunities. The findings of time-varying DCC-GARCH, in conjunction with MODWT may assist the market players at various levels. At d1 level, the visual insights from Figs. 4, 5, 6 and 7 and the range estimates indicate that the DCC can display homogenous overlap to positive and negative values. The value ranges between (− 0.75) and 0.75. Hence, this time scale accounts for the high risk and high return scenario.

A deeper inspection of the DCC figures in terms of mean and median measures implies that DJIA/Natural Gas, Natural Gas/NIFTY, etc. are the perfect combination for diversification. A similar phenomenon prevails at the d3 scale as well. Both the mean and median of the DCC between Crude Oil/DJIA, Crude Oil/Natural Gas, and Crude Oil/NIFTY are low but positive in both d1 and d3 scales. Hence, associating Crude Oil with any of these assets may marginally increase the risk in the short run. In the long run, the DCC between BSE Energy/NIFTY, Crude Oil/Natural Gas, and DJIA/NIFTY are on a substantially higher side as manifested by the positive mean and median values. Hence, in the long run, the said combinations may be avoided for the diversification process. Comparatively, BSE Energy/Crude Oil, Crude Oil/NIFTY, etc. are better options for diversification. The significant increase (− 0.91) to 1.00 approximately in the range of magnitude of the DCC in the long run eventually augments the risk. This implies that the long-run diversification is comparatively more ideal for investors with high-risk appetite than the short-run counterparts. Therefore, in the short-run, diversification is comparatively less susceptible to the risk than the long run counterparts, while the probability of getting a better return is more in the long run. The granular DCC-GARCH framework assists in choosing assets for the portfolio accordingly.

We estimate the hedge ratio for each scale. Table 9 presents the summary statistics of pairwise estimated hedge ratios at respective scales. Here, some selected pairs share negative average hedge ratios for all three scales. It happens due to the presence of a significant negative correlation between the pairs. The hedge can be performed by either being short or long on both assets. The positive hedge ratios suggest the opposite scenario. The average hedge ratio between NIFTY and BSE Energy is 0.27 at scale d1. It signifies that a 100 unit long position in NIFTY can hedge with 27 units in a short position in BSE Energy. Therefore, the hedge ratios can assist investors in seeking higher yield by hedging the risk through portfolio realignment.

Table 9 Summary statistics of hedge ratio
Full size table

6 Conclusions

This paper presents a framework to examine the behavioral pattern, interplay, and estimating hedge ratios of global energy and equity markets. For this purpose, we assess the temporal pattern using fractal modeling and recurrence analysis. The CWT delves the interaction among the markets, and MODWT based DCC-GARCH approach estimates dynamic correlations. Initial findings through fractal modeling reject the random walk hypothesis of five indices (energy and financial) for the period over January 2012 to March 2017. The strong presence of persistent trends identified through recurrence analysis eventually hints at the same behavioral pattern in future periods. Accordingly, market players at various levels can effectively manage resources. The wavelet coherence analysis uncovers the time-varying dynamic interactions among the markets at different scales. We detect significant long-duration associations among the assets. The study majorly focuses on studying the dynamic association. The findings of association analysis help us to construct and realign short term and long-term low-risk portfolio. The findings on the return series of selected financial time series through DCC-GARC can benefit traders in risk management and portfolio diversification. In the future, we may analyze the causality in terms of direction and magnitude of causal influence through the utilization of conventional Granger causality or unconventional nonlinear causality models. The proposed approach is also applicable to other markets and assets for empirical inspection, portfolio diversification and projecting future directions.