Opinion Formation with Imperfect Agents as an Evolutionary Process

Abstract

We develop and simulate an interaction-based model of continuous opinion formation under bounded confidence to identify conditions and understand circumstances that lead a society into either a consensus, multiple opinion classes or perpetual opinion dynamics. The society is modeled as a social network and random meetings are presumed. When only regular agents are present, we have shown that the small world networks may bring the society very close to consensus for even small threshold levels, but require higher tolerance than the complete network to reach consensus. We have identified the conditions under which the process with stubborn agents generates long-run consensus, permanent disagreement or permanent fluctuation in opinions. There cannot be a persistent fluctuation in opinions in the environment of regular agents nor in the presence of a single group of stubborn agents. In the runs with a single group of stubborn extremists, we have identified the Popper paradox despite the existence of a tolerance span in which the proportion of extremism decreases as the tolerance level increases. Further, in a highly tolerant society with two competing extremist groups, they have no supporters among the regular agents whose opinions are oscillating around the center of the opinion space. The influence of inconsistent agents is persistent and induces a perpetual opinion dynamics. The model is non-equilibrium and emerging, while consensus, if attainable, can be reached in a finite time.

1 Introduction

In the present paper, we examine the question of opinion formation in an integrated society of heterogeneous and interacting individuals. The importance of the topic stems from the fact that what people think determines the choices that they make in their everyday life. This may refer either to economics, finance, game theory, buying decisions, marketing and product recommendations, politics and voting, urban growth, norms. In a decentralized society which does not have a social planner to direct others’ behaviors, opinions are generated spontaneously by repeated local interactions between the large number of participants, we call them agents, and the feedback influences from the macrostructure onto the agents’ behaviors. It has been shown that the interacting society can produce very diverse outcomes. Even extreme and marginal views can prevail in certain conditions, including the outcomes that are considered undesired and condemned (Glaeser et al. 1996; Schelling 1971).

Economists have been for a long interested in how the interaction influences the individuals’ opinions and how this transforms into the opinion dynamics within the society. It has been found that the interacting society leads to the adoption of widespread opinions, directing the society towards consensus. In fact, the ability of autonomous and interacting individuals with different priors to reach consensus is remarkable and has been thoroughly studied (Bala and Goyal 1998; Banerjee and Fudenberg 2004; Baronchelli et al. 2008; DeGroot 1974; Gale and Kariv 2003; Golub and Jackson 2010; Hegselmann and Krause 2005; Motsch and Tadmor 2014; Olfati-Saber and Murray 2004; Vicsek et al. 1995). Over the years, the question of consensus has become a central concern within the research community.

However, the complex and dynamic large-scale societies exhibit much richer behavioral structures. In fact, the notion of consensus contrasts with empirical facts and can be considered an idealization of the reality and a theoretical construct, while disagreement is a norm in practice.¹ For instance, individuals regularly disagree on political agendas, movies, the cast, prefer some restaurants and places to others, have opposing views to the superstars, etc. One might mistakenly believe that disagreement is caused by the asymmetric and incomplete information alone, because it is present when individuals are exposed to the same data or news (Hirshleifer 2001). Some disagreement may be induced by the people’s attitude towards the opposing views, because some may have more firm beliefs than others. Anyway, disagreement in a society can be expressed either in the form of multiple opinion clusters or as a perpetual opinion dynamics. Recent research has demonstrated that stable diversity of opinions can be attained when bounded confidence or stubborn agents with fixed opinions are introduced (Deffuant et al. 2000, 2002; Weisbuch et al. 2002). Though very intuitive, these attempts cannot properly describe behavioral patterns on both, the individual and the aggregate level, that are induced by the joint influences of agents’ specifics and the interrelationships between the microscopic processes which both are complex. One aspect that has not received any attention yet is the agents’ sincerity in information-sharing, which is always relevant when agents refer to human beings. Relatedly, when agents update their opinions upon the opinions of others, they may contact an insincere counterpart and then make a decision upon the insincere opinion. In the large-scale societies with random meetings, insincere agents would be very hardly identified and then avoided. The interacting agents could thus not know whether the opinion they received was agents’ genuine or not. If it is not, the insincere opinion may be incorporated into their updated opinions and through interaction subsequently transferred further onto their counterparts, who then pass it over to their counterparts and so on across the society. Similar is the case with the stubborn agents who do not change their priors. Furthermore, it is well known from the theory of complex systems that even a slight modification of a single parameter may shape the process, inducing the macroscopic shifts. Multi-agent simulation based methods are used to examine the models of opinion dynamics principally because they allow for the mutual and causal influences of the micro-elements on the development of the complex system, which develops in a nonlinear way (Tesfatsion and Judd 2006).

To explain the very diverse opinion structures within the interacting and interconnected society, we extend the bounded confidence model of continuous opinion formation. In particular, our goal is to improve our understanding of how the process of opinion formation goes through the phase transitions as the circumstances and the network structures are modified. More specifically, we would like to identify the conditions that lead a complex society into either a consensus, multiple opinion clusters or a perpetual opinion dynamics, and examine the evolutionary dynamics. The model is based on the principal assumption that there is no true opinion towards which agents would like to converge.²

The society is modeled as a social network that consists of a large number of single agents who are represented as nodes and connected with one another with a set of links through which the opinions are regularly exchanged. Since reciprocal person-to-person communication is presumed, we use undirected links. A direct implication is that all of the interacting individuals can potentially affect one another. More specifically, the updating rule is conducted upon the difference in the two opinions and the adoption rate. The principle of bounded confidence implies that an agent will change his opinion if the opinion of a selected counterpart differs from his by less than his threshold level. The threshold level can be interpreted as the individuals’ tolerance to the opposing opinion and along with the adoption rate represents the crucial parameter in an agent’s choice function. Analogously, tolerance is interpreted as the agent’s willingness to consider the counterpart’s opinion. The adoption rate determines how much of the opponent’s opinion an agent will integrate into his priors. By using the continuous opinions, an agent can take only a slight portion of the counterpart’s opinion and the communication can end in an opinion which has not been present before. This would not be possible if we used discrete opinions which presume a fixed number of predetermined states. We compare the results on several different network topologies: the complete network, which considers the society an integrated entity in which everyone can meet and share his opinion with anyone, small world network (Watts and Strogatz 1998) which presume local clustering, and the scale free network in the sense of Barabási and Albert (1999).

We begin with a very general setting with only regular agents and show that a widespread consensus can be reached in even a moderately tolerant society, while there cannot be a persistent opinion dynamics if regular agents have homogeneous threshold levels. A less tolerant society will end up in several opinion classes. This also holds true in the small world network and the scale-free network. Here we show that the network topology plays an important role for the process of opinion formation. In particular, the small world networks have proved to be the most effective in bringing the society to very high degree of consensus, while higher threshold levels than in the complete network are required to reach consensus. Subsequently, we extend the model by introducing a subset of stubborn agents³ with extreme opinions and show the susceptibility of even a moderately tolerant society to extremism. Here, we have identified such a tolerance span where the higher tolerance is offset with less extremism in society. When another group of stubborn agents is added on the opposing extreme, the group of regular agents can end either in consensus, multiple opinion clusters or even in the perpetual opinion dynamics. In the latter case, no regular agent is the extremist. In the last part of the paper, we examine the cases with a subset of inconsistent agents, who report a random opinion to the selected counterparts and show that their influence is persistent.⁴ Important for the behavior of the model is the assumption that stubborn and insincere agents cannot be identified and avoided and that the regular agents’ threshold levels and opinions are also not observable to the counterparts. Our most important contribution is to show the phase transitions that are network-based and related to different tolerance levels and the social structure. We also show that the model is non-equilibrium and that consensus, if attainable, can be reached in a finite time.

The remainder of this paper is organized as follows. Section 2 discusses related literature. The model is described in Sect. 3. In Sect. 4, we examine the model with regular agents and conduct several simulations on different network topologies. In Sect. 5, the model includes a portion of stubborn counterparts with the extreme opinion. In Sect. 6, we add additional group of the stubborn agents located on the other extreme. Section 7 examines the model with inconsistent agents. The last section concludes.

2 Related Literature

There is a rich and still growing literature on the opinion formation that tries to find the explanations for agents’ very diverse behaviors.⁵ Following the pioneering work of DeGroot (1974), the early studies elucidated how the environment of autonomous and interacting individuals leads to consensus. Specifically, DeGroot shows that consensus is reached when agents constantly update their opinions upon the weighted average of neighbors’ opinions. The subsequent research has shown that the existence of consensus and its dynamics depend on how individuals receive, process and respond to information and what are the interaction patterns (Altafini 2013; Boccaletti et al. 2014; Motsch and Tadmor 2014).

Principally, our model is related to the models of bounded confidence, in which agents can influence each others’ opinions if and only if the two opinions were already sufficiently close (Acemoglu et al. 2013; Ben-Naim 2005; Blondel et al. 2009; Deffuant et al. 2000, 2002; Hegselmann and Krause 2002, 2005; Jadbabaie et al. 2003, 2012). The decision criterion behind the bounded confidence is the level of disagreement and this has proved to be very efficient in explaining the behavioral diversity. Lorenz (2010) examines the model in which agents have two different bounds and finds that consensus can be reached even when both bounds of confidence are significantly below the critical bound of confidence of a homogeneous society. Several other methods have also been conducted: the voter model (Krapivsky and Redner 2003; Sood and Redner 2005), the Ising model (Galam 2008). Some other models include forceful agents (Acemoglu et al. 2010), influential agents (Golub and Jackson 2010; Watts and Dodds 2007). Sznajd-Weron and Sznajd (2000) develop a discrete opinion model in which two agents unite their opinions first and then try to impose this common opinion onto their nearest neighbors. Glaeser et al. (1996) propose a model of crime rates, in which agents’ decisions are jointly affected by a combination of the behavior of their immediate neighbors and the average behavior within a society. This is a variant of the threshold model (Granovetter 1978) in which a certain number of counterparts must make one decision (hold a certain opinion in our case) before it is adopted by the agent. Galam (2004) examines the model with contrarian agents who deliberately oppose the prevailing choice. Decision-making upon the quorum was proposed by Ward et al. (2008). Our paper is also related to the models of dishonest behavior (Dutta and Sen 2012; Eliaz 2002). The common assumption postulates that agents honestly share their opinions with others, which may not be always satisfied.⁶ Most models presume direct agent-to-agent communication. Some models include media (DeMarzo et al. 2003; Gentzkow and Shapiro 2011) or social media (Gruhl et al. 2004; Kempe et al. 2003; Kwak et al. 2010).

Methodologically, the model of opinion formation embodies a diffusion process on a social network. These models provide a useful framework for studying the behavior of multi-agent systems from different disciplines (Albert et al. 2000; Axelrod 1997; Blume 1993; Boccaletti et al. 2006; Burnside et al. 2011; Granovetter 1995; Kauffman 1993; Leskovec et al. 2007; Newman 2002; Nowak and May 1992; Pastor-Satorras and Vespignani 2001; Szabó and Fath 2007; Valente 1995).

3 The Model

We provide a network-based model of discrete and finite time, defined over $t = 0, 1,2,{\ldots }\,,T$, with $t=0$ indicating initial states and, if not stated differently, $T=50{,}000$. Let ${\mathcal {G}} = \{{\mathcal {V}}, {\mathcal {E}}\}$ be a graph that consists of a finite set of agents $i \in {\mathcal {V}}=\{1,2,{\ldots }\,,n\}$ who are defined as nodes on a network and linked with one another with a finite set of links ${\mathcal {E}}$.⁷ Each agent is characterized by the triple: opinion, threshold level and a set of connections, hence $i = \{x_{i,t}, \epsilon _i, {\mathcal {N}}_i\}$. At each point in time t, agent i has opinion $x_{i,t} \in X(0,1)$. If not stated differently, at $t=0$, each agent is assigned an initial opinion $x_{i,0} \sim U(0,1)$, independent and identically distributed (i.i.d.) random variable, expressed by a real number. By the assumption, no “true” opinion exists and no payoff or utility is attached to agents’ opinions. Furthermore, agents have no knowledge about the counterpart’s opinion until it is revealed and do not know the type of a selected counterpart nor his threshold level nor the neighborhoods of their counterparts.

Links between the agents indicate the communication channels through which opinions are exchanged and the influence is imposed. Communication requires a direct link between the agents $(i,j) \in {\mathcal {E}}$. We use undirected links in which the two agents are either connected or not. Formally, if (i, j) denotes a link from agent i to j, then we say that the link is undirected if and only if $(i, j) \in {\mathcal {E}} \Leftrightarrow (j,i) \in {\mathcal {E}}$. That is, when agent i communicates his opinion to agent j, there is also a reciprocal transfer of opinion from j to i. This condition is very practical since information-sharing is usually both-sided, for which each of the two interacting agents can potentially influence the other.

In each period t, agent i selects a random counterpart j from his neighborhood ${\mathcal {N}}_i$ and the two share their opinions $x_{i,t}$ and $x_{j,t}$, respectively.⁸ The neighborhood of a node i is the set of nodes that i is linked to: ${\mathcal {N}}_i = \{j \in {\mathcal {V}} | (j,i) \in {\mathcal {E}}\}$. Since $(ij)\Leftrightarrow (ji)$ it follows that $j \in {\mathcal {N}}_i\Leftrightarrow i\in {\mathcal {N}}_j$. Neighborhoods of the agents are determined by the network structure. We consider the behavior of the model on three different network structures: the complete network, small world network and scale free network. There is only one neighborhood in a complete network since all agents are connected with each other. There are several different neighborhoods in the small world network and the scale free network. More precisely, in the small world network the average neighborhood is equal across the nodes, while the scale free network displays a large degree of heterogeneity. Moreover, in these networks different agents are members of different neighborhoods. If $i\notin {\mathcal {N}}_j$ and $j\notin {\mathcal {N}}_i$, then $k\in {\mathcal {N}}_i \cap {\mathcal {N}}_j$ represents the bridge between the two neighborhoods. Bridges transmit information between the neighborhoods and thus improve the network connectivity.

Agents meet in a sequential fashion. When the counterpart is chosen and the opinions are exchanged, agents establish the attitude towards the opinion they hear. If $x^{R}_{i,t}$ is the opinion that agent i reports to the selected counterpart, then $x^{R}_{i,t} \ne x_{i,t}$ in the case of insincere agents; for honest agents $x^{R}_{i,t} = x_{i,t}$. Subsequently, each of the two agents autonomously and simultaneously updates his opinion without knowing what the counterpart has selected. The process then repeates for agent 2, and so on until the last agent. The process then proceeds to the next period and repeats until $t=T$.

Agents adjust their opinion upon the principle of bounded confidence. If $x_{i,t}$ is the opinion of agent i in t and $x^{R}_{j,t}$ is the opinion that has been reported to him by agent j in t, then an agent with bounded confidence is willing to adjust his opinion if and only if $|x_{i,t} - x^{R}_{j,t}| < \epsilon _i$, with $\epsilon _i$ representing the threshold level of agent i, otherwise $x_{i,t+1} = x_{i,t}$.⁹ Distance between the two opinions $x_{i,t}$ and $x_{j,t}$ in t, denoted $d_{ij,t}$, is measured as $l_1$-norm

$$\begin{aligned} d_{ij,t}=|x_{i,t}-x^{R}_{j,t}|. \end{aligned}$$

(1)

Distance in (1) signifies the level of temporary disagreement between the two agents. The maximum distance at which an agent will take a portion of the counterpart’s opinion is determined by the agent’s threshold level $\epsilon _i$. Hence, one could also think of the threshold level as the agent’s tolerance for the distance or simply his tolerance. In a way, the threshold level determines the agent’s vulnerability to the opponents’ opinions. An agent with $\epsilon _i=1$ is absolutely vulnerable and will always take a portion $\mu$ of the counterpart’s opinion. An agent with $1>\epsilon _i>0$ is relatively vulnerable and approaches the counterpart’s opinion when $d_{ij,t}<\epsilon _i$. Most individuals from the reality would fall under this category. Threshold levels are assigned to each agent at $t=0$, with $\epsilon _i \in [0, 1]$. Because we assume that threshold levels are equal across the population of regular agents $(\epsilon _1 = \epsilon _2 =\cdots = \epsilon _n)$, we will simplify the notation and write $\epsilon _i = \epsilon$. The group of stubborn agents have $\epsilon _s = 0$ since the stubborn agents always keep their initial opinion. Thresholds are considered agents’ private information and are unknown to the counterparts.

We close the model by introducing the adoption rate $\mu \in [0, 1]$, representing the proportion of counterpart’s opinion an agent integrates into his prior. If $\mu =0$ we have a trivial case of a stubborn agent, because such agent evaluates the counterpart’s opinion but never approaches to it. These cases are not of interest for us.

Definition 1

A non-stubborn agent i has parameter values of $\epsilon _i>0$ and $\mu >0$.

Definition 2

A stubborn agent i has parameter values of $\epsilon _i=0$ and/or $\mu =0$.

This yields the principal equation of the model which drives the agent’s opinion dynamics and is considered a linear combination of the agent’s opinion $x_{i,t}$ and the counterpart’s reported opinion $x^{R}_{j,t}$

$$\begin{aligned} x_{i,t+1} = \left\{ \begin{array}{l l l} x_{i,t}+\mu (x^{R}_{j,t}-x_{i,t}) &{} \quad \text {if} &{} \quad d_{ij,t} < \epsilon _i\\ x_{i,t} &{} \quad \text {if} &{} \quad d_{ij,t} \ge \epsilon _i \end{array} \right. \end{aligned}$$

(2)

In (2), $x_{i,t+1}$ is the opinion of agent i at $t+1$. Notice that $x^{R}_{j,t} = x_{j, t}$ for honest agents. Because the information flows in both directions, agent j approaches to the opinion of agent i by the factor of $\mu$ if and only if $d_{ij,t}<\epsilon _j$. Analogically, the opinion dynamics for agent j is provided as $x_{j,t+1}=x_{j,t}+\mu (x^{R}_{i,t}-x_{j,t})$. Now, $x^{R}_{i,t}$ refers to the reported opinion by agent i to j.

Since $\epsilon _i = \epsilon$ for the regular agents, this implies that $d_{ij,t} = d_{ji,t}$. If $d_{ij,t} < \epsilon$, each of the two agents approaches to the counterpart by the $\mu$ portion of the disagreement $d_{ij,t}$, which reduces the distance between the two by the size of $2 \mu d_{ij,t}$, else, both agents remain at their prior opinions. There is a special case when $d_{ij,t}<\epsilon$ and $\mu = 0.5$, when $x_{i,t+1} = x_{j,t+1} = (x_{i,t} + x_{j,t}) / 2$, and the two agents end the discussion with the same opinion, which is the average opinion of the two. If agents have heterogeneous thresholds, for which $\epsilon _i \ne \epsilon _j$ for $i \ne j$, only an agent with a higher threshold may modify his opinion and approach to the counterpart. We will meet this sort of cases in the runs with the stubborn agents who are characterized by the zero tolerance $(\epsilon _s = 0)$.

The process of continuous opinion sharing between the agents promotes convergence. The process converges at $t_c \in t$, if and only if $x_{i,t_{c+l}} = x_{i,t_c}$ for all i and $l>0$, which means that no agent changes his opinion from this period on. The process which does not converge, exhibits a perpetual opinion dynamics. Convergence does not postulate consensus.

Definition 3

An opinion class $C = {c_1, c_2,{\ldots }\,, c_m}$ is a partition of the set of agents ${\mathcal {V}}$. $c_i \cap c_j = \emptyset$ for $i \ne j$ and $\cup ^{n}_{i=1} c_{i} = P$.

Consensus is reached when there is only one opinion class and $C = 1$. This means that the difference in the opinions between any two agents is zero and $\lim _{t\rightarrow \infty } (x_{j,t} - x_{i,t}) = 0$ for all i and j. The consensual opinion is denoted $x^{*}$. Society is polarized if two different opinions are present ($C=2$) and is pluralistic when $C > 2$.¹⁰ Such a description of the opinion classes and consensus is very strict and is prone to the existence of single isolated agents with unique opinions. For instance, if 199 of 200 agents belong to the class $c_1$ and a single agent to $c_2$, the notion of the polarized society would inadequately describe the opinion space. The society would actually be polarized when each of the two classes are sufficiently large. As a supplement, we also apply a weaker form of consensus and also report the size of the largest three opinion classes $c_1$, $c_2$ and $c_3$.

4 Opinion Formation with Regular Agents

We start with the simplest case, in which only regular agents are present. Each agent is assigned an initial opinion $x_{i,0} \sim U (0,1)$, all agents have the same threshold level $\epsilon _i = \epsilon$ and adoption rate $\mu$ and $x^{R}_{i,t} = x_{i,t}$ for every i.

Fig. 1

Time evolution of the opinion dynamics in two selected runs. (left plot): $\mu =0.05$, $\epsilon =0.35$, (right plot): $\mu =0.3$, $\epsilon =0.2$. First 50 iterations are displayed

The plots in Fig. 1 demonstrate that the process of opinion formation within the integrated society tends to self-organization and that the outcomes depend upon the threshold levels. The most fundamental feature in the process of harmonization of opinions is the contraction feature, therefore, we introduce the following proposition.

Proposition 1

Let $x_{i,t} \ne x^{R}_{j,t}, \mu \in (0,1), d_{ij,t}>0$ and $\epsilon >d_{ij,t}$ in (2) holds. Then the process of opinion formation exhibits a contraction feature.

Proof

Let us assume that there are two agents i and j at time t with opinions $x_{i,t}$ and $x_{j,t}$, respectively, and that they interact with each other. Under these conditions, the upper part of (2) applies. It may be provided as a linear combination of the two opinions: $x_{i,t+1}=(1-\mu )x_{i,t}+\mu x^{R}_{j,t}$. If $x_{i,t} > x^{R}_{j,t}$, then ${(x_{i,t}> x_{i,t+1} > x^{R}_{j,t})}$ for all $\mu > 0$, and, since $\epsilon _i = \epsilon _j = \epsilon$, ${(x_{j,t}< x_{j,t+1} < x^{R}_{i,t})}$, for all $\mu > 0$. Analogically, we can provide the opinion change for agent j, which goes towards the opinion of agent i. Because $x_{j,t+1} > x_{j,t}$ and $x_{i,t+1} < x_{i,t}$, it follows that $(x_{j,t+1} - x_{i,t+1}) < (x_{j,t} - x_{i,t})$, which means that the distance between the priors of the two agents has decreased. $\square$

If conditions from the proposition are not met and $\epsilon <d_{ij,t}$, then $x_{i,t+1}=x_{i,t}$ and $x_{j,t+1}=x_{j,t}$. The contraction principle bounds the agents’ opinions in $t+1$ by their opinions in time t, for which $d_{ij,t+1} \le d_{ij,t}$. This means that conversation cannot increase the level of disagreement between the two interacting agents. We introduce the following lemmas to show that the contraction principle prevents the expansion of disagreement over time on the aggregate level.

Lemma 1

No such pair of agents (k, l) exists in $t+1$ with a distance that is larger than the distance between the pair (i, j) who were in time t the farthest apart; i.e. $\max (d_{ij,t}) \ge \max (d_{kl,t+1})$.

Proof

Since the set of agents is fixed, the process of opinion dynamics is determined by Eq. (2) which is strictly bounded. If $\min (s_{ij,0}) > \epsilon$ for all $i \ne j$, $x_{i,t} = x_{i,0}$ for all i, which implies $\max (d_{kl,t+1}) = \max (d_{ij,t})$. $\square$

Analogically, if $\max (d_{kl,t+1}) \le \max (d_{ij,t})$, then $\max (d_{kl,t}) \le \max (d_{ij,t-1})$. Solving this recursively, with $t \rightarrow 0$, this gives $\max (d_{kl,1}) \le \max (d_{ij,0})$. So, we can derive the supplementary lemma.

Lemma 2

No such pair of agents (k, l) exists with a distance that is larger than the distance between the pair (i, j) who were initially the farthest apart; i.e. $\max (d_{kl,t}) \le \max (d_{ij,0})$.

Lemmas and the proposition state that the opinions of the two interacting agents can only converge to one another. Hence, direct implication is the following lemma.

Lemma 3

The interacting society of regular agents with $\epsilon _i = \epsilon$ converges.

Proof

Assume that $\epsilon >0$ and $\mu >0$. Then, if $s_{ij,t} < \epsilon$, $x_{i,t+1} = x_{i,t}+\mu (x_{j,t}-x_{i,t})$, else $x_{i,t+1} = x_{i,t}$, and analogically for j. Each agent approaches to the counterpart by the factor of $\mu d_{ij,t}$. If k was the closest to i at t in the opposite direction of the i’s move, then the contraction between i and j increases the i’s distance to k by the amount of i’s move towards j: $d_{ik,t+1} = d_{ik,t} + \mu s_{ij,t}$. Agents move across the opinion scale until $0< |x_{i,t} - x_{j,t}| < d$ for every i and j. This implies that at least the closest counterpart has to be located within the agent’s threshold level. Convergence is achieved when $x_{i,t_{c}+1} = x_{i,t_{c}}$ for every i. $\square$

On the aggregate level convergence occurs in the finite time $t_c \in t$ such that $\lim _{t\rightarrow t_c} (d_{ij, t+1} - d_{ij, t}) = 0$ for all i. Convergence is the state of no further changes and does not postulate consensus. Consensus is based on the following premises. The most fundamental premise is the existence of the appropriate counterpart j with the opinion $x_{j,t}$ so that $d_{ij,t} < d$. The second premise is accessibility, which presumes that $(i,j) \in {\mathcal {E}}$ and hence $j \in {\mathcal {N}}_i$. Yet, accessibility does not postulate contraction, since accessible agent should be chosen; this represents the well-known coordination problem (premise 3). Agents pick a random counterpart from the neighborhood with probability $p = \frac{1}{|{\mathcal {N}}_i|}$ with ${\mathcal {N}}_i$ representing the agent’s neighborhood. Clearly, the probability of being selected decreases with the increase of ${\mathcal {N}}_i$. In a complete network, the probability that a certain agent is selected is close to zero.

Let premise 1 be satisfied, then the network topology is crucial for the process of opinion dynamics as it affects premises 2 and 3. In a complete network, $j\in {\mathcal {N}}_i$ for all j and i. Hence, the contraction principle leads to consensus $(x^{*})$ if and only if in any period t there exists such neighbor j with $x_{j,t} \ne x_{i,t}$ where $|x_{j,t} - x_{i,t}| < \epsilon$, for every i. If $x_{j,t} \ne x_{i,t}$ and $\min (d_{ij,t}) > \epsilon$, agent i could not be affected by the opinion of any counterpart, since the closest neighbor to agent i with a distinct opinion is too distant and $C > 1$ with probability one. In a complete network, premise 1 postulates premise 2. Yet, the probability that a certain agent is selected is very small, which would impede the transition towards consensus when the number of appropriate and accessible counterparts is small.

The contraction feature brings two interacting agents closer to each other. If $x_{i,t}, x_{j,t} > x^{*}$,¹¹ then the agent who is closer to $x^{*}$ is by definition moving away from $x^{*}$, which increases his $t+1$ distance to the closest neighbor on the way towards $x^{*}$. If k was the i’s closest counterpart towards $x^{*}$ and did not move in t, while i has moved towards j, then the distance between i and k increased to $|x_{i,t} - x_{k,t}| + \mu d_{ij,t}$, thus imposing the additional burden on the required threshold level for harmonization in subsequent periods.

The results of the simulation-based experiments show some interesting differences in the opinion dynamics across the network topologies. Figure 2 shows that in a complete network some harmonization occurs even when $\epsilon =0.01$. For $\epsilon =0.15$ concentration in opinions is substantial in all network topologies. A global consensus is reached when $\epsilon =0.5$. Since initial opinions across the agents are the same in all experiments, the differences are due to the premises 2 and 3.

Fig. 2

Opinion dynamics within a complete network and small world network for selected threshold levels: $\epsilon = 0.0$ (top), $\epsilon = 0.01$ (line 2), $\epsilon = 0.15$ (line 3), $\epsilon = 0.5$ (bottom). Plots in the left column refer to the complete network and in the right column to the small world network

Corollary 1

Assume a connected society of $n>2$ regular agents with $x_{i,0} \sim U(0,1)$ and $\epsilon _i = \epsilon$. Further assume that they randomly meet with one another. Then such a threshold level $\epsilon _{c1} > 0$ exists, which assigns the outcome $C=1$ some positive probability.

Corollary 2

Assume a connected society of $n>2$ regular agents with $x_{i,0} \sim U(0,1)$ and $\epsilon _i = \epsilon$. Further assume that they randomly meet with one another. Then such threshold level $\epsilon _{c2}<1$ exists, which implies $C=1$ almost surely.

To get an idea of how the threshold level and consensus are related, we provide the following sketch of the proof. Assume a society of $n=4$ agents with initial opinions $x_{1,0}=0, x_{2,0}=0.33, x_{3,0}=0.67$ and $x_{4,0}=1$ and $\mu =0.5$. Due to the path-dependent nature of the opinion formation process, the required $\epsilon ^{*}$ for consensus depends upon the interaction pairs. Case 1: If $x_1$ interacts with $x_3$ and $x_2$ with $x_4$, then they settle for $x_{1,1} = x_{3,1} = 0.34$ and $x_{2,1} = x_{4,1} = 0.67$, which makes $\epsilon ^{*}=0.67$. Case 2: If $x_1$ interacts with $x_2$ and $x_3$ with $x_4$, then they settle for $x_{1,1} = x_{2,1} = 0.17$ and $x_{3,1} = x_{4,1} = 0.83$, but need $\epsilon =0.66$ to settle, which makes $\epsilon ^{*}=0.66$. Case 3: If $x_1$ interacts with $x_4$ and $x_2$ with $x_3$, then $\epsilon ^{*}=0.5$. At $t=1$ the first pair does not settle and the second settles at $x_{2,1} = x_{3,1} = 0.5$. This makes $\epsilon ^{*}=0.5$. Therefore, $\min (\epsilon ^{*})=0.5$ and $\max (\epsilon ^{*})=0.67$.

The corollaries imply that there is a minimum threshold level $\epsilon _{c1}$ at which consensus may be reached and the minimum threshold level $\epsilon _{c2}$ from where on consensus is always reached.

Lemma 4

Let $\overline{x}_t = \frac{1}{n} \sum _{i=1}^{n} x_{i,t}$ be the average opinion of n agents in t and $\overline{x}_0$ the average initial opinion. Assume that $\mu _i = \mu _j$ and $\epsilon _i = \epsilon _j$ for each i, j. Further assume that agents change their opinions according to Eq. (2). Then, $\overline{x}_t = \overline{x}_0$ for every t, $\mu$ and $\epsilon$.

Proof

$\overline{x}_0$ is the average of the initial opinions. From the updating rule it follows that if two interacting agents i and j change their opinions, then $x_{i,t}+\mu (x^{R}_{j,t}-x_{i,t})$ and $x_{j,t}+\mu (x^{R}_{i,t}-x_{j,t})$. For regular agents $x^{R}_{t} = x_{t}$. The cummulative change of the two agents equals to $\mu (x_{j,t}-x_{i,t}) + \mu (x_{i,t}-x_{j,t}) = 0$. If $d_{ij,t} > \epsilon \Rightarrow x_{i,t+1} = x_{i,t}, x_{j,t+1} = x_{j,t}$. $\square$

The lemma says that the average opinion within the society of regular agents with $\epsilon _i = \epsilon$ and $\mu$ is kept constant over time and equals to $\overline{x}_0$. This also means that consensus $x^{*}$ can only be reached in $\overline{x}_0$. Since $E[|X|] < \infty$, $x_{i,0} \sim U(0,1)$ and $n=10{,}000$, we have by the law of large numbers that $\frac{1}{n}\sum _{i=1}^{n} x_{i,0} \rightarrow E[X] = 0.5$ almost surely.¹² This implies that the threshold level $\epsilon ^{*} = 0.5$ brings the society into consensus almost surely since it can extract every agent from the most extreme points.

We simulate the model for 50 times for each threshold level on $0 \le \epsilon \le 1$ with an increment of $\varDelta \epsilon = 0.01$ and find that $\epsilon _{c2} = 0.5$, which is the theoretical condition for consensus. However, simulations show that $\epsilon _{c1} = 0.28$ which means that consensus may be attained for much smaller values of $\epsilon$ (Fig. 3). Moreover, $c_1 = 0.99$ when $\epsilon =0.28$.¹³ Hence, the values would suggest that even a moderately tolerant society actually reaches a consensus, while a larger threshold span is required that all outliers are captured and brought to consensus. The results also show that $\max (c_{2}) = 0.482$ when $\epsilon =0.24$ and $\max (c_{3}) = 0.317$ when $\epsilon =0.14$. Threshold level of $\epsilon =0.28$ represents a strict bifurcation point, increasing $c_1$ from 0.523 $(\epsilon =0.27)$ to 0.999 $(\epsilon =0.28)$. The society could be considered polarized when $\epsilon = 0.18$$(c_1 = 0.512, c_2 = 0.422, c_3 = 0.065)$.

Fig. 3

The average proportion of agents within the leading three opinion classes $c_1$, $c_2$ and $c_3$ as a function of $\epsilon$ in a complete network after 50 repetitions

Proposition 2

A society of n interacting regular agents with $x_{i,t} \sim U(0,1)$ and $\epsilon > 0$ exhibits either a consensus or persistent disagreement but not also a persistent fluctuation in opinions.

Proof

Lemma 3 claims that interacting society of regular agents with $\epsilon > 0$ converges. Convergence denies the existence of a perpetual dynamics, which implies that there cannot be a persistent fluctuation in opinions. We continue with the proof from the Lemma and have to show that the threshold level determines the number of opinion classes. Let there be agents i, j and k with opinions $x_{i,t}> x_{j,t} > x_{k,t}$, respectively. Assume that $s_{ij,t} = \epsilon$ and $d_{jk,t} < \epsilon$, then $d_{ik,t} > \epsilon$. If agent j picks agent k, then $x_{j,t+1} = x_{j,t}+\mu (x_{k,t}-x_{j,t}) \Rightarrow s_{ij,t+1} > \epsilon$. Since $d_{ij,t} = \epsilon$, any move of j increases the distance between the agents beyond $\epsilon$, preventing i to become a member of the opinion class of agents j and k, and $C > 1$. $\square$

The complexity of the process on the small world network and particularly the scale free network is determined by the fact that ${\mathcal {N}}_i \ll n$ for all i and ${\mathcal {N}}_i \ne {\mathcal {N}}_j$.¹⁴ In these networks, only a small proportion of $\frac{|{\mathcal {N}}_i|}{n}$ counterparts can directly affect the opinion of agent i. As a consequence, the validity of premise 1 does not postulate the validity of premise 2 since agent $j \notin {\mathcal {N}}_i$ cannot directly affect the opinion of agent i even though $|x_{j,t} - x_{i,t}| < \epsilon$. In a connected network there exists a connection between any pair of agents i and j through the sequence of links between the connected pairs $(i_i, i_1), (i_1, i_2), \ldots , (i_{j-1}, i_j)$, for which the opinion could be recursively transferred along the path. However, the sequential execution of influences along the path bounds the feasibility of the implementation since agent j would need to change the opinion of agent $j-1$, who would need to change the opinion of $j-2$ and so on until agent i, while the condition $|x_{j,t} - x_{i,t}| < \epsilon$ would need to be satisfied for each pair along the path. The feasibility of this plan is constrained by the fact that agents on the path may change their opinions over time and become too distant for the opinion change when needed. For these reasons, these networks require more tolerant society (higher threshold levels) or larger neighborhoods (Fig. 4) to reach consensus.

Fig. 4

Bifurcation diagrams across the threshold levels and the network topologies; top left: complete network; top right: scale free network; middle left: SW, k = 10; middle right: SW, k = 20; bottom left: SW, k = 30, bottom right: SW, k = 50. Results refer to $t = 50{,}000$

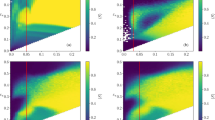
Bifurcation diagrams plot the average proportions of agents with a given opinion at $t=50{,}000$ across $\epsilon$. The color-palette shows proportions of agents with a given opinion. The top left plot refers to the complete network and demonstrates a large level of regularity and simmetry around $\overline{x}_0$. The shape of the most outern surface of the diagram indicates stable convergence sections at the frontier. Transitions across the opinion classes are clearly seen. For instance, in the neighborhood of $\epsilon = 0.15$, the network exhibits three major opinion classes; $x^1 \approx 0.2, x^2 \approx 0.5, x^3 \approx 0.8$.

The scale-free topography (BA), exhibited in the top right section, shows much less organization and symmetry than a complete network. Yet, the network is still capable of producing some leading opinion classes, even though the larger threshold levels are required for a contraction.

The figure reveals that the opinion dynamics on a small world network is very susceptible to the node degree k.¹⁵ Our experiments show that the small world networks efficiently bring the society very close to consensus for even small threshold levels, but fail to capture the outliers when connectivity is small. In the small world networks, consensus thus requires larger threshold levels. Moreover, bifurcation diagrams show that the SW10 network behaves very chaotically for the smallest values of $\epsilon$.

Further, we also examine the size of the largest opinion class $c_1$ within the runs and across the threshold levels (Fig. 5). In the left plot, the lowest value of $c_1$ across the runs for a given threshold level and the network topology is reported, denoted $\min (c_1)$. The right plot reports the highest value of $c_1$ across the runs and the network structures as a function of $\epsilon$, denoted $\max (c_1)$.

Fig. 5

Proportions of agents with the lowest [$\min (c_1)$, left plot] and the highest [$\max (c_1)$, right plot] value of $c_1$ in a single run across the repetitions as a function of $\epsilon$ in a given network topology. Number of repetitions: 50. BA—scale free network; FC—complete network; SW10, 20, 30, 50—small world networks

Comparing the plots, we notice very high variability across the runs in SW10, particularly for small threshold levels, indicating that the degree of consensus in a single run can also be very small, ceteris paribus. For instance, when $\epsilon =0.12$ in SW10, $\max (c_1)=5484, \min (c_1)=181$, making the difference of 5303 agents. This is also the biggest difference between $\max (c_1)$ and $\min (c_1)$ values across the simulations. The intuition is the following. On average, each agent i within the SW10 network only has 10 links, for which the probability that opinions within ${\mathcal {N}}_i$ are dense and evenly dispersed across the opinion scale is smaller than in any bigger community. Moreover, the process is path-dependent and is subject to the contraction principle. Hence, the opinion dynamics within the SW10 network is very susceptible to which counterpart from the neighborhood an agent picks. The smallest maximum difference of 2019 is observed in the complete network, denoted FC, when $\epsilon =0.18$$(\min (c_1)=4066, \max (c_1)=6085)$. A complete network also exhibits the smallest variability across the runs, which means that the outcomes in this network are the most predictable. However, within the range $0.13 \ge \epsilon \ge 0.27$, the complete network exhibits the lowest min–min values, which means that within this range the network is the least capable of reaching the desired level of consensus. For instance, when $\epsilon =0.27$, $\min (c_1) = 5076$ in a complete network, while $\min (c_1) > 9500$ in other networks that we use. Generally, opinions exhibit the largest variability when $\epsilon =0.12$. The largest variability at the single threshold level was observed in the scale free network when $\epsilon =0.26$, because the outcomes of $c_1$ fluctuated between 0.95 and 0.5.

Interesting results are observed within the small world networks. The figures show that a small and initially inhomogeneous group requires more tolerant members to reach consensus since agents may be located too far apart from each other. With the increase of the average node degree and hence the agents’ neighborhoods, the structure of the small world network becones similar to the structure of the complete network. On the one side, initial opinions are likely to be more evenly distributed and closer to one another. Yet, the enlarged neighborhoods increase the problem of a selection, as postulated by premise 3. We can thus confirm our previous expectations that the complete network faces the problem of selection (premise 3), while the small world networks face the problem of accessibility (premise 2). Those who would prefer sufficient degree of consensus would choose a SW10 network, while the preference towards consensus would prefer complete or SW50 network.

5 Opinion Formation with Regular and Stubborn Agents

Cases in which all agents are regular are rare. Assume now that the set of agents ${\mathcal {V}}$ is divided into two distinct groups, ${\mathcal {V}}^{R} \subset {\mathcal {V}}$ representing the subset of regular agents and ${\mathcal {V}}^{S} \subset {\mathcal {V}}$ representing the subset of stubborn agents, with ${\mathcal {V}}^S \cup {\mathcal {V}}^R = {\mathcal {V}}$ and ${\mathcal {V}}^S \cap {\mathcal {V}}^R = \emptyset$.

Definition 4

Agent i is denoted a stubborn agent if at least one of the two parameter values ($\epsilon _i$, $\mu$) is zero.

Stubborn agents may be described as highly persuaded individuals or extremely conservative individuals who do not change their initial opinion.¹⁶ According to Watts and Dodds (2007), they may be considered the opinion leaders in a sense that they have the ability to exert their extreme opinion onto others but are not willing to change theirs.

Let there be $\vert {\mathcal {V}}^{S} \vert = 1000$ and $\vert {\mathcal {V}}^{R} \vert = 10{,}000$. Stubborn agents are assigned the same initial opinion $x^{S}$. For simplicity, we put the stubborn agents on the bottom extreme $x^S = 0$. Since $x^{S}_{t} = x^{S}_{0}$, we omit the time index for the opinions of stubborn agents. We introduce the following two additional assumptions. First, stubborn agents cannot be distinguished from other regular agents and are members of the regular agents’ neighborhoods. Since regular agents cannot identify and avoid them, stubborn agents regularly interact with the neighbors. Second, stubborn agents do not know the threshold levels nor the opinions of their counterparts.

Using the result of Lemma 3, we show that the environment of regular and a single group of stubborn agents may either reach consensus or permanent disagreement and cannot end in a perpetual opinion dynamics.

Lemma 5

The interacting society of regular agents with $\epsilon _i = \epsilon$ and a group of stubborn agents with $x^S$ converges.

The proof follows the explanation of Lemma 3. However, the presence of the stubborn agents changes the conditions of Lemma 4, since $\epsilon _i \ne \epsilon _S$, except when $\epsilon _i = 0$. Principally, the opinion of the stubborn agents exhibits a relative dominance because if $d_{is,t} < \epsilon$, then $x^{S}_{t+1} = x^{S}_{t}$ and $x_{i, t+1} = x_{i,t}+\mu (x^{S}_{t}-x_{i,t})$. Since only regular agents tend to modify their opinions, the updating rule is not symmetric anymore. Hence, the average opinion in a society is not constant over time but, for sufficiently large threshold levels, tends to $x^S$. Because regular agents change their opinion on the proximity basis, the question of interest is how is the opinion process affected by the regular agents’ threshold levels. We start with the conditions for consensus, because any deviation means a permanent disagreement.

Corollary 3

If ${\mathcal {V}}^{R}$ is a subset of regular agents with $x_{i,0} \sim U(0,1)$ and $\epsilon _i = \epsilon$ and ${\mathcal {V}}^S$ is a subset of stubborn agents with $x^{S} = 0$ and $\epsilon _S = 0$, then with probability 1 such a minimal threshold level $\epsilon _{s} < 1$ exists in the complete network where $x_{i,t} = x^{S}$ for all i, almost surely.

Proof

Following the updating rule, consensus can only occur at $x^S$. By assumption $x^S = 0$, which implies $\max s(x^S, x_{i,0}) = 1$. Since the stubborn agents can reach every agent with $\epsilon =1$, this would require that regular agents themselves bring the extreme counterparts from the extreme. We can use the result of Lemma 3 and the Corollaries 1 and 2 to show that the system of perpetual interaction converges towards the center of the opinion space when $\epsilon \ll 1$. Since $x_{i,0} \sim U(0,1)$ and ${\mathcal {N}}_i = n$, agent with $x_{j,0}=1$ will be chosen by the non-extreme agent with probability 1, almost surely. Once the regular agent with $x_{j,0}=1$ is extracted from the extreme, $|x_{j,1}-x^S| < 1$. $\square$

For example, as shown on the left plot of Fig. 6, $\epsilon =0.6 \Rightarrow x^{*} = x^S$. Figure on the right displays the average proportions of regular agents with the extreme opinion as a function of $\epsilon$. It shows that society leads to extremism under the influence of minority of stubborn extremists when $\epsilon \ge 0.42$.

Fig. 6

Opinion dynamics in a society of regular agents and a group of stubborn agents with $x^{S}=0$. Left plot: $\epsilon =0.6$, $\mu = 0.2$. First 120 iterations are displayed. Right plot: proportion of regular agents with $x^S$ as a funcion of $\epsilon$

Notice that the proportion of regular agents who adopt the extreme opinion of the stubborn agents is not monotonically increasing in $\epsilon$, as one would expect. The results show that there is a tolerance span in which the proportion of extremism among regular agents decreases as the tolerance level increases. One can observe several phase transitions across $\epsilon$. At the beginning, the proportion of extremism increases with the agents’ tolerance until $\epsilon <0.2$, reaching 58% of regular agents. Agents who are grasped are those who would in an all-regular setting form a separate opinion class in the bottom half of the opinion space within the reach of the stubborn extremists. A decay occurs at $\epsilon =0.21$ and is followed by a sharp decay at $\epsilon =0.31$. Within the span $0.32< \epsilon < 0.42$, none regular agent adopts the extreme opinion. This is a striking result.

To explain the apparent inconsistency, we go back to the setting with only regular agents, where the strict tendency towards consensus $x^{*} = 0.5$ was identified from $\epsilon \ge 0.28$. Stubborn extremists can directly influence the regular agents in the proximity until $x_{i,t} \le \epsilon$ and bring them towards the bottom. In addition, regular agents themselves may keep themselves in the vicinity of the stubborn extremists. However, since $\vert {\mathcal {V}}^{S} \vert \ll n$, the intensity of contacts between regular and stubborn agents is strictly limited. Because opinions are agents’ private information until revealed, stubborn agents cannot identify vulnerable and accessible agents but pick them randomly. Hence, the number of actual contacts between the stubborn and accessible agents is strictly smaller from the number of potential contacts. The increased threshold level increases the proportion of regular agents from the above who could bring their counterparts out of the extremists’ reach. As long as the agents’ tolerance is below the distance to the stubborn agents, regular agents will tend to move away from the bottom extreme. As the number of regular agents that move upwards increases, the probability that agents from the bottom will meet an agent with the opinion that would be close to the bottom extreme decreases, while the probability that they will interact with a counterpart with the opinion from the upper side and whose opinion would be within his tolerance level increases. Even though some regular agents could be grabbed by the extreme stubborn agents, there is a sufficient number of other regular agents who may not be reached by the stubborn extremists but could and would attract the agents with the opinions close to the extreme, thus directing them towards the center of the opinion space. As a consequence, only a few of the regular agents would have adopted the extreme opinion of the stubborn agents.

As the threshold level still increases, the extreme stubborn agents can also reach more distant counterparts. Moreover, regular agents from the upper part of the opinion scale also tend to go towards the center because they are more easily influenced by their counterparts when the threshold is larger. This brings them closer to the stubborn extremists who can impose a direct influence when $x_{i,t} \le \epsilon$.

There is a a sharp reversal towards extremism at $\epsilon =0.42$, indicating the presence of the Paradox of tolerance, described by Popper (1945). The paradox says that the ability of a highly tolerant society to be tolerant will be seized by the intolerant members. Simulations have shown that the minimum threshold level at which at least one run converged into $x^{*} = x^S = 0$ is reached when $\epsilon =0.44$. Consensus is always reached when $\epsilon \ge 0.58$. We notice that both levels are well above the corresponding levels from the environment of only regular agents. This is because higher tolerance is needed to bring the agents from the upper extreme to the bottom, while in the setting of regular agents consensus was reached in the proximity of 0.5.

We may find several examples of this kind. The most representative may be the rise to power of several dictators and autocrats, such as in Germany in the 1930s, the Iranian revolution in the 1970s, which was much less escorted by the use of force than it grew from the influence of initially small group of ideological leaders. In the pop-culture, the sudden rise and fall of unknown artists also seems to follow this pattern.

6 Opinion Formation with Two Groups of Stubborn Agents

In the previous section there was only one group of stubborn extremists along the regular agents. In real life, one would often find the stubborn agents also on the opposing extreme. To consider for this, we extend the previous setting by introducing another group of stubborn agents with the extreme opinion. We thus have $x^{S0} = 0$ and $x^{S1} = 1$. We assume that the groups of stubborn agents are equally sized, consisting of 500 stubborn agents each. Again, $x_{i,0} \sim U(0,1)$. Let us put a very general proposition.

Proposition 3

Let there be a set of regular agents with $x_{i,0}\sim U(0,1)$ and $\epsilon >0$ and $\mu >0$ and two sets of stubborn agents ${\mathcal {V}}^{S0}$ and ${\mathcal {V}}^{S1}$ with opinions $x_{S0}=0$ and $x_{S1}=1$, respectively. Then such a threshold level $\epsilon > 0$ exists which exhibits:

• 1. consensus,

• 2. polarization,

• 3. pluralism or

• 4. perpetual opinion dynamics.

Before proceeding with the exposition of Proposition 3, we present some intuition and insights about these different states. Depending upon the regular agents’ tolerance level, the influence of the extremists can be local, they may attract a part of the population, the entire population or none. Under the proposition, the consensus means that all regular agents end up in the same opinion class after some finite time $t_c \in t$ and $C=1$. Polarization means that regular agents are split into two extremes after some finite time $t_c \in t$ and $C=2$. Pluralism means that regular agents are divided within the two extremes after some finite time $t_c \in t$ and $C>2$ such that a portion of them forms additional opinion classes. Perpetual opinion dynamics means that regular agents continuously change their opinions.

We test the proposition through a series of simulation-based experiments on a complete network. We do 50 repetitions for each threshold level $\epsilon$. Figure 7 presents the entire developments of selected runs. Figure 8 displays the average number of final opinion classes in $T=50{,}000$ across $\epsilon$.

Fig. 7

Opinion dynamics with regular agents and two groups of stubborn agents. Selected single runs for the given parameter values are displayed. The values for stubborn agents in the first four plots are the same and equal to: $x^{S0}=0$, $x^{S1}=1$. Regular agents: (top left) $\epsilon =0.28$; (top right) $\epsilon =0.6$; (bottom left) $\epsilon =0.55$; (bottom right) $\epsilon =0.47$

Fig. 8

Left: opinions of regular agents as the function of $\epsilon$. Right plot: proportion of regular agents with the extreme opinions across $\epsilon$

Both figures reveal that in the presence of two opposing stubborn groups the process of opinion dynamics is highly sensitive to $\epsilon$, exhibiting very rich and complex structure and some sharp phase transitions. A great part of this diversity is caused because the opinions of stubborn agents create a bandwidth in which the opinions of regular agents may be caught and influenced by both groups.

In a weakly tolerant society in which the value of $\epsilon$ is small, the group of regular agents exhibits a plurality of opinions, which is represented by a persistent disagreement in society but not also a persistent fluctuation in opinions. The level of extremism in a society is small and split between the two groups, since each extreme group grasps the agents in its proximity. The remainder of regular agents form a fixed number of intermediate opinion classes. As the threshold levels increase, the fraction of regular agents who are within reach of the extreme stubborn agents increases. Hence, the smaller is the number of these intermediate classes and the larger are the extremist groups. At a sufficiently large $\epsilon$, the majority of regular agents concentrate at both extremes and about a third move to the center of the opinion space, where the distance between the average opinion of the regular cluster and both extremes is the largest. After a slight increase of $\epsilon$ from this tipping point equilibrium at $\epsilon \approx 0.18$, the power of extremist agents collapses and two stable, but intermediate, opinion centers prevail at about half the distance between extreme poles and the middle of the opinion space. Up to this point, a homogenisation of the opinion space is observed with a manifold of opinion clusters without changes in the cluster membership after some time t.

Further increases of the threshold level in the society cause the reduction in the size of both non-extreme classes up to another tipping point at $\epsilon \approx 0.28$, where the extremism prevails and the society ends in a complete polarisation of the opinion space. This is demonstrated on the top-left diagram on Fig. 7 and both diagrams on Fig. 8. The polarisation phase in our simulation experiments is stable in all 50 repetitions and it seems that it appears only within a narrow threshold span.

Further increases of $\epsilon$ from the polarisation phase cause another sharp bifurcation of stable equilibrium opinion in which the regular agents all concentrate in the center, forming a large single opinion class. The bottom-right diagram on Fig. 7, the bifurcation diagram on Fig. 8 and the extremist-share diagram on the Fig. 8 confirm the existence of the phase transition from a complete polarisation to a complete consensus among the regular agents at around the middle of the opinion spectrum at moderate levels of $0.3<\epsilon <0.5$. Consensus can also be represented through the emergence of the totalitarianism, which occurs for $\epsilon \approx 0.5$. This is represented by the bottom left diagram on Fig. 7 and by both diagrams from Fig. 8.

Finally, there is a threshold level beyond which the society enters the perpetual opinion dynamics not only a long run disagreement. This occurs when opinions of highly tolerant regular agents are trapped between the opinions of stubborn agents and are regularly affected by members of both these groups, and also by the opinions of other regular agents. Each extreme pole pushes the opinion in the society towards itself, but jointly they stabilize in the middle of the opinion space. This result points us to the state in a highly tolerant society $\epsilon \ge 0.6$ in which the two competing extremist groups have no supporters among the regular agents whose opinions are oscillating around the center of the opinion space. Recall that in the model of a single extreme group, tolerance and the level of extremism were positively correlated. This is not the case here. This is very powerful conclusion with some meaningful policy implications as it says that extremism can be neutralized by introducing a competing extreme group with the opposing attitude. We denote this state the Paradox of extremism.

7 Opinion Formation with Inconsistent Agents

One of the model’s fundamental principles is that agents establish the attitude towards the opinion they hear. In the previous sections we have (implicitly) postulated sincere agents with $x^{R}_{i,t} = x_{i,t}$. This is also the assumption that one finds in other models of opinion formation. In this part, we slightly retract from this assumption and assume that the society includes a portion of insincere counterparts.¹⁷ Let us define the inconsistent agent first.

Definition 5

Let $x_{i,t}$ be the opinion of agent i in period t and $x^{R}_{i,t}$ the reported opinion to the counterpart in t. An agent is said to be inconsistent if $x^{R}_{i,t} \sim U(0,1)$.

With the inclusion of the inconsistent agents, the society ${\mathcal {V}}$ can be split onto a set regular agents ${\mathcal {V}}^{R} \subset {\mathcal {V}}$ with $x_{i,0} \sim U(0,1)$ and $x^{R}_{i,t} = x_{i,t}$, and a finite subset ${\mathcal {V}}^{F} \subset {\mathcal {V}}$ of insincere agents with $x^{F}_{i,0} \sim U(0,1)$ and $x^{R}_{i,t} \ne x_{i,t}$, with $F \ll n$ and ${\mathcal {V}}^{R} \cup {\mathcal {V}}^{F} = {\mathcal {V}}$. We assume $|{\mathcal {V}}^{F}| = 1000$.

Inconsistency is modeled as the agent’s inability to honestly report his opinion to the selected counterpart. For simplicity, we assume that an inconsistent agent reports a random opinion to the selected counterpart. Because $x^{R}_{i,t} \sim U(0,1)$, the assumption that insincere agents do not know the threshold levels of regular agents has no practical importance for the behavior of inconsistent agents and is thus irrelevant, although still kept. On the other side, regular agents are assumed to lack the ability to identify insincere agents, for which they cannot avoid them. Therefore, the inconsistent agents persistently affect the opinion dynamics of regular agents.

Fig. 9

Left plot: opinion dynamics with a set of 10, 000 regular agents and $F=1000$ inconsistent agents; $\epsilon =0.4, \mu =0.2$. Right plot: bifurcation as a function of $\epsilon$

Proposition 4

The environment of a subset of regular agents with $x_{i,0} \sim U(0,1)$ and a subset of inconsistent agents with $x^{R}_{i,t} \sim U(0,1)$ induces a perpetual opinion dynamics for any $\epsilon >0$ and $\mu >0$.

Proposition is the implication of the following lemma claiming that such an environment does not converge.

Lemma 6

The interacting society of regular agents with $\epsilon > 0$ and $\mu > 0$ and a group of inconsistent agents with $x^{R}_{i,t} \sim U(0,1)$ does not converge.

Proof

An inconsistent agent can affect the opinion of a regular agent if and only if he is contacted and $|x^{R}_{i,t} - x_{i,t}| < \epsilon$. Assumptions that agents meet randomly and that inconsistent agents cannot be identified and avoided induce that there is always a non-zero probability $p = \frac{F}{(n-1)}$ that an inconsistent agent is selected, with $0<F<n$ representing the number of inconsistent agents in society. The assumption that $x^{R}_{i,t} \sim U(0,1)$ for an inconsistent agent assures that for any $\epsilon >0$, there is almost surely an opinion of an inconsistent agent $x^{R}_{i,t}$ which would imply $|x^{R}_{i,t} - x_{i,t}| < \epsilon$.

$\square$

Since there is no convergence, the process exhibits a perpetual opinion dynamics.

In the left plot of Fig. 9, we display the opinion dynamics in a selected run with $x_{i,0} \sim U(0,1), \epsilon =0.4$ and a set of $F=1000$ inconsistent agents. The plot on the right side of the figure displays the average proportions of regular agents per opinion as a function of threshold level d. The figures show that inconsistent agents induce a permanent influence onto the opinion formation process, leading to a perpetual opinion dynamics. The influences of the inconsistent agents are not only direct. The second-order influences are induced through interaction between the agents, reflecting the idea of epidemic models and the spread of viruses (Newman 2002; Pastor-Satorras and Vespignani 2001). This may explain very unique shapes of the bifurcation diagram.

8 Conclusions

We have constructed and simulated a discrete-time continuous-opinion model under bounded confidence with random meetings to examine the role of different circumstances on the process of opinion formation. The model was simulated on a complete network, small world network and the scale free network. Our findings can be summarized as follows.

The society of regular agents with homogeneous threshold levels always converges to the fixed number of opinion classes, while the number of classes is determined by the agents’ threshold levels. At least moderate threshold levels are required for consensus to emerge. We have shown that the network topology is important for the opinion formation process. The runs with a single group of stubborn agents have shown that extremism is not epidemic but conditional upon the regular agents’ threshold levels. Here we show that even a moderately tolerant society can become fully extreme. Extremism can be avoided when the additional group of stubborn agents exists on the opposite extreme, because tolerant individuals will traverse between the two groups and will never become extreme. Moreover, the runs with two groups of stubborn agents exhibit a very rich and complex structure, ranging from consensus, multiple opinion clusters to the perpetual opinion dynamics. We also identified some sharp phase-transitions between different opinion states. Introduction of insincere agents substantially affect the opinion dynamics within the integrated community, particularly when they refer to inconsistent agents.

We have shown that even simple models of opinion formation are subject to nonlinearities in that the process of opinion dynamics constantly changes with the agents’ current opinions and that our analysis can help us understand these peculiarities and the circumstances that lead a society into either a consensus, multiple opinion clusters or a perpetual opinion dynamics.