Two-phase semi-Lagrangian relaxation for solving the uncapacitated distribution centers location problem for B2C E-commerce

Abstract

This paper develops a mixed integer programming model for determining uncapacitated distribution centers location (UDCL) for B2C E-commerce. Based on the characteristics of distribution system for B2C E-commerce firms, the impact of supply cost of multi-commodity is considered in this model. Combining with the properties of the semi-Lagrangian relaxation (SLR) dual problem in the UDCL case, a two-phase SLR algorithm with good convergency property is furthermore developed for solving the UDCL problem. For the sake of contrastive analysis, this paper has performed computational experiments on 15 UDCL instances by the mixed integer programming solver, CPLEX, and the approach obtained by combining two-phase SLR algorithm with CPLEX, respectively. The numerical results show that the two-phase SLR algorithm not only can improve the solving speed of the CPLEX solver, but also can provide better results in reasonable time for most instances.

1 Introduction

Compared with traditional commerce, business-to-consumer (B2C) E-commerce has advantages in reducing investment cost and selling cost by using internet and Web technologies [20]. However, since B2C E-commerce firms must deliver commodities to customers who have the characteristics of numerous multi-variety small batch demands and decentralized locations, their logistics cost is increased [20]. Therefore, with competition and economy fluctuations in recent years, it is very necessary for B2C E-commerce firms to reduce logistics cost and improve customer service.

Depots, distribution centers and customers are important members of a distribution network. When the distribution centers are constructed, the commodities will be shipped from the depots to the customers via the distribution centers. The more distribution centers are constructed, the better customer service will be, but the higher construction cost will be. If location-allocation of the distribution centers are not appropriate, the service level will be reduced and logistics cost will be increased. Appropriate distribution centers location can not only reduce logistics cost but also enhance service level and profits [30, 32]. Therefore, it is necessary for a B2C E-commerce firm to find the best plan to locate its distribution centers.

In the distribution system for B2C E-commerce firms, the establishment of distribution centers needs some installing and operating cost, while transporting commodities not only needs transportation cost but also needs supply cost and turnover cost at depots and distribution centers, respectively. Thus, the distribution centers location problem involves how to select locations of distribution centers from the potential candidates and how to transport commodities from the depots to customers via distribution centers so that the total relevant cost is minimized [32].

Distribution centers location (DCL) is one of the practical applications of facility location (FL) which has been a well-known research topic in the operation research community [18, 24]. The challenge for best locating facilities has attracted much attention and ever expanding family of models has emerged. FL models can be broadly classified into two categories: continuous location models and (mixed) integer programming models. Continuous location model was proposed in 1909 when Weber first considered how to locate a single warehouse so as to minimize the total distance between it and its customers [18]. Then several extended versions of this problem were investigated in literatures, such as multi-source Weber problem [18], the location problems of maximizing minimum distances, problems with barriers and so on. A rough classification of (mixed) integer programming models can be given as follows: (a) capacitated models versus uncapacitated models, (b) single-stage models versus multi-stage models [2, 22, 31, 33], (c) single-commodity models versus multi-commodity models [21, 26], (d) static models versus dynamic models [3], (e) deterministic models versus uncertain models [15, 20, 32], (f) single-source models versus multiple-source models, (g) single-objective models versus multi-objective models [12, 17], (h) single-level models versus multi-level models [8, 27]. A brief introduction and surveys of FL models appear in [18].

Numerous heuristic algorithms [14, 20, 32], approximate algorithms [1, 23] and exact algorithms [33] for solving the FL problems have been discussed in literatures. Although heuristic algorithms such as genetic algorithm [20] and tabu search algorithm [32], are widely used for solving complicated optimization problems [14], various heuristic algorithms have the disadvantages of premature convergence and low search efficiency. Thus, in order to overcome the limitation of a single heuristic algorithm, various hybrid heuristic algorithms were proposed to solve the FL problems in recent years, for instance, hybrid firefly-genetic algorithm [29], iterated tabu search heuristic [13], Lagrangian heuristic and ant colony system [7], swarm intelligence based on sample average approximation [4], improved genetic algorithm with particle swarm optimization [20]. Numerous exact algorithms for solving the FL problems usually combine branch-and-bound search with some bounding techniques, such as column generation and branch-and-price method [19], branch-and-bound-and-cut algorithm [28]. Lagrangian relaxation, one of the most popular bounding techniques, which has also been used to solve the FL problems [11, 34]. Recently, semi-Lagrangian relaxation (SLR) [5, 6, 10, 16, 25], an improved Lagrangian relaxation method, has been applied to solve the FL problems by means of general purpose mixed integer programming solvers, for example, CPLEX. The SLR shows no duality gap [5, 6, 16, 25] and therefore it constitutes exact solution procedures.

The objectives that are usually considered in FL problems can be different [9]. Most of them can be as follows: (a) minimizing the longest distance from the existing facilities, (b) minimizing fixed cost, (c) minimizing total annual operating cost, (d) minimizing the number of located facilities, (e) minimizing average time/distance traveled, (f) minimizing maximum time/distance traveled, (g) maximizing service, (h) maximizing responsiveness. Recently, environmental and social objectives based on energy cost, land use and construction cost, congestion, noise, quality of life, pollution, fossil fuel crisis and tourism are also becoming customary [9].

It is worth pointing out that most of the (mixed) integer programming models presented in DCL literatures, which aim to minimize the logistics cost, cannot be directly applied to optimize the location of distribution centers in B2C E-commerce. There is one main reason for this: the existing literatures focus almost exclusively on how to optimize the site and the number of distribution centers [20], and neglect the supply cost generated by all of the activities which are associated with distributing commodities at depots, such as handling, packing, loading and so on. Customers of B2C E-commerce firms are no longer a few retailers or wholesales with mass and centralized demands but lots of terminal customers whose demands are small, various and decentralized [20]. Therefore, the largely increasing supply cost in B2C E-commerce has a great impact on the location of the distribution centers.

Motivated by the special customer characteristics of B2C E-commerce, a multi-commodity, multi-stage and uncapacitated distribution centers location (UDCL) model considering the supply cost is proposed in this paper. Then, some good theoretical properties are investigated when semi-Lagrangian relaxation is applied to solve the proposed model.

The outline of this paper is as follows. In Sect. 2 we present a multi-commodity, multi-stage and uncapacitated distribution centers location model for the B2C E-commerce. In Sect. 3 we first briefly review the main properties of the SLR, then apply it to the UDCL model. In Sect. 4, in conjunction with the properties of the SLR dual problem in the UDCL case, we derive a two-phase SLR algorithm. In Sect. 5, the two-phase SLR algorithm is tested by solving a set of UDCL instances. Finally, concluding remarks are given in Sect. 6.

2 The uncapacitated distribution centers location (UDCL) problem for B2C E-commerce

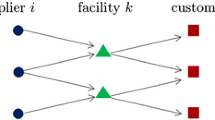
Considering the distribution network of a B2C E-commerce firm with a international/national presence and several inventory depots attached to it, the firm distributes different commodities from depots to its customers through a network of uncapacitated distribution centers located in different locations. It is assumed that one depot can deliver commodities to any distribution center and one customer can be served by one distribution center only. However, one distribution center can serve more than one customer. To understand this problem easily, we can consult Fig. 1.

Fig. 1

Distribution network of a B2C E-commerce firm

This paper considers five kinds of costs generated by the distribution into the model: (1) supply cost at each depot; (2) transportation cost from the depots to the distribution centers; (3) fixed cost of installing and operating distribution centers; (4) turnover cost of commodities at distribution centers; (5) transportation cost from the distribution centers to the customers. The total distribution cost is not only related to the units of commodities transacted but also relied on the locations of the distribution centers and the allocation of customers.

Decision makers need to perform three tasks: (1) choose the building sites of the uncapacitated distribution centers from the potential set; (2) allocate the customers to the selected distribution centers; (3) determine the amount of commodities transported from each depot to each selected distribution center without exceeding the supply of commodities. For the results of this decision, there are two requirements including satisfying the demand of each customer and minimizing the total cost.

In order to model the uncapacitated distribution centers location problem, the following notations for the parameters are defined:

• $I=\{i|i=1,2,\ldots , M\}$, set of commodity depots;

• $J=\{j|j=1,2,\ldots , N\}$, set of distribution center candidates;

• $K=\{k|k=1,2,\ldots , R\}$, set of customers;

• $L=\{l|l=1,2,\ldots , T\}$, set of commodity categories;

• $p_{il}=$ the cost of supplying one unit of commodity l at depot i;

• $c_{ijl}=$ the cost of transporting one unit of commodity l from depot i to distribution center j;

• $g_{j}=$ the fixed cost including installing and operating distribution center j;

• $t_{jkl}=$ the cost of transporting one unit of commodity l from distribution center j to customer k;

• $d_{kl}=$ the demands of customer k for commodity l;

• $h_{jl}=$ the turnover cost of one unit of commodity l at the distribution center j;

• $A_{il}=$ the maximal supply of commodity l at depot i in the planning period.

For this problem, we need to select several distribution centers from the potential set $J=\{1,2,\ldots , N\}$ and allocate each customer $k\in K$ to a single selected distribution center. We use the binary variables $y_j$ and $z_{jk}$ to denote whether the distribution center j is selected or not and whether the distribution center j serves customer k or not, respectively. That is,

$$\begin{aligned} y_{j}= & {} \left\{ \begin{array}{ll} 1, &{}\ \ \text {if the distribution center}\ j \ \text {is selected},\\ 0, &{}\ \ \text {otherwise.}\\ \end{array} \right. \\ z_{jk}= & {} \left\{ \begin{array}{ll} 1, &{}\ \ \text {if the distribution center}\ j \ \text {serves customer} \ k,\\ 0, &{}\ \ \text {otherwise.}\\ \end{array} \right. \end{aligned}$$

In addition, we use one set of nonnegative continuous variables to represent the multi-commodity flows from the depots to the selected distribution centers:

• $x_{ijl}=$ the amount of commodity l transported from the depot i to the distribution center j.

The model considers the minimization of the total relevant cost, subject to constraints on the supply of each depot and the conservation of commodity flow at each distribution center.

$$\begin{aligned} \begin{aligned} f(\mathbf {x,y,z})&= \sum _{i\in I}\sum _{l\in L}p_{il}\sum _{j\in J}x_{ijl}+\sum _{i\in I}\sum _{j\in J}\sum _{l\in L}c_{ijl}x_{ijl}\\&\quad + \sum _{j\in J}g_{j}y_{j}+\sum _{j\in J}\sum _{l\in L}h_{jl}\sum _{i\in I}x_{ijl}+ \sum _{j\in J}\sum _{k\in K}\sum _{l\in L}t_{jkl}d_{kl}z_{jk}&\end{aligned} \end{aligned}$$

(1)

Minimize $f(\mathbf {x,y,z})$ subjects to the following constraints:

$$\begin{aligned}&\sum _{i\in I}x_{ijl}= \sum _{k\in K}d_{kl}z_{jk},\quad j\in J,\ \ l\in L \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j\in J}z_{jk}= 1,\quad k\in K \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{j\in J}x_{ijl}\le A_{il},\quad i\in I,\ \ l\in L \end{aligned}$$

(4)

$$\begin{aligned}&z_{jk}\le y_{j},\quad j\in J,\ \ k\in K \end{aligned}$$

(5)

$$\begin{aligned}&x_{ijl}\ge 0,\quad i\in I ,\ \ j\in J,\ \ l\in L \end{aligned}$$

(6)

$$\begin{aligned}&y_{j}\in \{0,1 \},\quad j\in J \end{aligned}$$

(7)

$$\begin{aligned}&z_{jk}\in \{0,1 \},\quad j\in J, \ \ k\in K \end{aligned}$$

(8)

Equation (1) expresses the objective of minimizing the total cost of the whole distribution system. The total cost consists of 5 parts, which are the cost of supplying commodities at depots , the cost of shipping commodities from depots to distribution centers, the cost of fixed installing and operating distribution centers, commodity turnover cost at distribution centers and transportation cost from distribution centers to customers. Constraints (2) are the commodity flow conservation constrains which ensure the total amount of commodity $l\in L$ shipped from the depots to the distribution center $j\in J$ are equal to the amount shipped out from the distribution center $j\in J$. Constraints (3) guarantee only one distribution center serves one customer. Constraints (4) take care of limited supply of commodity $l\in L$ at depot $i\in I$. Constraints (5) couple the location and the assignment decision.

The supply cost is included in (1)–(8). As mentioned in Sect. 1, this is the main difference between the new model (1)–(8) and other location models presented in literatures.

3 Semi-Lagrangian relaxation and the UDCL problem

3.1 SLR concepts and properties

The semi-Lagrangian relaxation was introduced in [5] and applied to the uncapacitated facility location (UFL) problem in [6, 16, 25]. In this section, we briefly summarize the main results obtained in [5, 6]. Consider the following problem, to be named “primal” henceforth:

$$\begin{aligned} z^* =\min _x&c^Tx \end{aligned}$$

(9)

$$\begin{aligned} \text{ s.t. }&Ax = b, \end{aligned}$$

(10)

$$\begin{aligned}&x \in X \subset S \cap \mathbb {N}^n, \end{aligned}$$

(11)

where $A \in \mathbb {R}^m \times \mathbb {R}^n$ is a rational matrix, and the components of $b \in \mathbb {R}^m$ and $c \in \mathbb {R}^n$ are nonnegative. Furthermore, S is a polyhedral set and $0 \in X$. Unless otherwise stated, it will be assumed throughout the paper that (9)–(11) has an optimal solution.

The semi-Lagrangian relaxation consists in substituting the constraint $Ax = b$ by the equivalent pair of constraints $Ax \le b$ and $Ax \ge b$, and then relaxing $Ax \ge b$ only. We thus obtain the SLR dual problem

$$\begin{aligned} q^* = \max _{u\in U} q(u), \end{aligned}$$

(12)

where $U = \mathbb {R}^m_+$ and q(u) is the semi-Lagrangian dual function defined as

$$\begin{aligned} q(u) =\min _x&c^Tx + u^T(b-Ax) \end{aligned}$$

(13)

$$\begin{aligned} \text{ s.t. }&Ax \le b, \end{aligned}$$

(14)

$$\begin{aligned}&x \in X . \end{aligned}$$

(15)

Note that we have to solve problem (13)–(15) for calculating q(u), which we call the oracle at u. Also note that with our assumptions its feasible set is bounded. We also have that $x = 0$ is feasible to the oracle; hence it has an optimal solution. q(u) is well-defined, but the minimizer in (13)–(15) is not necessarily unique. With some abuse of notation, we write

$$\begin{aligned} x(u) = \arg \min _x\{ c^Tx + u^T(b-Ax) \mid Ax \le b,\quad x \in X\} \end{aligned}$$

to denote one such minimizer.

We denote $X^*, U^*$ and X(u) the set of optimal solutions of problem (9)–(11), (12) and (13)–(15), respectively. We say that $(x^*, u^*)$ is an optimal primal-dual point if $u^*\in \text{ int }(U^*)$ and $x^*\in X(u^*) \cap X^*.$ Given two sets $S_1$ and $S_2$, its addition corresponds to $S_1+S_2 = \{ s_1 + s_2 : s_1\in S_1 \text{ and } s_2\in S_2\}.$ For any set S, int(S) stands for its interior. Furthermore, given two vectors u and v, we will write $u\le v$ to mean that $u_i\le v_i$ for each component i. Finally, for any scalar x, we define the negative part of x as

$$\begin{aligned}{}[x]^- := -\min \{x, 0\} \end{aligned}$$

and its positive part as

$$\begin{aligned}{}[x]^+ := \max \{x, 0\}. \end{aligned}$$

Theorem 1

[5, 6] The following statements hold true.

• 1. q(u) is concave and $b - Ax(u)$ is a subgradient at u.

• 2. q(u) is monotone and $q(u') \ge q(u)$ if $u' \ge u$, with strict inequality if $u' > u$ and $u' \not \in U^*$.

• 3. $U^* + \mathbb {R}^m_+ = U^*$; thus $U^*$ is an unbounded (convex) set.

• 4. If x(u) is such that $Ax(u) = b$, then $u \in U^*$ and $x(u)\in X^*.$

• 5. Conversely, if $u\in \text{ int }(U^*)$, then any $x(u)\in X^*.$

• 6. The SLR closes the duality gap for problem (9)–(11), that is, $z^* = q^*.$

From the definition of the SLR of problem (9)–(11), it is easy to know that the SLR can be applied to both pure integer linear programming problem and mixed integer linear programming problem. Beltran et al. [5, 6] proposed the SLR of integer linear programming problem (9)–(11), and gave an explicit proof of Theorem 1. Note that all of the variables in (9)–(11) and (13)–(15) should be integer, which was not considered in the proof of Theorem 1 presented in [5, 6]. Therefore, the statements in Theorem 1 also hold true when the SLR is applied to mixed integer linear programming problem.

3.2 SLR applied to the UDCL problem

Following the ideas of the preceding section, we formulate the semi-Lagrangian relaxation of the UDCL problem (1)–(8). We obtain the SLR dual problem

$$\begin{aligned} \max _{u\in U,\ v\in V } \ \mathcal {L}_{SLR}(u,v ) \end{aligned}$$

(16)

and the dual function (note that, now, we keep the equality constraints (2) and (3) as inequalities)

$$\begin{aligned} \mathcal {L}_{SLR}(u,v )= \displaystyle \min _{x,y,z} &\mathcal {L}(u,v,x,y,z) \end{aligned}$$

(17)

$$\begin{aligned} \text{ s.t. } &\sum _{i\in I}x_{ijl}\le \sum _{k\in K}d_{kl}z_{jk},&j\in J,\ \ l\in L \end{aligned}$$

(18)

$$\begin{aligned}&\sum _{j\in J}z_{jk}\le 1,&k\in K \end{aligned}$$

(19)

$$\begin{aligned}&(4)-(8) \end{aligned}$$

(20)

where the Lagrangian function is defined as usual

$$\begin{aligned} \mathcal {L}(u,v,x,y,z)= & {} \sum _{i\in I}\sum _{l\in L}p_{il}\sum _{j\in J}x_{ijl}+\sum _{i\in I}\sum _{j\in J}\sum _{l\in L}c_{ijl}x_{ijl} + \sum _{j\in J} g_j y_j\\&\quad + \sum _{j\in J}\sum _{l\in L}h_{jl}\sum _{i\in I}x_{ijl} + \sum _{j\in J}\sum _{k\in K}\sum _{l\in L}t_{jkl}d_{kl}z_{jk}\\&\quad + \sum _{j\in J}\sum _{l\in L}u_{jl}\left( \sum _{k\in K}d_{kl}z_{jk}-\sum _{i\in I}x_{ijl}\right) +\sum _{k\in K}v_{k}\left( 1-\sum _{j\in J}z_{jk}\right) \\= & {} \sum _{i\in I}\sum _{j\in J}\sum _{l\in L}(p_{il}+c_{ijl}+h_{jl}-u_{jl})x_{ijl}+\sum _{j\in J}g_{j}y_{j}\\&\quad +\sum _{j\in J}\sum _{k\in K}\left( \sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}-v_{k}\right) z_{jk}+\sum _{k\in K}v_{k} \end{aligned}$$

As in the previous section, we denote (x(u, v), y(u, v), z(u, v)) an optimal point for the oracle (17)–(20) and get the following theorem.

Theorem 2

Let (x(u, v), y(u, v), z(u, v)) is an optimal point of the oracle $\mathcal {L}_{SLR}(u,v )$.

• 1. $x_{ijl}(u,v)=0$ if $p_{il}+c_{ijl}+h_{jl}-u_{jl}> 0$;

• 2. if $p_{il}+c_{ijl}+h_{jl}-u_{jl}> 0$ for all (i, j, l) ($i\in I, \ j\in J, \ l\in L$).

  • (a) For a given $k\in K$, if $\sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}-v_{k}> 0$, then $z_{jk}(u,v)=0$;

  • (b) For a given $k\in K$, if $\sum _{j\in J}z_{jk}(u,v)=1$, then

    $$\begin{aligned} v_{k}\ge \min _{j\in J}\left\{ \sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}\right\} ; \end{aligned}$$

• 3. For a given $k\in K$, if

  $$\begin{aligned} v_{k}\ge \min _{j\in J}\left\{ \sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}+g_{j}\right\} , \end{aligned}$$

  then there exists an optimal oracle solution (x(u, v), y(u, v), z(u, v)) with $\sum _{j\in J}z_{jk}(u,v)=1$.

Proof

• 1. (By contradiction) Suppose that there exists $x_{i'j'l'}(u,v)>0$ with $p_{i'l'}+c_{i'j'l'}+h_{j'l'}-u_{j'l'}> 0$ ($i'\in I, j'\in J, l'\in L$). In this case, we can define a new feasible solution for the oracle say ($\hat{x}(u,v),\hat{y}(u,v),\hat{z}(u,v)$) which is equal to (x(u, v), y(u, v), z(u, v)) except for component $\hat{x}_{i'j'l'}(u,v)$. We set $\hat{x}_{i'j'l'}(u,v)=0$. Thus,

  $$\begin{aligned}&(p_{i'l'}+c_{i'j'l'}+h_{j'l'}-u_{j'l'})\hat{x}_{i'j'l'}(u,v)\nonumber \\&\qquad< (p_{i'l'}+c_{i'j'l'}+h_{j'l'}-u_{j'l'})x_{i'j'l'}(u,v)\nonumber \\&\quad \Longrightarrow \mathcal {L}(u,v,\hat{x},\hat{y},\hat{z})< \mathcal {L}(u,v,x,y,z) \end{aligned}$$

  (21)

  However, this contradicts (x(u, v), y(u, v), z(u, v)), the optimal point of the oracle $\mathcal {L}_{SLR}(u,v )$.

• 2.

  • (a) Similar with the proof of the Theorem 2.1.

  • (b) Let us assume that $v_{k_0}< \min _{j\in J}\{\sum _{l\in L}t_{jk_0l}d_{k_0l}+\sum _{l\in L}u_{jl}d_{k_0l}\}$ for some $k_0\in K$ and see that contradicts $\sum _{j\in J}z_{jk_0}(u,v)=1$. If $v_{k_0}< \min _{j\in J}\{\sum _{l\in L}t_{jk_0l}d_{k_0l}+\sum _{l\in L}u_{jl}d_{k_0l}\}$, then $\sum _{l\in L}t_{jk_0l}d_{k_0l}+\sum _{l\in L}u_{jl}d_{k_0l}-v_{k_0}>0$ for all $j\in J$. Any optimal solution (x(u, v), y(u, v), z(u, v)) is such that $z_{jk_0}(u,v)=0$ by Theorem 2.2.(a). Hence, $0=\sum _{j\in J}z_{jk_0}(u,v)\ne 1$.

• 3. Assume $v_k \ge \min _{j\in J}\{\sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}+g_{j}\}$ for a given $k\in K$. If there exists an optimal solution of the oracle such that $\sum _{j\in J}z_{jk}(u,v)=1$, then statement 3 hold. Assume we have the oracle solution with $\sum _{j\in J}z_{jk}(u,v)=0$ for the given k. Let $j'$ be such that $\sum _{l\in L}t_{j'kl}d_{kl}+\sum _{l\in L}u_{j'l}d_{kl}+g_{j'} = \min _{j\in J}\{\sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}+g_{j}\}$. By hypothesis, $\sum _{l\in L}t_{j'kl}d_{kl}+\sum _{l\in L}u_{j'l}d_{kl}+g_{j'}-v_{k}\le 0$ and one can set $z_{j'k}=1$ and $y_{j'}=1$ without increasing the objective value. The modified solution is also optimal. Hence, there exists an optimal oracle solution with $\sum _{j\in J}z_{jk}(u,v)=1$ for the given k where $v_k \ge \min _{j\in J}\{\sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}+g_{j}\}$.

$\square$

Note that the statement 2 of Theorem 2 can not always hold if $p_{il}+c_{ijl}+h_{jl}-u_{jl}< 0$ for any (i, j, l) ($i\in I, \ j\in J, \ l\in L$). For example, $p_{i_0l_0}+c_{i_0j_0l_0}+h_{j_0l_0}-u_{j_0l_0}=-5<0$ and $A_{i_0l_0}=10$ for the given ($i_0,j_0,l_0$) ($i_0\in I, \ j_0\in J, \ l_0\in L$), $t_{j_0k_0l_0}d_{k_0l_0}+u_{j_0l_0}d_{k_0l_0}-v_{k_0}=1>0$ for the given ($j_0,k_0$) ($j_0\in J,\ k_0\in K$), and $d_{k_0l_0}=4$ and $g_{j_0}=2$. In this case, one can set $x_{i_0j_0l_0}=4$, $y_{j_0}=1$ and $z_{j_0k_0}=1$.

From Theorem 2, we can know that some $x_{ijl}(u,v)$ and $z_{jk}(u,v)$ can be fixed to “0” in advance if their $p_{il}+c_{ijl}+h_{jl}-u_{jl}> 0$ and $\sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}-v_{k}> 0$. This operation, which reduces the size of the oracle, is quite common in Lagrangian relaxation applied to combinatorial optimization. There, using some appropriate arguments, one fixes some of the oracle variables and obtains a reduced-size oracle called the core problem. Usually we have (much) fewer variables $x_{ijl}(u,v)$ and $z_{jk}(u,v)$ in the core problem. Roughly speaking, if the size of the core problem is small enough, it will be possible to solve it by an Integer Programming solver(e.g. CPLEX, etc.), and this is the main advantage of the core problem.

If the dual ascent method is applied to solve the dual problem (16), one should properly initialize and update multipliers v according to the value of u and vice versa for reducing the number of iterations and improving computational efficiency. Initializing and updating the Lagrangian multipliers (u, v) are not an easy task because they are interrelated. For the sake of convenience, in this paper we first set all of the multipliers $u_{jl}=0$ for all $j\in J$ and $l\in L$, and get the following dual problem (22) and core problem (23)–(27) by fixing all of the variables $x_{ijl}$ to “0” because of $p_{il}+c_{ijl}+h_{jl}-u_{jl}> 0$ ($i\in I, \ j\in J, \ l\in L$) . After solving the dual problem (22) optimally, we use its results to initialize u and solve (16). That is, the solution process is divided into two phases. We first solve dual problem (22), and then solve dual problem (16).

$$\begin{aligned} \max _{v\in V } \ \mathcal {L}_{SLR}^0( v ) \end{aligned}$$

(22)

and dual function

$$\begin{aligned} \mathcal {L}_{SLR}^0( v )=&\min _{y,z} \mathcal {L}^0(v,y,z) \end{aligned}$$

(23)

$$\begin{aligned} \text{ s.t. } &\sum _{j\in J}z_{jk}\le 1,&k\in K \end{aligned}$$

(24)

$$\begin{aligned}&z_{jk}\le y_{j},&j\in J,\ \ k\in K \end{aligned}$$

(25)

$$\begin{aligned}&y_{j}\in \{0,1 \},&j\in J \end{aligned}$$

(26)

$$\begin{aligned}&z_{jk}\in \{0,1 \},&j\in J, \ \ k\in K \end{aligned}$$

(27)

where

$$\begin{aligned} \mathcal {L}^0(v,y,z) = \sum _{j\in J}g_{j}y_{j}+\sum _{j\in J}\sum _{k\in K}\left( \sum _{l\in L}t_{jkl}d_{kl}-v_{k}\right) z_{jk}+\sum _{k\in K}v_{k} \end{aligned}$$

(28)

We denote ($U^*, V^*$), $V_0^*$, X(u, v) and X(v) the set of optimal solutions of problem (16), (22), (17)–(20) and (23)–(27), respectively. For each (i, j, l) ($i\in I$, $j\in J$, $l\in L$), we define its costs as $\mathcal {F}_{ijl}=p_{il}+c_{ijl}+h_{jl}$. For each customer k, we define its combined costs as $\mathcal {C}_k:=\min _{j\in J}\{\sum _{l\in L}t_{jkl}d_{kl}+g_{j}\}$ and its transportation cost from distribution center j as $\mathcal {T}_{jk}:=\sum _{l\in L}t_{jkl}d_{kl}$. The vector of combined costs is thus $\mathcal {C}:=(\mathcal {C}_1, \cdots , \mathcal {C}_R)$. Furthermore, we sort costs $\mathcal {T}_{jk}$ for each customer k and $\mathcal {F}_{ijl}$ for each (j, l), and get the sorted costs

$$\begin{aligned} \mathcal {T}_{k}^1 \le \mathcal {T}_{k}^2\le \cdots \le \mathcal {T}_{k}^N,\ \ \ \ \ \ \ \mathcal {F}_{jl}^1\le \mathcal {F}_{jl}^2\le \cdots \le \mathcal {F}_{jl}^M. \end{aligned}$$

The dual problem (22) and the oracle problem $\mathcal {L}_{SLR}^0( v )$ are very similar with the uncapacitated facility location (UFL) dual problem and oracle problem presented in [6], respectively. Thus the main results of the UFL oracle problem are applicable to the oracle problem $\mathcal {L}_{SLR}^0( v )$, which are summarized in Theorem 3.

Theorem 3

The following statements hold true [6].

• 1. $v\ge \mathcal {C}\Longrightarrow v\in V_0^*$;

• 2. $v> \mathcal {C}\Longrightarrow v\in int(V_0^*)$;

• 3. If $v\in int (V_0^*)$, then $v\ge \mathcal {T}^1$.

Corollary 1

If $u_{jl}\ge \mathcal {F}_{jl}^M$ for all (j, l) ($j\in J$, $l\in L$), and $v_{k}\ge \mathcal {C}_k + \max _{j\in J}\{\sum _{l\in L}u_{jl}d_{kl}\}$ for all $k\in K$, then $(u,v)\in (U^*, V^*)$.

Proof

Assume $u_{jl}\ge \mathcal {F}_{jl}^M$ for all (j, l) ($j\in J$, $l\in L$), and $v_{k}\ge \mathcal {C}_k + \max _{j\in J}\{\sum _{l\in L}u_{jl}d_{kl}\}$ for all $k\in K$. If there exists an optimal solution of the oracle problem $\mathcal {L}_{SLR}(u,v )$ such that $\sum _{i\in I}x_{ijl}=\sum _{k\in K}d_{kl}z_{jk}$ for all $j\in J$ and $l\in L$, and $\sum _{j\in J}z_{jk}=1$ for all $k\in K$, then, by Theorem 1, this solution is optimal for the original problem (1)–(8). Otherwise, we have two exclusive cases:

• 1. $\sum _{i\in I}x_{ijl}< \sum _{k\in K}d_{kl}z_{jk}$ for some (j, l) and $\sum _{j\in J}z_{jk}=1$ for all $k\in K$. In this case, we can increase the value of $x_{ijl}$ for some (i, j, l) such that the modified solution (x, y, z) satisfies constraints (2)–(8).

• 2. $\sum _{j\in J}z_{jk}=0$ for some $k\in K$. In this case, first let $j'$ be such that $\mathcal {C}_k=\sum _{l\in L}t_{j'kl}d_{kl}+g_{j'}$, and set $z_{j'k}=1$ and $y_{j'}=1$. Then we can also increase the value of $x_{ijl}$ for some (i, j, l) such that the modified solution (x, y, z) satisfies constraints (2)–(8).

By hypothesis, $p_{il}+c_{ijl}+h_{jl}-u_{jl}\le 0$ for all (i, j, l), and $\sum _{l\in L}t_{jkl}d_{kl}+\sum _{l\in L}u_{jl}d_{kl}+g_{j}-v_{k}\le 0$ for all $k\in \{k|\sum _{j\in J}z_{jk}=0, \ \ k\in K\}$. Thus, the modified solution does not increase the objective value and is also optimal. Hence, there exists an optimal oracle solution with $\sum _{i\in I}x_{ijl}=\sum _{k\in K}d_{kl}z_{jk}$ for all (j, l) ($j\in J$, $l\in L$), $\sum _{j\in J}z_{jk}=1$ for all $k\in K$ and $(u,v)\in (U^*,V^*)$. $\square$

Theorem 4

Let us consider $\tilde{v}\in V$. If $(y(\tilde{v}),z(\tilde{v}))\in X(\tilde{v})$ then $\sum _{k\in K}-[\sum _{l\in L} t_{jkl}d_{kl}-\tilde{v}_k]^{-}+g_{j}\le 0$ for all $j\in J(y)$, where J(y) is the set of selected distribution centers, i.e., $J(y):=\{ j\in J| y_{j}=1\}$.

Proof

(By contradiction) Let us assume that there exists $j'\in J(y)$ such that $\sum _{k\in K}-[\sum _{l\in L} t_{j'kl}d_{kl}-\tilde{v}_k]^{-}+g_{j'}> 0$. In this case, we can define a new feasible solution $(\hat{y}(\tilde{v}),\hat{z}(\tilde{v}))$ which is equal to $(y(\tilde{v}),z(\tilde{v}))$ except for components with $j=j'$, for these components, we set $\hat{y}_{j'}(\tilde{v})=0$ and $\hat{z}_{j'k}(\tilde{v})=0$ for all $k\in K$. Thus

$$\begin{aligned}&g_{j'}\hat{y}_{j'}(\tilde{v})+\sum _{k\in K}\left( \sum _{l\in L}t_{j'kl}d_{kl}-\tilde{v}_{k}\right) \hat{z}_{j'k}(\tilde{v})=0\\&\qquad < \sum _{k\in K}-[\sum _{l\in L} t_{j'kl}d_{kl}-\tilde{v}_k]^{-}+g_{j'} \\&\qquad \le \sum _{k\in K}\left( \sum _{l\in L}t_{j'kl}d_{kl}-\tilde{v}_{k}\right) z_{j'k}(\tilde{v})+g_{j'}y_{j'}(\tilde{v}) \end{aligned}$$

where the last inequality comes from the fact that $(\sum _{l\in L}t_{j'kl}d_{kl}-\tilde{v}_{k})z_{j'k}(\tilde{v}) \ge -[\sum _{l\in L} t_{j'kl}d_{kl}-\tilde{v}_k]^-$ for all $k\in K$, $j\in J$. This contradicts $(y(\tilde{v}),z(\tilde{v}))\in X(\tilde{v})$. $\square$

Theorem 5

Let us consider $\tilde{v}\in V$. If $(y(\tilde{v}),z(\tilde{v}))\in X(\tilde{v})$ and there exists $k'\in K$, $\sum _{j\in J}z_{jk'}(\tilde{v}) =1$, then

$$\begin{aligned} \tilde{v}_{k'}\ge \sum _{l\in L}t_{j'k'l}d_{k'l}=\min _{j\in J(y)}\left\{ \sum _{l\in L}t_{jk'l}d_{k'l}\right\} \end{aligned}$$

where $J(y):=\{ j\in J| y_{j}=1\}$, $j'$ is the closet open distribution center to client k(it may not be unique).

Proof

(By contradiction) Let us assume that there exist $k''\in K$ such that $\sum _{j\in J}z_{jk''}(\tilde{v}) =1$ and

$$\begin{aligned} \tilde{v}_{k''}< \sum _{l\in L}t_{j'k''l}d_{k''l}=\min _{j\in J(y)}\left\{ \sum _{l\in L}t_{jk''l}d_{k''l}\right\} \end{aligned}$$

In this case we can define a new feasible solution for the oracle $\mathcal {L}_{SLR}^0( v )$, say $(\hat{y}(\tilde{v}),\hat{z}(\tilde{v}))$, which is equal to $(y(\tilde{v}),z(\tilde{v}))$ except for components with $k=k''$. For these components, we set $\hat{z}_{jk''}(\tilde{v})=0$ for all $j\in J$. Thus

$$\begin{aligned} \sum _{j\in J(y)}\left( \sum _{l\in L}t_{jk''l}d_{k''l}-\tilde{v}_{k''}\right) \hat{z}_{jk''}(\tilde{v})=0<\sum _{j\in J(y)}\left( \sum _{l\in L}t_{jk''l}d_{k''l}-\tilde{v}_{k''}\right) z_{jk''}(\tilde{v}) \end{aligned}$$

Considering this inequality and the definition of $(\hat{y}(\tilde{v}),\hat{z}(\tilde{v}))$, we can conclude that $(y(\tilde{v}),z(\tilde{v}))\notin X(\tilde{v})$ which contradicts the hypothesis of the theorem. $\square$

4 Two-phase SLR algorithm to solve the UDCL problem

4.1 Computing the initial point for algorithm SLR

As pointed out in [6], it is likely to be impractical that solving the oracle (23)–(27) at any $\bar{v}>\mathcal {C}$ because the oracle is probably too difficult at that $\bar{v}$. It is also likely that there exists a $v_{0}^*\in V_{0}^*$ with small norm, for which the oracle subproblem is easier (with less binary variables) and hopefully tractable by an integer programming solver. In this paper, we use the optimal solution $v(\lambda ^*)$ of the following problem (29)–(31) to initialize the multiplier v.

$$\begin{aligned} \min _{0\le \lambda \le 1}&\sum _{k\in K}v_{k}(\lambda ) \end{aligned}$$

(29)

$$\begin{aligned} \mathrm {s.t.}&\sum _{k\in K}-\left[ \sum _{l\in L} t_{jkl}d_{kl}- v_k(\lambda )\right] ^{-}+g_{j}\le 0 \ \ \ \ \ \ j\in J \end{aligned}$$

(30)

$$\begin{aligned}&v(\lambda )=\lambda v^0 + (1-\lambda )\mathcal {C} \end{aligned}$$

(31)

where $\mathcal {C}$ is the vector of best combined costs defined in Sect. 3, $v^0$ is an initial guess for $v^*\in V_{0}^*$ such that $\mathcal {T}^1\le v^0 \le \mathcal {C}$. Obviously, $v(\lambda ^*)$ is one point in $[v^0, \mathcal {C}]$, the line segment is used for connecting points $v^0$ and $\mathcal {C}$ (notice that by Theorem 3, $\mathcal {C}\in V_{0}^*$).

4.2 Two-phase SLR algorithm

In this section, we propose a two-phase SLR algorithm for the UDCL problem, which is obtained by combining the semi-Lagrangian relaxation approach with the theoretical results presented in Sect. 3. The two-phase SLR algorithm employs a specialized version of the dual ascent method to solve the dual problems (22) and (16) in two consecutive phases. In the first phase, Theorem 4 is used for computing the initial dual point $v^{iter1}$ firstly, and then the processes of solving the oracle problem (23)–(27) and updating the dual point $v^{iter1}$ are executed iteratively until an optimal point of dual problem (22) is obtained. In the second phase, the optimal results obtained in the first phase are used for initializing the dual point $(u^{iter2}, v^{iter2})$ firstly, and then the processes of solving the oracle problem (17)–(20) and updating the dual point $(u^{iter2}, v^{iter2})$ are executed iteratively until a primal-dual optimal point is obtained. Theorem 5 and Theorem 2 are used for updating dual points $v^{iter1}$ in the first phase and $(u^{iter2}, v^{iter2})$ in the second phase (see the following algorithm for details), respectively. To maintain the oracle problems $\mathcal {L}_{SLR}^0( v^{iter1} )$ and $\mathcal {L}_{SLR}(u^{iter2}, v^{iter2})$ as small as possible, at each iteration, we only update the components of $v^{iter1}$ and $(u^{iter2}, v^{iter2})$ whose corresponding subgradients are not equal to “0”. The details of the solution procedure are as follows.

Algorithm 1

• Input: $v^0\ge \mathbf 0$ (0 represents a zero vector ) initial guess for an optimal point of the dual problem (22).

• Output: $(x(u^*,v^*), y(u^*,v^*), z(u^*,v^*), u^*, v^*)$ primal-dual optimal point for the UDCL problem (1)–(8).

First phase: solving the dual problem (22)

• 1. Initialization: For each customer $k\in K=\{1,2,\ldots , R\}$:

  • (a) compute its transportation costs:

    $$\begin{aligned} \mathcal {T}_{jk}=\sum _{l\in L}t_{jkl}d_{kl} \ \ \ \ \ \ \ \ j\in J=\{1,2,\cdots , N\}; \end{aligned}$$

  • (b) sort its costs $\mathcal {T}_{jk}$ such that

    $$\begin{aligned} \mathcal {T}_{k}^1 \le \mathcal {T}_{k}^2\le \cdots \le \mathcal {T}_{k}^N; \end{aligned}$$

  • (c) compute its best combined cost:

    $$\begin{aligned} \mathcal {C}_k:=\min _{j\in J}\left\{ \sum _{l\in L}t_{jkl}d_{kl}+g_{j}\right\} . \end{aligned}$$

  • (d) set $\mathcal {T}_{k}^{N+1}=\mathcal {C}_k +\varepsilon$ for an $\varepsilon >0$

• 2. Initial dual point:

  • (a) Solve problem (29)–(31) to obtain $v(\lambda ^*)$;

  • (b) Set $v^1$ such that

    $$\begin{aligned} v_{k}^1=\min \left\{ \mathcal {T}_{k}^r|\mathcal {T}_{k}^r\ge v_{k}(\lambda ^*),\quad r\in \{1,2,\ldots , N, N+1\} \right\} +\varepsilon \ \ \ (\varepsilon >0); \end{aligned}$$

  • (c) Set $iter1=1$.

• 3. Oracle call: compute $\mathcal {L}_{SLR}^0( v^{iter1} )$, $(y(v^{iter1}),z(v^{iter1}))$ and the subgradient $s^{iter1}$ where

  $$\begin{aligned} s_{k}^{iter1}=1-\sum _{j\in J} z_{jk}(v^{iter1}),\ \ \ \ k\in K. \end{aligned}$$

• 4. Stopping criterion: if $s^{iter1}=\mathbf 0$, then stop: $(\tilde{y}^*,\tilde{z}^*,\tilde{v}^*)=(y^{iter1},z^{iter1},v^{iter1})$, $\tilde{v}^*$ is the optimal point of the problem (22).

• 5. Dual point updating:

  • (a) Define $J(y^{iter1}):=\{j|y_{j}(v^{iter1})=1, \ j\in J\}$;

  • (b) For each $k\in K$ such that $s_{k}^{iter1}=0$, set $v_{k}^{iter1+1}=v_{k}^{iter1}$;

  • (c) For each $k\in K$ such that $s_{k}^{iter1}=1$, set

    $$\begin{aligned} v_{k}= & {} \min _{j\in J(y^{iter1})}\{\mathcal {T}_{jk}\},\\ v_{k}^{iter1+1}= & {} \min \left\{ \mathcal {T}_{k}^r|\mathcal {T}_{k}^r\ge v_{k},\ \ r\in \{1,2,\ldots , N, N+1\}\right\} +\varepsilon ; \end{aligned}$$

• 6. Set $iter1=iter1+1$ and go to Step 3.

Second phase: solving the dual problem (16)

• 1. Initialization:

  • (a) Compute $\mathcal {F}_{ijl}=p_{il}+c_{ijl}+h_{jl}$ for each (i, j, l) ( $i\in I$, $j\in J$, $l\in L$);

  • (b) For each (j, l) ($j\in J$, $l\in L$), sort cost $\mathcal {F}_{ijl}$ such that

    $$\begin{aligned} \mathcal {F}_{jl}^1\le \mathcal {F}_{jl}^2\le \cdots \le \mathcal {F}_{jl}^M; \end{aligned}$$

  • (c) Set $u_{jl}^{0}=0$ for each (j, l)($j\in J$, $l\in L$), and $v_{k}^0=\tilde{v}_{k}^*$ for all $k\in K$;

  • (d) Set $z(u^0,v^0)=\tilde{z}^*$;

  • (e) Set $iter2=1$.

• 2. Dual point setting (I):

  • (a) For each (j, l) ($j\in J$, $l\in L$), compute $D_{jl}$, the amount of commodity l transported from the distribution center j to customers:

    $$\begin{aligned} D_{jl}=\sum _{k\in K} d_{kl}z_{jk}(u^{iter2-1},v^{iter2-1}); \end{aligned}$$

  • (b) Define $u^{iter2}$ such that

    $$\begin{aligned} u_{jl}^{iter2}=\max \left\{ u_{jl}^{iter2-1}, \min \left\{ \mathcal {F}_{jl}^r|\sum _{i=1}^r A_{Locate(i)l}\ge D_{jl}, \ \ r\in I \right\} \right\} +\varepsilon , \end{aligned}$$

    where $Locate(\cdot )$ is the locating function such that $\mathcal {F}_{jl}^r=\mathcal {F}_{Locate(r)jl}$ for the given $r\in I$.

  • (c) Define $v^{iter2}$ such that

    $$\begin{aligned} v_{k}^{iter2}=v_{k}^{iter2-1}+\max \left\{ \sum _{l\in L}\left( u_{jl}^{iter2}-u_{jl}^{iter2-1}\right) d_{kl}, \ \ j\in J\right\} \end{aligned}$$

• 3. Oracle call: compute $\mathcal {L}_{SLR}(u^{iter2}, v^{iter2})$, $(x(u^{iter2},v^{iter2}),y(u^{iter2},v^{iter2}),z(u^{iter2},v^{iter2}))$ and the subgradient $s^{iter2}$ and $sub^{iter2}$ where

  $$\begin{aligned} s_{k}^{iter2}= & {} 1-\sum _{j\in J}z_{jk}(u^{iter2},v^{iter2}),\ \ \ \ \ k\in K\\ sub_{jl}^{iter2}= & {} \sum _{k\in K}d_{kl}z_{jk}(u^{iter2},v^{iter2})-\sum _{i\in I}x_{ijk}(u^{iter2},v^{iter2}), \ \ \ \ \ j\in J, l\in L \end{aligned}$$

• 4. Stopping criterion: If $s^{iter2}=\mathbf 0$ and $sub^{iter2}=\mathbf 0$, then stop:

  $(x(u^{iter2},v^{iter2}), y(u^{iter2},v^{iter2}), z(u^{iter2},v^{iter2}),u^{iter2},v^{iter2})$ is the primal-dual optimal point.

• 5. Dual point setting (II):

  • (a) If $s^{iter2}\ne \mathbf 0$ and $sub^{iter2}=\mathbf 0$,

    • i. set $u^{iter2+1}=u^{iter2}$.

    • ii. for each $k\in K$ such that $s_{k}^{iter2}=0$, set $v_{k}^{iter2+1} = v_{k}^{iter2}$.

    • iii. for each $k\in K$ such that $s_{k}^{iter2}=1$, set $v_{k}^{iter2+1}=\tilde{v}_{k} +\varepsilon$ where

      $$\begin{aligned} \tilde{v}_{k}=\min _{j\in J(y^{iter2})}\left\{ \mathcal {T}_{jk}+ \sum _{l\in L}u_{jl}^{iter2}d_{kl}\right\} \end{aligned}$$

      (32)

    • iv. set $iter2=iter2+1$ and go to Step 3.

  • (b) If $sub^{iter2}\ne \mathbf 0$,

    • i. for each $k\in K$ such that $s_{k}^{iter2}=1$, firstly set $\tilde{v}_{k}$ by using Eq. (32), then set $v_{k}^{iter2}=\tilde{v}_{k}$ and $z_{j'k}(u^{iter2},v^{iter2})=1$ where

      $$\begin{aligned} j'=\min \left\{ j| \tilde{v}_{k} = \mathcal {T}_{jk}+ \sum _{l\in L}u_{jl}^{iter2}d_{kl},\ \ j\in J\right\} \end{aligned}$$

      (33)

    • ii. set $iter2=iter2+1$ and go to Step 2.

Theorem 6

Algorithm 1 is a dual ascent method and after finitely many iterations, it converges to optimal dual points $\tilde{v}^*\in V_{0}^*$ ($V_{0}^*\ne \emptyset$) in the first phase and $(u^*,v^*)\in (U^*,V^*)$ ($U^*\ne \emptyset$ and $V^*\ne \emptyset$) in the second phase, respectively.

Proof

Considering the first phase, let $(y(v^{iter1}),z(v^{iter1}))$ be the optimal solution of the oracle $\mathcal {L}_{SLR}^{0}(v^{iter1})$ (iter1 is a finite positive integer). We have three exclusive cases:

• Case 1 At least for one component of $s(v^{iter1})$, say $k'$, there exists $s_{k'}(v^{iter1})=1$ and $v_{k'}^{iter1}<\mathcal {T}_{k'}^{N+1}$. In this case, the updating procedure of Algorithm 1 consists in increasing component $v_{k'}^{iter1}$ (step 5 in the first phase). Thus, $v^{iter1+1}>v^{iter1}$ and by Theorem 1.2 we have $\mathcal {L}_{SLR}^{0}(v^{iter1+1})>\mathcal {L}_{SLR}^{0}(v^{iter1})$.

• Case 2 All of the nonzero components of $s(v^{iter1})$ have the associated multipliers $v_{k}^{iter1}=\mathcal {T}_{k}^{N+1}$. However, by Theorem 3 we can know that this case cannot happen.

• Case 3 $s(v^{iter1})=\mathbf 0$. By Theorem 1.4, we have $v^{iter1} \in V_{0}^*$.

For the second phase, we can also proof $\mathcal {L}_{SLR}(u^{iter2+1},v^{iter2+1} )>\mathcal {L}_{SLR}(u^{iter2},v^{iter2} )$ by the updating procedure of dual point, Step 5 and Step 2. After finitely many iterations, if $u_{jl}^{iter2}\ge \mathcal {F}_{jl}^M$ for all (j, l) ($j\in J$, $l\in L$), and $v_{k}^{iter2}\ge \mathcal {C}_k + \max _{j\in J}\{\sum _{l\in L}u_{jl}^{iter2}d_{kl}\}$ for all $k\in K$, then $(u^*,v^*)\in (U^*,V^*)$ by Corollary 1. $\square$

5 Computational experiments

In order to assess the performance of two-phase SLR algorithm in terms of solution quality and CPU time, we solve a set of UDCL instances by using plain CPLEX and the approach obtained by combining two-phase SLR algorithm with CPLEX, respectively. The CPU time limit is set to 7200 s for the plain CPLEX. For the two-phase SLR algorithm, owing to the fact that our main purpose is to solve the dual problem (16) in the second phase which needs more CPU time, the CPU time limit is set to 10 s in the first phase and 7200 s in the second phase, respectively. The experiments are conducted on a laptop with a processor Intel Core $^\mathrm{TM}$ i7-2640M CPU 2.80 GHz, and 6.00 GB of RAM. CPLEX 12.5 (with default parameters) interfaced with MATLAB R2010a is used as mixed integer linear programming solver.

Note that, on the one hand, we use plain CPLEX to solve the UDCL instances, and on the other hand, we also use CPLEX as the integer programming solver to compute $\mathcal {L}_{SLR}^0( v )$ or $\mathcal {L}_{SLR}( u, v )$ at each iteration of two-phase SLR algorithm .

5.1 Instance description

For the sake of contrastive analysis, this paper tested 15 instances which can be divided into two groups. All of the instances distribute 5 different kinds of commodities ($l=1,2,\ldots ,5$) from depots to theirs customers through the distribution centers. For the 5 kinds of commodities, the unit transportation costs from depots to distribution centers $tc1_l$ and the unit transportation costs from distribution centers to customers $tc2_l$ are shown in Table 1. The parameters $p_{il}$ (unit supply cost of commodity l at depot i), $h_{jl}$ (the unit turnover cost of commodity l at distribution center j), $d_{kl}$(the demands of the customer k for commodity l), and $Dis1_{ij}$ (the distance between the depot i and distribution center j) are generated randomly in the intervals shown in Table 2. The transportation cost $c_{ijl}$ and the maximal supply $A_{il}$ are generated by $c_{ijl}=tc1_{l}\times Dis1_{ij}$ and $A_{il}=[\alpha \times \frac{\sum _{k\in K}d_{kl}}{M}+0.5]$ (M is the number of depots, $[\cdot ]$ is the sign of rounding off, $\alpha$ is a random number generated in the interval [1, 2]), respectively.

Table 1 Unit transportation cost

Table 2 Intervals of the parameters

The fixed costs $g_{j}$ and the shipping costs $t_{jkl}$ in the first group are generated as follows: in the Euclidian plane n points are randomly generated in the unit square $[0,1]\times [0,1]$. Each point simultaneously represents a distribution center and a customer ($N=R$), with $N=500$, 1000. The shipping costs $t_{jkl}$ are determined by the Euclidian connection distance $Dis2_{jk}$ and $tc2_l$, $t_{jkl}=Dis2_{jk}\times tc2_l$. In each instance all the fixed costs $g_{j}$ are equal and calculated by $\sqrt{N}/m$ with $m=$ 10, 100 or 1000. All values are rounded up to 4 significant digits and made integers. We use the label $N-m$ to name the 6 instances in the first group.

The second group has 9 instances with $N=R$. In these instances, the shipping costs $t_{jkl}$ are generated by $Dis2_{jk}$ and $tc2_l$, $t_{jkl}=Dis2_{jk}\times tc2_l$, where the connection distances $Dis2_{jk}$ are drawn uniformly at random from [1000, 2000]. The fixed costs $g_{j}$ are drawn uniformly at random from [100, 200] in class ‘a’, from [1000, 2000] in class ‘b’ and from [10, 000, 20, 000] in class ‘c’. We use the label YZ to name these instances, where Y is equal to ‘N’ and Z is the class (a, b, or c).

In Table 3 we further describe 15 instances used in our test, the number of depots (Nb. of depots), the number of clients (customers) (Nb. of clients), the number of variables (Nb. of vars.) and the number of constraints (Nb. of cons.). In the tables of this paper, P.ave. and G.ave. are the abbreviation for partial average and global average, respectively.

5.2 CPLEX performance

In Table 3 we report the results obtained with CPLEX 12.5 in default settings and 7200 s of CPU time limit. Column cost reports the objective function value. Column time (s) reports the CPU time (in seconds) for solving the UDCL. Column Nb. of cents. reports the number of selected distribution centers. Within the allowed time limit, 14 of the 15 instances obtained optimal solutions by plain CPLEX, which are presented with CPU time less than 7200 s. The instance 1000-10 which was not proved its optimality is marked with (*). The average CPU time for solving the first group of instances and the second group of instances are around 2704 s and 1496 s, respectively. For the first group of instances, the number of the selected distribution centers is around half of the number of the customers, that is, on average per selected distribution center serves 2–3 customers. For the second group of instances, the number of the selected distribution centers is around one-tenth of the number of the customers. For example, 21 selected instances serve 250 customers for instance 250c, and on average per selected distribution center serves 10–12 customers.

Table 3 Instances description and CPLEX performance

5.3 Two-phase SLR algorithm performance

Table 4 The performance of the two-phase SLR algorithm

In Table 4 we report the results obtained with the two-phase SLR algorithm. The results obtained in the first phase and in the second phase are presented in columns First phase and Second phase, respectively. Except instance 750c, other 14 instances obtained optimal solutions for the dual problem (22) within 10 s of CPU time limit in the first phase. All of the tested instances obtained optimal primal-dual solutions in the second phase. Obviously, the objective function value obtained in the first phase (presented in the second column) is the lower bound of the objective function value obtained in the second phase (presented in the sixth column). An important advantage of the two-phase SLR algorithm is that it can drastically reduce the number of relevant variables (otherwise said, we can fix many variables to 0). For example, instance 750a has 619,500 variables shown in Table 3, but as we can see in the fourth column of Table 4 only 2900 variables are relevant in the first phase (the remaining 616,600 variables are fixed to 0). Note that the number of variables in the second phase is different for each SLR iteration and therefore we give average figures corresponding to all the SLR iterations. On average, in the first phase we only use $0.71\%$ of the variables and $99.28\%$ of the constraints, and in the second we use $78.00\%$ of the variables. As expected, we have a similar reduction in the CPU time. We observe that the dual problem (22) for 14 instances other than 750c is solved optimally in a few seconds in the first phase.

Comparing Tables 3 and 4, although the CPU time spent in the second phase is slightly higher than the CPU time spent by plain CPLEX for instances 500-10, 500-100, 250a, 250c and 500c, the global average CPU time of the two-phase SLR algorithm is competitive because the sum of CPU time spent in the first phase and the second phase is reduced by around 750 s. Especially, the two-phase SLR algorithm took 5537.62 s to compute an optimal solution for the instance 1000-10 which was not solved optimally by plain CPLEX within 7200 s.

6 Conclusion

The contribution of this paper is threefold as following:

Modeling contribution: based on the characteristics of distribution system for B2C E-commerce firms, a mixed integer programming model for determining the location of distribution centers was developed. This model is a multi-commodity, multi-stage and uncapacitated distribution center location-allocation model considering the supply cost of different commodities. Compared with the models without considering the supply cost of commodities, the one established in this paper is closer to the real distribution system of B2C E-commerce firms.

Algorithmic contribution: we studied the theoretical properties of the SLR dual problem in the UDCL case. These properties are very useful for initializing and updating the Lagrangian multipliers. Furthermore, a two-phase SLR algorithm was proposed to solve the UDCL problem and we have proved its (finite) convergence.

Empirical contribution: the performance of a general mixed integer programming solver, as CPLEX, can be enhanced by combining it with the SLR algorithm. We compared the approach obtained by combining two-phase SLR algorithm with CPLEX versus plain CPLEX in our computational experiment. In this experiment we used a set of 15 UDCL instances. Within a CPU time limit of 7200 s, 14 and 15 instances were solved by using plain CPLEX and the combined approach, respectively. On average, the combined approach performed better than the plain CPLEX. The reason for this good result is that, the two-phase SLR algorithm drastically reduced the number of the UDCL relevant variables. Roughly speaking, on average the number of relevant variables was reduced to $0.71\%$ in the first phase and $78.00\%$ in the second phase, respectively.