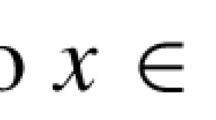A derivative-free descent method in set optimization

Abstract

Based on a vectorization result in set optimization with respect to the set less order relation, this paper shows how to relate two nonempty sets on a computer. This result is developed for generalized convex sets and polyhedral sets in finite dimensional spaces. Using this approach a numerical method for the determination of optimal scenarios is presented. A new derivative-free descent method for the solution of set optimization problems is given together with numerical results in low dimensions.

1 Introduction

Set optimization has developed from an extension of continuous optimization to problems with set-valued maps. For early contributions see the papers published by Borwein [1] in 1977 and Oettli [21] in 1980. Although most of the papers on set optimization work with the notion of a minimizer and variants of it, nowadays one works with a more realistic order relation for the comparison of sets which has been introduced to optimization by Kuroiwa (e.g., see [12]; a first publication has been given by Kuroiwa et al. [13]). Outside the optimization community this notion has been already used by Young [27] in algebra, by Nishnianidze [20] in fixed point theory and by Chiriaev and Walster [2] in computer science and interval analysis. Since Chiriaev and Walster introduced the name “set less” for the comparison of sets, which is also implemented in the FORTRAN compiler f95 of SUN Microsystems [24], we also use this name in the present paper. In [10] even more realistic order relations have been discussed.

Recently, Neukel [19] has shown that there are important socio-economic applications for these order relations. Applications of set optimization to finance can be found in a paper by Hamel and Heyde [6] among others.

This paper aims at the numerical solution of set optimization problems. The presented methods are based on a vectorization approach [8] by the author. Vectorization is a first step to a scalarization in set optimization. Direct scalarization approaches for set optimization problems have been introduced by Hernández and Rodríguez-Marín [7] in 2007 and in 2012 by Gutiérrez et al. [5], Khoshkhabar-amiranloo and Soleimani-damaneh [11] and Xiao et al. [26].

Löhne and Schrage [16] have given the first algorithm for the solution of polyhedral set optimization problems. Based on the vectorization approach a new descent method is now presented for generalized convex optimization problems which can also be used for the treatment of polyhedral sets. It turns out that these nonlinear problems can only be solved with a high numerical effort.

This paper is organized as follows. In Sect. 2, we present the basic theoretical results together with its application to numerical methods for the comparison of two sets with respect to the set less order relation. Using the definition of minimal elements Sect. 3 gives an algorithm for the determination of optimal scenarios. Finally, the descent method is described in Sect. 4 and numerical results are given.

2 Basic results

In this section we investigate set optimization problems in the following setting.

Assumption 2.1

Let $S$ be a nonempty subset of ${\mathbb {R}}^{n}$, let $C$ be a closed convex cone in ${\mathbb {R}}^{m}$ with $C\ne {\mathbb {R}}^{m}$, and let $F:S\rightrightarrows {\mathbb {R}}^{m}$ be a set-valued map with $F(x)\ne \emptyset$, $F(x)$ compact, $F(x)+C$ and $F(x)-C$ convex for all $x\in S$.

Under this assumption we investigate the finite dimensional set optimization problem

$$\begin{aligned} \min _{x\in S}\ F(x). \end{aligned}$$

(1)

In this paper minimal solutions of problem (1) are defined using the set less order relation.

Definition 2.1

Let Assumption 2.1 be satisfied.

• (a) Let nonempty sets $A,B\in {\mathbb {R}}^{m}$ be given and let $\le$ be a partial ordering induced by the convex cone $C$. Then the set less order relation $\preccurlyeq _{s}$ is defined by

  $$\begin{aligned} A\preccurlyeq _{s} B \ \ :\Longleftrightarrow \ \ \big ( \forall \ a\in A \ \exists \ b\in B: a\le b\big ) \ \text{ and }\ \big ( \forall \ b\in B \ \exists \ a\in A: a\le b\big ). \end{aligned}$$

  (2)

• (b) $\bar{x}\in S$ is called a minimal solution of the set optimization problem (1) iff $F(\bar{x})$ is a minimal element of the system of sets $F(x)$ (with arbitrary $x\in S$), i.e.

  $$\begin{aligned} F(x)\preccurlyeq _{s}F(\bar{x}),\; x\in S\ \ \Longrightarrow \ \ F(\bar{x})\preccurlyeq _{s}F(x). \end{aligned}$$

In the equivalence (2) one requires that two conditions are satisfied in order to have some kind of symmetry in the statement. It is well-known (e.g., see [10, Proposition 3.1,(a)]) that the equivalence (2) can be replaced by

$$\begin{aligned} A\preccurlyeq _{s}B\ \ \Longleftrightarrow \ \ B\subset A+C \text{ and } A\subset B-C. \end{aligned}$$

Figure 1 illustrates these two inclusions used in the characterization of the set less order relation $\preccurlyeq _{s}$.

Fig. 1

Illustration of the inequality $A\preccurlyeq _{s}B$, i.e. $B\subset A+C$ and $A\subset B-C$

Throughout this paper let $C^{*}$ denote the dual cone of $C$. Lower indices are used for the components of a vector in ${\mathbb {R}}^{n}$ (or ${\mathbb {R}}^{m}$) and different vectors in ${\mathbb {R}}^{n}$ (or ${\mathbb {R}}^{m}$) are distinguished by upper indices. All computations in this paper have been done with MATLAB.

For the comparison of two sets using the set less order relation we cite Theorem 2.1 in [8] in a specific form in finite dimensions.

Theorem 2.1

[8], Thm. 2.1] Under Asssumption 2.1 we have for all $x^{1},x^{2}\in S$

$$\begin{aligned} F(x^{1})\preccurlyeq _{s} F(x^{2})&\Longleftrightarrow \max \Big (\sup _{\ell \in C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\}}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})} \ell ^{T}y\big ) ,\nonumber \\&\sup _{\ell \in C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\}}\big ( \max _{y\in F(x^{1})} \ell ^{T}y - \max _{y\in F(x^{2})} \ell ^{T}y\big )\Big ) \le 0. \end{aligned}$$

(3)

We use this equivalence in order to decide on a computer whether $F(x^{1})\preccurlyeq _{s} F(x^{2})$ or not. Theorem 2.1 works with infinitely many vectors $\ell$ in the nontrivial dual cone and this result can be reduced to finitely many vectors $\ell$ in special cases.

2.1 The nonlinear case

It is remarked in [8, Remark 2.2] that the complexity of the set $C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\}$ is reduced, if it is restricted to the subset $C^{*}\cap \{y\in {\mathbb {R}}^{m}\ |\ \Vert y\Vert =1\}$ belonging to the unit sphere where $\Vert \cdot \Vert$ is an arbitrary norm in ${\mathbb {R}}^{m}$. Although this set also consists of infinitely many elements it can be discretized in small dimensions. Figure 2 illustrates such a discretization for $m=2$ and $C^{*}={\mathbb {R}}^{2}_{+}$.

Fig. 2

Discretization of $C^{*}$

If we replace the dual cone $C^{*}$ by such a subset of finitely many vectors $\ell ^{1},\ldots ,\ell ^{s}\in {\mathbb {R}}^{m}$ for a given $s\in {\mathbb {N}}$, then the equivalence (3) in Theorem 2.1 can be replaced by the approximate equivalence

$$\begin{aligned} F(x^{1})\preccurlyeq _{s} F(x^{2})&<\!\approx \! > \max \Big (\max _{\ell \in \{\ell ^{1},\ldots ,\ell ^{s}\}}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})} \ell ^{T}y\big ) ,\nonumber \\&\max _{\ell \in \{\ell ^{1},\ldots ,\ell ^{s}\}}\big ( \max _{y\in F(x^{1})} \ell ^{T}y - \max _{y\in F(x^{2})} \ell ^{T}y\big )\Big ) \le 0. \end{aligned}$$

(4)

For a given discretization $\{\ell ^{1},\ldots ,\ell ^{s}\}$ of the intersection of the unit sphere and the dual cone the inequality in (4) can be checked on a computer. One has to solve $4s$ nonlinear optimization problems. Since these optimization problems have the same constraint sets $F(x^{1})$ and $F(x^{2})$ and only the linear objective functions vary, it makes certainly sense to solve these $4s$ subproblems in parallel. So, the decision, whether $F(x^{1})\preccurlyeq _{s} F(x^{2})$ or not, can be made by highly parallelized computations.

In the following remark we investigate a possible error bound caused by the discretization of the set $C^{*}\cap \{y\in {\mathbb {R}}^{m}\ |\ \Vert y\Vert =1\}$.

Remark 2.1

For convenience we set $T:=C^{*}\cap \{y\in {\mathbb {R}}^{m}\ |\ \Vert y\Vert =1\}$, where the norm $\Vert \cdot \Vert$ now denotes the Euclidean norm, and for an arbitrary $x\in S$ we define the minimal value function $\varphi ^{x}_{min}:T\rightarrow {\mathbb {R}}$ with

$$\begin{aligned} \varphi ^{x}_{min}(\ell ):=\min _{y\in F(x)} \ell ^{T}y \text{ for } \text{ all } \ell \in T. \end{aligned}$$

For simplicity we investigate only one inner term in the max term in (4). For arbitrarily given $x^{1},x^{2}\in S$ we define the function $\varphi ^{x^{1}\!,\,x^{2}}:T\rightarrow {\mathbb {R}}$ with

$$\begin{aligned} \varphi ^{x^{1}\!,\,x^{2}}(\ell ) := \varphi ^{x^{1}}_{min}(\ell ) -\varphi ^{x^{2}}_{min}(\ell ) \text{ for } \text{ all } \ell \in T. \end{aligned}$$

By Assumption 2.1 the constraint sets $F(x^{1})$ and $F(x^{2})$ are compact and because the objective functions are linear, the minimal value functions $\varphi ^{x^{1}}_{min}$ and $\varphi ^{x^{2}}_{min}$ are continuous (e.g., see [9, Lemma 2.1]) and, therefore, the function $\varphi ^{x^{1}\!,\,x^{2}}$ is continuous as well. Since the set $T$ is compact, there is some $\bar{\ell }\in T$ with

$$\begin{aligned} \sup _{\ell \in T}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})} \ell ^{T}y\big ) = \sup _{\ell \in T}\;\varphi ^{x^{1}\!,\,x^{2}}(\ell ) = \max _{\ell \in T}\;\varphi ^{x^{1}\!,\,x^{2}}(\ell ) = \varphi ^{x^{1}\!,\,x^{2}}(\bar{\ell }). \end{aligned}$$

(5)

If we consider a discretization $\{\ell ^{1},\ldots ,\ell ^{s}\}$ (with $s\in {\mathbb {N}}$) of the set $T$, we get for some $\ell ^{j}$ with $j\in \{ 1,\ldots ,s\}$

$$\begin{aligned} \max _{\ell \in \{\ell ^{1},\ldots ,\ell ^{s}\}}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})} \ell ^{T}y\big ) = \max _{\ell \in \{\ell ^{1},\ldots ,\ell ^{s}\}}\varphi ^{x^{1}\!,\,x^{2}}(\ell ) = \varphi ^{x^{1}\!,\,x^{2}}(\ell ^{j}). \end{aligned}$$

(6)

Let $\ell ^{k}$ with $k\in \{ 1,\ldots ,s\}$ be a point of the discrete set $\{\ell ^{1},\ldots ,\ell ^{s}\}$ with smallest distance to the point $\bar{\ell }$ and let for every $\ell \in T$ the smallest distance to a point $\ell ^{1},\ldots ,\ell ^{s}$ be bounded by a number $d>0$ describing the fineness of discretization. If the sets $F(x^{1})$ and $F(x^{2})$ are given by inequality and equality constraints, it can be shown under strong assumptions (e.g., appropriate differentiability assumptions, the strong second-order sufficient condition and the linear independence constraint qualification) that the minimal value functions $\varphi ^{x^{1}}_{min}$ and $\varphi ^{x^{2}}_{min}$ are differentiable (for a similar result see [9, Lemma 4.1]). If the norm of the gradients $\nabla \varphi ^{x^{1}}_{min}$ and $\nabla \varphi ^{x^{2}}_{min}$ are bounded on the set $T$ by some $u>0$, then by the mean value theorem there is some $\vartheta \in (0,1)$ so that with the equalities (5) and (6)

$$\begin{aligned}&\Big |\sup _{\ell \in T}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})} \ell ^{T}y\big ) - \max _{\ell \in \{\ell ^{1},\ldots ,\ell ^{s}\}}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})}\ell ^{T}y\big )\Big |\\&\quad = \big |\varphi ^{x^{1}\!,\,x^{2}}(\bar{\ell }) -\varphi ^{x^{1}\!,\,x^{2}}(\ell ^{j})\big |\\&\quad \le \big |\varphi ^{x^{1}\!,\,x^{2}}(\bar{\ell }) -\varphi ^{x^{1}\!,\,x^{2}}(\ell ^{k})\big |\\&\quad = \big |\nabla \varphi ^{x^{1}\!,\,x^{2}}(\ell ^{k}+\vartheta (\bar{\ell }-\ell ^{k}))^{T}(\bar{\ell }-\ell ^{k})\big |\\&\quad = \big |\big (\nabla \varphi ^{x^{1}}_{min}(\ell ^{k}+\vartheta (\bar{\ell }-\ell ^{k})) -\nabla \varphi ^{x^{2}}_{min}(\ell ^{k}+\vartheta (\bar{\ell }-\ell ^{k}))\big )^{T} (\bar{\ell }-\ell ^{k})\big |\\&\quad \le \big ( \Vert \nabla \varphi ^{x^{1}}_{min}(\ell ^{k}+\vartheta (\bar{\ell }-\ell ^{k})\Vert + \Vert \nabla \varphi ^{x^{2}}_{min}(\ell ^{k}+\vartheta (\bar{\ell }-\ell ^{k})\Vert \big ) \Vert \bar{\ell }-\ell ^{k}\Vert \\&\quad \le 2u\cdot d. \end{aligned}$$

Recall that $d$ is a measure of the fineness of discretization of the set $T$. So, the obtained error bound decreases, if the fineness of discretization is increased.

2.2 The polyhedral case

In this subsection we restrict ourselves to polyhedral sets $F(x)$ (with $x\in S$). In this case the result of Theorem 2.1 can also be reduced to finitely many vectors $\ell \in C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\}$.

Theorem 2.2

Let Assumption 2.1 be satisfied. In addition, let the cone $C$ be polyhedral and let the set-valued map $F$ be given with

$$\begin{aligned} F(x):=\{ y\in {\mathbb {R}}^{m}\ | \ A(x)\cdot y\le b(x)\} \ \text{ for } \text{ all }\ x\in S \end{aligned}$$

where $A:S\rightarrow {\mathbb {R}}^{(p,m)}$ and $b:S\rightarrow {\mathbb {R}}^{p}$ are given maps. For every $x\in S$ let the set

$$\begin{aligned} L_{1}(x):=\{ -a^{1}(x),\ldots , -a^{p}(x)\} \cap (C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\} ) \end{aligned}$$

and

$$\begin{aligned} L_{2}:= \{\ell ^{1},\ldots ,\ell ^{s}\} \end{aligned}$$

be given where $a^{1}(x),\ldots ,a^{p}(x)$ denote the rows of the matrix $A(x)$ (with $x\in S$) and $\ell ^{1},\ldots ,\ell ^{s}$ are the normed extremal points of the dual cone $C^{*}$. Then for all $x^{1},x^{2}\in S$ it holds

$$\begin{aligned} F(x^{1})\preccurlyeq _{s} F(x^{2})&\Longleftrightarrow&\forall \ \ell \in L_{1}(x^{1}): b_{t}(x^{1})\ge \max _{y\in F(x^{2})} -\ell ^{T}y\end{aligned}$$

(7)

$$\begin{aligned}&\text{(for } t\in \{ 1,\ldots ,p\} \text{ with } \ell =-a^{t}(x^{1})\text{) }\nonumber \\&\forall \ \ell \in L_{2}: \min _{y\in F(x^{1})} \ell ^{T}y \le \min _{y\in F(x^{2})} \ell ^{T}y\nonumber \\&\text{ and }\nonumber \\&\forall \ \ell \in L_{1}(x^{2})\cup L_{2} : \max _{y\in F(x^{1})} \ell ^{T}y \le \max _{y\in F(x^{2})} \ell ^{T}y\nonumber \\&\Longleftrightarrow \max \Big (\max _{\ell \in L_{1}(x^{1})}\big ( - b_{t}(x^{1}) + \max _{y\in F(x^{2})} -\ell ^{T}y \big ),\nonumber \\&\max _{\ell \in L_{2}}\big ( \min _{y\in F(x^{1})} \ell ^{T}y - \min _{y\in F(x^{2})} \ell ^{T}y\big ), \nonumber \\&\max _{\ell \in L_{1}(x^{2})\cup L_{2}}\big ( \max _{y\in F(x^{1})} \ell ^{T}y - \max _{y\in F(x^{2})} \ell ^{T}y \big )\Big ) \le 0\\&( \text{ for } t\in \{ 1,\ldots ,p\} \text{ with } \ell =-a_{t}(x^{1})).\nonumber \end{aligned}$$

(8)

Proof

The proof of the second equivalence is obviuos. The proof of the first equivalence consists of two parts: an introductory part and the proof of this equivalence. Let $x^{1}, x^{2}\in S$ be arbitrarily chosen.

• (a) For an arbitrary $\ell \in L_{1}(x^{1})$ we have with the definition of the set $F(x^{1})$

  $$\begin{aligned} b_{t}(x^{1}) = \max _{y\in F(x^{1})} a^{t}(x^{1})^{T}y = - \min _{y\in F(x^{1})} - a^{t}(x^{1})^{T}y = - \min _{y\in F(x^{1})} \ell ^{T}y \end{aligned}$$

(for $t\in \{ 1,\ldots ,p\}$ with $\ell =-a^{t}(x^{1})$) and, therefore, the inequality (7) is equivalent to

$$\begin{aligned} \min _{y\in F(x^{1})} \ell ^{T}y \le \min _{y\in F(x^{2})} \ell ^{T}y. \end{aligned}$$

Thus, the right hand side of the equivalence in the assertion can be written as

$$\begin{aligned}&\forall \ \ell \in L_{1}(x^{1})\cup L_{2}: \min _{y\in F(x^{1})} \ell ^{T}y \le \min _{y\in F(x^{2})} \ell ^{T}y\\&\text{ and }\\&\forall \ \ell \in L_{1}(x^{2})\cup L_{2} : \max _{y\in F(x^{1})} \ell ^{T}y \le \max _{y\in F(x^{2})} \ell ^{T}y. \end{aligned}$$

(b) For the actual proof of the first equivalence we notice that the implication “$\Longrightarrow$” is obvious with Theorem 2.1 and part (a) of this proof. Finally, we prove the opposite direction “$\Longleftarrow$”. It is well-known that the polyhedron $F(x^{1})+C$ can be represented by the intersection of certain affine halfspaces generated by facets of this polyhedron, i.e. $\displaystyle F(x^{1})+C=\cap _{\ell \in L_{1}(x^{1})\cup L_{2}} H_{1}(\ell )$ for appropriate affine halfspaces $H_{1}(\ell )$ ($\ell \in L_{1}(x^{1})\cup L_{2}$). Because of the assumption and the equivalent transformation in part (a) of this proof we obtain

$$\begin{aligned} F(x^{2})\subset H_{1}(\ell ) \text{ for } \text{ all } \ell \in L_{1}(x^{1})\cup L_{2} \end{aligned}$$

which implies

$$\begin{aligned} F(x^{2})\subset \bigcap _{\ell \in L_{1}(x^{1})\cup L_{2}} H_{1}(\ell ) = F(x^{1})+C. \end{aligned}$$

(9)

With the same arguments one can consider the affine halfspaces generated by facets of the polyhedron $F(x^{2})-C$, one can apply part (a) of this proof and then one gets

$$\begin{aligned} F(x^{1})\subset F(x^{2})-C. \end{aligned}$$

(10)

From the inclusions (9) and (10) it follows with Definition 2.1,(a) that $F(x^{1})\preccurlyeq _{s} F(x^{2})$ which has to be shown. $\square$

Remark 2.2

The result of Theorem 2.2 has an important consequence from a numerical point of view. The decision whether $F(x^{1})\preccurlyeq _{s} F(x^{2})$ can be made by solving a finite number of linear optimization problems. The number of linear problems depends on the number of appropriate facets of the polyhedrons $F(x^{1})+C$ and $F(x^{2})-C$. So, for problems with a less complex polyhedral structure this number is small.

The result of Theorem 2.2 can be used in an algorithm in order to evaluate whether $F(x^{1})\preccurlyeq _{s} F(x^{2})$ or $F(x^{1})\not \preccurlyeq _{s} F(x^{2})$.

Algorithm 2.1

(Test of $F(x^{1})\preccurlyeq _{s} F(x^{2})$ for $x^{1},x^{2}\in S$)

The following corollary is a direct consequence of Theorem 2.2.

Corollary 2.1

Under the assumptions of Theorem 2.2 Algorithm 2.1 is well-defined and makes the decision whether $F(x^{1})\preccurlyeq _{s} F(x^{2})$ is true or not (for arbitrary $x^{1},x^{2}\in S$).

Example 2.1

We investigate the set-valued map $F:{\mathbb {R}}^{2}\rightrightarrows {\mathbb {R}}^{2}$ with

$$\begin{aligned} F(x):=\{ y\in {\mathbb {R}}^{2}\ | \ A(x)\cdot y\le b(x)\} \ \forall \ x\in {\mathbb {R}}^{2} \end{aligned}$$

where for arbitrary $x=(x_{1},x_{2})\in {\mathbb {R}}^{2}$

$$\begin{aligned} A(x):=\left( \begin{array}{cc} -\frac{1}{1+|x_2-x_1|} &{}\quad -\frac{1}{3+|x_2-x_1|}\\ [1ex] -\frac{1}{1+|x_1|} &{}\quad -x_2\\ [1ex] -\frac{5}{4} &{}\quad 1\\ [1ex] \frac{6}{5} &{}\quad -1\\ [1ex] \frac{5-|x_2-x_1|}{7} &{}\quad 1 \end{array}\right) \text{ and } b(x):=\left( \begin{array}{c} -1\\ [1ex] -1\\ [1ex] 2+x_{2}\\ [1ex] \frac{41}{5}-\frac{16}{25}(2x_1-x_2)\\ [0.5ex] 9+2x_1-\frac{2}{35}(x_1-3x_2) \end{array}\right) . \end{aligned}$$

Figure 3 illustrates the sets $F(1,2)$ and $F(3,1)$. For the cone $C:={\mathbb {R}}^{2}_{+}$ we obtain with Algorithm 2.1 the result $F(1,2)\preccurlyeq _{s} F(3,1)$.

Fig. 3

Illustration of the sets $F(1,2)$ and $F(3,1)$ in Example 2.1

3 Determination of optimal scenarios

In concrete applications, like socio-economic applications discussed by Neukel in [19], the constraint set $S$ only consists of some few points $\{x^{1},\ldots ,x^{k}\}\subset {\mathbb {R}}^{n}$ (with $k\in {\mathbb {N}}$). Every set $F(x^{i})$ (with $i\in \{ 1,\ldots ,k\}$) describes a certain scenario and it is the aim to find optimal scenarios. This means mathematically that one has to determine minimal elements of the system of sets $F(x^{i})$ with $i\in \{ 1,\ldots ,k\}$, if they exist. Based on the definition of minimal solutions the following algorithm determines optimal scenarios.

Algorithm 3.1

(Determination of minimal solutions)

Proposition 3.1

Let Assumption 2.1 be satisfied. Algorithm 3.1 is well-defined and determines all minimal solutions, if there exists at least one minimal solution.

Proof

The proof is obvious because the algorithm works according to the definition of minimal solutions. $\square$

Recently, Löhne [15] has proved by induction that every finite set $S$ has at least one minimal solution so that the corresponding assumption in Proposition 3.1 can be dropped.

Remark 3.1

In the nonlinear case the inequality in the approximate equivalence (4) can be used for the comparison of sets in Algorithm 3.1. In the polyhedral case one works with Algorithm 2.1 for the comparisons in the “if” parts of Algorithm 3.1.

As a simple example we consider a problem of finding an optimal scenario among given scenarios.

Example 3.1

For the set-valued map $F:{\mathbb {R}}^{2}\rightrightarrows {\mathbb {R}}^{2}$ defined in Example 2.1 we consider the sets $F(1,1)$, $F(1,2)$, $F(2.5,1)$, $F(2.5,1.2)$ and $F(3,1)$. These sets are illustrated in Fig. 4. It is obvious from this figure that for the natural order cone there is only one minimal scenario among these 5 scenarios. In other words, for $C={\mathbb {R}}^{2}_{+}$ and $S:=\{ (1,1),(1,2),(2.5,1),(2.5,1.2),(3,1)\}$ the point $(1,1)$ is a minimal solution of problem (1). This result is obtained with Algorithm 3.1.

Fig. 4

Illustration of the sets $F(1,1)$, $F(1,2)$, $F(2.5,1)$, $F(2.5,1.2)$ and $F(3,1)$ in Example 3.1

4 A descent method

Until now we have investigated set optimization problems with a constraint set consisting of a finite number of points. In this section we now consider unconstraint set optimization problems, i.e. in Assumption 2.1 with have $S={\mathbb {R}}^{n}$. We present a derivative-free descent method which works with a cluster of points. For instance, the well-known Nelder–Mead method (see [14, 17, 18]) is a classical method in nonlinear optimization which works with a cluster of points. In general, the Nelder–Mead method does not work in set optimization because $n+1$ points in a cluster in ${\mathbb {R}}^{n}$ are too less for comparisons of sets and it does not make sense to drop undesirable points since many sets are not comparable with respect to the set less order relation. Using a cluster of points we now construct a descent direction together with an appropriate step length.

Remark 4.1

Let $x^{i}\in {\mathbb {R}}^{2}$ be an arbitrary iteration point. As indicated in Fig. 5 eight equally distributed points with equal small $\ell _{\infty }$ distance to $x^{i}$ are considered and for each point $x$ of this cluster it is checked using the approximate equivalence (4) or the equivalence (8) whether $F(x)\preccurlyeq _{s} F(x^{i})$ or not. Among all cluster points satisfying this inequality one chooses the point for which the exact or approximated max term in (4) or (8) has the smallest value. For such a point $\tilde{x}$ the difference $h:=\tilde{x}-x^{i}$ gives the descent direction of this iteration. For the determination of the step length one considers the point $x^{i}+2h$. If $F(x^{i}+2h)\not \preccurlyeq _{s} F(\tilde{x})$, then one stops and $x^{i+1}:=\tilde{x}$ is the new iteration point. Otherwise one considers the point $x^{i}+3h$ and so on. This technique is implemented in Algorithm 4.1.

Fig. 5

Illustration of an iteration step of the descent method

We now present an algorithm for the improvement of feasible points.

Algorithm 4.1

(descent method)

It should be noted that in the “else” part of the “if” statement of the preceding algorithm, more than only one refinement of the grid should be implemented in order to have a better chance to find a new iteration point.

Theorem 4.1

Let Assumption 2.1 with $S={\mathbb {R}}^{n}$ be satisfied.

• (a) Algorithm 4.1 is well-defined for arbitrary input parameters.

• (b) For an arbitrary starting point $x^{0}\in {\mathbb {R}}^{n}$ let $x^{1}, x^{2}, \ldots \in {\mathbb {R}}^{n}$ denote the iteration points generated by Algorithm 4.1.

  • (i) In the polyhedral case we have

    $$\begin{aligned} F(x^{i+1})\preccurlyeq _{s} F(x^{i}) \text{ for } \text{ all } i=0,1,2,\ldots . \end{aligned}$$

    (11)

    This inequality is also satisfied in the nonlinear case, if one works with all $\ell \in C^{*}\backslash \{ 0_{{\mathbb {R}}^{m}}\}$.

  • (ii) If $x^{\prime }\in {\mathbb {R}}^{n}$ denotes the output vector, then we obtain in the polyhedral case

    $$\begin{aligned} F(x^{\prime })\preccurlyeq _{s} F(x^{0}). \end{aligned}$$

    This inequality is also satisfied in the nonlinear case, if one works with all $\ell \in C^{*}\backslash \{ 0_{{\mathbb {R}}^{m}}\}$.

• (c) For arbitrary input parameters where $i_{max}$ and $j_{max}$ are sufficiently large, let $S(0_{{\mathbb {R}}^{m}},\frac{\varepsilon }{d})$ denote the sphere around $0_{{\mathbb {R}}^{m}}$ with radius $\frac{\varepsilon }{d}$. If one works with the whole sphere $S(0_{{\mathbb {R}}^{m}},\frac{\varepsilon }{d})$ in Algorithm 4.1 (and not only with a cluster of points), then in the polyhedral case the output vector $x^{\prime }\in {\mathbb {R}}^{n}$ is minimal with respect to the set $S(x^{\prime },\frac{\varepsilon }{d})\cup \{ x^{\prime }\}$. This assertion is also true in the nonlinear case, if one works with all $\ell \in C^{*}\backslash \{ 0_{{\mathbb {R}}^{m}}\}$.

Proof

• (a) This part of the proof is obvious.

• (b),(i) For an arbitrary iteration point $x^{i}\in {\mathbb {R}}^{n}$ Algorithm 4.1 determines a new iteration point $x^{i+1}$, if the corresponding max term is nonpositive. In the polyhedral case we then get $F(x^{i+1})\preccurlyeq _{s} F(x^{i})$ by Theorem 2.2. In the nonlinear case we get the assertion using Theorem 2.1.

• (b),(ii) This assertion immediately follows from part (i) because the set less order relation $\preccurlyeq _{s}$ is transitive.

• (c) If Algorithm 4.1 stops at an iteration point $x^{\prime }\in {\mathbb {R}}^{n}$, then the method could not find any $x\in S(x^{\prime },\frac{\varepsilon }{d})$ with the property $F(x)\preccurlyeq _{s} F(x^{\prime })$. So, by Definition 2.1,(b) $x^{\prime }$ is a minimal solution with respect to the set $S(x^{\prime },\frac{\varepsilon }{d})\cup \{ x^{\prime }\}$.

$\square$

Remark 4.2

• (a) Because of the inequality (11) we use the concept descent method for Algorithm 4.1.

• (b) The assertion (c) in Theorem 4.1 says that the output vector $x^{\prime }$ is some kind of minimal solution. Since $\varepsilon >0$ is small and $d>1$, this means some kind of local minimality. At the best, the vector $x^{\prime }$ is a local minimal solution.

• (c) In practice, Algorithm 4.1 does not produce locally minimal solutions because various discretizations are included in this method. In the nonlinear case only finitely many vectors are chosen in $C^{*}\backslash \{ 0_{{\mathbb {R}}^{m}}\}$ and in both cases Algorithm 4.1 works only with finitely many vectors in the spheres $S(0_{{\mathbb {R}}^{m}},\varepsilon )$ and $S(0_{{\mathbb {R}}^{m}},\frac{\varepsilon }{d})$. If these discretizations are not fine enough, it may be that descent directions cannot be found. The radius $\varepsilon >0$ should be small enough in order to obtain local descent directions.

Algorithm 4.1 fits into the class of pattern search methods with one essential difference that we do not minimize an objective function but we work with a function $\varphi : {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}$ with

$$\begin{aligned} \varphi (\bar{x},\tilde{x})&= \max \Big (\sup _{\ell \in C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\}}\big ( \min _{y\in F(\bar{x})} \ell ^{T}y - \min _{y\in F(\tilde{x})} \ell ^{T}y\big ),\\&\sup _{\ell \in C^{*}\backslash \{0_{{\mathbb {R}}^{m}}\}}\big ( \max _{y\in F(\bar{x})} \ell ^{T}y - \max _{y\in F(\tilde{x})} \ell ^{T}y\big )\Big ) \text{ for } \text{ all } \bar{x},\tilde{x}\in {\mathbb {R}}^{n} \end{aligned}$$

which has a special meaning in this setting. In fact, we want to obtain negative function values which should finally tend to zero. Torczon [25] has developed a general convergence theory for pattern search algorithms which can be adapted to the special problem in this paper (see also [3])).

In order to obtain such a convergence result we have to extend Algorithm 4.1 with two additional specifications (in the following we set ${\mathbb {N}}_{0}={\mathbb {N}}\cup \{ 0\}$):

• (A) Assume that the pattern contains at least one direction of descent whenever a set $F(x^{i})$ ($i\in {\mathbb {N}}_{0}$) can be improved.

• (B) Let some $\beta \in (0,1)$ and an arbitrary null sequence $(\varepsilon ^{i})_{i\in {\mathbb {N}}_{0}}$ with $\varepsilon ^{i}<0$ for all $i\in {\mathbb {N}}_{0}$ be given. While $\varphi (x^{i}+\lambda h^{i},x^{i})\le \varepsilon ^{i}<0$ set $\lambda :=\beta ^{q}\lambda ^{0}$ for $q:=0,1,2,\ldots$ ($\lambda ^{0}$ and $h^{i}$ denote the initial step length and the descent direction at an iteration point $x^{i}$, respectively).

If an arbitrary point $x^{i}$ ($i\in {\mathbb {N}}_{0}$) is a non-final iteration point, then there exists a (strict) descent direction and an $\bar{x}\in {\mathbb {R}}^{n}$ with $\varphi (\bar{x},x^{i})<0$. Since the function $\varphi$ is continuous, there exists a ball $B(\bar{x},\delta )$ around $\bar{x}$ with radius $\delta >0$ so that

$$\begin{aligned} \varphi (x, x^{i})<0 \text{ for } \text{ all } x\in B(\bar{x},\delta ). \end{aligned}$$

So, it is obvious that a refinement of the grid leads to a descent direction so that the specification (A) is satisfied.

Specification (B) defines a step length control where various forms are possible. It should be ensured that the step lengths tend to zero. Since the function $\varphi$ is continuous, it is always possible to give some finite $q\in {\mathbb {N}}$ so that for $\lambda :=\beta ^{q}\lambda ^{0}$ the inequality $0\ge \varphi (x^{i}+\lambda h^{i},x^{i})>\varepsilon ^{i}$ holds (if $\varphi (x^{i}+\lambda h^{i},x^{i})\le 0$ for all $\lambda \in [0,1]$), i.e. the while loop in specification (B) can be carried out in finitely many steps.

With these two specifications we now formulate a convergence result.

Theorem 4.2

Let Assumption 2.1 be satisfied, let Algorithm 4.1 with the additional specifications (A) and (B) generate an iteration sequence $(x^{i})_{i\in {\mathbb {N}}_{0}}$ and let the level set

$$\begin{aligned} L_{x^{0}}:=\left\{ x\in {\mathbb {R}}^{n}\ |\ F(x)\preccurlyeq _{s} F(x^{0})\right\} \end{aligned}$$

be compact. Then it follows

$$\begin{aligned} \limsup _{i\rightarrow \infty } \varphi (x^{i+1},x^{i})=0. \end{aligned}$$

Proof

Since Algorithm 4.1 is a descent method, we have $x^{i}\in L_{x^{0}}$ for all $i\in {\mathbb {N}}_{0}$. Because of the compactness of the level set $L_{x^{0}}$ and the continuity of the function $\varphi$ (compare Remark 2.1), the function values $\varphi (x^{i+1},x^{i})$ with $i\in {\mathbb {N}}_{0}$ are bounded. Consequently, the limit superior exists.

Assume that $\displaystyle \limsup _{i\rightarrow \infty }\varphi (x^{i+1},x^{i})\ne 0$. Then there exists a subsequence $(x^{i_{r}})_{r\in {\mathbb {N}}}$ with $\displaystyle \lim _{r\rightarrow \infty } \varphi (x^{i_{r}+1},x^{i_{r}}) := \alpha \ne 0$. With the specification (A) we have $F(x^{i+1})\preccurlyeq _{s} F(x^{i})$ for all $i\in {\mathbb {N}}_{0}$ and then we get by Theorem 2.1

$$\begin{aligned} \varphi (x^{i+1},x^{i})\le 0 \text{ for } \text{ all } i\in {\mathbb {N}}_{0}. \end{aligned}$$

Consequently, we have $\alpha <0$. Then there is some $N_{1}\in {\mathbb {N}}$ with the property

$$\begin{aligned} \varphi (x^{i_{r}+1},x^{i_{r}})\le \frac{\alpha }{2}<0 \text{ for } \text{ all } r\ge N_{1}. \end{aligned}$$

Since $(\varepsilon ^{i})_{i\in {\mathbb {N}}_{0}}$ is a null sequence, there is some $N_{2}\in {\mathbb {N}}$ with

$$\begin{aligned} \frac{\alpha }{2}\le \varepsilon ^{i_{r}}<0 \text{ for } \text{ all } r\ge N_{2}. \end{aligned}$$

Then we obtain

$$\begin{aligned} \varphi (x^{i_{r}+1},x^{i_{r}})\le \frac{\alpha }{2}\le \varepsilon ^{i_{r}} \text{ for } \text{ all } r\ge N:=\max \{N_{1},N_{2}\}, \end{aligned}$$

but this contradicts the specification (B). $\square$

In the following Algorithm 4.1 is applied to various examples in ${\mathbb {R}}^{2}$.

Example 4.1

We investigate the set-valued map $F:{\mathbb {R}}^{2}\rightrightarrows {\mathbb {R}}^{2}$ with

$$\begin{aligned} F(x):=\{ y\in {\mathbb {R}}^{2}\ | \ A(x)\cdot y\le b(x)\} \ \forall \ x\in {\mathbb {R}}^{2} \end{aligned}$$

where for arbitrary $x=(x_{1},x_{2})\in {\mathbb {R}}^{2}$

$$\begin{aligned} A(x):=\left( \begin{array}{cc} -\frac{1}{1+|x_2|} &{}\quad -\frac{1}{3+|x_1|}\\ [1ex] -\frac{1}{1+|x_1|} &{}\quad -x_2\\ [1ex] -\frac{5}{4} &{}\quad 1\\ [1ex] \frac{6}{5} &{}\quad -1\\ [1ex] \frac{5-|x_2|}{7} &{}\quad 1 \end{array}\right) \text{ and } b(x):=\left( \begin{array}{c} -1\\ [1ex] -1\\ [1ex] 2+x_{2}\\ [1ex] \frac{41}{5}-\frac{16}{25}(2x_1-x_2)\\ [0.5ex] 9+2x_1-\frac{2}{35}(x_1-3x_2) \end{array}\right) . \end{aligned}$$

The matrix function $A$ is slightly different from the one in Example 2.1. Figure 6 illustrates the iteration process for $C:={\mathbb {R}}^{2}_{+}$. The chosen starting point is $x^{0}:=(3, 2.5)$, the radius is $\varepsilon := 0.01$ and $k:=8$ cluster points are selected as indicated in Fig. 5. Algorithm 4.1 then determines the iteration points $x^{1}:=(1.34, 0.84)$, $x^{2}:=(0.71, 0.84)$ and $x^{3}:=(0.18, 0.31)$. Using a discretization multiplier $d:=2$ the point $(0.175, 0.3075)$ cannot be improved. For this example totally 4,566 linear optimization problems have to be solved. Figure 7 illustrates the sets $F(x^{0})$ and $F(x^{3})$.

Fig. 6

Illustration of the iteration points in Example 4.1

Fig. 7

Illustration of the sets $F(3, 2.5)$ and $F(0.18, 0.31)$ in Example 4.1

Example 4.2

We investigate the set-valued map $F:{\mathbb {R}}^{2}\rightrightarrows {\mathbb {R}}^{2}$ with

$$\begin{aligned} F(x_{1},x_{2}):\!=\!\left\{ (y_{1},y_{2})\in {\mathbb {R}}^{2}\ |\ (y_{1}\!-\!2x_{1}^{2})^{2} \!+\!(y_{2}\!-\!2x_{2}^{2})^{2} \!\le \! (1\!+\!x_{2}^{2})^{2}\right\} \ \forall \ (x_{1},x_{2})\in {\mathbb {R}}^{2}. \end{aligned}$$

Here we choose the starting point $x^{0}:=(2.99, 1.01)$, the radius $\varepsilon :=0.1$, the discretization parameter $d:=2$ and the number $s:=10$ of vectors in the dual cone $C^{*}$ generated by the convex hull of the two points $(0.1111,0.8889)$ and $(1.1111,-0.1111)$. Figure 8 illustrates the iteration process and Table 1 gives the iteration points obtained by Algorithm 4.1. The iteration point $x^{9}$ cannot be improved. For this example totally 3,340 convex optimization problems have to be solved. The solution of these convex optimization problems has been done using the fmincon tool in MATLAB. Figure 9 illustrates the sets $F(x^{i})$ for $i=0,1,\ldots ,9$.

Table 1 Iteration points in Example 4.2

Fig. 8

Illustration of the iteration points in Example 4.2

Fig. 9

Illustration of the sets $F(x^{0})$,...,$F(x^{9})$ in Example 4.2 ($F(x^{0})$ is the set on the right and $F(x^{9})$ is the left circle)

Example 4.3

Again we consider the problem in Example 4.2; but now we work with $C:={\mathbb {R}}^{2}_{+}$ and a higher discretization in the dual cone. Here we choose $s:=100$ vectors in $C^{*}={\mathbb {R}}^{2}_{+}$. For the starting point $x^{0}:=(1, 1.2)$ we get with the parameter $\varepsilon :=0.1$ the iteration point $x^{1}:=(0.1, 0.3)$ which cannot be improved in this setting. Figure 10 illustrates the sets $F(x^{0})$ and $F(x^{1})$. With the multiplier $d:=2$ one obtains the slightly changed point $(1.9429\cdot 10^{-16}, 0.25)$ which cannot be improved. Because of the high discretization totally 21,000 convex optimization problems have to be solved.

Fig. 10

Illustration of the sets $F(x^{0})$ and $F(x^{1})$ in Example 4.3

5 Conclusion

The presented descent method in Algorithm 4.1 does not generally produce optimal solutions. But the conception may lead to better feasible points with respect to the set less order relation. In practice, the iteration process is very time-consuming. Since many comparisons can be done in parallel, the descent method can use parallel computation tools. Moreover, adaptive techniques can be applied for the step size control and the refinement of the cluster.

Using nonlinear scalarization results given by Rubinov [23], Tammer (Gerstewitz) [4] and Pascoletti and Serafini [22] in vector optimization and by Hernández and Rodríguez-Marín [7] in set optimization, one then gets other types of $\min$ problems which can be solved on a computer. Then even nonconvex set optimization problems should be solvable.