A heuristic method towards deadline-aware energy-efficient mapreduce scheduling problem in Hadoop YARN

Abstract

The MapReduce (MR) scheduling is a prominent area of research to minimize energy consumption in the Hadoop framework in the era of green computing. Very few scheduling algorithms have been proposed in the literature which aim to optimize energy consumption. Moreover, most of them are only designed for the slot-based Hadoop framework, and hence, there is a need to address this issue exclusively for container-based Hadoop (known as Hadoop YARN). In this paper, we consider a deadline-aware energy-efficient MR scheduling problem in the Hadoop YARN framework. First, we model the considered scheduling problem as an integer program using the time-indexed binary decision variables. Thereafter, a heuristic method is designed to schedule map and reduce tasks on the heterogeneous cluster machines by taking advantage of the fact that tasks have different energy consumption values on different machines. Our heuristic method works in two phases, where each phase is composed of multiple similar rounds. We evaluate the proposed method for large-scale workloads of three standard benchmark jobs, namely, PageRank (CPU-bound), DFSIO (IO-bound), and NutchIndexing (mix-bound). The experimental results show that the proposed method considerably minimizes the energy consumption for all benchmarks against the custom-made makespan minimizing scheme which does not consider energy-saving criteria. We observe that energy-efficiency of the schedule generated by proposed heuristic stays within the 5% of the optimal solution. Apart from this, we also evaluate the proposed heuristic against delay scheduler (the default task-level scheduler in Hadoop YARN), and found it to be 35% more energy-efficient.

1 Introduction

In the era of Big data analytics, large-scale data centers have huge energy demands and thus given rise to various energy efficiency issues. A typical data center consumes electricity equivalent to 25000 households. Moreover, the electricity consumption of worldwide data centers in 2012 was about 270 TWh [27]. This corresponds to almost 2% of the global electricity consumption and has an approximated annual growth rate of 4.3%. Since Hadoop MapReduce (MR) is a widely used framework in data centers to analyze a huge amount of data, we need to explore the various possibilities to optimize energy consumption in context to Hadoop.

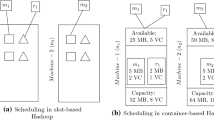
There are two variants of Hadoop framework: (i) slot-based [6] and (ii) container-based [28]. The container-based Hadoop employs a new cluster manager known as Yet Another Resource Negotiator (YARN). As depicted in Fig. 1, mainly four methodologies are used to minimize the energy consumption in any variant of Hadoop deployment. These methodologies include (i) energy-aware data placement at Hadoop Distributed File System (HDFS) layer (ii) Dynamic Voltage and Frequency Scaling (DVFS) technique (iii) cluster-level resource management, and (iv) energy-efficient job/task scheduling. In this paper, we have adopted the last approach to optimize energy consumption. In this approach, various map and reduce tasks are assigned/scheduled to suitable energy-efficient nodes by taking advantage of hardware heterogeneity in order to reduce energy consumption.

Fig. 1

Energy saving techniques in Hadoop

The MR schedulers for Hadoop can be classified as job-level or task-level [25]. The default job-level schedulers (i.e., FIFO, FAIR, and Capacity Schedulers), and a default task-level delay scheduler [40] do not consider energy minimization criteria while making scheduling decisions in both variants of Hadoop. To overcome this problem, some scheduling algorithms have been proposed in the literature, which target to reduce energy consumption. However, most of them are designed only for slot-based Hadoop. Thus, there is a need to look for an energy-efficient scheduling scheme exclusively for the YARN environment.

Besides minimizing power consumption, MR schedulers need to complete production jobs in data centers within a user-specified deadline. For example, the spam detection task of Facebook is executed periodically and needs to be completed before a given time. In view of this, we consider the problem of deadline-aware Energy-efficient MR Scheduling for YARN (EMRSY). Eventually, our problem turns out to be same as in [15,39] as far as the energy minimization objective and deadline constraint is concerned. However, authors in these references have considered a slot-based Hadoop which has a different mechanism for resource allocation and scheduling. Hence, the mathematical modeling of the EMRSY problem and subsequently designing a heuristic algorithm for it requires an entirely different approach and is a very challenging task, which we explain next.

1.1 Scheduling challenges in container-based Hadoop

The scheduling in both variants of Hadoop differs in the way various computing resources available of any node¹ are allocated to map and reduce tasks. In traditional (slot-based) Hadoop, resources are allocated in the form of a slot which represents a fixed portion of node’s overall resource capacity [28]. At each machine, a constant number of slots, equals to the number of computing cores available at that machine, are created separately for map and reduce tasks. Each computing slot represents the same resource capacity and can not exactly meet the heterogeneous resource demand of different tasks. During the job execution, map and reduce tasks are to be scheduled on their respective slots.

On the other hand, YARN discards the idea of separate computing slots for the map and reduce tasks. Moreover, it allows map and reduce tasks to place their resource requirements in the form a vector $\vec {q}=\langle q_{1}, \dots , q_{l}, \dots , q_{|{\mathcal{A}}|}\rangle$ where $q_{l}$ represents the amount of lth resource type and $|{\mathcal{A}}|$ represents total resource types available at any machine. The YARN allocates the exact amount of these resources in the form of containers. A container represents the logical collection of resources available at a node, and resembles as a virtual machine. Currently, YARN supports two resource types: memory and virtual cores. Therefore, resource request vector of any task is represented as $\langle q_{1}\, {\text{MB}},\, q_{2}\, {\text{VC}} \rangle$, where $q_{1}$ and $q_{2}$ denotes required amount of memory in megabytes (MB) and number of virtual cores (VC), respectively.

Figure 2 demonstrates the resource allocation concept in YARN. There are two map tasks $m_{1}$ and $m_{2}$, and a reduce task $r_{1}$ to be scheduled on a YARN cluster of two machines $n_{1}$ and $n_{2}$. Both map tasks have same resource request vector as $\langle 6\, {\text{MB}},\, 2\, {\text{VC}} \rangle$ each, and reduce task has request vector as $\langle 5\, {\text{MB}},\, 1\, {\text{VC}} \rangle$. Moreover, both machine has a total resource capacity² of $\langle 64\, {\text{MB}},\, 8\, {\text{VC}} \rangle$ each. And now suppose that tasks $m_{1}$ and $r_{1}$ are scheduled on machine $n_{1}$ by any scheduling algorithm. In that case, two containers of respective (and exact) resource demand are allocated within machine $n_{1}$ for both tasks as shown in Fig. 2. Similarly, if task $m_{2}$ is scheduled on machine $n_{2}$, a container of the exact amount of resources is created within machine $n_{2}$. After task allocation, machine $n_{1}$ is left with $\langle 54\, {\text{MB}},\, 5\, {\text{VC}} \rangle$ resources whereas machine $n_{2}$ is left with $\langle 58\, {\text{MB}},\, 6\, {\text{VC}} \rangle$ resources. Moreover, when the tasks finish their execution, both machines reclaim its allocated resources. In any case, total number of tasks (and eventually total number of containers) scheduled on any machine should not consume resources more than the machine’s total resource capacity. For example, if we have so many map tasks to be scheduled only on machine $n_{1}$, then at most four of them can be executed at a particular time instance.

Fig. 2

Task assignment and resource allocation in Hadoop YARN

1.2 Work done and contributions

We formulate the EMRSY problem for a single MR job as an integer program. To solve the formulated problem, we propose an offline heuristic algorithm which generates a static schedule before the actual execution of MR job begins. At the time of job execution, tasks are scheduled on a particular node and at a designated time as specified in the schedule. The algorithm uses a metric similar to the one used in [15]. However, in our case, it is now calculated for each node rather than for each slot. Based on this new metric, nodes are arranged in a particular order and picked one by one for task allocation. Apart from this, the proposed heuristic separately calculates the map and reduce deadlines unlike [15], to better schedule the tasks so that job may complete its execution before user-specified deadline.

Our algorithm schedules map and reduce tasks to various machines in two disjoint phases by calling two separate subroutines. In the first phase, it schedules all map tasks to cluster machines in multiple similar rounds. Once all map tasks are scheduled, it starts scheduling reduce tasks in the second phase. The scheduling of reduce tasks are also performed in various similar rounds. We evaluate the performance of the proposed technique for a wide variety of MR benchmark jobs and find that it saves a significant amount of energy in comparison to a scheme that considers only makespan minimization as its primary objective.

Being an offline scheduling algorithm, the proposed approach requires the values of various input parameters including processing time and energy consumption of tasks in advance. The values of these two parameters can be estimated with the help of profiling. In most data centers, many production jobs are run periodically which creates a huge amount of profiled historical data. For example, the Facebook process GigaBytes of data every few minutes to detect spams. The profiling technique has been successfully utilized in many MapReduce scheduler proposed in the past [3, 15, 17, 29, 30, 39]. To profile the desired input parameters, we have designed an MR energy profiler which do not rely on any external power meter as used in [15, 39].

1.3 Paper organization

The organization of the paper is as follows. Section 2 presents a brief discussion of energy-efficient scheduling techniques in both variants of the Hadoop framework. Section 3 formulates the EMRSY scheduling problem as an integer program. Section 4 proposes a offline heuristic method which produces sub-optimal schedules for map and reduce tasks. Next, Sect. 5 presents the experimental evaluation of the proposed technique followed by conclusion in Sect. 6.

2 Related work

In this section, we discuss existing energy-efficient MR scheduling schemes. For a better understanding, we classify the discussed techniques as slot-based and YARN-based schemes.

2.1 Energy-efficient scheduling schemes in slot-based Hadoop

To minimize the energy consumption, Yigitbasi et al. [38] took the advantage of hardware heterogeneity of a Hadoop cluster and proposed a scheme to schedule heterogeneous workload (mix of IO and CPU-bound) by intelligently assigning jobs to its corresponding energy-efficient node. Mashayekhy et al. [14, 15] proposed a task-level offline scheduler to improve the energy efficiency of a single MapReduce job over a cluster of heterogeneous machines while satisfying the service level agreement (SLA). The problem of map and reduce tasks assignment to respective slots has been modeled as an integer programming (IP) problem with a deadline as one of the constraints. To solve the formulated problem, two heuristics have been proposed which take the differences in energy efficiency of machines for different tasks into account and use a metric called energy consumption rate (ecr) which is calculated for each computing slot. The metric induces an order relation among the machines for tasks allocation i.e., the slot with the lowest ecr value is picked first for scheduling tasks on it.

In order to improve the performance of the heuristic method discussed in [15], Yousefi et al. [39] proposed a task-based greedy heuristic, to establish the mapping between slots and tasks. The heuristic minimizes the energy consumption of an MR job without significant loss in performance while satisfying a user-specific deadline. On average, the proposed greedy heuristic can meet deadlines as tight as 12% because it calculates map and reduce deadline separately before starting the task placement. The time complexity of the proposed greedy heuristic is $O(i (\log i + k \log k) + j(\log j + l \log l))$ where i and j represents the number of map and reduce tasks, respectively. And k and l represents the number of map and reduce slots, respectively.

Bampis et al. [2] considered the problem of minimizing the weighted completion time of n MapReduce jobs with a constraint of the energy budget in an environment where processors have DVFS technology. The authors assumed that the order of jobs is not fixed, and derived a polynomial-time constant-factor approximation algorithm to solve the formulated problem as integer program.

Wang et al. [32] considered a geo-distributed heterogeneous MapReduce clusters and proposed the energy-aware task scheduling scheme which also take care of deadlines, data locality and resource utilization. A mathematical model is constructed for the considered problem. It is well known that the energy consumption is closely related to resource utilization in data centers. Their scheme improves server resource utilization using fuzzy logic which ultimately optimizes the energy consumption.

Zhang et al. [41] aim to reduce the energy consumption of a MR job along with minimizing the makespan at the same time, thus, making it a bi-objective optimization problem. They model it as an integer linear program, while ignoring the temporal dependency constraint between map and reduce tasks. They propose a two phase heuristic allocation (TPHA) algorithm to find a high-quality initial feasible solution and then employ the NSGA-II meta-heuristic to find the set of pareto optimal solutions. The TPHA heuristic provides feasible schedule as the initial population to NSGA-II algorithm.

Chen [4] take multiple MapReduce jobs for scheduling and focus on the goal of jointly optimizing the scheduling time, job costs and energy consumption. The authors mainly rely on reducing the network traffic through data locality to reduce the energy consumption. Hamandawana et al. in [8] proposed a scheduling framework with two modules, namely, a task scheduler and power management module which coordinates with the scheduler to place the nodes in two different power transition pools: high and low state power pools by leveraging the node tagging information. Zhou et al. [42] proposed a window-based dynamic resource reservation and a heterogeneity-aware copy allocation technique to schedule the straggler tasks with an aim of energy minimization. Besides this new scheme, they also devised a performance and an energy consumption model to compare the different speculative execution solutions proposed in the literature.

2.2 Energy-efficient scheduling schemes in YARN-based Hadoop

Cai et al. [3] assumed a set of n MR jobs, each with its own user-specified deadline to be executed in the YARN environment. They designed a scheduler to minimize the energy consumption, which works at the job level and task level both. At job-level, the scheduler only attempts to complete the jobs within its deadline, leaving the objective of energy minimization at the task-level which is targeted through the user-space DVFS governor. Pandey et al. [16] presented a heuristic algorithm that greedily selects the best energy-efficient node for task allocation. The proposed scheme is capable of scheduling n number of MR jobs algorithm, however, it does not consider any deadline parameter.

Shao et al. [19] formulated the MR scheduling problem for YARN architecture as an m-dimensional knapsack problem (MKP) resulting in an integer program. Besides energy minimization, the authors also considered the fairness metric and proposed a heuristic approach to produce the sub-optimal solution. Their scheme also employs a power-down mechanism where in periods of low-utilization some servers are switched off to save more energy.

Jin et al [11] employed two types of binning algorithms for energy minimization in YARN environment. For CPU-intensive batch jobs, they proposed a D-based binning algorithm. On the other hand, for online jobs, they proposed a K-based binning algorithm that can adapt to continuously arriving tasks. Shinde et al. [20] proposed a algorithm for YARN environment and devised a metric called Rank, which uses the progress score (PS) of currently executing tasks. The algorithm assigns task to containers without negatively impacting the makespan.

Now, we briefly discuss and mention some pointers to other energy-saving techniques in the Hadoop framework as shown in Fig. 1. Few significant works have been done by Tiwari et al. in [22,23,24, 26] where authors have employed the DVFS technology to save processor energy. Li et al. [12] propose a temperature-aware power allocation (TAPA) scheme which adjusts frequencies of CPUs according to their temperature. Besides these works, Wirtz et al. [33] also proposed a user-space CPU governor to adjust processor frequency to save power, however, their scheme run Hadoop on commodity hardware comprising maximum 4 cores per node. An extensive analysis of the frequency scaling technique to optimize energy consumption in Hadoop is given in [10]. Wang et al. [31] built a power controller which scale up CPU frequency in case of CPU-intensive workloads and scale down CPU frequency when I/O-intensive or Network-intensive workloads emerge. The main goal is to dynamically search the performance-power consumption trade off by the proposed control model.

Although D’Souza et al. [7] has not proposed any new scheme for energy minimozation, they produce an empirical analysis of energy consumption in all three default job-level schedulers in Hadoop: FIFO, FAIR and Capacity Scheduler (CS) with a conclusion that CS performs best among them. As far as intelligent data placement techniques at the HDFS layer are concerned, authors in [13, 35,36,37] have proposed various schemes at the HDFS layer to minimize energy consumption. The interested readers are advised to refer to [18, 34] for a comprehensive discussion of energy saving techniques in Hadoop.

3 The problem formulation

In this section, we formulate the EMRSY problem as an integer programming (IP) problem and call it as EMRSY-IP. We consider a MapReduce job $\mathcal{J}$ which is represented by two sets of tasks: ${\mathcal{M}}{\mathcal{T}} =\{m_{1},\dots ,m_{|{\mathcal{M}}{\mathcal{T}}|}\}$ and ${\mathcal{R}}{\mathcal{T}}=\{r_{1},\dots ,r_{|{\mathcal{R}}{\mathcal{T}}|}\}$. The set ${\mathcal{M}}{\mathcal{T}}$ and ${\mathcal{R}}{\mathcal{T}}$ consist of $|{\mathcal{M}}{\mathcal{T}}|$ map tasks and $|{\mathcal{R}}{\mathcal{T}}|$ reduce tasks, respectively. The job ${\mathcal{J}}$ is to be processed by a YARN cluster comprising $|\mathcal{N}|$ heterogeneous machines represented by a set $\mathcal{N}=\{n_{1},\dots ,n_{|\mathcal{N}|}\}$. The energy consumption and processing time of a map task $m_{j} \in {\mathcal{M}}{\mathcal{T}}$ on machine $n_{i} \in \mathcal{N}$ is $e_{ij}$ and $p_{ij}$, respectively. Similarly, the energy consumption and processing time of a reduce task $r_{k} \in {\mathcal{R}}{\mathcal{T}}$ on machine $n_{i} \in \mathcal{N}$ is $e_{ik}$ and $p_{ik}$, respectively. Moreover, we also consider a set ${\mathcal{A}}=\{a_{1},\dots ,a_{|{\mathcal{A}}|}\}$ which represents $|{\mathcal{A}}|$ types of resources available at each machine.

Further, a two-dimensional resource capacity matrix RC of size $|\mathcal{N}| \times |{\mathcal{A}}|$ is used to represent the total amount of each resource type available at any node. The value RC[i, l] indicates the total amount of resource type $a_{l}\in {\mathcal{A}}$ available at machine $n_{i}$. Furthermore, a resource request matrix $RR^{m}$ of size $|{\mathcal{M}}{\mathcal{T}}| \times |{\mathcal{A}}|$ is defined to store the amount of each resource type required by any map tasks for its execution. Similarly, a two-dimensional matrix $RR^{r}$ of size $|{\mathcal{R}}{\mathcal{T}}| \times |{\mathcal{A}}|$ is also defined to store the amount of each resource type required by any reduce tasks. Particularly, the values $RR^{m} [j, l]$ and $RR^{r} [k, l]$ indicate the amount of a specific resource type $a_{l} \in {\mathcal{A}}$ required by map task $m_{j}$ and reduce task $r_{k}$ respectively during its execution.

The problem here is to schedule all map and reduce tasks over the cluster of machines in such a way so that the total energy consumption is minimized. It is also required that all tasks complete their execution within a given deadline D while maintaining the temporal dependency between map and reduce tasks i.e., a reduce task may start only after the execution of all map tasks. Moreover, as we have considered the YARN environment, scheduling process needs to fulfill the resource constraint, that is, at a particular time, no more tasks can be scheduled at any machine beyond its total capacity.

The problem is formulated using time-indexed (TI) decision variables [21], which is based on discretization of time horizon t ($t=0, 1, \dots ,T$) where time is divided into discrete intervals. our TI formulation (EMRSY-IP) uses two types of binary decision variables, $x_{ijt}$ and $y_{ikt}$, where $x_{ijt}=1$ ($y_{ikt}=1$) signals that map task $m_{j}$ (reduce task $r_{k}$) is scheduled on machine $n_{i}$ at time t. The formulation is as follows:

$$\begin{aligned} \min \sum _{i=1}^{|\mathcal{N}|}\sum _{j=1}^{|{\mathcal{M}}{\mathcal{T}}|}\sum _{t=0}^{T-p_{ij}}e_{ij}x_{ijt} + \sum _{i=1}^{|\mathcal{N}|}\sum _{k=1}^{|{\mathcal{R}}{\mathcal{T}}|}\sum _{t=0}^{T-p_{ik}}e_{ik}y_{ikt} \end{aligned}$$

(1)

subject to:

$$\begin{aligned}&\sum _{i=1}^{|\mathcal{N}|}\sum _{t=0}^{T-p_{ij}}x_{ijt}=1, \quad (j =1,\dots ,|{\mathcal{M}}{\mathcal{T}}|) \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i=1}^{|\mathcal{N}|}\sum _{t=0}^{T-p_{ik}}y_{ikt}=1, \quad (k=1,\dots ,|{\mathcal{R}}{\mathcal{T}}|) \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i=1}^{|\mathcal{N}|}\sum _{t=0}^{T-p_{ik}}(t+p_{ik})y_{ikt}\le D, \quad (k=1,\dots ,|{\mathcal{R}}{\mathcal{T}}|) \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{j=1}^{|{\mathcal{M}}{\mathcal{T}}|}\sum _{s=max(0,t-p_{ij})}^{t-1} RR^{m}[j,l]x_{ijs} \\&\quad +\sum _{k=1}^{|{\mathcal{R}}{\mathcal{T}}|}\sum _{s=max(0,t-p_{ik})}^{t-1} RR^{r}[k,l]y_{iks} \le RC[i,l], \quad \\&\quad (i=1,\dots ,|{\mathcal{N}}|, \, t=0,1,\dots ,T-1, \, l=1,\dots ,|{{\mathcal{A}}}|) \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{i=1}^{|{\mathcal{N}}|}\sum _{s=max(0,t-p_{ij})}^{T-p_{ij}} x_{ijs} +\sum _{i=1}^{|{\mathcal{N}}|}\sum _{s=0}^{t-1} y_{iks} \le 1, \\&\quad (j=1,\dots ,|{\mathcal{M}}{\mathcal{T}}|, k=1,\dots ,|{\mathcal{R}}{\mathcal{T}}|,t=0,1,\dots ,T-1) \end{aligned}$$

(6)

$$\begin{aligned}&x_{ijt} \in \{0,1\} \quad (i=1,\dots ,|{\mathcal{N}}|, \, j =1,\dots ,|{\mathcal{M}}{\mathcal{T}}|, \\&\quad t=0,1,\dots ,T-1) \end{aligned}$$

(7)

$$\begin{aligned}&y_{ikt} \in \{0,1\} \quad (i=1,\dots ,|{\mathcal{N}}|, k=1,\dots ,|{\mathcal{R}}{\mathcal{T}}|, \\&\quad t=0,1,\dots ,T-1) \end{aligned}$$

(8)

The decision variables of the formulation include:

$x_{ijt}$:

binary variable equals to 1 if map task $m_{j}$ is scheduled on machine $n_{i}$ at time t and 0 otherwise

$y_{ikt}$:

binary variable equals to 1 if reduce task $r_{k}$ is scheduled on machine $n_{i}$ at time t and 0 otherwise

And, indices used in the formulation have following meaning:

Index	Meaning
i	Index of cluster machines $(i=1,\dots ,|\mathcal{N}|)$
j	Index of map task to be scheduled $(j=1,\dots ,|{\mathcal{M}}{\mathcal{T}}|)$
k	Index of reduce task to be scheduled $(k=1,\dots ,|{\mathcal{R}}{\mathcal{T}}|)$
l	Index of resource type $(l=1,\dots ,|{\mathcal{A}}|)$
t	Index of time $(t=0,1,\dots ,T)$

In this IP formulation, the objective 1 is to minimize total energy consumption. Constraint 2 and 3 are assignment constraints that require each map and reduce task to be assigned to one machine only once. Constraint 4 is deadline constraint, which requires all tasks must finish their computation before the user-specified deadline.Constraint 5 is a capacity constraint which requires that at any instance of time, the number of tasks assigned to any machine should not exceed its capacity limit. The constraint 6 establishes the temporal dependency between map and reduce tasks. And lastly, constraints 7 and 8 ensure that decision variables $x_{ijt}$ and $y_{ikt}$ take values either 0 or 1. The formulation has $\mathcal{O}(|\mathcal{N}|(|{\mathcal{M}}{\mathcal{T}}|+|{\mathcal{R}}{\mathcal{T}}|)T)$ decision variables and $\mathcal{O}(|{\mathcal{M}}{\mathcal{T}}|+|{\mathcal{R}}{\mathcal{T}}|+ |{\mathcal{M}}{\mathcal{T}}||{\mathcal{R}}{\mathcal{T}}|T+|\mathcal{N}||{\mathcal{A}}|T)$ constraints, that is, exponential in the input size of the problem. Therefore, exponential time is required to solve it optimally. However, LP relaxation of time-indexed IP formulations provides a good lower bound to optimal solutions in less time [1].

Table 1 Processing time and energy consumption of MR tasks

An example of optimal schedule We show an example of an optimal schedule for an MR job comprising 5 map tasks $\{m_{1}, m_{2}, m_{3}, m_{4}, m_{5}\}$ and 2 reduce tasks $\{r_{1}, r_{2}\}$ when executed on a cluster of 2 machines $\{n_{1}, n_{2}\}$. The resource requirement, processing time in seconds (s), and energy consumption in joule (J) of all map and reduce tasks on both machines are shown in Table 1. The machine $n_{1}$ has resource capacity of $\langle 10\, {\text{MB}},\, 3\, {\text{VC}} \rangle$, whereas machine $n_{2}$ has $\langle 15\, {\text{MB}},\, 4\, {\text{VC}} \rangle$. We use IBM ILOG CPLEX studio v12.8 to exactly solve the EMRSY-IP formulation for the above problem instance. For small problems, CPLEX generates the optimal schedule in very quick time. Figure 3 shows the generated optimal schedule when the deadline D = 15 s. The decision variables, which have value one, are shown in the diagram itself. The total energy consumption of 7 tasks for the generated optimal schedule is 24 J.

Fig. 3

An example of optimal schedule when deadline D = 15 s

4 The Heuristic algorithm

This section presents the proposed (deadline-aware) energy-efficient MapReduce scheduling algorithm for YARN (EMRSAY) to solve the problem formulated in Sect. 3. The algorithm is based upon a metric known as the average energy consumption rate ($avg\_ecr$) similar to the metric given in [15]. However, the avg_ecr metric in our work has a difference, that is, in spite of each map and reduce slot, the metric is now calculated for each cluster machine separately for map tasks and reduce tasks. For a particular machine $n_{i}$, The metric avg_ecr is calculated as the average ratio of energy consumption and processing time as follows:

$$\begin{aligned} avg\_ecr_{i}^{m}= & \dfrac{\sum _{j=1}^{|{\mathcal{M}}{\mathcal{T}}|} \dfrac{e_{ij}}{p_{ij}}}{|{\mathcal{M}}{\mathcal{T}}|} \quad (i=1,\dots ,|\mathcal{N}|)\\ avg\_ecr_{i}^{r}= & \dfrac{\sum _{k=1}^{|{\mathcal{R}}{\mathcal{T}}|} \dfrac{e_{ik}}{p_{ik}}}{|{\mathcal{R}}{\mathcal{T}}|} \quad (i=1,\dots ,|\mathcal{N}|) \end{aligned}$$

where $avg\_ecr_{i}^{m}$ and $avg\_ecr_{i}^{r}$ represent average energy consumption rate of machine $n_{i}$ for map and reduce tasks respectively.

The proposed EMRSAY algorithm schedule the map and reduce tasks to cluster machines in two separate non-overlapping phases, namely, map phase and reduce phase. The map phase is triggered first by subroutine $sched\_map()$ in which scheduling decisions regarding all map tasks are fixed. Whereas, in the reduce phase, triggered next by subroutine $sched\_reduce()$, scheduling decisions for reduce tasks are taken. Both these phases are comprised of multiple similar rounds and in each round (of any phase), one by one all machines are packed with as many tasks as its total resource capacity. The order in which machines are selected for task allocation (or packing) is decided on the basis of $avg\_ecr$ metric. As we will see later that these metrics are dynamic in nature and are repeatedly calculated at the start of each round. The proposed algorithm also estimates the map and reduce deadlines separately as in [39]. This better guides the algorithm to schedule map and reduce tasks within the user-specified deadline. The detailed working of the algorithm is as follows.

The main EMRSAY algorithm has been shown in Algorithm 1 where it first initializes the time horizon variable $t=0$, and then estimates map deadline $D^{m}$ and reduce deadline $D^{r}$. To achieve this, the algorithm requires two parameters $\overline{T}_{j}^{m}$ and $\overline{T}_{k}^{r}$ for each map and reduce task respectively. These parameters represent average processing time of a respective task over all machines in the cluster. After calculating these parameters in lines 3 and 5, the algorithm calculates map deadline according to the expression given in line 6. Next, the reduce deadline $D^{r}$ is set as the job deadline D . Afterward, it simply calls two sub-routines: $sched\_map()$ and $sched\_reduce()$, one after another to schedule map and reduce tasks to different machines in multiple rounds. After returning from $sched\_reduce()$ subroutine, if there are some map or reduce task still unallocated (line 10), the main algorithm tells that no feasible schedule is possible and returns. Otherwise, it outputs the values of decision variables x and y.

The subroutine $sched\_map()$ has been shown in Algorithm 2, which schedules map tasks on cluster machines in multiple rounds. It starts with initializing the variable $v=1$. An iteration of the first while loop (lines 2–21) represents a single round. At the starting of any round (say vth), the subroutine initializes the variable round to v and $round\_time_{v}$ to zero. The variable round represents the current round and $round\_time_{v}$ represents the total duration of vth round and equals to the maximum processing time of any map task scheduled in that round. After initialization, it creates a priority queue ${\mathcal{Q}}$ of all machines on the basis of $avg\_ecr$ metrics (lines 5–7). This priority queue $\mathcal{{\mathcal{Q}}}$ is created afresh in each round.

Next, during the while loop of lines 8–19, the subroutine extracts a machine one at a time from this queue and assigns as many map tasks to it as its resource capacity while satisfying map phase deadline criteria. This process is repeated until all machines are extracted or all map tasks are allocated. The detailed explanation of this loop is as follows. First of all, a node $n_{i}$ is extracted from this priority queue in line 9. The machine which has the lowest average rate of energy consumption has the highest priority of being extracted from the queue. After extracting $n_{i}$, all unassigned map tasks $m_{j}$ are stored as a set $\tau ^{m}_{i}$ on the basis of processing time $p_{ij}$ on this extracted machine (line 10). Once the subroutine has the extracted machine $n_{i}$ and the sorted set $\tau ^{m}_{i}$ at hand, it starts assigning map tasks from the set $\tau ^{m}_{i}$ to the extracted node till the node $n_{i}$ is not full and $\tau ^{m}_{i}$ is not empty (lines 11–19).

During this scheduling process, the algorithm first takes the map task $m_{j}$ which has maximum processing time on node $n_{i}$ (line 12). And if its resource requirement can be fulfilled by node $n_{i}$ and total processing time do not exceed map deadline (line 13), the algorithm schedules this map task $m_{j}$ on node $n_{i}$ in line 14 ($x_{ijt}=1$). The fulfillment of resource requirement is checked by the expression $\vec {RR^{m}_{j}} + \vec {RO_{i}} \le \vec {RC_{i}}$ in line 13, where the vector $\vec {RO_{i}}$ of size $(|{\mathcal{A}}|)$ represents the total amount of currently occupied (busy) resources on $n_{i}$. Apart from this, the vector $\vec {RC_{i}}$ represents the resource capacity of node $n_{i}$ and $\vec {RR^{m}_{j}}$ represents the resource request vector of map task $m_{j}$. After the assignment, various data structures are updated in lines 15–17. At last, if the processing time of task $m_{j}$ is greater than the current $round\_time_{v}$, its value is updated as the value of $p_{ij}$. This process is repeated till the node $n_{i}$ has some unallocated resources and ordered set $\tau ^{m}_{i}$ is not empty. After this node becomes full, the algorithm extracts the next node from queue ${\mathcal{Q}}$ and repeat the process (lines 8–19). Once all nodes are extracted from the queue ${\mathcal{Q}}$, the algorithm updates the scheduling time horizon t in line 20 and enters into the next round by incrementing the round counter by one in line 21.

After the subroutine $sched\_map()$ finishes the scheduling of map tasks, the main EMRSAY algorithm calls the $sched\_reduce()$ procedure (second phase) which schedules reduce tasks also in multiple rounds. The procedure $sched\_reduce()$ has been shown in algorithm 3 with necessary modification as required. The detailed working of this procedure is similar to $sched\_map()$ procedure and we skip its discussion.

4.1 Time complexity

The time complexity of EMRSAY is $\mathcal{O}(|{\mathcal{M}}{\mathcal{T}}|\varvec{+}|{\mathcal{R}}{\mathcal{T}}| \varvec{+} |{\mathcal{M}}{\mathcal{T}}|(|{\mathcal{N}}|\lg |\mathcal{N}|+|{\mathcal{M}}{\mathcal{T}}|^{2}) \varvec{+} |{\mathcal{R}}{\mathcal{T}}|(|\mathcal{N}|\lg |{\mathcal{N}}|+|{\mathcal{R}}{\mathcal{T}}|^{2}))$. There are four additive terms in this expression. The first two terms correspond to two for loops of lines 2–3 and lines 4–5, respectively in Algorithm 1. The third and forth term correspond to time complexities of $sched\_map()$ and $sched\_reduce()$ subroutines, which are $\mathcal{O}(|{\mathcal{M}}{\mathcal{T}}|(|\mathcal{N}|\lg |\mathcal{N}|+|{\mathcal{M}}{\mathcal{T}}|^{2}))$ and $\mathcal{O}(|{\mathcal{R}}{\mathcal{T}}|(|\mathcal{N}|\lg |\mathcal{N}|+|{\mathcal{R}}{\mathcal{T}}|^{2}))$ respectively. The complexity of $sched\_map()$ subroutine is calculated as follows. The while loop of lines 8–19 has the complexity of $\mathcal{O}(|\mathcal{N}|(\lg |\mathcal{N}| + |{\mathcal{M}}{\mathcal{T}}|\lg |{\mathcal{M}}{\mathcal{T}}| + |{\mathcal{M}}{\mathcal{T}}|^{2})$ where first additive term is for extracting an element form priority queue in line 9, second term is for sorting in line 10, and finally third term is for inner while loop of lines 11–19. The previous time complexity of lines 8–19 simply reduces to $\mathcal{O}(|\mathcal{N}|\lg |\mathcal{N}| + |{\mathcal{M}}{\mathcal{T}}|^{2} )$. Further, the for loop of lines 5–7 contributes $\mathcal{O}(|\mathcal{N}|\lg |\mathcal{N}|)$ in running time. Hence, running time of outer while loop of lines 2–21 is calculated as $\mathcal{O}(|{\mathcal{M}}{\mathcal{T}}|(|\mathcal{N}|\lg |\mathcal{N}| +|{\mathcal{M}}{\mathcal{T}}|^{2}))$ which is also equal to running time of $sched\_map()$ subroutine. Similarly, the complexity of $sched\_map()$ subroutine is calculated as $\mathcal{O}(|{\mathcal{R}}{\mathcal{T}}|(|\mathcal{N}|\lg |\mathcal{N}| +|{\mathcal{R}}{\mathcal{T}}|^{2}))$.

4.2 A numerical example

We show an example to explain the working of our proposed EMRSAY heuristic algorithm. We take same set of 5 map tasks $\{m_{1}, m_{2}, m_{3}, m_{4}, m_{5}\}$, and a set of 2 reduce tasks $\{r_{1}, r_{2}\}$ as assumed in Sect. 3. The tasks are to be scheduled on 2 machines $n_{1}$, $n_{2}$ with resource capacity of $\langle 10\, {\text{MB}},\, 3\, {\text{VC}} \rangle$ and $\langle 15\, {\text{MB}},\, 4\, {\text{VC}} \rangle$, respectively. All other characteristics has been shown in Table 1, with a user deadline D is set as 15 s. We deliberately consider the same problem instance to compare the sub-optimal schedule generated by EMRSAY algorithm with the optimal schedule in Sect. 3.

The algorithm starts by initializing time horizon variable $t=0$ and then it calculates map and reduce deadlines. For this purpose, it first calculates $\overline{T}^{m}$ $= \{2.5, 5, 5.5, 5.5, 4\}$ and $\overline{T}^{r} = \{3.5, 2.5\}$. Afterwards the algorithm calculates map deadline $D^{m}=11.84\,{\text{s}}$ and fixes the reduce deadline $D^{r}=D=15\,{\text{s}}$. After this, it calls the subroutines $sched\_map()$ and $sched\_reduce()$ one after another. The subroutine $sched\_map()$ starts by initializing variable $v=1$. The detailed explanation of different rounds of $sched\_map()$ procedure is as follows:

${sched\_map()}$, Round 1: At the starting of the first round ($round=v=1$), the subroutine sets $round\_time_{1}=0s$. Then, it calculates $avg\_ecr^{m}=\{0.93, 0.96\}$ for both machines $n_{1}$ and $n_{2}$. After this, a priority queue ${\mathcal{Q}}=\{n_{1}, n_{2}\}$ is created based on $avg\_ecr^{m}$ values. The subroutine extracts $n_{1}$ as the first node for scheduling map tasks. For that purpose, it creates an ordered set $\tau _{1}^{m}=\{m_{4}, m_{2}, m_{3}, m_{5}, m_{1}\}$ on the basis of processing time of unallocated map tasks on the first extracted machine $n_{1}$. The first map task $m_{4}$ of ordered set $\tau _{1}^{m}$ is scheduled on machine $n_{1}$ ($x_{1,4,0}=1$). After this, the machine $n_{1}$ has remaining capacity of $\langle 5\, {\text{MB}}, 1\, {\text{VC}} \rangle$ and is unable to accommodate more map tasks. Hence, the second machine $n_{2}$ is extracted from the priority queue ${\mathcal{Q}}$ and remaining unallocated map tasks $(m_{1}, m_{2}, m_{3}, m_{5})$ are again sorted on the basis of processing time on $n_{2}$ to form the new ordered set $\tau _{2}^{m} = \{m_{3}, m_{2}, m_{5}, m_{1}\}$. Next, the map tasks $m_{3}$ and $m_{2}$ are scheduled in that order on machine $n_{2}$ ($x_{1,3,0}=1,\, x_{1,2,0}=1$). After this assignment, node $n_{2}$ left with capacity of $\langle 5\, {\text{MB}}, 0\, {\text{VC}} \rangle$ and unable to accommodate more tasks further. At this point of time, the $round\_time_{1}$ parameter is calculated as 7 s (the maximum processing time of a map task scheduled on any machine in this round) and the priority queue ${\mathcal{Q}}$ becomes empty. Hence, the subroutine enters into second round of scheduling after setting the time horizon variable $t=0+7=7\,{\text{s}}$ and incrementing the variable v.

${sched\_map()}$, Round 2: At the starting of second round, the variable round is set to 2 and $round\_time_{2}$ is initialized as 0 s. Here, we have two map task $m_{1}$ and $m_{5}$ left for scheduling. Hence, on the basis of energy consumption of only these two task, the parameter average energy consumption rate ($avg\_ecr$) of both machine is calculated as $avg\_ecr^{m}=\{1.34, 1.33\}$ and again a priority queue is created as ${\mathcal{Q}}=\{n_{2}, n_{1}\}$. First $n_{2}$ is extracted and map tasks $m_{1}$ and $m_{5}$ are scheduled on it ($x_{2,1,7}=1,\, x_{2,5,7}=1$). After the scheduling of last map task, $round\_time_{2}$ is calculated as 4 s and time horizon variable is set as $t=11\,{\text{s}}$.

After the $sched\_map()$ finishes its scheduling process, the main algorithm calls the $sched\_reduce()$ subroutine which schedules reduce tasks in multiple rounds (quite similar to $sched\_map()$ subroutine). It also starts by initializing the variable $v=1$. The detailed working of the $sched\_reduce()$ procedure is as follows:

${sched\_reduce()}$, Round 1: In the first round, we calculate $avg\_ecr^{r}=\{1.1, 2.58\}$ and on the basis of these values, priority queue ${\mathcal{Q}}=\{n_{1}, n_{2}\}$ is created. First, machine $n_{1}$ is extracted and ordered set $\tau _{1}^{r}=\{r_{1}, r_{2}\}$ is implemented. Thereafter, both these reduce tasks are scheduled on $n_{1}$ ($y_{1,1,11}=1 \, \text {and} \, y_{1,2,11}=1$). The parameter $round\_time_{1}$ is calculated as 4 s and time variable t is set to 15 s at the end of first round. Now, we have no more reduce task to schedule hence, the procedure terminates and returns to main EMRSAY algorithm.

As all the map and reduce tasks are scheduled on machines within a given deadline, the main algorithm EMRSAY produces the values of decision variables x and y as the output. The total energy consumption of the generated schedule is 28 J, whereas the optimal schedule in Sect. 3 consumes 24 J. However, optimal schedule generation costs much more time than the EMRSAY algorithm as observed through experimental evaluations as explained in the next section.

5 Experiments

We perform two sets of experiments to evaluate the performance of proposed EMRSAY heuristic algorithm. In the first set of experiments, we compare EMRSAY with two different custom-made offline algorithms, namely, L-BOUND and L-MSPAN. Both these algorithms are designed especially for comparison with EMRSAY and have the following interpretations:

The L-BOUND algorithm provides a lower bound to the optimal solution of EMRSY-IP problem. This lower bound is obtained by optimally solving the relaxed version of EMRSY-IP problem that can be derived by relaxing the binary integer restrictions on decision variables. We call the relaxed problem as EMRSY-LP, where LP stands for linear programming. For large scale big-data jobs, the optimal solution to EMRSY-IP problem takes a huge amount of time. Hence, we take the L-BOUND algorithm to compare our results, which produces the result in a very quick time. The L-MSPAN algorithm provides lower bound to NP-hard makespan minimization (MSPAN) problem which minimizes the completion time of last reduce task. The MSPAN problem can also be formulated as an IP problem (say MSPAN-IP) by simply changing the objective function of Eq. 1, and its relaxed version (i.e., MSPAN-LP) is solved by L-MSPAN to derive a lower bound. The L-BOUND and L-MSPAN have been implemented using the JAVA API provided with IBM CPLEX optimization studio which internally uses Simplex algorithm [5] to solve the relaxed LP problems. Both L-BOUND and L-MSAPN generate partial schedules as the value of a decision variable can be any value between 0 and 1 which results in the partial assignment of tasks to machines. Hence, the generated schedule can not be used in practice but serves as a lower bound to their respective optimal solutions.

In the second set of experiments, we compare the performance of EMRSAY with delay scheduler [40] which is the default task-level scheduler in Hadoop YARN. It is used by all three default job-level FIFO, FAIR and Capacity Scheduler to assign map and reduce tasks to different machines on the basis of data-locality and fairness. The delay scheduler does not consider any energy-efficiency metric while tasks assignment.

As mentioned earlier, the EMRSAY, L-BOUND, and L-MSPAN are offline scheduling algorithms that require the value of different input parameters including processing time and energy consumption of all map and reduce tasks on each machine in advance to produce the static schedule even before the actual execution of MR job begins. Therefore, to profile the input parameters for the first set of experiments, a five node experimental YARN cluster is built using heterogeneous machines. Once the profiling is done, all three offline algorithms are compared through the simulations performed on a single machine, and for that, we implement the EMRSAY algorithm in JAVA.

On the other hand, when EMRSAY is compared with the delay scheduler, the same experimental YARN cluster is used as a testbed for analysis. Before discussing the details of the YARN cluster, we mention the benchmark jobs and workload sizes which are used in both sets of experiments. The performance metrics, used for evaluations in both sets of experiments, are described in Sects. 5.3 and 5.4.

5.1 Benchmark jobs used for evaluations

Experiments have been performed using three MapReduce jobs from the HiBench benchmark suite. These benchmarks have been listed in Table 2 where PageRank is a CPU-bound, DFSIO is an IO-bound and NutchIndexing is a mix-bound MR job. HiBench is a big data benchmark suite that helps evaluate different big data frameworks in terms of speed, throughput, and system resource utilization. There are a total of 19 workloads in HiBench. The workloads are divided into 6 categories: micro, machine learning (ML), SQL, graph, web search, and streaming.

Particularly, for experiment set-1, we take all three selected benchmarks to compare the performances of EMRSAY against L-BOUND and L-MSPAN algorithms. On the other hand, for the experiment set-2, we use only PageRank job.

Table 2 Selected HiBench workload

5.2 YARN cluster configuration and profiling

A five node Hadoop YARN cluster has been used to profile the processing time and energy consumption of map and reduce tasks. The cluster is composed of five nodes with one node as master and remaining four nodes as slaves. The master node has a 10-core Intel Xeon W-2155 processor, 64 GB RAM, and 2 TB hard disk. One of the slave nodes has the same configuration as the master node, two slave nodes have a 6-core Intel Xeon E5645 processor, 8 GB RAM, and 1 TB hard disk each, and lastly, one slave node has a 2-core Intel Core i5-7200U processor, 12 GB RAM, and 1 TB hard disk. We use Hadoop 2.7.2 framework with an inbuilt FAIR scheduler for profiling. The HDFS block size is kept as 128 MB with a file replication factor of 3. All nodes are connected through a 1Gbps network switch. The cluster configuration has been summarized in Table 3.

Table 3 Cluster configuration

To profile energy consumption and processing time, a single benchmark job is executed at a time. The processing time of various tasks on different machines can directly be noted down from YARN log files. However, to compute the energy consumption $e_{ij}$ of a map task $m_{j}$ at the machine $n_{i}$ during the execution, we use power model as shown in Eq. 9. Similarly, the energy consumption $e_{ik}$ of a reduce task $r_{k}$ at the machine $n_{i}$ during the execution is calculated using the power model shown in Eq. 10. Table 4 shows the meaning of various symbols used in both power models. The values of $P^{cpu}_{i},\, P^{mem}_{i}$ can directly be taken from hardware specification sheets provided by the manufacturer of the respective component. Whereas, the values of $E^{disk}_{i}$, and $E^{nic}_{i}$ can easily be calculated by using the power consumption of disk and network interface card (NIC) that can also be taken from hardware specification sheets. The values of $p_{ij}/p_{ik}$, $d_{ij}/d_{ik}$, and $N_{ij}/N_{ik}$ are taken from YARN log files.

$$\begin{aligned} e_{ij}= & P^{cpu}_{i} \times p_{ij} + P^{mem}_{i} \times p_{ij} + E^{disk}_{i} \times d_{ij} + E^{nic}_{i} \times N_{ij} \end{aligned}$$

(9)

$$\begin{aligned} e_{ik}= & P^{cpu}_{i} \times p_{ik} + P^{mem}_{i} \times p_{ik} + E^{disk}_{i} \times d_{ik} + E^{nic}_{i} \times N_{ik} \end{aligned}$$

(10)

Table 4 The meaning of symbols used in power functions

In order to better predict the energy consumption and processing time of tasks at the time actual performance evaluation, we execute the single benchmarks jobs multiple times during the profiling stage with different input file sizes: 40 GB, 60 GB, 80 GB, and 100 GB. Moreover, for each input file size, the process is repeated five times resulting in 20 runs for each benchmark.

on a particular run, say u ($1 \le u \le 20$), we take the average energy consumption of all map tasks scheduled on machine $n_{i}$ and denote it as $\overline{e}^{mu}_{i}$. Next, we calculate the minimum of all twenty average energy consumption of map tasks scheduled on machine $n_{i}$ and denote it as $\min \nolimits _{u}(\overline{e}^{mu}_{i})$. Similarly, the expression $\max \nolimits _{u}(\overline{e}^{mu}_{i})$ is calculated as the maximum of all twenty average energy consumption of map tasks scheduled on machine $n_{i}$. In the same manner, we calculate the values of $\min \nolimits _{u}(\overline{p}^{mu}_{i})$ and $\max \limits _{u}(\overline{p}^{mu}_{i})$ as the minimum and maximum of average processing time of all map tasks scheduled at machine $n_{i}$. The same procedure is followed for reduce tasks and the values of $\min \nolimits _{u}(\overline{e}^{ru}_{i})$, $\max \limits _{u}(\overline{e}^{ru}_{i})$, $\min \nolimits _{u}(\overline{p}^{ru}_{i})$, and $\max \limits _{u}(\overline{p}^{ru}_{i})$ are calculated where all expressions have usual meaning.

During the actual performance evaluation, the values of processing time $p_{ij}(i=1,\dots ,|\mathcal{N}|;j=1,\dots ,|{\mathcal{M}}{\mathcal{T}}|)$ and the energy consumption $e_{ij}(i=1,\dots ,|\mathcal{N}|;j=1,\dots ,|{\mathcal{M}}{\mathcal{T}}|)$ of the map tasks on machine $n_{i}$ are taken in such a way so that these values may remain uniformly distributed in [$\min \nolimits _{u}(\overline{e}^{mu}_{i})$, $\max \nolimits _{u}(\overline{e}^{mu}_{i})$] and [$\min \nolimits _{u}(\overline{p}^{mu}_{i})$, $\max \nolimits _{u}(\overline{p}^{mu}_{i})$], respectively. Similarly, the processing time and the energy consumption of the reduce tasks on machine $n_{i}$ are kept uniformly distributed in [$\min \nolimits _{u}(\overline{e}^{ru}_{i})$, $\max \nolimits _{u}(\overline{e}^{ru}_{i})$] and [$\min \nolimits _{u}(\overline{p}^{ru}_{i})$, $\max \nolimits _{u}(\overline{p}^{ru}_{i})$], respectively.

The EMRSAY, L-BOUND, and L-MSPAN also require the user specified deadline (D) as one of the input parameters. And its value influences the possibility of getting the feasible schedule under each algorithm. We set user specified deadline according to Eq. 11 and denote it as $D_{S}$ so that every time we get a feasible schedule during the experiments. In Eq. 11, $\overline{T}_{j}^{m} = \dfrac{\sum _{i=1}^{|\mathcal{N}|}p_{ij}}{|\mathcal{N}|}$ and $\overline{T}_{k}^{r} = \dfrac{\sum _{i=1}^{|\mathcal{N}|}p_{ik}}{|\mathcal{N}|}$ represents the average processing time of any map task $m_{j}$ and reduce task $r_{k}$, respectively.

$$\begin{aligned} D_{S}= \dfrac{\sum _{j=1}^{|{\mathcal{M}}{\mathcal{T}}|}\overline{T}_{j}^{m}+\sum _{k=1}^{|{\mathcal{R}}{\mathcal{T}}|}\overline{T}_{k}^{r}}{|\mathcal{N}|} \end{aligned}$$

(11)

Although L-BOUND and L-MSPAN solve the relaxed problem of their respective IPs and thereby take less CPU time, it may further be reduced by choosing a suitable value for the input parameter T (the total discrete time intervals). In this case, the value of the deadline parameter D serves as a lower bound (LB) to T and we set $T^{LB}=D$. It is to be noted that parameter T is only required in L-BOUND and L-MSPAN algorithms.

5.3 Results and discussion: experiment set-1

As mentioned earlier, the experiment set-1, where we compare EMRSAY with L-BOUND and L-MSPAN, is performed for three different benchmark jobs as shown in Table 2. For each job, we choose to evaluate three performance metrics: total energy consumption (TEC) in joule (J), schedule generation time (SGT) in seconds (s), and tightest satisfiable deadline (TSD) in seconds (s). The metric TEC represents the total energy consumption of all tasks following a schedule generated by a particular scheduling algorithm. The metric SGT represents the execution time (i.e., running time) of any scheduling algorithm to generate a feasible schedule. The TSD represents the lowest value of deadline below which EMRSAY, L-BOUND, and L-MSPAN fail to generate a feasible schedule. Obviously, it is better to have a lower TSD value, which means the algorithm can schedule jobs under harder conditions. To measure the TSD parameter, we ran EMRSAY, L-BOUND, and L-MSPAN several times in a binary search manner for each workload to find the tightest deadline that each algorithm can meet. For each MR job, the values of these metrics are evaluated for eight different workload sizes, as shown in Table 5. The smallest workload is represented by (128M, 64R) which has 128 map tasks and 64 reduce tasks, i.e., 192 tasks in total. Whereas the largest workload, represented by (512M, 512R), has a total of 1024 tasks consisting of 512 map and 512 reduce tasks.

Apart from these metrics, we also analyze the sensitivity of total energy consumption on the deadline parameter. For that, the number of map and reduce tasks are fixed as (256M, 256R), and the deadlines are varied from $D_{S}-40$ to $D_{S}+60$ where $D_{S}$ represents the satisfiable deadline calculated by Eq. 11.

Table 5 Workload size for the CPU, IO and mix-bound experiments

5.3.1 CPU-bound load

Figure 4 shows the performance of EMRSAY against the L-BOUND, and L-MSPAN algorithms for the CPU-bound PageRank benchmark. Particularity, Fig. 4a shows the total energy consumption of tasks following the schedules generated by all three algorithms for different workload sizes. It is observed that energy consumption in EMRSAY is very close to the L-BOUND algorithm for all workload sizes. This indicates that our proposed scheme is also very close to optimal energy consumption. On the other hand, the energy consumption in L-MSPAN scheme is far more than EMRSAY and L-BOUND schemes as the main objective of L-MSPAN is to minimize the completion time of the last reduce task. Further, these results show that the schedules produced by EMRSAY consume on average 37.23% less energy in comparison to L-MSPAN and just 4.6% more energy in comparison to L-BOUND algorithm. This reduction of 37.23% in energy consumption makes EMRSAY a suitable choice to replace makespan minimizing schedulers in YARN framework. In addition, the results also clearly show the sensitivity of energy consumption on the total number of map and reduce tasks. We note that energy consumption of tasks in all three algorithms continuously increases when the total tasks are increased from 192 to 1024.

Fig. 4

Performance evaluation of EMRSAY for CPU-bound (PageRank) job

Figure 4b shows the SGT of all three algorithms for different workload sizes. It is seen that all algorithms manage to produce a feasible schedule within one second for all workloads sizes. Particularly, the proposed algorithm EMRSAY generates a feasible schedule in less than 0.01 seconds for the biggest workload (512M, 512R). It should be noted that L-BOUND and L-MSPAN solve the relaxed version of their respective (NP-hard) IP problems, and thus both manage to produce the near-optimal schedule very fast. We could not get the optimal solution even after one hour. As far as the sensitivity analysis of SGT on the workload is concerned, it increases very slowly as the number of map and reduce task is increased.

Figure 4c shows the tightest satisfiable deadline (TSD) under EMRSAY, L-BOUND, and L-MSAPN for different workload sizes. It shows that the TSDs under these algorithms increases swiftly as the number of map and reduce tasks are increased. Further, the experiments show that L-BOUND and L-MSPAN can meet the deadline 17.18% and 19.78% shorter than EMRSAY respectively.

Lastly, Fig. 5 shows the sensitivity analysis of energy consumption on different user deadline. The results show that as we relax (i.e., increase) the deadline, total energy consumption in all algorithms is reduced. For example, at deadline $D_{S}$, TEC of EMRSAY, L-BOUND, and L-MSPAN is 35,152, 32,519, and 56,176 J respectively while at deadline $D_{S}+20$, it is 34,252, 31,287, and 54,173 J respectively. When a production job in any data center (e.g., spam detection job in Facebook) is executed over a fixed-size input file, it creates a constant number of map and reduce tasks. In that case, it is concluded that the value of the user deadline supplied with these jobs affects the total energy consumption during the execution.

Fig. 5

Energy consumption sensitivity on deadline for CPU-bound (PageRank) job

5.3.2 IO bound load

To evaluate the performance of EMRSAY for the IO-bound load, we take the DFSIO benchmark job and perform the same sets of experiments as in Sect. 5.3.1. Figures 6 and 7 shows the various experimental results obtained for the experiments.

Fig. 6

Performance evaluation of EMRSAY for IO-bound (DFSIO) job

Fig. 7

Energy consumption sensitivity on deadline for IO-bound (DFSIO) job

Particularly, Fig. 6a shows the TEC of tasks in EMRSAY, L-BOUND, and L-MSPAN algorithms for a different number of map and reduce tasks. The results show that the energy consumption in EMRSAY is very close to the L-BOUND algorithm where tasks consume only 4.6% more energy on average. Also, as in the case of CPU-bound load, EMRSAY performs far better than L-MSPAN algorithm and saves 41.21% more energy on average. If we compare these results with the CPU-bound (PageRank) experiments shown in Fig. 4a, we observe that for the same number of map and reduce tasks, the energy consumption of EMRSAY, L-BOUND, and L-MSPAN is always less as the CPU consumes more power than the other IO components. As far as the energy sensitivity on the number of map and reduce tasks is concerned, energy consumption is always large on bigger workloads. For example, the total energy consumption of EMRSAY, L-BOUND, and L-MSPAN algorithms for workload (256M, 128R) are 22,896, 20,319, and 34,193 J respectively, while the total energy consumption for workload (256M, 256R) are 31,358, 28,083, and 52,552 J respectively.

Figure 6b shows the SGT of EMRSAY for different DFSIO workload sizes in comparison with L-BOUND and L-MSPAN. The results conclude that EMRSAY produces the feasible schedule within 0.006 s on average that makes it suitable for even IO-bound workloads. Further, Fig. 6b presents the TSDs of these offline algorithms for different workloads. It is observed that the value of TSD increases for all algorithms as the number of map and reduce tasks are increased. The L-BOUND and L-MSPAN algorithms perform better than EMRSAY and achieves 15.56% and 18.12% shorter deadline in case IO-bound loads. Moreover, in case of DFSIO job, all algorithms could not achieve deadline as tight as PageRank job. For example, EMRSAY achieves the TSD of 199 and 190 s for DFSIO and PageRank jobs respectively for the workload (256M, 128R). Thus, the user can provide tighter deadlines in case of CPU-bound loads.

At last, Fig.7 shows the sensitivity analysis of energy consumption on different deadline parameters. The results show same behavior as PageRank job, that is, under tighter deadlines more energy is consumed in comparison to relaxed deadlines.

5.3.3 Mix-bound load

In the last experiment, we choose NutchIndexing job which is CPU-bound during map stage and more disk IO-bound in the reduce stage, making it a mix-bound job overall [9]. Figure 8a presents the TEC in all three algorithms under a variety of workloads of NutchIndexing benchmarks. It shows the same behavior as PageRank and DFSIO benchmarks, that is, energy consumption increases as the number of map and reduce tasks are increased. However, for mix-bound benchmark job, energy consumption in EMRSAY is higher than CPU and IO-bound jobs for the same number of map and reduce tasks. For example, energy consumption is 22,703 J under EMRSAY for the mix-bound job while under CPU and IO-bound jobs, it is 17,501 and 16,128 J, respectively when workload is (128M, 128R).

Fig. 8

Performance evaluation of EMRSAY on mix-bound (NutchIndexing) job

Figure 8b shows the schedule generation time (SGT) of EMRSAY for different workloads in comparison with the SGT of L-BOUND and L-MSPAN algorithms. The results show that SGT follows the same trends as in the case of PageRank and DFSIO benchmarks. We observe that EMRSAY produces the feasible schedule within 0.006s on average that makes it suitable for even mix-bound workloads. Further, TSD of all three algorithms for NutchIndexing job shows the same behavior as in PageRank and DFSIO benchmarks as shown in Fig. 8c. The results show that TSD increases as the number of map and reduce tasks are increased. However, in NutchIndexing job, the algorithms fail to meet deadlines as tight as PageRank and DFSIO jobs. For example, EMRSAY achieves the TSD of 203 s while L-BOUND and L-MSPAN achieve the TSD of 196 and 190 s respectively for the workload (256M, 128R). Thus, the user can provide tighter deadlines in case of CPU and IO-bound loads. At last, Fig. 9 shows the result of the sensitivity analysis of energy consumption on different deadline parameters. The results show that under tight deadlines more energy is consumed in comparison to relaxed deadlines.

Fig. 9

Energy consumption sensitivity on deadline for mix-bound (NutchIndexing) job

5.4 Results and discussion: experiment set-2

In the second set of experiments, we compare the performance of EMRSAY against the delay scheduler, the default task-level scheduler in YARN. We choose two performance metrics: total energy consumption (TEC) in joule (J), and the tightest satisfiable deadline (TSD) in seconds (s). Both these metrics (i.e., TEC, and TSD) are evaluated for the following input data size: 15 GB, 25 GB, 35 GB, 45 GB, 55 GB, 65 GB, and 75 GB. As this is the real testbed experiments, we do not have direct control over the number of map and reduce tasks. All we can do is to increase the size of input file which eventually increases the number of map and reduce tasks. For a input file of size X GB, the $\lceil (X \times 1024) \div 128 \rceil$ number of map tasks are created as we keep the HDFS block size as 128 MB. The number of reduce tasks are set as one-third of map tasks. we also evaluate the sensitivity of energy consumption on deadline. To achieve that, the input data size is kept as 35 GB, and the deadlines are varied from $D_{S}-40$ to $D_{S}+60$ where $D_{S}$ represents the satisfiable deadline.

Figure 10a shows the TEC of tasks when they follow the schedule generated by EMRSAY and delay algorithms. We notice that for a particular workload size, the EMRSAY schedule consumes less energy than delay scheduler. For instance, energy consumption in EMRSAY and delay scheduler is 17,490 and 24,079 J, respectively for input data size of 35 GB. Moreover, as we increase the size of input data, the TEC also increases in both algorithms. Figure 10b shows that TSD in case of EMRSAY is always less than delay scheduler for particular data size. Also, TSD for both EMRSAY and delay scheduler increases as we increase the input data size. This concludes that EMRSAY is able to generate a feasible schedule in tighter deadline constraints. Finally, Fig. 11 compare both algorithms on the basis of energy sensitivity on deadline. The figure shows that energy consumption in both of them decreases as we relax the deadline. For example, when the deadline is $D_{S}+20$, energy consumption is 34,252 and 37,465 J in EMRSAY and delay scheduler respectively. On the other hand, when the deadline is $D_{S}+40$, energy consumption is 33,154 and 36,176 J, respectively.

Fig. 10

Performance of EMRSAY against default delay scheduler of Hadoop YARN

Fig. 11

Energy consumption sensitivity on deadline

6 Conclusion

The minimization of energy consumption in the Hadoop framework is a very important research field in the era of big data and green computing. In this paper, we considered the problem of scheduling map and reduce tasks of a single MR job in order to minimize energy-consumption in Hadoop YARN, and formulated this problem as an integer program. As the formulated problem is strongly NP-hard, we proposed a heuristic approach called EMRSAY, which generates sub-optimal schedules in polynomial time. Experimental results for a wide variety of benchmarks show that the proposed heuristic algorithm saves a significant amount of energy. We have also compared the proposed EMRSAY algorithm with the default task-level delay scheduler in Hadoop and conclude that EMRSAY saves up to 35% energy. As the Hadoop YARN can be used for a variety of big data applications other than MapReduce, EMRSAY may be redesigned with suitable modification for other applications too.

Our future plan has two directions, first is to design a dynamic MapReduce scheduler which does not require any profiling and can be used for ad-hoc jobs. Second is to build an energy-efficient YARN scheduler that can handle a mix of Big Data jobs e.g., MapReduce and Spark simultaneously.