1 Introduction

As an important way to trip, metro has become more and more popular. There are many advantages of metro station, such as high speed, energy conservation, environment protection, less prone to traffic jam. Nevertheless, metro station is narrow and long space with massive pedestrian flows, which leads it to be a main target of terrorist. For example, there were serious terrorist attacks at Paris in 1996, at London in 2005, at the republic of Belarus in 2004, 2010, 2011, at Belgium in 2016. In addition, there are some other emergency events like fire, flood, earthquake, high passenger flow which cause the metro station under emergency environment. Therefore, the safety of metro station attracts people’s attention at the same time. One of the most important issues is how to select a suitable evacuation strategy to evacuate the pedestrians to the safety places as quickly as possible. There are different kinds of strategies to counter the emergency evacuation in a metro station. Meanwhile, there exist some works addressing the issues of how to choose a suitable evacuation strategy.

This paper proposes a new decision making approach to choose a suitable evacuation strategy under the metro station in emergency context. A group decision system is introduced for metro station in emergency requires quick decision-making and swift action. Under emergency conditions, there are various limitations, such as a lack of information, uncertainty of the decision-making environment, and difficulties in information extraction [1]. Therefore, it is very difficult to provide crisp data under an emergency environment to make a decision. Meanwhile, the interval type-2 fuzzy sets (IT2FSs) are suitable to handle high complexity and uncertainty for they involve more uncertainties and more flexible than type-1 fuzzy sets [2]. This paper presents the weights of all criteria and the ratings of alternatives using the interval type-2 fuzzy numbers (IT2FNs), which allow higher degrees of impreciseness than the exact values. It is a better way to represent the uncertainty and the fuzziness information of the metro station in the evacuation process. TOPSIS is a widely applied model for multiple criteria decision-making (MCDM) problems [3,4,5,6]. In this paper, an improved TOPSIS method will be proposed for evacuation strategy selection under interval type-2 fuzzy environment.

The reminder of the paper is organized as follows. Section 2 briefly reviews the evacuation strategy and TOPSIS method in IT2FSs. Then some basic concepts related to IT2FSs and TOPSIS method are introduced in Sect. 3. In Sect. 4, an evacuation strategy selection model and the specific calculation steps are formulated. Section 5 discusses and applies the proposed methods to the evacuation strategy selection of metro station in emergency context, and gives a sensitivity analysis of the parameters. Moreover, a comparison analysis is conducted in Sect. 6. Finally, some further discussions on the proposed methodology and conclusions are given in Sect. 7.

2 Literature review

An effective evacuation strategy is necessary to minimize the number of victims and the extent of property damages caused by emergency events in metro station. Reviewed below, the past efforts to evacuation strategy fall into two categories: the categories of strategies and the methods of choosing strategies.

There have been many categories of evacuation strategies proposed by researchers in recent years. From the view of time, Lovell and Daganzo [7] presented a real-time strategy. This strategy minimizes total time in a network for a special case in which queues are only allowed at the network’s access points. Cepolina [8] implemented a phased evacuation to minimize the building evacuation time by controlling the alarm times and the egress routes of a building. Based on the heterogeneous population, a partially dedicated evacuation strategy was proposed by Noh et al. [9], there are two paths, one for high-speed subpopulation of people without disabilities, and the other for the remaining heterogeneous population to minimize the blocking effect. Koo et al. [10] studied the evacuation behaviors of a heterogeneous population in a semi-panic evacuation scenario. You et al. [11] denoted a strategy for small group evacuation, in which the pedestrians tend to move to low-density areas during the evacuation processes. In addition, total evacuation strategy, phased evacuation strategy, stay-in-place strategy [12], adaptive strategy for evacuations along touts [13], and nearest-gate immediate evacuation strategy [14] were proposed by some scholars. There are two important senses to strategy selection: (i) it evacuates the maximum number of people at all times, and (ii) it finishes the evacuation in the least possible time [13]. Zhang et al. [15] proposed four key performance indicators (KPIs) to assess the evacuation performance within different route planning strategies, namely average pedestrian density, average evacuation length, average evacuation time and average evacuation capacity. Fry and Binner [16] formulated a Bayesian algorithm and constructed a model individual people for deriving optimal strategies. Vanlandegen and Chen [17] developed a framework to simulate emergency evacuations using rail transit by GIS-based network analysis. There are many kinds of proposed strategies, and have made some significant contributions on the research on evacuation study in the metro station under emergency environment. However, few MCDM approaches are applied to select a suitable strategy.

The problem of evacuation strategy selection in emergency context can be regarded as a fuzzy MCDM problem based on IT2FSs. Meanwhile, TOPSIS is viewed as a widely used model for solving MCDM problems. Chen and Lee [18, 19] presented a family of approaches for fuzzy multiple criteria group decision making (MCGDM) based on the interval type-2 fuzzy TOPSIS method. Baykasoğlu and Gölcük [20] presented a new hybrid MCDM method combining DEMATEL and TOPSIS methods within the context of interval type-2 fuzzy information. Moreover, Chen [21] developed a novel IT2F-TOPSIS method for MCDM analysis based on interval type-2 trapezoidal fuzzy numbers. Nasab and Malkhalifeh [22] introduced an extension of fuzzy TOPSIS with the aid of IT2FSs for handling fuzzy MCDM problems. Nehi and Keikha [23] proposed a new method to calculate the distance measure between IT2FNs, and further introduced a hybrid method based on TOPSIS and Choquet integral in type-2 fuzzy environment. Zamri and Abdullah [24] proposed a new linguistic variable that considers positive and negative sides of the TOPSIS approach based on IT2FSs. Sang and Liu [25] introduced an analytical solution to IT2FSs based TOPSIS model, the proposed method operates the IT2FSs directly and keeps the IT2FSs formats in the whole process, and the result of which is precise in analytical. Definitely, interval type-2 fuzzy TOPSIS method is widely used in many areas, such as supplier selection [26], airline route selection [27], initial aircraft training evaluation [28], environmental risk evaluation [29], metro station dynamic risk assessment [30], recommend personal diabetic-diet [31], medical decision making [32]. Above all, the application of type-2 fuzzy MCDM methods to evacuation strategy selection problems is very rare. In this paper, the interval type-2 fuzzy TOPSIS method will be proposed to select a suitable evacuation strategy for the metro station under emergency environment.

3 Preliminaries

Definition 1

[33] A type-2 fuzzy set (T2FS) denoted as \(\tilde{A}\), is characterized by a type-2 membership function \(\mu _{\tilde{A}} (x,u)\), where \(x\in X\),\(u\in [0,1]\),\(0\le \mu _{\tilde{A}} \left( {x,u} \right) \le 1 \), i.e.,

$$\begin{aligned} \tilde{A}=\left\{ {\left. {\left( {\left( {x,u} \right) ,\mu _{\tilde{A}} \left( {x,u} \right) } \right) } \right| x\in X,u\in [0,1]} \right\} \end{aligned}$$
(1)

\(\tilde{A}\) can also be expressed as

$$\begin{aligned} \tilde{A}=\int _{x\in X} {\int _{u\in J_x } {{\mu _{\tilde{A}} \left( {x,u} \right) }/{\left( {x,u} \right) }} } , \end{aligned}$$
(2)

where \(J_x =\left\{ {\left. {\left( {x,u} \right) } \right| u\in \left[ {0,1} \right] ,\mu _{\tilde{A}} \left( {x,u} \right) >0} \right\} \).

Definition 2

[33] If all \(\mu _{\tilde{A}} \left( {x,u} \right) =1\), then \(\tilde{A}\) is called an IT2FS which is a special case of the type-2 fuzzy sets.

$$\begin{aligned} \tilde{A}=\int _{x\in X} {\int _{u\in J_x } {1/{\left( {x,u} \right) }} } ={\int _{x\in X} {\left( {\int _{u\in J_x } {1/u} } \right) } }/x, \end{aligned}$$
(3)

where \(J_x =\left\{ {\left. {\left( {x,u} \right) } \right| u\in \left[ {0,1} \right] ,\mu _{\tilde{A}} \left( {x,u} \right) =1} \right\} \).

Definition 3

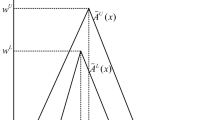
[34] Let \(\tilde{A}^{L}\) and \(\tilde{A}^{U}\) be two generalized fuzzy sets, where the height of a generalized fuzzy number is positioned in \(\left[ {0,1} \right] \). Let \(h_{\tilde{A}}^L \) and \(h_{\tilde{A}}^U \) be the heights of \(\tilde{A}^{L}\) and \(\tilde{A}^{U}\), respectively. An interval type-2 fuzzy number \(\tilde{A}\) (as shown in Fig. 1) in the universe of discourse X is defined as:

$$\begin{aligned} \tilde{A}= & {} \left( {\tilde{A}^{L},\tilde{A}^{U}} \right) =\left( \left( {a_1^L ,a_2^L ,a_3^L ,a_4^L ;h_{\tilde{A}}^L }\right) ,\right. \nonumber \\&\times \left. \left( {a_1^U ,a_2^U ,a_3^U ,a_4^U ;a_{\tilde{A}}^U } \right) \right) , \end{aligned}$$
(4)

where \(a_1^L \le a_2^L \le a_3^L \le a_4^L \), \(a_1^U \le a_2^U \le a_3^U \le a_4^U ,0\le h_{\tilde{A}}^L \le h_{\tilde{A}}^U \le 1\).

Fig. 1
figure 1

An interval type-2 fuzzy sets \(\tilde{A}\)

Full size image

The upper membership function and the lower membership function are defined as \(\tilde{A}^{U}(x)\),\(\tilde{A}^{L}(x)\), respectively.

$$\begin{aligned}&\tilde{A}^{U}(x)=\left\{ {\begin{array}{lll} \frac{\left( {x-a_1^U } \right) h_{\tilde{A}}^U }{a_2^U -a_1^U } &{}\quad a_1^U \le x\le a_2^U\\ h_{\tilde{A}}^U &{}\quad a_2^U \le x\le a_3^U\\ \frac{\left( {a_4^U -x} \right) h_{\tilde{A}}^U }{a_4^U -a_3^U } &{}\quad a_3^U \le x\le a_4^U\\ 0&{}\quad {\hbox {otherwise}} \\ \end{array}} \right. \end{aligned}$$
(5)
$$\begin{aligned}&\tilde{A}^{L}(x)=\left\{ {\begin{array}{lll} \frac{\left( {x-a_1^L } \right) h_{\tilde{A}}^L }{a_2^L -a_1^L } &{}\quad a_1^L \le x\le a_2^L \\ h_{\tilde{A}}^L &{}\quad a_2^L \le x\le a_3^L \\ \frac{\left( {a_4^L -x} \right) h_{\tilde{A}}^L }{a_4^L -a_3^L } &{}\quad a_3^L \le x\le a_4^L \\ 0&{}\quad {\hbox {otherwise}} \\ \end{array}} \right. \end{aligned}$$
(6)

Definition 4

[35] The arithmetic operations between the IT2FSs \(\tilde{A}_1 =\left( {\tilde{A}_1^L ,A_1^U } \right) =\left( {\left( {a_{11}^L ,a_{12}^L ,a_{13}^L ,a_{14}^L ;h_1^L } \right) } \right. , \left. {\left( {a_{11}^U ,a_{12}^U ,a_{13}^U ,a_{14}^U ;h_1^U } \right) } \right) \) and \(\tilde{A}_2 =\left( {\tilde{A}_2^L ,A_2^U } \right) = \left( \left( {a_{21}^L ,a_{22}^L ,a_{23}^L ,a_{24}^L ;h_2^L } \right) \right. \) ,\(\left. \left( {a_{21}^U ,a_{22}^U ,a_{23}^U ,a_{24}^U ;h_2^U } \right) \right) \) are defined as follows:

$$\begin{aligned} \tilde{A}_1 \oplus \tilde{A}_2&=\left( {\tilde{A}_1 ^{L},\tilde{A}_1 ^{U}} \right) \oplus \left( {\tilde{A}_2 ^{L},\tilde{A}_2 ^{U}} \right) \nonumber \\&=\left( {{\begin{array}{ll} \left( a_{11}^L +a_{21}^L ,a_{12}^L +a_{22}^L ,a_{13}^L +a_{23}^L ,\right. \\ \quad \left. a_{14}^L+\,a_{24}^L;\min \left( {h_1^L ,h_2^L } \right) \right) , \\ \left( a_{11}^U +a_{21}^U ,a_{12}^U +a_{22}^U ,a_{13}^U +a_{23}^U ,\right. \\ \quad \left. a_{14}^U +\,a_{24}^U ;\min \left( {h_1^U ,h_2^U } \right) \right) \\ \end{array} }} \right) , \end{aligned}$$
(7)
$$\begin{aligned} \tilde{A}_1 \Theta \tilde{A}_2&=\left( {\tilde{A}_1 ^{L},\tilde{A}_1 ^{U}} \right) \Theta \left( {\tilde{A}_2 ^{L},\tilde{A}_2 ^{U}} \right) \nonumber \\&=\left( {\;{\begin{array}{lll} \left( a_{11}^L -a_{21}^L ,a_{12}^L -a_{22}^L ,a_{13}^L -a_{23}^L ,\right. \\ \quad \left. a_{14}^L -a_{24}^L ;\min \left( {h_1^L ,h_2^L } \right) \; \right) , \\ \left( a_{11}^U -a_{21}^U ,a_{12}^U -a_{22}^U ,a_{13}^U -a_{23}^U ,\right. \\ \quad \left. a_{14}^U -a_{24}^U ;\min \left( {h_1^U ,h_2^U } \right) \; \right) \\ \end{array} }\;} \right) , \end{aligned}$$
(8)
$$\begin{aligned} \tilde{A}_1 \otimes \tilde{A}_2&=\left( {\tilde{A}_1 ^{L},\tilde{A}_1 ^{U}} \right) \otimes \left( {\tilde{A}_2 ^{L},\tilde{A}_2 ^{U}} \right) \nonumber \\&=\left( {{\begin{array}{l} \left( a_{11}^L \times a_{21}^L ,a_{12}^L \times a_{22}^L ,a_{13}^L \times a_{23}^L ,\right. \\ \quad \left. a_{14}^L \times a_{24}^L ;\min \left( {h_1^L ,h_2^L } \right) \right) , \\ \left( a_{11}^U \times a_{21}^U ,a_{12}^U \times a_{22}^U ,a_{13}^U \times a_{23}^U ,\right. \\ \quad \left. a_{14}^U \times a_{24}^U ;\min \left( {h_1^U ,h_2^U } \right) \right) \\ \end{array} }}\right) , \end{aligned}$$
(9)
$$\begin{aligned} k\otimes \tilde{A}_1&=k\otimes \left( {\tilde{A}_1 ^{L},\tilde{A}_1 ^{U}} \right) \nonumber \\&=\left( \left( {k\times a_{11}^L ,k\times a_{12}^L ,k\times a_{13}^L ,k\times a_{14}^L ;h_1^L } \right) ,\right. \nonumber \\&\left. \quad \times \left( k\times a_{11}^U ,k\times a_{12}^U, k\times a_{13}^U ,k\times a_{14}^U ;h_1^U \right) \right) ,\nonumber \\ \end{aligned}$$
(10)

where \(k>0\).

$$\begin{aligned} A_1^\alpha= & {} \left( \left( {(a_1^L )^{\alpha },(a_2^L )^{\alpha },(a_3^L )^{\alpha },(a_4^L )^{\alpha };h_1^L } \right) ,\right. \nonumber \\&\times \left. \left( (a_1^U )^{\alpha },(a_2^U )^{\alpha },(a_3^U )^{\alpha },(a_4^U )^{\alpha };h_1^U \right) \right) , \end{aligned}$$
(11)
$$\begin{aligned} A_1^{\frac{1}{\alpha }}= & {} \left( \left( {\root \alpha \of {a_1^L },\root \alpha \of {a_2^L },\root \alpha \of {a_3^L },\root \alpha \of {a_4^L };h_1^L } \right) ,\right. \nonumber \\&\left. \times \left( {\root \alpha \of {a_1^U },\root \alpha \of {a_2^U },\root \alpha \of {a_3^U },\root \alpha \of {a_4^U };h_1^U } \right) \right) , \end{aligned}$$
(12)

where \(\alpha \) is a real number excluding 0.

Table 1 Linguistic terms and their corresponding IT2FSs [37]
Full size table

In order to compare the size of IT2FS, Chen presents a signed-distance-based method in the context of IT2FS, the definition is defined as follows.

Definition 5

[36] \(\tilde{A}=\big ( \left( {a_1^L ,a_2^L ,a_3^L ,a_4^L ;h_A^L } \right) ,\big ( a_1^U ,a_2^U ,a_3^U, a_4^U ;h_A^U \big ) \big )\) is an IT2FS, then the ranking of \(\tilde{A}\) can be defined as the signed based distance from \(\tilde{A}\) to \(\tilde{1}_1 \):

$$\begin{aligned} d(\tilde{A},\tilde{1}_1 )= & {} \frac{1}{8}\left( a_1^L +a_2^L +a_3^L +a_4^L +4a_1^U +2a_2^U +2a_3^U \right. \nonumber \\&\left. +\,4a_4^U +3\left( a_2^U +a_3^U -a_1^U -a_4^U \right) \frac{h_A^L }{h_A^U}-16 \right) ,\nonumber \\ \end{aligned}$$
(13)

where \(\tilde{1}_1 =\left( {\left( {1,1,1,1;1} \right) ,\left( {1,1,1,1;1} \right) } \right) \).

When \(d\left( {\tilde{A},\tilde{1}_1 } \right) =0\), \(\tilde{A}\)is located at \(\tilde{1}_1 \).

When \(0<h_A^L =h_A^U \le 1\), the Eq. (13) is reduced to a simplified form, which is shown as follows:

$$\begin{aligned} d(\tilde{A},\tilde{1}_1 )= & {} \frac{1}{8}\left. \left( a_1^L +a_2^L +a_3^L +a_4^L +a_1^U +5a_2^U \right. \right. \\&\left. \left. +\,5a_3^U \right. +a_4^U -16 \right) . \end{aligned}$$

Definition 6

[36] The ranking of \(\tilde{A}\) and \(\tilde{B}\) by the signed based distance \(d\left( {\tilde{A},\tilde{1}_1 } \right) \) and \(d\left( {\tilde{B},\tilde{1}_1 } \right) \) on \(\tilde{X}\) can be defined as the following:

  1. (1)

    When \(d\left( {\tilde{A},\tilde{1}_1 } \right) >d\left( {\tilde{B},\tilde{1}_1 } \right) \), then \(\tilde{A}\) is better than or preferred to \(\tilde{B}\), denoted by \(\tilde{A}\succ \tilde{B}\);

  2. (2)

    When \(d\left( {\tilde{A},\tilde{1}_1 } \right) =d\left( {\tilde{B},\tilde{1}_1 } \right) \), then \(\tilde{A}\) is indifferent to \(\tilde{B}\), denoted by \(\tilde{A}\sim \tilde{B}\);

  3. (3)

    When \(d\left( {\tilde{A},\tilde{1}_1 } \right) <d\left( {\tilde{B},\tilde{1}_1 } \right) \), then \(\tilde{A}\) is worse than or less preferred to \(\tilde{B}\), denoted by \(\tilde{A}\prec \tilde{B}\).

4 Evacuation strategy selection model and calculation steps

In order to make a quick and effective decision and swift action, a model of evacuation strategy selection is constructed and the specific calculation steps are introduced as follows.

Table 2 The interval type-2 fuzzy decision matrix of expert \(E_k \)
Full size table

4.1 Description of evacuation strategy selection model

The problem to select a suitable evacuation strategy can be treated as a MCGDM problem. The experts who involve in the decision process consist of the group of decision makers (DMs), expressed by a set \(D=\left\{ {\left. {D_k } \right| k=1,2,\ldots ,p} \right\} \), and \(\lambda =\left( {\left. {\lambda _k } \right| k=1,2,\ldots ,p} \right) ^{T}\) is the weight set of the DMs, where \(\lambda _k >0\) and \(\sum _{k=1}^p {\lambda _k } =1\). The alternative strategies come from the emergency preparedness plan database which has been screened. The alternative strategies are expressed as a set \(A=\left\{ {\left. {A_i } \right| i=1,2,\ldots ,m} \right\} \). The criteria set evaluating the strategies is denoted as \(C=\left\{ {\left. {C_j } \right| j=1,2,\ldots ,n} \right\} \), and the criteria weights set is expressed as \(W=\left\{ {\left. {w_j } \right| j=1,2,\ldots ,n} \right\} \). The decision criteria can be divided into two sets, benefit criteria set \(C_b \) and cost criteria set \(C_c \) which satisfy \(C_b \cup C_c =C\), and \(C_b \cap C_c =\varnothing \). Let \(X=\left\{ {\left. {x_{ij} } \right| i=1,2,\ldots ,m;j=1,2,\ldots ,n} \right\} \) denotes the decision matrix, where \(x_{ij} \) is the performance measure of the alternative \(A_i \) with respect to the criterion \(C_j \).

In this study, it can be assumed that the decision maker expects to form linguistic terms (see Table 1) to assign linguistic values to express their decision preferences with IT2FSs [37].

4.2 Model and calculation of evacuation strategy selection

In the following, the TOPSIS method is extended to present a new model for handling the evacuation strategy selection problem of the metro station under emergency environment based on interval type-2 fuzzy sets.

Step 1 Construct the decision matrix \(X_k \) of the kth decision maker, as Table 2 shows, and construct the evaluate matrix W of the importance of the criteria, as is shown in Table 3.

Table 3 Evaluate the importance of the criteria
Full size table
Table 4 The aggregation decision matrix
Full size table

Step 2 Construct the average decision matrix \(\tilde{Z}\) by Eqs. (14) and (15), the decision matrix as shown in Table 4 can be obtained, and the weights of the criteria are shown in Eq. (16).

$$\begin{aligned} \tilde{z}_{ij}= & {} \sum _{k=1}^p {\lambda _k \tilde{x}_{ij}^k } , \quad 1\le i\le m,1\le j\le n,1\le k\le p, \end{aligned}$$
(14)
$$\begin{aligned} \tilde{w}_j= & {} \sum _{k=1}^p {\lambda _k \tilde{w}_{kj} } , \quad 1\le j\le n,1\le k\le p. \end{aligned}$$
(15)
$$\begin{aligned} \tilde{W}=(\tilde{w}_1 ,\tilde{w}_2 ,\ldots ,\tilde{w}_n ) \end{aligned}$$
(16)

Step 3 Acquire the weighted normalized decision matrix using Eq. (17), and the value of \(\tilde{z}_{ij}^{\prime } \) can be expressed as \(\tilde{z}_{ij}^{\prime } =((z_{ij1}^L ,z_{ij2}^L ,z_{ij3}^L ,z_{ij4}^L ;h_{ij}^L );(z_{ij1}^U ,z_{ij2}^U ,z_{ij3}^U ,z_{ij4}^U ;h_{ij}^U ))\).

$$\begin{aligned} \tilde{Z}_{ij}^{\prime } =\tilde{Z}_{ij} \otimes \tilde{W}_j . \end{aligned}$$
(17)

Step 4 Determine the positive ideal solution (PIS), choose the biggest values for the benefit criteria and the smallest values for the cost criteria, i.e., \(D^{+}=\left( {v_{_1 }^+ ,v_2^+ ,\ldots ,v_n^+ } \right) \), and the negative ideal solution (NIS) is opposite, i.e., \(D^{-}=\left( {v_{_1 }^- ,v_2^- ,\ldots ,v_n^- } \right) \). The ideal solutions are calculated as Eqs. (18), (19), (20), (21).

$$\begin{aligned} v_j^+ =((v_{j1}^L ,v_{j2}^L ,v_{j3}^L ,v_{j4}^L ;h_{v_j }^L ),(v_{j1}^U ,v_{j2}^U ,v_{j3}^U ,v_{j4}^U ;h_{v_j }^U )), \end{aligned}$$

where

$$\begin{aligned} v_{jg}^L= & {} \left\{ {\begin{array}{l} \mathop {\mathop {\max }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^L } \right\} ,\;\;if\;C_j \in C_b \\ \mathop {\mathop {\min }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^L } \right\} ,\;\;if\;C_j \in C_c \\ \end{array}} \right. ,\quad h_{v_j }^L =\mathop {\min }\limits _{1\le i\le m} (h_{ij}^L ), \quad 1\le i\le m,1\le j\le n,1\le g\le 4, \end{aligned}$$
(18)
$$\begin{aligned} v_{jg}^U= & {} \left\{ {\begin{array}{ll} \mathop {\mathop {\max }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^U } \right\} ,\;\;if\;C_j \in C_b \\ \mathop {\mathop {\min }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^U } \right\} ,\;\;if\;C_j \in C_c \\ \end{array}} \right. ,\quad h_{v_j }^U =\mathop {\min }\limits _{1\le i\le m} (h_{ij}^U ),\quad 1\le i\le m,1\le j\le n,1\le g\le 4.\nonumber \\ v_j^-= & {} ((v_{j1}^L ,v_{j2}^L ,v_{j3}^L ,v_{j4}^L ;h_{v_j }^L ),(v_{j1}^U ,v_{j2}^U ,v_{j3}^U ,v_{j4}^U ;h_{v_j }^U )), \end{aligned}$$
(19)

where

$$\begin{aligned} v_{jg}^L= & {} \left\{ {\begin{array}{l} \mathop {\mathop {\min }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ij\hbox {g}}^L } \right\} ,\;\;if\;C_j \in C_b \\ \mathop {\mathop {\max }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^L } \right\} ,\;\;if\;C_j \in C_c \\ \end{array}} \right. ,\quad h_{v_j }^L =\mathop {\min }\limits _{1\le i\le m} (h_{ij}^L ),\quad 1\le i\le m,1\le j\le n,1\le g\le 4, \end{aligned}$$
(20)
$$\begin{aligned} v_{jg}^U= & {} \left\{ {\begin{array}{l} \mathop {\mathop {\min }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^U } \right\} ,\;\;if\;C_j \in C_b \\ \mathop {\mathop {\max }\limits _{1\le i\le m} }\limits _{1\le g\le 4} \left\{ {z_{ijg}^U } \right\} ,\;\;if\;C_j \in C_c \\ \end{array}} \right. ,\quad h_{v_j }^U =\mathop {\min }\limits _{1\le i\le m} (h_{ij}^U ),\quad 1\le i\le m,1\le j\le n,1\le g\le 4. \end{aligned}$$
(21)
Table 5 The ranking value of decision matrix \(Y_{ij} \)
Full size table
Fig. 2
figure 2

The frame diagram of evacuation strategy selection

Full size image

Step 5 Based on Eq. (14), calculate the ranking value \(Rank\left( {\tilde{Z}^{{\prime }}_{ij} } \right) \) of the IT2FSs \(\tilde{Z}^{{\prime }}\) to obtain the ranking value decision matrix \(Y_{ij} \), where \(1\le i\le m\),\(1\le j\le n\), and \(v_{ij} =Rank(\tilde{Z}_{ij}^{\prime } )\), \(v^{+{*}}=Rank(v^{+})\), \(v^{-{*}}=Rank(v^{-})\) (Table 5).

Step 6 Calculate the distance \(d^{+}\) between each alternative \(A_i \) and the corresponding PIS \(D^{+}\), the distance \(d^{-}\) between each alternative \(A_i \) and the corresponding PIS \(D^{-}\) which are shown as follows:

$$\begin{aligned} d^{+}(A_i )= & {} \sqrt{\sum _{j=1}^n {\left( {v_{ij} -v_j^{+{*}} } \right) ^{2}} } \qquad 1\le i\le m, \end{aligned}$$
(22)
$$\begin{aligned} d^{-}(A_i )= & {} \sqrt{\sum _{j=1}^n {\left( {v_{ij} -v_j^{-{*}} } \right) ^{2}} } \qquad 1\le i\le m. \end{aligned}$$
(23)

Step 7 Balance the separations of an alternative from the PIS and the NIS, and calculate the relative closeness \(C(A_i )\) of each alternative [38].

$$\begin{aligned} C(A_i )=\delta ^{+}\left( {\frac{d_i^- }{\sum _{i=1}^m {d_i^- } }} \right) -\delta ^{-}\left( {\frac{d_i^+ }{\sum _{i=1}^m {d_i^+ } }} \right) , \end{aligned}$$
(24)

where \(\delta ^{+}+\,\delta ^{-}=1\) and \(\delta ^{-},\delta ^{+}\ge 0\). \(\delta ^{+}\) denotes the weight of the \(\frac{d_i^- }{\sum _{i=1}^m {d_i^- } }\), indicating the higher value of \(\frac{d_i^- }{\sum _{i=1}^m {d_i^- } }\) is better. \(\delta ^{-}\) denotes the weight of the \(\frac{d_i^+ }{\sum _{i=1}^m {d_i^+ } }\), indicating the smaller value of \(\frac{d_i^+ }{\sum _{i=1}^m {d_i^+ } }\) is better.

Step 8 Sort the values of \(C(A_i )\) in a descending sequence, where \(1\le i\le m\). The larger the values of \(C(A_i )\), the higher preference of the alternative \(A_i \).

Step 9 End.

The frame diagram of evacuation strategy selection of the metro station under emergency environment is shown in Fig. 2.

5 An illustrative example

In this section, an emergency evacuation example in metro station is provided to verify the efficiency of the proposed method for strategy selection problem.

5.1 Problem description

Metro station is a huge and complex system. It is very important to choose a suitable strategy to improve evacuation efficiency. After preliminary screening, five potential evacuation strategies \((A_1 ,A_2 ,A_3 ,A_4 ,A_5 )\) have been identified for further selection. Six criteria to be considered in the selection process are \(C_1 \) (i.e., match degree of equipment and pedestrians), \(C_2 \) (i.e., evacuation capacity of metro station), \(C_3 \) (i.e., response extent), \(C_4 \) (i.e., crowd panic), \(C_5 \) (i.e., destructive emergency event), \(C_6 \) (i.e., heterogeneous population). A group including four decision makers can be denoted as \(D=(D_1 ,D_2 ,D_3 ,D_4 )\), and the weight vector of the decision makers is \(\lambda =\left( {0.25,0.3,0.3,0.15} \right) ^{T}\).

5.2 Steps of selection strategy

  1. (1)

    Since \(C_1 ,C_2 ,C_3 \) are the benefit criteria, \(C_4 ,C_5 ,C_6 \) are the cost criteria. Construct the decision matrix \(D_k \) of the kth decision maker, as is shown in Table 6, and the evaluate matrix W of the importance of the criteria can be constructed (see Table 7) by the linguistic terms values.

Table 6 The decision matrices of DMs
Full size table
Table 7 Linguistic weights of the attributes
Full size table
  1. (2)

    Transform linguistic terms values in Table 6 to IT2FNs, and construct the average decision matrix \(\tilde{Z}\) using Eq. (14), the results are shown in Table 8. Aggregate the individual criteria weights into group criteria weights using Eq. (15), the result is shown in Eq. (25).

    $$\begin{aligned}&\left( {{\begin{array}{ll} {\tilde{w}_1 } \\ {\tilde{w}_2 } \\ {\tilde{w}_3 } \\ {\tilde{w}_4 } \\ {\tilde{w}_5 } \\ {\tilde{w}_6 } \\ \end{array} }} \right) \nonumber \\&\quad =\left[ {{\begin{array}{lll} {(0.515,0.595,0.595,0.665;0.9),(0.435,}\\ \quad {0.595,0.595,0.735;1)} \\ {(0.695,0.78,0.78,0.838;0.9),(0.61,0.78,}\\ \quad {0.78,0.895;1)} \\ {(0.41,0.495,0.495,0.573;0.9),(0.325,0.495,}\\ \quad { 0.495,0.65;1)} \\ {(0.575,0.66,0.66,0.723;0.9),(0.49,0.66,}\\ \quad { 0.66,0.785;1)} \\ {(0.596,0.685,0.685,0.76;0.9),(0.51,0.685,}\\ \quad {0.685,0.835;1)} \\ {(0.5,0.6,0.6,0.68;0.9),(0.4,0.6,0.6,0.76;1)} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$
    (25)
Table 8 The aggregation decision matrix
Full size table
  1. (3)

    In virtue of Eq. (17), acquire the weighted normalized decision matrices, which are shown in Table 9.

Table 9 The weighted normalized decision matrix
Full size table
  1. (4)

    Based on Table 9 and Eqs. (18), (19), (20), (21), the PIS and NIS can be obtained respectively. The PIS and NIS are shown in the below:

$$\begin{aligned} D^{+}= & {} \left\{ {[(0.299,} \right. 0.405,0.405,0.509;0.900),\\&(0.209,0.405,0.405,0.625;1)], \\&{[}0.514,0.655,0.655,0.758;0.900),\\&(0.390,0.655,0.655,0.868;1], \\&{[}(0.267,0.371,0.371,0.471;0.900),\\&(0.179,0.371,0.371,0.582;1)], \\&{[}(0.283,0.383,0.383,0.470;0.900),\\&(0.196,0.383,0.383,0.565;1)], \\&{[}(0.257,0.360,0.360,0.454;0.900),\\&(0.168,0.360,0.360,0.559;1)], \\&{[}(0.186,0.276,0.276,0.371;0.900),\\&(0.114,0.276,0.276,0.475;1]\} \\ D^{-}= & {} \left\{ {[(0.131,} \right. 0.187,0.187,0.268;0.900),\\&(0.085,0.187,0.187,0.360;1)], \\&{[}0.101,0.156,0.156,0.239;0.900),\\&(0.055,0.156,0.156,0.331;1], \\&{[}(0.049,0.089,0.089,0.149;0.900),\\&(0.020,0.089,0.089,0.221;1)], \\&{[}(0.443,0.574,0.574,0.67;0.900),\\&(0.328,0.574,0.574,0.773;1)], \\&{[}(0.406,0.534,0.534,0.642;0.900),\\&(0.296,0.534,0.534,0.760;1)], \\&{[}(0.375,0.510,0.510,0.621;0.900),\\&(0.260,0.510,0.510,0.741;1]\} \end{aligned}$$
  1. (5)

    Based on Eq. (13), calculate the ranking value \(Rank\left( {\tilde{Z}^{{\prime }}_{ij} } \right) \) of the IT2FS\(\tilde{Z}^{{\prime }}\), where \(1\le j\le n\) (see Table 10), and the ranking value of \(D^{+},D^{-}\).

    $$\begin{aligned} v^{+{*}}= & {} (-\,1.187,-\,0.631,-\,1.255,-\,0.1.237,\\&-\,1.280,-\,1.441),\\ v^{-{*}}= & {} (-\,1.611,-\,0.613,-\,1.809,-\,0.864,\\&-\,0.936,-\,0.986). \end{aligned}$$
  2. (6)

    Calculate the distances \(d_i^+ \), \(d_i^- \) of alternatives \(A_i \) to the PIS and NIS respectively, and the relative closeness coefficients to the ideal solution \(C(A_i )\) using Eqs. (22), (23), (24), which are shown in Table 11.

  3. (7)

    Rank the alternatives and select the best one(s) via the relative closeness coefficient value \(C(A_i )\), and the higher value of \(C(A_i )\) is better. According to Table 11, obviously

    $$\begin{aligned} A_3 \succ A_5 \succ A_1 \succ A_2 \succ A_4 . \end{aligned}$$

Therefore, the strategy \(A_3 \) is the best.

Table 10 The ranking value of matrix \(\tilde{Z}^{{\prime }}\)
Full size table
Table 11 The distance \(d_i^+ \), \(d_i^- \) to the ideal solution and \(C(A_i )\)
Full size table

5.3 Sensitivity analysis

In order to reflect the influence of different values of parameters \(\delta ^{+},\delta ^{-}\)on the results, different obtained rankings of the alternatives can be assessed under different \(\delta ^{+},\delta ^{-}\) values, where \(\delta ^{+}+\delta ^{-}=1\). The corresponding results are obtained in Table 12. In order to visualize the influence of fluctuating values of \(\delta ^{+},\delta ^{-}\), a radar diagram based on Table 12 showing the results according to the sensitivity analysis is given in Fig. 3.

From Table 12, it is obvious that the ranking orders obtained by different values of \(\delta ^{+},\delta ^{-}\) from 0 to 1 have changed in this example. This means the ranking results are sensitive to the values of \(\delta ^{+},\delta ^{-}\). In other words, the final ranking results change with the different values of the parameters \(\delta ^{+},\delta ^{-}\) in the process of decision. In the case 0, when \(\delta ^{+}=1\) and \(\delta ^{-}=0\), then \(C(A_i)=\delta ^{+}\left( {\frac{d_i^- }{\sum _{i=1}^m {d_i^- } }} \right) \), which means the DMs prefer the alternative that is the furthest to the NIS. In the case 10, when \(\delta ^{+}=0\) and \(\delta ^{-}=1\), then \(C(A_i )=-\,\delta ^{-}\left( {\frac{d_i^+ }{\sum _{i=1}^m {d_i^+ } }} \right) \), which means the DMs prefer the alternative that is the closest to the PIS.

Table 12 Ranking orders of alternatives with different \(\delta ^{+},\delta ^{-}\)
Full size table
Fig. 3
figure 3

The radar plot showing the result of the sensitivity analysis (Color figure online)

Full size image

As can be seen in Table 12 and Fig. 3, the ranking orders of alternatives change with the increasing different between \(\delta ^{+}\) and \(\delta ^{-}\). The ranking order of these five alternatives is \(A_3 \succ A_5 \succ A_1 \succ A_2 \succ A_4 \) when \((\delta ^{+},\delta ^{-})\) changes among (1,0), (0.9, 0.1), (0.8, 0.2), (0.7, 0.3), (0.6, 0.4), (0.5, 0.5), (0.4, 0.6), \(A_5 \succ A_3 \succ A_1 \succ A_2 \succ A_4 \) when \((\delta ^{+},\delta ^{-})\) changes between (0.3, 0.7) and (0.2, 0.8), and \(A_5 \succ A_1 \succ A_3 \succ A_2 \succ A_4 \) when \((\delta ^{+},\delta ^{-})\) changes between (0.1, 0.9) and (0, 1). When \((\delta ^{+},\delta ^{-})\) takes the values of (0.3, 0.7) and (0.2, 0.8), the ranks are the same as the best strategy, when \((\delta ^{+},\delta ^{-})\) takes the values of (0.1, 0.9) and (0, 1), the ranks are the same as the worst strategy. This phenomenon confirms that the ranking of the alternatives should consider the relative importance of the two separations. The ranking order varies with the value of \((\delta ^{+},\delta ^{-})\) because of different preferences of DMs. It should be noted that inflection point causing change of the ranking order is not always when \(\delta ^{+}=0.5\),\(\delta ^{-}=0.5\), because the values of \(d_i^+ \) and \(d_i^- \) also affect the turning point.

6 Comparative analysis

In order to verify the validity of the developed method, comparative analysis is conducted with the interval type-2 fuzzy TOPSIS method, which was proposed by Chen [18]. In [18], the ranking values of IT2Fs is calculated using Eq. (26) before determining the PIS \(D^{+}=(v_1^+ ,v_2^+ ,\ldots ,v_n^+ )\) and the NIS \(D^{-}=(v_1^- ,v_2^- ,\ldots ,v_n^- )\), which is different from this paper, the PIS and the NIS are determined before calculating the ranking value of IT2Fs in this paper.

$$\begin{aligned} Rank(\tilde{A}_i )= & {} M_1 (\tilde{A}_i^U )+M_1 (\tilde{A}_i^L )+M_2 (\tilde{A}_i^U )+M_2 (\tilde{A}_i^L )\nonumber \\&+\,M_3 (\tilde{A}_i^U )+M_3 (\tilde{A}_i^L ) \nonumber \\&-\,\frac{1}{4}\left( \;S_1 \left( {\tilde{A}_i^U } \right) +S_1 \left( {\tilde{A}_i^L } \right) \right. \nonumber \\&\left. +\,S_2 \left( {\tilde{A}_i^U } \right) +S_2 \left( {\tilde{A}_i^L } \right) +S_3 \left( {\tilde{A}_i^U } \right) \right. \nonumber \\&\left. +\,S_3 \left( {\tilde{A}_i^L } \right) +S_4 \left( {\tilde{A}_i^U } \right) +S_4 \left( {\tilde{A}_i^L } \right) \; \right) \nonumber \\&+\,H_1 \left( {\tilde{A}_i^U } \right) +H_1 \left( {\tilde{A}_i^L } \right) \nonumber \\&+\,H_2 \left( {\tilde{A}_i^U } \right) +H_2 \left( {\tilde{A}_i^L } \right) , \end{aligned}$$
(26)

Determine the PIS \(D^{+}=(v_1^+ ,v_2^+ ,\ldots ,v_n^+ )\) and the NIS,\(D^{-}=(v_1^- ,v_2^- ,\ldots ,v_n^- )\), where,

$$\begin{aligned} v_i^+ =\left\{ {\begin{array}{l} \mathop {\max }\limits _{1\le j\le n} \left\{ {Rank(\tilde{v}_{ij} )} \right\} ,\;\;\hbox {if}\;f_i \in C_b \\ \mathop {\min }\limits _{1\le j\le n} \left\{ {Rank(\tilde{v}_{ij} )} \right\} ,\;\;\hbox {if}\;f_i \in C_c \\ \end{array}} \right. \end{aligned}$$
(27)

and

$$\begin{aligned} v_i^- =\left\{ {\begin{array}{l} \mathop {\min }\limits _{1\le j\le n} \left\{ {Rank(\tilde{v}_{ij} )} \right\} ,\;\;\hbox {if}\;f_i \in C_b \\ \mathop {\max }\limits _{1\le j\le n} \left\{ {Rank(\tilde{v}_{ij} )} \right\} ,\;\;\hbox {if}\;f_i \in C_c \\ \end{array}} \right. \end{aligned}$$
(28)

where \(C_b \) denotes the set of the benefit criteria, \(C_c \) denotes the set of the cost criteria, and \(C_b \cup C_c =C\), \(C_b \cap C_c =\emptyset \).

The relative degree of closeness \(C(A_i )\) of \(A_i \) with respect to the PIS \(D^{+}\) can be calculated using Eq. (29) in the following way.

$$\begin{aligned} C(A_i )=\frac{d_i^- }{d_i^+ +d_i^- }. \end{aligned}$$
(29)

According to Eqs. (22), (23), (26)–(29), the corresponding distance measures \(d_i^+ ,d_i^- \) and the closeness degree \(C(A_i )\) can be calculated, which are shown in Table 13. The ranking order is \(A_3 \succ A_1 \succ A_5 \succ A_2 \succ A_4 \).

Table 13 The distance of \(d_i^+ ,d_i^- \)and the value of \(C(\tilde{A}_i )\)
Full size table

From Eq. (29), the same weight is given to the distances \(d_i^+\) and \(d_i^-\), i.e., \(\delta ^{+}=0.5\) and \(\delta ^{-}=0.5\). Comparing the results of the two approaches, as is shown in Table 13, it is obvious that the ranking orders using these two methods are similar, when \(\delta ^{+}=0.5\) and \(\delta ^{-}=0.5\). They have the same best alternative \(A_3 \) and worst alternative \(A_4 \). It is evident that the ranking result obtained by the proposed approach is reasonable.

From Tables 12 and 13, it can be known that the ranking orders by these two methods are similar from case 0 to case 6. They have the same best alternative \(A_3 \) and worst alternative \(A_4 \). While, from case 7 to case 10, the ranking order by these two methods are slightly different. The main reasons behind the differences can be concluded as follows: (1) the proposed approach in this study considers the preferences of DMs using the different values of \((\delta ^{+},\delta ^{-})\), but Chen [14] fails to consider the preferences of DMs and can’t reflect the decision makers’ preferences. (2) The different approaches that calculate the ranking value of IT2FSs cause a bit of bias of the ranking order.

7 Conclusions and further study

It’s one of the most important issues to select a suitable evacuation strategy for the metro station under emergency environment, which directly impacts the safety of the people and the loss of property. From this perspective, the development and extension of a strategy selection decision method is of substantial significance. In this study, the evacuation strategy selection model and the special calculation are proposed. All the decision information and criteria weight information provided by DMs are represented by IT2FSs, which can reflect the complex uncertainty and fuzzy information. And then, a sensitivity analysis about \((\delta ^{+},\delta ^{-})\) and the effects on results are discussed. The results show that difference values of \((\delta ^{+},\delta ^{-})\) cause the different ranking orders of alternatives which represents the difference preferences of DMs. Finally, the proposed method is compared with Chen’s approach. It’s obvious that the proposed approach is effective and good enough for being widely used.

This research has made important contribution to the current study on the emergency management of metro station in emergency context. First, an effective approach has been provided to select evacuation strategy when an emergent event occurs the metro station. Second, it is very meaningful to help managers of metro stations to choose a suitable evacuation strategy quickly. Finally, the TOPSIS approach has been extended considering the IT2FSs which has made an important contribute to the current literature. In summary, this paper is of important theoretical and practical significance.

There are some flaws in this study, such as neglecting the effects of pedestrians’ behaviors and the cooperation degrees of the pedestrians during the evacuation organization in the emergency context of metro station. In the future work, we will remedy defects and extend different decision approaches to the emergency decision area. It’s worth extending different classical decision methods in the context of generalized type-2 fuzzy sets, such as ELECTER (Elimination et Choice Translating Reality), TODIM(Decision Making Trial and Evaluation Laboratory), PROMETHEE (Preference Ranking Organization Method for Enrichment Evolutions). Furthermore, the study could be continued with anticipation that the method could be found applicable to metro station decision problem, such as metro address selection, planning and designing the route for emergency evacuation, emergency evacuation evaluation.