Interval type-2 fuzzy TOPSIS approach with utility theory for subway station operational risk evaluation

Abstract

As a distributing center for passengers, the subway station directly affects the entire subway system’s safe operation. Accurate operational subway station risk evaluation has an important significance in risk avoidance and accident emergency response. By analyzing the application of interval type-2 fuzzy TOPSIS (IT2-FTOPSIS) method in risk evaluation, the existing research lacks consideration of the utility function and cannot reflect the actual operational risk of the subway station. To overcome these shortcomings, we develop an IT2-FTOPSIS approach with a utility function and utilize it to evaluate the subway station’s operational risk. Finally, the example of Beijing Subway is selected to illustrate the developed risk evaluation approach’s performance. The results show that the same event has different effects on subway station safe operation at different times or spaces. Namely, the same event may have different risk utility values in different situations. Thus, the developed IT2-FTOPSIS model with a utility function can improve the risk evaluation’s accuracy and reflect the subway station’s operational risk state more reasonable than the previous method.

1 Introduction

With the continuous expansion of the subway network in many cities in China, the subway acts as an extremely important role in the public transport system because of its fast speed and large transportation capacity. As a distributing center for passengers, the subway station directly affects the entire subway system's safe operation. Moreover, the environment of the subway station is relatively closed. Once there is an accident, for instance, a fire, it will cause a huge loss of life and property. Therefore, risk evaluation of subway stations is significant to ensure the operation risk of the subway station. The subway station's risk evaluation evaluates the subway station’s risk state at a certain time based on the factors affecting the operation risk. The operation risk state of the subway station can be real-time displayed by the risk evaluation. Through risk evaluation, we can find out risk sources and monitor the risks that exist in the operation of the subway station, then assist the managers of the subway station in reducing or eliminating operational risks in a timely and targeted manner, and avoid accidents and guarantee the safe and reliable operation of the subway as much as possible. In recent years, subway station risk evaluation has attracted more and more scholars’ attention (Kyriakidis et al. 2012; Wan et al. 2015; Lu et al. 2013).

In the research on subway station operational risk evaluation, some different methods have been introduced into the subway station's risk state classification. After analyzing the relationship between passenger numbers and congestion level, Wu and Ma (2012) applied the K-means clustering method to classify subway station passengers’ crowding degree. Qin et al. (2013) analyzed Guangzhou Metro’s safety state by establishing a PSO-SVM based metro safety state prediction model. Meanwhile, due to the complexity of the subway environment and the uncertainty of evaluation information, many scholars have introduced the fuzzy set theory into the subway safety evaluation. Lu et al. (2011) put forward fuzzy signal detection theory (FSDT) methods to evaluate the risk state of subway workers, predict the possible risks, and ensure the subway’s safe operation. Sari et al. (2012) analyzed the urban rail transit system’s risk factors, investigated fuzzy AHP to evaluate the risk state, and found the most dangerous urban rail system. Actually, evaluating the safety of subway stations is a very complex process, including selecting and calculating the safety indicators of the subway station, identifying the weights of the indicators, and can be regarded as a typical multi-criteria decision-making (MCDM) problem. Considering the uncertainty of the risk information on subway station, the fuzzy TOPSIS method is sort by detecting the distance between the evaluation object and the positive ideal solution and the negative solution, which is suitable to solve such cases.

The fuzzy TOPSIS method has been widely applied in many fields, such as service quality, road traffic safety, and project selection. Awasthi et al. (2011) studied a fuzzy TOPSIS method to evaluate the service quality of Montreal Subway system. Besides, Bao et al. (2012) analyzed road traffic safety in many European countries by the improved hierarchical fuzzy TOPSIS method. Mahmoudi et al. (2020) constructed the TOPSIS based framework of project selection. In the framework, principal component analysis and the K-means clustering method were applied to extract the project features and cluster the projects, and the TOPSIS method was used to find out the best projects. Sattarpour et al. (2018) obtained the best placement strategy of allocating the remote terminal units and distributed generations by the GA-TOPSIS method. Considering the hesitance and uncertainty information in industrial firms’ carbon performance evaluation problem, Peng et al. (2019) developed an IVHF-TOPSIS method to measure firms’ separations. Karaaslan and Hunu (2020) discussed some distance measures’ properties of type-2 single-valued neutrosophic sets and introduced a type-2 single-valued neutrosophic TOPSIS method.

Furthermore, to represent the uncertain evaluation information more accurately, the TOPSIS method has been extended to an interval type-2 fuzzy environment. Chen and Lee (2010a) proposed a TOPSIS method based on interval type-2 fuzzy sets (IT2FSs) to deal with fuzzy MCDM problems. Kilic and Kaya (2015) developed a decision-making model based on IT2FSs to select investment projects. Celik et al. (2013) combined IT2-FTOPSIS and GRA to evaluate Istanbul’s public transport passenger satisfaction. Wu et al. (2018) extracted the evaluation information by social network analysis and used the interval type-2 fuzzy TOPSIS (IT2-FTOPSIS) method to select the most valued restaurant. Celik and Akyuz (2018) chose the appropriate ship loader type for handling bulk materials by the interval type-2 fuzzy AHP-TOPSIS method to reduce the shipping service cost. Deveci et al. (2018) selected the car-sharing stations by the interval type-2 WASPAS-TOPSIS method and made service providers expand their market. In terms of the subway station, the IT2-FTOPSIS-based subway station evaluation method can often achieve better results because of its complexity. Mei and Xie (2019) constructed a metro station evacuation strategy selection model using the IT2-FTOPSIS method, helping the passengers escape the subway station in case of emergency. Qin et al. (2015) investigated an IT2-FTOPSIS method to assess the risk status of Beijing Metro. The existing research has focused on combining TOPSIS and other MCDM methods and applying the IT2-FTOPSIS method.

However, the existing IT2-FTOPSIS method lacks consideration of the utility values, especially applying the subway station risk evaluation problem. The utility function reflects the relationship between the risk utility value and the original risk value (Zhang et al. 2020). The subway station has different operation characteristics in a different time or space, and the same event may have different risk utility values. For instance, elevator failures occurring in the morning or evening peak hours have a different impact on subway station operational safety than during other times. At the morning or evening peak hours, the elevator failure has a more serious effect on the subway station’s safety. Namely, the elevator failure may have a different risk utility value in the morning or evening peak hours or other times. Similarly, the elevator failure occurring in different subway stations may have a different utility value on the subway station’s safety. To overcome this drawback, we introduce the utility function to reflect the subway station’s actual risk value in a different time or different space, develop an IT2-FTOPSIS approach with a utility function, and apply it to the subway station risk evaluation.

The contributions of our work are as follows. Firstly, the subway station risk evaluation framework considering the risk utility in different time or space is put forward. It can more accurately express the station operation risk in different time or space, which provide a theoretical basis for station safety management. Secondly, a novel IT2-FTOPSIS method with utility function is developed, which enriches the IT2-FTOPSIS method. Thirdly, IT2FSs with alpha-cut express the uncertainty of subway operational risk more accurately.

The structure of our work is shown as follows: Sect. 2 introduces some basic concepts of IT2FSs and fuzzy TOPSIS approach based on α-level sets; Sect. 3 develops an IT2-FTOPSIS approach with utility function for subway station risk evaluation; Sect. 4 introduces time risk utility function and space risk utility function of the subway station and gives risk evaluation examples of Beijing Subway to illustrate the performance of the developed method; Sect. 5 gives a conclusion of our work.

2 Preliminary

2.1 Some basic concepts of IT2FSs

Compared with type-1 fuzzy sets, IT2FSs provide a more accurate tool to express uncertain information. Therefore, IT2FSs are widely used to solve the MCDM problem with many uncertain information (Chakravarty and Dash 2012; Wagner and Hagras 2010). Then, we introduce some basic concepts of IT2FSs.

Definition 1

(Mendel et al. 2006). Suppose that $\tilde{\tilde{A}}$ is a type-2 fuzzy set (T2FS) in the universe of discourse $X$, the T2FS $\tilde{\tilde{A}}$ is represented as

$$\tilde{\tilde{A}} = \{ (x,u),\mu_{{\tilde{\tilde{A}}}} (x,u)|\forall x \in X,\forall u \in J_{x} \subseteq [0,1]\}$$

(1)

where $0 \le \mu_{{\tilde{\tilde{A}}}} (x,u) \le 1$.

If the universe is continuous, Eq. (1) is also represented as

$$\tilde{\tilde{A}} = \int_{x \in X} {\int_{{u \in J_{x} }} {\mu_{{\tilde{\tilde{A}}}} } } (x,u)/(x,u), \, J_{x} \subseteq [0,1]$$

(2)

where $\smallint$ represents the union of the sets. If the universe is discrete, $\smallint$ can be used instead of $\sum$.

Definition 2

(Chen and Lee 2010b). Suppose that $\tilde{\tilde{A}}$ is a type-2 fuzzy set in the universe of discourse $X$, the type-2 fuzzy set $\tilde{\tilde{A}}$ can be represented by a membership function $\mu_{{\tilde{\tilde{A}}}}$. If all $\mu_{{\tilde{\tilde{A}}}} (x,u) = 1$, then $\tilde{\tilde{A}}$ is an IT2FS, can be expressed as

$$\tilde{\tilde{A}} = \int_{x \in X} {\int_{{u \in J_{x} }} {1/(x,u)} } { , }J_{x} \subseteq [0,1]$$

(3)

Definition 3

(Chen and Lee 2010b). The footprint of uncertainty (FOU) of IT2FS is the set of all elements and values of the main membership function.

$$FOU(\tilde{\tilde{A}}) = \bigcup\limits_{x \in X} {J_{x} } = \{ (x,y):y \in J_{x} = [\tilde{A}^{U} (x),\tilde{A}^{L} (x)]\}$$

(4)

Definition 4

(Chen and Lee 2010b). The upper membership function (UMF) $\overline{\mu }_{{\tilde{\tilde{A}}}} (x)$ or the lower membership function (LMF) $\underline {\mu }_{{\tilde{\tilde{A}}}} (x)$ of IT2FS $\tilde{\tilde{A}}$ is a type-1 membership function. The UMF $\overline{\mu }_{{\tilde{\tilde{A}}}} (x)$ is the union of all the largest membership values, and the LMF $\underline {\mu }_{{\tilde{\tilde{A}}}} (x)$ is the union of all the smallest membership values.

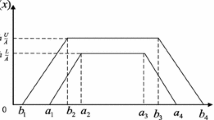
Throughout this paper, we use the triangular interval type-2 fuzzy numbers (IT2FNs) to represent IT2FSs. The triangular IT2FN $\tilde{\tilde{A}}$ can be expressed as $\tilde{\tilde{A}} = (\tilde{A}^{U} ,\tilde{A}^{L} ) = ((a_{1}^{U} ,a_{2}^{U} ,a_{3}^{U} ;w^{U} ),(a_{1}^{L} ,a_{2}^{L} ,a_{3}^{L} ;w^{L} ))$, as shown in Fig. 1.

Fig. 1

An example of the triangle IT2FN

Suppose that $\tilde{\tilde{A}}_{1} = (\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} ) = ((a_{11}^{U} ,a_{12}^{U} ,a_{13}^{U} ;w_{1}^{U} ),(a_{11}^{L} ,a_{12}^{L} ,a_{13}^{L} ;w_{1}^{L} ))$ and $\tilde{\tilde{A}}_{2} = (\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} ) = ((a_{21}^{U} ,a_{22}^{U} ,a_{23}^{U} ;w_{2}^{U} ),(a_{21}^{L} ,a_{22}^{L} ,a_{23}^{L} ;w_{2}^{L} ))$ are two triangular IT2FSs. The operational laws are as following (Chen et al. 2012).

• 1. $\begin{gathered} \tilde{\tilde{A}}_{1} + \tilde{\tilde{A}}_{2} = (\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} ) \oplus (\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} ) \hfill \\ = ((a_{11}^{U} + a_{21}^{U} ,a_{12}^{U} + a_{22}^{U} ,a_{13}^{U} + a_{23}^{U} ;\min (w_{1}^{U} ,w_{2}^{U} )),(a_{11}^{L} + a_{21}^{L} ,a_{12}^{L} + a_{22}^{L} ,a_{13}^{L} + a_{23}^{L} ;\min (w_{1}^{L} ,w_{2}^{L} ))) \hfill \\ \end{gathered}$,

• 2. $\begin{gathered} \tilde{\tilde{A}}_{1} \otimes \tilde{\tilde{A}}_{2} = (\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} ) \otimes (\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} ) \hfill \\ = ((a_{11}^{U} \times a_{21}^{U} ,a_{12}^{U} \times a_{22}^{U} ,a_{13}^{U} \times a_{23}^{U} ;\min (w_{1}^{U} ,w_{2}^{U} )),(a_{11}^{L} \times a_{21}^{L} ,a_{12}^{L} \times a_{22}^{L} ,a_{13}^{L} \times a_{23}^{L} ;\min (w_{1}^{L} ,w_{2}^{L} ))) \hfill \\ \end{gathered}$,

• 3. $k\tilde{\tilde{A}}_{1} = k(\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} ) = ((k \times a_{11}^{U} ,k \times a_{12}^{U} ,k \times a_{13}^{U} ;w_{1}^{U} ),(k \times a_{11}^{L} ,k \times a_{12}^{L} ,k \times a_{13}^{L} ;w_{1}^{L} ))$, k > 0.

2.2 Fuzzy TOPSIS method based on α-level sets

TOPSIS is a sort method for approaching the ideal solution, which was first developed by Hwang and Yoon. The main idea is to establish the initial decision matrix firstly, then find out the positive ideal solution (PIS) and the negative ideal solution (NIS) in the limited alternatives, calculate the distance between each evaluation object and PIS or NIS separately, and obtain the relative closeness between each evaluation object and the PIS, and finally rank them by the relative closeness. In recent years, the TOPSIS method provides a suitable tool to handle with MCDM problem and has been widely used (Lourenzutti and Krohling 2016; Ishizaka and Siraj 2018; Zhang et al. 2019).

However, due to the complex and changeable decision-making environment, different -makers may have different experiences, knowledge, and preferences for the same problem. It is difficult to quantify some criteria that reflect the impact of society and the environment. For the above-mentioned reasons, the information of criteria values is often incomplete, and it is difficult to describe the quantitative criteria with a crisp number. With the extension of fuzzy set theory (Zadeh 1965; Liang and Mendel 2000), various forms of fuzzy numbers are often put forward to represent the values of criteria in the MCDM problem. In the past decade, a lot of research has extended the classical TOPSIS method into the fuzzy environment and put forward many fuzzy TOPSIS methods (Amiri 2010; Büyüközkan and Çifçi 2012).

According to Zedeh’s decomposition theorem (Zimmermann 2011), if $\tilde{A}$ is a fuzzy set in the universe U, $\tilde{A}_{\alpha }$ is $\alpha$-level set of A, $\alpha \in [0,1]$, then

$$\tilde{A} = \bigcup\limits_{\alpha \in [0,1]} {\alpha A_{\alpha } }$$

(5)

The steps of the fuzzy TOPSIS method based on α-level sets are as follows.

• Step 1: construct the fuzzy decision matrix

Suppose that a MCDM problem has n alternatives, $B_{1} ,....,B_{n}$ and m criteria, $E_{1} ,...,E_{m}$. The decision matrix $\tilde{Z}_{ij} = (\tilde{z}_{ij} )_{n \times m}$ and the fuzzy weight $\tilde{S} = [\tilde{s}_{1} ,\tilde{s}_{2} ,...,\tilde{s}_{n} ]$ are shown as:

$$\tilde{Z}_{ij} = \left[ \begin{gathered} \tilde{z}_{11} \, \tilde{z}_{12} ... \, \tilde{z}_{1m} \hfill \\ \tilde{z}_{21} \, \tilde{z}_{22} ... \, \tilde{z}_{2m} \hfill \\ ... \, ... \, ... \, ... \hfill \\ \tilde{z}_{n1} \, \tilde{z}_{n2} ... \, \tilde{z}_{nm} \hfill \\ \end{gathered} \right]$$

(6)

$$\tilde{S} = [\tilde{s}_{1} ,\tilde{s}_{2} ,...,\tilde{s}_{n} ],\begin{array}{*{20}c} {} & {} \\ \end{array} \sum\limits_{j = 1}^{m} {\tilde{s}_{j} = 1}$$

(7)

• Step 2: normalize the fuzzy decision matrix.

If $\tilde{y}_{ij} = (a_{ij} ,b_{ij} ,d_{ij} )(i = 1,...n,j = 1,...,m)$ is a triangular fuzzy number, the standardization process is accomplished by the following formula

$$\tilde{t}_{ij} = \left( {\frac{{a_{ij} }}{{d_{j}^{*} }},\frac{{b_{ij} }}{{d_{j}^{*} }},\frac{{d_{ij} }}{{d_{j}^{*} }}} \right),{{ i = 1,}}...{{n; j}} \in \Omega_{b} ,\quad d_{j}^{*} = \mathop {\max }\limits_{i} d_{ij} {{ j}} \in \Omega_{b}$$

(8)

$$\tilde{t}_{ij} = \left( {\frac{{a_{j}^{ - } }}{{d_{ij} }},\frac{{a_{j}^{ - } }}{{b_{ij} }},\frac{{a_{j}^{ - } }}{{a_{ij} }}} \right),{{ i = 1,}}...{{n; j}} \in \Omega_{c} \quad a_{j}^{ - } = \mathop {\min }\limits_{i} a_{ij} {{ j}} \in \Omega_{c}$$

(9)

• Step 3: identify the PIS and the NIS.

The normalized value $t_{ij}$ is between 0 and 1, and the PIS and NIS are defined as follows.

$$O^{ + } = \{ z_{1}^{ + } ,...,z_{m}^{ + } \} \, = \{ (\mathop {\max }\limits_{j} c_{ij} |j \in \Omega_{b} ),(\mathop {\min }\limits_{j} a_{ij} |j \in \Omega_{c} )\}$$

(10)

$$O^{ - } = \{ z_{1}^{ - } ,...,z_{m}^{ - } \} \, = \{ (\mathop {{minx}}\limits_{j} c_{ij} |j \in \Omega_{b} ),(\mathop {\max }\limits_{j} a_{ij} |j \in \Omega_{c} )\}$$

(11)

• Step 4: calculate the relative closeness of each alternative.

$(t_{ij} )_{\alpha } = [(t_{ij} )_{\alpha }^{L} ,(t_{ij} )_{\alpha }^{U} ]$, $(s_{j} )_{\alpha } = [(s_{j} )_{\alpha }^{L} ,(s_{j} )_{\alpha }^{U} ]$ are α-level sets of $t_{ij}$,$s_{j}$, the formula for calculating the relative closeness of the alternatives(Wang and Elhag 2006) are as follows.

$$\begin{gathered} (RC_{i} )_{\alpha }^{L} = Min\frac{{\sqrt {\sum\limits_{j = 1}^{m} {(s_{j} ((t_{ij} )_{\alpha }^{L} - t_{j}^{ + } ))^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{m} {(s_{j} ((t_{ij} )_{\alpha }^{L} - t_{j}^{ - } ))^{2} } } + \sqrt {\sum\limits_{j = 1}^{m} {(s_{j} ((t_{ij} )_{\alpha }^{L} - t_{j}^{ + } ))^{2} } } }}{{, i = 1,}}...{{,n}} \hfill \\ \text{s}\text{.t}\text{.}\quad (s_{j} )_{\alpha }^{L} \le s_{j} \le (s_{j} )_{\alpha }^{U} ,{{ j = 1,}}...{{,m}} \hfill \\ (t_{ij} )_{\alpha }^{L} \le t_{ij} \le (t_{ij} )_{\alpha }^{U} ,{{ j = 1,}}...{{,m}} \hfill \\ \end{gathered}$$

(12)

$$\begin{gathered} (RC_{i} )_{\alpha }^{U} = Max\frac{{\sqrt {\sum\limits_{j = 1}^{m} {(s_{j} ((t_{ij} )_{\alpha }^{U} - t_{j}^{ + } ))^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{m} {(s_{j} ((t_{ij} )_{\alpha }^{U} - t_{j}^{ - } ))^{2} } } + \sqrt {\sum\limits_{j = 1}^{m} {(s_{j} ((t_{ij} )_{\alpha }^{U} - t_{j}^{ + } ))^{2} } } }}{{ i = 1,}}...{{n}} \hfill \\ \text{s}\text{.t}\text{.}\quad (s_{j} )_{\alpha }^{L} \le s_{j} \le (s_{j} )_{\alpha }^{U} ,{{ j = 1,}}...{{,m}} \hfill \\ (t_{ij} )_{\alpha }^{L} \le t_{ij} \le (t_{ij} )_{\alpha }^{U} ,{{ j = 1,}}...{{,m}} \hfill \\ \end{gathered}$$

(13)

According to the extension principle (Zimmermann 2011), the relative closeness $RC_{i}$ of each alternative can be defined as

$$RC_{i} = \mathop \cup \limits_{\alpha } \alpha [(RC_{i} )_{\alpha }^{L} ,(RC_{i} )_{\alpha }^{U} ]{,0 < }\alpha \le 1$$

(14)

• Step 5: Defuzzify each alternative's fuzzy relative closeness and rank the alternative by sorting the $RC_{i}$ value.

The defuzzified value of $RC_{i}$ is defined as

$$RC_{i}^{*} = \frac{1}{N}\sum\limits_{j = 1}^{N} {\left( {\frac{{(RC_{i}^{L} )_{{\alpha_{j} }} + (RC_{i}^{L} )_{{\alpha_{j} }} }}{2}} \right)} ,\quad i = 1,...,n$$

(15)

3 IT2-FTOPSIS approach with utility function for subway station risk evaluation

In this section, we develop an IT2-FTOPSIS approach with a utility function for subway station risk evaluation, and the flowchart of the developed IT2-FTOPSIS approach is shown in Fig. 2. The main idea of the approach is as follows. Firstly, construct the subway station risk evaluation matrix. Secondly, calculate the utility risk value of each risk criterion of each subway station and normalize the risk evaluation matrix. Thirdly, identify the PIS and NIS from the normalized risk evaluation matrix. Fourthly, obtain each subway station’s relative closeness by calculating the distance between the subway station and the PIS or NIS. Finally, calculate the risk value of each subway station by defuzzifying the relative closeness. The IT2-FTOPSIS approach with a utility function for subway station risk evaluation is presented as follows.

Fig. 2

Flowchart of the developed IT2-FTOPSIS approach for subway station risk evaluation

• Step 1: Construct the subway station risk evaluation matrix $\tilde{\tilde{Y}} = \{ \tilde{\tilde{y}}_{ij} \}_{n \times m}$.

Suppose that the subway station risk evaluation approach has n subway stations at the same time or n periods in the same subway station, and m criteria. The subway station risk evaluation matrix $\tilde{\tilde{Y}} = \{ \tilde{\tilde{y}}_{ij} \}_{n \times m} ,i = 1,2,...,m;j = 1,2,...,n$ can be represented by

$$\tilde{\tilde{Y}} = \left[ {\begin{array}{*{20}c} {\tilde{\tilde{y}}_{11} } & {\tilde{\tilde{y}}_{12} } & {...} & {\tilde{\tilde{y}}_{1m} } \\ {\tilde{\tilde{y}}_{21} } & {\tilde{\tilde{y}}_{22} } & {...} & {\tilde{\tilde{y}}_{2m} } \\ {...} & {...} & {...} & {...} \\ {\tilde{\tilde{y}}_{n1} } & {\tilde{\tilde{y}}_{n2} } & {...} & {\tilde{\tilde{y}}_{nm} } \\ \end{array} } \right]$$

(16)

In the subway station risk evaluation approach, the risk evaluation indexes utilize the index system and calculating methods of risk value of each index by Qin et al. (2015) and are shown in Fig. 3. The risk evaluation index system is established from people, equipment, environment, management and accident. Passengers are the most important and flexible factor that affects the risk, and the indexes I₁–I₆ are the capacity of some important conflict points, such as auto fare collection (AFC). The indexes I₇–I₁₂ are considered from several important types of equipment. The environment significantly affect the operational safety of the subway station; the indexes select from temperature, humidity, PM2.5, PM10, and CO₂. Meanwhile, safety management and emergency evacuation capacity are important risk factors. Based on operational experience, the occurrence of accidents is somewhat influenced by historical accidents. Thus, we take historical accidents into account. The risk value of each index can be expressed as a crisp number.

Fig. 3

The framework of subway station risk evaluation by Qin et al. (2015)

• Step 2: Calculate the risk utility value $\tilde{\tilde{x}}_{ij}^{{}}$ of each index and ensure the weight $\tilde{\tilde{\omega }}_{i}$ of the indexes by representing by IT2FSs.

In the process of subway station risk evaluation, there has different risk utility value in different periods of the same subway station or in different subway stations under the same period. For example, elevator failure has different risk utility values to the operational safety of the subway station in a different period or different space. At the morning peak hours, the elevator failure has more serious on the safety of the subway station. And the elevator failure happens in the subway stations with different node degrees. It will cause somewhat impacts on operational safety. Therefore, the risk evaluation matrix with utility function is presented as

$$\tilde{\tilde{X}} = \mu \left( {\tilde{\tilde{Y}}} \right) = \left[ {\begin{array}{*{20}c} {\tilde{\tilde{x}}_{11}^{{}} } & {\tilde{\tilde{x}}_{12}^{{}} } & {...} & {\tilde{\tilde{x}}_{1m}^{{}} } \\ {\tilde{\tilde{x}}_{21}^{{}} } & {\tilde{\tilde{x}}_{22}^{{}} } & {...} & {\tilde{\tilde{x}}_{2m}^{{}} } \\ {...} & {...} & {...} & {...} \\ {\tilde{\tilde{x}}_{n1}^{{}} } & {\tilde{\tilde{x}}_{n2}^{{}} } & \ldots & {\tilde{\tilde{x}}_{nm}^{{}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{\tilde{y}}_{11}^{f\left( \beta \right)} } & {\tilde{\tilde{y}}_{12}^{f\left( \beta \right)} } & {...} & {\tilde{\tilde{y}}_{1m}^{f\left( \beta \right)} } \\ {\tilde{\tilde{y}}_{21}^{f\left( \beta \right)} } & {\tilde{\tilde{y}}_{22}^{f\left( \beta \right)} } & {...} & {\tilde{\tilde{y}}_{2m}^{f\left( \beta \right)} } \\ {...} & {...} & {...} & {...} \\ {\tilde{\tilde{y}}_{n1}^{f\left( \beta \right)} } & {\tilde{\tilde{y}}_{n2}^{f\left( \beta \right)} } & \ldots & {\tilde{\tilde{y}}_{nm}^{f\left( \beta \right)} } \\ \end{array} } \right] = \left( {\tilde{\tilde{Y}}} \right)^{f\left( \beta \right)}$$

(17)

where $f\left( \beta \right)$ is the risk utility parameter.

And the weights of the indexes are

$$\tilde{\tilde{W}} = [\tilde{\tilde{\omega }}_{1} ,\tilde{\tilde{\omega }}_{2} ,...,\tilde{\tilde{\omega }}_{m} ]^{T}$$

(18)

where, i is the i-th period in the same subway station or i-th subway station in the same period, j is the j-th index, $\tilde{\tilde{W}}$ is the weight of the risk indexes.

• Step 3: Normalize the subway station risk evaluation matrix $\tilde{\tilde{X}}$.

The normalized risk evaluation matrix method is shown as Eqs. (19, 20).

$$\begin{gathered} \tilde{\tilde{x}}_{ij} = ((\frac{{a_{ij}^{L} }}{{c_{j}^{*} }},\frac{{b_{ij}^{L} }}{{c_{j}^{*} }},\frac{{c_{ij}^{L} }}{{c_{j}^{*} }}),(\frac{{a_{ij}^{U} }}{{c_{j}^{*} }},\frac{{b_{ij}^{U} }}{{c_{j}^{*} }},\frac{{c_{ij}^{U} }}{{c_{j}^{*} }})),i = 1,2,...,n,j \in \Omega_{c} \hfill \\ s.t.\begin{array}{*{20}c} {} & {} \\ \end{array} c_{j}^{*} = \mathop {\max }\limits_{i} c_{ij} ,j \in \Omega_{c} \hfill \\ \end{gathered}$$

(19)

$$\begin{gathered} \tilde{\tilde{x}}_{ij} = ((\frac{{\overline{a}_{j} }}{{c_{ij}^{U} }},\frac{{\overline{a}_{j} }}{{b_{ij}^{U} }},\frac{{\overline{a}_{j} }}{{a_{ij}^{U} }}),(\frac{{\overline{a}_{j} }}{{c_{ij}^{L} }},\frac{{\overline{a}_{j} }}{{b_{ij}^{L} }},\frac{{\overline{a}_{j} }}{{a_{ij}^{L} }})),i = 1,2,...,n,j \in \Omega_{c} \hfill \\ s.t.\begin{array}{*{20}c} {} & {} \\ \end{array} \overline{a}_{j} = \mathop {\min }\limits_{i} a_{ij} ,j \in \Omega_{c} \hfill \\ \end{gathered}$$

(20)

• Step 4: Identify the PIS A⁺ and NIS A⁻ from the risk evaluation matrix.

The PIS and NIS can be defined as

$$A^{ + } = \{ x_{1}^{ + } ,...,x_{m}^{ + } \} = \{ (\mathop {\max }\limits_{j} c_{ij} \left| {j \in \Omega_{c} } \right.),(\mathop {\min }\limits_{j} a_{ij} \left| {j \in \Omega_{c} } \right.)\}$$

(21)

$$A^{ - } = \{ x_{1}^{ - } ,...,x_{m}^{ - } \} = \{ (\mathop {\min }\limits_{j} a_{ij} \left| {j \in \Omega_{b} } \right.),(\mathop {\max }\limits_{j} c_{ij} \left| {j \in \Omega_{b} } \right.)\}$$

(22)

• Step 5: Set different α levels, and calculate the corresponding α-level sets of $\tilde{\tilde{x}}_{ij} ,i = 1,2, \ldots ,n;j = 1,2, \ldots ,m$.

• Step 6: Calculate the fuzzy relative closeness RC_i by Eqs. (23)–(26) for each α level. The UMF and the LMF of the risk value represented by IT2FSs are defined as follows.

$$\begin{gathered} ((RC_{i}^{U} )^{U} )_{\alpha } = \max \frac{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{U} )_{\alpha } - x_{j}^{ + } ))^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{U} )_{\alpha } - x_{j}^{ - } ))^{2} } } + \sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} (((x_{ij}^{U} )_{\alpha } - x_{j}^{ + } )))^{2} } } }} \hfill \\ s.t.\begin{array}{*{20}c} {} & {} \\ \end{array} ((w_{j} )^{U} )_{\alpha }^{L} \le \omega_{j} \le ((w_{j} )^{U} )_{\alpha }^{U} ,j = 1,2,...,m \hfill \\ \end{gathered}$$

(23)

$$\begin{gathered} ((RC_{i}^{U} )^{L} )_{\alpha } = \min \frac{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{L} )_{\alpha } - x_{j}^{ + } ))^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{L} )_{\alpha } - x_{j}^{ - } ))^{2} } } + \sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} (((x_{ij}^{L} )_{\alpha } - x_{j}^{ + } )))^{2} } } }} \hfill \\ s.t.\begin{array}{*{20}c} {} & {} \\ \end{array} ((w_{j} )^{U} )_{\alpha }^{L} \le \omega_{j} \le ((w_{j} )^{U} )_{\alpha }^{U} ,j = 1,2,...,m \hfill \\ \end{gathered}$$

(24)

$$\begin{gathered} ((RC_{i}^{L} )^{U} )_{\alpha } = \max \frac{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{U} )_{\alpha } - x_{j}^{ + } ))^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{U} )_{\alpha } - x_{j}^{ - } ))^{2} } } + \sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} (((x_{ij}^{U} )_{\alpha } - x_{j}^{ + } )))^{2} } } }} \hfill \\ s.t.\begin{array}{*{20}c} {} & {} \\ \end{array} ((w_{j} )^{L} )_{\alpha }^{L} \le \omega_{j} \le ((w_{j} )^{L} )_{\alpha }^{U} ,j = 1,2,...,m \hfill \\ \end{gathered}$$

(25)

$$\begin{gathered} ((RC_{i}^{L} )^{L} )_{\alpha } = \min \frac{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{L} )_{\alpha } - x_{j}^{ + } ))^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} ((x_{ij}^{L} )_{\alpha } - x_{j}^{ - } ))^{2} } } + \sqrt {\sum\limits_{j = 1}^{m} {(\omega_{j} (((x_{ij}^{L} )_{\alpha } - x_{j}^{ + } )))^{2} } } }} \hfill \\ s.t.\begin{array}{*{20}c} {} & {} \\ \end{array} ((w_{j} )^{L} )_{\alpha }^{L} \le \omega_{j} \le ((w_{j} )^{L} )_{\alpha }^{U} ,j = 1,2,...,m \hfill \\ \end{gathered}$$

(26)

where $[(w_{j} )^{U} ]_{\alpha } = [((w_{j} )^{U} )_{\alpha }^{L} ,((w_{j} )^{U} )_{\alpha }^{U} ]$, $[(w_{j} )^{L} ]_{\alpha } = [((w_{j} )^{L} )_{\alpha }^{L} ,((w_{j} )^{L} )_{\alpha }^{U} ]$ are the UMF and LMF of the weight vector $\tilde{\tilde{W}}$.

• Step 7: Defuzzify the relative closeness $RC_{i}^{*}$ of each subway station risk value.

The risk value calculated by Step 6 is an interval, and the interval needs to be defuzzified according to the following formula.

$$RC_{i}^{*} = \frac{1}{N}\sum\limits_{k = 1}^{N} {(\frac{{(RC_{i}^{L} )_{{\alpha_{j} }} + (RC_{i}^{U} )_{{\alpha_{j} }} }}{2})} ,k = 1,2,...,N$$

(27)

where k represents the k-th level, and N is the total number of α levels.

• Step 8: Calculate the risk value of the subway station by defuzzifying the relative closeness and identify the risk state.

$RC_{i}^{*}$ is the risk value of the same station at different periods or the different stations at the same time. The larger the risk value, the greater the risk of the subway station. The risk state is divided into five levels, shown in Table 1.

Table 1 Risk rating of subway station (Qin et al. 2015)

4 Case study of subway station risk evaluation

4.1 Risk utility parameter of the subway station

Before the subway station risk evaluation, we firstly introduce risk utility parameter function of the subway station. Combined with the practical operation experience of subway station, the linear mapping relationship between time risk utility parameter and time or between space risk utility parameter and node degree is used for risk utility parameter function of the subway station.

4.1.1 Time risk utility parameter function

It is noted that the passenger flow at the station is different at different periods. On weekdays, there have a morning rush hour and an evening rush hour. At the weekend, most passengers travel between 9:00 and 20:00. Combined with the changing characteristics of passenger flow, the linear mapping between time and time risk utility parameter is shown in Fig. 4. At rush hours of weekday, the time risk utility parameter value f (β) is [0.8, 1], and at flat hump period, the time risk utility parameter value f (β) is [1, 1.2]. At 9:00–20:00 of weekend, f (β) is [0.8, 1.0], and at other times, f (β) is [1.0, 1.2].

Fig. 4

The time utility function of the subway station risk evaluation

4.1.2 Space risk utility parameter function

It is obvious that different stations have different importance in the subway network. The important transfer stations have an important impact on the operation safety of the whole subway network. Considering the node degree of the subway station, the linear mapping between node degree and space risk utility parameter is shown in Fig. 5. The greater the node degree of the subway station, the more important it is.

Fig. 5

The space utility function of the subway station risk evaluation

4.2 Process of subway station risk evaluation

The subway station’s risk state is evaluated by passenger flow, equipment, environment, management, and accident. The evaluation system of the subway station’s risk state is established and shown in Fig. 3. We take Beijing Subway as examples to discuss the performance of the developed approach.

Example 1

Different subway stations at the same time.

Fuchengmen Station, Chegongzhuang Station, and Xizhimen Station of Beijing Subway Line 2 are selected as the risk evaluation objects. According to the calculation method of node degree (Meng et al. 2014), the node degrees of the three stations are 2, 4, 5, and the corresponding risk utility parameters of the three stations are 1.0, 0.8, and 0.7 by the mapping relationship shown in Fig. 5.

Take the practical risk values of Fuchengmen Station at 18:00 as an example to explain the risk evaluation process.

• Step 1: Construct the risk evaluation matrix of Fuchengmen Station. Table 2 shows the original risk values of each index calculated by Qin et al. (2015).

• Step 2: Calculate the risk utility of the risk evaluation and identify the weights of the indexes.

Table 2 The calculated values of each index during 18:00 at Fuchengmen station

The space risk utility parameter of Fuchengmen Station is 1.0, then the risk utility values of each index are equal to the original risk values shown in Table 2. And the linguistic variables of the weights of subway station risk indexes and their corresponding IT2FNs are shown in Table 3.

Table 3 Linguistic variables of weights of the indexes and their corresponding IT2FNs (Mendel and Wu 2010)

The passenger flow risk, including six sub-indexes (I₁–I₆) is selected as an example to calculate the relative closeness of passenger flow risk. The relative importance information of the indexes is given by three decision-makers: DM1, DM2, and DM3, and $\tilde{w}_{j} = (\tilde{w}_{j}^{1} + \tilde{w}_{j}^{2} + \tilde{w}_{j}^{3} )/3$ is used to aggregate the three decision-makes’ information on the weights, as shown in Table 4.

Table 4 The normalized relative importance weights of passenger flow index

• Step 3: Normalize the Fuchengmen station risk evaluation matrix. Because the maximum risk value is 1, there is no need to normalize the risk matrix.

• Step 4: Identify the PIS and NIS from the risk evaluation matrix. According to Eqs. (21, 22), the PIS of the passenger flow risk is $A^{ + } = \{ 0,...,0\}$, and the NIS is $A^{ - } = \{ 1,...,1\}$.

• Step 5: Set different α levels, and calculate the corresponding α-level sets of $\tilde{\tilde{x}}_{ij}$. To make the fuzzy relative closeness of each subway station more accurate, we set up 11 α-level sets, $\alpha = 0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9{\text{ and 1}}{.0}$.

• Step 6: Calculate the fuzzy relative closeness by Eqs. (23)–(26) for each α level. The calculated relative closeness of the passenger flow index is shown in Fig. 6.

Fig. 6

The relativeness closeness calculation process of Fuchengmen Station

Similarly, the relative closeness of equipment (B₂), environment (B₃), management (B₄), and accident (B₅) are calculated respectively and shown in Figs. 5e and 6b.

And the risk value of Fuchengmen Station consists of the relative closeness of the five indexes (B₁–B₅). The relative importance weights of B₁–B₅ are shown in Table 5. The risk value of Fuchengmen Station represented by the relative closeness is shown in Fig. 6f.

Table 5 The relative importance weights of the five indexes (B₁–B₅)

• Step 7: Defuzzify the relative closeness of Fuchengmen Station risk value. The defuzzified risk value of Fuchengmen Station is 0.3506 by Eq. (27).

• Step 8: Identify the risk state of Fuchengmen Station, the risk state is Level 4 (safe).

Similarly, the original risk value of Xizhimen Station and Chegongzhuang Station are in Table 6, and the relative closeness in different α-level sets at the same time is calculated as shown in Table 7 and Fig. 7. In the evening rush hour, the passenger flow ranking: Xizhimen Station > Chegongzhuang Station > Fuchengmen Station. With the increase of passenger flow, the overall risk of the metro station has enhanced. Therefore, the risk of Xizhimen Station is higher than the other two stations, and the risk state is unsafe. At this time, the managers of Xizhimen Station need to take measures to reduce the risk, such as restricting passenger flow and troubleshooting equipment safety hazards.

Table 6 The original risk values of each index at 18:00 in Chegongogzhuang Station and Xizhimen Station

Table 7 The fuzzy relative closeness of different subway stations in different α-level sets

Fig. 7

The fuzzy relative closeness of three stations at 18:00

Compared with the results of the method by Qin et al. (2015), the risk values of Xizhimen Station and Chegongzhuang Station are higher, and the risk evaluation results are shown in Fig. 8. Although the three subway stations all belong to Beijing Subway Line 2, the space risk utility is different because of their different roles and positions in the whole subway network. Xizhimen Station is connected with Line 2, Line 4, Line 13, and Beijing North Railway Station. Obviously, it plays an extremely important role in the whole subway network. Once Xizhimen Station has an accident, it will have a greater impact on the whole Subway Line 2. Therefore, the space risk utility value of Xizhimen Station may be higher than the original risk information. Chegongzhuang Station is a transfer station for Line 2 and Line 6. And Fuchengmen Station is a common station on Line 2. Suppose that the risk values of entrance AFC in the three stations are 0.5, then the risk utility values are (0.5)^0.7 = 0.62, (0.5)^0.8 = 0.57, (0.5)^1.0 = 0.5. By adding the space risk utility function, the risk utility values accurately reflect the risk state differences of different subway stations at the same time. In other words, the accident consequence of the same accident in Xizhimen Station and the input of resources needed to resume normal operation are often greater than those of the other two stations. From the perspective of complex network theory, the node degrees of the three stations are 5, 4, and 2, respectively. And the corresponding risk utility parameters of the three stations are 1.0, 0.8 and 0.7. Then, the risk value ranking: Xizhimen Station > Chegongzhuang Station > Fuchengmen Station. Therefore, the introduction of spatial risk utility can improve the accuracy of subway station risk evaluation.

Fig. 8

The risk values of the three stations in the same period by the two methods

Example 2

The same subway station at different times.

Compared with the method by Qin et al. (2015), we select Chegongzhuang Station as the object of risk evaluation. Three different periods of operation data are carried out to evaluate the risk state, as shown in Table 8. According to the time risk utility parameter in Fig. 4, the corresponding time risk parameters corresponding to 8:00, 9:00, and 10:00 can be 0.8, 1.0, and 1.05, respectively.

Table 8 The original risk values of each index at different times

Similarly, the relative closeness of Chegongzhuang Station in different α-level sets at three different times are calculated by the developed IT2-FTOPSIS approach. The risk evaluation results are shown in Table 9 and Fig. 9. At 8:00, the morning rush hour, there are a lot of passengers in Chegongzhuang Station, and the risk value is larger than the other times. With the passing of the early peak, the station risk is reduced. Therefore, the risk ranking: 8:00 > 9:00 > 10:00.

Table 9 The fuzzy relative closeness of different times in different α-level sets

Fig. 9

The fuzzy relative closeness of different times of Chegongzhuang station

Figure 10 shows the differences between the developed IT2-FTOPSIS method and the method in Qin et al. (2015). We can see that there is no significant difference in the risk values between the two methods at 9:00, but there are some significant differences in the risk values at 8:00 and 10:00. Combined with the operation state of the subway station, it is found that 8:00 is the morning rush period of the subway station. The sudden failure of the power supply system in Line 2 causes the train to be delayed, and a large number of passengers are stranded on the platform, which brings tremendous pressure to the equipment and management of the station. Considering the time factor, once an accident occurs in the subway station at 8:00, it will have a greater impact than other times. Therefore, the actual risk caused by the event is greater than the risk calculated by the previous method, and the risk states by the new method and the previous method are very unsafe (0.81, Level 1) and unsafe (0.79, Level 2). At 10:00, a series of measures have been taken to deal with the accident, the power supply equipment has been restored to normal, then the operation of Chegongzhuang station has been restored to normal, the passenger flow has also dropped significantly in the morning rush hour, and the risk sources affecting the safety of the subway station are in a good state, the actual risk value is less than the risk value calculated by the previous method. The risk states by the new method and the previous method are safe (0.39, Level 4) and medium (0.41, Level 3). In summary, the introduction of the time risk utility function can more accurately reflect the subway station's safety state.

Fig. 10

The risk values of Chegongzhuang station at different times by the two methods

4.3 Discussion

The difference between the subway station’s risk utility values from the developed IT2-FTOPSIS method and the risk values from the previous methods is low. The main reasons are as follows. Firstly, the risk evaluation process involves 22 indexes. Changes in individual index values hardly change the safety of the subway station system. For example, the number of passengers at entrance AFC suddenly increase and hardly change the subway station's overall safety. Secondly, the risk utility values calculated by the time risk utility parameter function or space risk utility parameter function are slightly different from the original risk values.

However, the risk states from the developed IT2-FTOPSIS method and the previous methods are different in some cases. For example, the risk values of Chegongzhuang Station calculated by the two methods are 0.79 and 0.81 at 8 o’clock, respectively. The management measures of subway stations are different when the subway stations have different risk states. The station managers will use flow restrictions to reduce risk when the station is very unsafe (Risk value is 0.81). Meanwhile, the station managers keep track of the subway station’s safety operation when the station’s risk is unsafe (Risk value is 0.79). Thus, the developed IT2-FTOPSIS method is closer to the actual operation of the subway station according to the station mangers’ experience.

Overall, the developed IT2-FTOPSIS method evaluating the subway station’s risk state is more reasonable than the previous methods. The developed IT2-FTOPSIS method considers the risk utility function, which is closer to the practical experience. The subway station has different operation characteristics in a different time or space, and the same event may have different risk utility values. The same event occurring in the morning or evening peak hours has a more serious effect on subway station operational safety than during other times. Namely, the event may have a different risk utility value in the morning or evening peak hours or at other times. Similarly, the same event occurring in different subway stations may have a different utility value on the subway station’s safety.

5 Conclusions

In this study, a new subway station operational risk evaluation framework is proposed by using an IT2-FTOPSIS approach with a utility function. The risk factors of subway stations are assessed by crisp numbers, and IT2FNs represent the weights of each risk factor. Furthermore, the introduction of time risk utility function and space risk utility function provides a useful tool to improve the risk accuracy of the subway station and reflect the risk state more objectively. Besides, the IT2-FTOPSIS approach based on α-level sets is used to solve the subway station operational risk evaluation, which improves the practicality and flexibility of the risk evaluation approach. Finally, an example of Beijing Subway is selected to illustrate the developed risk evaluation approach’s performance. The results show that the developed IT2-FTOPSIS approach with time risk utility function or space risk utility function can improve the accuracy of the risk evaluation and reflect the subway station's operational risk state more objectively than the previous method.

However, many aspects need to be further improved. Firstly, considering excluding the influence of the subway line on the risk evaluation result, the three subway stations are selected to explain the developed IT2-FTOPSIS method’s effectiveness. We will discuss the heterogeneous subway stations’ risk evaluation that belongs to the different subway lines. Secondly, risk thresholds are determined by expert subway station operation managers. Three-way decisions provide a useful tool to calculate the risk thresholds scientifically and assess subway stations’ risk status (Liang et al. 2018; Gao et al. 2020). We will combine the IT2-FTOPSIS with three-way decisions to improve the risk evaluation framework of the subway station.