1 Introduction

Clustering is a key machine learning and data mining task used for extracting useful patterns in diverse fields. Over the period of decades, various clustering techniques have been proposed [1]. Connectivity-based clustering, centroid-based clustering, distribution-based clustering, and density-based clustering are a few of the most commonly used approaches for cluster analysis. Clustering has many real-world applications. A few cases in point are extracting coherent groups from a protein–protein interaction network, wireless sensor network with uncertain edges, and social networking. Depending on the problem domain, cluster analysis is also focused on finding non-spherical clusters. Traditional partitioning-based clustering methods, like k-means and k-medoids fail to find non-spherical clusters [2]. Graph-based approaches have shown promising results for this task. Generally, the goal of clustering is to extract strongly connected, coherent groups from the underlying data. Graphs provide a convenient representation of items having a direct or indirect relation. Where related items in a graph are represented by an edge between nodes or a series of edges among scattered nodes. Spanning trees represent a structure that completely covers the graph having a path to every node. Minimum spanning trees (MSTs) are similar to the spanning tree, however, the overall sum of edges’ weight in the MST is minimum. Two nodes closer to each other in a graph will have lesser value of the edge weight connecting them as compared to the nodes placed far apart. However, a different interpretation of an edge weight is also possible, specific to the problem domain. Keeping the distance-based interpretation in view, an MST thus represents a closely connected group of nodes that can be interpreted as a cluster. When utilizing MSTs for cluster formation, using a complete MST to represent a single cluster is not an appropriate concept [3]. Reason being the inclusion of all nodes in the MST for a connected graph, thus forming a single cluster. Techniques employing MSTs for clustering address this concern by restricting growth of an MST for a specific threshold weight. This enables to construct coherent groups that are strongly connected. These MST-based extracted groups can further be optimized by rearranging their connections within the tree. However, this rearrangement needs to be done in line with the actual connections in the graph. It needs to be done gradually and evaluated for improvement in cluster quality before accepting it. This is an area where evolutionary computing can be utilized. Genetic algorithm and genetic programming can be controlled to converge steadily using mutation and crossover rates. However, evolution strategy (ES) seems to be a better choice here, where the reproduction operator of mutation is only used. An approach can be devised that extracts MST from a graph representing a cluster/pattern. Later, this MST can be optimized using ES-based approach. Since a graph may have multiple MSTs, these can become candidate solutions (population) for the ES. Previously, ES-based approaches for optimizing solutions in the domain of pattern recognition, independent learning, and bioinformatics have shown better results [4,5,6]. Clustering data using evolutionary algorithms has been studied before, however, most of the existing literature is either focused on similarity measures for data [7] or is an extension of existing algorithms for graphs [8]. There are a few existing methods that rely on the graph-based representation of the MST-based methodology for clustering [9], similar to the approach proposed in this work, but the amount of data lost in these methods is much higher [10, 11]. MST-based clustering is known for extracting irregular boundaries and outlier detection [12]. The MST-based clustering techniques have widely been used for efficient clustering. However, creating a single MST from a graph is not a good idea for efficient clustering. To overcome this limitation this work proposes to optimize MSTs for efficient clustering formations. The main idea is to extract multiple MSTs from a graph and then optimize the clustering formations using ES. This work utilizes (1+1)-ES for the optimization of MST-based extracted clusters. Details on the existing approaches for clustering data and how the proposed approach is different from the existing work are listed in Sect. 2.

This work focuses on optimizing the MST-based clustering using the ES. A graph may have many MSTs and by selecting any particular MST different clustering formation can be achieved. In order to obtain the optimal MST-based clustering (1+1)-ES is used in this work. Mutation is the only reproduction operator used in ES for the creation of new individuals by modification of the parent solutions. The ES population is generated using multiple MSTs of the same input graph. Later, these MST-based clustering formations are optimized using the objective function. The Davies–Bouldin Index (DBI) is used as a fitness function to evaluate the quality of clusters formed by each individual of the ES population. This proposal can be adopted as a generic framework, where DBI is one of the many possible fitness functions to guide this framework for better clustering formations. The reason for opting for DBI here is its wide utility in the clustering algorithms and much less complex than the computation of other cluster validity indices like Silhouettes coefficient (SC). Additionally, DBI being an internal validity index enables to assess the cluster quality in the absence of the ground truth. Thus, justifying the utility of DBI as an objective function here. The ES is executed for 1000 iterations having a population of ten individuals. Population size of ten individuals is opted due to the limited number of disjoint MSTs in a graph. There can be a case where the input graph having all edges with same weight has only a single MST for any root node selection. The proposed approach is evaluated using eleven benchmark datasets. Seven of these are based on microarray and the rest are taken from the UCI machine learning repository. This evaluation is performed using the external cluster validity measure adjusted rand index (ARI) and the internal cluster validation indices of DBI, Dunn index (DI) and SC. The results of the proposed approach are also compared with two state-of-the-art MST-based clustering algorithms, i.e., B-MST [13] and information theoretic MST-based (ITM) clustering [14], where the results suggest better performance of the proposed approach in the majority of the cases.

The rest of the paper is organized as follows: Sect. 2 presents the related work; Sect. 3 explains the proposed solution covering chromosome structure, reproduction operators and the fitness functions. Section 4 lists the detailed experiments, obtained results and discussion, including comparison with the state-of-the-art methods. Finally, Sect. 5 concludes the paper with a few of the future directions.

2 Related work

Clustering data and extracting useful patterns attracts interest from an assortment of fields. The MST-based clustering is specifically useful to identify clusters with irregular boundaries [15]. MSTs have been used to group data, in the fields of biology [16], pattern recognition [16], and image processing [17, 18]. There are many clustering algorithms available depending on the type of data and the problem statement at hand. Broadly, these can be divided into three categories; partitioning algorithms, hierarchical algorithms, and graph-based algorithms. This section covers the literature that presents clustering using MSTs and the evolutionary algorithms.

Zhong et al. [19] use the k-means approach for extracting MST-based clusters from a graph. Their approach utilizes divide-and-conquer scheme to produce an approximate MST having a time complexity of O (\(N^{1.5})\), where N is the number of nodes in a complete graph. The approach initially partitions the data into \(\sqrt{N}\) clusters using k-means algorithm and then these clusters are combined using an exact MST algorithm. The algorithm’s performance is evaluated using real-world and synthetic datasets. Internally, Prim’s algorithm is employed to extract the MSTs. The computational cost of their framework is dominated by the number of partitions initially created through k-means. However, this can be reduced by producing same sized partitions. The approach can also be applied to larger datasets. Perim et al. [13] report an MST-based heuristic called B-MST for clustering. An objective function consisting of tightness and separation index (TSI) is utilized to guide the algorithm. The method is reported to work on co-expression network topology. A local search procedure is developed for TSI minimization. The results are compared with established methods, such as, gene ontology and ARI. The authors report that B-MST produced superior results as compared to other complex clustering algorithms. Muller et al. [14] present an information-theoretic clustering algorithm. Information-theoretic grouping produces non-convex groups by expressing the numerical information in data through the likelihood density function. It is based on Euclidean minimum spanning tree, which is a fast and efficient optimization algorithm. The edge weights in the Euclidean minimum spanning tree represent the Euclidean distances between points. It is a non-parametric algorithm. The only known parameter is the number of classes. Zhou et al. [20] present an adaptive MST-based clustering algorithm (AMST). Their proposal is useful to extract irregular shaped clusters. It works by initially determining the optimal number of partitions in the region using a validity index. Afterwards the candidate clusters are evaluated for their significance. The validity index takes into consideration both compactness and isolation of data. This enables to select the best portion of an MST for clustering. Their approach is compared with static MST (SMST) and dynamic MST (DMST) clustering approaches. The AMST method extracts multiple clusters from the data as opposed to the single cluster formed by SMST and DMST. Simulations also support better accuracy of AMST in comparison with SMST and DMST. Zhou et al. [21] present two MST-based clustering algorithms using Euclidean distance. These include the k-constrained algorithm and unconstrained algorithm. The k-constrained algorithm extracts an MST from a graph and repeatedly removes edges from it based on a predefined constraint to form k clusters. Whereas, the unconstrained algorithm partitions the data into multiple clusters without describing the number of clusters. This is done by reducing the overall standard deviation of the edges in the Euclidean minimum spanning tree. The algorithm is named maximum standard deviation reduction algorithm (MSDR). It is evaluated using four benchmark datasets from the UCI repository and is compared with the scale-free minimum spanning tree clustering algorithm (SFMST) and k-means approach. Although the authors attempt to reduce the time complexity of their approach by using sorting in each node, however, it is still a performance bottleneck. The work in [9] is like the one presented in [21]. Wang et al. [22] introduce an MST-based clustering algorithm that detects clusters by removing inconsistent edges. Edges are considered inconsistent if their weight is larger than the average edge weight of the MST. The algorithm also removes outliers based on density. Density-based outliers are considered for object status, which is the ratio between local density of the object’s neighbors and the local densities of their neighboring objects. Density for each object is calculated by assigning an object a local outlier factor (LOF). LOF is compared with a threshold. If LOF is higher than the pre-specified threshold, it is considered an outlier. Several experiments are reported by comparing the solution against other clustering algorithms where the proposal performs better in identifying a relatively small number of density-based outliers during MST construction. Jothi et al. [23] propose two MST-based clustering algorithms. Most of the MST-based clustering algorithms first generate a complete graph from the input dataset and then perform clustering. This usually takes \(O(n^{2})\) time. The work in [23] aims to reduce the time for constructing MST. The execution time of their approach is \(O\left( {n^{\frac{3}{2}}} \right) .\) However, the MST is constructed with computational time of \(O\left( {n^{\frac{3}{2}}lgn} \right) .\) Experiments are used to perform evaluations using four artificial datasets. The results show that their algorithm reduces running time as well as gives efficient clustering. Yu et al. [25] explain the hierarchical structures in MST. They state that the already established algorithms and the proposed theories are inadequate for the identification and explanation of the clusters in trees. They devised a method which can first identify a cluster in a tree and subsequently grow into MSTs. The tree agglomerative hierarchical clustering (TAHC) method is introduced for the identification of the clusters in MSTs. The approach is efficient for the detection of the clusters in artificial trees. Normalized mutual information is utilized to quantify the similarity between the underlying real clusters and the clusters detected by the TAHC method. Their method is reported to have application in the identification of the clusters. Xu et al. [16] present a framework to represent multi-dimensional gene expression data as MST. The framework avoids the loss of information during the partitioning process. Their MST-based clustering approach utilizes three objective functions, namely, clustering through removing long MST edges, iterative clustering, and globally optimal clustering. The first objective function is to minimize the total edge distance of multiple trees by partitioning an MST in k subtrees. The second objective function optimizes the k-clustering by reducing the total distance between cluster centers and their data points. The third objective function partitions the MST into k trees by globally minimizing the distance between the data points and the cluster centers. This is done by grouping the data points around the best representative. The framework is tested using three datasets. Huang et al. [26] present a modified density-based minimum spanning tree (MST) clustering algorithm. Their algorithm has two phases; a density-based micro-cluster and MST-based tree formation. The initial clustering is performed using the density-based part that detects noise. In the next step the \(k-1\) longest edges of the MST are removed, which results in the generation of k clustering. The clustering results are optimized using an objective function. They further report that micro-MST-cluster algorithm performs better and exhibit good clustering effect. Their algorithm is reported to have various applications in domains with large datasets. Zhong et al. [27] present a hierarchical clustering method by splitting and merging an MST. They employ MST to guide the processes of merging and splitting. During the splitting process the higher degree MST vertices are selected as initial prototypes, while k-means is used to split the dataset. The merging process involves the filtration of the subgroup pairs. The neighboring pairs are considered for merging.

As evident from the above literature survey and to the best of our knowledge, the majority of work in MST-based clustering focuses on partitioning the MST for better cluster formations. The use of an evolutionary approach is missing that may produce promising results. This proposal focuses on using evolutionary algorithm for optimizing the MST-based clusters. The works closely related to this proposal are B-MST clustering [13] and Information Theoretic MST-based (ITM) clustering [14]. These are used for comparing the results of the current proposal. The key difference between the proposed work and previous approaches is that it is not based on any assumption about the underlying data. Like in case of ITM, absolute continuous data distribution is assumed. Additionally, in the previous works complex pointer-based data structures were utilized for storing the MSTs and the extracted clusters. This increased the processing time. However, in this case, the trees are avoided to permanently store clusters; instead, one-dimensional arrays are utilized. There is a limited utility of trees while extracting the MSTs, however its cost is minimized by keeping less population size.

3 Proposed solution

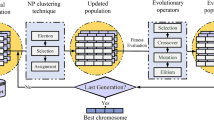
This proposal presents an MST-based clustering approach to extract optimized clustering using (1+1)-ES. Previously, work has been reported that indicate MST-based clustering as an efficient method for clustering because of its ability to extract arbitrary shaped clusters and outliers [9]. This work initially extracts multiple MSTs from a graph and later ES is used to optimize the clusters represented by these. The (1+1)-ES has benefits in solving optimization problems due to its simplicity and flexibility of strong response in varying circumstances [28]. The advantage of ES over genetic programming (GP) is its ability to avoid premature convergence thus resulting in better clustering. A key issue in ES is its population size. Small population causes ES to converge too quickly, however larger population waste computational resources. The ES population here consists of ten individuals. The initial individuals of the ES population are MSTs extracted from the input graph using Prim’s algorithm by selecting varying nodes as the root. Depending on the input graph there may be multiple MSTs. However, this number is usually small thus restricting our framework to have a population size of ten chromosomes. Once the ES population is initialized, one child is produced from each parent through mutation resulting in a parent child pool of 20 chromosomes. Fitness of both, parent, and the child solution is computed. If the child’s fitness is higher than the parent, it replaces the parent in the next iteration. Otherwise, the parent chromosome is moved to the next generation. The rate at which mutations occur is often small because large mutation rates alters the structure of the chromosome quickly thereby resulting in the loss of good genetic material in highly fit individuals. The Davies–Bouldin index (DBI) [29] is utilized as a fitness function in the proposed solution. Since a lower value of DBI indicates better clustering, the individuals with minimum DBI values survive in the next generation. This proposal requires the datasets to be represented as a graph by considering each data point as a node and edge indicating distance between them. The proposal is evaluated using various distance measures for the edge weight, such as: Euclidean, Minkowski, Chebyshev, Correlation, Mahalanobis and city block. Figure 1 shows the overall working of the proposed solution. For the proposed system, the input dataset is represented as a graph. The data samples become the graph nodes and an edge between two nodes represent their Euclidean distance. For N samples, we have an N \(\times \) N adjacency matrix. Where, each cell containing a non-zero entry shows the distance between two nodes, which is computed by applying the distance measure to its attributes.

Fig. 1
figure 1

Overall system working

Full size image
Fig. 2
figure 2

A sample graph with two of its MSTs a input graph, b MST-1, c MST-2

Full size image
Fig. 3
figure 3

Pseudocode to generate clusters using MSTs

Full size image

3.1 Chromosome encoding

To initialize the ES population multiple MSTs are derived from a single graph by arbitrarily selecting a node as the MST root. This results in dissimilar MSTs. The MSTs are derived using Prim’s algorithm. However, to have multiple MSTs in the graph there must be multiple edges having the same weight. This result in multiple MSTs having same total weight, but varying shape. Figure 2 shows two MSTs extracted from the sample graph. Once multiple MSTs are extracted from the graph, the next step is to extract coherent partitions (i.e., clusters) from these MSTs. Initial clusters from each MST are generated using a specific threshold. For a given MST \(^{1}\), edges are extracted from the MST and added to cluster \(C_{MST}^{1}\), this process is repeated until the cumulative weight of the cluster \(C_{MST}^{1}\) exceeds a threshold (\(t_{c})\). This threshold is the ratio between the total weight of an MST divided by the number of clusters. When the sum of the cluster’s edges reaches a value greater than the threshold, the cluster growth is stopped [See Eq. (1)].

$$\begin{aligned} \hbox {Threshold}\,(t_c )=\left( \mathop \sum \limits _{k=0}^n W_k \right) /n_c \end{aligned}$$
(1)

Where, \(n_c \) is the total number of clusters and w is the sum of all the edges in the MST. Upon exceeding the threshold, cluster \(C_{MST}^{2 }\)is constructed and the process is repeated until all edges in the MST are exhausted. This approach is used in all MSTs for creating clusters. From M MSTs, we have M sets of clustering formations. The chromosomes are represented as a one-dimensional array where a cell containing −1 is used to separate clusters. These cells are called separators. The consecutive series of cells in the chromosome (until a cell having −1 is reached) represents one cluster. Each cell can contain an integer between 1 and n, where n is the total number of nodes in the graph. This integer value represents the node number of the graph. Once a node is assigned to a cell in the chromosome, it cannot repeat in other cells. The initial assignment of the nodes to the chromosome’s cell comes from the extracted MSTs. This provides the ES with a logical initial clustering formation to start with. Figure 3 lists the pseudocode that generates clusters using the MSTs.

3.2 Objective function

The Davies Bouldin Index (DBI) is used as a fitness to evaluate the cluster quality represented by the ES chromosomes. DBI is a clustering algorithm evaluation metric which checks for the inter-cluster as well as intra-cluster similarity. Being an internal evaluation scheme, DBI validates the clustering based on quantities and dimensions inherent to the dataset. Equation (2) shows the mathematical formulation of DBI, where n represents the number of clusters, \(\sigma _x \) represents the average distance of all the nodes in the cluster to the center of the cluster \(c_{i,} \)and \(d(c_i ,c_j )\) is the distance between the centroids of two clusters \(c_i \) and \(c_j \).

$$\begin{aligned} DBI=\frac{1}{n}\mathop \sum \limits _{i=1}^n { }_{i\ne j}^{max} \left( {\frac{\sigma _{i} +\sigma _j }{d(c_i ,c_j )}} \right) . \end{aligned}$$
(2)

The minimum value of DBI indicates better clustering. The time complexity of computing DBI is \(O(d(K^{2}+N))\).

3.3 Reproduction

Mutation is the only reproduction operator used in ES to guide the population towards convergence. Population’s each individual is mutated to produce one offspring. The mutation rate of 5% is set in this proposal. For mutation, two sets of nodes are utilized. The first set includes the original cluster’s nodes (called the cluster-nodes) and the second set is of nodes that are used for mutation, referred to as the mutation-nodes. The mutation-nodes and the cluster-nodes are two disjoint sets. Nodes in set cluster-node and the ones in mutation-nodes have equal chances to be selected for the replacement and mutation respectively. For example, consider a dataset with nine nodes numbered as 1, 2, 3, 4, 5, 6, 7, 8, and 9. We have a cluster-node set with members 2, 3, 5, 7 and mutation-nodes set having 1, 4, 6, 8, 9 as members. If the mutation rate is 50%, it means that two nodes are randomly selected from the mutation-nodes to be replaced by any two randomly selected nodes from the set cluster-nodes. This results in a new cluster with changed structure. However, the connectivity of various nodes is validated to be present in the original graph before the mutated chromosome is accepted. This mechanism avoids creation of any false-negative clusters. Figure 4 demonstrates an example mutation.

Fig. 4
figure 4

An example mutation

Full size image

4 Experiments and results

This section lists the experiments and their results. The section shows the outcomes of experiments for the proposed approach referred to as evolution strategy towards clustering (ES-TCL) from this point onwards. Performance of ES-TCL is compared with B-MST [13] and Information Theoretic MST-based (ITM) clustering [14], these being the closely related work to the current proposal. B-MST is proposed in [13] that use R and the igraphFootnote 1 library [30] for implementation. ITM is proposed in [14] and is implemented using python. ES-TCL is evaluated using eleven benchmark datasets. Seven of these are microarray datasets with known clusters, and remaining four are taken from the UCI repository.Footnote 2 The comparison is based on both internal and external cluster validity indices. These include, DBI, DI, SC, and ARI. Table 1 lists the description of the eleven datasets. Microarray data represent the measurement technology used for gene expression. Gene expression is the process of finding the rules due to which the information is stored in DNA. BreastA dataset is about breast cancer produced using one-channel oligonucleotide with 98 objects and 1213 attributes. BreastA is originally clustered into three classes with 51, 11, and 36 samples. BreastB is also a breast cancer dataset produced using two-channel oligonucleotide with 48 objects and 1213 attributes. DLBCLA stands for diffuse large B-cell lymphoma A, it is a dataset having 141 objects and 661 attributes. CNS and LungA datasets are utilized in [31] and [13] respectively. Novartis represent MultiA gene expression dataset having 5565 genes which are normalized for reduction to 100 and 103 objects. The digits, vowels, vehicle, and iris datasets are taken from the UCI repository. Table 2 lists the parameter setting for the ES. The ES is run for 1000 iterations having a population size of ten chromosomes. A mutation rate of 5% is used in the experiments, however, convergence is also evaluated on three other mutation rates.

Table 1 Datasets description
Full size table
Table 2 EA parameter settings
Full size table

4.1 Cluster validity measures

Once a chromosome represents a clustering formation of the given graph, its quality, i.e., fitness is evaluated using the DBI. However, additional clustering quality indices will help in evaluating the formed clusters by the proposed approach. For this purpose, both internal and external cluster validity indices are utilized. The internal validity index does not require prior knowledge about the clustering structure [32]. Whereas, the external validity indices require this information. External validity indices compare two portions on equality. Other than DBI, the two internal validity indices and one external validity index used for evaluation are listed as follows.

4.1.1 Dunn index (DI)

Dunn index (DI) is an internal measure for gauging the results of a clustering algorithm. It aims to find solid and disjoint clusters. DI is the ratio between intra-cluster and inter-cluster similarity. Equation (3) lists the formula to find the intra-cluster similarity.

$$\begin{aligned} intra_{cluster} =\frac{1}{n}\sum _{i=1}^c \sum _{a\in Ci} ||a-centeri|| \end{aligned}$$
(3)

where, n is the number of points in a cluster, c is the total number of clusters, \(C_{i}\) is the cluster and centeri is the center of \(C_{i}.\) The intra-cluster distance is to be minimized. The inter-cluster similarity shows the separation between clusters which measure the distance between them. For good clustering, it should be maximum. Formula for inter-cluster similarity is given in Eq. (4).

$$\begin{aligned}&inter_{cluster}\nonumber \\&\quad =\sum \nolimits _{k=0}^n {{\begin{array}{l} {\min \left( {\hbox {||C}i-\hbox {C}j\hbox {||}^{2}} \right) ,i=1,2,3,\ldots ,c-1} \\ \qquad \qquad \qquad \qquad \qquad {j=1,2,3,\ldots ,c} \\ \end{array} }} \end{aligned}$$
(4)

Where, C represents the cluster center.

$$\begin{aligned} \hbox {DI}=\frac{\mathop {\min }\nolimits _{1\le j\le C} (\hbox {inter}_\_ \hbox {cluster})}{\mathop {\hbox {max}}\nolimits _{1\le J\le C} (\hbox {intra}_\_ \hbox {cluster})} \end{aligned}$$
(5)

where, min (inter-cluster) represent the minimum distance between two clusters. Max (intra-cluster) is the maximum distance between two points in cluster k. Dunn index is inversely proportional to \(mix(inter-cluster)\). The higher values of DI represent good clustering.

4.1.2 Silhouettes coefficient

Silhouettes coefficient (SC) provides a graphical representation of the clustered objects. SC is an internal validity measure showing the similarity and dissimilarity of the object assigned to a cluster. If the object is well clustered, it is more connected to its own cluster’s members, and disconnected to other clusters. For example, if an object i is assigned to cluster C1 then average dissimilarity AVGa(i) of i with all other objects of C1 is calculated. Next, the average dissimilarity of i to objects of other clusters except C1 is computed. The SC value ranges between −1 and 1. Formula for computing SC is listed in Eq. (6). The higher SC value is considered better.

$$\begin{aligned} { SC}({i})=\frac{{ AVGb}\left( { i} \right) -{ AVGa}({i})}{{ max}\{{ AVGa}\left( { i} \right) ,{ AVGab}({ i})\}} \end{aligned}$$
(6)

4.1.3 Adjusted rand index (ARI)

ARI, an external cluster validity index, finds the resemblance between two clusters by identifying how much two clusters are like each other. Consider the data points in a dataset represented as a set SD.

Table 3 Notations used in ARI formula
Full size table
$$\begin{aligned} SD=\left\{ {d_1 ,d_2 ,d_3 \ldots d_n } \right\} \end{aligned}$$
(7)

Let two clusters of SD be \(C1=\left\{ {a_1 ,a_2 ,a_3 \ldots d_s } \right\} \) and \(C2=\left\{ {b_1 ,b_2 ,b_3 \ldots b_s } \right\} \)

Where, C1 is an external index containing \(a_i \) classes, and C2 is a result of clustering algorithm containing \(b_i \) classes. The formula for ARI is:

$$\begin{aligned} ARI= \frac{a+b}{a+b+c+d} \end{aligned}$$
(8)

Table 3 lists the description of a, b, c, and d. The value of ARI ranges between 0 and 1. If both clusters are same, ARI is 1. The value \(a+b\) shows the connection between C1 and C2, while \(c+d\) shows disparity between two clusters. The higher ARI value indicates better clustering formation.

4.2 Distance measures

ES-TCL utilizes Prim’s algorithm to extract initial MSTs from a given graph and later clusters are formed. All this involves computation of distance between various nodes. In the experiments six distance measures are utilized, including: Euclidean, Chebyshev, Minkowski, Mahalanobis, correlation, and city block distance. These distance measures are shown in Eq. (9–14).

$$\begin{aligned}&d (a, b)=\sqrt{(b_1 -a_1 )^{2}+(b_2 -a_2 )^{2}+\cdots +(b_n -a_n)^{2}} \end{aligned}$$
(9)
$$\begin{aligned}&\mathop {d_{chebyshev} (\hbox {a},\hbox {b})=\mathop {\max }\nolimits _i \mid a_i -b_i \mid }.\end{aligned}$$
(10)
$$\begin{aligned}&{{d}_{minkowski}}({\mathrm a,b})={{\left( \sum \nolimits _{i=0}^{n-1}{|{{a}_{i}}-{{b}_{j}}{{|}^{p}}}\right) }^{1/p}}\end{aligned}$$
(11)
$$\begin{aligned}&{{d}_{mahalanobis}}({\mathrm a,b})={{\left( {{\left( \vec {a}-\vec {b} \right) }^{T}}{{S}^{-1}}\left( \vec {a}-\vec {b} \right) \right) }^{1/2}}\end{aligned}$$
(12)
$$\begin{aligned}&d_{correlation}\nonumber \\&\quad =\frac{n\left( {\mathop \sum \nolimits _{i=0}^{n-1} a_i b_i } \right) -\left( \mathop \sum \nolimits _{i=0}^{n-1} a_i \right) \left( \mathop \sum \nolimits _{i=0}^{n-1} b_i \right) }{\sqrt{\left[ {n\mathop \sum \nolimits _{i=0}^{n-1} a_i^2 -\left( \mathop \sum \nolimits _{i=0}^{n-1} a_i \right) ^{2}} \right] \left[ {\mathop \sum \nolimits _{i=0}^{n-1} b_i^2 -\left( \mathop \sum \nolimits _{i=0}^{n-1} b_i \right) ^{2}} \right] }}\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned}&d_{cityblock} =\mathop \sum \nolimits _{i=1}^N \mid a_i -b_i \mid ^{} \end{aligned}$$
(14)
Fig. 5
figure 5

(1+1)-ES convergence graphs for five datasets

Full size image
Fig. 6
figure 6

Four mutation rates and convergence speed

Full size image
Table 4 Cluster validity indices using Euclidean distance
Full size table

4.3 ES results

Fig. 7
figure 7

Silhouettes coefficient plot using the LungA dataset

Full size image

The ES-TCL is executed over the eleven datasets for 1000 iterations. After each iteration, fitness of the best individual (from the parent child pool) is recorded. This enables to compute the population’s average fitness indicating the convergence or otherwise of the proposed methodology. Figure 5 shows the convergence using five datasets, i.e., BreastA, BreastB, CNS, DLBCLA, and DLBCLB. Depending on the features and other dataset specific characteristics the fitness function values, i.e., DBI may vary across the datasets. Due to this reason, these values are normalized in Fig. 5 for demonstration purpose. All the datasets converge before 1000 iterations. Figure 6 shows the convergence speed on four mutation rates. These results represent the average values obtained from ten runs. Each run evolved the population for 1000 iterations. The figure indicates quicker convergence of 5% mutation, thus the same is opted for further experiments.

4.4 Comparison

For the purpose of comparison, B-MST and Information Theoretic MST-based (ITM) clustering are utilized, these being the closely related recent approach to ES-TCL. Both, the proposed algorithm and B-MST, are distance-based clustering algorithms. For the similarity between objects, six distance measures were evaluated (Sect. 4.2). ES-TCL obtained the results using these six measures (one at a time), and a comparison was made with B-MST. Out of the eleven datasets utilized in this study, seven are microarray datasets, which were originally used in the evaluation of B-MST. Table 4 shows the comparison of the proposed solution with B-MST using Euclidean distance. ES-TCL and B-MST were executed five times and the average value was used for evaluation. The lowest value for DBI and the highest values for DI, SC, and ARI indicate better clustering. The table presents the validity indices of partitions generated by ES-TCL and B-MST. The results suggest that using the Euclidean measure, the proposed approach has better DBI values for all datasets as compared to the B-MST, while DI value is better only for LungA dataset. The SC value for ES-TCL is better for all datasets except CNS. Similarly, ES-TCL gives better ARI values for BreastB, DLBCLA, DLBCLB, CNS, and Novartis. Figure 7 shows an SC plot using the LungA dataset. The dissimilarity between objects was also computed using Chebyshev distance for ES-TCL and B-MST. The DBI, DI, SC, ARI values for B-MST and ES-TCL are listed in Table 5. The minimum value of DBI is achieved for ES-TCL on all datasets. ES-TCL has better DI values for four among the seven datasets. ES-TCL has better SC value for all the datasets with an exception of CNS. ARI values for three datasets, i.e., BreastA, DLBCLA, and DLBCLB, are better for the ES-TCL. The proposed approach takes minimum running time on all datasets except for CNS as compared to B-MST. Table 6 lists the validity indices using Minkovski distance. As is the case for Euclidean and Chebyshev distances, ES-TCL has better DBI values for all datasets. It has better DI values only for two datasets; CNS and lungA. SC values of ES-TCL are better for five datasets. Table 7 mentions the DBI, DI, SC, and ARI measured when correlation is used for clustering in ES-TCL and B-MST. Four datasets have better DBI values using correlation with the current proposal. For DI, no dataset gives better results for ES-TCL. Four datasets have better SC values by using correlation. For ARI, ES-TCL has better values for all datasets, except lungA and Novartis. Table 8 shows the results using Mahalanobis distance. For this distance measure, all the datasets produce better DBI values excluding CNS, over the proposed solution. DI values of ES-TCL are worst only for BreastA and CNS datasets. Excluding the CNS dataset, SI value on all datasets are better using the proposed solution. Novartis is the only dataset that does not provide good values on the proposed solution. Table 9 lists the results using city block distance. The results show that DBI is better for all datasets, DI is better for four datasets, i.e., DLBCLA, DLBCLB, CNS, and Novartis.

Analysis of the results reveals that the ES-TCL performs better than B-MST in most of the cases. However, there are few instances in the results where B-MST’s performance is better. Since the objective function used by ES-TCL is the DBI, it has a success rate of 85.71% for this metric. Considering time, other than the six instances, ES-TCL consumed less running time than B-MST. This is due to the fewer individuals in the ES-TCL’s population as compared to B-MST. Additionally, the initial individuals of the ES-TCL were a good estimate of the cluster formation in shape of MSTs. This enabled the approach to converge quickly.

Performance of ES-TCL is also compared with ITM. For this comparison, four UCI repository datasets were used, including: digits, vowel, vehicle, and iris. These datasets were also evaluated using three internal and one external validity index. The comparison is also performed on running time. Table 10 lists the results. The current proposal produces better DBI for all the datasets. The four datasets, digits, vowel, vehicle, and iris also produce better DI for ES-TCL. ITM is a Euclidean distance based clustering algorithm. While comparing it with the ES-TCL, the highest value among all distance measure is selected. However, it is observed that the ITM performed better using the cluster validity indices of SC and ARI. A deeper investigation of the results in Table 10 reveals that on average the clustering solution provided by ES-TCL is four times better than the one provided by ITM based on the DBI metric. Whereas, the clustering solution provided by ITM is only half or one-third times better than the ones provided by ES-TCL. The ES-TCL is slower than ITM due to being an evolutionary approach.

Table 5 Cluster validity indices using Chebyshev distance
Full size table
Table 6 Cluster validity indices using Minkovski distance
Full size table
Table 7 Cluster validity indices using correlation
Full size table

4.5 Discussion

The proposal presented in this work aims at optimizing the clusters represented by the MSTs using evolutionary computation approach. For this purpose, (1+1)-ES is utilized. There are many other evolutionary approaches, including: genetic algorithms, genetic programming, evolutionary programming, and differential evolution. However, the (1+1)-ES seems to be the most suitable evolutionary approach for the problem at hand. The reason for this is the less complications in the reproduction procedure due to the mutation-only strategy as compared to the other algorithms in this domain. Additionally, the problem at hand starts with an initial well-calculated solution instead of a random initial population. This makes ES more suitable for the current task. The ES population is restricted to only ten individuals because of the limited number of unique MSTs extracted from the same input graph. Increasing the population size would not only cause duplication, but will also increase the running time of ES-TCL. DBI, a widely-used cluster validity index guides the ES-TCL. DBI has the advantage of being an internal cluster validity index, that quantifies the quality of clustering using features inherent to the dataset. However, once the ES-TCL converges, the final clustering formations are evaluated using two other internal and one external cluster validity indices, namely, DI, SC, and ARI. This enables to evaluate the results over other independent metrics previously unknown to the proposed algorithm. The ARI has an added advantage of computing the clustering accuracy even in the absence of the class labels [33]. The proposal is compared with two other MST-based clustering approach, namely: B-MST and ITM. ITM utilizes MSTs, whereas, B-MST employs an evolutionary computing approach for clustering in addition to the utility of MSTs. This makes the comparison rational.

Table 8 Cluster validity indices using Mahalanobis distance
Full size table
Table 9 Cluster validity indices using city block distance
Full size table
Table 10 Cluster validity indices for ES-TCL and ITM
Full size table

The current proposal is compared with B-MST using six distance measures based on four cluster validity indices and time. The results are listed in Tables 4, 5, 6, 7, 8, and 9. Using the seven datasets, five performance measures (four validity indices and time), and six distance measures a total of 210 indicators are presented for B-MST and ES-TCL. Where, the ES-TCL perform better in 143 instances turning to be 68.0952% better than B-MST. Overall, ES-TCL performs best with the Euclidean distance having an average accuracy of 74.29% for all datasets and all cluster validity indices. Considering all datasets and all validity indices, ES-TCL performs worst using Mahalanobis and city block distances. For the DBI, ES-TCL performs best, i.e., 85.71% of the times, it achieves better performance than B-MST considering all distance measures. ES-TCL performs better than B-MST 71.43% of the times considering SC. However, it performs only 23.81% times better than B-MST for DI. Considering time, B-MST consumes less running time and executes quicker than B-MST 88.10% of the times for all datasets and distances. Reason for this is ES-TCL’s initial population being computed logically and the lesser number of individuals in each iteration. Keeping in view the above discussion, ES-TCL works at its optimal to optimize the clusters with the DBI as a fitness function and Euclidean/Chebyshev/Minkovski distance as a measure to compute node detachment. With this configuration, ES-TCL performs better than B-MST for all datasets (Tables 4, 5, 6).

ITM is the other MST-based clustering approach used to compare the performance of ES-TCL. ITM’s approximate optimization formulation leads it to be an efficient algorithm with low runtime complexity. Whereas, ES-TCL being an evolutionary computing-based approach requires additional time for convergence. The results in Table 10 show that ES-TCL performs better than ITM on all datasets using the cluster validity indices of DBI and DI. ITM does perform better on the cluster validity indices of SC and ARI. Investigating this in depth reveals that the solution produced by ES-TCL is at least two times better based on DBI and DI in comparison to the ones produced by ITM. Whereas, the better clustering solutions provided by ITM based on SC and ARI are only at maximum, half times better than those provided by ES-TCL. However, the key strength of ITM remains to be its much less computation time. Overall, ES-TCL performs better than ITM and B-MST using all cluster validity indices, all datasets, and all distances. Thus, generalizing the results. Like any other research, there are some limitations of the proposed work. Although this work has performed a detailed set of experiments on evaluating the ES-TCL’s performance, where this proposal generally performs better than the two closely related clustering approaches. However, a limitation of the work is duplication of MST’s. Though care has been taken for the datasets considered in this study to discard any duplicate MST to be considered as a candidate solution, however, for datasets with many duplicate MSTs ES-TCL will suffer with performance issues. The proposed framework, ES-TCL, can be utilized for various software visualization tasks that benefit from clustering [34, 35] and in extracting social circles in the ego networks [36, 37].

5 Conclusions and future work

This work proposed a MST-based clustering procedure to extract coherent groups from a dataset represented as a graph. An input dataset was transformed into a graph where, nodes of the graph represented the samples and an edge indicated the distance between them. Multiple MSTs from a graph were extracted using Prim’s algorithm. The (1+1)-ES was utilized for the optimization of the MST-based extracted clusters. The ES used DBI as its guiding function. Eleven benchmark datasets were used to evaluate the performance of the proposed methodology. The (1+1)-ES-based cluster optimization approach, named, ES-TCL, was executed using 10 chromosomes for 1000 iterations. A mutation rate of 5% was used. The results were compared with two state-of-the-art MST-based clustering algorithms, B-MST and ITM. For this comparison three internal validity indices (DBI, DI, and SC), and one external validity index, ARI was used. The proposed solution was also compared with the two algorithms with respect to execution time. B-MST and the proposed solution both use distance-based clustering, so these were evaluated using seven microarray datasets. The results suggested that the proposed solution on average performed better as compared to B-MST and ITM. The proposed approach can be explored further in the future. A limitation of the proposed solution is that it finds n MST in a graph which may cause to build identical MSTs. This needs to be looked into in the future. Evolutionary approaches are slow by their nature, in the future other faster optimization techniques can be used to extract MST-based clustering formations.