Multisite statistical downscaling model for daily precipitation combined by multivariate multiple linear regression and stochastic weather generator

Abstract

This study provides a multi-site hybrid statistical downscaling procedure combining regression-based and stochastic weather generation approaches for multisite simulation of daily precipitation. In the hybrid model, the multivariate multiple linear regression (MMLR) is employed for simultaneous downscaling of deterministic series of daily precipitation occurrence and amount using large-scale reanalysis predictors over nine different observed stations in southern Québec (Canada). The multivariate normal distribution, the first-order Markov chain model, and the probability distribution mapping technique are employed for reproducing temporal variability and spatial dependency on the multisite observations of precipitation series. The regression-based MMLR model explained 16 % ~ 22 % of total variance in daily precipitation occurrence series and 13 % ~ 25 % of total variance in daily precipitation amount series of the nine observation sites. Moreover, it constantly over-represented the spatial dependency of daily precipitation occurrence and amount. In generating daily precipitation, the hybrid model showed good temporal reproduction ability for number of wet days, cross-site correlation, and probabilities of consecutive wet days, and maximum 3-days precipitation total amount for all observation sites. However, the reproducing ability of the hybrid model for spatio-temporal variations can be improved, i.e. to further increase the explained variance of the observed precipitation series, as for example by using regional-scale predictors in the MMLR model. However, in all downscaling precipitation results, the hybrid model benefits from the stochastic weather generator procedure with respect to the single use of deterministic component in the MMLR model.

1 Introduction

Simultaneous generation of temporal and spatial variability of climate variables at multiple local points is often required in many hydrological, agricultural, and ecological research and applications, including climate change impact analysis (Wilby et al. 2003; Mehrotra and Sharma 2007). Atmosphere-Ocean Global Climate Models (AOGCMs) provide large-scale information for the analysis of impacts of climate change. It is broadly recognized that AOGCMs produce reliable climatology for large-scale upper-air variables (e.g. wind, temperature, humidity, air pressure, etc) (Giorgi et al. 2001) and at the annual and seasonal time scales over broad continental scales (McAveney et al. 2001; Schoof et al. 2007). However, outputs of the AOGCMs are generally too coarse, with horizontal resolutions generally larger than 2°longitude and longitude (e.g., 3.75°longitude × 3.75°latitude for the Canadian AOGCM), to be applied directly at the local scale in the assessment of climate change impacts. Furthermore, they generally demonstrate only temporal variability and spatial dependency on a global-scale and cannot reproduce those at a more local-scale (Prudhomme et al. 2002).

Downscaling techniques have been developed to fill the gap between large scale atmospheric variables simulated by AOGCMs and the local scale climate information (Huth 2002). Downscaling techniques include dynamic downscaling, which uses regional climate models (RCMs) driven by AOGCM outputs to generate climate information over a limited area, and statistical downscaling (SD), which uses statistical relationship between large scale climate predictors from AOGCMs and local-scale predictand (Wilby et al. 1998). SD approaches are often used because of their relative ease of implementation, they require low computation, and provide climate information at the equivalent of point climate observations (Wilby et al. 2002). SD methods, as reviewed in several studies (Xu 1999; Wilby et al. 2002), can be divided into three main groups (e.g. Wilby et al. 2004): regression-based approaches, stochastic weather generator approaches, and weather typing (or analog) approaches. Regression-based are common and simple where an empirical relationship between predictors and predictands is derived directly by linear or non-linear transfer functions. In the regression-based approaches, multiple linear regression (MLR) (Hellström et al. 2001; Palutikof et al. 2002; Wilby et al. 2002; Huth 2004; Hessami et al. 2008), canonical correlation analysis (CCA) combined to MLR (Trigo and Palutikof 2001; Huth 2002, 2004), and principle component analysis (PCA) with MLR (Huth 2004; Buishand and Brandsma 2001) have all been used as transfer functions. Despite the fact that SDs are easily adaptable to local scale and applicable to any output of AOGCM (Hellström et al. 2001), these large-scale predictors used in the regression-based approaches explain only a fraction of the observed variance of the predictand, especially for precipitation (Wilby et al. 2002). Moreover, Wilby et al. (2003) and Harpham and Wilby (2005) experienced difficulty to reproduce spatial coherence among multisite precipitations using the regression-based approaches.

Stochastic weather generator approaches are fairly simple but flexible and computationally economical methodologies for daily weather data at a single site as well as multisite (Wilks 1998, 1999; Qian et al. 2002; Palutikof et al. 2002). A weather generator uses a random number conditioned upon large-scale model output state (Wilks 1999). They are also statistical models which mimic sequences of observed weather variables. The main limitation in the weather generator is the difficulty in adjusting the parameters in a physically realistic and consistent manner under future climate states (Wilby et al. 1998). Weather typing (or analog) approaches generate local climate variable by resampling from observed atmospheric data (Buishand and Brandsma 1997; von Zorita and Storch 1999; Hewitson and Crane 2002; Boé et al. 2006; Crimmins 2006).

A conditional re-sampling approach, a hybrid scheme combining a regression-based approach with a MLR model and a stochastic weather generator, was first proposed by Wilby et al. (2003) and was successfully applied by Harpham and Wilby (2005) for multisite precipitation simulation. This hybrid procedure could overcome weaknesses of both regression-based and stochastic weather generation approaches. Ideally, unexplained temporal variability and spatial dependence on a local-region by global-scale AOGCM predictors can be complemented by employing a stochastic weather generating technique. Moreover, this hybrid procedure can provide physically realistic information from AOGCM outputs to generate future climate scenarios. Including the conditional re-sampling approach introduced by Wilby et al. (2003), several studies have tested for multisite simulation of precipitation and temperature with or without downscaling. Wilks (1998, 1999), Qian et al. (2002), and Mehrotra and Sharma (2007) generated multisite precipitation using stochastic weather generation approaches based on Markov chain. Regression-based approaches have used to simulate precipitation at multiple sites by using AOGCM predictors (Harpham and Wilby 2005). They used artificial neural network techniques as transfer functions to downscale daily precipitation for multisite. Fowler et al. (2005) provided a multisite stochastic rainfall model based on weather types for climate impact assessment in UK.

In this study, a multi-site hybrid statistical downscaling procedure combining regression and stochastic weather generation approaches is provided for multisite generation of daily precipitation. As a transfer function, Multivariate Multiple Linear Regression (MMLR) is tested for simultaneous downscaling of daily precipitation occurrence and amount series for multiple observation sites over southern Québec (Canada). The MMLR is a logical extension of the multiple linear regression to allow for multiple response variables estimated from different input variables. Unexplained temporal variability and spatial dependency by the MMLR model are complemented by employing a stochastic weather generating technique.

This paper is organized as follows. Section 2 describes the methodology. Section 3 explains the study area and the procedure used to select the predictors. Section 4 contains results of the study, and Section 5 provides the conclusion.

2 Methodology

2.1 Multivariate multiple linear regression

It occasionally arises that prediction of several dependent variables are required from a set of independent variables. Statistical downscaling from multiple AOGCM predictors to numerous meteorological observation sites is one of these situations. To analyze relationships between multiple independent variables and multiple dependent variables, multivariate regression approaches have been used in many diverse scientific areas. The MMLR estimates the same coefficients and standard errors as one would obtain using separate MLRs by using the ordinary least squares (OLS) estimate.

Suppose that there are multiple predictor variables matrix X of dimension n×k and also multivariate predictand variables matrix Y of dimension n×m, where the measurement record length n is larger than the dimension of the explanatory variables k. One can estimate parameter matrix B of dimension k×m, which can define linear relationship between the two matrices X and Y . Therefore, for the m dependent variables and k independent variables, the MMLR can be expressed as:

$$ {\mathbf{Y}} = {\mathbf{X}} \cdot {\mathbf{B}} + {\mathbf{E}} $$

(1)

where the E is the residual matrix of dimension n×m.

The Ordinary Least Squares (OLS) estimates of the parameter matrix B in the k·n parameter space is given by:

$$ \widehat{{\mathbf{B}}} = {\left( {{{\mathbf{X}}^{\text{T}}}{\mathbf{X}}} \right)^{ - 1}}{{\mathbf{X}}^{\text{T}}}{\mathbf{Y}} $$

(2)

Under the assumption that the errors be normally distributed, OLS is the maximum likelihood estimators. The main concern of the MMLR is to find a parameter matrix B in the k·n parameter space. One of the problems to the parameter matrix B of MMLR is multi-collinearity which produces large standard errors of estimated parameters in the related independent variables. In order to limit the influence of multi-collinearity, many methods have been employed such as ridge regression, principal component regression, canonical correlation regression, and stepwise regression. In this study, backward stepwise regression (as in Hessami et al. 2008) was employed to deal with multi-collinearity problem and to select optimal predictors. Backward stepwise regression is initiated with all predictors being included in the model, and redundant predictors are eliminated one after the other based on F-statistic and associated P-value (Chatterjee and Price 1977).

2.2 Regression-based downscaling method

The deterministic series of daily precipitation occurrence probabilities can be modeled using the following MMLR equation and atmospheric predictors:

$$ \widehat{{\mathbf{O}}} = {\widehat{\alpha }_0} + {\mathbf{X}}\widehat{\alpha } $$

(3)

Where ${\widehat{O}_{ij}}$, an element of the matrix $\widehat{{\mathbf{O}}}$, is the downscaled deterministic series of precipitation occurrence probability on a day i (=1, 2, …, n) at a site j (=1, 2, …, m). X [n×k] is normalized atmospheric predictor variable matrix. Constant term matrix ${\widehat{\alpha }_0}\left[ {n \times m} \right]$ and the parameter matrix $\widehat{\alpha }\left[ {k \times m} \right]$ are estimated MMLR parameters by the OLS estimation method.

If precipitation amount variable vector Y _j for a site j is not normally distributed, appropriate transformation should be performed before developing regression-based precipitation amount model. The gamma distribution has been often fitted to rainfall amounts in many studies (Stephenson et al. 1999; Giorgi et al. 2001; Yang et al. 2005). Based on the approach proposed by Yang et al. (2005), the Anscombe transformation is employed for transforming the precipitation amount. If the vector Y _j has gamma distribution, the distribution of ${R_{ij}} = Y_{ij}^{1/3}$ on a day i at a site j, where the Rs are called Anscombe residuals, is normal as described by Terrell (2003) and Yang et al. (2005). The deterministic series of transformed precipitation amount matrix R [n×m] can be modeled using the following MMLR equation and atmospheric predictors:

$$ \widehat{{\mathbf{R}}} = {\widehat{\beta }_0} + {\mathbf{X}}\widehat{\beta } $$

(4)

where the $\widehat{{\mathbf{R}}}\left[ {n \times m} \right]$ is the downscaled deterministic series of Anscombe residuals matrix of precipitation amount. Constant term matrix ${\widehat{\beta }_0}\left[ {n \times m} \right]$, the parameter matrix $\widehat{\beta }\left[ {k \times m} \right]$ are estimated MMLR parameters by the OLS estimation method.

In this study, the MMLR amount model was developed from all daily series including zero values to downscale precipitation amounts conditional on nearby station being dry, which usually have smaller amounts than corresponding amounts conditional on near neighbors being wet. It also made it easy to reproduce cross-site correlation in the observed precipitation series by stochastic weather generation technique. The dry days at all observation sites were 25 % of the whole available days in the present study area. Therefore, the downscaled precipitation amount series from the MMLR amount were underestimated and had biases because of the inclusion of zero amounts of precipitation. Those biases should be removed by employing an appropriate statistical adjusting technique. In our case, a probability distribution mapping technique is used to deal with this problem.

2.3 Stochastic variation method

2.3.1 Precipitation occurrence

Residual (or error) matrix E _O [n×m] of the deterministic series of daily probability of precipitation occurrence is described below:

$$ {{\mathbf{E}}_{\mathbf{O}}} = \left( {{\mathbf{O}} - \widehat{{\mathbf{O}}}} \right) $$

(5)

In the equation, O [n×m] is the observed binary (0 or 1) matrix of precipitation occurrence where an O _ij , an element of the matrix O, is 0 for dry day and 1 for wet day (measured precipitation ≥1 mm) on a day i (=1, 2… n) at a site j (=1, 2… m). $\widehat{{\mathbf{O}}}\left[ {n \times m} \right]$ is the matrix of deterministic probability series of precipitation occurrence by the MMLR and atmospheric predictors.

Generally, the modeled probability matrix $\widehat{{\mathbf{O}}}$ cannot represent the at-site temporal variance and cross-site correlation of the observed matrix O. To reproduce those temporal variability and spatial dependency of the precipitation occurrence, the residual matrix ${\widetilde{{\mathbf{E}}}_{\mathbf{O}}}\left[ {n \times m} \right]$ is generated from a multivariate normal distribution having error variances [V _O ] and correlation matrix [Ω _O ] of the residual matrix E _O . Generated residuals are added to the deterministic probability matrix of the precipitation occurrence $\widehat{{\mathbf{O}}}$ as below:

$$ \widetilde{{\mathbf{O}}} = \widehat{{\mathbf{O}}} + {\widetilde{{\mathbf{E}}}_{\mathbf{O}}} $$

(6)

The continuous probability series of each station in the matrix $\widetilde{{\mathbf{O}}}$ have normal distribution rather than uniform distribution [0, 1]. However, eventually, the generated continuous probability matrix $\widetilde{{\mathbf{O}}}$ for precipitation occurrence should transport to the [0 or 1] binary series by selecting an appropriate threshold. This study employed first-order Markov chain model, which follows from the assumption that the probability of precipitation occurrence depends only on whether precipitation occurred or not on the previous day. The first-order Markov chain therefore involves two precipitation probabilities: (1) the probability of wet day following a dry day (p ₀₁) and (2) the probability of wet day following a wet day (p ₁₁). These transition probabilities are estimated separately for each observation site.

Let $\mathop {{\mathbf{O}}}\limits^\cdot$ denote the binary matrix of precipitation occurrence and ${\dot{O}_t}(k)$ is a [0 or 1] binary value of rainfall occurrence at location k on a day t. The ${\dot{O}_t}(k)$ is then determined as:

$$ {\dot{O}_t}(k)\left| {\matrix{{*{20}{c}} {1,} \hfill & {{\text{if}}\;{{\widetilde{O}}_t}(k) \geqslant {\Phi^{ - 1}}(k)\left[ {1 - {p_{01}}(k)} \right]\;{\text{and}}\;{{\dot{O}}_{t - 1}}(k) = 0} \hfill \\ {1,} \hfill & {{\text{if}}\;{{\widetilde{O}}_t}(k) \geqslant {\Phi^{ - 1}}(k)\left[ {1 - {p_{11}}(k)} \right]\;{\text{and}}\;{{\dot{O}}_{t - 1}}(k) = 1} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ } } \right. $$

(7)

where Φ⁻¹ (k) indicates normal cumulative distribution function which uses mean and standard deviation parameter estimates from time series of $\widetilde{O}(k)$.

One problem during the [0, 1] transformation is that the transferred binary series ${\mathbf{\dot{O}}}$ cannot represent the original multisite cross-correlation in the $\widetilde{{\mathbf{O}}}$, and also multisite cross-correlation in the observed matrix O. To deal with this problem, empirical relationships of cross-correlations between binary series (ξ(k,l)) and continuous series (ω(k,l)) at any locations k and l should be derived (Wilks 1998). This study employed a simple power function to derive the empirical relationships as below:

$$ \omega \left( {k,l} \right) = a \times \xi {\left( {k,l} \right)^b} $$

(8)

The multisite correlation matrix [Ω _O ] of the residual matrix E _O was adjusted using Eq. 8 to generate residuals ${\widetilde{{\mathbf{E}}}_{\mathbf{O}}}$ for reproducing multisite cross-correlation in the observed O matrix to the transformed binary matrix ${\mathbf{\dot{O}}}$. Therefore, the parameters a and b in Eq. 8 have been estimated to yield the smallest RMSE between every m(m-1)/2 pair of cross-site correlation coefficients in the observed binary series, and the same number of cross-site correlation coefficients in the transformed binary series ${\mathbf{\dot{O}}}$.

2.3.2 Precipitation amount

Residual (or error) matrix E _R [n×m] of the deterministic series of daily precipitation amount can be described as below:

$$ {{\mathbf{E}}_{\mathbf{R}}} = \left( {{\mathbf{R}} - \widehat{{\mathbf{R}}}} \right) $$

(9)

where R[n×m] is Anscombe residuals matrix of the observed precipitation amount Y [n×m] and $\widehat{{\mathbf{R}}}\left[ {n \times m} \right]$ is the matrix of deterministic series generated by the MMLR amount model and atmospheric predictors. In general, the downscaled $\widehat{{\mathbf{R}}}$ cannot represent at-site variances and multisite cross-correlations of the observed matrix R. Therefore, the residual matrix ${\widetilde{{\mathbf{E}}}_{\mathbf{R}}}\left[ {n \times m} \right]$ is generated from multivariate normal distribution having error variances [V _R ] and correlation matrix [Ω _R ] of the residual matrix E _R . Generated residuals are added to the modeled matrix $\widehat{{\mathbf{R}}}$ as below:

$$ \widetilde{{\mathbf{R}}} = \widehat{{\mathbf{R}}} + {\widetilde{{\mathbf{E}}}_{\mathbf{R}}} $$

(10)

The generated precipitation amounts are calculated as below:

$$ {\widetilde{Y}_{ij}} = \widetilde{R}_{ij}^3 $$

(11)

The ${\widetilde{Y}_{ij}}$ is counted as a nonzero precipitation amount only when the model described in the occurrence model simulates to be wet [${\mathop {Y}\limits^\cdot_{ij}} = {\mathop {O}\limits^\cdot_{ij}} \times {\widetilde{Y}_{ij}}$].

One problem is that generated precipitation series in the $\mathop {{\mathbf{Y}}}\limits^\cdot$ generally have different statistical properties (e.g. mean and standard deviation) than the observed precipitation amount series for each observation site. The main reason of these differences is that the Anscombe residuals R from the observed precipitation amount are not exactly normally distributed, and the modeled Anscombe residuals $\widehat{{\mathbf{R}}}$ from the MMLR are biased estimators. Moreover, this study included zero precipitation amounts to calibrate MMLR amount model. Therefore, residual matrix E _R of each site is not generally normally distributed and has skew. To overcome this problem, probability distribution mapping technique was adapted and the generated precipitation amount was adjusted. The precipitation amounts for each site in the $\mathop {{\mathbf{Y}}}\limits^\cdot$ are fitted to gamma distributions and their cumulative probabilities are calculated. Subsequently, precipitation amounts are recalculated with the gamma distributions fitted to observation data for each site using the calculated cumulative probabilities from the $\mathop {{\mathbf{Y}}}\limits^\cdot$. Figure 1 describes schematically the procedure of the multi-site hybrid model calibration of daily precipitation series

Fig. 1

Procedure to calibrate the multi-site hybrid model

3 Model application

3.1 Study area and data

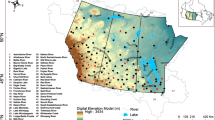
Figure 2 shows the area over eastern Canada where the studied meteorological stations are located. We have focused on the southern part of the province of Québec. As predictands, this study used daily precipitation data from Environment Canada station, which have been rehabilitated by Mekis and Hogg (1999). Small amount of missing data (less than 5 %) were excluded in this study. Table 1 reports names and latitude-longitude locations of the selected meteorological stations, as in Fig. 2 these stations are mapped with respect to their numbers given in the Table.

Fig. 2

Locations of CGCM3 grid points and observation stations of daily precipitation

Table 1 List of the 9 stations used in this study

3.2 Predictors source and selection

Predictors are derived from the National Center for Environmental Prediction (NCEP)/ National Center for Atmospheric Research (NCAR) reanalysis datasets (e.g., Kalnay et al. 1996; Kistler et al. 2001) over the period from 1961 to 2000. The NCEP/NCAR reanalysis at the horizontal original resolution of 2.5 latitude × 2.5° longitude have been interpolated onto the Canadian coupled AOGCM version 3 (i.e. CGCM3) grid which has a horizontal resolution of 3.75° latitude × 3.75° longitude (about 400 km). Indeed, as the ultimate goal of SD application is to develop climate change information, all reanalysis predictor products used for the calibration of the SD model need to be re-gridded at the resolution of the AOGCM that we use as source of predictors to simulate climate change daily values. As in the following work, we will use the CGCM3 predictors to generate climate change daily information, the NCEP predictors used here to calibrate and evaluate our downscaling approach come from the atmospheric variables interpolated onto the CGCM3 grid size. These reanalysis data usually mimic the temporal distribution of observed atmospheric variables, and they are used to calibrate SD model. They are developed from a high-resolution global atmospheric model and use a data assimilation system from observed measurements (i.e. from near surface and tropospheric column). Table 2 lists 25 predictor variables of NCEP/NCAR interpolated on a CGCM3 grid. In our study area, there are six grid points and 150 predictor variables. In the Fig. 2, the 6 grid points are represented as GP1 ~ GP6.

Table 2 NCEP/NCAR predictor variables

The MMLR parameters for precipitation occurrence and amount models were estimated separately for each month by using predictands and predictors from 1961 to 1990. The calibrated monthly MMLR models were validated with respect to observed data, by using predictors over the independent time window between 1991 and 2000. As the downscaled results are highly sensitive to the selection of predictor variables (Wilby et al. 2002), this choice needs to be carefully addresses (see further discussion in Wilby et al. 2004; IPCC 2001, 2007; and over southern and northern Canada in Choux 2005, and Dibike et al. 2008, respectively). Over the same area, Jeong et al. (2012) reported that the mean sea level pressure, specific humidity, geopotential heights, U- and V- components, at various pressure levels are important predictors for daily precipitation occurrence and amount. They also reported that these last variables are the most sensitive variables to potential changes in climate conditions based on CGCM3. These circulation and moisture related variables are both connected to large scale circulation precipitation occurrence and amount, at the scale of NCEP reanalysis data. Indeed, occurrence and intensity of precipitation are controlled by complex mechanisms which may be linked to: large-scale upward or downward motion of a relevant air mass; small-scale processes, such as localised convection; cloud development; turbulent motion of wet or dry air in the boundary layer; orographic effects, including convergence of an air mass, which may induce upward motion on a windward slope area. Hence, considering the coarse scale resolution of NCEP and its sub-grid scale parameterization, the regional scale predictors are not explicitly taken into account in the list of predictors used in this study.

As a statistical criterion, the backward stepwise approach was employed to select predictors from the potential predictor set during the calibration period from 1961 to 1990. As stated before, the backward stepwise approach starts with the all available potential predictors and successively eliminates redundant or non-significant predictors, one at a time. The backward stepwise approach was preferred to the forward method of predictor selection in order to give an initial equal change of selection to all predictors, as recommended by a number of authors (see McCuen 2003; Goyal and Ojha 2010). For the daily precipitation series of the nine observation sites, the optimal combination of predictors among the 150 NCEP/NCAR variables was identified by backward stepwise regression approach without monthly consideration. As a first step, the same combination of predictors is selected through the year to develop monthly downscaling models. Table 3 reports the selected 28 predictor variables of each grid point (GP1~GP6) and each predictor variable for precipitation modeling. The selected predictors by the backward stepwise approach are acceptable to calibrate statistical downscaling models and also projecting future climate scenarios by including sensitive predictors to climate changes such as specific humidities and geopotential heights (Boé et al. 2006; Dibike et al. 2008; Jeong et al. 2012) and predictors frequently employed in other downscaling studies over various regions across Canada such as mean sea level pressure and wind components (e.g. Hessami et al. 2008; Dibike et al. 2008; Jeong et al. 2011).

Table 3 Selected NCEP/NCAR predictors for MMLR model at each CGCM3 grid point

4 Results

For stability and robustness of the stochastic weather generating results of the hybrid model, 50 realizations are generated of the precipitation series of length equal to the precipitation record from 1961 to 2000. Hence, results of the hybrid model presented in this section were evaluated from the 50 realizations of precipitation occurrence and amount series. Note that the daily MMLR and the hybrid models were developed separately for each month.

4.1 MMLR models

Figure 3 presents explained variance of the daily MMLR occurrence and amount models for the whole series (annual, i.e. considering all 12 months together), spring (March, April, and May), summer (June, July, and August), autumn (September, October, and November), and winter (December, January, and February) during the calibration period (1961 ~ 1990) and for the whole series (annual) during the validation period (1991 ~ 2000). The R-squares of precipitation occurrence by the MMLR were varied from 0.16 (site 8) to 0.22 (site 9) for annual during the calibration period, and from 0.10 (site 2) to 0.20 (site 9) for annual during the validation period. The R-squares of precipitation amount by the MMLR were varied from 0.13 (site 2) to 0.25 (site 9) for the whole series during calibration period and from 0.09 (site 8) to 0.20 (site 9) for the whole series during validation period. Spatially, observation sites located in the eastern part of study area have larger values of R-squares for the MMLR than those in the western part except site 8 (Rimouski), which is the only observation station located in the Lower St-Lawrence valley, on the south shore. In general, the relative low R-square values of (i.e. between 0.1 and 0.3) underline the difficulty to downscale precipitation series. However, in the case of daily rainfall, and considering the stochastic character of daily rainfall, these values are quite respectable. At most sites, R-squares for summer and winter months were smaller than those for spring and autumn. Summer local convective activities and their associated intense rainfall events are not well captured at the scale of global NCEP reanalysis products, as compared to large-scale meteorological synoptic systems more explicitly resolved in that model and during fall through spring.

Fig. 3

R-squares of the daily MMLR occurrence and amount models for the whole series (annual), summer, and autumn during the calibration (cal.) period (1961 ~ 1990) and for the whole series (annual) during the validation (val.) period (1991 ~ 2000)

4.2 Precipitation occurrence

Figure 4 shows scatter plot of observed and generated total number of wet days (≥1 mm/day) by the hybrid and the MMLR models at all 9 stations and 12 months over the calibration (1961 ~ 1990) and (1991 ~ 2000) validation periods, where each point represents a month and station. For the hybrid model, 95th percentile, median, and 5th percentile values from 50 realizations are presented under the form of whisker plots. As can be seen from the figure, the hybrid model reproduces the observed total number of wet days fairly well for all months and all stations during both calibration and validation periods. However, the MMLR model tends to underestimate this value, and the difference is large when there is relatively small number of wet days of an observation site. This suggests that the hybrid model benefits from the stochastic weather generator procedure with respect to the single use of deterministic component in the MMLR model. Note that the wet day was determined when deterministic series of daily probability of precipitation occurrence by the MMLR occurrence model was larger than the threshold 0.5.

Fig. 4

Scatter plot of observed and modeled total number of wet days by hybrid and MMLR models at all stations and 12 months, where black solid and open circles are values of hybrid model for the calibration (cal.) and validation (val.) periods and gray solid and open triangles are values of MMLR for the calibration and validation periods, respectively. Note that the numbers of wet days of calibration period (i.e. 30 years) are larger than those of validation period (i.e. 10 years). a Calibration (Annual) b Validation (Annual) c Calibration (July) d Calibration (October)

Figure 5 shows cross-site correlation coefficients between pairs of daily precipitation occurrence series versus their station distance for all possible combinations of station pairs for the whole series (annual), during the calibration and validation periods and for July and October during the calibration period. The hybrid model was able to reproduce the cross-site correlation of the series fairly well on both calibration and validation periods (see Fig. 5a and b). This reveals the effectiveness of the stochastic weather generation procedure and the simple power function described in Eq. 8 to derive the empirical relationships between cross-site correlations between binary series and continuous series. The MMLR model showed more difficulty in representing the cross-site correlation of precipitation occurrence series which were consistently over-represented for almost all pairs. This is not surprising, since the MMLR occurrence model is able to explain only a part of observed variability of precipitation occurrence series from NCEP/NCAR coarse-scale predictors.

Fig. 5

Cross-site correlations between pairs of daily precipitation occurrence series versus their station distance for all possible combinations of station pairs for the whole series (annual) during the calibration and validation periods and for July and October during the calibration period as shown in Fig. 4. In this figure, black solid and black dotted lines represent exponential decay functions with interception of one on the y-axis fitted to observations and median values of hybrid model. a Wet spell probabilities of a day b Wet spell probabilities of 2 ~ 3 days c Wet spell probabilities of 4 ~ 6 days

Cross-site correlation between pairs of daily precipitation occurrence also showed obvious seasonal variability. In Fig. 5c and d, observed cross-site correlations between pairs are weaker in July than for the annual results, while they are stronger in October than for the whole year. As mentioned before, the weaker cross-site correlations in July is likely related to the effect of localized convective activities during summer. The stronger cross-site correlations in October and in fall/winter/spring months are notably associated with the large-scale precipitation events, mostly caused by synoptic low pressure systems rather than mesoscale events more prominent in summer. However, the hybrid model reproduced the cross-site correlations well in both months.

Figure 6 shows scatter plots of wet spell probabilities between observation and generation by the hybrid and the MMLR models for (a) a day, (b) 2 ~ 3 days, and (c) 4 ~ 6 days for the nine observed sites. The cases of the consecutive wet days for the the different periods from 1 to 6 days and then the probabilities have been calculated by the counted cases divided by the total number of possible cases for each site. The hybrid model reproduced one-day, 2 ~ 3 days, and 4 ~ 6 days wet spell probabilities fairly well for all stations, with a weak underestimation for shorter duration and a weak overestimation for longer duration. The MMLR model tended to consistently underestimate all wet spell probabilities. Spatially, sites 4, 5, 7 and 9, which are located in the eastern part of the study area (Near Lake St-Jean and the North shore of the St-Lawrence River), showed larger probabilities then the other sites at the 2 ~ 3 and 4 ~ 6 wet spell days and the hybrid model reproduced those spatial variability relatively well.

Fig. 6

Wet spell probabilities of observed and generated by hybrid and MMLR models for a a day, b 2 ~ 3 days, and c 4 ~ 6 days for the calibration period. Numbers in the figures represent observation sites. a Spring b Summer c Autumn d Winter

Figure 7 shows scatter plots of Lag-1 autocorrelation of daily precipitation occurrence of the hybrid and the MMLR models for each station and for each season during the calibration period. Each point on the figures represents a month and a station. Although, the hybrid model showed good ability in representing consecutive wet days, it yielded few over-estimated values for all seasons. However, of the hybrid model yielded better performance than the MMLR model except in spring. In spring, the hybrid model and the MMLR yielded similar performance. The hybrid model showed best performance in winter, and worst performance in spring. Lag-1 autocorrelation of daily precipitation occurrence showed obvious seasonal variability which was stronger in spring, weaker in summer than that in autumn and in winter. However, the hybrid model represents the seasonal variability fairly well.

Fig. 7

Scatter plots of lag-1 autocorrelation of daily precipitation occurrence of hybrid and MMLR models for each station and for each month, where results are presented for each season during calibration period. Numbers in the figures represent observation sites

4.3 Precipitation amounts

Figure 8 shows scatter plot of the observed and generated mean intensity of precipitations per wet days (≥1 mm/day) by the hybrid and the MMLR models at all stations and 12 months, for both the calibration (1961 ~ 1990) and the validation (1991 ~ 2000) periods. The hybrid model reproduced quite well the precipitation amount per wet days for the calibration period; furthermore, the 95th and 5th percentile values of 50 realization series were almost similar. For the validation period, the median values of 50 realizations of the hybrid model showed more scatter values than for the previous period. One reason of this scatter in the validation period is the differences of observed mean precipitation per wet days between the calibration and validation periods because of sampling errors. Note that the observed wet day means between calibration and validation period are slightly different. The MMLR model yielded large negative biases and tended to strongly underestimate the amount per wet days. This underestimation of precipitation amount by the MMLR is not surprising, because the MMLR amount model uses zero values in the predictand variables for model calibration.

Fig. 8

Scatter plot of observed and modeled mean precipitation of wet days by hybrid and MMLR models at all stations and 12 months. Solid symbols are values of calibration period and open symbols are values of validation period

Figure 9 shows scatter plot of observed and modeled standard deviation of wet day precipitation amounts by the hybrid and the MMLR models at all stations and over the 12 months. Again, for the hybrid model, 95th median, and 5th percentile values of 50 realizations are presented during the calibration period while median values of 50 realizations are presented during the validation period. The hybrid model showed fairly accurate values with respect to observed ones during the calibration period while it showed some scatter during the validation period. Similar to the mean precipitation per wet days, the MMLR model showed stronger under representation of the standard deviation of wet day precipitation amount, and yielded large negative bias in this statistic.

Fig. 9

Scatter plot of observed and modeled standard deviation of wet day precipitation amounts by hybrid and MMLR models at all stations and 12 months. Solid symbols are values of calibration period and open symbols are values of validation period. a Calibration (Annual) b Validation (Annual) c Calibration (July) d Calibration (October)

Figure 10 shows cross-site correlations between pairs of daily precipitation amount series versus station distances for all possible combinations of station pairs for the whole series (annual) during both the calibration and validation periods, and for July and October during the calibration period. Although, the hybrid model tended to under-estimate this spatial dependency of precipitation series for most station pairs for the whole year results during both calibration and validation periods, it reproduced the cross-site correlations of precipitation series fairly well (see Fig. 10a and b). This result implies that the stochastic weather generation procedure employed in the hybrid model is able to reproduce spatial dependency of the observed precipitation amount series fairly well. However, the MMLR model showed difficulty in representing the cross-site correlation of precipitation amount series which were consistently over-represented for almost all pairs. In Fig. 10c and d, observed cross-site correlations between pairs are weaker in July than in annual, while they are stronger in October than in annual. Again, the hybrid model reproduced this seasonal variability in the cross-site correlations well in both months. However, the difference between 95 % and 5 % values of this statistic in both months were larger than those in annual.

Fig. 10

Cross-site correlations between pairs of daily precipitation amount series versus their station distances for all possible combinations of station pairs for the whole series (annual) during calibration and validation periods and for July and October during calibration period, where black solid and black dotted lines represented exponential decay functions with interception of one on the y-axis fitted to observation and median values of hybrid model. a Spring b Summer c Autumn d Winter

Figure 11 shows scatter plots of maximum 3-days precipitation total amounts of the hybrid and the MMLR models for each station, where results are presented for each season during the calibration period. The hybrid model reproduced the maximum 3-days precipitation total amount fairly well; however, the statistic had large differences between 5 % and 95 % at site 9 in spring and autumn, when the observed value of this statistic was large. The MMLR model showed best performance in winter while it showed worst performance in summer. As shown in Figs. 8, 9, 10 and 11, the hybrid model reproduced daily precipitation amount and extreme values fairly well at all stations. Those results verify the effectiveness of stochastic weather generation procedure and probability distribution mapping technique in the hybrid model.

Fig. 11

Scatter plots of maximum 3-days precipitation total amount of hybrid and MMLR models for each station and for each month, where results are presented for each season during calibration period. Numbers in the figures represent observation sites. a Annual total precipitation of site 1 (Chelsea) b Annual maximum daily precipitation (mm) of site 1 (Chelsea)

The specific RMSE values of the provided scatter plots of the diagnostic indices of precipitation occurrence and amount are summarized in Table 4. As described above, hybrid model yielded better performance than MMLR for all indices except for the lag-1 autocorrelation in spring. The two models yielded similar values of RMSEs for the lag-1 autocorrelation in spring.

Table 4 RMSEs of diagnostic indices for MMLR and hybrid models of nine observation sites during calibration period, where the RMSEs of the hybrid model were calculated from median values of 50 realizations

5 Discussion

In general, the variability of a local predictand as precipitation is explained only a part by regression-based downscaling mapping from coarse-scale predictors (Wilby et al. 2002; Cannon 2009). As mentioned by von Storch (1999), predictors generated from synoptic-scale field cannot represent all variability at the sub-grid scale. Furthermore, spatial dependency among multisite local predictand variables are not reproduced accurately by regression mapping from large-scale predictors (Wilby et al. 2003; Harpham and Wilby 2005; Bürger and Chen 2005). In this study, cross-site correlations of precipitation occurrence and amount among the observation sites are obviously over-estimated (see Figs. 5 and 10) and this over-estimation is evident that one cannot reproduce local-scale spatial dependency by simply using coarse NCEP/NCAR predictors. Therefore, this study provided a statistical weather generation procedure based on randomization approach, which reproduced the cross-site correlation of precipitation occurrence and amount among the observation sites. However, reproducing cross-site correlation of precipitation amount (see Fig. 10) is more difficult than that of precipitation occurrence (see Fig. 5), because ultimately determined precipitation amount results are affected by the precipitation occurrence results.

Even though, a part of generated precipitation occurrence and amount series of the hybrid model are from the MMLR regression-based models using large-scale predictors, it is still much smaller than that from stochastic weather generation. Figure 12 shows scatter plots of (a) annual total precipitation and (b) annual maximum daily precipitation of the hybrid and the MMLR models at site 1 (Chelsea) over the entire period (1961–2000). As shown in the two panels of this Figure, the hybrid model and also the MMLR model shows difficulty in reproducing time-domain variability of these two statistics, and reproduces only average values of them. The hybrid model is however more able to reproduce the annual total and annual maximum of precipitation than the MMLR model, as in this last case, the simulated values are strongly underestimated with respect to observed ones. If the MMLR model could explain more variability on the precipitation series using NCEP/NCAR predictors, the hybrid and MMLR models also can represent more time-domain variability in the annual total or annual extreme precipitations.

Fig. 12

Scatter plots of a annual total precipitation and b annual maximum daily precipitation of the hybrid and MMLR models at site 1 (Chelsea), where numbers represent years from 1961 to 2000

6 Conclusion

For multisite downscaling of daily precipitation, this study provided a hybrid statistical downscaling procedure combined by regression-based and stochastic weather generation approaches. The developed hybrid procedure was then applied to generate daily precipitations of nine observation sites located in southern Québec (Canada). Application results of the hybrid model were compared with those of the regression-based MMLR model without stochastic variation, to explain abilities of stochastic weather generating scheme in the hybrid model.

The regression-based MMLR model yielded R-squares of 0.16 ~ 0.22 for daily precipitation occurrence series, and of 0.13 ~ 0.25 for daily precipitation amount series during the calibration period. The MMLR model showed difficulty in reproducing cross-site correlation among multiple observation sites, and systematically over-represented the spatial dependency of daily precipitation occurrence and amount. These low explained variances and over-representing of spatial dependency of observed daily precipitation from local observation sites underline the difficulty to downscale precipitation series from large-scale predictors using regression-based downscaling approaches. The daily MMLR occurrence and amount models were developed separately for each month to take into consideration seasonal variability of precipitation. These MMLR models showed clear different performance for each month. On average, the MMLR models showed worse performance in summer than in the other seasons.

In generating daily precipitation occurrence, the hybrid model showed good reproduction ability for number of wet days, cross-site correlation, and probabilities of consecutive wet days for various periods of observed precipitation occurrence series for all observation sites. These results indicate that the stochastic weather generation procedure and the first-order Markov chain model are successful in reproducing the temporal variability and spatial dependency of the observed precipitation occurrence. Although, the hybrid model reproduced various durations of wet days fairly well, it reproduced little over-represented values for lag-l auto-correlations. The hybrid model also reproduced seasonal variability of cross-site correlation, and lag-1 auto-correlation fairly well.

In generating daily precipitation amount, the hybrid model reproduced mean precipitation and standard deviation of wet days, cross-site correlation, and maximum 3-days precipitation total amount reasonably well for all observation sites. These results indicate that the stochastic weather generation procedure and probability distribution mapping technique are successful in reproducing the temporal variability and spatial dependency of the observed precipitation amount. However, this model tended to slightly under-estimate cross-site correlation coefficients of precipitation amounts of most station pairs. Unsurprisingly, the MMLR model yielded highly biased results for these statistics. The MMLR included zero amounts of precipitations for calibration so as to downscale precipitation amounts conditional on nearby station being dry which usually have smaller amounts than corresponding amounts conditional on near neighbors being wet. The hybrid and also the MMLR models however showed difficulty in reproducing time-domain variability of the daily precipitation series and represented only average values of them (see Fig. 12). However, the reproducing ability of the hybrid model for time-domain variations can be improved, if the MMLR model could explain more variance of the observed precipitation series by using both large and regional scale predictors. This can be done in further works, using regional reanalysis products available over the whole North America at higher resolution than global-scale NCEP/NCAR products (i.e. NARR products, e.g. Mesinger et al. 2006), in order to incorporate into the deterministic part of the MMLR model more spatial and temporal dependency between precipitation values over the area of interest. Some promising results (see Gachon et al. 2011) have been recently obtained over one specific Canadian station (Ottawa) when using regional-scale predictor variables from NARR (with respect to NCEP/NCAR) in the SD process, in order to improve both median and quantile values of daily precipitation amount and its variability. Further steps will also consist to evaluate the hybrid approach developed in our study using both global and regional climate models for climate change applications.