Constructing motion primitive sets to summarize periodic orbit families and hyperbolic invariant manifolds in a multi-body system

Abstract

Rapid trajectory design in multi-body systems often leverages individual arcs along natural dynamical structures that exist in an approximate dynamical model. To reduce the complexity of this analysis in a chaotic gravitational environment, a motion primitive set is constructed to represent the finite geometric, stability, and/or energetic characteristics exhibited by a set of trajectories and, therefore, support the construction of initial guesses for complex trajectories. In the absence of generalizable analytical criteria for extracting these representative solutions, a data-driven procedure is presented. Specifically, k-means and agglomerative clustering are used in conjunction with weighted evidence accumulation clustering, a form of consensus clustering, to construct sets of motion primitives in an unsupervised manner. This data-driven procedure is used to construct motion primitive sets that summarize a variety of periodic orbit families and natural trajectories along hyperbolic invariant manifolds in the Earth–Moon circular restricted three-body problem.

1 Introduction

Human exploration of the lunar surface through a cislunar waypoint, robotic exploration of asteroids and planetary systems, and the use of advanced space telescopes all require the operation of spacecraft in chaotic, multi-body gravitational environments (Bosanac et al. 2019; Restrepo et al. 2018; Whitley et al. 2018). These types of missions necessitate a rapid and intuitive trajectory design process that enables the design of complex trajectories during concept development and, potentially, post-launch. In multi-body systems, one current approach to rapid trajectory design begins with generating a large database of solutions discretized along families of fundamental solutions such as periodic and quasi-periodic orbits (Folta et al. 2015; Parker et al. 2010). Similarly, analysis of the natural transport of celestial bodies throughout a multi-body system leverages the generation of stable and unstable manifolds of periodic and quasi-periodic orbits (Koon et al. 2011). Specialized design tools then support the exploration and analysis of these families of solutions to identify arcs that are assembled to form an initial guess for a trajectory (Guzzetti et al. 2016). However, searching over a large and complex design space may impede analysis because it requires significant time and resources from a human-in-the-loop. Accordingly, strategies for simplifying the analysis of the design space support effectively exploring and leveraging natural motion for increasingly complex mission concepts, mission extensions, and real-time operations as well as the study of natural transport in a multi-body system.

To support continued advancement in trajectory design, the concept of a motion primitive is used in this paper to summarize sets of trajectories in a multi-body system. A motion primitive may be described as an average representation of a range of similar solutions. This concept has been explored extensively in robotic motion planning, transportation applications, and human body gesture analysis (Frazzoli 2001; Jenkins and Mataric 2002; Paranjape et al. 2015; Reng et al. 2005; Wang et al. 2018). In each of these fields, motion primitives are used to decompose complex actions or paths into a finite set of representative components, either via analytical or data-driven techniques. This paper focuses on applying this concept to the analysis of multi-body systems by constructing a motion primitive set that summarizes the characteristics of a set of trajectories seeded from a family of fundamental solutions; this definition is motivated by the eventual goal of reducing the complexity of analysis for a human analyst or in autonomous path planning.

In this paper, motion primitives are used to summarize trajectories within a multi-body system and in a manner that does not place a significant burden on a human analyst. Often used in preliminary trajectory design or the analysis of natural transport within multi-body systems, the circular restricted three-body problem (CR3BP) admits a solution space that exhibits distinctly different sensitivities in various regions and energy levels (Szebehely 1967). However, families of fundamental solutions supply a useful representation of the solution space (Guzzetti et al. 2016; Haapala et al. 2015; Koon et al. 2011). Thus, as a proof of concept, motion primitives are constructed to summarize families of periodic orbits and hyperbolic invariant manifolds in the CR3BP. In contrast to traditional applications in robotics, solutions with the same characteristics as a motion primitive in a specific system modeled by the CR3BP only exist within a limited region of the phase space; yet, the terminology motion primitive still applies as the associated representative trajectory summarizes similar solutions and may support initial guess construction during the trajectory design process. One challenge, however, in extracting a set of motion primitives in the CR3BP is that generalizable and exact analytical criteria for grouping solutions along a family according to both qualitative and quantitative characteristics do not currently exist. Thus, clustering, an unsupervised learning process, is employed to group similar solutions. From each cluster, a single representative member serves as the associated motion primitive.

The utility of clustering algorithms in grouping solutions to nonlinear dynamical systems has been demonstrated by a variety of researchers. For instance, spectral clustering has been employed by Hadjighasem, Karrasch, Teramoto, and Haller to identify coherent Lagrangian vortices within a dynamical system (Hadjighasem et al. 2016). In astrodynamics, the partition-based clustering algorithm, k-means, has been used by Nakhjiri and Villac to identify bounded motions in a specific region of a Poincaré map and by Villac, Anderson, and Pini to group periodic orbit solutions based on the locations of apses and orbital period in the augmented Hill three-body problem (Nakhjiri and Villac 2015; Villac et al. 2016). In addition, Bosanac and Bonasera and Bosanac have applied hierarchical density-based clustering methods to Poincaré maps in the CR3BP to group trajectories with similar geometries to facilitate analysis in the trajectory design process (Bonasera and Bosanac 2021; Bosanac 2020). These applications of clustering all demonstrate the value of a data-driven approach to grouping members of a family or set of trajectories in a chaotic dynamical system based on a defined set of features.

The focus of this paper is to present and demonstrate a systematic motion primitive construction process to summarize dynamical structures in the CR3BP. Generating a set of motion primitives to summarize families of periodic orbits and hyperbolic invariant manifolds supports analysis of the natural transport mechanisms that are often used in trajectory design and govern the natural motion of small celestial bodies (Davis et al. 2010; Gómez et al. 2004; Lo 2002). This paper presents an automated approach for motion primitive construction that limits the burden on a human analyst and may be applied to a variety of periodic and nonperiodic trajectories in the CR3BP. Specifically, the motion primitive construction process leverages k-means (a partition-based method), agglomerative clustering (a hierarchical method), and Weighted Evidence Accumulation Clustering (WEAC) (a consensus method) to extract motion primitives from a set of trajectories based on common trajectory design parameters such as geometry, stability, and energy. The procedure is outlined and demonstrated in detail by constructing motion primitives for the distant prograde orbit (DPO) family, the northern $L_1$ halo orbit family, and trajectories along the unstable manifold associated with an $L_1$ Lyapunov orbit in the Earth–Moon CR3BP. Then, this procedure is extended to a wide variety of planar and spatial periodic orbit families throughout the Earth–Moon CR3BP. Based on these results, this paper offers two contributions: (i) a data-driven procedure for constructing a set of motion primitives that summarizes a family or set of trajectories in an unsupervised manner, and (ii) a demonstration of this procedure in the context of a variety of natural motions throughout the Earth–Moon CR3BP. These contributions may, potentially, contribute to summarizing and reducing the complexity of exploring the solution space admitted by a multi-body system, reducing the analytical workload of a trajectory designer, and facilitating further advancement in rapid and informed trajectory design procedures; demonstrating the use of the constructed motion primitives in the initial guess construction process is the focus of ongoing work.

2 Background: dynamical model and fundamental solutions

The CR3BP is used to approximate the motion of a spacecraft (or small celestial body) under the point mass gravitational influences of the Earth and Moon, each assumed to travel along circular orbits. The spacecraft is assumed to possess a negligible mass compared to the larger primary, the Earth, with constant mass $M_1$ and the smaller primary, the Moon, with constant mass $M_2$ (Szebehely 1967). Following application of these assumptions, a rotating reference frame is defined using the system barycenter as the origin and axes $\hat{\varvec{x}}\hat{\varvec{y}}\hat{\varvec{z}}$: $\hat{\varvec{x}}$ is directed from the Earth to the Moon, $\hat{\varvec{z}}$ is aligned with the orbital angular momentum of the primary system, and $\hat{\varvec{y}}$ completes the right-handed triad (Szebehely 1967). Then, length, mass, and time quantities are nondimensionalized using the characteristic parameters $l^*$, $m^*$, and $t^*$, respectively (Szebehely 1967). Typically, $l^*$ is set equal to the distance between the Earth and Moon, $m^*$ corresponds to the total mass of the system, and $t^*$ is defined such that the nondimensional period of the primary system is equal to $2\pi$ (Koon et al. 2011). The state of the spacecraft is then written in the rotating frame as a nondimensional vector $\varvec{x} = [x, y, z, \dot{x}, \dot{y}, \dot{z}]^{T}$ relative to the barycenter of the system. Accordingly, the nondimensional equations of motion for the spacecraft in the CR3BP are written in the rotating frame as

$$\begin{aligned} \begin{aligned} \ddot{x}&= 2\dot{y} + x - \frac{(1-\mu )(x+\mu )}{r_1^3} - \frac{\mu (x-1+\mu )}{r_2^3} \\ \ddot{y}&= - 2\dot{x} + y - \frac{(1-\mu )y}{r_1^3} - \frac{\mu y}{r_2^3}, \\ \ddot{z}&= - \frac{(1-\mu )z}{r_1^3} - \frac{\mu z}{r_2^3} \end{aligned} \end{aligned}$$

(1)

where $\mu = M_2/(M_1 + M_2)$ is the mass ratio, while $r_1 = \sqrt{(x+\mu )^2 + y^2 + z^2}$ and $r_2 = \sqrt{(x-1+\mu )^2 + y^2 + z^2}$ are the distances between the spacecraft and the Earth and Moon, respectively. In this dynamical system, an integral of motion, labeled the Jacobi constant, exists and is equal to

$$\begin{aligned} C_J = (x^2 + y^2) + \frac{2(1-\mu )}{r_1} + \frac{2\mu }{r_2} - \dot{x}^2 - \dot{y}^2 - \dot{z}^2. \end{aligned}$$

(2)

At a single Jacobi constant, a variety of fundamental solutions exist throughout the phase space, including equilibrium points, periodic orbits, quasi-periodic orbits, and hyperbolic invariant manifolds (Koon et al. 2011; Szebehely 1967).

In the CR3BP, periodic orbits exist within continuous families and contribute to an underlying dynamical structure that influences natural transport within a multi-body system (Koon et al. 2011; Szebehely 1967). Periodic orbits correspond to trajectories that precisely repeat in the rotating frame, with the minimal time interval for repetition labeled the orbit period. Families of periodic orbits exist throughout the phase space and are often labeled using the location of some members relative to primaries and/or libration points, bifurcations that occur along the family, orbital resonance admitted by selected members, or direction of motion. The direction of motion is typically described in the rotating frame: a state that is labeled as prograde (or retrograde) with respect to a selected reference location produces an instantaneous orbital angular momentum vector of the spacecraft with respect to the reference that possesses a positive (or negative) z component.

Each family of periodic orbits used in this paper is computed numerically using multiple shooting in conjunction with pseudo-arclength continuation. To compute a single periodic orbit, an initial guess is constructed using either a stability analysis of a libration point, Poincaré mapping, resonance analysis in the two-body problem, or bifurcation analysis of another periodic orbit family (Bosanac 2016; Hadjidemetriou 1993; Koon et al. 2011; Szebehely 1967). The initial guess is then discretized into multiple arcs with equal integration times. The states at the beginning of all arcs along with the common integration time along all arcs are considered free variables. These free variables are adjusted iteratively using Newton’s method to ensure continuity between all neighboring arcs and, therefore, periodicity to within a specified tolerance of $10^{-12}$ (Bosanac 2016; Koon et al. 2011). Then, pseudo-arclength continuation is used to compute additional members along the periodic orbit family until one of several termination criteria are satisfied: a maximum number of members have been calculated, members pass within a specified minimum threshold on the distance from a primary, the entire family is computed, or the numerical corrections process fails to compute additional members (Bosanac 2016; Keller 1977). Upon completion of the corrections and continuation process, the computed segment of a family of periodic orbits is characterized and analyzed.

The stability of a periodic orbit offers preliminary insights into the solution space in its local neighborhood and the existence of associated dynamical structures. First, a monodromy matrix is calculated by propagating the state transition matrix from a selected point along the periodic orbit for precisely one orbital period (Koon et al. 2011). Then, the monodromy matrix is decomposed into a set of six eigenvalues and associated eigenvectors. In the CR3BP, the eigenvalues exist in reciprocal or complex conjugate pairs: one trivial pair corresponds to unity eigenvalues, while the two nontrivial pairs of eigenvalues are used to assess the stability of the periodic orbit. This stability information is often summarized using the stability indices, $s_1$ and $s_2$ (Howell 1984). Each of these indices is computed in this paper as the following sum of a pair of nontrivial eigenvalues, $\lambda _{j}$ and $\lambda _{k}$, of the monodromy matrix associated with the periodic orbit:

$$\begin{aligned} s_{i} = \lambda _{j}+\lambda _{k} \end{aligned}$$

(3)

for $i=1,2$. A value of the stability index between -2 and 2 indicates the existence of an oscillatory mode and, therefore, a center eigenspace that includes nearby quasi-periodic orbits. An index possessing a magnitude greater than 2, however, indicates the existence of stable and unstable eigenspaces that govern natural motion into and away from the orbit, respectively (Koon et al. 2011). When the order of magnitude of the stability index associated with stable and unstable modes is low, nearby trajectories exciting these modes are relatively slow to arrive into or depart from the orbit.

Global stable and unstable invariant manifolds govern the natural flow of trajectories that asymptotically approach and depart an unstable periodic orbit, respectively (Koon et al. 2011). In the CR3BP, global stable and unstable manifolds are computed numerically (Koon et al. 2011). First, the unstable periodic orbit is discretized into $N_{\text {PO}}$ points, equally spaced in time. Then, a single point is perturbed by a small step along the eigenvector associated with either the stable or unstable mode to produce an approximation of a state that lies in the stable or unstable eigenspace, respectively. This state is then used to produce a trajectory that lies in the global stable or unstable manifold by integrating backward or forward in time, respectively, until any termination criteria are satisfied. These termination criteria may include a maximum integration time, maximum number of apses, crossing a specified boundary in the configuration space, or impacting a primary body. This procedure is repeated for all $N_{\text {PO}}$ points to produce a set of trajectories that span the computed segment of the stable or unstable manifold associated with the unstable periodic orbit.

3 Background: extracting motion primitives via clustering

Motion primitives have been used in various disciplines to construct a reduced basis set of path segments, actions, configurations, or behaviors that reflects the characteristics of a solution space; however, the exact definition of a motion primitive depends on the field of application (Frazzoli 2001; Jenkins and Mataric 2002; Paranjape et al. 2015; Reng et al. 2005; Wang et al. 2018). In robotic motion planning, motion primitives may be defined as sets of control inputs that result in a common desired behavior, such as a circular path or an aggressive turn (Paranjape et al. 2015). Similarly, in transportation applications, motion primitives may be defined as steering and velocity profiles that result in different basic driving tasks such as a lane change or lane keeping (Wang et al. 2018). A set of Euler angles may be used in human body gesture analysis to define motion primitives as fundamental limb configurations (Reng et al. 2005). Frazzoli defines trajectory primitives in the context of autonomous vehicle motion planning as a set of path segments that capture the characteristics of the solution space, support complex path construction, and support extraction of key state description parameters (Frazzoli 2001). Based on these examples, a motion primitive set is defined in this paper as a set of arcs that capture the characteristics of a larger set of trajectories and support assembly of an initial guess for a more complex path in a multi-body system.

Although motion primitives may be extracted analytically or by a human analyst in simple environments, their extraction is significantly more challenging and time-consuming in complex and higher-dimensional dynamical systems (Jenkins and Mataric 2002; Jiang et al. 2016; Wang et al. 2018). In complex dynamical environments, data are often sampled or observed from the environment and then data mining techniques such as feature selection, dimensionality reduction, and clustering are employed to uncover the fundamental primitives in the system. Due to the complexity of the solution space in a multi-body system, this paper leverages clustering to group solutions that possess a similar set of characteristics; these characteristics of interest are defined using domain knowledge. A representative member from each cluster is then designated as a motion primitive (Bosanac 2020; Han et al. 2012; Jiang et al. 2016). Together, the reduced set of trajectories that form a motion primitive set summarize a larger set of arcs of trajectories that exist in a multi-body system.

Clustering is an unsupervised learning method for separating the members of a dataset into a finite number of groups based on a defined set of features (Han et al. 2012). Data in the same cluster possess similar properties, while data in different clusters possess dissimilar properties in a prescribed feature space. Each of the n members of a dataset is described by an m-dimensional feature vector $\varvec{f}$. A clustering algorithm is then applied to the $(n\times m)-$dimensional dataset to construct groupings of the members within the set. Note that sufficiently sampling the data source and constructing an appropriate feature space to produce a useful set of clustering results is determined by the human analyst. For the selected dataset, the resulting clusters are influenced by various factors including: the dataset supplied to the clustering algorithm, the type of clustering method and associated algorithm, the input parameters governing the algorithm, and the selected feature space description (Aggarwal and Reddy 2014). In addition, it is often challenging to select an appropriate algorithm and input parameters for a desired application because the structure of the dataset is typically not known a priori.

To facilitate parameter and algorithm selection in the clustering process, consensus clustering is employed: using an ensemble of individual clustering results to form a single clustering solution (Aggarwal and Reddy 2014; Fred and Jain 2005). This paper leverages the WEAC algorithm to perform consensus clustering due to its capacity to produce clusters of arbitrary shapes, sizes, and densities (Fred and Jain 2005; Huang et al. 2015). As an input to the WEAC algorithm, individual clustering results are constructed using k-means, a partition-based method, and agglomerative clustering, a hierarchical method, each governed by a variety of input parameters. The k-means algorithm is used due to its iterative nature and computational efficiency, while agglomerative clustering is used due to its deterministic nature and the useful insights gained from the resulting dendrogram. Furthermore, both of these clustering algorithms have been successfully used in shape-based time-series clustering applications (Aggarwal and Reddy 2014). This section supplies an overview of these clustering algorithms.

3.1 K-means

The k-means algorithm is a partition-based clustering method that groups members of a dataset according to their distance from k centroids. The centroid of a cluster is defined using the mean feature vector of the members assigned to the cluster (Han et al. 2012). The algorithm requires the number of clusters, k, as an input; then, the centroids are initialized by randomly selecting k members of the dataset (Han et al. 2012). Clusters are then formed by associating each member to the closest centroid using the $l^2$-norm as a distance metric. After assigning each member to a cluster, the centroid of each cluster is recomputed and the members are reassigned to their new closest centroids to form new clusters. This process is repeated iteratively with the goal of minimizing the sum of the squared Euclidean distances between the centroid of each cluster and the associated members. The algorithm terminates either when the clusters remain unchanged from one iteration to the next or a maximum number of iterations are exceeded. If k-means clustering converges on a clustering result prior to reaching the specified maximum number of iterations, the algorithm recovers a local minimum that depends on the selection of the initial centroids (Pedregosa et al. 2011). Furthermore, the primary limitation of k-means is selecting the desired number of clusters when the structure of the dataset is not known or understood a priori. However, using k-means within the consensus clustering process offers one approach to selecting an appropriate value of k without a priori knowledge of the dataset or significant reliance on a human-in-the-loop when applied to a variety of distinct datasets.

To increase the stability and robustness of using k-means clustering, the algorithm is often applied multiple times to the same dataset but with different initial centroids (Han et al. 2012; Pedregosa et al. 2011). Then, the clustering result with the lowest inertia, E, is selected; minimizing the inertia indicates the computation of more compact clusters that minimize the sum of the squared Euclidean distances between the centroid of each cluster and the associated members. The inertia is a metric that is defined as

$$\begin{aligned} E = \sum _{i=1}^{k} \sum _{\varvec{f} \in C_i} ||\varvec{f} - \varvec{c}_i||^2, \end{aligned}$$

(4)

where $C_i$ is the ith cluster, $\varvec{f}$ is the feature vector of a member in the ith cluster, and $\varvec{c}_i$ is the centroid of the ith cluster (Han et al. 2012; Pedregosa et al. 2011). By selecting the clustering result with the lowest inertia, the algorithm becomes more stable and less dependent on the selection of the initial centroids.

3.2 Agglomerative clustering

Agglomerative clustering uses a bottom-up approach to hierarchically represent a dataset as a tree with each node corresponding to a cluster. For a dataset composed of n members, the tree has n leaves, each initially corresponding to a separate cluster (Han et al. 2012). At each step of the algorithm, the distances between all of the current clusters are computed and the pair of clusters with the smallest inter-cluster distance is combined. This process continues until all members are grouped into a single cluster. The resulting tree of clusters is often summarized by a dendrogram that reflects the structure of the dataset at various inter-cluster distances (Han et al. 2012). The dendrogram also captures the lifetime of a specified number of clusters, defined as the range of inter-cluster distances at which those clusters are present and constant (Fred and Jain 2005); long lifetimes in the dendrogram often indicate natural groupings of the dataset. To generate the final clustering result, the dendrogram is cut at a specified inter-cluster distance and the corresponding clusters in the hierarchy are obtained. A suitable value of the inter-cluster distance may be selected either: manually, automatically as the midpoint of the inter-cluster distance range with the longest lifetime, or automatically as the midpoint of the inter-cluster distance range corresponding to a desired number of clusters.

The method used to compute the inter-cluster distance, known as the linkage type, fundamentally influences the underlying tree structure produced by agglomerative clustering. Common linkage types include single, complete, average, and Ward linkage (Aggarwal and Reddy 2014; Han et al. 2012). Single linkage measures the inter-cluster distance as the distance between the closest two members in the two clusters, whereas complete linkage uses the farthest two members. Average linkage measures the inter-cluster distance as the average of the distances between all of the members of the two clusters. Ward linkage, however, captures the increase in the sum of squared distances between each member of two clusters and its associated centroid due to merging the clusters. Mathematically, Ward linkage defines the inter-cluster distance between clusters $C_i$ and $C_j$ as

$$\begin{aligned} d(C_i, C_j) = \sqrt{\frac{2|C_i||C_j|}{|C_i| + |C_j|}} ||\varvec{c}_i - \varvec{c}_j||, \end{aligned}$$

(5)

where $|C_i|$ and $|C_j|$ are the number of members in the ith and jth clusters, respectively, and $\varvec{c}_i$ and $\varvec{c}_j$ are the centroids of the ith and jth clusters, respectively (Kaufman and Rousseeuw 2005). By minimizing the increase in the sum of squared distances of the merged clusters at each step of the algorithm, Ward linkage tends to produce compact and well-separated clusters while considering the overall structure of each cluster. Average linkage is also useful for considering the overall structure of clusters throughout the merging process. However, single and complete linkage only focus on the local and global structure of clusters, respectively, during the merging process and are more sensitive to noise and outliers in a dataset (Aggarwal and Reddy 2014). Distinctly different tree structures and, subsequently, clustering results may be produced using different definitions of inter-cluster distance.

3.3 Weighted evidence accumulation clustering

WEAC generates a consensus clustering result from an ensemble of base clustering results. A significant benefit of using consensus clustering is the capacity to produce better quality and more robust results than a single clustering solution for a variety of datasets, while also supporting automated input parameter selection (Aggarwal and Reddy 2014; Fred and Jain 2005; Huang et al. 2015). The WEAC algorithm requires an ensemble of $N_C$ base clustering results as an input, defined as the set ${\mathbb {P}}$. Each base clustering result, $\varvec{P}_i$ for $i=[1,N_C]$, is the set of cluster labels assigned to the members of a dataset. These base clustering results may be generated in any manner. For example, the ensemble may be generated by a single algorithm with varying input parameters and/or a variety of clustering algorithms (Fred and Jain 2005; Huang et al. 2015). In this paper, both k-means and agglomerative clustering with Ward linkage are used to generate an ensemble of clustering solutions, each for several distinct values of k within a specified range. Each base clustering solution is considered a piece of independent evidence for the natural groupings within the dataset that is used in generating a consensus result from the ensemble of accumulated evidence.

Given an ensemble of base clustering results, WEAC assumes two members of a dataset naturally belong to the same cluster if they are consistently co-located in the base clustering results. This characteristic is quantified by a weighted ensemble co-association matrix. First, a co-association matrix, $\varvec{S}_i$, is computed for each base clustering result. Each matrix is a $n\times n$ similarity matrix in which $\varvec{S}_i(a,b) = 1$ if members a and b are grouped in the same cluster and $\varvec{S}_i(a,b) = 0$ if members a and b are grouped in different clusters within a single base clustering result. Then, a weight, $w_i$, is computed for each base clustering result using its normalized crowd agreement index ($\text {NCAI}$) (Huang et al. 2015). To compute each weight, the crowd agreement index ($\text {CAI}$) for each base clustering is defined as

$$\begin{aligned} \text {CAI}(\varvec{P}_i) = \frac{1}{N_C-1} \sum _{\varvec{P}_j \in {\mathbb {P}}, i \ne j}^{N_C} \text {Sim}(\varvec{P}_i, \varvec{P}_j), \end{aligned}$$

(6)

where $\text {Sim}(\varvec{P}_i, \varvec{P}_j)$ measures the similarity between two base clustering results as the maximal normalized mutual information shared between the two solutions as defined by Strehl and Ghosh (Strehl and Ghosh 2002). Therefore, $\text {CAI}(\varvec{P}_i)$ quantifies the average amount of information that $\varvec{P}_i$ shares with the ensemble and is normalized as

$$\begin{aligned} \text {NCAI}(\varvec{P}_i) = \frac{\text {CAI}(\varvec{P}_i)}{\max _{\varvec{P}_j \in {\mathbb {P}}} \text {CAI}(\varvec{P}_j)} \end{aligned}$$

(7)

The $\text {NCAI}$ of each base clustering result ranges from 0 to 1 and is used to calculate the weight, $w_i$, for the co-association matrix of each clustering result $\varvec{P}_i$ as

$$\begin{aligned} w_i = \frac{I_{\text {NCAI}}(\varvec{P}_i)}{\sum _{j=1}^{N_C} I_{\text {NCAI}}(\varvec{P}_j)}, \end{aligned}$$

(8)

where $I_{\text {NCAI}}(\varvec{P}_i) = (\text {NCAI}(\varvec{P}_i))^\beta$ and $\beta$ is selected to adjust the influence of the $\text {NCAI}$ weighting. Based on the parameter analysis conducted by Huang et al. (2015) on a variety of datasets, a value of $\beta = 2$ is used in this paper. Finally, the weighted ensemble co-association matrix, $\varvec{A}$, is computed as

$$\begin{aligned} \varvec{A} = \sum _{i=1}^{N_C} w_i\varvec{S}_i. \end{aligned}$$

(9)

Then, agglomerative clustering with average linkage is applied to the dataset using $\varvec{A}$ as a precomputed similarity matrix to generate a consensus clustering result; average linkage is selected due to its capacity to support a general similarity metric and capture the average characteristics of entire clusters. Each element of $\varvec{A}$ is a measure of the similarity between two members of the dataset and approximately reflects the percentage of results in which the members are co-located in the same cluster throughout the clustering ensemble. Consequently, the distance between two members of the dataset, a and b, is equal to $1 - \varvec{A}(a,b)$. The final number of clusters is then selected by sampling the resulting dendrogram at the midpoint of the inter-cluster distance range with the longest lifetime above a specified threshold (Fred and Jain 2005; Huang et al. 2015). By introducing an alternative measure of similarity between members of a dataset, WEAC leverages the evidence accumulated by a large ensemble of clustering solutions to generate a single consensus result. As a result, WEAC reduces the sensitivity to and complexity of parameter and algorithm selection.

3.4 Motion primitive extraction

A motion primitive is extracted as the most representative member of a cluster of similar trajectories. In the data-driven approach employed in this paper, the medoid of a cluster is the member of the cluster that is most similar to all other members in the cluster within the prescribed feature space; as a guaranteed member of the cluster, this definition is particularly advantageous for arbitrarily shaped clusters (Han et al. 2012). Using the definition of a medoid, the motion primitive associated with the ith cluster is identified as

$$\begin{aligned} {\varvec{f}_{\text {MotionPrim}_i}} = \mathop {\hbox {argmin}}\limits _{\varvec{f} \in C_i} \sum _{j=1}^{|C_i|} ||\varvec{f} - \varvec{f}_j||, \end{aligned}$$

(10)

where ${\varvec{f}_{\text {MotionPrim}_i}}$ is the feature vector of the motion primitive of the ith cluster, $C_i$; $|C_i|$ is the number of members of the ith cluster; and $\varvec{f}_j$ is the feature vector of the jth member in the ith cluster (Van der Laan et al. 2003).

4 Translating trajectory characteristics into a feature vector

The results of a clustering approach depend on the feature space encoding that translates domain knowledge into a quantitative description of the dataset (Aggarwal and Reddy 2014). Selecting a feature vector is member-specific because the available features depend on the type of members in the dataset, but it is also application-specific because the features should be selected to recover a useful summary of the dataset for the desired application. During the early stages of trajectory design and the study of natural motion in complex gravitational environments, human analysts tend to examine the geometry, stability, and energy of fundamental dynamical structures (Guzzetti et al. 2016; Haapala et al. 2015; Koon et al. 2011). This section outlines the feature vectors formulated to reflect one approach to encoding these characteristics for periodic orbits and nonperiodic trajectories that lie along stable or unstable manifolds in the CR3BP to support the motion primitive extraction process presented in this paper.

4.1 Describing trajectory geometry

The geometry of a trajectory is quantitatively described by discretizing the solution into a sequence of states (Zheng 2015). Sampling a trajectory at equally spaced times may capture small geometric variations along the path. However, selecting a single time distribution or number of states that sufficiently represent a general set of trajectories in a chaotic dynamical system is challenging. Rather, this work uses a generalizable and curve-based approach to produce a lower-dimensional description: sampling a trajectory at apses relative to a specified reference point, such as a primary body or equilibrium point (Bosanac 2020; Zheng 2015); each apsis corresponds to either a local minimum or maximum distance from the reference point along the trajectory.

The state information at each apsis along a trajectory is scaled to prevent unintended feature biases during clustering (Han et al. 2012). Relative position components of the state at each apsis are normalized between -1 and 1 by dividing each position component by the global maximum distance of an apsis relative to the specified reference point along all members of the selected family or set of trajectories. Then, the velocity unit vector $\hat{\varvec{v}}=\dot{\tilde{x}}\hat{\varvec{x}}+\dot{\tilde{y}}\hat{\varvec{y}}+\dot{\tilde{z}}\hat{\varvec{z}}$ reflects the direction of motion at each apsis with components possessing values between -1 and 1; note that the tilde notation indicates a normalized quantity. With these definitions, the geometric component of a feature vector, $\varvec{f}_{g}$, describing a trajectory in the CR3BP is defined in this paper as

$$\begin{aligned} \varvec{f}_{g} = \left[ \tilde{x}_1 \quad \tilde{y}_1 \quad \tilde{z}_1 \quad \dot{\tilde{x}}_1 \quad \dot{\tilde{y}}_1 \quad \dot{\tilde{z}}_1 \quad \cdots \quad \tilde{x}_l \quad \tilde{y}_l \quad \tilde{z}_l \quad \dot{\tilde{x}}_l \quad \dot{\tilde{y}}_l \quad \dot{\tilde{z}}_l \right] , \end{aligned}$$

(11)

where l is the number of apses that occur along the trajectory and all features are in the range $[-1,1]$. This geometric component of a feature vector possesses a dimension of $1\times 6l_{\max }$ where $l_{\max }$ is the maximum number of apses that occur along any member of a set of trajectories. If the number of apses is not constant across all members of a set of trajectories, placeholder vectors are included in the remaining elements of $\varvec{f}_{g}$ (Bosanac 2020). When placeholders are employed, they are set equal to the zero vector to ensure that they are distinct from the vectors describing actual apses. Using these definitions, this component of the feature vector supplies a straightforward geometric description of an orbit that is computationally efficient to construct, limits unintended feature bias, may be generalized across various trajectories, and, when applied to the sets examined in this paper, does not produce an excessively high-dimensional description.

4.2 Describing orbital stability

A function is defined to incorporate stability indices into the feature vector for a periodic orbit. This function is designed to reduce unintended feature bias when the maximum value along the family possesses a large order of magnitude, offer a continuous stability description to avoid a loss of information, and mitigate excessive compression between the critical values of -2 and 2. To appropriately characterize the stability properties along a periodic orbit family, it may be desirable to capture complex variations of the stability indices within the oscillatory mode regime, differentiate between a pair of oscillatory or stable and unstable modes, and avoid an artificial separation between strictly oscillatory modes and the pairs of eigenvalues that possess magnitudes that are close to unity. Furthermore, it may not be essential to distinguish between stability indices with large magnitudes. To achieve these goals in characterizing a periodic orbit in the CR3BP, the stability component of a feature vector, $\varvec{f}_{s}$, is defined using a hyperbolic tangent function, which retains continuity and produces values between -1 and 1. Mathematically, the stability component of the feature vector is written as

$$\begin{aligned} \varvec{f}_{s} = \left[ \tanh \left( {\frac{s_1}{2}}\right) \quad \tanh \left( {\frac{s_2}{2}} \right) \right] . \end{aligned}$$

(12)

For a planar periodic orbit, $s_1$ and $s_2$ are calculated using the in-plane and out-of-plane modes, respectively. However, for a spatial periodic orbit, $s_1$ and $s_2$ each reflect the evolution of a single pair of eigenvalues along the family, ensuring continuity in the stability indices. Through the definition in Eq. 12, stability indices within the range $[-2,2]$ produce a feature vector component within the approximate range $[-0.7616, 0.7616]$ to maintain significant resolution in the stability component of the feature vector. Due to continuity in the hyperbolic tangent function, there is also no artificial separation between a stability index with a magnitude that is strictly below 2 and one that is only slightly above. In addition, the asymptotes of the hyperbolic tangent function limit the differentiation between stability indices with large magnitudes.

4.3 Describing orbital energy

Orbital energy is often used to supply preliminary insight into accessible regions of motion and heuristics for maneuver planning. In the CR3BP, the Jacobi constant, as defined in Eq. 2, is inversely proportional to the energy of the system (Koon et al. 2011): an increase in the Jacobi constant corresponds to a decrease in the energy of the system, and vice versa. Therefore, the energy component of a feature vector, $f_{e}$, for a trajectory in the CR3BP is defined as

$$\begin{aligned} f_{e} = {\tilde{C}}_{J}, \end{aligned}$$

(13)

where ${\tilde{C}}_{J}$ is the Jacobi constant normalized to within the range $[-1,1]$ using the minimum and maximum values of $C_J$ along the computed set of trajectories. This component of the feature vector supplies a single parameter to describe the energetic properties of each member of a set of trajectories in the CR3BP.

4.4 Defining feature vectors

Leveraging the geometric, stability, and energetic properties of a trajectory in the CR3BP, feature vector definitions are formulated separately for periodic orbits and trajectories along a stable or unstable manifold. The feature vector ${\varvec{f}_{\text {PO}}}$ is constructed to describe a periodic orbit and simultaneously capture a variety of considerations of interest to a trajectory designer during initial guess construction. This parametric feature vector is defined as

$$\begin{aligned} {\varvec{f}_{\text {PO}}} = [\varvec{f}_{g} \quad \varvec{f}_{s} \quad f_{e}] \end{aligned}$$

(14)

and possesses a length of $m=6l_{\max }+3$. For a planar periodic orbit, the out-of-plane position and velocity features are omitted, resulting in a feature vector with a length of $m=4l_{\max }+3$. Similarly, the feature vector ${\varvec{f}_{\text {Mani}}}$ is constructed to describe the geometry of a trajectory along either a stable or unstable manifold associated with an unstable periodic orbit. This feature vector is defined as

$$\begin{aligned} {\varvec{f}_{\text {Mani}}} = [\varvec{f}_{g} \quad \Delta {\tilde{t}}_1 \quad \cdots \quad \Delta {\tilde{t}}_{l-1}], \end{aligned}$$

(15)

where $\varvec{f}_{g}$ contains the states associated with apses along the trajectory with respect to a specified reference point and $\Delta {\tilde{t}}_i$ is the nondimensional time between two consecutive apses, normalized by the total integration time of the trajectory. Note, the terminal state of the trajectory is included in $\varvec{f}_{g}$, which may or may not correspond to a desired apsis. The additional normalized time features are included in ${\varvec{f}_{\text {Mani}}}$ to capture the variations in transit time along a nonperiodic trajectory. Similar to the use of placeholder vectors in $\varvec{f}_{g}$, values of zero are used for the remaining normalized time features in ${\varvec{f}_{\text {Mani}}}$ when $l < l_{\max }$ for a trajectory. Furthermore, $f_e$ is not included in the feature vector because in this paper all of the manifold trajectories in a given dataset are associated with one periodic orbit and, therefore, possess the same value of the Jacobi constant. Therefore, ${\varvec{f}_{\text {Mani}}}$ possesses a length of $m=7l_{\max }-1$ for a spatial manifold, or $m=5l_{\max }-1$ in the planar case, and quantitatively summarizes the geometry of a trajectory along a stable or unstable manifold. Both feature vector definitions supply a finite, quantitative description of trajectories along a family to create an $(n\times m)-$dimensional dataset that is input to a clustering algorithm for motion primitive extraction.

5 Summarizing periodic orbit families

The motion primitive construction process is defined for periodic orbits in the CR3BP and demonstrated in detail via application to the planar DPO and spatial northern $L_1$ halo periodic orbit families in the Earth–Moon CR3BP. Each of these periodic orbit families exhibits several changes in geometry, stability, and energy along the family. Some of these changes may be identified through analytical separation criteria capturing a change in the number of apses or locating when a critical value or turning point occurs for a parameter calculated along the family. These analytically identifiable changes supply a straightforward verification of some of the groupings within the clustering results. However, the clustering process should be able to produce additional differentiation between periodic orbits that a human may be able to visually identify but may not be described by an associated set of generalizable and clear analytical criteria formulated as a function of the feature space description. Thus, both of these families of periodic orbits serve as a suitable example for demonstrating the procedure for extracting motion primitives that summarize the finite set of geometric, stability, and energetic characteristics admitted by its members. Following a detailed demonstration in the context of these two families, the motion primitive extraction process is applied to a wider variety of periodic orbit families throughout the Earth–Moon CR3BP.

5.1 Motion primitive construction process for periodic orbits

For a family of periodic orbits, the motion primitive construction procedure consists of the following steps:

• 1. Compute a family of periodic orbits in the desired system in the CR3BP.

• 2. For n orbits sampled along the family, compute the full state at each apsis along the orbit with respect to a specified reference point, the stability indices, and the Jacobi constant.

• 3. Construct an $(n\times m)-$dimensional dataset containing the m-dimensional feature vector ${\varvec{f}_{\text {PO}}}$ of each orbit, as defined in Eq. 14, to reflect the geometry, stability, and energy of each periodic orbit.

• 4. Generate an ensemble of $N_C$ base clustering results by applying k-means and agglomerative clustering with Ward linkage to the dataset, each for $N_C/2$ values of k in a specified range.

• 5. Specify an inter-cluster distance threshold, t, ranging from 0 to 1 and apply WEAC to the ensemble of base clustering results computed in Step 4. The clustering result selected using WEAC possesses a number of clusters with the largest lifetime above t.

• 6. Extract a set of motion primitives as the medoids of clusters in the final consensus clustering result to summarize the periodic orbit family.

Once the desired set of trajectories is computed, this procedure only requires selection of the range of values of k to form the base clustering results and the value of t used within WEAC to select the final clustering result. In applying this procedure to the DPO and northern $L_1$ halo orbit families in the Earth–Moon system, the following values are selected: $k \in [3, 18]$ to produce $N_C = 2\times 16 = 32$ base clustering results that are input to WEAC, and $t = 0.4$. The range of selected k values is a wide range that encompasses a reasonable number of expected distinct characteristics along each family. The threshold value of $t = 0.4$ (i.e., a similarity value of 0.6) is selected because it ensures that clusters with members that are co-located more than approximately 60% of the time on average remain clustered together in the final consensus-derived result. The final “cut” of the dendrogram is above $t = 0.4$ and therefore identifies a natural cluster boundary where the additional merging of two smaller clusters no longer results in a cluster whose members are frequently co-located. Finally, all clustering results are produced using the Scikit-Learn v0.23.1 module available in Python and the components of the WEAC algorithm that do not involve clustering have been implemented by the authors in MATLAB^® (MathWorks 2020; Pedregosa et al. 2011). The computation time for this clustering procedure to generate motion primitives summarizing a periodic orbit family is on the order of $10^{0}$ seconds for each example in this section.

5.2 Summarizing the distant prograde orbit family

The DPO family is composed of members that exhibit multiple distinct geometric and stability properties while encircling the Moon (Broucke 1968; Lara and Russell 2006). Figure 1 displays a subset of the DPO family, computed in the Earth–Moon CR3BP using a multiple shooting algorithm for corrections and pseudo-arclength continuation. Each orbit in the computed segment of the family is plotted in the rotating frame with the arrows indicating direction of motion. The equilibrium points are displayed using red diamonds while the Moon is plotted, not to scale, using a gray circle. Additionally, the in-plane ($s_1$) and out-of-plane ($s_2$) stability indices along this segment of the DPO family are displayed in Fig. 2 as a function of the Jacobi constant. Note that the stability indices are scaled in Fig. 2 using the function $2\sinh ^{-1}(s_{i})/\sinh ^{-1}(2)$ to improve visualization. A stability index associated with oscillatory modes produces a value of this function within the range $[-2,2]$, while a stability index associated with a stable and unstable mode pair produces a function value that is greater than 2 in magnitude; note that the sign of the stability index is preserved through this normalization. In addition, four orbits, each denoted with a distinct color, are highlighted in Fig. 1 and their associated parameters are plotted in Fig. 2 to facilitate a clear description of the family. These two figures reveal distinct changes in geometry, stability, and energy along the DPO family: some changes may be described via quantitative separation criteria, whereas other changes are challenging to define in an analytical and generalizable manner. These complex variations render the planar DPO family a useful first scenario for demonstrating the motion primitive construction process.

Fig. 1

Computed segment of the DPO family in the Earth–Moon CR3BP, displayed in the rotating frame

Fig. 2

Stability indices, $s_1$ and $s_2$, along the computed segment of the DPO family in the Earth–Moon CR3BP

To support verification of the recovered motion primitives, the geometry and stability of members of the DPO family are characterized. At one end of the computed segment of the family near $C_J \approx 3.1487$, denoted in purple in Figs. 1 and 2, the orbits possess stable and unstable in-plane modes and oscillatory out-of-plane modes. In addition, motion along these orbits is generally prograde in the rotating frame: there are two prograde perilunes, with one occurring close to the Moon and one located close to $L_{2}$, and two retrograde apolunes that occur near $L_{2}$ and symmetrically about the x-axis. As the Jacobi constant increases, the magnitude of the velocity vector at the two apolunes decreases. After reaching a magnitude of zero in the rotating frame, the velocity vector changes direction and the associated orbit possesses two prograde apolunes. These prograde apolunes approach the x-axis as the Jacobi constant continues to increase. Eventually, the orbits evolve to possess only one perilune and one apolune; both apses relative to the Moon are prograde and located on the x-axis. This evolution of the geometry is accompanied by a change in the in-plane stability such that these members of the DPO family do not possess any stable or unstable modes. As the Jacobi constant increases further, the perilune distance increases and the apolune distance decreases until the orbit resembles an oval. Eventually, the orbits possess two prograde perilunes on the x-axis and two prograde apolunes symmetrically located about the x-axis. As the Jacobi constant reaches a maximum, denoted in red in Figs. 1 and 2, another change in the stability occurs and the associated members of the DPO family possess stable and unstable in-plane modes. With a decreasing Jacobi constant, the apolunes occur at increasing values of y and decreasing values of x, with a speed that decreases. After the velocity magnitude passes through zero, denoted in light blue in Figs. 1 and 2 and at low values of the Jacobi constant, orbits along the DPO family possess low prograde perilunes and high retrograde apolunes. The out-of-plane stability also changes, resulting in these members of the DPO family possessing only stable and unstable modes through the end of the computed segment of the family, as indicated in light brown in Figs. 1 and 2.

The observed distinct changes in geometry and stability are summarized to facilitate verification of the results. Table 1 lists these changes using labels beginning with “G” to indicate a change in the geometry, assessed via the number and direction of motion at each apsis, and a prefix “S” indicating a qualitative change in stability; the numbers in each label are assigned to changes that occur as the family is traversed from a Jacobi constant starting at $C_J \approx 3.1487$, reaching a maximum at $C_J \approx 3.1827$, and ending at $C_J \approx 2.9511$. A horizontal bar in Table 1 indicates that a change did not occur in a specific property. These distinct changes in the geometry and stability support verifying some of the cluster-based differentiation between orbits during the motion primitive construction process. Specifically, the final clustering result should at least separate solutions of distinct geometries, as listed in Table 1, while also admitting additional differentiation for geometric changes that are challenging to describe in an analytical and generalizable manner. Due to the form of the stability component of the feature vector for a periodic orbit, the stability changes listed in Table 1 may potentially, but not necessarily, lie close to the boundaries of some clusters.

Table 1 Dominant geometric and stability changes along the DPO family; prograde is abbreviated as ‘pro.’ and retrograde is abbreviated as ‘retro.’ to describe direction of motion

Consensus clustering is used to differentiate periodic orbits within the DPO family. First, the parametric feature vector defined in Eq. 14 is used to represent the geometric, stability, and energetic properties of 400 members of the family, computed using multiple shooting for corrections and pseudo-arclength continuation. The geometry of each orbit is represented as a sequence of apses relative to the Moon. Furthermore, the out-of-plane position and velocity features of each apsis are omitted because all members of the DPO family lie in the plane of the primaries. The feature vectors of the selected members of this family are used to form a $(400\times 19)-$dimensional dataset. Then, k-means and agglomerative clustering with Ward linkage are applied to the dataset, each for 16 values of k ranging from 3 to 18, to produce 32 base clustering results. The resulting dendrogram formed when WEAC is applied to this ensemble of clustering results is displayed in Fig. 3. Each vertical blue line represents a cluster, and each horizontal blue line represents the merging of two clusters at various values of the inter-cluster distance, displayed on the vertical axis. Values on the horizontal axis are not labeled because they indicate the cluster identification numbers, which are arbitrarily set by the algorithm as new clusters are formed with new values of inter-cluster distance. The solid black line indicates the specified inter-cluster distance threshold of $t = 0.4$. Analyzing the dendrogram, the number of clusters with the largest lifetime above this threshold is $k = 9$, as indicated by the bounding dashed red lines. Other potential natural cluster boundaries in the dataset occur for $k = 6$ and $k = 7$ as evident in the dendrogram based on the size of each cluster lifetime. However, $k = 9$ is selected consistent with possessing the largest lifetime above the threshold. Motion primitives are extracted from this clustering result as the medoid of each cluster.

Fig. 3

Dendrogram constructed via WEAC to determine clusters of periodic orbits in the DPO family

Fig. 4

Motion primitives constructed for the DPO family in the Earth–Moon CR3BP, displayed with respect to the corresponding clusters in the rotating frame; clusters and motion primitives are split across two subfigures for visual clarity

The motion primitives and associated clusters are depicted in the configuration space and as a function of Jacobi constant to support further analysis. First, the nine clusters of periodic orbits are displayed in Fig. 4 in the configuration space using unique colors, with the black arrows indicating direction of motion relative to the Moon. Within each cluster, the periodic orbit selected as the motion primitive is highlighted in bold, while additional members lie within the region of the same color. To support further analyzing these results, these clusters and motion primitives are also displayed on the left of Fig. 5 as a function of $C_J$. DPOs at various values of $C_J$ are displayed on the right of Fig. 5 for reference; the selected orbits correspond to those highlighted in Fig. 1. Each cluster in Fig. 5 is colored consistent with Fig. 4, and each motion primitive is located by a black diamond. Furthermore, the four dominant geometry changes (G1, G2, G3, G4) and the three dominant stability changes (S1, S2, S3) summarized in Table 1 are denoted with dashed black and gray lines, respectively.

Fig. 5

Clustering result and motion primitives for the DPO family in the Earth–Moon CR3BP as a function of $C_J$; dominant changes in geometry and stability are labeled on left of the figure

Analysis of the clustering results in Figs. 4 and 5 reveals that the motion primitive set successfully captures variations in geometry and stability of members along the DPO family: including those identified in Table 1 and more subtle changes that are challenging to describe in an analytical and generalizable manner. The presented procedure successfully identifies, at a minimum, all four distinct changes in geometry via changes in the number of and direction of motion at the apses. Additional clusters capture more subtle changes in Jacobi constant, stability, and geometry. For example, as $C_J$ decreases after the change in geometry at G4, WEAC identifies three different clusters of orbits with two high retrograde apolunes and two low prograde perilunes due to the variations in $C_J$ and stability. In fact, the third stability change, S3, is identified by the clustering approach but not exactly at the boundary due to the continuous feature description used to capture orbital stability. The distinct geometric differences between each of these clusters is visible in Fig. 4a: although members of these clusters admit a similar general shape, regions along each orbit with a different direction of motion possess a distinctly different relative size in the configuration space. Another example of successful geometric differentiation is visible in Fig. 4b: the gray cluster possessing members with the largest y-extension admit a significantly different geometry and evolution of the location of apses compared with members in the neighboring maroon cluster. This example demonstrates the capacity to use clustering to extract a small set of motion primitives representing a family of planar periodic orbits.

5.3 Summarizing the northern $L_1$ halo orbit family

Fig. 6

Subset of the northern $L_1$ halo orbit family in the Earth–Moon CR3BP, displayed in the rotating frame

The $L_1$ halo orbits comprise a spatial family that emerges from a bifurcation along the $L_1$ Lyapunov orbit family (Breakwell and Brown 1979; Zagouras and Kazantzis 1979). Figure 6 displays in black a subset of the northern $L_1$ halo family computed in the Earth–Moon CR3BP with selected members highlighted in distinct colors; note, only the northern orbits are analyzed due to their symmetry with the southern halo orbits about the plane of the primaries. At one end of the computed segment of the northern $L_1$ halo family, denoted in light brown in Fig. 6, members intersect the $L_1$ planar Lyapunov orbit family and revolve in a clockwise manner about $L_1$. At the other end of the computed segment of the family, denoted in purple in Fig. 6, members possess large z-extensions above the plane of the primaries and a low perilune. Analysis of Fig. 6 reveals a variation in the shape and three-dimensional geometry along this spatial family. However, unlike the previous example with the DPO family, these geometric changes cannot be straightforwardly identified or analytically separated because the number of apses and the direction of motion at each apsis relative to the Moon are constant along the family. There are some changes in the number of apses relative to $L_1$, but the direction of motion at these apses also remains constant along the family. With geometry changes that are visually identifiable but challenging to locate analytically, the northern $L_1$ halo orbit family offers a suitable second demonstration case for the motion primitive construction process.

Fig. 7

Stability indices, $s_1$ and $s_2$, of the northern $L_1$ halo orbits in the Earth–Moon CR3BP

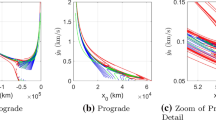
The stability indices of the computed segment of the northern $L_1$ halo family also admit multiple qualitative changes. Figure 7 displays the stability indices, $s_1$ and $s_2$, scaled using the same normalization function as Fig. 2 and plotted as a function of the Jacobi constant; the parameters associated with the highlighted orbits in Fig. 6 are indicated using the same color scheme. The qualitative changes in the orbital stability along the family are summarized in Table 2, using the same configuration as Table 1. There are five primary changes in stability along the computed segment of the family. The $s_1$ index exhibits three changes in stability, occurring in regions of the family where the halo orbits possess a large inclination and low perilune. For members of the family that approach the $L_{1}$ equilibrium point with a Jacobi constant that is above $C_J = 3.0$, $s_1$ possesses a large positive value, corresponding to the existence of stable and unstable modes governing fast arrival into or departure from the periodic orbit. Conversely, $s_2$ indicates two changes in stability: the value of $s_2$ passes through the critical value of -2 near Jacobi constants of $C_J \approx 2.9435$ and $C_J \approx 2.9986$. However, for members that possess a high inclination, low perilune, and values of the Jacobi constant that are less than $C_J = 3.0$, the magnitude of the stability index is on the order of $10^{0}$. As a result, natural arrival into and departure from the vicinity of these members via these stable and unstable modes is relatively slow.

Table 2 Dominant stability changes along the northern $L_1$ halo orbit family

Using the geometric, stability, and energetic properties of members along the northern $L_1$ halo orbit family, an associated set of motion primitives is constructed. Similar to the DPO example, multiple shooting and pseudo-arclength continuation are used to compute 498 orbits along the northern halo orbit family. Then, the feature space encoding is constructed using Eq. 14. The reference point used to compute the apses and relative position vectors along each halo orbit is selected as the Moon, consistent with the evolution of this family toward the Moon. Together, these orbits and feature vectors produce a $(498\times 15)$-dimensional dataset. K-means and agglomerative clustering with Ward linkage are then applied to the dataset, each for 16 values of k ranging from 3 to 18, to generate the ensemble of base clustering results. WEAC is then applied to this ensemble with an inter-cluster distance threshold of $t = 0.4$. Figure 8 displays the dendrogram produced by WEAC for this family of halo orbits. As denoted in Fig. 8 with dashed red lines, the clusters produced using $k = 11$ possess the largest lifetime. The associated clusters, denoted by unique colors, and the motion primitives, denoted with black diamonds, are displayed in Fig. 9a as a function of the discretized orbit number along the family; although this quantity does not possess a physical significance, it enables a clear and unique initial visualization of the results. Furthermore, the five dominant stability changes (S1, S2, S3, S4, S5) summarized in Table 2 are denoted with dashed gray lines. Figure 9b displays the members of each cluster in configuration space; the motion primitives are highlighted in bold and the corresponding clusters capture the region of existence of each primitive in the system.

Fig. 8

Dendrogram constructed via WEAC to determine clusters of periodic orbits in the northern $L_1$ halo family

Fig. 9

Clustering result and motion primitives for the northern $L_1$ halo orbits in the Earth–Moon CR3BP; dominant stability changes are labeled on left of the figure

Despite the absence of distinct or hard boundaries between members within the 15-dimensional feature space, the motion primitive set successfully captures the variety of geometric and stability characteristics exhibited by the northern $L_1$ halo orbit family. Figure 9a reveals that members are differentiated into separate clusters in the vicinity of, but not exactly at the location of, each qualitative change in orbital stability; such a result is not unexpected due to the definition of the stability component of the feature vector as a continuous function. S1, S2, S3, and S4 each describe stability changes where the two nontrivial pairs of eigenvalues of the monodromy matrix remain close to the unit circle in the complex plane and, therefore, the values of the stability component of the feature vector are similar on either side of each soft boundary. On the other hand, S5 is more closely captured by the clustering approach because it marks a more distinct change in stability as the magnitude of $s_1$ increases significantly away from the critical value of 2. The remaining clusters along the family above the dashed line for S5 in Fig. 9a primarily reflect changes in geometry. In fact, analysis of Fig. 9b reveals that these clusters capture the evolution of the eccentricity, inclination, shape, and location of members along this family as they evolve toward the plane of the primaries near $L_1$ and away from the Moon. The reduced set of motion primitives effectively captures the characteristics of the computed members of the northern $L_1$ halo orbit family, thereby supplying a simplified representation of the continuous family of spatial periodic orbits for future use in rapid and informed trajectory design strategies.

5.4 Summarizing periodic orbit families throughout the Earth–Moon system

To further demonstrate the utility of summarizing a subset of the solution space of a multi-body system, the motion primitive construction process is applied to a variety of planar and spatial periodic orbit families throughout the Earth–Moon CR3BP. Each family of orbits is summarized based on its geometric, stability, and energetic properties following the procedure outlined in Sect. 5.1. Figure 10 displays the set of motion primitives constructed to summarize a variety of planar periodic orbit families in the Earth–Moon system including: the low prograde orbits (LoPOs); distant retrograde orbits (DROs); $L_1$, $L_2$, and $L_3$ Lyapunov orbits; $L_5$ short and long period orbits; and 3:1 resonant orbits. The black arrows indicate direction of motion, while each color indicates a distinct cluster and the associated motion primitive is highlighted in bold. The corresponding cluster for each motion primitive also reflects the region of existence of the primitive in the configuration space of the Earth–Moon system. Note that although colors are frequently repeated across distinct families for visual clarity, each cluster is localized to a single family of periodic orbits. Using a similar configuration to Figs. 10, 11 displays the motion primitives generated to summarize the northern $L_2$ and $L_3$ halo orbits; the $L_1$, $L_2$, and $L_3$ axial orbits; and the $L_1$, $L_2$, and $L_3$ vertical orbits. These orbit families are diverse in terms of their geometric, stability, and energetic properties as well as their locations in the configuration space of the Earth–Moon system. Despite the diversity and complexity exhibited by each family of periodic orbits, the general motion primitive construction process presented in Sect. 5.1 is applied to each family in the same manner. This automated, unsupervised approach successfully constructs groupings that capture the fundamental characteristics of members along each family. As a result, these examples indicate the capacity for a data-driven procedure to extract smaller sets of motion primitives that summarize the wide variety of periodic orbits that influence the solution space within a multi-body system. This simpler representation of periodic orbit families may be used to reduce the complexity of constructing an initial guess for a complex trajectory; such use of the constructed motion primitives is the focus of ongoing work.

Fig. 10

Motion primitives summarizing planar periodic orbit families in the Earth–Moon CR3BP, displayed with respect to the corresponding clusters in the rotating frame

Fig. 11

Motion primitives summarizing spatial periodic orbit families in the Earth–Moon CR3BP, displayed with respect to the corresponding clusters in the rotating frame

6 Summarizing hyperbolic invariant manifolds

The role of hyperbolic invariant manifolds in governing natural transport throughout a multi-body system has resulted in trajectory designers analyzing the geometry of arcs of finite duration along stable and unstable manifolds and assembling them to construct initial guesses for complex transfers (Koon et al. 2011). In this section, the motion primitive construction process is defined and demonstrated by summarizing these arcs along the unstable manifold associated with a single $L_1$ Lyapunov orbit in the Earth–Moon CR3BP. This procedure is similar to the process presented in Sect. 5.1 for periodic orbit families with some modifications, primarily in the computation and description of the nonperiodic trajectories comprising the dataset and additional cluster refinement.

6.1 Constructing motion primitive sets for hyperbolic invariant manifolds

To construct a set of motion primitives summarizing arcs along a hyperbolic invariant manifold, the clustering procedure is defined as follows:

• 1. Select an unstable periodic orbit and discretize the orbit into ${N_{\text {PO}}}$ states, equally spaced in time. Then, generate the stable or unstable manifold by propagating each nearby state that lies in the approximation of the manifold backward or forward in time, respectively, until any termination criteria are satisfied. In this section, each trajectory along the unstable manifold of the selected periodic orbit is propagated until either 15 subsequent apses occur relative to the Moon, an impact with the Moon occurs, or the trajectory departs the lunar vicinity either through the $L_1$ or $L_2$ gateways.

• 2. Discretize each trajectory into multiple smaller arcs based on an apsis window, where each apsis is defined relative to a specified reference point. In this section, up to the first 12 apses that occur along each trajectory along the unstable manifold of the selected periodic orbit are used to define smaller arcs each composed of a total of 4 apses relative to the Moon. Along a given trajectory, the first arc is defined from the first apsis event of the trajectory propagated until the fourth apsis event, the second arc is defined from the second apsis event propagated until the fifth apsis event, and so forth until the final computed arc terminates at the final recorded apsis of the trajectory. If the apsis window is larger than the total number of apses along the trajectory, then the trajectory is considered a single arc.

• 3. Compute the feature vector ${\varvec{f}_{\text {Mani}}}$ defined by Eq. 15 for each arc constructed in Step 2. In this feature vector, the time between apses along an arc is normalized by the total integration time of the corresponding arc. Additionally, the terminal state of an arc is included in ${\varvec{f}_{\text {Mani}}}$ if the associated trajectory contains fewer apses than the specified apsis window.

• 4. Construct an $(n\times m)-$dimensional dataset containing the feature vectors computed in Step 3.

• 5. Generate an ensemble of $N_C$ base clustering solutions by applying k-means and agglomerative clustering with Ward linkage to the dataset, each for $N_C/2$ values of k in a specified range.

• 6. Specify an inter-cluster distance threshold, t, ranging from 0 to 1 and apply WEAC to the ensemble of base clustering solutions computed in Step 5. The clustering result selected using WEAC possesses a number of clusters with the largest lifetime above t.

• 7. If necessary, refine the clusters produced by WEAC. For each cluster with more than 10 members, construct a c-nearest neighbor graph from the members in the cluster using a specified value of c and compute the number of connected components in the graph. If there is more than one connected component, then split the original cluster into multiple sub-clusters that each contain one connected component in the graph. However, for clusters with 10 members or less, a c-nearest neighbor graph is well-connected for even small values of c due to its size. Therefore, the similarity values computed in WEAC are directly leveraged to refine small clusters and ensure the members have a high degree of similarity. Specifically, for clusters with 10 members or less, members in the cluster with similarity values greater than or equal to 0.75 are grouped; this value tends to split a small cluster of insufficiently similar members into multiple sub-clusters, each composed of members with a high degree of similarity.

• 8. Extract a set of motion primitives as the medoids of clusters in the final consensus clustering result to summarize the set of trajectories along the selected stable or unstable manifold.

Given a desired set of trajectories, this motion primitive construction process is an automated procedure that only requires selecting the range of k, specifying t, and, if applicable, specifying c. In applying this process to the unstable manifold associated with an $L_1$ Lyapunov orbit in the Earth–Moon system, the inter-cluster distance threshold is set at $t = 0.4$. Furthermore, the range of k values used to generate the cluster ensemble is selected based on the size of the dataset as $k \in [3,61]$ (Fred and Jain 2005; Huang et al. 2015). This range is selected to ensure the evidence supplied to WEAC in the form of base clustering results encompasses both a small number of clusters, which tends to raise the average similarity values between members in the matrix $\varvec{A}$, and a large number of clusters that tends to lower the average similarity values in $\varvec{A}$; as a result, a wide range of k values tends to balance out these effects to more clearly reflect the natural structure of this complex dataset (Fred and Jain 2005; Huang et al. 2015). Finally, all clustering results are produced using the Scikit-Learn v0.23.1 module available in Python and the components of the WEAC algorithm that do not involve clustering have been implemented by the authors in MATLAB^® (MathWorks 2020; Pedregosa et al. 2011). The computation time for this clustering procedure to generate motion primitives summarizing the arcs along a hyperbolic invariant manifold is on the order of $10^{1}$ seconds for the example in this section.

An additional step for cluster refinement is included in the motion primitive construction procedure due to the potential sparsity of arcs computed along a hyperbolic invariant manifold and for cases when related, yet visually distinct arcs are incorrectly clustered together; such issues may occur in high-dimensional feature spaces due to the curse of dimensionality (Aggarwal and Reddy 2014). Inspired by a previous use of graph theory for more complex cluster refinement in hierarchical clustering (Karypis et al. 1999), a c-nearest neighbor graph is a simple and powerful tool to autonomously determine if a cluster should be further split into smaller groups. For example, a homogeneous cluster will likely only contain one connected component in a c-nearest neighbor graph, while a cluster consisting of several smaller and separated sub-clusters may contain multiple connected components depending on the selected value of c. When $c = 1$, a sparse graph is produced and may contain a large number of connected components that each possess only two members, resulting in an excessive fragmentation of an original cluster. However, $c = 2$ generates a better-connected graph that avoids this issue and may preserve the structure of continuous, homogeneous clusters. A large value of c naturally results in a well-connected graph because c dictates the number of nearest neighbors each member is connected to in the graph (Han et al. 2012). Therefore, c may be selected based on the desired scale of cluster refinement; in this section, c is set equal to 2. This automated refinement process limits the burden on a human analyst when additional refinement is deemed appropriate.

A sub-cluster that is comprised of only one or two members cannot be identified using a c-nearest neighbor graph when $c \ge 2$; these types of sub-clusters may be considered as outliers. To address these edge cases and include outlier detection, two rules are formulated to identify sub-clusters with only one or two members during the cluster refinement in Step 7 of the motion primitive construction process. A member of a cluster is identified as the sole member of a sub-cluster when: (i) it is not a nearest neighbor of any other members in its cluster, and (ii) its average similarity to its nearest neighbors is less than 0.75. By leveraging this large similarity value threshold with the c-nearest neighbor graph, sub-clusters with only one member are automatically identified as outliers but only when there is not a high degree of similarity to the original cluster. Similarly, two members of a cluster form a sub-cluster when both members are not a nearest neighbor of any other members in their cluster aside from each other. These rules support outlier detection while also avoiding excessive fragmentation during cluster refinement.

6.2 Summarizing an unstable half-manifold of an $L_1$ Lyapunov orbit

A set of motion primitives is constructed to summarize segments of the global unstable half-manifold associated with an $L_1$ Lyapunov orbit and directed toward the Moon. The global unstable half-manifold is generated for a motion primitive in the $L_1$ Lyapunov orbit family; specifically, at a Jacobi constant of 3.1670. The trajectories that lie along this unstable manifold exhibit many close approaches and revolutions around the Moon, while some trajectories impact the Moon or leave the vicinity of the Moon through the $L_1$ gateway. Figure 12a displays short segments, denoted in red, of trajectories computed along the unstable half-manifold departing the $L_1$ Lyapunov orbit, denoted in black, and directed toward the Moon. The gray regions in Fig. 12 correspond to the forbidden regions and are bound by zero-velocity curves. Furthermore, Fig. 12b displays a Poincaré map with an apsis surface of section, defined with respect to the Moon, recording up to 15 perilunes and apolunes that lie along this unstable half-manifold of the selected $L_1$ Lyapunov orbit. Then, 500 trajectories that lie on this unstable manifold are sampled to produce up to 12 smaller arcs along each trajectory, each admitting 4 apses, unless impacting the Moon or passing through the $L_{1}$ or $L_2$ gateways first. These arcs are used to form the dataset that describes the unstable manifold and is summarized using the clustering procedure outlined in Sect. 6.1 for a general hyperbolic invariant manifold. Using the feature vector ${\varvec{f}_{\text {Mani}}}$ defined by Eq. 15, the resulting dataset is a $(951\times 19)-$dimensional dataset. Given the expected diverse and complex geometric variations along manifold structures as well as the size of the dataset, a large range of $k \in [3, 61]$ is selected to encompass a reasonable number of distinct characteristics in the dataset. WEAC is then applied to the resulting 118 base clustering results along with the cluster refinement procedure, identifying 40 clusters and their associated motion primitives.

Fig. 12

Trajectories along the unstable manifold of an $L_1$ Lyapunov orbit at $C_{J}=3.1670$ and directed toward the Moon along with the resulting apsis map relative to the Moon for up to 15 returns

Fig. 13

Subset of trajectory clusters U1–U16 along the unstable manifold directed toward the Moon for an $L_1$ Lyapunov orbit at $C_{J}=3.1670$ with x plotted on the horizontal axis and y plotted on the vertical axis; motion primitives are denoted in bold

Fig. 14

Subset of trajectory clusters U17–U32 along the unstable manifold directed toward the Moon for an $L_1$ Lyapunov orbit at $C_{J}=3.1670$ with x plotted on the horizontal axis and y plotted on the vertical axis; motion primitives are denoted in bold

Trajectory arcs lying along the unstable half-manifold of an $L_1$ Lyapunov orbit at $C_{J}=3.1670$ exhibit a variety of distinct geometries in the lunar vicinity. Following application of the presented procedure to this dataset, the resulting 40 clusters and motion primitives are displayed in Figs. 13, 14, and 15. Each cluster and corresponding motion primitive is labeled with the prefix “U” followed by a number to facilitate discussion of the results. In these figures, the corresponding trajectories for each cluster are plotted in configuration space with the motion primitives denoted in bold and unique colors assigned to distinct clusters. Focusing initially on arcs admitting fewer than 4 apses, the clustering approach generates five different clusters and motion primitives, U1–U5, as displayed in Fig. 13. Clusters that contain only two members, such as U4, depict both members of the cluster with one member arbitrarily selected as the motion primitive because either arc is suitable to summarize the motion in the cluster. Analysis of this figure reveals that clusters U2–U4 effectively capture several distinct geometries admitted by arcs that impact the Moon after departing the vicinity of the $L_1$ Lyapunov orbit. The motion primitives computed from clusters U1 and U5 capture arcs that leave the lunar vicinity via the $L_1$ gateway after a single revolution around the Moon, but with distinct geometries. The remaining 35 different clusters, U6–U40, in Figs. 13, 14, and 15 produce motion primitives that represent arcs admitting 4 apses. Multiple fundamental departure geometries from the initial $L_1$ Lyapunov orbit are uncovered via clusters U25–U30 in Fig. 14. The remaining motion primitives effectively summarize the variety of geometries admitted by subsequent arcs along the selected unstable manifold in the lunar vicinity: a variety of arcs revolving around the Moon with varying close approaches are recovered as well as the flow of trajectories toward the $L_2$ gateway. Some of the arcs revolving around the Moon possess segments that resemble known periodic orbits. For example, clusters U14–U16 in Fig. 13 and clusters U17–U24 in Fig. 14 contain segments with similar geometries to a member of the DPO family at $C_{J}=3.1670$. This set of motion primitives supplies a succinct summary of the trajectories along an unstable half-manifold that may be useful when designing a transfer in cislunar space; incorporating this summary into the initial guess construction process is the focus of ongoing work.

Fig. 15

Subset of trajectory clusters U33–U40 along the unstable manifold directed toward the Moon for an $L_1$ Lyapunov orbit at $C_{J}=3.1670$ with x plotted on the horizontal axis and y plotted on the vertical axis; motion primitives are denoted in bold

Due to the sparsity of the trajectories discretized along the unstable manifold and the feature space definition, the original WEAC results may sometimes produce clusters that appear to contain distinct smaller clusters. Before refining the clusters, the initial WEAC result for the arcs computed along the unstable manifold associated with the $L_1$ Lyapunov orbit at $C_{J}=3.1670$ identifies 25 distinct clusters; 13 of these clusters are refined. A majority of these clusters consisted of one dense sub-cluster and one or more smaller sparse sub-clusters containing only a few outlier members, typically ranging from 1 to 6 outliers; a total of 41 outliers are identified (approximately 4.3% of the total members of the dataset). For example, the WEAC approach originally produced the cluster displayed in Fig. 16a that appears to contain one dense sub-cluster and one smaller sparse sub-cluster consisting of 6 members; while there are some similarities in the general geometries of these clusters, they are distinct. This cluster is automatically refined using the process outlined in Step 7 of the motion primitive construction procedure for hyperbolic invariant manifolds, producing the two distinct clusters displayed in Fig. 16b using distinct shades of purple. Additionally, clusters composed of one or two members, such as U21–U24, are the result of splitting several denser clusters, such as U18–U20, as displayed in Fig. 14. As previously discussed, due to the sparsity of the dataset there may be clusters with only a few outlier members that are incorrectly clustered with trajectories that are most similar to them in the prescribed feature space. Therefore, the presented refinement process is able to successfully identify and form these smaller sub-clusters to separate outliers with distinct geometries. Of course, increasing the number of states sampled along the original periodic orbit and used to generate the associated unstable half-manifold may reduce the need for such refinement. However, in the absence of an iterative data generation and parameter selection procedure, driven by a human analyst, the additional cluster refinement approach ensures that the final set of motion primitives captures the variety of geometries admitted by arcs along the unstable half-manifold.

Fig. 16

Refinement of a single cluster, produced by WEAC, into two distinct clusters

7 Discussion

Generated through a data-driven approach, motion primitives summarize arcs along families of fundamental solutions that govern motion in a multi-body system. This process has been constructed with the goal of eventually simplifying and supporting rapid and informed trajectory design strategies. Specifically, ongoing work by the authors has focused on developing and demonstrating a preliminary procedure for analyzing, selecting, and assembling motion primitives to construct initial guesses of desired geometries for both natural and maneuver-enabled transfers in the Earth–Moon system. Although this work is the focus of a separate paper, Smith and Bosanac (2021), a brief summary is presented here to motivate the potential utility of motion primitives in the trajectory design process.

Consider the fundamental example of designing planar transfers from an $L_{1}$ Lyapunov orbit to an $L_{2}$ Lyapunov orbit in the Earth–Moon CR3BP. Two Lyapunov orbits are selected and displayed in Fig. 17 in solid purple and light brown, respectively, and each correspond to a motion primitive of their respective periodic orbit families; additional members of each family that possess similar geometric, stability, and energetic properties and are assigned to the same cluster lie within the associated transparent shaded regions. The selected $L_1$ and $L_{2}$ Lyapunov orbits possess Jacobi constants of $C_J = 3.1670$ and $C_J = 3.1666$, respectively. To assemble an initial guess for a maneuver-enabled transfer between two periodic orbits that possess a similar geometry to the selected Lyapunov orbits, the unstable and stable manifolds of these representative periodic orbits are generated. Motion primitive sets are then constructed to summarize the finite geometries of arcs that lie along these fundamental solutions that govern motion in the lunar vicinity. Using this summary, an initial guess for a transfer with a desired geometry is constructed by directly selecting and assembling motion primitives; in this example, lying within the pink- and maroon-shaded regions and displayed using dashed arcs. The selected motion primitives are then morphed within their associated regions of existence to improve the quality of the initial guess. This morphed initial guess, displayed using solid arcs, is input to a constrained optimization algorithm that uses collocation to recover a maneuver-enabled transfer. The trajectory designer may then construct additional transfers with distinct geometries by selecting a different number or combination of motion primitives. Through this procedure, motion primitives have the potential to: reduce the complexity of analyzing arcs along the families of fundamental solutions that are often used in trajectory design; offer additional insight into their distinct geometric, stability, and/or energetic properties; and support initial guess construction for a wide variety of complex trajectories throughout multi-body systems.

Fig. 17

Initial guess constructed using motion primitives and their corresponding regions of existence for a transfer between an $L_1$ and $L_2$ Lyapunov orbit in the Earth–Moon CR3BP with a single revolution around the Moon

8 Conclusion

In this paper, the concept of a motion primitive is used to summarize fundamental dynamical structures in a multi-body system with the goal of eventually reducing the complexity of analysis required in current strategies for trajectory design and examination of natural transport. Across a variety of disciplines, a motion primitive is a fundamental building block of complex motion in a dynamical environment, representing a range of similar solutions. In this paper, a motion primitive set is defined as a set of arcs that capture the characteristics of a larger set of trajectories and support assembly of an initial guess for a more complex path in a multi-body system. This paper presents a data-driven framework for autonomously extracting these primitives from a set of trajectories, without the need for significant human intervention or analytical separation criteria. A set of trajectories is first encoded in a feature space description that captures common design parameters of interest such as geometry, stability, and energy. Then, an ensemble of clustering results is computed for the dataset using k-means and agglomerative clustering evaluated for a variety of input parameters. WEAC, a consensus clustering method, is leveraged to generate the final clustering result. A set of motion primitives is then extracted as the medoids of the clusters. Utilizing a consensus clustering algorithm in conjunction with traditional clustering approaches produces results without requiring significant intervention from a human; rather, this approach learns from an ensemble of accumulated evidence to uncover the natural groupings within a set of trajectories.

Using the presented data-driven procedure, motion primitives are constructed to summarize families of periodic orbits and hyperbolic invariant manifolds in the Earth–Moon CR3BP. A set of motion primitives is constructed for the planar family of distant prograde orbits, the spatial family of northern $L_1$ halo orbits, and a variety of other periodic orbit families; in each case, the motion primitive sets capture the complex variations in geometry, stability, and energy along each family. A similar clustering approach is also employed to summarize a set of trajectories along an unstable half-manifold of an $L_1$ Lyapunov orbit. Each trajectory along the manifold is discretized into a series of smaller arcs based on an apsis window to identify the fundamental variations in geometry of arcs along the manifold. This approach effectively summarizes the departure geometries from the $L_1$ Lyapunov orbit toward the Moon and $L_2$, motion around the Moon, and trajectories that either directly impact the Moon or leave the lunar vicinity. For both the periodic orbit families and the manifold trajectories, the outputs of the developed approach include: (i) a set of fundamental trajectories that summarize larger sets of natural motions in a multi-body system, and (ii) a depiction of the regions in which the motion primitives exist. These outputs serve as a key, fundamental step toward future work in leveraging motion primitives for rapidly generating initial guesses for complex trajectories within multi-body systems.