Classifying four-body convex central configurations

Abstract

We classify the full set of convex central configurations in the Newtonian planar four-body problem. Particular attention is given to configurations possessing some type of symmetry or defining geometric property. Special cases considered include kite, trapezoidal, co-circular, equidiagonal, orthodiagonal, and bisecting-diagonal configurations. Good coordinates for describing the set are established. We use them to prove that the set of four-body convex central configurations with positive masses is three-dimensional, a graph over a domain D that is the union of elementary regions in ${\mathbb {R}}^{+^3}$.

1 Introduction

The study of central configurations in the Newtonian n-body problem is an active subfield of Celestial Mechanics. A configuration is central if the gravitational force on each body is a common scalar multiple of its position vector with respect to the center of mass. Perhaps the most well-known example is the equilateral triangle solution of Lagrange, discovered in 1772, consisting of three bodies of arbitrary mass located at the vertices of an equilateral triangle (Lagrange 1772). Released from rest, any central configuration will collapse homothetically toward its center of mass, ending in total collision. In fact, any solution of the n-body problem containing a collision must have its colliding bodies asymptotically approaching a central configuration (Saari 2005). On the other hand, given the appropriate initial velocities, a planar central configuration can rotate rigidly about its center of mass, generating a periodic solution known as a relative equilibrium. These are some of the only explicitly known solutions in the n-body problem. For more background on central configurations and their special properties, see Albouy and Chenciner (1998), Meyer and Offin (2017), Moeckel (1990; 2015), Saari (2005), Schmidt (2002), Wintner (1941) and the references therein.

In this paper, we focus on four-body planar central configurations that are convex. A configuration is convex if no body lies inside or on the convex hull of the other three bodies (e.g., a rhombus or a trapezoid); otherwise, it is called concave. Most of the results on four-body central configurations are either for a specific choice of masses or for a particular geometric type of configuration. For instance, Albouy proved that all of the four-body equal mass central configurations possess a line of symmetry. This in turn allows for a complete solution to the equal mass case (Albouy 1995, 1996). Albouy, Fu, and Sun showed that a convex central configuration with two equal masses opposite each other is symmetric, with the equal masses equidistant from the line of symmetry (Albouy et al. 2008). Recently, Fernandes, Llibre, and Mello proved that a convex central configuration with two pairs of adjacent equal masses must be an isosceles trapezoid (Fernandes et al. 2017). A numerical study for the number of central configurations in the four-body problem with arbitrary masses was done by Simó in Simó (1978). Other studies have focused on examples with one infinitesimal mass, solutions of the planar restricted four-body problem (Barros and Leandro 2011, 2014).

In terms of restricting the problem to a particular shape, Cors and Roberts classified the four-body co-circular central configurations in Cors and Roberts (2012), while Corbera et al. recently studied the trapezoidal solutions (Corbera et al. 2019) (see also Santoprete 2018). Symmetric central configurations are often the easiest to analyze. The regular n-gon ($n \ge 4$) is a central configuration as long as the masses are all equal. A kite is a symmetric quadrilateral with two bodies lying on the axis of symmetry, and the other two bodies positioned equidistant from it. A kite may either be convex or concave. Leandro showed that the number of kite central configurations (equivalence classes) ranges between one and five (Leandro 2003). A more recent investigation of the kite central configurations was carried out in Érdi and Czirják (2016).

One of the major results in the study of convex central configurations is that they exist. MacMillan and Bartky showed that for any four masses and any ordering of the bodies, there exists a convex central configuration (MacMillan and Bartky 1932). This was proven again later in a simpler way by Xia (2004). It is an open question as to whether this solution must be unique. This is problem 10 on a published list of open questions in Celestial Mechanics (Albouy et al. 2012). Uniqueness has been verified when restricting to the case of convex kite configurations (Leandro 2003). Hampton showed that for any four positive masses, there exists a concave central configuration (Hampton 2002). Uniqueness does not hold in the concave setting as the example of an equilateral triangle with an arbitrary mass at the center illustrates. Long studied the possible shapes of convex and concave four-body central configurations, obtaining bounds on the interior angles (Long 2003). Finally, Hampton and Moeckel showed that given four positive masses, the number of equivalence classes of central configurations under rotations, translations, and dilations is finite (Hampton and Moeckel 2006).

Here we study the full space of four-body convex central configurations, focusing on how various geometrically defined classes fit within the larger set. We introduce simple yet effective coordinates to describe the space up to an isometry, rescaling, or relabeling of the bodies. Three radial coordinates a, b, and c represent the distance from three of the bodies, respectively, to the intersection of the diagonals. The remaining coordinate $\theta$ is the angle between the two diagonals. Positivity of the masses imposes various constraints on the coordinates. We find a simply connected domain $D \subset {\mathbb {R}}^{+^3}$, the union of four elementary regions, such that for any $(a,b,c) \in D$, there exists a unique angle $\theta$ which makes the configuration central with positive masses. The angle $\theta = f(a,b,c)$ is a differentiable function on the interior of D. Thus, the set of convex central configurations with positive masses is the graph of a function of three variables. We also prove that $\pi /3 < \theta \le \pi /2$, with $\theta = \pi /2$ if and only if the configuration is a kite.

One of the surprising features of our coordinate system is the simple linear and quadratic equations that define various classes of quadrilaterals. The kite configurations lie on two orthogonal planes that intersect in the family of rhombi solutions. These planes form a portion of the boundary of D. The co-circular and trapezoidal configurations each lie on saddles in D, while the equidiagonal solutions are located on a plane. These three types of configurations intersect in a line corresponding to the isosceles trapezoid family. Our work provides a unifying structure for the set of convex central configurations and a clear picture of how the special subcases are situated within the broader set.

The paper is organized as follows. In the next section, we develop the equations for a four-body central configuration using mutual distance coordinates. In Sect. 3 we introduce our coordinate system and study the important domain D, proving that $\theta$ is a differentiable function on D. We also verify the bounds on $\theta$ and show that it increases with c. Section 4 focuses on four special cases—kite, trapezoidal, co-circular, and equidiagonal configurations—and how they fit together within D.

Figure 3 and all of the three-dimensional plots in this paper were created using MATLAB (2016). All other figures were made using the open-source software SageMath (2016).

2 Four-body planar central configurations

Let $q_i \in {\mathbb {R}}^2$ and $m_i$ denote the position and mass, respectively, of the ith body. We will assume that $m_i > 0 \; \forall i$, while recognizing that the zero-mass case is important for defining certain boundaries of our space. Let $r_{ij} = ||q_i - q_j||$ represent the distance between the ith and jth bodies. If $M = \sum _{i=1}^n m_i$ is the sum of the masses, then the center of mass is given by $c = \frac{1}{M} \sum _{i=1}^n m_i q_i$. The motion of the bodies is governed by the Newtonian potential function

$$\begin{aligned} U(q) \; = \; \sum _{i < j}^n \; \frac{m_i m_j}{r_{ij} }. \end{aligned}$$

The moment of inertia with respect to the center of mass is given by

$$\begin{aligned} I(q) \; = \; \sum _{i=1}^{n} \; m_i \Vert q_i - c \Vert ^2 \; = \; \frac{1}{M} \sum _{i < j} \; m_i m_j r_{ij}^2 . \end{aligned}$$

This can be interpreted as a measure of the relative size of the configuration.

There are several ways to describe a central configuration. We follow the topological approach.

Definition 2.1

A planar central configuration $(q_1, \ldots , q_n) \in {\mathbb {R}}^{2n}$ is a critical point of U subject to the constraint $I = I_0$, where $I_0 > 0$ is a constant.

It is important to note that, due to the invariance of U and I under isometries, any rotation, translation, or scaling of a central configuration still results in a central configuration.

2.1 Mutual distance coordinates

Our derivation of the equations for a four-body central configuration follows the nice exposition of Schmidt (2002). In the case of four bodies, the six mutual distances $r_{12}, r_{13}, r_{14}, r_{23}, r_{24}, r_{34}$ turn out to be excellent coordinates. They describe a configuration in the plane as long as the Cayley–Menger determinant

$$\begin{aligned} V \; = \; \left| \begin{array}{ccccc} 0 &{} \quad 1 &{} \quad 1 &{} \quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad r_{12}^2 &{}\quad r_{13}^2 &{}\quad r_{14}^2 \\ 1 &{}\quad r_{12}^2 &{}\quad 0 &{}\quad r_{23}^2 &{}\quad r_{24}^2 \\ 1 &{}\quad r_{13}^2 &{}\quad r_{23}^2 &{}\quad 0 &{}\quad r_{34}^2 \\ 1 &{}\quad r_{14}^2 &{} \quad r_{24}^2 &{} \quad r_{34}^2 &{}\quad 0 \end{array} \right| \end{aligned}$$

vanishes and the triangle inequality $r_{ij} + r_{jk} > r_{ik}$ holds for any choice of indices with $i \ne j \ne k$. The constraint $V=0$ is necessary for locating planar central configurations; without it, the only critical points of U restricted to $I = I_0$ are regular tetrahedra (a spatial central configuration for any choice of masses). Therefore, we search for critical points of the function

$$\begin{aligned} U + \lambda (I - I_0) + \mu V \end{aligned}$$

(1)

satisfying $I = I_0$ and $V = 0$, where $\lambda$ and $\mu$ are Lagrange multipliers.

A useful formula involving the Cayley–Menger determinant is

$$\begin{aligned} \frac{\partial V}{ \partial r_{ij}^2} \; = \; - 32 \, A_i A_j \, , \end{aligned}$$

(2)

where $A_i$ is the signed area of the triangle whose vertices contain all bodies except for the ith body. Formula (2) holds only when restricting to planar configurations.

Differentiating (1) with respect to $r_{ij}$ and applying formula (2) yield

$$\begin{aligned} m_i m_j (s_{ij} - \lambda ^{'}) \; = \; \sigma A_i A_j, \end{aligned}$$

(3)

where $s_{ij} = r_{ij}^{-3}, \lambda ^{'} = 2\lambda /M,$ and $\sigma = -64 \mu$. Arranging the six equations of (3) as

$$\begin{aligned} \begin{aligned}&m_1 m_2(s_{12} - \lambda ') = \sigma A_1 A_2, \qquad m_3 m_4(s_{34} - \lambda ') = \sigma A_3 A_4,\\&m_1 m_3(s_{13} - \lambda ') = \sigma A_1 A_3, \qquad m_2 m_4(s_{24} - \lambda ') = \sigma A_2 A_4,\\&m_1 m_4(s_{14} - \lambda ') = \sigma A_1 A_4, \qquad m_2 m_3(s_{23} - \lambda ') = \sigma A_2 A_3, \end{aligned} \end{aligned}$$

(4)

and multiplying together pairwise yield the well-known Dziobek relation (Dziobek 1900)

$$\begin{aligned} (s_{12} - \lambda ^{'})(s_{34} - \lambda ^{'}) \; = \; (s_{13} - \lambda ^{'})(s_{24} - \lambda ^{'})\; = \; (s_{14} - \lambda ^{'})(s_{23} - \lambda ^{'}). \end{aligned}$$

(5)

This assumes that the masses and areas are all nonzero. Eliminating $\lambda ^{'}$ from (5) produces the important equation

$$\begin{aligned} \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) \; = \; \left( r_{12}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) . \end{aligned}$$

(6)

In some sense, Eq. (6) is the defining equation for a four-body central configuration. It or some equivalent variation can be found in many papers and texts (e.g., see p. 278 of Wintner (1941).) Equation (6) is clearly necessary given the above derivation. However, it is also sufficient assuming the six mutual distances describe an actual configuration in the plane. The only other restrictions required on the $r_{ij}$ are those that insure solutions to system (4) yield positive masses, as explained in the next section.

2.2 Restrictions on the mutual distances

For the remainder of the paper, we will restrict our attention to four-body convex central configurations. We will assume the bodies are ordered consecutively in the counterclockwise direction. This implies that the lengths of the diagonals are $r_{13}$ and $r_{24}$, while the four exterior side lengths are $r_{12}, r_{23}, r_{14}$, and $r_{34}$. With this choice of labeling, we always have $A_1, A_3 > 0$ and $A_2, A_4 < 0$. We will also assume, without loss of generality, that the largest exterior side length is $r_{12}$.

First, note that $\sigma \ne 0$. If this was not the case, then Eq. (3) and nonzero masses would imply that all $r_{ij}$ are equal, which is the regular tetrahedron solution. If $\sigma < 0$, then system (4) and positive masses imply

$$\begin{aligned} r_{12}, r_{14}, r_{23}, r_{34} \;< \; \frac{1}{\root 3 \of {\lambda '}} \; < \; r_{13}, r_{24} \, . \end{aligned}$$

(7)

This means the two diagonals are strictly longer than any of the exterior sides. On the other hand, if we assume that $\sigma > 0$, then the inequalities in (7) would be reversed. But such a configuration is impossible since it violates geometric properties of convex quadrilaterals such as $r_{13} + r_{24} > r_{12} + r_{34}$ (see Lemma 2.3 in Hampton et al. 2014). The fact that $\sigma < 0$ is also proven in Albouy (2003) (see Proposition 9) where Dziobek configurations of arbitrary dimension are studied.

In addition to (7), further restrictions on the exterior side lengths follow from the Dziobek equation

$$\begin{aligned} (s_{12} - \lambda ^{'})(s_{34} - \lambda ^{'}) \; = \; (s_{14} - \lambda ^{'})(s_{23} - \lambda ^{'}). \end{aligned}$$

(8)

Since $r_{12}$ is the largest exterior side length, we have $r_{12} \ge r_{14}$ and $s_{14} - \lambda ' \ge s_{12} - \lambda ' > 0$. It follows that $s_{34} - \lambda ' \ge s_{23} - \lambda '$; otherwise, Eq. (8) is violated. We conclude that $r_{23} \ge r_{34}$. A similar argument shows that $r_{12} \ge r_{23}$ implies that $r_{14} \ge r_{34}$. Hence, the shortest exterior side is always opposite the longest one, with equality only in the case of a square. In sum, for our particular arrangement of the four bodies, any convex central configuration with positive masses must satisfy

$$\begin{aligned} r_{13}, r_{24} \; > \; r_{12} \; \ge \; r_{14}, r_{23} \; \ge \; r_{34}. \end{aligned}$$

(9)

According to the Dziobek Eq. (5),

$$\begin{aligned} \lambda ' \; = \; \frac{ s_{12} s_{34} - s_{13} s_{24} }{s_{12} + s_{34} - s_{13} - s_{24}} \; = \; \frac{ s_{12} s_{34} - s_{14} s_{23} }{s_{12} + s_{34} - s_{14} - s_{23}} \; = \; \frac{ s_{13} s_{24} - s_{14} s_{23} }{s_{13} + s_{24} - s_{14} - s_{23}} \, . \end{aligned}$$

These expressions generate nice formulas for the ratios between the masses. From system (4), a short calculation gives

$$\begin{aligned} \frac{m_2}{m_1} \; = \; -\frac{A_2(s_{14} - s_{13})}{ A_1 (s_{23} - s_{24}) }, \quad \frac{m_3}{m_1} \; = \; \frac{A_3(s_{14} - s_{12})}{ A_1 (s_{34} - s_{23}) }, \quad \frac{m_4}{m_1} \; = \; -\frac{A_4(s_{12} - s_{13})}{ A_1 (s_{34} - s_{24}) } \, \end{aligned}$$

(10)

and

$$\begin{aligned} \frac{m_3}{m_2} \; = \; -\frac{A_3(s_{12} - s_{24})}{ A_2 (s_{34} - s_{13}) }, \quad \frac{m_4}{m_2} \; = \; \frac{A_4(s_{23} - s_{12})}{ A_2 (s_{34} - s_{14}) }, \quad \frac{m_4}{m_3} \; = \; -\frac{A_4(s_{23} - s_{13})}{ A_3 (s_{14} - s_{24}) } \, . \end{aligned}$$

(11)

Due to Eq. (6), these formulas are consistent with each other. They are all well defined for configurations satisfying the inequalities in (9) unless $s_{34} = s_{23}$ (and thus $s_{12} = s_{14}$), or $s_{34} = s_{14}$ (and thus $s_{12} = s_{23}$). For these special cases, which correspond to symmetric kite configurations, we use the alternative formulas

$$\begin{aligned} \frac{m_3}{m_1} \; = \; \frac{A_3(s_{12} - s_{13})(s_{14} - s_{24})}{ A_1 (s_{23} - s_{13})(s_{34} - s_{24}) } \quad \text{ and } \quad \frac{m_4}{m_2} \; = \; \frac{A_4(s_{23} - s_{13})(s_{12} - s_{24})}{ A_2 (s_{34} - s_{13})(s_{14} - s_{24}) } \, . \end{aligned}$$

(12)

The formulas obtained for the mass ratios explain why Eq. (6) is also sufficient for obtaining a central configuration. If the mutual distances $r_{ij}$ satisfy both (9) and (6), then the mass ratios (which are positive) are given uniquely by (10), (11), or (12). We can then work backward and check that system (4) is satisfied so that the configuration is indeed central.

3 The set of convex central configurations

We now describe the full set of convex central configurations with positive masses, showing it is three-dimensional, the graph of a differentiable function of three variables.

3.1 Good coordinates

We begin by defining simple, but extremely useful coordinates. Since the space of central configurations is invariant under isometries, we may apply a rotation and translation to place bodies 1 and 3 on the horizontal axis, with the origin located at the intersection of the two diagonals. It is also permissible to rescale the configuration so that $q_1 = (1,0)$. This alters the value of the Lagrange multipliers, but preserves the special trait of being central.

Define the remaining three bodies to have positions $q_2 = (a \cos \theta , a \sin \theta ), q_3 = (-b, 0)$, and $q_4 = (-c \cos \theta , -c \sin \theta )$, where a, b, c are radial variables and $\theta \in (0, \pi )$ is an angular variable (see Fig. 1). If one or more of the three radial variables are negative, then the configuration becomes concave or the ordering of the bodies changes. If one or more of the radial variables vanish, then the configuration contains a subset that is collinear or some bodies coalesce (e.g., $b=c=0$ implies $r_{34} = 0$). Thus, we will assume throughout the paper that $a> 0, b > 0,$ and $c > 0$. The coordinates $(a,b,c,\theta )$ turn out to be remarkably well suited for describing different classes of quadrilaterals that are also central configurations (see Sect. 4).

Fig. 1

Coordinates for a convex configuration of four bodies: three radial variables $a, b, c > 0$ and an angular variable $\theta \in (0,\pi )$

In our coordinates, the six mutual distances are given by

$$\begin{aligned} r_{12}^2 = a^2 -2a \cos \theta + 1, \quad&r_{23}^2 = a^2 + 2ab \cos \theta + b^2,&\quad r_{13} = b + 1, \end{aligned}$$

(13)

$$\begin{aligned} r_{14}^2 = c^2 + 2c \cos \theta + 1, \quad&r_{34}^2 = b^2 - 2bc \cos \theta + c^2,&\quad r_{24} = a + c. \end{aligned}$$

(14)

Based on Eq. (6), define F to be the function

$$\begin{aligned} F(a,b,c,\theta ) \; = \; \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) - \left( r_{12}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) , \end{aligned}$$

where each mutual distance is treated as a function of the variables a, b, c,  and $\theta$.

The previous discussion justifies the following lemma.

Lemma 3.1

Let ${{{\mathcal {C}}}}$ and E denote the sets

$$\begin{aligned} {{\mathcal {C}}}= & {} \{ (a,b,c,\theta ) \in {\mathbb {R}}^{+^3} \! \times (0, \pi ): r_{13}, r_{24} > r_{12} \ge r_{14}, r_{23} \ge r_{34} \} , \\ E= & {} \{ s = (a,b,c,\theta ) \in {\mathbb {R}}^{+^3} \! \times (0, \pi ): s \in {{\mathcal {C}}} \text{ and } F(s) = 0 \}. \end{aligned}$$

Any point in E corresponds to a four-body convex central configuration with positive masses. Moreover, up to an isometry, rescaling, or relabeling of the bodies, E contains all such configurations.

3.2 Defining the domain D

We will find a set $D \subset {\mathbb {R}}^{+^3}$ such that for each $(a,b,c) \in D$, there exists a unique angle $\theta$ which makes the configuration central. Specifically, we prove that there exists a differentiable function $\theta = f(a, b, c)$ with domain D, whose graph is equivalent to E. In order to define D, we use the mutual distance inequalities in (9) to eliminate the angular variable $\theta$.

Lemma 3.2

The inequalities in (9) imply the following conditions on the positive variables a, b, c:

$$\begin{aligned} r_{12} \; \ge \; r_{14} \; \text{ and } \; r_{23} \; \ge \; r_{34}&\quad \Longrightarrow \quad&a \; \ge \; c , \end{aligned}$$

(15)

$$\begin{aligned} r_{12} \; \ge \; r_{23} \; \text{ and } \; r_{14} \; \ge \; r_{34}&\quad \Longrightarrow \quad&b \; \le \; 1 , \end{aligned}$$

(16)

$$\begin{aligned} r_{13} \; > \; r_{12} \; \ge \; r_{14}&\quad \Longrightarrow \quad&c \; < \; \frac{1}{a} (b^2 + 2b), \end{aligned}$$

(17)

$$\begin{aligned} r_{13} \;> \; r_{12} \; \ge \; r_{23} \; \text{ and } \; a> 1&\quad \Longrightarrow \quad&b \; > \; \frac{1}{2}\left( -1 + \sqrt{4a^2 - 3}\, \right) , \end{aligned}$$

(18)

$$\begin{aligned} r_{24} \;> \; r_{12} \; \ge \; r_{14} \; \text{ and } \; 0< a < 1&\quad \Longrightarrow \quad&c \; > \; \frac{1}{2} \left( -a + \sqrt{4 - 3a^2}\,\right) , \end{aligned}$$

(19)

$$\begin{aligned} r_{24} \;> \; r_{12} \; \ge \; r_{23}&\quad \Longrightarrow \quad&c \; > \; -a + \sqrt{a^2 + b} \, . \end{aligned}$$

(20)

Proof

From Eqs. (13) and (14), we compute that

$$\begin{aligned}&r_{12}^2 - r_{14}^2 \; = \; (a + c)(a - c - 2 \cos \theta ), \end{aligned}$$

(21)

$$\begin{aligned}&r_{12}^2 - r_{23}^2 \; = \; (1 + b)(1 - b - 2a \cos \theta ), \end{aligned}$$

(22)

$$\begin{aligned}&r_{23}^2 - r_{34}^2 \; = \; (a + c)(a - c + 2b \cos \theta ),\end{aligned}$$

(23)

$$\begin{aligned}&r_{14}^2 - r_{34}^2 \; = \; (1 + b)(1 - b + 2c \cos \theta ). \end{aligned}$$

(24)

Since a, b,  and c are all positive, $r_{12} \ge r_{14}$ and $r_{23} \ge r_{34}$ together imply that

$$\begin{aligned} a - c \; \ge \; \text{ max }\{2 \cos \theta , -2b \cos \theta \} \; \ge \; 0 . \end{aligned}$$

(25)

Similarly, $r_{12} \ge r_{23}$ and $r_{14} \ge r_{34}$ imply

$$\begin{aligned} 1 - b \; \ge \; \text{ max }\{2 a \cos \theta , -2c \cos \theta \} \; \ge \; 0. \end{aligned}$$

(26)

This proves implications (15) and (16).

Next, Eqs. (13) and (14) yield

$$\begin{aligned}&r_{13}^2 - r_{12}^2 \; = \; b^2 + 2b - a^2 + 2a \cos \theta \quad \text{ and } \end{aligned}$$

(27)

$$\begin{aligned}&r_{24}^2 - r_{12}^2 \; = \; c^2 + 2ac - 1 + 2a \cos \theta . \end{aligned}$$

(28)

Since $r_{12} \ge r_{14}$, Eq. (21) gives $a - 2 \cos \theta \ge c$ or $a^2 - 2a \cos \theta \ge ac$. Then $r_{13} > r_{12}$ implies that

$$\begin{aligned} b^2 + 2b \; > \; a^2 - 2a \cos \theta \; \ge \; ac, \end{aligned}$$

(29)

which verifies (17).

Similarly, $r_{12} \ge r_{23}$ and Eq. (22) yield $-2a \cos \theta \ge b - 1$. Then $r_{13} > r_{12}$ implies that

$$\begin{aligned} b^2 + 2b - a^2 \; > \; -2a \cos \theta \; \ge \; b - 1, \end{aligned}$$

(30)

which yields

$$\begin{aligned} b^2 + b + 1 - a^2 \; > \; 0. \end{aligned}$$

(31)

Since b and a are both positive, inequality (31) clearly holds if $a \le 1$. However, for any fixed choice of $a > 1$, the value of b must be chosen strictly greater than the largest root of the quadratic $Q_a(b) = b^2 + b + 1 - a^2$. This root is $\frac{1}{2}(-1 + \sqrt{4a^2 - 3})$, which verifies implication (18).

Next, $r_{24} > r_{12} \ge r_{14}$ yields

$$\begin{aligned} c^2 + 2ac -1 + a^2 \; > \; - 2a \cos \theta + a^2 \; \ge \; ac, \end{aligned}$$

(32)

which in turn gives

$$\begin{aligned} c^2 + ac + a^2 - 1 \; > \; 0. \end{aligned}$$

(33)

Since a and c are both positive, inequality (33) clearly holds if $a \ge 1$. However, for any fixed choice of $a \in (0,1)$, the value of c must be chosen strictly greater than the largest root of the quadratic $Q_a(c) = c^2 + ac + a^2 - 1$. This root is $\frac{1}{2}(-a + \sqrt{4 - 3a^2})$, which proves (19).

Finally, $r_{24} > r_{12} \ge r_{23}$ implies that

$$\begin{aligned} c^2 + 2ac -1 \; > \; -2a \cos \theta \; \ge \; b - 1, \end{aligned}$$

(34)

which gives

$$\begin{aligned} c^2 + 2ac - b \; > \; 0. \end{aligned}$$

(35)

Since $b > 0$, c must be chosen greater than the largest root of the quadratic $Q_{a,b}(c) = c^2 + 2ac - b$. This root is $-a + \sqrt{a^2 + b}$, which verifies (20) and completes the proof. $\square$

The combined inequalities between the radial variables a, b,  and c given in (15) through (20), along with $a> 0, b > 0,$ and $c > 0$, define a bounded set $D \subset {\mathbb {R}}^{+^3}$. We will show that this set is the domain of the function $\theta = f(a,b,c)$ and the projection of E into abc-space.

Note that D is simply connected. Using inequalities (31), (33), $c \le a$, and $b \le 1$, it is straightforward to check that D is contained within the box

$$\begin{aligned} \frac{1}{\sqrt{3}} \le a \le \sqrt{3}, \; 0 \le b \le 1, \; 0 \le c \le \sqrt{3} \,. \end{aligned}$$

Let ${\overline{D}}$ denote the closure of D. A plot of the boundary of D is shown in Fig. 2. It contains five vertices, six faces, and nine edges (six curved, three straight), in accordance with Poincaré’s generalization of Euler’s formula ${\overline{V}} -{\overline{E}} + {\overline{F}} = 2$. The vertices of ${\overline{D}}$ are

$$\begin{aligned} \begin{aligned}&P_1 = (1,0,0), \quad P_2 = \left( \frac{1}{\sqrt{3}}, \frac{2 - \sqrt{3}}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right) , \quad P_3 = \left( \frac{1}{\sqrt{3}}, 1, \frac{1}{\sqrt{3}}\right) , \\&P_4 = \left( \sqrt{3}, 1 , \sqrt{3}\right) , \text{ and } P_5 = \left( \sqrt{3}, 1, 2 - \sqrt{3}\right) , \end{aligned} \end{aligned}$$

each of which corresponds to a symmetric central configuration with at least two zero masses. $P_3$ and $P_4$ are rhombi with one diagonal congruent to the common side length, while $P_2$ and $P_5$ are kites with horizontal and vertical axes of symmetry, respectively. The point $P_1$ corresponds to an equilateral triangle with bodies 3 and 4 sharing a common vertex.

Fig. 2

The faces and vertices of ${\overline{D}}$ (face III not shown to improve the perspective). Faces II and V are vertical. For each point $(a, b, c) \in D$, there exists a unique angle $\theta$ that makes the corresponding configuration central

3.3 Configurations on the boundary of D

We now focus on points lying on the boundary of D. The next lemma shows that these points correspond to configurations where two or more of the mutual distance inequalities in (9) become equalities. Moreover, the only points for which this is true lie on the boundary of D.

Lemma 3.4

Suppose that $(a,b,c,\theta )$ are chosen so that $r_{13}, r_{24} \ge r_{12} \ge r_{14}, r_{23} \ge r_{34}$ with $a \ge 1/\sqrt{3}$, $b \ge 0$, and $c \ge 0$. Then

$$\begin{aligned} r_{12} = r_{14} \; \text{ and } \; r_{23} = r_{34}&\quad \text{ if } \text{ and } \text{ only } \text{ if } \quad&a \; = \; c , \end{aligned}$$

(36)

$$\begin{aligned} r_{12} = r_{23} \; \text{ and } \; r_{14} = r_{34}&\quad \text{ if } \text{ and } \text{ only } \text{ if } \quad&b \; = \; 1 , \end{aligned}$$

(37)

$$\begin{aligned} r_{13} \; = \; r_{12} \; = \; r_{14}&\quad \text{ if } \text{ and } \text{ only } \text{ if } \quad&c \; = \; \frac{1}{a} (b^2 + 2b), \end{aligned}$$

(38)

$$\begin{aligned} r_{24} \; = \; r_{12} \; = \; r_{14}&\quad \text{ if } \text{ and } \text{ only } \text{ if } \quad&c \; = \; \frac{1}{2} \left( -a + \sqrt{4 - 3a^2}\,\right) , \end{aligned}$$

(39)

$$\begin{aligned} r_{13} \; = \; r_{12} \; = \; r_{23}&\quad \text{ if } \text{ and } \text{ only } \text{ if } \quad&b \; = \; \frac{1}{2}\left( -1 + \sqrt{4a^2 - 3}\, \right) , \end{aligned}$$

(40)

$$\begin{aligned} r_{24} \; = \; r_{12} \; = \; r_{23}&\quad \text{ if } \text{ and } \text{ only } \text{ if } \quad&c \; = \; -a + \sqrt{a^2 + b} \, . \end{aligned}$$

(41)

Proof

We first note that under the assumptions of the lemma, the inequalities on a, b,  and c from Lemma 3.2 are still valid, except that the inequalities are no longer strict.

If $r_{12} = r_{14}$ and $r_{23} = r_{34}$, then Eqs. (21) and (23) imply $a - c = 2 \cos \theta$ and $a - c = -2b \cos \theta$, respectively. This yields $(1+b) \cos \theta = 0$ from which it follows that $\cos \theta = 0$ and $a = c$. Conversely, if $a = c$, (25) implies that either $\cos \theta = 0$ or $b = 0$. In the former case, $\theta = \pi /2$ and then $r_{12} = r_{14}$ and $r_{23} = r_{34}$ follows quickly. In the latter case, inequality (17) and $a = c$ implies that $a = c = 0$, which contradicts $a \ge 1/\sqrt{3}$. Thus, $b > 0$ and $r_{12} = r_{14}$ and $r_{23} = r_{34}$, proving (36).

If $r_{12} = r_{23}$ and $r_{14} = r_{34}$, then Eqs. (22) and (24) imply $1 - b = 2 a\cos \theta$ and $1 - b = -2c \cos \theta$, respectively. Thus, $(a+c) \cos \theta = 0$. Since $a \ge 1/\sqrt{3}$ and $c \ge 0$, we must have $\cos \theta = 0$ and hence $b = 1$. Conversely, if $b = 1$, (26) implies that either $\cos \theta = 0$, or $\cos \theta < 0$ and $c=0$. In the former case, $\theta = \pi /2$ and then $r_{12} = r_{23}$ and $r_{14} = r_{34}$ follows quickly. The latter case is impossible, since $c = 0$ and $b = 1$ contradict inequality (20). This proves (37).

If $r_{13} = r_{12}$, then Eq. (30) gives $a - 2 \cos \theta = \frac{1}{a}(b^2 + 2b)$. Likewise, if $r_{12} = r_{14}$, then $a - 2 \cos \theta = c$. Thus, $r_{13} = r_{12} = r_{14}$ implies $c = \frac{1}{a}(b^2 + 2b)$. Conversely, if $ac = b^2 + 2b$, then both inequalities in (29) become equalities. From this, we deduce that $r_{13} = r_{12} = r_{14}$, which verifies (38).

If $r_{24} = r_{12}$, then Eq. (31) gives $a(c + 2 \cos \theta ) = 1 - c^2 - ac$. Likewise, if $r_{12} = r_{14}$, then $c + 2 \cos \theta = a$. Thus, $r_{24} = r_{12} = r_{14}$ implies $c^2 + ac + a^2 - 1 = 0$. The quadratic $Q_a(c) = c^2 + ac + a^2 - 1$ has real roots for $1/\sqrt{3} \le a \le 2/\sqrt{3}$, but the smaller root is always negative for these a-values. Thus, c must be taken to be the larger root of $Q_a(c)$. Conversely, if $c = \frac{1}{2} (-a + \sqrt{4 - 3a^2}\,)$, then $c^2 + ac + a^2 - 1 = 0$ and both inequalities in (32) become equalities. From this, we deduce that $r_{24} = r_{12} = r_{14}$, which verifies (39). The proof of (40) and (41) follows in a similar fashion, using inequalities (30) and (34), respectively. $\square$

Lemma 3.4 shows that the six faces on the boundary of D, labeled I through VI, are given by the six equations (36) through (41), respectively. The first two faces are the only ones belonging to D (positive masses) and contain all of the kite configurations, where $\theta = \pi /2$. The remaining four faces on the boundary of D correspond to cases with one or three zero masses (see Table 1). Points on these faces are interpreted as limiting solutions of a sequence of central configurations with positive masses. The mass values shown in Table 1 follow from formulas (10), (11), and (12). Here we assume that the limiting solution lies in the interior of the given face.

Table 1 The six faces on the boundary of D along with their key attributes

For example, suppose there is a sequence of points $x^\epsilon = (a^\epsilon , b^\epsilon , c^\epsilon )$ in the interior of D converging to a point ${\overline{x}} = ({\overline{a}}, {\overline{b}}, {\overline{c}})$ located on the interior of face V. This corresponds to a sequence of central configurations, each with positive masses, that limits on a configuration with $r_{13} = r_{12} = r_{23}$. Since ${\overline{x}}$ does not lie on any of the other faces on the boundary of D, the other three limiting mutual distances, $r_{24}, r_{14},$ and $r_{34}$, must be distinct from $r_{13}$ and each other. Moreover, the limiting values of the areas $A_i$ do not vanish because ${\overline{a}}, {\overline{b}},$ and ${\overline{c}}$ are all strictly positive. Using either (10) or (11), it follows that the limiting mass value for $m_4$ must vanish, while the other limiting mass values are strictly positive. A similar argument applied to the other faces determines which masses must vanish in the limit.

Configurations on face IV or V, respectively, correspond to equilibria of the planar, circular, restricted four-body problem with infinitesimal mass $m_3$ or $m_4$, respectively (Barros and Leandro 2014, 2011; Kulevich et al. 2009). Configurations on face III or VI, respectively, correspond to relative equilibria of the $(1+3)$-body problem, where a central mass (body 1 or 2, respectively) is equidistant from three infinitesimal masses (Corbera et al. 2015; Hall 1988; Moeckel 1994). Note that we have not made any assumptions on the relative size of the masses. Each of the six faces satisfies either $r_{12} = r_{14}$ or $r_{12} = r_{23}$. Using Eqs. (21) and (22), it follows that there is a unique value of $\theta$ for each point on the boundary of D, $\theta = \cos ^{-1}(\frac{a-c}{2})$ if $r_{12} = r_{14}$ or $\theta = \cos ^{-1}(\frac{1-b}{2a})$ if $r_{12} = r_{23}$.

The masses at the vertices of ${\overline{D}}$ are not well defined because there are more options for the path of a limiting sequence. For example, the point $P_4$ represents a rhombus with one diagonal ($r_{13}$) congruent to all of the exterior sides. Approaching $P_4$ along the line (a, 1, a) as $a \rightarrow \sqrt{3}$ (a sequence of rhombi central configurations) yields the limiting mass values $m_2 = m_4 = 0$ and $m_1 = m_3 \ne 0$. On the other hand, it is possible to construct a sequence of kite central configurations on face I with masses $m_1 = 1, m_2 = m_4 = \epsilon ^2,$ and $m_3 = \epsilon$ that limits on $P_4$ as $\epsilon \rightarrow 0$. The first sequence has two limiting mass values that vanish, while the second sequence has three. The difference occurs because the mass ratio $m_3/m_1$ at $P_4$ is undefined in either formula (10) or (12).

Regardless of the particular limiting sequence, all five vertices of ${\overline{D}}$ will have at least two mass values that vanish in the limit. For $P_1$, this follows from Proposition 2 in Moeckel (1997). For the other four vertices, this fact is a consequence of formulas (10) and (11). In general, note that a limiting sequence with precisely two zero masses can only occur at vertices $P_1, P_3,$ or $P_4$. This somewhat surprising restriction is a consequence of Propositions 3 and 4 in Moeckel (1997) and the fact that the non-collinear critical points of the restricted three-body problem must form an equilateral triangle with the non-trivial masses.

3.4 The projection of ${\overline{D}}$ onto the ab-plane

The set ${\overline{D}}$ can be written as the union of four elementary regions in abc-space, where c is bounded by functions of a and b. The projection of ${\overline{D}}$ onto the ab-plane is shown in Fig. 3. It is determined by $\frac{1}{\sqrt{3}} \le a \le \sqrt{3} \,$ and $l(a) \le b \le 1$, where l(a) is the piecewise function

$$\begin{aligned} l(a) \; = \; \left\{ \begin{array}{cc} l_1(a) &{}\quad \text{ if } \, {\frac{1}{\sqrt{3}}} \le a \le 1 \\ l_2(a) &{}\quad \text{ if } \, 1 \le a \le \sqrt{3} \, . \end{array} \right. \end{aligned}$$

Here, $l_1(a) = -1 + \frac{1}{2} (a + \sqrt{4 - 3a^2} \, )$ is the projection of the intersection between faces III and IV, and $l_2(a) = \frac{1}{2} (-1 + \sqrt{4a^2 - 3}\, )$ is the projection of the vertical face V. The edge $a = \frac{1}{\sqrt{3}}$ is the projection of the intersection between faces I and IV, while the edge $b=1$ is the projection of the vertical face II.

Fig. 3

The projection of ${\overline{D}}$ into the ab-plane. The dashed red curves divide the region into four subregions over which c is bounded by functions of a and b. The orientation of the a-axis has been reversed to match Fig. 2

The decreasing dashed curve in Fig. 3 is the projection of the intersection of faces I and III, given by $b = -1 + \sqrt{1 + a^2} \, , \frac{1}{\sqrt{3}} \le a \le \sqrt{3}$. The increasing dashed curve is the projection of the intersection of faces IV and VI, given by $b = 1 - \frac{3}{2}a^2 + \frac{a}{2} \sqrt{4 - 3a^2} \, , \frac{1}{\sqrt{3}} \le a \le 1$. These curves divide the projection into four subregions over which c is bounded by different functions of a and b, as indicated below:

$$\begin{aligned} \begin{array}{cl} \mathrm{(i)} &{} \quad -a + \sqrt{a^2 + b} \; \le \; c \; \le \; a \\ \mathrm{(ii)} &{} \quad {\frac{1}{2}} \left( -a + \sqrt{4 - 3a^2}\,\right) \; \le \; c \; \le \; a \\ \mathrm{(iii)} &{} \quad {\frac{1}{2}} \left( -a + \sqrt{4 - 3a^2}\,\right) \; \le \; c \; \le \; {\frac{1}{a}} (b^2 + 2b) \\ \mathrm{(iv)} &{} \quad -a + \sqrt{a^2 + b} \; \le \; c \; \le \; {\frac{1}{a}} (b^2 + 2b) \, . \end{array} \end{aligned}$$

3.5 E is a graph $\theta = f(a,b,c)$ over D

We now prove our main result, showing that for each $(a,b,c) \in D$, there exists a unique angle $\theta$ that makes the configuration central. In general, for any point (a, b, c) in the interior of D, there is an interval of possible angles $\theta$ for which the mutual distance inequalities (9) hold. According to the identities given in Eqs. (21)–(24) and (27), (28), $\theta$ must be chosen to satisfy

$$\begin{aligned}&\text{ max } \Bigl \{ \frac{c-a}{2b}, \; \frac{b - 1}{2c}, \; \frac{a^2 - b^2 - 2b}{2a}, \; \frac{1 - c^2 - 2ac}{2a} \Bigl \}\nonumber \\&\qquad \le \; \cos \theta \le \; \text{ min } \Bigl \{ \frac{a-c}{2}, \; \frac{1 - b}{2a} \Bigl \} \end{aligned}$$

(42)

in order for (9) to be true. The following lemma shows that condition (42) is not vacuous on the interior of D.

Lemma 3.5

For any point (a, b, c) in the interior of D, define the constants $k_1$ and $k_2$ by

$$\begin{aligned} k_1= & {} \max \Bigl \{ \frac{c-a}{2b}, \; \frac{b - 1}{2c}, \; \frac{a^2 - b^2 - 2b}{2a}, \; \frac{1 - c^2 - 2ac}{2a} \Bigl \},\\ k_2= & {} \min \Bigl \{ \frac{a-c}{2}, \; \frac{1 - b}{2a} \Bigl \}. \end{aligned}$$

Then $-1< k_1< k_2 < 1$.

Proof

On the interior of D, the first two quantities in the definition of $k_1$ are strictly negative, while the two quantities defining $k_2$ are strictly positive. The inequality $(a^2 - b^2 - 2b)/(2a) < (a-c)/2$ follows from $c < (b^2 + 2b)/a$. The inequality $(a^2 - b^2 - 2b)/(2a) < (1-b)/(2a)$ is equivalent to $b^2 + b + 1 - a^2 > 0$, which is clearly valid for $a \le 1$. It also holds for $a > 1$ because $b > \frac{1}{2}(-1 + \sqrt{4a^2 - 3} \, )$. Likewise, $(1 - c^2 - 2ac)/(2a) < (a-c)/2$ is equivalent to $c^2 + ac + a^2 - 1 > 0$, which is clearly satisfied for $a \ge 1$. It also holds for $0< a < 1$ since $c > \frac{1}{2}(-a + \sqrt{4 - 3a^2} \,)$. Finally, $(1 - c^2 - 2ac)/(2a) < (1-b)/(2a)$ is satisfied because $c > -a + \sqrt{a^2 + b}$. This verifies that $k_1 < k_2$.

Since $a< \sqrt{3} < 2 + c$ and $1< \frac{2}{\sqrt{3}} < 2a + b$ on the interior of D, we see that $k_2 < 1$. Finally, $(1 - c^2 - 2ac)/(2a) > -1$ holds if $c < 1$. But if $c \ge 1$, then $b> 0 > 1 - 2c$ implies that $(b-1)/(2c) > -1$. Thus, at least one of the quantities in the definition for $k_1$ is larger than $-1$. This shows that $k_1 > -1$. $\square$

Lemma 3.5 shows that for any point (a, b, c) in the interior of D, there is an interval of $\theta$-values for which (9) holds. More specifically, if we let $\theta _l = \cos ^{-1} (k_2)$ and $\theta _u = \cos ^{-1} (k_1)$, with $k_1, k_2$ defined as in Lemma 3.5, then for any $\theta \in (\theta _l, \theta _u)$, we have $(a,b,c,\theta ) \in \mathcal{C}$.

Recall that

$$\begin{aligned} F(a,b,c,\theta ) \; = \; \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) - \left( r_{12}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) , \end{aligned}$$

and that $E = \{ s = (a,b,c,\theta ) \in {\mathbb {R}}^{+^3} \! \times (0, \pi ): s \in {{\mathcal {C}}} \text{ and } F(s) = 0 \}$ represents the set of convex central configurations with positive masses.

Theorem 3.6

Suppose that $(a, b, c) \in D$. Then there exists a unique angle $\theta$ such that $(a, b, c, \theta )$ determines a central configuration. More precisely, the set of four-body convex central configurations with positive masses is the graph of a differentiable function $\theta = f(a,b,c)$. The domain of this function is D, which is the projection of E onto abc-space.

Proof

Fix a point (a, b, c) in the interior of D and treat $F = F(\theta )$ as a one-variable function. We will show that F has a unique root $\theta$ satisfying the inequalities in (42).

(i) Existence: Suppose that $\theta$ is taken to be $\theta _l = \cos ^{-1} (k_2)$. This is the smallest possible value for $\theta$. If $\cos \theta = (a-c)/2$, then Eq. (21) gives $r_{12} = r_{14}$ and thus

$$\begin{aligned} F \; = \; \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) \; > \; 0, \end{aligned}$$

since (a, b, c) is in the interior of D. (If any of the differences above also vanished, then (a, b, c) would be on the boundary of D due to Lemma 3.4.) Similarly, if $\cos \theta = (1-b)/(2a)$, then Eq. (22) gives $r_{12} = r_{23}$ and we compute that

$$\begin{aligned} F= & {} \left( r_{13}^3 - r_{12}^3\right) \left[ \left( r_{24}^3 - r_{14}^3\right) \left( r_{12}^3 - r_{34}^3\right) - \left( r_{12}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{34}^3\right) \right] \\= & {} \left( r_{13}^3 - r_{12}^3\right) \left[ - r_{24}^3 r_{34}^3 - r_{14}^3 r_{12}^3 + r_{12}^3 r_{34}^3 + r_{14}^3 r_{24}^3 \right] \\= & {} \left( r_{13}^3 - r_{12}^3\right) \left( r_{24}^3 - r_{12}^3\right) \left( r_{14}^3 - r_{34}^3\right) \; > \; 0, \end{aligned}$$

since (a, b, c) is in the interior of D. In either case, we see that $F(a,b,c, \theta = \theta _l) > 0$.

Next, suppose that $\theta$ is chosen to be $\theta _u = \cos ^{-1} (k_1)$. This is the largest possible value for $\theta$. If $\cos \theta = (c-a)/(2b)$, then Eq. (23) gives $r_{23} = r_{34}$ and thus

$$\begin{aligned} F \; = \; - \left( r_{12}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) \; < \; 0. \end{aligned}$$

If $\cos \theta = (b-1)/(2c)$, then Eq. (24) gives $r_{14} = r_{34}$ and we find that

$$\begin{aligned} F= & {} \left( r_{24}^3 - r_{14}^3\right) \left[ \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{14}^3\right) - \left( r_{12}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{23}^3\right) \right] \\= & {} \left( r_{24}^3 - r_{14}^3\right) \left[ r_{13}^3 r_{23}^3 + r_{12}^3 r_{14}^3 - r_{12}^3 r_{13}^3 - r_{14}^3 r_{23}^3 \right] \\= & {} \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{14}^3\right) \left( r_{23}^3 - r_{12}^3\right) \; < \; 0, \end{aligned}$$

where the strict inequality follows once again from Lemma 3.4. If $\cos \theta = (a^2 - b^2 - 2b)/(2a)$, then Eq. (27) gives $r_{13} = r_{12}$ and thus

$$\begin{aligned} F \; = \; - \left( r_{12}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) \; < \; 0. \end{aligned}$$

Finally, if $\cos \theta = (1-c^2-2ac)/(2a)$, then Eq. (28) gives $r_{24} = r_{12}$ and we find that

$$\begin{aligned} F= & {} \left( r_{12}^3 - r_{14}^3\right) \left[ \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) - \left( r_{12}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) \right] \\= & {} \left( r_{12}^3 - r_{14}^3 \right) \left[ r_{13}^3 r_{23}^3 + r_{12}^3 r_{34}^3 - r_{12}^3 r_{13}^3 - r_{34}^3 r_{23}^3 \right] \\= & {} \left( r_{12}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{34}^3\right) \left( r_{23}^3 - r_{12}^3\right) \; < \; 0. \end{aligned}$$

In all four cases, we find that $F(a,b,c, \theta = \theta _u) < 0$. Since F is a continuous function with opposite signs at $\theta = \theta _l$ and $\theta = \theta _u$, the intermediate value theorem implies that there exists an angle $\theta \in (\theta _l, \theta _u)$ such that $F(a,b,c,\theta ) = 0$.

(ii) Uniqueness: To see that this solution is unique, we show that $\frac{ \partial F}{\partial \theta } < 0$ for any (a, b, c) in the interior of D and any $\theta \in (\theta _l, \theta _u)$. From Eqs. (13) and (14), we have

$$\begin{aligned}&\frac{\partial r_{12}}{\partial \theta } = \frac{a \sin \theta }{r_{12}}, \quad \frac{\partial r_{23}}{\partial \theta } = \frac{- ab \sin \theta }{r_{23}}, \quad \frac{\partial r_{14}}{\partial \theta } = \frac{- c \sin \theta }{r_{14}}, \quad \frac{\partial r_{34}}{\partial \theta } = \frac{bc \sin \theta }{r_{34}}, \quad \text{ and } \quad \\&\frac{\partial r_{13}}{\partial \theta } = \frac{\partial r_{24}}{\partial \theta } = 0. \end{aligned}$$

Then we compute

$$\begin{aligned} \frac{\partial F}{\partial \theta } \; = \; -3 \sin \theta \left( a r_{12} \, \alpha _1 + ab r_{23} \, \alpha _2 + c r_{14} \, \alpha _3 + bc r_{34} \, \alpha _4 \right) , \end{aligned}$$

where

$$\begin{aligned} \alpha _1= & {} \left( r_{24}^3 - r_{14}^3\right) \left( r_{23}^3 - r_{34}^3\right) + \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) , \nonumber \\ \alpha _2= & {} \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) + \left( r_{24}^3 - r_{34}^3\right) \left( r_{12}^3 - r_{14}^3\right) , \nonumber \\ \alpha _3= & {} \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) - \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) , \nonumber \\ \alpha _4= & {} \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) - \left( r_{12}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{23}^3\right) . \end{aligned}$$

(43)

By (9) and Lemma 3.4, both $\alpha _1$ and $\alpha _2$ are strictly positive. After adding and subtracting $r_{23}^6$ to $\alpha _3$, we can rewrite that expression as

$$\begin{aligned} \alpha _3 \; = \; \left( r_{24}^3 - r_{23}^3\right) \left( r_{13}^3 - r_{23}^3\right) + \left( r_{12}^3 - r_{23}^3\right) \left( r_{23}^3 - r_{34}^3\right) , \end{aligned}$$

(44)

which is also strictly positive on the interior of D. Finally, we find that

$$\begin{aligned} \alpha _1 + \alpha _4 \; = \; \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3 + r_{23}^3 - r_{34}^3\right) + \left( r_{13}^3 - r_{23}^3\right) \left( r_{24}^3 - r_{12}^3 + r_{14}^3 - r_{34}^3\right) , \end{aligned}$$

which is strictly positive by (9). The conditions $a> c, 1 > b,$ and $r_{12} > r_{34}$, which are valid on the interior of D, combine to yield $a r_{12} > bc r_{34}$. Then we have

$$\begin{aligned} a r_{12} \, \alpha _1 + bc r_{34} \, \alpha _4 \;> \; bc r_{34} \, \alpha _1 + bc r_{34} \, \alpha _4 \; = \; bc r_{34} (\alpha _1 + \alpha _4) \; > \; 0 . \end{aligned}$$

This shows that $\frac{ \partial F}{\partial \theta } < 0$, which proves uniqueness.

By the implicit function theorem, there exists a differentiable function $\theta = f(a,b,c)$ on the interior of D such that $F(a,b,c,f(a,b,c)) = 0$. The point $(a,b,c,\theta =f(a,b,c))$ describes a convex central configuration with positive masses. Since $k_2 - k_1$ approaches zero as (a, b, c) approaches the boundary of D, we may extend the function f continuously to the boundary of D, where it is defined as $\theta = \theta _l = \theta _u$.

Finally, if $(a,b,c) \not \in D$, then Lemma 3.2 shows that one of the mutual distance inequalities in (9) will be violated. For example, if $c > a$, then either $r_{12} < r_{14}$ or $r_{23} < r_{34}$. Likewise, if $c \ge \frac{1}{a}(b^2 + 2b)$, then either $r_{12} < r_{14}$ or $r_{13} \le r_{12}$. In any case, such a configuration, assuming it is central, will contain a negative or zero mass. It follows that D is precisely the domain of the implicitly defined function f and that the projection of E into abc-space equals D. $\square$

3.6 Properties of the angle between the diagonals

Next we focus on the possible values of the angle $\theta$ between the two diagonals, showing that it is always between $60^\circ$ and $90^\circ$. Moreover, the value of $\theta$ increases as the radial variable c increases.

Lemma 3.7

Suppose that $(a,b,c) \in D$ and $\theta = \pi /2$. Then $r_{12}^3 + r_{34}^3 \ge r_{14}^3 + r_{23}^3$.

Proof

When $\theta = \pi /2$, the formulas in (13) and (14) reduce to $r_{12}^2 = a^2 + 1, r_{14}^2 = c^2 + 1, r_{23}^2 = a^2 + b^2,$ and $r_{34}^2 = b^2 + c^2$. Define the function $G(a,b,c) = r_{12}^3 + r_{34}^3 - r_{14}^3 - r_{23}^3$. Note that $G(a,b,c=a) = 0$ since $r_{12} = r_{14}$ and $r_{23} = r_{34}$ when $c = a$ (a kite configuration). We compute that

$$\begin{aligned} \frac{ \partial G}{\partial c} \; = \; 3r_{34}^2 \frac{\partial r_{34}}{\partial c} - 3 r_{14}^2 \frac{\partial r_{14}}{\partial c} \; = \; 3c (r_{34} - r_{14}) \; \le \; 0, \end{aligned}$$

because $b \le 1$ on D. Since $G(a,b,c=a) = 0$, it follows that $G(a,b,c < a) \ge 0$, as desired. $\square$

Theorem 3.8

For a convex central configuration with positive masses, the angle $\theta$ between the two diagonals satisfies $\pi /3 < \theta \le \pi /2$. If $\theta = \pi /2$, the configuration must be a kite.

Proof

We first show that $\theta \le \pi /2$. For any point $(a,b,c) \in D$, we have $r_{34} \le r_{14}$ and $r_{23} \le r_{12}$. If $\theta = \pi /2$, we also have $r_{23}^3 - r_{34}^3 \le r_{12}^3 - r_{14}^3$ by Lemma 3.7. Thus, when $\theta = \pi /2$, we have

$$\begin{aligned} \left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) \le \left( r_{24}^3 - r_{34}^3\right) \left( r_{13}^3 - r_{23}^3\right) \left( r_{12}^3 - r_{14}^3\right) , \end{aligned}$$

(45)

since all factors in (45) are nonnegative and each factor on the left-hand side of the inequality is less than or equal to the corresponding factor on the right. This shows that $F(a,b,c,\theta = \pi /2) \le 0$. From the proof of Theorem 3.6, $\partial F/\partial \theta < 0$ on the interior of $D \times [\theta _l, \theta _u]$. Thus, for a fixed point (a, b, c) in the interior of D, the unique solution to $F(a,b,c,\theta ) = 0$ must satisfy $\theta \le \pi /2$.

Next, from (42), we have that $2 \cos \theta \le a - c$ and $2a \cos \theta \le 1 - b$. We have just shown that $\cos \theta \ge 0$, and since $b > 0$ and $c > 0$ on the interior of D, we conclude that

$$\begin{aligned} 2 \cos \theta \;< \; 2 \cos \theta + c \; \le a \; \le \; \frac{1 - b}{2 \cos \theta } \; < \; \frac{1}{2 \cos \theta } . \end{aligned}$$

(46)

It follows that $\cos ^2 \theta < 1/4$, which means $\theta > \pi /3$.

Finally, inequality (45) is strict unless $r_{14} = r_{34}$ and $r_{12} = r_{23}$, or a factor on each side of the inequality vanishes. By Lemma 3.4, this can only occur if (a, b, c) lies on the boundary of D. Thus, $F(a,b,c,\theta = \pi /2) < 0$ on the interior of D. Since $\theta = \cos ^{-1}(\frac{a-c}{2})$ or $\theta = \cos ^{-1}(\frac{1-b}{2a})$ on the boundary of D, we see that a central configuration with $\theta = \pi /2$ must satisfy either $a = c$ or $b = 1$. By (36) or (37), the configuration must be a kite. $\square$

Remark 3.9

• 1. The fact that a convex central configuration with perpendicular diagonals must be a kite was proven earlier by the authors in Corbera et al. (2018).

• 2. If $\theta = \pi /3$, then all inequalities in (46) must become equalities. This can only happen at the point $P_1 = (1,0,0)$, a vertex of ${\overline{D}}$ corresponding to an equilateral triangle configuration with bodies 3 and 4 coinciding ($r_{34} = 0$).

• 3. A related result proven by Long (2003) is that every interior angle of a convex central configuration must lie between $\pi /3$ and $5\pi /6$.

Next we show that the value of $\theta$ increases as we move upward (increasing in c) through the domain D. We will need the following lemma. Recall that E is the set of four-body convex central configurations with positive masses in our particular coordinate system.

Lemma 3.10

Consider the following three quantities:

$$\begin{aligned} \beta _1= & {} \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) - \left( r_{13}^3 - r_{23}^3\right) \left( r_{12}^3 - r_{14}^3\right) , \\ \beta _2= & {} \left( r_{13}^3 - r_{23}^3\right) \left( r_{24}^3 - r_{34}^3\right) - \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) , \\ \beta _3= & {} \left( r_{13}^3 - r_{23}^3\right) \left( r_{12}^3 - r_{14}^3\right) - \left( r_{13}^3 - r_{12}^3\right) \left( r_{24}^3 - r_{14}^3\right) . \end{aligned}$$

Then, $\beta _1 \ge 0, \, \beta _2 > 0, \, \beta _3 < 0,$ and $\beta _2 + \beta _3 \ge 0$ for any configuration in E.

Proof

Since we are working in E, the equation $F = 0$ implies

$$\begin{aligned} \left( r_{13}^3 - r_{23}^3\right) \left( r_{12}^3 - r_{14}^3\right) \; = \; \frac{\left( r_{24}^3 - r_{14}^3\right) \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) }{r_{24}^3 - r_{34}^3} \, . \end{aligned}$$

(47)

Then we have

$$\begin{aligned} \beta _1 \; = \; \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) \left( 1 - \frac{r_{24}^3 - r_{14}^3}{r_{24}^3 - r_{34}^3} \right) \; = \; \frac{\left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 - r_{34}^3\right) \left( r_{14}^3 - r_{34}^3\right) }{r_{24}^3 - r_{34}^3} , \end{aligned}$$

which is nonnegative due to the inequalities in (9).

Note that the quantity $\beta _2$ is identical to $\alpha _3$ used in the proof of Theorem 3.6 (Eq. 43). By Eq. (44), we see that $\beta _2 > 0$ on E.

Next, using Eq. (47), we have

$$\begin{aligned} \beta _3 \; = \; \left( r_{13}^3 - r_{12}^3\right) \left( r_{24}^3 - r_{14}^3\right) \left( \frac{r_{23}^3 - r_{34}^3}{r_{24}^3 - r_{34}^3} - 1 \right) \; = \; - \frac{\left( r_{13}^3 - r_{12}^3\right) \left( r_{24}^3 - r_{14}^3\right) \left( r_{24}^3 - r_{23}^3\right) }{r_{24}^3 - r_{34}^3} , \end{aligned}$$

which is strictly negative due to the inequalities in (9).

Finally, we compute that

$$\begin{aligned} \beta _2 + \beta _3= & {} \left( r_{13}^3 - r_{23}^3\right) \left( r_{12}^3 + r_{24}^3 - r_{14}^3 - r_{34}^3\right) - \left( r_{13}^3 - r_{12}^3\right) \left( r_{23}^3 + r_{24}^3 - r_{14}^3 - r_{34}^3\right) \\= & {} r_{13}^3 \left( r_{12}^3 - r_{23}^3\right) - r_{23}^3 \left( r_{24}^3 - r_{14}^3 - r_{34}^3\right) + r_{12}^3\left( r_{24}^3 - r_{14}^3 - r_{34}^3\right) \\= & {} \left( r_{12}^3 - r_{23}^3\right) \left( r_{13}^3 + r_{24}^3 - r_{14}^3 - r_{34}^3\right) , \end{aligned}$$

which is nonnegative on E. This completes the proof. $\square$

Theorem 3.11

On the interior of D, the angle $\theta$ between the two diagonals increases with c. In other words, $\frac{\partial \theta }{\partial c} > 0$ on the interior of D.

Proof

Recall that the angle $\theta = f(a,b,c)$ is a differentiable function on the interior of D, determined by the solution to the equation $F(a,b,c, f(a,b,c)) = 0$. Using the implicit function theorem, we have $\frac{\partial \theta }{\partial c} = - \frac{\partial F}{\partial c} / \frac{\partial F}{\partial \theta } .$ From the proof of Theorem 3.6, $\frac{\partial F}{\partial \theta } < 0$. Thus, it suffices to show that $\frac{\partial F}{\partial c} > 0$, where the partial derivative is evaluated at $(a,b,c, \theta = f(a,b,c)) \in E$ with (a, b, c) in the interior of D.

Using Eqs. (13) and (14), we have that

$$\begin{aligned} \frac{\partial r_{14}}{\partial c} = \frac{c + \cos \theta }{r_{14}}, \quad \frac{\partial r_{34}}{\partial c} = \frac{c - b \cos \theta }{r_{34}}, \quad \frac{\partial r_{24}}{\partial c} = 1, \quad \text{ and } \quad \frac{\partial r_{12}}{\partial c} = \frac{\partial r_{13}}{\partial c} = \frac{\partial r_{23}}{\partial c} = 0. \end{aligned}$$

Then we compute

$$\begin{aligned} \frac{\partial F}{\partial c} \; = \; 3r_{24}^2 \beta _1 + 3r_{14}(c + \cos \theta ) \beta _2 + 3r_{34} (c - b \cos \theta ) \beta _3 \, , \end{aligned}$$

(48)

where the $\beta _i$ is given as in Lemma 3.10. Since we are working in the interior of D, the central configuration is not a kite and Theorem 3.8 implies that $\cos \theta > 0$. Hence, applying Lemma 3.10, each term on the right-hand side of (48) is nonnegative except for $3r_{34} c \beta _3$. However, since $r_{14} \ge r_{34}$ and $\beta _2 > 0$, we have

$$\begin{aligned} 3r_{14}c \beta _2 + 3r_{34} c \beta _3= & {} 3c(r_{14} \beta _2 + r_{34} \beta _3) \\\ge & {} 3c( r_{34} \beta _2 + r_{34} \beta _3) \\= & {} 3c r_{34} (\beta _2 + \beta _3) \\\ge & {} 0 \end{aligned}$$

by Lemma 3.10. This shows that $\frac{\partial F}{\partial c} > 0$. The inequality is strict because the term $3r_{14} \beta _2 \cos \theta$ is strictly positive on the interior of D. This completes the proof. $\square$

Remark 3.12

• 1. Regarding Fig. 1, if we fix the values of a and b, then one interpretation of Theorem 3.11 is that as the configuration widens in the vertical direction (c increasing), the diagonals become closer and closer to perpendicular. If (a, b) is chosen from subregion i or ii (see Fig. 3), then the angle $\theta$ increases monotonically to $\pi /2$ where $c = a$ (a kite configuration). On the other hand, if (a, b) belongs to subregion iii or iv, then $\theta$ is bounded above by $\cos ^{-1}(\frac{a-{\bar{c}}}{2}) < \pi /2$ where ${\overline{c}} = \frac{1}{a}(b^2 + 2b) < a$.

• 2. For kite configurations lying on the vertical face II ($b = 1, r_{12} = r_{23},$ and $r_{14} = r_{34}$), it is straightforward to check that $\frac{\partial F}{\partial c} = 0$. This in turn implies that $\frac{\partial \theta }{\partial c} = 0$, which agrees with the fact that $\theta$ is constant ($\theta = \pi /2$) on all of face II. Thus, the strict inequality of Theorem 3.11 only holds on the interior of D.

4 Special classes of central configurations

In this section, we use our coordinates in D to classify different types of quadrilaterals that are also central configurations. The analysis and defining equations are remarkably simple in our coordinate system, resulting in only linear or quadratic equations in a, b, and c. Certain cases can be handled quickly due to the constraints on the mutual distances given by (9). For example, the only parallelogram that can be a central configuration is a rhombus. Likewise, the only possible rectangle is a square.

4.1 Kites

The kite configurations play a particularly important role in the overall classification of convex central configurations, occupying two of the six boundary faces of D. Recall that a kite configuration is a symmetric quadrilateral with two bodies lying on the axis of symmetry and two bodies located equidistant from that axis. The diagonals are always perpendicular, and the two bodies not lying on the axis of symmetry must have equal mass.

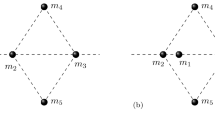
Based on our ordering of the bodies, there are two possible types of kite configurations. A kite with bodies 1 and 3 on the axis of symmetry, denoted ${\textit{kite}}_{13}$, is symmetric with respect to the x-axis and must satisfy $c = a$ (left plot in Fig. 4). These kites lie on face I and have $m_2 = m_4$, as can be verified by the middle formula in (11). A kite with bodies 2 and 4 on the axis of symmetry, denoted ${\textit{kite}}_{24}$, is symmetric with respect to the y-axis and must satisfy $b = 1$ (right plot in Fig. 4). These kites occupy face II and require $m_1 = m_3$, as can be checked using the middle formula in (10).

Fig. 4

Two kite central configurations with different axes of symmetry. Kites with a horizontal axis of symmetry ($\hbox {kite}_{13}$) lie in the plane $c=a$, while those with a vertical axis of symmetry ($\hbox {kite}_{24}$) lie in the plane $b=1$. All kites have $\theta = \pi /2$; these are the only possible convex central configurations with perpendicular diagonals

It is important to note that due to statements (36) and (37) in Lemma 3.4, any point in D lying on one of the two planes $c = a$ or $b = 1$ must correspond to a kite central configuration. While two pairs of mutual distances must be congruent in order to distinguish a kite configuration from a general convex quadrilateral, only one equation is required to imply a kite when restricting to the set of convex central configurations. An alternative interpretation of this fact is the following theorem.

Theorem 4.1

A convex central configuration with one diagonal bisecting the other must be a kite.

Proof

In our coordinate system, if one of the diagonals bisects the other, then either $a = c$ or $b = 1$. By (36) and (37) in Lemma 3.4, either case must correspond to a kite configuration. $\square$

Remark 4.2

Theorem 4.1 also follows directly from Conley’s perpendicular bisector theorem (Moeckel 1990).

The intersection of the planes $c = a$ and $b = 1$ is a line that corresponds to the one-dimensional family of rhombi central configurations. This line is an edge on the boundary of D between vertices $P_3$ and $P_4$. We regard a as a parameter describing this family, with $1/\sqrt{3}< a < \sqrt{3}$. From (10) and (11), we have $m_1 = m_3, m_2 = m_4,$ and

$$\begin{aligned} \frac{m_2}{m_1} \; = \; \frac{8a^3 - a^3(a^2 + 1)^{3/2} }{ 8a^3 - (a^2 + 1)^{3/2}} \, . \end{aligned}$$

Note that $m_1$ and $m_3$ vanish as $a \rightarrow 1/\sqrt{3}$, while $m_2$ and $m_4$ approach 0 as $a \rightarrow \sqrt{3} \,$. The length of the diagonal $r_{24}$ increases with a, stretching the rhombus in the vertical direction. The point $a = 1$ corresponds to the equal mass square configuration with congruent diagonals ($r_{13} = r_{24} = 2$).

4.2 Trapezoids

Next we consider the two possible types of trapezoids. Let $\overline{q_i q_j}$ denote the side of the trapezoid between vertices i and j. If exterior sides $\overline{q_1 q_2}$ and $\overline{q_3 q_4}$ are parallel, then we have

$$\begin{aligned} \frac{a \sin \theta }{a \cos \theta - 1} \; = \; \frac{c \sin \theta }{c \cos \theta - b} \, , \end{aligned}$$

which reduces to $(ab - c) \sin \theta = 0.$ Since $\sin \theta \ne 0$, $c = ab$ is both necessary and sufficient to have a trapezoid of this kind (left plot in Figure 5). On the other hand, if $\overline{q_1 q_4}$ is parallel to $\overline{q_2 q_3}$, then we quickly deduce that $a = bc$. However, since $a \ge c$ and $1 \ge b$ on D, we have $a \ge bc$ always, with equality only if both $a = c$ and $b =1$ are satisfied. It follows that the only trapezoid of this type is necessarily a rhombus, a subset of the first type of trapezoids. This proves the following theorem.

Fig. 5

Trapezoidal central configurations lie on the surface $c = ab$. The isosceles trapezoid family (right figure) lies on the line formed by the intersection of the planes $a = 1$ and $c = b$

Theorem 4.3

Suppose that s is a central configuration in E. Then $s = (a,b,c,\theta )$ is a trapezoid if and only if $c = ab$. The exterior sides $\overline{q_1 q_2}$ and $\overline{q_3 q_4}$ are always parallel.

Remark 4.4

Theorems 3.6 and 4.3 together show that the set of trapezoidal central configurations with positive masses is two-dimensional, a graph over the surface $c = ab$ in D (a portion of a saddle). This concurs with the recent results in Corbera et al. (2019).

Fig. 6

The trapezoidal central configurations (purple) lie on the surface $c = ab$ within D. The violet line shows the isosceles trapezoid central configurations, where $a = 1$ and $c = b$

Figure 6 demonstrates how the surface of trapezoidal central configurations lies within the full space D. This surface intersects the boundary of D along the straight edge between vertices $P_3$ and $P_4$ corresponding to the rhombi family (the intersection of faces I and II). It also meets the boundary of D in two curves of relative equilibria for the restricted four-body problem, one curve on face V connecting vertices $P_1$ and $P_4$ and the other on face IV joining vertices $P_1$ and $P_3$.

Next, suppose that $s \in E$ is a trapezoid. If we substitute $c = ab$ into Eqs. (13) and (14), we obtain

$$\begin{aligned} r_{23}^2 - r_{14}^2 \; = \; (a^2 - 1)(1 - b^2) \, . \end{aligned}$$

(49)

If $b = 1$, then $c = ab$ implies $c = a$ and hence s is a rhombus. Assuming that $b < 1$, it follows from Eq. (49) that $r_{23} > r_{14}$ for $a > 1$, and $r_{14}> r_{23}$ when $a < 1$. The border between these two cases is the isosceles trapezoids, where $r_{23} = r_{14}$ (right plot in Fig. 5). In other words, the isosceles trapezoid family of central configurations corresponds to a line formed by the intersection of the planes $a=1$ and $c = b$. This line slices through the interior of D, crossing from the degenerate equilateral triangle at (1, 0, 0) to the square at (1, 1, 1) (violet line in Fig. 6). By Theorem 3.11, the angle between the diagonals monotonically increases from $\pi /3$ to $\pi /2$ as c increases from 0 to 1. The family of isosceles trapezoids was studied in Cors and Roberts (2012) and Xie (2012).

4.3 Co-circular configurations

Another interesting class of central configurations is those where the four bodies lie on a common circle, a co-circular central configuration (see Fig. 7). One of the main results in Cors and Roberts (2012) is that the set of four-body co-circular central configurations is a two-dimensional surface, a graph over two of the exterior side lengths. We reproduce that result here, showing that the co-circular central configurations are a graph over the saddle $b = ac$ in D.

Fig. 7

A co-circular central configuration, where the bodies all lie on a common circle, must satisfy $b = ac$

Theorem 4.5

Suppose that s is a central configuration in E. Then $s = (a,b,c,\theta )$ is a co-circular central configuration if and only if $b = ac$.

Proof

We make use of the cross-ratio¹ from complex analysis (Ahlfors 1979). The cross-ratio of four points $z_1, z_2, z_3, z_4$ is defined as the image of $z_1$ under the linear transformation that maps $z_2$ to 1, $z_3$ to 0, and $z_4$ to $\infty$. It is given by the expression

$$\begin{aligned} \frac{ (z_1 - z_3)(z_2 - z_4) }{ (z_1 - z_4)(z_2 - z_3) } . \end{aligned}$$

(50)

One of the nice properties of the cross-ratio is that it is real if and only if the four points lie on a circle or a line. Regarding the position of each body as a point in ${\mathbb {C}}$, we have $z_1 = 1, z_2 = ae^{i \theta }, z_3 = -b$, and $z_4 = -ce^{i \theta }$. Substituting into (50), we find the cross-ratio to be

$$\begin{aligned} \frac{ (a+c)(b+1) }{ ac e^{i \theta } + b e^{-i \theta } + a + bc} \, , \end{aligned}$$

which is real if and only if $\sin \theta (ac - b) = 0$. Since $\theta \in (\pi /3, \pi /2]$, we obtain $b = ac$ as a necessary and sufficient condition for the four bodies to be lying on a common circle. $\square$

In Fig. 8 we plot the surface of co-circular central configurations within D. This surface intersects the boundary of D on four faces. On face I we have co-circular kite configurations ($\hbox {kite}_{13}$) defined by the parabola $c = a, b = a^2, 1/\sqrt{3} < a \le 1$. We also have co-circular kites on face II with the opposite axis of symmetry ($\hbox {kite}_{24}$), lying on the hyperbola $b = 1, c = 1/a, 1 \le a < \sqrt{3}$. This latter curve of co-circular kites is equivalent to the family studied in Mello and Fernandes (2011) after rescaling and relabeling the configuration. The surface $b = ac$ also intersects faces IV and V, tracing out curves of relative equilibrium solutions to the restricted four-body problem.

Fig. 8

Co-circular central configurations lie on the surface $b = ac$ (light red) in D. The violet line corresponds to the isosceles trapezoid family, where $a = 1$ and $b = c$

Substituting $b = ac$ into Eqs. (13) and (14), we find that $r_{23} = a \, r_{14}$ and $r_{34} = c \, r_{12}$. The line $a=1$ (violet line in Fig. 8) divides the surface $b = ac$ into two pieces. As was the case for the trapezoids, if $1< a < \sqrt{3}$, then we have co-circular central configurations with $r_{23} > r_{14}$, while if $1/\sqrt{3}< a < 1$, then $r_{14} > r_{23}$. Configurations on the line $a=1$ are isosceles trapezoids, where $r_{14} = r_{23}$. Since $r_{12} \ge r_{34}$, the equation $r_{34} = c \, r_{12}$ implies that $c \le 1$ for any co-circular central configuration. The maximum value of c occurs at the square $a = b = c = 1$.

4.4 Equidiagonal configurations

The final class of convex central configurations we choose to explore is equidiagonal quadrilaterals, where the two diagonals are congruent (left plot in Fig. 9). These configurations are characterized by the equation $r_{13} = r_{24}$, which is the plane $a - b + c = 1$ in our coordinates. This plane intersects the boundary of D in four places (right plot in Fig. 9). On face I we find equidiagonal kites ($\hbox {kite}_{13}$) along the line $c = a, b = 2a - 1, 1/\sqrt{3} < a \le 1$. Similarly, there is a line of equidiagonal kites ($\hbox {kite}_{24}$) on face II parameterized by $b = 1, c = 2 - a, 1 \le a < \sqrt{3}$. These two kite families intersect at the square $a = b = c = 1$. The equidiagonal plane also meets the boundary of D along two curved edges, one where faces III and IV intersect and the other where faces V and VI meet. This follows directly from the equations given in Table 1.

Fig. 9

Equidiagonal central configurations (left) are located on the plane $a - b + c = 1$ in D (right). The violet line consists of the isosceles trapezoids ($a=1$ and $b=c$)

As with the trapezoidal and co-circular cases, the isosceles trapezoid family ($a = 1, b = c$) divides the equidiagonal plane into two regions distinguished by whether $r_{23} > r_{14}$ (when $1< a < \sqrt{3}$) or $r_{14} > r_{23}$ (when $1/\sqrt{3}< a < 1$).

4.5 Summary

Table 2 summarizes the different classes of configurations along with their defining equations in abc-space or in the mutual distance variables $r_{ij}$. In addition to the simplicity of the defining equations, perhaps one of the more striking features of Table 2 is that all of the configurations shown are defined by linear or quadratic equations. Moreover, due to Theorem 3.6, the dimension of each set is equivalent to the dimension of the corresponding geometric figure in abc-space. Each type of configuration can be represented as the graph of a function over a one- or two-dimensional set in D, where the function is $\theta = f(a,b,c)$ restricted to the given set.

Table 2 Some special classes of central configurations and their surprisingly simple defining equations in abc-space

Figure 10 illustrates how the surfaces corresponding to trapezoidal, co-circular, and equidiagonal configurations lie within D. All three intersect at the line corresponding to the isosceles trapezoid configurations. For $1< a < \sqrt{3}$, the trapezoids are located above the co-circular configurations, which in turn lie above the equidiagonal solutions. This is a consequence of comparing the c-values on each surface. Since $b \le 1 < a$, we have

$$\begin{aligned} ab \;> \; \frac{b}{a} \; > \; 1 - a + b \, . \end{aligned}$$

(51)

On the other hand, for the portion of D with $1/\sqrt{3}< a < 1$, the inequalities in (51) are reversed and the equidiagonal configurations lie above the co-circular solutions, which lie above the trapezoids.

Fig. 10

The left figure shows how the trapezoidal (purple) and co-circular (red) central configurations lie within D, while the right figure demonstrates how the co-circular (red) and equidiagonal (brown) central configurations fit together in D. All three classes of central configurations intersect at the isosceles trapezoid family ($a = 1$ and $b = c$)

The symmetric configurations play a particularly important role in the overall structure of D, occupying two boundary faces (kites), a boundary edge (rhombi), or a line of intersection between three classes of configurations (isosceles trapezoids). Two classes of convex quadrilaterals must be kites in order to be central configurations. Configurations with either orthogonal or bisecting diagonals must be kites by Theorems 3.8 and 4.1, respectively.

5 Conclusion and future work

We have established simple, yet effective coordinates for describing the space E of four-body convex central configurations. Using these coordinates, we prove that E is a three-dimensional set, the graph of a differentiable function over three radial variables. The domain D of this function has been carefully defined, analyzed, and plotted in ${\mathbb {R}}^{+^3}$. Our coordinates provide elementary descriptions of several important classes of central configurations, including kite, rhombus, trapezoidal, co-circular, and equidiagonal configurations. The dimension and location of each of these classes within D have been explored in detail. We have also shown that the angle between the diagonals of a four-body convex central configuration lies between $60^\circ$ and $90^\circ$. As the configuration widens, the diagonals become closer and closer to orthogonal. The diagonals are perpendicular if and only if the quadrilateral is a kite.

In future research, we intend to investigate the values of the masses as a function over the domain D. The mass ratios in (10) and (11) reduce fairly nicely in our coordinate system, although the dependence on the angle $\theta = f(a,b,c)$ is complicated. Nevertheless, we hope to build on our current work to show that the mass map from D into ${\mathbb {R}}^{+^3}$ (suitably normalized) is injective. Given a particular ordering of the bodies, this would prove that there is a unique convex central configuration for any choice of four positive masses.